Alkaline Water Electrolysis Powered by Renewable Energy: A Review
Abstract
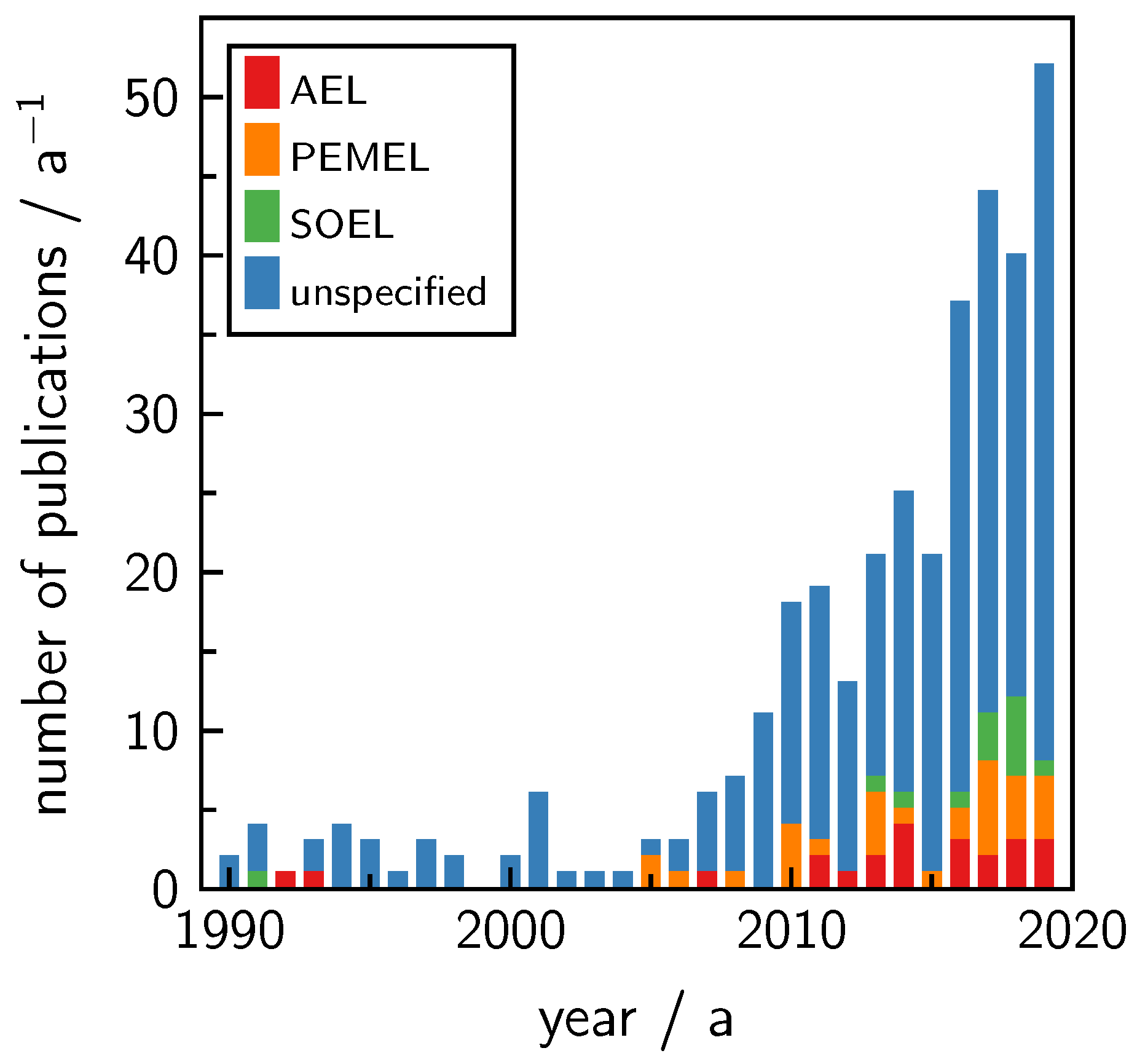
1. Introduction
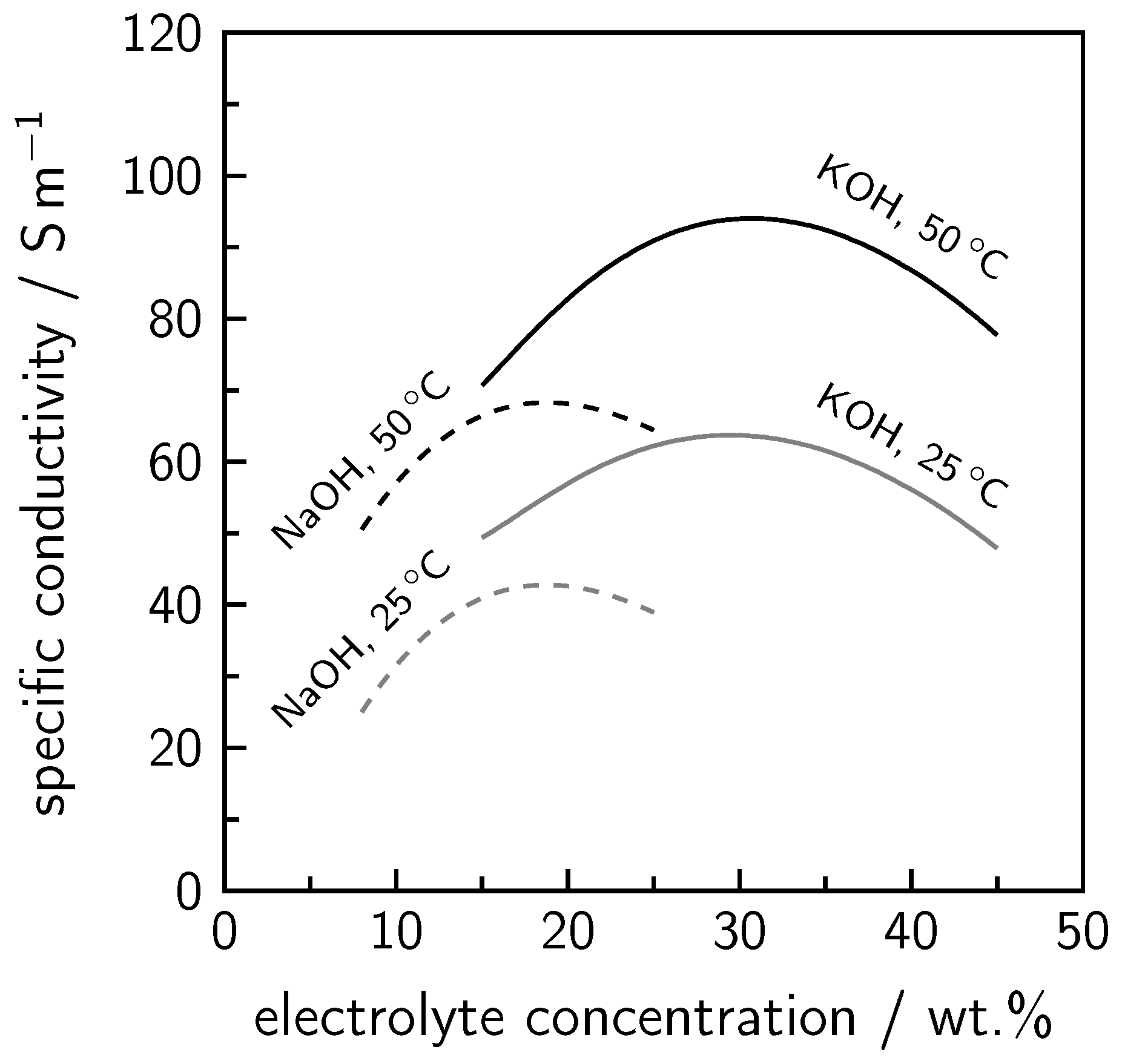
2. Alkaline Water Electrolysis
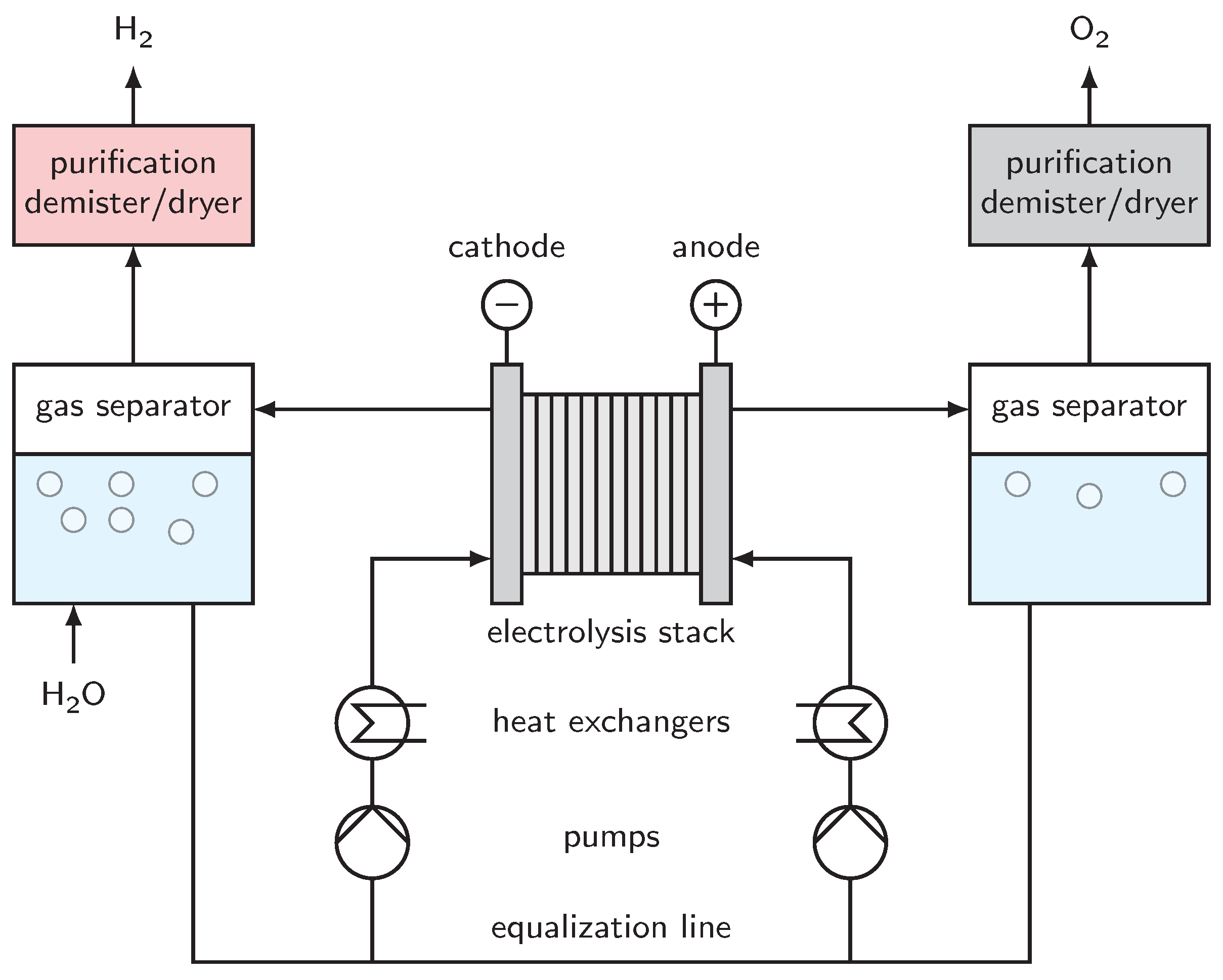
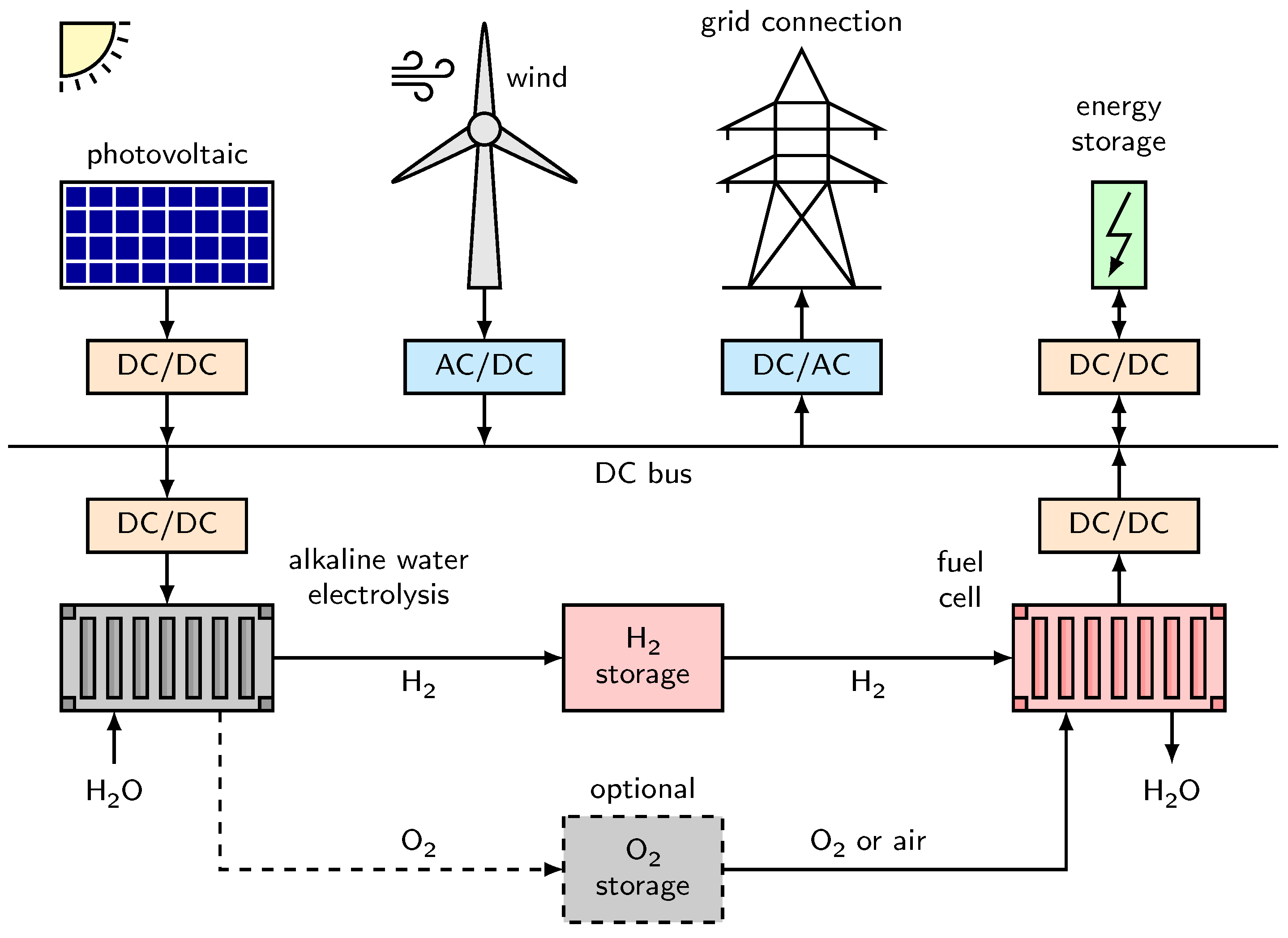
3. System
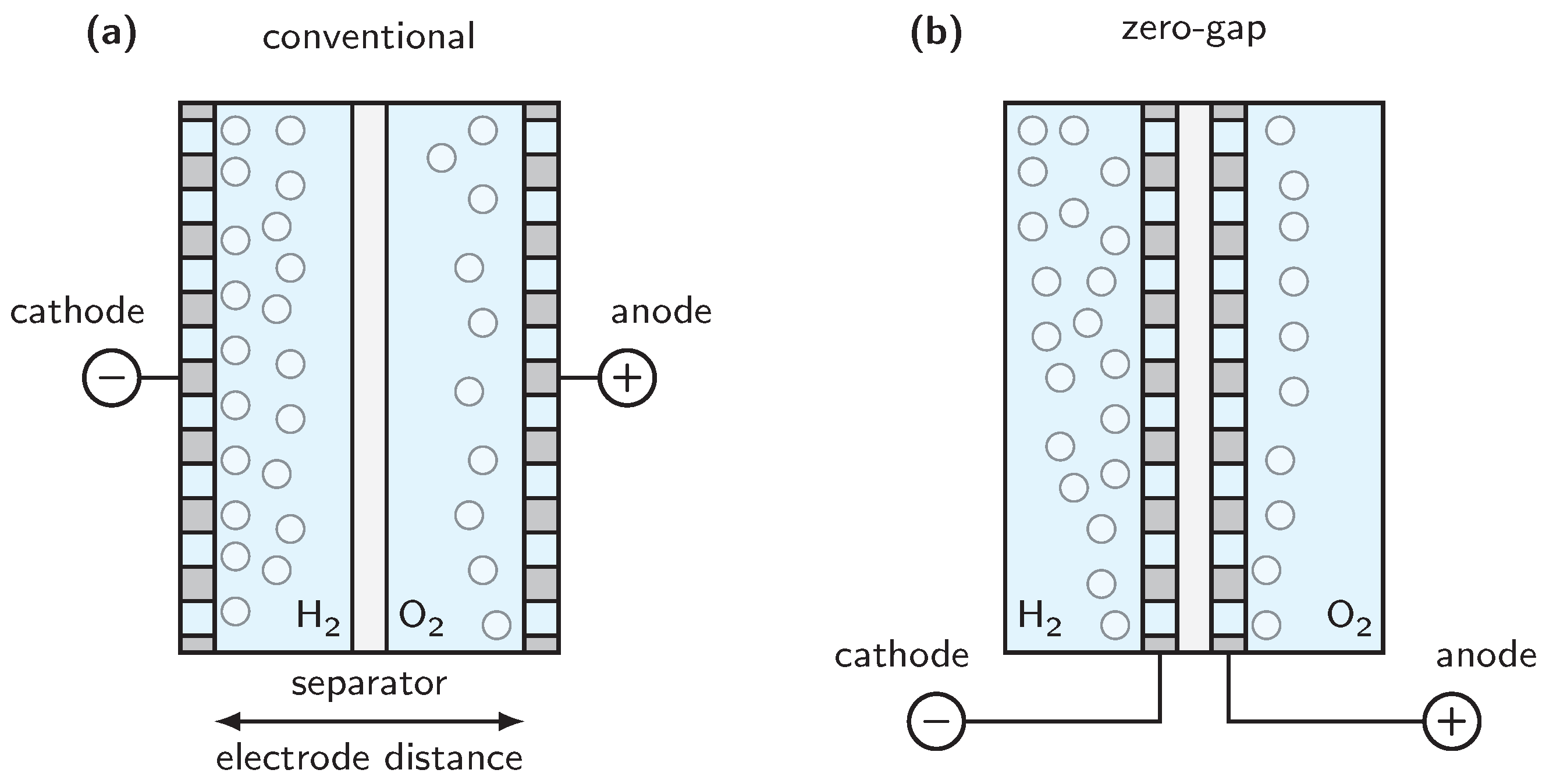
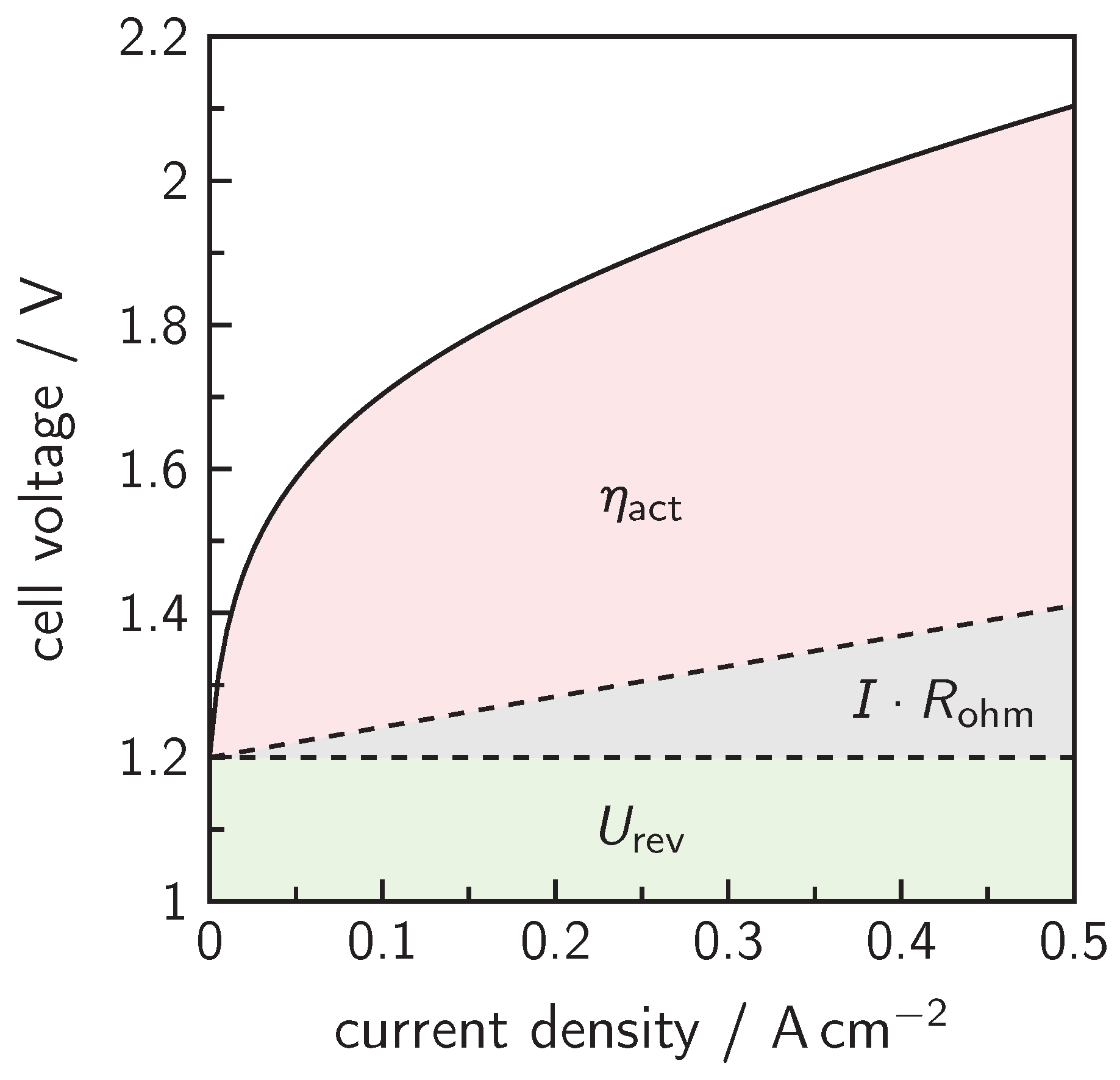
4. Cell Design and Cell Voltage
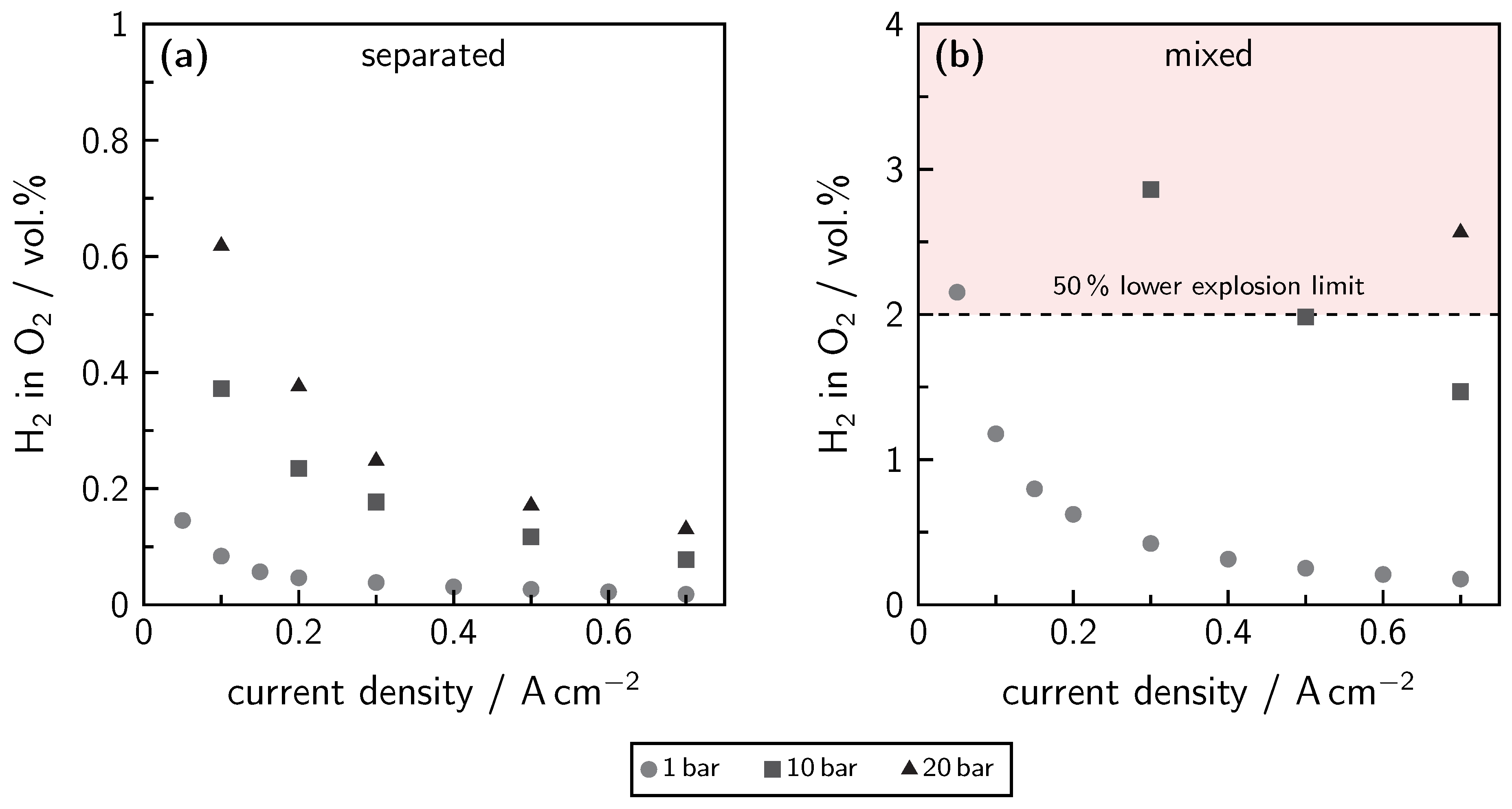
5. Gas Purity
6. Periphery
7. Renewable Energy
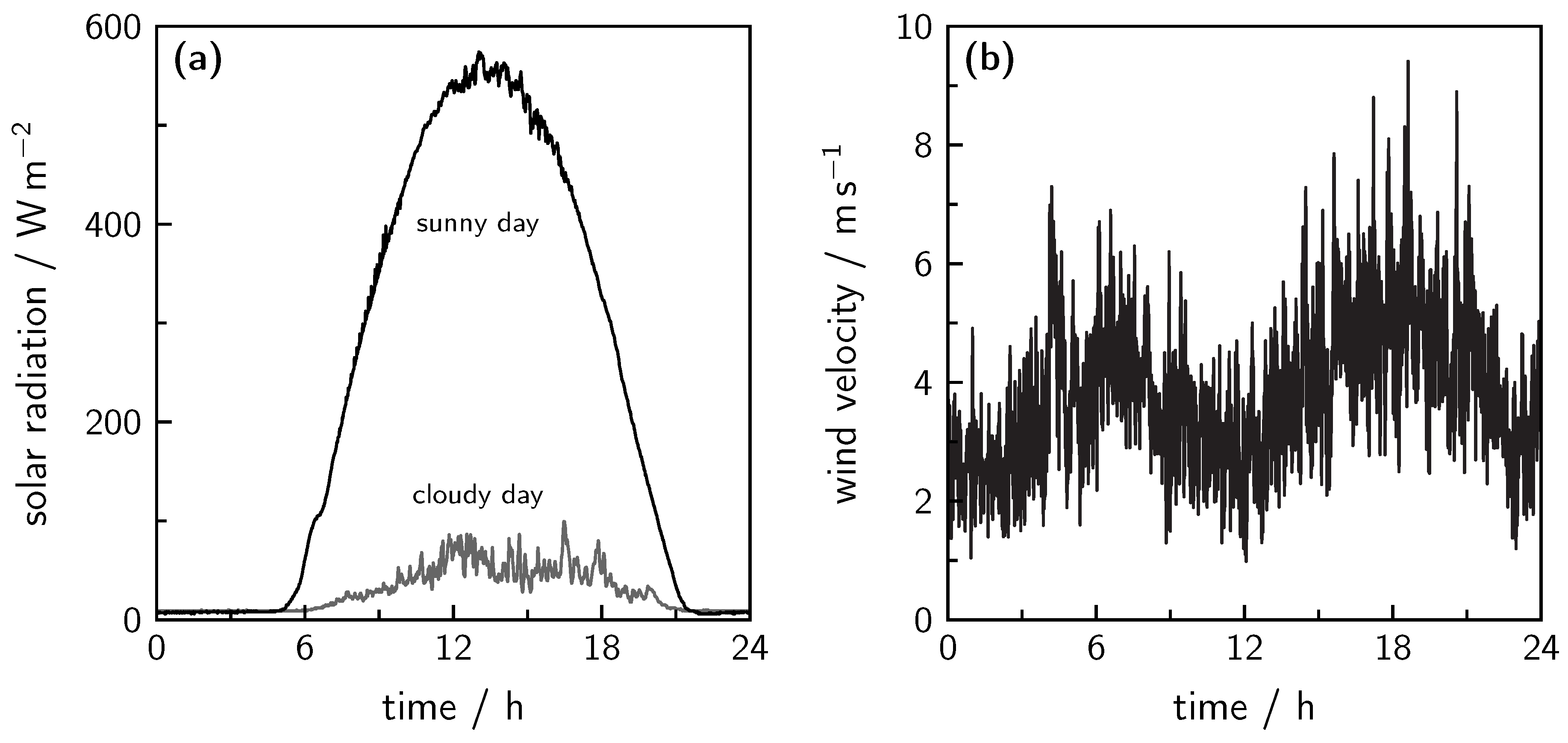
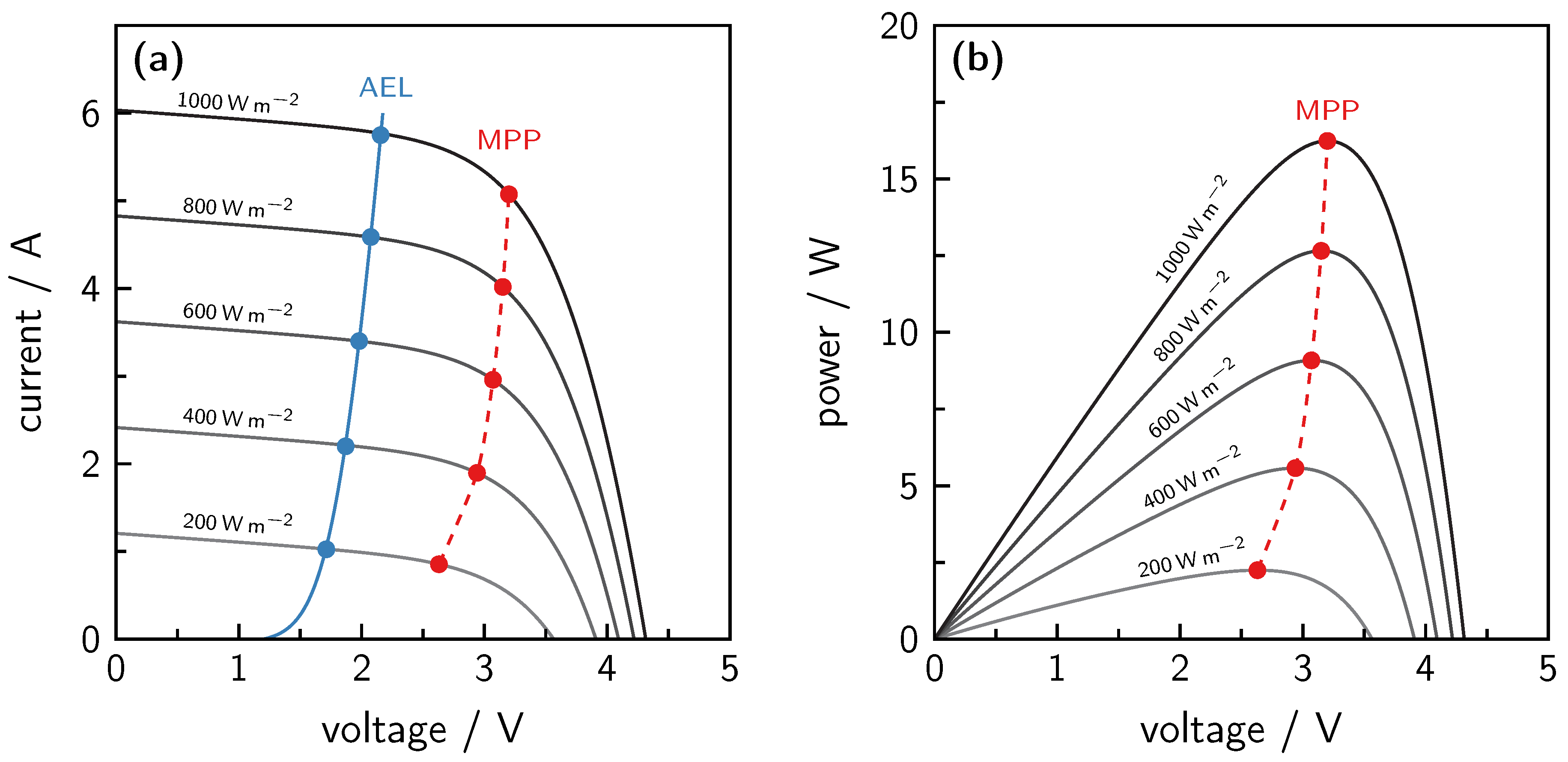
7.1. Solar Photovoltaic Power
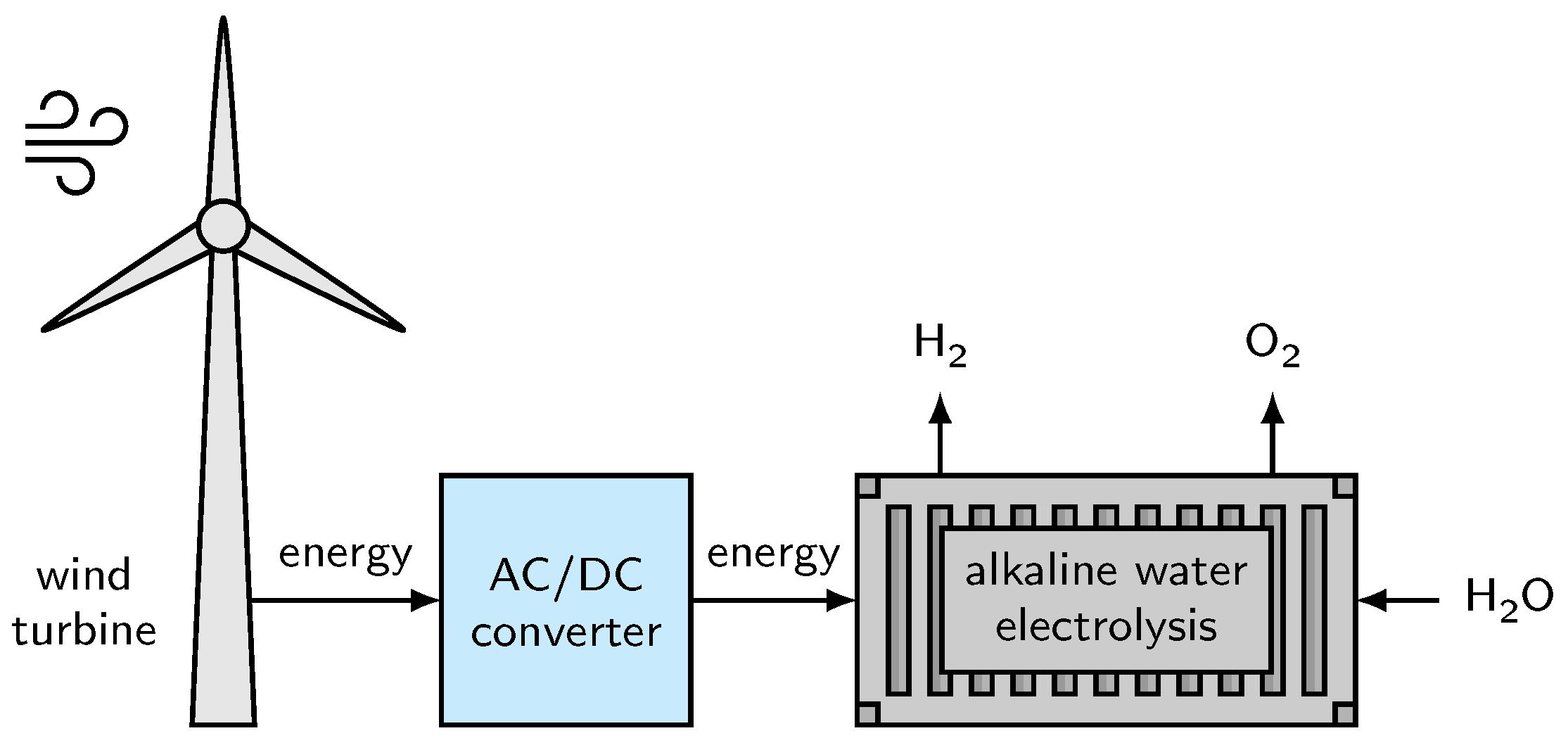
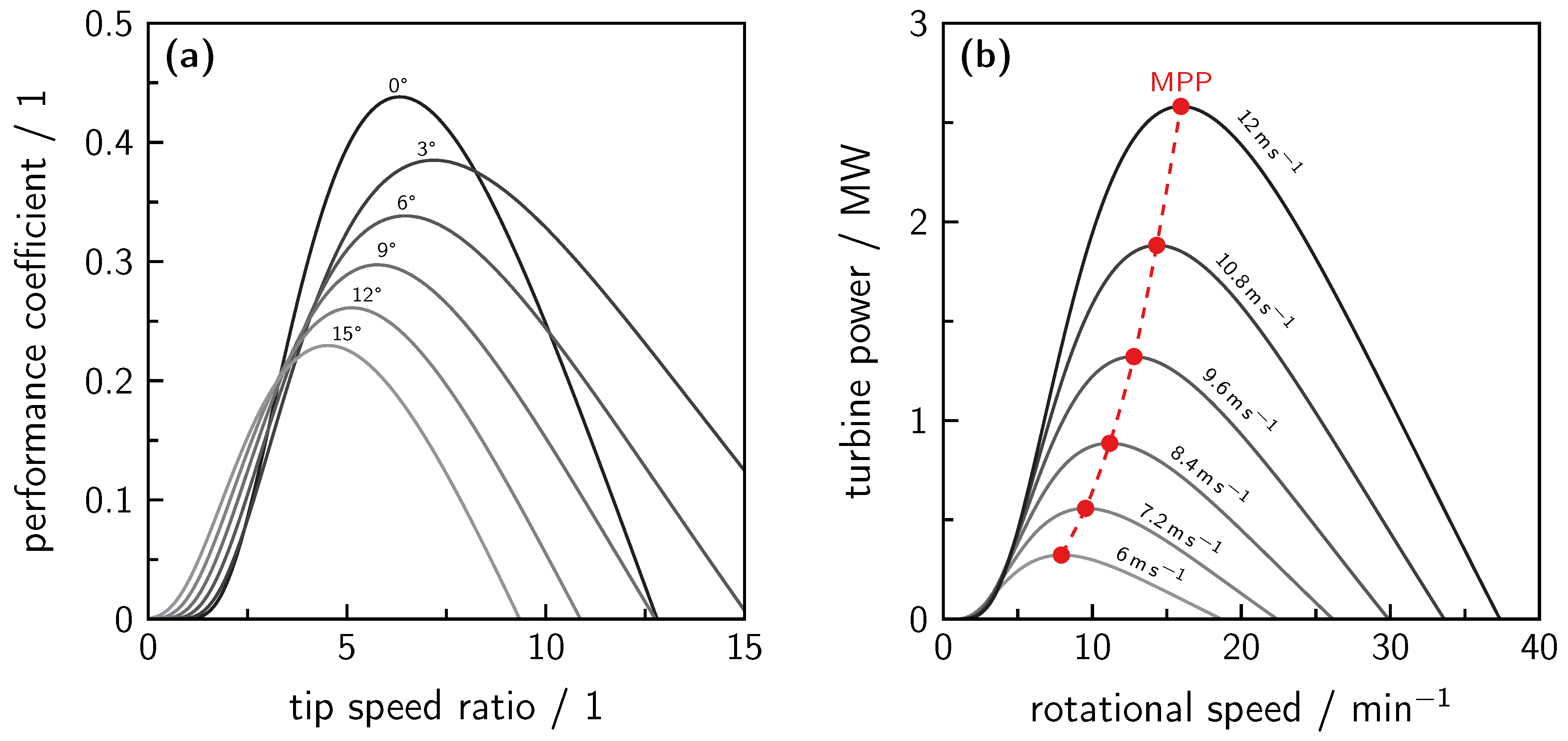
7.2. Wind Power
8. Hydrogen Energy System and Power Grid Stabilization
9. Limitations and Solution Approaches
9.1. Limited Operation Time
9.2. Optimal System Design and Operation Strategies
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| AEL | Alkaline water electrolysis |
| CFD | Computational fluid dynamics |
| DC | Direct current |
| HTEL | High-temperature electrolysis |
| ILs | Ionic liquids |
| MPP | Maximum power point |
| PEMEL | Proton exchange membrane electrolysis |
| PV | Photovoltaic |
| SOEL | Solid oxide electrolysis |
Appendix A. Correlations and Parameters
| Parameter | Equation (7) [28,94] | Equation (8) [39] | Unit |
|---|---|---|---|
| 8.05 | 4.45153 | ||
| −2.5 | 6.88874 | °C−1 | |
| s | 0.185 | 0.33824 | |
| 1.002 | −0.01539 | ||
| 8.424 | 2.00181 | °C A−1 | |
| 247.3 | 15.24178 | °C2 A−1 | |
| – | −3.12996 | ||
| – | 4.47137 |
| Parameter | Equation (A2) [57] | Unit | Equation (A3) [52] | Unit |
|---|---|---|---|---|
| 27.9844803 | −45.7 | |||
| −0.924129482 | 1.02 | °C−1 | ||
| −0.0149660371 | 3200 | |||
| −0.0905209551 | −2990 | |||
| 0.0114933252 | 784 | |||
| 0.1765 | – | – | – | |
| 6.96648518 | – | – | ||
| −2898.15658 | – | – |
References
- Sherif, S.; Barbir, F.; Veziroglu, T. Towards a Hydrogen Economy. Electr. J. 2005, 18, 62–76. [Google Scholar] [CrossRef]
- Suleman, F.; Dincer, I.; Agelin-Chaab, M. Environmental Impact Assessment and Comparison of Some Hydrogen Production Options. Int. J. Hydrog. Energy 2015, 40, 6976–6987. [Google Scholar] [CrossRef]
- Dincer, I.; Acar, C. Review and Evaluation of Hydrogen Production Methods for Better Sustainability. Int. J. Hydrog. Energy 2015, 40, 11094–11111. [Google Scholar] [CrossRef]
- Gandía, L.M.; Oroz, R.; Ursúa, A.; Sanchis, P.; Diéguez, P.M. Renewable Hydrogen Production: Performance of an Alkaline Water Electrolyzer Working under Emulated Wind Conditions. Energy Fuels 2007, 21, 1699–1706. [Google Scholar] [CrossRef]
- Santos, D.M.F.; Sequeira, C.A.C.; Figueiredo, J.L. Hydrogen Production by Alkaline Water Electrolysis. Quim. Nova 2013, 36, 1176–1193. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Gong, X.; Guo, Z. The Intensification Technologies to Water Electrolysis for Hydrogen Production—A Review. Renew. Sustain. Energy Rev. 2014, 29, 573–588. [Google Scholar] [CrossRef]
- Gahleitner, G. Hydrogen from Renewable Electricity: An International Review of Power-to-Gas Pilot Plants for Stationary Applications. Int. J. Hydrog. Energy 2013, 38, 2039–2061. [Google Scholar] [CrossRef]
- Carpetis, C. Estimation of Storage Costs for Large Hydrogen Storage Facilities. Int. J. Hydrog. Energy 1982, 7, 191–203. [Google Scholar] [CrossRef]
- Michalski, J.; Bünger, U.; Crotogino, F.; Donadei, S.; Schneider, G.S.; Pregger, T.; Cao, K.K.; Heide, D. Hydrogen Generation by Electrolysis and Storage in Salt Caverns: Potentials, Economics and Systems Aspects with Regard to the German Energy Transition. Int. J. Hydrog. Energy 2017, 42, 13427–13443. [Google Scholar] [CrossRef]
- Pellow, M.A.; Emmott, C.J.M.; Barnhart, C.J.; Benson, S.M. Hydrogen or Batteries for Grid Storage? A Net Energy Analysis. Energy Environ. Sci. 2015, 8, 1938–1952. [Google Scholar] [CrossRef]
- Qadrdan, M.; Abeysekera, M.; Chaudry, M.; Wu, J.; Jenkins, N. Role of Power-to-Gas in an Integrated Gas and Electricity System in Great Britain. Int. J. Hydrog. Energy 2015, 40, 5763–5775. [Google Scholar] [CrossRef]
- Schouten, J.; Janssenvanrosmalen, R.; Michels, J. Modeling Hydrogen Production for Injection into the Natural Gas Grid: Balance between Production, Demand and Storage. Int. J. Hydrog. Energy 2006, 31, 1698–1706. [Google Scholar] [CrossRef]
- Goncharov, A.; Guglya, A.; Melnikova, E. On the Feasibility of Developing Hydrogen Storages Capable of Adsorption Hydrogen Both in Its Molecular and Atomic States. Int. J. Hydrog. Energy 2012, 37, 18061–18073. [Google Scholar] [CrossRef]
- Goncharov, A.; Guglya, A.; Melnikova, E. Corrigendum to “On the Feasibility of Developing Hydrogen Storages Capable of Adsorption Hydrogen Both in Its Molecular and Atomic States” [Int J Hydrogen Energy, 37 (2012) 18061–18073]. Int. J. Hydrog. Energy 2013, 38, 3521. [Google Scholar] [CrossRef]
- Schmidt, O.; Gambhir, A.; Staffell, I.; Hawkes, A.; Nelson, J.; Few, S. Future Cost and Performance of Water Electrolysis: An Expert Elicitation Study. Int. J. Hydrog. Energy 2017, 42, 30470–30492. [Google Scholar] [CrossRef]
- Schalenbach, M.; Zeradjanin, A.R.; Kasian, O.; Cherevko, S.; Mayrhofer, K.J. A Perspective on Low-Temperature Water Electrolysis-Challenges in Alkaline and Acidic Technology. Int. J. Electrochem. Sci. 2018, 13, 1173–1226. [Google Scholar] [CrossRef]
- Zeng, K.; Zhang, D. Recent Progress in Alkaline Water Electrolysis for Hydrogen Production and Applications. Prog. Energy Combust. Sci. 2010, 36, 307–326. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A Comprehensive Review on PEM Water Electrolysis. Int. J. Hydrog. Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- David, M.; Ocampo-Martínez, C.; Sánchez-Peña, R. Advances in Alkaline Water Electrolyzers: A Review. J. Energy Storage 2019, 23, 392–403. [Google Scholar] [CrossRef]
- Buttler, A.; Spliethoff, H. Current Status of Water Electrolysis for Energy Storage, Grid Balancing and Sector Coupling via Power-to-Gas and Power-to-Liquids: A Review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Rashid, M.; Mesfer, M.K.A.; Naseem, H.; Danish, M. Hydrogen Production by Water Electrolysis: A Review of Alkaline Water Electrolysis, PEM Water Electrolysis and High Temperature Water Electrolysis. Int. J. Eng. Adv. Technol. 2015, 4, 80–93. [Google Scholar]
- Götz, M.; Lefebvre, J.; Mörs, F.; McDaniel Koch, A.; Graf, F.; Bajohr, S.; Reimert, R.; Kolb, T. Renewable Power-to-Gas: A Technological and Economic Review. Renew. Energy 2016, 85, 1371–1390. [Google Scholar] [CrossRef]
- Marini, S.; Salvi, P.; Nelli, P.; Pesenti, R.; Villa, M.; Berrettoni, M.; Zangari, G.; Kiros, Y. Advanced Alkaline Water Electrolysis. Electrochim. Acta 2012, 82, 384–391. [Google Scholar] [CrossRef]
- Seibel, C.; Kuhlmann, J.W. Dynamic Water Electrolysis in Cross-Sectoral Processes. Chem. Ing. Tech. 2018, 90, 1430–1436. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Li, G.; Lie, T.T.; Hong, L. Experimental Study on the External Electrical Thermal and Dynamic Power Characteristics of Alkaline Water Electrolyzer. Int. J. Energy Res. 2018, 42, 3244–3257. [Google Scholar] [CrossRef]
- Clarivate Analytics. Web of Science Database. 2020. Available online: http://apps.webofknowledge.com (accessed on 14 January 2020).
- Ehret, O.; Bonhoff, K. Hydrogen as a Fuel and Energy Storage: Success Factors for the German Energiewende. Int. J. Hydrog. Energy 2015, 40, 5526–5533. [Google Scholar] [CrossRef]
- Ulleberg, O. Modeling of Advanced Alkaline Electrolyzers: A System Simulation Approach. Int. J. Hydrog. Energy 2003, 28, 21–33. [Google Scholar] [CrossRef]
- Đukić, A.; Firak, M. Hydrogen Production Using Alkaline Electrolyzer and Photovoltaic (PV) Module. Int. J. Hydrog. Energy 2011, 36, 7799–7806. [Google Scholar] [CrossRef]
- LeRoy, R.L. The Thermodynamics of Aqueous Water Electrolysis. J. Electrochem. Soc. 1980, 127, 1954. [Google Scholar] [CrossRef]
- Haug, P.; Koj, M.; Turek, T. Influence of Process Conditions on Gas Purity in Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2017, 42, 9406–9418. [Google Scholar] [CrossRef]
- Haug, P.; Kreitz, B.; Koj, M.; Turek, T. Process Modelling of an Alkaline Water Electrolyzer. Int. J. Hydrog. Energy 2017, 42, 15689–15707. [Google Scholar] [CrossRef]
- Renaud, R.; Leroy, R. Separator Materials for Use in Alkaline Water Electrolysers. Int. J. Hydrog. Energy 1982, 7, 155–166. [Google Scholar] [CrossRef]
- Kraglund, M.R.; Aili, D.; Jankova, K.; Christensen, E.; Li, Q.; Jensen, J.O. Zero-Gap Alkaline Water Electrolysis Using Ion-Solvating Polymer Electrolyte Membranes at Reduced KOH Concentrations. J. Electrochem. Soc. 2016, 163, F3125–F3131. [Google Scholar] [CrossRef]
- Kraglund, M.R.; Carmo, M.; Schiller, G.; Ansar, S.A.; Aili, D.; Christensen, E.; Jensen, J.O. Ion-Solvating Membranes as a New Approach towards High Rate Alkaline Electrolyzers. Energy Environ. Sci. 2019, 12, 3313–3318. [Google Scholar] [CrossRef]
- Hnát, J.; Paidar, M.; Schauer, J.; Žitka, J.; Bouzek, K. Polymer Anion-Selective Membranes for Electrolytic Splitting of Water. Part II: Enhancement of Ionic Conductivity and Performance under Conditions of Alkaline Water Electrolysis. J. Appl. Electrochem. 2012, 42, 545–554. [Google Scholar] [CrossRef]
- Hnát, J.; Plevová, M.; Žitka, J.; Paidar, M.; Bouzek, K. Anion-Selective Materials with 1,4-Diazabicyclo[2.2.2]Octane Functional Groups for Advanced Alkaline Water Electrolysis. Electrochim. Acta 2017, 248, 547–555. [Google Scholar] [CrossRef]
- Phillips, R.; Dunnill, C.W. Zero Gap Alkaline Electrolysis Cell Design for Renewable Energy Storage as Hydrogen Gas. RSC Adv. 2016, 6, 100643–100651. [Google Scholar] [CrossRef]
- Sánchez, M.; Amores, E.; Rodríguez, L.; Clemente-Jul, C. Semi-Empirical Model and Experimental Validation for the Performance Evaluation of a 15 kW Alkaline Water Electrolyzer. Int. J. Hydrog. Energy 2018, 43, 20332–20345. [Google Scholar] [CrossRef]
- Hammoudi, M.; Henao, C.; Agbossou, K.; Dubé, Y.; Doumbia, M. New Multi-Physics Approach for Modelling and Design of Alkaline Electrolyzers. Int. J. Hydrog. Energy 2012, 37, 13895–13913. [Google Scholar] [CrossRef]
- Koj, M.; Gimpel, T.; Schade, W.; Turek, T. Laser Structured Nickel-Iron Electrodes for Oxygen Evolution in Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2019, 44, 12671–12684. [Google Scholar] [CrossRef]
- Koj, M.; Qian, J.; Turek, T. Novel Alkaline Water Electrolysis with Nickel-Iron Gas Diffusion Electrode for Oxygen Evolution. Int. J. Hydrog. Energy 2019, 44, 29862–29875. [Google Scholar] [CrossRef]
- Hall, D.E. Electrodes for Alkaline Water Electrolysis. J. Electrochem. Soc. 1981, 128, 740. [Google Scholar] [CrossRef]
- Huot, J.Y. Low Hydrogen Overpotential Nanocrystalline Ni-Mo Cathodes for Alkaline Water Electrolysis. J. Electrochem. Soc. 1991, 138, 1316. [Google Scholar] [CrossRef]
- Rauscher, T.; Bernäcker, C.I.; Mühle, U.; Kieback, B.; Röntzsch, L. The Effect of Fe as Constituent in Ni-Base Alloys on the Oxygen Evolution Reaction in Alkaline Solutions at High Current Densities. Int. J. Hydrog. Energy 2019, 44, 6392–6402. [Google Scholar] [CrossRef]
- Fan, C. Study of Electrodeposited Nickel-Molybdenum, Nickel-Tungsten, Cobalt-Molybdenum, and Cobalt-Tungsten as Hydrogen Electrodes in Alkaline Water Electrolysis. J. Electrochem. Soc. 1994, 141, 382. [Google Scholar] [CrossRef]
- Rauscher, T.; Müller, C.I.; Schmidt, A.; Kieback, B.; Röntzsch, L. Ni–Mo–B Alloys as Cathode Material for Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2016, 41, 2165–2176. [Google Scholar] [CrossRef]
- Ursúa, A.; San Martín, I.; Barrios, E.L.; Sanchis, P. Stand-Alone Operation of an Alkaline Water Electrolyser Fed by Wind and Photovoltaic Systems. Int. J. Hydrog. Energy 2013, 38, 14952–14967. [Google Scholar] [CrossRef]
- Henao, C.; Agbossou, K.; Hammoudi, M.; Dubé, Y.; Cardenas, A. Simulation Tool Based on a Physics Model and an Electrical Analogy for an Alkaline Electrolyser. J. Power Sources 2014, 250, 58–67. [Google Scholar] [CrossRef]
- Balabel, A.; Zaky, M.S.; Sakr, I. Optimum Operating Conditions for Alkaline Water Electrolysis Coupled with Solar PV Energy System. Arab. J. Sci. Eng. 2014, 39, 4211–4220. [Google Scholar] [CrossRef]
- Vermeiren, P. Zirfon®: A New Separator for Ni-H2 Batteries and Alkaline Fuel Cells. Int. J. Hydrog. Energy 1996, 21, 679–684. [Google Scholar] [CrossRef]
- Le Bideau, D.; Mandin, P.; Benbouzid, M.; Kim, M.; Sellier, M. Review of Necessary Thermophysical Properties and Their Sensivities with Temperature and Electrolyte Mass Fractions for Alkaline Water Electrolysis Multiphysics Modelling. Int. J. Hydrog. Energy 2019, 44, 4553–4569. [Google Scholar] [CrossRef]
- Shoor, S.K.; Walker, R.D.; Gubbins, K.E. Salting out of Nonpolar Gases in Aqueous Potassium Hydroxide Solutions. J. Phys. Chem. 1969, 73, 312–317. [Google Scholar] [CrossRef]
- Grover, P.K.; Ryall, R.L. Critical Appraisal of Salting-Out and Its Implications for Chemical and Biological Sciences. Chem. Rev. 2005, 105, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Randall, M.; Failey, C.F. The Activity Coefficient of Non-Electrolytes in Aqueous Salt Solutions from Solubility Measurements. The Salting-out Order of the Ions. Chem. Rev. 1927, 4, 285–290. [Google Scholar] [CrossRef]
- Lang, W.; Zander, R. Salting-out of Oxygen from Aqueous Electrolyte Solutions: Prediction and Measurement. Ind. Eng. Chem. Fundam. 1986, 25, 775–782. [Google Scholar] [CrossRef]
- See, D.M.; White, R.E. Temperature and Concentration Dependence of the Specific Conductivity of Concentrated Solutions of Potassium Hydroxide. J. Chem. Eng. Data 1997, 42, 1266–1268. [Google Scholar] [CrossRef]
- De Souza, R.F.; Padilha, J.C.; Gonçalves, R.S.; Rault-Berthelot, J. Dialkylimidazolium Ionic Liquids as Electrolytes for Hydrogen Production from Water Electrolysis. Electrochem. Commun. 2006, 8, 211–216. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Huang, Y.; Zhou, Q.; Zhang, X.; Zhang, S. Toxicity of Ionic Liquids: Database and Prediction via Quantitative Structure–Activity Relationship Method. J. Hazard. Mater. 2014, 278, 320–329. [Google Scholar] [CrossRef]
- Zhao, Y.; Gani, R.; Afzal, R.M.; Zhang, X.; Zhang, S. Ionic Liquids for Absorption and Separation of Gases: An Extensive Database and a Systematic Screening Method. AIChE J. 2017, 63, 1353–1367. [Google Scholar] [CrossRef]
- Zhao, Y.; Pan, M.; Kang, X.; Tu, W.; Gao, H.; Zhang, X. Gas Separation by Ionic Liquids: A Theoretical Study. Chem. Eng. Sci. 2018, 189, 43–55. [Google Scholar] [CrossRef]
- De Souza, R.F.; Padilha, J.C.; Gonçalves, R.S.; de Souza, M.O.; Rault-Berthelot, J. Electrochemical Hydrogen Production from Water Electrolysis Using Ionic Liquid as Electrolytes: Towards the Best Device. J. Power Sources 2007, 164, 792–798. [Google Scholar] [CrossRef]
- Schalenbach, M.; Lueke, W.; Stolten, D. Hydrogen Diffusivity and Electrolyte Permeability of the Zirfon PERL Separator for Alkaline Water Electrolysis. J. Electrochem. Soc. 2016, 163, F1480–F1488. [Google Scholar] [CrossRef]
- Trinke, P.; Haug, P.; Brauns, J.; Bensmann, B.; Hanke-Rauschenbach, R.; Turek, T. Hydrogen Crossover in PEM and Alkaline Water Electrolysis: Mechanisms, Direct Comparison and Mitigation Strategies. J. Electrochem. Soc. 2018, 165, F502–F513. [Google Scholar] [CrossRef]
- Roy, A.; Watson, S.; Infield, D. Comparison of Electrical Energy Efficiency of Atmospheric and High-Pressure Electrolysers. Int. J. Hydrog. Energy 2006, 31, 1964–1979. [Google Scholar] [CrossRef]
- Ursúa, A.; Sanchis, P. Static–Dynamic Modelling of the Electrical Behaviour of a Commercial Advanced Alkaline Water Electrolyser. Int. J. Hydrog. Energy 2012, 37, 18598–18614. [Google Scholar] [CrossRef]
- Dobó, Z.; Palotás, Á.B. Impact of the Voltage Fluctuation of the Power Supply on the Efficiency of Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2016, 41, 11849–11856. [Google Scholar] [CrossRef]
- Dobó, Z.; Palotás, Á.B. Impact of the Current Fluctuation on the Efficiency of Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2017, 42, 5649–5656. [Google Scholar] [CrossRef]
- Speckmann, F.W.; Bintz, S.; Birke, K.P. Influence of Rectifiers on the Energy Demand and Gas Quality of Alkaline Electrolysis Systems in Dynamic Operation. Appl. Energy 2019, 250, 855–863. [Google Scholar] [CrossRef]
- De Fátima Palhares, D.D.; Vieira, L.G.M.; Damasceno, J.J.R. Hydrogen Production by a Low-Cost Electrolyzer Developed through the Combination of Alkaline Water Electrolysis and Solar Energy Use. Int. J. Hydrog. Energy 2018, 43, 4265–4275. [Google Scholar] [CrossRef]
- Hug, W.; Bussmann, H.; Brinner, A. Intermittent Operation and Operation Modeling of an Alkaline Electrolyzer. Int. J. Hydrog. Energy 1993, 18, 973–977. [Google Scholar] [CrossRef]
- Firak, M.; Djukic, A. An Investigation into the Effect of Photovoltaic Module Electric Properties on Maximum Power Point Trajectory with the Aim of Its Alignment with Electrolyzer U-I Characteristic. Therm. Sci. 2010, 14, 729–738. [Google Scholar] [CrossRef]
- Đukić, A. Autonomous Hydrogen Production System. Int. J. Hydrog. Energy 2015, 40, 7465–7474. [Google Scholar] [CrossRef]
- Dai, J.; Liu, D.; Wen, L.; Long, X. Research on Power Coefficient of Wind Turbines Based on SCADA Data. Renew. Energy 2016, 86, 206–215. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell Modelling and Model Parameters Estimation Techniques for Photovoltaic Simulator Application: A Review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Vergura, S. A Complete and Simplified Datasheet-Based Model of PV Cells in Variable Environmental Conditions for Circuit Simulation. Energies 2016, 9, 326. [Google Scholar] [CrossRef]
- Kovač, A.; Marciuš, D.; Budin, L. Solar Hydrogen Production via Alkaline Water Electrolysis. Int. J. Hydrog. Energy 2019, 44, 9841–9848. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Misra, A.; Sandeep, K. Photovoltaic Solar Energy Conversion for Hydrogen Production by Alkaline Water Electrolysis: Conceptual Design and Analysis. Energy Convers. Manag. 2017, 133, 1–13. [Google Scholar] [CrossRef]
- Khalilnejad, A.; Riahy, G. A Hybrid Wind-PV System Performance Investigation for the Purpose of Maximum Hydrogen Production and Storage Using Advanced Alkaline Electrolyzer. Energy Convers. Manag. 2014, 80, 398–406. [Google Scholar] [CrossRef]
- Badwal, S.P.S.; Giddey, S.S.; Munnings, C.; Bhatt, A.I.; Hollenkamp, A.F. Emerging Electrochemical Energy Conversion and Storage Technologies. Front. Chem. 2014, 2. [Google Scholar] [CrossRef]
- Kolli, A.; Gaillard, A.; De Bernardinis, A.; Bethoux, O.; Hissel, D.; Khatir, Z. A Review on DC/DC Converter Architectures for Power Fuel Cell Applications. Energy Convers. Manag. 2015, 105, 716–730. [Google Scholar] [CrossRef]
- Ursúa, A.; Barrios, E.L.; Pascual, J.; San Martín, I.; Sanchis, P. Integration of Commercial Alkaline Water Electrolysers with Renewable Energies: Limitations and Improvements. Int. J. Hydrog. Energy 2016, 41, 12852–12861. [Google Scholar] [CrossRef]
- Zini, G.; Tartarini, P. Wind-Hydrogen Energy Stand-Alone System with Carbon Storage: Modeling and Simulation. Renew. Energy 2010, 35, 2461–2467. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Akpinar, S. An Assessment on Seasonal Analysis of Wind Energy Characteristics and Wind Turbine Characteristics. Energy Convers. Manag. 2005, 46, 1848–1867. [Google Scholar] [CrossRef]
- Babu, N.R.; Arulmozhivarman, P. Wind Energy Conversion Systems-A Technical Review. J. Eng. Sci. Technol. 2013, 8, 493–507. [Google Scholar]
- Douglas, T.G.; Cruden, A.; Infield, D. Development of an Ambient Temperature Alkaline Electrolyser for Dynamic Operation with Renewable Energy Sources. Int. J. Hydrog. Energy 2013, 38, 723–739. [Google Scholar] [CrossRef]
- Kiaee, M.; Cruden, A.; Infield, D.; Chladek, P. Utilisation of Alkaline Electrolysers to Improve Power System Frequency Stability with a High Penetration of Wind Power. IET Renew. Power Gener. 2014, 8, 529–536. [Google Scholar] [CrossRef]
- Varone, A.; Ferrari, M. Power to Liquid and Power to Gas: An Option for the German Energiewende. Renew. Sustain. Energy Rev. 2015, 45, 207–218. [Google Scholar] [CrossRef]
- Parra, D.; Swierczynski, M.; Stroe, D.I.; Norman, S.; Abdon, A.; Worlitschek, J.; O’Doherty, T.; Rodrigues, L.; Gillott, M.; Zhang, X.; et al. An Interdisciplinary Review of Energy Storage for Communities: Challenges and Perspectives. Renew. Sustain. Energy Rev. 2017, 79, 730–749. [Google Scholar] [CrossRef]
- Kiaee, M.; Infield, D.; Cruden, A. Utilisation of Alkaline Electrolysers in Existing Distribution Networks to Increase the Amount of Integrated Wind Capacity. J. Energy Storage 2018, 16, 8–20. [Google Scholar] [CrossRef]
- Hug, W.; Divisek, J.; Mergel, J.; Seeger, W.; Steeb, H. Highly Efficient Advanced Alkaline Electrolyzer for Solar Operation. Int. J. Hydrog. Energy 1992, 17, 699–705. [Google Scholar] [CrossRef]
- Kuroda, Y.; Nishimoto, T.; Mitsushima, S. Self-Repairing Hybrid Nanosheet Anode Catalysts for Alkaline Water Electrolysis Connected with Fluctuating Renewable Energy. Electrochim. Acta 2019, 323, 134812. [Google Scholar] [CrossRef]
- Djafour, A.; Matoug, M.; Bouras, H.; Bouchekima, B.; Aida, M.; Azoui, B. Photovoltaic-Assisted Alkaline Water Electrolysis: Basic Principles. Int. J. Hydrog. Energy 2011, 36, 4117–4124. [Google Scholar] [CrossRef]
- Artuso, P.; Zuccari, F.; Dell’Era, A.; Orecchini, F. PV-Electrolyzer Plant: Models and Optimization Procedure. J. Sol. Energy Eng. 2010, 132, 031016. [Google Scholar] [CrossRef]

| m | |||||||
|---|---|---|---|---|---|---|---|
| – | – | A | V | Ω | Ω | – | °C |
| 9 | 2 | 5.98 | 4.615 | 0.099 | 20 | 1.6 | 48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brauns, J.; Turek, T. Alkaline Water Electrolysis Powered by Renewable Energy: A Review. Processes 2020, 8, 248. https://doi.org/10.3390/pr8020248
Brauns J, Turek T. Alkaline Water Electrolysis Powered by Renewable Energy: A Review. Processes. 2020; 8(2):248. https://doi.org/10.3390/pr8020248
Chicago/Turabian StyleBrauns, Jörn, and Thomas Turek. 2020. "Alkaline Water Electrolysis Powered by Renewable Energy: A Review" Processes 8, no. 2: 248. https://doi.org/10.3390/pr8020248
APA StyleBrauns, J., & Turek, T. (2020). Alkaline Water Electrolysis Powered by Renewable Energy: A Review. Processes, 8(2), 248. https://doi.org/10.3390/pr8020248






