Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method
Abstract
1. Introduction
2. Method for Determining Rotordynamic Coefficients
3. Numerical Investigation
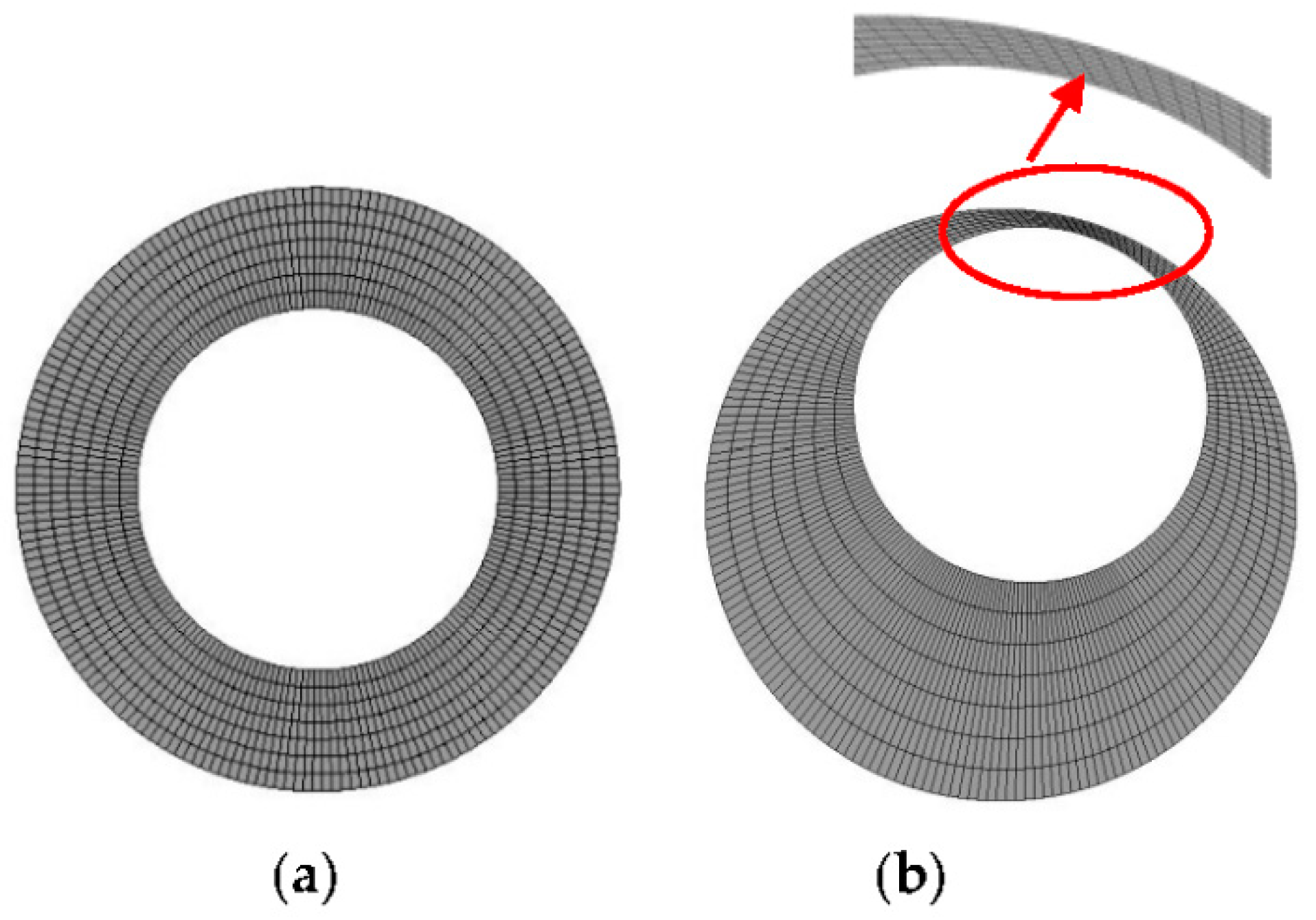
3.1. Geometry Model and Grid
3.2. Mesh Movement
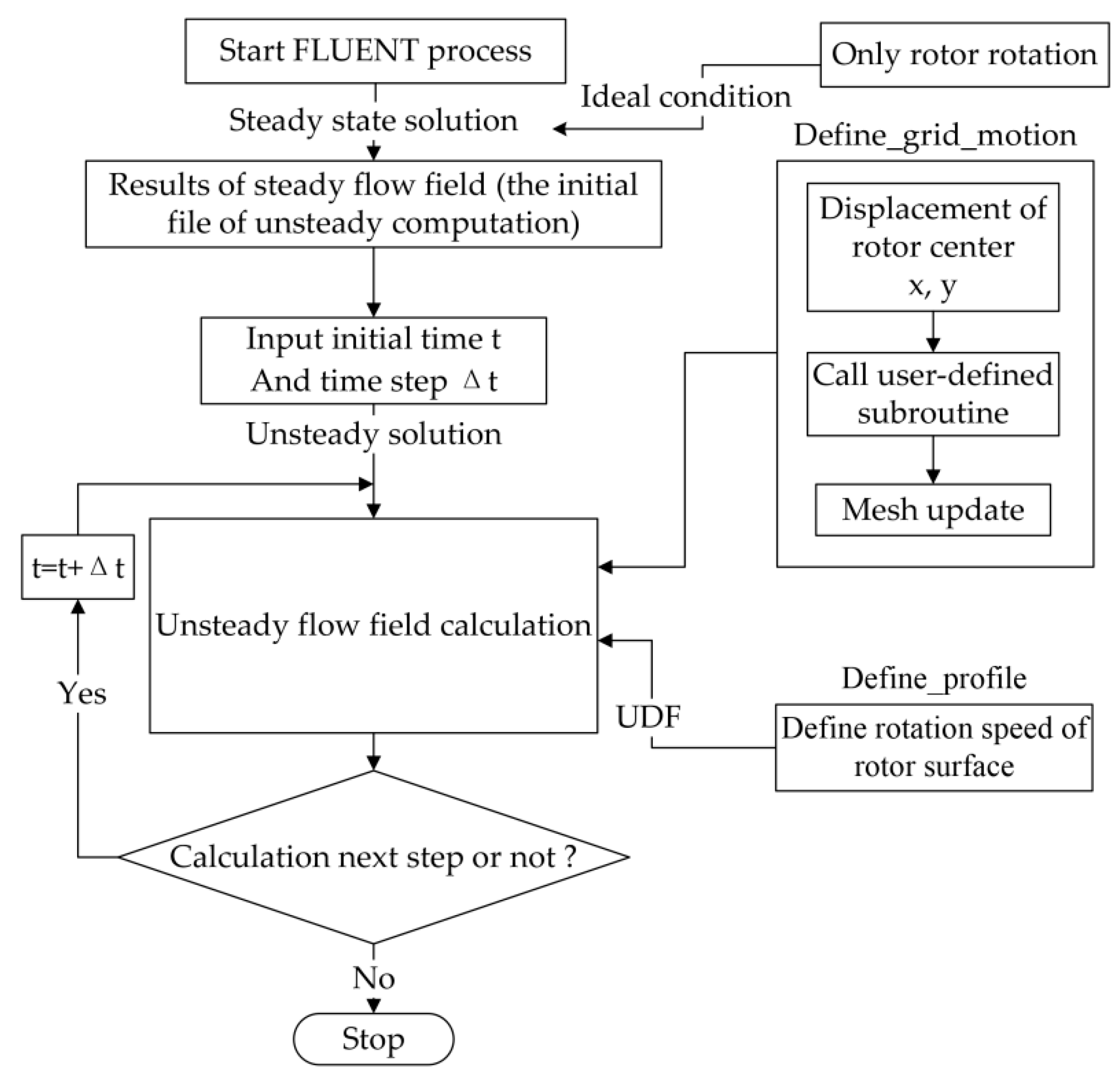
3.3. 3D Transient Analysis and Verification
3.3.1. Numerical Method
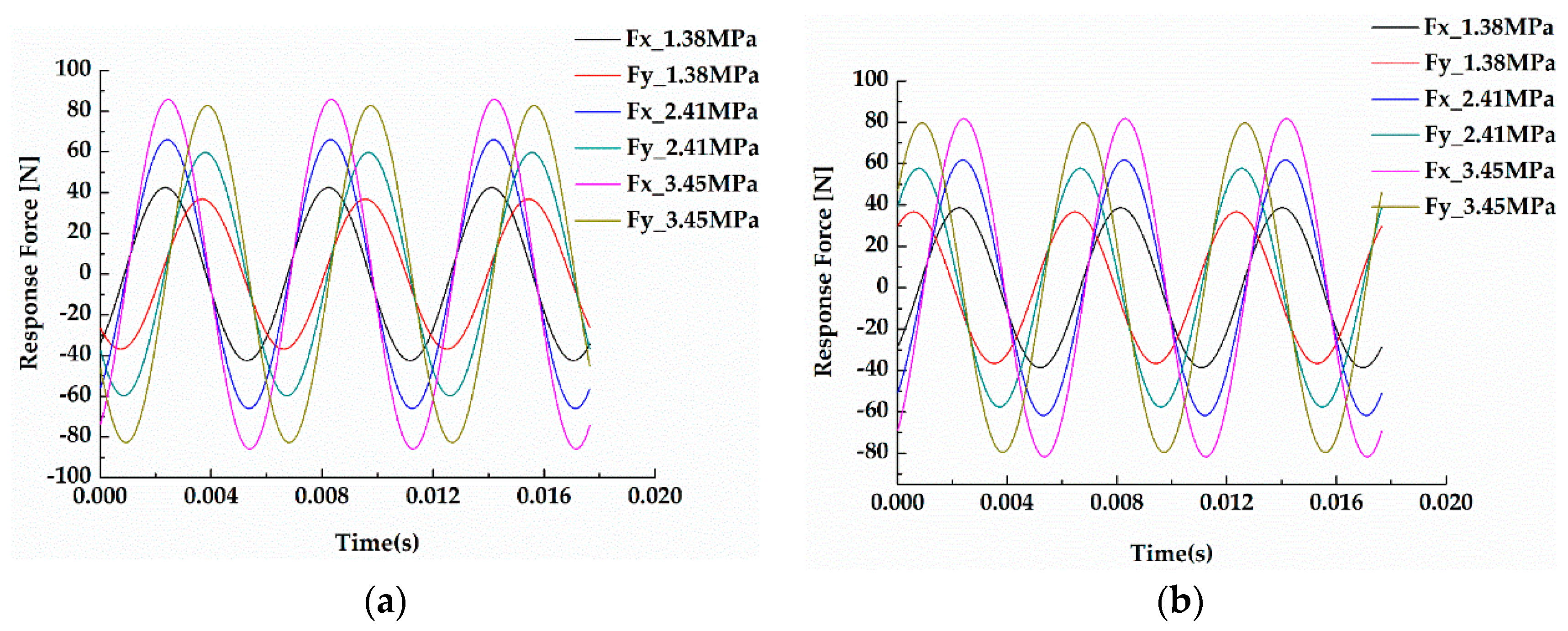
3.3.2. Fluid Reaction Forces
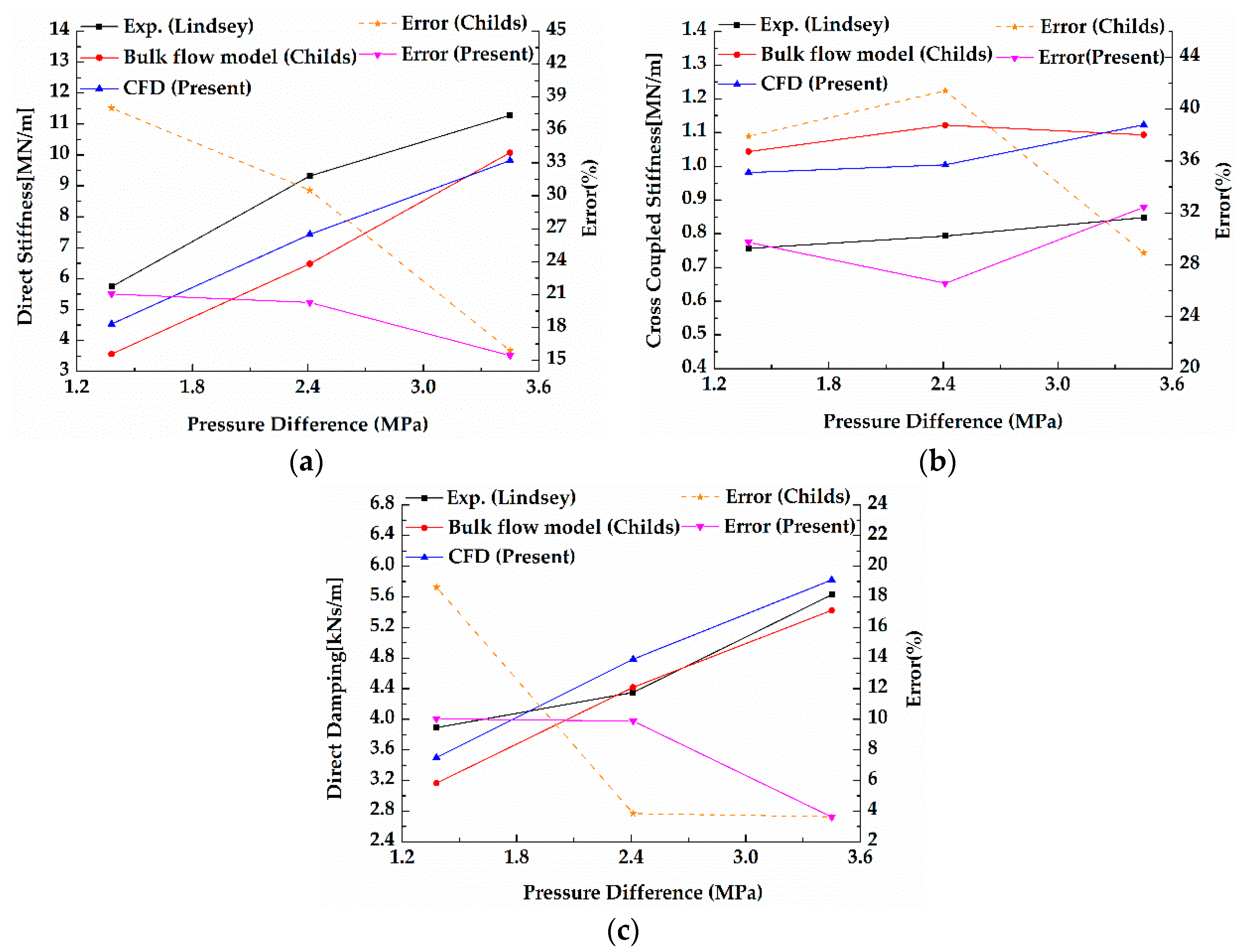
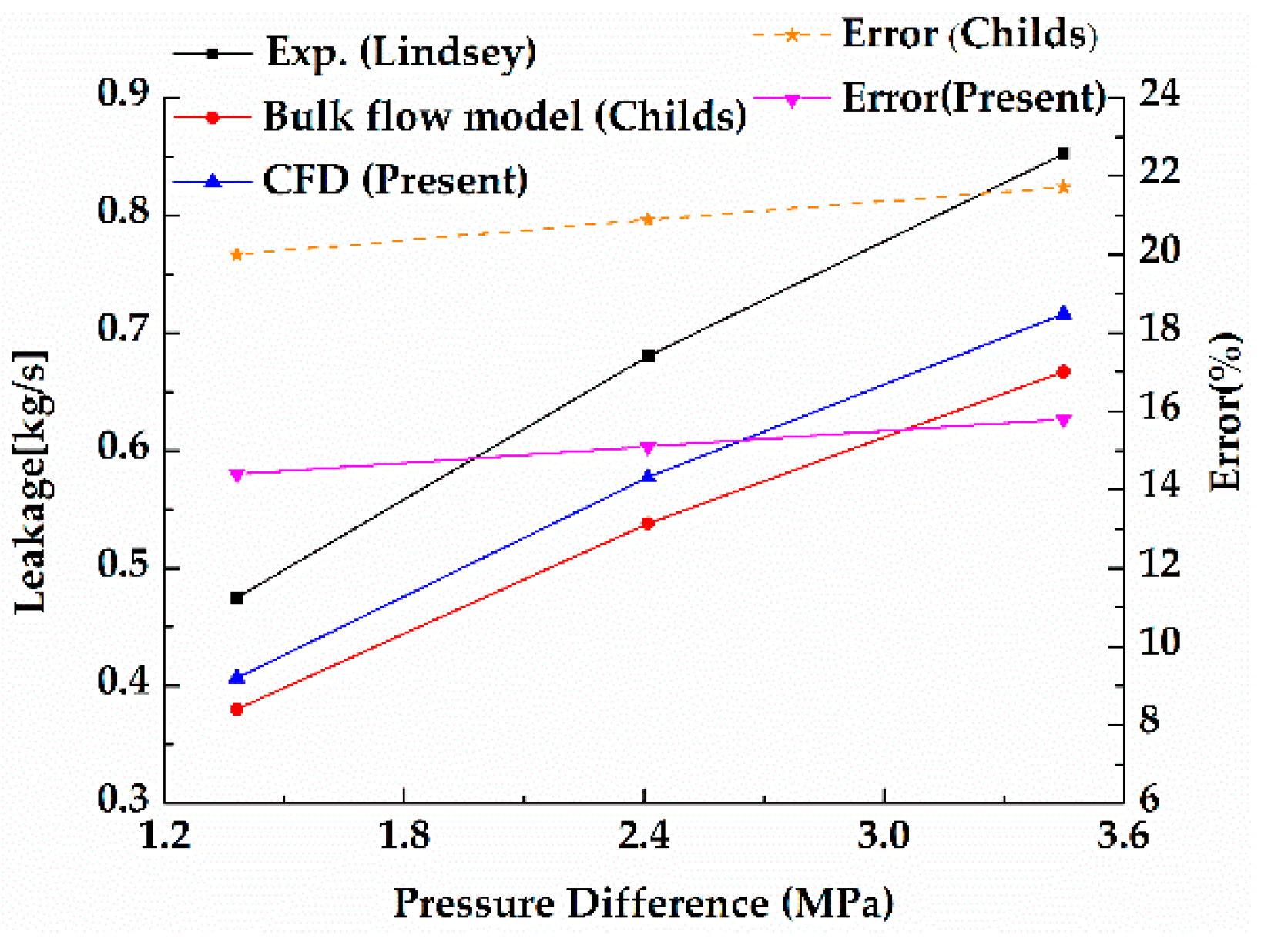
3.3.3. Theoretical and Experimental Verification
4. Results and Discussion
5. Conclusions
- (1)
- The proposed transient CFD method can control the grid movement at each time step and achieve optimal grid quality of the displacement grid at any time step. The CFD results were compared with the results from the experiment and the bulk-flow method. It was shown that the transient CFD analysis can provide better improvements than the bulk-flow analysis. The dynamic characteristics of annular seals can be predicted accurately by the transient CFD method.
- (2)
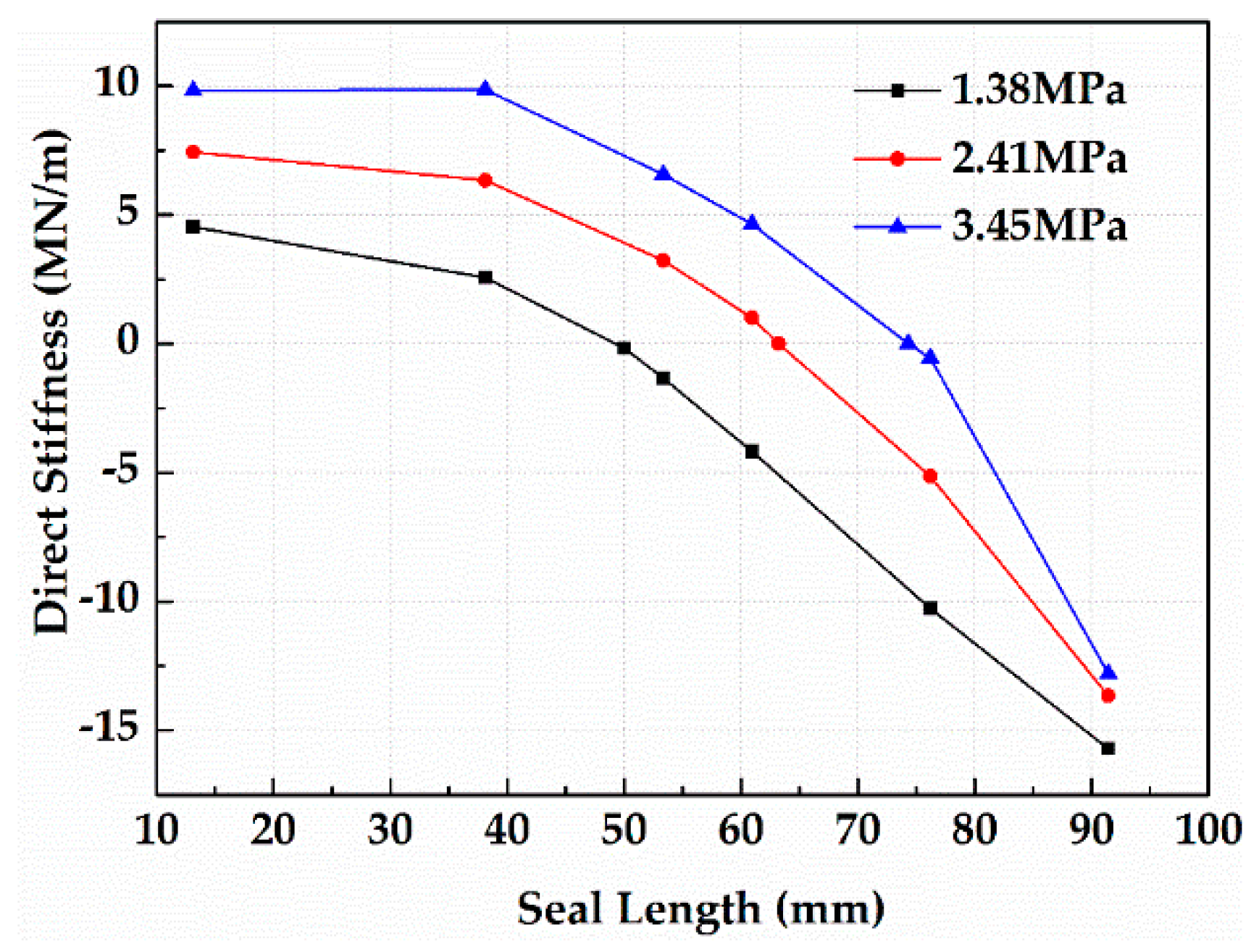
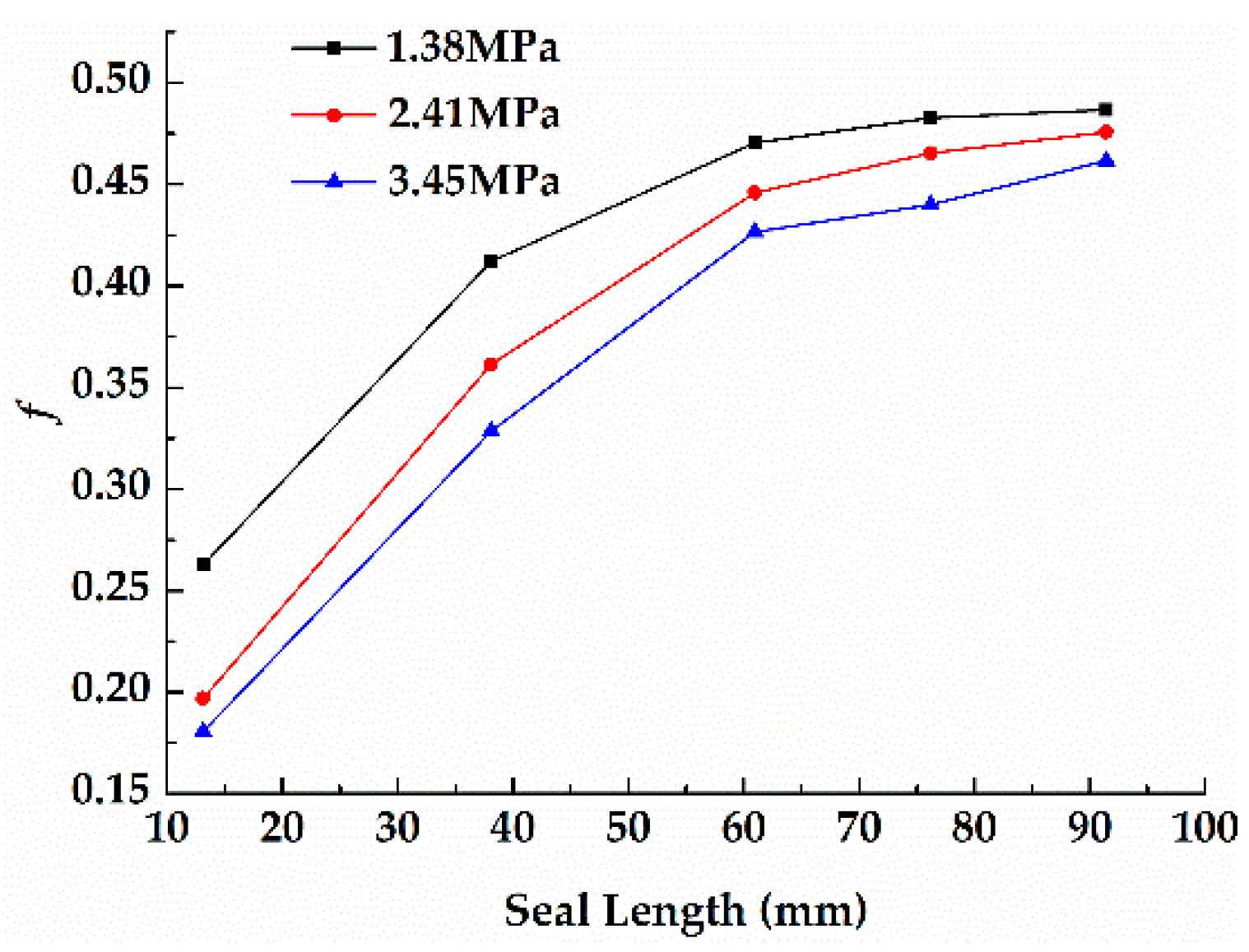
- The relationship between the seal length and rotordynamic characteristics was also investigated by the transient CFD method. The results show that direct stiffness changes from positive to negative as the seal length increases. This phenomenon can change the direction of the fluid force on the rotor surface and reduce the supporting effect of the annular seal on the pump rotor.
- (3)
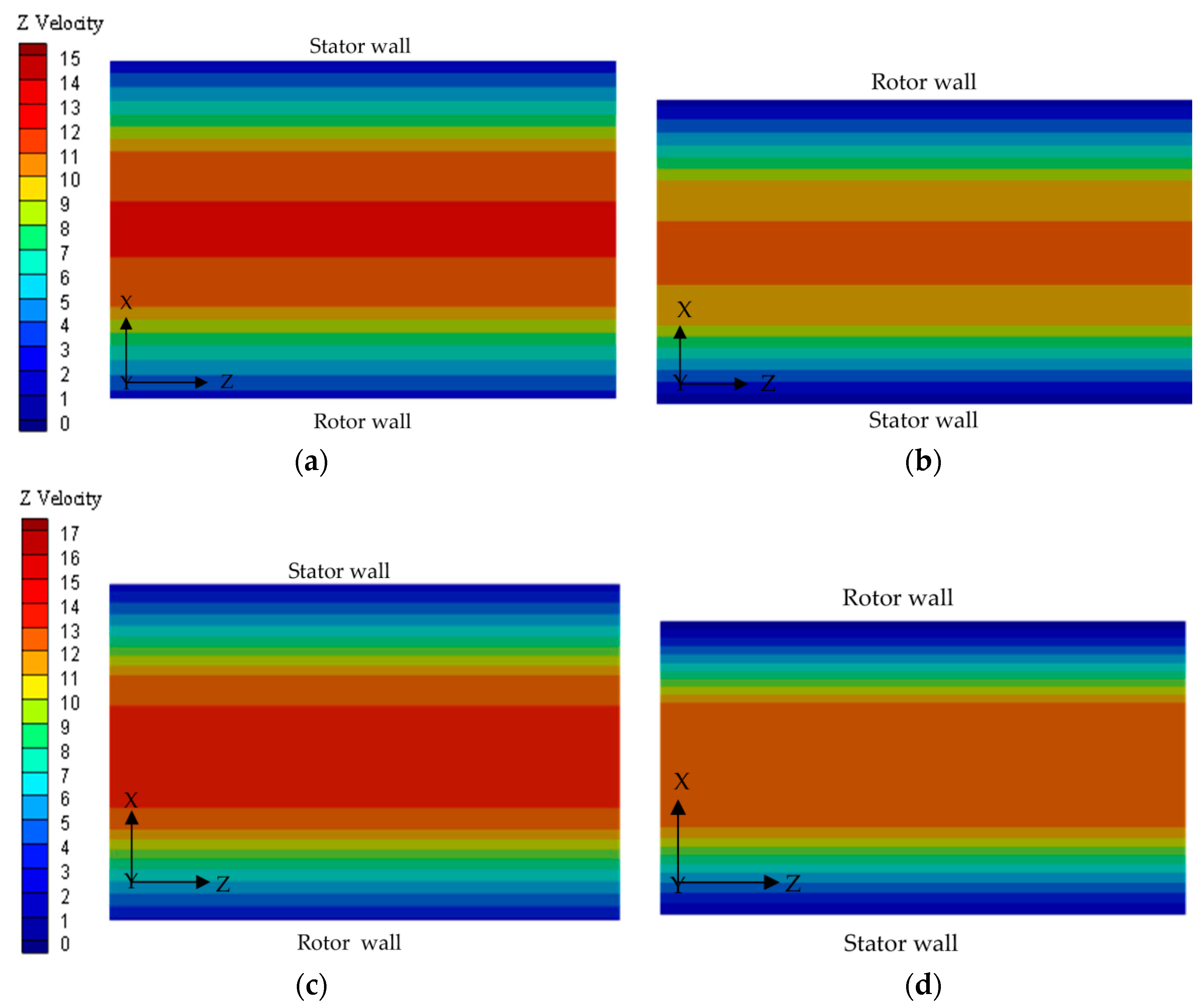
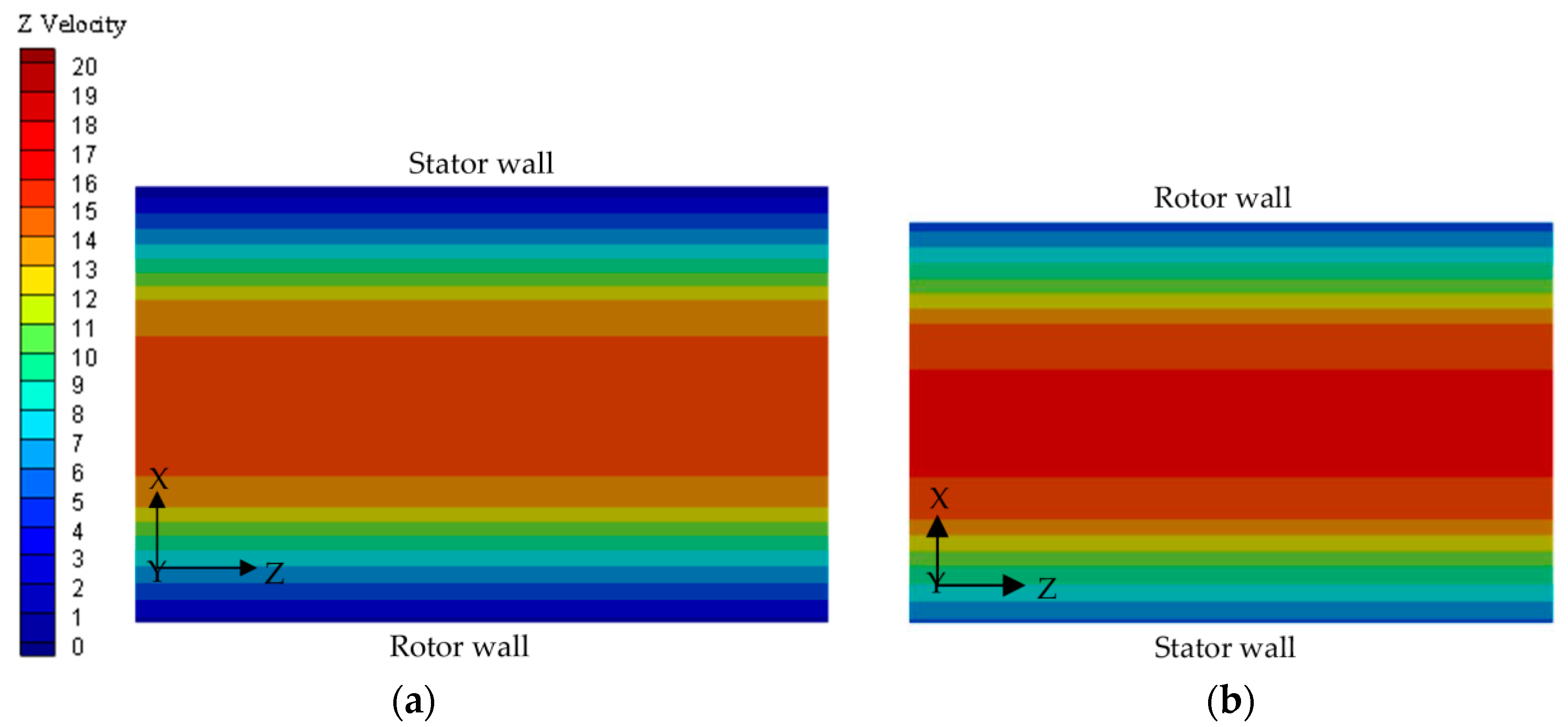
- For the short seal, the static pressure of the eccentric side is almost larger than that of the reverse side and direct stiffness is positive. For the long seal, a cross point exists in the axial position that makes Bernoulli effects predominant and direct stiffness negative. With the increasing seal length, the whirl-frequency ratio becomes larger, which decreases the stability of the pump rotor system.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| D | Seal diameter [mm] |
| L | Seal length [mm] |
| Cr | Seal clearance [mm] |
| e | Whirl radius [mm] |
| ω | Rotor velocity [rpm] |
| Ω | Whirl velocity [mm] |
| PD | Pressure difference [MPa] |
| θ | Initial angular of Pi0 [rad] |
| Rr | Rotor radius [mm] |
| K | Direct stiffness [N/m] |
| k | Cross coupled stiffness [N/m] |
| C | Direct damping [Ns/m] |
| c | Cross coupled damping [Ns/m] |
| M | Inertia mass [kg] |
| f | Whirl frequency ratio |
References
- Wang, C.; Chen, X.; Qiu, N.; Zhu, Y.; Shi, W. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Childs, D.W. Turbomachinery Rotordynamics: Phenomena, Modeling and Analysis; Wiley-Interscience: New York, NY, USA, 1993; pp. 229–243. [Google Scholar]
- Dietzen, F.J.; Nordmann, R. Calculating Rotordynamic Coefficients of Seals by Finite-Difference Techniques. J. Tribol. 1987, 109, 388–394. [Google Scholar] [CrossRef]
- Marquette, O.R.; Childs, D.W. An Extended Three-Control-Volume Theory for Circumferentially-Grooved Liquid Seals. J. Tribol. 1996, 118, 276–284. [Google Scholar] [CrossRef]
- Sun, D.; Yang, J.; Guo, R.; Zhang, W.; Ai, Y. A Trigonometric Series Expansion Based Method for the Research of Static and Dynamic Characteristics of Eccentric Seals. J. Mech. Sci. Technol. 2014, 28, 2111–2120. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Cheng, L.; Luo, C.; Xu, J.; Chen, K.; Jiao, W. Numerical Simulation on Hydraulic Characteristics of Nozzle in Waterjet Propulsion System. Processes 2019, 7, 915. [Google Scholar] [CrossRef]
- Tam, L.T.; Przekwas, A.J.; Muszynska, A.; Hendricks, R.C.; Braun, M.J.; Mullen, R.L. Numerical and Analytical Study of Fluid Dynamic Forces in Seals and Bearings. J. Vib. Acoust. 1988, 110, 315–325. [Google Scholar] [CrossRef]
- Mortazavi, F.; Palazzolo, A. Prediction of Rotordynamic Performance of Smooth Stator-Grooved Rotor Liquid Annular Seals Utilizing Computational Fluid Dynamics. J. Vib. Acoust. 2018, 140, 031002. [Google Scholar] [CrossRef]
- Ha, T.W.; Choe, B.S. Numerical Prediction of Rotordynamic Coefficients for an Annular-Type Plain-Gas Seal Using 3D CFD Analysis. J. Mech. Sci. Technol. 2014, 28, 505–511. [Google Scholar] [CrossRef]
- Ha, T.W.; Choe, B.S. Numerical Simulation of Rotordynamic Coefficients for Eccentric Annular-Type-Plain-Pump Seal Using CFD Analysis. J. Mech. Sci. Technol. 2012, 26, 1043–1048. [Google Scholar] [CrossRef]
- Moore, J.J. Three-Dimensional CFD Rotordynamic Analysis of Gas Labyrinth Seals. J. Vib. Acoust. 2003, 125, 427–433. [Google Scholar] [CrossRef]
- Untaroiu, A.; Hayrapetian, V.; Untaroiu, C.D.; Wood, H.G.; Schiavello, B.; McGuire, J. On the Dynamic Properties of Pump Liquid Seals. J. Fluids Eng. 2013, 135, 051104. [Google Scholar] [CrossRef]
- Untaroiu, A.; Migliorini, P.; Wood, H.G.; Allaire, P.E.; Kocur, J.A. Hole-Pattern Seals: A Three Dimensional CFD Approach for Computing Rotordynamic Coefficient and Leakage Characteristics. In Proceedings of the ASME 2009 International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009; pp. 981–990. [Google Scholar] [CrossRef]
- Subramanian, S.; Sekhar, A.; Prasad, B. Rotordynamic characteristics of rotating labyrinth gas turbine seal with centrifugal growth. Tribol. Int. 2016, 97, 349–359. [Google Scholar] [CrossRef]
- Moore, J.J.; Ransom, D.L.; Viana, F. Rotordynamic Force Prediction of Whirling Centrifugal Compressor Impellers Using Computational Fluid Dynamics. J. Eng. Gas Turbines Power 2010, 133, 042504. [Google Scholar] [CrossRef]
- Williams, M.; Chen, W.; Brozowski, L.; Eastland, A. Three-Dimensional Finite Difference Method for Rotordynamic Fluid Forces on Seals. AIAA J. 1997, 35, 1417–1420. [Google Scholar] [CrossRef]
- Jiang, X.K.; Wu, D.Z. Numerical Study of the Fluid Forces for a Whirling Annular Seal: CFD Simulation versus Experiment. In Proceedings of the 6th ISFMF, Wuhan, China, 22 October 2014; pp. 836–843. [Google Scholar] [CrossRef]
- Chochua, G.; Soulas, T.A. Numerical Modeling of Rotordynamic Coefficients for Deliberately Roughened Stator Gas Annular Seals. J. Tribol. 2007, 129, 424–429. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Janck, K.; Underbakke, H. Hole-Pattern and Honeycomb Seal Rotordynamic Forces: Validation of CFD-based Prediction Techniques. J. Eng. Gas Turbine Power 2012, 7, 122505. [Google Scholar] [CrossRef]
- Sreedharan, S.S.; Vannini, G.; Mistry, H. CFD Assessment of Rotordynamic Coefficients in Labyrinth Seals. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; pp. 26999–27007. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.G.; Feng, Z.P. Investigations on the Rotordynamic Coefficients of Pocket Damper Seals Using the Multifrequency, One- Dimensional, Whirling Orbit Model and RANS Solutions. J. Eng. Gas Turbines Power 2012, 134, 102510. [Google Scholar] [CrossRef]
- Li, Z.G.; Li, J.; Yan, X. Multiple Frequencies Elliptical Whirling Orbit Model and Transient RANS Solution Approach to Rotordynamic Coefficients of Annular Gas Seals Prediction. J. Vib. Acoust. 2013, 135, 031005. [Google Scholar] [CrossRef]
- Yan, X.; He, K.; Li, J.; Feng, Z.P. A Generalized Prediction Method for Rotordynamic Coefficients of Annular Gas Seals. J. Eng. Gas Turbines Power 2015, 137, 092506. [Google Scholar] [CrossRef]
- Jiang, X.K. Transient CFD Simulation on the Flow Field and Dynamic Characteristics of Annular Seals. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Wu, D.; Jiang, X.K.; Li, S.; Wang, L.Q. A New Transient CFD Method for Determining the Dynamic Coefficients of Liquid Annular Seals. J. Mech, Sci. Technol. 2016, 30, 3477–3486. [Google Scholar] [CrossRef]
- Lindsey, W.T.; Childs, D.W. The Effect of Converging and Diverging Axial Taper on the Rotordynamic Coefficients of Liquid Annular Pressure Seals: Theory versus Experiment. J. Vib. Acoust. 2000, 122, 126–131. [Google Scholar] [CrossRef]
- ANSYS FLUENT 16.0 Theory Guide [CP/DK]; ANSYS Inc.: Canonsburg, PA, USA, 2011.
- Luis, S.A.; Lu, X.L.; Zhu, J. Leakage and Force Coefficients for Pump Annular Seals Operating with Air/Oil Mixtures: Measurements Vs Predictions and Air Injection to Increase Seal Dynamic Stiffness; Turbomachinery Laboratory, Texas A & M Engineering Experiment Station: College Station, TX, USA, 2018; Available online: http://hdl.handle.net/1969.1/175007 (accessed on 15 February 2020).
- Chen, J.C.; Gunter, E.J. Introduction to Dynamics of Rotor-Bearing Systems; Trafford Publishing: Victoria, BC, Canada, 2005; pp. 297–304. [Google Scholar]
- Lund, J.W. The Stability of an Elastic Rotor in Journal Bearings with Flexible, Damped Supports. J. Appl. Mech. 1965, 32, 911–920. [Google Scholar] [CrossRef]
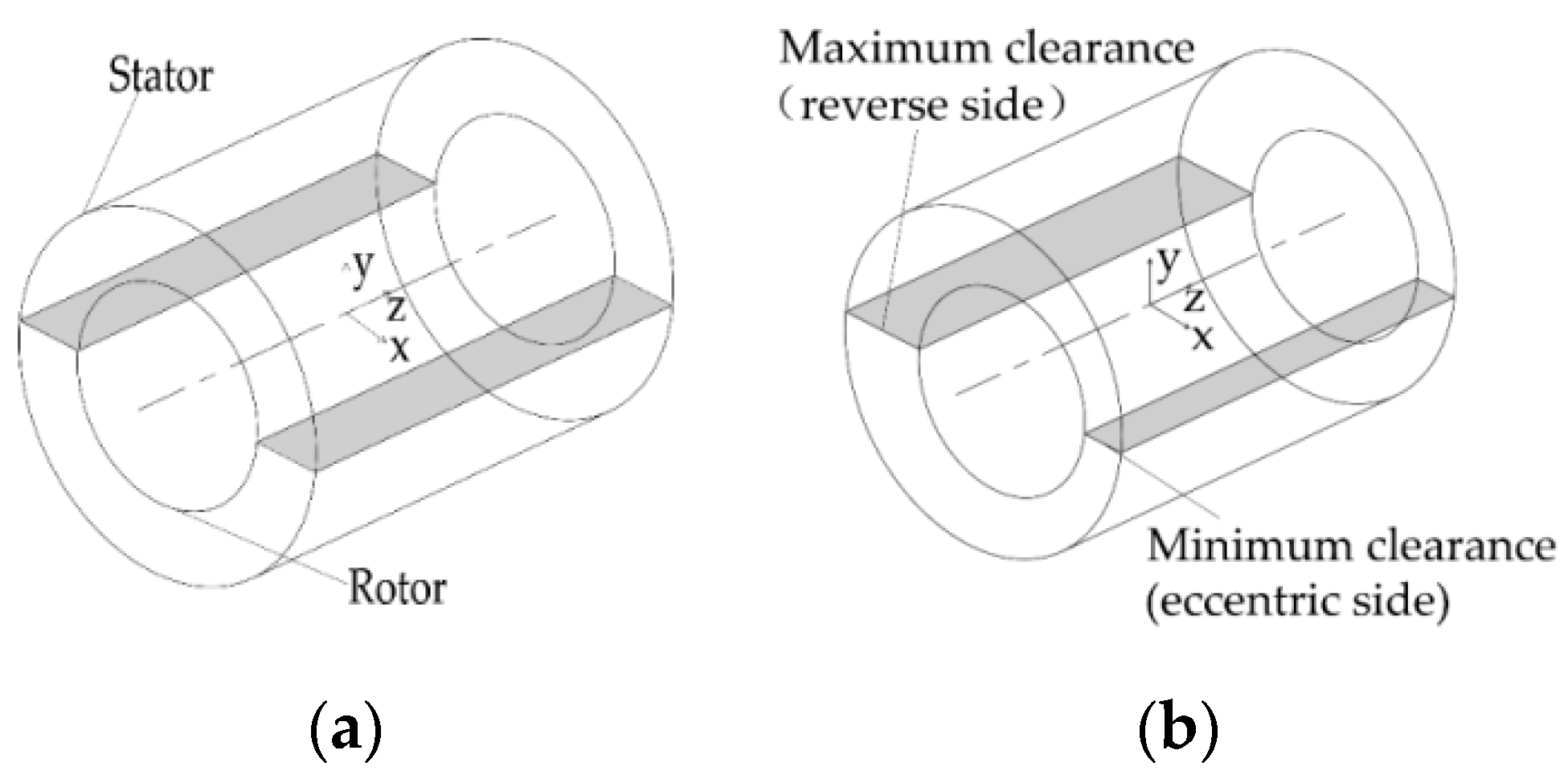
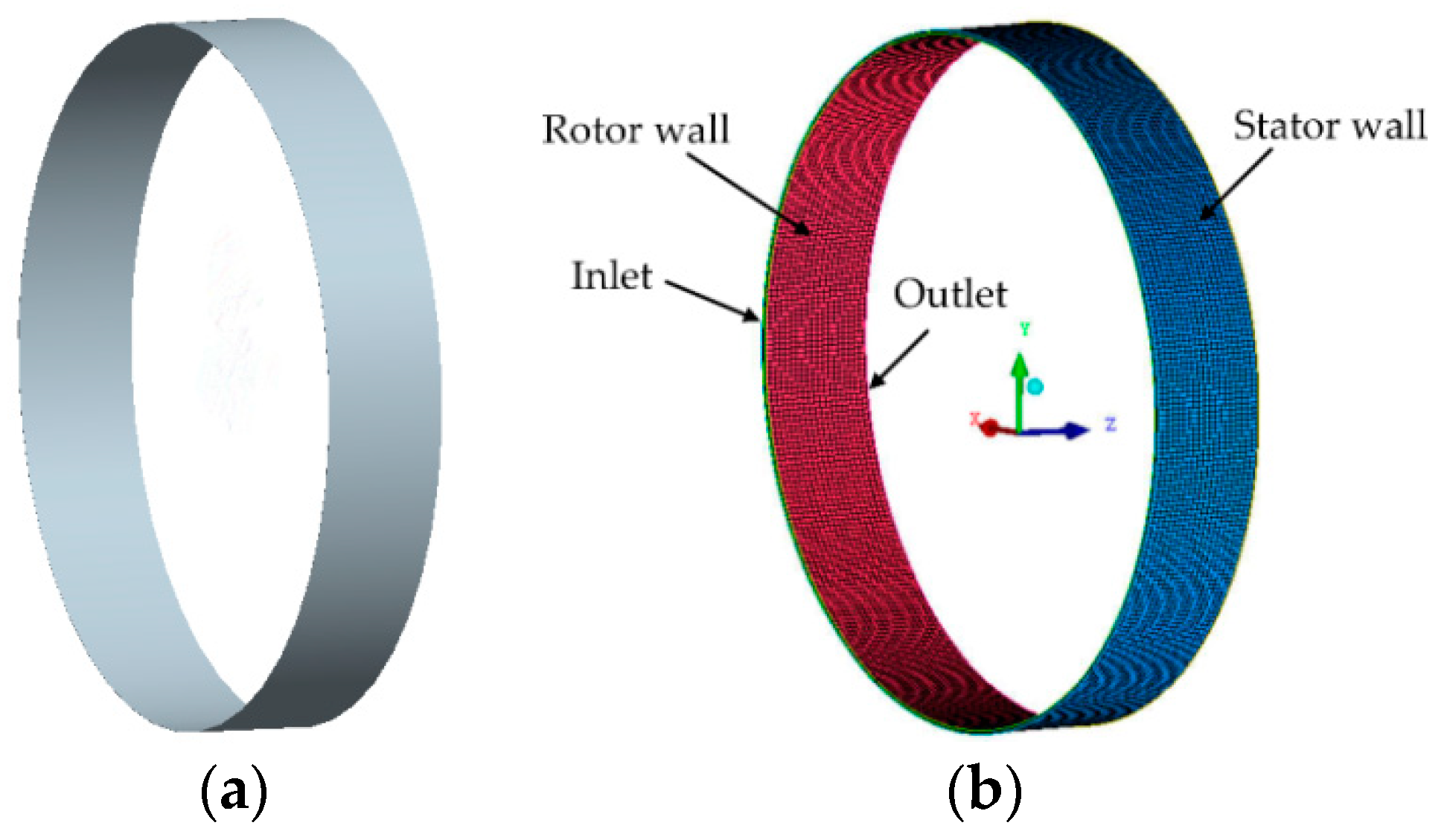
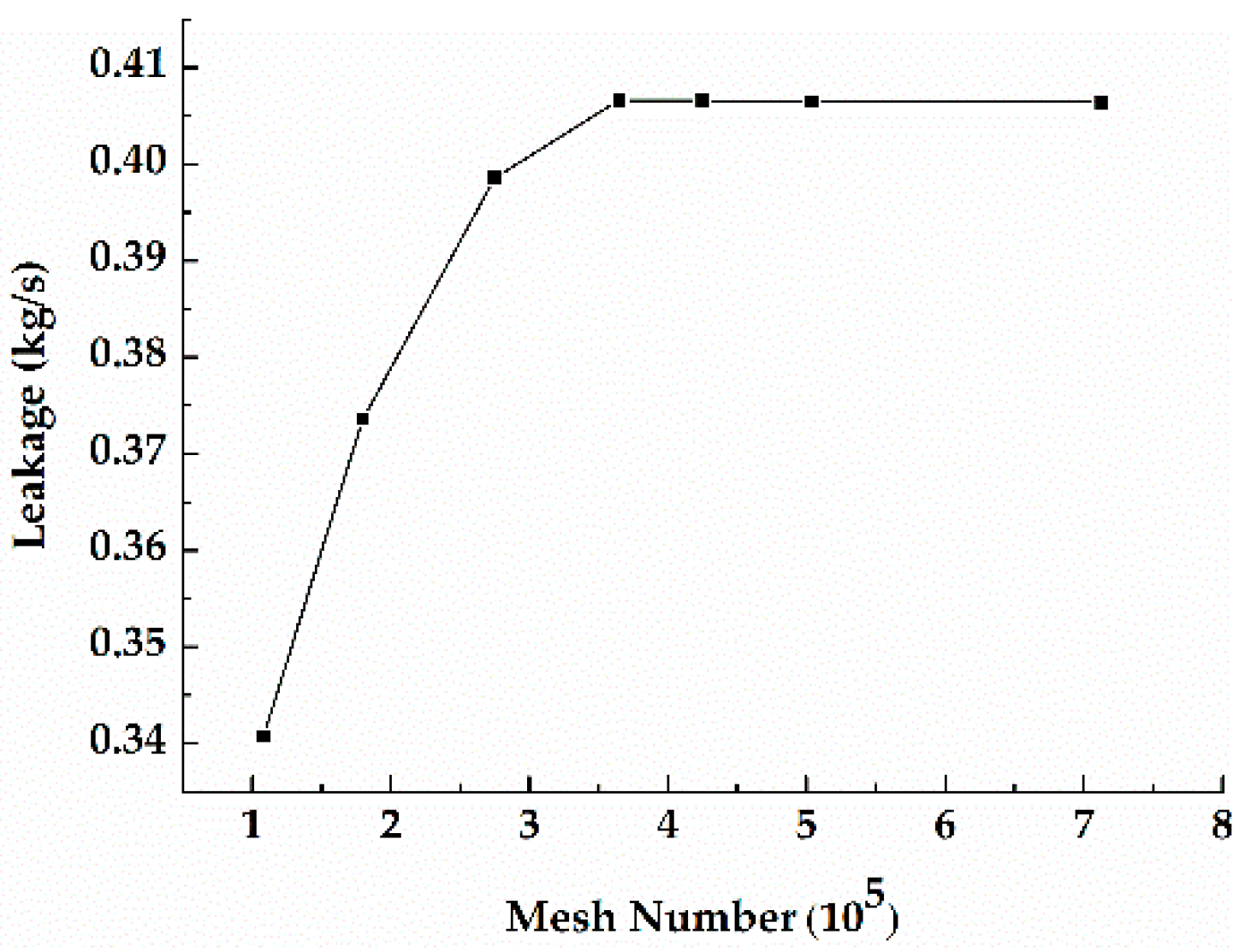
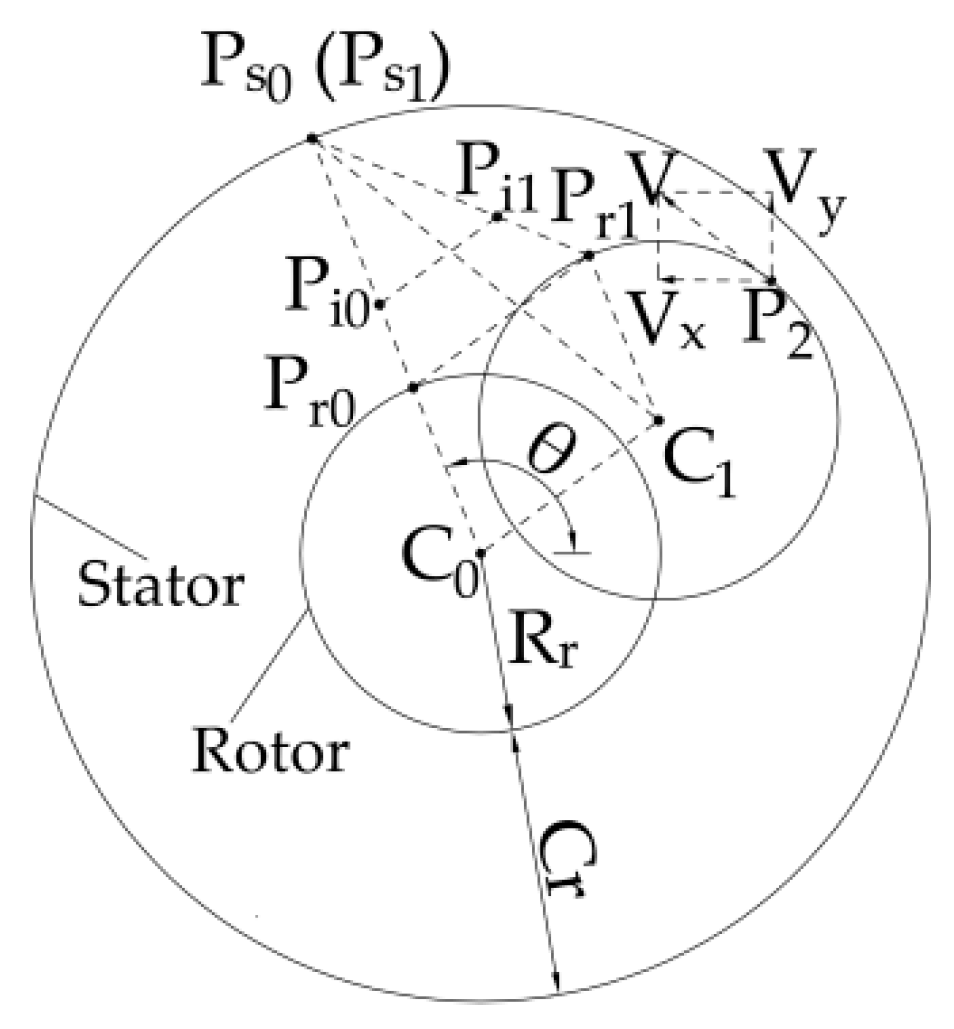
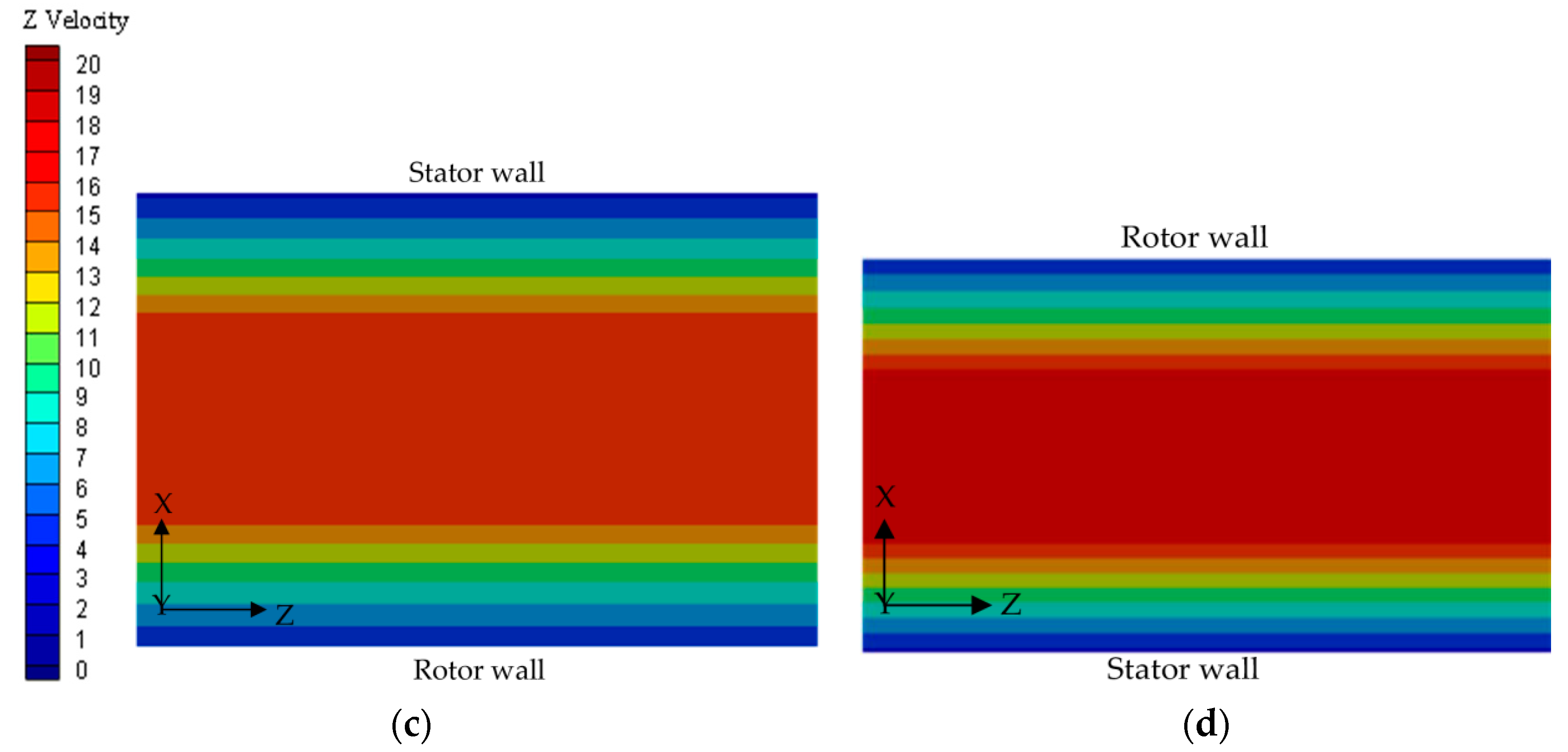
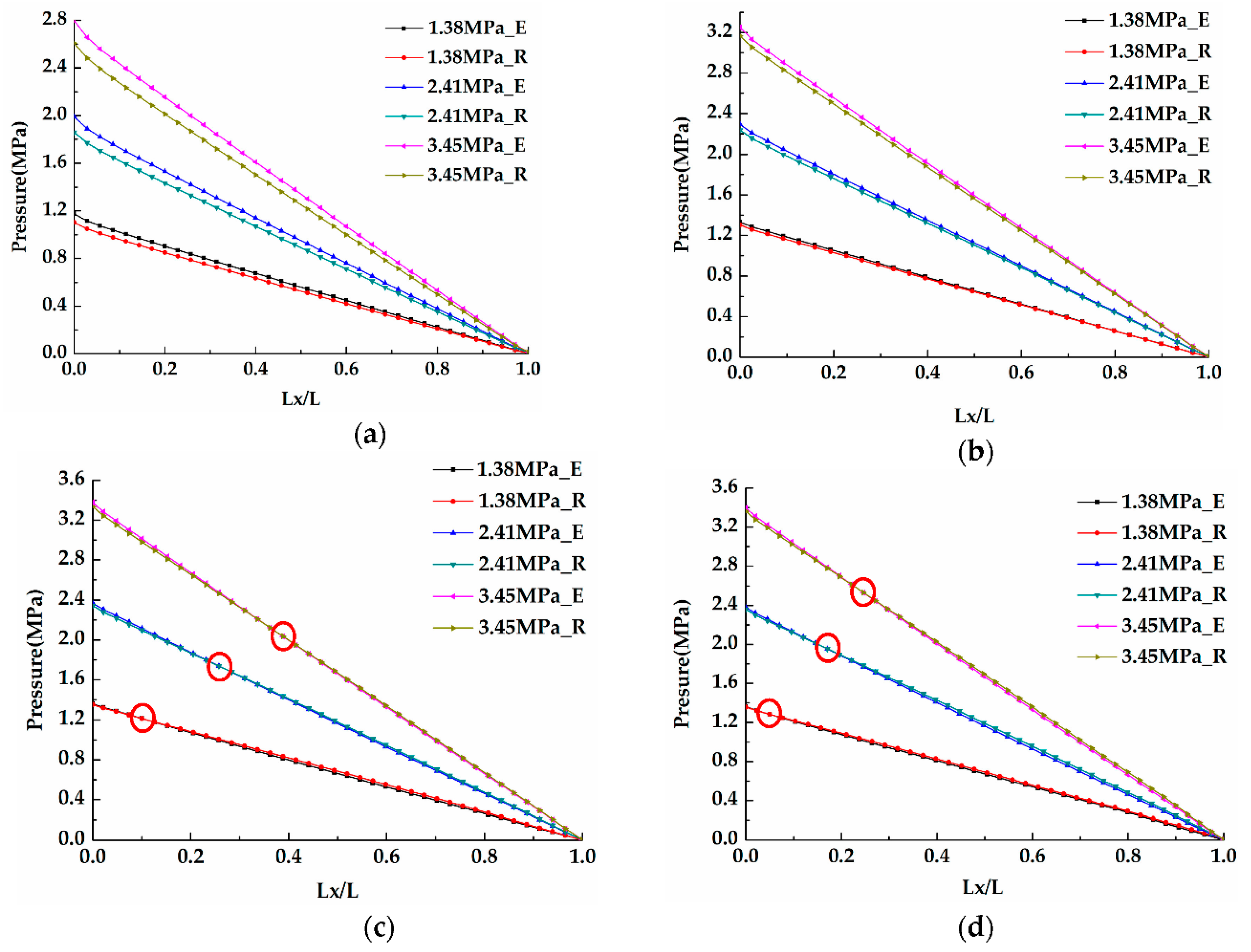
| Main Parameters | Signs | Values | Units |
|---|---|---|---|
| Seal diameter | D | 76.2 | mm |
| Seal clearance | Cr | 0.076 | mm |
| Seal length | L | 13.13 | mm |
| Whirl radius | e | 0.0076 | mm |
| Rotor velocity | ω | 10200 | rpm |
| Whirl velocity | Ω | 10200 | rpm |
| Pressure difference | PD | 1.38/2.41/3.45 | MPa |
| L/D ratio | - | 0.172 | - |
| PD MPa | L mm | K1 × 106 N/m | K1 × 106 N/m | C1 × 103 Ns/m | C1 × 103 Ns/m | M kg |
|---|---|---|---|---|---|---|
| 1.38 | 13.13 | 4.53 | 0.98 | 3.50 | 1.63 | 3.63 |
| 38.1 | 2.57 | 14.43 | 32.81 | 7.11 | 7.86 | |
| 60.96 | −4.17 | 47.59 | 94.74 | 27.27 | 27.40 | |
| 76.2 | −10.27 | 81.85 | 158.84 | 47.80 | 46.30 | |
| 91.44 | −15.76 | 110.78 | 222.44 | 72.87 | 71.81 | |
| 2.41 | 13.13 | 7.43 | 1.00 | 4.78 | 2.40 | 3.75 |
| 38.1 | 6.34 | 16.35 | 42.40 | 6.85 | 7.81 | |
| 60.96 | 1.01 | 54.45 | 114.38 | 25.75 | 26.67 | |
| 76.2 | −5.14 | 90.65 | 182.47 | 46.92 | 46.99 | |
| 91.44 | −13.67 | 134.89 | 265.61 | 73.81 | 72.18 | |
| 3.45 | 13.13 | 9.81 | 1.12 | 5.92 | 3.12 | 3.89 |
| 38.1 | 9.85 | 17.72 | 50.53 | 6.85 | 7.86 | |
| 60.96 | 4.64 | 60.07 | 131.95 | 25.86 | 27.68 | |
| 76.2 | −0.56 | 95.56 | 203.51 | 46.71 | 49.23 | |
| 91.44 | −12.80 | 138.17 | 280.38 | 69.27 | 65.82 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Cui, B.; Zhai, L. Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method. Processes 2020, 8, 227. https://doi.org/10.3390/pr8020227
Li F, Cui B, Zhai L. Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method. Processes. 2020; 8(2):227. https://doi.org/10.3390/pr8020227
Chicago/Turabian StyleLi, Fengqin, Baoling Cui, and Lulu Zhai. 2020. "Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method" Processes 8, no. 2: 227. https://doi.org/10.3390/pr8020227
APA StyleLi, F., Cui, B., & Zhai, L. (2020). Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method. Processes, 8(2), 227. https://doi.org/10.3390/pr8020227





