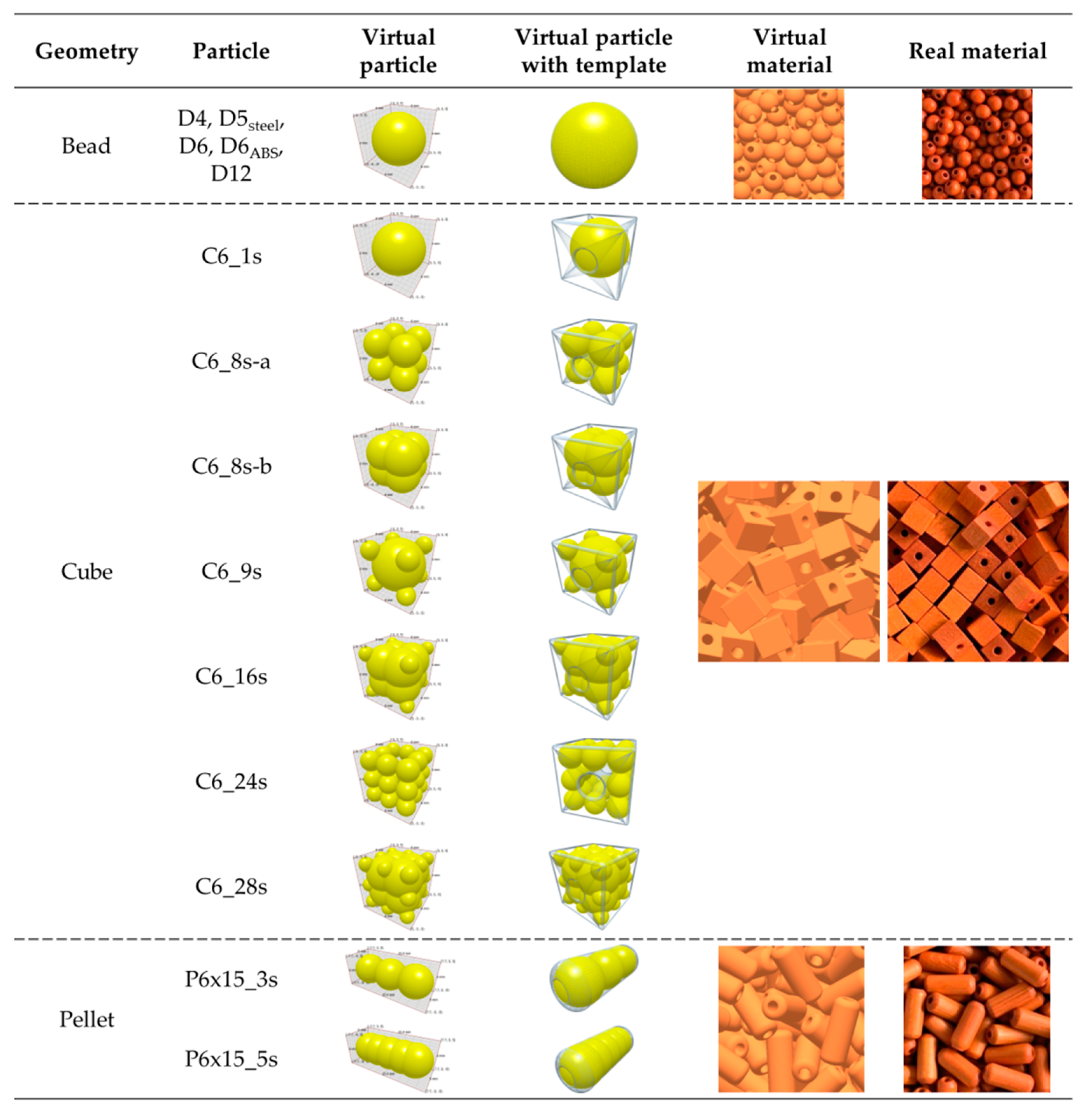
2.2.1. Determination of Interaction Coefficients
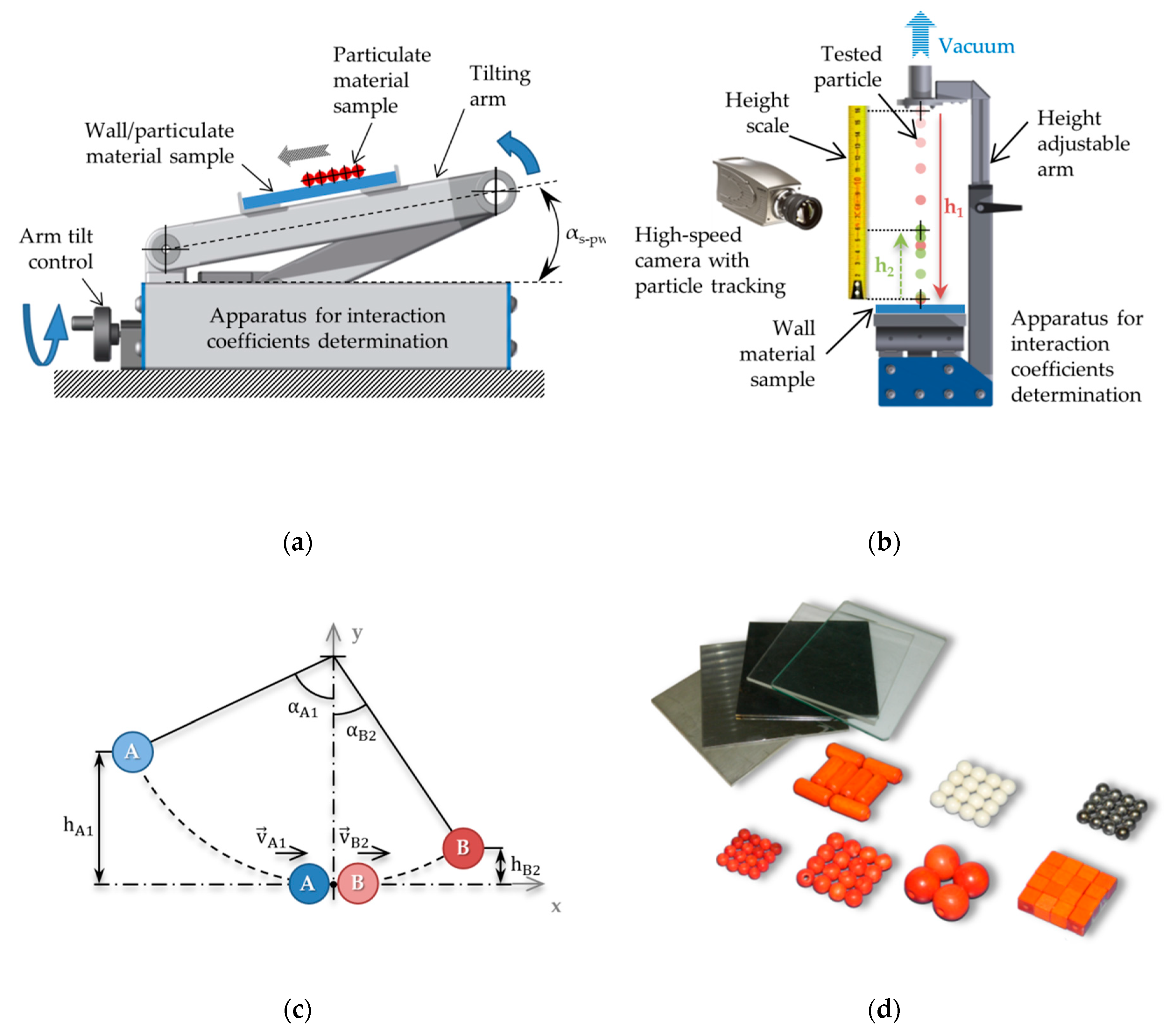
The interaction coefficients define how particles of particulate matter interact with each other or with other materials in contact. The three basic DEM interaction coefficients used in the Hertz-Mindlin contact model include the coefficient of static friction μs, the coefficient of rolling friction μr and the coefficient of restitution e. While some values of these interaction coefficients (e.g., static friction between a particle and a contact material) can be measured quite easily using test apparatus, the experimental determination of the coefficients defining interactions between the particles themselves (and their subsequent use in DEM) is often challenging. In order to measure all three interaction parameters, a test apparatus designed with regard to accuracy and simplicity of measurements was constructed. To measure the coefficient of restitution, the device features a height-adjustable arm with a head. A vacuum source can be connected to this head, allowing one to suck a test particle onto a fine screen of the head. The tilting arm controlled by a screw facilitates a fine pitch for smooth operation serves to measure the friction parameters.
The static friction measurement scheme is shown in
Figure 3a. The coefficient of static friction between the particle and the contact material
μs–pw is determined from the measured angle
αs–pw using the following equation:
Grains of a shape approaching a sphere (i.e., grains start to roll rather than slip on the wall material) are more challenging. This phenomenon has to be eliminated by clumping several particles into one compact unit (clump). In the particle surface thusly formed (see
Figure 3d), the free rotation of the grains is prevented, and only static resistance, not rolling resistance, is measured. The same methodology was used to measure the initial static friction values between particles
μs–pp, but the contact material was replaced with the surface of another particle clump.
The coefficient of rolling friction has been widely discussed, as evidenced by a number of publications dealing with this topic [
16,
43]. When spherical particles are used, rolling friction should be included, but this is not necessary when working with non-spherical particles [
36]. Wensrich and Katterfeld (2012) discuss this issue in their publications, among others. The same methodology was used for the spherical shape particles as for the measurement of static friction. The rolling friction coefficient for the particle μr is calculated from the measured angle
αr according to the following equation:
The coefficient of restitution (denoted by
e) is the ratio of the final to the initial relative velocity between two objects after they collide. It usually ranges from 0 to 1, where 1 refers to a perfectly elastic collision. The coefficient of restitution can be considered as the degree to which the mechanical energy of bodies is maintained when reflected from a surface or other body. In cases where the frictional forces can be neglected, and in the perfect progression of the collision and bounce, the ratio between the potential energy before the fall
EP1 and the potential energy after the reflection
EP2 can generally be calculated as follows:
For experimental measurements of the particle-wall restitution coefficient, an apparatus for measuring the interaction coefficients was used (
Figure 3b). A vacuum source was attached to a holder mounted on an extendable arm to hold a test particle on the holder screen. After switching off the vacuum source, the particle dropped from the height
h1 vertically onto a contact material, from which it bounced to the height
h2. The entire course of the experiment was captured using a high-speed camera. The movement was evaluated using tracking software that allows one to accurately track the particle trajectory. After reading the respective drop and rebound heights, the coefficient of restitution was determined according to Equation (5). A method published by Hlosta et al. (2018) was used to measure the coefficient of restitution of two particles. The coefficient of restitution of two particles is based on the laws of momentum conservation and energy conservation. When two particles collide, the total impulse introduced to the system (the two particles) is equal to zero. In the case of the collision of two particles that travel in one plane at different velocities before and after collision, it is assumed that the contact force between the particles is also in the same plane and the state of momentum is maintained. In this case, the coefficient of restitution is defined as the ratio of the relative velocities of the particles before and after they collide. If modelling of the flow of bulk material is required, damping behavior often becomes a factor of secondary importance. This is because many bulk materials demonstrate relatively strong damping properties. In most cases (e.g., in friction dominates processes), a value between 0.2 and 0.4 is appropriate and drop tests can be neglected in order to reduce the number of parameters to be calibrated [
36].
Particle A is hanged on a hinge and released from height
hA1. At the lowest point, particle A collides with particle B. It transmits its kinetic energy to particle B, which is reflected to the height
hB2. The coefficient restitution of two particles can be determined based on the Equation (5). Another way to determine the coefficient of restitution is using the ratio of the angle of reflection
αB2 to the angle of drop
αA1. The principle of this measurement is shown in
Figure 3c. Here again, the coefficient of restitution is a measure of how much energy is lost in a collision. The values range is 0 < e < 1. In an ideal plastic collision (
epp = 0), the particles remain together after they collide. In a perfect elastic collision (
epp = 1), no energy is lost so that the kinetic energy of the system is maintained and the velocity of the particles after the collision is equal to the velocity preceding the collision. In this study, a two-particle collision experiment using a double pendulum is employed to measure the coefficient of restitution of two particles [
44]. All measurements of interaction parameters were repeated ten times for each particulate material. From these ten values, the average value was determined including the standard deviation.
2.2.2. Bulk Density Measurement and Calibration
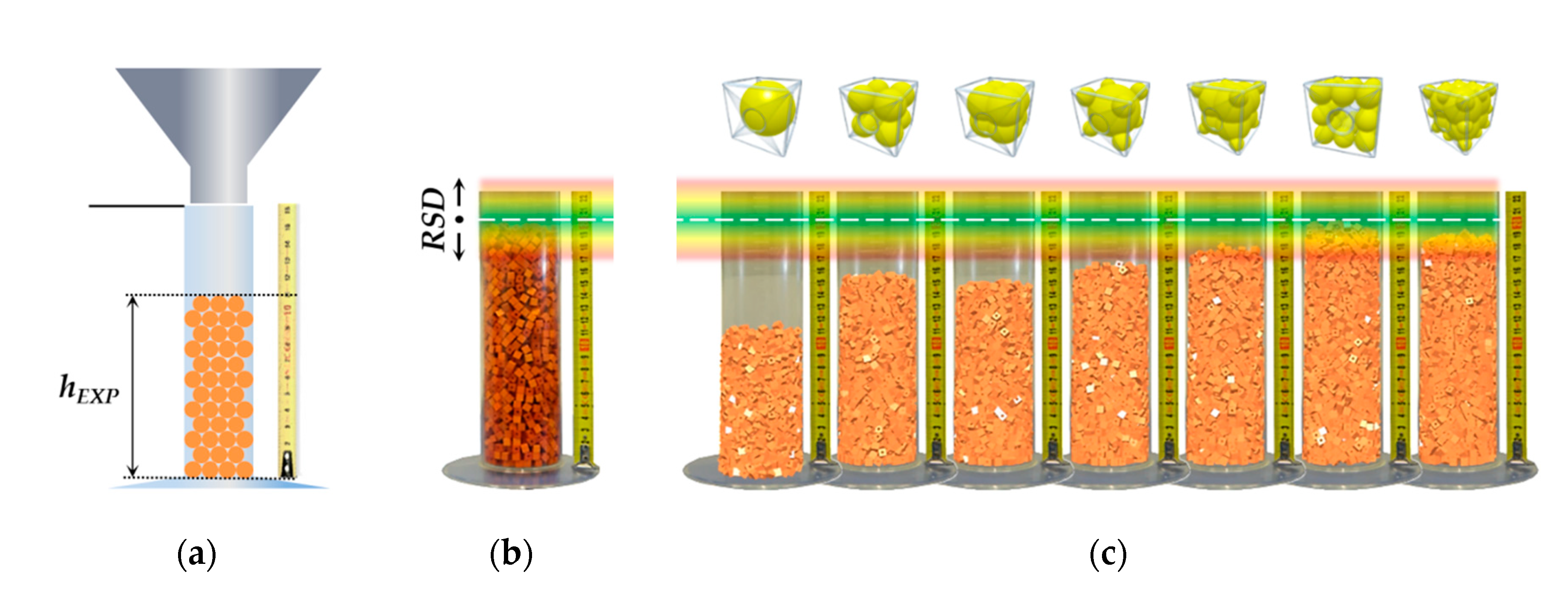
Particles packed in a bed are probably the simplest state of particulate matter, which is present both in nature and in a number of industries. The understanding of the particle deposition is also important in industrial applications due to the particle compaction (which is utilized in powder metallurgy), and the characterization of porosity, since air permeability and thermal conductivity of particulate materials can be quantitatively linked to the pore content and inter-particle contact properties. The bulk density verification parameter was the bed height of a particulate material of a known number of particles in a cylinder during the experiment and the DEM simulation. Differences in the resulting height can be resolved by shape accuracy and particle size. The weight of each individual DEM particle was always identical to the weight of actual particles according to
Table 3. The second use of the packing test is the initial estimation and determination of the friction parameters
μs and a
μr, as the values of static and rolling friction affect the height of a bed [
45]. A 1000 mL cylinder, stand, hopper, length gauge, tripod camera and slide shutter were used for the packing test. Each of the seven particulate materials was gradually placed in the hopper above the measuring cylinder and closed by the slide. The slide was then removed, and the material was freely poured into the cylinder. The camera took a photograph which was later used for reading the height of the material bed using the length gauge that was part of the apparatus and was placed in a vertical plane intersecting the axis of the cylinder. This procedure was repeated ten times for each material. From these ten values, the average was determined including the standard deviation. Based on DEM, the computational cost re-calculated to seconds per particle was also recorded as a possible criterion for the subsequent selection of shape accuracy for C6 and P6 × 15 particles. Material constants shown in
Table 2 and specific densities of particles in
Table 3 were used as input parameters. The scheme and principle used for the packing test are shown in
Figure 4.
2.2.3. Shear Modulus Value Optimization
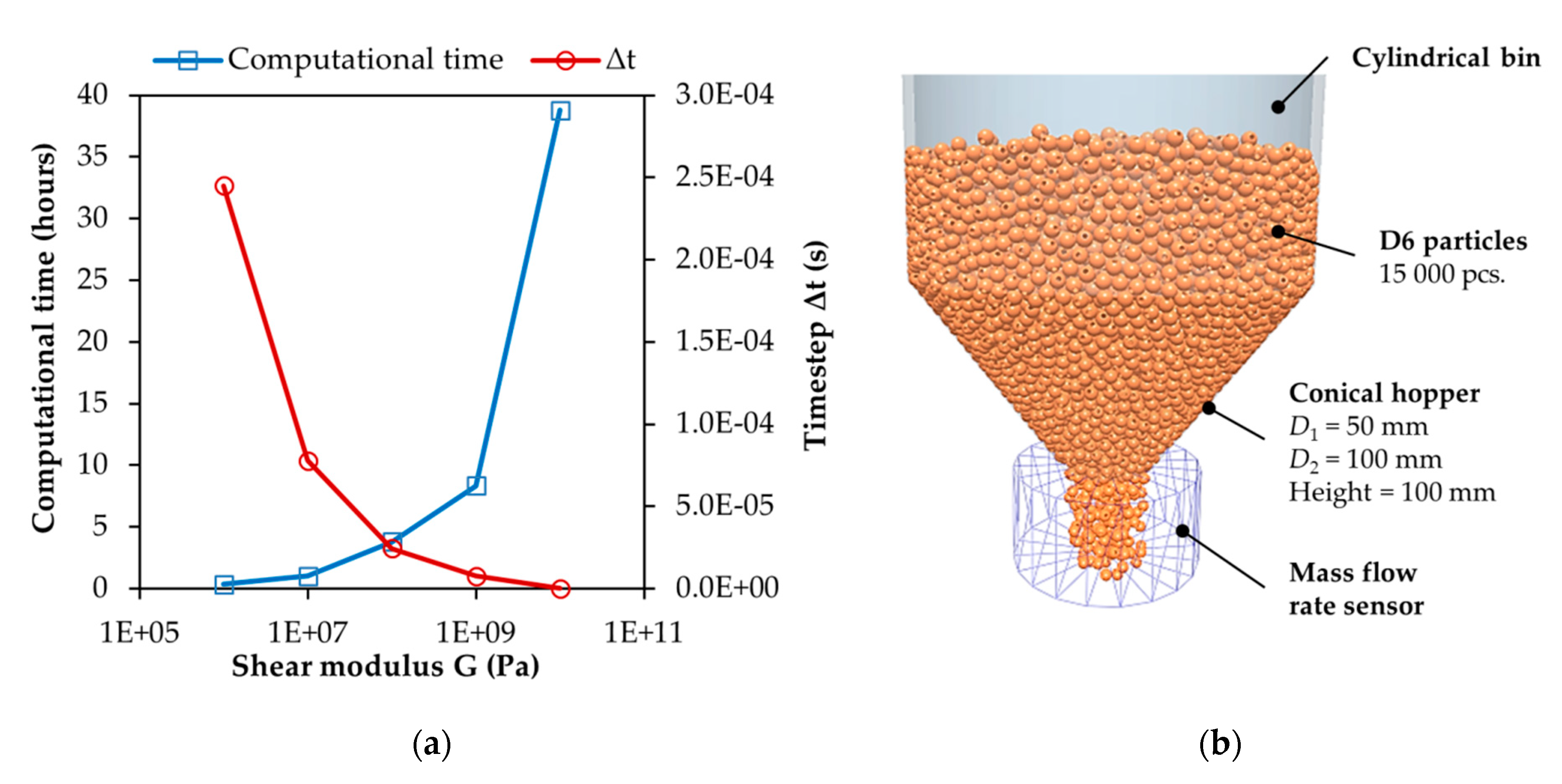
Using Young’s modulus and a shear modulus, respectively, which are lower than their actual values, is common practice in DEM. The main reason is to reduce the computational time. Chen et al. (2017) presented a study on the relationship between Young’s modulus in the range 0.01–0.0001 of the real value of Young’s modulus
E0 and the results of DEM simulations in which mixing of particles inside a rotary drum was investigated. The results showed that Young’s modulus has a significant influence on the behavior of individual particles during collisions, but only a small effect when mixing individual layers. Convective mixing due to random particle collisions is negligible compared to diffusion and friction mechanisms. The study also showed that a value of Young’s modulus reduced by up to 0.0007 times of the real value does not affect the results of the mixing simulation, and the DEM models with these values corresponded to the experiments performed. Additionally, the effect of the drum rotation speed or filling level on the relationship between the Young’s modulus value and the simulated mixing results was not observed in Chen’s study [
46]. In the case of DEM, isotropic materials, material properties, Young’s modulus
E, the shear modulus
G and Poisson’s ratio
υ are related as follows:
One of the key numbers in DEM simulation is the Rayleigh time step. This is the time taken for a shear wave to propagate through a solid particle. It is therefore a theoretical maximum time step for a DEM simulation of a quasi-static particulate collection in which the coordination number (total number of contacts per particle) for each particle remains above 1. It is given by:
where
R is the particle’s radius,
ρ its density,
G the shear modulus and
ν the Poisson’s ratio. This formula assumes that the relative velocity between contacting particles is very small. Other than for quasi-static systems, in practice some fraction of this maximum value is used, and for high coordination numbers (4 and above) a typical time step of 20% Δ
tmax has been shown to be appropriate. For lower coordination numbers, 40% Δ
tmax is more suitable [
47]. Choosing a suitable time step represents a compromise between the computational complexity/time, calculation error and simulation stability. Generally, the time step ranges between 20% and 80% of the critical time step according to Rayleigh. With regard to the duration of the calculation and its accuracy, a value of about 30% Δ
tmax was chosen for all simulations. In the proposed experiment, the influence of the shear modulus value on the process of discharging a hopper was investigated. A virtual cylindrical hopper with a conical discharge hopper of a 50 mm diameter was modelled. The conical hopper of a height of 100 mm was connected to the cylindrical part of a diameter of 100 mm. The experiment was performed for 15,000 pieces of D6 particles generated into the hopper. Subsequently, the flow rate of particles from the discharge hopper and the simulation calculation time were monitored for 5 s.
2.2.4. Static and Dynamic Angle of Repose Test
The process of forming a pile of particles is important in all industries where particulate materials are used. The angle of repose represents one of the basic properties of particulate matter, which affects transport and storage. In contrast to liquids or solids, granular materials create an angle of repose that depends on many of the material’s properties. Parameters such as internal friction between particles, particle size and shape, size distribution, surface, moisture and electrostatic or cohesive forces may influence the value of the natural angle of repose. The angle of repose (static: S-AoR, and dynamic: D-AoR) is also one of the most important parameters for characterizing the flowability of particulate materials. The dynamic angle of repose represents the angle of slope at which a given flowing cohesionless material comes to stable dynamic state. Calibrations based on the angle of repose are generally performed by comparing experiments and simulations on a 1:1 scale. The interaction coefficients can be gradually optimized by systematically changing the input parameters or by simulations managed by the optimization algorithm [
48,
49]. At the end of the calibration, a set of DEM parameters is determined that provides the closest simulation results to those of the experiment. In particular, rolling and static friction are parameters which affect the macroscopic behavior of cohesionless bulk materials.
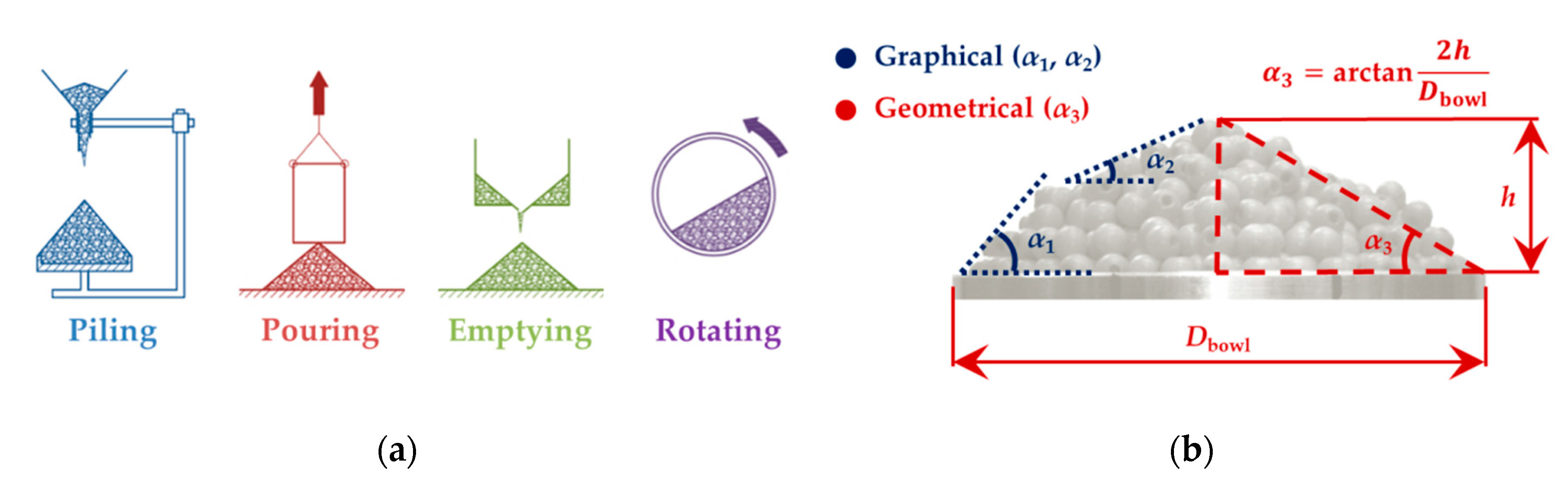
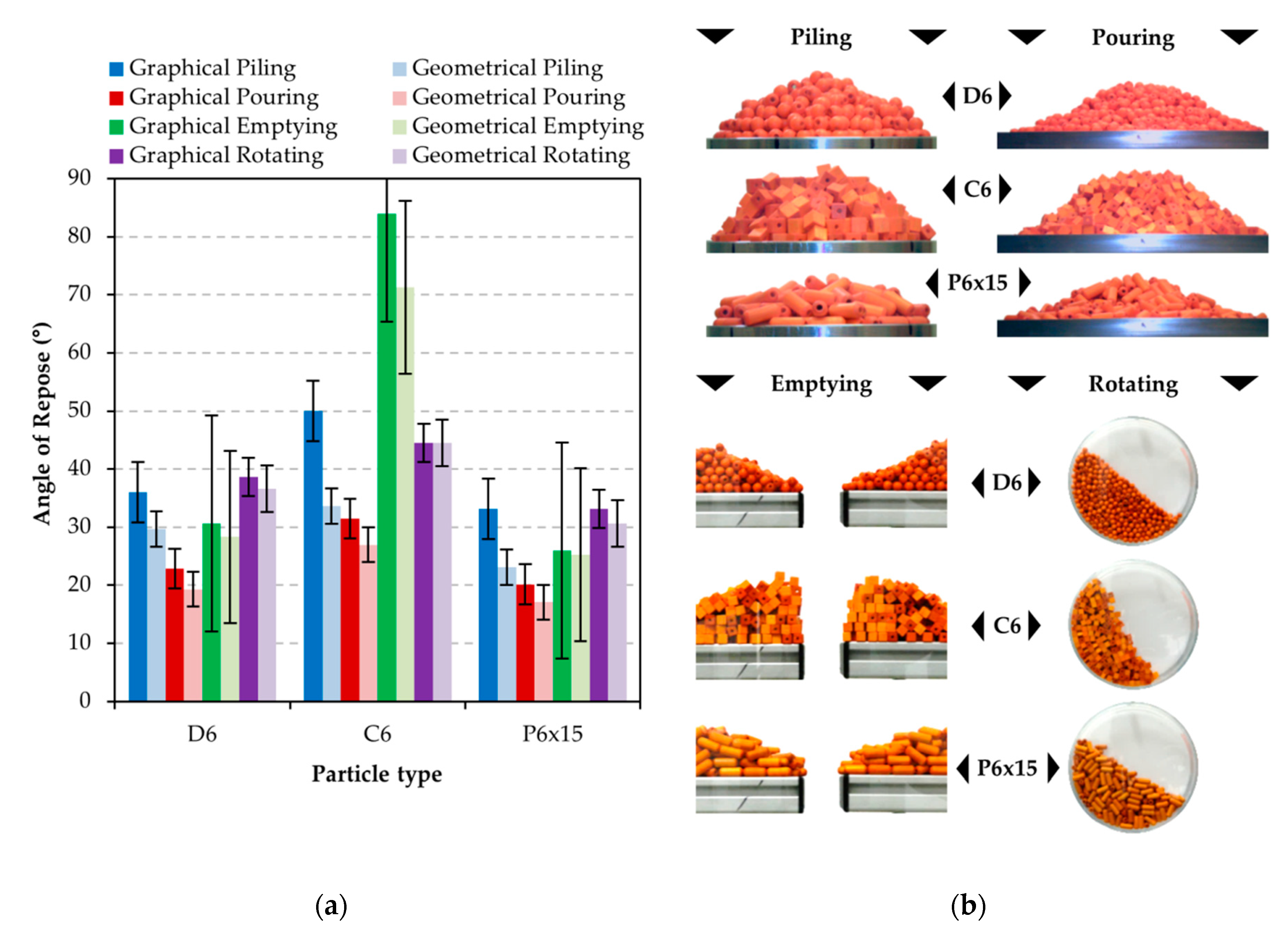
AoR of particulate material is influenced by many factors, such as the static and rolling frictions of particles, particle sizes and shapes, the quantity of material used during measurement and the measurement method (see
Figure 5a). It is necessary to choose a particular measurement method based on the application, since each method provides slightly different AoR values. Particular materials were chosen for the experiments with regard to their grain shape so it would be possible to evaluate the advantages and disadvantages of the individual methods. The “piling” and “rotating” methods (see
Figure 5a) proved to be the most universal and most credible for the determination of the AoRs of particular materials. If simple conditions are observed, these methods are able to provide high quality AoR values for a wide range of bulk materials. Angle of repose has been widely discussed in the literature for many decades and has been researched by many scientists, even outside of the process engineering field. This issue is first to be divided into two parts: (1) a study of how a pile of particulate material is formed; and (2) how the angle of repose is determined. Piling, pouring, emptying and slowly rotating in a drum leads to the determination of the static angle of repose. The dynamic angle of repose may be obtained in a rotary drum at higher rotational speeds [
50]. Each of these methods in a way influences the resulting angle of repose.
Calibration using the static angle of repose is primarily used to optimize interparticle interaction parameters. For the calibration via the dynamic angle of repose, a rotating drum was used with the static friction between particles and a PMMA cylinder. A rotating drum was also used for an experimental study of homogenization. The drum diameter of 140 mm corresponds to a number of about 25 particles across the surface profile. An adequate number of particles is important for determining the dynamic angle of repose. A low number of particles may lead to distorted results. Similarly, if there are too many particles in the drum, the DEM calculation times increase significantly. As some materials travel in different ways in the drum, their trajectories were in all cases compared with the recordings of the experiment. This comparison allowed for the evaluation of whether a particular material could be retained with existing properties or if any of the parameters needed to be adjusted. Each of methods was evaluated in two ways, both graphically and geometrically (see
Figure 6b).
2.2.5. Hopper Discharge Test
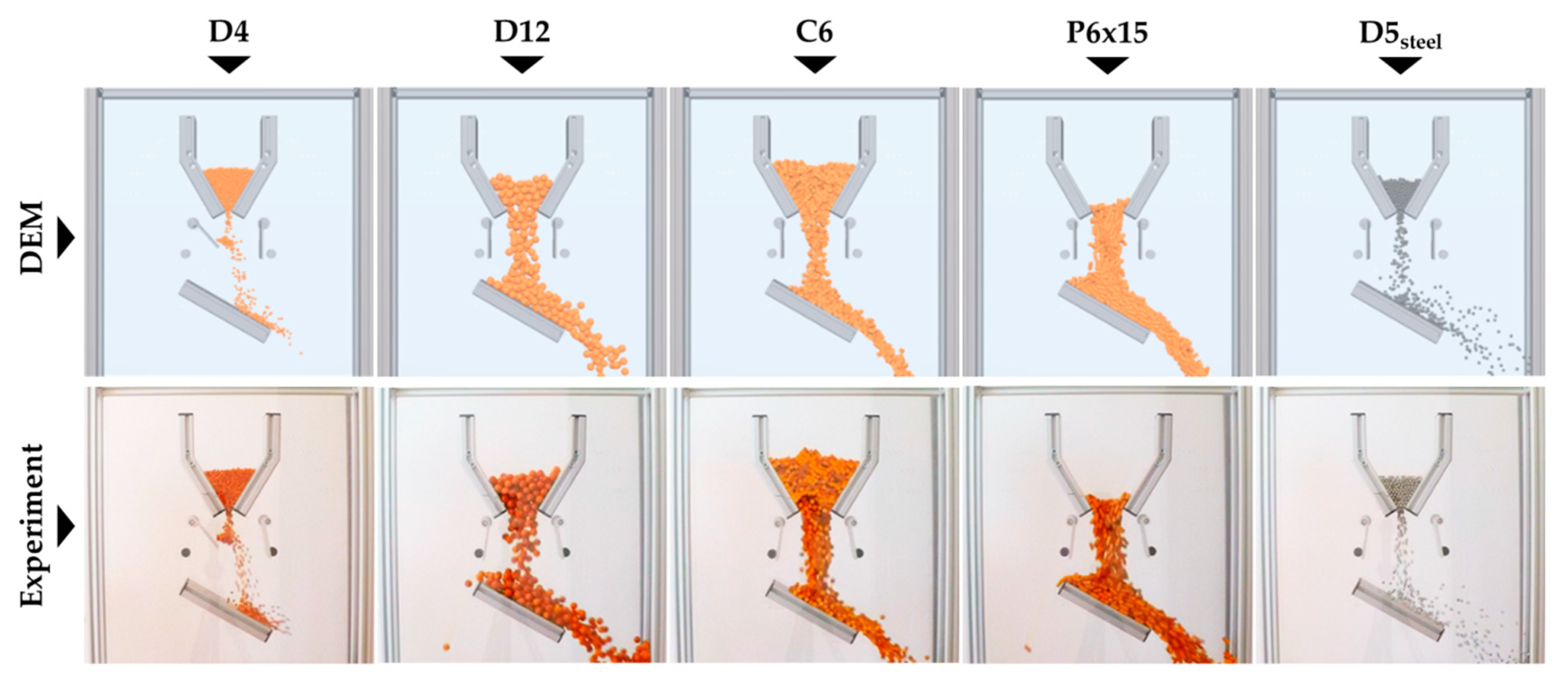
The calibration of the virtual material based on the discharge time of the hopper is important not only in terms of setting adequate flow properties, but also the rates of dispersion and diffusion of particles in the volume, which are crucial for all processes involving mixing. For all calibration experiments, it is important to find a suitable compromise between the number of particles used in the calibration test and the calculation time of single experiment. The more particles in one experiment that are calibrated, the more accurate the results which can be achieved. However, the experiments must be well-performed (simple movements of the apparatus, particles must not cause changes in the position of the apparatus, etc.) and reproducible over time. The hopper model was used to calibrate free-flowing materials. After filling the hopper with a particulate material and opening the discharge orifice, the material starts to flow onto a slide and slides/bounces to the bottom part of the model, where it forms a slope of a natural angle of repose. In addition to subjective observation and comparison of the course of the experiment with the simulation, this method makes it possible to calibrate the material using several different quantifiable aspects. For example, the particle speed at various points, particle tracking, the angle of repose defined after the experiment, the flow through the discharge orifice, the discharge time of the hopper and the mass loss characteristics of the hopper over time. Another option would be to use PIV analysis and compare the shape of vector fields with quantifiable velocity results. The inclination of the walls of the hopper and the slide is variable and the size of the discharge orifice and can be adjusted according to the material being calibrated.
In this study, calibration was based on the discharge time of the hopper, which contained a given number of particles. Furthermore, a visual assessment of the material flow from the hopper and through the slide was performed. First, an experiment was performed for each particle type. The hopper inclination was 60° in all cases while the discharge orifice width was set for each material so that the particles could flow freely. The whole experiment was recorded at a frame rate of 240 fps. Therefore, the exported record could to be slowed down to 12% of the real time of the experiment. This made it possible to determine the time period from opening the discharge orifice to the point when the last particle left the hopper with an accuracy of 0.004 s. DEM simulations were saved in steps of 0.01 s. Interaction parameters were then optimized and validated for the static and dynamic angles of repose.