1. Introduction
Conceptualizing and understanding the shock/boundary-layer interaction (SBLI) phenomena has been a challenging task for the scientific community since the dawn of supersonic flights, due to their effects on the performance of the vehicle and its parts. The diverse consequences of SBLIs are not restricted to excessive viscous dissipation, boundary layer degradation, and frequently to flow separation. The most apparent way for the SBLIs to occur is for an externally-produced shockwave to intrude on a boundary layer, formed over a surface. However, the interactions of shockwaves with the boundary layer can also be frequently observed in the supersonic/hypersonic flow past a compression corner created by changing the slope of the surface adjacent to the flow. For instance, at the leading edge of a fin or in front of an isolated object attached to a surface, e.g., a vertical fin. This type of compression corner generally creates a compression wave or a shockwave which has its root inside the boundary layer. Essentially, it has the same effect to an interaction where a shock originates from an external object and impinges upon the boundary layer. The property of the shockwave to increase the static pressure in the flow past it is utilized in supersonic and hypersonic intakes. In other words, the incoming high-speed air is compressed to a suitable combustor-friendly subsonic speed. However, even in these intentional-shock-utilization scenarios, the higher shock strength and their uncontrolled interactions with the viscous boundary layer might produce large drag. Subsequently, this incurs a higher cost to the propulsive efficiency. One of the vital reasons why the only supersonic passenger aircraft in history, the Concorde, was retired is due to its higher cost to propulsive efficiency.
In addition to the above briefed counter-productive characteristics, the SBLIs may even disturb the flow at the entrance into the compressor [
1,
2]. These interactions may cause noticeable changes in the shock system which may lead to the smearing or the splitting of the shock [
3,
4]. Additionally, the most important result of SBLI is the expansion of the pressure gradient caused because of shockwaves, so the impact of a sudden pressure change is experienced well upstream. When a sufficiently strong shock impinges on a surface to separate the boundary layer, there is a significant outcome on the advancement of the boundary layer and the adjoining inviscid flow field. Evidently, the impact of an SBLI taking place inside a flow is various and their outcomes are almost enduringly adverse in some respect. These undesired phenomena are the unsteady flow field, separation of flow, total pressure loss, and severe localized heating, which eventually results in engine failure [
5,
6,
7]. Hence, for a smooth and efficient operation of a high-speed intake, the necessary criteriona is to control SBLIs. Here, “control” signifies the modification of flow behavior, either previously or amid the interaction phenomena [
8]. Essentially, a control technique either modifies the structure of the shockwave that occurs naturally or suppresses the shock-induced separation. Accordingly, the SBLI control techniques are broadly classified into two types: the shock controls and the boundary layer controls. The SBLI control techniques can also be classified into active and passive controls. The active control methods require external energy input and a sensor to measure and respond to real-time flow characteristics in a feedback loop. Some examples of the established active control techniques are: fluid injection into the boundary layer, boundary layer bleed, and plasma actuators, etc. The importance of active control techniques such as suction, bleed jet actuators, and their role in controlling the SBLIs in supersonic and hypersonic flows has explored by several researchers [
9,
10]. Souverein and Debiève (2010) experimentally investigated the effect of upstream injection by means of continuous air-jet vortex generators (AJVGs) in shock boundary layer interactions. From the stereoscopic particle image velocimetry (SPIV) and hot wire anemometry (HWA) investigations to study the unsteady characteristics of the reflected shock, it is shown that the AJVGs cause a reduction of the separation bubble length and height [
11]. Furthermore, Sriram and Jagadeesh (2014) recently studied the ability of surface blowing and suction in controlling SBLIs inside the shock tunnel. In both cases, the separation length was found to decrease significantly [
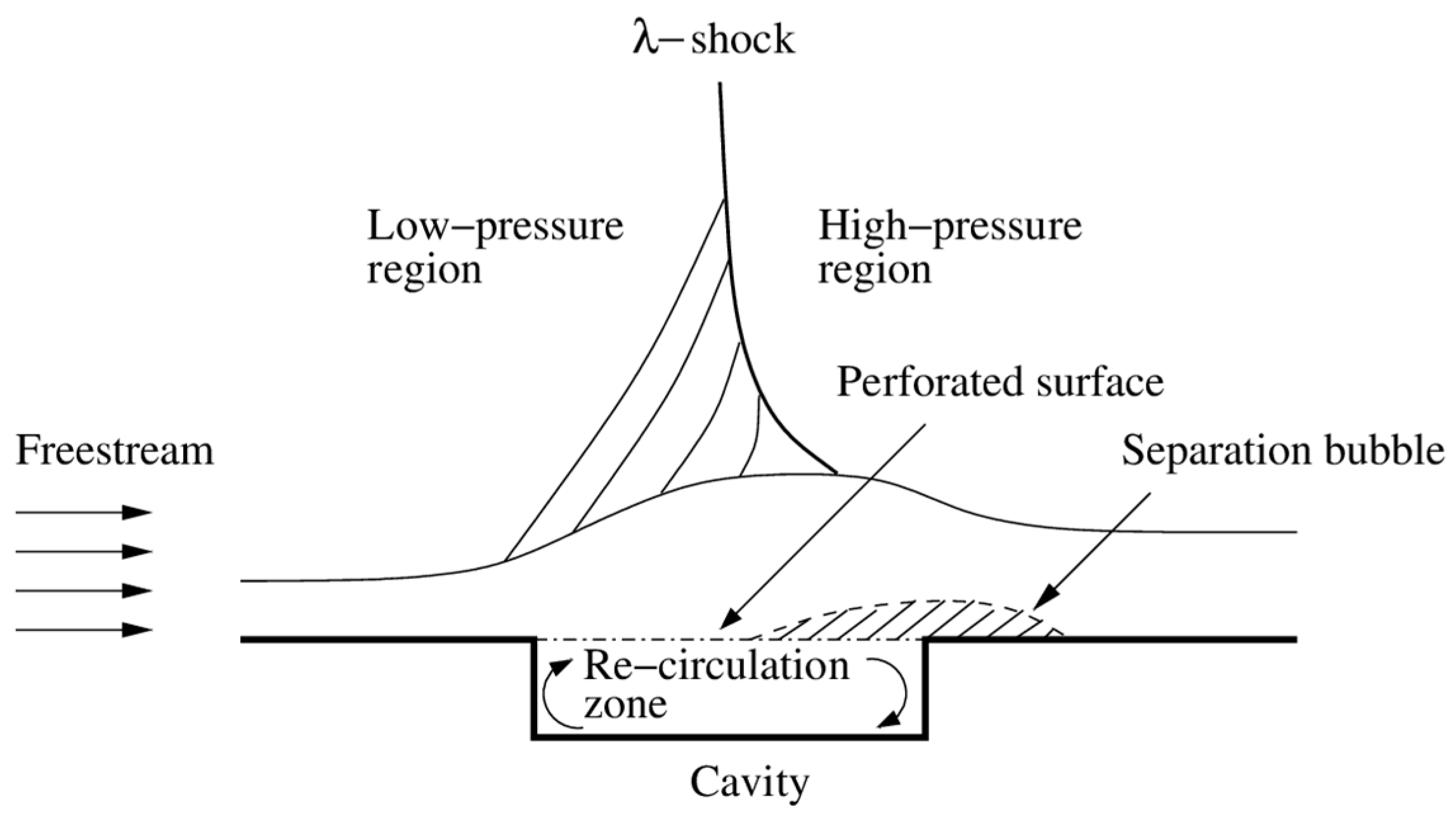
12]. It is important to note that these methods come with extravagant costs and, also, due to the requirement of additional components, the overall weight of the component increases. However, influencing the shock structure using carefully-configured passive shock controls has gained prominence in recent times. Indeed, the principal aim of a shock control is to reduce the stagnation pressure loss due to interactions by increasing the size of the smeared region and stretching the flow domain. Instead of attempting to generate a large smeared shock foot with continuous compression waves it is generally easier to aim for a large λ-shock which replaces the shock foot with an oblique shock followed by a near-normal shock, similar to the image illustrated in
Figure 1. It is proved that the flow downstream of control generated λ-shock exhibits a significant stagnation pressure recovery. Shock control through wall-ventilation promises to be one of the most fail-proof techniques for practical application in high flights. Here, a cavity covered with a porous surface is placed underneath the shock location [
13]. A natural flow circulation occurring inside the cavity from the downstream high-pressure region to the upstream low-pressure region produces a suction effect in the upper boundary layer. Thus, the strong interacting shock is split into a weak λ-shock (
Figure 1). In subsequent studies, the effectiveness of the cavity covered with perforated surface in controlling the interactions were tested in supersonic and hypersonic flow regimes [
14,
15]. The dependency of the control effectiveness on the dimensions of the cavity (length, depth) and porosity over a flat plate at Mach 1.3 has been studied by Roy et al. (2017) [
16]. It is observed that, at this Mach number, the cavity length had a strong influence on the drag reduction compared to the other tested parameters. This result was in accordance with Doerffer and Bohning (2003), who suggested that a shallow cavity of aspect ratio greater than 2.0, covered with a porous wall, is quite efficient in controlling the SBLI over a flat plate. This study was further extended by to test the active as well as hybrid control techniques [
17]. Here, when the suction was applied by external means along the cavity, it becomes a hybrid control, whereas, if the suction was applied on the cavity itself then the configuration was considered to be active-controlled. Various passive devices including conventional porous plate, micro-porous plate, streamwise slots, and flaps were studied in a Mach 1.42 flow [
18]. However, in all the slot and flap controlled cases, the flow fields downstream of the SBLIs were found to have high levels of turbulence compared to the predominantly two-dimensional flow over the conventional porous surfaces. Szulc et al. (2018) also found that in the presence of surface ventilation, the normal shock transforms into a new structure. This type of shock structure is based on the relative length of the cavity which might either lead to a large lambda-foot structure (classical cavity), or to a sequence of oblique waves (extended cavity with larger aspect ratios), or to a gradual compression [
19]. It was also proposed by Szulc et al. (2016), that the transformation of this normal shock forced by an extended cavity of large aspect ratio leads to noise reduction for high-speed impulsive helicopter rotors [
20]. Compared to the other SBLI shock control techniques, the wall-ventilation through a shallow cavity has shown a considerable increase in losses due to boundary layer thickening. However, the shock strength was significantly reduced due to the formation of a recirculation zone inside the cavity. Indeed, the passive cavity placed beneath the interaction region establishes a re-circulation zone by injecting the flow upstream of the shock through the cavity. As a consequence, the pressure difference across the shock becomes more uniform and the flow experiences nearly an isentropic compression, leading to a greater pressure recovery downstream of the shock [
21].
From the above discussion, it is clear that an extensive amount of research on wall ventilation has been carried out using simple idealized configurations, such as a 2D and 3D flat plate or aircraft wing. The porous cavity is a well-established drag reduction technique for an airfoil, however, in the present study it is deployed in the supersonic intake to smear and manipulate the shock structure for a minimal total pressure loss. In the literature, the researchers have investigated the ‘boundary-layer-bleed’ for a long time to suppress the separation bubble and minimize the total pressure loss. However, this technique causes a decrease in the effective mass flow rate. Thus, this study explores the cavity covered with porous surface which creates a natural recirculation by extracting the high-pressure fluid from the downstream and injecting it into the upstream low-pressure region. This phenomena extends the interaction zone, thereby transforming a single strong shock into several weak shocks. In addition, the flow structures and characteristics observed in simple geometries, such as the flat plate and aircraft wings cannot be easily extended to complex vehicle components, e.g., the intake.
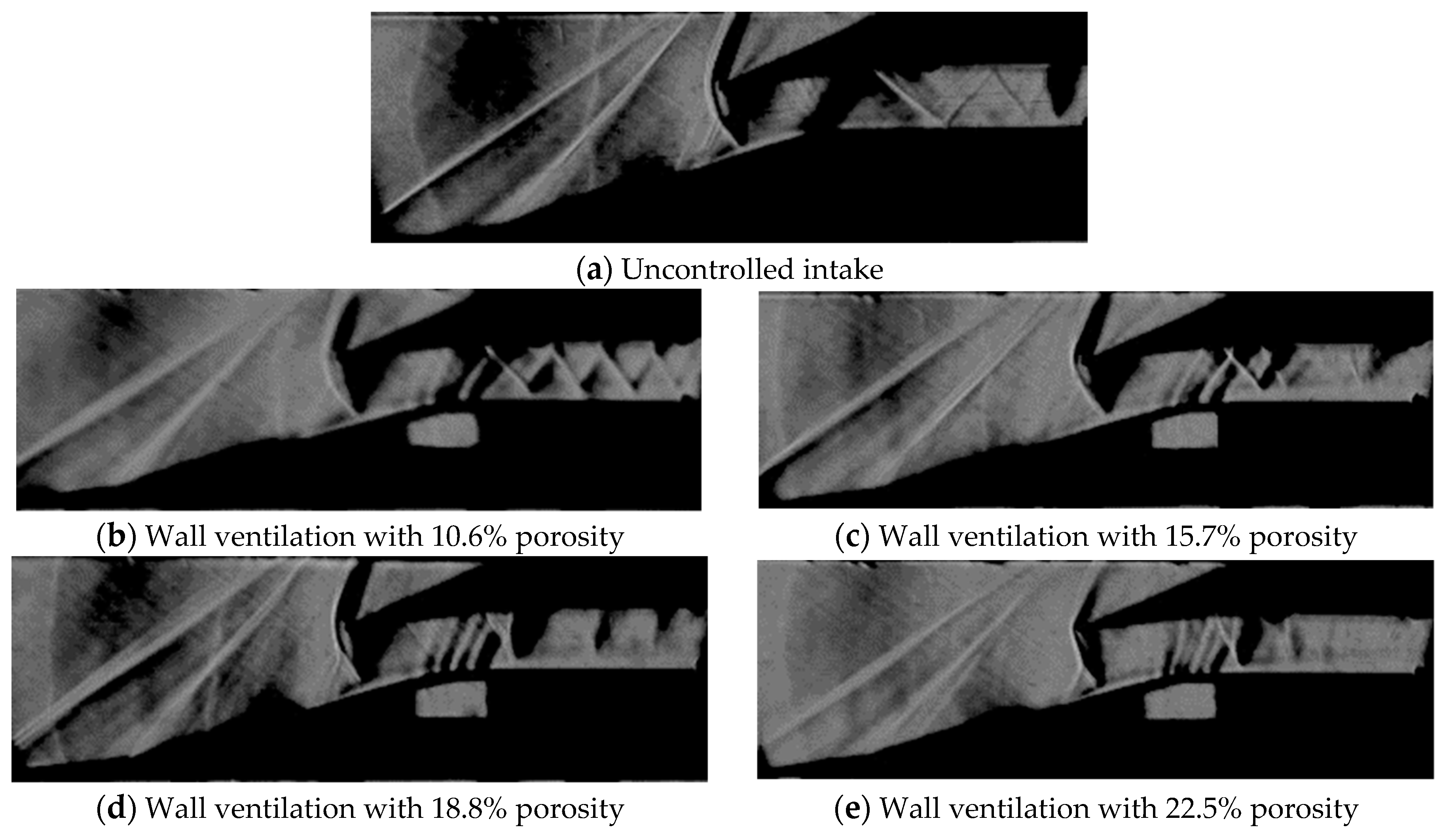
In most of the previous studies, a supersonic intake is modeled as a flat surface or a single-compression ramp. A single-ramp intake, however, experiences a large amount of drag due to an oblique shock of considerable strength, produced at the concave corner of the ramp. Thus, one method of drag reduction could be to generate another oblique shock downstream of the first one, using a double-ramp configuration. The compressed flow exiting the double-ramp would be made to pass through the intake-isolator, which, in turn, is designed to generate a series of weak shocks and expansion waves. This further compresses the flow with minimal pressure losses and, hence, contributing to less wave drag. Thus, cavity ventilation with a truncated angle was deployed in the present study to manipulate the shockwave/boundary layer interactions in a double-ramp mixed-compression supersonic intake, where the shock, generated at the cowl-lip, is located near the convex corner of the ramp. In order to provide significant recirculation, the porous cavity should be deployed right at the shock impinging point. In a series of experiments, it was observed that, with a Mach 2.2 ‘intake-start’ condition, the interaction of shock wave and the boundary layer takes place near the convex corner of the ramp. Due to the typical nature of the intake geometry, a truncated cavity is being used at the cowl shock impingement location.
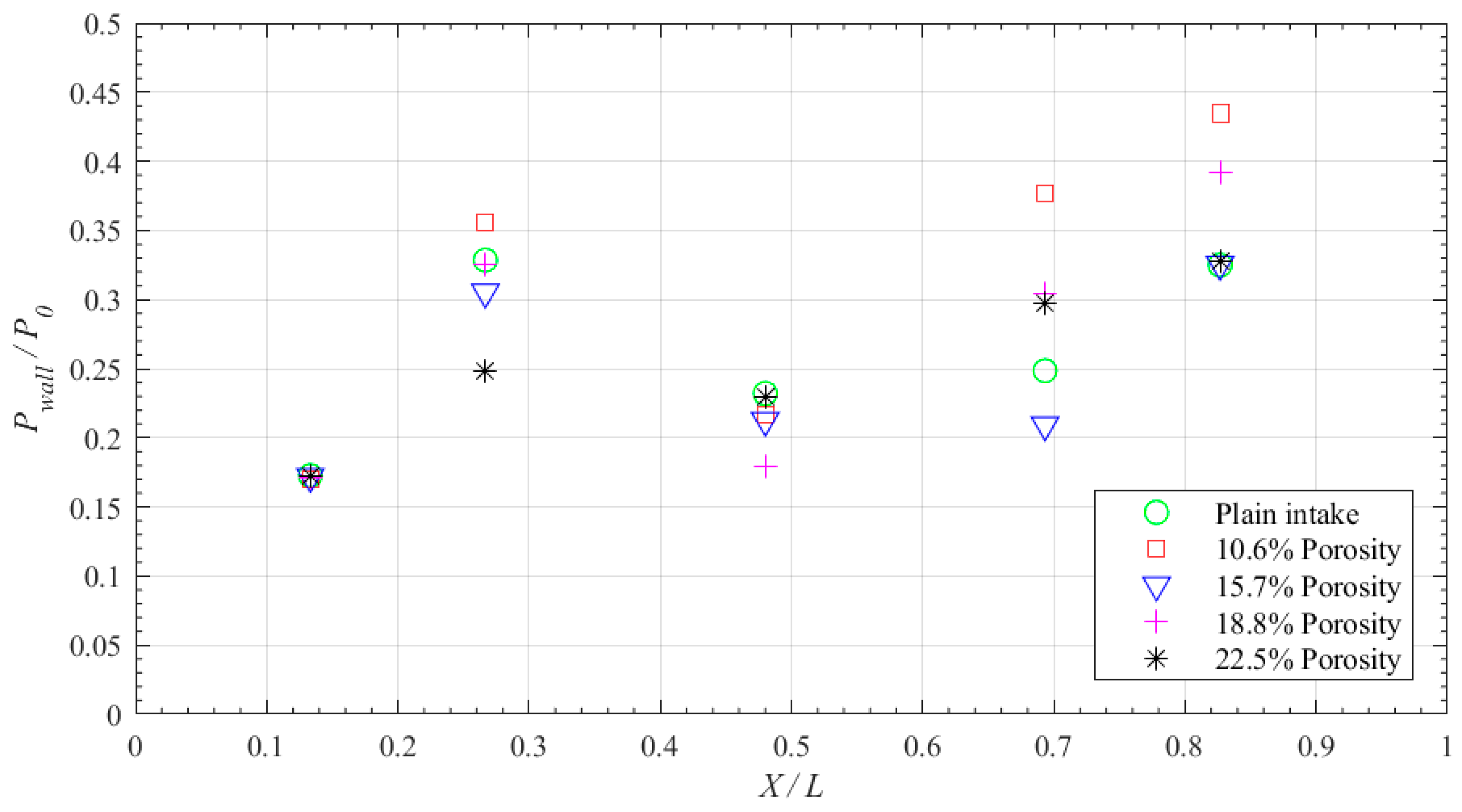
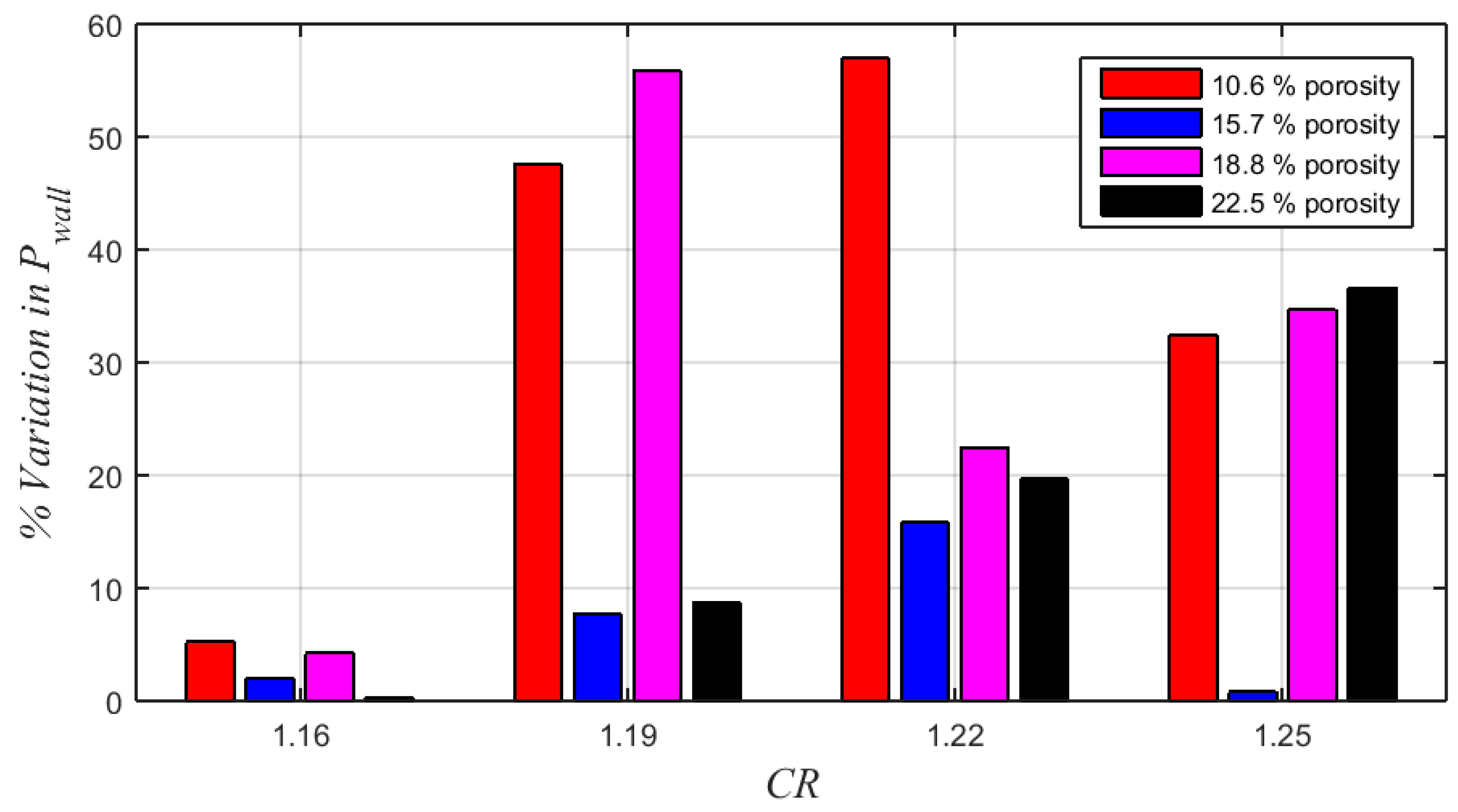
Interestingly, the cavity covered with a porous upper surface demonstrates two entirely distinct flow characteristics. It inflicts a significant reduction in the shock strength by causing the formation of a lambda shock. However, this advantage is not stand alone and comes with a penalty of boundary layer degradation. Our objective is to optimize the porosity level at different contraction ratios to maximize the benefit in controlling the SBLIs.
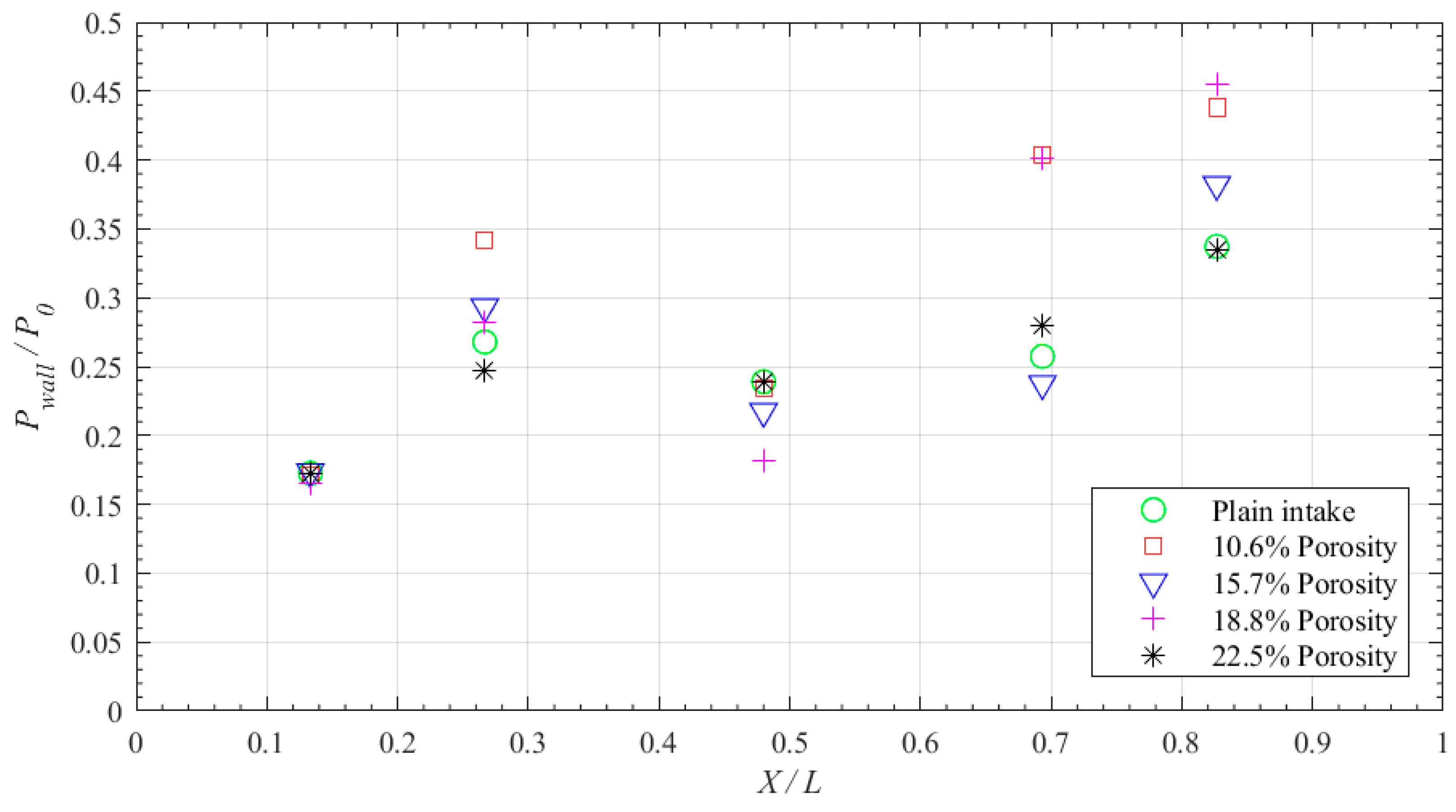
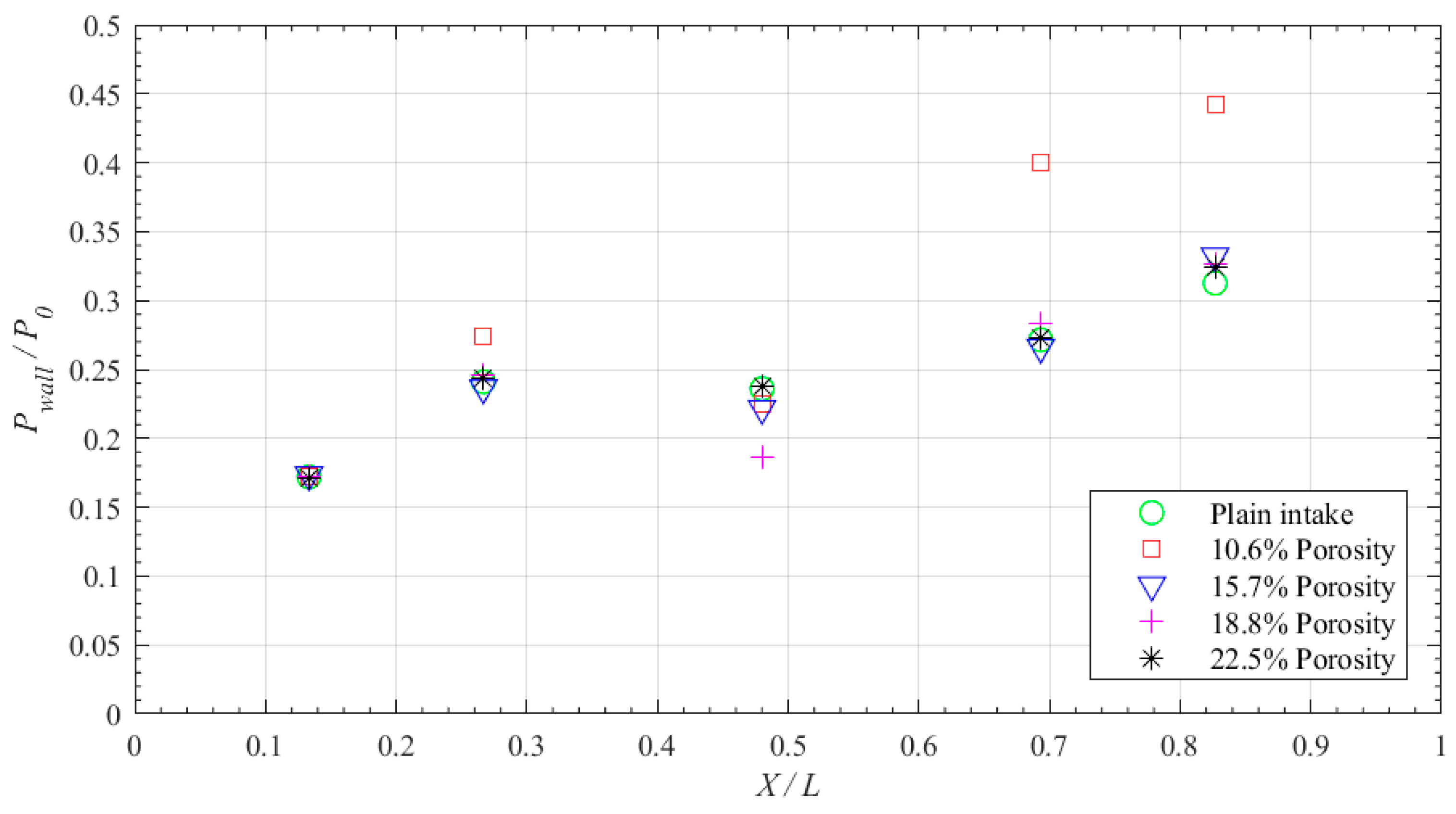
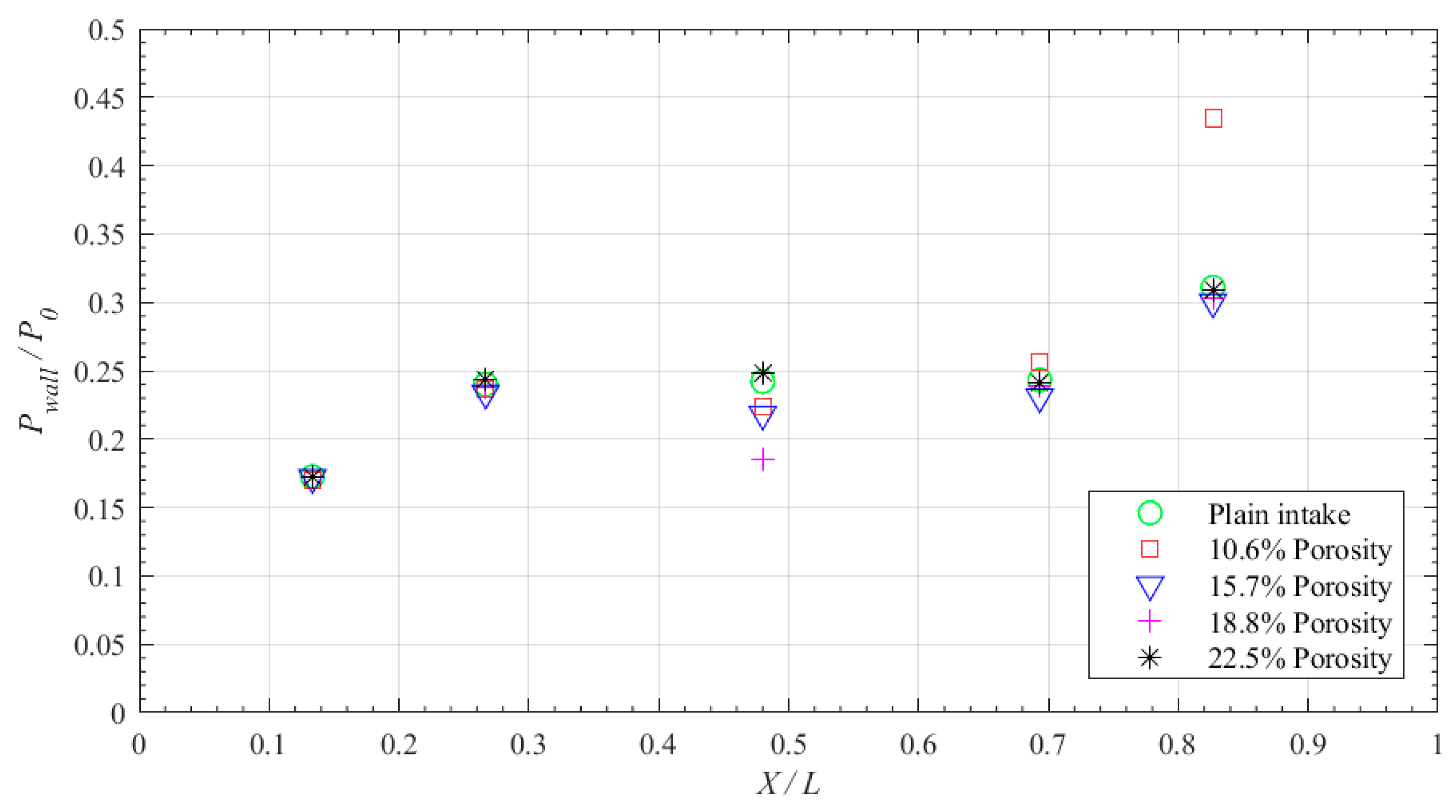
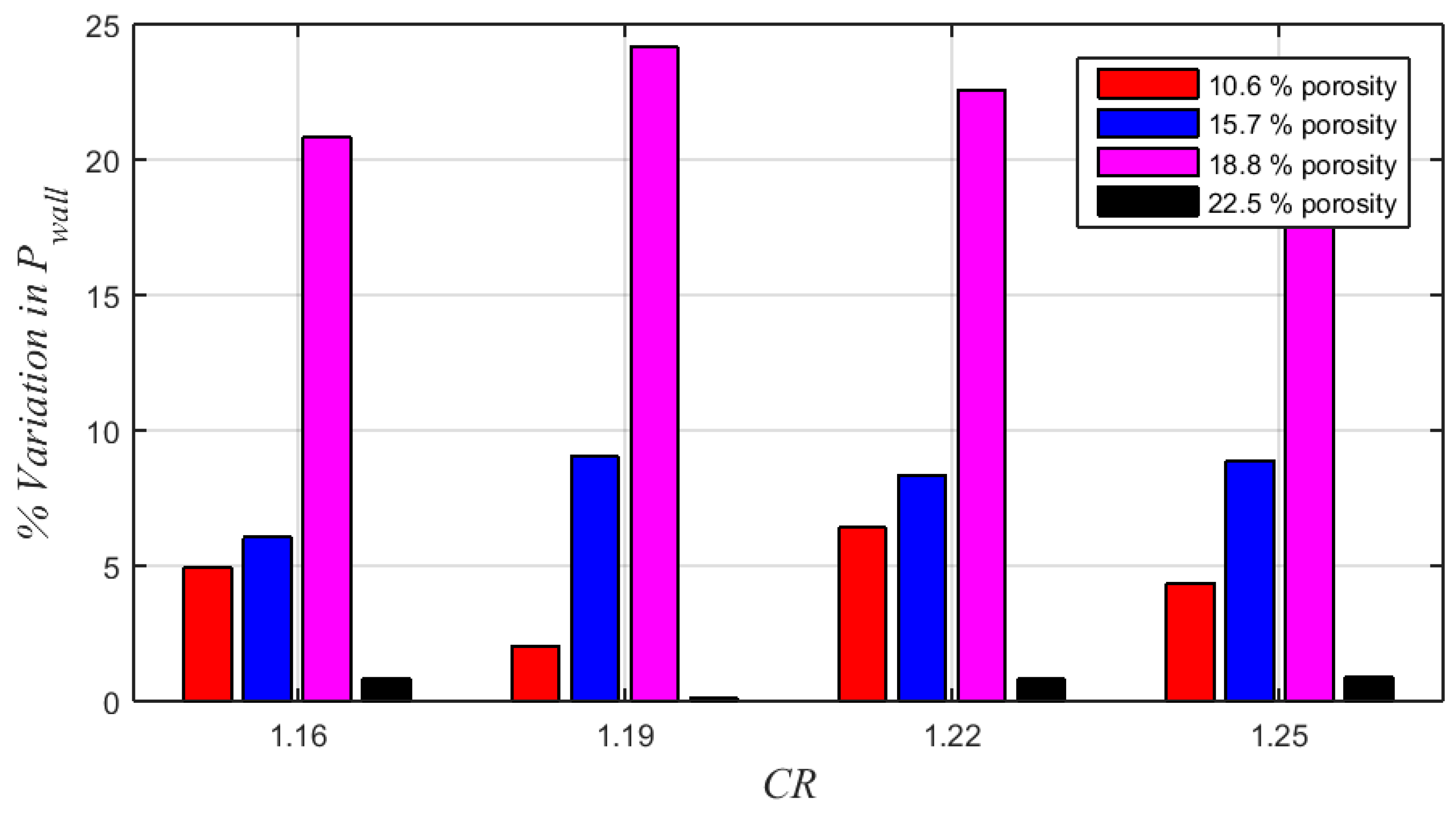
Keeping these observations in mind, an attempt is made in the present study to evaluate the efficacy of wall ventilation deployed at the intake-core at the region of shock impingement. The wall ventilation, on the whole, can be explained as a combination of two parts: a shallow cavity with a truncated-rectangular cross-section and a porous plate enveloping the cavity. This wall ventilation technique is deployed in our test model, which is a Mach 2.2 double-ramp mixed-compression intake. The porosity the ventilated wall is varied (by changing the diameter and pitch of the pores) as 10.6%, 15.7%, 18.8%, and 22.5%. A major focus of this work is dedicated to analyzing the effect of porosity in the control of SBLIs at various intake contraction ratios. The analysis is carried out based on two types of flow measurements. One is by measuring the static pressures for both uncontrolled and controlled intakes, using pressure ports mounted along the length of the intake-core. Another is by capturing the shock and expansion waves prevailing in the intakes using a Schlieren density field.
2. Experimental Methodology
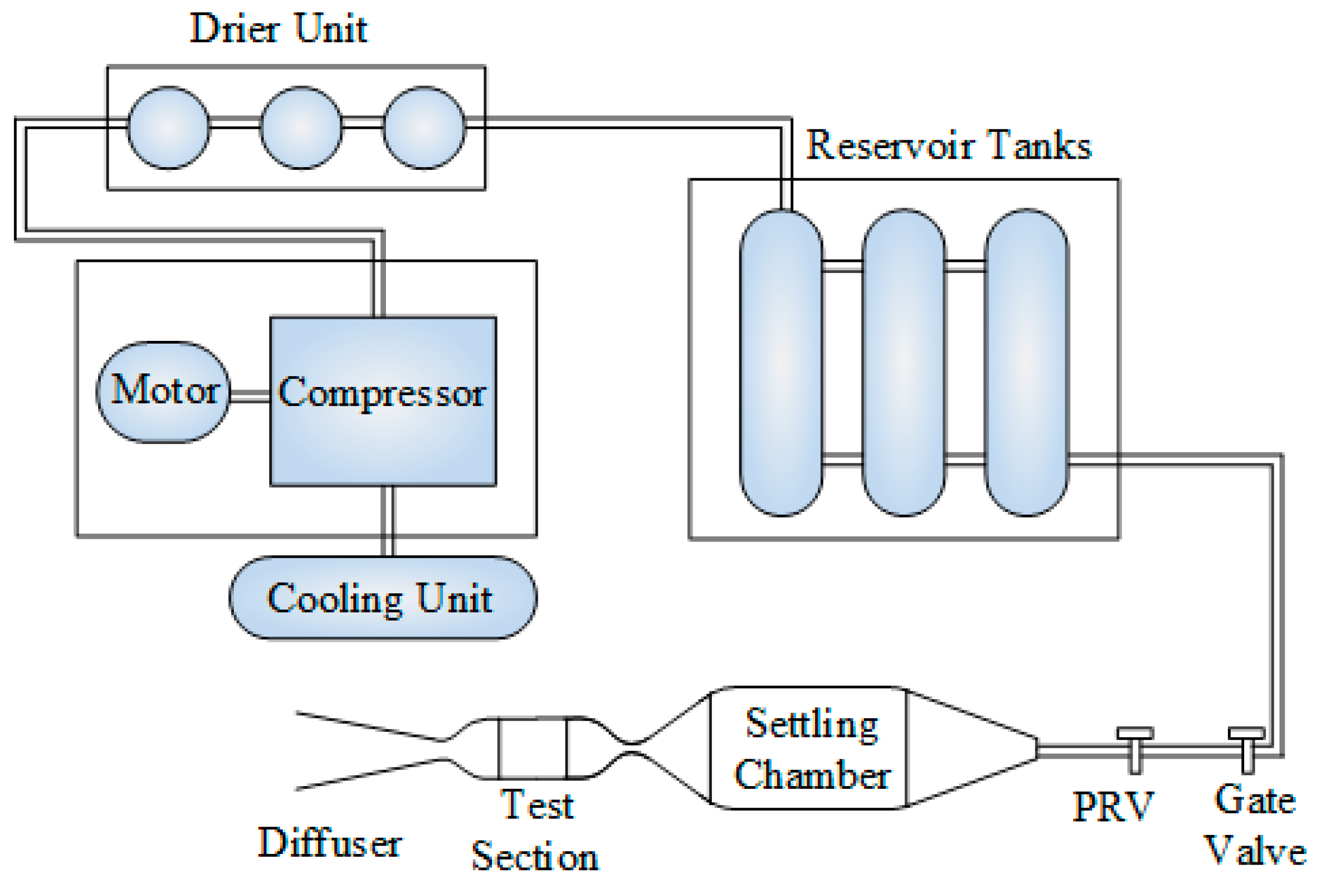
In the present investigation, the experiments were carried out in the supersonic blow-down wind tunnel facility situated at the Indian Institute of Technology Madras, India. The experimental facility is sketched schematically with important notations in
Figure 2. In the experimental facility, the pressurized air is used as the operating fluid. The compressed air is filtered, dried, and heated to remove the moisture and impurities before entering the tunnel section.
During each test run, the stagnation pressure (
) and the stagnation temperature (
) in the settling chamber were held constant around at 340 kPa and 27 °C, respectively. The fluctuation in stagnation temperature throughout the current study was about ±0.5 °C. The measurement of static pressure (
) at the intake model was conducted at different ports, located along the intake-core wall using piezo-resistive pressure transducers (GE DRUCK PMP-4110, New York City, New York, USA). The accuracy in the pressure measurement was estimated as ±0.1%. LabView was used to collect the output from the pressure sensors. The Schlieren setup was arranged with a monochromatic halogen light source with a wavelength of 580 nm. Three concave mirrors of focal length 1.4 m, 2 m, and 1.4 m were used along with a bi-convex lens of focal length 0.48 m. The parallel rays passing through the test section were focused at the knife-edge location by means of a concave mirror. Here, the amount of light blocked by the knife-edge essentially governs the sensitivity of the Schlieren images. The images were captured using an IDT NX4-S3 high frame rate camera equipped with a 100 mm f/2 lens, and having a sampling rate of 300 fps. The camera is focused to capture the flow development in the mid-plane of the model with a focal plane thickness of around 1 mm. From the measured test-section static pressure (
) (without the presence of model or the mounting mechanisms and, hence, with an unobstructed flow field in the test section) and the settling chamber stagnation pressure (
), the calibrated test section Mach number (
) using the isentropic relation (Equation (1)) was found to be 2.2. Further, the Reynolds number of the flow was estimated to be 4.6 × 10
7 per unit length, which is much higher than the troublesome Reynolds number of 500 [
22], thus, in this study, the viscous effects on the pressure measurements were almost insignificant.
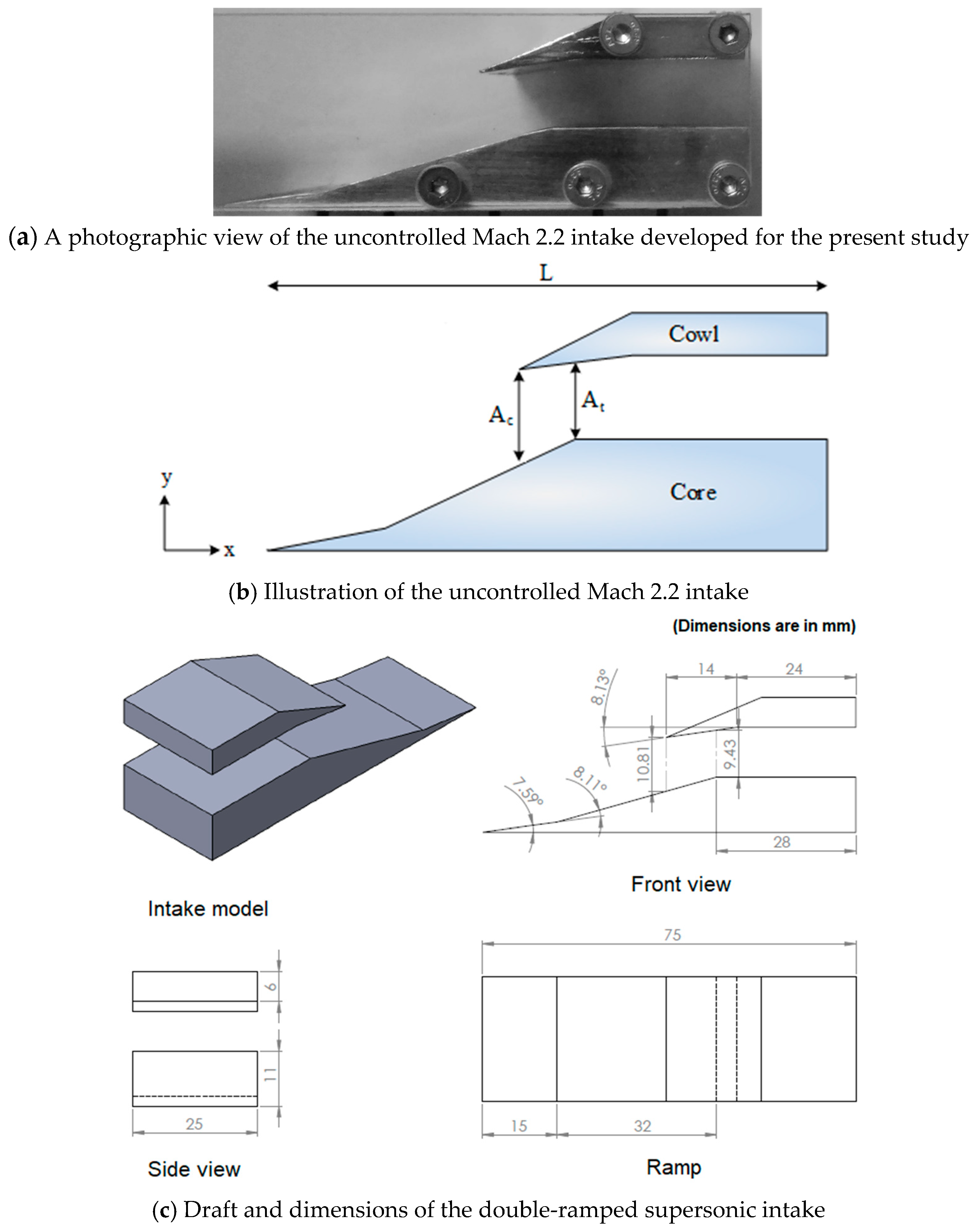
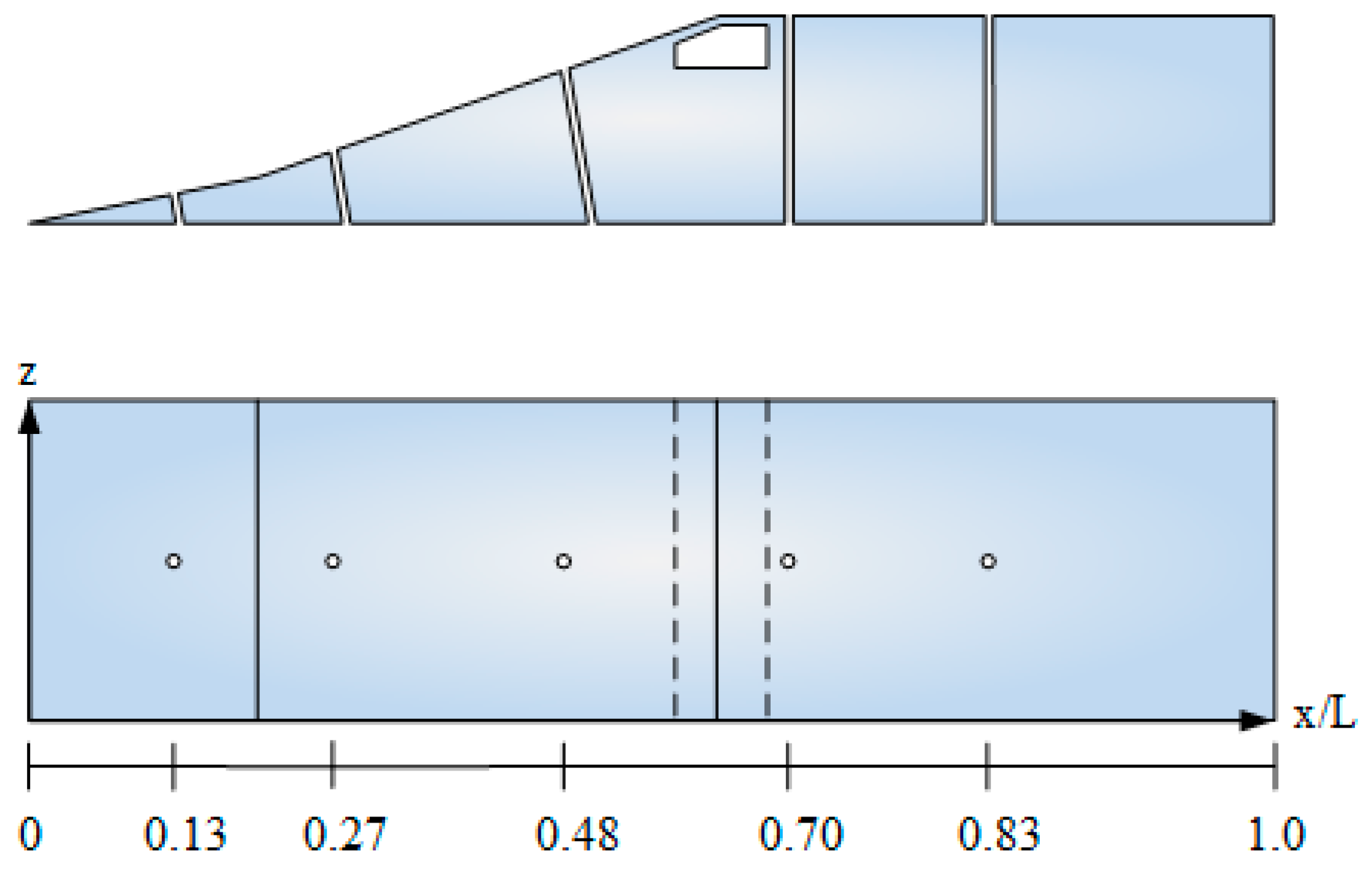
Generic two-dimensional mixed-compression intake models at Mach 2.2 (at five different contraction ratios) with dual-compression ramps and a constant area isolator, has been designed and experimentally investigated. The contraction ratio (
) of the intake, defined as the ratio of the flow capture area (A
c) to the throat area (A
t), has been varied as 1.16, 1.19, 1.22, and 1.25. The photographic and schematic views of the intake model are shown in
Figure 3a,b, respectively. In addition, the typical specifications of the intake model are shown in
Figure 3c. The Mach 2.2 intake is designed such that the incoming air is compressed by means of both internal and external shocks with the minimum total pressure loss. According to Oswatitsch (1947), Equation (2) shows the maximum pressure recovery condition in two-dimensions for a system of (n − 1) oblique shocks [
23]. Further, Ran and Mavris (2005) [
24] have shown that, for a freestream Mach number
and the specific heat ratio of γ = 1.4, the Mach numbers at each downstream location can be found using the oblique shock relations, given by Equations (3) and (4).
The contraction ratio
, has a crucial aspect in regulating the flow behavior in the intake-isolator and the limit is set to this ratio (
) by the Kantrowitz condition (Equation (5)) [
25]. It depicts that the intake unstart phenomenon might be observed if the value of the contraction ratio for an intake is higher than
.
At the freestream condition of
, the limiting contraction ratio from Equation (5) is
(i.e.,
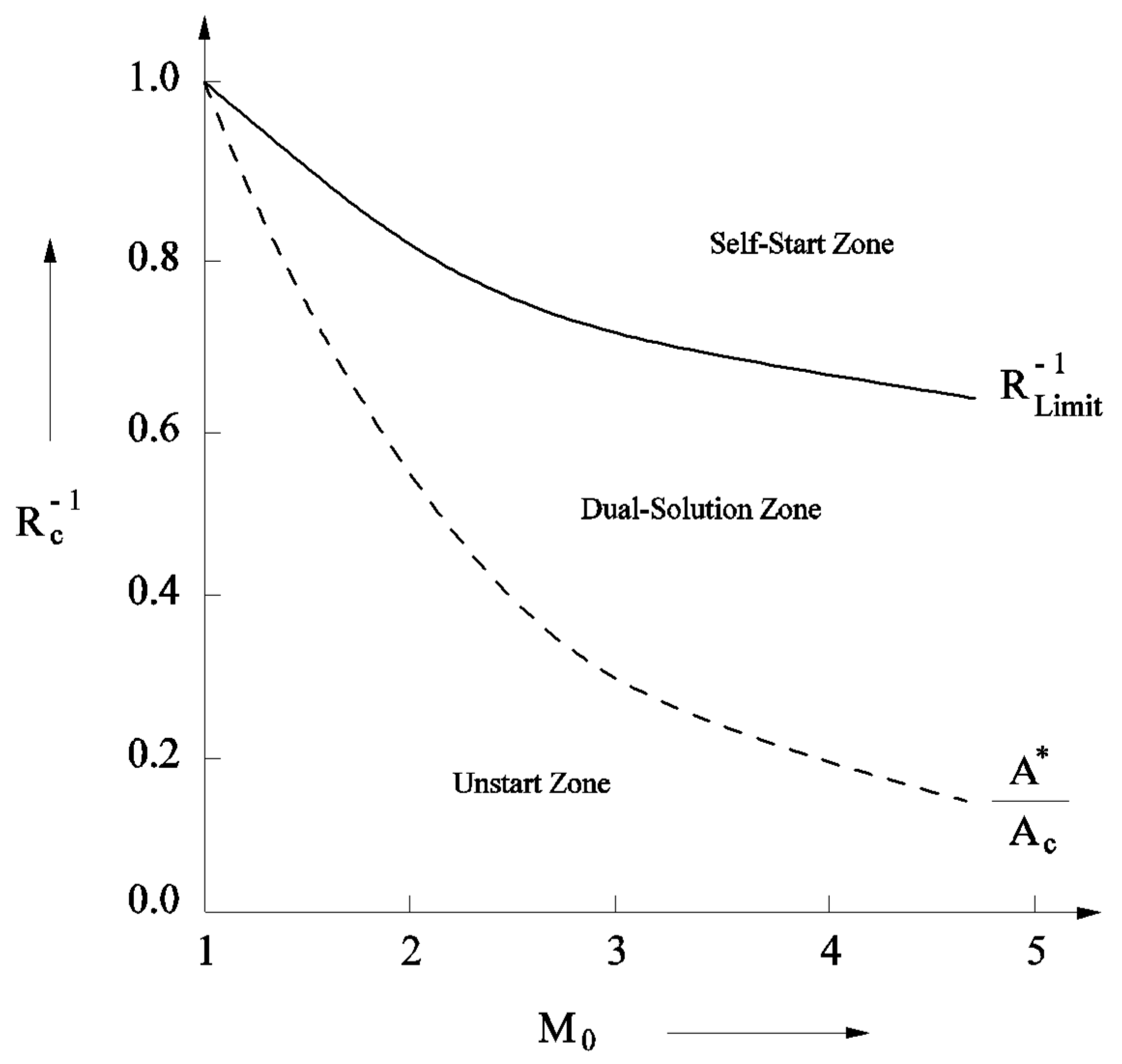
). Further, the variation of
with respect to
is plotted in
Figure 3, which shows the ideal intake-start and unstart zones for a specific
. The R
Limit variation is estimated by using the quasi-one-dimensional theory proposed by Kantrowitz, and is depicted as a thick line. Further, the variation of the sonic area ratio
, which corresponds to the minimum contraction ratio to start the intake, is obtained through isentropic relations (Equation (6)). The area between these two curves represents the dual solution zone where the intake might exhibit either start or unstart characteristics.
Since the objective of the present study is to evaluate the intake models at both intake-start and unstart conditions, the contraction ratios of
= 1.16, 1.19, 1.22, and 1.25 are chosen from the self-start zone and the dual-solution zone of
Figure 4. Here, the flow capture area (
) and the throat area (
) were varied by altering the throat height, between the cowl and intake-core (
Figure 3b), which, in turn, changes the contraction ratio of the intake. In
Table 1, for the mixed compression intake at Mach 2.2, the intake contraction ratios and their corresponding inverse values are shown. Note that the geometric flow blockage at the test-section, offered by the intake models at these contraction ratios were found to be in the range of 7.51% to 7.99%. The flow blockage was estimated by using Equation (7), which is essentially a ratio of the projected area of intake (
) to the cross-sectional area of the test section (
).
In the literature, it is a well-known fact that the blockage generated by the model should be less than 10% for a smooth operation in supersonic flow. Therefore, in the present study, along with the side plate, the maximum blockage generated by the model (made of polycarbonates sheets) was maintained at approximately 8%. Additionally, the intake models were mounted in the test section with a gap of about 38.5 mm from the top wall, 37.5 mm from the bottom wall and 31.5 mm from both the side walls of the test section.
Figure 3 shows that the intake with contraction ratio,
falls in the self-start region since its corresponding inverse value
= 0.862 is higher than the value of
. However, the intake with contraction ratios
= 1.19, 1.22, and 1.25 fall in the dual-solution zone since the corresponding inverse values associated with them (i.e.,
= 0.84, 0.819 and 0.8) are lower than
but higher than
= 0.57 for
= 2.2.
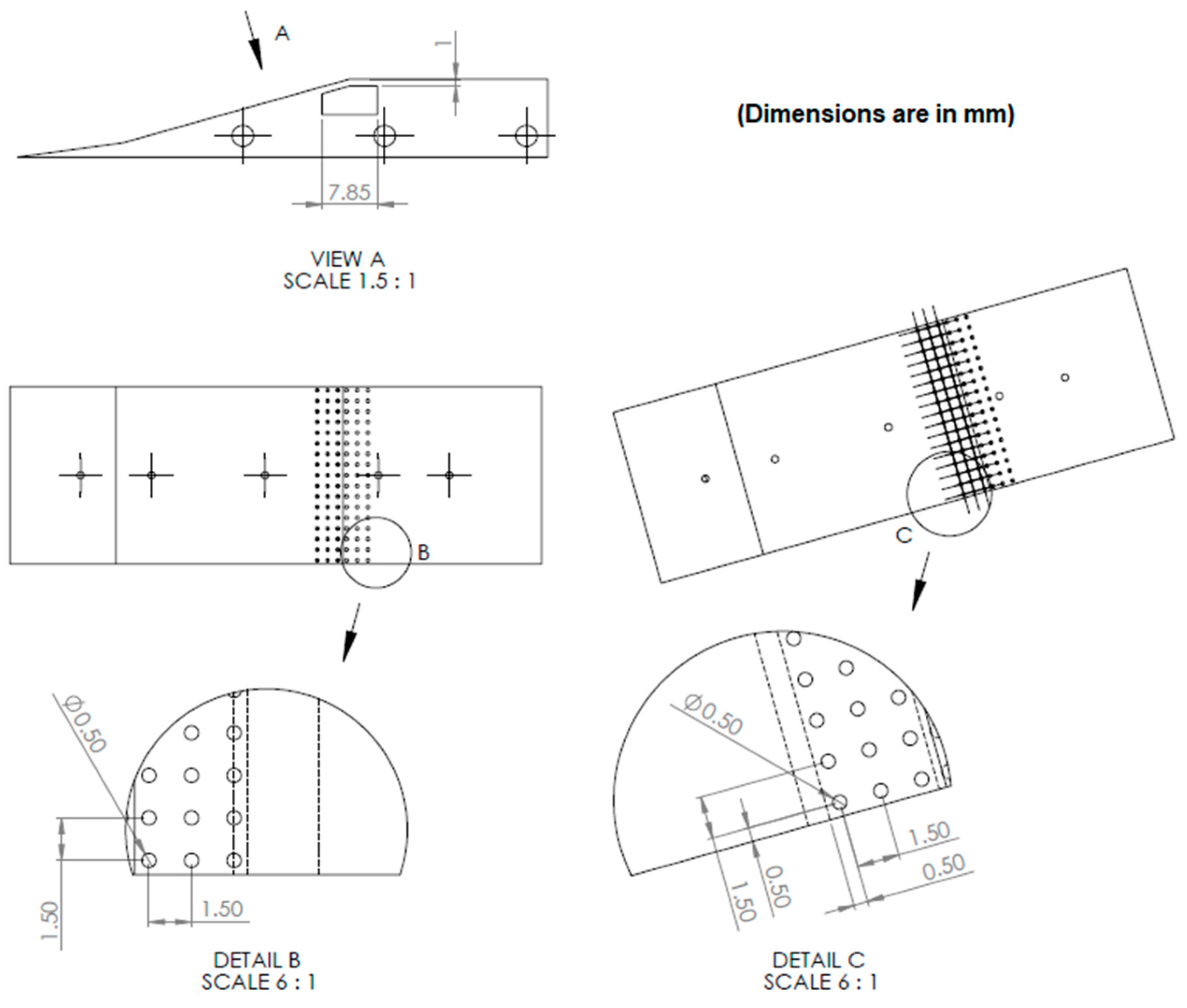
The preliminary experiments are conducted to identify the regions of the adverse pressure gradient and also the location of the impinging shock generated by the intake-cowl. As a shock control technique, wall ventilation through a shallow cavity is deployed at the region of the adverse pressure gradient (
Figure 3a). The cavity under the porous wall (the ventilated region of the intake-core wall) is not a regular rectangular cavity but is designed to have an angular cut at one of the corners. This cut angle is equal to the angle subtended by the second ramp of the intake with respect to the horizontal axis. A parametric study is conducted by varying the porosity of the ventilated wall. The diameter and the pitch of the uniformly distributed pores are varied (as shown in
Table 2) such that the corresponding porosity of the surface is varied as well at 10.6%, 15.7%, 18.8%, and 22.5%. These cavities are tested for their effectiveness in controlling the SBLI due to the impinging shock at varied intake contraction ratios as given in
Table 1. It can be seen that, in both uncontrolled and wall-ventilated intakes, the geometric blockage is essentially constant, i.e., the cavity with a porous upper surface contributes to no additional blockage to the flow through the intake. Photographic views of the intake-cores deployed with wall ventilation through the shallow cavity are shown in
Figure 5 with different porous surfaces. In addition, the specifications of the cavity covered with the 10.6% porous surface placed on the intake-core is sketched in
Figure 6.