Numerical Study on Bubble Rising in Complex Channels Saturated with Liquid Using a Phase-Field Lattice-Boltzmann Method
Abstract
1. Introduction
2. Numerical Method
2.1. Phase-Field LB Model
2.1.1. Macroscopic Governing Equations
2.1.2. LBE for Interface Tracking
2.1.3. LBE for Hydrodynamics
2.2. Numerical Implementation
2.2.1. Discretization
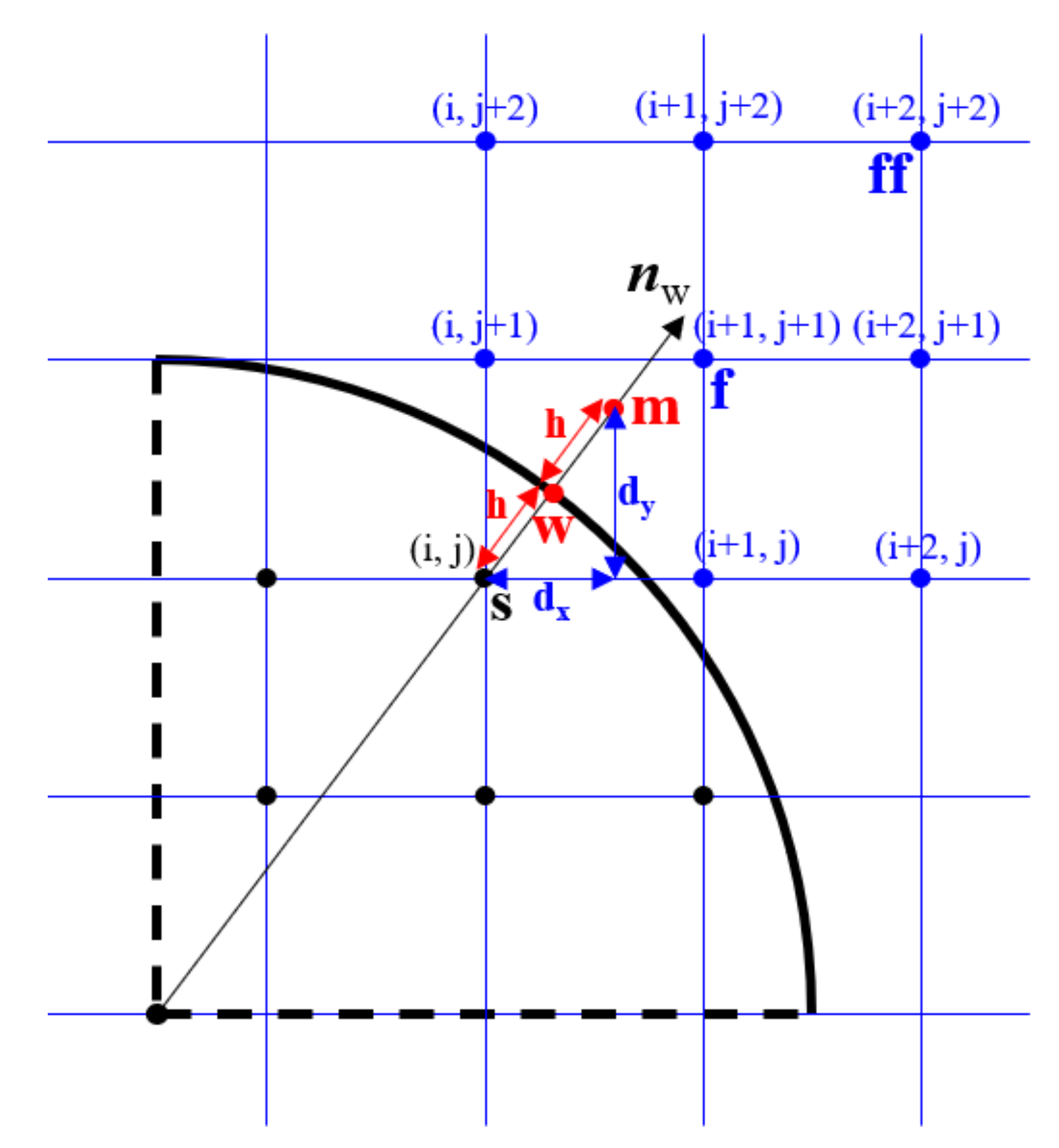
2.2.2. Curved Boundary Treatment
3. Numerical Validation
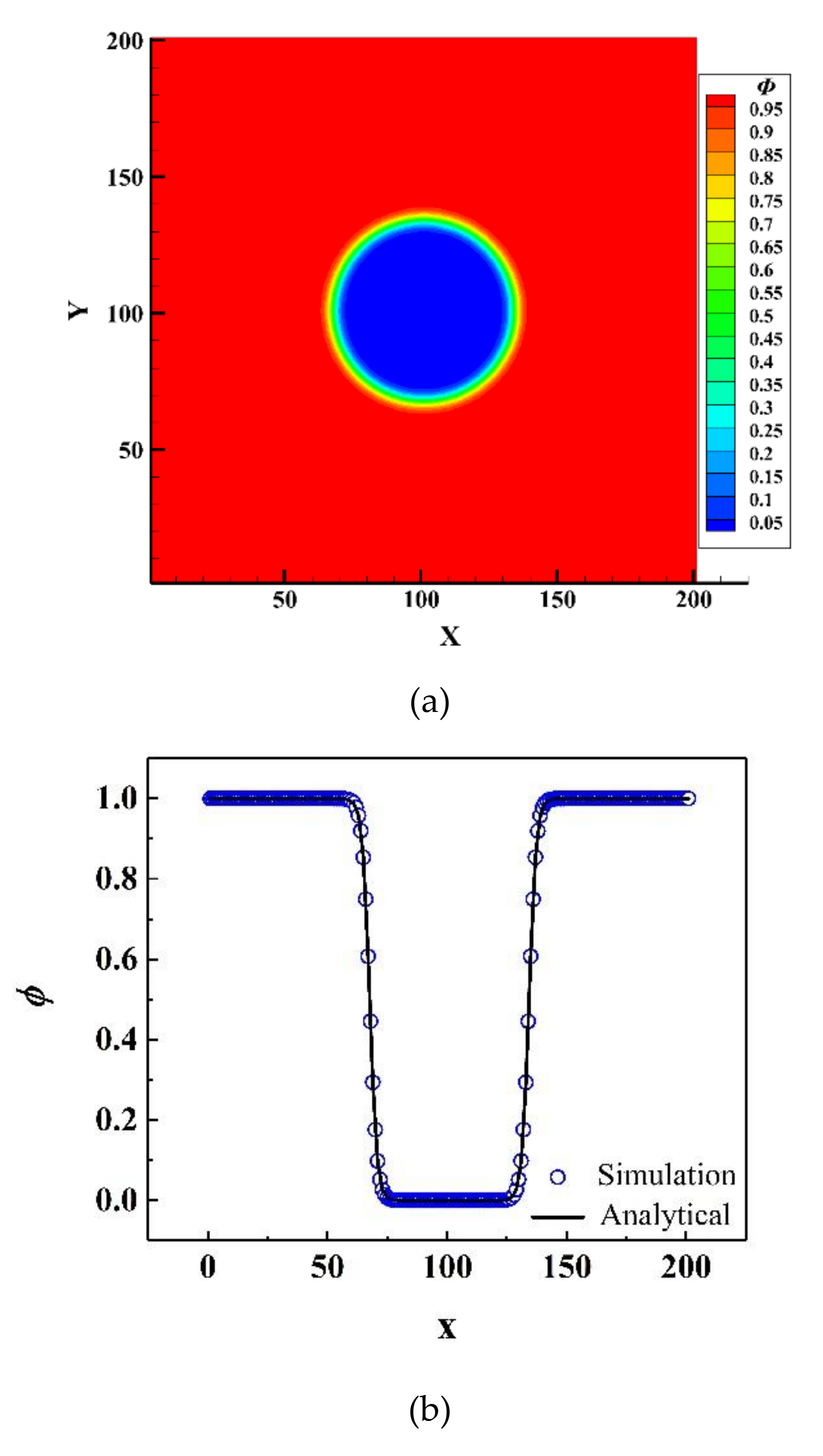
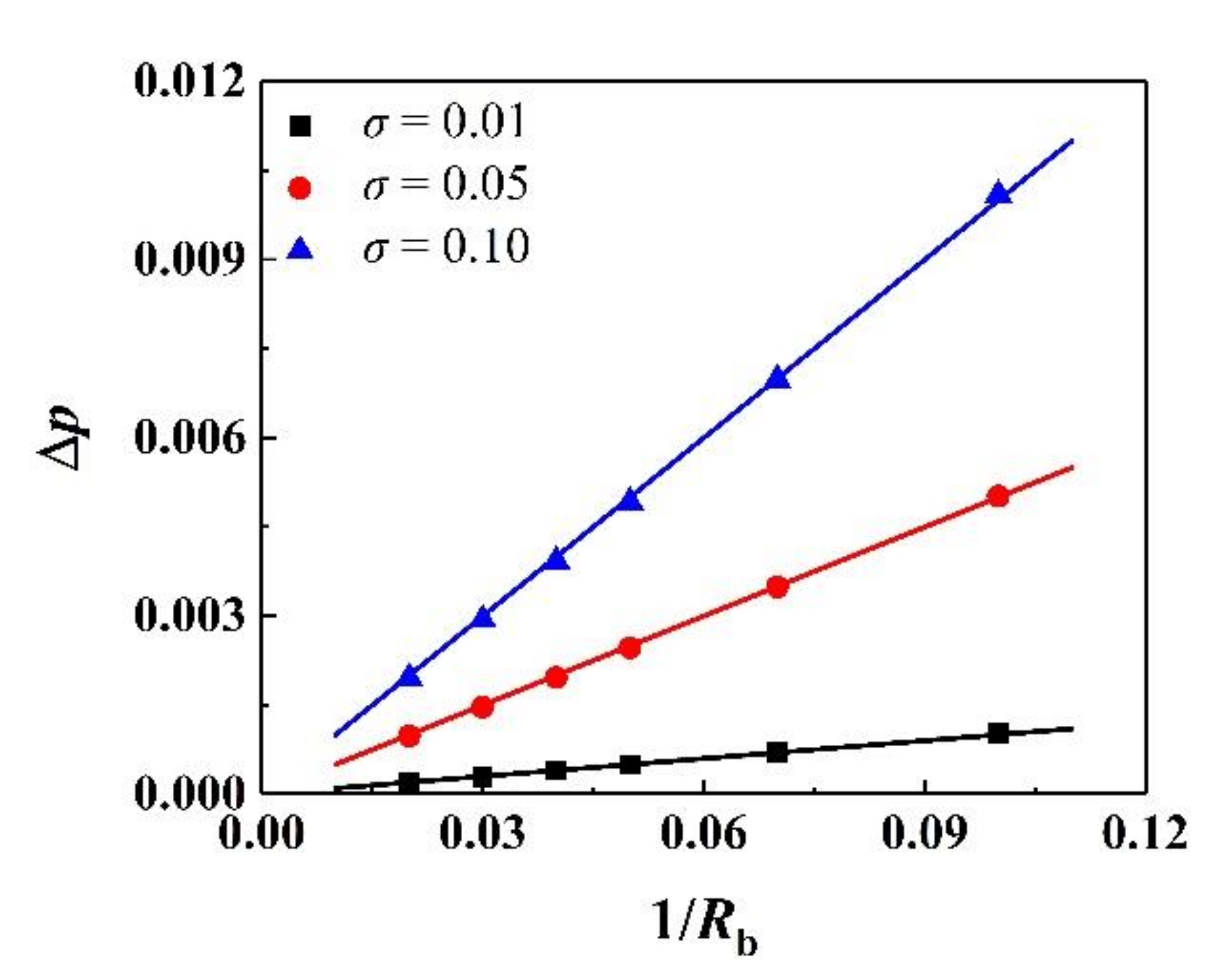
3.1. Laplace Law
3.2. Bubble Deformation
- (1)
- The gravity Reynolds number (ReGr),
- (2)
- The Eötvös number (Eo),
- (3)
- The Morton number (Mo),
- (4)
- The above three are not independent, since .
4. Numerical Results and Discussion
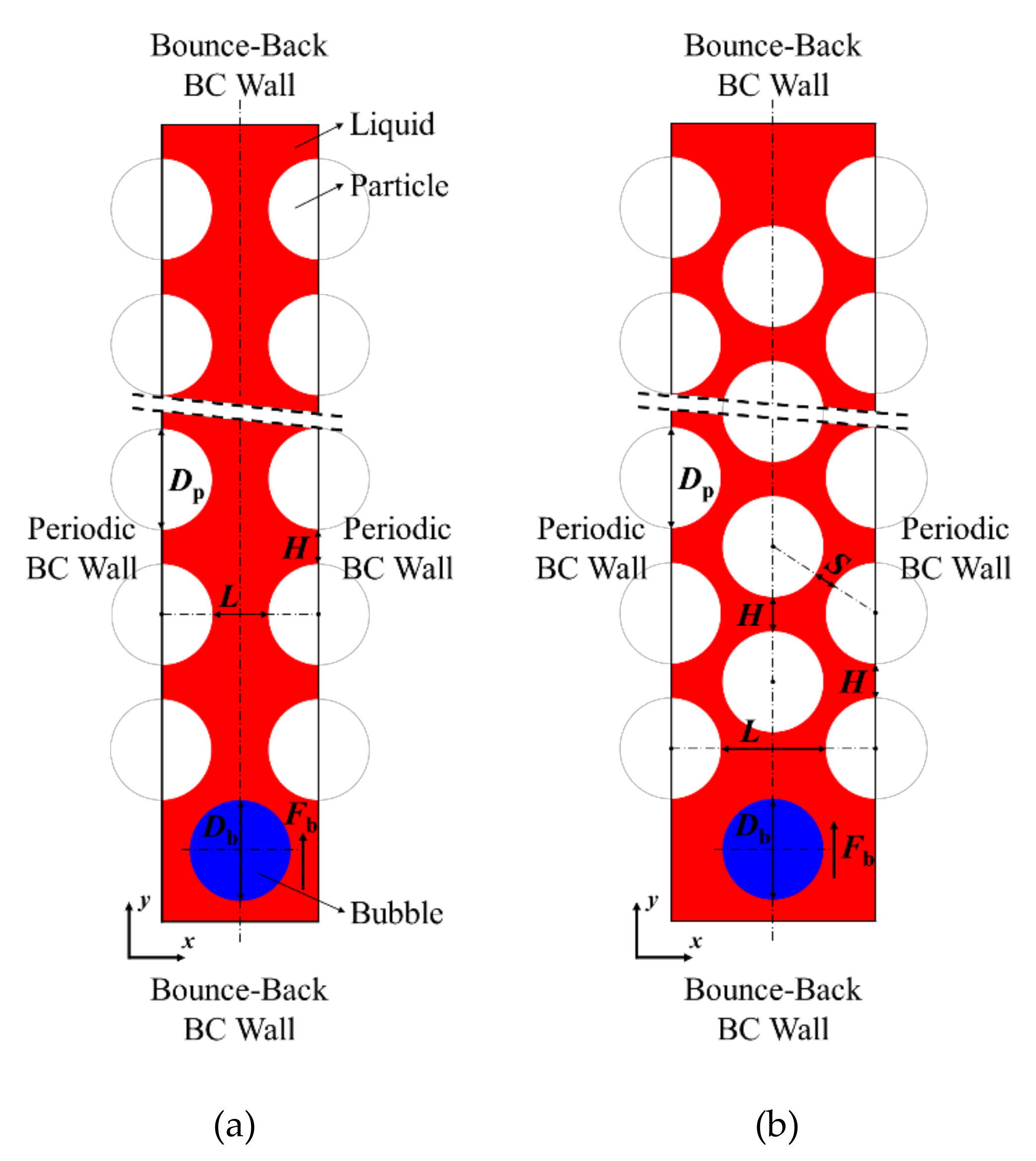
4.1. Channel Construction and Numerical Initialization
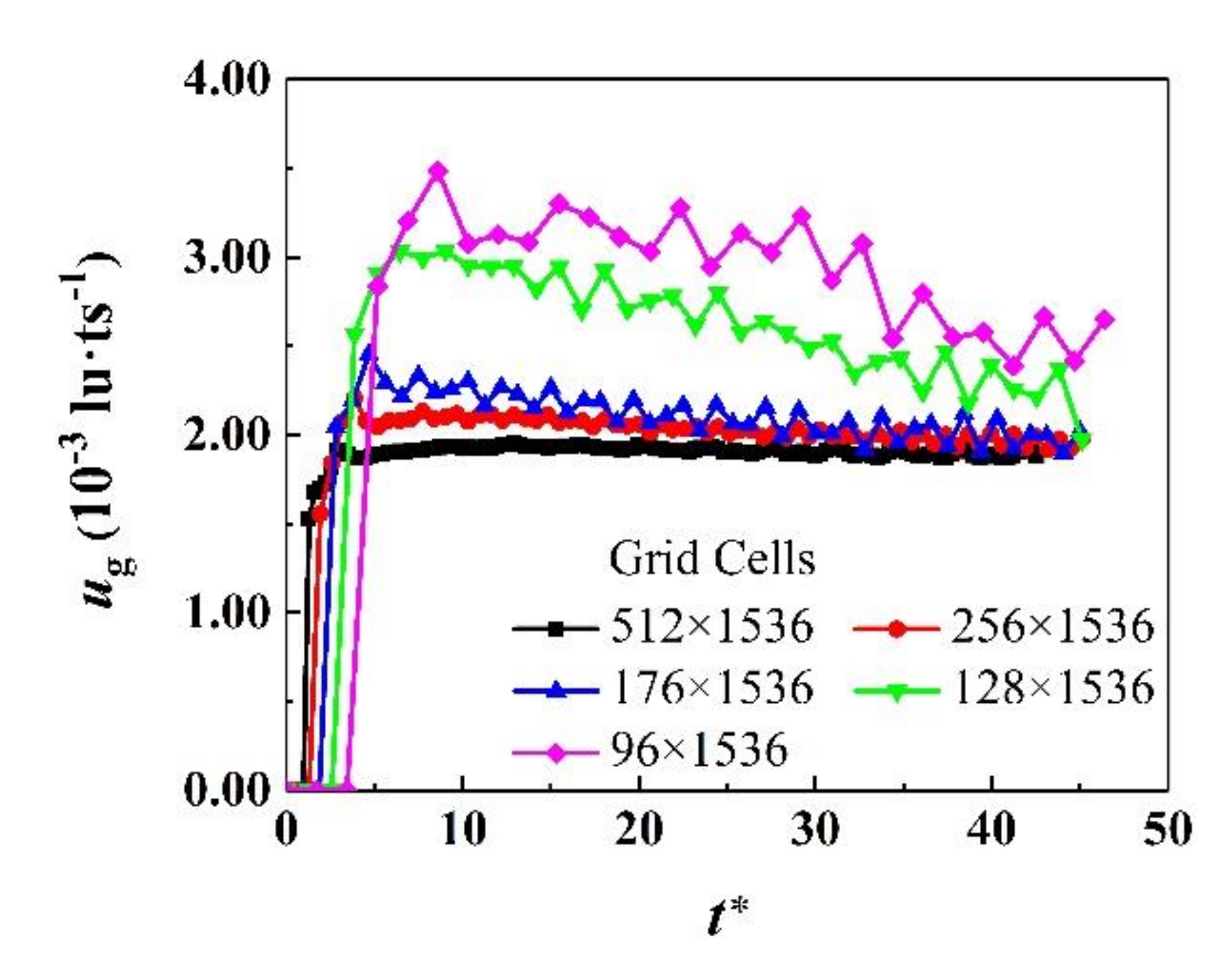
4.2. Grid Independence
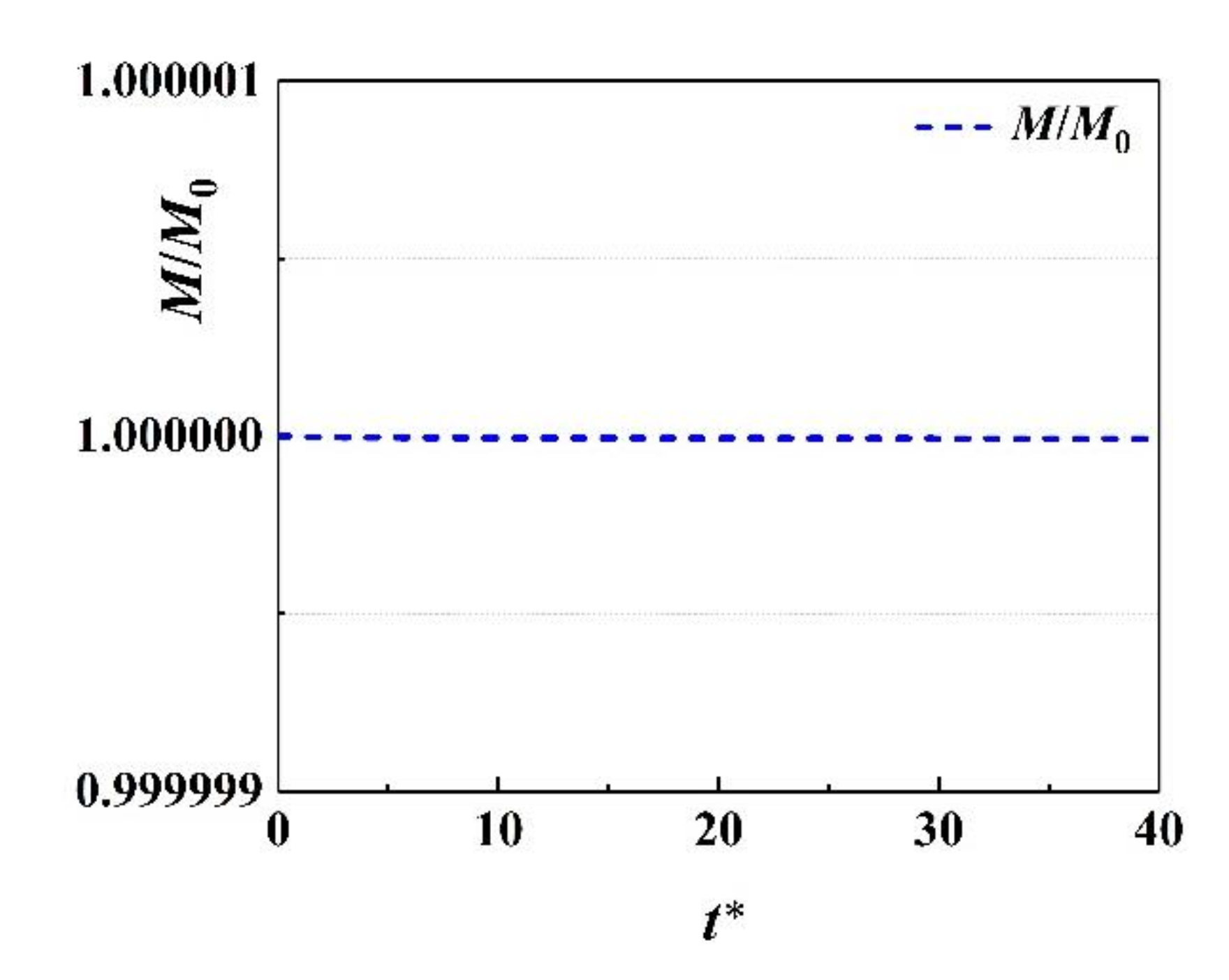
4.3. Mass Conservation
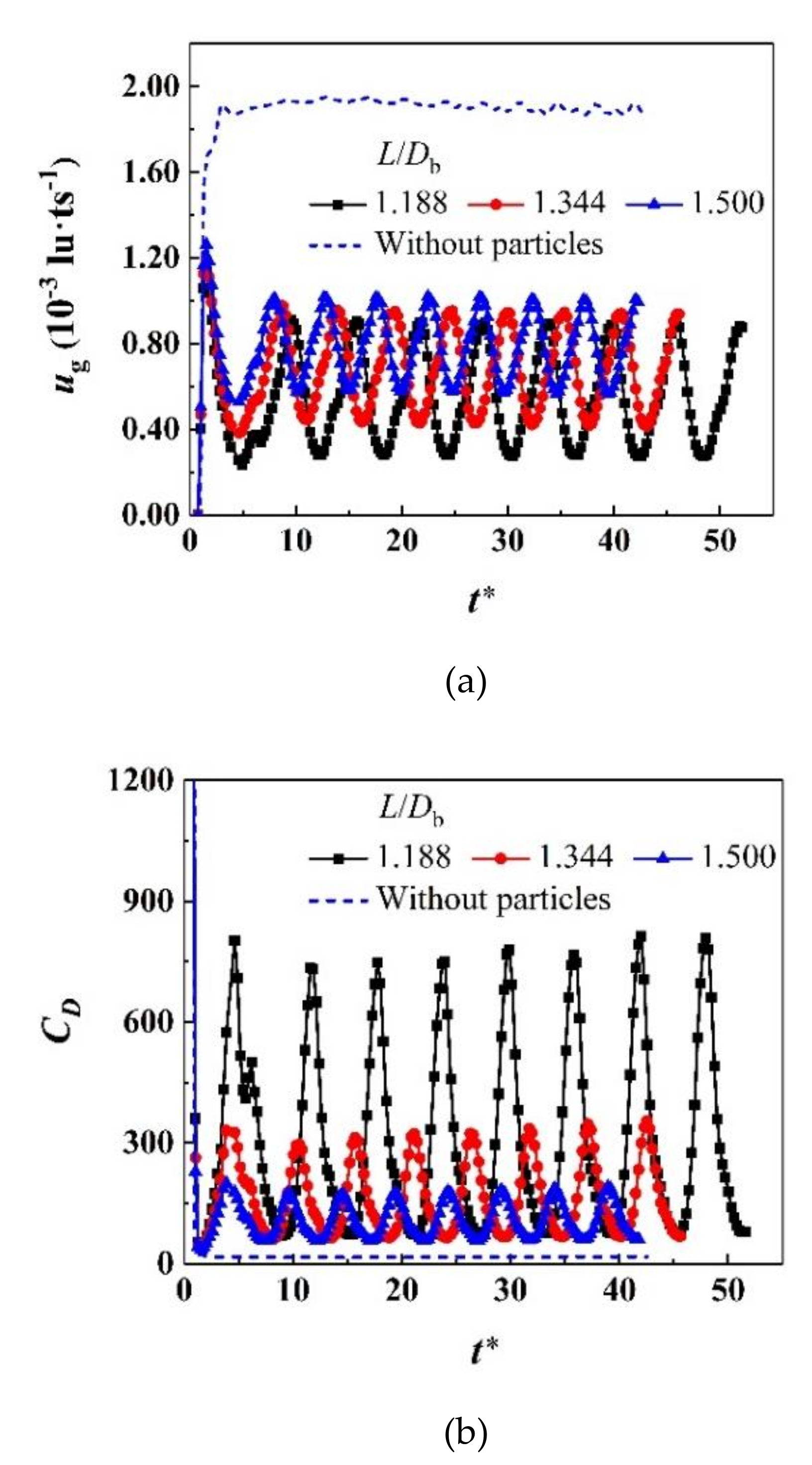
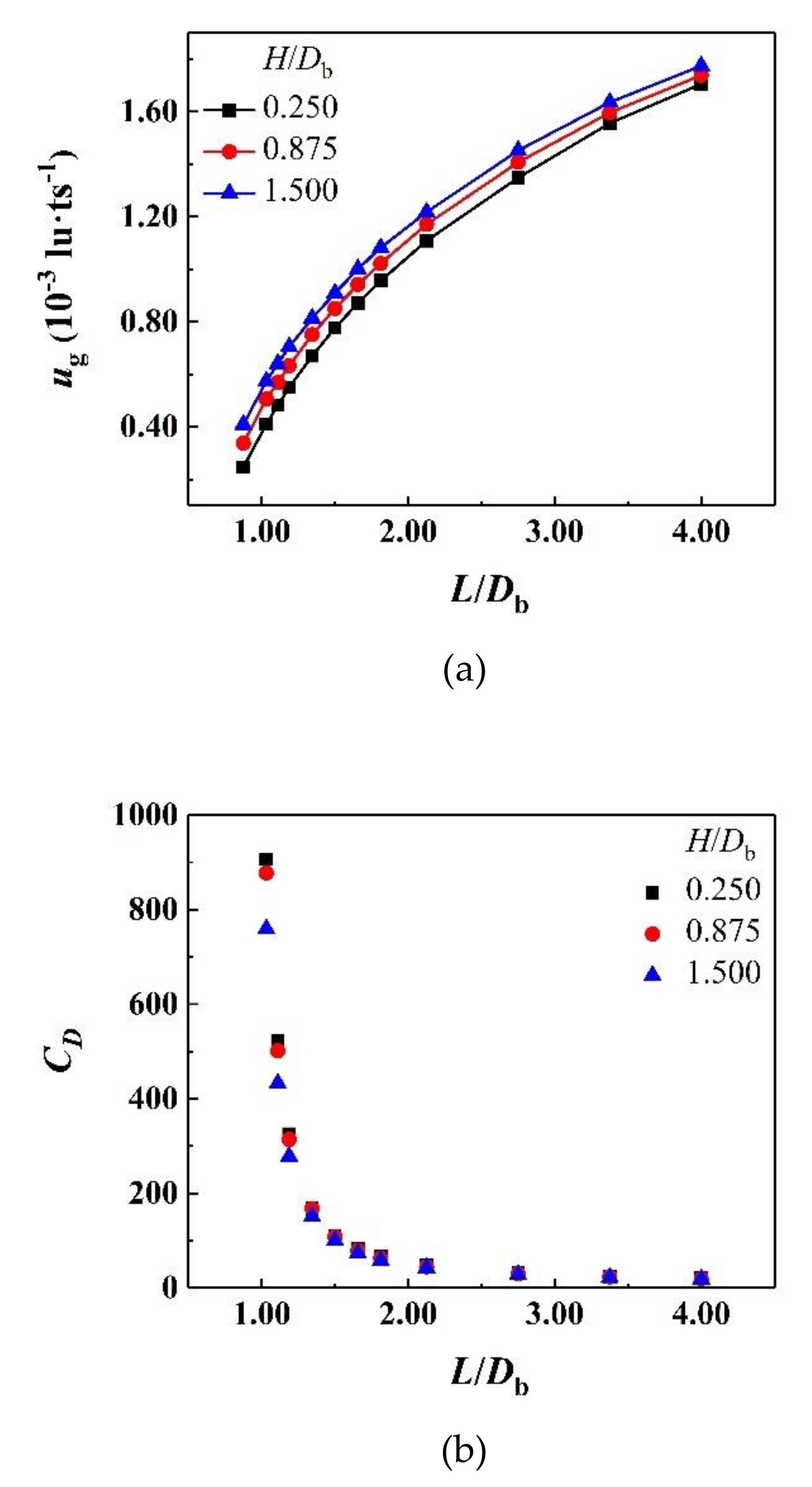
4.4. Channel Width Effect
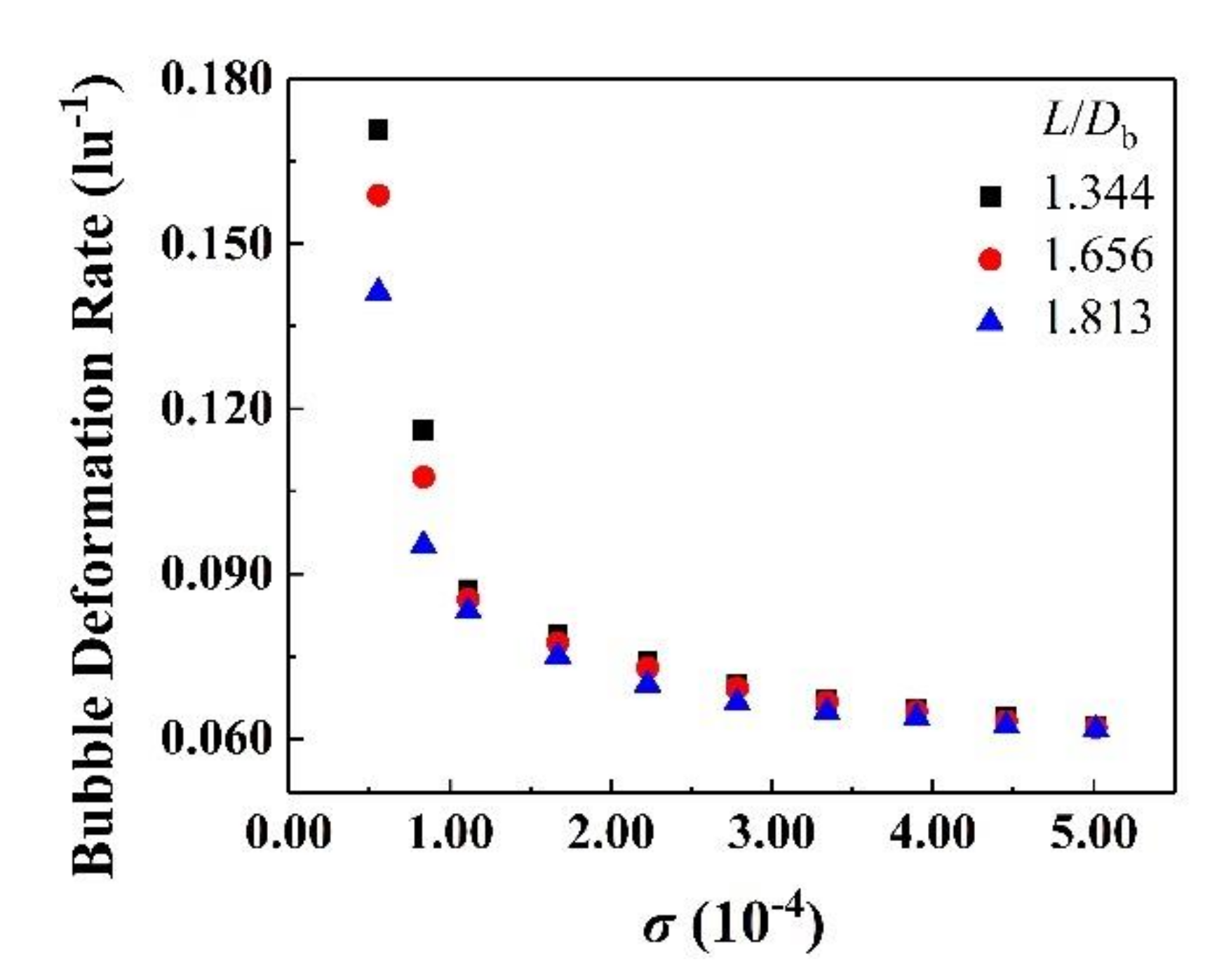
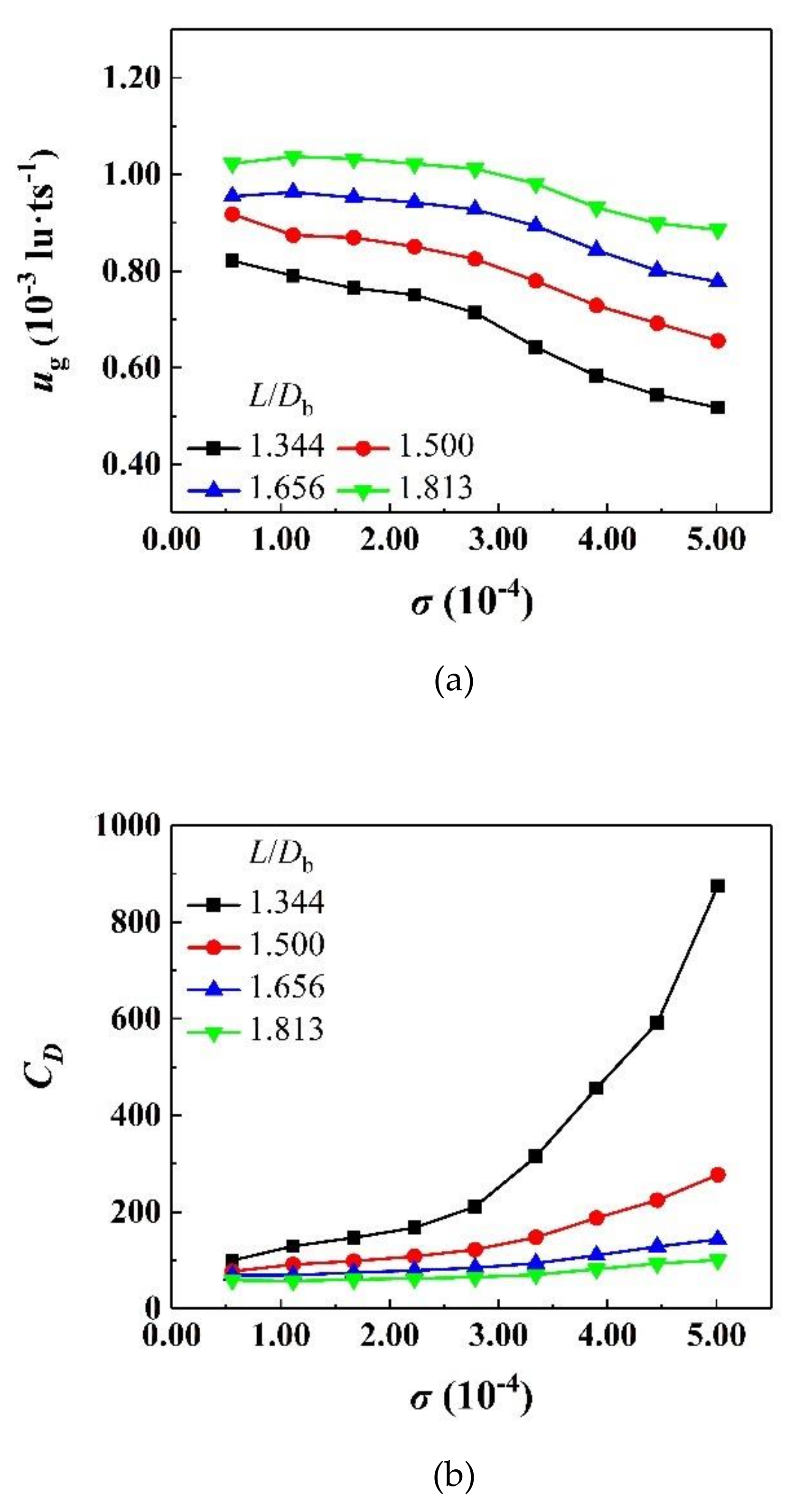
4.5. Surface Tension Effect
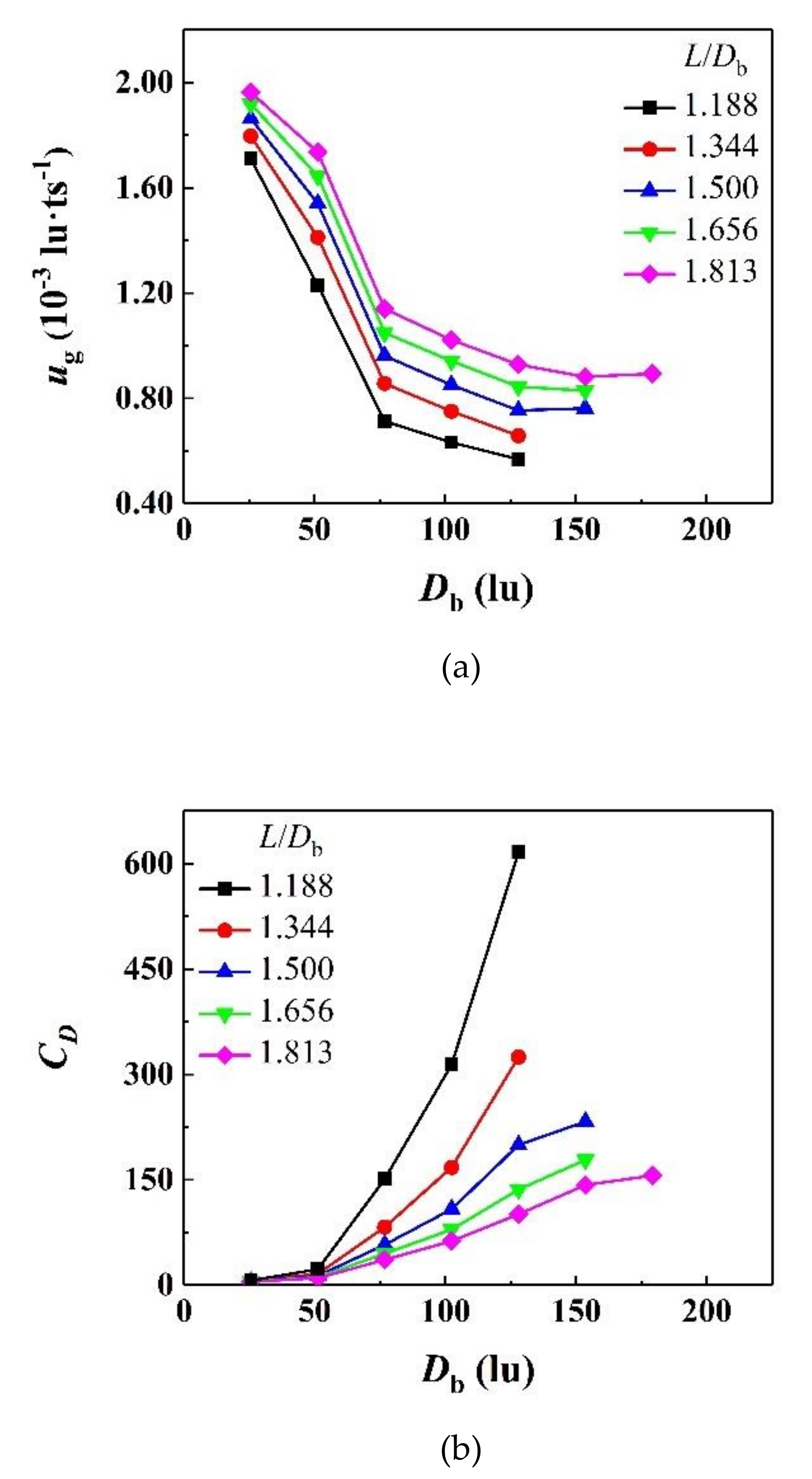
4.6. Bubble Diameter Effect
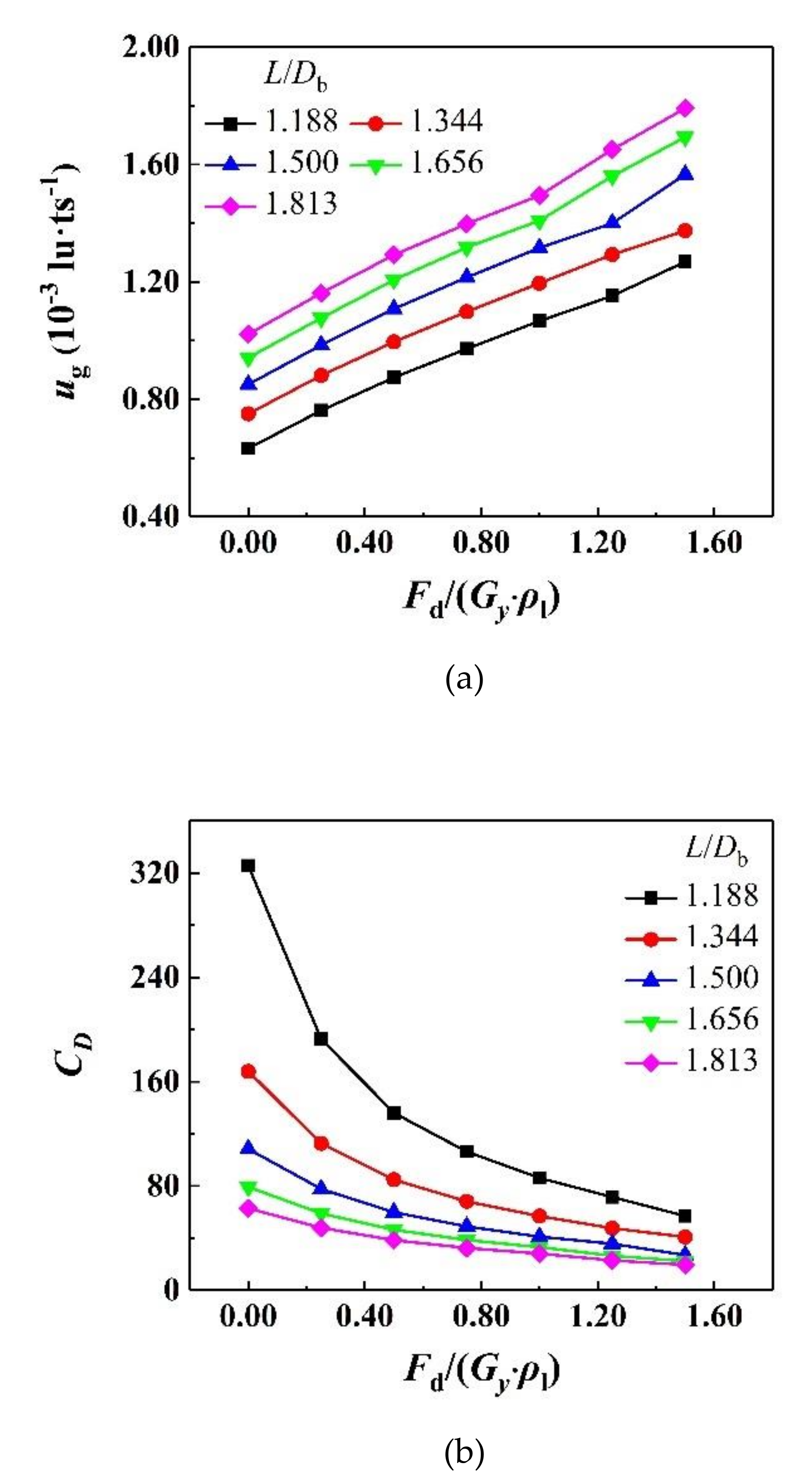
4.7. Driving Force Effect
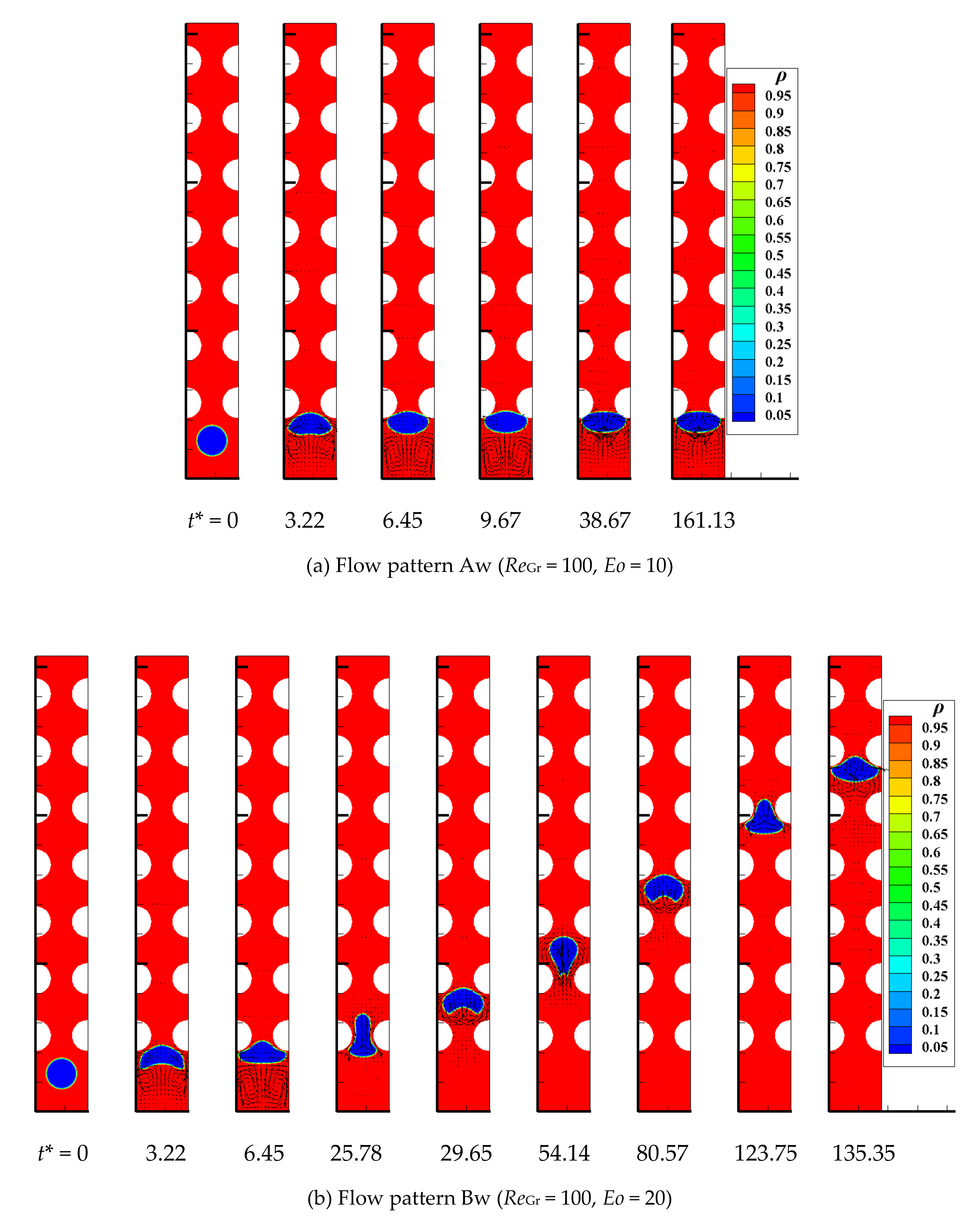
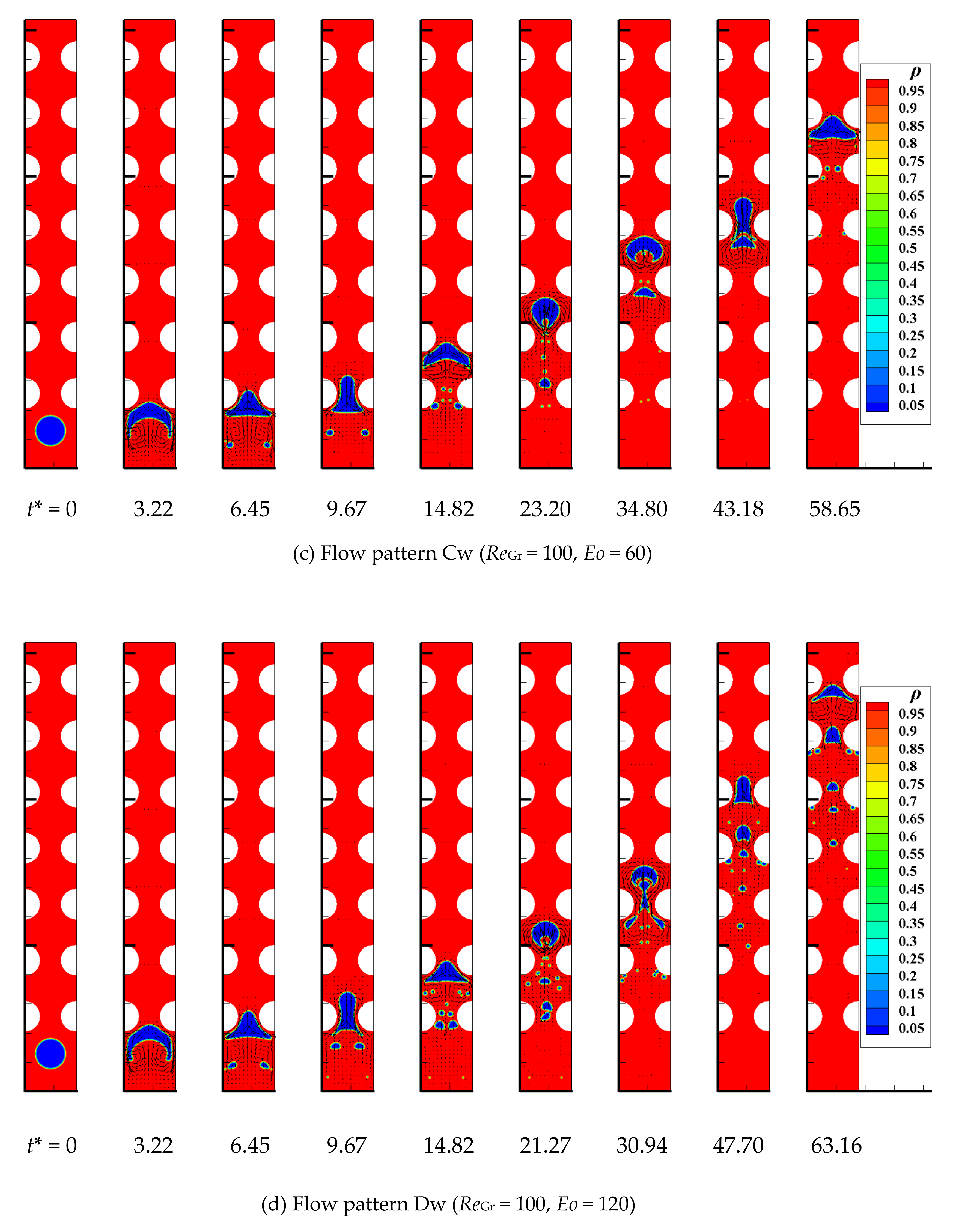
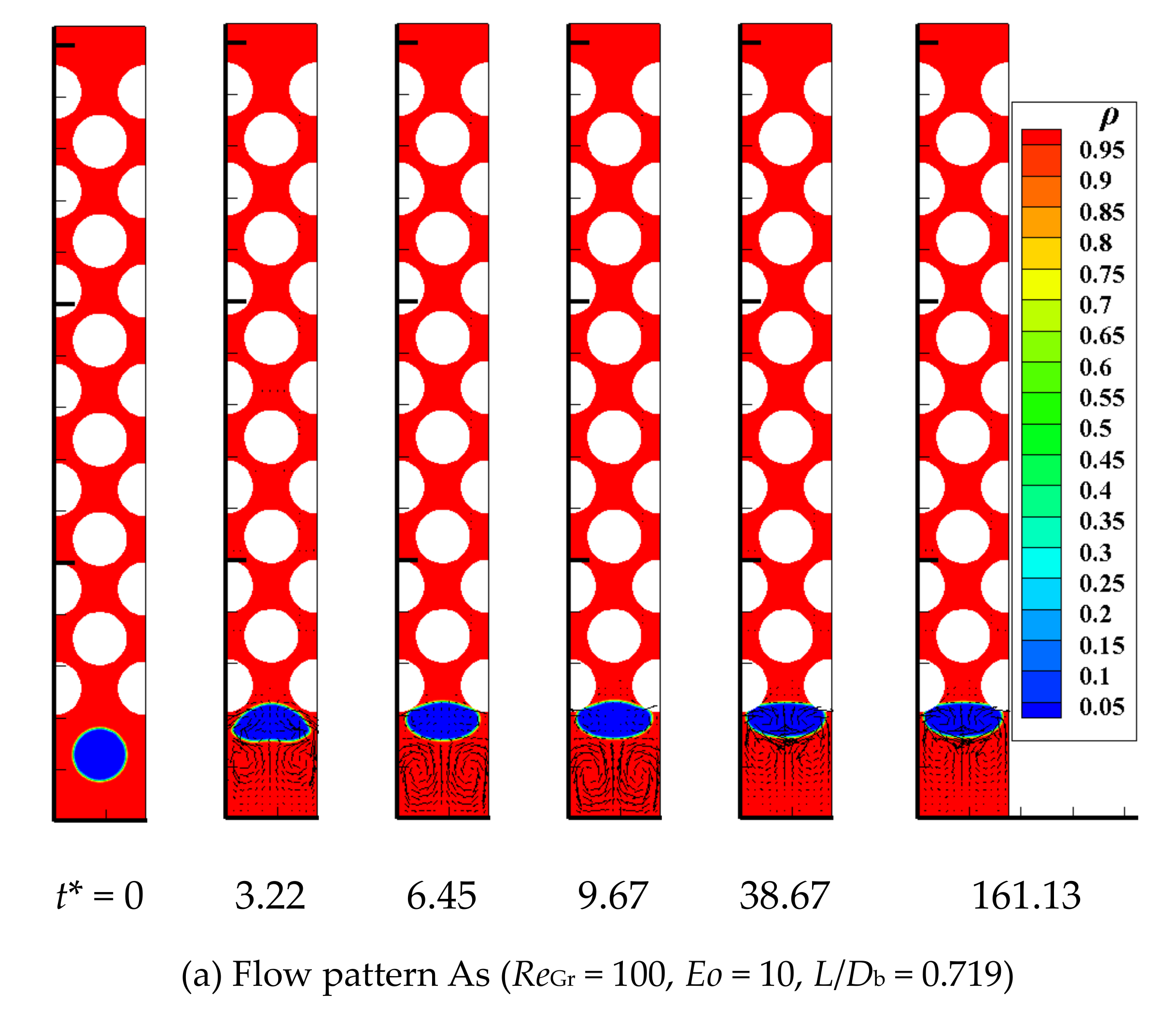
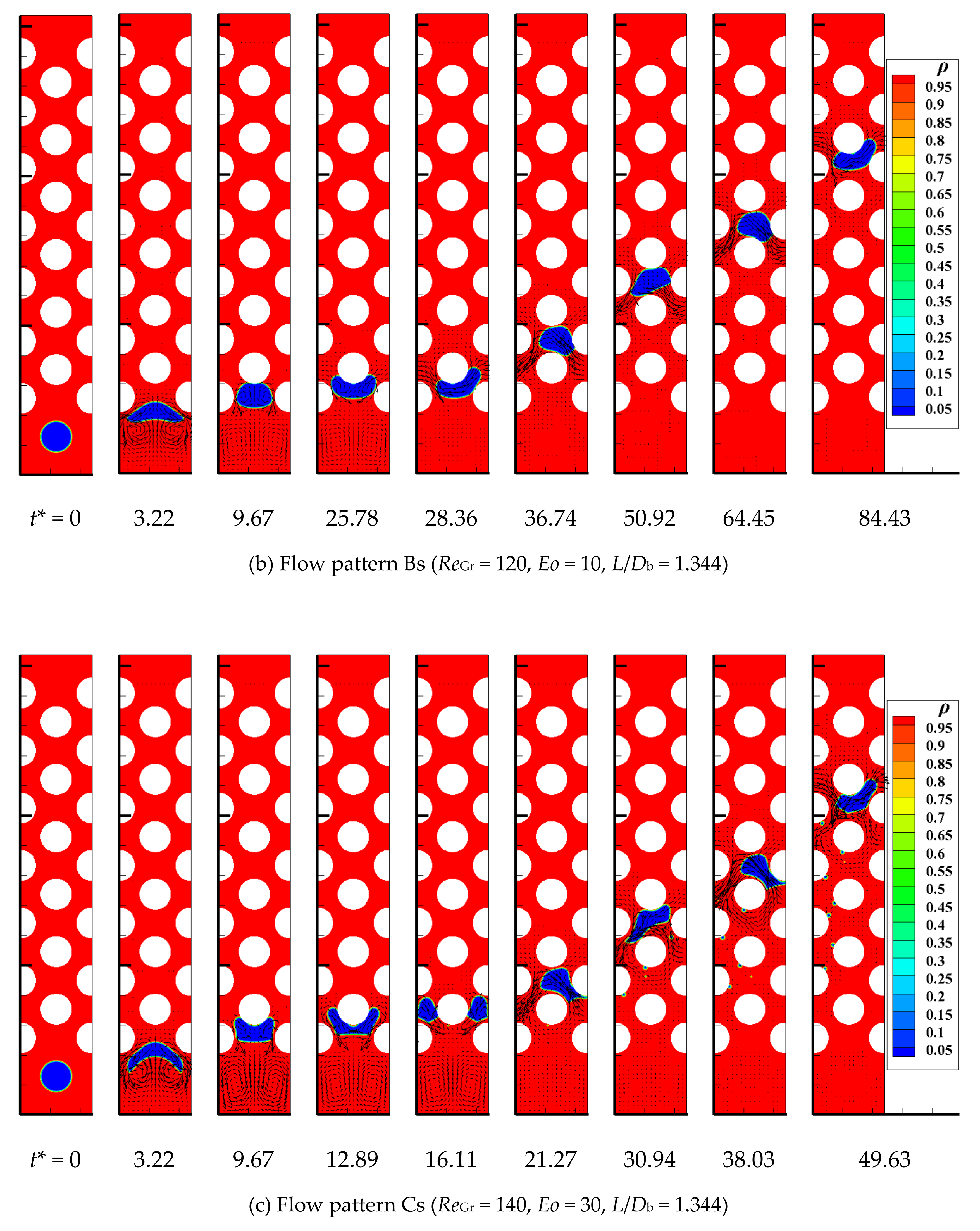
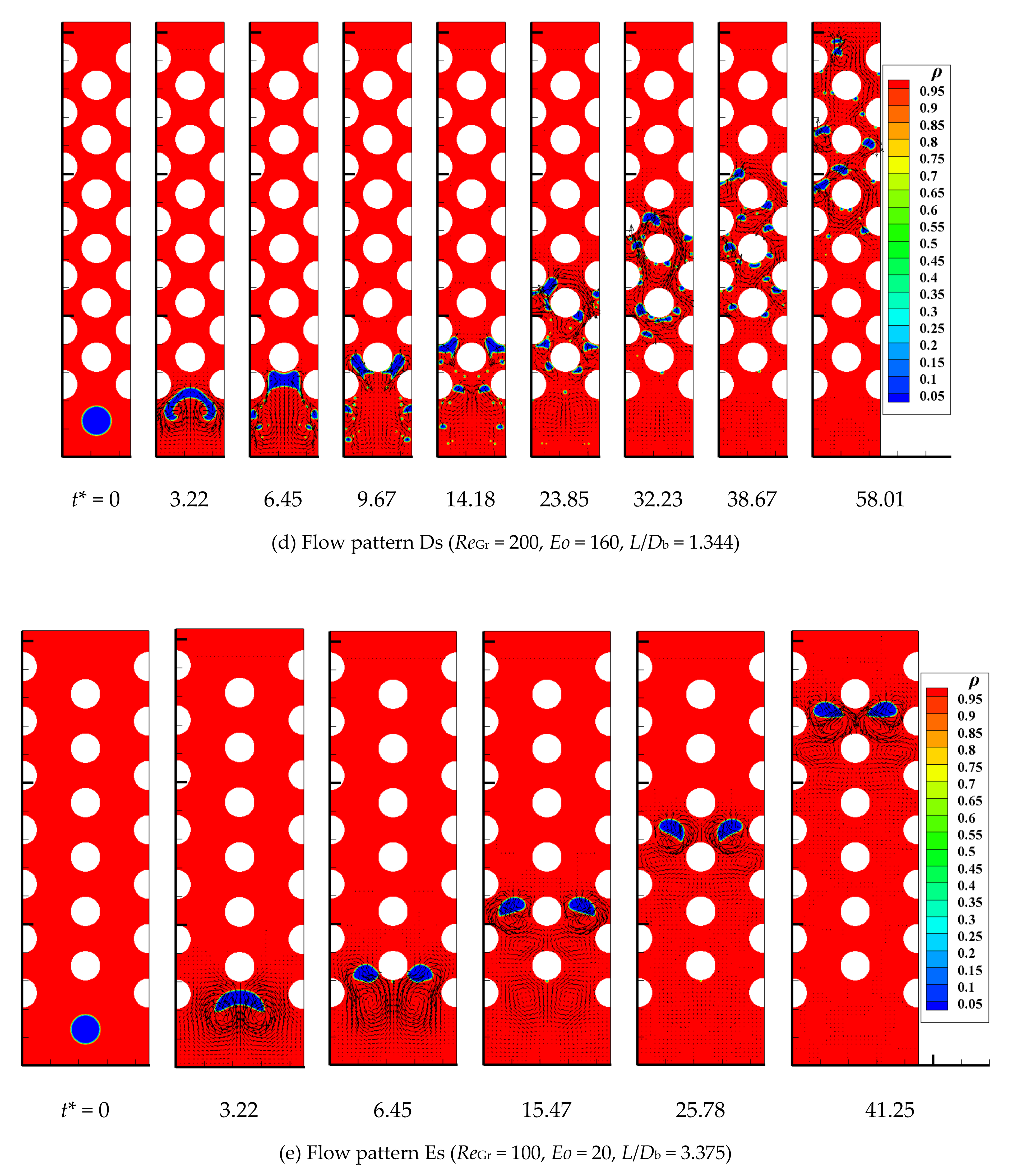
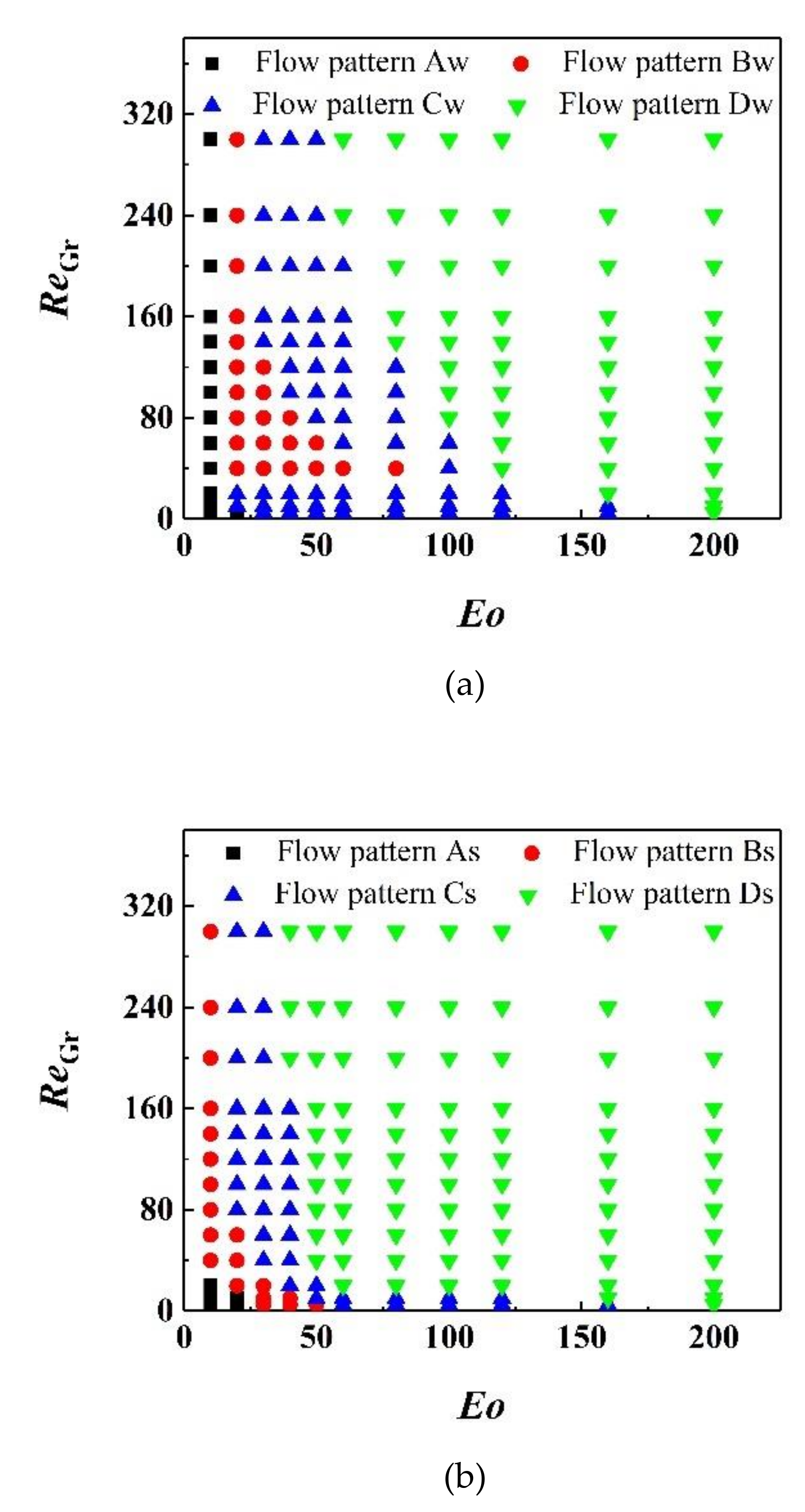
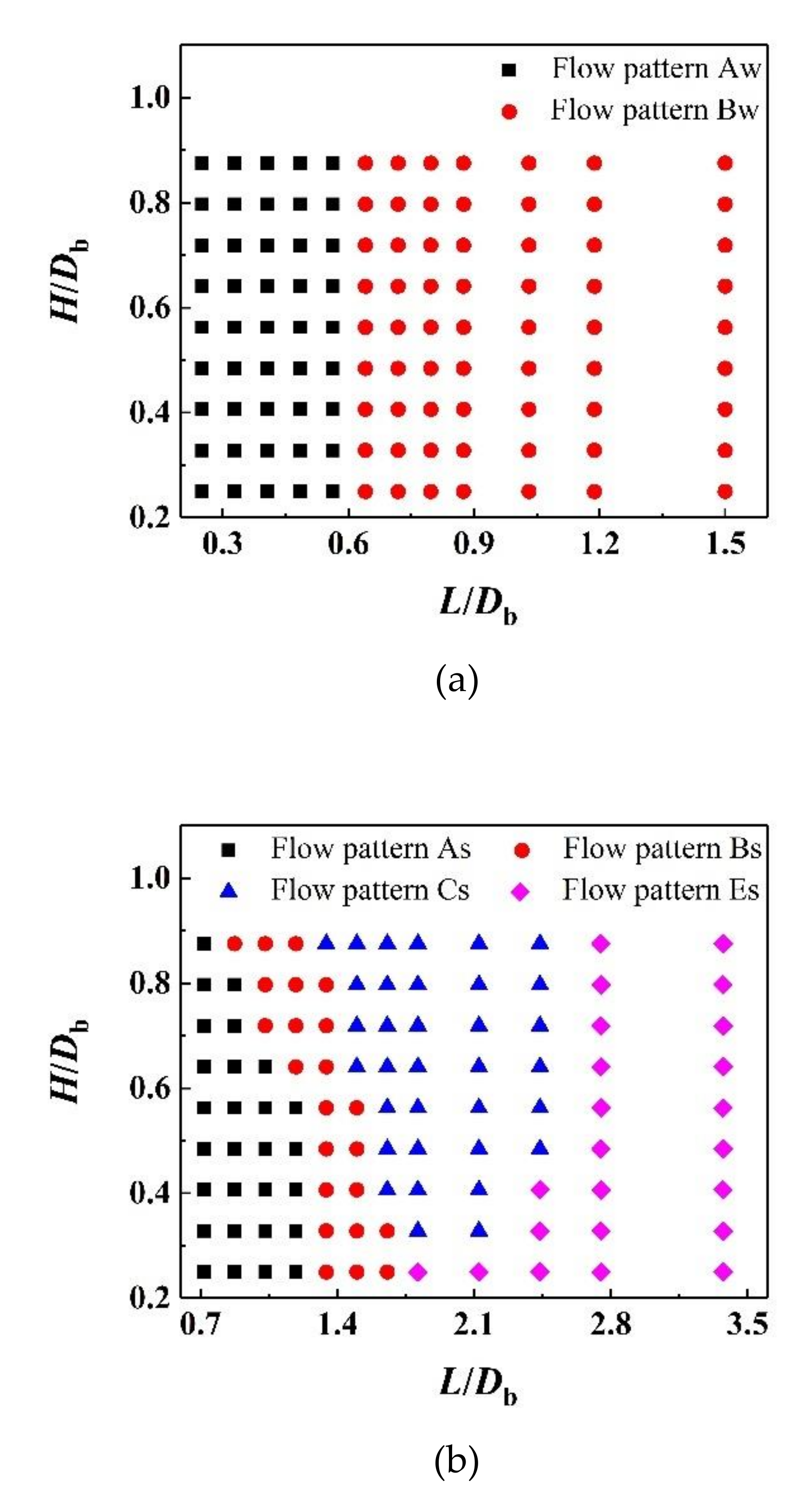
4.8. Bubble Flow Pattern
5. Conclusions
- (1)
- The present LB model is tested through three aspects of Laplace law, bubble deformation, and mass conservation, and it has been proven to have good stability, accuracy, and conservation from both qualitative and quantitative perspectives.
- (2)
- In the simulations of bubble rising in complex channels, the effects of channel width, surface tension, bubble diameter and additional driving force on bubble motion are investigated in detail. The larger channel width and additional driving force as well as smaller bubble diameter and surface tension lead to lower drag coefficients, which are conducive to smooth passage through the channels for the bubble.
- (3)
- Four and five types of bubble flow patterns are divided according to different bubble evolution processes under different ReGr, Eo and channel structures conditions in the wavy vertical channel and S-shaped curved channel, respectively. The detailed flow pattern diagrams are drawn for flow pattern recognition. To some extent, this study has some guiding significance for the regulation of bubble flow patterns in the industrial packed beds.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Symbols | |
| cs | Lattice sound speed |
| CD | Drag coefficient |
| Db | Bubble diameter |
| Dp | Particle diameter |
| eα | Lattice-related mesoscopic velocity set |
| Ef | Volumetric free energy |
| Eo | Eötvös number |
| Fα | Forcing term of the hydrodynamic LBE |
| Fb | Body force |
| Fd | Additional driving force |
| Fs | Surface tension force |
| Equilibrium hydrodynamic distribution function | |
| Modified hydrodynamic distribution function | |
| Modified equilibrium hydrodynamic distribution function | |
| Gy | Gravitational acceleration |
| Phase-field distribution function | |
| Equilibrium phase-field distribution function | |
| H | Vertical spacing between two vertically adjacent particles |
| L | Horizontal spacing between two horizontally adjacent particles |
| M | Mobility |
| M | Orthogonal transformation matrix |
| M | Total mass of the gas-liquid system |
| M0 | Initial total mass of the gas-liquid system |
| Mo | Morton number |
| Unit vector normal to the gas-liquid interface | |
| Unit vector normal to the solid boundary | |
| p | Macroscopic pressure |
| Δp | Pressure difference between inside and outside the bubble |
| Rb | Bubble radius |
| Re | Reynolds number of the rising bubble |
| ReGr | Gravity Reynolds number |
| S | Shortest spacing between two diagonally adjacent particles |
| Diagonal relaxation matrix | |
| t | Time |
| t* | Gravity-based dimensionless time |
| u | Macroscopic velocity vector |
| ug | Bubble rising velocity |
| wα | Lattice-related weight coefficient set |
| x | Coordinates of the lattice nodes |
| xw | Position of the point on the solid boundary |
| Unit vector with a vertical downward direction | |
| δt | Unit time |
| δx | Unit lattice length |
| ξ | Interface thickness |
| μ | Fluid mixed viscosity |
| μg | Gas viscosity |
| μl | Liquid viscosity |
| μϕ | Chemical potential |
| ϕ | Phase-field variable |
| ϕm | Phase field value of the interpolated point |
| ϕw | Phase field value of the point on the solid boundary |
| ρ | Fluid mixed density |
| ρg | Gas density |
| ρl | Liquid density |
| σ | Surface tension |
| τ | Hydrodynamic relaxation time |
| τϕ | Phase-field relaxation time |
| θ | Contact angle |
| Ωα | Collision operator of the hydrodynamic LBE |
| Ψ(ϕ) | Bulk free energy |
References
- Tailleur, R.G.; Hernandez, J.; Rojas, A. Selective hydrogenation of olefins with mass transfer control in a structured packed bed reactor. Fuel 2008, 87, 3694–3705. [Google Scholar] [CrossRef]
- Yuan, R.; He, Z.; Zhang, Y.; Wang, W.; Chen, C.; Wu, H.; Zhan, Z. Partial oxidation of methane to syngas in a packed bed catalyst membrane reactor. AIChE J. 2016, 62, 2170–2176. [Google Scholar] [CrossRef]
- Miladinovic, N.; Weatherley, L.R. Intensification of ammonia removal in a combined ion-exchange and nitrification column. Chem. Eng. J. 2008, 135, 15–24. [Google Scholar] [CrossRef]
- Huggins, T.M.; Haeger, A.; Biffinger, J.C.; Ren, Z.J. Granular biochar compared with activated carbon for wastewater treatment and resource recovery. Water Res. 2016, 94, 225–232. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Swift, M.R.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 1995, 75, 830–833. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys. 2004, 198, 628–644. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.L. A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio. J. Comput. Phys. 2005, 206, 16–47. [Google Scholar] [CrossRef]
- Lee, T.; Liu, L. Lattice Boltzmann simulations of micron-scale drop impact on dry surfaces. J. Comput. Phys. 2010, 229, 8045–8063. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar]
- Chiappini, D.; Bella, G.; Succi, S.; Toschi, F.; Ubertini, S. Improved lattice Boltzmann without parasitic currents for Rayleigh-Taylor instability. Commun. Comput. Phys. 2010, 7, 423–444. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Force imbalance in lattice Boltzmann equation for two-phase flows. Phys. Rev. E 2011, 83, 036707. [Google Scholar] [CrossRef]
- Zheng, H.W.; Shu, C.; Chew, Y.T. A lattice Boltzmann model for multiphase flows with large density ratio. J. Comput. Phys. 2006, 218, 353–371. [Google Scholar] [CrossRef]
- Fakhari, A.; Rahimian, M.H. Phase-field modeling by the method of lattice Boltzmann equations. Phys. Rev. E 2010, 81, 036707. [Google Scholar] [CrossRef]
- Fakhari, A.; Lee, T. Finite-difference lattice Boltzmann method with a block-structured adaptive-mesh-refinement technique. Phys. Rev. E 2014, 89, 033310. [Google Scholar] [CrossRef]
- Fakhari, A.; Geier, M.; Lee, T. A mass-conserving lattice Boltzmann method with dynamic grid refinement for immiscible two-phase flows. J. Comput. Phys. 2016, 315, 434–457. [Google Scholar] [CrossRef]
- Fakhari, A.; Bolster, D. Diffuse interface modeling of three-phase contact line dynamics on curved boundaries: A lattice Boltzmann model for large density and viscosity ratios. J. Comput. Phys. 2017, 334, 620–638. [Google Scholar] [CrossRef]
- Fakhari, A.; Mitchell, T.; Leonardi, C.; Bolster, D. Improved locality of the phase-field lattice-Boltzmann model for immiscible fluids at high density ratios. Phys. Rev. E 2017, 96, 053301. [Google Scholar] [CrossRef] [PubMed]
- Fakhari, A.; Bolster, D.; Luo, L.S. A weighted multiple-relaxation-time lattice Boltzmann method for multiphase flows and its application to partial coalescence cascades. J. Comput. Phys. 2017, 341, 22–43. [Google Scholar] [CrossRef]
- Fakhari, A.; Li, Y.; Bolster, D.; Christensen, K.T. A phase-field lattice Boltzmann model for simulating multiphase flows in porous media: Application and comparison to experiments of CO2 sequestration at pore scale. Adv. Water Resour. 2018, 114, 119–134. [Google Scholar] [CrossRef]
- Mitchell, T.; Leonardi, C.; Fakhari, A. Development of a three-dimensional phase-field lattice Boltzmann method for the study of immiscible fluids at high density ratios. Int. J. Multiph. Flow 2018, 107, 1–15. [Google Scholar] [CrossRef]
- Magaletti, F.; Picano, F.; Chinappi, M.; Marino, L.; Casciola, C.M. The sharp-interface limit of the Cahn-Hilliard/Navier-Stokes model for binary fluids. J. Fluid Mech. 2013, 714, 95–126. [Google Scholar] [CrossRef]
- Chiu, P.H.; Lin, Y.T. A conservative phase field method for solving incompressible two-phase flows. J. Comput. Phys. 2011, 230, 185–204. [Google Scholar] [CrossRef]
- Jacqmin, D. Calculation of two-phase Navier-Stokes flows using phase-field modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Geier, M.; Fakhari, A.; Lee, T. Conservative phase-field lattice Boltzmann model for interface tracking equation. Phys. Rev. E 2015, 91, 063309. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Shyy, W. A unified boundary treatment in lattice Boltzmann method. AIAA J. 2003. [Google Scholar] [CrossRef]
- Hua, J.; Lou, J. Numerical simulation of bubble rising in viscous liquid. J. Comput. Phys. 2007, 222, 769–795. [Google Scholar] [CrossRef]
- Fakhari, A.; Rahimian, M.H. Simulation of an axisymmetric rising bubble by a multiple relaxation time lattice Boltzmann method. Int. J. Mod. Phys. B 2009, 23, 4907–4932. [Google Scholar] [CrossRef]
- Huang, H.; Huang, J.J.; Lu, X.Y. A mass-conserving axisymmetric multiphase lattice Boltzmann method and its application in simulation of bubble rising. J. Comput. Phys. 2014, 269, 386–402. [Google Scholar] [CrossRef]
- Liang, H.; Li, Y.; Chen, J.; Xu, J. Axisymmetric lattice Boltzmann model for multiphase flows with large density ratio. Int. J. Heat Mass Transf. 2019, 130, 1189–1205. [Google Scholar] [CrossRef]
- Bhaga, D.; Weber, M.E. Bubbles in viscous liquids: Shapes, wakes and velocities. J. Fluid Mech. 1981, 105, 61–85. [Google Scholar] [CrossRef]
- Patel, T.; Patel, D.; Thakkar, N.; Lakdawala, A. A numerical study on bubble dynamics in sinusoidal channels. Phys. Fluids 2019, 31, 052103. [Google Scholar] [CrossRef]
- Shi, Y.; Tang, G.H.; Lin, H.F.; Zhao, P.X.; Cheng, L.H. Dynamics of droplet and liquid layer penetration in three-dimensional porous media: A lattice Boltzmann study. Phys. Fluids 2019, 31, 042106. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
| Case | ReGr | Eo | Experiments (Bhaga and Weber, 1981) [37] | Front Tracking Method (Hua and Lou, 2007) [33] | LBM (Liang et al., 2019) [36] | Present LBM |
|---|---|---|---|---|---|---|
| A1 | 1.67 | 17.7 |  |  |  |  |
| A2 | 79.88 | 32.2 |  |  |  | 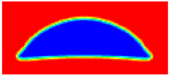 |
| A3 | 134.63 | 115 | 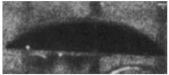 |  |  |  |
| A4 | 30.83 | 339 | 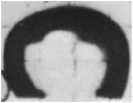 |  |  | 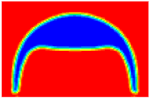 |
| A5 | 49.72 | 641 |  |  |  | 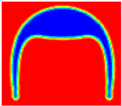 |
| Case | Re of Experiments [37] | Re of Present LBM | Relative Error (%) |
|---|---|---|---|
| A1 | 0.232 | 0.211 | 9.05 |
| A2 | 55.3 | 47.8 | 13.56 |
| A3 | 94.0 | 87.5 | 6.91 |
| A4 | 18.3 | 16.4 | 10.38 |
| A5 | 30.3 | 27.5 | 9.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Yong, Y.; Yang, C. Numerical Study on Bubble Rising in Complex Channels Saturated with Liquid Using a Phase-Field Lattice-Boltzmann Method. Processes 2020, 8, 1608. https://doi.org/10.3390/pr8121608
Yu K, Yong Y, Yang C. Numerical Study on Bubble Rising in Complex Channels Saturated with Liquid Using a Phase-Field Lattice-Boltzmann Method. Processes. 2020; 8(12):1608. https://doi.org/10.3390/pr8121608
Chicago/Turabian StyleYu, Kang, Yumei Yong, and Chao Yang. 2020. "Numerical Study on Bubble Rising in Complex Channels Saturated with Liquid Using a Phase-Field Lattice-Boltzmann Method" Processes 8, no. 12: 1608. https://doi.org/10.3390/pr8121608
APA StyleYu, K., Yong, Y., & Yang, C. (2020). Numerical Study on Bubble Rising in Complex Channels Saturated with Liquid Using a Phase-Field Lattice-Boltzmann Method. Processes, 8(12), 1608. https://doi.org/10.3390/pr8121608




