Monitoring, Diffusion and Source Speculation Model of Urban Soil Pollution
Abstract
1. Introduction
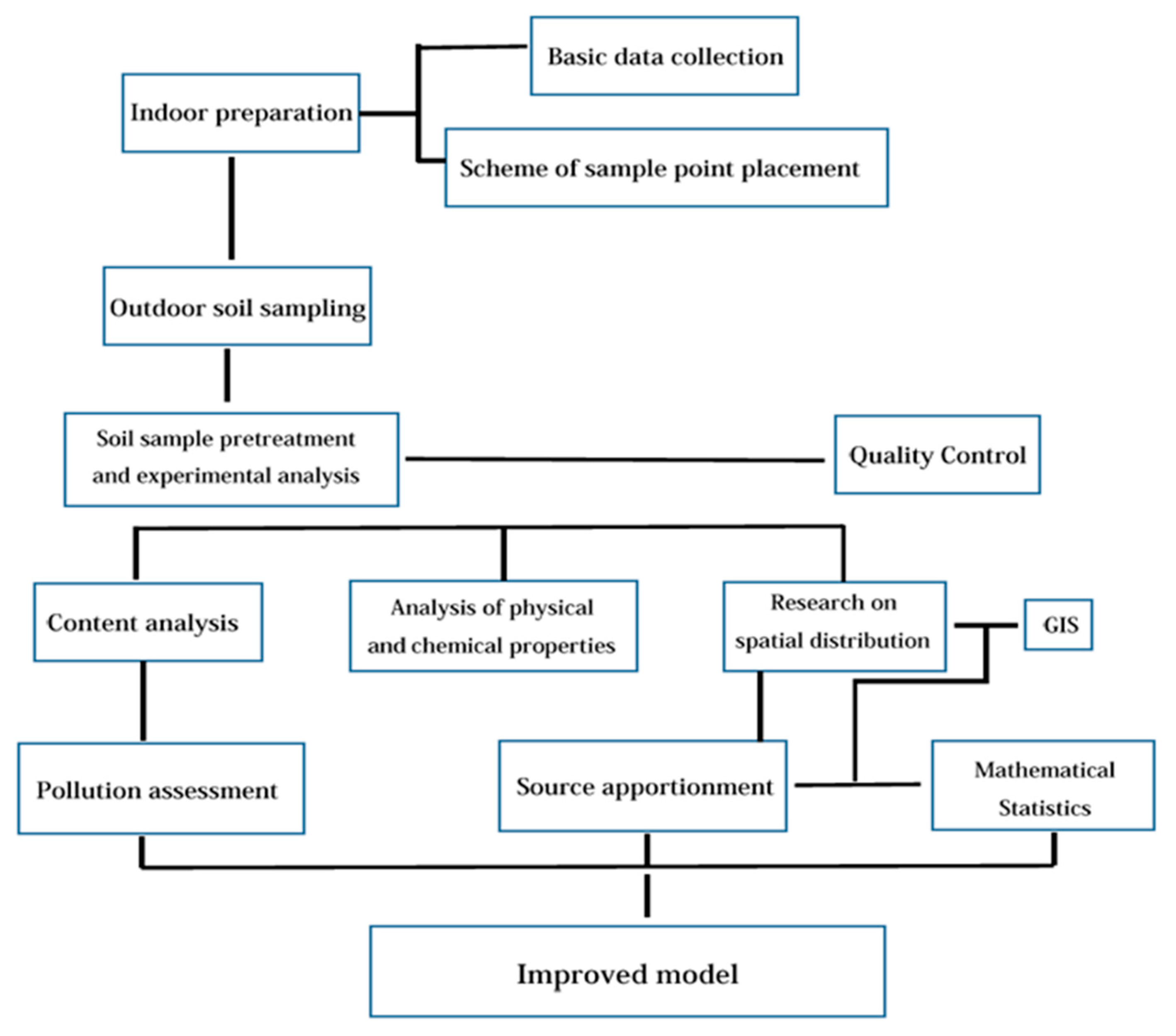
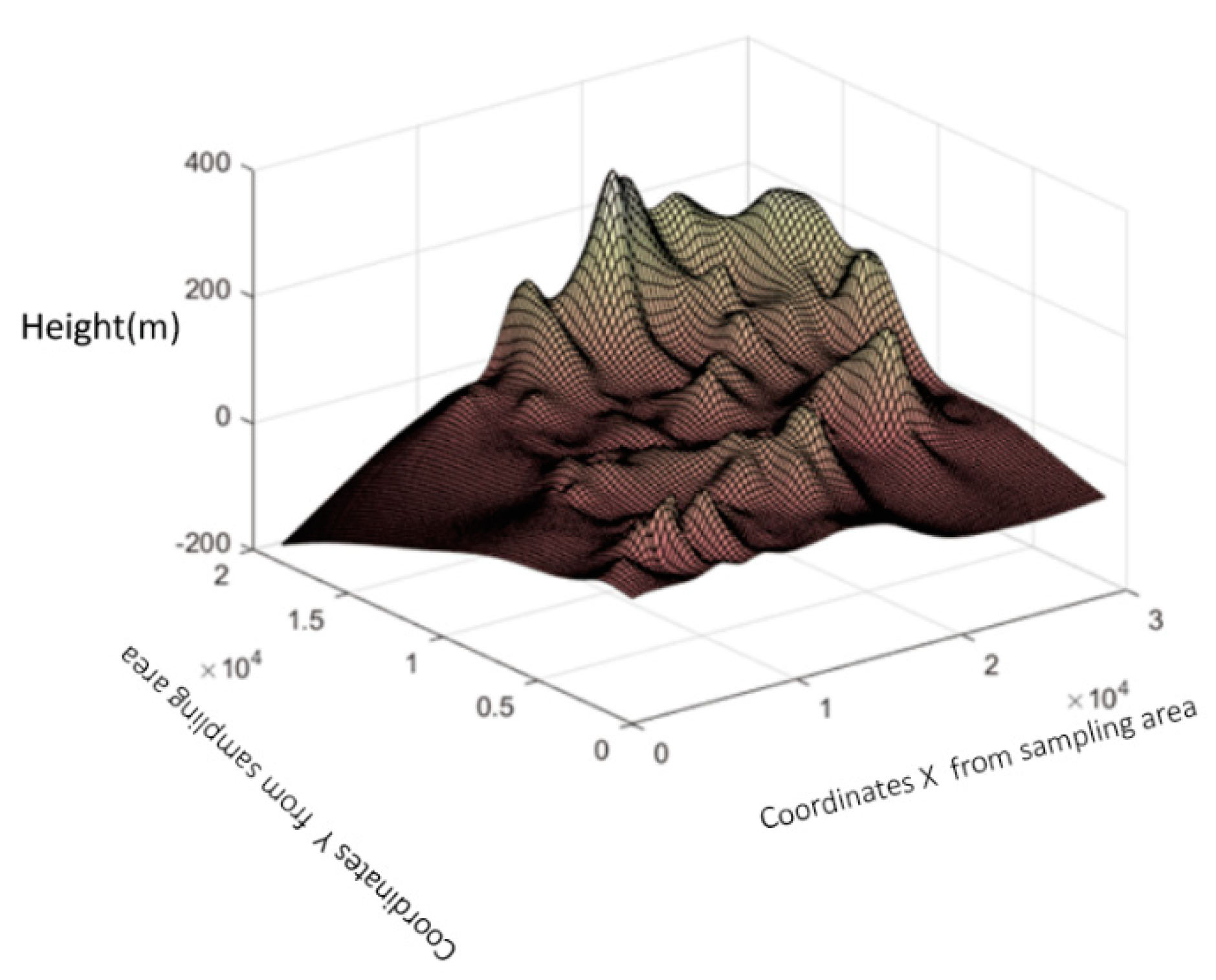
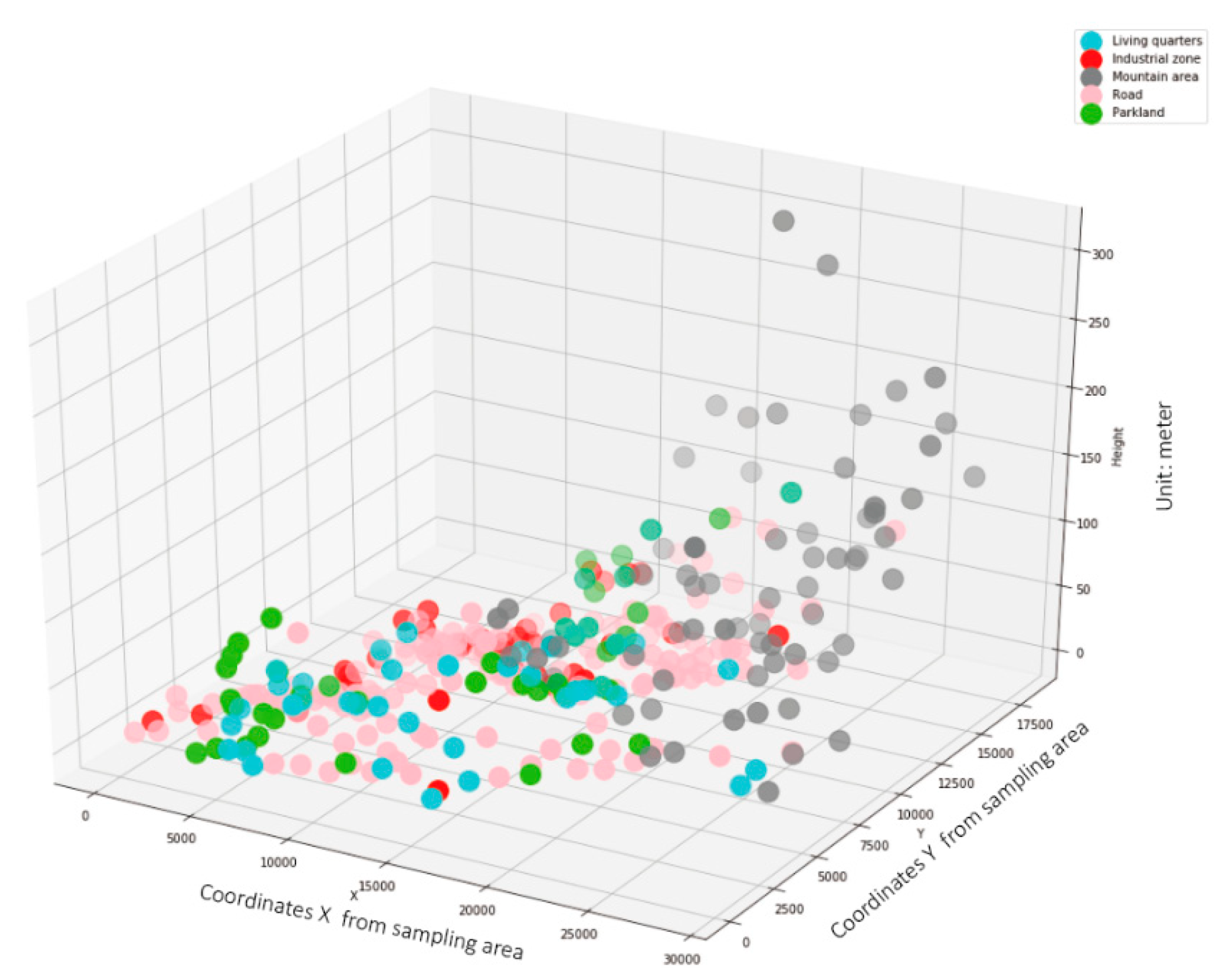
2. Data and Modeling Preparation
Kriging Spatial Interpolation
3. Pollutant Diffusion Model
3.1. Improved Convective Dispersion Model
3.2. Air Subsidence Model
3.2.1. Simple Air Subsidence Model
3.2.2. Improved Air Subsidence Model
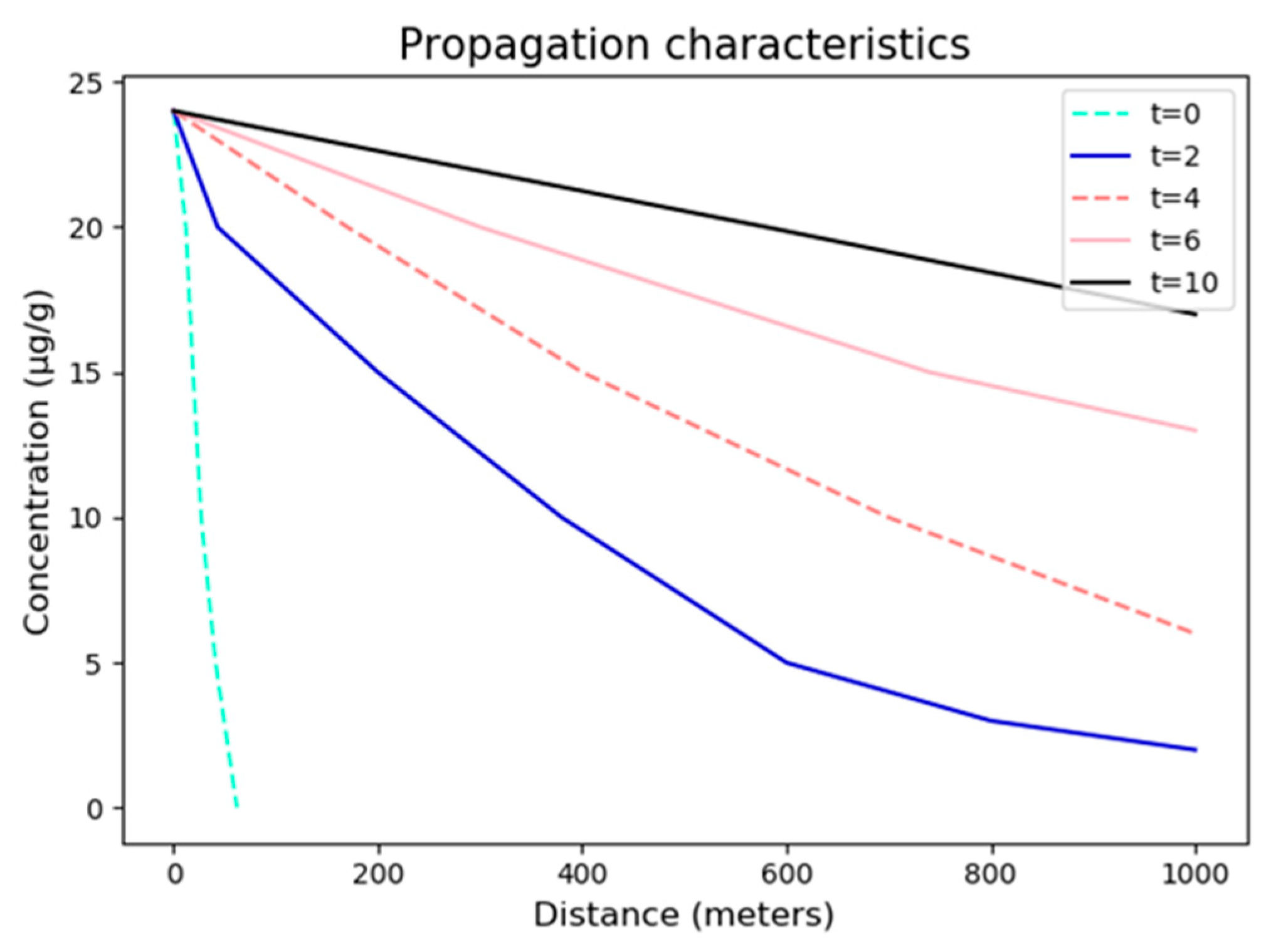
3.3. Propagation Characteristics of Pollutants
4. Discussion
4.1. Prediction of Pollution Source Location
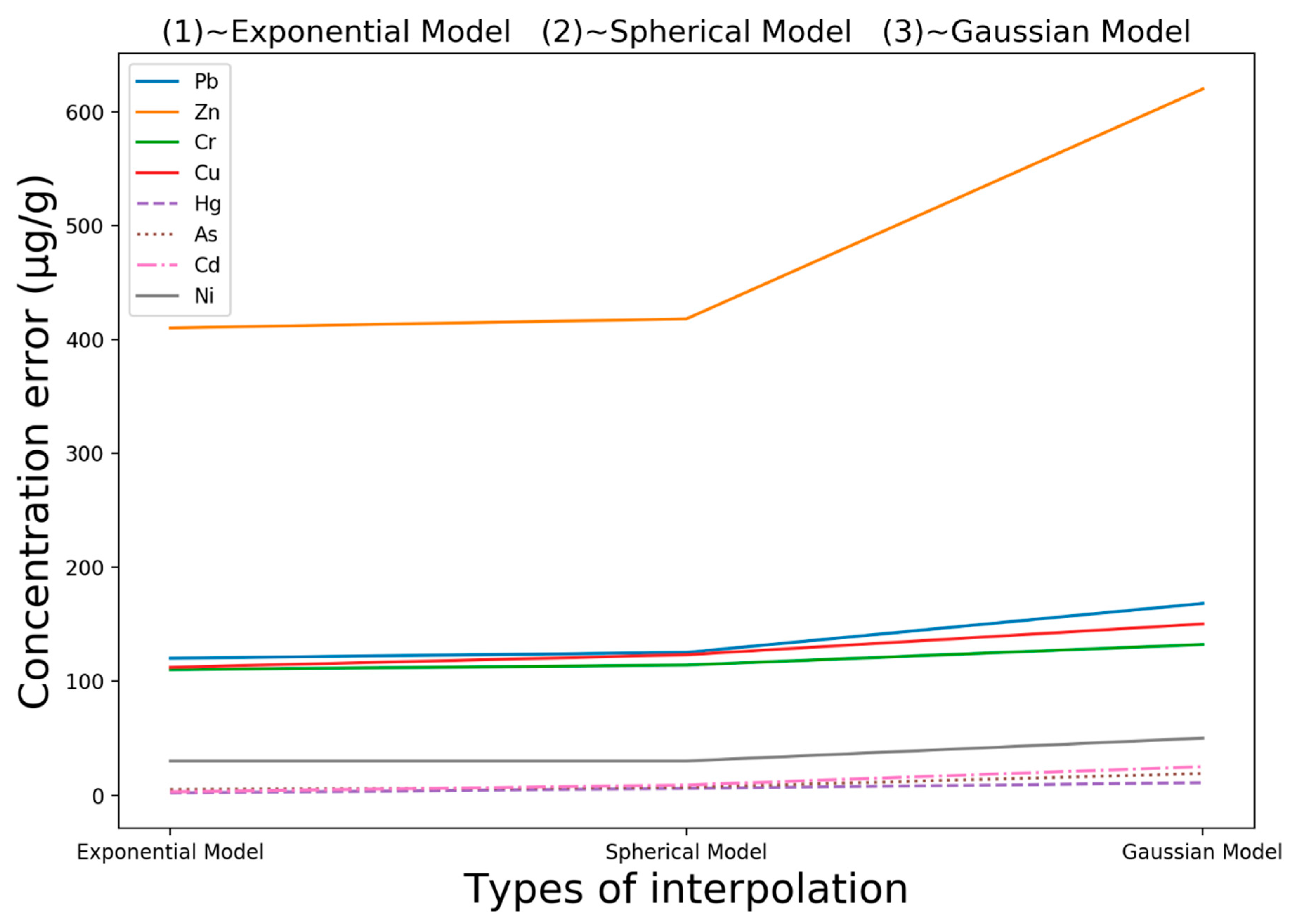
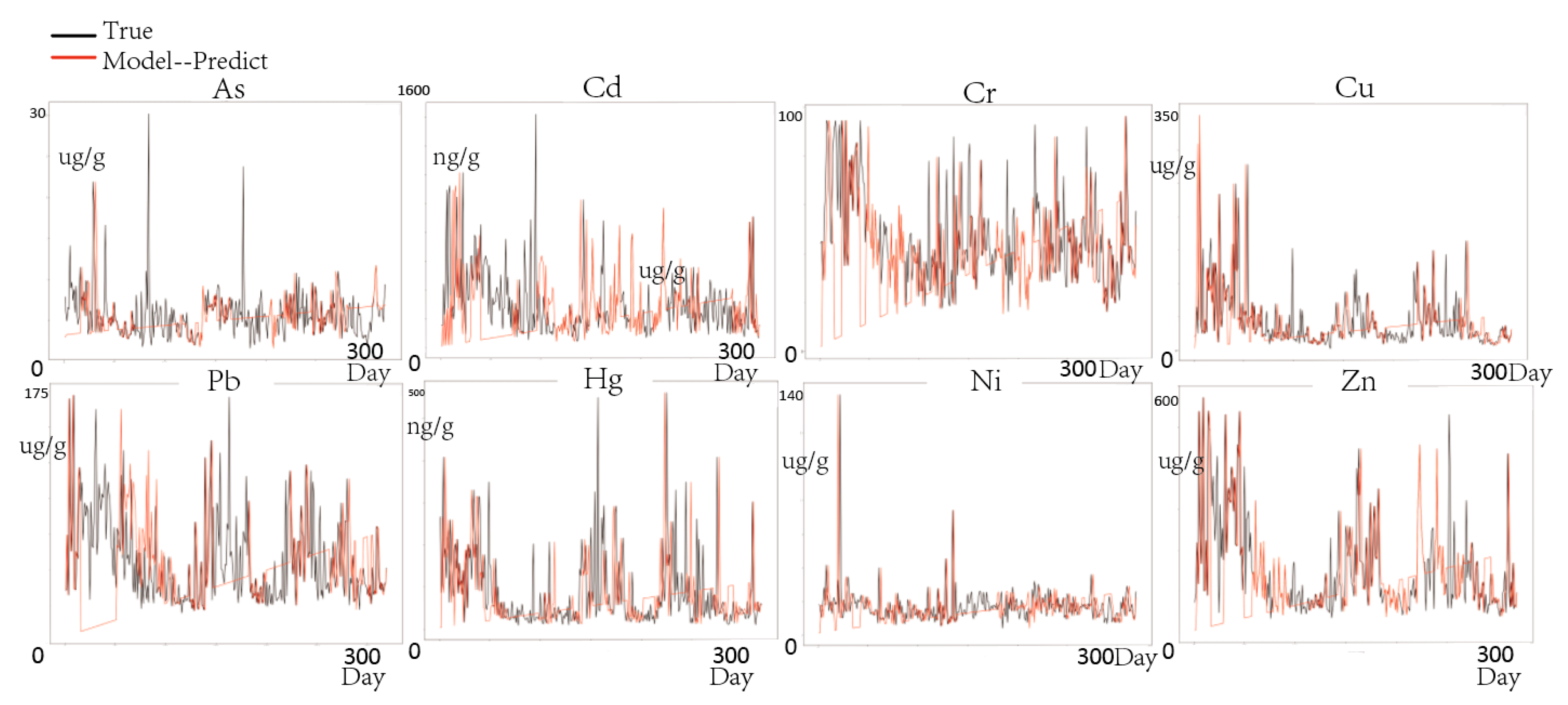
4.2. Prediction Effect of the Improved Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sennett, R. The Open City; Routledge: New York, NY, USA, 2017; pp. 97–106. [Google Scholar]
- Douglas, I. Urban ecology. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2016; pp. 1–13. [Google Scholar] [CrossRef]
- Mehr, M.R.; Keshavarzi, B.; Moore, F.; Sharifi, R.; Lahijanzadeh, A.; Kermani, M. Distribution, source identification and health risk assessment of soil heavy metals in urban areas of Isfahan province. J. Afr. Earth Sci. 2017, 132, 16–26. [Google Scholar] [CrossRef]
- Zhichao, L.; Tianqu, S. An Improved Ecological Services Valuation Model in Land Use Project. Int. J. Environ. Res. Public Health 2019, 16, 1474. [Google Scholar] [CrossRef]
- Maas, S.; Scheifler, R.; Benslama, M.; Crini, N.; Lucot, E.; Brahmia, Z.; Benyacoub, S.; Giraudoux, P. Spatial distribution of heavy metal concentrations in urban, suburban and agricultural soils in a Mediterranean city of Algeria. Environ. Pollut. 2010, 158, 2294–2301. [Google Scholar] [CrossRef] [PubMed]
- Manta, D.S.; Angelone, M.; Bellanca, A.; Neri, R.; Sprovieri, M. Heavy metals in urban soils: A case study from the city of Palermo (Sicily), Italy. Sci. Total Environ. 2002, 300, 229–243. [Google Scholar] [CrossRef]
- Andersson, M.; Ottesen, R.T.; Langedal, M. Geochemistry of urban surface soils—Monitoring in Trondheim, Norway. Geoderma 2020, 156, 112–118. [Google Scholar] [CrossRef]
- Morton-Bermea, O.; Hernández-Álvarez, E.; González-Hernández, G.; Romero, F.; Lozano, R.; Beramendi-Orosco, L.E. Assessment of heavy metal pollution in urban topsoils from the metropolitan area of Mexico City. J. Geochem. Explor. 2009, 101, 218–224. [Google Scholar] [CrossRef]
- Harrison, R.M.; Chirgawi, M.B. The assessment of air and soil as contributors of some trace metals to vegetable plants I. Use of a filtered air growth cabinet. Sci. Total Environ. 1989, 83, 13–34. [Google Scholar] [CrossRef]
- Kasassi, A.; Rakimbei, P.; Karagiannidis, A.; Zabaniotou, A.; Tsiouvaras, K.; Nastis, A.; Tzafeiropoulou, K. Soil contamination by heavy metals: Measurements from a closed unlined landfill. Bioresour. Technol. 2008, 99, 8578–8584. [Google Scholar] [CrossRef]
- Qing, X.; Yutong, Z.; Shenggao, L. Assessment of heavy metal pollution and human health risk in urban soils of steel industrial city (Anshan), Liaoning, Northeast China. Ecotoxicol. Environ. Saf. 2015, 120, 377–385. [Google Scholar] [CrossRef]
- Selim, H.M.; Sparks, D.L. (Eds.) Heavy Metals Release in Soils; CRC Press: Boca Raton, FL, USA, 2001; pp. 10–21. [Google Scholar]
- Qiao, P.; Lei, M.; Guo, G.; Yang, J.; Zhou, X.; Chen, T. Quantitative analysis of the factors influencing soil heavy metal lateral migration in rainfalls based on Geographical detector software: A case study in Huanjiang county, China. Sustainability 2017, 9, 1227. [Google Scholar] [CrossRef]
- Ishchenko, V. Soil contamination by heavy metal mobile forms near landfills. Int. J. Environ. Waste Manag. 2017, 20, 66–74. [Google Scholar] [CrossRef]
- Ukpaka, C. Empirical model approach for the evaluation of pH and conductivity on pollutant diffusion in soil environment. Chem. Int. 2016, 2, e278. [Google Scholar]
- Murray, K.; Bazzi, A.; Carter, C.; Ehlert, A.; Kopec, M.; Richardson, J.; Sokol, H. Distribution and mobility of lead in soils at an outdoor shooting range. Soil Sediment Contam. 1997, 6, 79–93. [Google Scholar] [CrossRef]
- Wu, G.; Li, L.Y. Modeling of heavy metal migration in sand/bentonite and the leachate pH effect. J. Contam. Hydrol. 1988, 33, 313–336. [Google Scholar] [CrossRef]
- Goovaerts, P.; Webster, R.; Dubois, J.P. Assessing the risk of soil contamination in the Swiss Jura using indicator geostatistics. Environ. Ecol. Stat. 1997, 4, 49–64. [Google Scholar] [CrossRef]
- Fallah, B.; Richter, A.; Ng, K.T.W.; Salama, A. Effects of groundwater metal contaminant spatial distribution on overlaying kriged maps. Environ. Sci. Pollut. Res. 2019, 26, 22945–22957. [Google Scholar] [CrossRef] [PubMed]
- Higham, D.J.; Higham, N.J. MATLAB Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016; pp. 445–446. [Google Scholar]
- Chambers, J.M. Graphical Methods for Data Analysis: 0; Chapman and Hall/CRC: New York, NY, USA, 2017; pp. 48–50. [Google Scholar]
- Gowd, S.S.; Reddy, M.R.; Govil, P.K. Assessment of heavy metal contamination in soils at Jajmau (Kanpur) and Unnao industrial areas of the Ganga Plain, Uttar Pradesh, India. J. Hazard. Mater. 2010, 174, 113–121. [Google Scholar] [CrossRef]
- Khalid, N.; Hussain, M.; Young, H.S.; Boyce, B.; Aqeel, M.; Noman, A. Effects of road proximity on heavy metal concentrations in soils and common roadside plants in Southern California. Environ. Sci. Pollut. Res. 2018, 25, 35257–35265. [Google Scholar] [CrossRef]
- Wildeboer, R.R.; Sloun, R.J.G.V.; Schalk, S.G.; Mannaerts, C.K.; Linden, J.C.V.D.; Huang, P.; Wijkstra, H.; Mischi, M. Convective-dispersion modeling in 3D contrast-ultrasound imaging for the localization of prostate cancer. IEEE Trans. Med. Imaging 2018, 37, 2593–2602. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Daniel, D.E. Diffusion in saturated soil. I: Background. J. Geotech. Eng. 1991, 117, 467–484. [Google Scholar] [CrossRef]
- Acar, Y.B.; Haider, L. Transport of low-concentration contaminants in saturated earthen barriers. J. Geotech. Eng. ASCE 1990, 116, 1031–1052. [Google Scholar] [CrossRef]
- Foose, G.J.; Benson, C.H.; Edil, T.B. Comparison of solute transport in three composite liners. J. Geotech. Geoenviron. Eng. 2002, 128, 391–403. [Google Scholar] [CrossRef]
- Nazir, M.H.; Khan, Z.; Stokes, K. Modelling of metal-coating delamination incorporating variable environmental parameters. J. Adhes. Sci. Technol. 2015, 29, 392–423. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Tack, F.; Marc, M.G.; Verloo, G. Chemical speciation and fractionation in soil and sediment heavy metal analysis: A review. Int. J. Environ. Anal. Chem. 1995, 59, 225–238. [Google Scholar] [CrossRef]
- Ogunbanjo, O.; Onawumi, O.; Gbadamosi, M.; Ogunlana, A.; Anselm, O. Chemical speciation of some heavy metals and human health risk assessment in soil around two municipal dumpsites in Sagamu, Ogun state, Nigeria. Chem. Speciat. Bioavailab. 2016, 28, 142–151. [Google Scholar] [CrossRef]
- Nevedrov, N.P.; Protsenko, E.P.; Glebova, I.V. The relationship between bulk and mobile forms of heavy metals in soils of Kursk. Eurasian Soil Sci. 2018, 51, 112–119. [Google Scholar] [CrossRef]

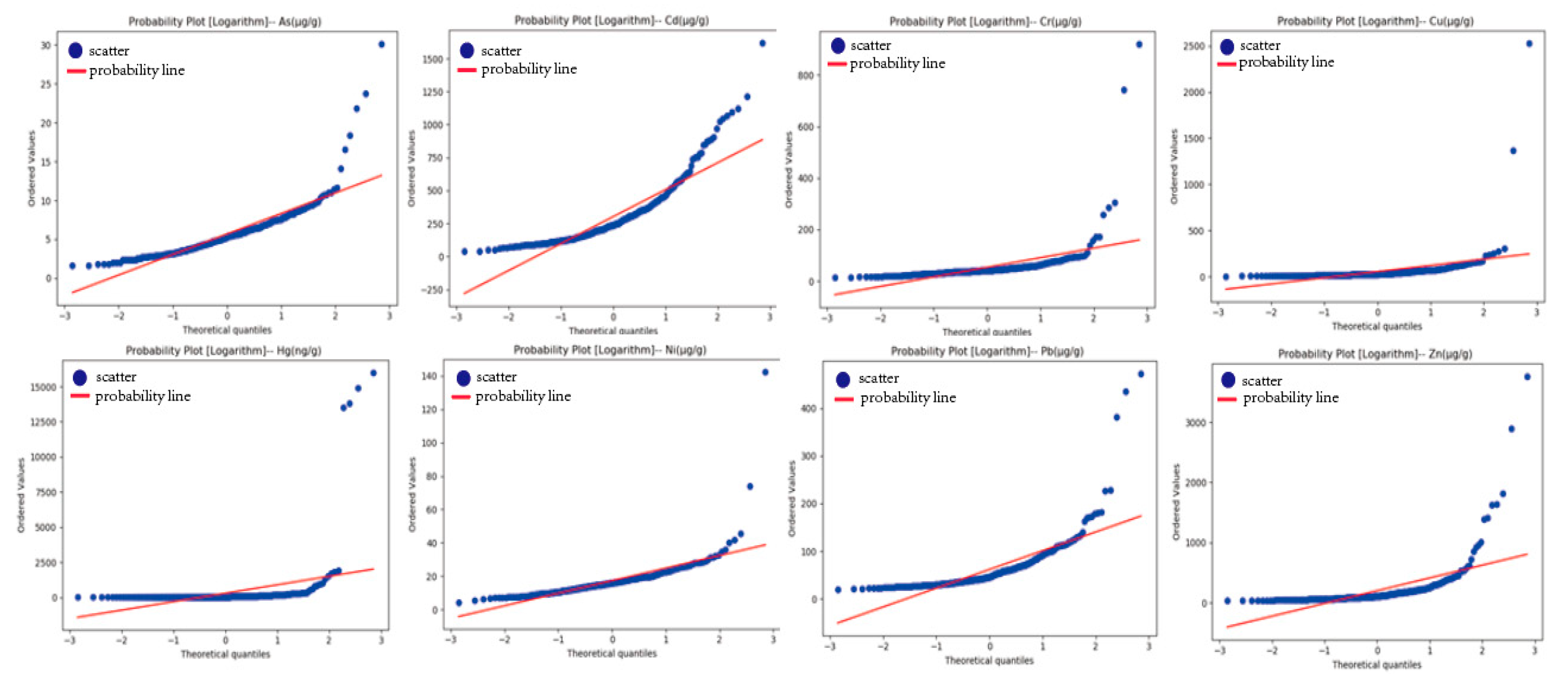
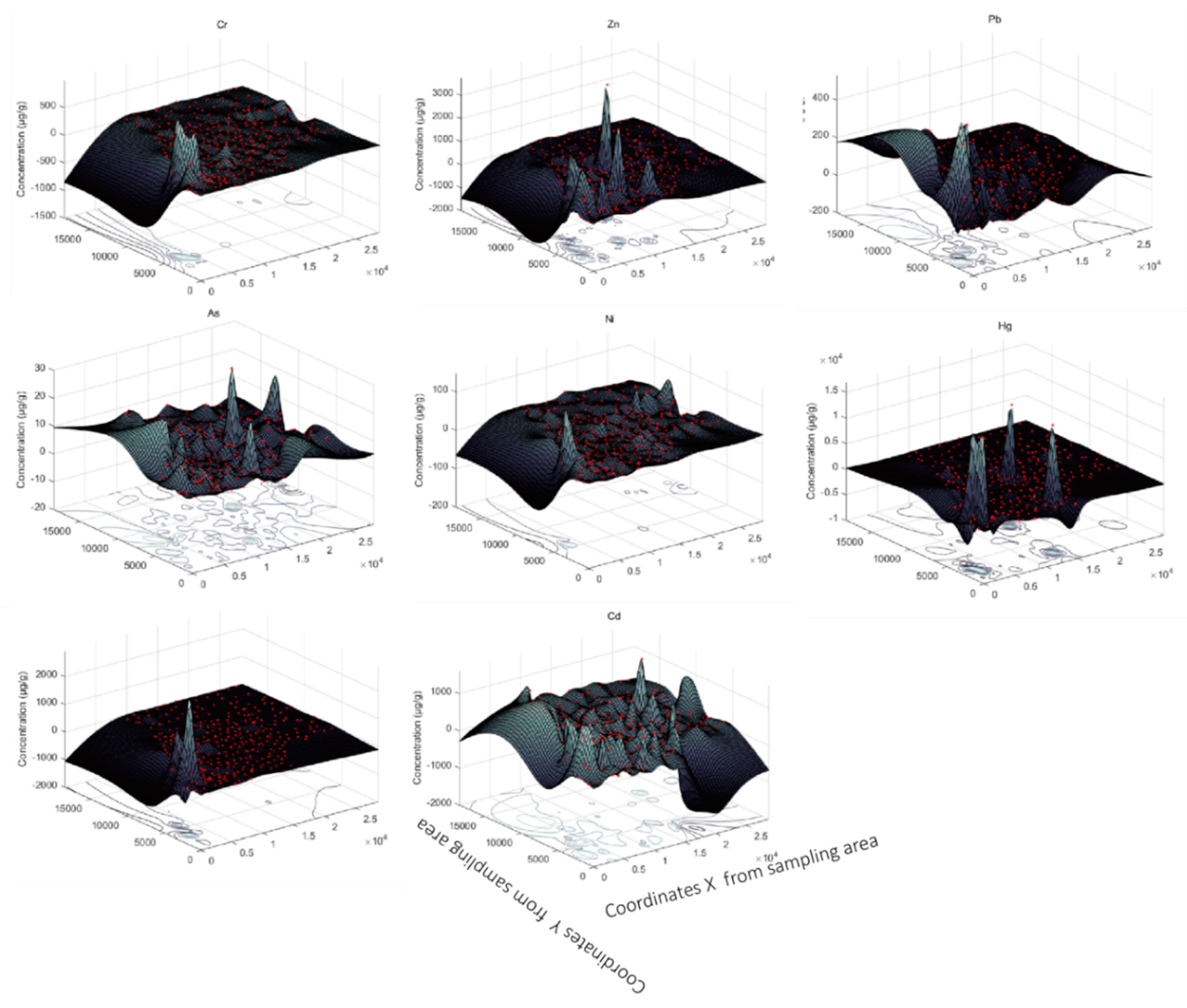
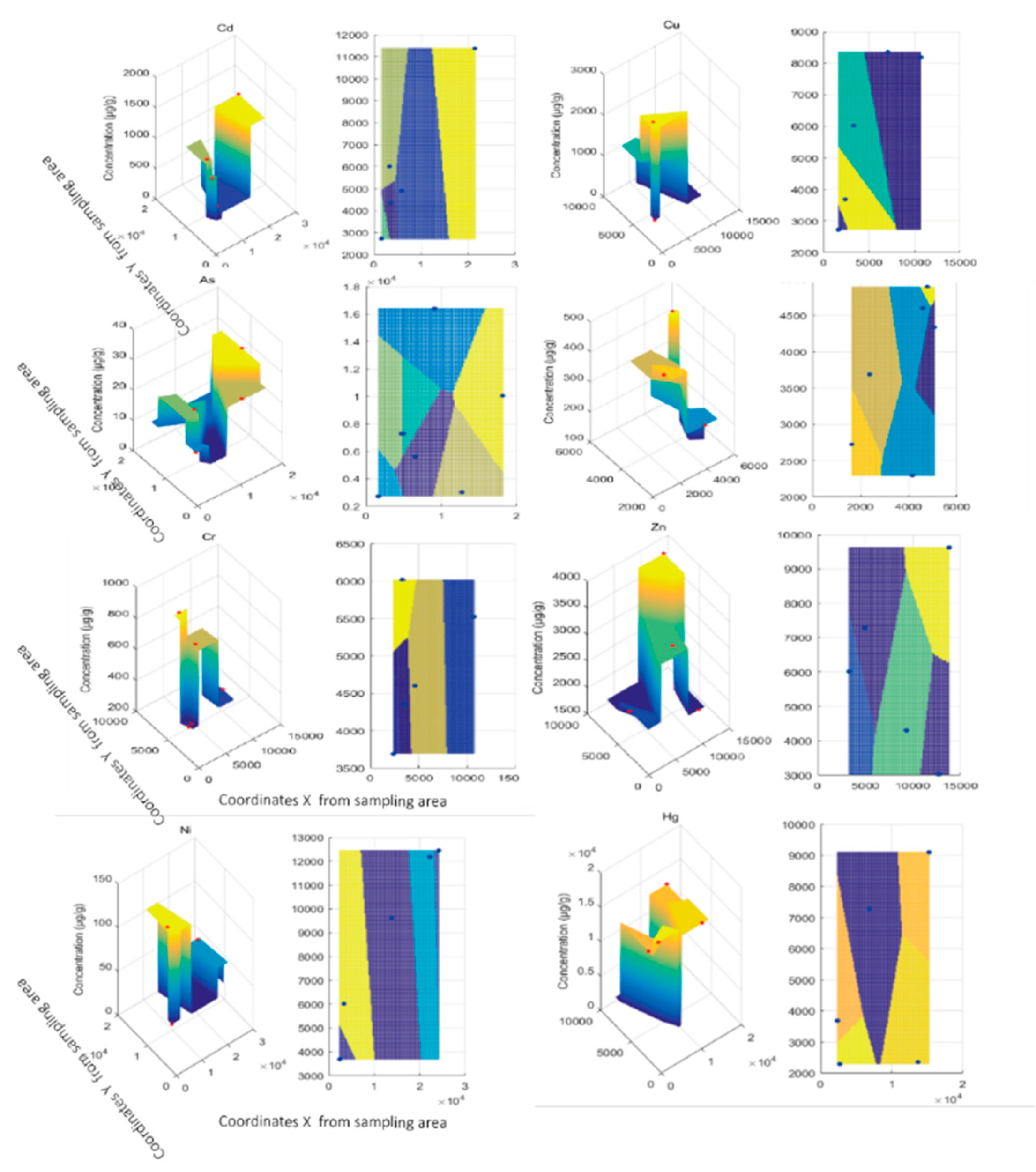
| Element | Nugget | Structural Variance | Sill Value | Model | |
|---|---|---|---|---|---|
| As | 2.446 | 0.719 | 3.165 | 77.28% | Exponential |
| Cd | 0.002 | 0.009 | 0.011 | 18.18% | Spherical |
| Cr | 3.581 | 2.215 | 5.796 | 61.78% | Exponential |
| Cu | 0.207 | 0.035 | 0.242 | 85.54% | Exponential |
| Hg | 0.257 | 0.192 | 0.449 | 57.24% | Exponential |
| Ni | 1.216 | 2.182 | 3.398 | 35.79% | Exponential |
| Zn | 0.814 | 1.057 | 1.871 | 43.51% | Exponential |
| Pb | 0.916 | 2.490 | 3.406 | 26.89% | Exponential |
| Migration Mode | Simulation | Sensitivity Factors in the Model | |||||
|---|---|---|---|---|---|---|---|
| Heavy Metal Properties | Soil Physical and Chemical Properties | Vegetation Properties | Climatic Factors | ||||
| Type | Form | Organic Matter, pH Value, Texture and Moisture Content | Cumulative Effect | ||||
| Degree of Influence | Degree of Influence | Degree of Influence | |||||
| Vertical migration | Integral model | Convective dispersion model | / | +++ | ++ | / | / |
| Air subsidence model | + | / | / | ++ | +++ | ||
| Improved model | + | / | ++ | ++ | ++ | ||
| Horizontal migration | SWAT model | ++ | ++++ | +++ | +++ | +++ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, W.; Huang, J. Monitoring, Diffusion and Source Speculation Model of Urban Soil Pollution. Processes 2020, 8, 1339. https://doi.org/10.3390/pr8111339
Li Z, Lu W, Huang J. Monitoring, Diffusion and Source Speculation Model of Urban Soil Pollution. Processes. 2020; 8(11):1339. https://doi.org/10.3390/pr8111339
Chicago/Turabian StyleLi, Zhichao, Wanchun Lu, and Jilin Huang. 2020. "Monitoring, Diffusion and Source Speculation Model of Urban Soil Pollution" Processes 8, no. 11: 1339. https://doi.org/10.3390/pr8111339
APA StyleLi, Z., Lu, W., & Huang, J. (2020). Monitoring, Diffusion and Source Speculation Model of Urban Soil Pollution. Processes, 8(11), 1339. https://doi.org/10.3390/pr8111339




