Mathematical Model of COVID-19 Transmission Dynamics in South Korea: The Impacts of Travel Restrictions, Social Distancing, and Early Detection
Abstract
1. Introduction
2. Data and Model
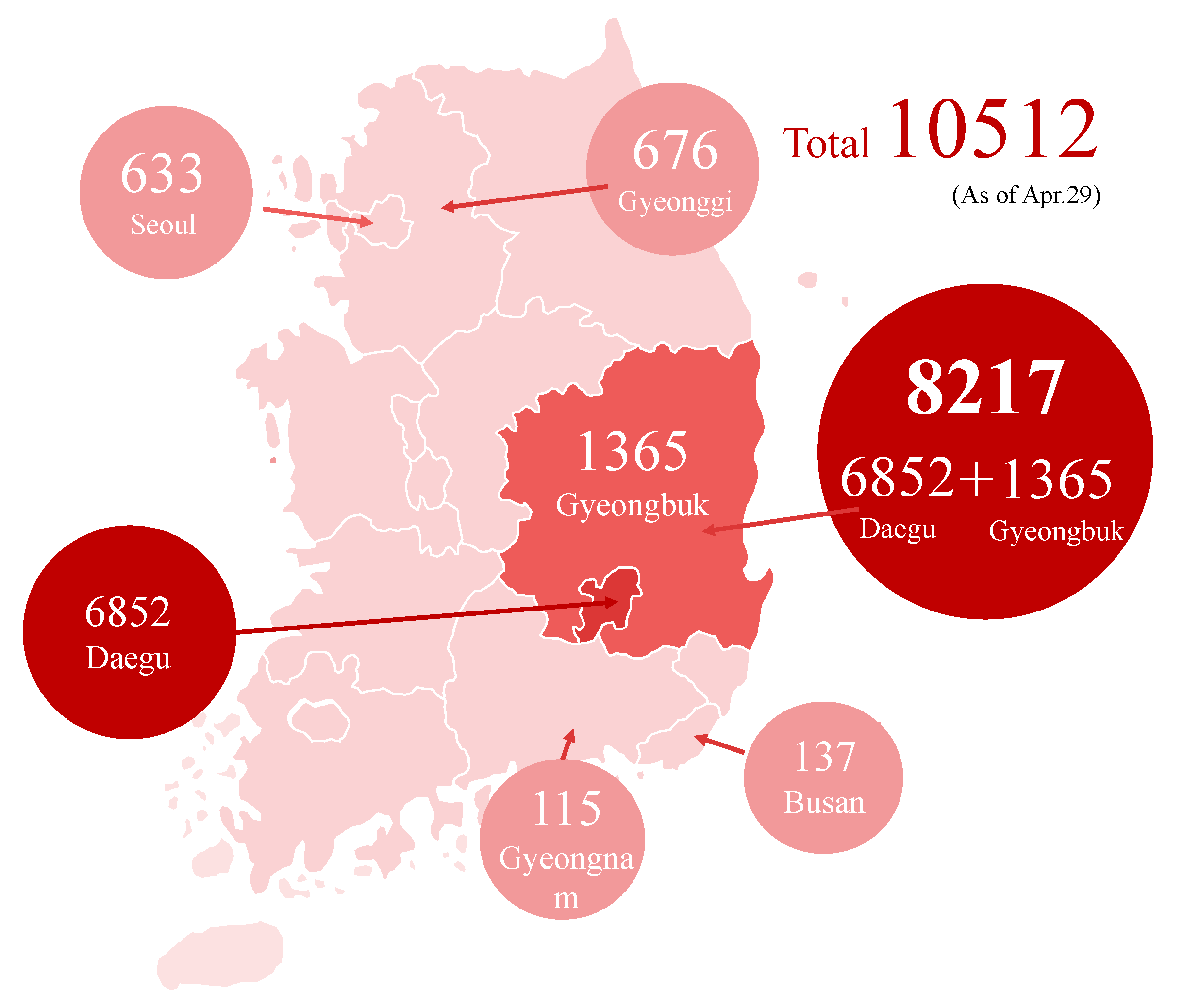
2.1. Characteristics of the Early COVID-19 Outbreaks in South Korea
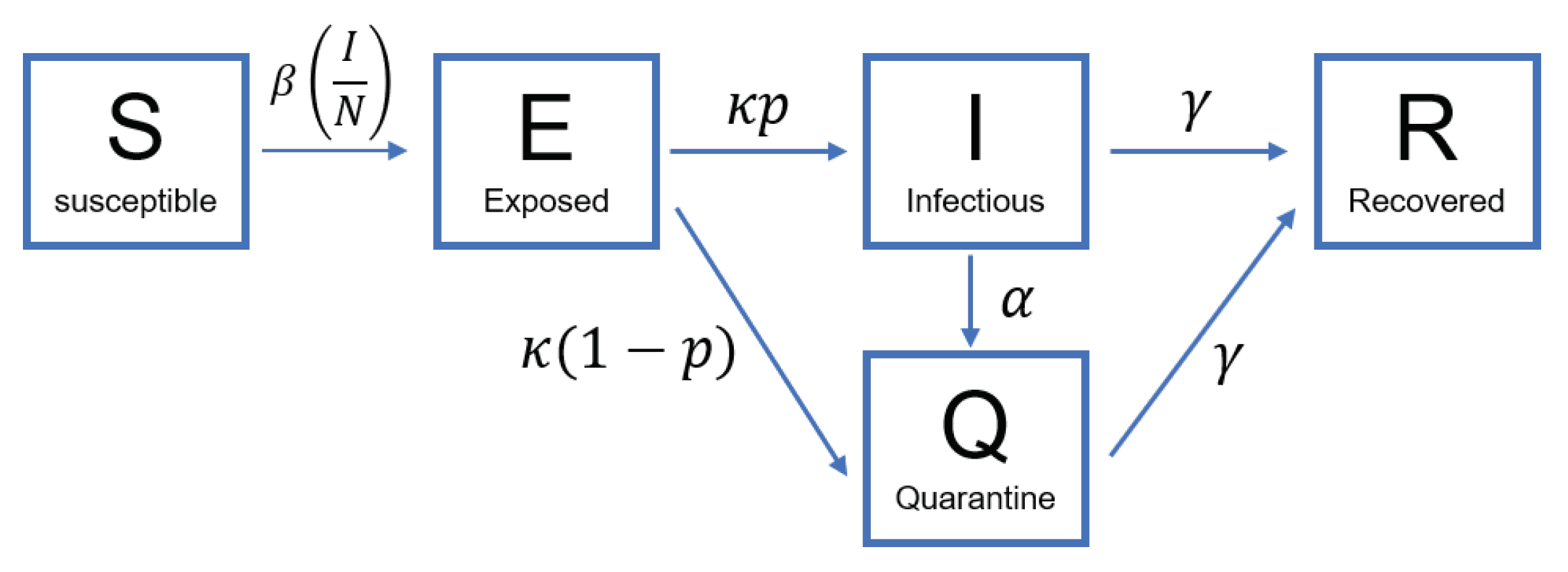
2.2. A Single-Patch Model: SEIQR Model
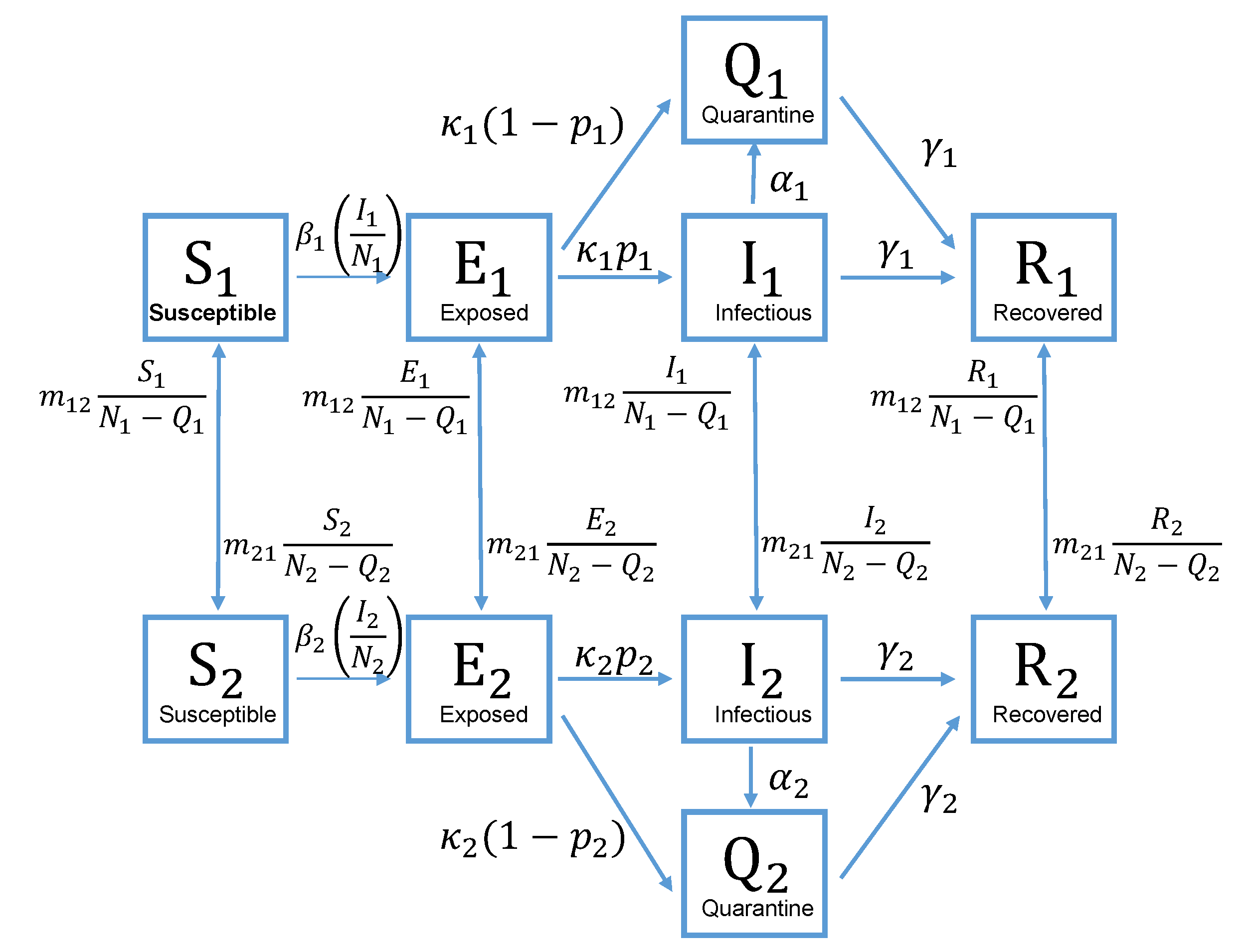
2.3. Two-Patch Transmission Model
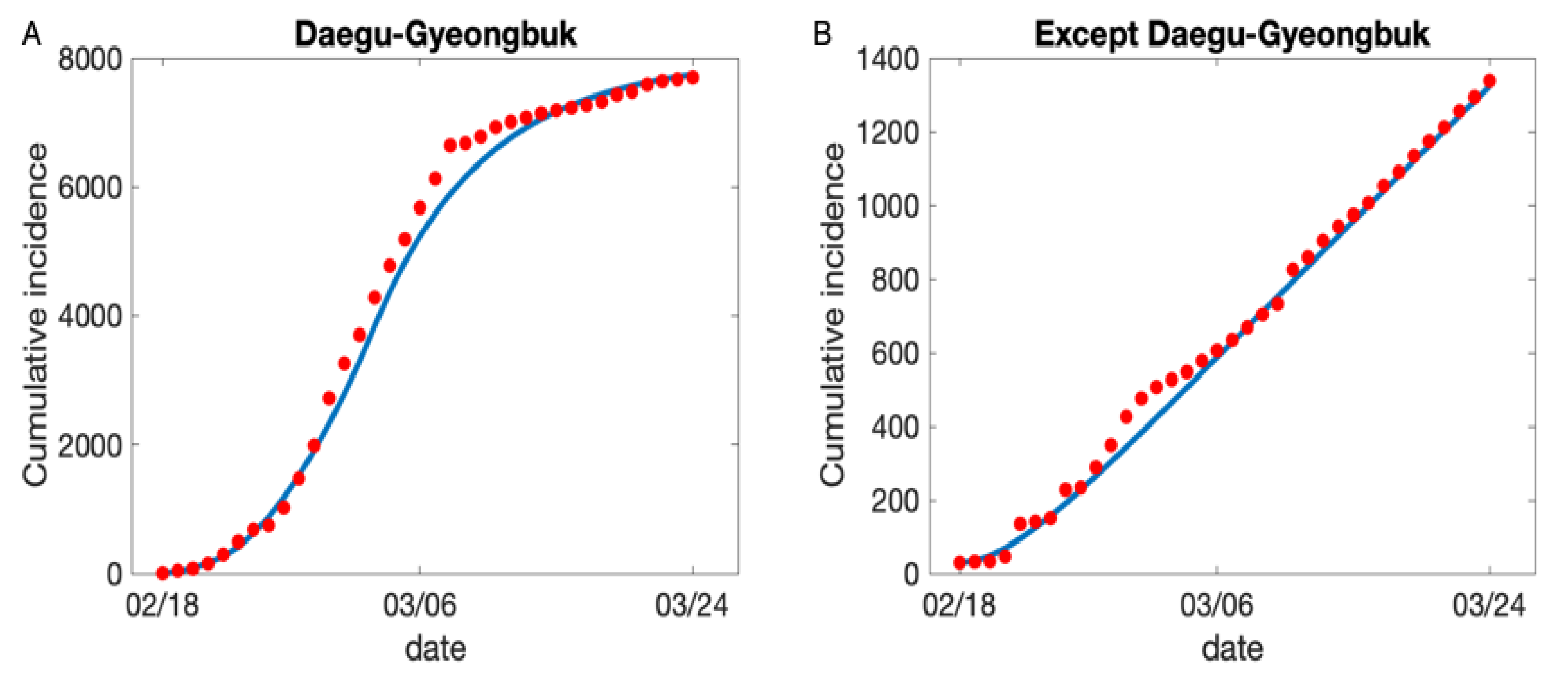
3. Parameter Estimation
3.1. Estimated Parameter
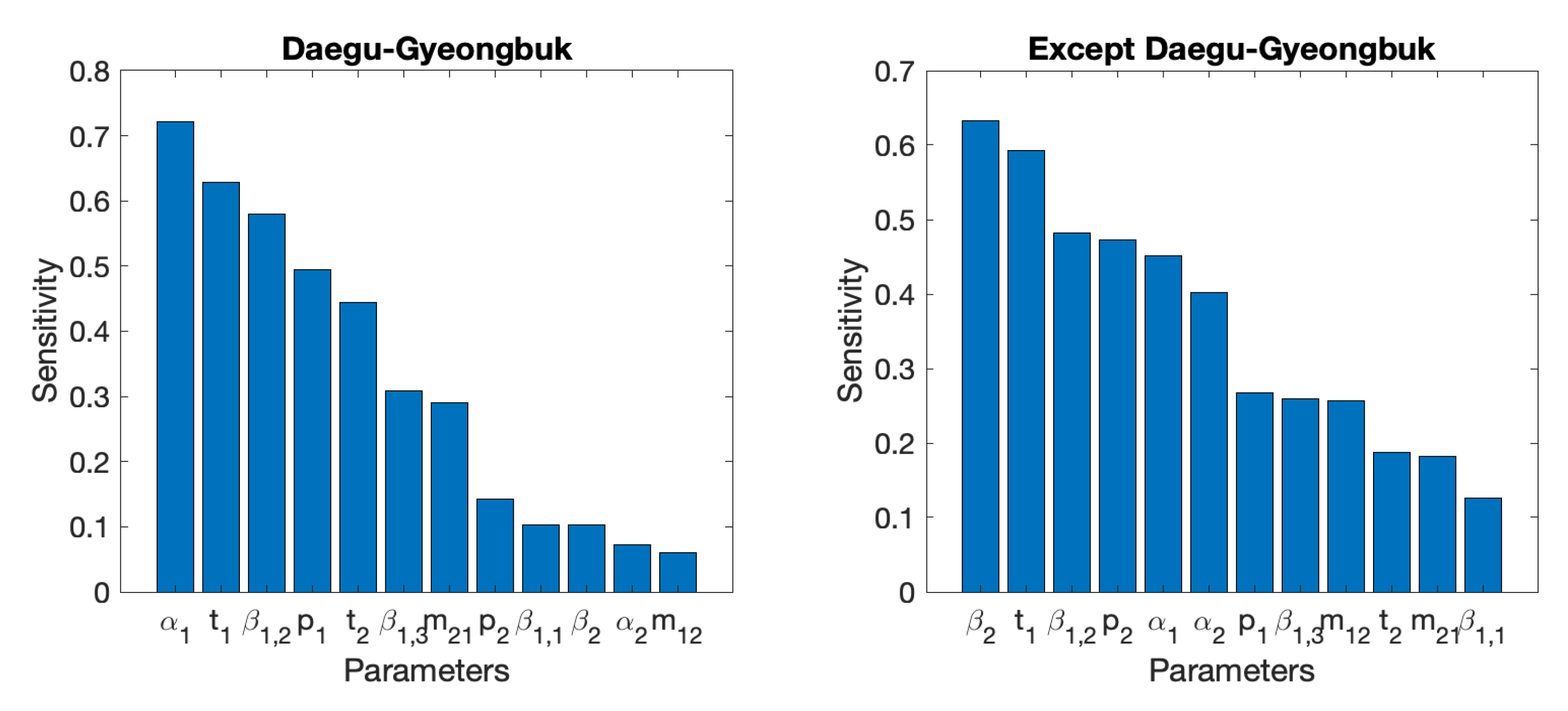
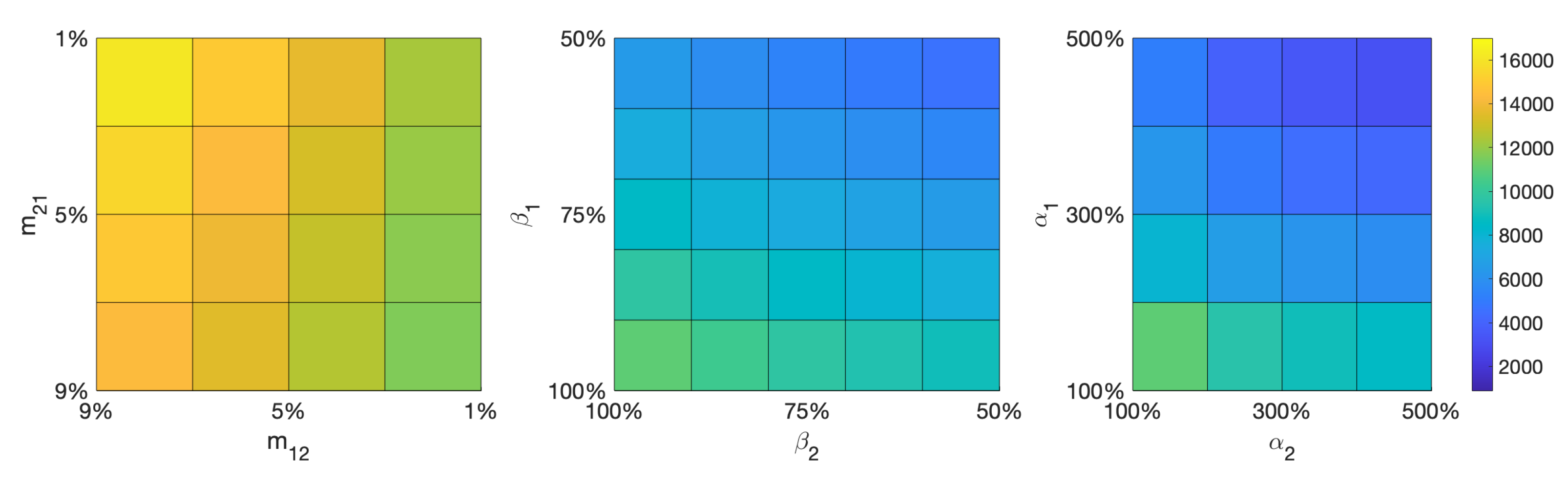
3.2. Sensitivity Analysis
4. Numerical Simulations
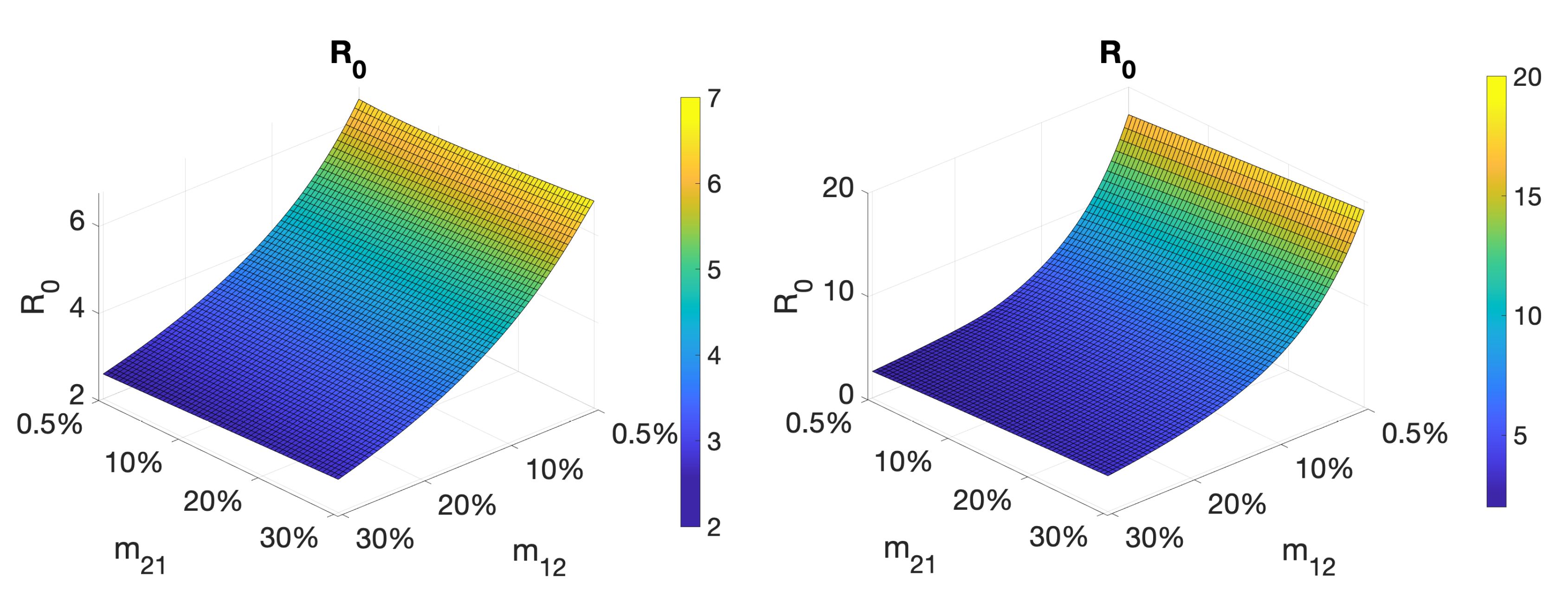
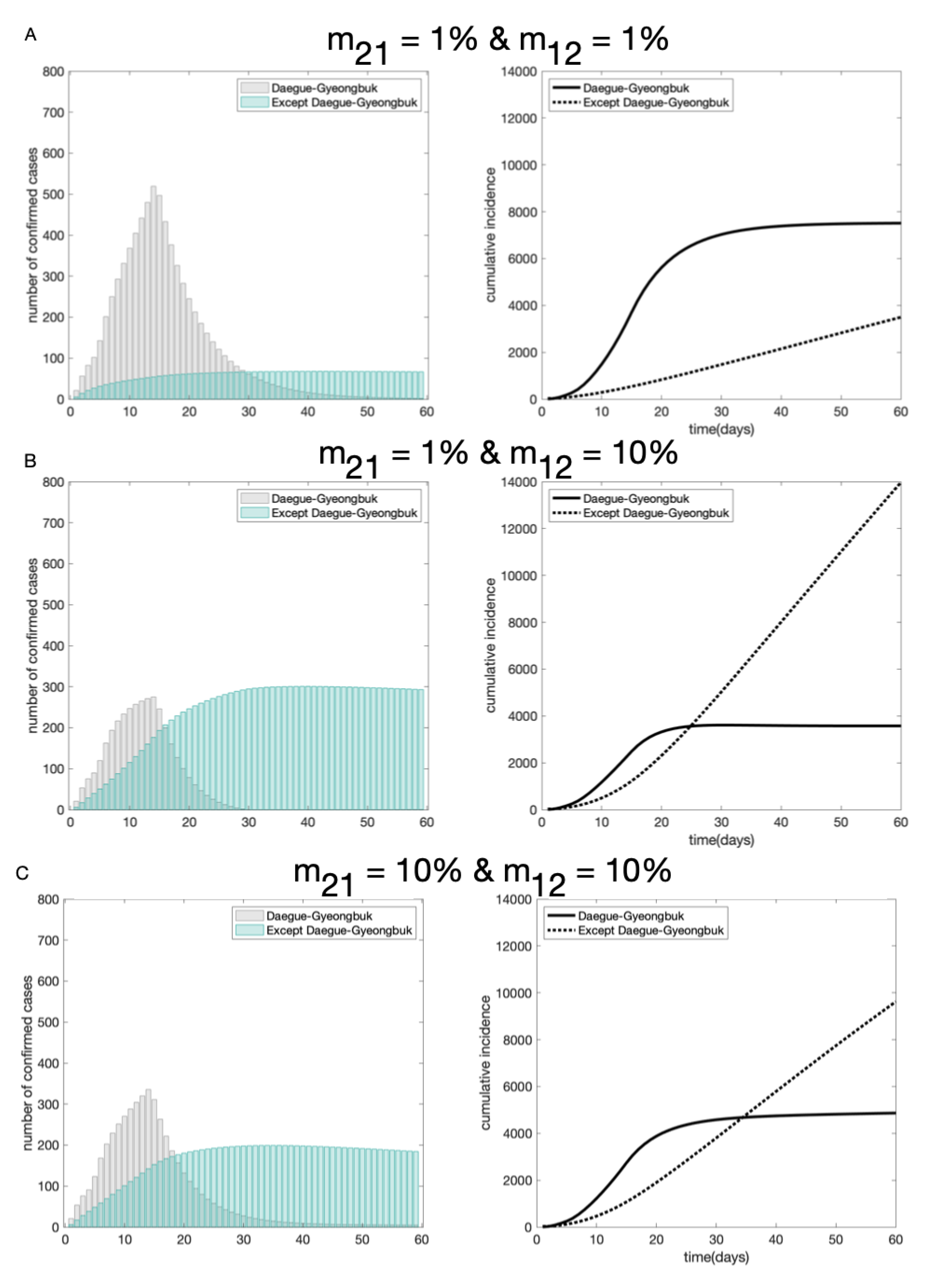
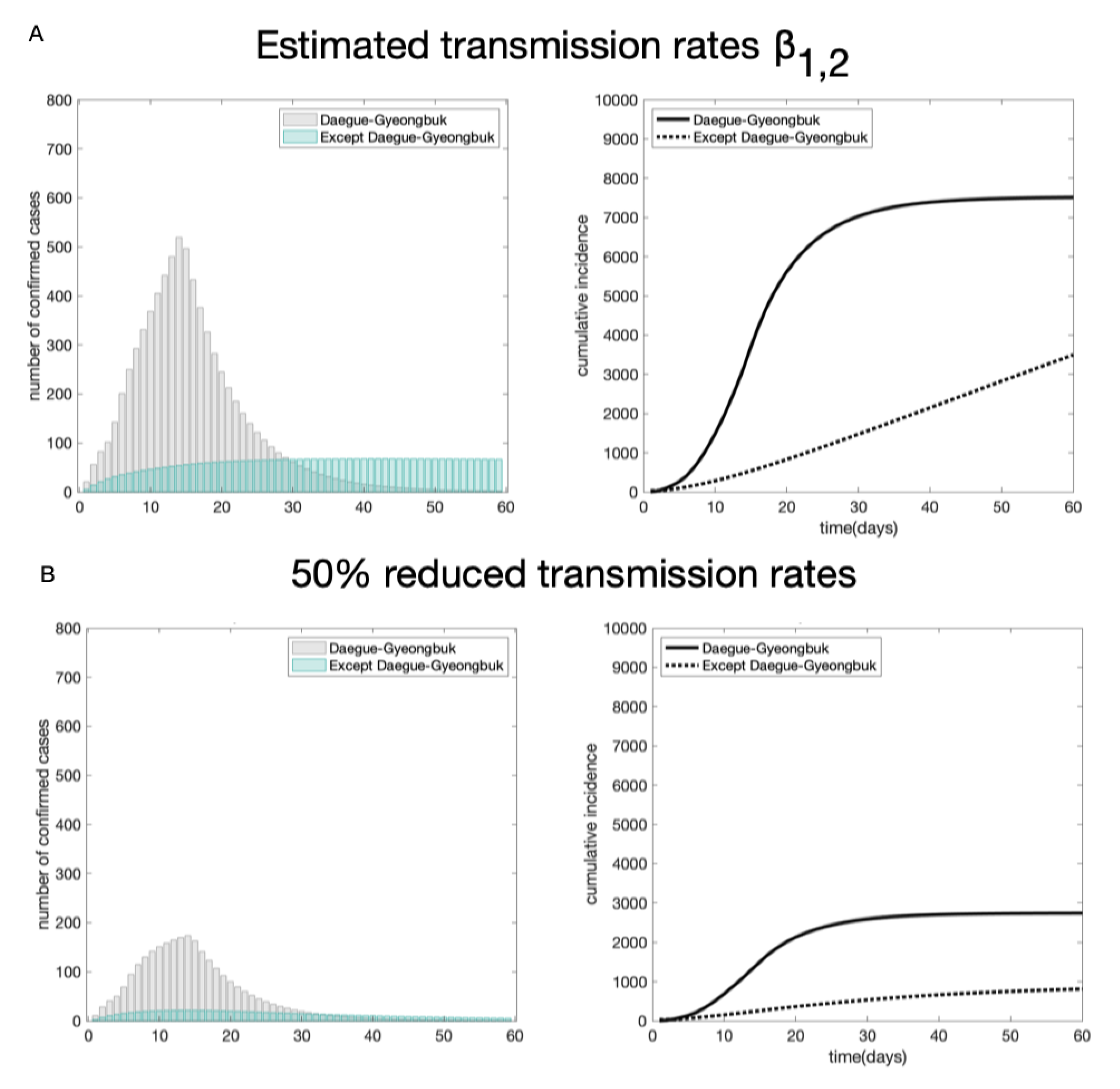
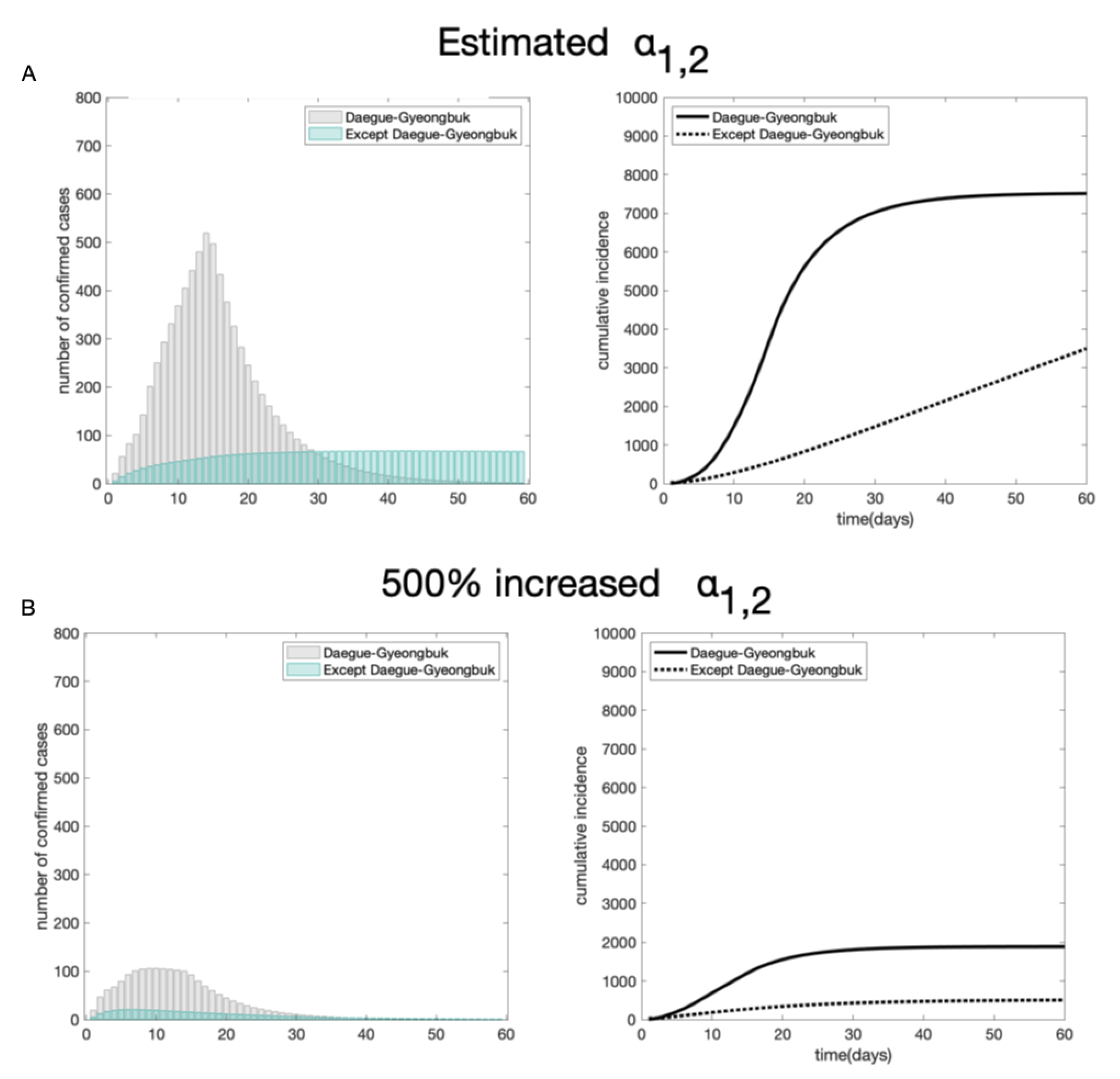
4.1. The Impact of Mobility on the COVID-19 Transmission Dynamics
4.2. The Impact of Social Distancing and Early Detection on the COVID-19 Transmission Dynamics
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
The Global Basic Reproduction Number
References
- Mayo Clinic. Available online: https://www.mayoclinic.org/diseases-conditions/coronavirus/symptoms-causes/syc-20479963 (accessed on 27 May 2020).
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.; Fu, H.; et al. Estimates of the severity of COVID-19 disease. medRxiv 2020. [Google Scholar] [CrossRef]
- Center for Disease Control (CDC). Available online: https://www.cdc.gov/coronavirus/2019-ncov/symptoms-testing/symptoms.html (accessed on 27 May 2020).
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science 2020, 6490, 489–493. [Google Scholar] [CrossRef]
- World Health Organization(WHO). Coronavirus. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 31 March 2020).
- Johns Hopikins University and Medicine. Coronavirus Resource Center. Available online: https://coronavirus.jhu.edu/map.html (accessed on 31 March 2020).
- The Korea Herald. Available online: http://www.koreaherald.com/view.php?ud=20200305000889$&$np=85$&$mp=9 (accessed on 6 March 2020).
- Korea Center for Disease Control (KCDC). Available online: https://www.cdc.go.kr/board/ (accessed on 2 March 2020).
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2000. [Google Scholar]
- Murray, J.D. Mathematical Biology. II: Spatial Models and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Sattenspiel, L.; Dietz, K. A structured epidemic model incorporating geographic- mobility among regions. Math. Biosci. 1995, 128, 71–91. [Google Scholar] [CrossRef]
- Lee, S.; Castillo-Chavez, C. The Role of Residence Times in Two-Patch Dengue Transmission Dynamics and Optimal Strategies. J. Theor. Biol. 2015, 374, 152–164. [Google Scholar] [CrossRef]
- Hyman, J.M.; Laforce, T. Modeling the Spread of Influenza Among Cities. In Biomathematical Modeling Applications in Homeland Security; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Lee, J.M.; Choi, D.; Cho, G.; Kim, Y. The effect of public health interventions on the spread of influenza among cities. J. Theor. Biol. 2012, 293, 131–142. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-Based Analysis, Modelling and Forecasting of the novel Coronavirus (2019-nCoV) outbreak. medRxiv 2020. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Q.; Liu, M.; Wang, Y.; Zhang, A.; Jalali, N. Epidemiological and clinical features of the 2019 novel coronavirus outbreak in China. medRxiv 2020. [Google Scholar] [CrossRef]
- You, C.; Deng, Y.; Hu, W.; Sun, J.; Lin, Q.; Zhou, F. Estimation of the Time-Varying Reproduction Number of COVID-19 Outbreak in China. Int. J. Hyglene Environ. Health 2020. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaga, K.; Chowell, G. Early epidemiological assessment of the transmission potential and virulence of 2019 Novel Coronavirus in Wuhan City: China, 2019. medRxiv 2020. [Google Scholar] [CrossRef]
- Wu, J.; Leung, K.; Leung, G. Now casting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of 2019-nCoV: A mathematical modelling study. medRxiv 2020. [Google Scholar] [CrossRef]
- Piccolomiini, E.L.; Zama, F. Monitoring Italian COVID-19 spread by an adaptive SEIRD model. medRxiv 2020. [Google Scholar] [CrossRef]
- Sadun, L. Effects of Latency on Estimates of the COVID-19 Replication Number. Bull. Math Biol. 2020, 82, 114. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 6490, 493–497. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 6489, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J.; El-harakeh, A.; Bognanni, A.; Lotfi, T.; Loeb, M.; et al. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Rashid, H.; Ridda, I.; King, C.; Begun, M.; Tekin, H.; Wood, J.G.; Booy, R. Evidence Compendium and Advice on Social Distancing and Other Related Measures for Response to an Influenza Pandemic. Paediatr. Respir. Rev. 2015, 16, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Jiang, B.; Yuan, J.; Tao, Y. The impact of social distancing and epicenter lockdown on the COVID-19 epidemic in mainland China: A data-driven SEIQR model study. medRxiv 2020. [Google Scholar] [CrossRef]
- Choi, S.; Ki, M. Estimating the reproductive number and the outbreak size of COVID-19 in Korea. Epidemiol. Health 2020, 42, e2020011. [Google Scholar] [CrossRef]
- Ryu, S.; Ali, S.T.; Jang, C.; Kim, B.; Cowling, B.J. Effect of Nonpharmaceutical Interventions on Transmission of Severe Acute Respiratory Syndrome Coronavirus 2, South Korea, 2020. Emerg. Infect. Dis. 2020, 26, 2406. [Google Scholar] [CrossRef]
- Korea Transfortation DataBase. Available online: https://www.ktdb.go.kr (accessed on 15 May 2020).
- KCDC Briefing Report. Available online: http://ncov.mohw.go.kr/tcmBoardList.do?brdId=3&brdGubun= (accessed on 22 March 2020).
- Daegu Briefing Report. Available online: https://www.daegu.go.kr/icms/bbs/selectBoardArticle.do (accessed on 28 February 2020).
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Coronavirus Incubation Period: 2–14 days. Available online: https://www.worldometers.info/coronavirus/coronavirus-incubation-period/ (accessed on 12 March 2020).
- Byrne, A.W.; McEvoy, D.; Collins, A.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020, 10, e039856. [Google Scholar] [CrossRef]
- Workman, J. Proportion of COVID-19 Cases that Are Asymptomatic in South Korea: Comment on Nishiura et al. Int. J. Infect. Dis. 2020, 96, 398. [Google Scholar] [CrossRef] [PubMed]
- Korean Statistical Information Service. Available online: http://kosis.kr (accessed on 15 May 2020).
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D. E A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Park, S.J.; Lee, G.R.; Kim, J.E.; Lee, J.H.; Jung, Y.; Nam, E.W. The relationship between trends in COVID-19 prevalence and traffic levels in South Korea. Int. J. Infect. Dis. 2020, 96, 399–407. [Google Scholar]
- Moreno, V.; Espinoza, B.; Barley, K.; Paredes, M.; Bichara, D.; Mubayi, A.; Castillo-Chavez, C. Role of Mobility and Health Disparities on the Transmission Dynamics of Tuberculosis. Theor. Biol. Med. Model. 2017, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Lavezzo, E.; Franchin, E.; Ciavarella, C.; Cuomo-Dannenburg, G.; Barzon, L.; Del Vecchio, C.; Rossi, L.; Manganelli, R.; Loregian, A.; Navarin, N.; et al. Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo’. Nature 2020, 584, 425–429. [Google Scholar] [CrossRef] [PubMed]
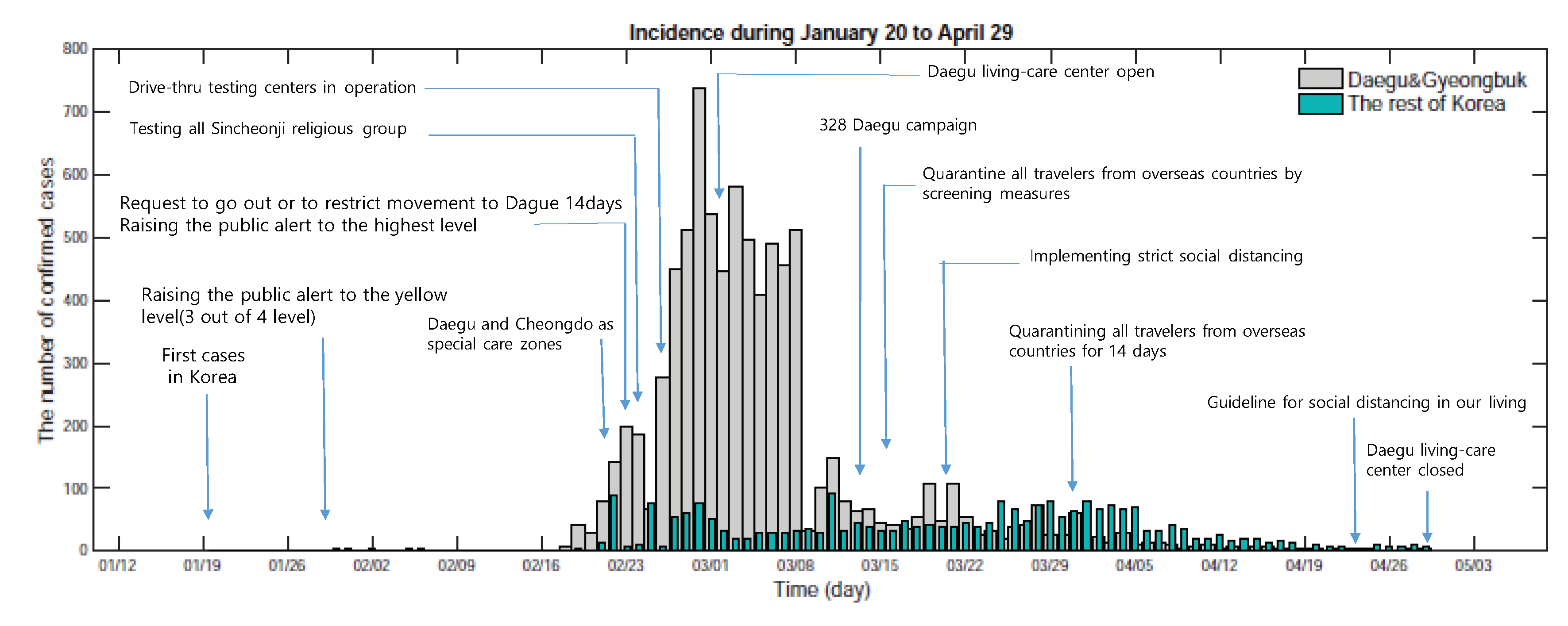
| Date | Administrative Countermeasures | |
|---|---|---|
| 20 January | The first case reported in Korea | |
| 28 January | Raising the public alert to the yellow level (3 out of 4 level) | |
| 3 February | Self-quarantine followed by contact-tracing | |
| 21 February | Declare Daegu and Cheongdo as special care zones | |
| 23 February | Restrict movement in Dague 2 weeks | |
| Raising the public alert to the highest level | ||
| 24 February | Testing all Sincheonji religious group, - Delay schools open | |
| 26 February | Supply of face masks export restriction and sale for public purpose | |
| Drive-through testing centers in operation | ||
| 2 March | Daegu living-care center open | |
| 5 March | Gyeongbuk as a special management zone | |
| 15 March | 328 Daegu campaign (minimization of movement, and social distancing) | |
| 17 March | Quarantine all travelers from overseas countries | |
| 21 March | Strict social distancing | |
| 22 March | COVID-19 testing at all nursing hospitals in Daegu almost completed | |
| 1 April | Quarantining all travelers from overseas countries for 14 days | |
| 4 April | Strict social distance extended | |
| 9 April | Schools begin online classes | |
| 20 April | Mitigated social distancing | |
| 22 April | Prepare sustainable social distancing | |
| 24 April | Guideline for social distancing in our living | |
| 30 April | Daegu living-care center closed |
| Parameter | Description | Value | Reference |
|---|---|---|---|
| The number of people traveling from patch 1 to patch 2 per day | 2,192,794 | [30] | |
| The number of people traveling from patch 2 to patch 1 per day | 1,693,727 | [30] | |
| Progression rate from E to I in patch 1 per day | 1/7 | [34] | |
| Progression rate from E to I in patch 2 per day | 1/7 | [34] | |
| Recovery rate in patch 1 | 1/14 per day | [35] | |
| Recovery rate in patch 2 | 1/14 per day | [35] | |
| The proportion of undetected infectious individuals in patch 1 | 0.33 | [36] | |
| The proportion of undetected infectious individuals in patch 2 | 0.33 | [36] | |
| Population size in patch1 (Daegu and Gyeongbuk) | 5.12 | [37] | |
| Population size in patch2 (the rest of Korea) | 46.52 | [37] | |
| Initial number of asymptomatic individuals in patch1 | 1442 | Estimated | |
| Initial number of asymptomatic individuals in patch2 | 330 | Estimated | |
| The starting point of the rapid increase interval | 4 | Estimated | |
| The starting point of the slower increase interval | 10 | Estimated | |
| Transmission rate of patch 1 during | 0.338 | Estimated | |
| Transmission rate of patch 1 during | 0.99 | Estimated | |
| Transmission rate of patch 1 during | 0.01 | Estimated | |
| Transmission rate of patch 2 during | 0.3575 | Estimated | |
| Early detection and diagnostic rate of patch 1 per day | 0.0312 | Estimated | |
| Early detection and diagnostic rate of patch 2 per day | 0.3575 | Estimated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.N.; Kim, E.; Lee, S.; Oh, C. Mathematical Model of COVID-19 Transmission Dynamics in South Korea: The Impacts of Travel Restrictions, Social Distancing, and Early Detection. Processes 2020, 8, 1304. https://doi.org/10.3390/pr8101304
Kim BN, Kim E, Lee S, Oh C. Mathematical Model of COVID-19 Transmission Dynamics in South Korea: The Impacts of Travel Restrictions, Social Distancing, and Early Detection. Processes. 2020; 8(10):1304. https://doi.org/10.3390/pr8101304
Chicago/Turabian StyleKim, Byul Nim, Eunjung Kim, Sunmi Lee, and Chunyoung Oh. 2020. "Mathematical Model of COVID-19 Transmission Dynamics in South Korea: The Impacts of Travel Restrictions, Social Distancing, and Early Detection" Processes 8, no. 10: 1304. https://doi.org/10.3390/pr8101304
APA StyleKim, B. N., Kim, E., Lee, S., & Oh, C. (2020). Mathematical Model of COVID-19 Transmission Dynamics in South Korea: The Impacts of Travel Restrictions, Social Distancing, and Early Detection. Processes, 8(10), 1304. https://doi.org/10.3390/pr8101304






