A Novel Approach Integrating Intuitionistic Fuzzy Analytical Hierarchy Process and Goal Programming for Chickpea Cultivar Selection under Stress Conditions

Abstract

Chickpea (Cicer arietinum L.) is a quite high nutrient and widespread legume that is consumed globally. Similar to many plants, chickpea is sensitive to environmental stresses. The major goal of the breeders is to achieve the most tolerant cultivars. This study aims to determine the tolerance level of chickpea cultivars against cold and drought stresses. The cultivars in the scope of this study are the ones that are officially identified and grown in Turkey. Ranking alternatives according to multiple criteria is difficult and requires a systematic approach. Thus, a coherent multi criteria decision making (MCDM) methodology is proposed in order to ease the ranking process. The methodology includes integration of intuitionistic fuzzy analytical hierarchy process (IF-AHP) with group decision making (GDM) and goal programming (GP). This integration presents a robust ranking according to criteria that are appraised by talented experts. Applying the methodology to the data, results in the order of chickpea cultivars with regard to their cumulative tolerance to cold and drought stresses. Diyar 95 spearheads this list with its utmost performance. The main contribution of this study is the proposition of the powerful MCDM approach with systematic procedure for the ranking process of cultivars. The proposed methodology has a generic structure that can be applied to various stress problems for different plants.

1. Introduction

As one of the earliest domesticated grain legumes, the roots of cultivated chickpea (Cicer arietinum L.) dates back to nearly 7500 years ago [1]. Chickpea cultivars are believed to have originated in the Old World, where south eastern part of Turkey and adjoining Syria lie today [2]. Archeological explorations at this region provided evidence that chickpea cultivars already existed in the early times of Neolithic revolution [3]. Today, cultivation of chickpea has global interest with numerous variants to satisfy distinct dietary habits. According to 2018 data by Food and Agriculture Organization of the United Nations (FAO) [4], India is the top producer by far over the world with a volume of over 11 million tons a year. India is followed by Australia with nearly 1 million tons. By ascending on the list year by year, Turkey is the third global producer with 630,000 tons.

Domesticated plants may be confronted by many biotic and abiotic stress elements. Remarkable yield loss is observed globally due to external impacts. Specific to chickpea cultivation, biotic stress includes pathogens and pests such as Ascochyta rabiei, Fusarium oxysporum, Liriomyza cicerina, and Callosobruchus chinensis L., where cold (both chilling and freezing) and drought stresses are prominent types of abiotic stresses that delimitate both nutritional value and development of plant, particularly in semiarid regions [5,6]. Kashiwagi et al. [7] determined the variability of root length and its contribution to crop productivity under drought stress. Molina et al. [8] applied Super Serial Analysis of Gene Expression (SuperSAGE) technology in order to observe the response of chickpea seeds to drought stress by analyzing gene expression. Mafakheri et al. [9] researched the results of drought stress on 3 types of chickpea cultivars concerning selected characteristics, where Çiçek et al. [5] screened 21 cultivars by chlorophyll $\alpha$ fluorescence measurement at 3 different severity levels of drought. Arslan et al. [6] focused on biochemical and molecular changes of three chickpea cultivars at freezing temperatures. Nayyar and Chander [10] observed the protection response of polyamines in case of oxidative stress that is arisen in consequence of water and cold stress. Nayyar et al. [11] exposed chickpea cultivars to chilling stress, assisted the plants by injecting glycine betaine additive, and observed the recovery with respect to control cultivar. Gao et al. [12] created two cDNA libraries, selected random clones from the libraries, performed sequencing analysis on expressed sequence tags (ESTs) and revealed gene regulations against dehydration stress. Unlike many studies on this topic, Croser et al. [13] tried to determine the effects of low temperature by fusing findings of a wide range of study in the literature, nevertheless the study is lacking in a generic mathematical model.

There are many distinct studies in the literature that have their own focus. Rather than having a specific and focused conceptual research on chickpeas, this study concentrates on developing an analytical decision-making approach by comparing different cultivars in terms of key characteristics that are changed during stress conditions. The aim of constructing such an analytical model is to provide an efficient decision making process for breeders to select cultivars to achieve the best results under abiotic stress conditions, to compare efficiency of crop cultivars with regard to their traits, and to encourage agricultural policy makers to revise their cultivation strategies by generalizing this approach for crops of interest. This study handles the cultivation of chickpea under cold and drought stress conditions with a holistic perspective. These abiotic stresses have an aggregated effect of nearly 65–70% on crop loss. Hence, a vital portion of agents that engender yield loss is covered for a more accurate ranking. The proposed multi criteria decision making (MCDM) model provides a ranking sequence for chickpea cultivars with regard to their durability under cold and drought stress conditions to enhance optimum results.

Many statistical approaches are applied to agricultural data to culminate in intended solution, conclusion, or inference. These models implicitly reveal patterns with pure numerical methods without intervention and should be interpreted with a defined hypothesis. Analysis of variance (ANOVA) is a very common example that is widely used in agricultural studies. MCDM methods deal with suggesting an order or ranking of alternatives. Many MCDM algorithms were developed to overcome various types of real-world decision-making problems. In contradistinction to statistical methods, MCDM methods encourage decision makers to contribute to the solution methodology for achieving more accurate and preferable results. MCDM methods may be reinforced with fuzzy theory to adjoin linguistic evaluations of decision makers with regard to selection criteria and handle uncertainties of decision makers on concluding judgments. Analytical hierarchy process (AHP) is widely implemented to determine weights of the criteria of decision model by pairwise comparisons of expert decision makers. As an extension, intuitionistic fuzzy-AHP (IF-AHP) can be administered for decision models where decision makers have suspicion on comparing criteria. IF-AHP can manage linguistic judgments or comparisons without disregarding the uncertainties of decision makers. Goal programming (GP) has been used in many studies to rank alternatives according to the closeness to the goal values with regard to weighted criteria.

Table 1. A review for goal programming (GP) studies.

Study	Methodology	Sensitivity Analysis	GDM	Application Area
Gong et al. [14]	IF-GP	No	No	Fuzzy preference relations
Dey and Roy [15]	IF-GP	No	No	Nonlinear multi objective structural problems
Razmi et al. [16]	IF-GP	No	No	Finding pareto-optimal solutions
Gupta et al. [17]	IF-GP	No	No	Portfolio optimization
Ku et al. [18]	Fuzzy AHP-Fuzzy GP	No	No	Supplier selection
Liao [19]	Fuzzy AHP-GP	No	No	New product segmented under price strategy
Trivedi & Singh [20]	Fuzzy AHP-GP	Yes	Yes	Emergency shelter location–relocation projects
Ervural et al. [21]	Fuzzy AHP-GP	No	Yes	Sustainable energy investment planning
Alegoz and Yapicioglu [22]	Fuzzy TOPSIS-Type II Fuzzy AHP-GP	No	Yes	Supplier selection
Proposed Methodology	IF AHP-GP	Yes	Yes	Chickpea cultivars ranking

summarizes preceding studies that are similar to our methodology. The methodologies of these studies will be compared in the discussion and conclusion sections.

Aydemir and Akçakaya [23] pioneered the implementation of the MCDM approach on chickpea cultivars and applied the technique for order preference by similarity to ideal solution (TOPSIS) method to rank cultivars according to their growth on regular fields. Sudha and Jeba [24] proposed a TOPSIS model for evaluating five different crops versus five criteria.

The MCDM methodology, instead of statistical methods, is preferred for this study since subjective evaluations of decision makers were paramount to overcome the ambiguity of the stress conditions. For instance, drought stress plays a more important role on the growth of chickpea cultivars according to the judgments by decision makers. It would be hard to reveal this sophisticated decision tree with statistical methods.

From this standpoint, this study proposes an integrated IF-AHP and GP approach for development of a systematic procedure for agricultural decision-making processes. Multiple decision makers may judge the evaluation criteria with imprecise linguistic terms from which the weights of the criteria are derived. The integrated GP model analytically suggests the ranks and scores of the alternatives concerning their closeness to the goal values. The distinguishing feature of this methodology in comparison to statistical methods is the capability of comprising the judgements of decision makers considering uncertainties.

To the best of the author’s knowledge, the proposed methodology, which integrates IF-AHP and GP, is the first intelligent MCDM methodology for the field of agriculture that is empowered by a sensitivity analysis to determine bounds of weights. The MCDM studies on agricultural data in the literature have not yet handled sensitivity analysis.

The rest of this study is organized as follows: Section 2 explains the materials and methods in detail. Case study and results are given in Section 3. Discussion, conclusions, and recommendations are emphasized in Section 4.

2. Materials and Methods

2.1. Data

The data of this study consist of two datasets by two different experiments that belong to a project named ‘’Physiological and Molecular Approaches for Determining the Tolerance of Chickpea Cultivars Registered in Turkey to Cold and Drought’’ of the Hacettepe University Scientific Research Unit (Project No. 801601007). The cultivars were provided from the official office in Turkey, namely Ankara Central Research Institute for Field Crops. Both studies have examined 21 cultivars. Our study utilizes parameters of 18 cultivars, which are common in both experiments. Because this study deals with only states of the experiments and the measurements of parameters during these states, no detailed setup and configuration are shared. This information is included in a corresponding reference study. Datasets are described with their own states and parameters. Each state is a transition period between the stages of the experiment. More clearly, states are the milestones of the experiment where environmental conditions are changed. Parameters are the critical indicators that depict the status of the chickpea cultivars.

2.1.1. Cold Stress Dataset

The dataset consists of 4 control states and 5 experimental states. The parameters of chickpea cultivars in experimental states are measured and compared with parameters of corresponding control state. The states of the dataset are illustrated in Figure 1.

C₀ is the state in which all seeds are grown under control conditions for 15 days at 25 °C. Until this state, the seeds are allowed to be germinated in controlled conditions and seedlings have 4–5 leaves. At this state, the process is divided into 3 branches. The first branch involves control chickpea cultivars that are persistently grown with control conditions at 25 °C. States C₁, C₂, and C₃ are 22, 37, 44 days old control plants, respectively. The second branch has chickpea cultivars that are subjected to three successive cold stress conditions. Control plants that are 15 days old are subjected to a cold acclimation process for 7 days at 10 °C during State CA, which is followed by State CA + S at 1 °C for 15 days. Then, a rewarming process is applied for 7 days as State CA + S + R at 25 °C. The chickpea cultivars in the last branch are exposed directly to cold stress condition without an acclimation process for 15 days at 1 °C as State S. Until State S, seedlings were grown at 25 °C for 22 days. Finally, a rewarming process is applied for 7 days as State S + R at 25 °C.

Five parameters are measured for each state of cold stress experiment to figure out the responses of chickpea cultivars. Chlorophyll fluorescence is a very useful tool to monitor the successive steps of excitation energy transformation of photosystem II (PSII). Maximum Quantum Efficiency of PSII of Dark Adapted Plants (F_V/F_M) is the ratio of variable fluorescence to maximum fluorescence, which is the measurement of maximum quantum yield of PSII, and the alterations of this parameter are correlated with degradation of membrane integrity. Performance Index on Absorption Basis (PI_ABS) is an aggregated performance index parameter that hosts three independent parameters that cumulatively quantify total functionality of the electron flux through PSII and indicates the vitality of the plant [26]. Absorption Flux per Reaction Centre (ABS/RC) specifies effective antenna size by proportioning absorbed photons to active reaction centers, and an increase of ABS/RC indicates a decrease in the antenna size and inactivation of PSII units. Dissipation Energy Flux per Reaction Centre (DIo/RC) is the ratio of dissipated excitation energy to active reaction centers. Enhancement of DIo/RC reflects that the samples dissipate the excitation energy as heat and fluorescence more than photochemistry. Malondialdehyde (MDA) content is used to examine the oxidative damage level of the cell membranes.

2.1.2. Drought Stress Dataset

Drought stress experiment is based on two branches where chickpea cultivars in the first branch are grown under control conditions and the second branch has chickpea cultivars under stress conditions. The dataset has an initial state, namely C₀, 6 experimental states, and their corresponding control states. Chickpeas are exposed to consecutive stress and recovery phases during experiment. The experimental states are named with S_x for stress states and R_x for recovery states where x is the index number of the states. The states of the dataset are demonstrated in Figure 2.

Five parameters were observed for drought stress, where F_V/F_M, PI_ABS and MDA are common with cold stress experiment. Total Performance Index (PI_TOTAL) is the performance index parameter that measures the performance of electron flux to the final photosystem I (PSI) electron acceptors. The PI_TOTAL is a very sensitive chlorophyll fluorescence parameter and is defined as the probability of an electron moving from the reduced intersystem electron acceptors to the PSI end-electron acceptors. Hydrogen peroxide (H₂O₂) content of the cultivars reflects oxidative stress levels of the cells.

2.2. Method

The proposed methodology consists of two integrated MCDM methods. IF-AHP with group decision making is applied to determine weights of the criteria in accordance with opinions by competent decision makers without strict decisions. Decision makers are encouraged to state their judgements by comparing criteria with linguistic scales so that they can express both their level of certainty and hesitation. Linguistic terms are quantified with intuitionistic fuzzy sets (IFS) during the decision-making process. Once the weights are acquired, integrated GP model is executed to evaluate and rank the alternatives. Resulting order of alternatives indicates the level of common tolerance to both cold and drought stress depending on weighted criteria.

2.2.1. Intuitionistic Fuzzy Sets

Most real-world characteristics encompass uncertainty in its nature that complicates mathematical representation by crisp values. i.e., a temperature of 24 °C may refer to both “warm” or “hot” in some senses. This definition may change according to environment, sense of person, age of person, state of the sun etc. More precisely, 24 °C may refer to warm in a South African country, while it could be classified as hot in a Scandinavian country. Zadeh [27] introduced fuzzy set theory to overcome this uncertainty. This theory suggests that a fuzzy set may be characterized by assigning a degree of membership to all objects by membership functions. Since 1965, many updated models are introduced to the literature to overcome gaps of fuzzy sets theory. As a result of his improvement study on fuzzy sets, Atanassov introduced IFS theory as an extension [28]. Lean fuzzy set theory defines the degree of membership for an element regarding a set. Moreover, all elements are assigned a degree of membership, a nondegree of membership, and a hesitancy value to propound a more realistic rating in IFS theory. Hesitancy value states the tentativeness on conclusion to a concrete decision. All IFS numbers are assigned a membership, nonmembership, and hesitancy mathematically. Let $C$ be a crisp set where $I\subset C$. Then an IFS, $I$, in $C$ can be defined as follows;

$$I=\left\{\langle x,{\mu }_I\left(x\right),{\nu }_I\left(x\right),{\pi }_I\left(x\right)\rangle |x\in C\right\}$$

(1)

where the function ${\mu }_I\left(x\right):C\to \left[0,1\right]$ shows the degree of membership, ${\nu }_I\left(x\right):C\to \left[0,1\right]$ represents the nonmembership degree, and ${\pi }_I\left(x\right):C\to \left[0,1\right]$ defines the hesitancy.

For such a definition, the following equations hold:

$$\begin{array}{l}0\le {\mu }_I\left(x\right)+{\nu }_I\left(x\right)\le 1,\\ {\pi }_I(x)=1-{\mu }_I\left(x\right)-{\nu }_I\left(x\right)\end{array}$$

(2)

Then, ${\pi }_I(x)$ indicates the uncertainty degree of the membership of element $x\in C$ in set $I$. The equation ${\pi }_I(x)=0$ holds for classical fuzzy sets for all $x\in C$.

Hence, an IF set $I$ in $X=\left\{x\right\}$ may be defined as

$$\begin{array}{l}I=\left\{\langle x,{\mu }_I\left(x\right),{\nu }_I\left(x\right)\rangle |x\in C\right\},\\ \mathrm{where}\\ {\mu }_I\left(x\right)\to \left[0,1\right];{\nu }_I\left(x\right)\to \left[0,1\right];{\pi }_I\left(x\right)\to \left[0,1\right]\end{array}$$

(3)

The membership and nonmembership functions of the triangular IF number $\tilde{I}$ may be stated as follows:

The membership function:

$${\mu }_{\tilde{I}}(x)=\{\begin{array}{ll}\frac{\left(x-a\right){\mu }_{\tilde{I}}}{b-a}& (a\le x<b)\\ {\mu }_{\tilde{I}}& (x=b)\\ \frac{(c-x){\mu }_{\tilde{I}}}{c-b}& (b<x\le c)\\ 0& \mathrm{otherwise}\end{array}$$

(4)

The nonmembership function:

$${\nu }_{\tilde{I}}(x)=\{\begin{array}{ll}\frac{\left(b-x\right)+{\nu }_{\tilde{I}}(x-a^{\prime }))}{b-a^{\prime }}& (a^{\prime }\le x<b)\\ {\nu }_{\tilde{I}}& (x=b)\\ \frac{(x-b+{\nu }_{\tilde{I}}(c^{\prime }-x))}{c^{\prime }-b}& (b<x\le c^{\prime })\\ 0& \mathrm{otherwise}\end{array}$$

(5)

2.2.2. Intuitionistic Fuzzy Analytic Hierarchy Process (IF-AHP)

Analytic hierarchy process (AHP) is one of most prominent MCDM methods, which is introduced by Saaty [29]. Each criterion has a different importance level that determines its contribution to the selection process in a MCDM problem. Thus, criteria should be assigned “weights” in advance of selection calculations of alternatives. Apart from being capable of evaluating alternatives like most of the MCDM algorithms, AHP is widely applied to determine weights divergently to remaining algorithms [30]. However, traditional AHP has shortcomings in terms of consistency and uncertainty [31]. IF-AHP is one of the integrations that overcomes these shortcomings. IF-AHP may be formulated by the following steps:

Step 1: Transform metadata into the MCDM problem by defining alternatives to be evaluated, categories and their subcategories/criteria and objectives. Construct the net of hierarchy of the defined problem.

Step 2: Determine and build the scale for pairwise comparisons. This scale is applied to reveal mutual importance of defined categories, subcategories, and criteria. The scale proposed by Abdullah and Najib [31] is applied in this study for pairwise comparisons except for reciprocal Intuitionistic Fuzzy Number (IFN) of the linguistic term “equally important (EI)”. We propose that both IFN and its reciprocal IFN should be equal as (0.02, 0.18, and 0.80) if they are counted as EI. The scale is defined like shown in

Table 2. Linguistic variables for pairwise comparison [31].

Linguistic Variables	Preference Numbers	Intuitionistic Fuzzy Numbers	Reciprocals Preference Numbers	Reciprocal Intuitionistic Fuzzy Numbers
Equally Important (EI)	1	(0.02,0.18,0.80)	1/1	(0.02,0.18,0.80)
Intermediate Value (IV1)	2	(0.06,0.23,0.70)	1/2	(0.23,0.06,0.70)
Moderately More Important (MI)	3	(0.13,0.27,0.60)	1/3	(0.27,0.13,0.60)
Intermediate Value (IV2)	4	(0.22,0.28,0.50)	1/4	(0.28,0.22,0.50)
Strongly More Important (SI)	5	(0.33,0.27,0.40)	1/5	(0.27,0.33,0.40)
Intermediate Value (IV3)	6	(0.47,0.23,0.30)	1/6	(0.23,0.47,0.30)
Very Strong More Important (VSI)	7	(0.62,0.18,0.20)	1/7	(0.18,0.62,0.20)
Intermediate Value (IV4)	8	(0.80,0.10,0.10)	1/8	(0.10,0.80,0.10)
Extremely More Important (EMI)	9	(1.00,0.00,0.00)	1/9	(0.00,1.00,0.00)

by linguistic terms and their corresponding IFNs as 9 levels.

Step 3: Decide the weight that are used to figure out the relative importance of each Decision Maker (DM). It would be complicated to suggest concrete numerical values to determine influences of DM. Thus, linguistic term based IFNs should be defined to cover uncertainties, as demonstrated in

Table 3. Linguistic variables for importance degrees of Decision Makers [32].

Linguistic Variables	Intuitionistic Fuzzy Numbers
Very Important (VI)	(0.90,0.05,0.05)
Important (I)	(0.75,0.20,0.05)
Medium (M)	(0.50,0.40,0.10)
Unimportant (UNIMP)	(0.25, 0.60, 0.15)
Very Unimportant (VUNIMP)	(0.10, 0.80,0.10)

. By this way, the level of contribution of each DM to the model should be evaluated subjectively with respect to his/her experience, relativeness, and knowledge. Then, DMs may be assigned by calculating the formula in Equation (6), where ${\lambda }_n$ is the crisp weight value of the nth DM:

$$\begin{array}{l}{\lambda }_n=\frac{\left({\mu }_n+{\pi }_n\left(\frac{{\mu }_n}{{\mu }_n+{\nu }_n}\right)\right)}{{\displaystyle \sum _{n=1}^l\left({\mu }_n+{\pi }_n\left(\frac{{\mu }_n}{{\mu }_n+{\nu }_n}\right)\right)}}\\ an\mathrm{and}\\ {\displaystyle \sum _{n=1}^l{\lambda }_n=1}\end{array}$$

(6)

Step 4: Let DMs compare each category, subcategory, and criterion mutually. Derive the decision matrices for each DM from comparisons where each linguistic term demonstrates preference level of the item (category, subcategory, or criterion) versus item in the column.

Step 5: Convert linguistic terms in the matrices to IF numbers, so that IF decision matrices are obtained. In this step first, each linguistic term is represented by an IF number.

Step 6: Aggregate each row of IF decision matrices into a single column with Intuitionistic Fuzzy Weighted Average (IFWA) operator. Thus, aggregated IF decision matrices are gained, which show the preference of DMs for the specific category, subcategory, and criterion.

Step 7: Aggregate IF decision matrices of all DMs into a collective form, so that each category, subcategory, and criteria are represented with a single IF number in IF weighted aggregated decision matrices. IFWA operator by Xu [33] is implemented to obtain this collective form. Let $W_j^{\left(n\right)}=\left[{\mu }_j^{\left(n\right)},{\nu }_j^{\left(n\right)},{\pi }_j^{\left(n\right)}\right]$ be an IF number that indicates the evaluation of nth DM for the category, subcategory, or criteria $X_j$. Then, Equation (7) explicitly defines the aggregation calculations:

$$\begin{array}{ll}{W}_j& =IFW{A}_{\lambda }\left(W_j^{\left(1\right)},W_j^{\left(2\right)},\dots ,W_j^{\left(l\right)}\right)\\ & ={\lambda }_1{W}_j^{\left(1\right)}\oplus {\lambda }_2{W}_j^{\left(2\right)}\oplus {\lambda }_3{W}_j^{\left(3\right)}\oplus \dots \oplus {\lambda }_l{W}_j^{\left(l\right)}\\ & =\left[1-{\displaystyle \prod _{n=1}^l{\left(1-{\mu }_j^{\left(n\right)}\right)}^{{\lambda }_n},{\displaystyle \prod _{n=1}^l{\left({\nu }_j^{\left(n\right)}\right)}^{{\lambda }_n},}{\displaystyle \prod _{n=1}^l{\left(1-{\mu }_j^{\left(n\right)}\right)}^{{\lambda }_n},}-{\displaystyle \prod _{n=1}^l{\left({\nu }_j^{\left(n\right)}\right)}^{{\lambda }_n},}}\right]\\ W& =\left[W_1,W_2,W_3,\dots ,W_j\right]\\ W_j& =\left[{\mu }_j,{\nu }_j,{\pi }_j\right]\left(j=1,2,\dots ,n\right).\end{array}$$

(7)

Step 8: Check the consistency of each IF aggregated weighted decision. The consistency ratio (CR) is calculated for each matrix with Equation (8). CR formula is the adapted version by Abdullah and Najib [31,34] of the original CR Formula by Saaty [29]. The adaptation is required to enable application with IF numbers. The aim of this check is for estimating the consistency of pair-wise comparisons. A CR value less than 0.10 hints that the comparisons are consistent enough to be accepted. A value over 0.10 suggests reviewing initial comparisons made by DMs for consistency.

$$CR=\frac{\left({\lambda }_{\max }-k\right)/\left(k-1\right)}{RI}$$

(8)

$\left({\lambda }_{\max }-k\right)$ may be assumed as the average of ${\pi }_{\left(x\right)}$ values for each matrix. Here, $k$ denotes the size of the matrix.

Step 9: Final weights for each category, subcategory, and criterion are calculated using Equation (9) [35].

$$\begin{array}{l}{w}_n=\frac{\left({\mu }_n+{\pi }_n\left(\frac{{\mu }_n}{{\mu }_n+{\nu }_n}\right)\right)}{{\displaystyle \sum _{n=1}^l\left({\mu }_n+{\pi }_n\left(\frac{{\mu }_n}{{\mu }_n+{\nu }_n}\right)\right)}}\\ \mathrm{and}\\ {\displaystyle \sum _{n=1}^l{w}_n=1}\end{array}$$

(9)

2.2.3. Goal Programming

GP is among the earliest MCDM algorithms to deal with decision-making problems with multiple objectives by Charnes and Cooper [36]. The aim of the algorithm is to find the optimum set among feasible sets that minimizes the deviation from the defined goals. Algorithm may be applied with the following steps:

Step 1: Decision matrix is constructed. Because each cultivar has distinctly varying parameter values, naive parameter values do not provide an occasion for meaningful comparisons. Hence, instead of using parameter values directly, the decision matrix is built on the difference values of cultivars under stress from their control cultivar of equal age in the experiment.

$$D=\left[\begin{array}{lll}di{f}_{11}& \cdots & di{f}_{1a}\\ ⋮& \ddots & ⋮\\ di{f}_{b1}& \cdots & di{f}_{ba}\end{array}\right]$$

(10)

Step 2: Allowing each criterion to have its own value range would lead to biased solutions. Therefore, each column of criterion in the matrix is normalized. Min–max normalization is applied to transform values of each column to [0,1] scale. The normalized decision matrix is denoted by $\overline{D}={\left[{\stackrel{\sim }{dif}}_{ba}\right]}_{jxl}$.

Step 3: GP model is constructed. The model can be formulated as below by utilizing the following parameters, objective function, decision variables, and hard constraints [37]:

• Parameters:
  • $w_{ijk}$ is the weight of the $k_{th}$ criteria under $i_{th}$ category and $j_{th}$ subcategory.
  • $c_{ijkl}$ is the deviation coefficient of alternative $l$ on $k_{th}$ criteria of $i_{th}$ category and $j_{th}$ subcategory.
  • $g_{ijk}$ is the goal value for $k_{th}$ criteria under $i_{th}$ category and $j_{th}$ subcategory.
• Decision Variables:
  • $d_{ijk}^{+}$ is the positive deviation of $k_{th}$ criteria from $g_{ijk}$
  • $d_{ijk}^{-}$ is the negative deviation of $k_{th}$ criteria from $g_{ijk}$
  • $x_l$ is the binary decision variable for alternative $l$ (0 if alternative $l$ is nor selected, 1 otherwise)
• Objective function:

  $$\mathrm{Minimize} z={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{k=1}^p{w}_{ijk}(d_{ijk}^{+}}}}+d_{ijk}^{-})$$

  (11)
• Constraints:

  $$\underset{i}{\forall }\underset{j}{\forall }\underset{k}{\forall }{\displaystyle \sum _{l=1}^r{c}_{ijkl}}.x_l+d_{ijk}^{+}-d_{ijk}^{-}=g_{ijk}$$

  (12)

  $$\underset{l}{\forall }{\displaystyle \sum _{l=1}^r{x}_l=1}$$

  (13)

  $$\underset{l}{\forall }{x}_l\in \left\{0,1\right\}$$

  (14)

  $$d_{ijk}^{+},d_{ijk}^{-}\ge 0$$

  (15)

  where $i$ is the index for categories, $j$ is the index for subcategories, $k$ is the index for criteria, $l$ is the index for alternatives.

In the GP formulation above, Equation (11) is the objective function, which aims to minimize total value of weighted deviation from goal values. Constraint in Equation (12) measures the deviations from goals in case of selection of alternative $l$. In this GP formulation, the goals are set to limit values in the column of criterions. More clearly, goal value for each criterion is the best value for this criterion that is achieved by a cultivar in the experiment. Thus, goal for criterion $ijk$ is recognized $g_{ijk}=\min \left\{{\stackrel{\sim }{dif}}_{ba}\right\}$ for criteria if decrease of the values is better and $g_{ijk}=\max \left\{{\stackrel{\sim }{dif}}_{ba}\right\}$ if increase of the values is better. The hard constraint (13) ensures that only one alternative is selected. Constraints in Equations (14) and (15) are domains for variables.

Solving the GP model optimally advises the best alternative that has minimum objection function value, which is minimal weighted deviation from goal values. The objective function value also indicates the performance of the best alternative. The model should be run $l-1$ times to rank alternatives and calculate their scores. Best alternative should be dispatched from the model after each solution. Thus, the order of the alternatives with regard to tolerance to cold and drought stress and their scores are gained.

2.2.4. Proposed Methodology

Hybrid or integrated methodologies are applied to overcome gaps of the unique techniques and attain more robust and reliable solutions. This study utilizes IF theory to handle uncertainty of the decision-making process, AHP with GDM to calculate weights of the criteria by evaluations of decision makers, and GP to rank alternatives according to their durability against cold and drought stress. As a result, IF-AHP with GDM hybrid methodology is integrated to GP model. The proposed methodology consists of four stages:

Stage 1:

Setup of the problem, initializing the model.

Stage 2:

Determining weights of the criteria by applying IF-AHP with GDM.

Stage 3:

Obtaining optimal solution for GP model.

Stage 4:

Evaluation of the results and sensitivity analysis.

Figure 3 shows the flow of the proposed methodology.

3. Case Study and Results

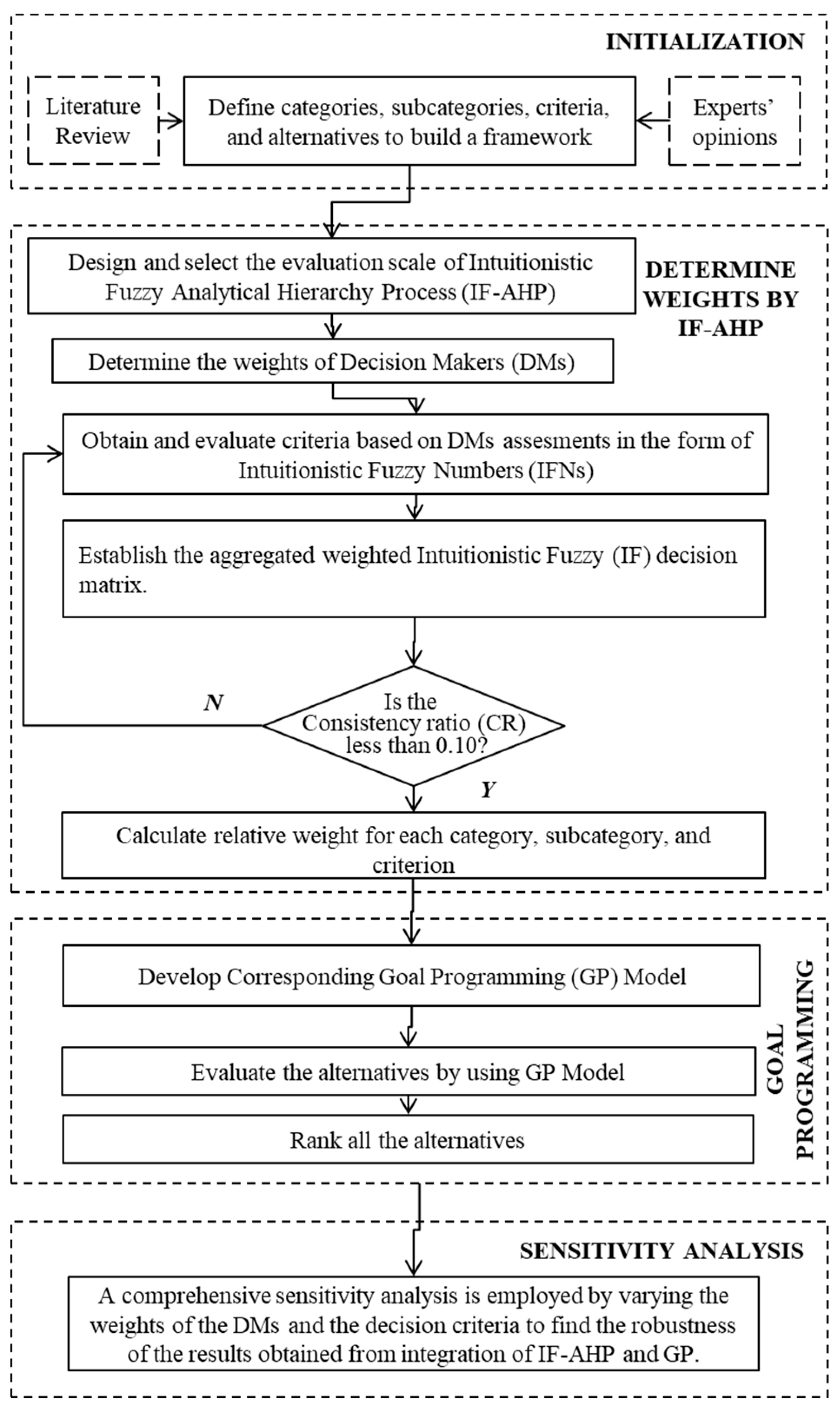
Proposed methodology is applied step by step to evaluate durability of chickpea cultivars.

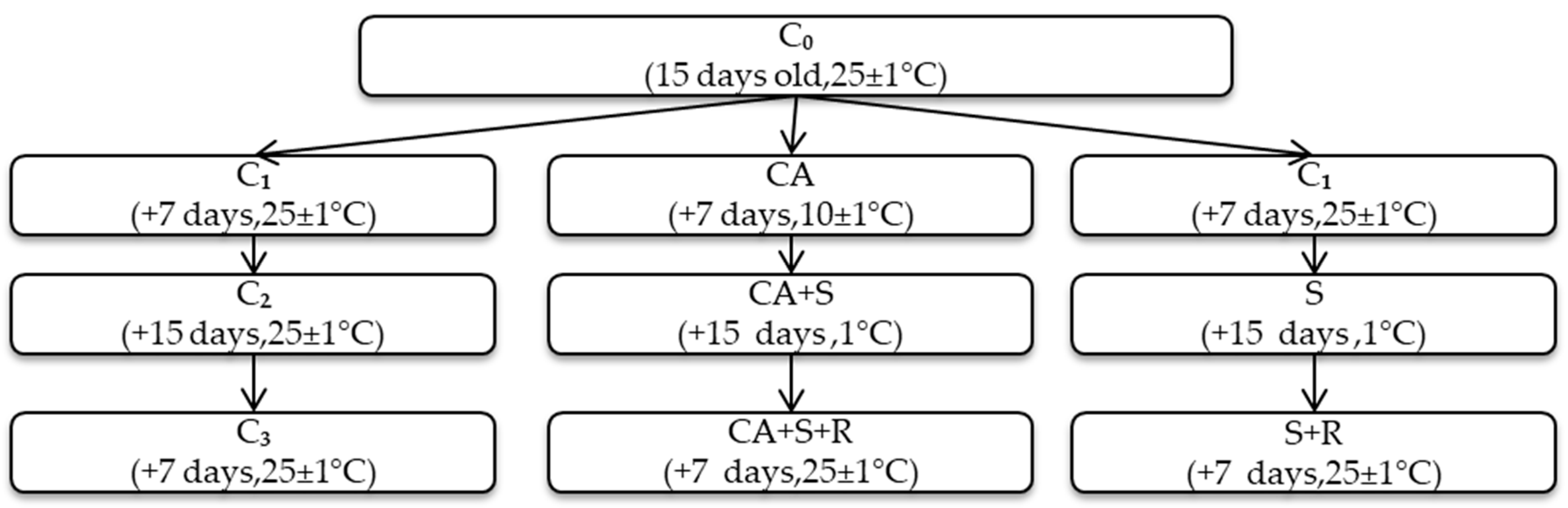
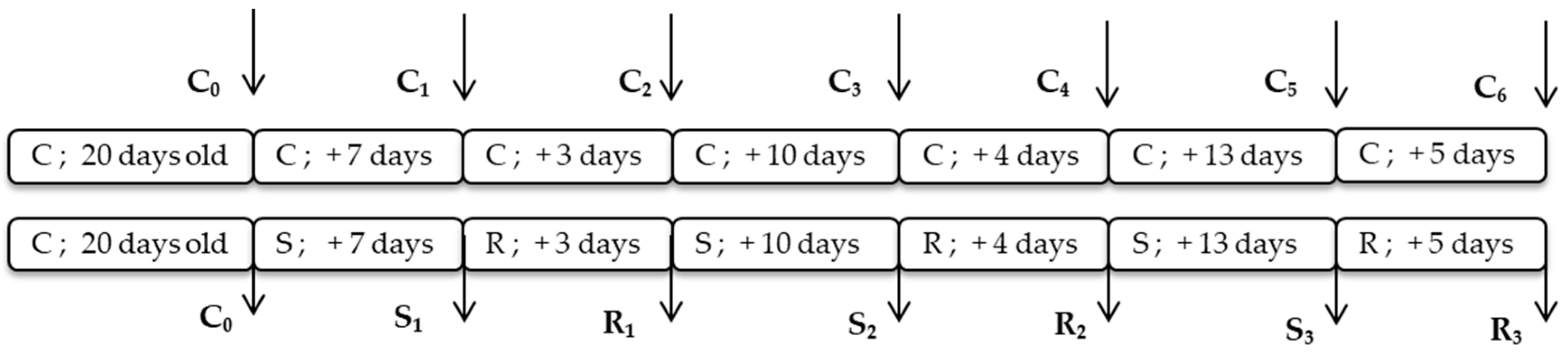
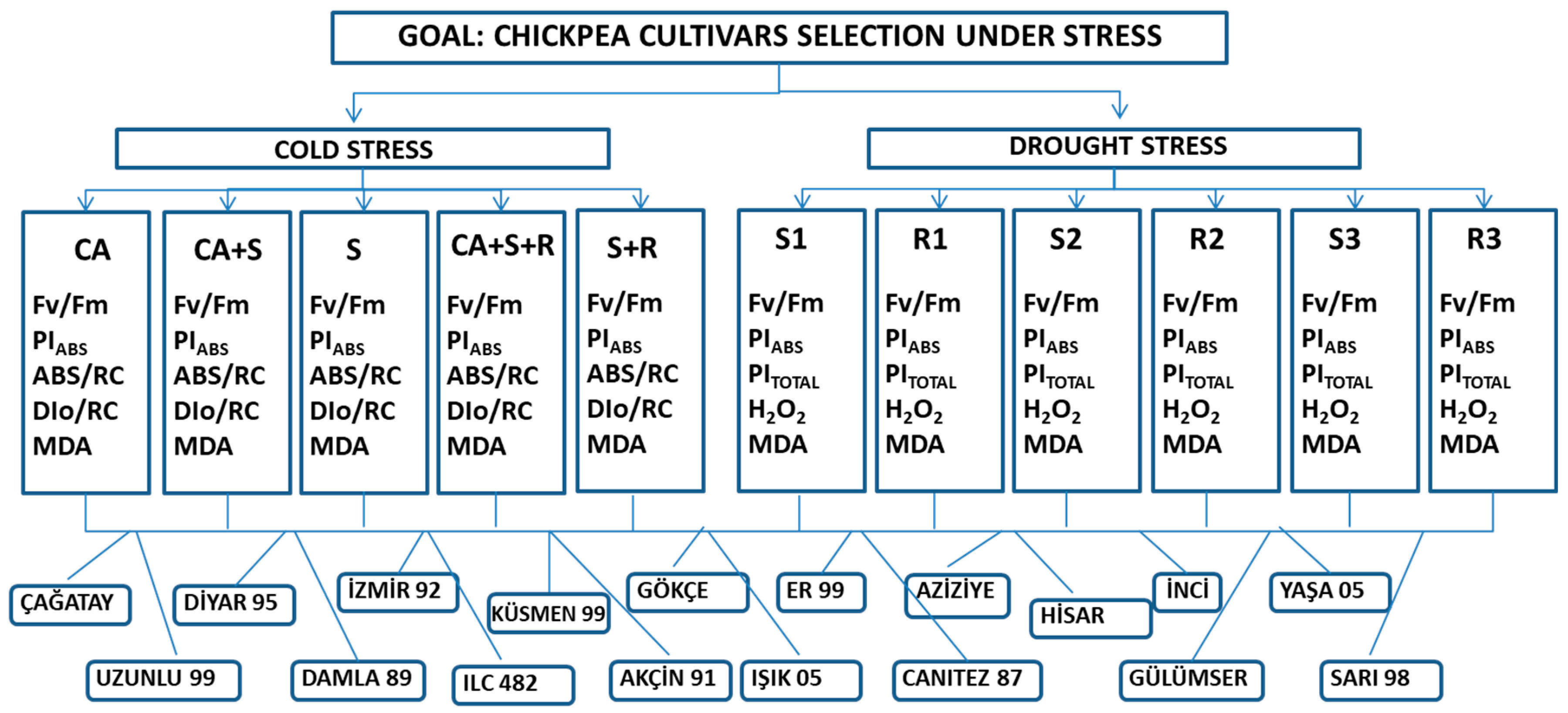
Step-1: To establish the MCDM problem, 18 chickpea cultivars are defined as alternatives. Alternatives are evaluated in line with a three-layer structure. Cold stress and drought stress are described as categories. Each state of both stress experiments that has calculated values for variables are introduced as subcategories. Hence, the number of subcategories under cold stress and drought stress are five and six, respectively. Finally, each calculated variable in the experiment is counted as criterion linked to subcategories. As a result, each subcategory has five criteria. The resulting MCDM model is represented in Figure 4.

Step-2: The scale in Table 2 by Abdullah and Najib [31] is assigned to be utilized in pairwise comparisons.

Step-3: To achieve group decision making, three decision makers expressed their judgments. The scale in Table 3 by Boran et al. [32] is used to resolve weights of decision makers. The weights of decision makers are determined as VI, I, and M for DM1, DM2, and DM3 according to their experience and relevance to the subject, respectively. Transforming linguistic weights by suggested formulation ensues crisp values as 0.413, 0.344, and 0.242, which can be seen in

Table 4. Decision makers’ weights.

DMs	DM1	DM2	DM3
Linguistic Terms	VI	I	M
IFNs	(0.90,0.05,0.05)	(0.75,0.20,0.05)	(0.50,0.40,0.10)
Weights	0.413	0.344	0.242

.

Step-4: Decision makers are requested to compare 2 categories, 11 subcategories, and 5 criteria mutually.

Table 5. Pairwise comparisons of decision makers concerning criteria of cold stress.

	Decision Maker 1					Decision Maker 2					Decision Maker 3
Criteria	FV/FM	PIABS	ABS/RC	DIo/RC	MDA	FV/FM	PIABS	ABS/RC	DIo/RC	MDA	FV/FM	PIABS	ABS/RC	DIo/RC	MDA
FV/FM			SI	SI				VSI	IV2				IV2	SI
PIABS	IV3		IV4	VSI	SI	IV2		IV4	IV3	VSI	IV2		IV3	SI	IV3
ABS/RC
DIo/RC			IV2					IV2					MI
MDA	SI		IV3	SI		IV3		IV4	IV3		SI		SI	IV2

and

Table 6. Pairwise comparisons of decision makers concerning criteria of drought stress.

	Decision Maker 1					Decision Maker 2					Decision Maker 3
Criteria	FV/FM	PIABS	PITOTAL	H2O2	MDA	FV/FM	PIABS	PITOTAL	H2O2	MDA	FV/FM	PIABS	PITOTAL	H2O2	MDA
FV/FM				IV2	SI				SI	IV2			IV2	SI	IV2
PIABS	IV2			VSI	IV3	MI			VSI	IV3	SI		IV2	IV3	IV4
PITOTAL	IV3	MI		SI	IV3	IV3	IV2		IV4	IV4					VSI
H2O2										SI			IV3
MDA				IV3										VSI

demonstrate sample pairwise comparison matrices by decision makers concerning criteria of cold stress and drought stress states, respectively. These matrices express the preference or importance level of a criterion in the rows versus a criterion on the columns.

Step-5: The linguistic expressions in the decision matrices are converted into IF values referenced to scale defined in the methodology.

Table 7. Pairwise comparison matrices with intuitionistic fuzzy values for criteria of cold subcategories.

		FV/FM			PIABS			ABS/RC			DIo/RC			MDA
DMs	Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
DM1	FV/FM	0.02	0.18	0.80	0.23	0.47	0.30	0.33	0.27	0.40	0.33	0.27	0.40	0.27	0.33	0.40
	PIABS	0.47	0.23	0.30	0.02	0.18	0.80	0.80	0.10	0.10	0.62	0.18	0.20	0.33	0.27	0.40
	ABS/RC	0.27	0.33	0.40	0.10	0.80	0.10	0.02	0.18	0.80	0.28	0.22	0.50	0.23	0.47	0.30
	DIo/RC	0.27	0.33	0.40	0.18	0.62	0.20	0.22	0.28	0.50	0.02	0.18	0.80	0.27	0.33	0.40
	MDA	0.33	0.27	0.40	0.27	0.33	0.40	0.47	0.23	0.30	0.33	0.27	0.40	0.02	0.18	0.80
DM2	FV/FM	0.02	0.18	0.80	0.28	0.22	0.50	0.62	0.18	0.20	0.22	0.28	0.50	0.23	0.47	0.30
	PIABS	0.22	0.28	0.50	0.02	0.18	0.80	0.80	0.10	0.10	0.47	0.23	0.30	0.62	0.18	0.20
	ABS/RC	0.18	0.62	0.20	0.10	0.80	0.10	0.02	0.18	0.80	0.28	0.22	0.50	0.10	0.80	0.10
	DIo/RC	0.28	0.22	0.50	0.23	0.47	0.30	0.22	0.28	0.50	0.02	0.18	0.80	0.23	0.47	0.30
	MDA	0.47	0.23	0.30	0.18	0.62	0.20	0.80	0.10	0.10	0.47	0.23	0.30	0.02	0.18	0.80
DM3	FV/FM	0.02	0.18	0.80	0.28	0.22	0.50	0.22	0.28	0.50	0.33	0.27	0.40	0.27	0.33	0.40
	PIABS	0.22	0.28	0.50	0.02	0.18	0.80	0.47	0.23	0.30	0.33	0.27	0.40	0.47	0.23	0.30
	ABS/RC	0.28	0.22	0.50	0.23	0.47	0.30	0.02	0.18	0.80	0.27	0.13	0.60	0.27	0.33	0.40
	DIo/RC	0.27	0.33	0.40	0.27	0.33	0.40	0.13	0.27	0.60	0.02	0.18	0.80	0.28	0.22	0.50
	MDA	0.33	0.27	0.40	0.23	0.47	0.30	0.33	0.27	0.40	0.22	0.28	0.50	0.02	0.18	0.80

and

Table 8. Pairwise comparison matrices with intuitionistic fuzzy values for criteria of drought subcategories.

		FV/FM			PIABS			PITOTAL			H2O2			MDA
DMs	Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
DM1	FV/FM	0.02	0.18	0.80	0.28	0.22	0.50	0.23	0.47	0.30	0.22	0.28	0.50	0.33	0.27	0.40
	PIABS	0.22	0.28	0.50	0.02	0.18	0.80	0.27	0.13	0.60	0.62	0.18	0.20	0.47	0.23	0.30
	PITOTAL	0.47	0.23	0.30	0.13	0.27	0.60	0.02	0.18	0.80	0.33	0.27	0.40	0.47	0.23	0.30
	H2O2	0.28	0.22	0.50	0.18	0.62	0.20	0.27	0.33	0.40	0.02	0.18	0.80	0.23	0.47	0.30
	MDA	0.27	0.33	0.40	0.23	0.47	0.30	0.23	0.47	0.30	0.47	0.23	0.30	0.02	0.18	0.80
DM2	FV/FM	0.02	0.18	0.80	0.27	0.13	0.60	0.23	0.47	0.30	0.33	0.27	0.40	0.22	0.28	0.50
	PIABS	0.13	0.27	0.60	0.02	0.18	0.80	0.28	0.22	0.50	0.62	0.18	0.20	0.47	0.23	0.30
	PITOTAL	0.47	0.23	0.30	0.22	0.28	0.50	0.02	0.18	0.80	0.80	0.10	0.10	0.80	0.10	0.10
	H2O2	0.27	0.33	0.40	0.18	0.62	0.20	0.10	0.80	0.10	0.02	0.18	0.80	0.33	0.27	0.40
	MDA	0.28	0.22	0.50	0.23	0.47	0.30	0.10	0.80	0.10	0.27	0.33	0.40	0.02	0.18	0.80
DM3	FV/FM	0.02	0.18	0.80	0.27	0.33	0.40	0.22	0.28	0.50	0.33	0.27	0.40	0.22	0.28	0.50
	PIABS	0.33	0.27	0.40	0.02	0.18	0.80	0.22	0.28	0.50	0.47	0.23	0.30	0.80	0.10	0.10
	PITOTAL	0.28	0.22	0.50	0.28	0.22	0.50	0.02	0.18	0.80	0.23	0.47	0.30	0.62	0.18	0.20
	H2O2	0.27	0.33	0.40	0.23	0.47	0.30	0.47	0.23	0.30	0.02	0.18	0.80	0.18	0.62	0.20
	MDA	0.28	0.22	0.50	0.10	0.80	0.10	0.18	0.62	0.20	0.62	0.18	0.20	0.02	0.18	0.80

show converted values for IF decision matrices demonstrated in Table 5 and Table 6.

Step-6: Each row of the decision matrices is aggregated into one single IF value, so that evaluations of decision makers regarding each criterion can be expressed with a single IF value. IFWA operator is applied for this operation. Applying IFWA operator to Table 7 results in the aggregated IF decision matrices in

Table 9. Aggregated IF decision matrices for criteria of cold subcategories.

	Agg. DM1			Agg. DM2			Agg. DM3
Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
FV/FM	0.24	0.29	0.47	0.31	0.25	0.45	0.23	0.25	0.52
PIABS	0.52	0.18	0.30	0.50	0.18	0.32	0.32	0.24	0.44
ABS/RC	0.19	0.35	0.47	0.14	0.44	0.42	0.22	0.24	0.54
DIo/RC	0.20	0.32	0.48	0.20	0.30	0.50	0.20	0.26	0.54
MDA	0.30	0.25	0.45	0.46	0.23	0.31	0.23	0.28	0.49

.

Table 10. Aggregated IF decision matrices for criteria of drought subcategories.

	Agg. DM1			Agg. DM2			Agg. DM3
Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
FV/FM	0.22	0.27	0.51	0.22	0.24	0.54	0.22	0.26	0.52
PIABS	0.35	0.19	0.45	0.34	0.21	0.45	0.44	0.20	0.36
PITOTAL	0.31	0.23	0.46	0.56	0.16	0.28	0.32	0.24	0.45
H2O2	0.20	0.33	0.47	0.19	0.38	0.43	0.25	0.33	0.42
MDA	0.26	0.31	0.43	0.19	0.35	0.47	0.28	0.32	0.40

shows the aggregated results after applying IFWA operator to Table 8.

Step-7: Weights of the decision makers and aggregated decision matrices are combined into weighted aggregated IF decision matrices by IFWA operator. Weighted aggregated IF decision matrix for criteria of cold subcategories and drought subcategories is shown in

Table 11. Weighted aggregated IF decision matrix for criteria of cold subcategories.

Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
FV/FM	0.26	0.27	0.47
PIABS	0.47	0.19	0.34
ABS/RC	0.18	0.34	0.48
DIo/RC	0.20	0.30	0.50
MDA	0.35	0.25	0.41

and

Table 12. Weighted aggregated IF decision matrix for criteria of drought subcategories.

Criteria	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
FV/FM	0.22	0.26	0.52
PIABS	0.37	0.20	0.43
PITOTAL	0.41	0.21	0.38
H2O2	0.21	0.35	0.45
MDA	0.24	0.33	0.44

, respectively.

Step-8: Each weighted aggregated IF decision matrix is checked for consistency. Sample calculation for the matrix in Table 11 and Table 12 is formulated in Equation (8). Because the CR value is 0.098 for cold subcategories and 0.099 for drought subcategories, which is below 0.10, the matrix is accepted to be consistent. The matrices with a CR value higher than 0.10 should be evaluated again by DMs.

Step-9: Relative weights for each category, subcategory, and criterion are calculated using Equation (9). Results are shown in

Table 13. Criterion weights.

Category	Weights	Subcategory	Local Weights	Criterion	Global Weights
Cold	0.407966008	CA	0.127848430	FV/FM	0.010264840
				PIABS	0.014577722
				ABS/RC	0.007080202
				DIo/RC	0.008251389
				MDA	0.011983660
		CA + S	0.251228975	FV/FM	0.020170957
				PIABS	0.028646001
				ABS/RC	0.013912975
				DIo/RC	0.016214418
				MDA	0.023548531
		S	0.151669812	FV/FM	0.012177438
				PIABS	0.017293919
				ABS/RC	0.008399422
				DIo/RC	0.009788830
				MDA	0.014216518
		CA + S + R	0.274637131	FV/FM	0.022050378
				PIABS	0.031315080
				ABS/RC	0.015209310
				DIo/RC	0.017725190
				MDA	0.025742656
		S + R	0.194615653	FV/FM	0.015625523
				PIABS	0.022190753
				ABS/RC	0.010777748
				DIo/RC	0.012560572
				MDA	0.018241975
Drought	0.592033992	S1	0.113622264	FV/FM	0.012051467
				PIABS	0.016973839
				PITOTAL	0.017357286
				H2O2	0.009836406
				MDA	0.011049245
		R1	0.150530920	FV/FM	0.015966222
				PIABS	0.022487561
				PITOTAL	0.022995566
				H2O2	0.013031629
				MDA	0.014638442
		S2	0.184976509	FV/FM	0.019619731
				PIABS	0.027633330
				PITOTAL	0.028257580
				H2O2	0.016013622
				MDA	0.017988118
		R2	0.200942717	FV/FM	0.021313203
				PIABS	0.030018495
				PITOTAL	0.030696627
				H2O2	0.017395835
				MDA	0.019540759
		S3	0.159284879	FV/FM	0.016894720
				PIABS	0.023795300
				PITOTAL	0.024332848
				H2O2	0.013789469
				MDA	0.015489725
		R3	0.190642712	FV/FM	0.020220722
				PIABS	0.028479794
				PITOTAL	0.029123167
				H2O2	0.016504152
				MDA	0.018539130

.

Step-10: Crisp weights are added to the GP model and the GP model is solved. Cultivars are ranked according to their difference scores from the goal values in ascending order. That is, a lower score grants a cultivar a better rank. Ranking results are shown in

Table 14. Rank of chickpea cultivars.

Chickpea Cultivars	Score	Rank
Diyar 95	0.272232	1
Yaşa 05	0.356107	2
Gökçe	0.376673	3
İnci	0.384299	4
ILC 482	0.390989	5
Uzunlu 99	0.400761	6
Aziziye	0.412080	7
Çağatay	0.439445	8
Damla 89	0.439734	9
Küsmen 99	0.447208	10
Hisar	0.461131	11
Gülümser	0.469239	12
İzmir 92	0.483987	13
Akçin 91	0.484900	14
Canıtez 87	0.522043	15
Er 99	0.530245	16
Sarı 98	0.539006	17
Işık 05	0.637592	18

.

The solution steps only cover sample calculations and tables because of space limitations. The resulting order presents the cumulative performance against cold and drought stress conditions. The scores of the cultivars also provides evidence for the degree of performance distinction. With this focus, Diyar 95 shows a prominent performance against remaining cultivars, while Işık 05 performs worst with the lowest value.

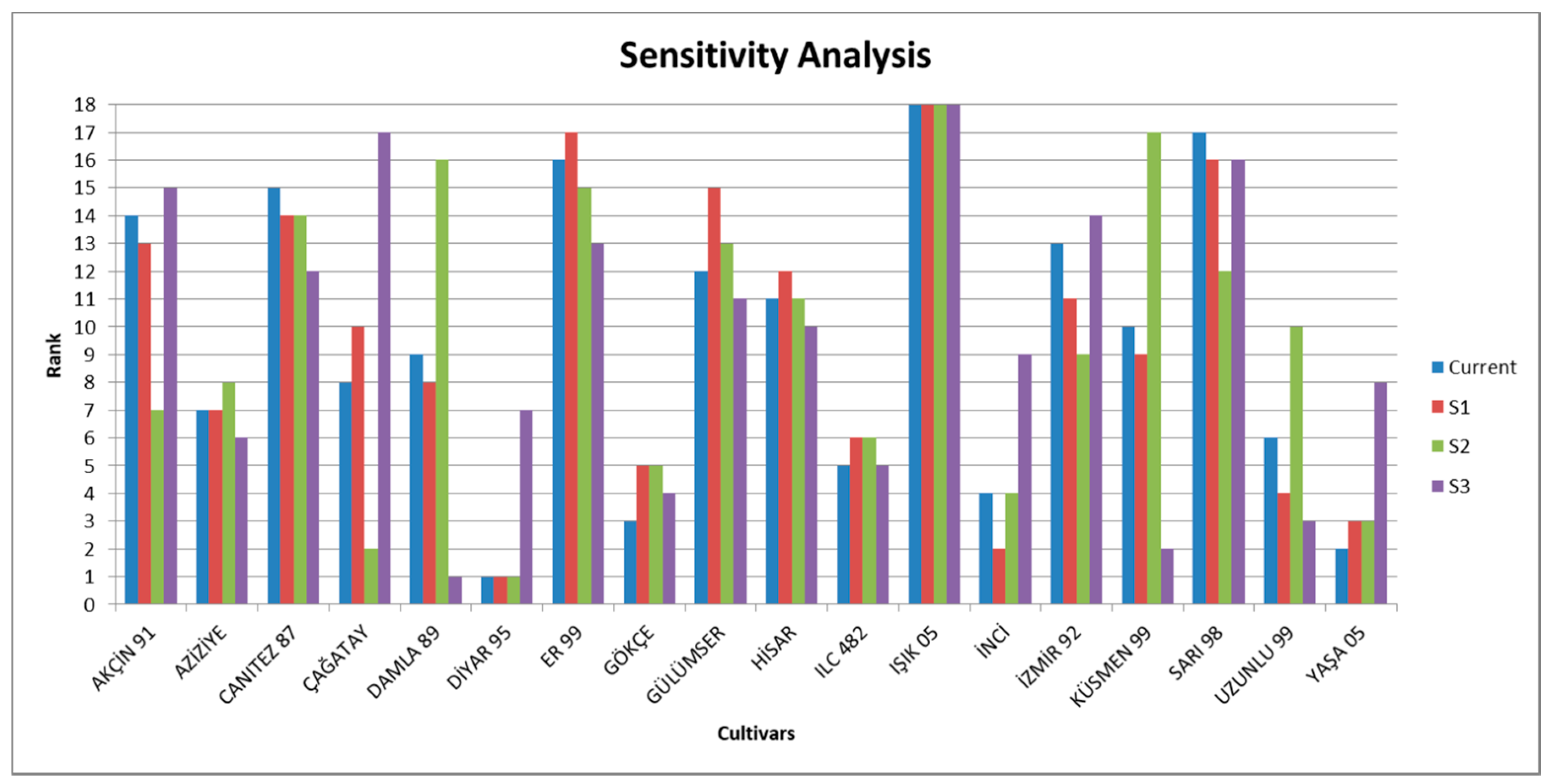
Sensitivity Analysis

Final ranks of alternatives are sensitive to the weights of the criteria. As a result of this assumption, relative changes of criteria may lead to a completely different ranking of alternatives. The weights are acquired from the subjective judgments of decision makers. Any perturbation on ranking may bias rational solution of any MCDM problem. Because the judgments of decision makers change according to knowledge, experience, and relativeness, a sensitivity analysis should be added to the methodology to evaluate boundaries of the solution rather than having a point solution.

A set of scenarios with changing weights were considered for sensitivity analysis. In Scenario 1, the weight of each criterion was accepted as equal. In Scenario 2, the effect of drought stress is assessed solely, thus weight of drought stress was 1.00 where the weight of cold stress was 0. Scenario 3 was the opposite case of Scenario 2 where weight of drought stress was 0 and the weight of cold stress was 1.00. Results for these scenarios are demonstrated in Figure 5. The scenarios have given rise to significant results. The most significant result is Diyar 95 remains as best alternative except in Scenario 3 where the weight of the drought stress is 0. This result advises that the performance of Diyar 95 under cold stress avoids it to remain as best alternative. Another significant result is Işık 05 remains as worst alternative in all scenarios. Damla 89 presents a highly varying performance, which keeps it as best alternative in Scenario 3 where cold stress is considered and 16th alternative in Scenario 2 where drought stress is considered. Çağatay presents an opposing performance to the Damla 89, thus it becomes 2nd in Scenario 2 and 17th in Scenario 3.

In addition to scenarios, limits regarding the best three alternatives are evaluated. The results are shown in

Table 15. Weight limits for best three alternatives.

	Interval for Weight of
Result	Drought Stress	Cold Stress
Best alternative (Diyar 95) not changing	0.25–1.00	0.00–0.75
Best two (Diyar 95 and Yaşa 05) not changing	0.46–0.91	0.09–0.54
Best three (Diyar 95, Yaşa 05 and Gökçe) not changing	0.46–0.64	0.36–0.54

.

4. Discussion and Conclusions

In this paper, a MCDM methodology is proposed to rank chickpea cultivars with respect to their cumulative tolerance to cold and drought stress conditions. The methodology integrates two important algorithms, namely AHP and goal programming. AHP is applied to determine the weights of the categories, subcategories, and criteria. Goal programming is handled to rank the alternatives with regard to their distances from their target values. AHP is widely used in literature to determine weights since it eases the process by pairwise comparisons. It enables GDM, in which the evaluations of multiple experts are aggregated to achieve a more concrete decision. However, classical AHP forces DMs to compare the criteria with crisp values. Thus, the comparison should be conducted numerically without any regret. However, in some cases DMs may be required to avoid definitive judgments. That is, they may need to express their uncertainties. Fuzzy sets are integrated to MCDM methodology to overcome this deficiency in the literature. Fuzzy numbers allow DMs to express the degree of membership and the degree of nonmembership to a set. Nevertheless, by expressing their evaluation with fuzzy numbers, DMs are still required to express exact levels of membership and nonmembership. As an extension of fuzzy theory, IF theory has been preferred to allow DMs to express their hesitancy while declaring their judgments. Various similar methodologies are surveyed and listed in Table 1. Studies [14] through [17] propose an IF-GP, in which the “performances” of alternatives may be evaluated with hesitancies. However, they lack evaluation of criteria by GDM experts and also a sensitivity analysis. The studies [18] and [19] suggest a fuzzy AHP-GP integration without GDM and sensitivity. The common deficit of studies from [18] to [21] is their integration with classical fuzzy sets that avoids DMs expressing their uncertainties. The methodology by Alegoz and Yapicioglu [22] is reinforced by type 2 fuzzy set that supports hesitancy with similar fashion to IF Set. However, GP methodology in this methodology cannot be applied to rank alternatives. Aggregating all these aspects, to the best of the author’s knowledge, this is the first study in this field that suggests a MCDM methodology for ranking alternatives that encourages a GDM process in which DMs also express their hesitancies by proposing an integration IF-AHP with GDM and GP followed by a sensitivity analysis. The distinguishing features of the methodology are the generic structure that allows the application to any other selection process, GDM where IF theory is applied to help DMs to evaluate the criteria by also indicating their uncertainties, and sensitivity analysis that helps to determine the limit values that change the result. The methodology may be applied to any MCDM problem without any change, where expert DMs exist to express their linguistic evaluations for criteria and alternatives have crisp performance values for each criterion.

The MCDM model of the case study has been built on chickpea cultivars as alternatives and stress conditions as categories, states of the stress experiments as subcategories, and critical parameters of chickpea cultivars as criteria. The experimental data consist of critical numerical parameters that decrease or increase under stress conditions. F_V/F_M, PI_ABS, and PI_TOTAL keep a decreasing trend whereas ABS/RC, DIo/RC, MDA, and H₂O₂ have an increase under stress conditions. Goal programming of the proposed methodology penalizes these deviations with respect to control cultivars to calculate cumulative capability of durability, since an increase or decrease in the values indicates sensitivity to stress conditions. In other words, cultivars are qualified as more tolerant to stress conditions provided that they have as little difference as possible from control cultivar parameter values. As a result, Diyar 95 outperforms with a highly separated score. Sensitivity analysis shows that Diyar 95 has the best capability to protect itself under drought stress. However, Damla 89 performs slightly well if the weight of cold stress is adjusted over 75%, since Damla 89 has better durability under cold stress conditions. The worst performing cultivar is Işık 05 with a distinctly low score.

Evaluating the final weights of categories, subcategories, and criteria, it can be inferred that real-life conditions of the geography are effective on evaluations by DMs. Drought stress condition is counted as more important than cold stress condition, in line with the conditions in Turkey. Discussing the subcategories, it can be recognized that the states followed by adaptation in cold stress and recovery state for drought stress are more important. The reason behind these preferences may be considered as also the similarities of these states to cultivations in Turkey. Among the criteria, PI_ABS and PI_TOTAL have the highest importance levels after comparisons. This result should not be surprising since these indicators collectively show the vitality level of the cultivars. All these deductions are consistent with the conditions in Turkey and may result in differences after evaluations by DMs in different regions.

The results in this study may be compared to the experimental studies by Turan [25] for cold stress and Çiçek et al. [5] for drought stress. Rather than having totally mathematical formulations, both studies have heuristic scoring approaches. Turan [25] partitioned the cultivars into three sets, namely tolerant, moderately tolerant, and sensitive. The proposed algorithm in this study has been run with weight values “0” for drought category and “1” for cold category to have the same scale with the study by Turan [25]. Dividing the ranking list of this study into same sets yields to have exactly the same cultivars within the same clusters. With the same manner, the algorithm has been run with weight values “1” for drought category and “0” for cold category to compare with the study by Çiçek et al. [5]. Both studies perform similar results. Four out of five cultivars at the top of both lists are the same cultivars. Hence, the comparisons with both studies suggest that the proposed methodology and results are consistent with experimental deductions.

This study aims to support decision makers on agriculture to select best alternatives for cultivation planning. For future research directions, new decision categories like cost, availability, etc. may be included to enhance the decision-making process for cultivar ranking. More parameters would enrich the quality of the decision process. Furthermore, integrated Z-Score AHP, neutrosophic sets, or Pythagorean fuzzy AHP may be applied to enhance the capability of handling uncertainties of the decision processes. Because the alternatives have numerical parameters, the model cannot be applied to data that include linguistic parameters. Instead of pure GP, IF-GP may be applied to transform linguistic terms into numerical values to involve them in calculations.