Thermal Radiation and MHD Effects in the Mixed Convection Flow of Fe3O4–Water Ferrofluid towards a Nonlinearly Moving Surface
Abstract
1. Introduction
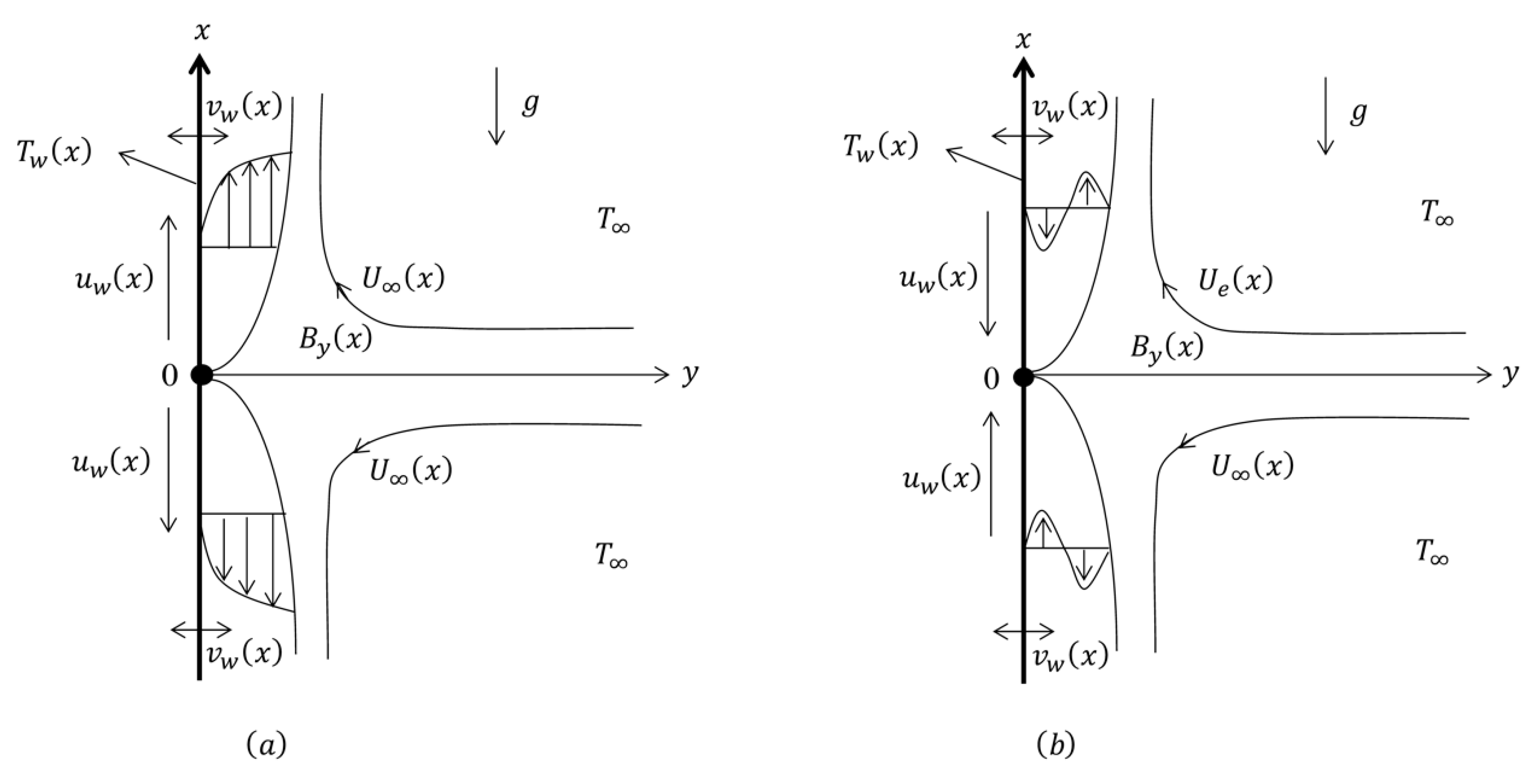
2. Formulation of the Problem
3. Stability Analysis
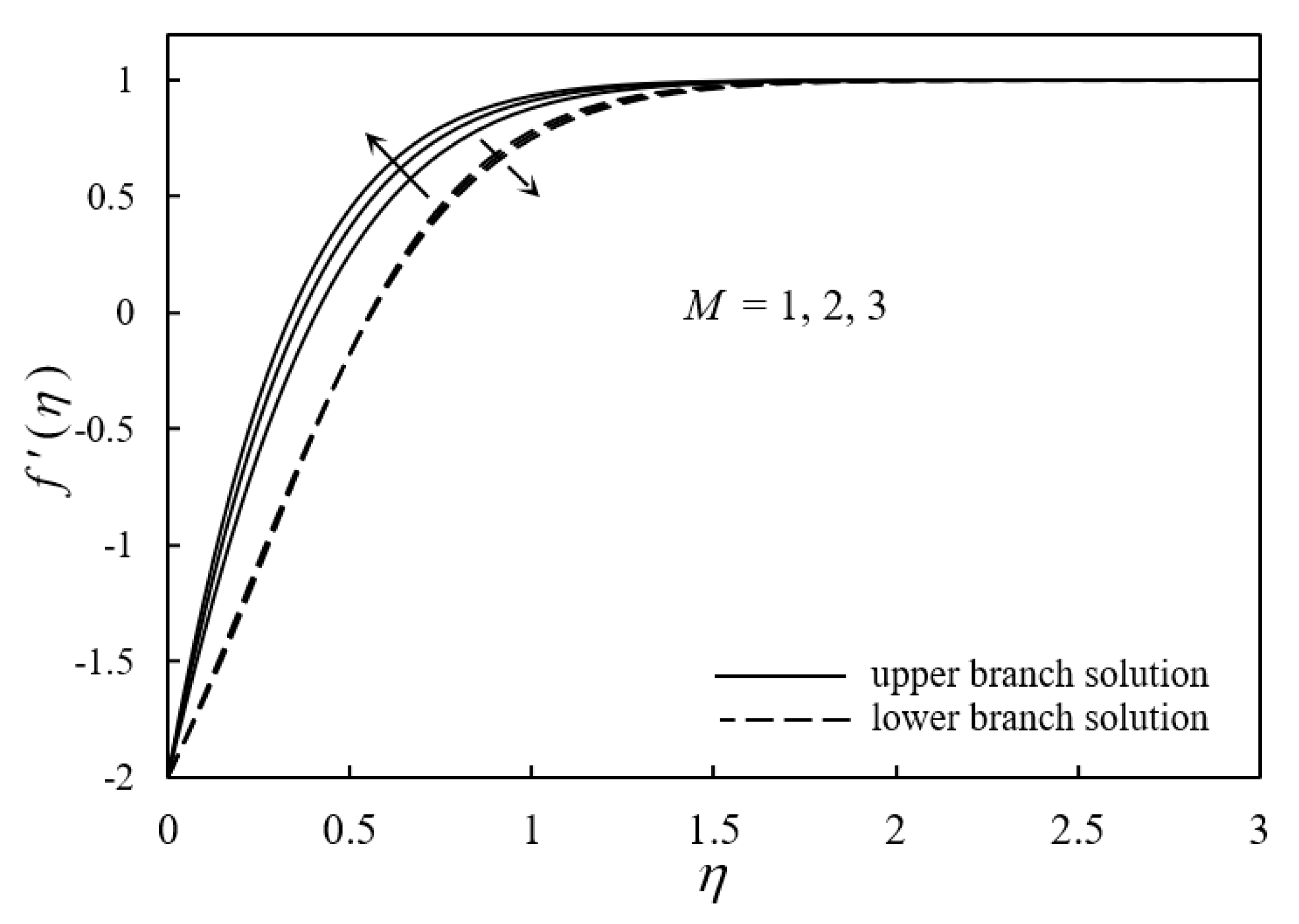
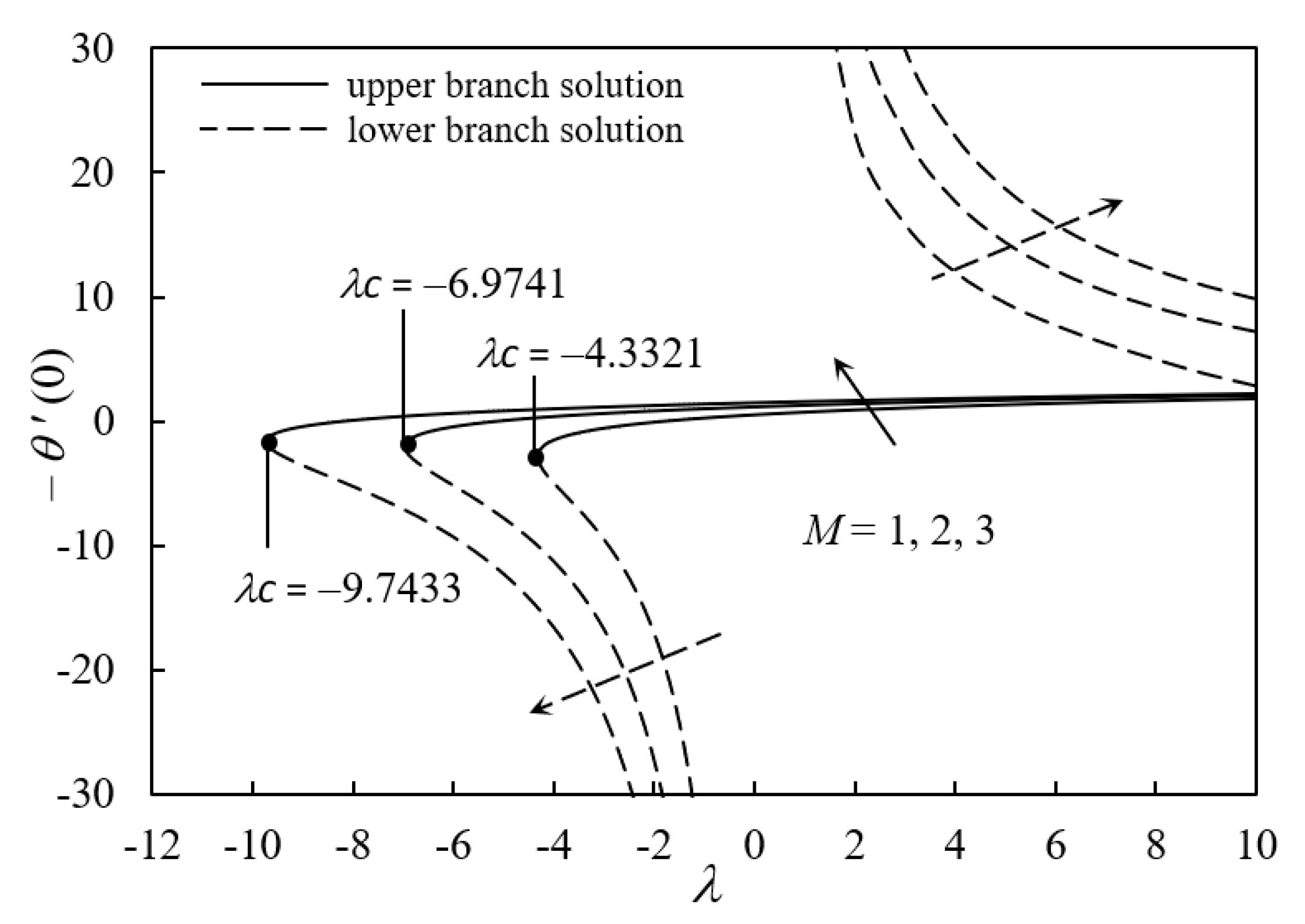
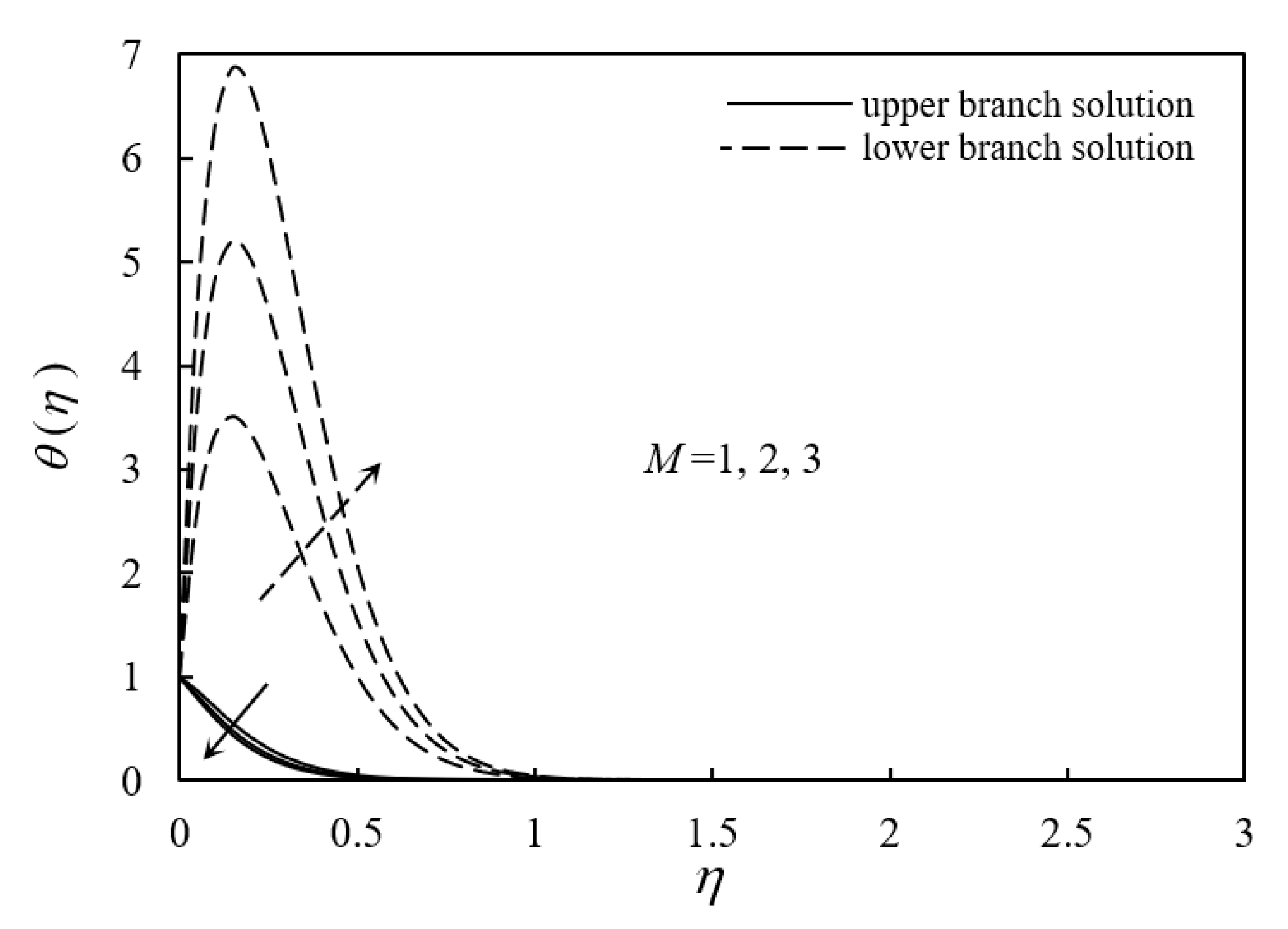
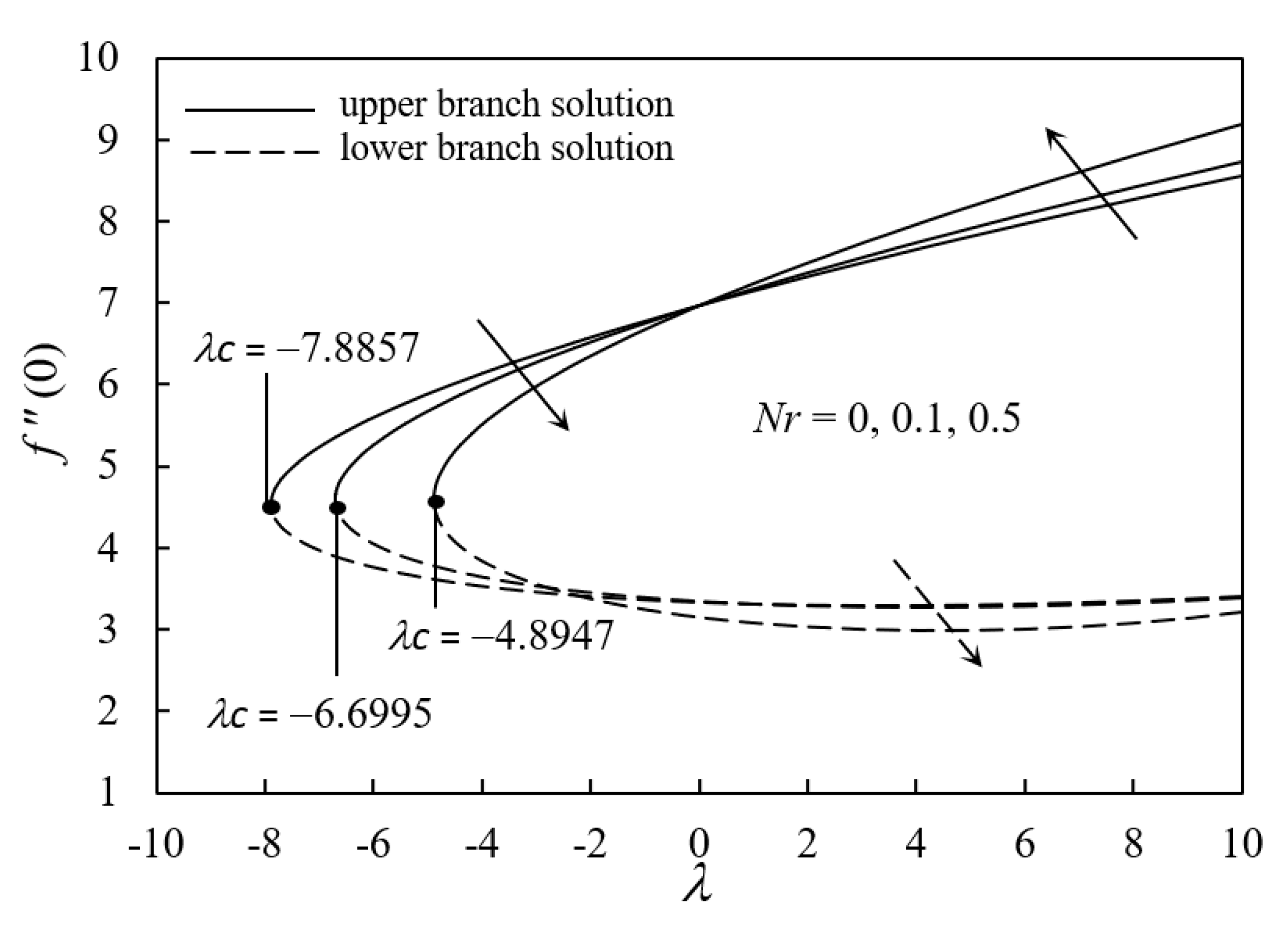
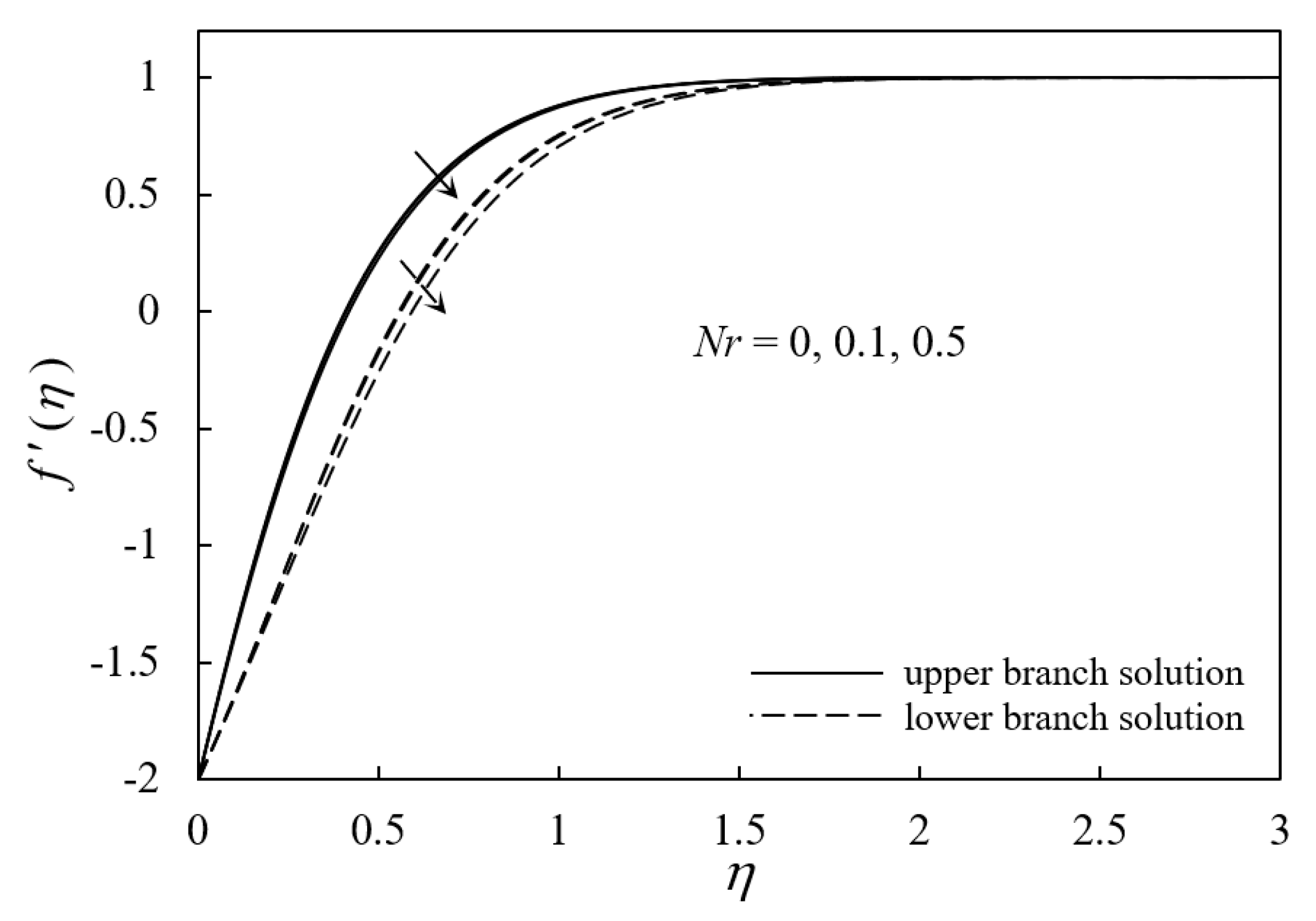
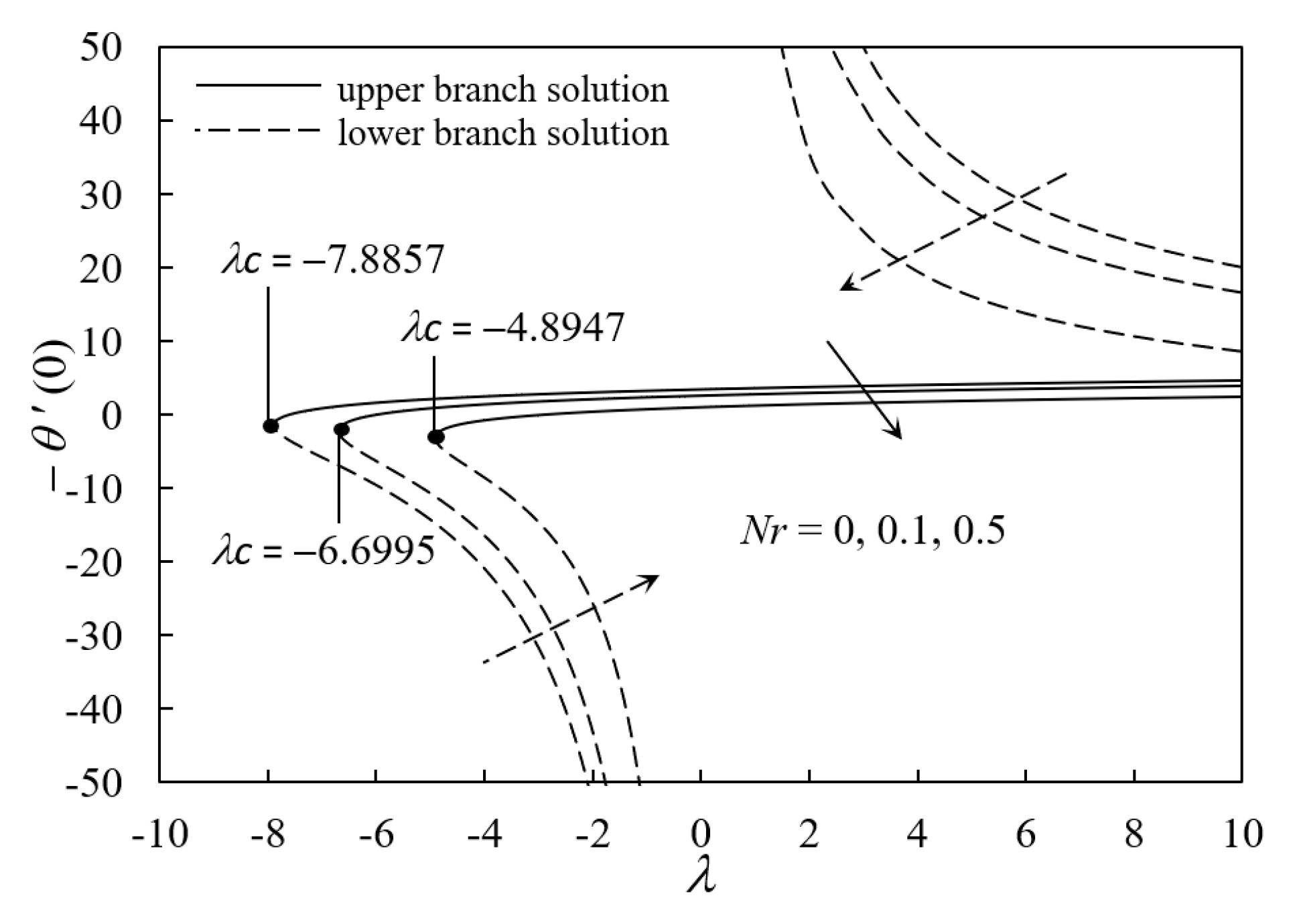
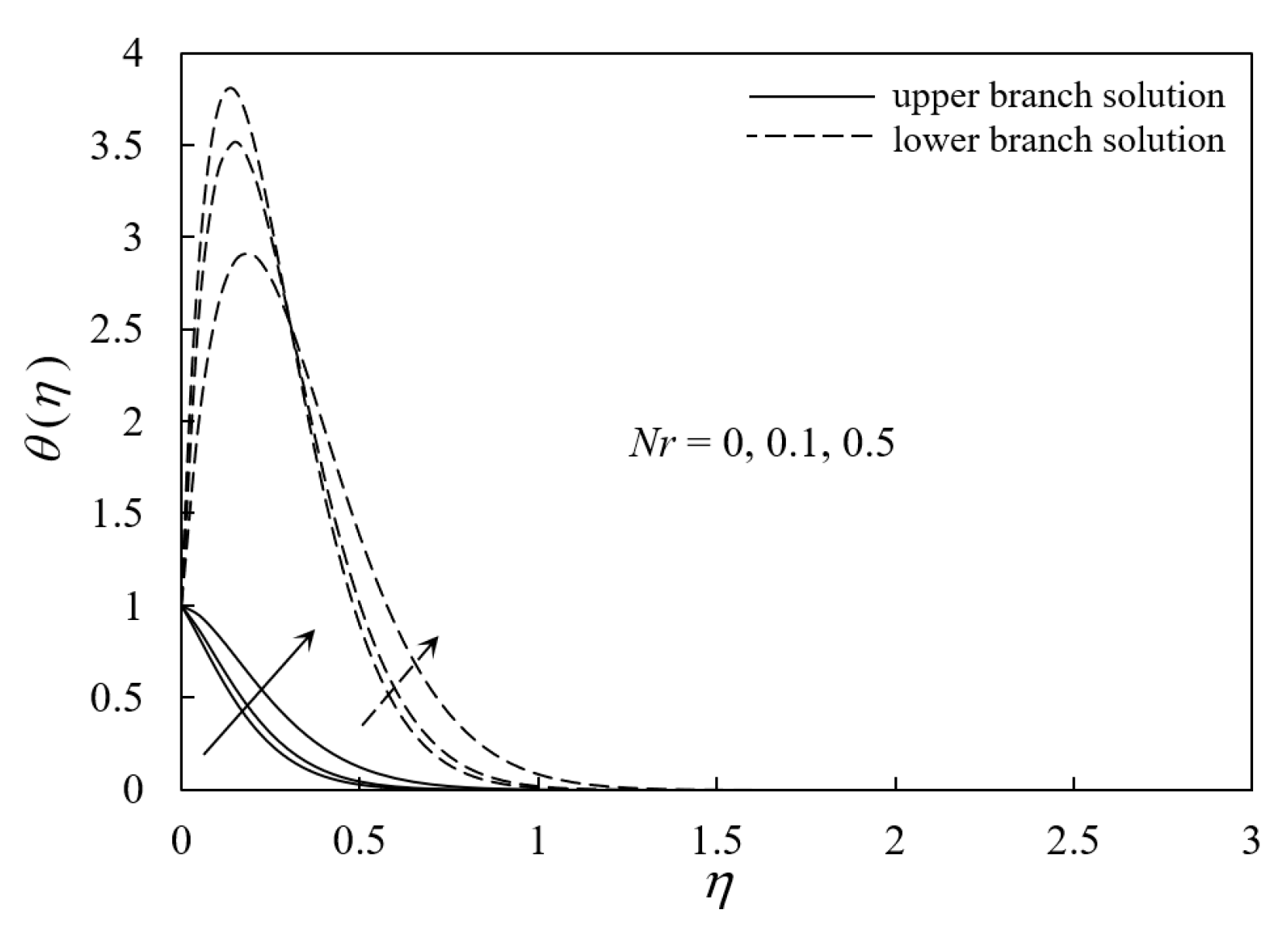
4. Results and Discussion
5. Conclusions
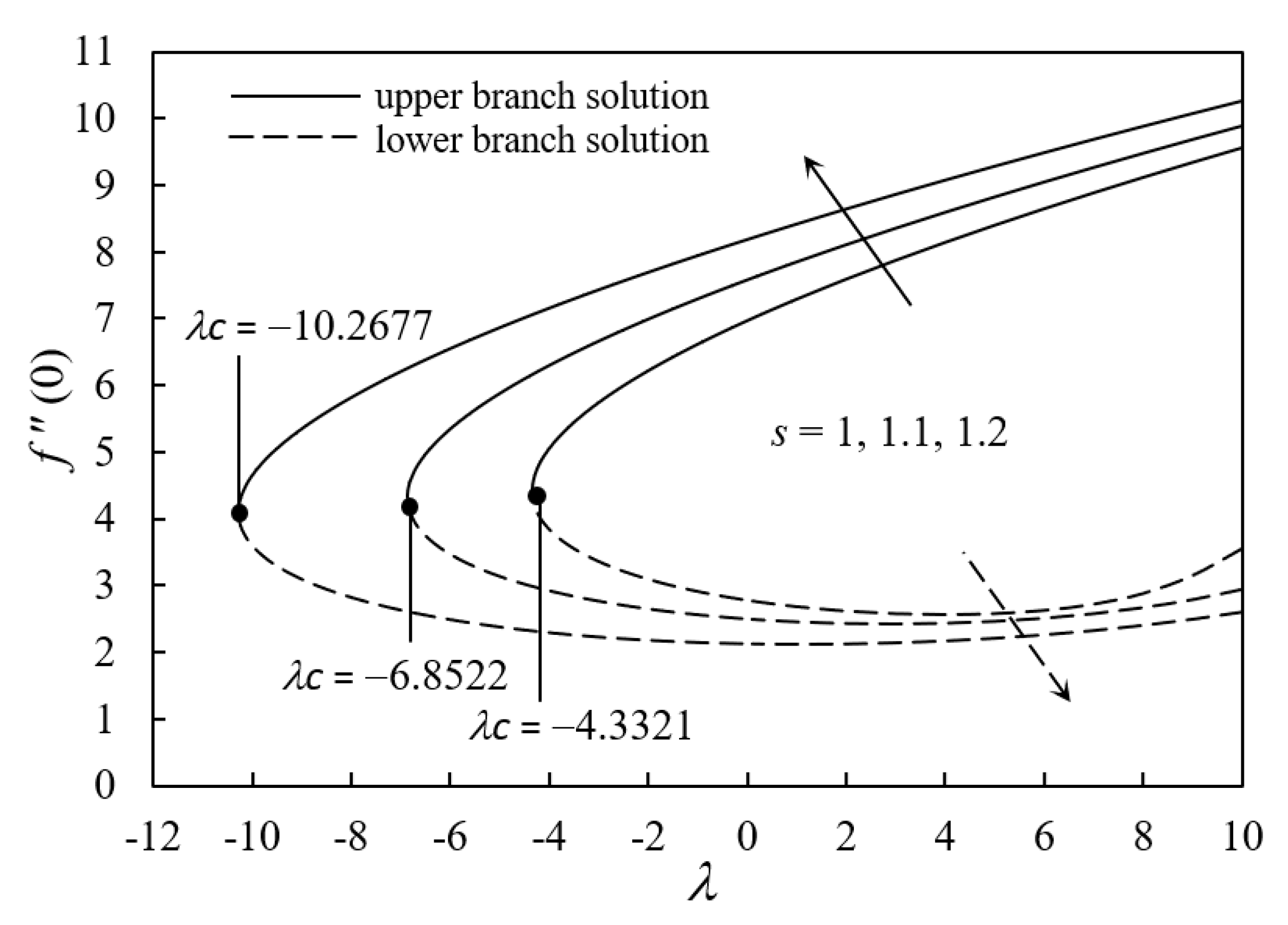
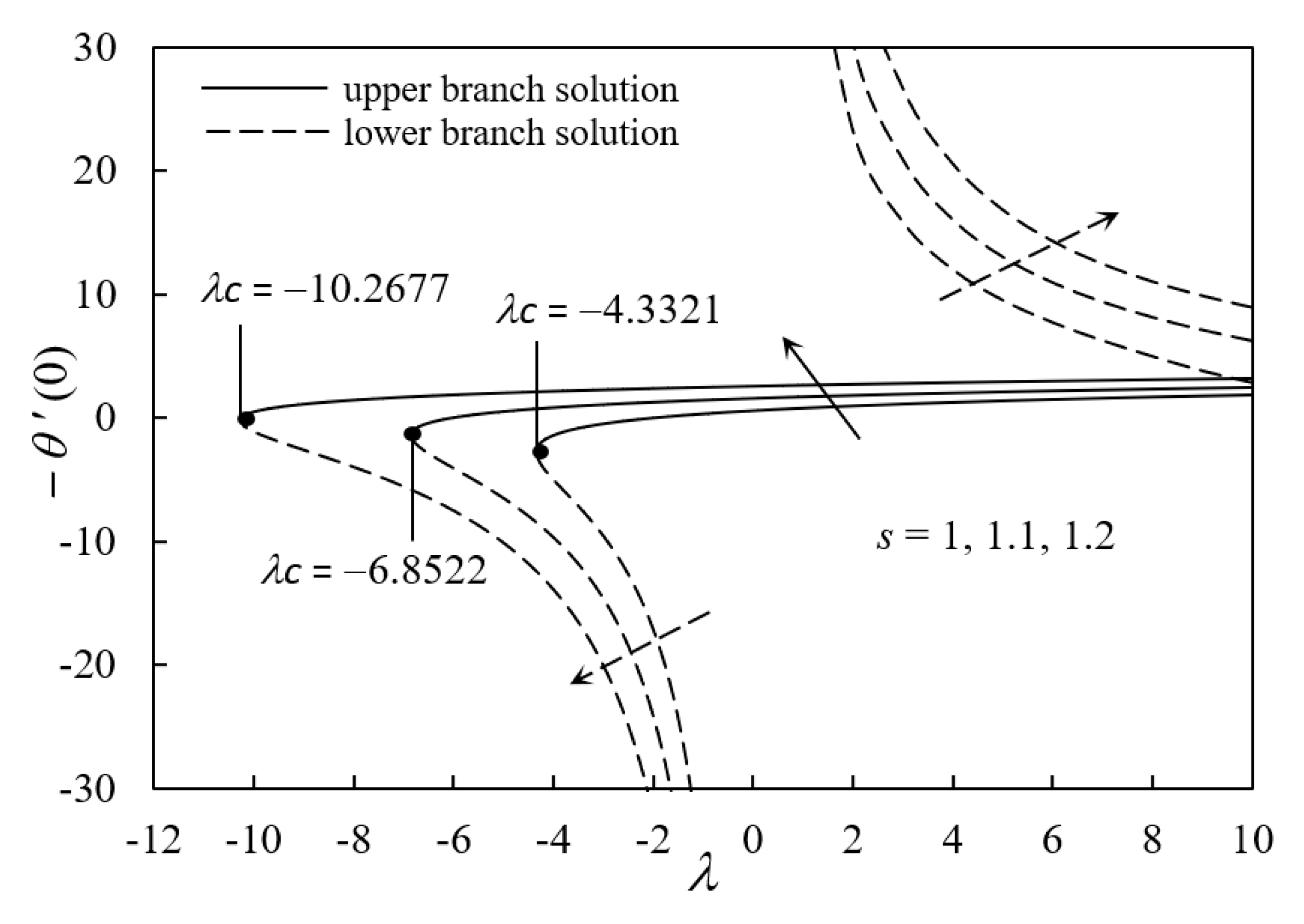
- The existence and duality of solutions were clearly demonstrated for the opposing flow and assisting flow.
- The solutions failed to exist for values of λ lower than the specified critical value for the opposing flow region.
- The stability of the dual solutions validated that the upper branch solution was stable while it was unstable for the lower branch solution.
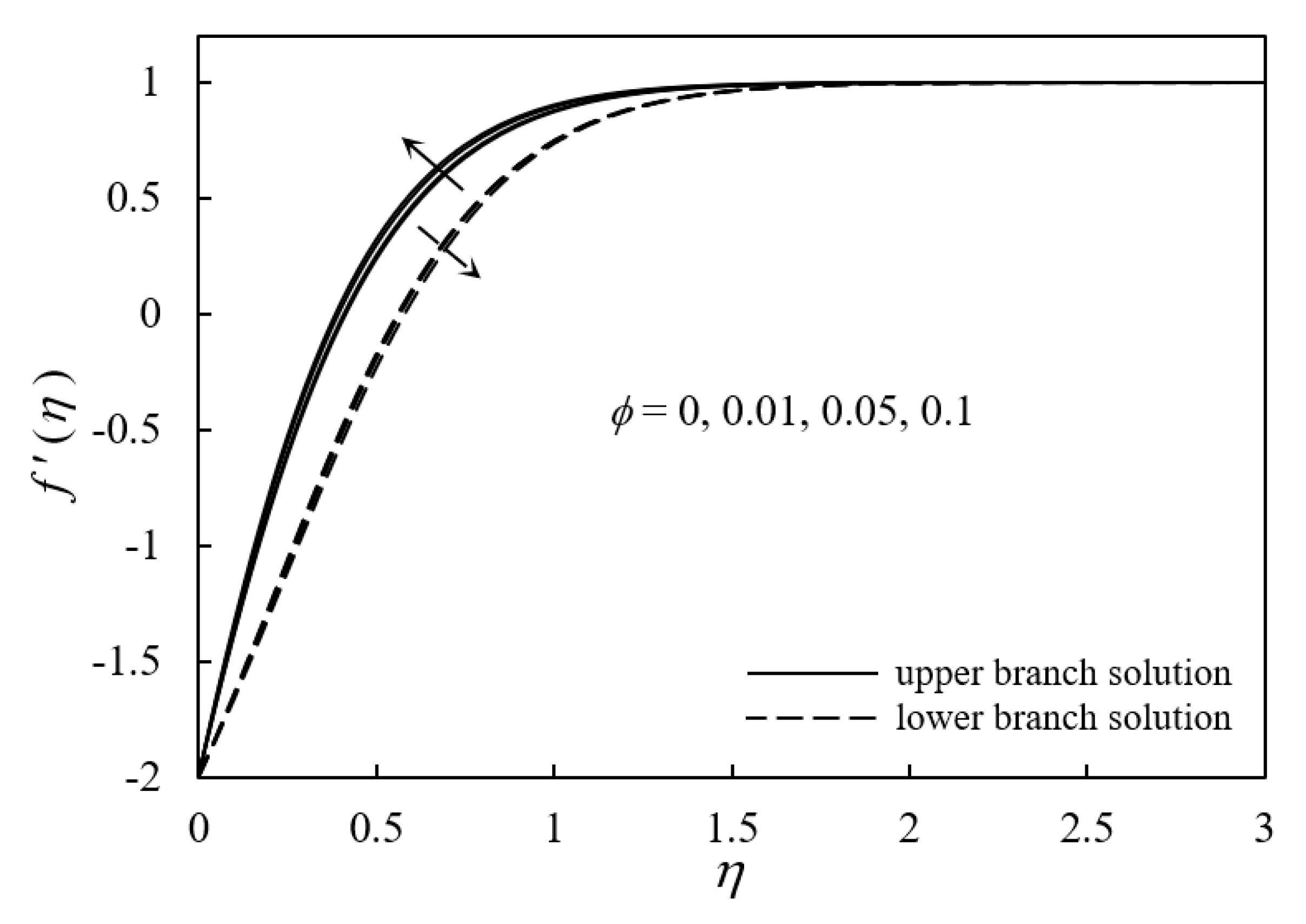
- Ferrofluid velocity profiles increased with an increase in M and ϕ but decreased with an increment in Nr.
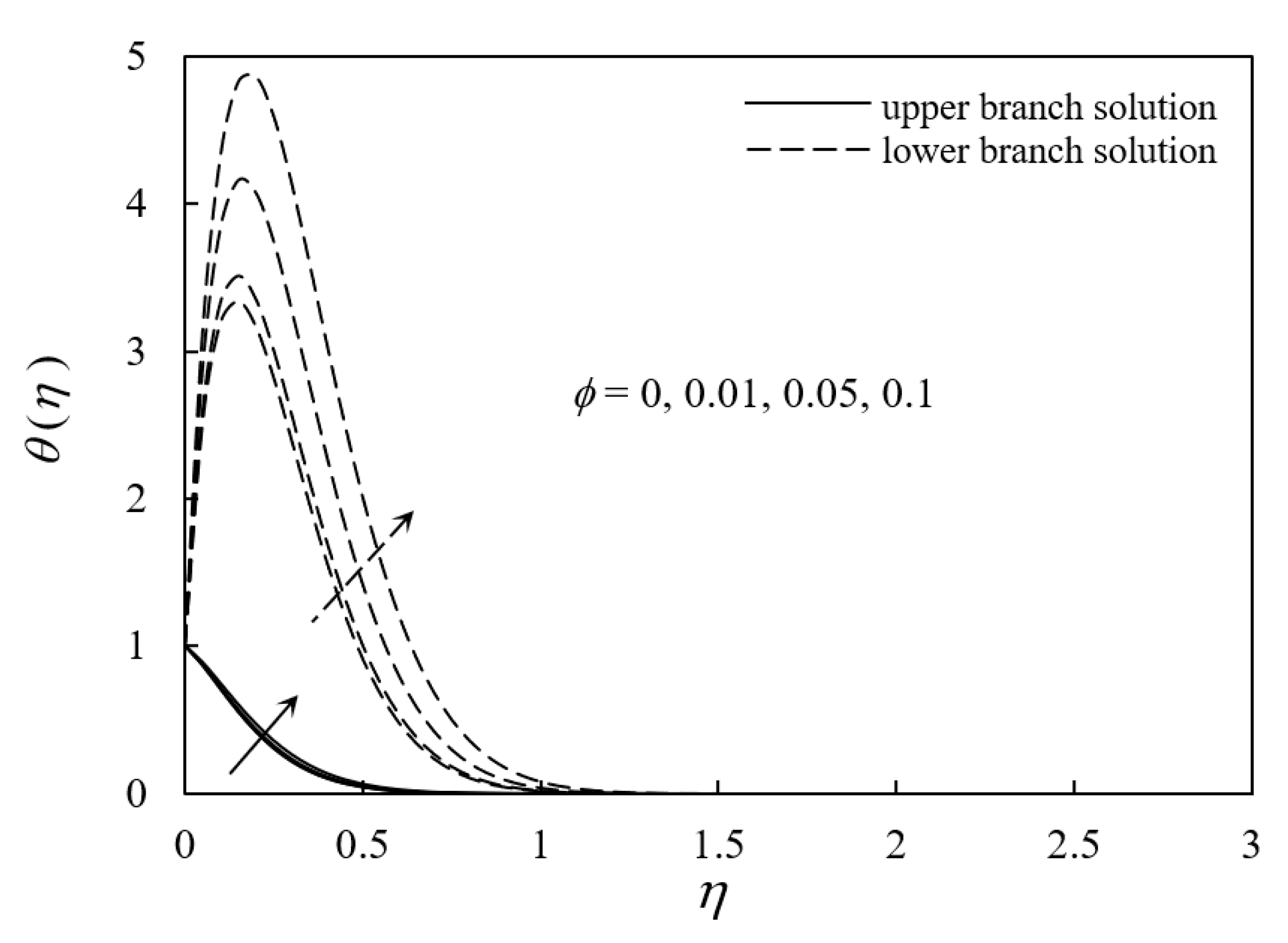
- Temperature profiles of the ferrofluid decreased with an increase in M; however, they increased with increasing ϕ and Nr.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–106. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammad, H. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 987–991. [Google Scholar] [CrossRef]
- Mahdy, A. Unsteady mixed convection boundary layer flow and heat transfer of nanofluids due to stretching sheet. Nucl. Eng. Des. 2012, 249, 248–255. [Google Scholar] [CrossRef]
- Tamim, H.; Dinarvand, S.; Hosseini, R.; Pop, I. MHD mixed convection stagnation-point flow of a nanofluid over a vertical permeable surface: A comprehensive report of dual solutions. Heat Mass Transf. 2014, 50, 639–650. [Google Scholar] [CrossRef]
- Mustafa, I.; Javed, T.; Majeed, A. Magnetohydrodynamic (MHD) mixed convection stagnation point flow of a nanofluid over a vertical plate with viscous dissipation. Can. J. Phys. 2015, 93, 1365–1374. [Google Scholar] [CrossRef]
- Subhashini, S.V.; Sumathi, R.; Momoniat, E. Dual solutions of a mixed convection flow near the stagnation point region over an exponentially stretching/shrinking sheet in nanofluids. Meccanica 2014, 49, 2467–2478. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Yazdi, M.; Moradi, A.; Dinarvand, S. MHD mixed convection stagnation-point flow over a stretching vertical plate in porous medium filled with a nanofluid in the presence of thermal radiation. Arab. J. Sci. Eng. 2014, 39, 2251–2261. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Influence of thermal radiation on mixed convection heat and mass transfer stagnation-point flow in nanofluids over stretching/shrinking sheet in a porous medium with chemical reaction. Nucl. Eng. Des. 2014, 273, 644–652. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Mixed convection–radiation on stagnation-point flow of nanofluids over a stretching/shrinking sheet in a porous medium with heat generation and viscous dissipation. J. Pet. Sci. Eng. 2015, 126, 16–25. [Google Scholar] [CrossRef]
- Haroun, N.A.; Mondal, S.; Sibanda, P. Effects of thermal radiation on mixed convection in a MHD nanofluid flow over a stretching sheet using a spectral relaxation method. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2017, 11, 52–61. [Google Scholar]
- Rosensweig, R.E. Magnetic fluids. Annu. Rev. Fluid Mech. 1987, 19, 437–463. [Google Scholar] [CrossRef]
- Pîslaru-Dănescu, L.; Morega, A.M.; Morega, M.; Stoica, V.; Marinică, O.M.; Nouraş, F.; Păduraru, N.; Borbáth, I.; Borbáth, T. Prototyping a ferrofluid-cooled transformer. IEEE Trans. Ind. Appl. 2013, 49, 1289–1298. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Çelik, Ö.; Can, M.M.; First, T. Size dependent heating ability of CoFe2O4 nanoparticles in AC magnetic field for magnetic nanofluid hyperthermia. J. Nanopart. Res. 2014, 16, 2321. [Google Scholar] [CrossRef]
- Golneshan, A.A.; Lahonian, M. Diffusion of magnetic nanoparticles in a multi-site injection process within a biological tissue during magnetic fluid hyperthermia using lattice Boltzmann method. Mech. Res. Commun. 2011, 38, 425–430. [Google Scholar] [CrossRef]
- Sharifi, I.; Shokrollahi, H.; Amiri, S. Ferrite-based magnetic nanofluids used in hyperthermia applications. J. Magn. Magn. Mater. 2012, 324, 903–915. [Google Scholar] [CrossRef]
- Lajvardi, M.; Moghimi-Rad, J.; Hadi, I.; Gavili, A.; Isfahani, T.D.; Zabihi, F.; Sabbaghzadeh, J. Experimental investigation for enhanced ferrofluid heat transfer under magnetic field effect. J. Magn. Magn. Mater. 2010, 322, 3508–3513. [Google Scholar] [CrossRef]
- Gavili, A.; Zabihi, F.; Isfahani, T.D.; Sabbaghzadeh, J. The thermal conductivity of water base ferrofluids under magnetic field. Exp. Therm. Fluid Sci. 2012, 41, 94–98. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A.; Qasim, M.; Shah, I.A. MHD stagnation point ferrofluid flow and heat transfer toward a stretching sheet. IEEE Trans. Nanotechnol. 2014, 13, 35–40. [Google Scholar] [CrossRef]
- Mustafa, I.; Javed, T.; Ghaffari, A. Heat transfer in MHD stagnation point flow of a ferrofluid over a stretchable rotating disk. J. Mol. Liq. 2016, 219, 526–532. [Google Scholar] [CrossRef]
- Ilias, M.R.; Rawi, N.A.; Shafie, S. MHD Free Convection Flow and Heat Transfer of Ferrofluids over a Vertical Flat Plate with Aligned and Transverse Magnetic Field. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar]
- Abbas, Z.; Sheikh, M. Numerical study of homogeneous–heterogeneous reactions on stagnation point flow of ferrofluid with non-linear slip condition. Chin. J. Chem. Eng. 2017, 25, 11–17. [Google Scholar] [CrossRef]
- Reddy, J.R.; Sugunamma, V.; Sandeep, N. Effect of frictional heating on radiative ferrofluid flow over a slendering stretching sheet with aligned magnetic field. Eur. Phys. J. Plus 2017, 132, 7. [Google Scholar] [CrossRef]
- Sivakumar, N.; Prasad, P.D.; Raju, C.S.; Varma, S.V.; Shehzad, S.A. Partial slip and dissipation on MHD radiative ferro-fluid over a non-linear permeable convectively heated stretching sheet. Results Phys. 2017, 7, 1940–1949. [Google Scholar] [CrossRef]
- Shen, M.; Wang, F.; Chen, H. MHD mixed convection slip flow near a stagnation-point on a nonlinearly vertical stretching sheet. Bound. Value Probl. 2015, 2015, 78. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Three-dimensional magnetohydrodynamic mixed convection flow of nanofluids over a nonlinearly permeable stretching/shrinking sheet with velocity and thermal slip. Appl. Sci. 2018, 8, 1128. [Google Scholar] [CrossRef]
- Hamid, R.A.; Nazar, R.; Pop, I. The non-alignment stagnation-point flow towards a permeable stretching/shrinking sheet in a nanofluid using Buongiorno’s model: A revised model. Z. Nat. A 2016, 71, 81–89. [Google Scholar] [CrossRef]
- Bachok, N.; Najib, N.; Arifin, N.M.; Senu, N. Stability of dual solutions in boundary layer flow and heat transfer on a moving plate in a Copper-water nanofluid with slip effect. WSEAS Trans. Fluid Mech. 2016, 11, 151–158. [Google Scholar]
- Roşca, N.C.; Pop, I. Axisymmetric rotational stagnation point flow impinging radially a permeable stretching/shrinking surface in a nanofluid using Tiwari and Das model. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Pop, I.; Naganthran, K.; Nazar, R. Numerical solutions of non-alignment stagnation-point flow and heat transfer over a stretching/shrinking surface in a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 6, 1747–1767. [Google Scholar] [CrossRef]
- Naganthran, K.; Nazar, R.; Pop, I. Effects of heat generation/absorption in the Jeffery fluid past a permeable stretching/shrinking disc. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–12. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Three-dimensional mixed convection stagnation-point flow over a permeable vertical stretching/shrinking surface with a velocity slip. Chin. J. Phys. 2017, 55, 1865–1882. [Google Scholar] [CrossRef]
- Naganthran, K.; Nazar, R.; Pop, I. Stability analysis of impinging oblique stagnation-point flow over a permeable shrinking surface in a viscoelastic fluid. Int. J. Mech. Sci. 2017, 131–132, 663–671. [Google Scholar] [CrossRef]
- Yatsyshin, P.; Kalliadasis, S. Coupled Mathematical Models for Physical and Biological Nanoscale Systems and Their Applications; Springer: Basel, Switzerland, 2018; pp. 171–185. [Google Scholar]
- Lee, J.W.; Nilson, R.H.; Templeton, J.A.; Griffiths, S.K.; Kung, A.; Wong, B.M. Comparison of molecular dynamics with classical density functional and Poisson-Boltzmann theories of the electric double layer in nanochannels. J. Chem. Theory Comput. 2012, 8, 2012–2022. [Google Scholar] [CrossRef]
- Garnett, J.M. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Med. 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. World J. Mech. 2013, 3, 4. [Google Scholar]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: New York, NY, USA, 2003; pp. 133–211. [Google Scholar]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N.; Raju, C.S.; Reddy, J.V.; Sugunamma, V. Nonlinear thermal radiation and induced magnetic field effects on stagnation-point flow of ferrofluids. J. Adv. Phys. 2015, 5, 1–7. [Google Scholar]
- Nazar, R.; Jaradat, M.; Arifin, N.; Pop, I. Stagnation-point flow past a shrinking sheet in a nanofluid. Cent. Eur. J. Phys. 2011, 9, 1195–1202. [Google Scholar] [CrossRef]

| Physical Properties | Cu | Al2O3 | TiO2 | Fe3O4 | Water |
|---|---|---|---|---|---|
| 385 | 765 | 686.2 | 670 | 4179 | |
| 8933 | 3970 | 4250 | 5180 | 997.1 | |
| 400 | 40 | 8.9538 | 9.7 | 0.613 | |
| 1.67 | 0.85 | 0.9 | 0.5 | 21 | |
| 59.6 106 | 35 106 | 2.6 106 | 0.74 106 | 5.5 10−6 |
| Cu-Water | Al2O3-Water | TiO2-Water | ||||
|---|---|---|---|---|---|---|
| Nazar et al. [48] | Present | Nazar et al. [48] | Present | Nazar et al. [48] | Present | |
| −1.1 | 1.81414 | 1.81414 | 1.54239 | 1.54239 | 1.55898 | 1.55898 |
| (0.07526) | (0.07526) | (0.06399) | (0.06399) | (0.06467) | (0.06467) | |
| −1.15 | 1.65447 | 1.65447 | 1.40663 | 1.40663 | 1.42176 | 1.42176 |
| (0.17841) | (0.17841) | (0.15168) | (0.15168) | (0.15332) | (0.15332) | |
| −1.2 | 1.42552 | 1.42552 | 1.21198 | 1.21198 | 1.22502 | 1.22502 |
| (0.35719) | (0.35719) | (0.30369) | (0.30369) | (0.30695) | (0.30695) | |
| Cu-Water | Al2O3-Water | TiO2-Water | ||||
|---|---|---|---|---|---|---|
| Nazar et al. [48] | Present | Nazar et al. [48] | Present | Nazar et al. [48] | Present | |
| −1.1 | 0.07358 | 0.07358 | −0.06258 | −0.06258 | −0.06716 | −0.06716 |
| (−2.78699) | (−2.78732) | (−3.69342) | (−3.69356) | (−3.66295) | (−3.66305) | |
| −1.15 | −0.03334 | −0.03334 | −0.18285 | −0.18287 | −0.18567 | −0.18567 |
| (−1.83645) | (−1.83645) | (−2.41407) | (−2.41407) | (−2.39321) | (−2.39321) | |
| −1.2 | −0.18352 | −0.18353 | −0.35356 | −0.35359 | −0.35396 | −0.35395 |
| (−1.25320) | (−1.25364) | (−1.65139) | (−1.65140) | (−1.63698) | (−1.63698) | |
| M | Nr | |||
|---|---|---|---|---|
| 1 | 0 | −7 | 1.1886 | −1.1165 |
| −7.5 | 0.7752 | −0.7442 | ||
| −7.88 | 0.0923 | −0.0919 | ||
| 1 | 0.5 | −4 | 1.6649 | −1.5358 |
| −4.5 | 1.0874 | −1.0318 | ||
| −4.89 | 0.1150 | −0.1144 | ||
| 1 | 1 | −4 | 1.1699 | −1.1104 |
| −4.1 | 0.9728 | −0.9315 | ||
| −4.33 | 0.0861 | −0.0858 | ||
| 2 | 1 | −6 | 1.8845 | −1.7512 |
| −6.5 | 1.2976 | −1.2338 | ||
| −6.97 | 0.1160 | −0.1155 | ||
| 3 | 1 | −9 | 1.5448 | −1.4634 |
| −9.5 | 0.8729 | −0.8466 | ||
| −9.74 | 0.0993 | −0.0990 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. Thermal Radiation and MHD Effects in the Mixed Convection Flow of Fe3O4–Water Ferrofluid towards a Nonlinearly Moving Surface. Processes 2020, 8, 95. https://doi.org/10.3390/pr8010095
Jamaludin A, Naganthran K, Nazar R, Pop I. Thermal Radiation and MHD Effects in the Mixed Convection Flow of Fe3O4–Water Ferrofluid towards a Nonlinearly Moving Surface. Processes. 2020; 8(1):95. https://doi.org/10.3390/pr8010095
Chicago/Turabian StyleJamaludin, Anuar, Kohilavani Naganthran, Roslinda Nazar, and Ioan Pop. 2020. "Thermal Radiation and MHD Effects in the Mixed Convection Flow of Fe3O4–Water Ferrofluid towards a Nonlinearly Moving Surface" Processes 8, no. 1: 95. https://doi.org/10.3390/pr8010095
APA StyleJamaludin, A., Naganthran, K., Nazar, R., & Pop, I. (2020). Thermal Radiation and MHD Effects in the Mixed Convection Flow of Fe3O4–Water Ferrofluid towards a Nonlinearly Moving Surface. Processes, 8(1), 95. https://doi.org/10.3390/pr8010095






