Abstract
Chemical–biological systems, such as bioreactors, contain stochastic and non-linear interactions which are difficult to characterize. The highly complex interactions between microbial species and communities may not be sufficiently captured using first-principles, stationary, or low-dimensional models. This paper compares and contrasts multiple data analysis strategies, which include three predictive models (random forests, support vector machines, and neural networks), three clustering models (hierarchical, Gaussian mixtures, and Dirichlet mixtures), and two feature selection approaches (mean decrease in accuracy and its conditional variant). These methods not only predict the bioreactor outcome with sufficient accuracy, but the important features correlated with said outcome are also identified. The novelty of this work lies in the extensive exploration and critique of a wide arsenal of methods instead of single methods, as observed in many papers of similar nature. The results show that random forest models predict the test set outcomes with the highest accuracy. The identified contributory features include process features which agree with domain knowledge, as well as several different biomarker operational taxonomic units (OTUs). The results reinforce the notion that both chemical and biological features significantly affect bioreactor performance. However, they also indicate that the quality of the biological features can be improved by considering non-clustering methods, which may better represent the true behaviour within the OTU communities.
1. Introduction
Process analytics in the chemical and biotechnology industries is currently reaping the rewards from a data revolution, which was initiated in the 1980s in the field of computer science and communications. This sparked the development of machine learning (ML) modeling paradigms. Simpler models such as random forests [1] and support vector machines [2] have demonstrated widespread success in a variety of classification problems; some examples include invasive plant species prediction [3] and speech recognition [4]. The highly complex neural networks [5] have been recognized as universal approximators [6] for non-linear functions. Neural networks are being successfully applied to modern problems such as natural language processing [7], image prediction [8], and recommender systems [9]. The success of neural nets lie in their ability to handle datasets with exorbitant numbers of samples (e.g., billions), which are known as big-N problems.
On the other hand, data are relatively scarce in the field of process engineering. For example, concentrations of chemicals or populations of biological specimens are usually measured intermittently in laboratories; this limits the frequency at which these data can be acquired. Currently there are few online, ML-based soft sensors for these measurements that are both accurate and inexpensive. Due to both the economical and physical limitations of obtaining abundant data in these cases, biological systems are usually known as small-N problems. In addition to being small-N, these datasets are often also high-dimensionality or big-d. The high number of features in these cases render many simple ML algorithms infeasible, due to the curse of dimensionality [10]. In light of these marked distinctions, these problems warrant an entirely different modeling and analysis paradigm. This study will address some of these challenges, by providing a sensible analysis workflow that identifies key features correlated with a predicted outcome.
The challenges of analyzing chemical, biological, and process data are non-trivial. Interpretable patterns—such as correlations between process performance and features—are often confounded due to the following inexhaustible list of factors:
- Non-uniform and inconsistent sampling intervals.
- Order-of-magnitude differences in dimensionalities.
- Complex interactions between participating species in a bioreactor (e.g., protagonistic vs. antagonistic members, functionally-redundant members).
- Conditionally-dependent effects of features (i.e., some features only affect the outcome in the presence or absence of other features).
Biological system data often includes the relative abundances of operational taxonomic units (OTUs). An OTU represents a taxonomic group (e.g., species or genus) based on the similarity (e.g., or for species and genus, respectively) of their 16S rRNA variable regions. These are determined using high-throughput sequencing of microbial community DNA [11]. The environment inside a bioreactor contains chemical and physical factors, which influence the types of OTUs that thrive. Conversely, the OTUs themselves also affect the environmental conditions inside the bioreactor, since microorganisms mediate many different types of chemical reactions. Microorganisms are known to interact and form communities with members that are protagonistic, antagonistic, or simply bystanders [12]. These profound coupling effects are difficult to identify as closed-form expressions, due to the non-linear stochastic nature of OTU communities. The individual and group effects of members comprising of thousands of OTUs are extremely difficult to isolate. However, the overall confusion can be significantly alleviated by first grouping or clustering OTUs together, according to pre-specified similarity metrics [13]. This reduces the dimensionality of analysis exponentially (e.g., from a few hundred down to several features), which in turn allows the predictive models to be much more focused. Grouping or clustering of OTUs is done with the purpose of identifying so-called keystone microorganisms, or biomarkers, which correlate to successful versus poor process performance.
The overall goal for bioreactor modeling is to extract, out of the many chemical, biological, and process features, those that have a proportionally significant effect on process performance. These can be incorporated into a process control algorithm (e.g., involving soft sensors) to improve performance and reliability, by using easy-to-measure features or biomarkers. Given historical data, the process outcome is identified and preferably separated into discrete classes. The high feature-space of the raw data associated with these classes are “compressed” using dimensionality-reduction techniques. This produces smaller subsets of meaningful, representative features. Predictive models are built using these high-impact features, instead of the original feature set (which may contain irrelevant or redundant data). Finally, the representative features are ranked in terms of importance—with respect to their contributions to the final process outcomes—using univariate feature selection techniques. The results from this approach serve as an informative pre-cursor to decision-making and control, especially in processes where little to no prior domain knowledge is available. The entire framework can also be depicted as a closed-loop feedback control diagram [14], as shown in Figure 1.
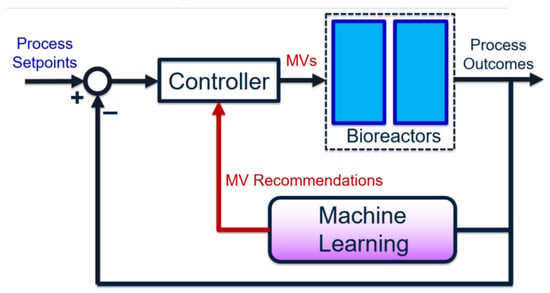
Figure 1.
Machine learning (ML)-guided process control and decision-making. Manipulated variables (MVs) selected from the original process features may be high-dimensional and full of confounding effects. Instead, the small subset of MVs most responsible for causing observed process changes is identified using ML algorithms. The key MVs may change from one operating stage to another, but they can be re-identified given the corresponding new data.
In the proposed workflow, the choice of manipulated variables (MVs) is dynamic—it is re-identified given each influx of new data. On the other hand, traditional feedback control uses a static set of pre-specified MVs, which may not always be impactful variables if the process and/or noise dynamics vary with time. Specifically, the use of machine learning achieves a three-fold goal:
- During each operating stage, operators would only need to monitor a small set of variables, instead of hundreds or thousands. This simplifies the controller tuning and maintenance drastically, and undesirable multivariable effects (such as input coupling [14]) are reduced.
- By using data-based ML models, the process outcomes can be predicted ahead of time, such that unsatisfactory outcomes are prevented. Moreover, the models can be updated using new data collected from each new operating stage, eliminating the need for complete re-identification.
- The ranking of feature impacts can be performed using grey-box models, which are mostly empirical but are guided by a modest amount of system domain knowledge. This combination is exceptionally powerful if the domain knowledge is accurate, since it defines otherwise-unknown prior assumptions. This improves both prediction accuracy and feature analysis accuracy. The task of control and monitoring is also much more feasible, since the focus is only on a handful of variables (as opposed to hundreds).
This work represents a framework of the feature extraction workflow that precedes the development of the aforementioned process control philosophy. Within the framework, we test several popular techniques for dimensionality reduction and machine learning. The explored techniques are applied on a biological wastewater treatment process aimed at removing selenium. The first part of this paper outlines a systematic data pre-processing workflow, which combines both chemical and biological data in a way that ensures both exert equal weights on the model outcome. Then, three unsupervised learning techniques, hierarchical clustering, Gaussian mixtures, and Dirichlet mixtures, are used dimensionality-reduction techniques to extract biomarkers. These key features, along with water chemistry features, are passed as inputs into three state-of-the-art predictive models to predict the final process outcome of selenium removal rate. The supervised learning techniques used are random forests (RFs), support vector machines (SVMs), and artificial neural networks (ANNs). Finally, important process features are correlated with the selenium removal rate using two techniques: mean decrease in accuracy (MDA), and the conditionally-permutated variant, C-MDA. The quality of modeling and feature selection results are compared and contrasted across all explored methods.
One key difference between this work and others in the literature is the broad range of exploration, as well as the extensive use of compare and contrast for several methodologies of data analysis. Most papers focus on the proof-of-concept and results of a single technique, with focus on either the prediction task or feature analysis task. When reading this paper, the reader should focus more on the strengths and limitations of each method, given the results obtained, rather than the numerical values of the results themselves. The main goal of this work is to bring clarity to the appropriate use of analytics, given the various characteristics and circumstances of the available raw process data.
2. Methods
This section introduces the details behind the wastewater treatment process, as well as the machine learning algorithms used for dimensionality reduction, prediction, then finally feature selection.
2.1. Process Flow Diagram and Description
The relevant case study is a wastewater treatment process located downstream of a mining operation. Due to proprietary reasons, the descriptions provided are kept at a general level. The overall process can be visualized as the general bioreactor shown in Figure 2:
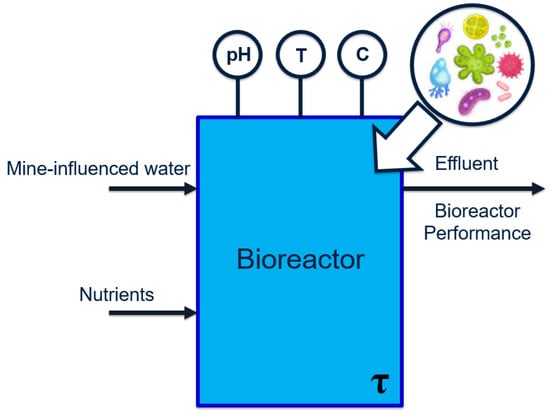
Figure 2.
A simple bioreactor schematic, with wastewater and biological nutrients as inlets, and treated effluent as outlet. The system contains directly-measurable macro variables related to water chemistry (such as contact time ), and difficult-to-measure micro variables reflecting the metabolism of micro-organisms.
Selenate and nitrate concentrations in the bioreactor effluent must be reduced to below and , respectively [15,16]. These chemical species bio-accumulate in the marine ecosystem [17] and thus reach harmful levels at the top of the food chain.
The feed to the first reactor is wastewater, which contains the main pollutant selenate (SeO). The selenate is to be reduced to elemental selenium (Se) by a series of two bioreactors. Samples are extracted from the bioreactors during each operating stage (at irregular intervals) and analyzed in order to determine and record values of various water chemistry variables. These features are summarized in Table 1.

Table 1.
Water chemistry variables.
In addition to the water chemistry data, data pertaining to the microbial presence is available in the form of operational taxonomic units (OTUs). In this case study, the numerical values associated with each OTU are known as raw abundance counts. These counts can be considered normalized population counts of each bacterial species, which fall within the range of 0∼16,000.
2.2. Data Pre-Treatment
Before the raw water chemistry and micro-biological data can be used for any analysis, they must be transformed into a meaningful form. The steps involved can be visualized as a workflow in Figure 3.
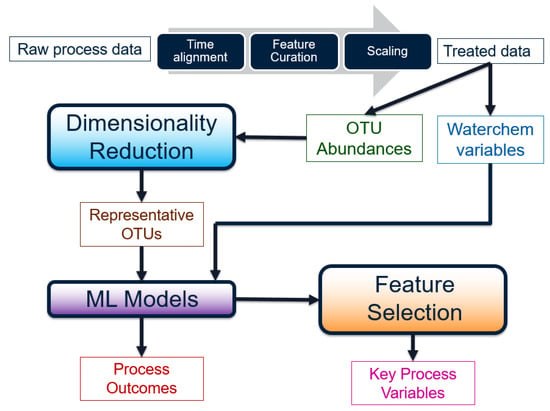
Figure 3.
Workflow of the pre-processing, dimensionality reduction, modeling, and feature selection steps. The final goal is to transform the input data into predicted outcomes, as well as key variables responsible for said outcomes.
The data pre-processing was performed using Jupyter iPython notebooks. The raw dataset originally consists of two files: one containing water chemistry data, and one containing OTU counts. First, samples containing missing or values were removed using the dropna function in pandas. Then, spurious process values (such as negative flowrates) were removed by Boolean functions. The remaining samples were then cross-matched between the water chemistry and OTU files, by use of tags which identify common operating stages. This results in a total of samples containing both water chemistry and microbial information. Although this is a small sample-size, it is unfortunately all the data that could be collected from this treatment plant.
Each water chemistry variable outlined in Table 1 (except SampleID) is standardized via mean-centering and unit-variance operations. This removes any weight-skewing effects during modeling, due to varying feature ranges. The OTU raw abundance counts are recorded in a matrix where the number of samples and number of OTUs are and , respectively. The raw counts fall within the range of 0∼16,000. The abundance distribution is heavily skewed towards the lower population numbers, as shown in Figure 4.
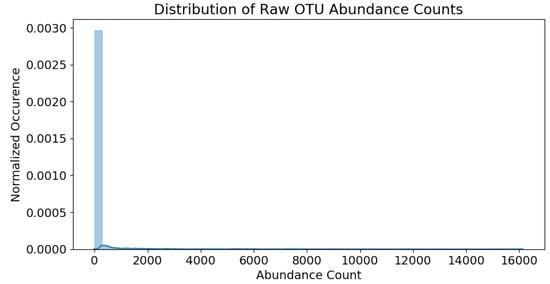
Figure 4.
Distribution of all available raw operational taxonomic unit (OTU) abundance counts.
The skew is partially remedied by applying a -transformation to all raw counts. Since many raw counts are equal to zero, 1 is added to every value before the transformation, to ensure the operation is valid. Counts equal to zero would still remain zero after transformation, since . The overall operation is:
The resulting distribution of the scaled counts can be observed in Figure 5. Note that the skew is not as severe as before; the OTU population distribution is now much clearer.
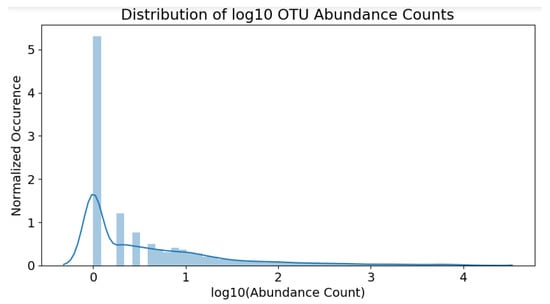
Figure 5.
Distribution of OTU abundance counts, after transformation.
These counts are now in a suitable form for analysis methods outlined in the following sections.
2.3. Unsupervised Learning Methods
The goal of unsupervised data analysis is to delve within the existing data, to search for patterns (e.g., clusters or latent variables) that serve as indicators responsible for the observed outcomes. Although some popular algorithms such k-Means [18] or density-based clustering [19] come to mind, they are not suitable for this case study. This is due to the relatively poorer performance of these methods in high-dimensional datasets, a phenomenon known as the curse of dimensionality.
Instead, this work will primarily focus on three clustering algorithms. The first is known as hierarchical clustering [20,21], which groups organisms together according to a similarity metric. The sizes of the groups can be arbitrarily selected, by deciding the position on the ranking system of said organisms. The benefit of this method lies in the ability to visualize not only the individual groups, but also the relationship between various groups on a dendrogram (see Figure A6), as well as their comparative sizes. Pertinent details behind this technique can be found in Appendix H.
The second and third clustering methods are probabilistic mixtures: namely, the Gaussian [22] and Dirichlet multinomial mixtures [23,24]. These mixture models are used to cluster OTUs based on assumptions of their underlying distributions, rather than their pairwise similarities. The optimal clusters are identified by using the well-known expectation–maximization (EM) algorithm [25]. The remaining details behind these mixtures can be found in Appendix I.
2.4. Network Analysis
Network analysis is a pre-processing technique used in this work, which transforms raw data (such as OTU abundance counts) into association values. These associations can be considered a statistical verification of co-occurrence between OTUs, which estimates true partial correlations between pairwise species.
The basis for this method comes from the observation that communities of microorganisms are extremely complex, and exert confounding effects on process outcomes. For example, OTU communities consist of members which are protagonistic, antagonistic, bystanding, and functionally- redundant species. Although the predatory-prey Lotka-Volterra model [26,27] is a popular method of clarifying such relationships, the network analysis and networks to models strategies [28] are a more modern and relevant approach to the case study at hand. The results from [29] show that not only can dominant microbial groups be directly linked to a certain outcome, but indirect species which faciliate these interactions can also be identified. These network associations can be readily computed using the netassoc algorithm [30]. In summary, this algorithm models the indirect effects of a possible third species (or more) that affects the primary interaction between the main two pairwise species, which is akin to conditionally-dependent modeling in Bayesian networks [31]. The main advantage of this approach is the ability to identify both biomarkers and secondary OTUs, which either facilitate or inhibit a specified process outcome (e.g., removal rate).
2.5. Supervised Learning Methods
After the key variables have been identified using the previous dimensionality reduction and network analysis methods, they are used to perform predictions of the final process outcome. Prediction plays a vital role in process control; if the variable(s) of interest are estimated before actual occurrence, then remedial actions can be formulated ahead of time. In this case study, the primary process outcome of selenium removal rate is predicted using three supervised learning techniques. These include random forests [1], support vector machines [2] (Figure A3), and artificial neural networks [32] (Figure A4 and Figure A5). The details behind these well-known models can be found in Appendix E, Appendix F and Appendix G respectively.
2.6. Feature Selection
After the key features have been identified and used to predict the final process outcome, a natural question to ask from a process engineering perspective is: “Which of these features contribute the most to the predictions?” Although most feature selection approaches in literature are often selected and customized on a case-by-case basis, two overarching groups of methods can be identified:
- Hypothesis testing: A model is trained with all features left untouched. Then, features are either removed or permutated (scrambled), either individually or conditionally according to other features. The model is re-trained, and its accuracy is compared to the base-case accuracy. The features which cause the largest decreases in model accuracy are considered “most important,” and vice versa.
- Scoring: A metric or “score” based on information or cross-entropy is defined and calculated for all features. Features with the highest scores are identified as the “most relevant,” and vice versa.
In the hypothesis testing framework, univariate (or single-feature) algorithms such as mean decrease in accuracy (MDA), and mean Gini impurity (MGI) [33] have been developed for simple models such as random forests. The MDA method can be visualized in Figure 6.
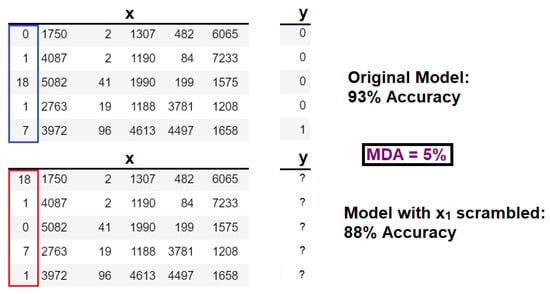
Figure 6.
Mean decrease in accuracy (MDA) applied on a dataset with six features. During each outer iteration, the values of a single feature are scrambled or permutated sample-wise. The model accuracy with the scrambled feature is compared against the base-case model accuracy. If the accuracy decreases significantly, then the feature is considered “important.” On the other hand, if the accuracy decreases negligibly, then the feature is “irrelevant” to the model.
Unfortunately, these univariate approaches have the following shortcomings:
- Inability to recognize coupling effects between multiple features, such as correlations or redundancies [34].
- Inability to distinguish conditional effects between features, i.e., whether a feature is “relevant” given the presence of other feature(s).
The second point above confounds the definition of “relevance.” A classic example is the prediction of presence of genetic disease (the outcome) using the genetic information of a person’s mother and grandmother. If information from the mother is absent, then the grandmother’s genes may be identified as a “relevant” feature. However, if genetic information is present from both the mother and grandmother, then the grandmother’s genes may become “redundant” and thus an “irrelevant” feature. Therefore, the “relevance” of a feature can be contingent or conditional on the presence of other features. The authors in [35] have made significant contributions to the modeling of conditional dependencies. The authors proposed an approach known as conditional mean decrease in accuracy (C-MDA), which is a variation on classic MDA, where conditional permutations are performed given the presence of other features. The conditional is defined as the appearance of secondary features within specified ranges of values. The difference in permutation between MDA and C-MDA can be realized in Figure 7.

Figure 7.
In the conditional mean decrease in accuracy (C-MDA) approach, the permutation is only performed on the values of a feature given the presence of another feature falling within a range of values. By contrast, permutation in traditional MDA (as shown in Figure 6) is performed on all values of a feature, with no consideration of other features.
3. Results
The following sections contain the pertinent results of this case study: clustering, prediction, and feature analysis. The most important part is the comparison of different results obtained from the clustering algorithms, as well as the key variables identified by the feature selection techniques. An overall summary of the results can be found in Section 3.6. Normalized time-plots of each process variable can be found in Appendix K, in Figure A7, Figure A8, Figure A9, Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15, Figure A16, Figure A17, Figure A18, Figure A19, Figure A20, Figure A21 and Figure A22. To access the data and code used to generate the results, please visit the main author’s GitHub repository (https://github.com/yitingtsai90/Bioreactor-data-analysis).
3.1. Hierarchical Clustering of OTUs
The -transformed counts obtained from pre-processing are first analyzed in terms of biological associations. This provides preliminary knowledge into the possible co-existing and/or antagonistic interactions between OTUs. In order to prevent spurious correlations (which are possible using methods such as Pearson or Spearman correlations), the netassoc algorithm by [30] is used. The result is a 305-by-305 matrix acting as a “pseudo” distance matrix between all OTUs, which can then be used for hierarchical clustering.
Before the netassoc distances can be used, however, it must undergo one final transformation: normalization of values between 0 and 1. This follows the concept of similarity being analogous to small distances (i.e., distances close to zero), and dissimilarity being analogous to large distances. The operation in Equation (2) accomplishes this scaling:
At this point, the hierarchical clustering models can finally be constructed. First, the following four hierarchical clustering methods are performed on the scaled netassoc distance matrix:
- Unweighted pair-group method with arithmetic means (UPGMA)
- Ward’s minimum variance method (Ward)
- Nearest-neighbour method (Single-linkage)
- Farthest-neighbour method (Complete-linkage)
This was accomplished using the scipy package cluster.hierarchy. In order to determine the “optimal” clustering method out of the four, the cophenetic correlation values (see Appendix H) were obtained using the cluster.cophenet command, for all four methods. The results are shown in Table 2.

Table 2.
Cophenetic (coph.) correlations. Unweighted pair-group method with arithmetic means (UPGMA).
Cophenetic correlations can be interpreted as how well a clustering method preserves the similarites between raw samples. Since the UPGMA method has the highest cophenetic correlation, it was selected as the most suitable clustering method. A dendrogram was then constructed using this method, and it can be visualized in Figure 8.
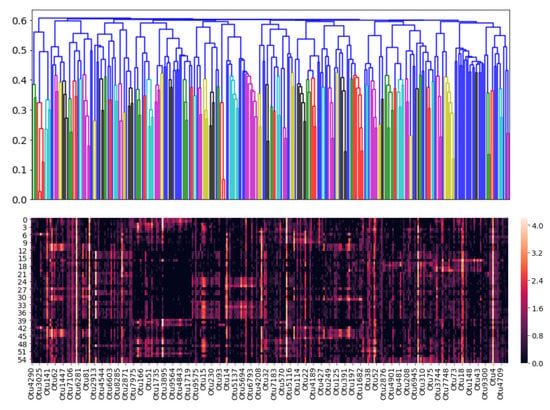
Figure 8.
UPGMA dendrogram (top) and heatmap (bottom) showing log-transformed OTU abundances. The rows of the heatmap represent individual samples, while the columns represent individual OTUs. Dark colours on the heatmap represent distances close to zero and hence similar OTUs, while light colours represent large distances and hence dissimilar OTUs.
The optimal number of clusters on this UPGMA dendrogram is determined by silhouette analysis (see Appendix H), which is a measure of how well cluster members belong to their respective clusters, given the number of desired clusters K. Silhouette values are computed for cluster numbers through , and the results are plotted on Figure 9.
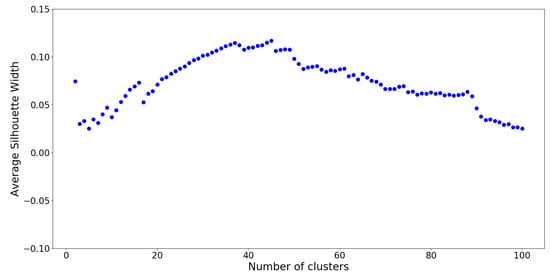
Figure 9.
Silhouette numbers for clusters . The highest value of occurs at .
From silhouette analysis, groups appear to be the “optimal” cut-off with the overall highest silhouette value. However, this is assuming that all netassoc distances are suitable for use. Recall that a normalized distance of 0 resembles similarity, and a distance of 1 resembles dissimilarity. A distance of corresponds to neither similarity nor dissimilarity. Values in that vicinity represent “neutral” OTU interactions which act as noise, confounding the clustering model. To remedy this issue, a distance cut-off approach inspired by [36] was employed. If a hierarchy with a distance cut-off value of is constructed, it means that no cluster contains members which are spread apart by a distance greater than . This reduces the amount of overlap between distinct clusters. To determine the precise value of , several UPGMA hierarchies were constructed using distance cutoffs within the set of values . The resulting silhouette values are reported in Figure 10:
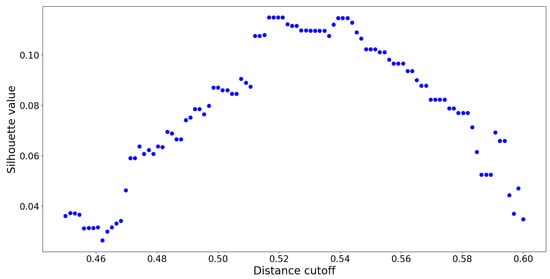
Figure 10.
Silhouette values as a function of distance cut-off in UPGMA clustering. The optimal cutoff value is the one corresponding to the maximum silhouette value.
The optimal distance cut-off is located at with a corresponding maximum silhouette value of . By constructing a UPGMA hierarchy with this cut-off, no two members within any cluster are spread apart by a normalized distance of . This UPGMA hierarchy yields a total of clusters, and its dendrogram is provided in Figure 11:
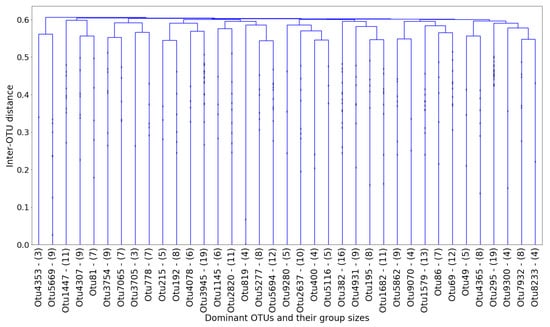
Figure 11.
Dendrogram of the UPGMA hierarchy with optimal distance cut-off, at a depth of groups. Each branch is labelled with the dominant OTU, and the number of its followers.
In each cluster, the “dominant” OTU was determined as the one closest (in terms of normalized netassoc distance) to the cluster centroid. The coordinates of each centroid were readily calculated using the distances in the dendrogram. The remaining OTUs in the cluster were therefore considered “followers.” The entire cluster could then be considered a co-existing community of OTUs. In Figure 12, the number of members in each cluster (which is also shown in Figure 11) is plotted against the cluster number.
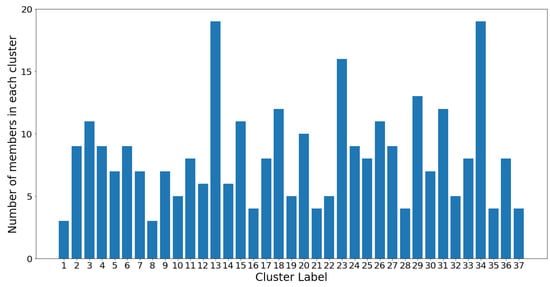
Figure 12.
Cluster populations for UPGMA dendrogram with groups.
On one hand, clusters 13 and 34 are the largest communities, with 19 OTUs in each. On the other hand, clusters 1 and 8 are the smallest communities, with three OTUs in each, followed by groups 16, 21, 28, 35, and 37 which all contain four OTUs. Despite the considerable variance in community sizes, no communities contain less than three OTUs or more than 20 OTUs. The membership distribution can be observed in the reverse histogram, where the number of groups for each membership size is shown:
Figure 13 shows that most clusters contain four, eight, and nine OTUs, followed by five and seven OTUs. Most clusters have a population ranging between four and 12 OTUs, which indicates a healthy clustering distribution.
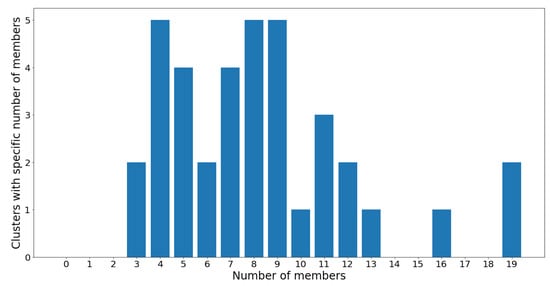
Figure 13.
Membership distribution for UPGMA dendrogram with clusters.
For the subsequent prediction and feature extraction steps, only the 37 dominant OTUs shown in Figure 11 are considered, out of the total 305 OTUs to begin with. Although 37 is still a reasonably large number (and not between two and 10, ideally), the choice is based on a combination of statistically-justified methods.
3.2. Gaussian Mixture Analysis of OTUs
Instead of using hierarchical clustering, another possible approach is to group OTUs using gaussian mixture models (GMMs). The assumption here is that the underlying distribution behind the OTU abundances can be modelled as a sum of multivariate Gaussians. Each Gaussian can be considered as a “cluster” of OTUs, with its centroid represented by the mean, and its spread (or size) represented by its variance. The overall GMM is built using the scikitlearn subpackage mixture.GaussianMixture. In order to determine the “optimal” number of Gaussians K, the Akaike information criterion (AIC) and Bayesian information criterion (BIC) values are determined for each value of K. This is performed by calling the .aic and .bic attributes of the GMM models within scikitlearn. The results are plotted in the following Figure 14 and Figure 15.
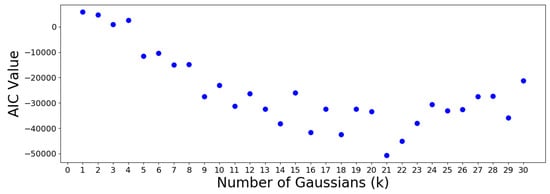
Figure 14.
Akaike information criterion (AIC) values for Gaussian mixture models (GMMs) with cluster sizes . The minimum occurs at , which is selected as the desired number of groups.
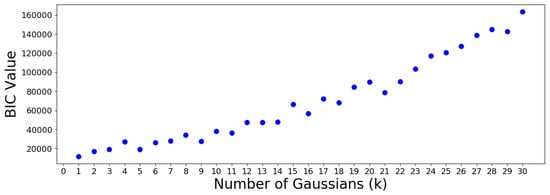
Figure 15.
Bayesian information criterion (BIC) values for GMMs of cluster sizes . The minimum occurs at , indicating that one single group should be considered. This is an impractical result and is therefore discarded.
The AIC minimum suggests that the 305 OTUs should be optimally clustered into a GMM with groups. On the other hand, the BIC minimum suggests that a GMM with only one cluster is optimal. This is a meaningless result which should be discarded, since it suggests that all OTUs are similar. Note that the BIC values increase almost monotonically from group onwards, meaning no suitable number of clusters can be determined using this criterion. Therefore, the AIC result is used to move forward.
The cluster population and membership plots can be observed in the following Figure 16 and Figure 17.
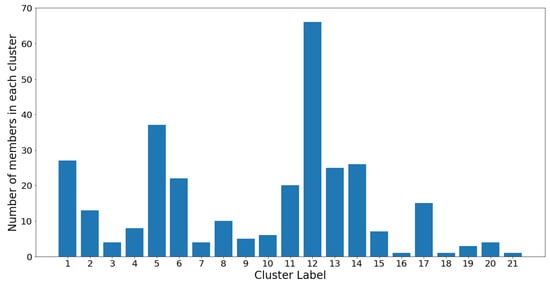
Figure 16.
Populations for the AIC-optimal GMM model with clusters.
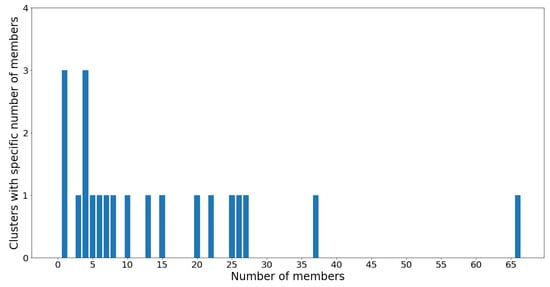
Figure 17.
Membership for the AIC-optimal GMM model with clusters.
Notice that the GMM cluster sizes have a much higher variance than the hierarchical clusters. Cluster 12 contains 66 out of the 305 total OTUs, while most other clusters contain between two and 40 OTUs. The skewed nature of the results is most likely due to the log-transformed OTU abundances being skewed towards the low counts. Therefore, the underlying Gaussian assumption (which assumes symmetrical distributions) is inaccurate. Moreover, the Gaussian mixture models were constructed using the abundance counts of OTUs, and not the associations as the hierarchical models were in Section 3.1. These two reasons alone suggest that the Gaussian clusters may not be the best representation of OTU groups. Nevertheless, the results are summarized in Table 3, which highlights the biomarker OTU in each GMM cluster as well as the cluster size.

Table 3.
Dominant OTUs from Gaussian mixture clusters.
3.3. Dirichlet Mixture Analysis of OTUs
In the previous Section 3.2, the OTU abundances were assumed to follow an underlying Gaussian distribution. In light of Figure 4 and Figure 5, this assumption is clearly inaccurate, since even the distribution of log-transformed values appears to be skewed towards the low counts. Therefore, a more suitable assumption for the OTU clusters is the Dirichlet multinomial mixture (DMM) (see Appendix J). Instead of using Python, the Dirichlet Multinomial R package developed by [37] is used. This algorithm is capable of constructing a set of DMM models, assessing the optimal model(s) using AIC, BIC, or Laplace information criterion (LIC), then producing heatmaps of the clustering results based on the Dirichlet weights of each cluster.
Unlike the hierachical or Gaussian approaches where the clustering is performed on the OTUs and not the samples, the DMM clustering is the exact opposite: The samples are clustered and not the OTUs. The results, however, can still be interpreted to identify the dominant OTUs for further analysis. For the 55 existing samples, the heatmap in Figure 18 shows the BIC-optimal DMM clusters, labelled with the 20 OTUs of highest Dirichlet weights.
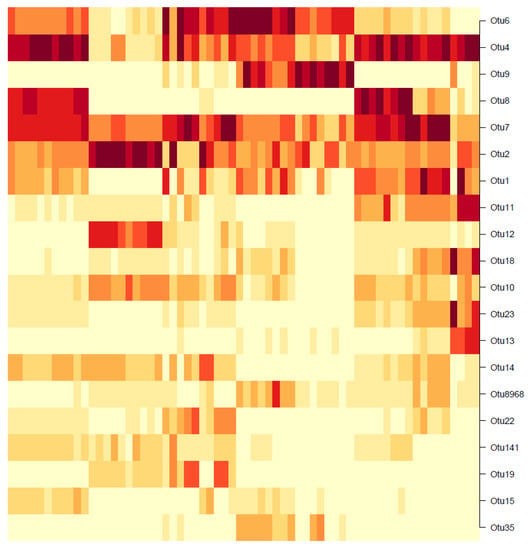
Figure 18.
Heatmap of the BIC-optimal DMM model, with respect to the 20 highest-weighting OTUs. Colours are coded according to log-transformed OTU abundances; a dark colour indicates high OTU abundance, and vice versa.
Note that the rows of the heatmap represent individual OTUs. In the first row (OTU6), a dark-shaded band exists in the mid-samples, including a commonly high abundance of OTU6 in those samples and low abundances elsewhere. Similarly, for the second row (OTU4), a common high-abundance band is observed for the first and last few samples, with low abundances elsewhere. This visual result reinforces the concept that the DMM model clusters the individual samples (columns) and not the OTUs. However, notice that going down the heatmap from OTU6 to OTU35, the dark- shaded bands appear less frequently. The colours become increasingly white, indicating an overall decrease in OTU abundance. Below the 20th-OTU cutoff (of OTU35), the rows are entirely white with close to zero abundance, and therefore those results have been truncated from the figure. Therefore, the 20 OTUs shown in Figure 18 are considered as the biomarker OTUs, akin to those in the hierarchical and GMM clustering results. However, the followers of these 20 biomarker OTUs cannot be determined, since the clustering was not performed OTU-wise.
3.4. Prediction Results
The 10 water chemistry variables (outlined in Table 1) are combined with representative OTUs obtained from Section 3.1, Section 3.2 and Section 3.3. Together, these serve as inputs. When combined with the corresponding, labelled process outcomes of selenium removal rate (SeRR), predictive models are trained for the estimation of the SeRR of new samples.
The models can be categorized in terms of their inputs, as follows:
- Base case: Water chemistry variables only.
- Hierarchical: Water chemistry variables plus representative OTUs obtained using hierarchical clustering.
- Gaussian: Water chemistry variables plus representative OTUs obtained using GMMs.
- Dirichlet: Water chemistry variables plus representative OTUs obtained using DMMs.
The idea is to observe whether the addition of biological features improves or confounds the predictive capabilities of these models. The actual models consist of the following three types:
- Random forests (RFs)
- Support vector machines (SVMs)
- Artificial neural nets (ANNs)
The raw SeRR values obtained from plant data were normalized and discretized into two (binary) classes, 0 and 1. Class 0 (poor) corresponds to SeRR values which fall below the mean SeRR, and Class 1 (satisfactory) corresponds to values above the mean. Out of the total data samples, 29 have a class label of 0 and 27 have a class label of 1, therefore the overall distribution is fairly even (i.e., not skewed towards one label).
For each model, of samples from each class are randomly selected as test samples for performance assessment, and the remaining of samples as training samples for model construction. Note that this approach eliminates the possibility of biased selection from either class. If the training and testing sets were instead selected arbitrarily from the entire dataset, then they could possibly be skewed (e.g., many samples selected from Class 1, but few from Class 0).
No validation (development) set was required, since the hyperparameters of each model (i.e., regularization constants, model complexity, etc.) were selected to be fixed values for simplicity. The RF model was constructed using the RandomForestClassifier module from scikitlearn.ensemble, with bootstrapping disabled. Although bootstrapping is normally recommended, the data sample-size in this case is extremely small for modeling purposes. Therefore, all of the existing samples are required for training; any arbitrary selection of samples without replacement could skew the training set. The SVM model was constructed using the sklearn.svm.svc module, with a regularizer value of and the default linear kernel. Finally, the ANN model was constructed using tensorflow, with 10 layers of 20 neurons each, a learning rate of and a -regularizer of . In order to maintain the reasonable computational times required by each model, a maximum of 1000 epochs (or “outer iterations”) were allowed. The ANN model was allowed 50 steps (or “inner iterations”) per epoch.
The prediction accuracy of each model on the test set (of samples) is reported in Table 4, with respect to the type of inputs used.

Table 4.
Prediction results for each model type. Random forests (RFs), support vector machines (SVMs), and artificial neural networks (ANNs).
The RF models produced the most accurate test predictions for every case, followed by SVMs then ANNs. When comparing the input types, the base case accuracy turned out to be the highest for both RF and SVM models. The addition of hierarchical OTU clusters had the largest detrimental effect on the test accuracy, as observed by the uniform, marked decreases across all three model types. The addition of Gaussian OTU clusters improved the test accuracy for the ANN model, but proved to be detrimental for the RF and SVM models, albeit with the least impact. The addition of Dirichlet OTU clusters also decreased the model accuracy for all three models, but not as much as the hierarchical. These results clearly show that the addition of biological data, which was initially expected to improve quality of prediction, actually degrades it. Even though the OTU abundances should contain valuable insight into the biological community interactions, the observed confounding effect is most likely due to the undesirable qualities of the data. These include the inherent noise present in the OTU abundances, and also the relatively low sample size to begin with. Another reason could be that the explored clustering methods are incapable of clearly extracting information related to coupling effects between OTUs and water chemistry variables.
If a model were to be selected for actual prediction of process outcomes, it would be the RF using base-case, water chemistry variables. This model achieves a respectable > accuracy on the binary classification of SeRR.
3.5. Feature Selection Results
The relevant features in the prediction framework are defined as those which contribute significantly to the accuracy of the model. The results in Section 3.4 showed the RF model as the most accurate one out of the three modeling approaches, and therefore it will be used for feature analysis in this section. The univariate feature selection strategy, mean decrease in accuracy (MDA), was first used to determine “relevant” features in terms of predicting the outcome . An RF model was constructed for each of the input types of hierarchical, Gaussian, and Dirichlet clustering. 10,000 permutations of MDA were performed for each RF model; the averaged feature importances for each are summarized in the following Table 5, Table 6 and Table 7. Only the top four water chemistry and top five OTU features are reported for conciseness.

Table 5.
Mean decrease in accuracy (MDA) feature importances for hierarchical clustering.

Table 6.
MDA feature importances for Gaussian clustering.

Table 7.
MDA feature importances for Dirichlet clustering.
Notice that consistently appears in each table as the most “relevant” feature, as MDAs of ∼ are observed as this feature is permutated. appears to be the second contender, causing accuracy drops of ∼ in most cases when permutated. and are the next most “relevant” features, however permutating them causes smaller accuracy drops of on the RF models. Therefore and can be comfortably concluded as the main deciders of overall selenium removal rate, in terms of all water chemistry variables. This result is logical from a domain-knowledge perspective, since both variables are used for selenium removal rate calculations using a mass-balance approach.
Note that the MDA approach is univariate, which means it ignores possible correlations between multiple features. In order to address this issue partially, the conditional mean decrease in accuracy (C-MDA) approach is also explored. In C-MDA, the permutations of features are performed, given the presence of other features. For example, when the feature is permutated, it is conditioned on the fact that the feature falls within a certain bracket of values. The R package developed by [35] is used to perform these C-MDA experiments, since the algorithm systematically decides the best values for the secondary variables to be conditioned upon. The detailed results can be found in Figure A23, Figure A24 and Figure A25 in Appendix L. The “relevant” variables from each RF model can be summarized in Table 8:

Table 8.
Overall Conditional Permutation feature importances.
3.6. Summary and Critique of Results
Of the supervised learning techniques tested, Section 3.4 show that RFs were the best model in terms of test-set accuracy, followed by SVMs and ANNs. RFs are an ensemble method which averages the predictions from a large number of randomly constructed models, as opposed to the SVMs or ANNs which were constructed in one shot. The ANNs performed the worst, due to the fact that deep learning models typically require an exorbitant number of samples (e.g., millions) to predict well, and only 56 samples were available in the dataset.
Inconsistent results (Section 3.1 and Section 3.2) were obtained for biomarkers identified through the three unsupervised techniques. This is due to two reasons: First, assocation values were used for hierarchical clustering, while abundance counts were used for the Gaussian and Dirichlet mixtures. Secondly, the three clustering methods also differ significantly from a statistical perspective. Specifically, the hierarchical clustering was based on pair-wise similarity calculations, whereas the Gaussian mixtures modelled OTU groups as a sum of overlapping distributions. The Dirichlet mixtures are distinct from the previous two clustering methods, since they were calculated using the 56 data sample rows rather than the 305 OTU columns. When modeling OTUs using multinomial distributions, an OTU can occur in several different groups associated with different operating stages or levels of process performance. This may be a closer representation of reality, instead of constraining each OTU to belong to one particular group only. Evidence supporting this conclusion includes, for example, the low Silhouette values (i.e., qualities of clusters) shown in Figure 9 and Figure 10.
Finally, the feature selection results are also quite nuanced. Specifically, note that and were identified as key variables in Table 5, Table 6 and Table 7. These are obvious contributory features from a domain knowledge perspective, since their numerical values directly determine the selenium removal rate. Non-obvious features such as , , and are also identified as important. Surprisingly, however, the carbon source variables or are never identified as contributory features. The type of carbon source is known to directly impact microbial community compositions in other studies (such as [38]), and therefore they were expected to influence selenium removal significantly. Finally, note that , , and have been identified as key biomarkers of high importance in Table 5, Table 6 and Table 7. Their feature importances are higher than several of the top four process variables in each case, which reinforces the hypothesis that microorganisms do in fact noticeably affect final selenium removal rate. Interestingly, appears as an important feature in both Gaussian and Dirichlet clusters, which are two models with entirely different statistical assumptions and properties. However, note that these biomarker OTUs represent clusters, which may be a sub-optimal way of characterizing the true OTU interactions. The clarity and robustness of these results can be improved, for example, by modeling OTUs as individuals rather than agglomerates. A possible avenue in this direction is explored in the following Section 4, and is recommended as a follow-up study to this work.
4. Conclusions and Future Work
The main objectives of this work are as follows: To compare the prediction capabilities of three predictive models (RFs, SVMs, and ANNs), as well as the abilities of three clustering methods (hierarchical, Gaussian, and Dirichlet mixtures) and two feature selection techniques (MDA and C-MDA) to identify key process variables. On one hand, the main process outcome of the selenium removal rate was observed to be best predicted by RF models. The obvious features of selenium loading and retention time were both identified as key contributors to the selenium removal rate. Non-obvious features such as ammonia outflow, nitrite outflow, and chemical oxygen demand were also identified as contributors, but surprisingly these exclude carbon source (a known factor which significantly alters OTU communities). On the other hand, the three clustering methods identified several different biomarker OTUs, which had feature importances similar to those of the aforementioned process variables. This result supports the notion that the OTUs play a substantial role in the removal of selenium from the bioreactor.
The results of this study suggest many possible avenues for future work. In terms of predictive modeling, the small-N issue can be mitigated by building a data simulator, which generates artificial samples based on the existing data. This can be accomplished by adapting the use of generative adversarial nets (GANs) [39], which is popular in image datasets. If a sufficient number (e.g., thousands) of samples are generated, then neural nets with much higher prediction accuracies can be constructed. The parameters as well as architecture of the neural nets can both be adaptively updated on each iteration, using the stochastic configuration network (SCN) method established by [40]. This method has demonstrated success in similar wastewater treatment applications such as [41,42,43].
In order to extract clearer conclusions from the biological data, the unsupervised learning paradigm can be changed from clustering models to graphical models. Instead of forcing the OTUs into clusters that they may not sensibly belong to, an alternative is to use Bayesian networks [31] for causality analysis. In this approach, the OTUs are instead modelled as individual entities or states, as nodes on a graph. The interactions between OTUs are modelled by state-transition probabilities, or graph edges, instead of overlapping clusters. Root-cause identification can then be performed by tracking the graph backwards from the process outcome (the last event) to the key trigger(s) at the start. This strategy has seen success in [44], as well as in the alarm management literature by [45,46] using Granger causality. A follow-up paper could explore the efficacy of these suggested methods, by identifying new OTU biomarkers using graphical models and observing whether they contribute more to the predictive models (in Table 4).
Author Contributions
Conceptualization, Y.T. and S.A.B.; methodology, Y.T. and S.A.B.; software, Y.T. and L.C.S.; formal analysis, Y.T. and S.A.B.; investigation, Y.T. and S.A.B.; resources, Y.T. and S.A.B. and L.C.S.; data curation, Y.T. and S.A.B. and L.C.S.; writing—original draft preparation, Y.T. and S.A.B.; writing—review and editing, Y.T., S.A.B. and B.G.; visualization, Y.T. and L.C.S.; supervision, S.A.B. and B.G.; project administration, S.A.B. and B.G.; funding acquisition, S.A.B. and B.G.
Funding
This research was funded by the Genome British Columbia User Partnership Program, grant number UPP026 to S.A. Baldwin (P.I.) and B. Gopaluni (co P.I.)
Acknowledgments
The authors would like to gratefully acknowledge Shams Elnawawi, a senior undergraduate student whose extensive coding expertise contributed significantly to the software development in Python.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike Information Criterion |
| ANN | Artificial Neural Net |
| ARIMA | Autoregressive with Integrated Moving Average |
| ARMA | Autoregressive with Moving Average |
| ARX | Autoregressive with Exogenous Inputs |
| BIC | Bayesian Information Criterion |
| C | Total number of discrete classes for a classification problem |
| C-MDA | Conditional Mean Decrease in Accuracy |
| COD | Chemical Oxygen Demand |
| CP | Conditional Permutations |
| d | Dimensionality of a dataset: number of variables or features |
| DMM | Dirichlet Mixture Model |
| DNA | Deoxyribonucleic Acid |
| EBCT | Empty-Bed Contact Time |
| DL | Deep Learning |
| DR | Dimensionality Reduction |
| FIR | Finite Impulse Response |
| GAN | Generative Adversarial Network |
| GMM | Gaussian Mixture Model |
| IID | Independent and Identically Distributed |
| K | Number of clusters or latent variables |
| Lebesgue p-norm (value of p may vary) | |
| LIC | Laplace Information Criterion |
| LTI | Linear Time Invariant |
| MA | Moving Average |
| MDA | Mean Decrease in Accuracy |
| MGI | Mean Gini Impurity |
| ML | Machine Learning |
| MPC | Model Predictive Control |
| MV | Manipulated Variable |
| N | Total number of samples in a dataset |
| NaN | Not a Number |
| OTU | Operational Taxonomic Unit |
| PID | Proportional-Integral-Derivative |
| SCN | Stochastic Configuration Network |
| SVM | Support Vector Machine |
| rRNA | Ribosomal Ribonucleic Acid |
| RF | Random Forest |
| RL | Reinforcement Learning |
| Se | Selenium |
| SeD | Selenium Dissolved |
| SeRR | Selenium Removal Rate |
| UPGMA | Unweighted Pair-Group Method with Arithmetic Means |
| ZOH | Zero-Order Hold |
Appendix A. Machine Learning Nomenclature
The nomenclature in this paper will follow machine learning literature by [10] and [47]. Historical data can be divided into input data which contains time measurements of all process variables, and output data which contains desired process outcomes. Input data are compactly expressed using the matrix , where N denotes the total number of samples and the total number of variables. Examples of these process variables or features include temperature, pH, valve actuator positions, pump speeds, etc. Output data are denoted by , assuming only one outcome is considered in any model. Furthermore, it is assumed that all outcome variables are independent of one another. If multiple outcomes are to be analyzed at once, or if correlations exist between individual outcomes, then they can be concatenated into a matrix . Examples of these outcomes include yields, final concentrations or flowrates, extents of reaction, removal rates, etc.
When the input data are expressed as a matrix , its N samples are oriented as rows and its features as columns, i.e.,
The bracket-enclosed superscript denotes samples, which differentiates it from the subscript which denotes features. From a physically-intuitive perspective, these input features can be further differentiated into macro variables and micro variables. Macro variables mostly consist of sensor-measurable quantities, such as temperatures, flowrates, pressures, or pH. However, they can also include inferential or soft-sensed variables [14], which are not directly measurable but can be inferred from other easily-measurable variables. An example of this is the chemical oxygen demand (COD), which is measured by extracting liquid samples from the system and performing analytical laboratory tests. On the other hand, micro variables are related to microbial properties, such as abundance counts or Spearman’s/Pearson’s correlations (which account for microbial interactions). In most cases, micro variables are inferential; a good example is operational taxonomic unit (OTU) counts, which are obtained via 16S gene sequencing.
Appendix B. Model Training, Validation, and Testing
Training, validation, and testing sets are defined with subtle differences in the scientific, engineering, and machine learning communities. This paper will adhere to the definitions accepted by the machine learning communities, which are as follows:
- Training: Samples used to obtain mathematical mappings (or models) between the input and output data.
- Validation (or development): Samples used to select optimal values of hyperaparameters—for example: model complexity (or order), regularization constants, etc. Systematic methods such as k-fold cross-validation are used.
- Testing: Samples restricted for assessing the performance (e.g., accuracy) of the selected model. This reflects its capability of generalizing to new, unseen samples.
When building a model, the test set cannot influence the selection of model structure, parameters or hyperparameters in any way. This is known as the “Golden Rule of Machine Learning” [10]. Both [10] and [32] recommend a training/validation/testing split ratio between 50/25/25 and 90/5/5, for data containing up to a few thousand samples. For data with more than a million samples, split ratios between 90/10/10 and 98/1/1 are recommended. In these data-abundant cases, the goal is to use as many samples as possible for training, while maintaining a respectable number of samples available for validation and testing.
Training, validation and testing errors are usually evaluated in two different forms, depending on whether the models are of a classification or regressive nature:
The symbol represents the indicator function and the estimated output for the ith sample using the selected model. In the case of classification, the error is calculated as a fraction of mismatched samples. In the case of regression, the error is computed as an average sum of errors in with respect to the selected error function f (e.g., mean squared error).
Finally, the bias-variance tradeoff is another important consideration when building a predictive model. The user must compromise between a simple model which “under-fits” (high bias, small variance) and a complex model that “over-fits” (small bias, high variance). The optimal point of balance can be determined by techniques such as k-fold cross validation or information criteria measures.
Appendix C. Standardization of Data
Prior to predictive modeling, features of a dataset are often standardized or normalized in order to homogenize the importance of each feature, such that each ends up with zero mean and unit variance. Mathematically, each feature is scaled by the operation , using the respective feature means and feature standard deviations .
Appendix D. Pretreatment of Data
- Uncalibrated, aging, or malfunctioning sensors
- Unexpected plant disruptions or shutdowns
- Human errors in data recording (either incorrect or missing values)
- Unmeasured, drifting disturbances (such as seasonal ambient temperatures)
Data must be cleaned prior to any modeling task, as the model quality is directly influenced by the data quality. The following approaches are well-known and straightforward to employ, but are of paramount importance in terms of obtaining high-quality predictive models:
- Outlier removal based on human intuitions: The elimination of spurious sensor values (e.g., negative flowrates recorded through a valve) using a priori knowledge. These values can either be replaced by NaN (missing) values, or estimates via imputation.
- Standardization: The scaling of each feature to zero-mean and unit variance, equalizing the effect of each individual feature. This prevents features with relatively large ranges (e.g., flowrate with range ) from dominating model weights over features with relatively small ranges (e.g., pH with range ).
- Imputation: The estimation of missing values, using a priori knowledge if available, or using standard techniques such as interpolation—for example, zero-order-hold (ZOH) or linear interpolation.
- Smoothing: The flattening of spiky measurements due to sensor noise, using techniques such as moving-average (MA) filters.
- Common time-grid alignment: The unification of sampling intervals for time-series data. For example, consider a variable measured every second, and another measured every 0.5 s. In order to model using both variables, each variable must contain the same number of samples. Therefore the uniform time-grid can either be taken at every second (losing half the resolution of the second variable) or every 0.5 s (requiring interpolation of the first variable).
Appendix E. Details of the Random Forest (RF) Model
Random forests are a well-known model covered in many texts, such as [48] and [47]. Its main advantage is the convenience of implementation; many optimized packages (such as scikitlearn) exist which allow users to obtain results quickly even for large datasets. The goal of RFs is to map the raw features of a dataset to outcomes, which are discrete class labels . Each of the original variables is split into two regions, one above and one below a threshold value . These regions become the branches of the first split on said variable. Each split is a conditional partition of a variable, which decides the final outcome. If a split on the first feature is insufficient to decide the final outcome, then a second split is performed off of the two branches from the first split. This continues until a clear outcome is realized.
A simple example demonstrating the partitioning of two features is provided in Table A1.

Table A1.
Feature partitioning for a two-feature decision tree, with possible partitions. Each partition is labelled using a number between 0 and 3. The threshold values decide which partition each sample falls under.
Table A1.
Feature partitioning for a two-feature decision tree, with possible partitions. Each partition is labelled using a number between 0 and 3. The threshold values decide which partition each sample falls under.
| 0 | 1 | |
| 2 | 3 |
To model all possible outcomes, partitions or branches are potentially required in total (where is the total number of features). The computation cost of this calculation becomes impractically large for common computing devices (such as PCs or laptops), as approaches numbers as small as 15. If is extremely large (e.g., hundreds or thousands), the outcome-space cannot be feasibly mapped out in its entirety. However, it can be approximately sampled using the concept of Random forests (RFs) [48]. In this approach, a random subset of all d features is selected and split on; the tree constructed using these arbitrarily-selected features is called a RF. Since not all features can be accounted for in a single RF, a large number of RFs are constructed (i.e., thousands or more) and the predicted class labels are determined by taking a majority vote across all obtained outcomes. An example of this is illustrated in Figure A1.
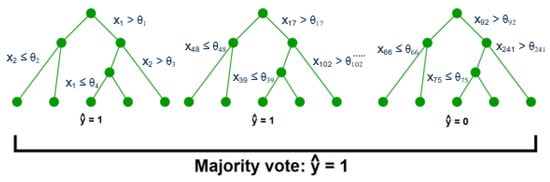
Figure A1.
Multiple random forests constructed for a binary-class problem. The outcomes (either Class 0 or 1) are decided by combining sequential splits of randomly selected features, from the original -dimensional feature space. The final outcome is determined by a majority vote of individual outcomes from all trees.
The threshold value used for each split is determined by a simple scoring rule in most cases [1]. For example, the feature may have a range of values . A computational routine would define an arbitrary step-size (usually a fraction of the gap ), then start with the threshold value and work all the way up to . The final threshold value is selected as the one resulting in the highest model accuracy (in terms of training).
In order to construct RFs which produce an unbiased estimate of the true class label for each given data sample, a technique known as bootstrapping or bootstrap aggregating (“bagging") can be used, according to [1] and [49]. Each RF randomly selects from the total N data samples to train on, with replacement, such that over a large number of RFs the total number of samples selected turns out to be approximately 0.63 N. Bootstrapping also mitigates numerical instabilities, which can occur with RFs and are especially common in complex models such as ANNs. However, it is only viable if the sample size N is sufficiently large (thousands or more). When bootstrapping on small datasets (N on the order of hundreds or less), special care must be taken to bootstrap over a large number of iterations.
Appendix F. Details of the Support Vector Machine (SVM) Model
The support vector machine maps existing samples of a training set to their corresponding given classes, such that the classes of new samples can be predicted. However, instead of partitioning on binary splits of each feature like RFs, SVMs directly find the separating boundaries between the classes of data. Support vectors are the vectors between the closest data sample in each class to the separating boundaries [2]; the distances of these vectors are maximized in order to optimize the extent of separation between classes. Although the boundaries can be found using the hinge-loss function, computational routines today instead use the softmax function as a smooth approximation of the hinge-loss. This approximation improves the numerical stability in solving for the SVM model via gradient descent, while not hindering its accuracy [50]. The softmax calculates the probability p that each sample belongs in class . The well-known logistic regression is the special-case of softmax for the binary (2-class) scenario. The parameters represents the model coefficients corresponding to each specific class. Specifically, the terms represent the model weights, assuming sample belongs in class c. Similarly, the terms represent coefficients assuming sample has a class label . Using these concepts, the softmax probability for any sample can be expressed as:
An example of multi-class SVM with four classes () is shown in Figure A2.
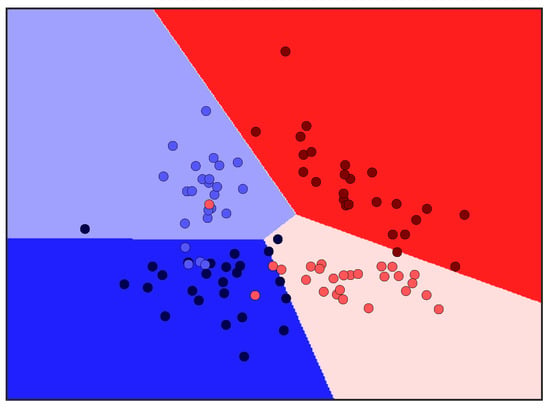
Figure A2.
Multi-class SVM for four classes. The hyperplanes (lines) in the 2-D space clearly separate the four distinct classes with acceptable misclassification rates. A smooth approximation can be made using a four-class softmax function.
Data that is linearly-separable allows linear boundaries to be drawn to separate the different classes. The equations of these separating hyperplanes can be obtained using methods described in [2]. On the other hand, data that is non-linearly-separable cannot be accurately modelled by linear separating boundaries. In these cases, the kernel trick [10] can be used to construct high-dimensional feature spaces in which the data becomes linearly separable.
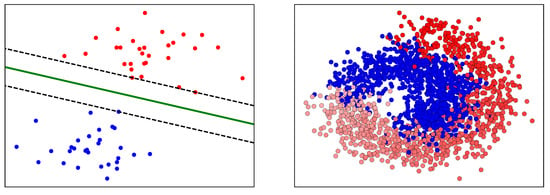
Figure A3.
A linearly-separable dataset (left), versus a non-linearly-separable dataset (right), adapted from [51].
Appendix G. Details Behind Artificial Neural Networks (ANNs)
Unlike least squares or SVMs which can only perform regression or classification, respectively, ANNs can predict either continuous (regression) or discrete (classification) outputs. The first layer in an ANN consists of an activation function acting upon an affine, i.e., . The function A is usually a non-linear transformation of its linear argument . If A were chosen to be linear in every layer of the network, the whole ANN would trivially reduce to a linear least-squares model.
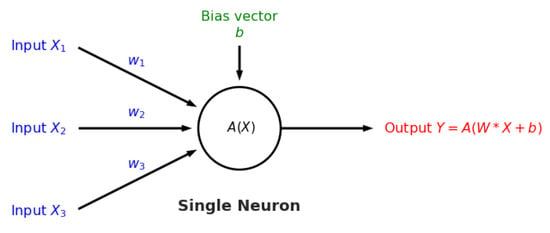
Figure A4.
Visualization of the operation in a single ANN node. The weighted sum of its inputs is added to a bias term; the final sum is transformed by a nonlinear activation function chosen by the user.
Subsequent layers follow the same affine-activation transformation, i.e., . For each neuron z, the subscript represents the neuron number, while the superscript represents the layer in which the neuron is located. The following Table A2 contains some commonly-used activation functions within ANNs:

Table A2.
Typical activation functions for neural networks.
Table A2.
Typical activation functions for neural networks.
| Activation | Abbreviation | Formula |
|---|---|---|
| Affine | ||
| Step | ||
| Sigmoid | ||
| Hyperbolic Tangent | ||
| Rectified Linear Unit | ||
| Leaky Rectified Linear Unit |
The entire neural net can be visualized as the following structure, with inputs entering the leftmost side and outputs exiting right-most side.
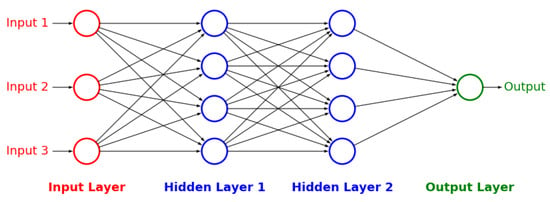
Figure A5.
Conventional ANN structure with two hidden layers.
An interesting, recent advancement in this field is the work of [40]. The authors developed the Stochastic Configuration Network, which is an improved, adaptive version of ANNs. On each training iteration, it learns not only the optimal parameters (i.e., weights and biases) that minimize prediction error, but also the optimal architecture (i.e., number of layers, number of neurons in each layer).
Appendix H. Details of Hierarchical Clustering
In biological systems, organisms (including microbial species) can be clustered together based on a similarity metric, which is evaluated between pairs of organisms. The underlying assumption is that all organisms are similar to others to some varying extent, and the “levels of similarity” can be realized using a ranking system. Some popular metrics used to compute similarities are included in Table A3:

Table A3.
Typical similarity formulas used.
Table A3.
Typical similarity formulas used.
| Type | |
|---|---|
| Euclidean Distance | |
| Manhattan Distance | |
| Cosine Similarity | |
| Jaccard Similarity | |
| Bray-Curtis Similarity |
The result of a hierarchical clustering can be expressed using a tree-like structure known as a dendrogram, which shows the overall hierarchy or ranking of clusters. Obviously, different similarity metrics result in different-looking dendrograms. Moreover, each dendrogram has various “depths” which represent sample clusters of various sizes. The corresponding labels for new samples can be quickly identified by determining which clusters these samples are closest to, based on the desired similarity metric. Finally, dendrograms can be drawn using the following two different methods:
- Agglomerative (bottom-up): Start with individual samples, then gradually merge them into clusters until one big cluster remains. This is the most common method.
- Divisive (top-down): Samples start as one big cluster, then gradually diverge into an increasing number of clusters, until one cluster is formed for each individual sample.
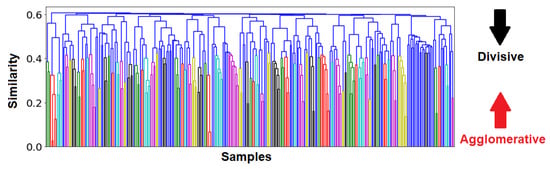
Figure A6.
A dendrogram representation of hierarchical clustering. At the bottom, each individual sample belongs to its own cluster. Going up the dendrogram, samples are merged together based on the desired distance metric. At the top, all samples are merged into one giant cluster.
Four main types of hierarchical clustering are commonly used [52]. These are accompanied by two metrics, which determine the optimal clustering method among the four (i.e., cophenetic correlations [53]) as well as the optimal number of clusters (i.e., silhouette analysis [21]):
- Single linkage (Nearest-neighbour): “Nearest-neighbour” clustering. Initially, each sample is considered a centroid. The pair of samples with the smallest distance between them is merged together; subsequent clusters are merged according to the distances between their closest members. The linkage function is expressed as:and represent two arbitrary clusters, and D the distance between them.
- Complete linkage (Farthest-neighbour): Also known as “farthest-neighbour” clustering. Identical to single linkage, except clusters are merged together according to distances between their farthest members. The linkage function is expressed as:
- Agglomerative averages: Also known as “average” clustering. Identical to single linkage, except clusters are merged together according to average distances between their members. The linkage function is expressed as:where represents the number of samples in each cluster, during each iteration.
- Ward’s method: Also known as “minimum-variance” clustering. Instead of merging samples or clusters together based on distance, it starts by assigning “zero variance” to all clusters. Then, an Analysis of Variance (ANOVA) test is performed: Two arbitrarily-selected clusters are merged together. The “increase in variance” is calculated as:for all pairwise clusters. represents the centroid coordinates for cluster . The pair of clusters that results in the smallest increase in variance is then merged at each iteration.
The agglomerative average approach includes the subroutines unweighted pair-group method with averages (UPGMA), unweighted pair-group method with centroids (UPGMC), weighted pair-group method with averages (WPGMA), and weighted pair-group method with centroids (WPGMC), which are discussed in detail in [13]. The difference between these methods lie within the use of averaged Euclidean coordinates versus pre-determined centroids, and whether each data sample contribution is equal or weighted (with the weights determined by some a priori information).
The confidence of clustering results can be quantitatively assessed by two metrics:
- cophenetic correlations [53]: Measures how well a specified clustering method preserves original pairwise distances between samples. In other words, how similar are the average inter- cluster distances between pairwise points compared to their actual distances. The formula is:which returns a value between 0 and 1, where represents average distances from all pairs of ,. represents the cophenetic distance between two pairwise points and , defined as the distance from the base of the dendrogram to the first node joining and .
- Silhouette analysis [21]: Measures the optimal depth of a specified clustering method. Mathematically, it assesses how well each sample belongs to its assigned cluster . Each individual Silhouette number is evaluated as:where represents the closest cluster to each . At each depth on the dendrogram, the average silhouette number is evaluated across all samples and calculated as . The depth with the highest is then selected for that particular clustering scheme.
By combining the cophenetic and silhouette analyses as outlined above, the “most confident” clustering method (i.e., UPGMA vs. Ward vs. single-linkage vs. complete-linkage) and the optimal clustering depth, respectively, can both be selected.
Appendix I. Details Behind Probabilistic Mixtures
The motivation behind using probabilistic mixtures is to model the underlying distributions of the given data. Models using one distribution are sufficient for uni-modal systems, but fail to capture multi-modal systems effectively. Therefore, data are usually modelled as the sums of various probabilistic distributions, with the structure of said distributions specified as a prior assumption. Mixture models are different from the hierarchical models. The difference lies in the assumption that in mixtures, each individual species is assigned a group to which it is similar, but overlaps may occur between multiple groups. In other words, each species may belong to more than one group. This introduces a degree of stochasticity which makes these models more flexible. The two mixtures used in this paper are:
- Gaussian Mixtures [47]:; the underlying distribution is assumed to be a sum of K weighted multivariate Gaussians with individual means and covariances. The term represents the weighting factor for each Gaussian. Each Gaussian has the formula .
- Dirichlet Mixtures [24]: Define as a vector containing the probabilities that sample belongs to each community species. The Dirichlet mixture prior over K distributions is , where are the Dirichlet parameters and are the Dirichlet weights.
The Gaussian assumption is reasonable for most natural processes, which assumes that the underlying distributions are symmetric. When little a priori knowledge is available, it is a popular choice. However, if domain knowledge is available, it should be used to guide the choice of distribution used. For example, if OTU data mostly contains abundances skewed towards low counts, then the Dirichlet mixture will model the data more accurately than Gaussian. This type of mixture model is discussed in greater detail in the following Appendix J.
Appendix J. Details Behind the Dirichlet Mixture
The detailed modeling equations behind Dirichlet distributions and mixtures can be found in [24]. A summary of the paper’s results is as follows:
- The likelihood of observing each sample is:where is the total number of OTU species, the probability that sample i belongs to species j, and the abundance count of species j in sample i.
- The total likelihood across all samples is therefore:
- The Dirichlet distribution is modelled as:where represents the Dirichlet precision (i.e., large implies all values lie close to the mean p value, and vice versa), a normalization constant such that , and the Dirac delta function which ensures further normalization.
- The Dirichlet mixture prior over distributions is:where are the Dirichlet parameters, the Dirichlet weights, and the complete set of mixture hyperparameters.
- The Dirichlet mixture posterior over distributions is:
Appendix K. Time Plots of Process Variables over Time
The time-plots of all water chemistry variables are provided here. This enables a visual analysis of the variations over time. Due to proprietary reasons, the values have been normalized. The plots are separated by reactor number, i.e., and to distinguish the behaviour in the two different reactors. The horizontal time-axis represents the duration measured in hours.
Appendix K.1. Time-Plots from Reactor 1
The time-plots of all water chemistry variables from Reactor 1 are provided here.
Figure A7.
Normalized empty-bed contact time for Reactor 1.
Figure A8.
Normalized ammonia outlet flowrate for Reactor 1.
Figure A9.
Normalized nitrate inlet flowrate for Reactor 1.
Figure A10.
Normalized nitrite outlet flowrate for Reactor 1.
Figure A11.
Normalized selenium inlet flowrate for Reactor 1.
Figure A12.
Normalized chemical oxygen demand for Reactor 1.
Figure A13.
Normalized categorical carbon source (MicroC) for Reactor 1.
Figure A14.
Normalized categorical carbon source (Acetate) for Reactor 1.
Appendix K.2. Time-Plots from Reactor 2
The time-plots of all water chemistry variables from Reactor 2 are provided here.
Figure A15.
Normalized empty-bed contact time for Reactor 2.
Figure A16.
Normalized ammonia outlet flowrate for Reactor 2.
Figure A17.
Normalized nitrate inlet flowrate for Reactor 2.
Figure A18.
Normalized nitrite outlet flowrate for Reactor 2.
Figure A19.
Normalized selenium inlet flowrate for Reactor 2.
Figure A20.
Normalized chemical oxygen demand for Reactor 2.
Figure A21.
Normalized categorical carbon source (MicroC) for Reactor 2.
Figure A22.
Normalized categorical carbon source (Acetate) for Reactor 2.
Appendix L. Feature Selection Results from C-MDA
The following figures show the feature importances obtained using the conditional permutation algorithm developed by [35]. The plots are separated for the three cases of hierarchical, Gaussian, and Dirichlet OTU-clusters.
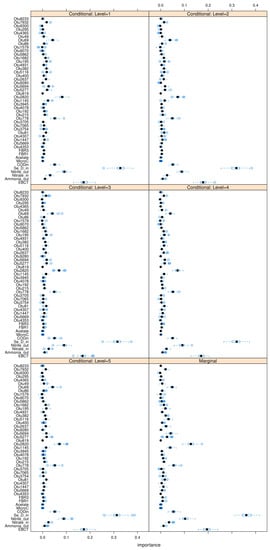
Figure A23.
Conditional feature importances for hierarchical clustering.
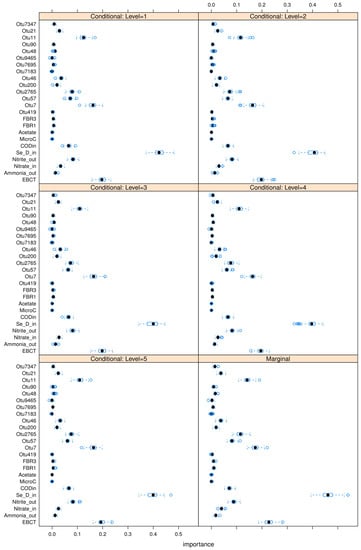
Figure A24.
Conditional feature importances for GMM clustering.
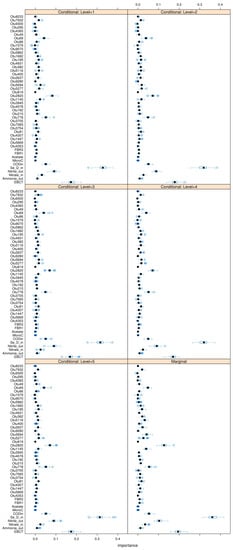
Figure A25.
Conditional feature importances for Dirichlet multinomial mixture (DMM) clustering.
References
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Campbell, W.M.; Campbell, J.P.; Reynolds, D.A.; Singer, E.; Torres-Carrasquillo, P.A. Support vector machines for speaker and language recognition. Comput. Speech Lang. 2006, 20, 210–229. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 1 June–3 September 2012; pp. 1097–1105. [Google Scholar]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; Volume 1. [Google Scholar]
- Chen, W.; Zhang, C.K.; Cheng, Y.; Zhang, S.; Zhao, H. A comparison of methods for clustering 16S rRNA sequences into OTUs. PLoS ONE 2013, 8, e70837. [Google Scholar] [CrossRef]
- Cernava, T.; Müller, H.; Aschenbrenner, I.A.; Grube, M.; Berg, G. Analyzing the antagonistic potential of the lichen microbiome against pathogens by bridging metagenomic with culture studies. Front. Microbiol. 2015, 6, 620. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology, Volume 24, (Developments in Environmental Modelling); Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Seborg, D.E.; Mellichamp, D.A.; Edgar, T.F.; Doyle, F.J., III. Process Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- CCME. Canadian Water Quality Guidelines for the Protection of Aquatic Life: NITRATE ION. Available online: http://ceqg-rcqe.ccme.ca/download/en/197 (accessed on 25 May 2019).
- CCME. Soil Quality Guidelines: SELENIUM Environmental and Human Health Effects. Available online: https://www.ccme.ca/files/Resources/supporting_scientific_documents/soqg_se_scd_1438.pdf (accessed on 24 May 2019).
- Lemly, A.D. Aquatic selenium pollution is a global environmental safety issue. Ecotoxicol. Environ. Saf. 2004, 59, 44–56. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. KDD 1996, 96, 226–231. [Google Scholar]
- Reynolds, A.P.; Richards, G.; de la Iglesia, B.; Rayward-Smith, V.J. Clustering rules: A comparison of partitioning and hierarchical clustering algorithms. J. Math. Modell. Algorithms 2006, 5, 475–504. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Rasmussen, C.E. The infinite Gaussian mixture model. In Proceedings of the Neural Information Processing Systems 1999, Denver, CO, USA, 29 November–4 December 1999; pp. 554–560. [Google Scholar]
- La Rosa, P.S.; Brooks, J.P.; Deych, E.; Boone, E.L.; Edwards, D.J.; Wang, Q.; Sodergren, E.; Weinstock, G.; Shannon, W.D. Hypothesis testing and power calculations for taxonomic-based human microbiome data. PLoS ONE 2012, 7, e52078. [Google Scholar] [CrossRef] [PubMed]
- Holmes, I.; Harris, K.; Quince, C. Dirichlet multinomial mixtures: Generative models for microbial metagenomics. PLoS ONE 2012, 7, e30126. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Matsuda, H.; Ogita, N.; Sasaki, A.; Satō, K. Statistical mechanics of population: The lattice Lotka-Volterra model. Prog. Theor. Phys. 1992, 88, 1035–1049. [Google Scholar] [CrossRef]
- Yasuhiro, T. Global Dynamical Properties of Lotka-Volterra Systems; World Scientific: Singapore, 1996. [Google Scholar]
- Faust, K.; Raes, J. Microbial interactions: From networks to models. Nat. Rev. Microbiol. 2012, 10, 538–550. [Google Scholar] [CrossRef]
- Gonze, D.; Lahti, L.; Raes, J.; Faust, K. Multi-stability and the origin of microbial community types. ISME J. 2017, 11, 2159–2166. [Google Scholar] [CrossRef]
- Morueta-Holme, N.; Blonder, B.; Sandel, B.; McGill, B.J.; Peet, R.K.; Ott, J.E.; Violle, C.; Enquist, B.J.; Jørgensen, P.M.; Svenning, J.C. A network approach for inferring species associations from co-occurrence data. Ecography 2016, 39, 1139–1150. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2014. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Han, H.; Guo, X.; Yu, H. Variable selection using mean decrease accuracy and mean decrease gini based on random forest. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, S.C.; Ott, J.E.; McArthur, E.D.; Harper, K.T. RCLUS, a new program for clustering associated species: A demonstration using a Mojave Desert plant community dataset. West. N. Am. Nat. 2006, 66, 285–297. [Google Scholar] [CrossRef]
- Morgan, M. Dirichlet Multinomial: Dirichlet-Multinomial Mixture Model Machine Learning for Microbiome Data; R package; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Xu, Z.; Dai, X.; Chai, X. Effect of different carbon sources on denitrification performance, microbial community structure and denitrification genes. Sci. Total Environ. 2018, 634, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Wang, D.; Li, M. Stochastic configuration networks: Fundamentals and algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef] [PubMed]
- Han, H.G.; Zhang, L.; Qiao, J.F. Data-based predictive control for wastewater treatment process. IEEE Access 2017, 6, 1498–1512. [Google Scholar] [CrossRef]
- Qiao, J.F.; Hou, Y.; Zhang, L.; Han, H.G. Adaptive fuzzy neural network control of wastewater treatment process with multiobjective operation. Neurocomputing 2018, 275, 383–393. [Google Scholar] [CrossRef]
- Han, H.G.; Zhang, L.; Liu, H.X.; Qiao, J.F. Multiobjective design of fuzzy neural network controller for wastewater treatment process. Appl. Soft Comput. 2018, 67, 467–478. [Google Scholar] [CrossRef]
- Runge, J.; Nowack, P.; Kretschmer, M.; Flaxman, S.; Sejdinovic, D. Detecting causal associations in large nonlinear time series datasets. arXiv 2017, arXiv:1702.07007. [Google Scholar]
- Izadi, I.; Shah, S.L.; Shook, D.S.; Chen, T. An introduction to alarm analysis and design. IFAC Proc. Vol. 2009, 42, 645–650. [Google Scholar] [CrossRef]
- Wang, J.; Yang, F.; Chen, T.; Shah, S.L. An overview of industrial alarm systems: Main causes for alarm overloading, research status, and open problems. IEEE Trans. Autom. Sci. Eng. 2015, 13, 1045–1061. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Cambridge, UK, 2006. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, USA, 1998; Volume 1. [Google Scholar]
- Lemm, S.; Blankertz, B.; Dickhaus, T.; Müller, K. Introduction to machine learning for brain imaging. Neuroimage 2011, 56, 387–399. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. The comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).