Some Eccentricity-Based Topological Indices and Polynomials of Poly(EThyleneAmidoAmine) (PETAA) Dendrimers

Abstract

Topological indices have been computed for various molecular structures over many years. These are numerical invariants associated with molecular structures and are helpful in featuring many properties. Among these molecular descriptors, the eccentricity connectivity index has a dynamic role due to its ability of estimating pharmaceutical properties. In this article, eccentric connectivity, total eccentricity connectivity, augmented eccentric connectivity, first Zagreb eccentricity, modified eccentric connectivity, second Zagreb eccentricity, and the edge version of eccentric connectivity indices, are computed for the molecular graph of a PolyEThyleneAmidoAmine (PETAA) dendrimer. Moreover, the explicit representations of the polynomials associated with some of these indices are also computed.

1. Introduction

The rapid growth in the field of medicine is resulting in the production of unknown nanomaterials, crystalline materials and drugs. To investigate the chemical properties of these compounds, huge efforts of pharmaceutical researchers are required and are being made. One way to understand it is by using mathematics; in mathematical chemistry, many concepts of graph theory are being used to formulate the mathematical model for chemical phenomena. Molecules and molecular compounds can be considered as graphs, if we map atoms to vertices and chemical bonds to edges, respectively. Such graphs are called molecular graphs. A graph can be identified by a uniquely defined number (or finite numbers), a matrix or a polynomial that describe the graph. Topological index (TI) is a mathematical quantity which is assigned to a graph (or molecular graph structure). Topological indices (TIs) provide relationships between structure of a molecule and several physical properties, biological activity or chemical reactivity. A TI is an invariant, that is if Top($H_1$) represents a TI of a graph $H_1$ and $H_2$ (another graph) with $H_1\cong H_2$ then Top($H_1$) = Top($H_2$).

The notions of TIs help pharmacists by providing several information based upon the structure of materials which reduce their workload. Computing TIs of a compound may help in approximating its medicinal behavior [1]. With the passage of time, the idea of understanding compounds through TIs has gained significant importance in the field of medicine because it requires no chemical-related apparatus to study [2]. TIs are also used for studying quantitative structure–activity relationships (QSAR) and quantitative structure property relationships (QSPR) for predicting many properties of chemical compounds. QSPR and QSAR approaches are used to study the properties (chemical, physical and biological) of a chemical substance from its molecular structure. QSAR and QSPR are the significant descriptors of chemical compounds in mathematical formulation of various properties [3]. TIs, in recent years, have been used to study the molecular complexity, chemical documentation, chirality, isomer discrimination, QSAR/QSPR, similarity/dissimilarity, lead optimization, drug design and database selection, deriving multilinear regression models and rational combinatorial library design [1,4]. Absence of degeneracy and high discriminating power are two properties of an ideal topological index.

Dendrimers are macromolecular structures with a central core, an interior dendritic structure (also called branches), and an exterior functional surface group. Initially, these molecules were discovered (and studied) by E. Buhleier [5], D. Tomalia [6] and G.R. Newkome [7]. For a given size and structure, one may construct a dendrimer inductively by using a chemical synthesis approach with low polydispersity index. Mainly two approaches, divergent and convergent, are used to synthesize the dendrimers. There are many known dendrimers with biological properties such as chemical stability, solubility, polyvalency, electrostatic interactions, low cytotoxicity and self-assembling. Dendrimers have applications in blood substitution as they have fluorocarbon and hydrophillic moieties. These varying properties are useful in the field of medical science, such as diagnostic imaging and anticancer therapies. Other than that, the linear growth in the size of dendrimers makes them ideal delivery vehicle candidates for the study of effects of composition and size of polymers in biological properties such as blood plasma retention time, cytotoxicity, lipid bilayer interactions and filtration; see [8] and references therein.

The study of Polyamidoamine (PAMAM) dendrimers has remained the most important topic of research in this field due to properties. PAMAM Dendrimers have hydrophilic interiors and exteriors which play roles in its unimolecular micelle properties. Moreover, PAMAM-based carriers increase the possibility of bioavailability of problematic drugs. Hence, PAMAM nano carriers enhance the potential of the bioavailability of drugs which are not so soluble for efflux transporters; see [8] and references therein. PAMAM dendrimers are also used in gene delivery for encapsulation of biodegradable functional polymer films. Moreover, these dendrimers also have potential applications in biosensors; for example, Ferrocenyl dendrimer (Fc-D). PAMAMs also have a usage in the delivery of agrochemicals to make plants healthier and less susceptible to diseases, but the complex synthesis of PAMAM limits the clinical translation of PAMAM-based materials. Interestingly, PolyEThyleneAmidoAmine (PETAA) dendrimers with more complete and uniform structure than PAMAM possess several properties of PAMAM such as the number of chemical bonds between the dendrimer core and the surface, number of surface primary amino groups and the number of tertiary amino groups. Other than that, the unique synthesis process of the PETAA enhances its potential for large-scale production, which results more application in biomedical sciences [9]. Consequently, the study of PETAA becomes a very important topic of research.

The purpose of this paper is to compute several distance-based TIs. Moreover, we also formulate explicit polynomials corresponding to some of these indices.

2. Materials and Methods

In this article, we understand a molecular graph to be a simple graph, representing the carbon atom skeleton of an organic molecule (usually, of a hydrocarbon). Let $G(V,E)$ be a graph, where V and E are the sets of vertices and set of edges respectively. Vertices $u,v\in V$ are said to be adjacent if $\{u,v\}\in E$. The degree of a $v\in V$ is denoted by $d_v$ and is the number of edges incident to the vertex v. A $(u_1,u_n)$-path with n vertices is defined as a graph with vertex set $\{u_i:1\le i\le n\}$ and edge set $\{u_i{u}_{i+1}:1\le i\le n-1\}$. The distance between two vertices u and w is the length of the shortest path between u and w and is denoted by $d(u,w)$. For a given vertex $u\in V$, the eccentricity $\epsilon \left(u\right)$ is defined as $\epsilon \left(u\right)=max\left\{d\right(w,u\left)\right|w\in V\}$.

Harold Wiener was the first who used the topological index in 1947. The path number of a graph, which is the sum of all distances between the carbon atoms of a molecule was introduced by H. Wiener, see [10]. Mathematically, the Wiener index ($W\left(G\right)$) is the count of all shortest distances in a graph G [11]. This molecular modeling is used to investigate the relationships between properties, structure and activity of chemical compounds. Another distance-based topological index is the eccentric-connectivity index $\xi \left(G\right)$ of the graph G which is defined as [12]

$$\xi \left(G\right)=\sum _{v\in V\left(G\right)}^{}\epsilon \left(v\right)d_v.$$

(1)

The comparisons of $\xi \left(G\right)$ and $W\left(G\right)$ in terms of estimation of biological activity have been done for several drugs, such as those used in Alzheimer’s disease, see [13], hypertension, see [14], inflammation, see [15], HIV, see [16] and as diuretics, see [17]. In most of these cases, the prediction power of the $\xi \left(G\right)$ was much superior to those correspondingly obtained from the $W\left(G\right)$ which provide motivation to find the $\xi \left(G\right)$. Some properties and applications of this index are discussed in [18,19,20,21]. The eccentric-connectivity polynomial of G is defined as [22]

$$ECP(G,y)=\sum _{v\in V\left(G\right)}{d}_v{y}^{\epsilon \left(v\right)}.$$

(2)

If the degrees of vertices are not used, then the total eccentricity index and total eccentric-connectivity polynomial are as follows [22]:

$$\varsigma \left(G\right)=\sum _{v\in V\left(G\right)}\epsilon \left(v\right),$$

(3)

$$TECP(G,y)=\sum _{v\in V\left(G\right)}{y}^{\epsilon \left(v\right)}.$$

(4)

For more information on different aspects of eccentric-connectivity and total eccentric-connectivity polynomials, one can see [23,24,25,26]. Zagreb indices of a graph G in terms of eccentricity were given in [27] as follows:

$$Z_1\left(G\right)=\sum _{v\in V\left(G\right)}{\left(\epsilon \left(v\right)\right)}^2,$$

(5)

$$Z_2\left(G\right)=\sum _{uv\in E\left(G\right)}\epsilon \left(u\right)\epsilon \left(v\right).$$

(6)

Some mathematical and computational properties of $Z_1\left(G\right)$ and $Z_2\left(G\right)$ have been established in [28,29,30,31]. The augmented eccentric-connectivity index of a graph G which is the generalization of $\xi \left(G\right)$, is defined as [32]

$$A_{\epsilon }\left(G\right)=\sum _{v\in V\left(G\right)}\frac{M\left(v\right)}{\epsilon \left(v\right)},$$

(7)

here, $M\left(v\right)={\displaystyle \prod _{u\in N\left(v\right)}}{d}_u$, $N\left(v\right)$ denoted the neighbors of v. It has been scrutinized in [33] that the $A_{\epsilon }\left(G\right)$, is much better then the $W\left(G\right)$ to high discriminating power, higher predictive accuracy and practically no degeneracy. This index has been studied in [34,35]. The modified eccentric-connectivity index and polynomial are defined as

$$\mathsf{\Lambda }\left(G\right)=\sum _{v\in V\left(G\right)}{S}_v\epsilon \left(v\right),$$

(8)

$$MECP(G,y)=\sum _{v\in V\left(G\right)}{S}_v{y}^{\epsilon \left(v\right)},$$

(9)

where $S_v={\sum }_{u\in N\left(v\right)}$, $N\left(v\right)$ denoted the neighbors of v. In [36,37] several chemical and mathematical aspects of $\mathsf{\Lambda }\left(G\right)$ and $MECP(G,y)$ have been comprehensively studied. The edge version of the $\xi \left(G\right)$, denoted by ${\epsilon }_e\left(G\right)$, was introduced by Xinli Xu and Yun Guo [38] as

$${\epsilon }_e\left(G\right)=\sum _{f\in E\left(G\right)}d\left(f\right)\epsilon \left(f\right),$$

(10)

where $d\left(f\right)$ represents the degree of an edge and $\epsilon \left(f\right)$ is defined as the largest distance of f with any other edge g in G. This index has been computed for different dendrimer structures in [39,40,41,42].

TIs are descriptors based upon the structure of a compound which brief facts about shape, branching, molecular size, presence of multiple bonds and heteroatoms in the numerical form [1]. Therefore, TIs may provide more insights into the interpretation of the molecular properties and/or is able to take part in a model like QSPR and QSAR for the forecast of different properties of the molecules. For instance, in [1,43,44,45,46,47] various properties of several chemical compounds were studied by using TIs. Based upon the computation of TIs and some known values of these properties, linear equations were developed in which TIs were the independent variable and a certain physical property was the dependent variable. Thereby, the computation of TIs is one of the flourishing lines of research. The significance of the above-mentioned indices in formulating mathematical models for various biological activities can be seen in [14,17,48,49,50,51,52,53]. In the next section, we compute these eccentricity-based indices for a PolyEThyleneAmidoAmine (PETAA) dendrimer.

3. Eccentricity-Based Indices and Polynomials for the PETAA Dendrimer

Let us denote the molecular graph of a PETAA dendrimer by $D\left(n\right)$, where n is representing the generation stage. Figure 1 depicts the molecular graph of a PETAA dendrimer for the growth stage $n=5$. The cardinality of vertex set of $D\left(n\right)$ is $44\times 2^n-18$, and edge set is $44\times 2^n-19.$ To compute the indices and polynomials described in previous section for $D\left(n\right),$ we determine the required values for the sets of representatives. Now, make two sets of representatives, say $A=\{{\alpha }_1,{\alpha }_2\}$ and $B=\{a_i,b_i,c_i,d_i,e_i,f_i,g_i,h_i\},$ where $0\le i\le n$, as shown in Figure 2. The representatives, degree, $S_v$, $M\left(v\right)$, $\epsilon \left(v\right)$ and frequency of each v in A and b are shown in

Table 1. Sets A and B with degree of element v, $S_v$, $M\left(v\right)$, eccentricity, and frequency.

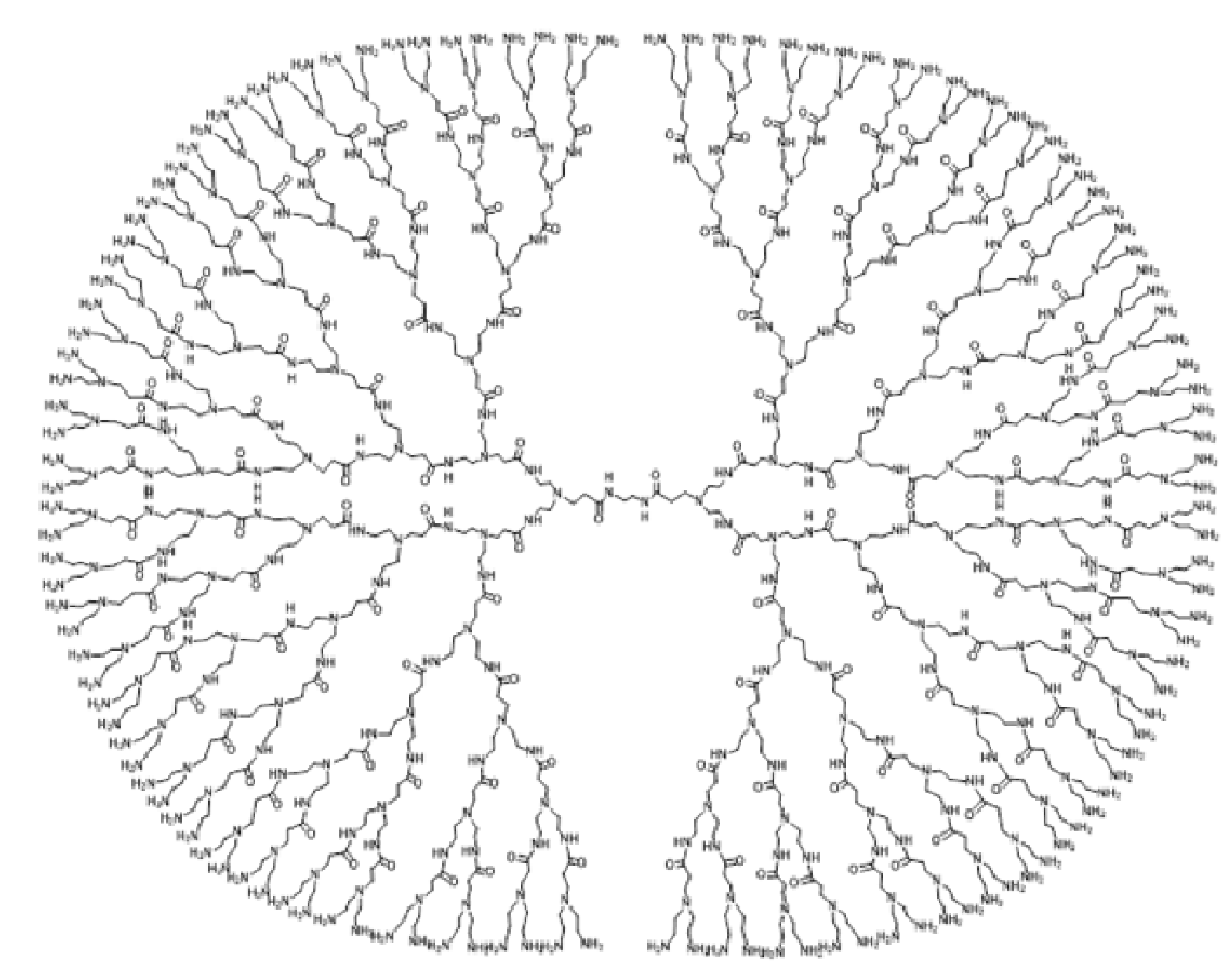
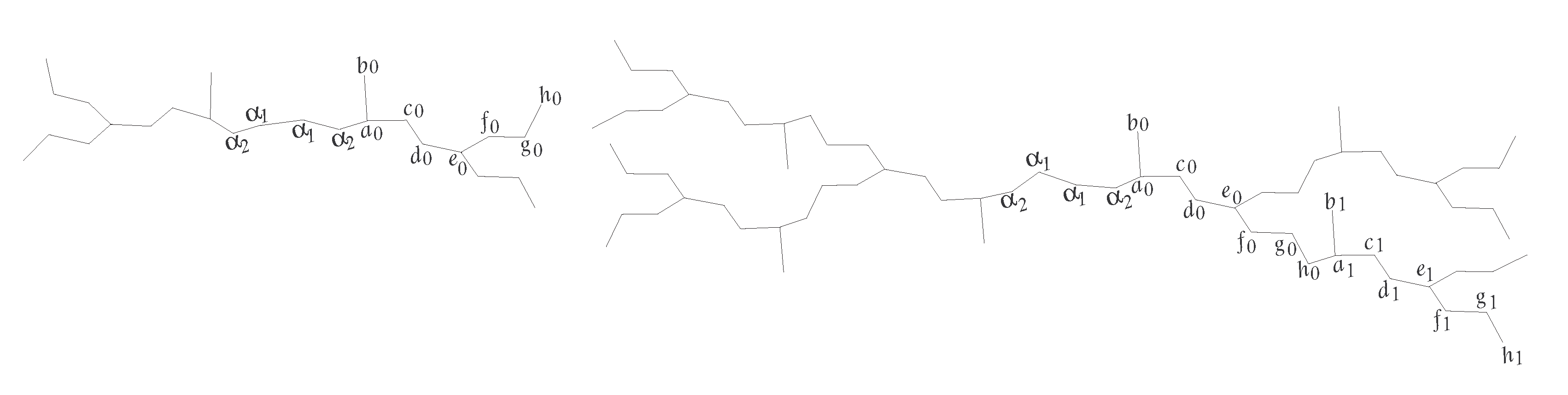
Representative	Degree	${\mathit{S}}_{\mathit{v}}$	$\mathit{M}\left(\mathit{v}\right)$	Eccentricity	Frequency
${\alpha }_1$	2	4	4	$7n+9$	2
${\alpha }_2$	2	5	6	$7n+10$	2
$a_i$	3	5	4	$\beta +4$	$2^{i+1}$
$b_i$	1	3	3	$\beta +5$	$2^{i+1}$
$c_i$	2	5	6	$\beta +5$	$2^{i+1}$
$d_i$	2	5	6	$\beta +6$	$2^{i+1}$
$e_i$	3	6	8	$\beta +7$	$2^{i+1}$
$f_i$	2	5	6	$\beta +8$	$2^{i+2}$
$g_i$	2	4	4	$\beta +9$	$2^{i+2}$
$h_i$ when $i\ne n$	2	5	6	$\beta +10$	$2^{i+2}$
$h_n$	1	2	2	$14n+17$	$2^{n+2}$

. Let $\beta =7(n+i+1)$ throughout this section.

Now with the help of Table 1, we are ready to compute different eccentricity-based indices and their corresponding polynomials for $D\left(n\right)$. We start with $\xi \left(G\right)$ for $D\left(n\right)$.

Theorem 1.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\xi \left(D\left(n\right)\right)=(1232n+604)2^n-266n+62.$$

Proof. 

The values of $\epsilon \left(v\right)$, $d_v$ from Table 1 in Equation (1) yield

$$\begin{array}{cc}\xi \left(D\right(n\left)\right)\hfill & =\xi \left(A\right)+\xi \left(B\right)=\sum _{v\in V\left(A\right)}\epsilon \left(v\right)d_v+\sum _{v\in V\left(B\right)}\epsilon \left(v\right)d_v\hfill \\ \hfill & =(2\times 2)(7n+9)+(2\times 2)(7n+10)+\sum _{i=0}^n((3\times 2^{i+1})(\beta +4)+(1\times 2^{i+1})(\beta +5)\hfill \\ \hfill & +(2\times 2^{i+1})(\beta +5)+(2\times 2^{i+1})(\beta +6)+(3\times 2^{i+1})(\beta +7)+(2\times 2^{i+2})(\beta +8)\hfill \\ \hfill & +(2\times 2^{i+2})(\beta +9))+2^{n+2}(14n+17)+\sum _{i=0}^{n-1}\left((2\times 2^{i+2})(\beta +10)\right).\hfill \end{array}$$

(11)

Here, ${\sum }_{i=0}^n\left((3\times 2^{i+1})(\beta +4)+(1\times 2^{i+1})(\beta +5)+(2\times 2^{i+1})(\beta +5)+(2\times 2^{i+1})(\beta +6)+(3\times 2^{i+1})(\beta +7)+(2\times 2^{i+2})(\beta +8)+(2\times 2^{i+2})(\beta +9)\right)=1064n\times 2^n+512\times 2^n-266n+10,$

and

${\sum }_{i=0}^{n-1}\left((2\times 2^{i+2})(\beta +10)\right)=112n\times 2^n+24\times 2^n-24-56n.$

Using these values in Equation (11), we have

$$\xi \left(D\left(n\right)\right)=(1232n+604)2^n-266n+62.$$

□

If the degrees of vertices are not used, then Table 1 and Equation (3) produce the following result:

Corollary 1.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\varsigma \left(D\left(n\right)\right)=(616n+324)2^n-126n+30.$$

In the next theorem, the $ECP(G,y)$ for $D\left(n\right)$ is derived.

Theorem 2.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\begin{array}{c}\begin{array}{cc}ECP\left(D\right(n),y)\hfill & =\frac{2(4y^5+4y^4+3y^3+3y^2+3)y^{7n+11}(2^{n+1}{y}^{7n+7}-1)}{2y^7-1}\hfill \\ \hfill & +\frac{8y^{7n+17}(2^n{y}^{7n}-1)}{2y^7-1}+4y^{7n+9}(1+y+2^n{y}^{7n+8}).\hfill \end{array}\hfill \end{array}$$

Proof. 

The values of $\epsilon \left(v\right)$, $d_v$ from Table 1 in Equation (2) yield

$$\begin{array}{c}\begin{array}{cc}ECP\left(D\right(n),y)\hfill & =ECP(A,y)+ECP(B,y)=\sum _{v\in V\left(A\right)}{d}_v{y}^{\epsilon \left(v\right)}+\sum _{v\in V\left(B\right)}{d}_v{y}^{\epsilon \left(v\right)}\hfill \\ \hfill & =(2\times 2)y^{7n+9}+(2\times 2)y^{7n+10}+\sum _{i=0}^n((3\times 2^{i+1})y^{\beta +4}+(1\times 2^{i+1})y^{\beta +5}\hfill \\ \hfill & +(2\times 2^{i+1})y^{\beta +5}+(2\times 2^{i+1})y^{\beta +6}+(3\times 2^{i+1})y^{\beta +7}+(2\times 2^{i+2})y^{\beta +8}\hfill \\ \hfill & +(2\times 2^{i+2})y^{\beta +9})+2^{n+2}{y}^{14n+17}+\sum _{i=0}^{n-1}\left((2\times 2^{i+2})y^{\beta +10}\right).\hfill \end{array}\hfill \end{array}$$

(12)

Moreover, ${\sum }_{i=0}^n\left((3\times 2^{i+1})y^{\beta +4}+(1\times 2^{i+1})y^{\beta +5}+(2\times 2^{i+1})y^{\beta +5}+(2\times 2^{i+1})y^{\beta +6}+(3\times 2^{i+1})y^{\beta +7}+(2\times 2^{i+2})y^{\beta +8}+(2\times 2^{i+2})y^{\beta +9}\right)={\displaystyle \frac{2(4y^5+4y^4+3y^3+2y^2+3y+3)y^{7n+11}(2^{n+1}{y}^{7n+7}-1)}{2y^7-1}},$

and

${\sum }_{i=0}^{n-1}\left((2\times 2^{i+2})y^{\beta +10}\right)={\displaystyle \frac{8y^{7n+17}(2^n{y}^{7n}-1)}{2y^7-1}}.$

Using these values in Equation (12), we get the desired result.□

Similarly, the values from Table 1 in (4) produce the $TECP(G,y)$ for $D\left(n\right)$.

Corollary 2.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\begin{array}{c}\begin{array}{cc}TECP\left(D\right(n),y)\hfill & =\frac{2(2y^5+2y^4+y^3+y^2+2y+1)y^{7n+11}(2^{n+1}{y}^{7n+7}-1)}{2y^7-1}\hfill \\ \hfill & +\frac{4y^{7n+17}(2^n{y}^{7n}-1)}{2y^7-1}+2y^{7n+9}(1+y+2^{n+1}{y}^{7n+8}).\hfill \end{array}\hfill \end{array}$$

In the next theorem, we determine $Z_1\left(G\right)$ for $D\left(n\right)$.

Theorem 3.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$Z_1\left(D\left(n\right)\right)=(8624n^2+9072n+6876)2^n-882n^2+420n-1886.$$

Proof. 

By using the values of eccentricity from Table 1 in Equation (5), we get

$$\begin{array}{c}\begin{array}{cc}{Z}_1\left(D\left(n\right)\right)\hfill & =Z_1\left(A\right)+Z_1\left(B\right)=\sum _{v\in V\left(A\right)}{\left[\epsilon \left(v\right)\right]}^2+\sum _{v\in V\left(B\right)}{\left[\epsilon \left(v\right)\right]}^2\hfill \\ \hfill & =2{(7n+9)}^2+2{(7n+10)}^2+2^{n+2}{(14n+17)}^2+\sum _{i=0}^n(2^{i+1}{(\beta +4)}^2+2^{i+1}{(\beta +5)}^2\hfill \\ \hfill & +2^{i+1}{(\beta +5)}^2+2^{i+1}{(\beta +6)}^2+2^{i+1}{(\beta +7)}^2+2^{i+2}{(\beta +8)}^2+2^{i+2}{(\beta +9)}^2)\hfill \\ \hfill & +\sum _{i=0}^{n-1}\left(2^{i+2}{(\beta +10)}^2\right).\hfill \end{array}\hfill \end{array}$$

(13)

Moreover, ${\sum }_{i=0}^n\left(2^{i+1}{(\beta +4)}^2+2^{i+1}{(\beta +5)}^2+2^{i+1}{(\beta +5)}^2+2^{i+1}{(\beta +6)}^2+2^{i+1}{(\beta +7)}^2+2^{i+2}{(\beta +8)}^2+2^{i+2}{(\beta +9)}^2\right)=7056n^2\times 2^n+6832n\times 2^n-882n^2+5292\times 2^n+56n-1820,$

and

${\sum }_{i=0}^{n-1}\left(2^{i+2}{(\beta +10)}^2\right)=784n^2\times 2^n+336n\times 2^n+428\times 2^n-196n^2-168n-428.$

By using these values in Equation (13), we get

$$Z_1\left(D\left(n\right)\right)=(8624n^2+9072n+6876)2^n-882n^2+420n-1886,$$

which proves our theorem. □

Now, we compute $A_{\epsilon }\left(G\right)$ for $D\left(n\right)$ in the next theorem.

Theorem 4.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\begin{array}{c}\begin{array}{cc}{A}_{\epsilon }\left(D\left(n\right)\right)\hfill & =\frac{8}{7n+9}+\frac{12}{7n+10}+\frac{2^{n+3}}{14n+17}+\left(\frac{8}{7n+11}+\cdots +\frac{2^{n+3}}{14n+11}\right)\hfill \\ \hfill & +\left(\frac{6}{7n+12}+\cdots +\frac{6\times 2^n}{14n+12}\right)+\left(\frac{12}{7n+12}+\cdots +\frac{12\times 2^n}{14n+12}\right)\hfill \\ \hfill & +\left(\frac{12}{7n+13}+\cdots +\frac{12\times 2^n}{14n+13}\right)+\left(\frac{16}{7n+14}+\cdots +\frac{16\times 2^n}{14n+14}\right)\hfill \\ \hfill & +\left(\frac{24}{7n+15}+\cdots +\frac{24\times 2^n}{14n+15}\right)+\left(\frac{16}{7n+16}+\cdots +\frac{16\times 2^n}{14n+16}\right)\hfill \\ \hfill & +\left(\frac{24}{7n+17}+\cdots +\frac{12\times 2^n}{14n+10}\right).\hfill \end{array}\hfill \end{array}$$

Proof. 

By using the values of $M\left(v\right)$ and $\epsilon \left(v\right)$ from Table 1 in (7), we get:

$$\begin{array}{c}\begin{array}{cc}{A}_{\epsilon }\left(D\left(n\right)\right)\hfill & =A_{\epsilon }\left(A\right)+A_{\epsilon }\left(B\right)=\sum _{v\in V\left(A\right)}\frac{M\left(v\right)}{\epsilon \left(v\right)}+\sum _{v\in V\left(B\right)}\frac{M\left(v\right)}{\epsilon \left(v\right)}\hfill \\ \hfill & =\frac{2\times 4}{7n+9}+\frac{2\times 6}{7n+10}+\frac{2\times 2^{n+2}}{14n+17}\hfill \\ \hfill & +\sum _{i=0}^n(\frac{4\times 2^{i+1}}{\beta +4}+\frac{3\times 2^{i+1}}{\beta +5}+\frac{6\times 2^{i+1}}{\beta +5}+\frac{6\times 2^{i+1}}{\beta +6}\hfill \\ \hfill & +\frac{8\times 2^{i+1}}{\beta +7}+\frac{6\times 2^{i+2}}{\beta +8}+\frac{4\times 2^{i+2}}{\beta +9})+\sum _{i=0}^{n-1}\left(\frac{6\times 2^{i+2}}{\beta +10}\right).\hfill \end{array}\hfill \end{array}$$

(14)

Furthermore, ${\sum }_{i=0}^n\left({\displaystyle \frac{4\times 2^{i+1}}{\beta +4}}+{\displaystyle \frac{3\times 2^{i+1}}{\beta +5}}+{\displaystyle \frac{6\times 2^{i+1}}{\beta +5}}+{\displaystyle \frac{6\times 2^{i+1}}{\beta +6}}+{\displaystyle \frac{8\times 2^{i+1}}{\beta +7}}+{\displaystyle \frac{6\times 2^{i+2}}{\beta +8}}+{\displaystyle \frac{4\times 2^{i+2}}{\beta +9}}\right)=\left({\displaystyle \frac{8}{7n+11}}+\cdots +{\displaystyle \frac{2^{n+3}}{14n+11}}\right)+\left({\displaystyle \frac{6}{7n+12}}+\cdots +{\displaystyle \frac{6\times 2^n}{14n+12}}\right)+\left({\displaystyle \frac{12}{7n+12}}+\cdots +{\displaystyle \frac{12\times 2^n}{14n+12}}\right)+\left({\displaystyle \frac{12}{7n+13}}+\cdots +{\displaystyle \frac{12\times 2^n}{14n+13}}\right)+\left({\displaystyle \frac{16}{7n+14}}+\cdots +{\displaystyle \frac{16\times 2^n}{14n+14}}\right)+\left({\displaystyle \frac{24}{7n+15}}+\cdots +{\displaystyle \frac{24\times 2^n}{14n+15}}\right)+\left({\displaystyle \frac{16}{7n+16}}+\cdots +{\displaystyle \frac{16\times 2^n}{14n+16}}\right),$

and

${\sum }_{i=0}^{n-1}\left({\displaystyle \frac{6\times 2^{i+2}}{\beta +10}}\right)=\left({\displaystyle \frac{24}{7n+17}}+\cdots +{\displaystyle \frac{12\times 2^n}{14n+10}}\right).$

The above two equations along with (14) yield the required result.□

We now determine $\mathsf{\Lambda }\left(D\right(n\left)\right)$ for $D\left(n\right)$.

Theorem 5.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\mathsf{\Lambda }\left(D\left(n\right)\right)=(2744n+1332)2^n-602n+132.$$

Proof. 

By using the values $S_v$ and $\epsilon \left(v\right)$ from Table 1 in (8), we obtain

$$\begin{array}{c}\begin{array}{cc}\mathsf{\Lambda }\left(D\right(n\left)\right)\hfill & =\mathsf{\Lambda }\left(A\right)+\mathsf{\Lambda }\left(B\right)=\sum _{v\in V\left(A\right)}{S}_v\epsilon \left(v\right)+\sum _{v\in V\left(B\right)}{S}_v\epsilon \left(v\right)\hfill \\ \hfill & =(2\times 4)(7n+9)+(2\times 5)(7n+10)+\sum _{i=0}^n((5\times 2^{i+1})(\beta +4)+(3\times 2^{i+1})(\beta +5)\hfill \\ \hfill & +(5\times 2^{i+1})(\beta +5)+(5\times 2^{i+1})(\beta +6)+(6\times 2^{i+1})(\beta +7)+(5\times 2^{i+2})(\beta +8)\hfill \\ \hfill & +(4\times 2^{i+2})(\beta +9))+2\times 2^{n+2}(14n+17)+\sum _{i=0}^{n-1}\left((5\times 2^{i+2})(\beta +10)\right).\hfill \end{array}\hfill \end{array}$$

(15)

Here, ${\sum }_{i=0}^n\left((5\times 2^{i+1})(\beta +4)+(3\times 2^{i+1})(\beta +5)+(5\times 2^{i+1})(\beta +5)+(5\times 2^{i+1})(\beta +6)+(6\times 2^{i+1})(\beta +7)+(5\times 2^{i+2})(\beta +8)+(4\times 2^{i+2})(\beta +9)\right)=2352n\times 2^n+1136\times 2^n-588n+20,$

and

${\sum }_{i=0}^{n-1}\left((5\times 2^{i+2})(\beta +10)\right)=280n\times 2^n+60\times 2^n-60-140n.$

Lastly by using these values in Equation (15), we have

$$\mathsf{\Lambda }\left(D\left(n\right)\right)=(2744n+1332)2^n-602n+132.$$

□

In the following theorem, we determine the $MECP(G,y)$ for $D\left(n\right)$.

Theorem 6.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$$\begin{array}{c}\begin{array}{cc}MECP\left(D\right(n),y)\hfill & =\frac{2(8y^5+10y^4+6y^3+5y^2+8y+5)y^{7n+11}(2^{n+1}{y}^{7n+7}-1)}{2y^7-1}\hfill \\ \hfill & +\frac{20y^{7n+17}(2^n{y}^{7n}-1)}{2y^7-1}+2y^{7n+9}(4+5y+2^{n+2}{y}^{7n+8}).\hfill \end{array}\hfill \end{array}$$

Proof. 

By using the values from Table 1 in Equation (9), we get:

$$\begin{array}{c}\begin{array}{cc}MECP\left(D\right(n),y)\hfill & =MECP(A,y)+MECP(B,y)=\sum _{v\in V\left(A\right)}{S}_v{y}^{\epsilon \left(v\right)}+\sum _{v\in V\left(B\right)}{S}_v{y}^{\epsilon \left(v\right)}\hfill \\ \hfill & =(2\times 4)y^{7n+9}+(2\times 5)y^{7n+10}+\sum _{i=0}^n((5\times 2^{i+1})y^{\beta +4}+(3\times 2^{i+1})y^{\beta +5}\hfill \\ \hfill & +(5\times 2^{i+1})y^{\beta +5}+(5\times 2^{i+1})y^{\beta +6}+(6\times 2^{i+1})y^{\beta +7}+(5\times 2^{i+2})y^{\beta +8}\hfill \\ \hfill & +(4\times 2^{i+2})y^{\beta +9})+2\times 2^{n+2}{y}^{14n+17}+\sum _{i=0}^{n-1}\left((5\times 2^{i+2})y^{\beta +10}\right).\hfill \end{array}\hfill \end{array}$$

(16)

Moreover, ${\sum }_{i=0}^n\left((5\times 2^{i+1})y^{\beta +4}+(3\times 2^{i+1})y^{\beta +5}+(5\times 2^{i+1})y^{\beta +5}+(5\times 2^{i+1})y^{\beta +6}+(6\times 2^{i+1})y^{\beta +7}+(5\times 2^{i+2})y^{\beta +8}+(4\times 2^{i+2})y^{\beta +9}\right)={\displaystyle \frac{2(8y^5+10y^4+6y^3+5y^2+8y+5)y^{7n+11}(2^{n+1}{y}^{7n+7}-1)}{2y^7-1}},$

and

${\sum }_{i=0}^{n-1}\left((5\times 2^{i+2})y^{\beta +10}\right)={\displaystyle \frac{20y^{7n+17}(2^n{y}^{7n}-1)}{2y^7-1}}.$

By using these values in Equation (16), we get the required result. □

The edge partition of sets A and B with respect to the representatives of pairs of end vertices, eccentricity and degree of each edge of the corresponding representative, and their frequencies of occurrence are shown in

Table 2. The edge partition of set B with respect to the representatives of pairs of end vertices, eccentricity, and degree of each edge, and their frequencies.

Representative	Eccentricity	Frequency	Eccentricity of an Edge	Degree of an Edge
$[{\alpha }_1,{\alpha }_1]$	$[7n+9,7n+9]$	1	$7n+7$	2
$[{\alpha }_1,{\alpha }_2]$	$[7n+9,7n+10]$	2	$7n+8$	2
$[{\alpha }_2,a_0]$	$[7n+10,7n+11]$	2	$7n+9$	3
$[a_i,b_i]$	$[\beta +4,\beta +5]$	$2^{i+1}$	$\beta +3$	2
$[a_i,c_i]$	$[\beta +4,\beta +5]$	$2^{i+1}$	$\beta +3$	3
$[c_i,d_i]$	$[\beta +5,\beta +6]$	$2^{i+1}$	$\beta +4$	2
$[d_i,e_i]$	$[\beta +6,\beta +7]$	$2^{i+1}$	$\beta +5$	3
$[e_i,f_i]$	$[\beta +7,\beta +8]$	$2^{i+2}$	$\beta +6$	3
$[f_i,g_i]$	$[\beta +8,\beta +9]$	$2^{i+2}$	$\beta +7$	2
$[g_i,h_i]$ when $i\ne n$	$[\beta +9,\beta +10]$	$2^{i+2}$	$\beta +8$	2
$[g_n,h_n]$	$[14n+16,14n+17]$	$2^{n+2}$	$14n+15$	1
$[h_i,a_{i+1}]$ when $i\ne n$	$[\beta +10,\beta +11]$	$2^{i+2}$	$\beta +9$	3

. The eccentricities of vertices are taken from Table 1.

In the next theorem, we determine $Z_2\left(G\right)$ for $D\left(n\right)$.

Theorem 7.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then,

$$Z_2\left(D\left(n\right)\right)=2^n(8624n^2+8456n+6552)-931n^2+434n-1979.$$

Proof. 

By using the values from Table 2 in Equation (6), we compute the second Zagreb eccentricity index of $D\left(n\right)$ as follows:

$$\begin{array}{c}\begin{array}{cc}{Z}_2\left(D\left(n\right)\right)\hfill & =Z_2\left(A\right)+Z_2\left(B\right)=\sum _{uv\in E\left(A\right)}\left[\epsilon \left(u\right)\epsilon \left(v\right)\right]+\sum _{uv\in E\left(B\right)}\left[\epsilon \left(u\right)\epsilon \left(v\right)\right]\hfill \\ \hfill & =(7n+9)(7n+9)+2(7n+9)(7n+10)+2(7n+10)(7n+11)\hfill \\ \hfill & +2^{n+2}(14n+16)(14n+17)+\sum _{i=0}^n(2^{i+1}(\beta +4)(\beta +5)+2^{i+1}(\beta +4)(\beta +5)\hfill \\ \hfill & +2^{i+1}(\beta +5)(\beta +6)+2^{i+1}(\beta +6)(\beta +7)+2^{i+2}(\beta +7)(\beta +8)\hfill \\ \hfill & +2^{i+2}(\beta +8)(\beta +9))+\sum _{i=0}^{n-1}\left(2^{i+2}(\beta +9)(\beta +10)+2^{i+2}(\beta +10)(\beta +11)\right).\hfill \end{array}\hfill \end{array}$$

(17)

Furthermore, ${\sum }_{i=0}^n\left(2^{i+1}(\beta +4)(\beta +5)+2^{i+1}(\beta +4)(\beta +5)+2^{i+1}(\beta +5)(\beta +6)+2^{i+1}(\beta +6)(\beta +7)+2^{i+2}(\beta +7)(\beta +8)+2^{i+2}(\beta +8)(\beta +9)\right)=6272n^2\times 2^n+5936n\times 2^n-784n^2+4608\times 2^n+84n-1604,$

and

${\sum }_{i=0}^{n-1}\left(2^{i+2}(\beta +9)(\beta +10)+2^{i+2}(\beta +10)(\beta +11)\right)=1568n^2\times 2^n+672n\times 2^n-392\times n^2+856\times 2^n-336n-856,$ which along with (17) give

$$Z_2\left(D\left(n\right)\right)=2^n(8624n^2+8456n+6552)-931n^2+434n-1979,$$

which was required. □

Finally, we determine the ${\epsilon }_e\left(D\left(n\right)\right)$ for $D\left(n\right)$.

Theorem 8.

Let $D\left(n\right)$ be the molecular graph of PETAA Dendrimer. Then

$${\epsilon }_e\left(D\left(n\right)\right)=(1456n+500)2^n-336n+144.$$

Proof. 

By using the values from Table 2 in (10), we get

$$\begin{array}{c}\begin{array}{cc}{\epsilon }_e\left(D\left(n\right)\right)\hfill & ={\epsilon }_e\left(A\right)+{\epsilon }_e\left(B\right)=\sum _{f\in E\left(A\right)}{d}_f\epsilon \left(f\right)+\sum _{f\in E\left(B\right)}{d}_f\epsilon \left(f\right)\hfill \\ \hfill & =(2\times 1)(7n+7)+(2\times 2)(7n+8)+(2\times 3)(7n+9)+\sum _{i=0}^n((2\times 2^{i+1})(\beta +3)\hfill \\ \hfill & +(3\times 2^{i+1})(\beta +3)+(2\times 2^{i+1})(\beta +4)+(3\times 2^{i+1})(\beta +5)+(3\times 2^{i+2})(\beta +6)\hfill \\ \hfill & +(2\times 2^{i+2})(\beta +7))+2^{n+2}(14n+15)+\sum _{i=0}^{n-1}\left((2\times 2^{i+2})(\beta +8)+(3\times 2^{i+2})(\beta +9)\right).\hfill \end{array}\hfill \end{array}$$

(18)

Here, ${\sum }_{i=0}^n\left((2\times 2^{i+1})(\beta +3)+(3\times 2^{i+1})(\beta +3)+(2\times 2^{i+1})(\beta +4)+(3\times 2^{i+1})(\beta +5)+(3\times 2^{i+2})(\beta +6)+(2\times 2^{i+2})(\beta +7)\right)=1120n\times 2^n+408\times 2^n-280n+76,$

and

${\sum }_{i=0}^{n-1}\left((2\times 2^{i+2})(\beta +8)+(3\times 2^{i+2})(\beta +9)\right)=280n\times 2^n+32\times 2^n-140n-32.$

By using these values in Equation (18), we get

$${\epsilon }_e\left(D\left(n\right)\right)=(1456n+500)2^n-336n+144.$$

This gives the required result. □

4. Discussion

In recent times, several techniques such as SARs model, QSAR model, QSPR model, least square regression analysis and other models are being used to predict chemical and biological behavior of compounds. By using graphs corresponding to compounds, non-experimental parameters are used to predict chemical behavior of these compounds. Among these parameters, several (distance based) indices have been formulated, such as the eccentric connectivity index (denoted by $\xi \left(G\right)$), total-eccentricity index ($\varsigma \left(G\right)$), augmented eccentric-connectivity index ($A_{\epsilon }\left(G\right)$) and modified eccentric-connectivity index ($\mathsf{\Lambda }\left(G\right)$). In order to demonstrate the importance of $\xi \left(G\right)$ in predicting biological activity, Gupta et. al [32] used nonpeptide N-benzylimidazole derivatives with respect to antihypertensive activity. After comparison between the results obtained by using $\xi \left(G\right)$ and the corresponding values obtained by using other TIs, they found the accuracy of prediction to be about 80%. In [12], Sharma et al. investigated the discrimination power of $\xi \left(G\right)$ with regard to biological/physical properties of molecules. By using $\xi \left(G\right)$ in several datasets, they obtained the correlation coefficients, ranging from 95% to 99%, with regard to physical properties of diverse nature. It was observed that the $\xi \left(G\right)$ shows excellent correlations with regard to analgesic activity of piperidinyl methyl ester and methylene methyl ester analogs. In the current work, we have extended the pool of information related to important PETTA dendrimers. This information can be used by the other researchers who are doing lab work. They may develop connections with the properties by using these values in different ways, for example, to decide the size of suitable dendrimers for a certain property. Furthermore, some physical and biological properties can be a topic of interest in the future.

5. Conclusions

The theoretical formulation studied in this article has received remarkable interest of researchers due to its extensive application in the fields of pharmacy, medical science, chemical engineering, and applied sciences. In this paper, we deal with the molecular structure of PETAA dendrimers. We compute some distance-based indices for PETAA dendrimers, along with the exact values of eccentric connectivity, total eccentricity, augmented eccentric connectivity, first Zagreb eccentricity, modified eccentric connectivity, second Zagreb eccentricity, and edge version of eccentric-connectivity indices for PETAA. The associated polynomials have also been computed for PETAA dendrimers. Since PETAA dendrimers have a wide variety of biomedical applications, therefore, these theoretical results may play a vital role in upcoming research in medical sciences.