Abstract
In order to gain a knowledge of the heat emitted from a variety of sources at the blind heading of an underground gold mine, the present study conducts an in situ measurement study in a blind heading within the load haul dumps (LHDs) that are operating. The measurements can provide a reliable data basis for the setting of numerical simulations. The results demonstrate that the distances between the forcing outlet and the mining face (denoted as Zm), as well as the heat generation from LHDs (denoted as QL), has brought significant impacts on the airflow velocity, relative humidity, and temperature distributions in the blind heading. Setting Zm to 5 m could achieve a relative optimal cooling performance, also indicating that when the LHD is fully operating in the mining face, employing the pure forcing system has a limited effect on the temperature decrease of the blind heading. According to the numerical simulations, a better cooling performance can be achieved based on the near-forcing-far-exhausting (NFFE) ventilation system.
1. Introduction
With the development of the global economy, the demands for mineral resources are persistently increased by human beings. In recent years, shallow resources have displayed a declining trend annually and the underground mining depth will become deeper and deeper in the future [1,2,3]. In addition, the higher-powered machinery that increases production levels impose an increased burden on ventilation systems to maintain an acceptable working environment [4]. As a result, the worsening thermal environments in underground mining resulted from higher virgin rock temperature and heat emitted from mechanical equipment gave rise to a lot of concerns regarding the health and safety of miners [5]. In the blind headings, the heat transferred from fragmented rock, explosives and LHDs (or roadheaders, continuous miners) with the existence of an auxiliary ventilation system could make the aerodynamic much more complex in the face area [6]. Auxiliary ventilation can be classified into three basic types, Pure Forcing (PF), Pure Exhausting (PE), and overlap systems (FFNE and NFFE) as shown in Figure 1. Therefore, to design the optimal ventilation and cooling systems, it is of great significance to carry out in-depth research on the thermal environment for high-speed ramp and tunnel developments [7].
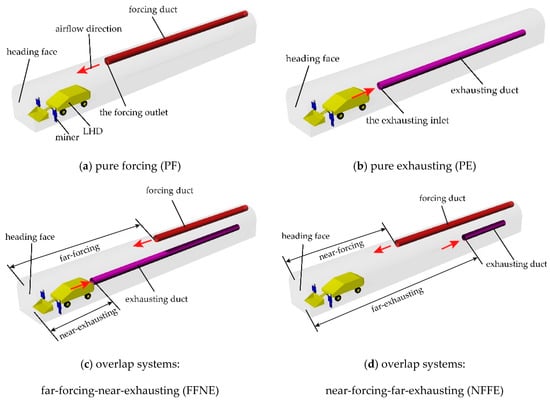
Figure 1.
Geometry model of the PF (a), PE (b), FFNE (c), and NFFE (d) ventilation systems.
Traditionally, researchers mainly adopt the following three methods for examining the thermal environment in blind headings: in situ measurement, laboratory experiment and numerical simulation [8]. The in situ measurement and experimental research has always been a challenge and only a few related studies are available due to the safety issue. For example, Bluhm et al. quantified the different heat sources by field measurements [7]. The heat flow from the rock was found to be the principal source of heat. Lowndes et al. measured the thermal environmental conditions in a representative development drivage in a coal mine during the non-production period and production period. The input values for the tunnel model were modified based on the measured data [9]. Shimada utilized a one-tenth scale model experimental apparatus to investigate the cooling effectiveness of the auxiliary ventilation systems and heat transfer at the heading face [10]. Jia et al. designed a thermal exchange simulation test platform for a blind heading that can be employed to investigate the cooling factor for the ventilation and cooling system [11]. However, most of the previous studies are mainly focused on the heat load transferred from rock.
With the emergence of computational fluid dynamics (CFD) in the 1960s, numerical simulations aiming at the thermal management in heading faces have become efficient and low cost [12]. Gao et al. employed the finite volume method for simulating the airflow velocity and temperature fields in a heading face. They obtained the distribution of heat transfer coefficient in the heading face [13]. Sasmito et al. developed a three-dimensional blind heading model for studying the effects of the ventilation flow rate, cooling load, virgin rock temperature, and the heat rejection from mining machinery [12]. To date, much more researchers have conducted a large number of numerical simulations to investigate the airflow ventilation-methane behavior and airflow ventilation-dust control [14,15,16,17,18] in PF and PE, respectively. Based on these research findings, the constraint conditions for Zm and Ze (the distances between the exhausting outlet and the heading face) in PF and PE can be written as Equations (1) and (2), respectively [19]:
where S is the section area of a blind heading (m2).
As stated above, in all numerical studies performed so far, much more attention was concentrated on the methane and dust distributions at the face area. The numerical models targeting thermal environment research were over-simplified. The heat sources such as the heat generation from diesel engines were mainly calculated by a simple equation proposed by McPherson [20]. The key parameters are regulated mostly based on field experience. There is still no ventilation scheme that has been proposed from the view point of thermal environment. In practical ventilation and cooling engineering, doubts still exist when determining Zm or Ze based on the Equations (1) and (2).
This study was organized as follows: firstly, an in situ measurement was performed in a selected blind heading. The heat emitted from surrounding rock and LHDs was calculated based on the measured airflow velocity, temperature and relative humidity. Secondly, FLUENT software was employed to study the airflow velocity, temperature and relative humidity distributions when the forcing outlet was set at different positions. An optimal position that can achieve a favorable cooling performance was determined. Then, effect of the heat emitted from LHDs is also discussed with respect to the temperature distributions. Finally, NFFE ventilation was proposed in the numerical simulation. Moreover, this study could help extend the existing thermal environment research and provide theoretical support for the design and operation of the auxiliary ventilation systems in blind headings that are mined using LHDs.
2. Field Measurements
2.1. Measuring Setup
This case study relates to a 40 m multi-blast development heading about 230 m below surface in an underground gold mine located in Japan. The drill and blast methods with the use of diesel equipment (such as LHD) were applied in the mine. There was no wet source in the heading and the surface of the walls was dry. To verify the heat load from the surrounding rock and diesel equipment in an actual blind heading, the dry bulb temperatures were continuously measured and digitally recorded within the mining stope during production periods. Due to the existence of hot spring water in the deep strata, the virgin rock temperature reaches above 80 °C and the rock stratum is andesite. The mining stope was 40 m in length with an arch cross-sectional area of 21.6 m2 and a perimeter of 15.5 m. Hence, the hydraulic diameter of the airway was 5.6 m. The heading face was ventilated by PF. The air duct (80 cm diameter) was being installed in the roof of the airway which was producing an airflow velocity of 12.0 m/s with a volume airflow of 7.0 m3/s. The average airflow velocity can be calculated as 0.3 m/s in the airway. The heat capacity of the airflow per unit time (W/°C) in this airway can be determined as 8442 W/°C by Equation (3):
where F is volume flow of air (m3/s), ρa is air density (kg/m3), Ca is specific heat capacity of air (J/(kg·°C)). In this paper, ρa is 1.2 kg/m3 and Ca is 1005 J/(kg·°C).
Figure 2 illustrates the location of the air duct and the measuring points near the heading from the side view. Zm was maintained about 20 m. The blind heading would advance about three meters in each blasting. Data loggers (midi LOGGER GL200, Graphtec Corporation, Yokohama City, Prefecture of Kanagawa, Japan) and thermocouples of Type K (diameter is 0.5 mm, Graphtec Corporation, Yokohama City, Prefecture of Kanagawa, Japan) were used for these measurements. The measuring interval of the data loggers was set at 30 s. The thermocouples were installed in nine locations of the cross-section (Figure 3). One of them was employed to measure the air temperature in the air duct. A blast may cause damage to the data loggers and sensors. Therefore, the sensors had to be installed about one meter from the surface of the airway and the measuring points were 30 m from the face and thus the heat exchange area was 424.6 m2.
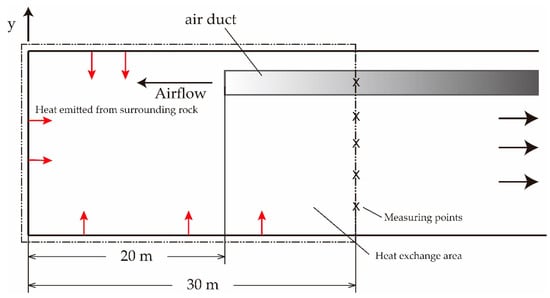
Figure 2.
Side view of the blind heading, the measuring points and the heat exchange area.
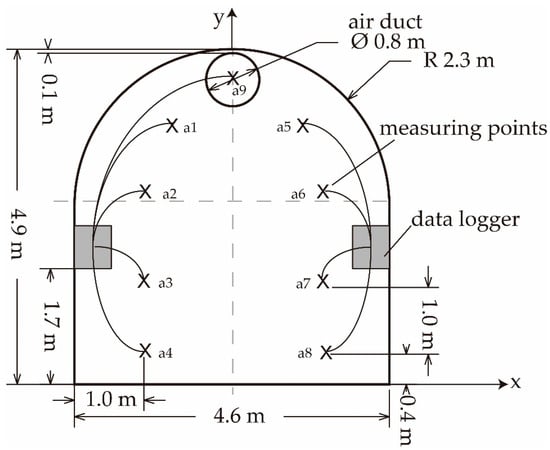
Figure 3.
Cross-sectional view of the measuring points.
2.2. Results and Discussion
Figure 4 presents the measured results of air temperature variation with time. The average air temperature of the airway represented the average measured results of the eight thermocouples. The air temperature of the outlet of the air duct represented the measure results at the outlet of the air duct. Table 1 introduces the mining operation process. The brief discussion of the measured results is shown below:
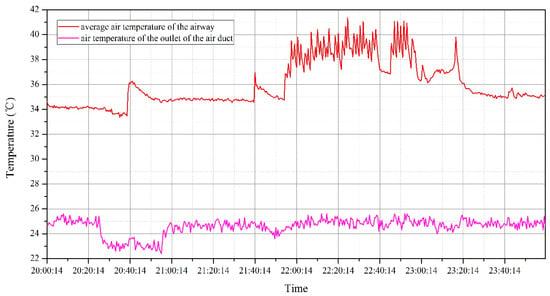
Figure 4.
Measuring result of the variation of air temperature with time.

Table 1.
Mining process record.
- No mining operation before 20:40;
- Air temperature increased due to the blasting at 20:40; and
- Air temperature increased due to the moving of LHD between 21:50 and 23:30.
2.2.1. Heat Emitted from Surrounding Rock
Before 20:40, there were no working activities that took place. Hence, it can be considered that the surrounding rock would be the major heat source to the air stream. Figure 5 which was magnified from Figure 4 shows the strata heat resulted in airflow temperatures increased by about 9.7 °C within the heat exchange area. The strata heat before a blasting in the vicinity of the head end could be determined as 81.9 kW by Equation (4), which can serve as the boundary conditions for subsequent numerical simulation:
where Qr is strata heat before the blasting (W), Cf is heat capacity of air in per unit time (W/°C) as shown in Equation (3), Θf0 is the stable air temperature before blasting (°C), Θi is air temperature at the outlet of the air duct (°C), here Θf0 − Θi = 9.7 °C.
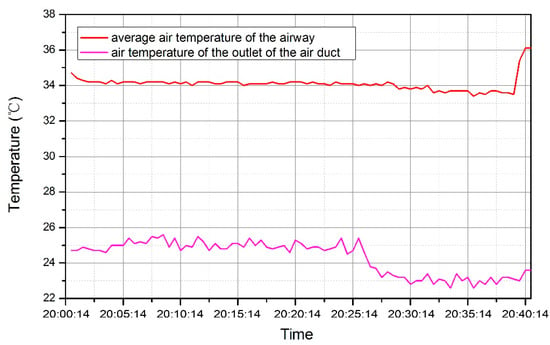
Figure 5.
Measuring result of the variation of air temperature with time before 20:40.
The Reynolds number could be determined as 1.1 × 105 by Equation (5):
where de is hydraulic diameter of the airway (m), um is average airflow velocity (m/s), vf is kinematic viscosity (N·m s/kg). In this paper de is 5.6 m, um is 0.3 m/s and vf is 15.3 × 10−6 N·m s/kg.
The local heat-transfer coefficient mostly depends on the distribution of air velocity which is influenced by the shape of the airway, the size and position of the duct outlet and the airflow rate. When the geometrical conditions are identical, it only depends on the airflow rate. Numerous studies have been carried out on the correlation between heat-transfer coefficient and the Reynolds number in a straight pipe with through airflow. Gao et al. recommended the following Equation (6) to calculate the heat transfer coefficient [13]:
where λ is heat conductivity of air (W/(m·°C)). Pr is Prandtl number given by:
where μ is viscosity of air (Pa·s). Cp is isobaric specific heat capacity (J/(kg·°C)). In this paper λ is 0.02 W/(m·°C), Cp is 1005 J/(kg·°C), Pr can be calculated as 0.77, h0 can be calculated as 0.8 W/m2·°C.
As airflow in the heading face is the typical forced turbulence in the semi-closed space, the airflow velocity distribution is uneven near the mining face. The local heat transfer coefficient varies with location in a wide range. Gao et al. suggested that the dimensionless heat transfer coefficients (h/h0) of roof, side wall, floor and mining face were 9.7, 5.1, 3.5, and 6.8, respectively, with the average of 5.6 [13]. Hence, the heat transfer coefficient can be determined at 4.5 W/(m2∙K).
2.2.2. Heat Transferred from LHD
The cyclical nature of mechanized loading and hauling operations can produce periodic fluctuation in the thermal environmental conditions created within these workings [9]. Table 2 shows the specifications of the LHD. Figure 6 presents the variation of the air temperature from 21:50 to 23:30 which was magnified from Figure 4. There are two kinds of heat source, respectively, heat produced by LHD and strata heat. The average temperature difference increases to 12.9 °C. The total heat that is produced by LHD and strata can be calculated as 108.9 kW. Hence, the LHD can produce approximately 27 kW heat during the working period.

Table 2.
Specifications of the LHD.
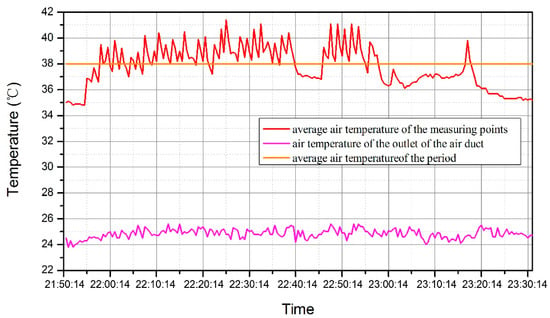
Figure 6.
Variation of air temperature with time from 21:50 to 23:30.
3. Numerical Study
3.1. Geometry Model
Two three-dimensional blind headings without and with the use of an LHD employing PF auxiliary ventilation system were built by Rhino 6 (Robert McNeel & Assoc, Seattle City, State of Washington, the United States) as shown in Figure 7a,b, respectively. The positive X direction points to the mining face from the entrance of the blind heading, the positive Y direction points to the left side-walls from the right side-walls and the positive Z direction points to the airway roof from the airway floor. The geometry model was an arch tunnel, 40 m long, 4.6 m wide, and 4.9 m high. A forcing duct with a diameter of 0.8 m was hung at 4 m from the floor. Its setback distance from the mining face was 20 m. An LHD was 8.0 m long, 2.5 m wide and 2 m high. The front part of the LHD was 2 m from the mining face and the miner’s height was 1.75 m, 3 m away from the mining face.
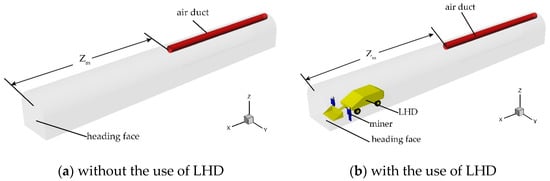
Figure 7.
Geometric model (a,b).
3.2. Mesh Generation
The mesh quality determines the computational results and accuracy [21]. The mesh generation was completed with ANSYS Meshing (ANSYS, Inc., Canonsburg City, PA, USA) and the globe mesh controls were applied. The element size was set to 1 m. Both Capture Curvature and Capture Proximity were set to Yes. With these settings, the combined effect of both the proximity and curvature sizing can be obtained. Finally, 0.83 × 106 elements were generated. Skewness and orthogonal quality are two of the primary quality measures for a mesh. The statistics of the skewness and orthogonal quality is shown in Table 3. The maximal skewness was lower than 0.95 and the minimal orthogonal quality was higher than 0.1, suggesting that the high-quality mesh had been generated as shown in Figure 8.

Table 3.
The mesh metric information.

Figure 8.
The original computational mesh.
3.3. Mesh Independence Test
The 3D inflation capability provides high quality mesh generation close to wall boundaries to resolve changes in physical properties. In order to ensure a mesh independent solution, another two different amount of elements 1.28 × 106 and 1.75 × 106 were generated by setting different element size and local inflation mesh controls. The comparison with the element amount of 0.83 × 106 and 1.28 × 106 is shown in Figure 9. It can be observed that a finer mesh and the inflation layers were generated in the boundary layers between the airflow and LHD. Figure 10 shows the distribution curves of the airflow velocities and temperatures at the position of Y = 4.1 m, Z = 1.7 m along the airway with three different amount of elements. It can be found that the element amount of 1.28 × 106 gives about 2% deviation compared to the element size of 1.75 × 106. Whereas, the results from the mesh size of 0.83 × 106 deviate up to 15% as compared to those from the finest one. Therefore, a mesh of 1.28 × 106 elements was sufficient for the numerical simulation purposes.
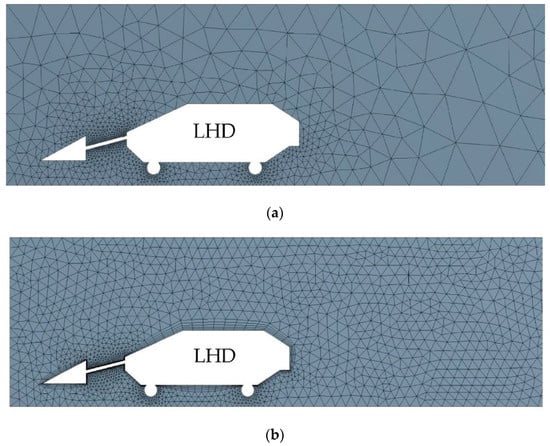
Figure 9.
Comparison with the original mesh (a) and first adaptive mesh (b).
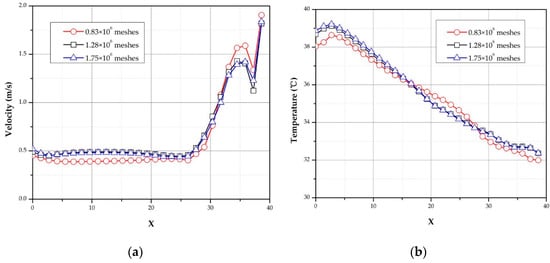
Figure 10.
Airflow velocities and temperatures distribution of calculating three times along the airway. (a) Airflow velocities distribution; and (b) airflow temperatures distribution.
3.4. Boundary Conditions
The boundary conditions for the model are summarized in Table 4.

Table 4.
Boundary conditions of the CFD method.
3.5. Turbulence Model
The turbulence model is the key component in representing flow behavior in underground thermal environment [24]. A commercial CFD code (Fluent, ANSYS, Inc., Canonsburg City, State of Pennsylvania, the United States) was applied to solve the mass conversion equation (continuous equation), momentum equation (Navier–Stokes equation), energy conversion equation and the turbulence model equation. The flow behavior of various turbulence models, i.e., Spalart-Allmaras, Standard K-Epsilon, Standard K-Omega and Reynolds stress model (RSM) had been compared with the experimental data while the Standard K-Epsilon model provided better results [25]. Table 5 shows the measured results of velocity value as compared to simulation results for various models.

Table 5.
Comparison between the measurement data of airflow velocity and the simulation data for various models.
To test whether there were differences between the measurements and the simulation results, a Wilcoxon signed rank test (IBM SPSS Statistics 19, IBM Corporation, Armonk City, State of New York, the United States) was conducted (significance was accepted at p < 0.05) as shown in Table 5. Because the minimum threshold airflow velocity measured by the anemometer was 0.3 m/s, “unmeasurable” indicates that the airflow velocities at the measured points were less than 0.3 m/s. Hence, only the measured points of a2, a3, a4, a7, and a8, with LHD and the measured points of a1, a3, a4, a7, and a8 without LHD were analyzed. No significant differences have been found between the measurements and the simulation without and with LHD, respectively (p = 0.414 and p = 0.083), when K-Epsilon model was employed. Figure 11a,b show the airflow temperature distributions in the cross-section of X = 14 m without and with LHD, respectively, using the K-Epsilon model.
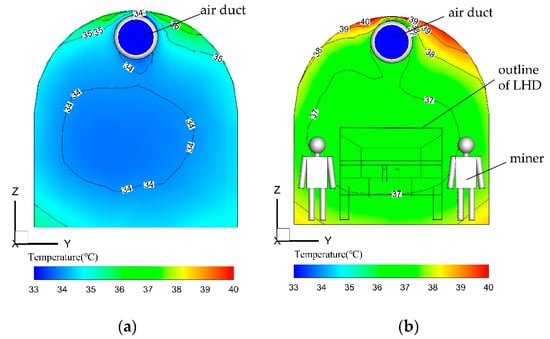
Figure 11.
Airflow temperature distributions in the cross section of X = 14 m without and with LHD: (a) without LHD; (b) with LHD.
The average temperatures were 34.1 °C and 37.4 °C, respectively. Figure 12a,b display the comparison between the measured data of the airflow temperature and the simulation results without and with LHD respectively. The results suggest that K-Epsilon model can give reasonably good prediction, which is in line with the finding of Agus P. Sasmito [26]. The effectiveness of the K-Epsilon model with regard to airflow velocity and temperature simulation was verified. K-Epsilon model considers two-equation model which deals with turbulent kinetic energy, k, and its rate of dissipation, ε, which is coupled with turbulent viscosity. This model is given as:
where Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients, C1ε and C2ε are model constants, σk and σε are the turbulent Prandtl numbers corresponding to the k equation and the ε equation, respectively, and μt is turbulent viscosity given by:
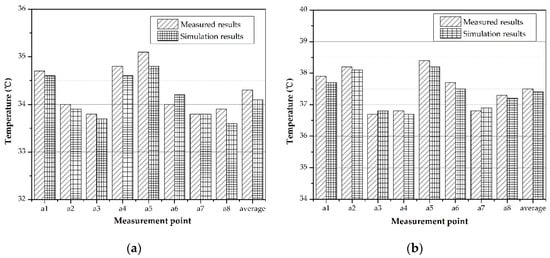
Figure 12.
Comparison between the measured data and the simulation results without and with LHD: (a) without LHD; and (b) with LHD.
The values of C1ε, C2ε, Cμ, σk, and σε are 1.44, 1.92, 0.09, 1, and 1.3, respectively.
4. Results and Discussion
The simulation results were mainly focused on the two different planes as shown in Figure 13 including the Y = 2.3 m plane that is vertical to Y-axis (Plane A), as well as Z = 1.7 m (Plane B) which are vertical to Z-axis. The miners are typically located at the area near to the mining face. Hence, the region surrounded by X = 27 m to 37 m and Z = 0 m to 4 m was defined as the occupied zone while the remaining region was defined as the unoccupied zone in accordance with the regional distribution of miners.
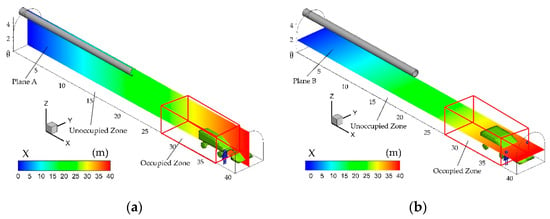
Figure 13.
Selection of planes. (a) Plane A; and (b) Plane B.
4.1. Effect of Different Zm on the Thermal Environment
Figure 14 shows the airflow velocity distributions in Plane A, when Zm was set at five different values (specifically 5 m, 10 m, 15 m, 20 m, and 25 m). According to the International Tunnelling Association, the minimum airflow velocity should be greater than 0.3 m/s [27]. Obviously, the airflow velocity was maintained below 0.3 m/s in many regions from Figure 14 when Zm = 5 m, Zm = 10 m, and Zm = 15 m, respectively. On the contrary, when Zm = 20 m, it can be observed that the regions of low airflow velocity can achieve less coverage. With this consideration, when Zm = 5 m, Zm = 10 m and Zm = 15 m, the forcing duct outlet was too close to the mining face, and the airflow could rapidly enter the relatively closed mining region after free expansion. The LHD greatly obstructed the return airflow, resulting in low reflux velocity.
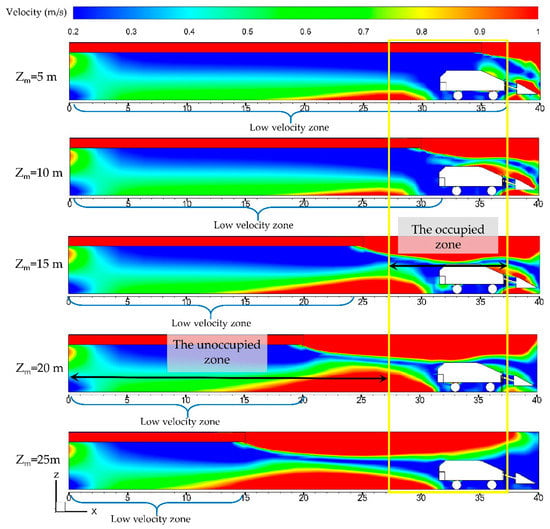
Figure 14.
Airflow velocity distributions in plane A when Zm = 5 m, Zm = 10 m, Zm = 15 m, Zm = 20 m, and Zm = 25 m.
When Zm = 20 m, the tail of the LHD restricted the development and diffusion of the jet flow and it reflowed back to the airway due to the blocking effect of the LHD. When Zm = 25 m, the distance exceeded the effective range of the jet flow. The airflow will form a circulating eddy zone before reaching the mining face and, thus, the effective reflux cannot be formed. Therefore, it can be concluded that the blocking effect of ventilation barriers such as LHDs or roadheaders on the airflow velocity distributions should be considered when repositioning the forcing duct.
Figure 15 depicts the airflow temperature distributions in Plane A when Zm was set at five different values as mentioned above. It can be observed that, there are no obvious differences in the temperature distributions in the unoccupied zone under different values of Zm. It can be considered that the airflow in unoccupied zone is mostly constituted by reflux and similar heat transfer has taken place between the airflow and the LHD as well as the surrounding rock. On the contrary, obvious differences in the temperature distributions are observed in the occupied zone. Obviously, the smaller Zm has better cooling performance in the occupied zone from Figure 15 considering that the smaller Zm can encourage more fresh airflow to involve the cooling process.
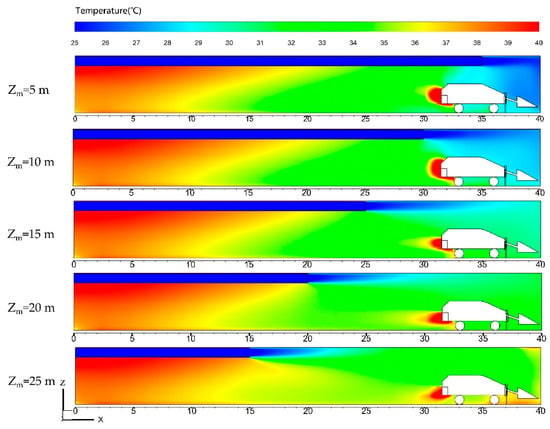
Figure 15.
Airflow temperature distributions in plane A when Zm = 5 m, Zm = 10 m, Zm = 15 m, Zm = 20 m, and Zm = 25 m.
Figure 16 shows the distribution curves of the airflow temperature at the position of Y = 4.1 m, Z = 1.7 m along the airway. It can be concluded that the different positions of the forcing duct will remarkably affect the airflow temperature distributions in the blind heading, especially in the occupied zone. It can be observed that the airflow temperature fluctuated to various degrees when Zm is set at five different values at X = 30 m of the airway due to the heat emitted from the LHD. More obvious fluctuations can be seen at Zm = 5 m, Zm = 10 m, and Zm = 25 m.
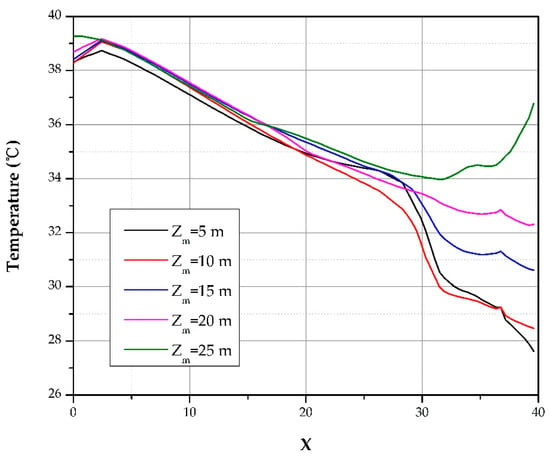
Figure 16.
Airflow temperature distributions of different Zm along the airway.
Figure 17 depicts the airflow relative humidity distributions in Plane A when Zm was set at five different values. It can be observed that, the smaller Zm, the higher relative humidity in the occupied zone. The relative humidity gradually decreases along the length of the airway (from the heading face to the outlet of the airway). In the case of the same moisture content of the airflow (the moisture content of the airflow was 13.7 g/m3), the relative humidity decreases with the increasing dry bulb temperature. If Zm is set to a higher value, the cooling airflow cannot fully involve in the cooling process in the occupied Zone due to the blocking effect of the LHD. To sum up, the temperature in the occupied zone is about 29 °C and the relative humidity is about 55% when Zm = 5 m, which is more comfortable for miners. Hence, Zm = 5 m should be adopted in subsequent analysis. Much care should be taken that the position of the LHD and the heat generated from the LHD are the important factors when optimizing the ventilation and cooling system.
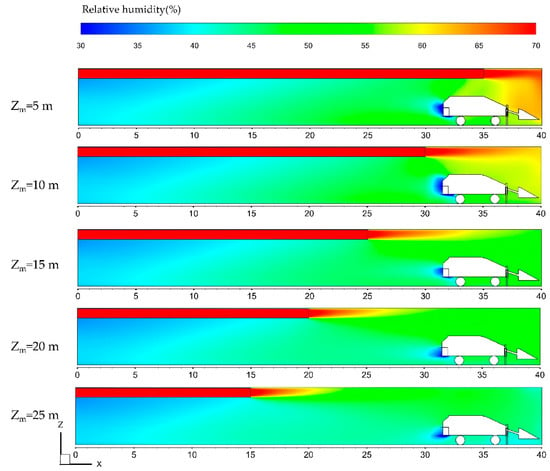
Figure 17.
Airflow relative humidity distributions in plane A when Zm = 5 m, Zm = 10 m, Zm = 15 m, Zm = 20 m, and Zm = 25 m.
4.2. Effect of Heat Emitted from LHD on the Thermal Environment
In most cases, an LHD operates continuously, but uses only full power (100%) while loading buckets and hauling up a ramp for 15 min per hour, operates at 50% maximum power tramming horizontally or downhill for 30 min per hour, and idles at 10% maximum power for the remaining 15 min per hour [28]. Investigating the variation of airflow temperature under different heat generation from a LHD can provide foundation for determining which heat removal/cooling should be applied. It provides great significance to realize the intelligent underground mining.
Figure 18 shows the temperature distributions in the unoccupied zone and occupied zone when QL is set at five different values (specifically, 10 kW, 20 kW, 30 kW, 40 kW, and 50 kW) which represent the heat generation from LHD under different working conditions. Obviously, when the QL increased from 10 kW to 50 kW, the average air temperature in the occupied zone increased from 30 °C to 34 °C. The airflow in the unoccupied zone is mostly constituted by the reflux. The heat transferred between the airflow and the LHD will result in the reflux temperature increasing to above 37 °C. Moreover, there is a long range and high flow velocity of the forcing system in the ventilation duct outlet that is frequently employed in the hot blind headings but it still has a limited cooling effect. Therefore, great efforts should be made to explore better ventilation and cooling schemes.
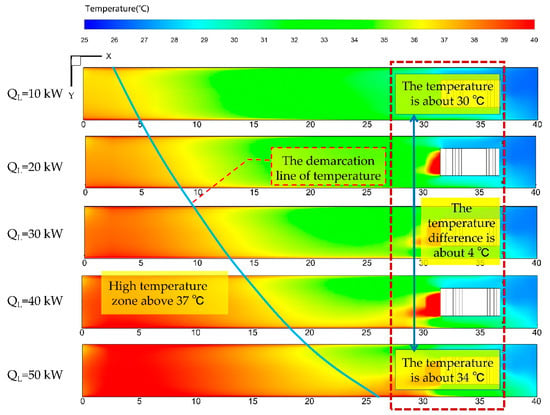
Figure 18.
Airflow temperature distributions in Plane B with different QL.
Figure 19 depicts the airflow relative humidity distributions in Plane B when QL is set at five different values. It can be observed that the raise of QL, can decrease the relative humidity in the airway. As mentioned above, the more heat generated by the LHD leads to the higher dry bulb temperature. In the case of the same moisture content of the airflow, the relative humidity decreases with the increasing dry bulb temperature.
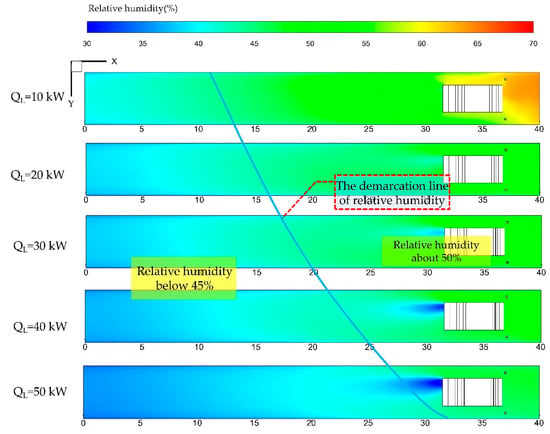
Figure 19.
Airflow relative humidity distributions in Plane B with different QL.
4.3. Effect of Auxiliary Ventilation on Thermal Environment of Airway
Sasmito et al. conducted CFD-based studies on the effect of ventilation airflow velocity. They found that increasing the forcing airflow velocity from 12 m/s to 20 m/s only reduced average temperature by 0.2 °C [12]. Limitations exist in PF to achieve a better cooling effect. However, the overlap systems, as shown in Figure 1, combine the advantages of the PF and PE, which provides another alternative to ameliorate adverse thermal environment. Many researchers carried out in situ measurements and numerical simulation studies on the auxiliary ventilation system from the viewpoint of dust and methane control [14,17]. However, few studies on the field of thermal environment are available. Therefore, the current work will employ the overlap systems to investigate the cooling effect.
As shown in Figure 1 and Figure 20, four systems will be analyzed. The first one is PF, which is the same as the previous study. The second one is PE with an exhausting duct of 800 mm in diameter, Ze = 5 m and the exhaust airflow velocity is 24 m/s. The exhausting duct is located on the airway floor. The third one is FFNE. The diameter of the forcing duct and the exhausting duct are the same as PF and PE, respectively, but Zm = 15 m and Ze = 5 m. To prevent recirculation, the total quantity of air exhausted must be at least twice the quantity delivered by the force fan. Therefore, the force airflow velocity was 12 m/s and the exhaust airflow velocity was 24 m/s. The fourth one is NFFE, which is similar to the FFNE but Zm = 5 m and Ze = 15 m [7].
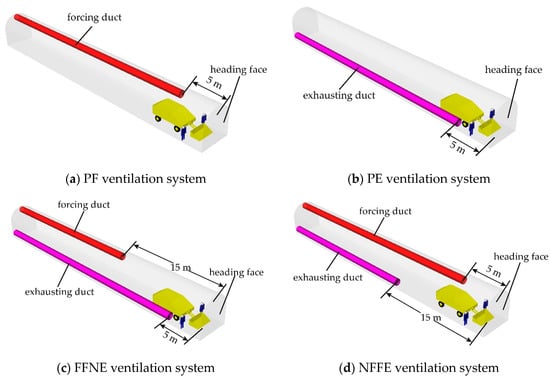
Figure 20.
Geometry model of the PF (a), PE (b), FFNE (c), and NFFE (d) ventilation systems.
Figure 21 displays the airflow temperature distributions of the four auxiliary ventilation systems at the Plane B, respectively. The simulation results show that the cooling performance in the occupied zone reaches the optimal level when applying NFFE. The airflow temperatures were reduced by about 3 °C compared with that of PF in the occupied zone when adopting the NFFE ventilation system. The temperature in the unoccupied zone would be increased but fewer miners would have to work in this region, which would enhance the energy utilization coefficient (EUC) based on EUC = (tuz − ts)/(toz − ts), where tuz was the average temperature in the unoccupied zone, ts was the supply air temperature, and toz was the average temperature in the occupied zone. Thus, it had conformed to the reasonable distribution of the cold flow [29].
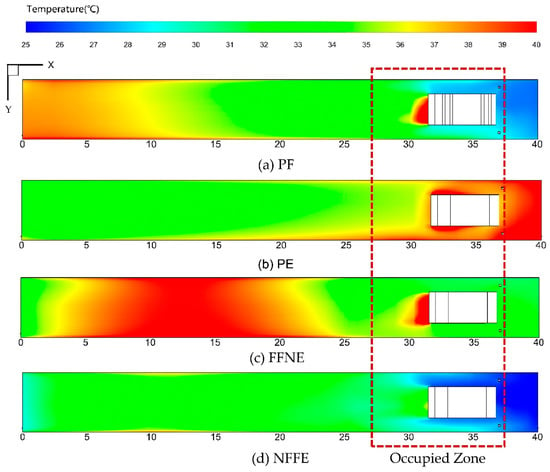
Figure 21.
Airflow temperature distributions of the four auxiliary ventilation systems.
Figure 22 shows the relative humidity distributions of the four auxiliary ventilation systems at the Plane B respectively. The average relative humidity is 56.4%, 62.1%, 42.6%, and 53.5% in the occupied zone, respectively. It can be concluded that when the overlap systems (FFNE and NFFE) is applied, the relative humidity of the airflow can be controlled to an optimal level. This is mainly due to the moist air being continuously migrated by the exhaust duct.
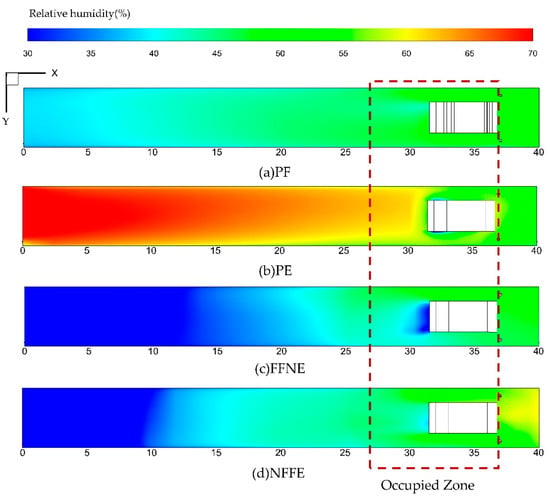
Figure 22.
Airflow relative humidity distributions of the four auxiliary ventilation systems.
Figure 23 presents the streamlines under the NFFE ventilation system. As can be seen, within the region of X = 20~30 m, the airflow is mainly subject to the negative pressure engulfment of the exhausting fan, supplemented by the positive pressure effect of the jet flow by the blowing fan. The engulfment confluence of the exhausting fan will be enhanced under the joint action of negative and positive pressure. This region can be defined as the effective engulfment region of the exhausting duct. As the working face is far from the forcing ventilation duct, the local eddy current can be generated at the interval of X = 30~35 m. Literature [30] indicates that it is beneficial to ventilation, since the circulating airflow can absorb a large amount of moisture, thus reducing the airflow temperature and humidity in the working face.
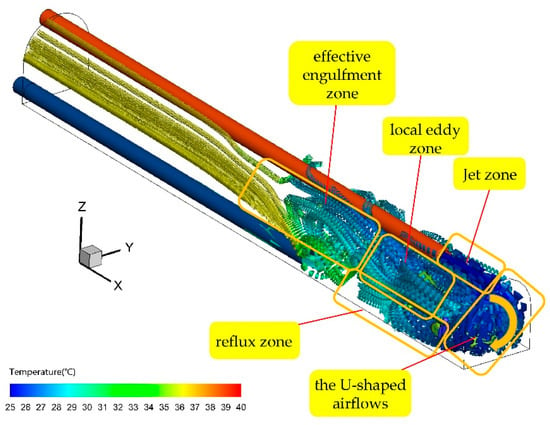
Figure 23.
Streamlines of the NFFE ventilation system.
Figure 24 illustrates the airflow temperature distributions in the plane B under the NFFE ventilation system and the different heat generations from LHD. Compared with Figure 18, it can be clearly observed that the NFFE ventilation system can remarkably reduce the temperature in the occupied zone.
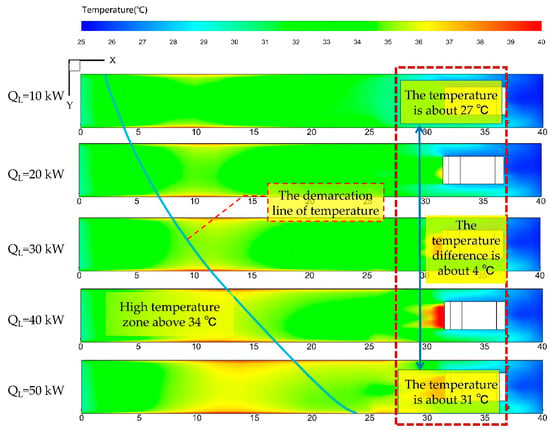
Figure 24.
Air temperature distributions in Plane B with different QL under the NFFE ventilation system.
5. Conclusions
This study suggests that, in the presence of ventilation barriers such as LHD, the blocking action of LHDs will have great influences on the airflow velocity field and temperature field. As a result, the influence of mechanical equipment like LHDs on the thermal environment should be taken into account when designing the local ventilation system.
In this case, the optimal ventilation duct position to achieve the optimal cooling effect is 5 m after simulating the airflow velocity, dry-bulb temperature, and relative humidity distributions under different distances between ventilation duct outlet to the mining face. Such results demonstrate that the optimal ventilation duct position should be explored for airways with different specifications to achieve the goal of energy conservation and environmental protection.
It can be clearly observed based on the simulation that the airflow temperature is increased with the increase of QL, indicating that the airflow temperature distribution is closely correlated with the heat emitted from the mechanical equipment. However, how to further improve the local ventilation cooling performance needs to be further investigated.
Finally, this study employs the NFFE ventilation pattern for numerical simulation and the results suggest that such ventilation patterns can remarkably reduce the temperatures in the occupied zone compared with the traditional ventilation pattern, thus achieving better energy utilization efficiency and cooling performance.
Author Contributions
W.Y. contributed to the conception of the study; W.W. and C.Z. provided the research data; G.Q. and C.L. analyzed the data; S.L. and H.X. helped perform the analysis with constructive discussions; W.W. and H.M. proposed the numerical simulation scheme and implemented; and W.W. and W.Y. wrote the paper.
Funding
This work has been funded by the National Natural Science Foundation of China, grant numbers 51804183, 51774197, and 51804185, Focus on Research and Development Plan in Shandong Province, grant number 2018GSF116012, the Natural Science Foundation of Shandong Province, grant number ZR2016EEP02 and Scientific Research Foundation of Shandong University of Science and Technology for Recruited Talents, grant number 2014RCJJ031.
Conflicts of Interest
We especially declare here this paper is not simultaneously submitted for publication elsewhere. There is no conflict of interest.
References
- Greth, A.; Roghanchi, P.; Kocsis, K. A review of cooling system practices and their applicability to deep and hot underground US mines. In Proceedings of the 16th North American Mine Ventilation Symposium, Golden, CO, USA, 17–22 June 2017; Volume 11, pp. 1–9. [Google Scholar]
- Kong, B.; Li, Z.H.; Wang, E.Y.; Yang, Y.L.; Chen, L.; Qi, G.S. An experimental study for characterization the process of coal oxidation and spontaneous combustion by electromagnetic radiation technique. Process Saf. Environ. Prot. 2018, 119, 285–294. [Google Scholar] [CrossRef]
- Kong, B.; Wang, E.Y.; Li, Z.H.; Lu, W. Study on the feature of electromagnetic radiation under coal oxidation and temperature rise based on multi-fractal theory. Fractals 2019, 27, 14–38. [Google Scholar]
- Lowndes, I.S.; Crossley, A.J.; Yang, Z.Y. The ventilation and climate modelling of rapid development tunnel drivages. Tunn. Undergr. Space Technol. 2004, 19, 139–150. [Google Scholar] [CrossRef]
- Yang, W.Y.; Inoue, M.; Miwa, S.H.; Kobayashi, Y. Heat form fragmented rock, explosives and diesel equipment in blind headings of underground mines. Mem. Fac. Eng. Kyushu Univ. 2013, 73, 13–26. [Google Scholar]
- Wala, A.M.; Vytla, S.; Taylor, C.D.; Huang, G. Mine face ventilation: A comparison of CFD results against benchmark experiments for the CFD code validation. Min. Eng. 2007, 59, 49–55. [Google Scholar]
- Glehn, F.H.V.; Bluhm, S.J. Practical aspects of the ventilation of high-speed developing tunnels in hot working environments. Tunn. Undergr. Space Technol. 2000, 15, 471–475. [Google Scholar] [CrossRef]
- Liu, C.Q.; Nie, W.; Bao, Q.; Liu, Q.; Wei, C.H.; Hua, Y. The effects of the pressure outlet’s position on the diffusion and pollution of dust in tunnel using a shield tunneling machine. Energy Build. 2018, 176, 232–245. [Google Scholar] [CrossRef]
- Lowndes, I.S.; Yang, Z.Y.; Jobling, S.; Yates, C. A parametric analysis of a tunnel climatic prediction and planning model. Tunn. Undergr. Space Technol. 2006, 21, 520–532. [Google Scholar] [CrossRef]
- Shimada, S.; Ohmura, S. Experimental study on cooling of heading face by local ventilation. Shigen-to-Sozai 1990, 106, 725–729. [Google Scholar] [CrossRef]
- Jia, M.T.; Chen, Y.H.; Wu, L.J.; Wang, S.; Qi, C.G. The heat exchange simulation test platform for deep excavation roadway in metal mine. Met. Mine 2014, 461, 113–116. [Google Scholar]
- Sasmito, A.P.; Kurnia, J.C.; Birgersson, E.; Mujumdar, A.S. Computational evaluation of thermal management strategies in an underground mine. Appl. Therm. Eng. 2015, 90, 1144–1150. [Google Scholar] [CrossRef]
- Gao, J.L.; Uchino, K.; Inoue, M. Simulation of Thermal Environmental Conditions in heading face with Forcing Auxiliary Ventilation-control of thermal environmental conditions in locally ventilated working face. Shigen-to-Sozai 2002, 118, 9–15. [Google Scholar] [CrossRef][Green Version]
- Hua, Y.; Nie, W.; Wei, W.L.; Liu, Q.; Liu, Y.H.; Peng, H.T. Research on multi-radial swirling flow for optimal control of dust dispersion and pollution at a fully mechanized tunnelling face. Tunn. Undergr. Space Technol. 2018, 79, 293–303. [Google Scholar] [CrossRef]
- Zhou, G.; Feng, B.; Yin, W.J.; Wang, J.Y. Numerical simulations on airflow-dust diffusion rules with the use of coal cutter dust removal fans and related engineering applications in a fully-mechanized coal mining face. Powder Technol. 2018, 339, 354–367. [Google Scholar] [CrossRef]
- Cai, P.; Nie, W.; Chen, D.W.; Yang, S.B.; Liu, Z.Q. Effect of airflow rate on pollutant dispersion pattern of coal dust particles at fully mechanized mining face based on numerical simulation. Fuel 2019, 239, 623–635. [Google Scholar] [CrossRef]
- Torano, J.; Torno, S.; Menendez, M.; Gent, M. Auxiliary ventilation in mining roadways driven with roadheaders: Validated CFD modelling of dust behaviour. Tunn. Undergr. Space Technol. 2011, 26, 201–210. [Google Scholar] [CrossRef]
- Ren, T.; Wang, Z.; Cooper, G. CFD modelling of ventilation and dust flow behaviour above an underground bin and the design of an innovative dust mitigation system. Tunn. Undergr. Space Technol. 2014, 41, 241–254. [Google Scholar] [CrossRef]
- Cheng, W.M. Mining Ventilation and Safety; China Coal Industry Publishing House: Beijing, China, 2016. [Google Scholar]
- McPherson, M.J. Subsurface Ventilation and Environmental Engineering; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. Simulation of a novel intermittent ventilation system for underground mines. Tunn. Undergr. Space Technol. 2014, 42, 206–215. [Google Scholar] [CrossRef]
- Shim, B.O.; Park, J.M.; Kim, H.C.; Lee, Y. Statistical Analysis on the Thermal Conductivity of Rocks in the Republic of Korea. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–30 April 2010. [Google Scholar]
- Mao, N.; Pan, D.; Deng, S.; Chan, M. Thermal, ventilation and energy saving performance evaluations of a ductless bed-based task/ambient air conditioning (TAC) system. Energy Build. 2013, 66, 297–305. [Google Scholar] [CrossRef]
- Parra, M.T.; Villafruela, J.M.; Castro, F.; Mendez, C. Numerical and experimental analysis of different ventilation systems in deep mines. Build. Environ. 2006, 41, 87–93. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Birgersson, E.; Ly, H.C.; Mujumdar, A.S. Some approaches to improve ventilation system in underground coal mines environment—A computational fluid dynamic study. Tunn. Undergr. Space Technol. 2013, 34, 82–95. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Xu, P.; Sasmito, A.P. A novel concept of enhanced gas recovery strategy from ventilation air methane in underground coal mines—A computation investigation. J. Natl. Gas Sci. Eng. 2016, 35, 661–672. [Google Scholar] [CrossRef]
- Yang, L.X. Modern Tunwnel Construction Ventilation Technology; China Communications Press: Beijing, China, 2012. [Google Scholar]
- Mkhwanazi, D. Optimizing LHD utilization. South. Afr. Inst. Min. Metall. 2011, 111, 273–280. [Google Scholar]
- Liu, W.W.; Lian, Z.W.; Yao, Y. Optimization on indoor air diffusion of floor-standing type room air-conditioners. Energy Build. 2008, 40, 59–70. [Google Scholar] [CrossRef]
- Ren, T.; Wang, Z.W. CFD modelling of ventilation, dust and gas flow dispersion patterns on a longwall face. In Proceedings of the 11th International Mine Ventilation Congress; Springer: Singapore, 2019. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).