Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation
Abstract
1. Introduction
2. Problem Formulation
2.1. Continuity Equation:
2.2. Momentum Equation
2.3. Equation of Thermal Energy
2.4. Equation of Mass Transfer
3. Parameters of Interest
3.1. Skin Friction
3.2. Nusselt Number
3.3. Sherwood Number
4. Entropy Analysis and Its Mathematical Description
5. Solution by HAM
6. HAM Solution Convergence
7. Results and Discussion
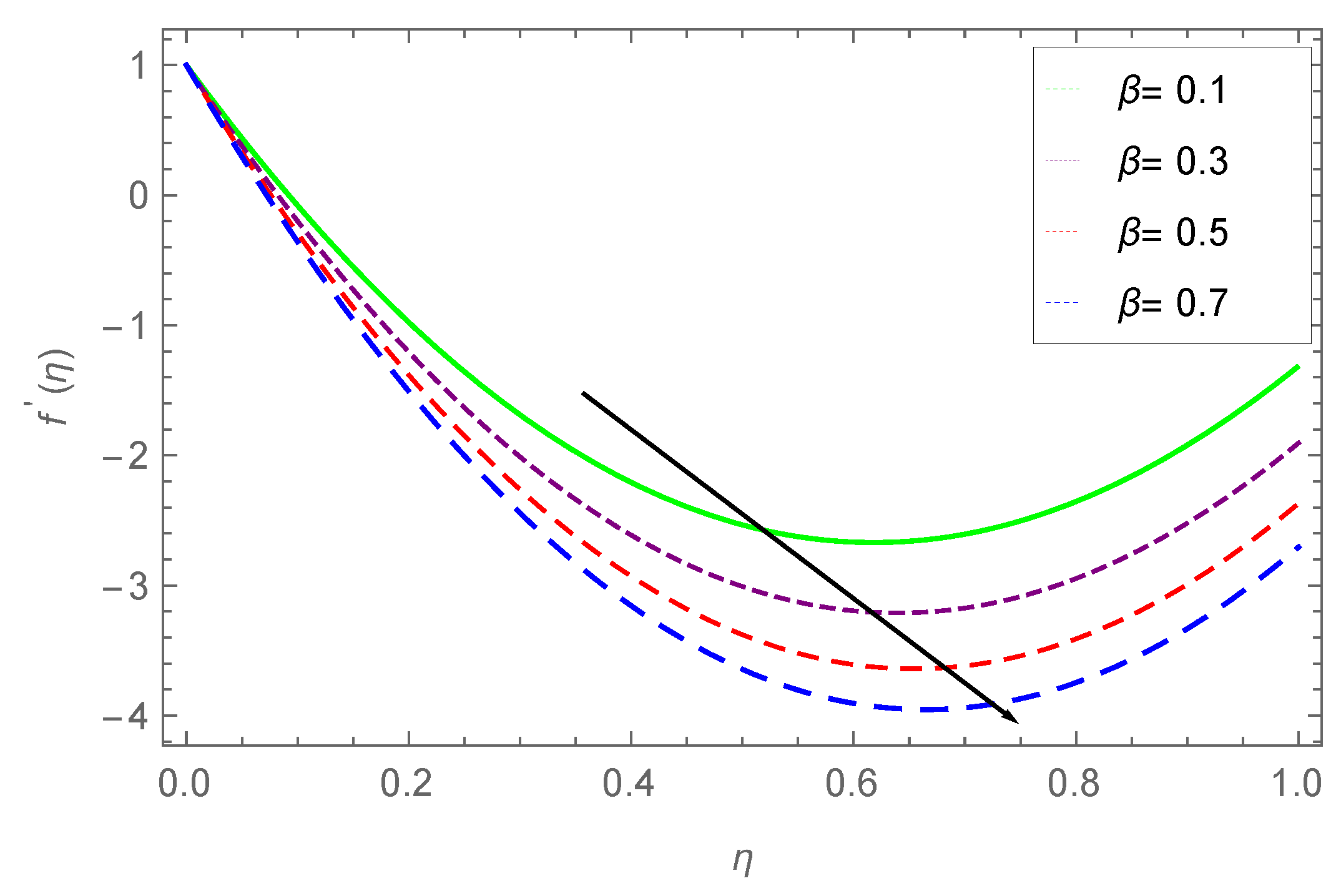
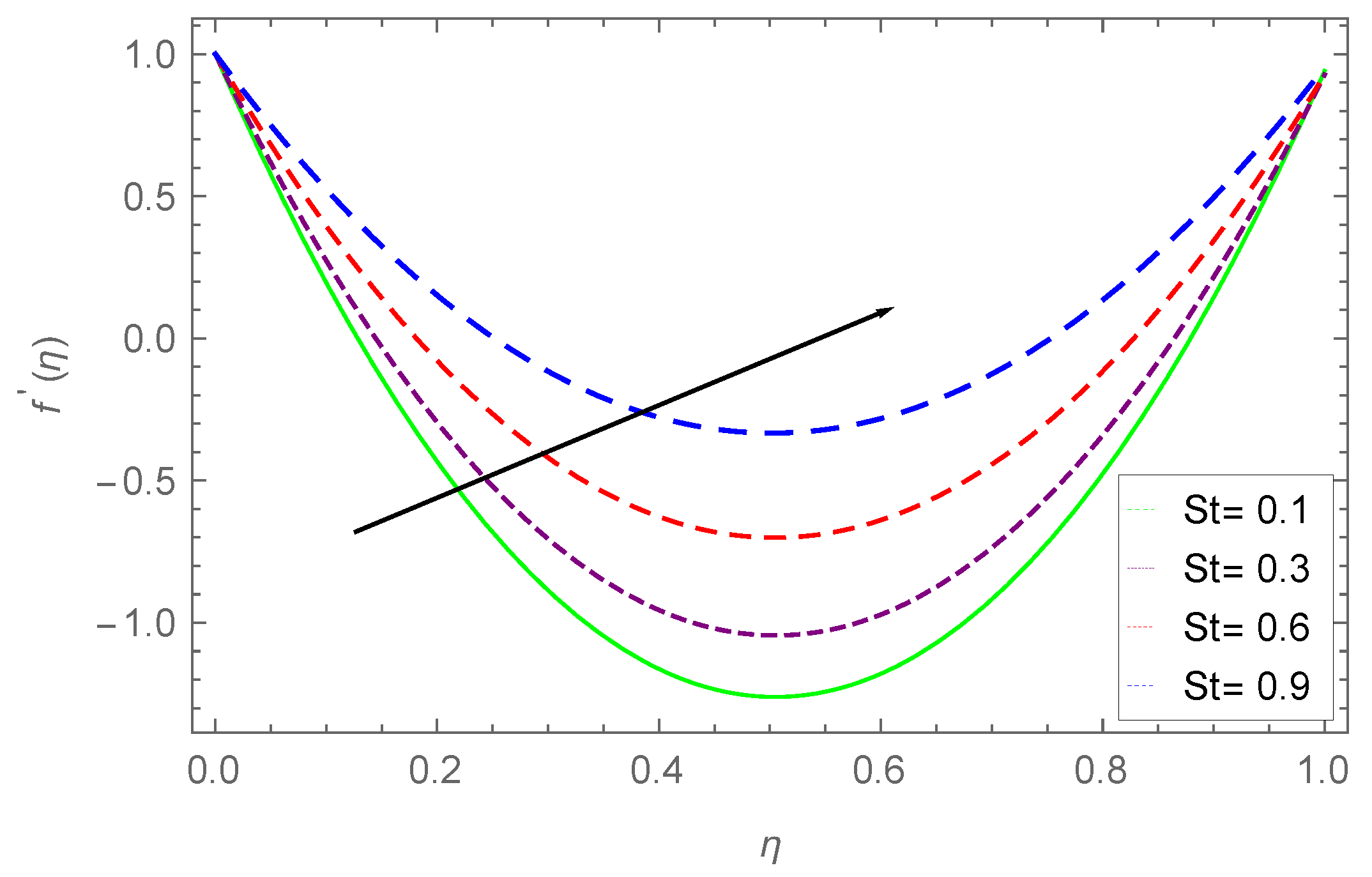
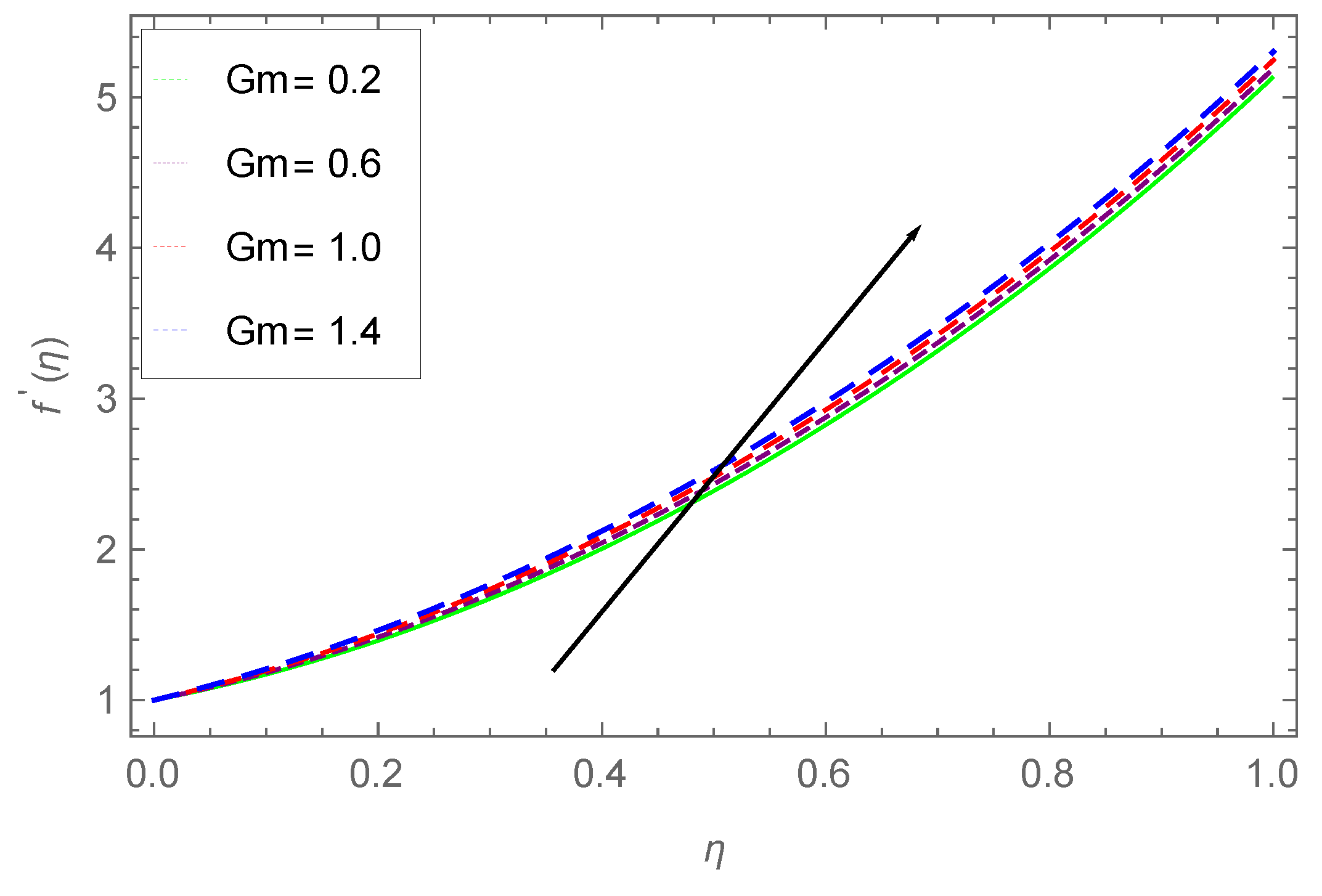
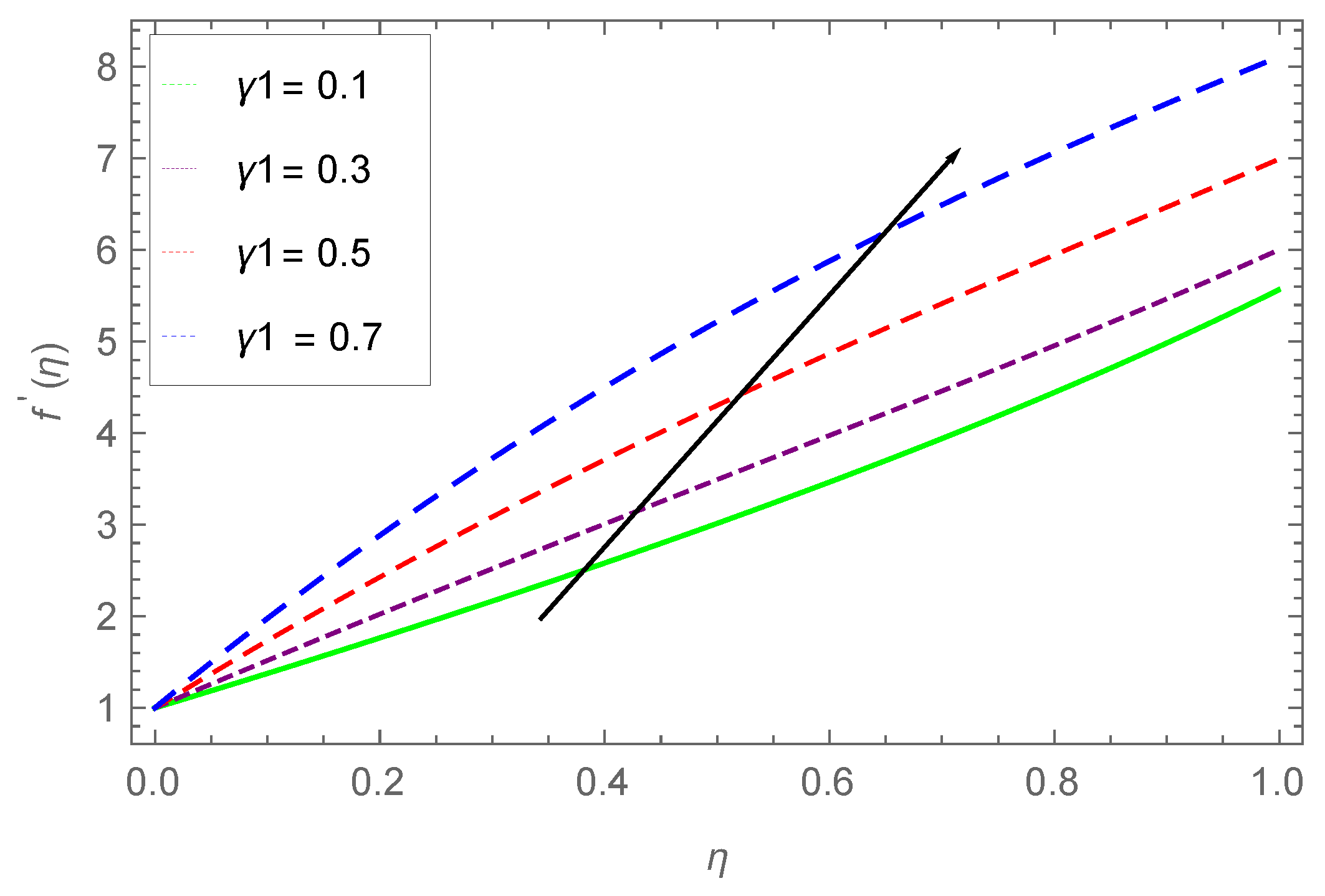
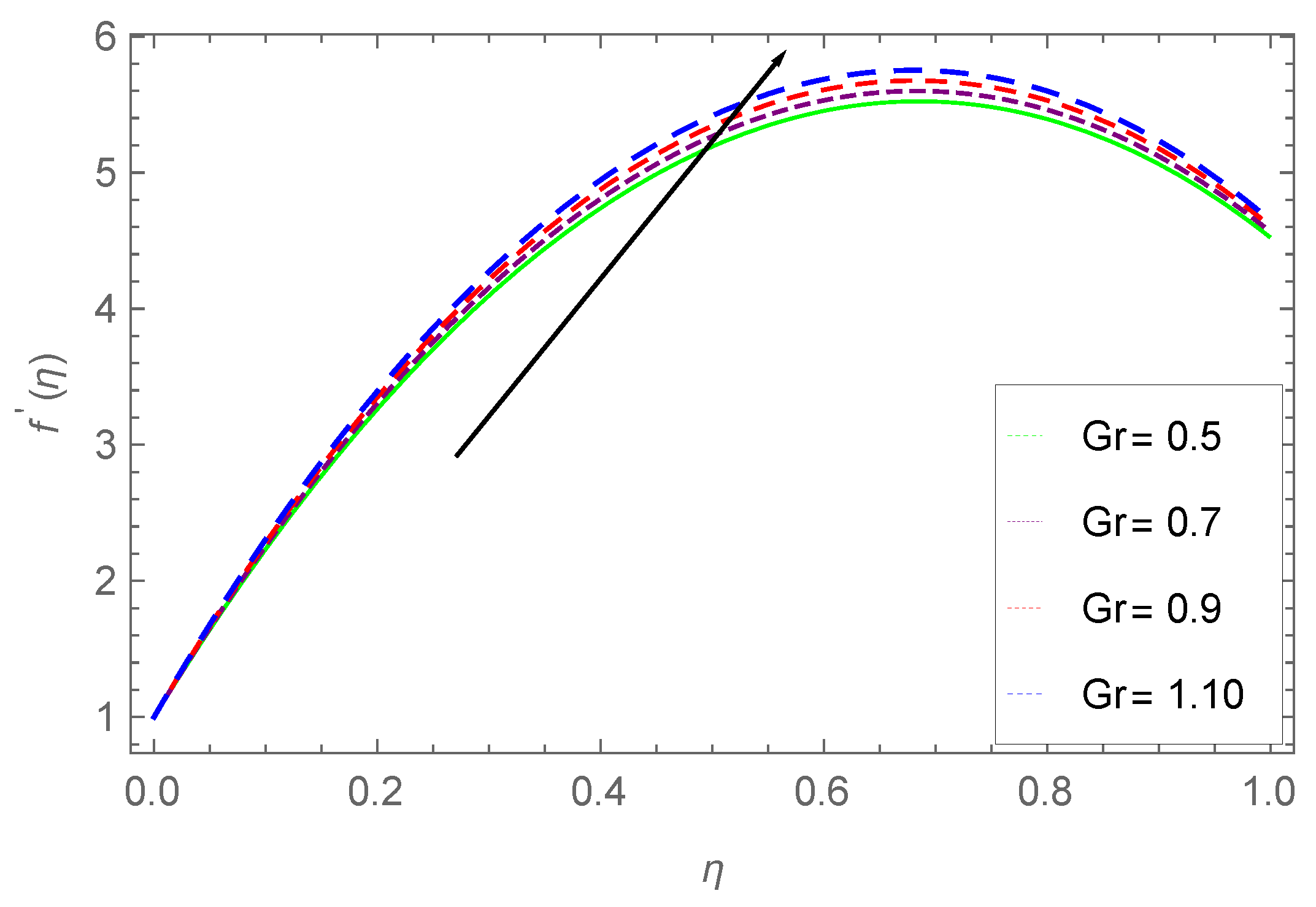
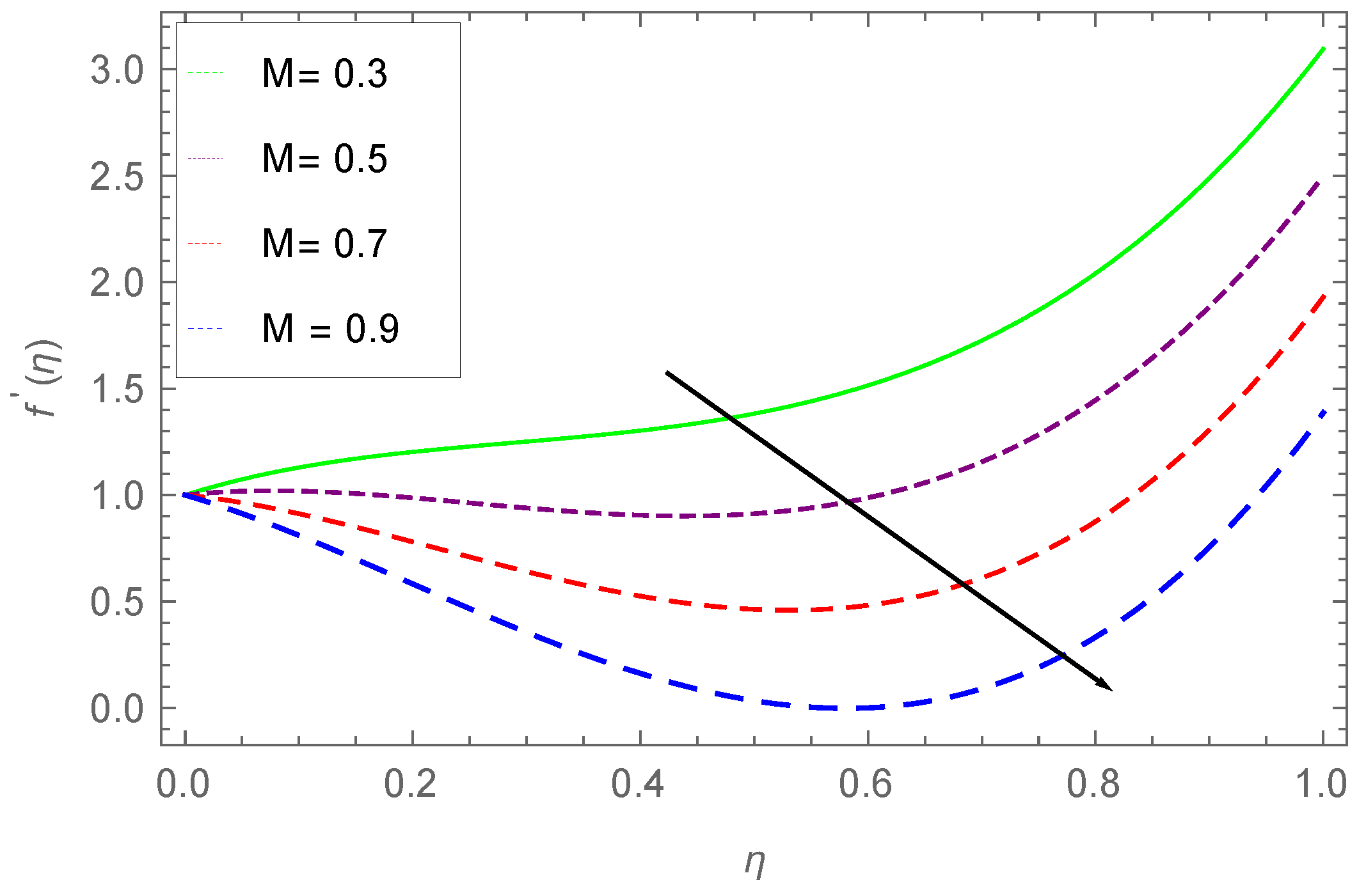
7.1. Velocity Profile
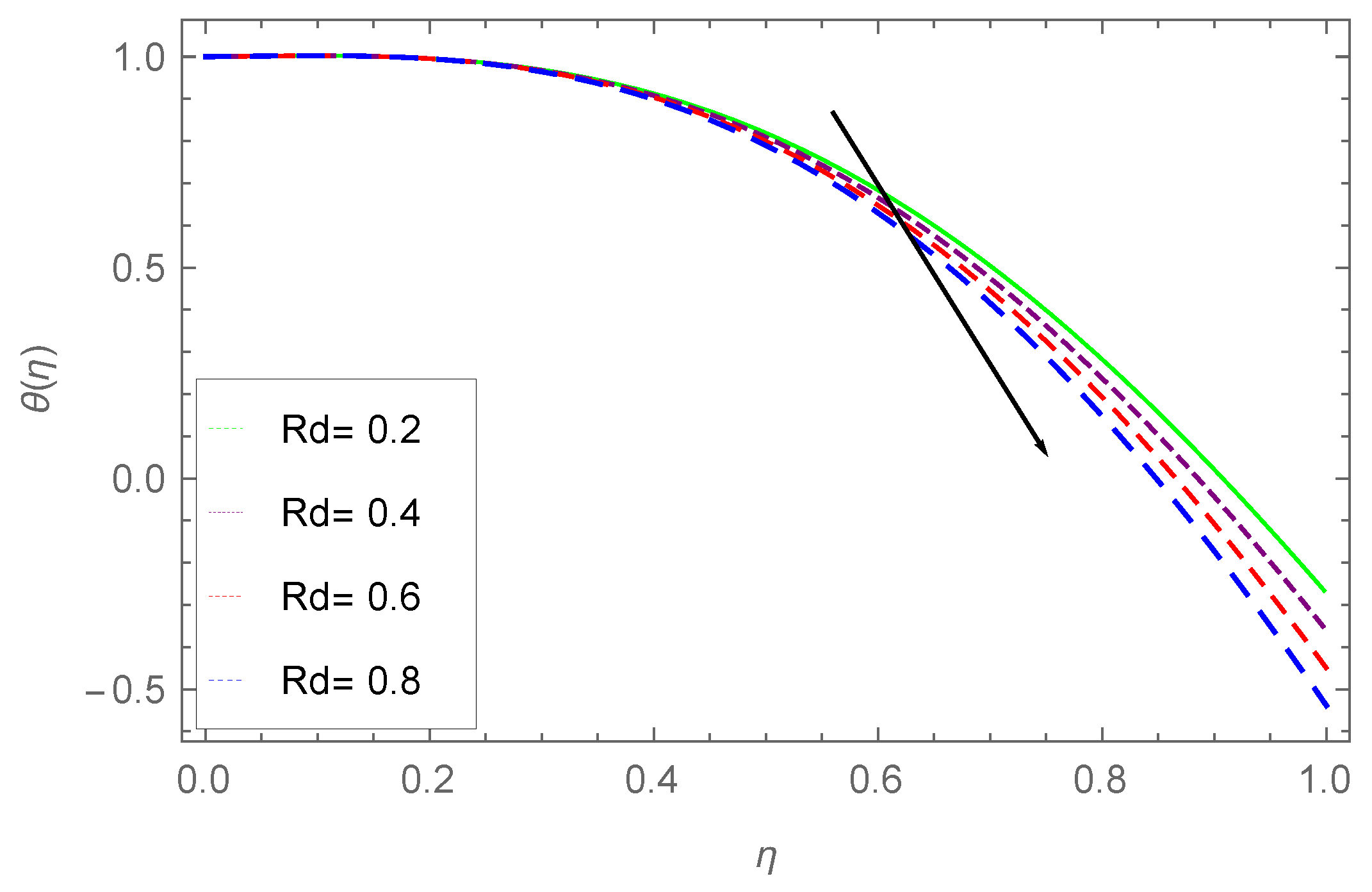
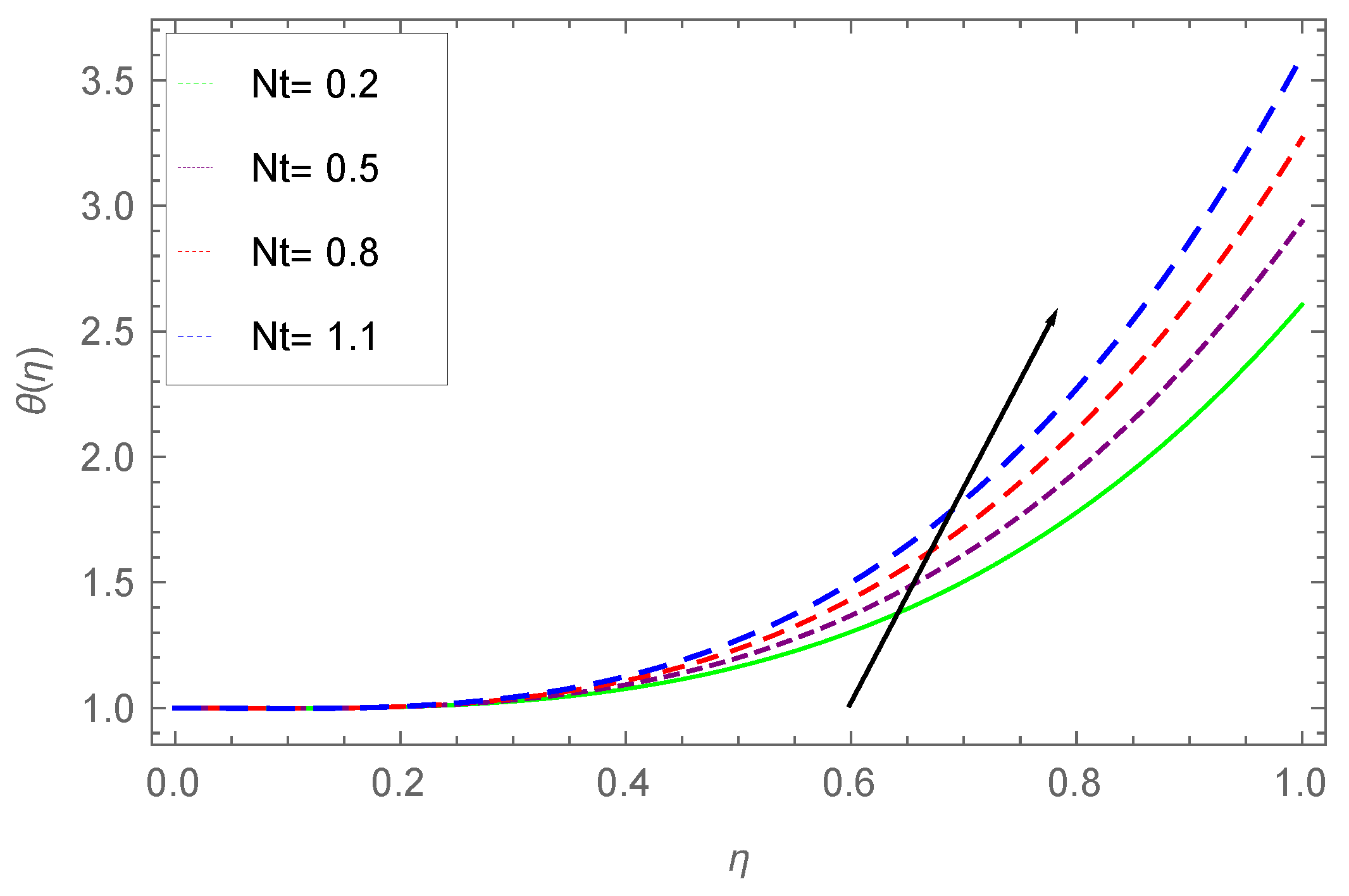
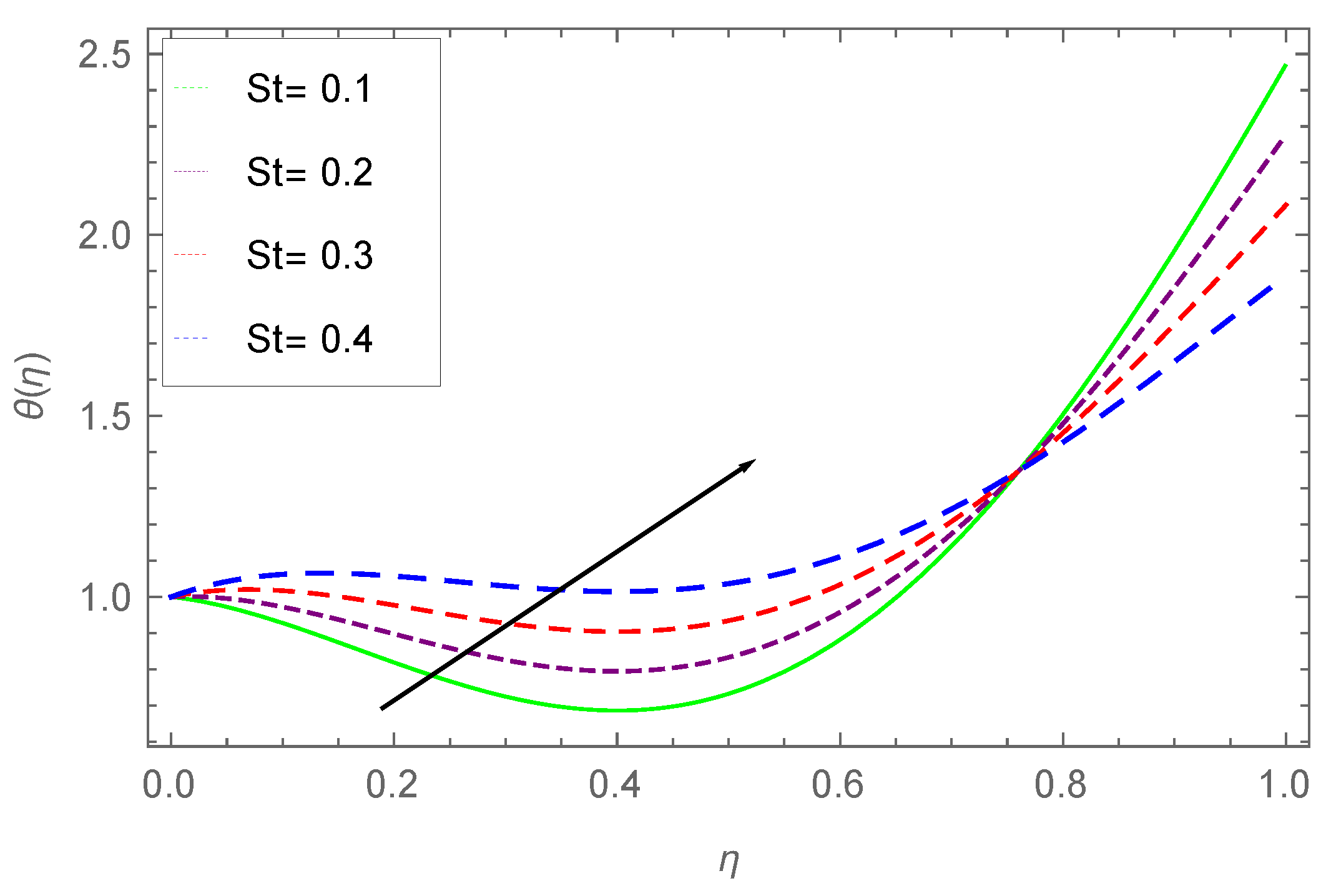
7.2. Temperature Profile
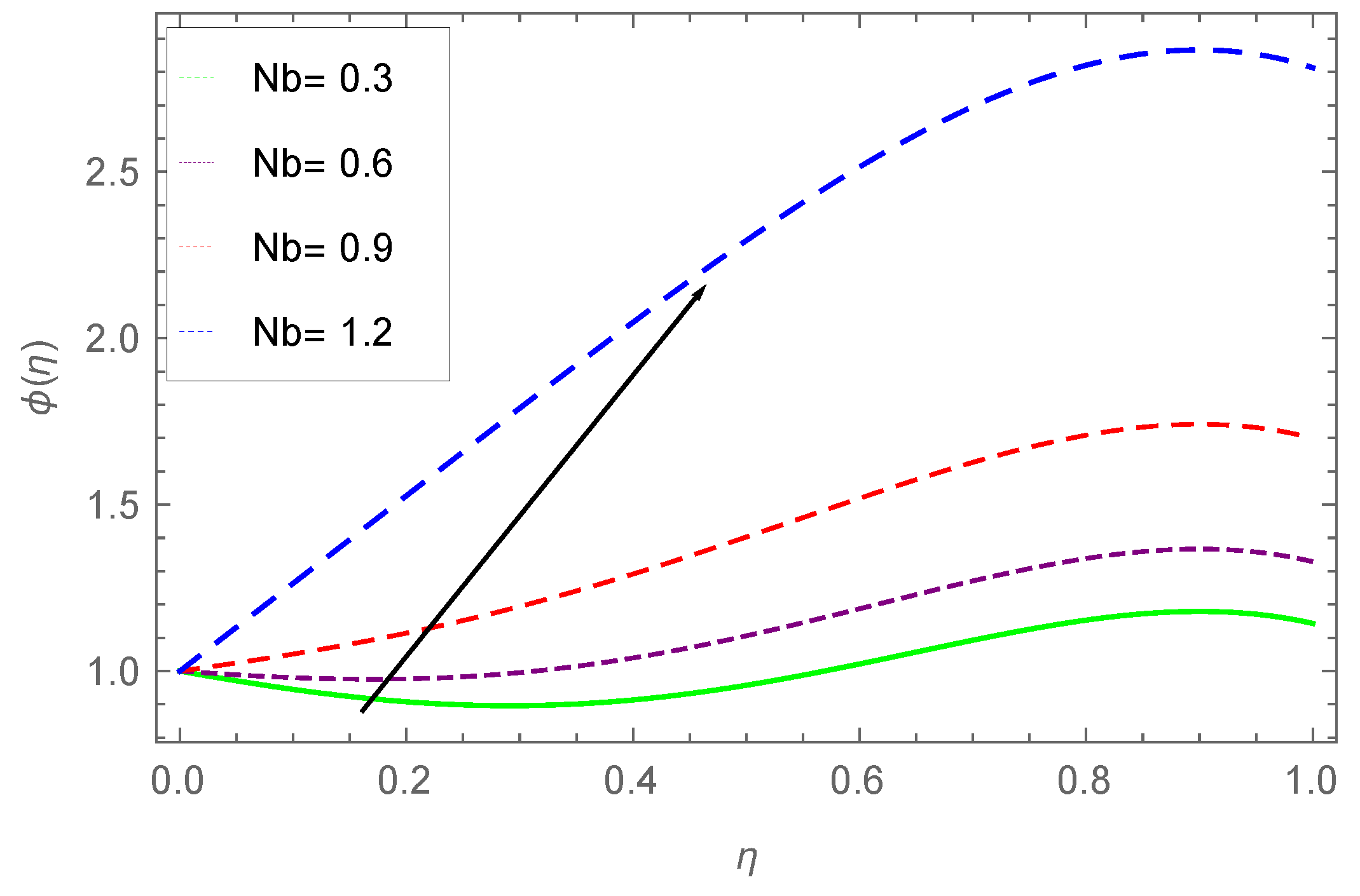
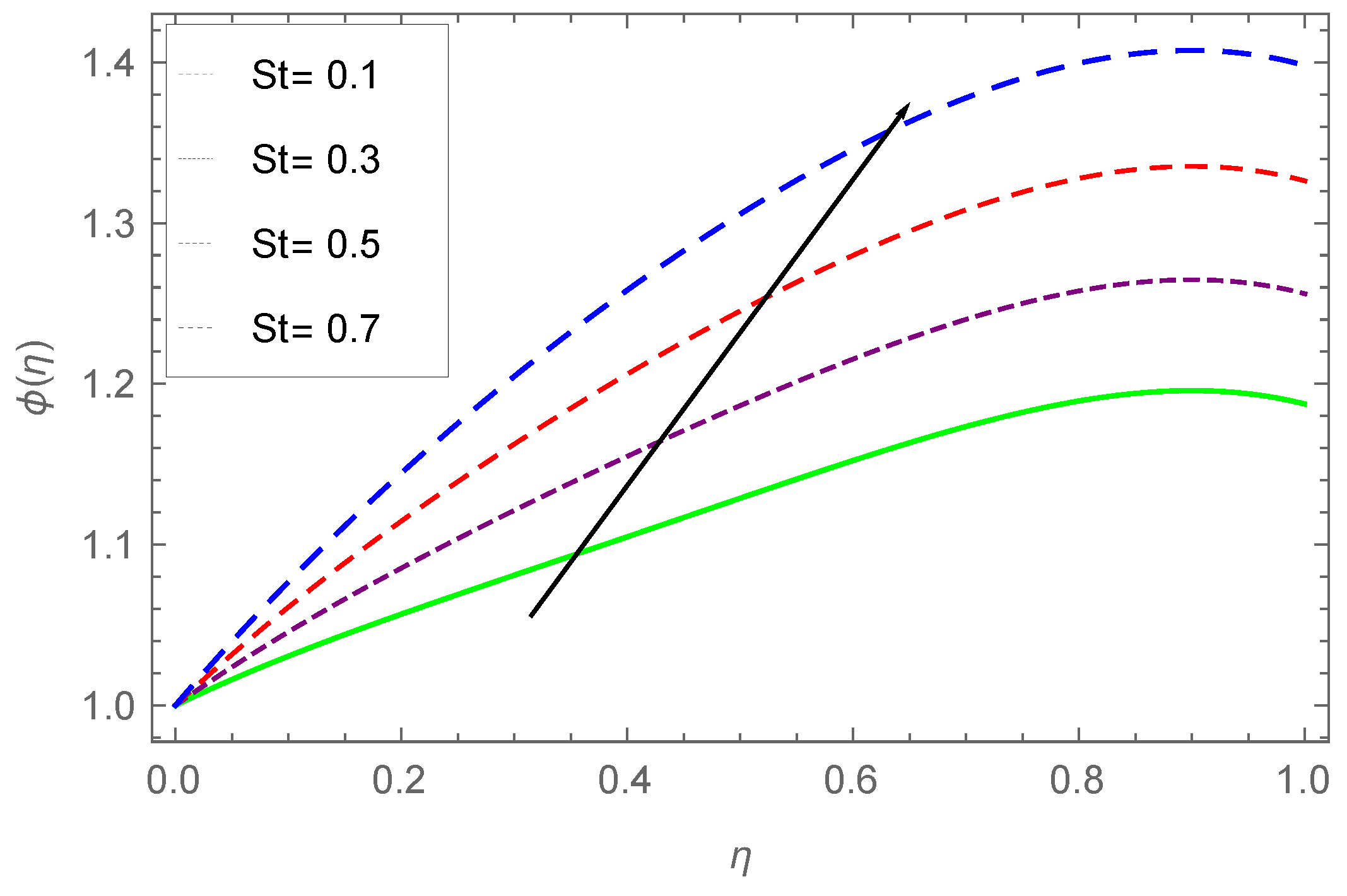
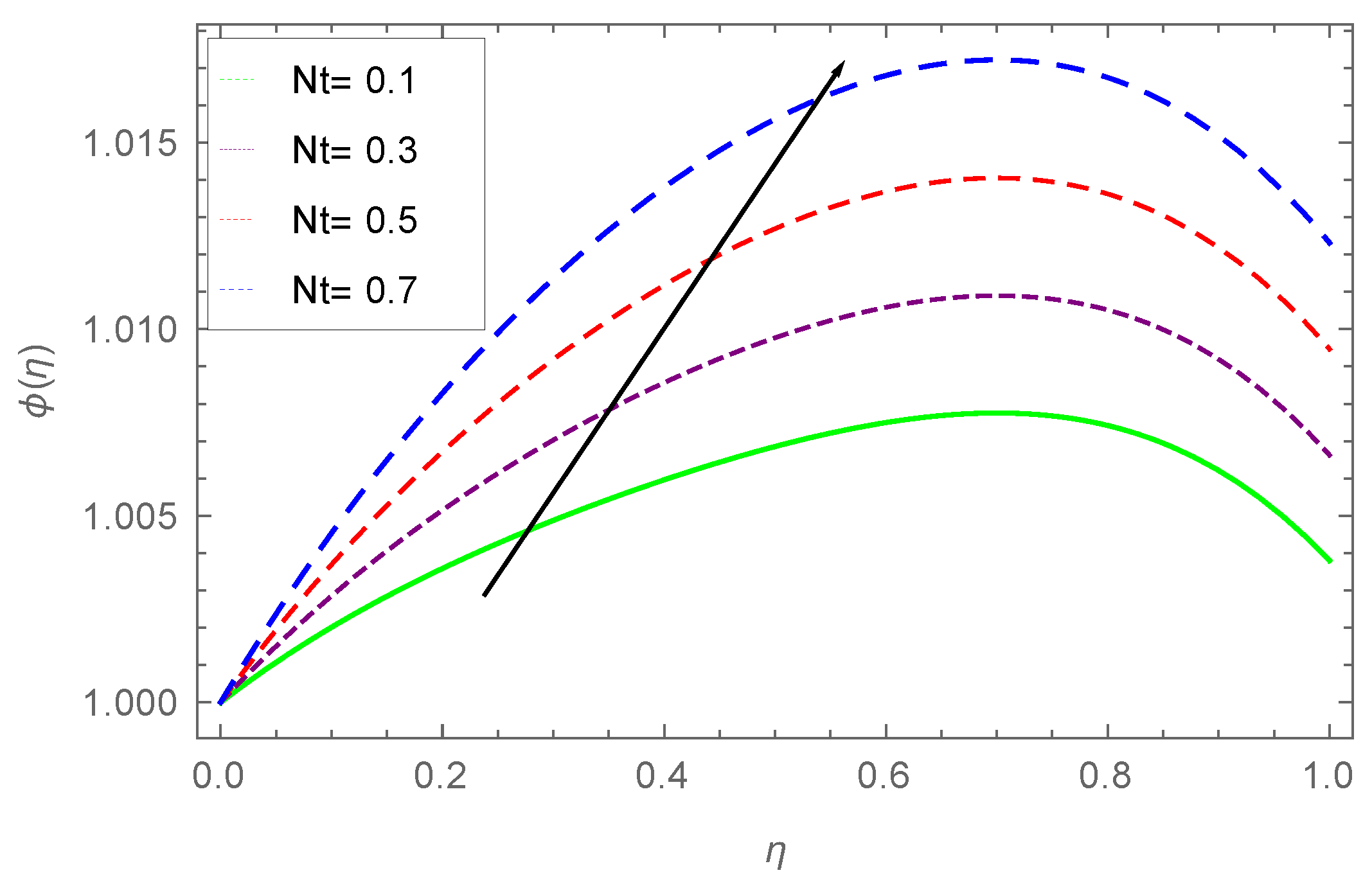
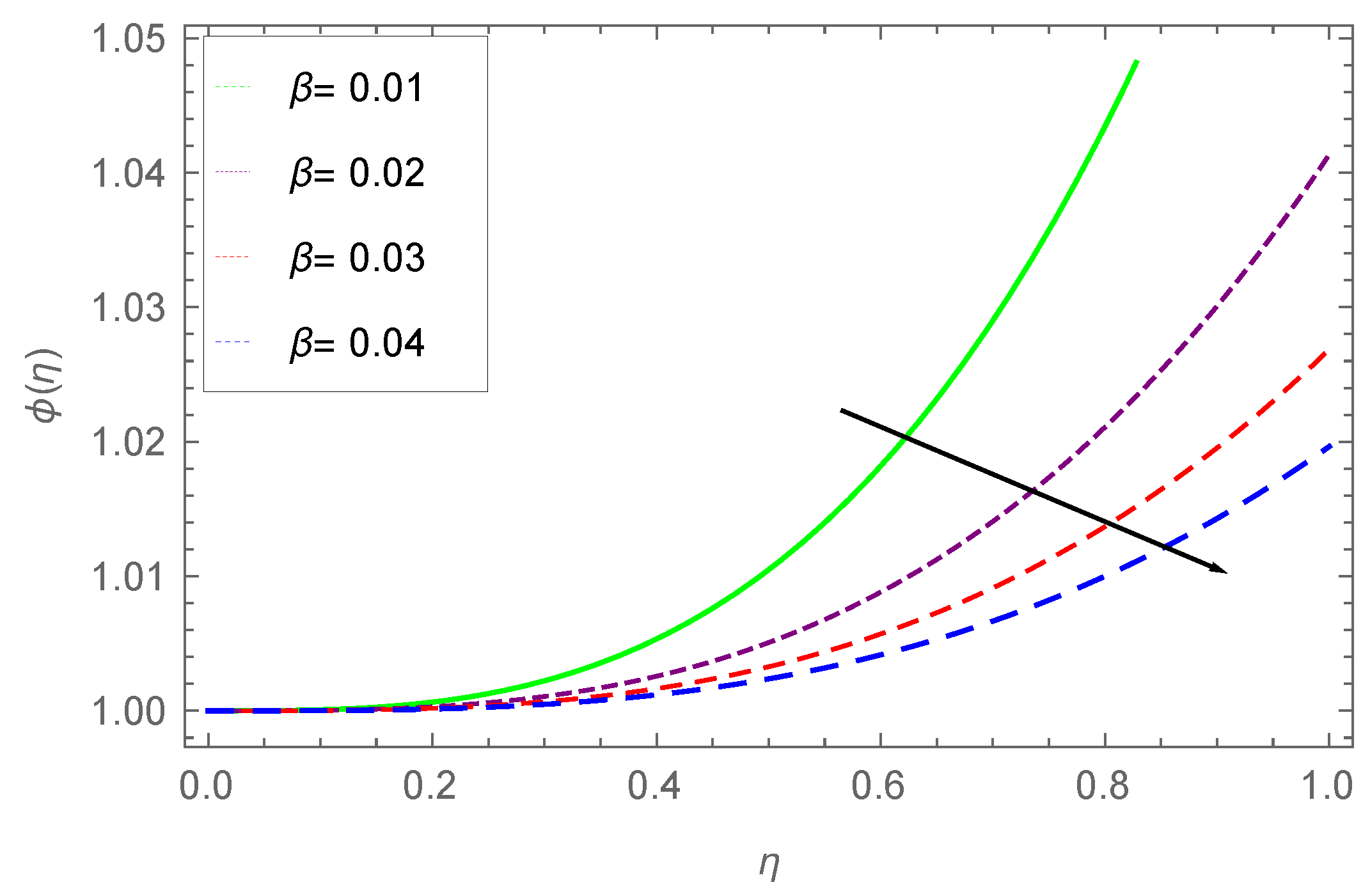
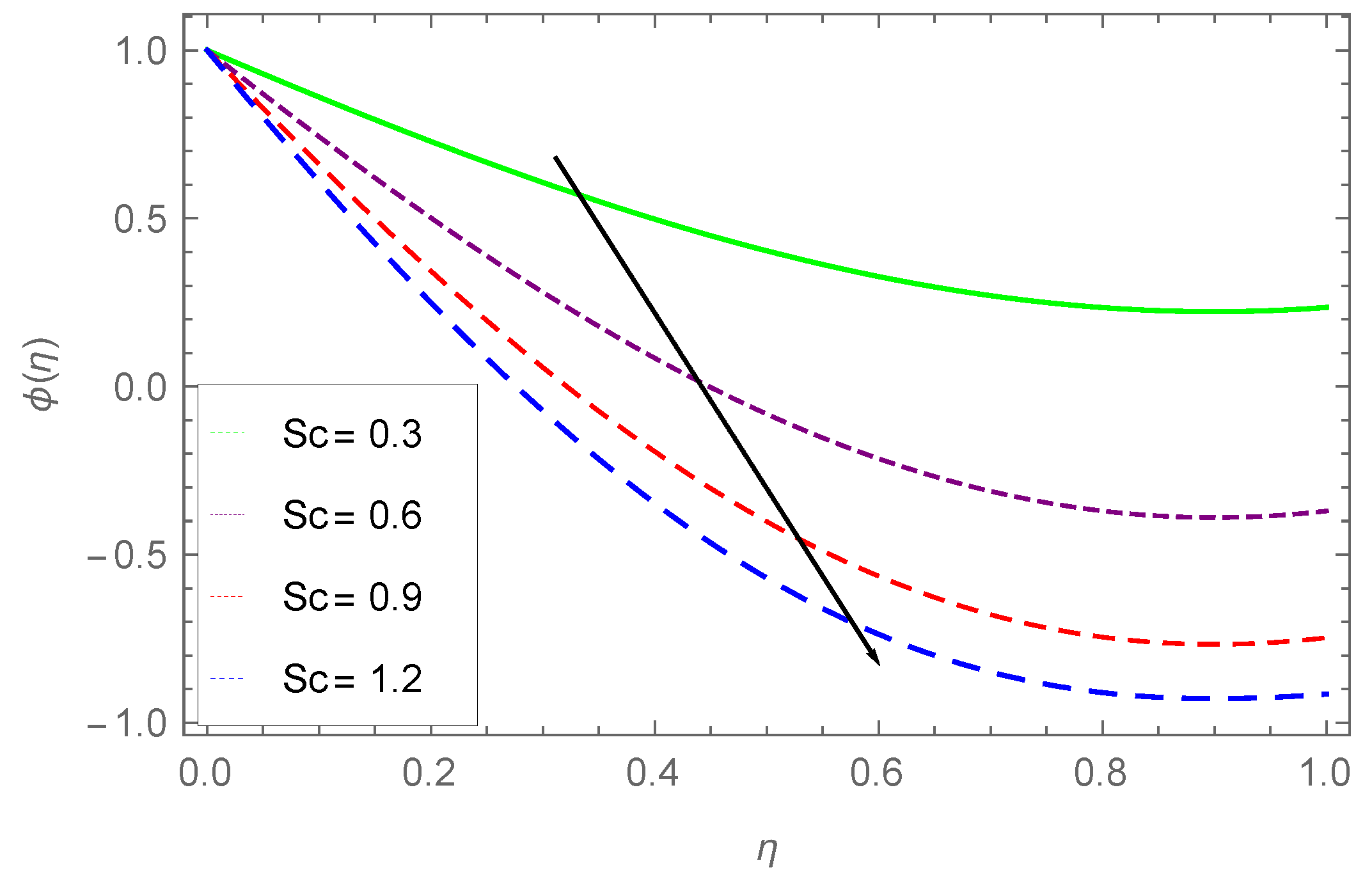
7.3. Concentration Profile
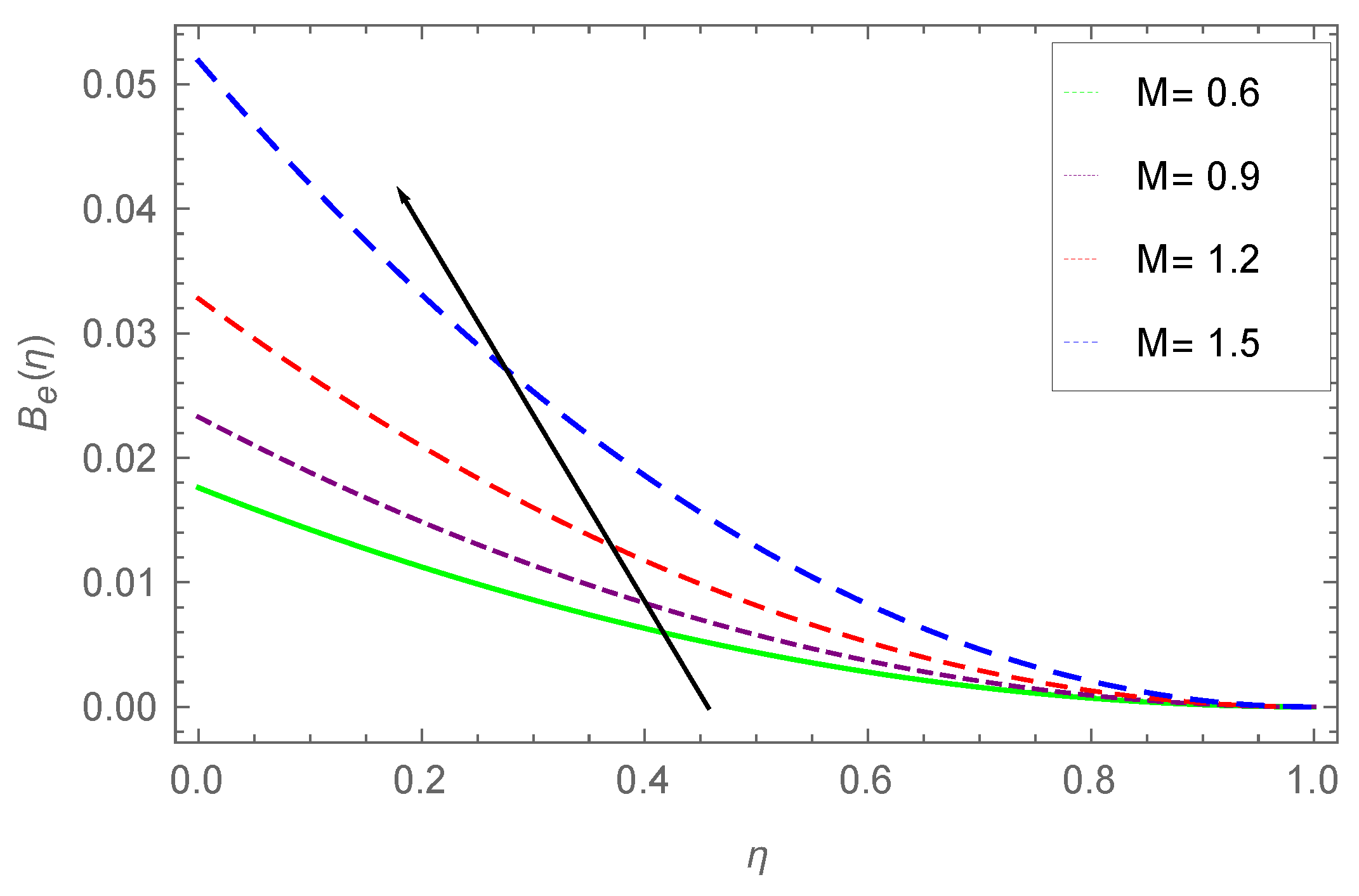
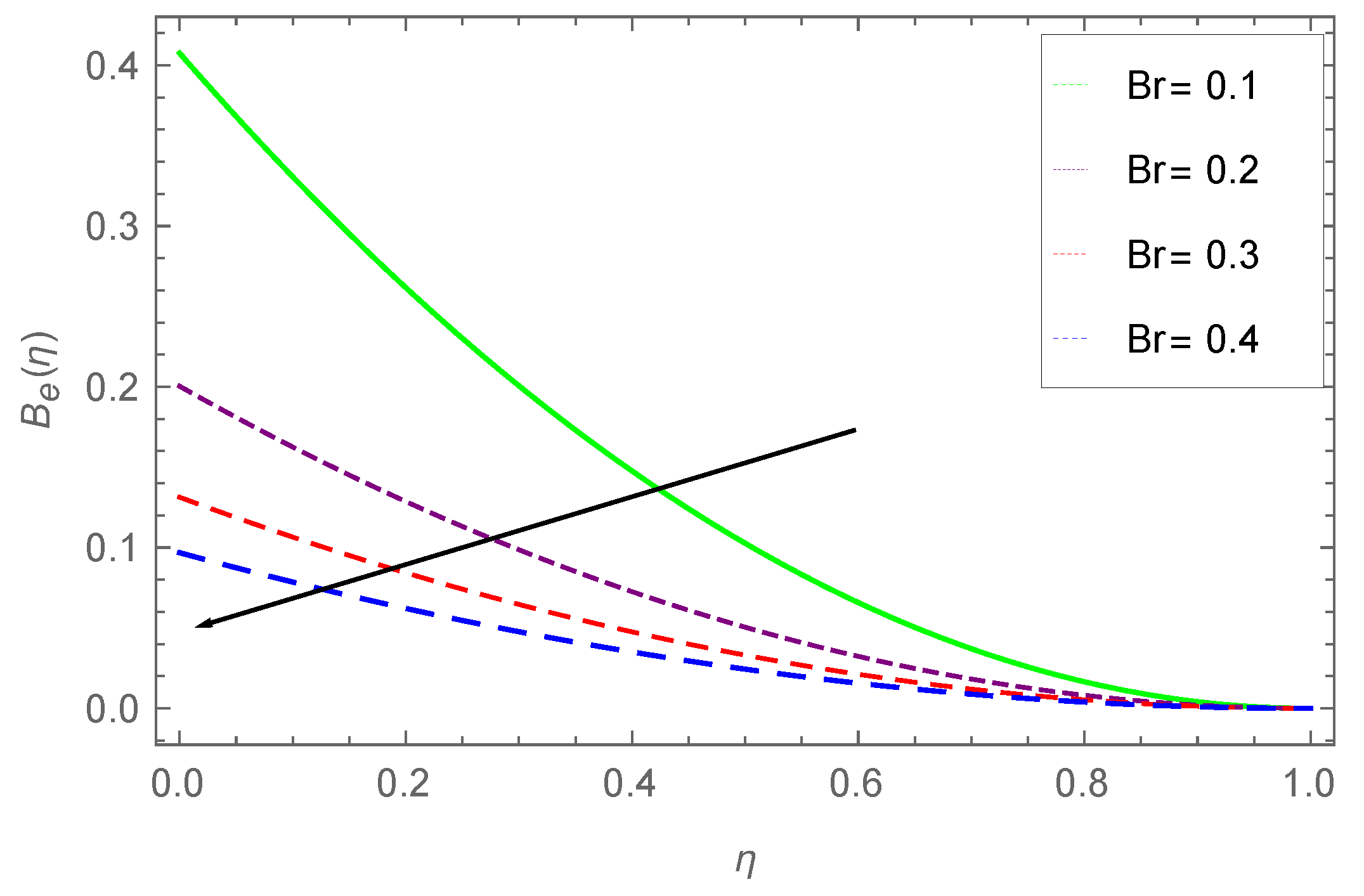
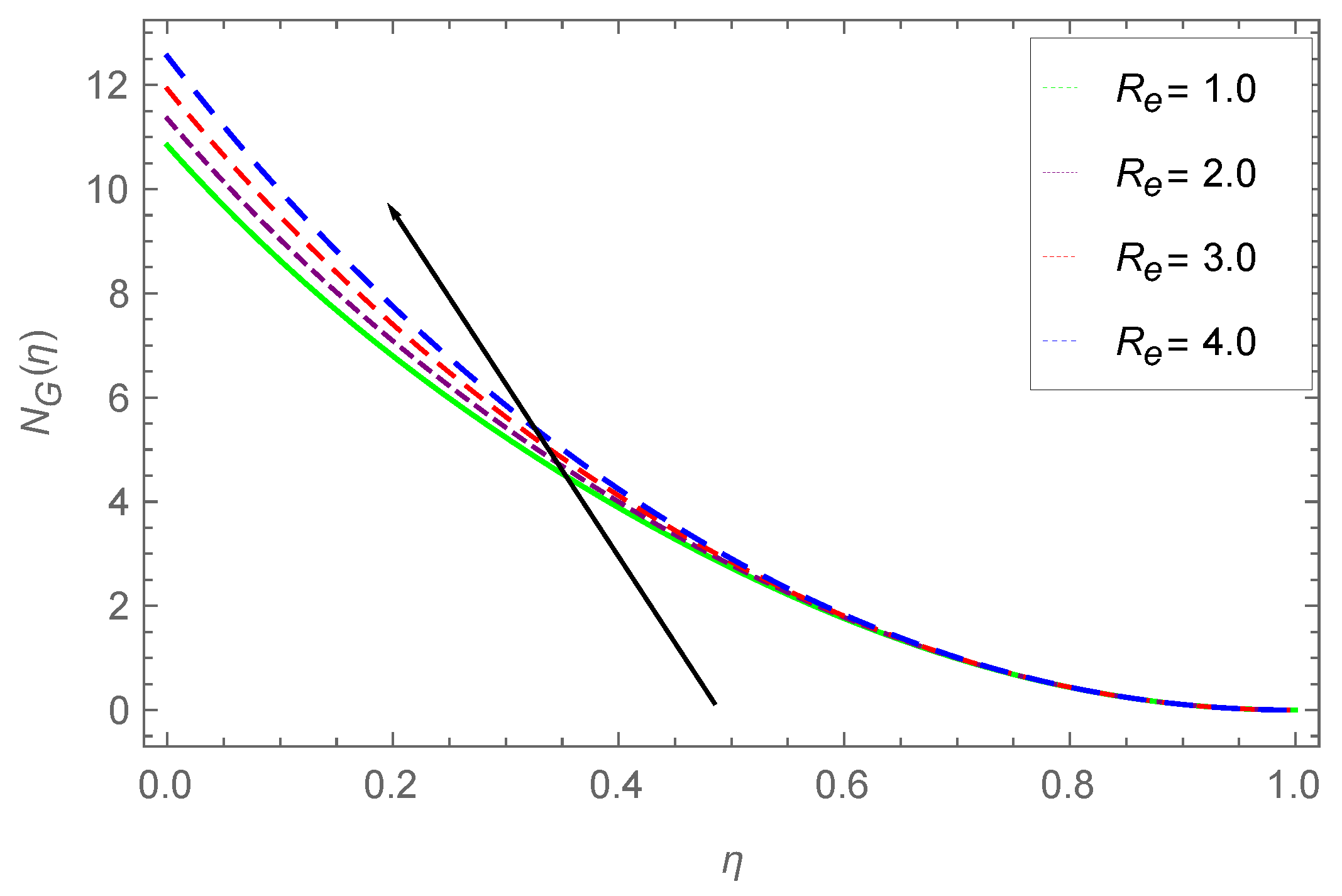
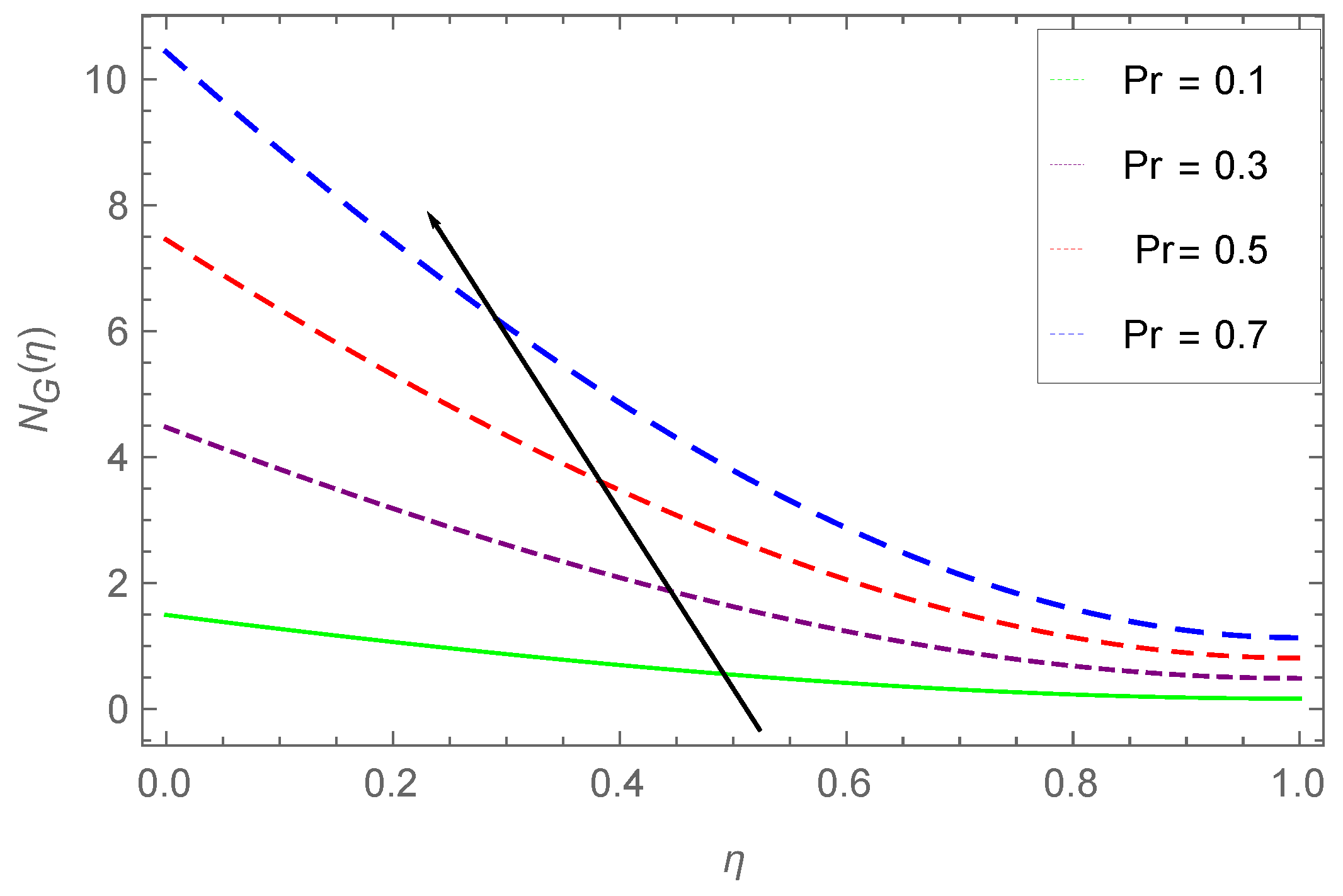
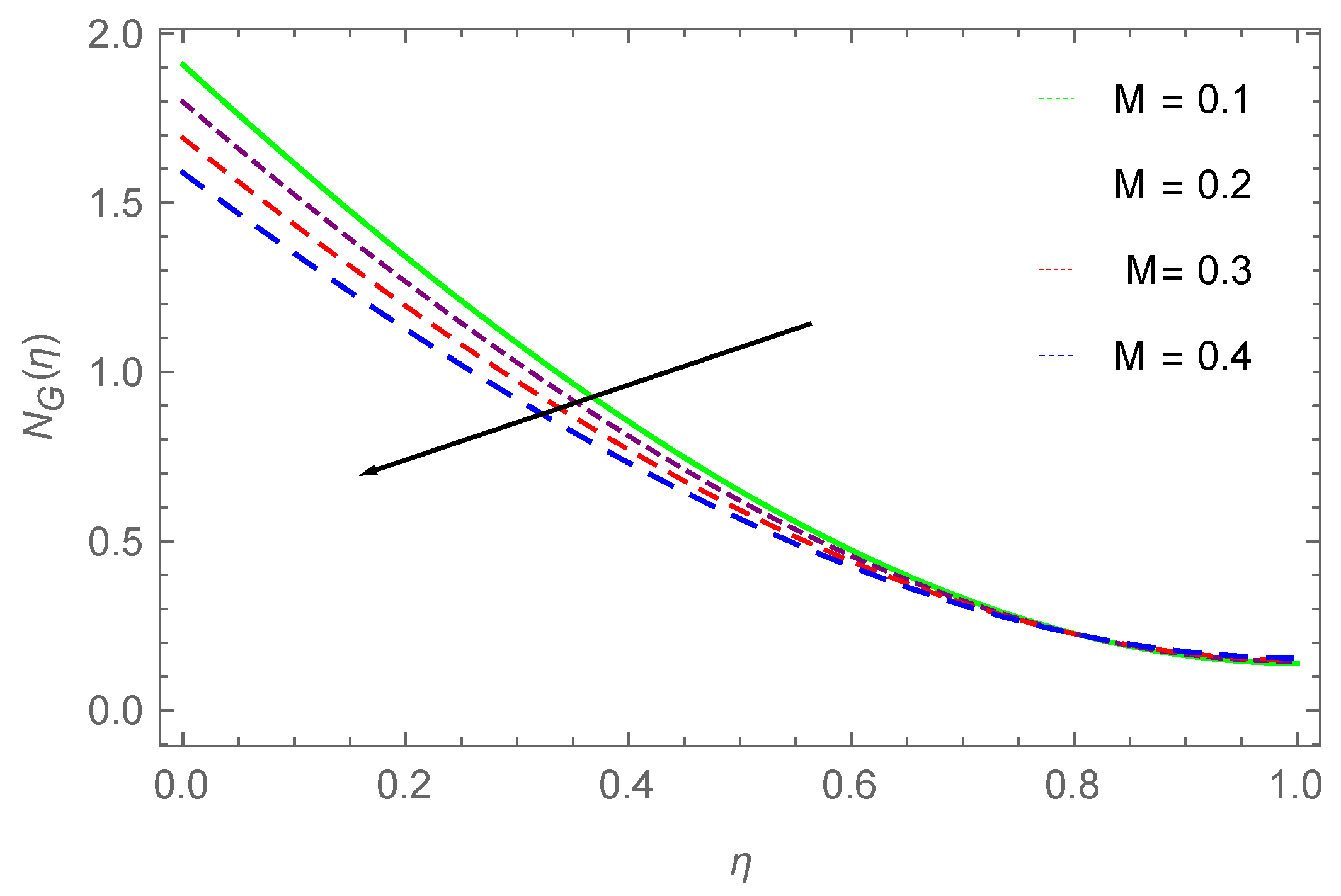
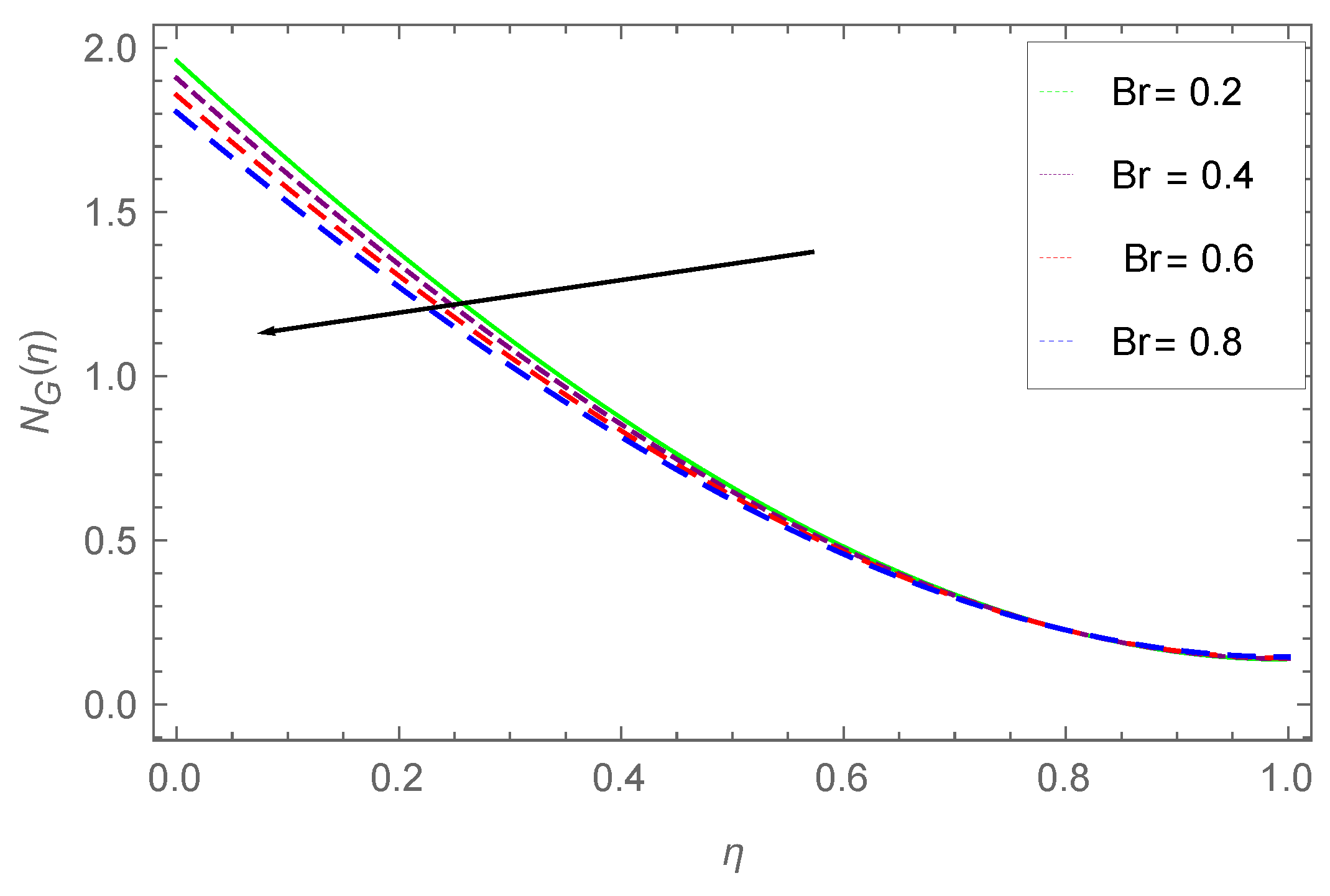
7.4. Entropy Profile
7.5. Table Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Sherwood number | |
| Film thickness parameter | |
| Nusselt number | |
| Unsteady parameter | |
| Reynolds number | |
| Prandtl number | |
| Stretching parameter | |
| Schmidt number | |
| Stretching velocity () | |
| Thermophoretic parameter | |
| Skin-friction coefficient | |
| Brownian motion parameter | |
| Cauchy stress tensor | |
| T | Fluid temperature |
| I | Identity tensor |
| Kinematic viscosity | |
| Density | |
| Dynamic viscosity | |
| Specific heat | |
| Thickness of liquid | |
| Heat Flux ) | |
| Mass flux | |
| f | Dimensionless velocity |
| ∞ | Condition at infinity |
| 0 | Reference condition |
| Velocity component in direction | |
| Velocity component in direction | |
| Coordinates | |
| Similarity variable | |
| t | Time () |
| Frequency parameter | |
| , and | Revilin Erickson Tensor |
| E | Electric Field |
| Non-Newtonian Parameter | |
| Magnetic Permeability | |
| and | Material constants |
| Mixing parameter | |
| Electric conductivity | |
| J | Current density |
References
- Myers, T. Application of non-Newtonian models to thin film flow. Phys. Rev. E 2005, 72, 066302. [Google Scholar] [CrossRef] [PubMed]
- Marinca, V.; Herişanu, N.; Nemeş, I. Optimal homotopy asymptotic method with application to thin film flow. Open Phys. 2008, 6, 648–653. [Google Scholar] [CrossRef]
- Sandeep, N.; Malvandi, A. Enhanced heat transfer in liquid thin film flow of non-Newtonian nanofluids embedded with graphene nanoparticles. Adv. Powder Technol. 2016, 27, 2448–2456. [Google Scholar] [CrossRef]
- Wang, C. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar]
- Usha, R.; Sridharan, R. On the motion of a liquid film on an unsteady stretching surface. ASME Fluids Eng. 1993, 150, 43–48. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, H.I. Heat transfer in a liquid film on an unsteady stretching sheet. Int. J. Therm. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Alomari, A. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica 2011, 46, 349–357. [Google Scholar] [CrossRef]
- Tawade, L.; Abel, M.; Metri, P.G.; Koti, A. Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation, internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 2016, 3, e40. [Google Scholar]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat transfer in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Chen, C.H. Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat Mass Transf. 2003, 39, 791–796. [Google Scholar] [CrossRef]
- Chen, C.H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Ishaq, M.; Ali, G.; Shah, S.I.A.; Shah, Z.; Muhammad, S.; Hussain, S.A. Nanofluid Film Flow of Eyring Powell Fluid with Magneto Hydrodynamic Effect on Unsteady Porous Stretching Sheet. J. Math. 2019, 51, 131–153. [Google Scholar]
- Shah, Z.; Bonyah, E.; Islam, S.; Gul, T. Impact of thermal radiation on electrical MHD rotating flow of Carbon nanotubes over a stretching sheet. AIP Adv. 2019, 9, 015115. [Google Scholar] [CrossRef]
- Khan, A.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef]
- Megahed, A. Effect of slip velocity on Casson thin film flow and heat transfer due to unsteady stretching sheet in presence of variable heat flux and viscous dissipation. Appl. Math. Mech. 2015, 36, 1273–1284. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative heat and mass transfer analysis of micropolar nanofluid flow of Casson fluid between two rotating parallel plates with effects of Hall current. J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Bonyah, E.; Khan, A.Z. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018, 2, 115014. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Khan, S.; Khan, W.; Khan, A.Z. Darcy–Forchheimer flow of micropolar nanofluid between two plates in the rotating frame with non-uniform heat generation/absorption. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Dawar, A.; Bonyah, E.; Ullah, H.; Khan, A. Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics. AIP Adv. 2018, 8, 125024. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer flow of radiative carbon nanotubes with microstructure and inertial characteristics in the rotating frame. Case Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, A.; Shah, Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J. Nanofluids 2017, 6, 812–829. [Google Scholar] [CrossRef]
- Tahir, F.; Gul, T.; Islam, S.; Shah, Z.; Khan, A.; Khan, W.; Ali, L. Flow of a nano-liquid film of Maxwell fluid with thermal radiation and magneto hydrodynamic properties on an unstable stretching sheet. J. Nanofluids 2017, 6, 1021–1030. [Google Scholar] [CrossRef]
- Chu, R.C.; Simons, R. Recent development of computer cooling technology. In Proceedings of the International Symposium on Transport Phenomena in Thermal Engineering, Seoul, Korea, 9–13 May 1993; pp. 17–25. [Google Scholar]
- Dixit, T.; Ghosh, I. Review of micro-and mini-channel heat sinks and heat exchangers for single phase fluids. Renew. Sustain. Energy Rev. 2015, 41, 1298–1311. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Z.; He, Y.; Tao, W. Numerical study of laminar heat transfer and pressure drop characteristics in a water-cooled minichannel heat sink. Appl. Therm. Eng. 2009, 29, 64–74. [Google Scholar] [CrossRef]
- Srivastava, L.; Srivastava, V.; Sinha, S. Peristaltic transport of a physiological fluid. Biorheology 1983, 20, 153–166. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Shehzad, S.A.; Alsaadi, F.; Altoaibi, N. Hydromagnetic peristaltic transport of copper–water nanofluid with temperature-dependent effective viscosity. Particuology 2016, 27, 133–140. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.; Alsaedi, A. Three-dimensional boundary layer flow of Maxwell nanofluid: mathematical model. Appl. Math. Mech. 2015, 36, 747–762. [Google Scholar] [CrossRef]
- Malik, M.; Khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 2015, 5, 117118. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N.; Malvandi, A. Free convective heat and mass transfer of MHD non-Newtonian nanofluids over a cone in the presence of non-uniform heat source/sink. J. Mol. Liq. 2016, 221, 108–115. [Google Scholar] [CrossRef]
- Rokni, H.B.; Alsaad, D.M.; Valipour, P. Electrohydrodynamic nanofluid flow and heat transfer between two plates. J. Mol. Liq. 2016, 216, 583–589. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl. Nanosci. 2014, 4, 625–631. [Google Scholar] [CrossRef]
- Shehzad, S.; Hayat, T.; Alsaedi, A. MHD flow of Jeffrey nanofluid with convective boundary conditions. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 873–883. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tlili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Kandelousi, S. Kerosene- alumina nanofluid flow and heat transfer for cooling application. J. Cent. South Univ. 2016, 23, 983–990. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Islam, S.; Khan, M.A.; Bonyah, E.; Hussain, F.; Mukhtar, S.; Ullah, M. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. 2018, 10, 36–45. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.; Ali, I.; Islam, S.; Husain, F. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, e296. [Google Scholar]
- Shah, Z.; Dawar, A.; Kumam, P.; Khan, W.; Islam, S. Impact of Nonlinear Thermal Radiation on MHD Nanofluid Thin Film Flow over a Horizontally Rotating Disk. Appl. Sci. 2019, 9, 1533. [Google Scholar] [CrossRef]
- Saeed, A.; Islam, S.; Dawar, A.; Shah, Z.; Kumam, P.; Khan, W. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry 2019, 11, 439. [Google Scholar] [CrossRef]
- Kumam, P.; Shah, Z.; Dawar, A.; Rasheed, H.U.; Islam, S. Entropy Generation in MHD Radiative Flow of CNTs Casson Nanofluid in Rotating Channels with Heat Source/Sink. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z. Impact of Thermal Radiation and Heat Source/Sink on MHD Time-Dependent Thin-Film Flow of Oldroyed-B, Maxwell, and Jeffry Fluids over a Stretching Surface. Processes 2019, 7, 191. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Khan, S.N. Radiative flow of magneto hydrodynamics single-walled carbon nanotube over a convectively heated stretchable rotating disk with velocity slip effect. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Bonyah, E.; Ayaz, M.; Khan, A. Three dimensional Darcy-Forchheimer radiated flow of single and multiwall carbon nanotubes over a rotating stretchable disk with convective heat generation and absorption. AIP Adv. 2019, 9, 035031. [Google Scholar] [CrossRef]
- Saeed, A.; Shah, Z.; Islam, S.; Jawad, M.; Ullah, A.; Gul, T.; Kumam, P. Three-Dimensional Casson Nanofluid Thin Film Flow over an Inclined Rotating Disk with the Impact of Heat Generation/Consumption and Thermal Radiation. Coatings 2019, 9, 248. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M. Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int. J. Heat Mass Transf. 2017, 111, 1039–1049. [Google Scholar] [CrossRef]
- Monfared, M.; Shahsavar, A.; Bahrebar, M.R. Second law analysis of turbulent convection flow of boehmite alumina nanofluid inside a double-pipe heat exchanger considering various shapes for nanoparticle. J. Therm. Anal. Calorim. 2019, 135, 1521–1532. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shamlooei, M.; Moradi, R. Fe3O4-Ethylene glycol nanofluid forced convection inside a porous enclosure in existence of Coulomb force. J. Mol. Liq. 2018, 249, 429–437. [Google Scholar] [CrossRef]
- Munkhbayar, B.; Tanshen, M.R.; Jeoun, J.; Chung, H.; Jeong, H. Surfactant-free dispersion of silver nanoparticles into MWCNT-aqueous nanofluids prepared by one-step technique and their thermal characteristics. Ceram. Int. 2013, 39, 6415–6425. [Google Scholar] [CrossRef]
- Esfe, M.H.; Wongwises, S.; Naderi, A.; Asadi, A.; Safaei, M.R.; Rostamian, H.; Dahari, M.; Karimipour, A. Thermal conductivity of Cu/TiO2–water/EG hybrid nanofluid: Experimental data and modeling using artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015, 66, 100–104. [Google Scholar] [CrossRef]
- Akhgar, A.; Toghraie, D. An experimental study on the stability and thermal conductivity of water-ethylene glycol/TiO2-MWCNTs hybrid nanofluid: Developing a new correlation. Powder Technol. 2018, 338, 806–818. [Google Scholar] [CrossRef]
- Keyvani, M.; Afrand, M.; Toghraie, D.; Reiszadeh, M. An experimental study on the thermal conductivity of cerium oxide/ethylene glycol nanofluid: Developing a new correlation. J. Mol. Liq. 2018, 266, 211–217. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Meghdadi, A.H.; Hojaji, M. The analysis of experimental process of production, stabilizing and measurement of the thermal conductivity coefficient of water/graphene oxide as a cooling nanofluid in machining. J. Mod. Process. Manuf. Prod. 2016, 5, 43–53. [Google Scholar]
- Carreau, P.; Kee, D.D.; Daroux, M. An analysis of the viscous behaviour of polymeric solutions. Can. J. Chem. Eng. 1979, 57, 135–140. [Google Scholar] [CrossRef]
- Kefayati, G.R.; Tang, H. MHD thermosolutal natural convection and entropy generation of Carreau fluid in a heated enclosure with two inner circular cold cylinders, using LBM. Int. J. Heat Mass Transf. 2018, 126, 508–530. [Google Scholar] [CrossRef]
- Olajuwon, B.I. Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion. Therm. Sci. 2011, 15, S241–S252. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Boundary layer flow of Carreau fluid over a convectively heated stretching sheet. Appl. Math. Comput. 2014, 246, 12–22. [Google Scholar] [CrossRef]
- Alsarraf, J.; Moradikazerouni, A.; Shahsavar, A.; Afrand, M.; Salehipour, H.; Tran, M.D. Hydrothermal analysis of turbulent boehmite alumina nanofluid flow with different nanoparticle shapes in a minichannel heat exchanger using two-phase mixture model. Phys. A Stat. Mech. Its Appl. 2019, 520, 275–288. [Google Scholar] [CrossRef]
- Azari, A.; Kalbasi, M.; Rahimi, M. CFD and experimental investigation on the heat transfer characteristics of alumina nanofluids under the laminar flow regime. Braz. J. Chem. Eng. 2014, 31, 469–481. [Google Scholar] [CrossRef]
- Munir, A.; Shahzad, A.; Khan, M. Convective flow of Sisko fluid over a bidirectional stretching surface. PLoS ONE 2015, 10, e0130342. [Google Scholar] [CrossRef] [PubMed]
- Olanrewaju, P.; Adigun, A.; Fenwa, O.; Oke, A.; Funmi, A. Unsteady free convective flow of sisko fluid with radiative heat transfer past a flat plate moving through a binary mixture. Therm. Energy Power Eng. 2013, 2, 109–117. [Google Scholar]
- Khan, M.; Munawar, S.; Abbasbandy, S. Steady flow and heat transfer of a Sisko fluid in annular pipe. Int. J. Heat Mass Transf. 2010, 53, 1290–1297. [Google Scholar] [CrossRef]
- Khan, M.; Shahzad, A. On boundary layer flow of a Sisko fluid over a stretching sheet. Quaest. Math. 2013, 36, 137–151. [Google Scholar] [CrossRef]
- Patel, M.; Patel, J.; Timol, M. Laminar boundary layer flow of Sisko fluid. Appl. Appl. Math. 2015, 10, 909–918. [Google Scholar]
- Darji, R.; Timol, M. Similarity analysis for unsteady natural convective boundary layer flow of Sisko fluid. Int. J. Adv. Appl. Math. Mech. 2014, 1, 22–36. [Google Scholar]
- Siddiqui, A.; Hameed, A.; Haroon, T.; Walait, A. Analytic solution for the drainage of Sisko fluid film down a vertical belt. Appl. Appl. Math. 2013, 8, 465–480. [Google Scholar]
- Khan, M.; Abbas, Q.; Duru, K. Magnetohydrodynamic flow of a Sisko fluid in annular pipe: A numerical study. Int. J. Numer. Methods Fluids 2010, 62, 1169–1180. [Google Scholar] [CrossRef]
- Sarı, G.; Pakdemirli, M.; Hayat, T.; Aksoy, Y. Boundary layer equations and Lie group analysis of a Sisko fluid. J. Appl. Math. 2012, 2012. [Google Scholar] [CrossRef]
- Khan, H.; Haneef, M.; Shah, Z.; Islam, S.; Khan, W.; Muhammad, S. The combined magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid flow over a stretching surface under the influence of variable heat and thermal radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Moallemi, N.; Shafieenejad, I.; Novinzadeh, A. Exact solutions for flow of a Sisko fluid in pipe. Bull. Iran. Math. Soc. 2011, 37, 49–60. [Google Scholar]
- Dawar, A.; Shah, Z.; Islam, S.; Idress, M.; Khan, W. Magnetohydrodynamic CNTs Casson Nanofl uid and Radiative heat transfer in a Rotating Channels. J. Phys. Res. Appl. 2018, 1, 017–032. [Google Scholar]
- Shah, Z.; Dawar, A.; Khan, I.; Islam, S.; Ching, D.L.C.; Khan, A.Z. Cattaneo-Christov model for electrical magnetite micropoler Casson ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. Case Stud. Therm. Eng. 2019, 13, 100352. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2018, 8, 115302. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Osiac, M. The electrical and structural properties of nitrogen Ge1Sb2Te4 thin film. Coatings 2018, 8, 117. [Google Scholar] [CrossRef]
- Bahgat Radwan, A.; Abdullah, A.; Mohamed, A.; Al-Maadeed, M. New electrospun polystyrene/Al2O3 nanocomposite superhydrophobic coatings; synthesis, characterization, and application. Coatings 2018, 8, 65. [Google Scholar] [CrossRef]
- Chen, X.; Dai, W.; Wu, T.; Luo, W.; Yang, J.; Jiang, W.; Wang, L. Thin film thermoelectric materials: Classification, characterization, and potential for wearable applications. Coatings 2018, 8, 244. [Google Scholar] [CrossRef]
- Yamamuro, H.; Hatsuta, N.; Wachi, M.; Takei, Y.; Takashiri, M. Combination of electrodeposition and transfer processes for flexible thin-film thermoelectric generators. Coatings 2018, 8, 22. [Google Scholar] [CrossRef]
- Khan, Z.; Shah, R.; Islam, S.; Jan, H.; Jan, B.; Rasheed, H.U.; Khan, A. MHD Flow and Heat Transfer Analysis in the Wire Coating Process Using Elastic-Viscous. Coatings 2017, 7, 15. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of Reiner-Philippoff fluid over an unstable stretching surface with Brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1982; Volume 15, pp. 1–58. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Weigand, B.; Birkefeld, A. Similarity solutions of the entropy transport equation. Int. J. Therm. Sci. 2009, 48, 1863–1869. [Google Scholar] [CrossRef]
- Makinde, O.D. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Khan, T.A.; Khan, M.I.; Ahmad, S.; Alsaedi, A. Entropy generation in Darcy-Forchheimer bidirectional flow of water-based carbon nanotubes with convective boundary conditions. J. Mol. Liq. 2018, 265, 629–638. [Google Scholar] [CrossRef]
- Makinde, O. Thermodynamic second law analysis for a gravity-driven variable viscosity liquid film along an inclined heated plate with convective cooling. J. Mech. Sci. Technol. 2010, 24, 899–908. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Abdollahzadeh, M. Free convection and entropy generation of nanofluid inside an enclosure with different patterns of vertical wavy walls. Int. J. Therm. Sci. 2012, 52, 127–136. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S. Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Feroz, N.; Shah, Z.; Islam, S.; Alzahrani, E.O.; Khan, W. Entropy Generation of Carbon Nanotubes Flow in a Rotating Channel with Hall and Ion-Slip Effect Using Effective Thermal Conductivity Model. Entropy 2019, 21, 52. [Google Scholar] [CrossRef]
- Alharbi, S.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink. Appl. Sci. 2018, 8, 2588. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Jalili, M. Determination of optimal convergence-control parameter value in homotopy analysis method. Numer. Algorithms 2013, 64, 593–605. [Google Scholar] [CrossRef]
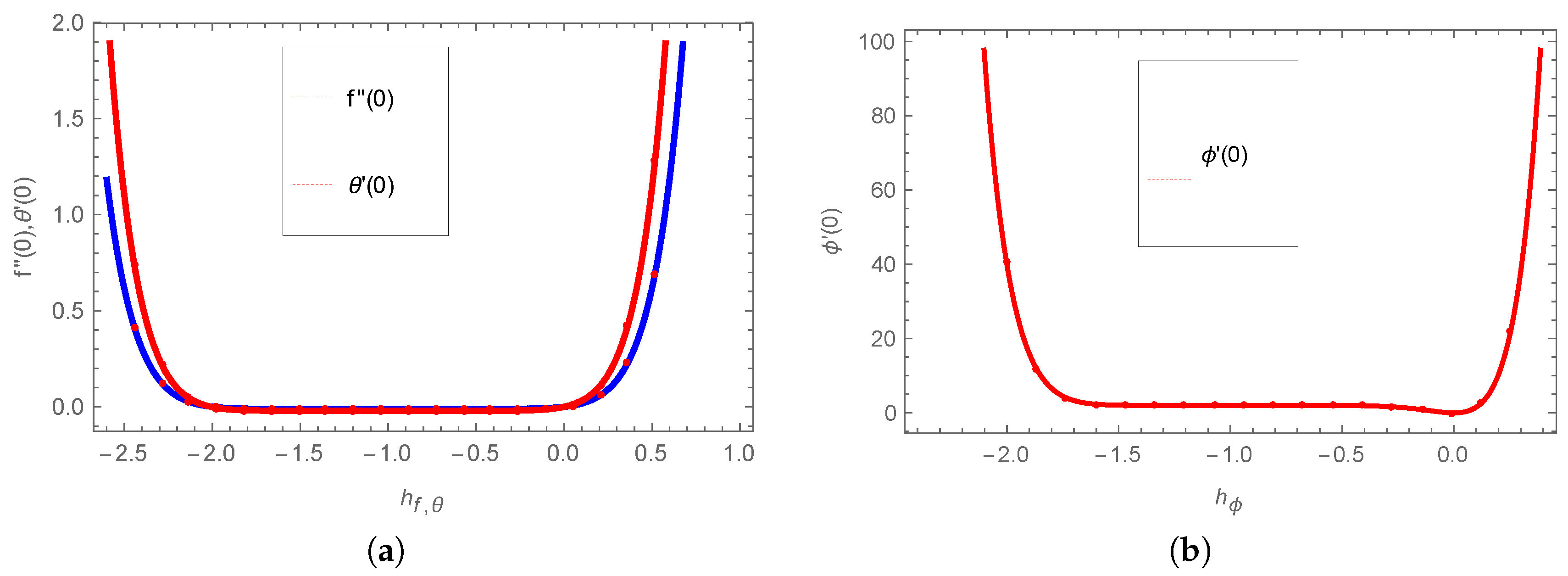


| Approximation Order | |||
|---|---|---|---|
| 1 | −0.0600000 | −1.107500 | 0.0537500 |
| 3 | −0.104656 | −0.106980 | 0.0856833 |
| 5 | −0.115692 | −0.106849 | 0.0935671 |
| 7 | −0.118420 | −0.106817 | 0.0955156 |
| 9 | −0.119090 | −0.106809 | 0.0095997 |
| 11 | −0.119261 | −0.106807 | 0.0961163 |
| 13 | −0.119303 | −0.106807 | 0.0961457 |
| 15 | −0.119313 | −0.106806 | 0.0961530 |
| 17 | −0.119315 | −0.106806 | 0.0961548 |
| 19 | −0.119316 | −0.106806 | 0.0961552 |
| 23 | −0.119316 | −0.106806 | 0.0961554 |
| 25 | −0.119316 | −0.106806 | 0.0961554 |
| M | ||||
|---|---|---|---|---|
| 0.1 | 0.5 | 0.1 | 1.5 | −0.1708 |
| 0.5 | −0.2034 | |||
| 1.0 | −0.2460 | |||
| 1.5 | 0.1 | −0.1776 | ||
| 0.5 | −0.1708 | |||
| 1.0 | −0.1708 | |||
| 1.5 | 0.1 | 0.3434 | ||
| 0.5 | 0.7463 | |||
| 1.0 | −6.9860 | |||
| 1.5 | 0.1 | −1.8672 | ||
| 0.5 | −0.2217 | |||
| 1.0 | −0.1320 |
| M | ||||
|---|---|---|---|---|
| 0.1 | 0.1 | 1.5 | 1.5 | 0.3523 |
| 0.5 | 0.3521 | |||
| 1.0 | 0.3519 | |||
| 1.5 | 0.1 | 0.3523 | ||
| 0.5 | 1.5145 | |||
| 1.0 | 2.2616 | |||
| 1.5 | 0.1 | 1.6248 | ||
| 0.5 | 0.2284 | |||
| 1.0 | 0.2904 | |||
| 1.5 | 1.5 | 0.3523 | ||
| 3.0 | 0.3243 | |||
| 5.0 | 0.3087 | |||
| 7.0 | 0.3012 |
| 0.1 | 0.5 | 0.1 | 1.5 | 1.5 | −1.3582 |
| 0.5 | −0.2388 | ||||
| 1.0 | −0.0988 | ||||
| 1.5 | 0.1 | 0.0223 | |||
| 0.5 | −1.3582 | ||||
| 1.0 | −2.7537 | ||||
| 1.5 | 0.1 | −4.1455 | |||
| 0.5 | −3.9667 | ||||
| 1.0 | −3.7453 | ||||
| 1.5 | 0.1 | −1.8105 | |||
| 0.5 | −2.3059 | ||||
| 1.0 | −2.9193 | ||||
| 1.5 | 1.5 | −3.5263 | |||
| 3.0 | −5.6130 | ||||
| 5.0 | −6.7706 | ||||
| 7.0 | −7.3323 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes 2019, 7, 262. https://doi.org/10.3390/pr7050262
Ullah A, Shah Z, Kumam P, Ayaz M, Islam S, Jameel M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes. 2019; 7(5):262. https://doi.org/10.3390/pr7050262
Chicago/Turabian StyleUllah, Asad, Zahir Shah, Poom Kumam, Muhammad Ayaz, Saeed Islam, and Muhammad Jameel. 2019. "Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation" Processes 7, no. 5: 262. https://doi.org/10.3390/pr7050262
APA StyleUllah, A., Shah, Z., Kumam, P., Ayaz, M., Islam, S., & Jameel, M. (2019). Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes, 7(5), 262. https://doi.org/10.3390/pr7050262








