Abstract
Shuttle-based storage and retrieval systems (SBS/RSs), a new type of “part-to-picker” system, have attracted public attention because of their flexibility and robustness. The systems consist of two sub-systems—shuttles and lifts—which are responsible for horizontal movements and vertical movements, respectively. SBS/RSs are categorized into tier-to-tier shuttles and tier-captive shuttles. This paper mainly researches SBS/RSs with tier-to-tier shuttles. New challenges have emerged since the commercial simulation-based optimization software has become widely applied for, for instance, task scheduling problems. Specifically, to decrease the idle time of lifts and the waiting time of shuttles, an integer programming scheduling model is proposed to minimize total task time with constraints on orders and devices. The Gurobi linear programming solver was utilized to obtain the optimal order sequence and the shortest operation time. The overall system efficiency was improved using our model. Moreover, the results are significant for reducing capital investment and operating cost.
1. Introduction
With the rapid development of science and technology, logistics equipment has developed in the direction of Intelligent, automation, and flexibility. Part-to-Picker systems play a supportive role in improving order-picking operations, which utilize a form of automatic storage sorting and conveying, as well as manual picking. The system provides a prompt when a pick order appears. The automated equipment can find the totes of targeted goods accurately and quickly, and can pick out the totes from their storage positions to a picking station. At the picking station, the staff does not need to walk and only needs to select totes according to the required items and quantity displayed on the screen of the picking station.
Shuttle-based storage and retrieval systems (SBS/RSs) are a kind of Part-to-Picker system. In the past five years, SBS/RSs have gradually seen increasing use in E-commerce or pharmaceutical industries. Warehouse equipment providers, such as Dematic and Knapp, have already implemented them in practice.
There are two types of shuttle-based systems: tier-to-tier and tier-captive SBS/RSs. The distinction is the achievement of cross-tier movement. In detail, for a tier-captive SBS/RS, there is one shuttle in each tier that is limited to move only on its own tier. Lifts installed at the end of aisles enable the transfer of loads between tiers. In contrast, in a tier-to-tier SBS/RS, the number of shuttles is less than the number of racks, which means shuttles can transport cross-tier with the help of lifts. In sum, tier-to-tier SBS/RSs have advantages in flexibility and robustness. For instance, if there is a malfunctioning shuttle in a tier-captive SBS/RS, the picking operations on this tier cannot be processed further. However, tier-to-tier SBS/RSs can schedule shuttles on other tiers to assist the picking process. In this paper, we focus on tier-to-tier SBS/RSs. We aim to study the device setting and task scheduling problems, provide a theoretical basis for improving system design and operational efficiency, and offer technological support for storage and retrieval tasks. Specifically, for a batch of orders accumulated during a single fixed time window, we set up an integer programming scheduling model to obtain the optimal task sequence.
The rest of the article is organized as follows. Section 2 reviews the relevant literature. Section 3 mainly describes the structure of the system and its operational process. The integer programming scheduling model is illustrated in detail in Section 4. Section 5 introduces a case study and compares the simulation results. Section 6 covers the summary and the direction of further research.
2. Literature Review
To the best of our knowledge, SBS/RSs are a relatively new technology and have similarities with the Automated Guided Vehicle (AGV) in terms of working principles and procedures. Compared with AGVs, there are few studies considering SBS/RSs in the literature. Thus, references regarding AGVs are included.
Due to the increase of fixed costs in logistics, studies on AGVs have gradually become more popular. However, AGV studies focus mainly on modeling, task scheduling, and path optimization. Many scholars have analyzed the model properties of the systems from application scenarios. Qiu et al. illustrated how AGVs work in the logistics field, modeled by Petri Web, and analyzed the system efficiency [1]. The results proved that the model could accurately describe system operations. Additionally, some scholars studied task scheduling and path optimization. Li et al. proposed a dynamic planning principal for task path optimization and compared several heuristic paths [2,3]. Liu ran a simulation and analyzed the offered heuristic paths under dual cycle command (DCC) [4]. Andrea et al. offered one self-stabilizing distributed traffic control protocol which adopted partition control. Specifically, they divided the control plane into several independent control sections. When the robot accessed the control section, it calculated the collision route from the origin to the objective [5]. Zhang et al. achieved the optimal task scheduling for the robot model according to mathematical model research about the adoptability and features of a heterogeneous robot system model [6].
The automated warehouse is inseparable from the efficiency of stackers. The mechanical parameters of stackers cannot be modified. However, the optimization of task scheduling can improve the system efficiency. Yang et al., Shia et al., and Cheng et al. modeled the task scheduling of stackers as a travelling salesman problem, and solved the model by genetic algorithms [7,8,9]. Li established a mathematical model based on the shortest task time of the stacker and the stability of racks. After solving it by a particle swarm algorithm and comparing with a genetic algorithm, it was found that the particle swarm algorithm was convergent [10]. Under a limitation on task completion, Kumar set the objective as the time of consignment delay and solved the model by simulated annealing algorithms [11]. Tian et al. modeled optimally based on the operational specialties fixed rack and stackers and solved the model by combining with new mixed genetic algorithms [12].
An AGV can drive horizontally cross-aisle. It is similar to the operation of tier-to-tier SBS/RSs that can also achieve the goal of cross-tier handover by lifts. Zou et al. established a fork–join queueing model for SBS/RSs, solved by the maximum entropy method (MEM), and compared the properties of shuttles and lifts under parallel work command and sequential operation tasks [13]. Wang et al. studied the retrieval tasks of SBS/RS. The two-step open queueing web was established for solving the waiting time of devices and applied ant colony algorithms for the results of a position distribution optimization model [14].
For multiple-cross-aisle warehouse systems, Kulak et al. studied a novel tabu search (TS) algorithm to solve order-batching and picker-routing problems. By modeling the routing problem of pickers as a classical Traveling Salesman Problem (TSP), they found that the TS algorithms were the most efficient methods in terms of solution quality and computational efficiency [15]. Mou determined the factors influencing the operational efficiency of SBS/RSs. Moreover, he established an optimization model for position distribution and task scheduling, and solved it using ant colony and non-domination genetic algorithms [16]. Li et al. formulated an integer programming to minimize the total travelling distance involved in order batching and picker routing. They proposed a joint optimization algorithm which includes an effective batching procedure based on a similarity coefficient and an improved ant colony optimization algorithm with local search, and the joint optimization algorithm has potential advantages under various order sizes and order structures [17].
Ekren et al. found the best rack design for SBS/RSs under a class-based storage policy (CSP) and utilized a simulation for modeling purposes. They found that warehouse design with CSP may tend to have lower investment cost [18]. Lerher et al. presented an analytical travel time model for the computation of travel (cycle) time for SBS/RSs. Under the assumption of uniform distributed storage rack locations and using probability theory, the model enables the calculation of the mean travel (cycle) time for single and dual command cycles [19]. In the same year, Lerher et al. presented a simulation-based performance evaluation of SBS/RSs, and results showed that SBS/RSs are effective in increasing the throughput capacity as well as reducing the mean cycle time [20]. In 2016, Lerher et al. continued to put forward an analytical travel time model for computing cycle times for double-deep SBS/RSs, and analysis proved that this model demonstrated good performances for evaluating double-deep SBS/RSs [21]. Ning et al. developed a simulation model which could auto-remodel for different rack configurations. The optimal rack design was determined in a simulation case study containing 81 different rack alternatives under 15 different retrieval rates within 48 hours [22]. Ekren et al. first provided a graph-based solution for performance evaluation of an SBS/RS, which could help decision-makers decide the best design among thousands of alternative design scenarios [23]. Lerher et al. explored statistically significant factors affecting the performance of SBS/RSs under pre-defined factors by using design of experiment (DOE) [24]. Borovinšek et al. built a multi-objective optimization solution of an SBS/RS which contains the minimization of average transaction cycle time (average throughput time), amount of energy (electricity) consumption, and total investment cost [25]. Ha et al. suggested system controls to prove the effectiveness of free balancing; they verified the system by running a simulation analysis [26].
Although SBS/RSs have been applied tentatively in many logistics distribution centers, most of the application scenarios do not make full use of the advantage that the shuttle systems can improve efficiency in parallel operations. Thus, there is large space for improvement. Further research is needed due to the lack of theoretical support. As for the task scheduling of SBS/RSs, the majority of studies focus on systems with higher task arrival rates. Additionally, researchers mostly use heuristics to optimize the task scheduling. Ordinarily, heuristics cannot guarantee the global optimality of their solution results.
In this paper, we first specifically illustrate the features of a tier-to-tier SBS/RS, which are usually applied with relatively fewer tasks (usually no more than 30 tasks per hour). Thus, modelling the task scheduling can accurately obtain the optimum solution. Second, an integer programming model is established to minimize the total task time, with constraints of shuttle and lift subsystems, and retrieval tasks. Moreover, this paper uses the Gurobi linear solver to solve the model, which can calculate the optimized retrieval task sequence quickly. This study focuses on the effect of the number of shuttles on task cycle time under different conditions.
3. System Description
Figure 1 demonstrates the design of a tier-to-tier SBS/RS. Here, shuttles transport the stock keeping unit (SKU) horizontally in each tier. Lifts placed at the end of each aisle are used for vertical transport. Additionally, shuttles can access any tier of the rack with the help of lifts. The shuttle buffer is at the bottom tier for resting shuttles when they complete tasks. This paper focuses on the performance with a single aisle, since there are similarities between aisles.
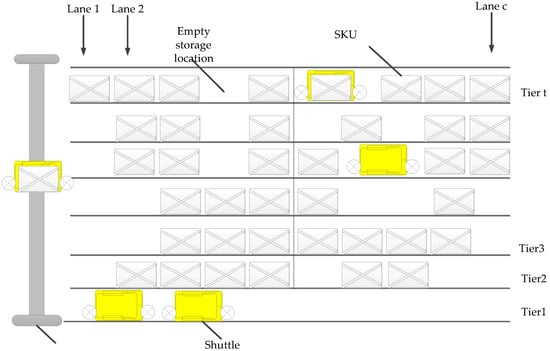
Figure 1.
Tier-to-tier SBS/RS configuration.
The operation procedure includes storage tasks, picking operation, and retrieval tasks. Since the storage task is similar to the retrieval tasks in terms of logic, we focus on the retrieval task. The procedure of retrieval tasks are introduced next.
Figure 2 shows the retrieval operation of an SBS/RS with a flowchart, where First Come First Served (FCFS) policy is used. A principal computer locates the aisle, tier, and column of the SKU based on the retrieval task. There are two situations: Firstly, if there is an idle shuttle, the principal computer will automatically assign an idle shuttle to the task. Secondly, if all shuttles are under tasks, the order will be listed in the waiting sequence. Next, when the idle shuttle gets the task, it will request the lift immediately, which will be put into the lift waiting sequence. Similarly, an idle lift will respond. In detail, a lift moves from the current position to the first tier, then the shuttle gets into the lift. The lift conveying the shuttle moves to the tier where the SKU locates, and the lift is released for other tasks after the shuttle has left. Shuttles start from the first column in one tier to the position where the SKU is located and go back to the initial location, requesting the lift service. Similar to the first request for lifts, the task waits in the line of lift tasks. The idle lift transports the loading shuttle to tier 1 and it is released for further tasks when the shuttle has left. The shuttle is free for the next task after unloading.
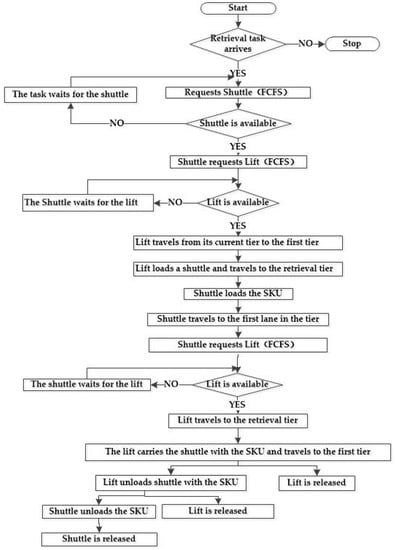
Figure 2.
Flowchart of the retrieval operation in a tier-to-tier SBS/RS.
The primary objective of task scheduling is to reduce the waiting time between shuttles and lifts. In other words, each retrieval task consists of one shuttle and one lift, and a lift works with idle shuttles and loading shuttles once, respectively. Thus, when we model the task scheduling, in order to decrease the waiting time of each order, we categorize the lift request for a retrieval task into two phases: fetching idle shuttles and fetching loading shuttles. Moreover, essential operations of the lift are classified into five categories, as shown in Figure 3. Figure 3a,b represents the movement of the idle and loading shuttles, respectively, from tier i to tier 1. Under the assumption of constant velocity of idle and loading shuttles, both situations can be combined as the movement of lifts from tier i to tier 1. Figure 3c shows the movement of a lift from tier i to tier j (may be idle in practical situations). Figure 3d,e illustrates the movement of the idle lift and shuttle from tier 1 to tier i.
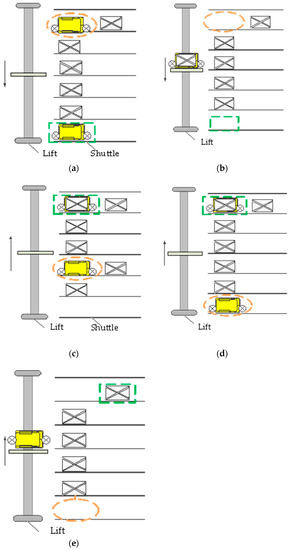
Figure 3.
Operation of Lifts. (a) The movement of an idle shuttle; (b) The movement of a loading shuttle; (c) The movement of a lift between two tiers; (d) The movement of an idle lift; (e) The movement of a loaded lift.
To describe the task scheduling, we define the following variables as Table 1.

Table 1.
Scenario settings.
Since the movement of shuttles and the lift need to undergo at least two stages (i.e., acceleration and deceleration), the features can be divided into two situations based on the longitude of traveling distance and parameters [27]:
- If shuttles and lifts reach the maximum velocity before deceleration, the operation includes three steps: accelerating from 0 to maximum velocity , traveling at , and decelerating from to 0. The patterns of acceleration and velocity are shown in Figure 4a.
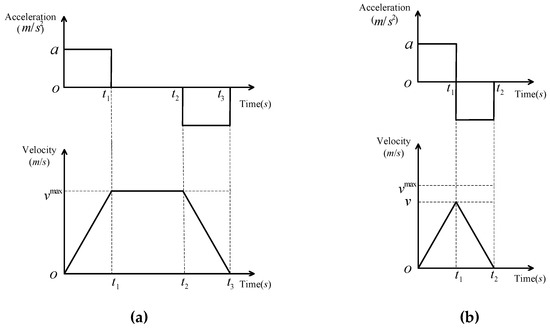 Figure 4. Operation Features of shuttles and lifts. (a) Patterns of acceleration and velocity for situation 1; (b) Patterns of acceleration and velocity for situation 2.
Figure 4. Operation Features of shuttles and lifts. (a) Patterns of acceleration and velocity for situation 1; (b) Patterns of acceleration and velocity for situation 2. - If shuttles and lifts do not reach the maximum velocity before deceleration, the operation includes two steps: accelerating from 0 to v and decelerating from v to 0. The patterns of acceleration and velocity are shown in Figure 4b.
Thus, based on the assumptions above, one retrieval task completion can be described in several steps.
1. The lift moves from the current position to tier 1 to fetch shuttles. Then, the vertical traveling distance is:
Combined with the acceleration and velocity of lifts, the traveling time of the lift is:
2. The lift conveying shuttles moves from tier 1 to the tier where the SKU is located. When the shuttle leaves the lift, the lift will be free. Let the SKU be located at tier y. The traveling distance of the lift is:
The traveling time of the lift is:
3. The shuttle moves horizontally from the first column to the column where SKU is located and returns to the first column waiting for the lift at one particular tier. Let the SKU be located at column c, then the horizontal distance of the shuttle is:
The traveling distance of the lift moving from tier z to where shuttle loaded the SKU:
Considering the acceleration and deceleration of the shuttle, the vertical distance of the shuttle is:
4. The lift conveying loading shuttles moves to tier 1 and unloads. The lift is then released. The vertical traveling distance of the lift is:
Then, the traveling time of the lift is:
were the lift’s time of moving from tier i to tier 1 is:
denotes the time spent in fetching the loading shuttle in tier i, unloading in tier i, and traveling back to tier j:
denotes the time spent in fetching the idle shuttle in tier 1 and traveling to tier i to unload:
denotes the time spent in fetching the idle shuttle in tier 1, unloading in tier i, and traveling to tier j:
denotes the time spent in fetching the idle shuttle in tier 1, unloading in tier i, and traveling back to tier 1:
denotes the time spent in traveling from column 1 to column q for picking and traveling back to column 1:
4. Integer Programming Scheduling Model
The integer programming scheduling model is used to regulate and schedule a batch of retrieval tasks to minimize the total time of a batch of orders. The goal for task scheduling of automated storage/retrieval systems (AS/RSs) is to determine the minimum travel time of stockers, and to obtain the minimum task time under single cycle command (SCC) or dual cycle command (DCC). In SBS/RSs, repeatedly transporting the picked SKU is a waste of time. Additionally, there is limited space for storing picked SKUs in sorting platforms. Thus, we sorted the tasks in batches. To be specific, we determine a single time window according to a particular strategy, and then assign the tasks in a time window to the sorting platform. The proposed integer programming scheduling model is established on the solid basis of all retrieval tasks in a time window. Based on the tiers and columns of the retrieval SKU in a particular time window, we scheduled and optimized the task sequence of shuttles and lifts to decrease the waiting time of shuttles and lifts, improve the efficiency, and develop the productivity of SKU storage and retrieval.
To better illustrate the model, we made the following assumptions:
- The retrieval SKU can be found in its assigned aisles randomly within a single time window.
- At the beginning of retrieval tasks, all shuttles remain at rest in the buffer area on tier 1. When the first shuttle is in a task with new tasks emerging, the system schedules the second shuttle for the next task, and this pattern is followed for shuttles third through h.
- While a shuttle performs a task in a certain tier, it is forbidden to allow other shuttles to step in since it could lead to deadlock or conflict.
- For retrieval tasks, lifts firstly transport the shuttles to the tier where the tasks is located, then the starting times of the first lift task, first shuttle task, and first retrieval task are set equal to 0.
Since each task completion requires lift scheduling, the total time of one task within a single time window can be illustrated by the sum of the starting time of the last lift task, the working time of lifts, the time of unloading shuttles, and the time of unloading goods. Specifically, the last lift task is to transport loading shuttles. In order to describe the integer programming scheduling model, we defined the parameters in Table 2 and variables in Table 3.

Table 2.
Parameters and meanings.

Table 3.
Variables and meanings.
The aim of the model is to minimize the task cycle time (TCT) within a single time window. So, the objective function is:
The constraints are as follows:
Equation (17) is the objective function, which represents the completion time of the last task—that is, the total time of all retrieval tasks within a fixed time window. Equation (18) represents that the lift can perform one function only for each time: to fetch the idle shuttle or the loading shuttle. Equation (19) illustrates that the position of each retrieval task is exclusive. Equation (20) indicates that the total number of retrieval tasks is O (i.e., the number of tasks of all shuttles is O). Equations (21) and (22) state that there are two requests for lifts for each retrieval task. Specifically, Equation (21) is the request for lifts of loading shuttles, and Equation (22) represents the request for lifts of idle shuttles. Equation (23) demonstrates that each retrieval task can be processed by one shuttle only. Equations (24)–(28) explain the relationship between the lift tasks. Here, Equation (24) means that the starting time of conveying loading shuttles of lifts is greater than idle shuttles for one retrieval order. Moreover, Equations (25)–(28) represent the relationship between lift tasks m and m − 1. Specifically, Equation (25) means that both lift requests are to fetch the loading shuttles. Equation (26) represents that task m is to fetch loading shuttles, and task m − 1 is to fetch the idle shuttle. Additionally, Equation (28) states that both tasks are to fetch the idle shuttles. Equations (29) and (30) demonstrate the relationship between two retrieval tasks on one tier. The relationship between the starting time of shuttles and retrieval tasks is shown in Equations (31) and (35). Equation (32) then explains the relationship between the starting time of the first task for shuttle h and shuttle h − 1. Equation (33) represents the relationship between each task of every shuttle. Equations (36) and (37) states the relationship between retrieval tasks and shuttles.
5. Case Study
Gurobi is a mathematical planning solver for solving large data sets. Since Gurobi can rapidly and accurately solve linear problems, quadratic problems, and mixed integer linear and quadratic problems, it has been widely applied for mathematical planning optimization in logistics, manufacture, transportation, and other fields. We used Gurobi 6.5.0 for the integer programming scheduling model, and Python (Pycharm) for solving the large-size model. Gurobi and Pycharm both offer free versions for universities. Pycharm is especially easy to debug.
To verify the model, we set up six simulation scenarios (shown in Table 3), which used the results of the precise calculation method above. In each scenario, we recorded the TCT in four random picking sequences, and compared the values with the model results. The data are shown in Table 4. Other parameters set in this paper are based on practical storage construction and device conditions, as shown in Table 5.

Table 4.
Scenario settings.

Table 5.
Parameter setting.
The results are shown in Table 6.

Table 6.
Model calculation analysis.
Obviously, the model’s TCT was far less than that under random sequences. For scenarios A, B, and C, the number of positions increased from 1200 to 2000, while the number of tiers was fixed. As the number of positions increased, the optimized percentage decreased. When the number of columns was kept consistent (i.e., scenarios A and D, scenarios B and E, and scenarios C and F), the average number of storage positions that each shuttle was responsible for was reduced, and the optimized percentage was reduced. In general, the scheduling sequence derived from the integer programming model could enhance the efficiency of the system by at least 7%.
6. Conclusions
Tier-to-tier SBS/RSs have advantages in robustness and cost-saving when the number of tasks is relatively small. After analyzing SBS/RS procedures, we established the integer programming scheduling model, which avoided the simulation complexity and inaccuracy of heuristic algorithms. Using the Gurobi optimizer in conjunction with Python, we could control the information of the input order, and the automated program written according to the model could calculate the total TCT of the optimal task picking sequence. By processing the value of the identification variable, the optimal pickup sequence could be found. Thus, the integer programming scheduling model helped to obtain the minimum time of retrieval tasks within a fixed time window and the optimized the retrieval task sequence for tier-to-tier SBS/RSs.
Although this paper achieved practical progress in modeling and optimizing an SBS/RS, further investigations are needed due to the complexity of the system.
- This paper only considers retrieval tasks, without considering storage tasks. In practice, SBS/RSs normally perform both storage and retrieval tasks. Besides, under dual cycle command (DCC), methods to model and schedule the SBS/RSs require further research.
- The integer programming scheduling model established here can obtain the optimized result by Gurobi. However, model-solving time will increase as the number of orders increases. Thus, determining the best heuristic algorithm for optimization requires further study.
- The developed automated computing program can be further packaged into software. Then, the decision maker would be able to control the inputs and read the best retrieval sequence. By sending information about the best sequence to the automation device, the automatic system’s efficiency could be improved, and the costs of the warehouse could be cut.
Author Contributions
Conceptualization, X.Z. and Y.W. (Yanyan Wang); Data calculation, Y.W. (Yunge Wang) and K.H.; Analysis, X.Z.; Investigation, Y.W. (Yanyan Wang) and Y.W. (Yunge Wang); Methodology, X.Z.; Resources, X.Z.; Validation, Y.W. (Yanyan Wang), Y.W. (Yunge Wang), and K.H.; Writing—original draft, X.Z.; Writing—editing and review, Y.W. (Yunge Wang) and K.H.; Supervision, Y.W. (Yanyan Wang).
Funding
This research was funded by the Shandong Province Key Research Funds, grant number 2017GGX60103, and the Fundamental Research Funds for Shandong University, grant number 2018JC035.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qiu, Y.; Tao, D. Research on Modeling of AGV Dispatching System in Container Terminal Based on Timed Petri Net. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2006, 30, 958–960. [Google Scholar]
- Li, S.; Wang, C. An Optimal Method of Finding Routing Orderpickers in Distribution Centers Using Dynamic Programming. Oper. Res. Manag. Sci. 2003, 12, 117–121. [Google Scholar]
- Li, S.; Du, W.; Peng, Q. Research on Routing Policies of Low-level Fixed-rack Warehouse. Hoisting Convey. Mach. 2007, 8, 5–9. [Google Scholar]
- Liu, J. The Research on Routing Method Selection for an Order Picking System in the Distribution Center. Oper. Res. Manag. Sci. 2010, 11, 179–183. [Google Scholar]
- D’Andrea, R. A Revolution in the Warehouse: A Retrospective on Kiva Systems and the Grand Challenges Ahead. IEEE Trans. Autom. Sci. Eng. 2012, 9, 638–639. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, X.; Zhao, J.; Lu, E.; Li, Y. The task allocation for improved fitness-based heterogeneous multi-robot. J. Northwest Univ. (Nat. Sci. Ed.) 2013, 43, 22–26. [Google Scholar]
- Yang, H.; Li, X.; Zhong, M. Research on Optimal Path in AS/RS Orderpicking Operation Allocation. Hoisting Convey. Mach. 2005, 3, 23–26. [Google Scholar]
- Shiau, J.Y.; Lee, M.C. A warehouse management system with sequential picking for multi-container deliveries. Comput. Ind. Eng. 2010, 58, 382–392. [Google Scholar] [CrossRef]
- Cheng, Y. Research on Modelling and Optimization of AS/RS Orderpicking Operation Allocation. Master’s Thesis, University of Xiamen, Xiamen, China, 2009. [Google Scholar]
- Li, C. Research on Scheduling Optimization of Automated Warehouse Based on PSO. Master’s Thesis, Shaanxi University of Science and Technology, Xian, China, 2015. [Google Scholar]
- Kumar, V. Hybrid TSSA algorithm-based approach to solve warehouse-scheduling problems. Int. J. Prod. Res. 2009, 47, 919–940. [Google Scholar]
- Tian, G.; Zhang, P.; Li, X.; Yin, J.; Lu, F. Research on One Class of Optimization Problem of the Automated Warehouse Using a New Kind of Hybrid Genetic Algorithm. J. Syst. Simul. 2004, 16, 1198–1201. [Google Scholar]
- Zou, B.; Xu, X.H.; Gong, Y.; Koster, R.D. Modeling parallel movement of lifts and vehicles in tier-captive vehicle-based warehousing systems. Eur. J. Oper. Res. 2016, 254, 51–67. [Google Scholar] [CrossRef]
- Wang, Y.; Mou, S.; Wu, Y. Task scheduling for multi-tier shuttle warehousing systems. Int. J. Prod. Res. 2015, 53, 5884–5895. [Google Scholar] [CrossRef]
- Kulak, O.; Taner, M.E. Joint order batching and picker routing in single and multiple-cross-aisle warehouses using cluster-based tabu search algorithms. Flex. Serv. Manuf. J. 2012, 24, 52–80. [Google Scholar] [CrossRef]
- Mou, S. Modelling and Optimization in Shuttle-based Storage and Retrieval System. Master’s Thesis, University of Shandong, Jinan, China, 2013. [Google Scholar]
- Li, J.; Huang, R.; Dai, J.B. Joint optimisation of order batching and picker routing in the online retailer’s warehouse in China. Int. J. Prod. Res. 2017, 55, 447–461. [Google Scholar] [CrossRef]
- Ekren, B.Y.; Sari, Z.; Lerher, T. Warehouse Design under Class-Based Storage Policy of Shuttle-Based Storage and Retrieval System. Ifac Pap. 2015, 48, 1152–1154. [Google Scholar] [CrossRef]
- Lerher, T.; Ekren, B.Y.; Dukic, G.; Rosi, B. Travel time model for shuttle-based storage and retrieval systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1705–1725. [Google Scholar] [CrossRef]
- Lerher, T.; Ekren, Y.B.; Sari, Z.; Rosi, B. SIMULATION ANALYSIS OF SHUTTLE BASED STORAGE AND RETRIEVAL SYSTEMS. Int. J. Simul. Model. (Ijsimm) 2015, 14, 48–59. [Google Scholar] [CrossRef]
- Lerher, T. Travel time model for double-deep shuttle-based storage and retrieval systems. Int. J. Prod. Res. 2016, 54, 1–22. [Google Scholar] [CrossRef]
- Ning, Z.; Lei, L.; Zhang, S.; Lodewijks, G. An efficient simulation model for rack design in multi-elevator shuttle-based storage and retrieval system. Simul. Model. Pract. Theory 2016, 67, 100–116. [Google Scholar] [CrossRef]
- Ekren, B.Y. Graph-based solution for performance evaluation of shuttle-based storage and retrieval system. Int. J. Prod. Res. 2017, 55, 1–11. [Google Scholar]
- Lerher, T. Design of Experiments for Identifying the Throughput Performance of Shuttle-Based Storage and Retrieval Systems. Procedia Eng. 2017, 187, 324–334. [Google Scholar] [CrossRef]
- Borovinšek, M.; Ekren, B.Y.; Burinskienė, A.; Lerher, T. Multi-objective optimisation model of shuttle-based storage and retrieval system. Transport 2017, 32, 1–18. [Google Scholar] [CrossRef]
- Ha, Y.; Chae, J. Free balancing for a shuttle-based storage and retrieval system. Simul. Model. Pract. Theory 2018, 82, 12–31. [Google Scholar] [CrossRef]
- Lerher, T.; Sraml, M.; Kramberger, J.; Potrc, I.; Borovinsek, M.; Zmazek, B. Analytical travel time models for multi aisle automated storage and retrieval systems. Int. J. Adv. Manuf. Technol. 2006, 30, 340–356. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).