1. Introduction
In recent decades, many electricity generation problems have been caused by their high production cost and environmental impact [
1]. It is generally accepted that renewable energy can provide promising solutions for the problems, and much research has been focused on numerous techniques, such as hydropower [
2,
3,
4], fuel cells [
5], biofuels [
6], wind power [
7,
8,
9], and solar power generation [
10]. Pumped hydroelectric storage (PHES) has attracted widespread interest because of its great flexibility and storage capacity in improving grid stability of other renewable energy sources [
11,
12]. The lateral inlet/outlet plays a critical role in the connecting tunnels of the water delivery system in a PHES, and its flow conditions can affect the economic benefit and operation stability of the PHES to a great extent. The PHES operates under pumped or generation conditions according to the command, and the water flows between the upper and lower reservoir through the inlet/outlet. Compared with ordinary hydropower stations, the hydraulic requirements for the inlet/outlet structure of the PHES require more attention.
Much research in recent years has focused on the hydraulic performances of the inlet/outlet experimentally and numerically. Müller et al. [
13] carried out prototype measurements by Acoustic Doppler Current Profiler (ADCP) to study flow velocities in the reservoir; subsequently a numerical model was built to further understand the flow development near the inlet/outlet. In order to ensure satisfactory hydraulic performances, Bermúdez et al. [
14] conducted numerical and physical model studies on the inlet/outlet of the Belesar-III power station in Northwest Spain. The initial design was optimized by numerical method, and the new design presented a more homogenous flow distribution and a reduced head loss. Cai et al. [
15] performed an experimental study on the effects of the shape and position of separation piers on the flow characteristics with two operations. Gao et al. [
16] tried to improve the velocity distribution at the intake-outlet orifices through 20 types of shape optimization experiments. Sun et al. [
17] found the incorrect arrangement of separation piers probably contributes to disadvantageous velocity distribution for the trash rack. Ye et al. [
18] simulated turbulent flow in a lateral inlet/outlet to explore the diffusion segment shape that can obtain better velocity and discharge distributions. Based on the validation of the experiment, flows in the lateral inlet/outlet were numerically simulated focusing on the variations in discharge distributions over different orifices; the results showed that the flow non-uniformity was improved successfully by adjusting the diffusion segment and width between the separation piers [
19]. The investigations indicate that computational fluid dynamics (CFD) has been used frequently to optimize the structure parameters of the inlet/outlet that can easily influence the hydraulic objectives. However, the process mentioned above is a trial-and-error approach requiring intensive work and a lot of time [
20], and the results may be subjective to some extent.
CFD coupled with optimization techniques has been used to determine the best design scheme for wind turbine devices [
21,
22,
23], and the adopted methods provide a reference for inlet/outlet optimization. For complex optimization problems, two methods have been generally applied to achieve optimization. When there are many individual objective functions, the functions can be combined into a single composite one; nonetheless it can be difficult to determine the proper and typical selection of the weights. In addition, the combination method would provide only a single result that cannot be chosen to make a trade-off. Therefore, multi-objective evolutionary algorithms (MOEAs) are more desired by decision makers. For MOEAs, it is common to use the concept of Pareto solutions. Pareto solutions consist of many non-dominated solutions where some gain in objectives always causes some sacrifice to others. MOEAs, such as Non-dominated Sorting Genetic Algorithm II (NSGA-II) [
24,
25], can offer many Pareto results in one single simulation process and have been extensively applied in engineering optimization.
Although MOEAs can obtain many solutions, these algorithms also require an even larger number of simulations and an unacceptable computation time in practice. Thus, multi-objective optimization based on the surrogate methods is receiving increasingly more support and attention. These approaches present objective functions by surrogate models, replacing expensive high-fidelity design simulations. The model is an effective engineering technique that can considerably save computing expense while still providing reasonably accuracy. Therefore, the multi-objective surrogate-based optimization method makes it more feasible to perform exhaustive global searches in the design space for complicated shape optimization. The optimization result will be more satisfactory because the exploration is not subjected to a limited number of simulating data and computing resources. General surrogate models contain Response Surface Methodology (RSM) [
26,
27], Radial Basis Function (RBF) [
28,
29,
30,
31,
32], and Kriging [
33,
34,
35]. However, owing to the diverse functional characteristics of the popular models, it is important to choose the most appropriate models for the responses of hydraulic objectives to diffusion segment parameters. For that reason, a recently surrogated model selection method proposed by Mehmani et al. [
36], called the Concurrent Surrogate Model Selection (COSMOS), was adopted to construct suitable models in this paper.
Although a multi-objective CFD optimization process for the inlet/outlet was developed in previous works [
37,
38], there are some drawbacks in the original process: (1) The CFD method was indirectly validated only by comparing the result with that of a published reference [
18], which weakened the reliability of the optimization process. (2) Only a single surrogated model (RSM) was considered to accelerate the optimization procedure. However, there is no universal surrogate model for every practical problem, and suitable model selection is critical for accuracy. (3) The objectives for the pump and generation mode were simply added up to estimate the total performance. Nevertheless, the significance of the pump mode and generation mode is probably not equal in many cases. Therefore, in this study a physical model experiment was well-designed to meet the requirement of bi-directional flow, and a more extensive validation of the CFD model was performed. Based on the validated CFD model, the COSMOS method was applied to select suitable surrogate models for the objectives of the inlet/outlet, to further improve the accuracy of the original optimization process. In addition, in order to better evaluate the overall hydraulic performance, the selection of objective functions was reconsidered and weight coefficients of different operation modes were introduced. In the present article, the shape of an inlet/outlet was improved through CFD optimization based on optimal surrogate models. The aim of this work was to apply the optimal surrogate optimization process to determine the optimum shape of the inlet/outlet, to simultaneously obtain better hydraulic performances under bidirectional flow conditions.
2. Problem Description
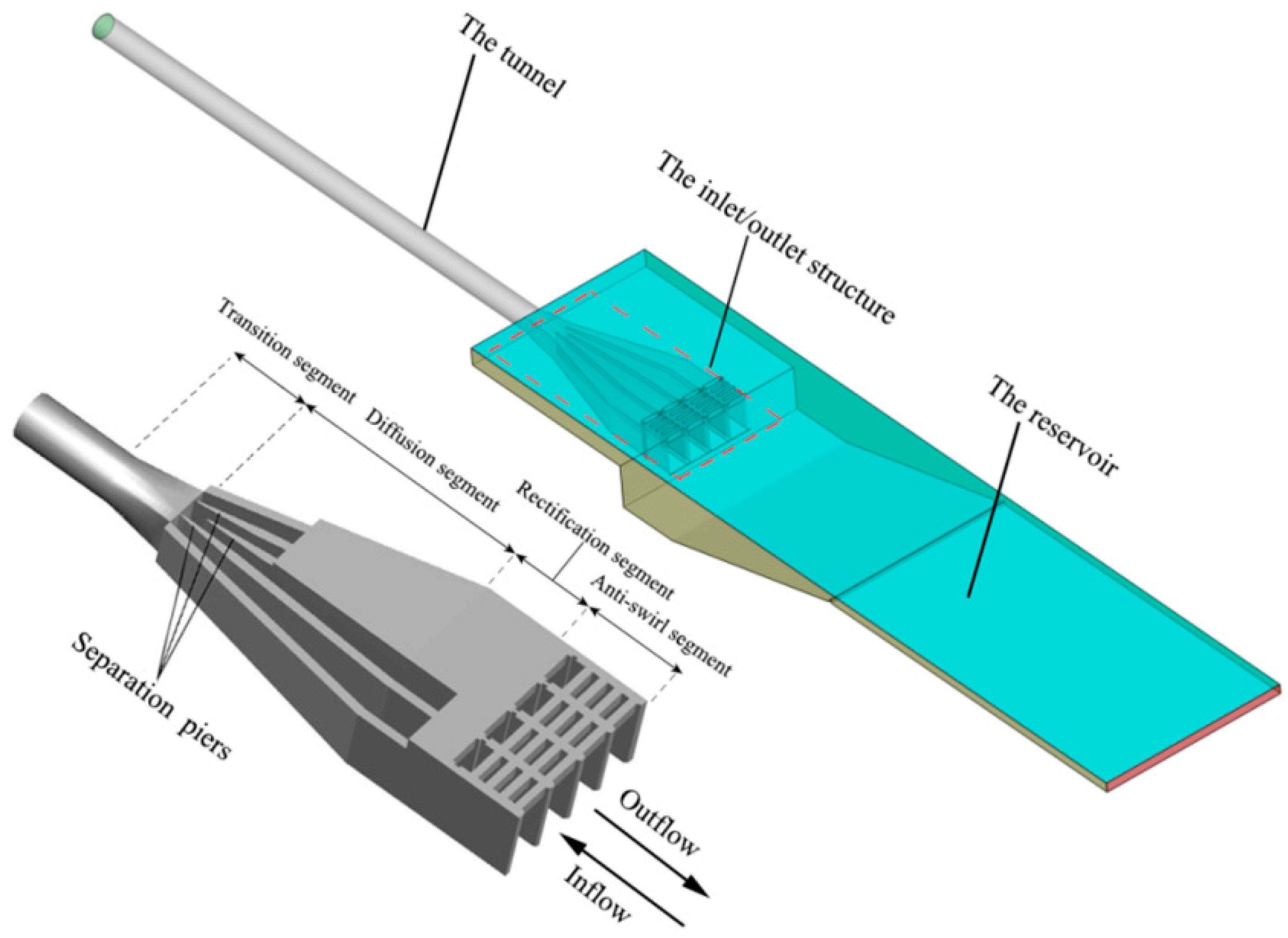
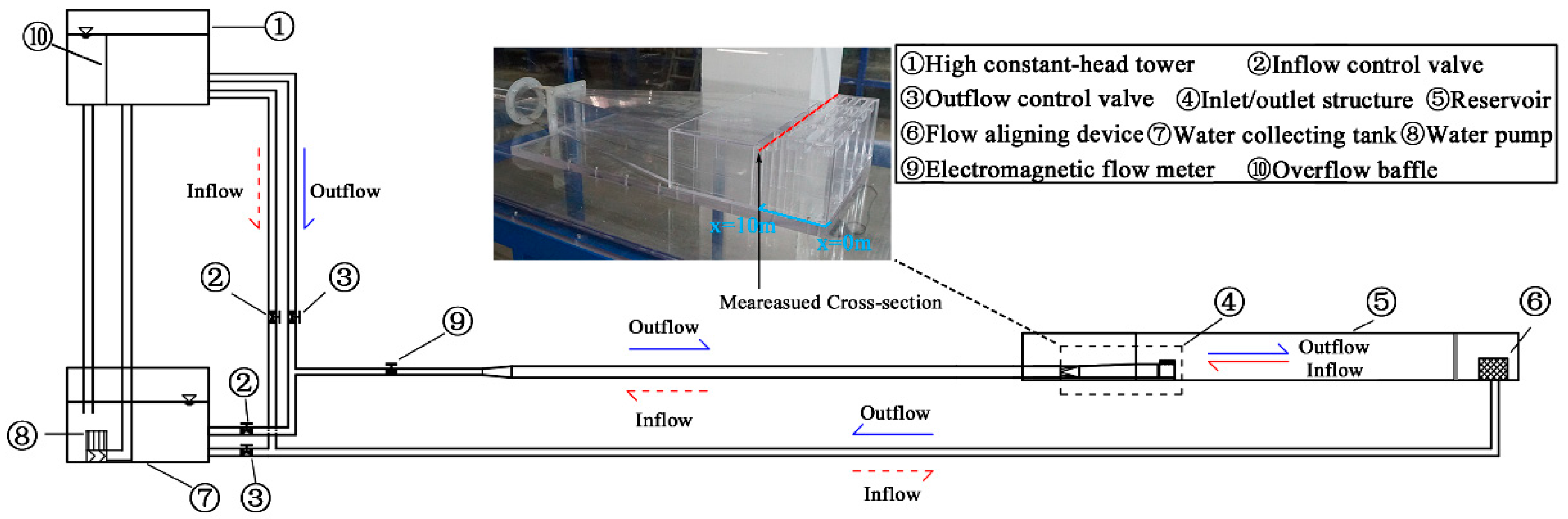
The typical shape of the lateral intake is shown in
Figure 1. When the PHES is in the generation mode, water flows into the lower reservoir through the tunnel and the inlet/outlet structure. Because water flows out from the inlet/outlet in this mode, the phenomenon is also called “outflow”. Along the outflow direction, the structure generally contains a transition part (a structure connecting a circular cross-section tunnel and a diffusion part), a diffusion part, a rectification part, and an anti-swirl part.
The diffusion part is very sensitive to the performance of the intake, and it is generally improved for the structure design.
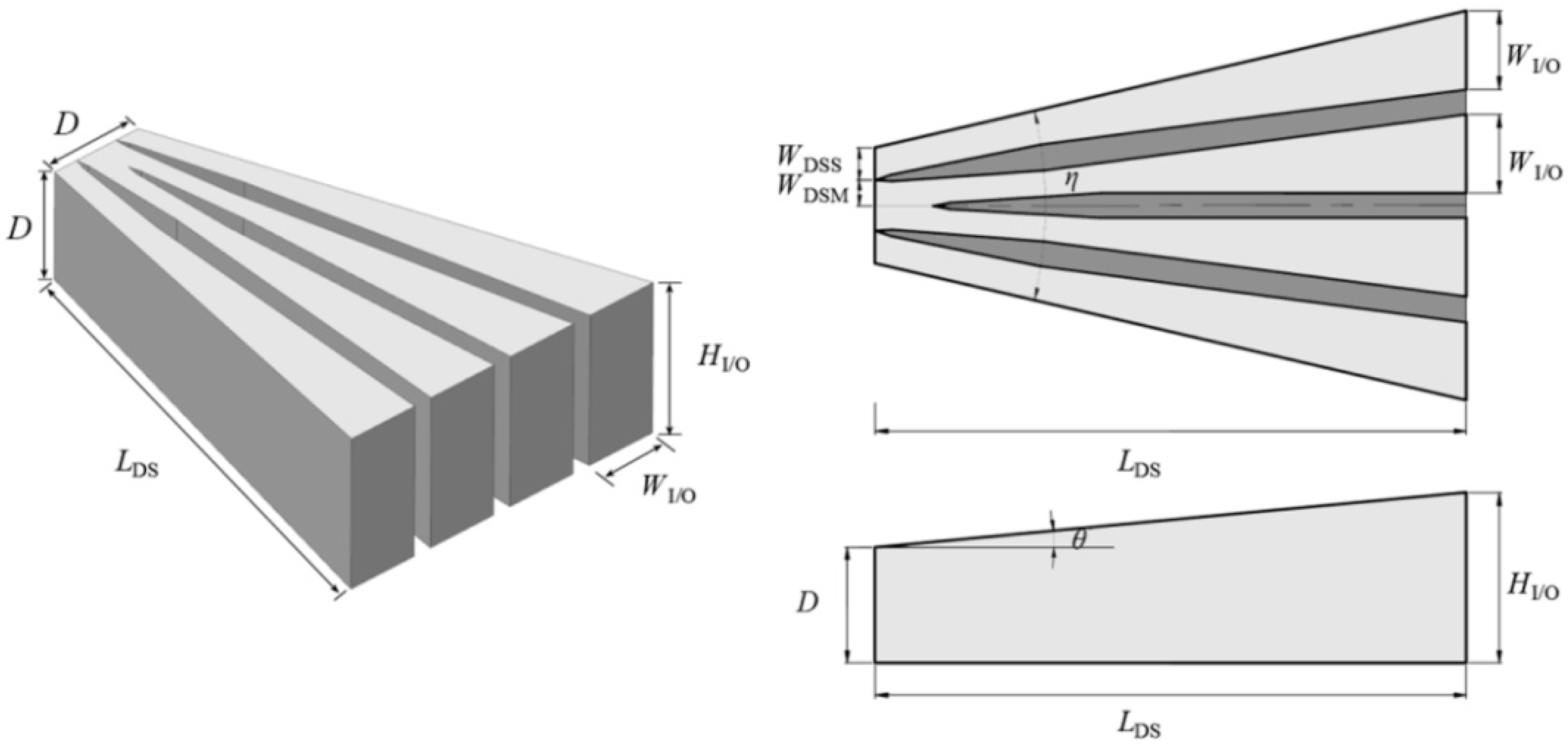
Figure 2 present flow passages and basic parameters in the diffusion part. This parameters include the length of the diffusion part (
LDS),height of the inlet/outlet orifices (
HI/O),wide of the separation pier in the middle orifices (
WDSM),width of the separation pier in the side orifices (
WDSS),horizontal diffusion angle (
), and vertical angle (
). The left side displays the 3D model for the flow passage. On the right side, plane sections of the model are demonstrated, and the flow passage and separation piers are marked out with light grey and dark grey, respectively. It should be noted that the tunnel diameter D in the PHES is generally decided beforehand by the difference of the water head between the upper and lower reservoir, the installed capacity of turbines, topographic and geological conditions etc. For the inlet/outlet optimization, the value of D is fixed (D = 7.2 m in the current study) because a change may need adjustment of the whole layout of the water conveyance system resulting in excessive costs. Besides, the number of orifices (4) is also fixed in view of it being the most commonly used form of the lateral inlet/outlet in the PHES of China. For more information about the shape parameters, readers can refer to the previous work [
38].
The lateral inlet/outlet hydraulic performance is characterized by three parameters: the head loss, the velocity, and the flowrate distribution [
37,
38,
39]. According to the Bernoulli equation, the head loss is computed as:
where the head loss
and
are used for the inflow and outflow mode, respectively;
is the coefficient of the head loss;
and
are the piezometric head in the reservoir and tunnel;
is the bulk velocity at the boundary of the tunnel;
is the kinetic energy correction coefficient.
Numerous vibration-caused trash rack failures have occurred because the trash rack may be exposed to high velocities at the orifice cross-section [
40]. Hence
is proposed as a typical index evaluating the uniformity of the flow velocity at orifices [
39,
41], and a lower
implies a better velocity distribution in the inlet/outlet. Considering there are four orifices divided by the separation pier,
could change with different orifices due to the influence of horizontal diffusion. In order to represent the overall performance of the velocity distribution, the worst case i.e., the maximum value of
among the four orifices, is selected. Thus
is defined as:
where
is the maximum value among the velocities at the orifice cross-section;
i indicates the index of orifices;
indicates the average velocity at the orifice cross-section.
In order to further improve the discharge distribution in the horizontal direction, the separation piers are designed to divide the flow passage into sub-tunnels. Then
is used to estimate the degree of flux uniformity by comparing the discharge between adjacent orifices, which can be defined as:
where
indicates the rate of flow at the different orifices (
i = 1, 2, 3).
For the purpose of determining a good compromise between the two modes of operation, these parameters under inflow and outflow conditions should be carefully combined. In a recent study, Gao et al. [
38] simply added up the parameters for the pump mode and the generation mode to estimate the total performance. However, the performance of the generation mode is probably more significant than that of the pump mode in many cases. The pumped water can be stored in the upper reservoir under the pump mode during the low load period of the power grid, while under the generation mode the water will flow into the lower reservoir to generate electricity during the peak load period. Designers tend to pay more attention to the head loss under the generation mode in order to achieve higher economic benefits. Therefore, a more reasonable approach is to use weights to deal with the combinations of the two modes. For that reason, the new combined objectives to evaluate the overall performance of the inlet/outlet are defined as follows:
where
and
are the overall head loss coefficient and velocity distribution coefficient, respectively;
and
are the weight coefficients of the objective function under the conditions of inflow and outflow, and
. In this article, the values of
and
are taken as 0.33 and 0.67 based on the specific engineering designer’s suggestion. However, they can be flexibly selected according to different projects.
Another drawback of their study [
37,
38] is the definition for the overall
, which is expressed as the difference of
between the pump and generation mode.
is the discharge uneven distribution coefficient under inflow condition,
is the discharge uneven distribution coefficient under outflow condition. When it is regarded as an objective function, it seeks to minimize the difference between
and
, rather than
and
themselves. If there are some bad points in the design space, on which the values of both
and
may be large, the difference (i.e., the overall
) may be small. Besides, according to the guideline the discharge distribution is sufficiently uniform when
is less than 10% [
39]. As a result it is more appropriate to choose
as the constraint, and the head loss and velocity distribution (
,
) can be optimized more flexibly.
Therefore, the objective functions were set to find the minimum values for
and
, while
,
η, and
θ were treated as constraint conditions.
Table 1 lists the design parameters and constraints in this study.
6. Conclusions
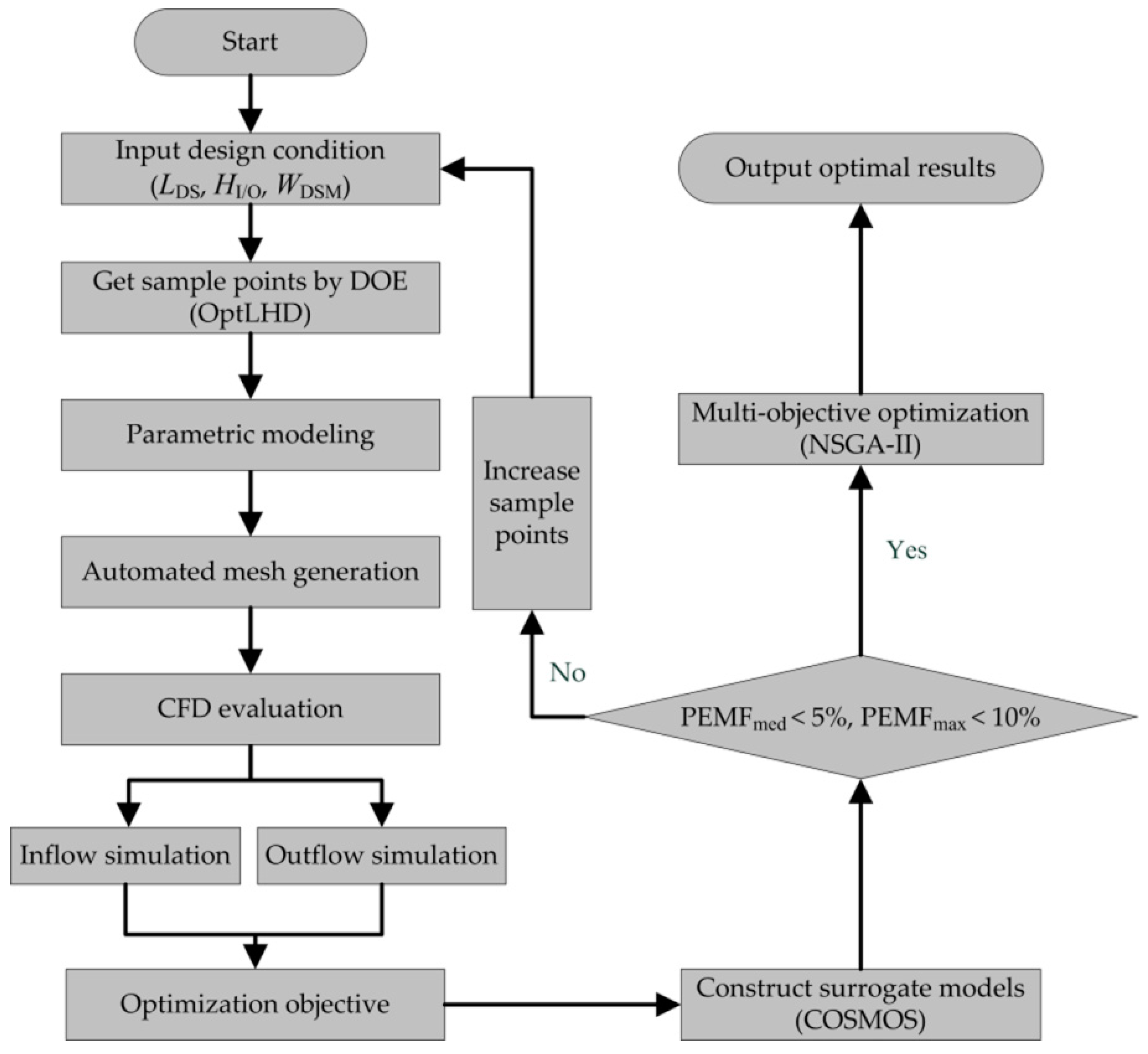
In this article, the CFD numerical simulation and multi-objective surrogate-based optimization strategy method (COSMOS and NSGA-II) were combined to optimize intake shape effectively. The CFD method applied in this paper was validated by a physical experiment carefully designed to meet bidirectional flow requirements for the inlet/outlet. For the purpose of determining a good compromise between the two modes of operation, reasonable weights were defined to better evaluate the overall performance. Then, suitable surrogate models based on COSMOS were utilized to build functions, and NSGA-II was chosen to complete the optimization.
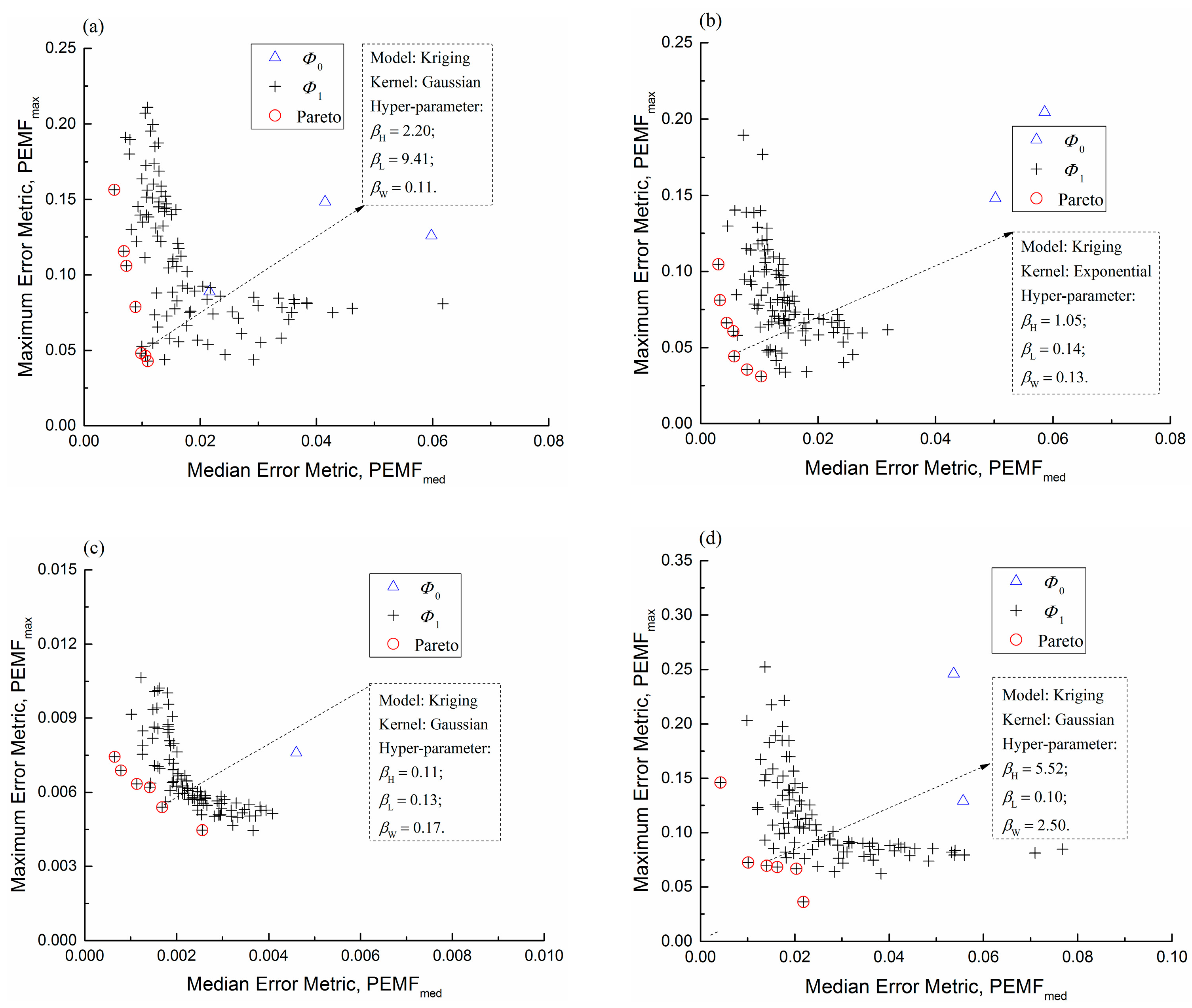
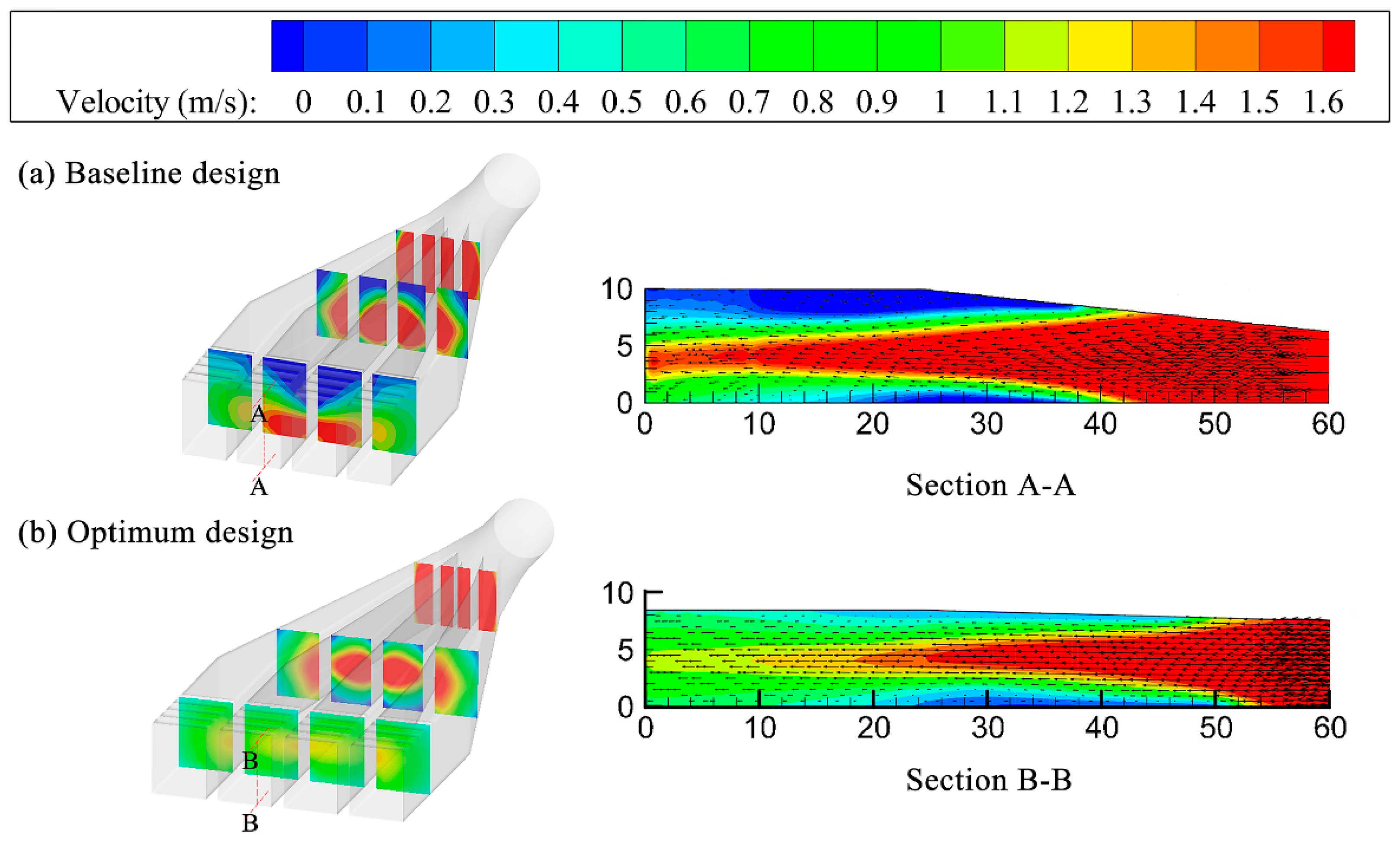
The optimum shape of the diffusion part in a PHES can be achieved automatically through the whole process, including numerical model building, CFD simulation, optimal surrogate model selection, and multi-objective optimization strategy. There were 60 sampling points generated by the OLHS employed to establish suitable surrogate models based on COSMOS, while the PEMF method was applied to estimate errors. The results indicate that the Kriging with a Gaussian kernel is best for the overall head loss coefficient and the shape parameter βH = 2.20, βL = 9.41, βW = 0.11; the best configuration of the overall velocity distribution coefficient is the Kriging model with an Exponential kernel and βH = 1.05, βL = 0.14, βW = 0.13.
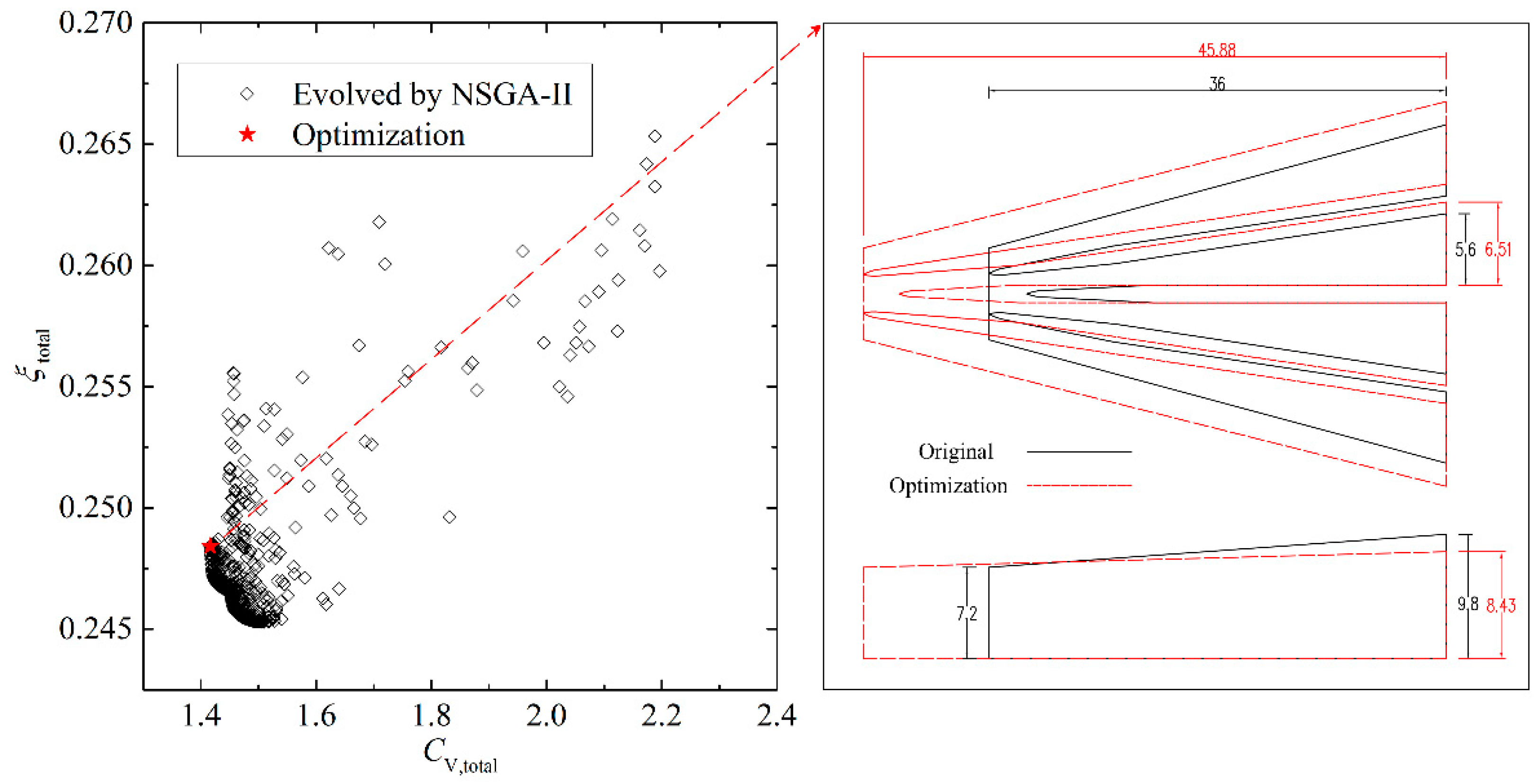
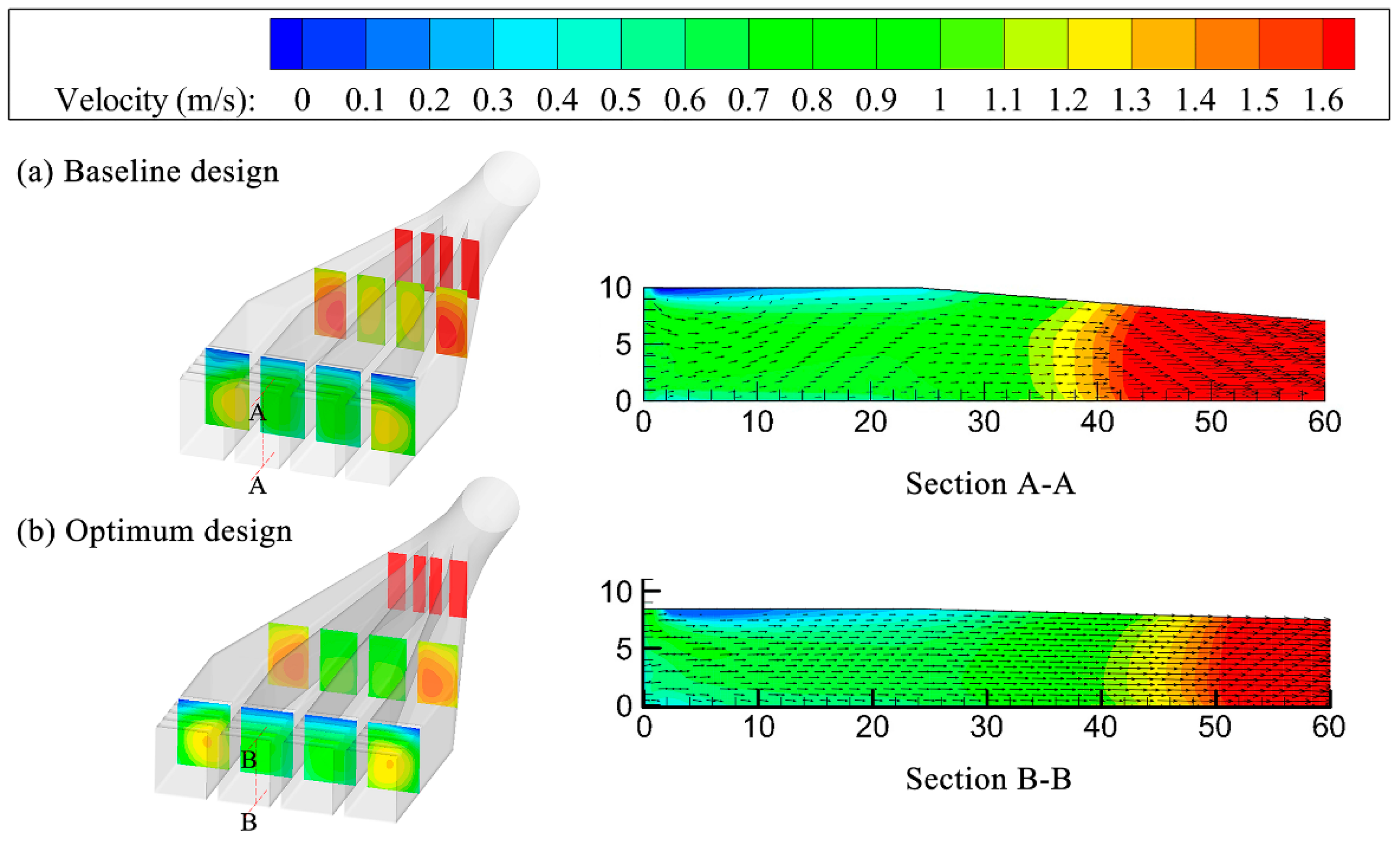
Finally, the NSGA-II algorithm was applied to generate Pareto optimal results, and the final optimal point was selected from the Pareto set through the TOPSIS decision making method. The optimization results show that compared with the original shape the overall head loss coefficient decreases by 6.42% and the overall velocity distribution coefficient decreases by 40.28%. This study demonstrates this new optimization process is a good choice for inlet/outlet engineering designers.