Study of Industrial Naphtha Catalytic Reforming Reactions via Modelling and Simulation
Abstract
:1. Introduction
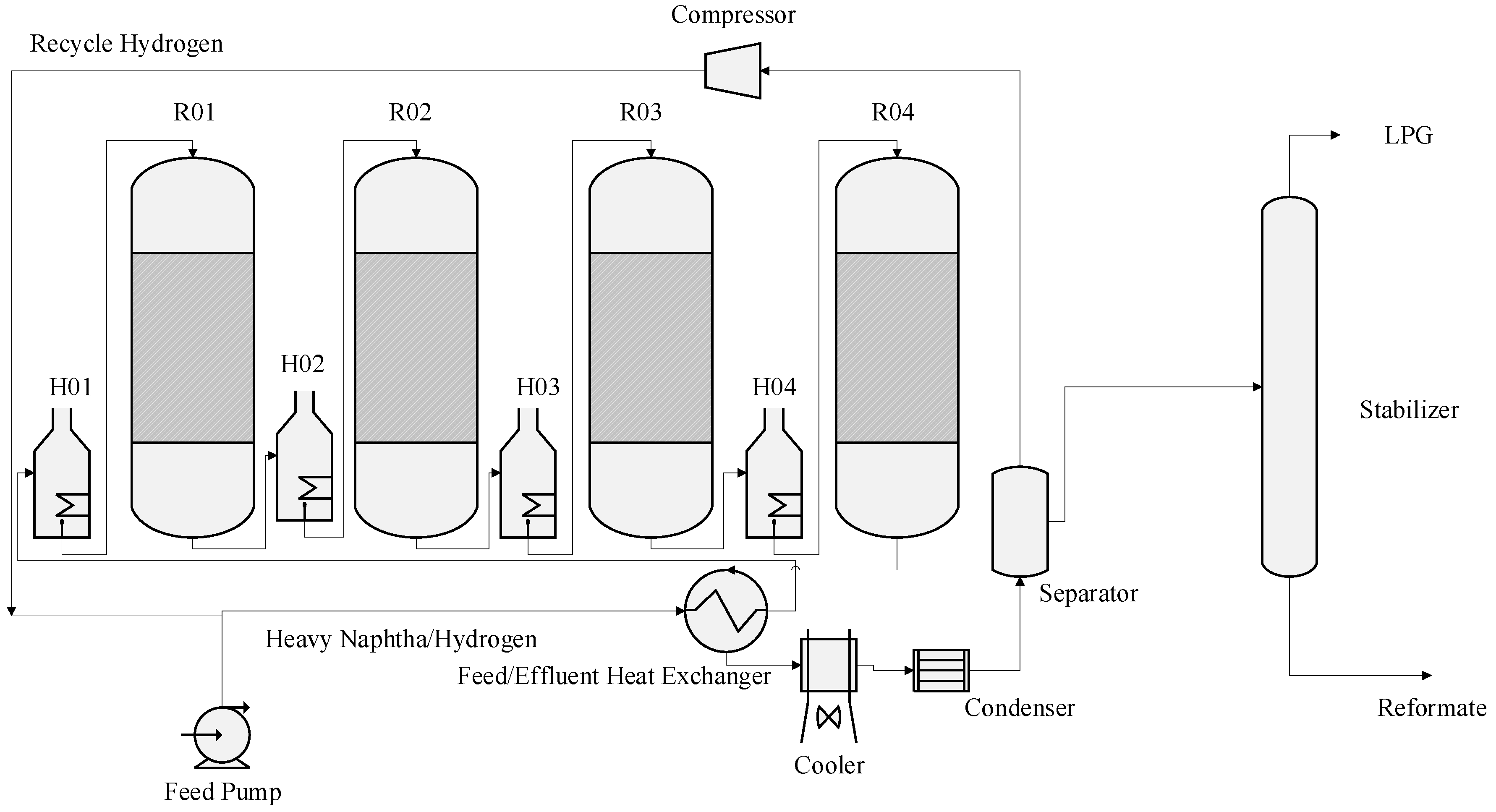
2. Process Description and Process Variables
| Dehydrogenation | Metallic function |
| Dehydrocyclization | Metallic + acidic functions |
| Isomerization | Metallic + acidic functions |
| Hydrogenolysis | Metallic function |
| Hydrocracking | Metallic + acidic function |
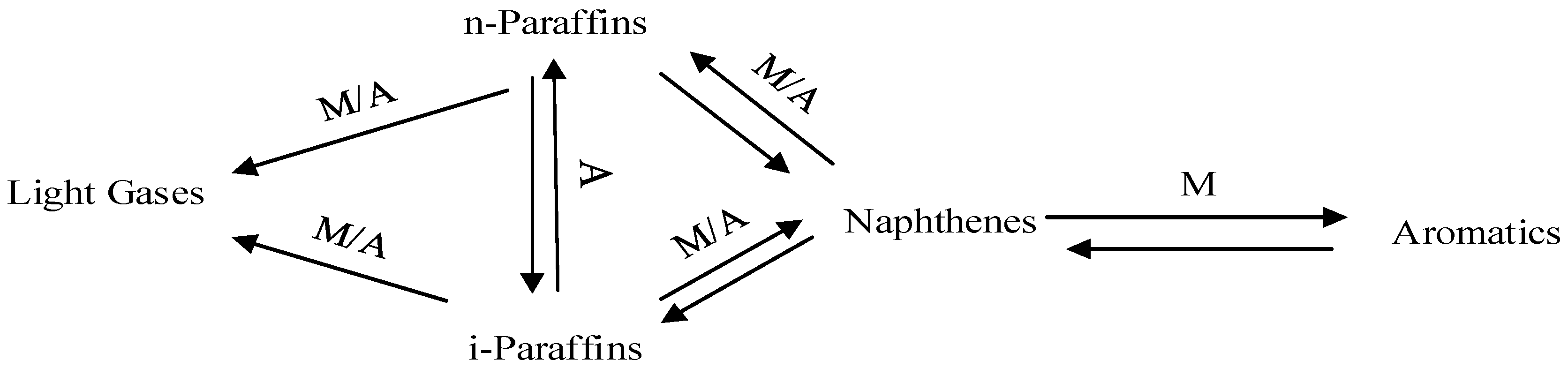
Process Classification
3. Kinetic Models
4. Mathematical Model
5. RON Model
6. Model Validation
7. Results and Discussion
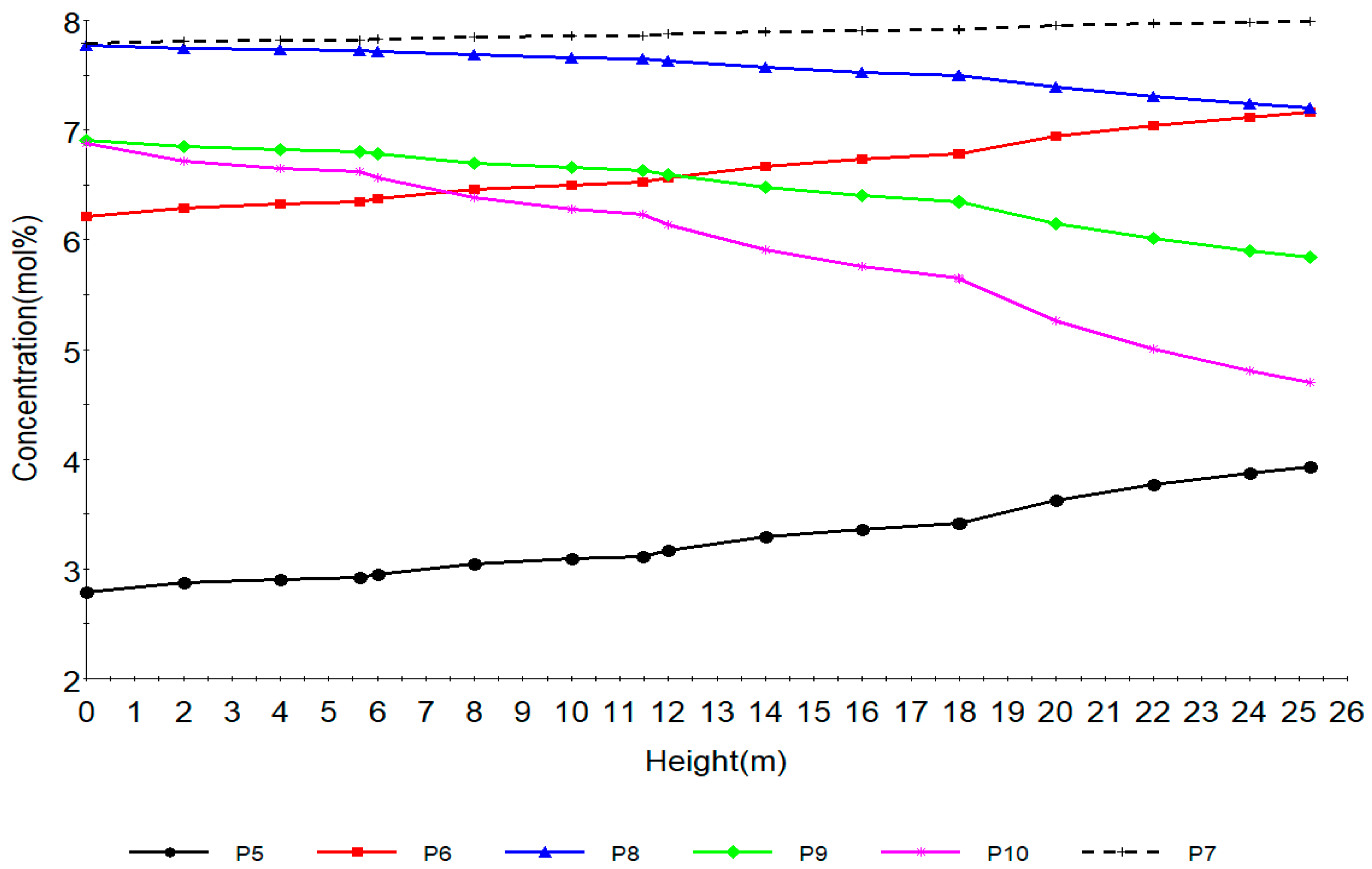
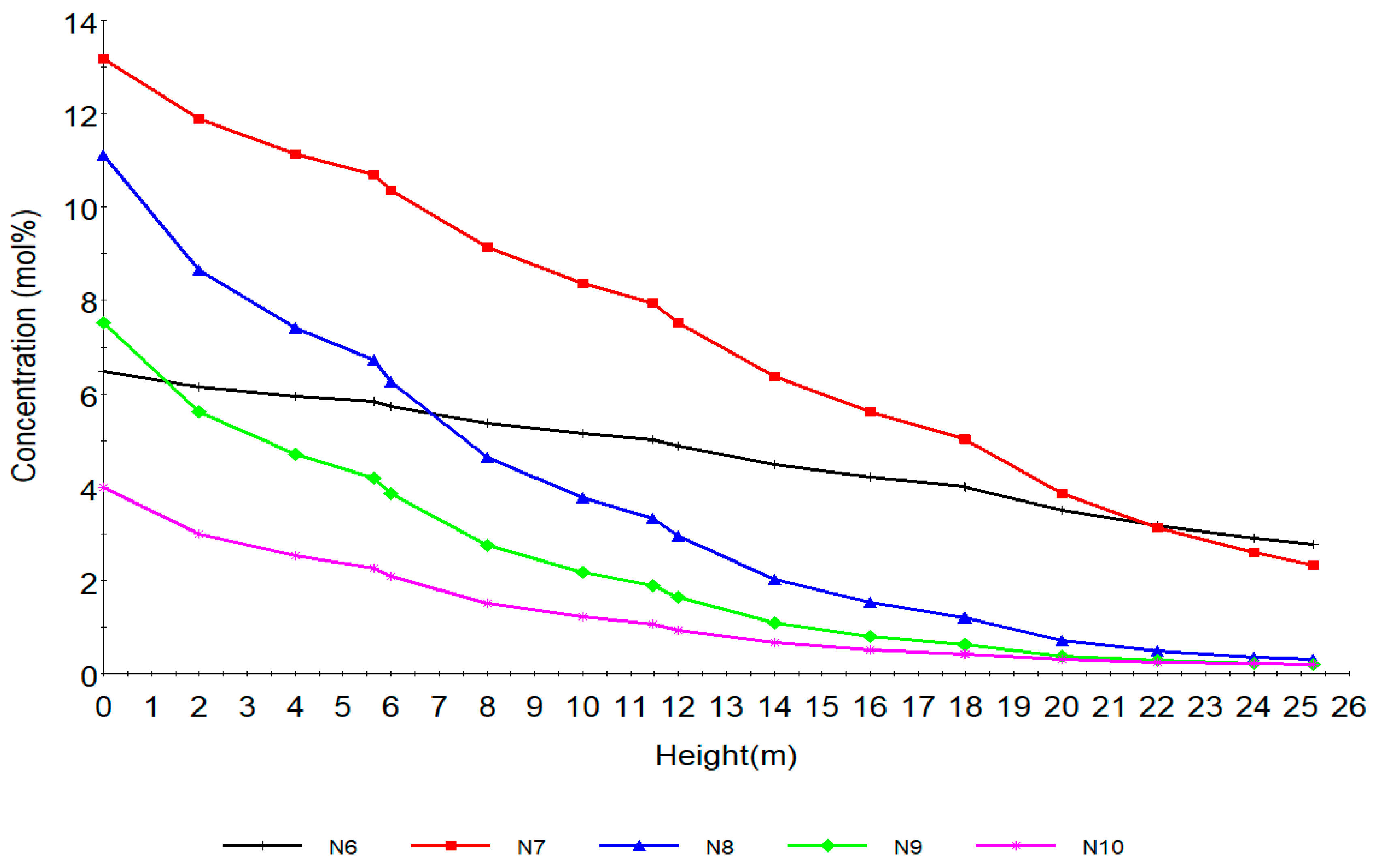
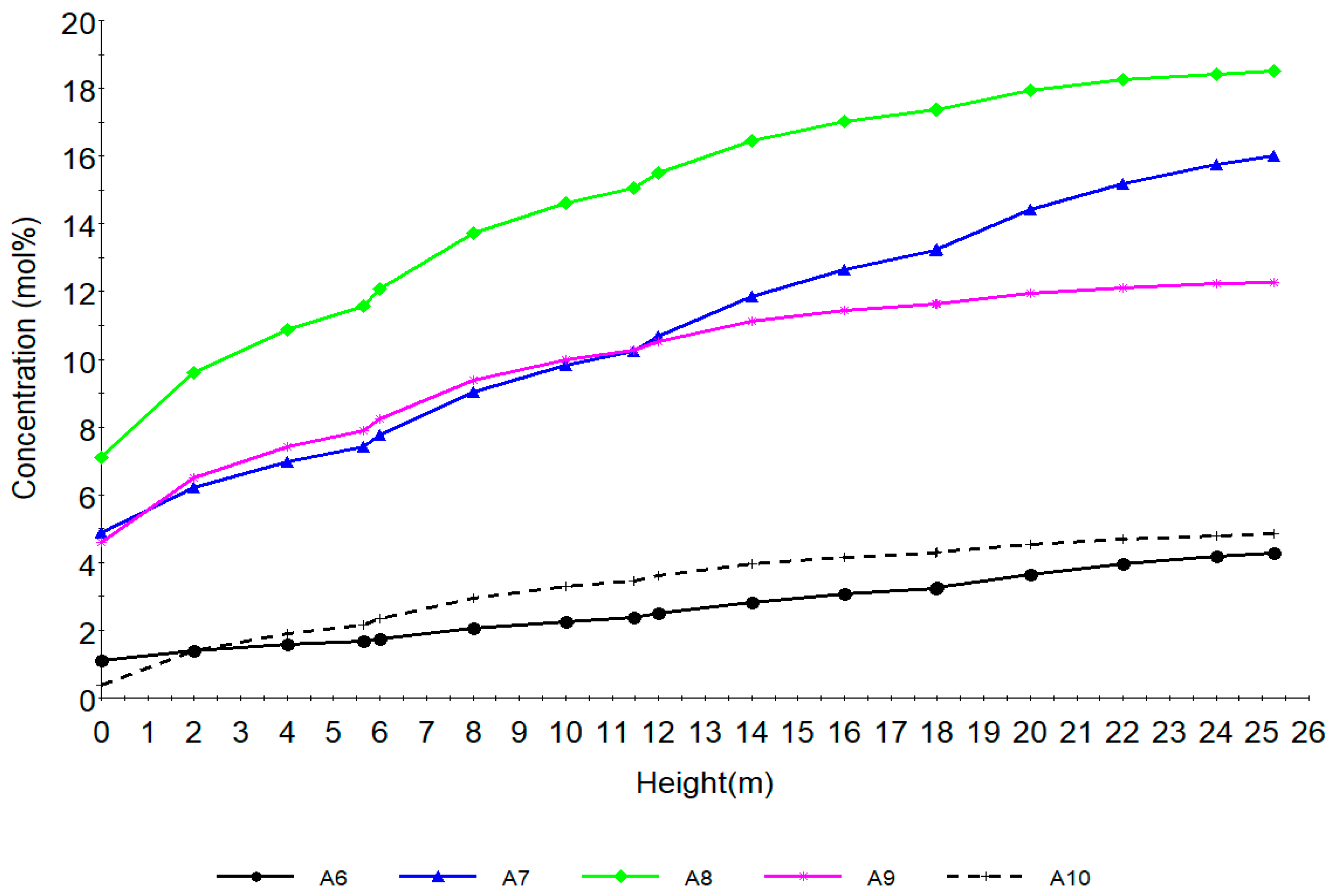
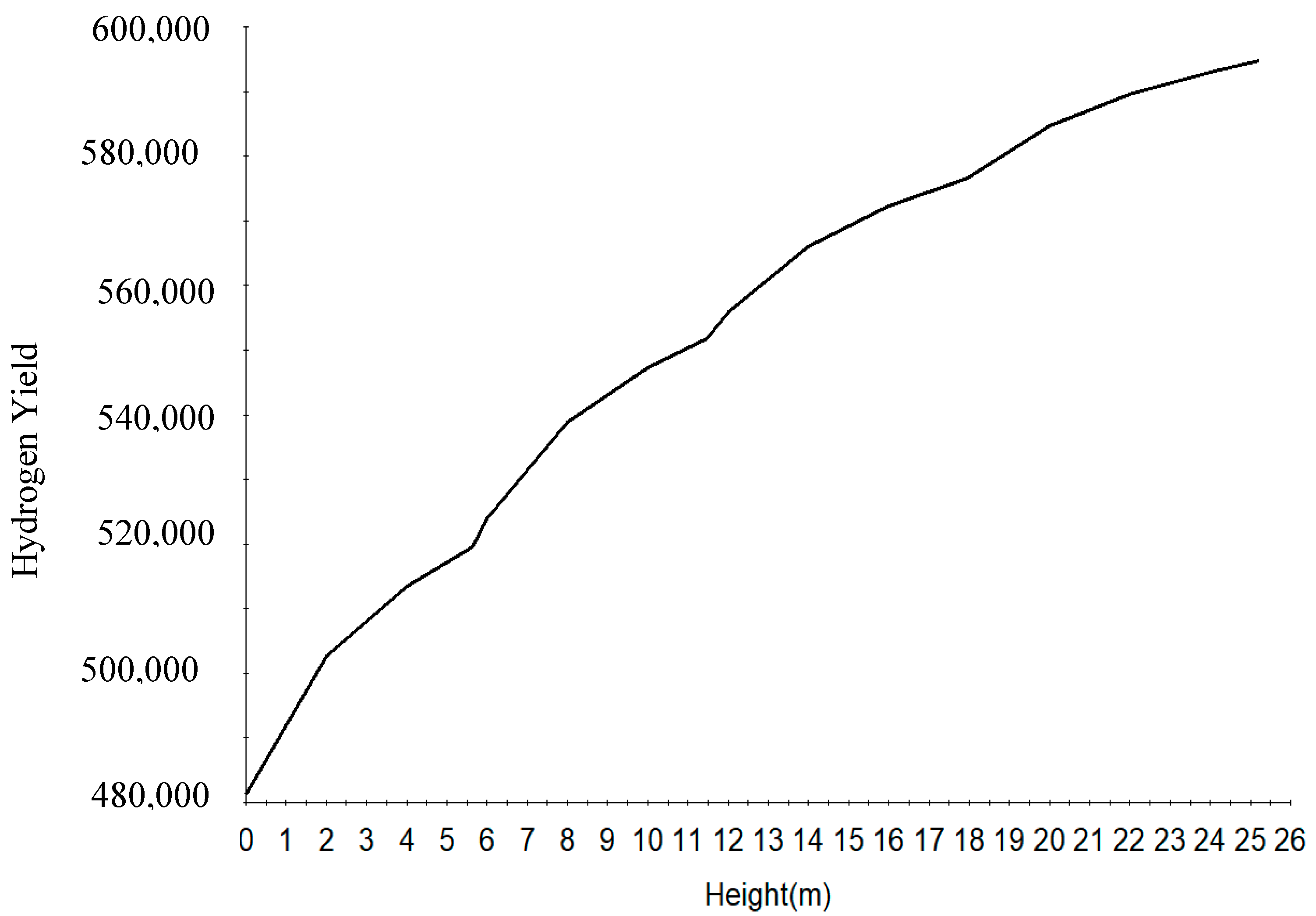
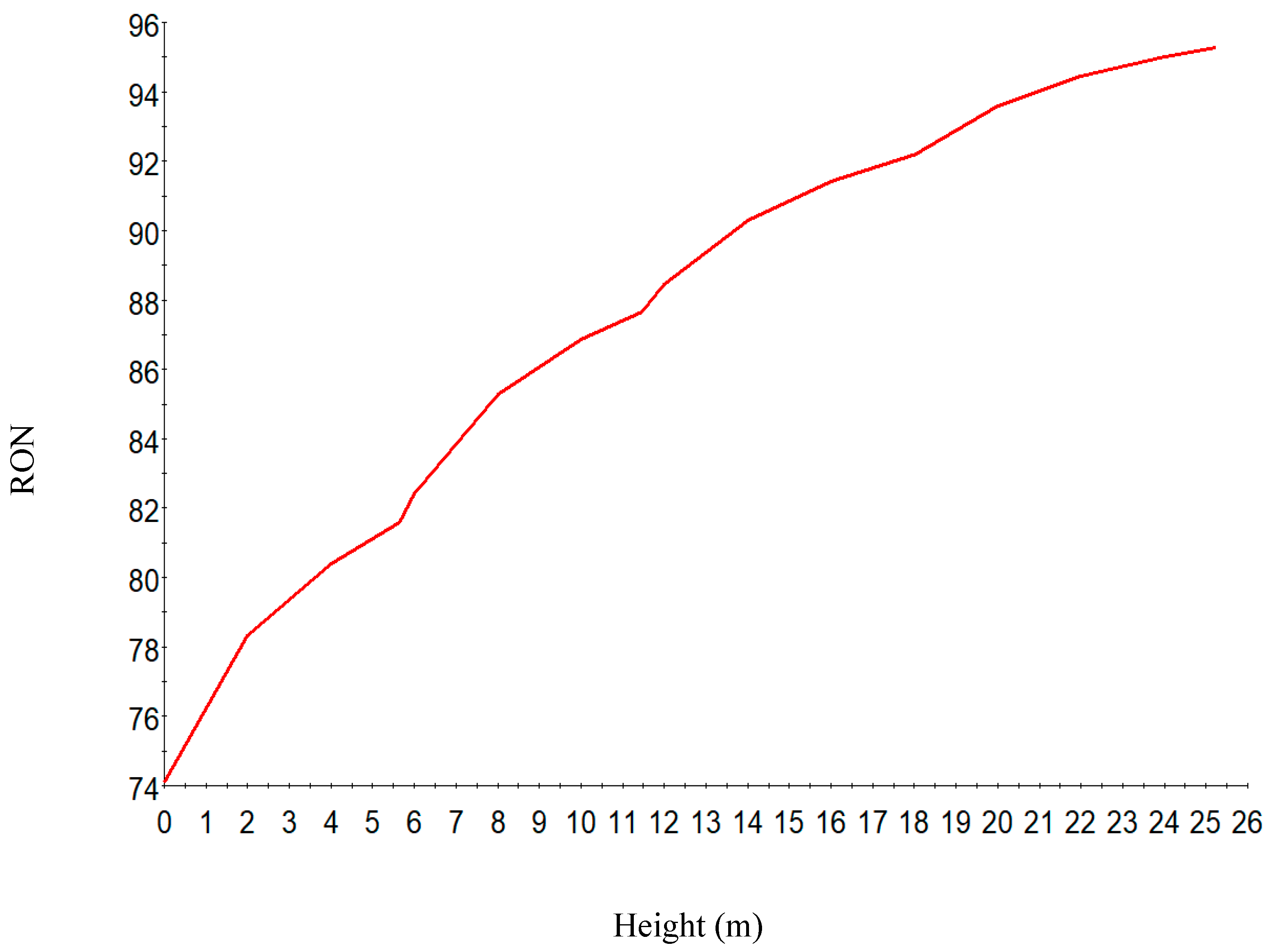
7.1. Steady State Simulation Results
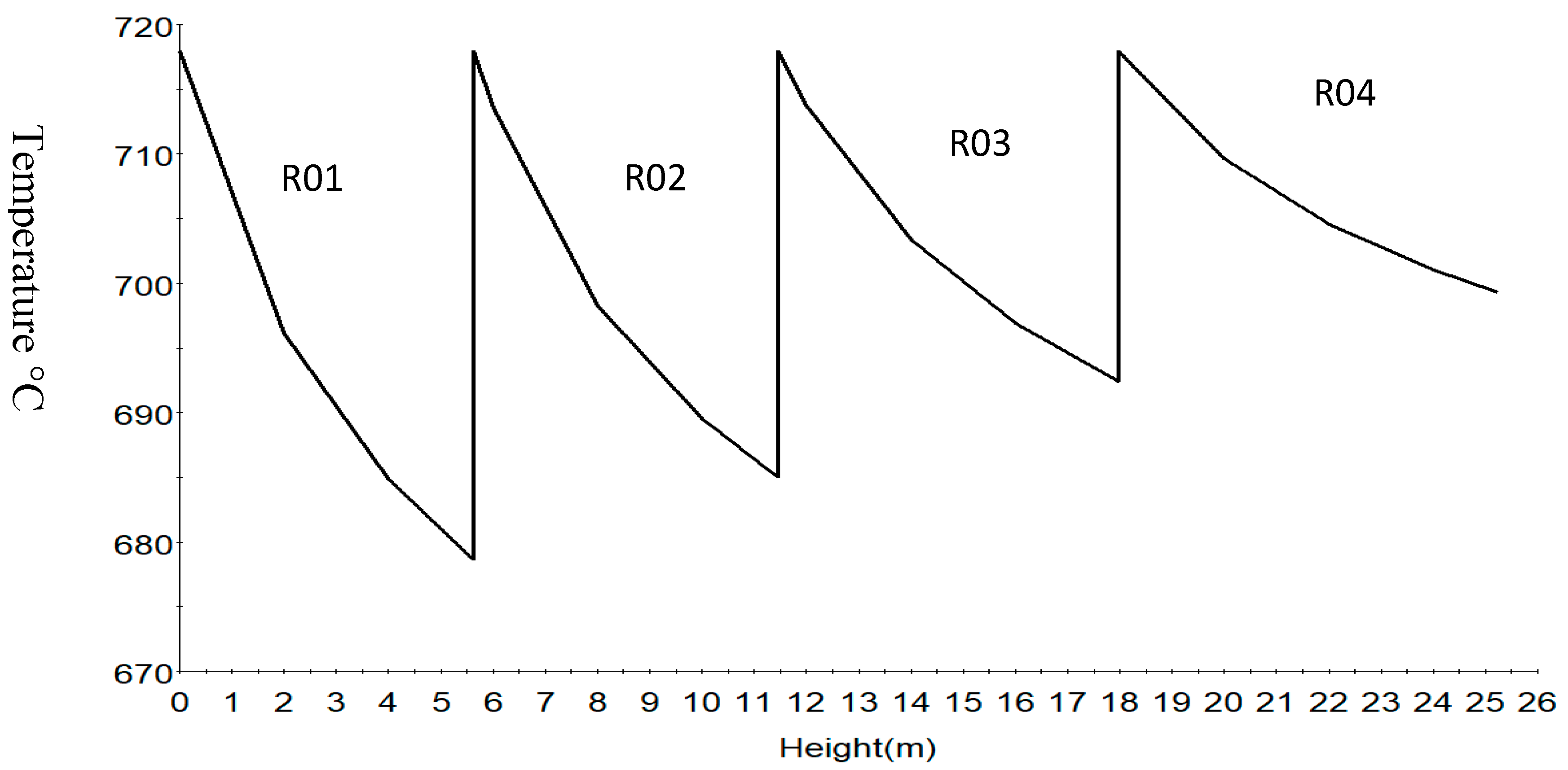
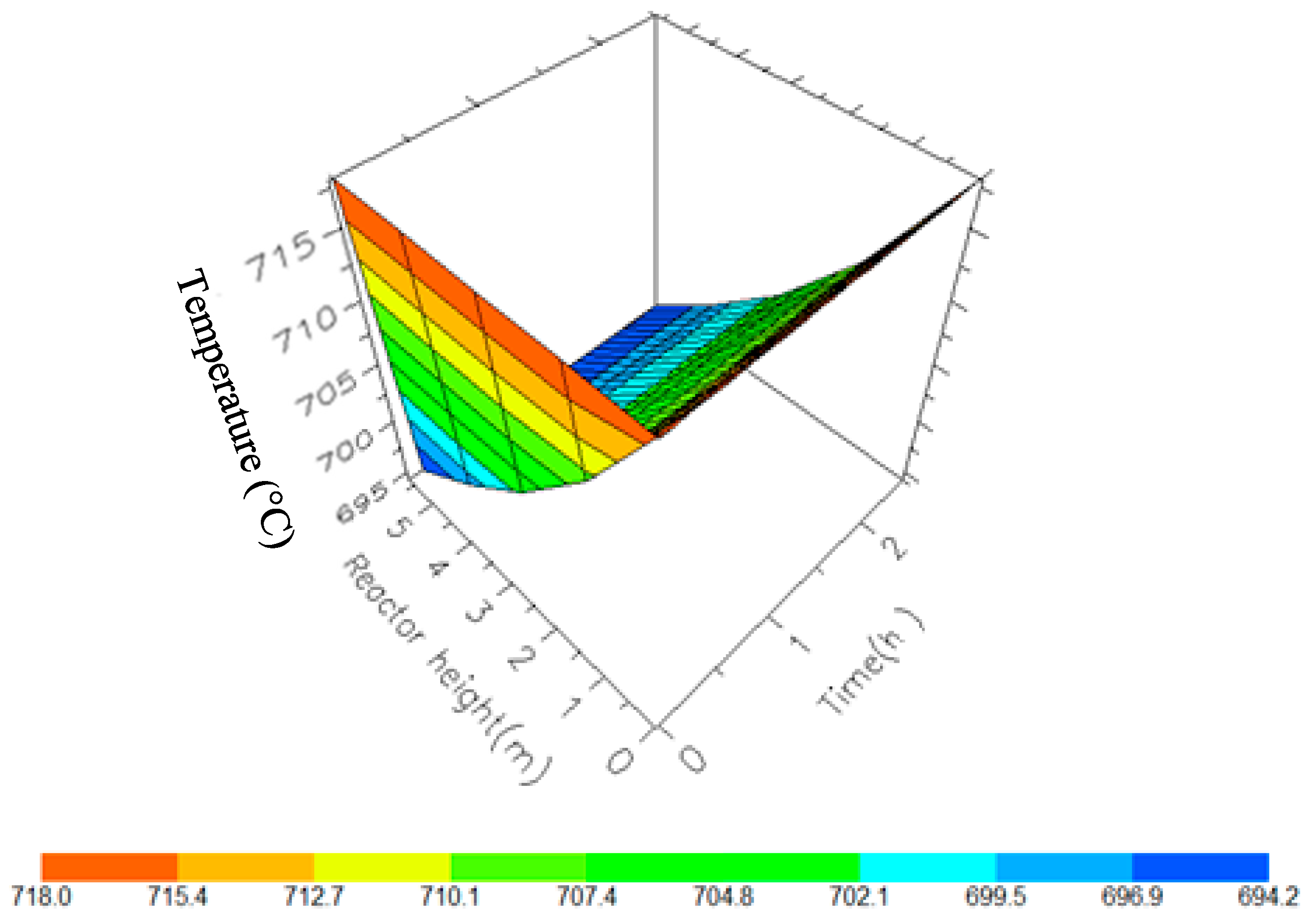
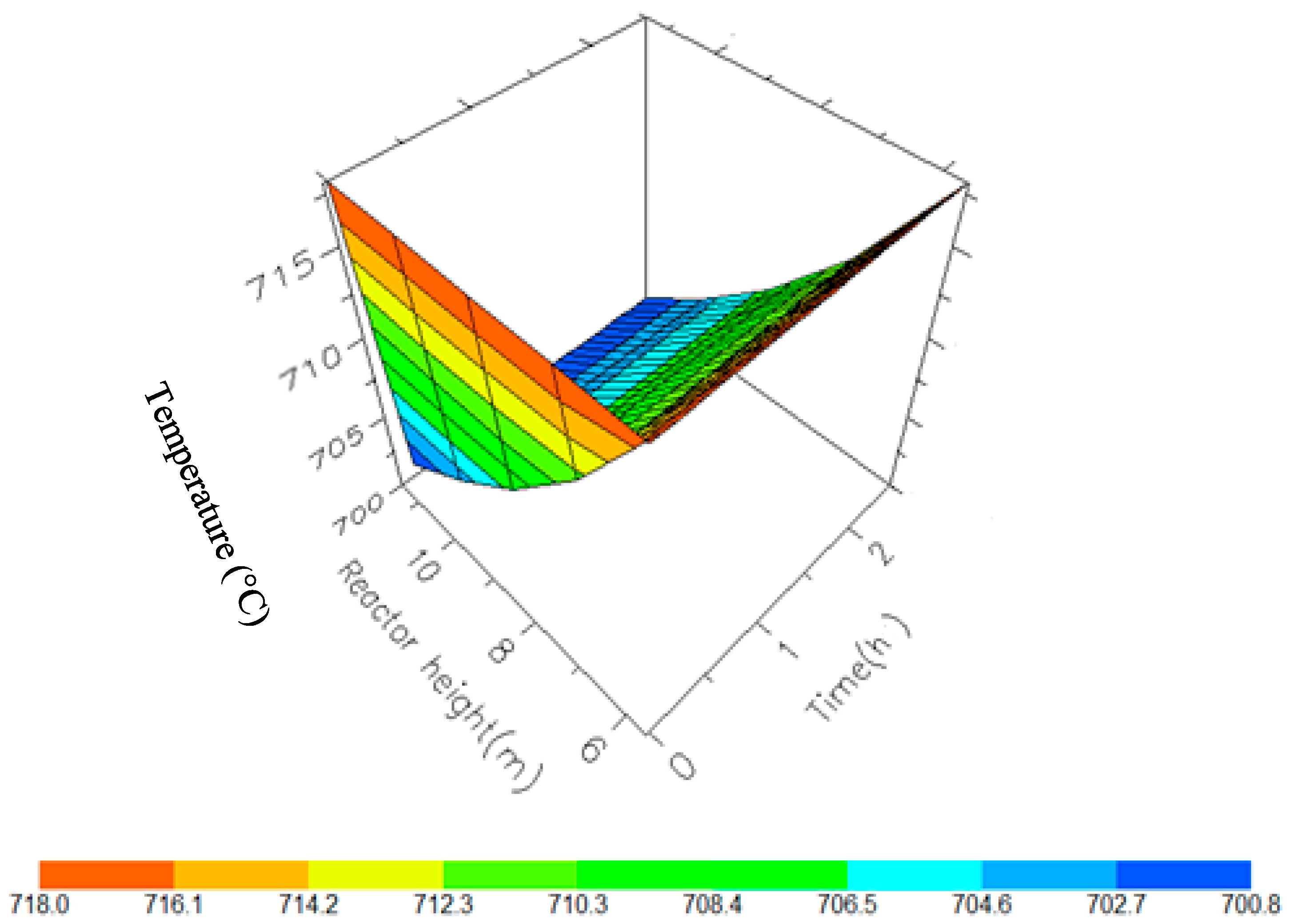
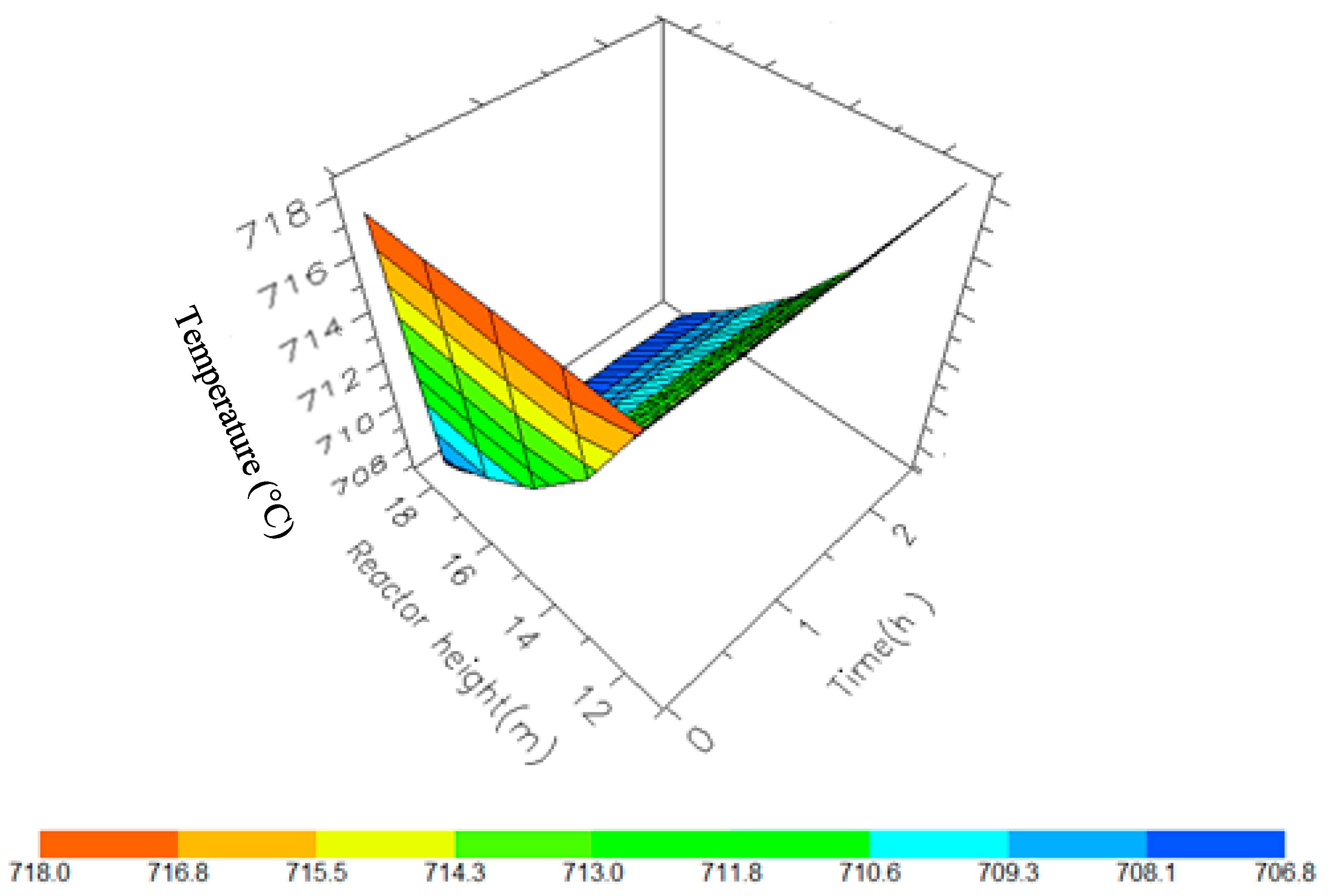
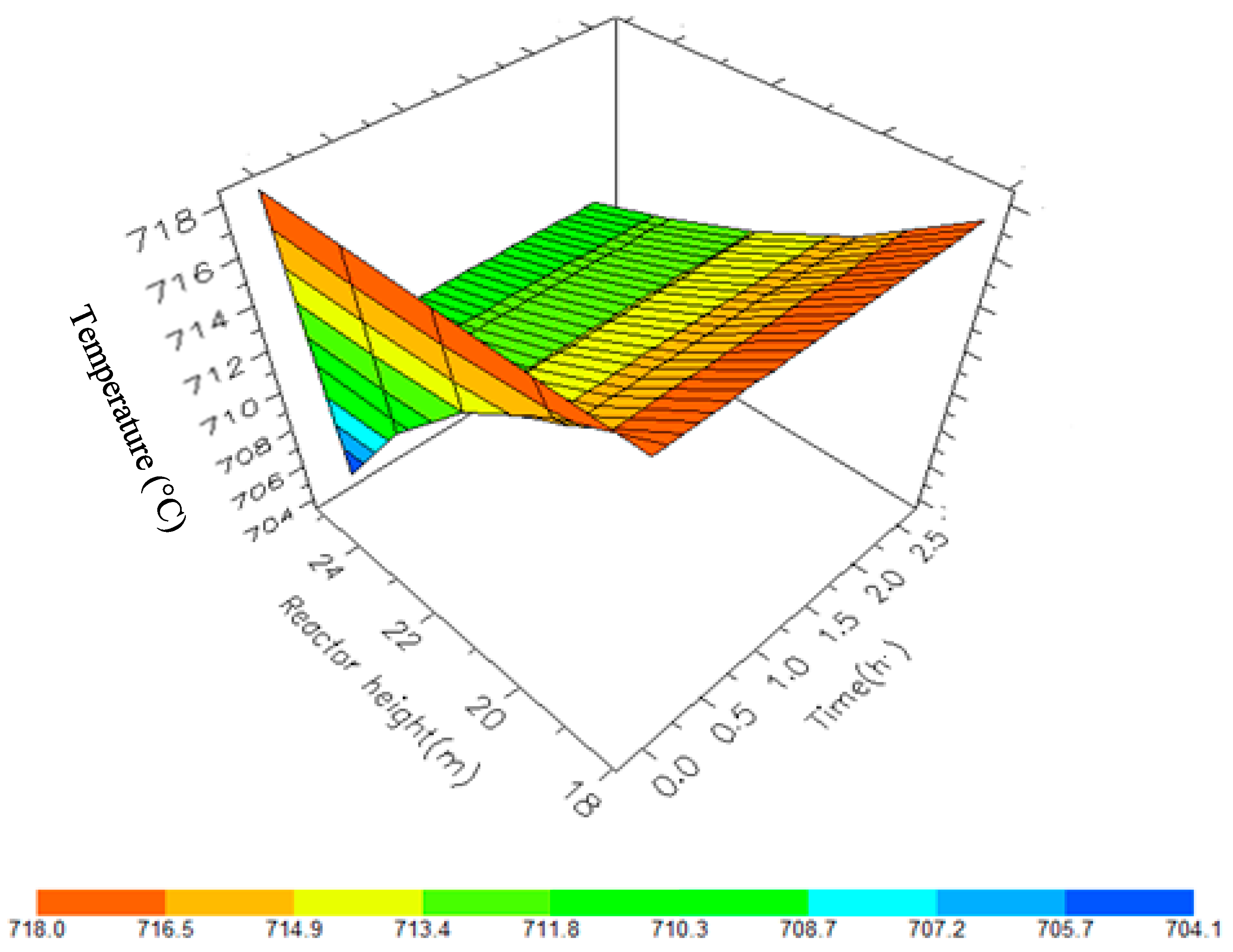
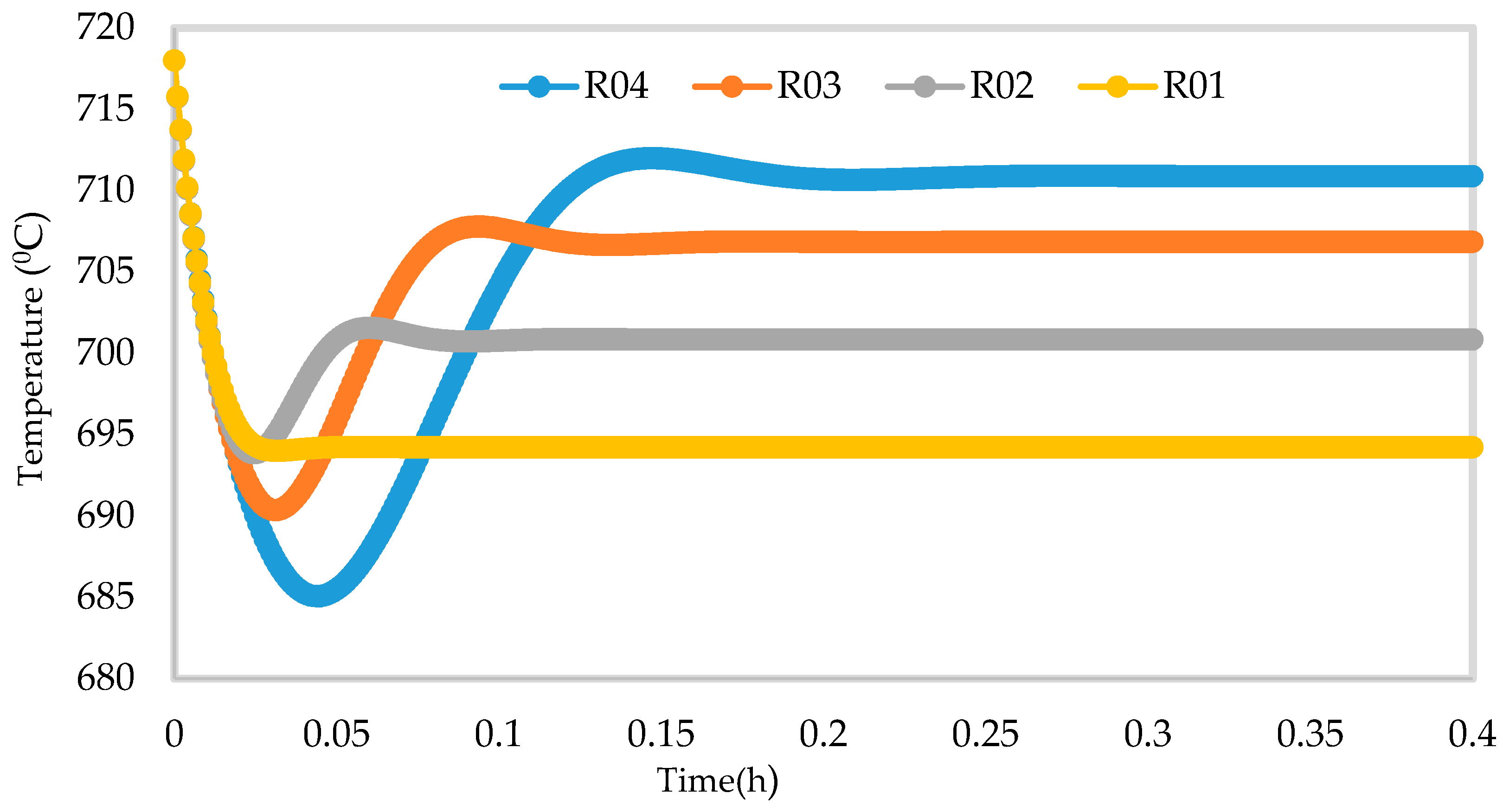
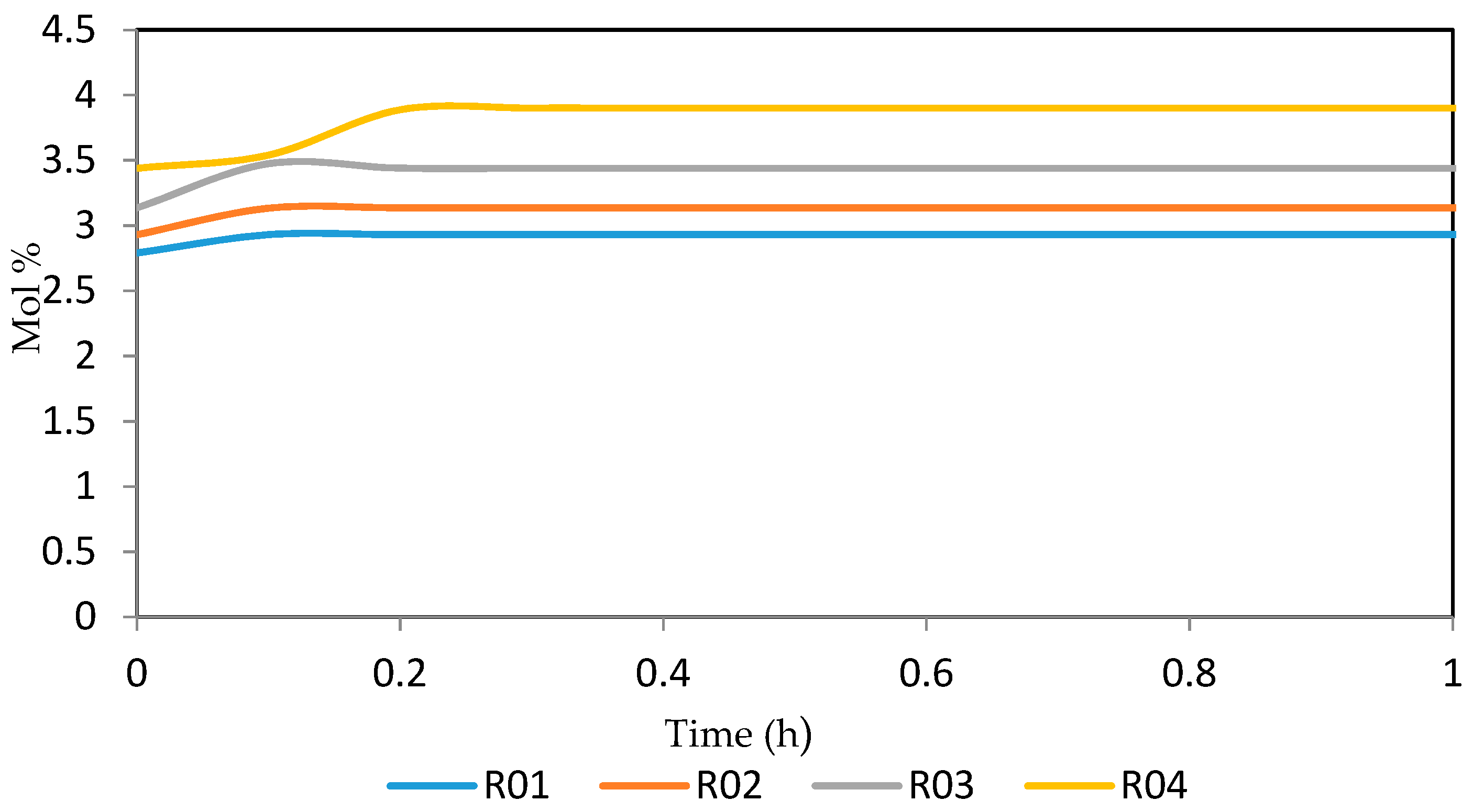
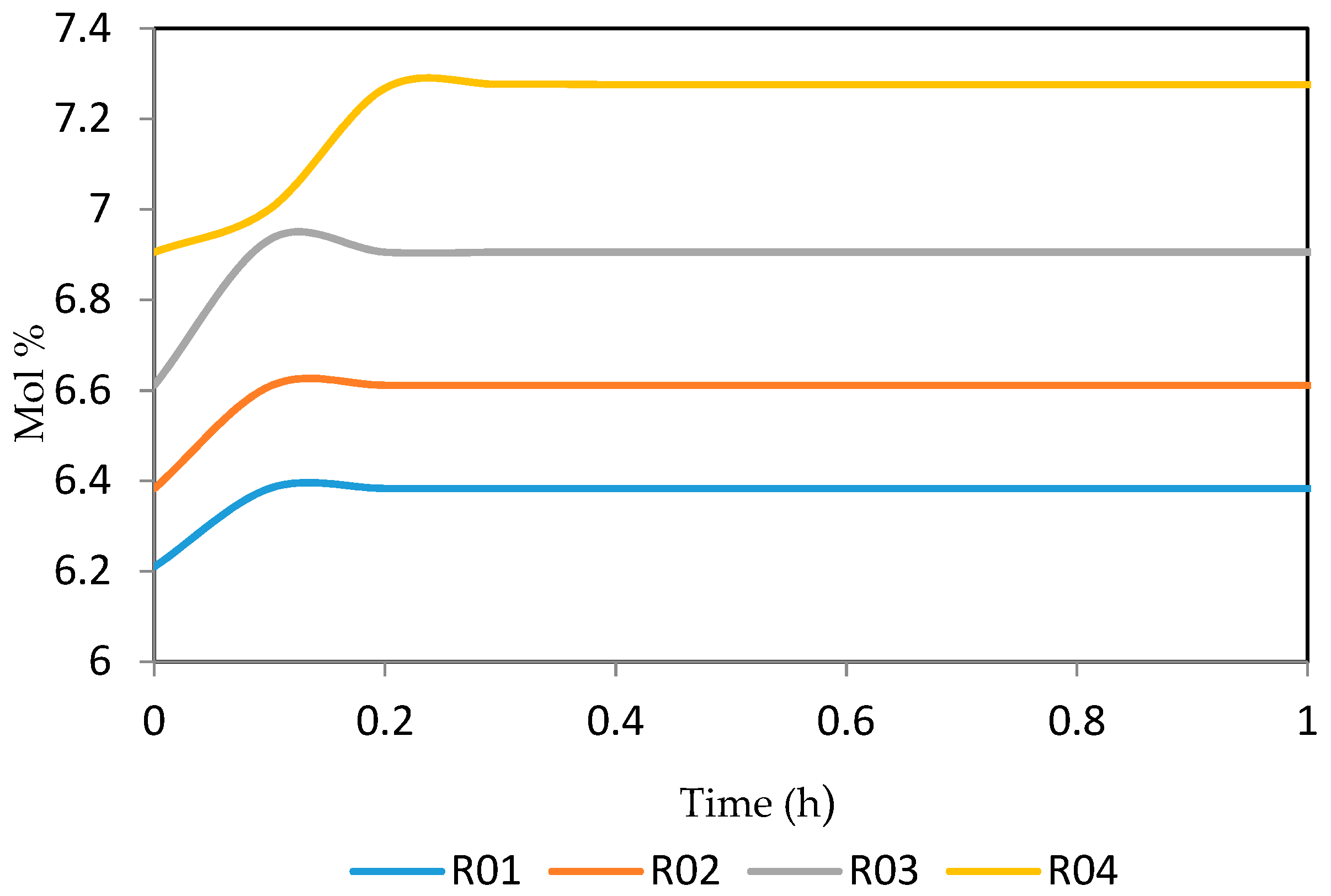
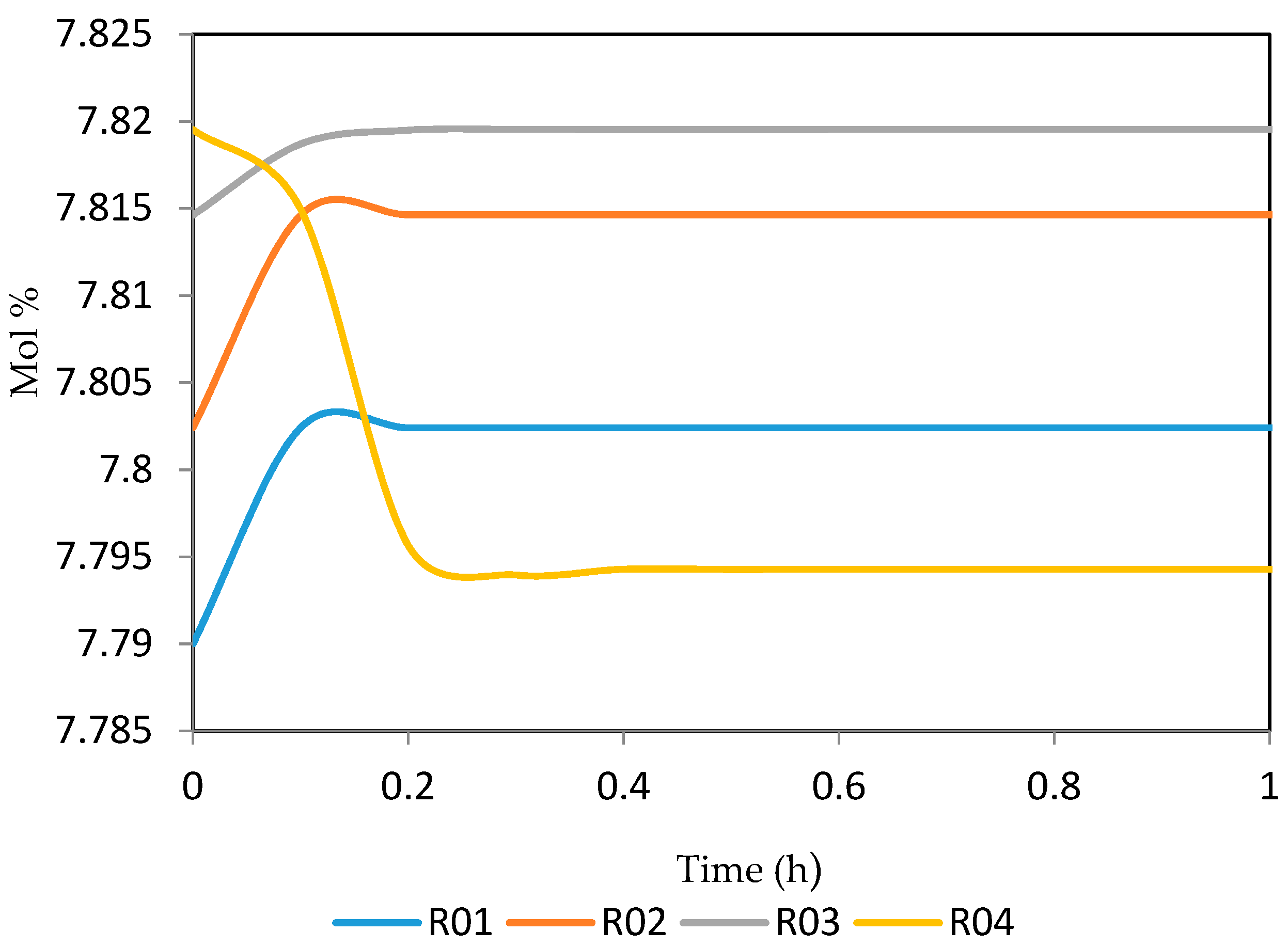
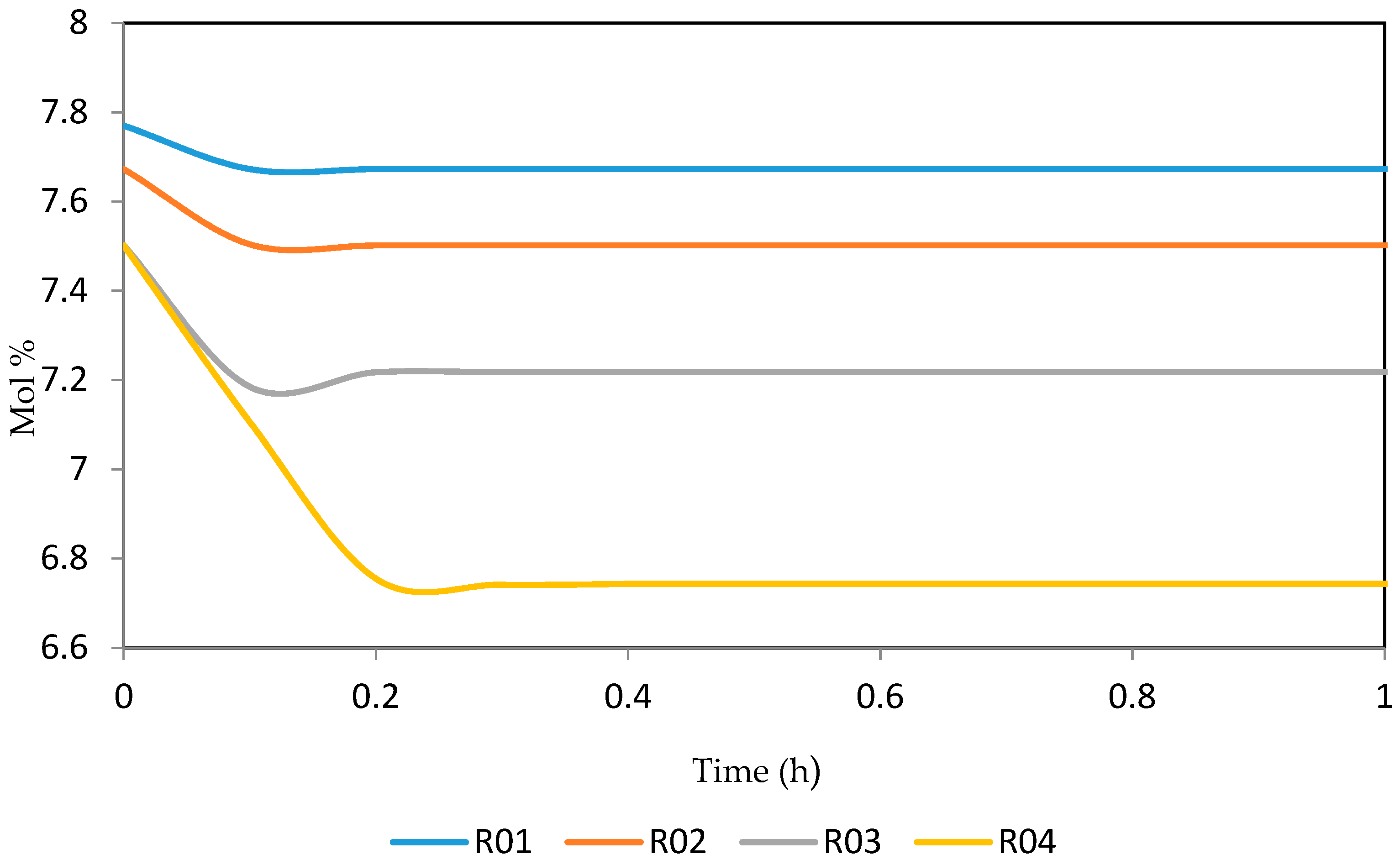
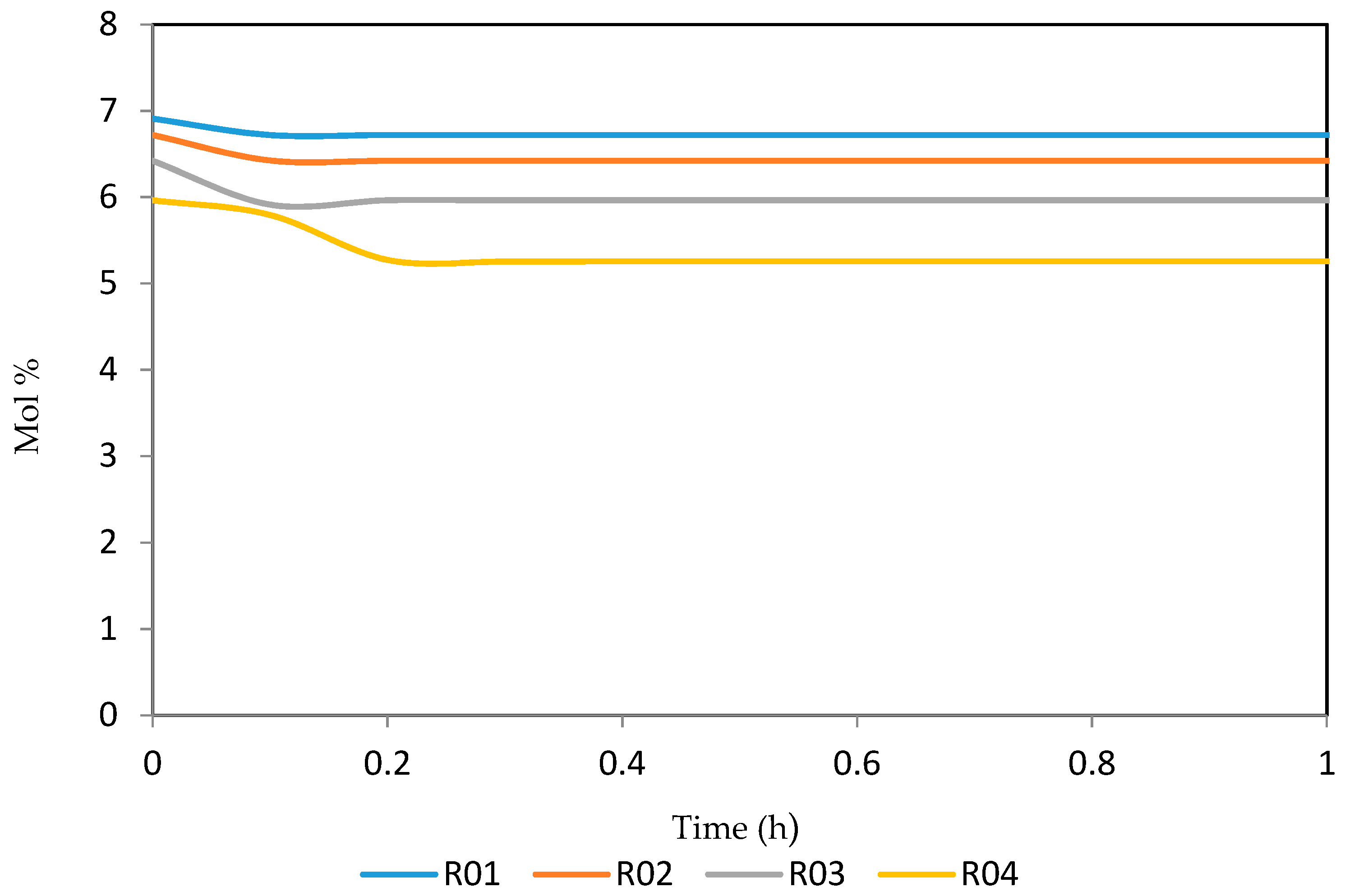
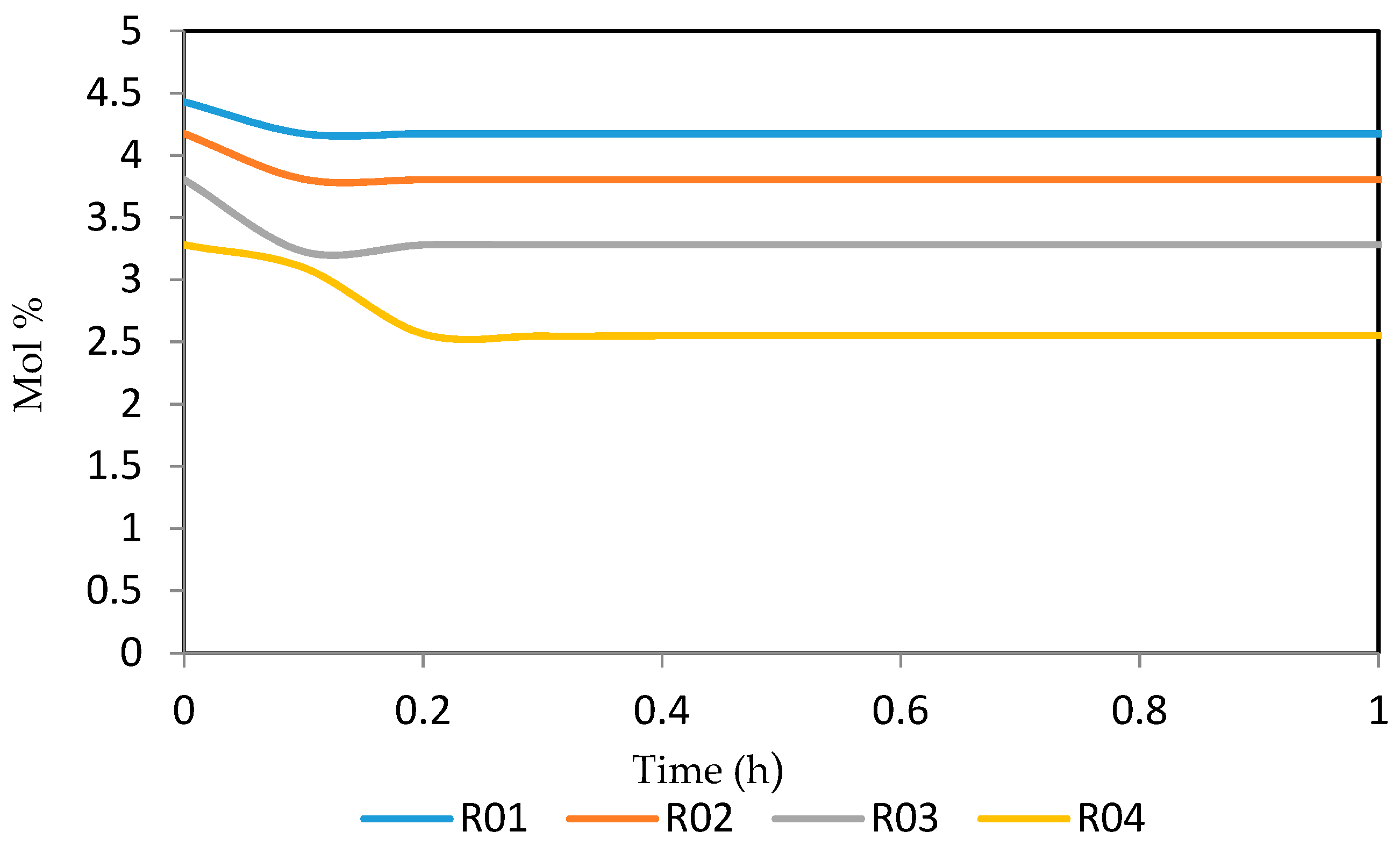
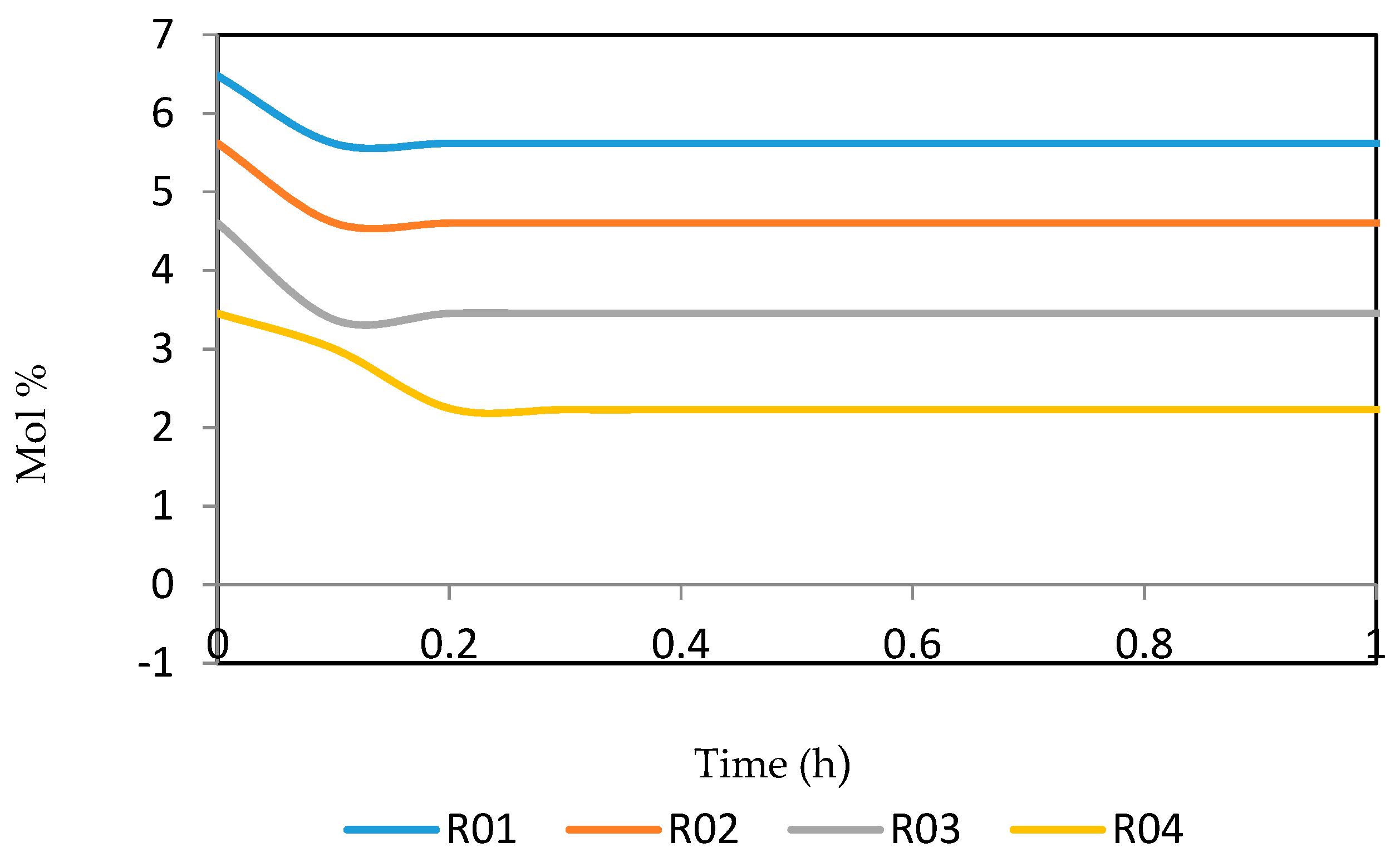
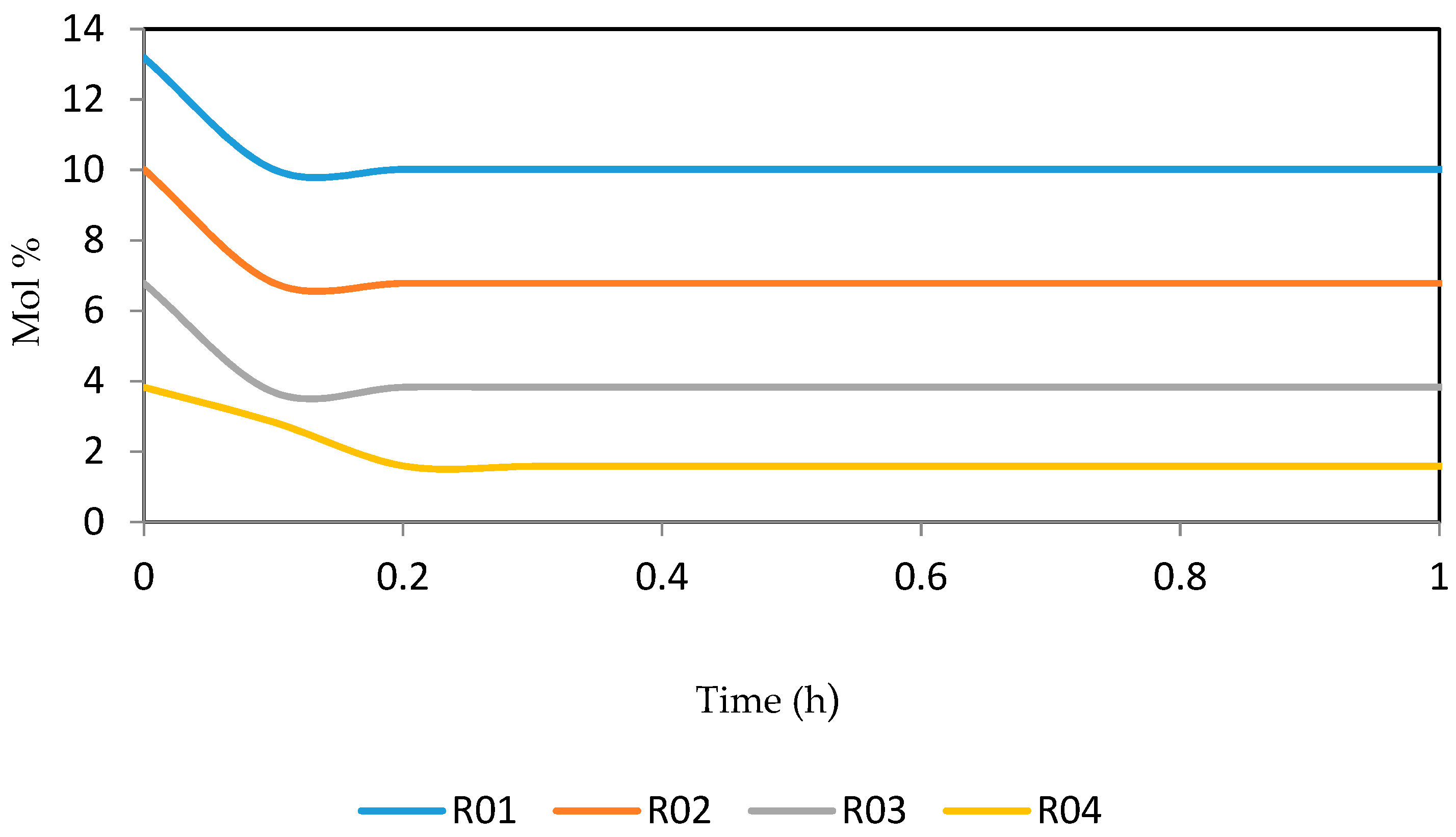
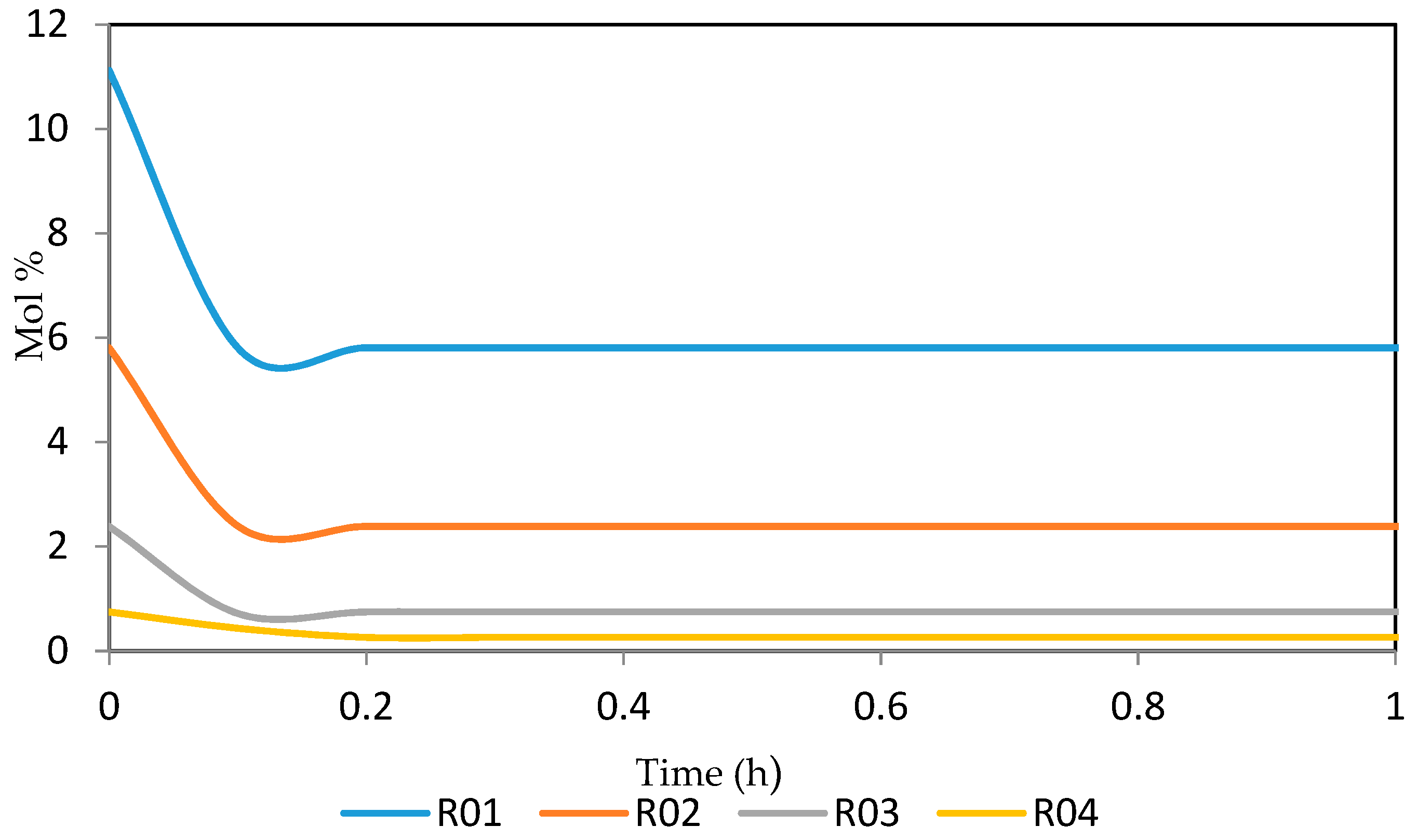
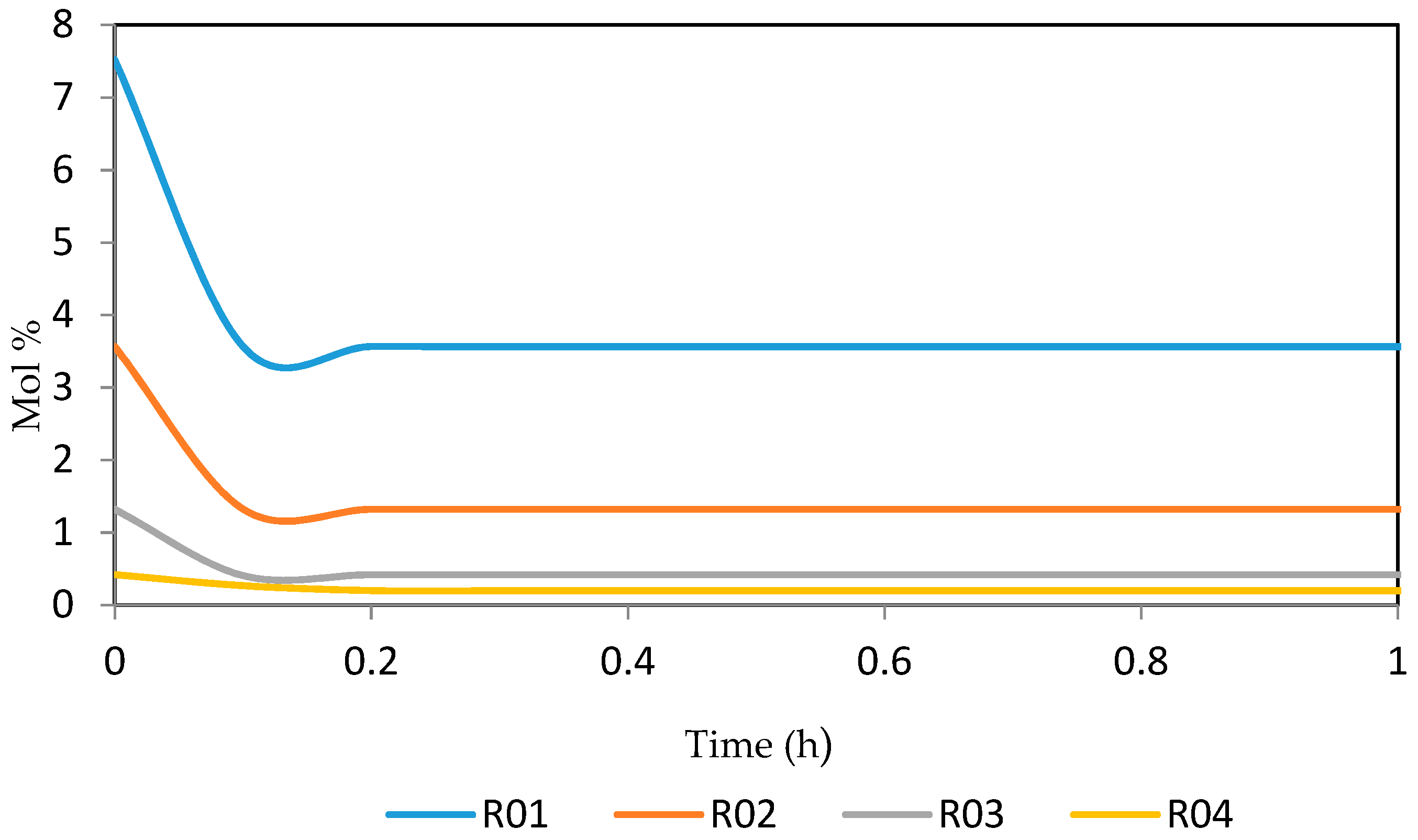
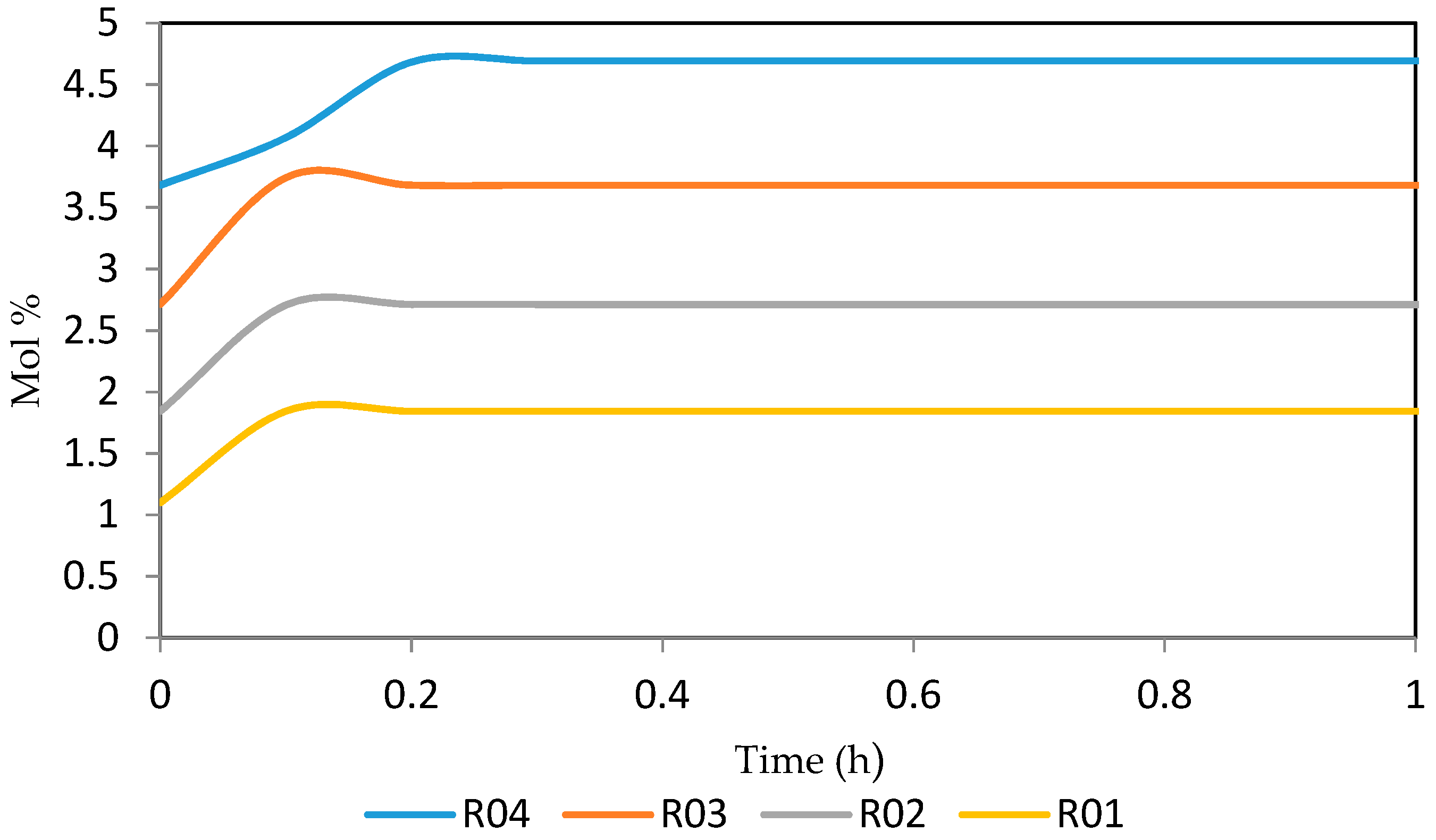
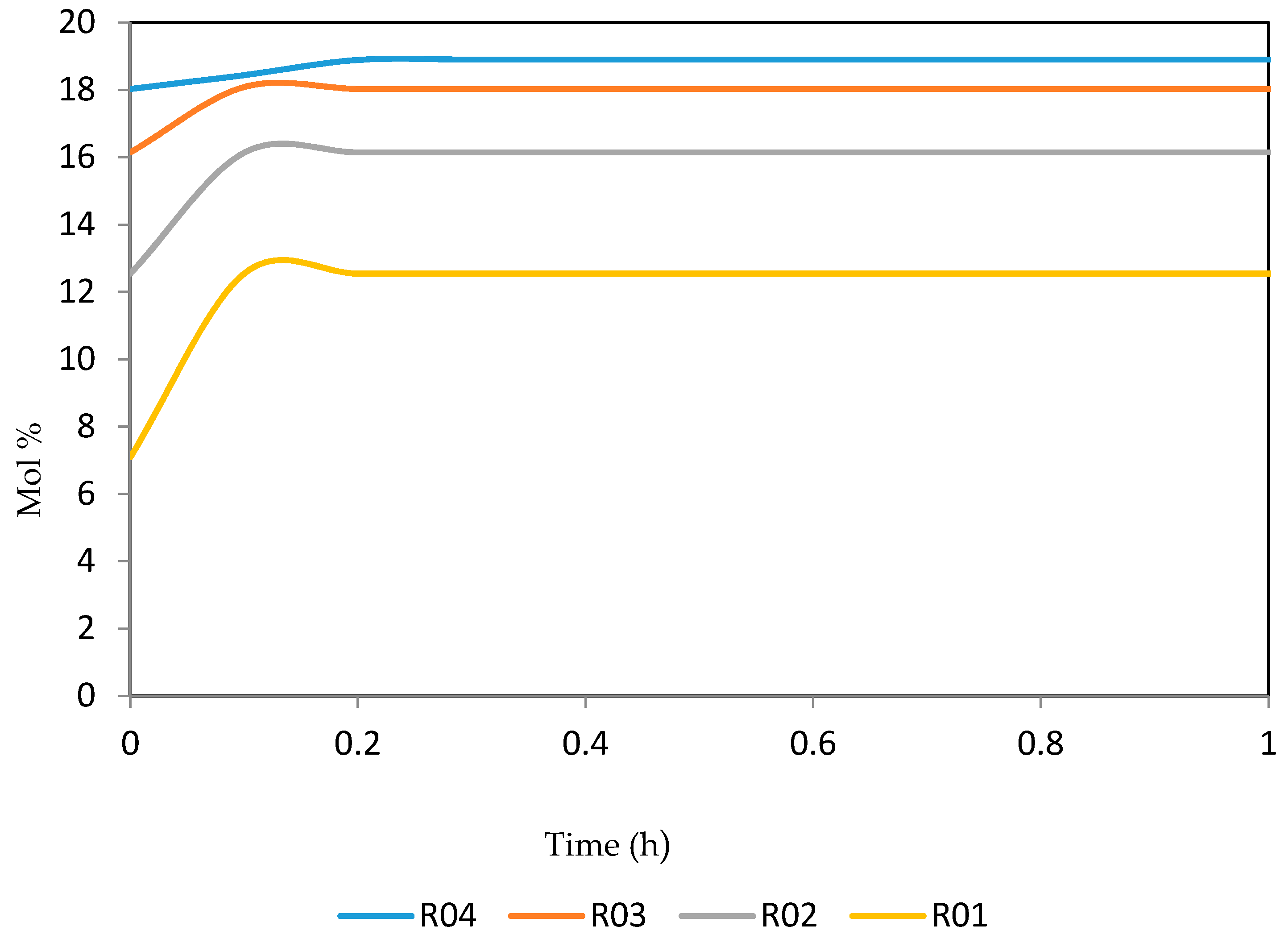
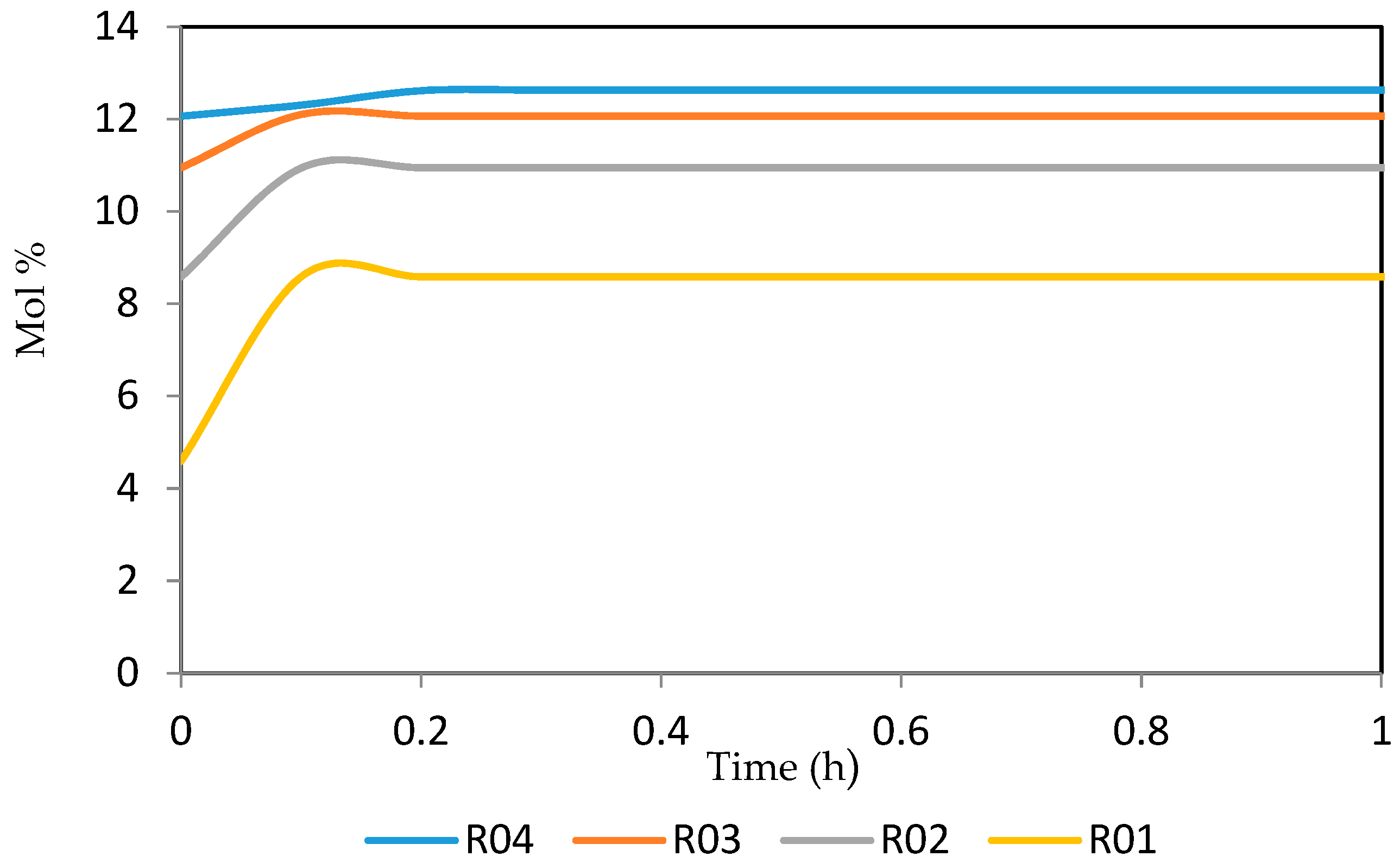
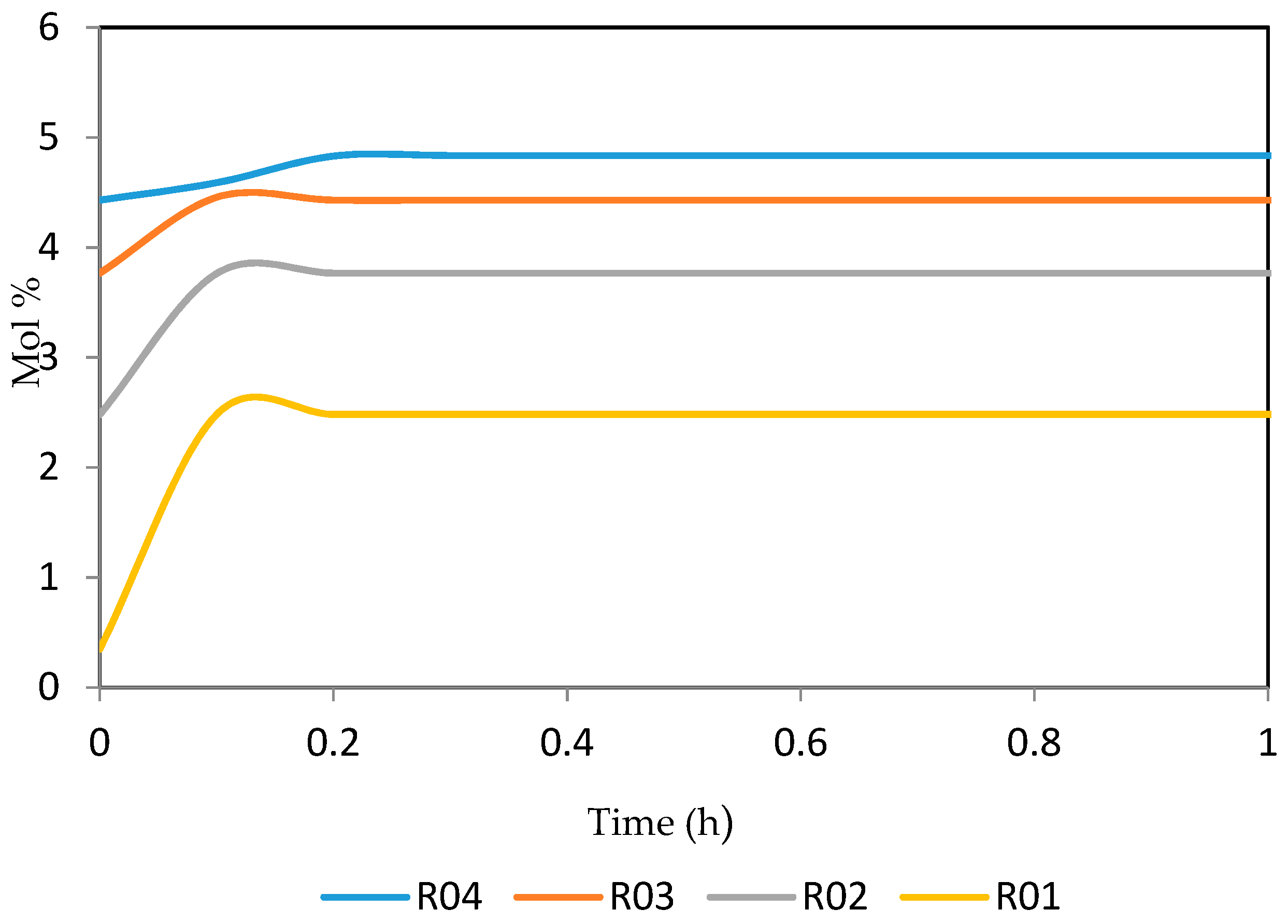
7.2. Dynamic Simulation of the Four Reactors
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Parameters from hydrogen reaction rate equation | |
| P | Paraffins |
| N | Naphthenes |
| Aromatics | |
| Constants for calculating heat capacities | |
| Constants for calculating Research octane Number (RON) | |
| Aromatics having 10 atoms of carbon | |
| Naphthenes having 10 atoms of carbon | |
| Paraffins having 10 atoms of carbon | |
| Heat capacity (KJ/kmol k) | |
| Particle diameter (m) | |
| Activation energy (KJ/kmol) | |
| Molar flow (Kmol/h) | |
| Force to mass conversion factor, 9.8066 ( m)/() | |
| Mass velocity (kg/m2 h) | |
| Reaction standard Gibbs energy (KJ/kmol k) | |
| Heat of reaction (KJ/kmol k) | |
| Kinetic constant at T (Kmol/h) | |
| Kinetic constant at T (Kmol/h) | |
| Equilibrium constant | |
| Weight hourly space velocity (h−1) | |
| Molecular weight (g/gmol) | |
| Reaction order | |
| N | Number of reactions naphthenes |
| Number of components | |
| Pi | Partial pressure of component i (Pa) |
| Pressure (Pa) | |
| Standard base pressure (Pa) | |
| Rate of reaction of component i (Kmol/h) | |
| Universal constant of gases (KJ/mol k) | |
| Cross sectional area (m2) | |
| Space-velocity (h−1) | |
| Reaction temperature (K) | |
| Base reaction temperature (K) | |
| Molar composition of component i (mol %) | |
| Reactor Height (m) | |
| SG | Specific Gravity |
| IBP | Initial Boiling Point (°C) |
| EBP | Final Boiling Point (°C) |
| RVP | Reid Vapor Pressure (Bar) |
| PPM | Parts Per Million |
| MBPD | Million Barrels Per Stream Day |
| Space velocity |
Greek Letters
| Void fraction of catalyst bed | |
| Density of gas mixture | |
| Density of catalyst | |
| Viscosity of gas mixture |
References
- Fawzi, M.E. Catalytic Naphtha Reforming; Challenges for Selective Gasoline an Overview and Optimization Case Study. J. Adv. Catal. Sci. Technol. 2016, 3, 27–42. [Google Scholar]
- George, J.A.; Abdullah, M.A. Catalytic Naphtha Reforming, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2004. [Google Scholar]
- George, A. Modelling and Simulation of Catalytic Reactors for Petroleum Refining; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hu, Y.; Su, H.; Chu, J. Modeling, Simulation and Optimization of Commercial Naphtha Catalytic Reforming Process. In Proceedings of the 2003 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 6206–6211. [Google Scholar]
- Stijepovic, M.Z.; Linke, P.; Kijevcanin, M. Optimization approach for continuous catalytic regenerative reformer processes. Energy Fuels 2010, 24, 1908–1916. [Google Scholar] [CrossRef]
- Mohaddecy, R.S.; Sadighi, S.; Bahmani, M. Optimisation of Catalyst Distribution in the Catalytic Naphtha Reforming of Tehran Refinery. Pet. Coal 2008, 50, 60–68. [Google Scholar]
- Arani, H.M.; Shokri, S.; Shirvani, M. Dynamic Modeling and Simulation of Catalytic Naphtha Reforming. Int. J. Chem. Eng. Appl. 2010, 1, 159–164. [Google Scholar] [CrossRef]
- Gyngazova, M.S.; Kravtsov, A.V.; Ivanchina, E.D.; Korolenko, M.V.; Chekantsev, N.V. Reactor modelling and simulation of moving-bed catalytic reforming process. Chem. Eng. J. 2011, 176–177, 134–143. [Google Scholar] [CrossRef]
- Iranshahi, D.; Rahimpour, M.R.; Asgari, A. A novel dynamic radial-flow, spherical-bed reactor concept for naphtha reforming in the presence of catalyst deactivation. Int. J. Hydrogen Energy 2010, 35, 6261–6275. [Google Scholar] [CrossRef]
- Elizalde, I.; Ancheyta, J. Dynamic modelling and simulation of a naphtha catalytic reforming reactor. Appl. Math. Model. 2015, 39, 764–775. [Google Scholar] [CrossRef]
- Ancheyta, J.; Villafuerte-Marclas, E.; Diaz-Garcia, L. Modelling and Simulation of four catalytic reactors in series for Naphtha Reforming. Energy Fuels 2001, 15, 887–893. [Google Scholar] [CrossRef]
- Rodríguez, M.A.; Ancheyta, J. Detailed description of kinetic and reactor modelling for naphtha catalytic reforming. Fuel 2011, 90, 3492–3508. [Google Scholar] [CrossRef]
- Unmesh, T.; James, B.R. Modeling and Optimization of a Semi regenerative Catalytic Naphtha Reformer. AIChE J. 1997, 43, 740–753. [Google Scholar] [CrossRef]
- Pieck, C.L.; Vera, C.R.; Parea, J.M.; Gimenez, G.N.; Sera, L.R.; Carvalho, L.S. Metal dispersion and catalytic activity of trimetallic Pt-Re-Sn/Al2O3 naphtha reforming catalysts. Catal. Today 2005, 107–108, 637–642. [Google Scholar] [CrossRef]
- Axens. RG Series Catalyst Handbook Catalytic Reforming Catalyst; A.I.G. Technologies, Inc.: Paris, France, 2004. [Google Scholar]
- Riazi, M. Characterization and Properties of Petroleum Fractions, 1st ed.; International Standards (ASTM): Philadephia, PA, USA, 2005. [Google Scholar]
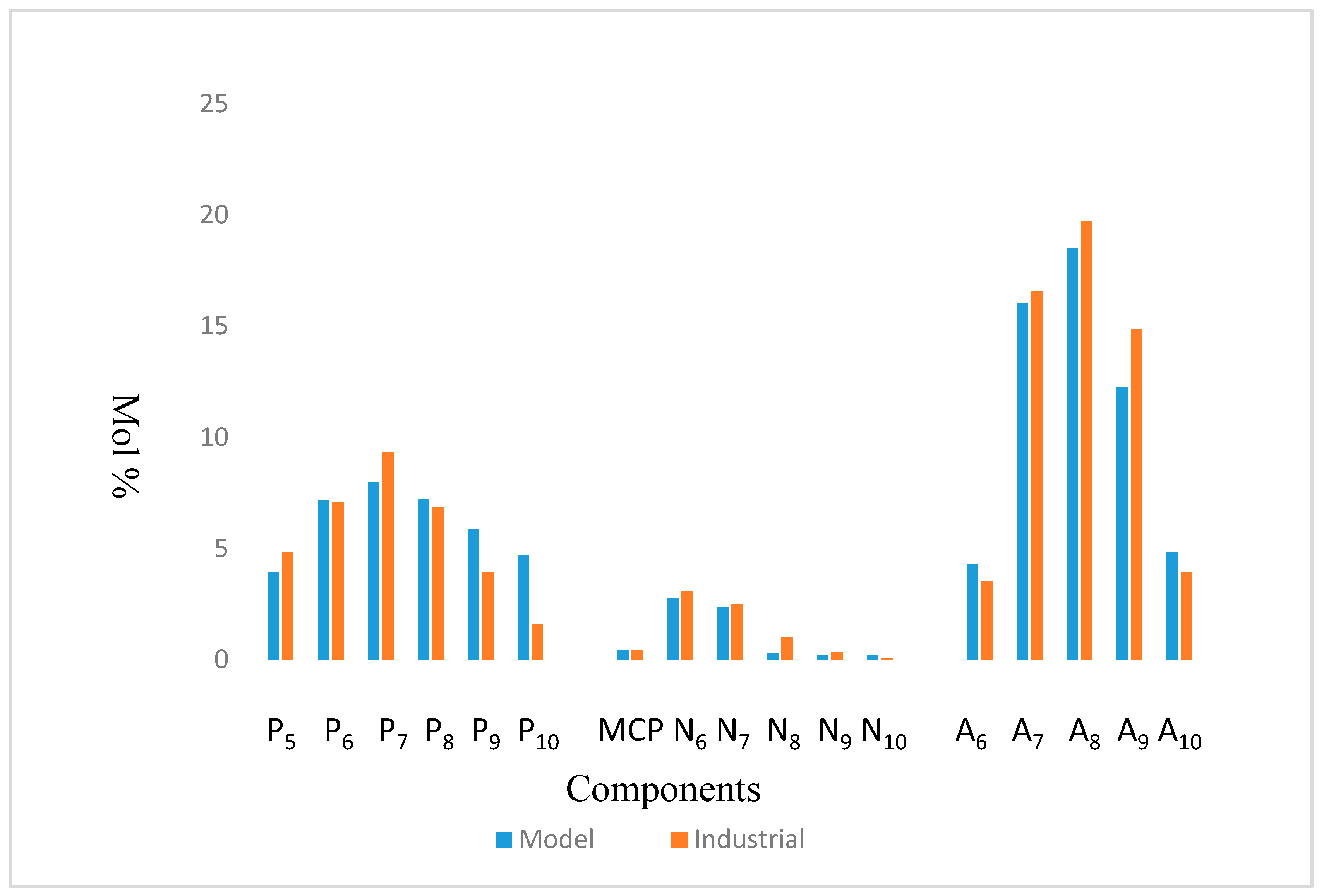

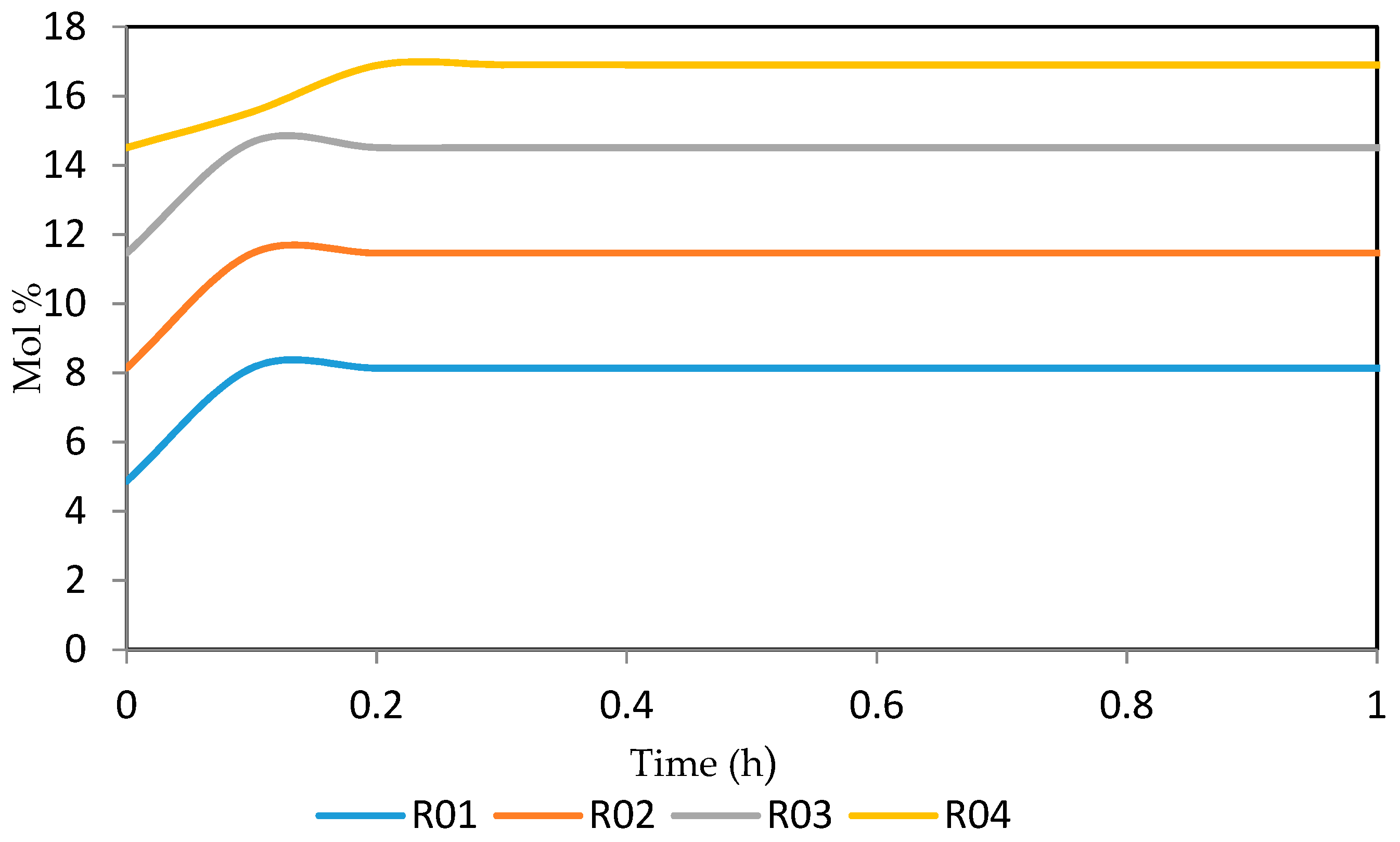
| Increased | RON | Reformate Yield | H2 Yield | Coke Deposit | |
|---|---|---|---|---|---|
| Pressure |  |  |  |  | |
| Temperature |  |  |  |  | |
| Space velocity |  |  |  |  | |
| H2/Hc ratio |  |  |  |  | |
| Naphtha Quality | A + 0.85 N |  |  |  |  |
| End boiling point |  |  |  |  | |
| Initial boiling point |  |  |  |  | |
| Reaction Steps of the Reactions | Rate Constants (kg/h·kg)−1 | |
|---|---|---|
| Dehydrogenation reactions of paraffins (P) to naphthenes (N) | ||
| 1. + | 0.00 | k1 |
| 2. + | 2.54 | k7 |
| 3. + | 1.81 | k13 |
| 4. + | 1.33 | k18 |
| 5. + | 0.58 | k23 |
| 6. + | 0.00 | k27 |
| 7. + | 0.00 | k28 |
| Hydrocracking reactions of paraffins (P) | ||
| 8. + + | 0.00 | k2 |
| 9. + + | 0.00 | k3 |
| 10. + + | 0.00 | k4 |
| 11. + + | 0.00 | k5 |
| 12. + + | 0.00 | k6 |
| 13. + + | 0.49 | k8 |
| 14. + + | 0.63 | k9 |
| 15. + + | 1.09 | k10 |
| 16. + + | 0.89 | k11 |
| 17. + | 1.24 | k12 |
| 18. + + | 0.30 | k14 |
| 19. + + | 0.39 | k15 |
| 20. + + | 0.68 | k16 |
| 21. + + | 0.55 | k17 |
| 22. + + | 0.19 | k19 |
| 23. + + | 0.25 | k20 |
| 24. + + | 0.43 | k21 |
| 25. + | 0.35 | k22 |
| 26. + + | 0.14 | k24 |
| 27. + + | 0.18 | k25 |
| 28. + + | 0.32 | k26 |
| 29. + + | 0.14 | k27 |
| 30. + + | 0.18 | k29 |
| 31. + | 0.27 | k31 |
| 32. + + | 0.12 | k32 |
| 33. + + | 0.15 | k33 |
| Dehydrogenation reactions of Naphthenes(N) | ||
| 34. + | 0.00 | k35 |
| 35. + | 24.5 | k40 |
| 36. + | 24.5 | k44 |
| 37. | 21.5 | k49 |
| 38. | 9.03 | k52 |
| 39. | 4.02 | k54 |
| 40. + | 0.00 | k34 |
| 41. + | 0.54 | k39 |
| 42. + | 0.54 | k44 |
| 43. + | 0.47 | k48 |
| 44. | 0.20 | k51 |
| 45. | 1.48 | k53 |
| 46. | 0.00 | k55 |
| 47. | 0.00 | k56 |
| 48. | 0.00 | k57 |
| Hydrocracking reactions of Naphthenes(N) | ||
| 49. + + | 0.00 | k36 |
| 50. + + | 0.00 | k37 |
| 51. + + | 0.00 | k38 |
| 52. + + | 1.84 | k41 |
| 53. + + | 1.34 | k42 |
| 54. + + | 0.80 | k43 |
| 55. + + | 1.27 | k45 |
| 56. + + | 1.27 | k46 |
| 57. | 0.09 | k47 |
| Hydrodealkylation reactions of Aromatics(A) | ||
| 58. | 0.00 | k59 |
| 59. | 0.00 | k60 |
| 60. | 0.06 | k62 |
| 61. | 0.06 | k63 |
| 62. | 0.00 | k64 |
| 63. | 0.05 | k66 |
| 64. | 0.05 | k67 |
| 65. | 0.01 | k69 |
| 66. | 0.00 | k58 |
| 67. | 0.00 | k61 |
| 68. | 0.16 | k65 |
| 69. | 0.16 | k68 |
| 70. | 0.16 | k70 |
| 71. | 0.45 | k71 |
| Activation Energy of Reactions | |
|---|---|
| Reactions | Activation Energy(kcal/mol) |
| Dehydrocyclization of paraffins ( ) | 45.00 |
| Hydrocracking of paraffins ( ) | 55.00 |
| Dehydrogenation of naphthenes ( ) | 30.00 |
| Hydrodealkylation of naphthenes ( ) | 55.00 |
| Ring opening of naphthenes ( ) | 45.00 |
| Hydrodealkylation of aromatics ( ) | 40.00 |
| Ring opening of aromatics ( ) | 45.00 |
| Hydrogenation of aromatics ( ) | 30.00 |
| Exponential values of Pressure | |
| Reaction | w |
| Other reactions | 0 |
| Hydrocracking of paraffins | 0.433 |
| Dehydrogenation/hydrogenation of aromatics | 0.0 |
| Hydrodealkylation of aromatic & naphthenes | 0.5 |
| Dehydrocyclization of paraffins | −0.7 |
| Reactor | Height (m) | Diameter (m) | Catalyst (Kg) | WHSV (h−1) |
|---|---|---|---|---|
| 1 | 4.902 | 2.438 | 9130 | 16 |
| 2 | 5.410 | 2.819 | 13,820 | 10.6 |
| 3 | 6.452 | 2.971 | 22,820 | 6.4 |
| 4 | 8.208 | 3.505 | 42,580 | 3.4 |
| Property | |
|---|---|
| MW | 104.8 |
| Specific gravity | 0.7406 |
| IBP | 88 |
| 10% | 101 |
| 90% | 155 |
| EBP | 180 |
| Total paraffins | 59.11 |
| Total naphthenes | 20.01 |
| Total aromatics | 20.88 |
| Components | Actual | Simulated [11] | Simulated gPROMs | Absolute Difference [11] | Absolute Difference gPROMs |
|---|---|---|---|---|---|
| P5 | 4.83 | 5.37 | 5.94 | 0.21 | 1.11 |
| P6 | 15.08 | 15.17 | 13.18 | 0.25 | 1.9 |
| P7 | 11.2 | 11.32 | 11.31 | 0.28 | 0.11 |
| P8 | 4.79 | 4.44 | 5.52 | 0.18 | 0.73 |
| P9 | 2.3 | 2.20 | 2.21 | 0.10 | 0.09 |
| P10 | 0.15 | 0.16 | 0.33 | 0.01 | 0.18 |
| P11 | 0.01 | 0.01 | 0.00 | 0.00 | 0.01 |
| MCP | 1.25 | 1.22 | 1.23 | 0.11 | 0.02 |
| N6 | 0.19 | 0.07 | 0.23 | 0.04 | 0.04 |
| N7 | 0.38 | 0.35 | 0.50 | 0.03 | 0.12 |
| N8 | 0.59 | 0.56 | 0.36 | 0.03 | 0.23 |
| N9 | 0.14 | 0.15 | 0.11 | 0.01 | 0.03 |
| N10 | 0.02 | 0.02 | 0.023 | 0.00 | 0.003 |
| N11 | 0.00 | 0.00 | 0.00 | 0.00 | 0 |
| A6 | 5.43 | 5.68 | 5.36 | 0.25 | 0.07 |
| A7 | 15.03 | 14.96 | 13.62 | 0.07 | 0.41 |
| A8 | 18.63 | 19.22 | 17.78 | 0.61 | 0.85 |
| A9 | 13.68 | 13.07 | 12.15 | 0.61 | 1.53 |
| A10 | 4.72 | 4.56 | 4.34 | 0.16 | 0.38 |
| A11 | 1.58 | 1.51 | 1.32 | 0.07 | 0.26 |
| Reactor Number | Height (m) | Diameter (m) | Catalyst (Kg) | WHSV (h−1) |
|---|---|---|---|---|
| 1 | 5.63 | 1.9 | 9572 | 5.56 |
| 2 | 5.83 | 2.1 | 12119 | 4.39 |
| 3 | 6.51 | 2.3 | 16231 | 3.28 |
| 4 | 7.26 | 2.7 | 24938 | 2.13 |
| FEED STOCK PROPERTIES | |
|---|---|
| MW | 103.7 |
| SG | 0.76 |
| IBP | 88 |
| 5% | 97 |
| 10% | 102 |
| 15% | 110 |
| 30% | 118 |
| 50% | 131 |
| 75% | 147 |
| 95% | 152 |
| EBP | 170 |
| RVP | 0.97 |
| SULFUR(PPM) | 0.32 |
| COMP | Simulated | Industrial | Error |
|---|---|---|---|
| P5 | 4.22 | 4.81 | 0.595 |
| P6 | 7.16 | 7.07 | 0.089 |
| P7 | 8.22 | 9.35 | 1.135 |
| P8 | 7.20 | 7.01 | 0.194 |
| P9 | 5.84 | 3.94 | 1.902 |
| P10 | 4.70 | 1.59 | 3.111 |
| MCP | 0.42 | 0.42 | 0 |
| N6 | 2.76 | 3.09 | 0.326 |
| N7 | 2.34 | 2.49 | 0.152 |
| N8 | 0.31 | 0.68 | 0.365 |
| N9 | 0.20 | 0.34 | 0.136 |
| N10 | 0.19 | 0.12 | 0.077 |
| A6 | 4.29 | 3.53 | 0.764 |
| A7 | 16.02 | 16.57 | 0.550 |
| A8 | 18.71 | 19.72 | 1.009 |
| A9 | 12.27 | 14.87 | 2.597 |
| A10 | 4.86 | 4.21 | 0.646 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusuf, A.Z.; Aderemi, B.O.; Patel, R.; Mujtaba, I.M. Study of Industrial Naphtha Catalytic Reforming Reactions via Modelling and Simulation. Processes 2019, 7, 192. https://doi.org/10.3390/pr7040192
Yusuf AZ, Aderemi BO, Patel R, Mujtaba IM. Study of Industrial Naphtha Catalytic Reforming Reactions via Modelling and Simulation. Processes. 2019; 7(4):192. https://doi.org/10.3390/pr7040192
Chicago/Turabian StyleYusuf, Aminu Zakari, B. O. Aderemi, Raj Patel, and Iqbal M. Mujtaba. 2019. "Study of Industrial Naphtha Catalytic Reforming Reactions via Modelling and Simulation" Processes 7, no. 4: 192. https://doi.org/10.3390/pr7040192
APA StyleYusuf, A. Z., Aderemi, B. O., Patel, R., & Mujtaba, I. M. (2019). Study of Industrial Naphtha Catalytic Reforming Reactions via Modelling and Simulation. Processes, 7(4), 192. https://doi.org/10.3390/pr7040192







