Realizing Energy Savings in Integrated Process Planning and Scheduling

Abstract

The integration of scheduling and process planning can eliminate resource conflicts and hence improve the performance of a manufacturing system. However, the focus of most existing works is mainly on the optimization techniques to improve the makespan criterion instead of more efficient uses of energy. In fact, with a deteriorating global climate caused by massive coal-fired power consumption, carbon emission reduction in the manufacturing sector is becoming increasingly imperative. To ease the environmental burden caused by energy consumption, e.g., coal-fired power consumption in use of machine tools, this research considers both makespan as well as environmental performance criteria, e.g., total power consumption, in integrated process planning and scheduling using a novel multi-objective memetic algorithm to facilitate a potential amount of energy savings; this can be realized through a better use of resources with more efficient scheduling schemes. A mixed-integer linear programming (MILP) model based on the network graph is formulated with both makespan as well as total power consumption criteria. Due to the complexity of the problem, a multi-objective memetic algorithm with variable neighborhood search (VNS) technique is then developed for this problem. The Kim’s benchmark instances are employed to test the proposed algorithm. Moreover, the TOPSIS decision method is used to determine the most satisfactory non-dominated solution. Several scenarios are considered to simulate different machine automation levels and different machine workload levels. Computational results show that the proposed algorithm can strike a balance between the makespan criterion and the total power consumption criterion, and the total power consumption can be affected by machine tools with different automation levels and different workloads. More importantly, results also show that energy saving can be realized by completing machining as early as possible on a machine tool and taking advantage of machine flexibility.

1. Introduction

Process planning and scheduling are two important functions in a flexible manufacturing system (FMS) [1,2,3]. Process planning determines the best-fitting technological requirements as well as corresponding manufacturing schemes with desired equipment to convert raw material to qualified parts [4,5]. In contrast to process planning, scheduling relates more closely to shop floor activities; it allocates operations to one of the available machines from another perspective, e.g., makespan minimization [2]. Traditionally, these two functions are treated separately and sequentially [6,7,8,9], and the critical failing is that this will cause resource conflicts in the shop floor. For instance, a previously determined process plan may not be used in actual manufacturing procedure due to some bottleneck machines on shop floor because the real-life shop floor status has not been considered in generating the process plan. Therefore, such resource conflicts greatly restrict the flexibility in a FMS. Due to such limitations and shortcomings in applications of FMSs, relative studies on integrated process planning and scheduling have been performed to achieve an efficient use of an FMS. According to existing publications [8,9,10,11,12,13,14,15,16], corresponding research on integrated process planning and scheduling (IPPS) are quite fruitful, and significant improvements have been achieved with the objective of makespan minimization, which is a primary criterion to evaluate the effectiveness of a schedule scheme. For instance, Doh et al. [10] adopted the priority dispatch rules to quickly determine a feasible scheduling scheme; nevertheless, this method usually cannot ensure a competitive solution. Kim et al. [8] proposed a symbiotic evolutionary algorithm for the IPPS problem. However the proposed symbiotic evolutionary algorithm lacks effective local search methods. Mathematical models of the IPPS problem have also been studied [15]; due to the complexity of the problem, existing mathematical models cannot capture satisfactory results.

Nevertheless, with a rapidly deteriorating global climate and the urgency of energy efficiency and carbon emission reduction requirements [17], environmental friendliness, which has never been a major concern in existing research on the IPPS problem, should be considered to be a serious topic [18,19]. The absence of sustainable practices will lead to negative impacts on the environment and society [20,21]. Although there are many approaches to realize energy savings in manufacturing processes, energy-effective scheduling is a very effective way with no capital investment to reduce energy consumption in manufacturing processes. Li et al. [22] have pointed out that machine tools have huge potential for energy saving. With a different perspective, energy savings have been achieved through the optimization of CNC machining parameters in their research. By reasonably determining machine tools, operation permutations (process plans), and operation sequences on machines, lot of energy consumption can be reduced.

This research mainly considers the energy consumption reduction (also carbon emission reduction) for the IPPS problem. The makespan and the total energy consumption have been considered as two criteria. The main idea of the proposed method is to take the advantage of the flexibilities in the IPPS problem and the idle time intervals on machines can be shortened or eliminated by properly assigning operations to machines with the optimal operation starting times, and hence energy consumption reduction caused by idle energy consumption on machines can thus be reduced. In this research, a novel mixed-integer linear programming (MILP) model is established first, and, in tandem with the complexity of the problem, a multi-objective memetic algorithm is then developed to capture the non-dominated solutions in the optimal Pareto front. The TOPSIS decision method is also adopted to determine the most promising non-dominated solution to strike a balance between the makespan criterion and the energy consumption criterion. Different machine automation levels and workload levels are considered and analyzed in both the MILP model as well as the proposed memetic algorithm; computational results indicate that these two factors will affect the total energy consumption.

2. Literature Review

At the beginning of the research on the IPPS problem, process planning and scheduling are integrated in a sequential manner [13]; this paradigm takes no advantage of the flexibilities in both the process planning module and the scheduling module since there are still serious bottlenecks in actual manufacturing activities. After that, relative research tends to integrate the two functions coherently to achieve a superior overall system performance mainly by three means: (1) mathematical modelling and corresponding solutions; (2) meta-heuristic-based approaches, such as genetic algorithm (GA); and (3) other approaches, e.g., agent-based methods [14].

For the first kind of approach, Özgüven et al. [15] give a MILP model for small-scale IPPS instances; nevertheless, their model belongs to the sequential paradigm where all the alternative process plans should be generated in advance to accommodate the scheduling constraints. In cases where flexible process plans are expressed in network graphs and process plans cannot be generated manually, their model cannot be used. Similar models can also be find in Tan et al.’s research [23]. In our previous research [2], we presented some MILP models to achieve a true integration of process planning and scheduling based on Wagner’s and Manne’s approach; complex network graph-based IPPS instances have been solved. However, existing MILP models cannot efficiently solve middle- or large-scale IPPS instances, since the Branch and bound method is a non-polynomial time algorithm. Therefore, practical solution approaches, represented by meta-heuristic algorithms, received noteworthy research attention. Kim et al. [8] first generalize the IPPS problem and give a set of benchmark instances with various flexibilities; they proposed a novel meta-heuristic algorithm—the symbiotic evolutionary algorithm—to optimize both process planning and scheduling schemes. Later, Li et al. [7] gives a GA combined with learning effects to solve IPPS instances. They also developed a tabu search (TS)-based hybrid meta-heuristic algorithm to obtain more promising results [24]. According to existing publications regarding meta-heuristic-based approaches, embedding local search methods in plain meta-heuristic algorithms can improve the quality of solutions. Lian et al. [6] adopted a novel algorithm, imperialist competitive algorithm (ICA), to address the IPPS problem, and they obtained more promising results on Kim’s benchmark. Other meta-heuristic algorithms have also been considered, such as the particle swarm optimization (PSO) algorithm [25,26,27], honey bee mating optimization (HBMO) algorithm [12], hybrid simulated annealing (SA) and TS algorithm [11], and the ant colony algorithm [28]. Recently, Liu et al. [29] proposed a quantum-inspired hybrid algorithm to minimize the makespan of IPPS instances, and outstanding outcomes have been observed. Other approaches in solving the IPPS problem concentrate mainly on agent-based approaches [14,30] and priority dispatch rule (PDR)-based approaches. PDR-based methods are practical and efficient; nevertheless, this kind of method has been given less emphasis due to the lack of efficaciousness. Recently, Zhang et al. [31] considered an IPPS problem in a flexible assembly job shop with sequence-dependent setup times and part sharing; they use constraint programming, MILP and dispatching rules to tackle the problem and the results show that constraint programming is the most effective approach while dispatching rules are simple to implement.

In general, the IPPS problem can be described in a network graph [8]. As illustrated in Figure 1, the network graph corresponds to a job to be processed; the starting node ’S’ and the ending node ’E’ are dummy nodes; representing the beginning and the end of a job. Most of the nodes are operation nodes, in which the operation ID and alternative machine tools with corresponding processing times are specified. Operation flexibility (OF) means that there is more than one feasible machine tool to finish an operation. Arrows between nodes indicate the precedence relations: if node A points to node B, operation B can only be processed after operation A directly or indirectly (sequencing flexibility, SF). The OR node appears in a bifurcation of two link-paths and only one of the two OR link-paths will be visited (processing flexibility, PF); otherwise, operations in both link-paths should be visited. For instance, a feasible operation permutation in Figure 1 is $1\to 7\to 2\to 8\to 4\to 5\to 6\to 10$.

Unfortunately, as one shortcoming of previous research, environmental friendliness has seldom been considered in IPPS optimizations. With carbon emission and global warming becoming increasingly severe problems, energy-efficient scheduling is attracting much more attention than before. Massive consumption of coal-fired electricity in manufacturing sectors causes more greenhouse gas and lots of carbon dioxide (CO${}_2$) will be released into the atmosphere directly; finally, the greenhouse effect has arisen [32]. Therefore, carbon emission reduction appears especially urgent [33]. To cope with such a grim situation, critical environmental regulations in many countries have forced relevant parties to take actions for carbon emission reduction. Clearly, considering only the economic criteria, e.g., makespan, in IPPS problems cannot satisfy the requirement of environmental friendliness presently.

Recently, researchers have performed some explorations on carbon emission reduction or energy saving in manufacturing activities (exact scheduling problems). He et al. [34] applied a nested partitions algorithm to realize energy saving by reasonably sequencing operations for each machine. May et al. [35] investigated the energy efficiency of a job shop manufacturing system; machine “switch ons” and “switch offs” have been considered to save energy. Similar to their research, Lin et al. [36] consider carbon footprint optimization in flow shop scheduling with parameter optimization; they developed three strategies to reduce carbon emission where the machine “switch on”-“switch off” technique was also adopted. As an intuitionistic method, the machine “switch on”-“switch off” technique was first proposed by Mouzon et al. [37] to reduce the energy consumption of non-bottleneck machines. Dai et al. [38] adopted the same technique for both makespan and total energy consumption reduction using a genetic-SA algorithm in flexible flow shop scheduling optimization. Recently, Meng et al. [39] developed some novel MILP models for the energy-conscious hybrid flow shop scheduling problem with unrelated parallel machines; again, the strategy of machines turning off and on has been adopted in their model.

Due to the considerable amount of additional energy in restarting machines as well as the damage to the machine tools caused by frequent machine switch “ons” and “offs”, Zhang et al. [40] adopted the machine speed scaling-based paradigm [41] to reduce energy consumption in a job shop. Later, based on the novel shuffled frog-leaping algorithm, Lei et al. [42] realized the minimization of both workload balance and total energy consumption in flexible job shop scheduling; in their work, the energy consumption model is also constructed based on the “machine speed scaling” paradigm. In the machine speed scaling-based paradigm, a machine tool can work at different speed levels with corresponding energy consumption levels and processing times. Wu et al. [43] suggested a green scheduling algorithm in flexible job shop scheduling; they divided the machining speed into three levels with corresponding machining power values; they adopted the NSGA-II algorithm to optimize the makespan, the energy consumption, and the numbers of turning-on/off machines. In their model, machine “turning-ons” and “offs” can minimize the energy consumption, but the number of turning-on/off machines is minimized to avoid the damage to the machines. Since the short processing times corresponds to high machining power values, generally, their model is a variant of machine speed scaling-based paradigm. However, this paradigm sometimes goes against real-life mechanical manufacturing environments, since the cutting speed is usually quite slow to increase the cutting moment in rough machining, while the cutting speed in fine machining is fast to ensure a satisfactory surface roughness. In addition, the cutting speed cannot be changed by traditional machine tools, and in such a case the “machine speed scaling” technique cannot be applied to realize energy saving.

Other researchers also developed energy-saving methods with corresponding optimization algorithms in different scheduling situations. Wang et al. [44] developed a genetic algorithm-based two-stage optimization technique to realize energy reduction in flexible job shop scheduling. Based on the energy consumption characteristics, they performed machine selection in the first stage to reduce both energy consumption and production cost; the operation sequencing on each machine is performed in the second stage to obtain a feasible scheduling scheme. However, since the integrated optimization of the flexible job shop scheduling problem can reduce conflicts of resources, the two-stage optimization technique in their research may not be the best optimization scheme. Giglio et al. [45] solved an integrated lot sizing and energy-efficient job shop scheduling problem using a relax-and-fix heuristic algorithm; they show that their method can reduce energy consumption, machines idle times, and the overall cost of the system. Some researchers also considered the optimal scheduling method with time-sharing prices [46,47]; however, that belongs to another topic where only the time period with low electric charge is considered, and this goes out of the scope of this research. For the IPPS problem, owing to complexity in the integration of process planning and scheduling, studies on the IPPS problem with energy-saving criteria appear to be limited according to existing publications. Recently, Zhang et al. [48] considered the energy consumption during setup and inspection times for the IPPS problem using the nonlinear process planning (NLPP) paradigm. However, the NLPP mode is a very elementary integration pattern in the IPPS problem, and it cannot truly ingrate the process planning function and the scheduling function closely [2]. For the cases where flexible process plans are expressed using network graphs (Figure 1) the NLPP paradigm becomes totally powerless. More importantly, as pointed out by Dahmus et al. [49], the energy consumption in a job shop is affected by many factors, such as the type of machine tools (e.g., general-purpose machine tools or CNC machine tools). Dahmus et al.’s research [49] also reveals that the workload of machines is the other factor that determines energy consumption in a job shop.

3. Methodological Approach and Advantages

According to the literature review presented above, the energy consumption reductions in scheduling problems are realized mainly by reducing the idle energy consumption; that is, avoid any energy consumptions as much as possible when a machine is in the non-cutting state. Based on this principle, there are mainly two methods in solving energy-efficient (or low carbon emission) production scheduling problems in early research. In the first kind of method, the energy consumption reduction is realized by turning off machine tools when they are in idle time intervals; in the other method, the total energy consumption can be reduced by controling the processing time to edge out the idle time intervals. In other words, the cutting times of an operation can be lengthened or shortened to occupy the idle time intervals. Although the two methods seem very effective according to previous publications, in many real-life situations in a flexible job shop frequent machine turning “ons” and “offs” will cause damage to machine tools. Moreover, a changeable processing time paradigm for energy consumption is also impractical due to technical requirements in cutting processes; for example, the surface roughness of a part highly relies on the cutting speed: with changeable cutting speed, the actual cutting speed will deviate from the predesigned one and the surface roughness of a part will not match the desired values specified in blueprint.

In general, the energy consumption in a job shop can be classified into three categories [50]: the common energy consumption, the processing energy consumption and the idle energy consumption; among the three, the common energy consumption stands for the indirect energy consumed, such as lighting, air conditioning, ventilation, etc., and this indirect energy consumption is not considered in this research. For the other two kinds of energy consumptions, Dahms et al. [49] have presented an energy use breakdown of a machine tool as shown in Figure 2. It can be seen that the total energy consumption can be divided into two parts—the constant part and the variable part—and the two parts exactly correspond to the idle energy consumption and the processing energy consumption respectively. In other words, there must be energy consumption whether the workpiece is being processed or not if the machine tool is turned on. The constant energy consumption is mainly determined by machine types (machine automation levels) and non-machining procedures, e.g., the use of oil pumps. The variable part, however, relies on the workpiece being processed.

In contrast to previous research that energy consumption is reduced by machine “turning-ons” and “offs” or controling the operation processing time, this research gives a novel perspective in both energy consumption reduction and makespan minimization for the IPPS problem. As analyzed above, there are some drawbacks in existing mainstream optimization methods in production scheduling problems with energy awareness. To make the optimization results more practical or make the optimal scheduling scheme match the real-life production situations as much as possible, machines are not allowed to be shut down during idle time intervals and the operation machining times are also fixed in this research; all the machines in this research have two statuses only: cutting status and standby status (idle status). By properly allocating operations to the machines and determining the starting times of operations, an energy-efficient scheduling scheme can be obtained.

Since the machine automation levels and the workload levels will affect the energy consumptions, two kinds of scenarios are considered to simulate different processing scenes in a job shop: the first kind of scenario is the machine tool types (that is, the automation levels of machine tools); the other kind of scenario relates to different machine workload levels. For different types of machine tools, based on their automation degree, the constant energy use may be different. In general, the higher degree of automation of a machine, the larger proportion of constant energy consumption it will occupy [49].

The research on the energy-efficient IPPS problem is rather limited, according to the literature mentioned in Section 2. The advances of this research can be summarized as follows:

• In this research, frequent machine turning “ons” and “offs” as well as changeable processing times are not allowed to make the resultant scheduling scheme of the energy-efficient IPPS problem more practical. The energy consumption reduction of the IPPS problem is realized by the optimal scheduling scheme.
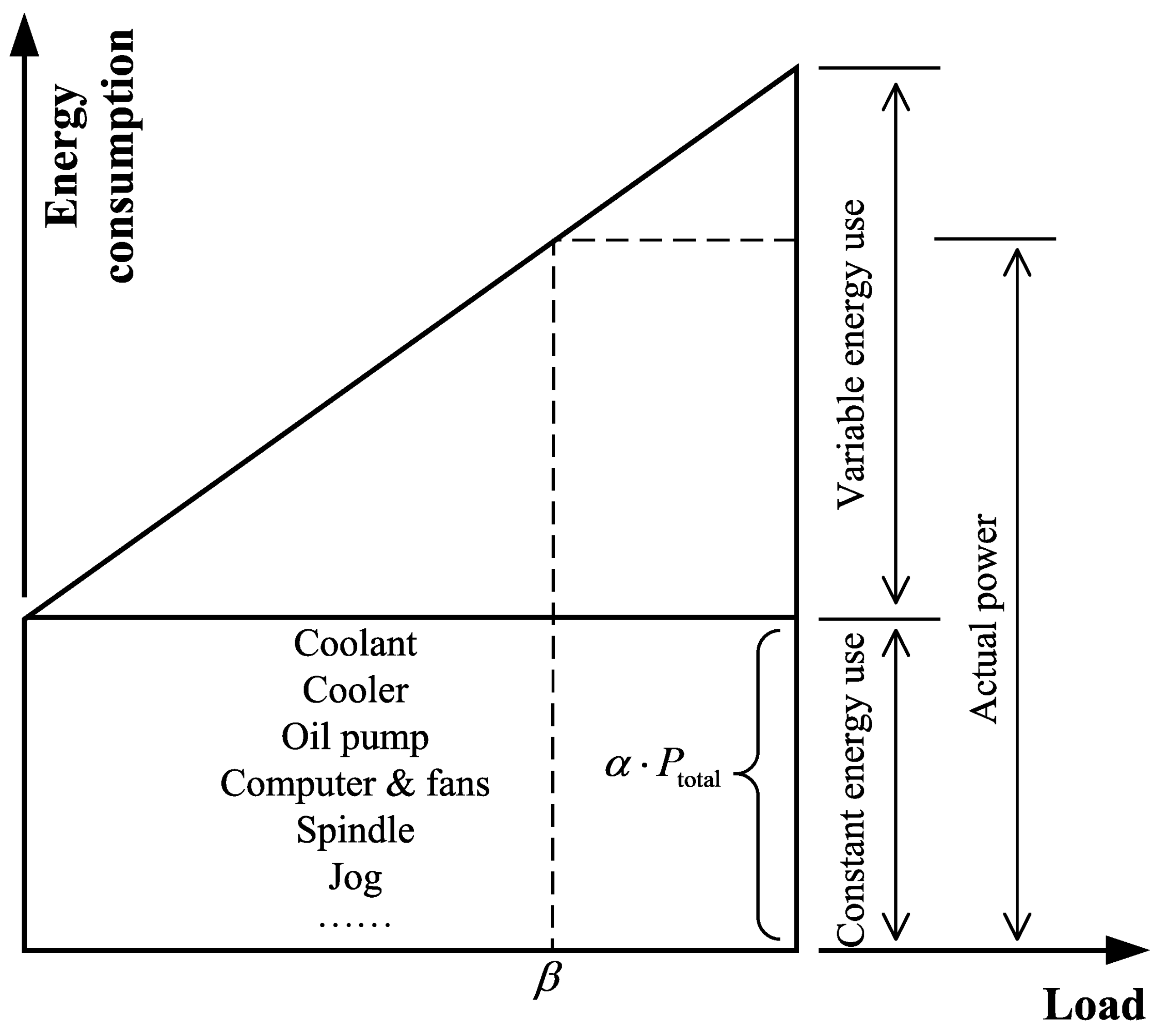
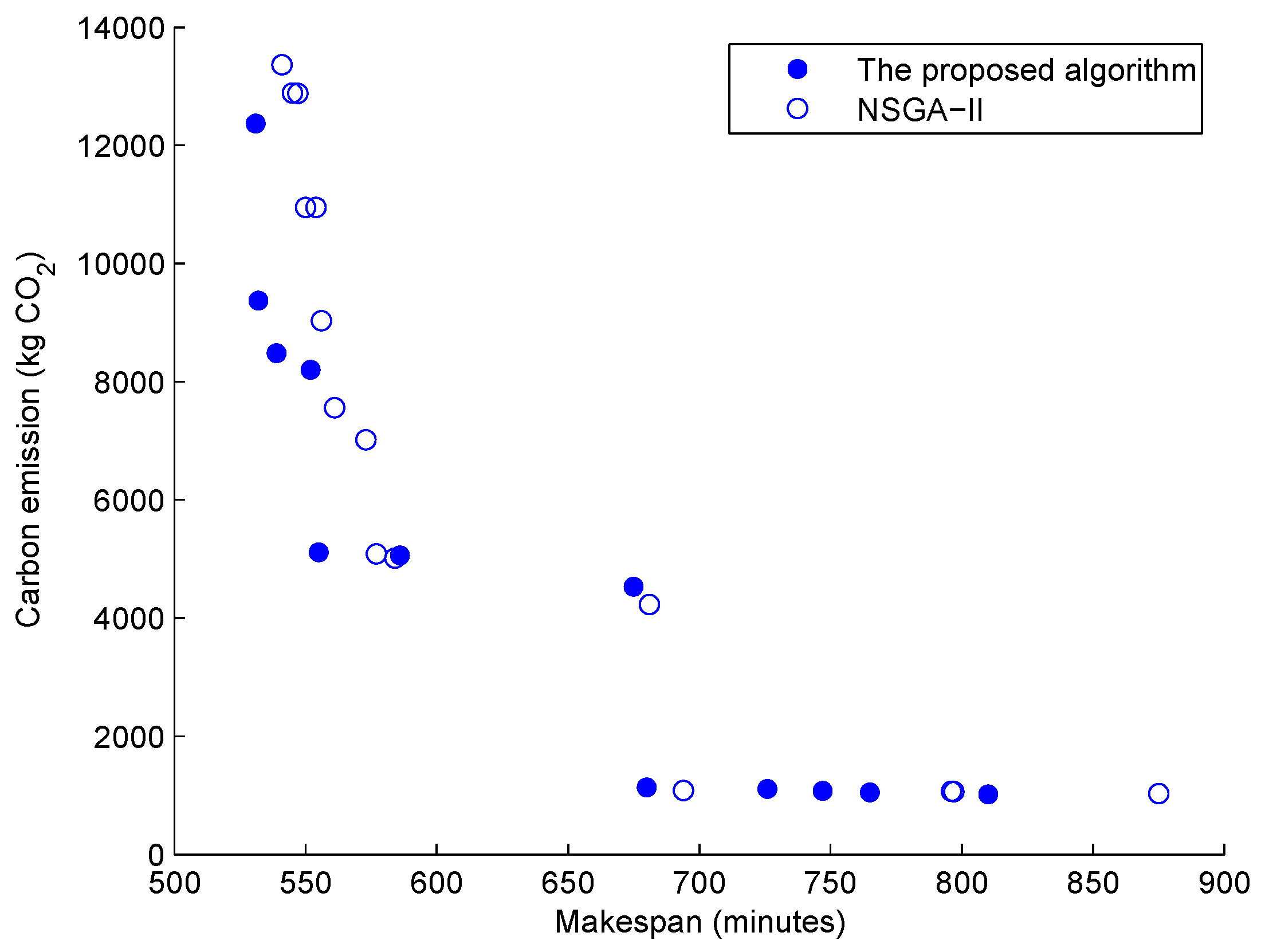
• Based on the two scenarios, we analyze the impacts of different machine automation levels (different types of machine tools, represented by the $\alpha$ value in Figure 2) and different workloads (represented by the $\beta$ value in Figure 2) on the energy consumptions of IPPS instances. Before this research, the impacts of machine automation levels on the energy consumption reductions have seldom been discussed in energy-efficient production scheduling optimizations.
• There are two types of MILP models for the IPPS problem, and the Type-2 MILP model can realize a true integration of process planning and scheduling [2]. Based on our previous Type-2 MILP model [2], this research reports a novel multi-objective MILP model for the energy-efficient IPPS problem for the first time where the energy consumption criterion together with the makespan criterion is optimized simultaneously.
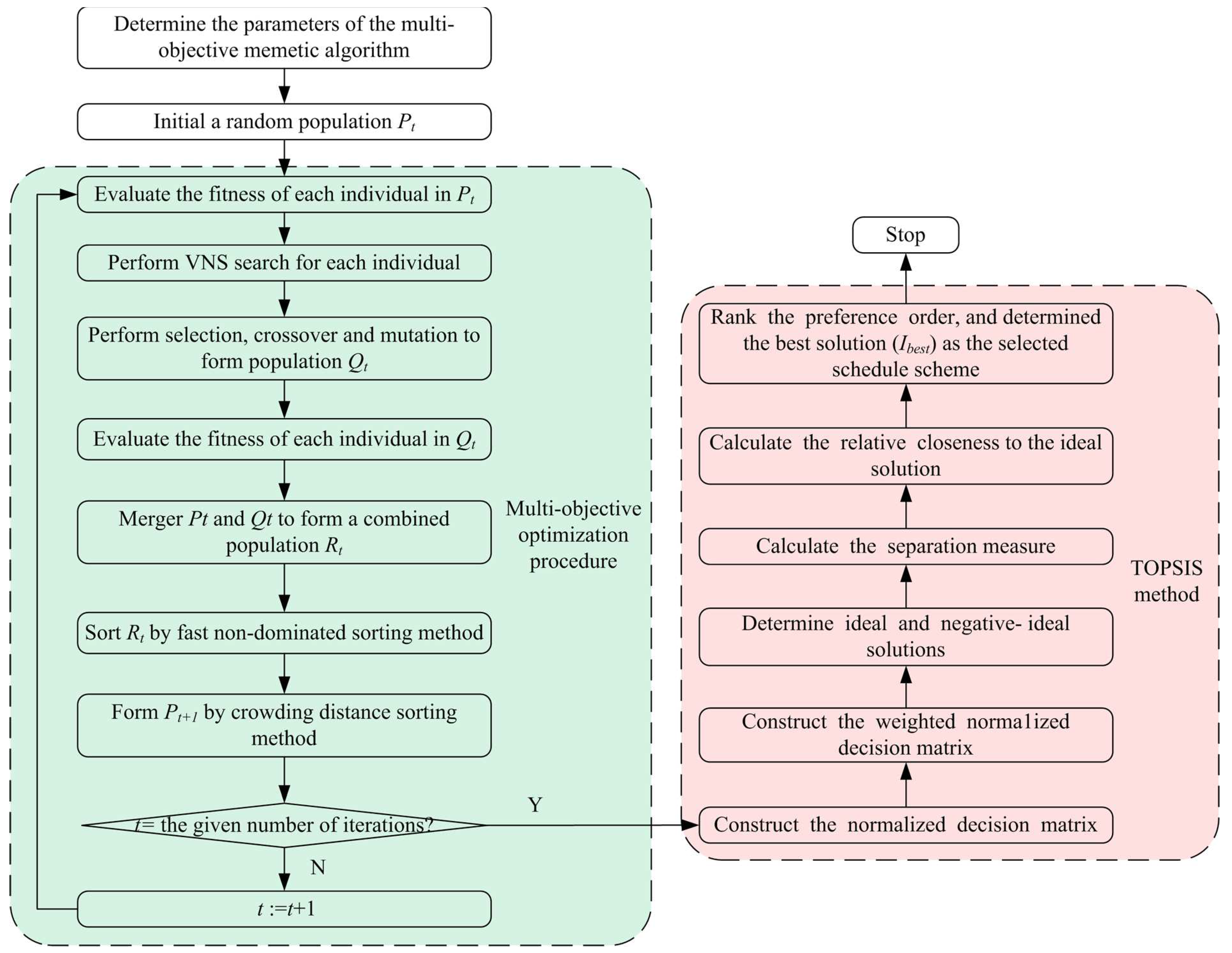
• Due to the complexity in solving the MILP model, a multi-objective memetic algorithm is developed to accommodate multi-objective optimization of the IPPS problem. In the proposed algorithm, the variable neighborhood search (VNS) is adopted to enhance the search ability of the algorithm. Instead of the abusive weighted sum method, the Pareto-based method [51] is adopted in the proposed memetic algorithm; this multi-objective optimization paradigm allows a set of non-dominated solutions for the decision maker. To determine the most promising scheduling scheme from the Pareto front, the TOPSIS decision method is adopted.

Figure 3 presents the flowchart of the proposed multi-objective memetic algorithm. It can be seen that the algorithm can be divided into two parts. The first part is the procedure of multi-objective memetic algorithm where the VNS local search method is introduced to explore more competitive solutions. The other part is the procedures of the TOPSIS method; the main steps of TOPSIS are elaborated in the figure.

To summarize, compared with existing research, this paper performs energy-efficient scheduling optimization from a novel and practical perspective: the energy-efficient scheduling optimization without machine turning “ons” and “offs” is performed; moreover, a novel MILP model is established and a VNS-based memetic multi-objective algorithm together with the TOPSIS decision method is presented to obtain an energy-efficient scheduling scheme. The remainder of this paper will be organized as follows. Section 4 presents the MILP model for the multi-objective IPPS problem. Section 5 introduces the proposed multi-objective memetic algorithm, and corresponding results with discussions will be reported in Section 6. Last section gives the conclusion as well as further research directions.

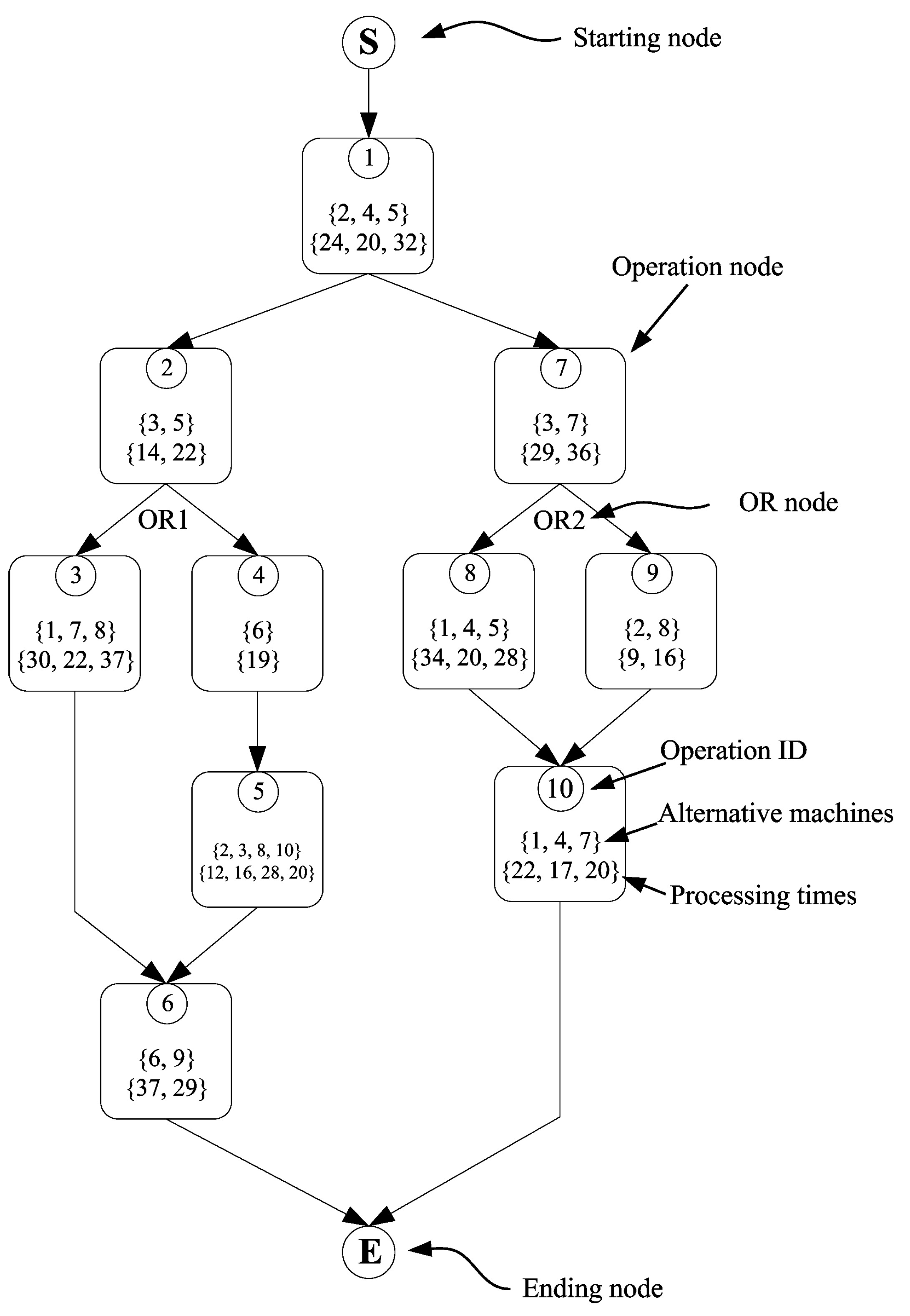
4. Mathematical Modelling

In traditional MILP models of the IPPS problem, all the available operation permutations (process plans) should be generated in advance; however, this method is total powerless in dealing with network graph-based IPPS instances in this paper because one cannot generate all the possible operation permutations in advance. In our previous research [2], novel MILP models (called Type-2 models) are reported to address such drawbacks. The MILP model for the energy-efficient IPPS problem in this paper is established based on the Type-2 model and the Manne’s modelling technique [52]. In a Type-2 model, operation precedence relationships are described by a pre-ordered set, a back-ordered set and a set of 0–1 variables to determine which operation should appear or be processed before the other one. In Manne’s approach, there is a set of variables $Z_{ij{j}^{\prime }}$ to determine whether operation j before operation $j^{\prime }$ in the same job; besides, the operation sequence on the same machine should also be determined using the corresponding 0-1 variables. After this, the whole scheduling scheme can be determined. In the following, each constraint set will be detailed. For the sake of completeness, the subscripts, notations, sets, parameters, and variables are listed below.

Subscripts and notations

$i,i^{\prime }$	jobs, 1 $\le i\le \left|n\right|$,
$j,j^{\prime }$	operations, $1\le i\le |n_i|$,
$k,k^{\prime }$	machines,
h	combinations,
$O_{ij}$	the j-th operation of job i,
$O_{ihj}$	the j-th operation of job i using the h-th combination of that job.

Sets and parameters

A	a very large positive integer,
$p_{ijk}$	the processing time of $O_{ij}$ on machine k,
$R_{ih}$	the set that contains the operations belonging to the h-th combination of job i,
$K_i$	the set of combinations of job i,
n	the set of all the jobs,
$n_i$	the set of all the operations in the network graph of job i,
$M_{ij}$	the set of available machines for $O_{ij}$,
$V_{ij{j}^{\prime }}$	1, if $O_{ij}$ is to be processed before $O_{i{j}^{\prime }}$ represented directly by the network graph; 0, otherwise,
$Q_{ij{j}^{\prime }}$	1, $O_{ij}$ should be processed directly or indirectly before $O_{ij}$; 0, otherwise,
$P_k$	the rated power of machine k,
$Pcu{t}_k$	the cutting power of machine k, $Pcu{t}_k=Pidl{e}_k+(1-\alpha )\beta P_k$,
$Pidl{e}_k$	the idle power of machine k, $Pidl{e}_k=\alpha P_k$.

Variables

$C_{max}$	makespan,
$EC$	total energy consumption,
$Y_{ih}$	1, if the h-th combination of job i is selected; 0, otherwise,
$X_{ihjk}$	1, if operation $O_{ihj}$ is processed on machine k; 0, otherwise,
$Z_{ij{j}^{\prime }}$	1, if operation $O_{ij}$ is processed directly or indirectly before $O_{i{j}^{\prime }}$; 0, otherwise,
$C_{ihj}$	the completion time of $O_{ihj}$,
$W_{ij{i}^{\prime }{j}^{\prime }}$	1, if $O_{ij}$ is processed before $O_{i^{\prime }{j}^{\prime }}$ on a machine; 0, otherwise,
$M{C}_k$	the completion time of the last operation on machine k,
$MC{T}_k$	the total production time of the operations on machine k (the time in cutting on machine k).

Objectives

The first objective is to minimize the makespan, and the other one is to minimize the total energy consumption.

$$min{C}_{max}$$

(1)

Constraints

$$minEC=\sum _{k}MC{T}_k·Pcu{t}_k+\sum _k\left[\left(M{C}_k-MC{T}_k\right)Pidl{e}_k\right]$$

(2)

Constraints

$$\sum _{h\in K_i}{Y}_{ih}=1,\forall i$$

(3)

$$\sum _{k\in M_{ij}}{X}_{ihjk}=Y_{ih},\forall i,\forall h\in K_i,\forall j\in R_{ih}$$

(4)

$$A·Y_{ih}\ge C_{ihj},\forall i,\forall h\in K_i,\forall j\in R_{ih}$$

(5)

$$C_{ih{j}^{\prime }}\ge C_{ihj}+\sum _{k^{\prime }\in M_{i{j}^{\prime }}}{X}_{ih{j}^{\prime }{k}^{\prime }}{p}_{i{j}^{\prime }{k}^{\prime }},\forall i,\forall h\in K_i,\forall j,j^{\prime }\in R_{ih},j\ne j^{\prime },V_{ij{j}^{\prime }}=1$$

(6)

$$Z_{ij{j}^{\prime }}+Z_{i{j}^{\prime }j}=1,\forall i,\forall j,j^{\prime }\in n_i,Q_{ij{j}^{\prime }}+Q_{i{j}^{\prime }j}=0,j\ne j^{\prime }$$

(7)

$$C_{ih{j}^{\prime }}\ge C_{ihj}+\sum _{k^{\prime }\in M_{i{j}^{\prime }}}{X}_{ih{j}^{\prime }{k}^{\prime }}{p}_{i{j}^{\prime }{k}^{\prime }}-A\left(1-Z_{ij{j}^{\prime }}\right),\forall i,\forall h\in K_i,\forall j,j^{\prime }\in R_{ih},j\ne j^{\prime },$$

(8)

$$\begin{array}{c}\hfill C_{i^{\prime }{h}^{\prime }{j}^{\prime }}\ge C_{ihj}+X_{i^{\prime }{h}^{\prime }{j}^{\prime }{k}^{\prime }}{p}_{i^{\prime }{j}^{\prime }{k}^{\prime }}-A\left(1-W_{ij{i}^{\prime }{j}^{\prime }}\right)-A\left(2-X_{ihjk}-X_{i^{\prime }{h}^{\prime }{j}^{\prime }{k}^{\prime }}\right),\\ \hfill \forall i,i^{\prime },i\ne i^{\prime },\forall h\in K_i,\forall h^{\prime }\in K_{i^{\prime }}\forall j\in R_{ih},\forall j^{\prime }\in R_{i^{\prime }{h}^{\prime }},k,k^{\prime }\in M_{ij}\cap M_{i^{\prime }{j}^{\prime }},k=k^{\prime }\end{array}$$

(9)

$$\begin{array}{c}\hfill C_{ihj}\ge C_{i^{\prime }{h}^{\prime }{j}^{\prime }}+X_{ihjk}{p}_{ijk}-A·W_{ij{i}^{\prime }{j}^{\prime }}-A\left(2-X_{ihjk}-X_{i^{\prime }{h}^{\prime }{j}^{\prime }{k}^{\prime }}\right),\\ \hfill \forall i,i^{\prime },i\ne i^{\prime },\forall h\in K_i,\forall h^{\prime }\in K_{i^{\prime }}\forall j\in R_{ih},\forall j^{\prime }\in R_{i^{\prime }{h}^{\prime }},k,k^{\prime }\in M_{ij}\cap M_{i^{\prime }{j}^{\prime }},k=k^{\prime }\end{array}$$

(10)

$$C_{max}\ge C_{ihj},\forall i,\forall h\in K_i,\forall j\in R_{ih}$$

(11)

$$M{C}_k\ge C_{ihj}-A\left(2-Y_{ih}-X_{ihjk}\right),\forall i,\forall j\in R_{ih},\forall k\in M_{ij},\forall h\in K_i$$

(12)

$$MC{T}_k=\sum _{i=1}^n\sum _{j\in R_{ih}}\sum _{h\in K_i}{p}_{ijk}\left(Y_{ih}+X_{ihjk}\right)/\phantom{\left(Y_{ih}+X_{ihjk}\right)2}2,\forall i$$

(13)

In the proposed MILP model, the network representation of a job is first decomposed into at least one combination; a feasible process plan can thus be obtained by properly arranging the operations belonging to a certain combination. For example, there are four operation combinations in the example in Figure 1, according to the two OR nodes. Once any one of the four combination is selected, e.g., the combination $(O_1,O_2,O_3,O_6,O_7,O_9,O_{10})$ is selected, a part can be completed by properly arranging the operations in the combination. Constraint set (3) states that exactly one combination is selected for each job to generate a process plan. Constraint set (4) relates the variables $X_{ihjk}$ and $Y_{ih}$; this means that if the h-th combination of job i is used, the corresponding operation of this combination of job i, e.g., $O_{ihj}$, will be assigned to an available machine. Constraint set (5) forces the completion time of the operations in an unselected combination of job i to be zero. Constraint set (6) schedules two operations of the same job by determining the completion time of the two operations. If the completion time of operation j is less than or equal to the starting time of operation $j^{\prime }$, then operation j should be scheduled before operation $j^{\prime }$. For two operations of the same job that have no precedence relationships, constraint set (7) determines which operation should be processed ahead; in other words, one of the two 0-1 variables should take value 1 and the other take value 0. Following this line, constraint set (8) schedules the operations that have no precedence relationships. Constraint sets (9) and (10) arrange different operations on a machine by determining the completion times of two operations that will be processed on the same machine. Constraint (11) determines the makespan of the whole schedule scheme. Constraint set (12) is introduced to obtain the latest completion time of operations on machine k; it includes the time in cutting and the time in the idle state of that machine. Finally, the actual time in cutting of machine k is expressed in constraint (13). Since the IPPS problem is an NP-hard problem, the model proposed above cannot be used due the intolerable computational time; therefore, this research suggests a multi-objective memetic algorithm to address such NP-hard problem.

5. Multi-Objective Memetic Algorithm

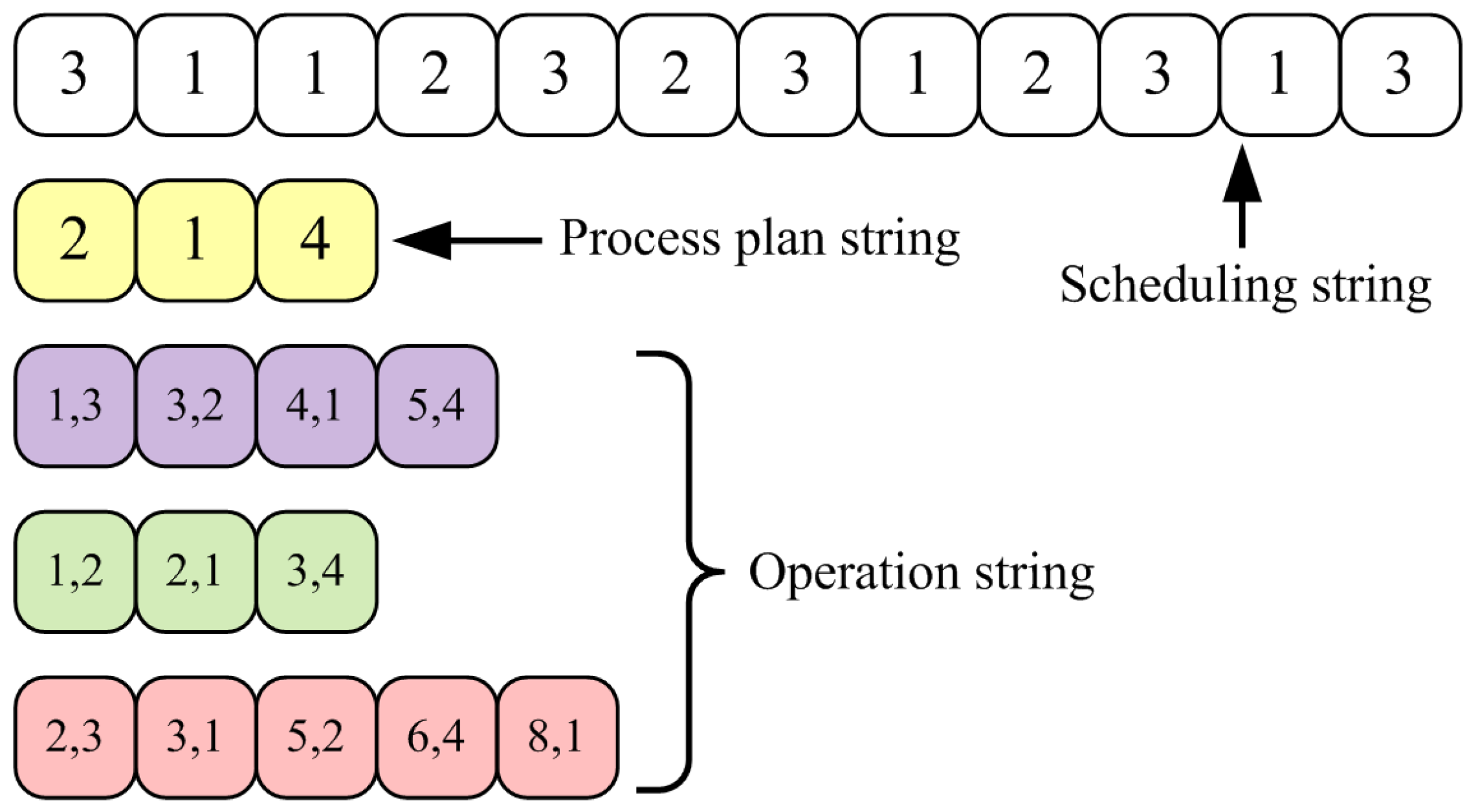
5.1. Encoding & Decoding

Compared with well-known NSGA-II algorithm, the proposed multi-objective memetic algorithm can achieve both the local exploitation and global exploration since a local search method is added in the memetic algorithm. As shown in Figure 4, the multi-string coding method is adopted in the proposed algorithm. The first part is the scheduling string; it adopts the operation-based representation paradigm [53]. In the scheduling string, the permutation of job IDs means the sequence of the operations to be processed in the decoding procedure: if number i appears exactly for the j-th time, the corresponding operation can be found in the j-th position of job i’s operation string. The number of positions of the scheduling string is predetermined and it equals the sum of the maximum possible number of operations of each job, e.g., ${\sum }_i{\left|R_{ih}\right|}_{max}$. If the actual number of operations in a selected combination of a job is less than the maximum one, e.g., $\left|R_{ih}\right|<{\left|R_{ih}\right|}_{max}$, corresponding zeros will be filled in the positions. This operation-based coding scheme avoids unfeasible scheduling schemes in the decoding procedure. In Figure 4, there are 12 positions in the scheduling string, and this means that each job adopts the process plan with the maximum number of operations.

The second string is the process plan string; it contains the information of the selected process plan (combination) of a job. The number i in the j-th position corresponds to the i-th process plan (combination) of job j, and this combination is adopted. According to Figure 4, the number in the third position of the process plan string is 4; this means that the forth combination is adopted in job 3.

The third string is the operation strings. The number of operation strings corresponds to the number of jobs. In each operation string, each position stands for an operation of that job, and the operation ID as well as the ID of the selected machine are specified. The number of positions is exactly the number of actual operations of the job using the correspond process plan (combination). It can be seen that such coding scheme reflects the logical relationship of the process planning module and the scheduling module.

Table 1. Description of three strings.

Names	Number of Positions	Purpose
Scheduling string	${\sum }_i{\left|R_{ih}\right|}_{max}$ at most	Operations belonging to different jobs will be processed sequentially according to the sequence in this string.
Process plan string	$\left|n\right|$	Indicate which operation combination will be adopted for each job.
Operation string	There are $\left|n\right|$ operation strings; each has ${\left|R_{ih}\right|}_{max}$ positions at most	The operation IDs and machine IDs of the corresponding operations are specified in each position; each operation string stands for an operation combination.

gives a clear description of the three strings.

The active scheduling paradigm [54] is adopted in the decoding procedure. For each position in the scheduling string, if the number i in the position is not equal to zero, then the operation of job i can be determined: if number i appear exactly for j times, the target operation can be located in the j-th position in the operation string of job i. If there is a ${}^{\prime }{0}^{\prime }$ in the scheduling string, jump to the next position directly. For the case of Figure 4, the number in the first position is 3, and it is the first time the number 3 appears; therefore, the corresponding operation is operation 2 of job 3 which can be located in the first position of the third operation string and further, this operation is to be processed by machine 3 according to Figure 4. Then, the processing time can be obtained based on the target operation with the machine. The operation is then assigned to the selected machine: if no operation has been assigned to the machine, the target operation is assigned to the machine directly with the starting time $max\{C_{ih,j-1},0\}$; in the other case, if the target operation is to be assigned to a machine which has already processed at least one operation, the machine idle time intervals between two operations will be checked. Suppose $M{S}_{kl}$ and $M{E}_{kl}$ stand for the starting and the ending time of the l-th idle time interval of machine k, the target operation can be inserted into the interval only if $max\{C_{ih,j-1},M{S}_{kl}\}+p_{ijk}\le M{E}_{kl}$; otherwise, this operation will be appended to the current last position of the machine with the starting time $max\{C_{ih,j-1},M{S}_{kl}\}$. The procedures discussed above repeat until all the operations have been assigned to the machines.

5.2. Crossover & Local Search

The crossover operator is used for elite retention as well as new individual exploitation. The crossover procedure is responsible for the evolution of individuals. Based on the proposed coding scheme, the crossover process in this multi-objective memetic algorithm is decomposed into two parts. For the two individuals, first, some jobs are randomly selected with the corresponding job IDs recorded; the process strings as well as operation strings in each individual are selected and they are exchanged in two individuals. In the case of Figure 5, the first two jobs have been selected and the process plan strings together with corresponding operations strings in the dashed boxes will be exchanged. Second, the scheduling strings of the two individuals must be adjusted using a position-based crossover method [55]. As presented in Figure 5, “P1” and “P2” are two former or old scheduling strings in the first and the second individuals while “O1” and “O2” in the figure stands for the newly generated scheduling strings of the first and the second individuals. The two new scheduling strings are generated from the old ones. For the new scheduling string of individual 1 (marked with “O1” in Figure 5), all its positions are set with “0”s at first and then the job IDs of the selected jobs in the former scheduling string of the other individuals, e.g., “P2”, are copied into the corresponding positions of “O1”. The job IDs of the unselected jobs in the former scheduling string of the individual “P1” are filled into the remainder positions of “O1” with the same order as they appear in “P1”. With the same method, the other new scheduling string, “O2”, can also be obtained.

In the regular multi-objective optimization algorithms, e.g., NSGA-II, local search methods are usually neglected. Existing research papers show that embedding local search methods into the main body of an algorithm can enhance the search ability of the algorithm. In the proposed multi-objective memetic algorithm, the problem specific VNS-based local search method is considered. In VNS, two neighborhood structures are adopted and they are used repeatedly in VNS procedure. Since the neighborhood structure usually uses the knowledge of a certain problem, it can provide more promising results. The first one is the N5 neighborhood structure [56] where only the operations in the head and the rear of a critical block are needed to be swapped to shorten the makespan. The other neighborhood structure [57] tries to shift an operation in the critical path to another available machine to shorten the critical path. The VNS procedure continues till there is no further improvements.

5.3. Multi-Objective Optimization

In this research, the makespan criterion as well as the energy consumption have both been paid attention to; therefore, the two criteria are treated equally. Traditionally, the weighted sum method is widely applied in multi-objective optimization; nevertheless, such a method ignores the variety of solutions and hence this brings difficulty for the decision makers. Deb’s NSGA-II algorithm [51] gives another perspective in multi-objective optimization based on the GA; they developed a systemic classification method called the fast non-dominated sorting method to distinguish the individuals and a selection method to retain the diversity of solutions. The whole population are divided into several parts according to the resultant Pareto fronts; The individuals in the optimal Pareto front are first considered. Usually, only part of the individuals is required to be selected in a certain Pareto front to form the new population, and in such a case, the crowding distance values are used to judge whether an individual in this Pareto front should be selected. Since the resultant optimal Pareto front can bring convenience to the decision makers, the proposed multi-objective memetic algorithm adopts Deb’s approach. After that, the TOPSIS decision method is adopted and the most satisfied solution is determined among all the individuals in the optimal Pareto front. During the decision process, we assume that both the two criteria are equally important; that is, the weights vector in TOPSIS can be written as $w=[\frac{1}{2},\frac{1}{2}]$. As illustrated in Figure 3, a normalized decision matrix is first constructed; with the weights vector, the weighted decision matrix can then be established. Based on the ideal and negative-ideal solutions, the relative closeness to the ideal solution can be calculated, and the best solution will finally be determined.

6. Experiments with Discussions

The proposed algorithm is coded in C++ language and is implemented on a computer with an i7-7700 3.6 GHz CPU and 16 GB of memory. The well-known Kim’s benchmark instances [8] are adopted and the characteristics of energy consumption of the IPPS problem have been investigated in detail. Based on the initial trials, both the population scale as well as the number of iterations are set to 800, and the crossover probability is 0.7. In Kim’s benchmark, as shown in

Table 2. Instances in Kim’s benchmark.

Number	Jobs	Job ID	Operations
1	6	1, 2, 3, 10, 11, 12	79
2	6	4, 5, 6, 13, 14, 15	100
3	6	7, 8, 9, 16, 17, 18	121
4	6	1, 4, 7, 10, 13, 16	95
5	6	2, 5, 8, 11, 14, 17	96
6	6	3, 6, 9, 12, 15, 18	109
7	6	1, 4, 8, 12, 15, 17	99
8	6	2, 6, 7, 10, 14, 18	96
9	6	3, 5, 9, 11, 13, 16	105
10	9	1, 2, 3, 5, 6, 10, 11, 12, 15	132
11	9	4, 7, 8, 9, 13, 14, 16, 17, 18	168
12	9	1, 4, 5, 7, 8, 10, 13, 14, 16	146
13	9	2, 3, 6, 9, 11, 12, 15, 17, 18	154
14	9	1, 2, 4, 7, 8, 12, 15, 17, 18	151
15	9	3, 5, 6, 9, 10, 11, 13, 14, 16	149
16	12	1, 2, 3, 4, 5, 6, 10, 11, 12, 13, 14, 15	179
17	12	4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 17, 18	221
18	12	1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17	191
19	12	2, 3, 5, 6, 8, 9, 11, 12, 14, 15, 17, 18	205
20	12	1, 2, 4, 6, 7, 8, 10, 12, 14, 15, 17, 18	195
21	12	2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 16, 18	201
22	15	2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 16, 17, 18	256
23	15	1, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18	256
24	18	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18	300

, there are 24 instances and the number of instances varies from 6 to 18. For example, the first instance contains 6 jobs and the maximum number of operations are 79; however, for the extreme case (Instance 24), all the 18 jobs are scheduled and there will be 300 operations at most. This benchmark instance set covers all the three flexibilities, e.g., OF, sequencing flexibility, and processing flexibility.

Table 3. Machine power values used in computation.

Machine ID	Power (kW)	Machine ID	Power (kW)	Machine ID	Power (kW)
1	25	6	19	11	7
2	12	7	7	12	21
3	17	8	5	13	9
4	18	9	23	14	13
5	12	10	16	15	28

gives the power values of 15 machines [58], and the power values range from 5 kw to 28 kw. To calculate the corresponding carbon emission values, we assume that the processing times in Kim’s benchmark are counted in minutes.

The influences induced by different machine types and machine workloads on the energy consumptions have been discussed in this research. Three scenarios have been generated to simulate machine tools with different automation levels by setting the $\alpha$ values to 0.35, 0.55, and 0.75, respectively. As discussed in Section 3, the low automation level machine tool takes less idle energy and this corresponds to a small $\alpha$ value. Similarly, three scenarios for different machine workloads can be realized by setting the $\beta$ values to 0.3, 0.5, and 1.0, respectively. In the case where $\beta =0.3$, it means that the workload is relatively light and $\beta =1$ means machines work in full loads.

For the most complex instance, Instance 24, the average computational time is about 460 s and the computational time of other instances is less than 460 s. For the plain NSGA-II algorithm, since there is no local search method and the algorithm takes no extra time to perform the local search procedure, the computational time is about 200 s and it is less than that of the proposed algorithm; nevertheless, as shown in Section 6.1, the proposed algorithm captures more promising non-dominated solutions.

6.1. Experiment 1

To reflect the advantage of the proposed multi-objective memetic algorithm, we first compare the Pareto fronts obtained by the proposed algorithm and the traditional NSGA-II algorithm, and corresponding Pareto fronts of Instance 24 are presented in Figure 6. It can be seen that the optimal non-dominated solution obtained by the proposed multi-objective algorithm are generally better than the ones obtained by the plain NSGA-II algorithm because the local search methods have not been considered in traditional NSGA-II algorithm and therefore the Pareto front of NSGA-II is distributed inferior to the Pareto front of the proposed algorithm. This reflects the powerful search capability of the multi-objective memetic algorithm. For the makespan criterion, the minimum value of the makespan is about 530 min using the proposed memetic algorithm, and the best makespan value obtained by the plain NSGA-II algorithm is about 545 min, and this means that the proposed multi-objective memetic algorithm performs better than the plain NSGA-II algorithm: due to the VNS local search in memetic algorithm, the search ability have been enhanced in the proposed algorithm.

Figure 7, Figure 8 and Figure 9 present three Gantt charts of Instance 24. The first and the second Gantt charts represent the two extreme cases in the optimal Pareto front: The first Gantt chart considers the makespan more than the other criterion while the second scheduling scheme puts more emphasis on the carbon emission minimization criterion; the third scheduling scheme is obtained by the TOPSIS method and it strikes a balance between the two criteria. The makespan as well as the carbon emission values of the three scheduling cases are summarized in

Table 4. Results comparisons of Instance 24.

Case 1 (in Figure 7)		Case 2 (in Figure 8)		Case 3 (in Figure 9)
makespan	carbon emission	makespan	carbon emission	makespan	carbon emission
531 (min)	13,340.3 (kg)	810 (min)	2036.32 (kg)	680 (min)	2267.88 (kg)

. Clearly, the first scheduling scheme has the minimum makespan while the value of the other criterion is relatively worse than other two cases. For the second case, as discussed above, it moves to the other extreme: the makespan value is the largest among the three cases while the carbon emission value reaches the lowest. According to the two extreme cases, it is quite necessary to consider both the two criteria and considering only the makespan or the carbon emission criterion is not enough to meet the low-carbon manufacturing requirement. The third scheduling scheme presented in Figure 9 is obtained by the TOPSIS decision method and it strikes the balance between the two criteria. According to Table 4, both the values of the two criteria are acceptable. Compared with the operation scheduling in Figure 8, the production efficiency of Figure 7 is much better. By compactly assigning operations to machines, the makespan is shortened. However, the carbon emissions in this case have not been emphasized and the massive carbon emissions caused by energy consumption in this case reflects the necessity of multi-objective optimizations in energy-efficient IPPS problem. In Figure 8, the carbon emission has been considered as a priority and it can be seen that the low-carbon scheduling strategy can be concluded as follows:

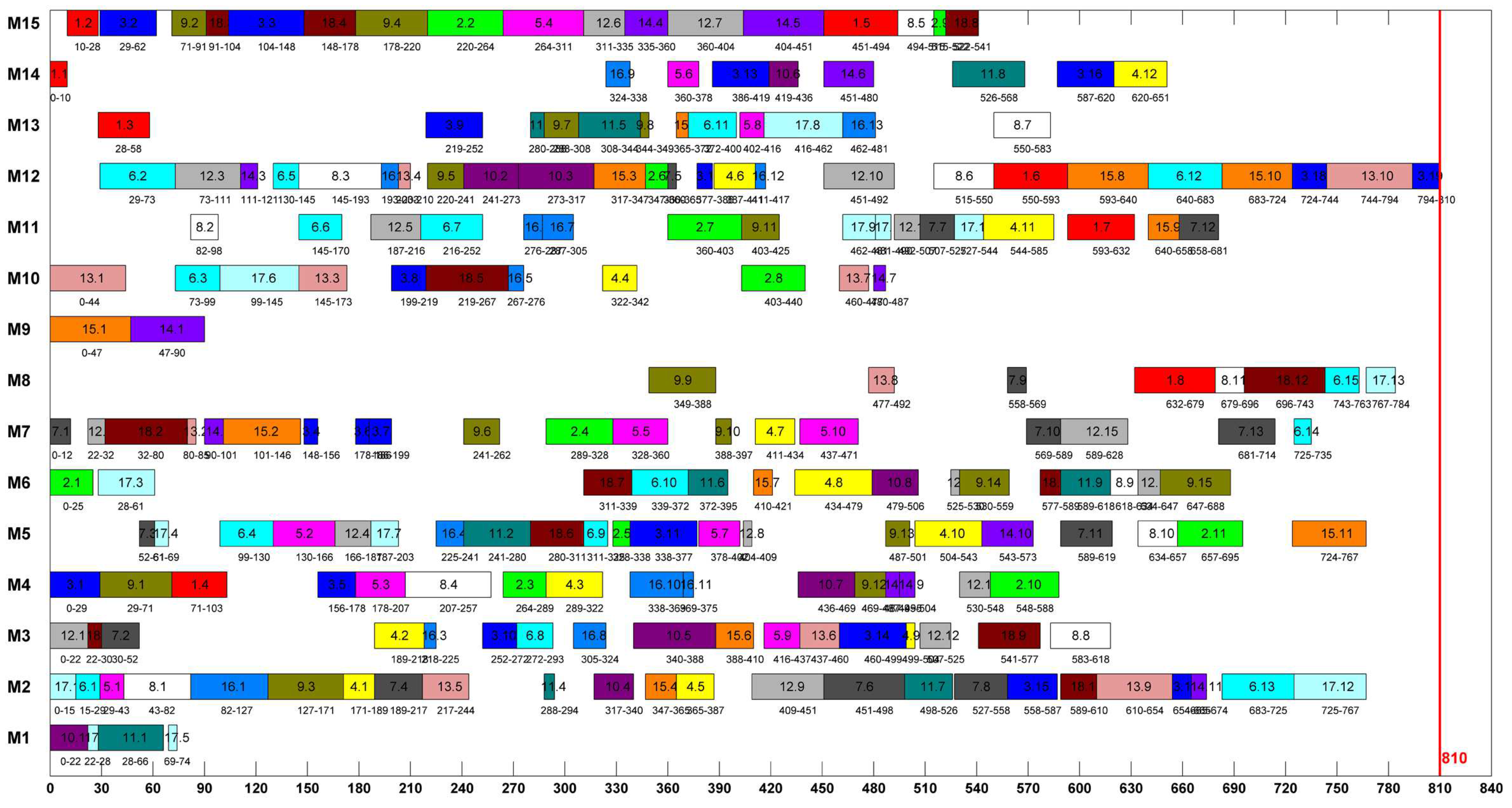
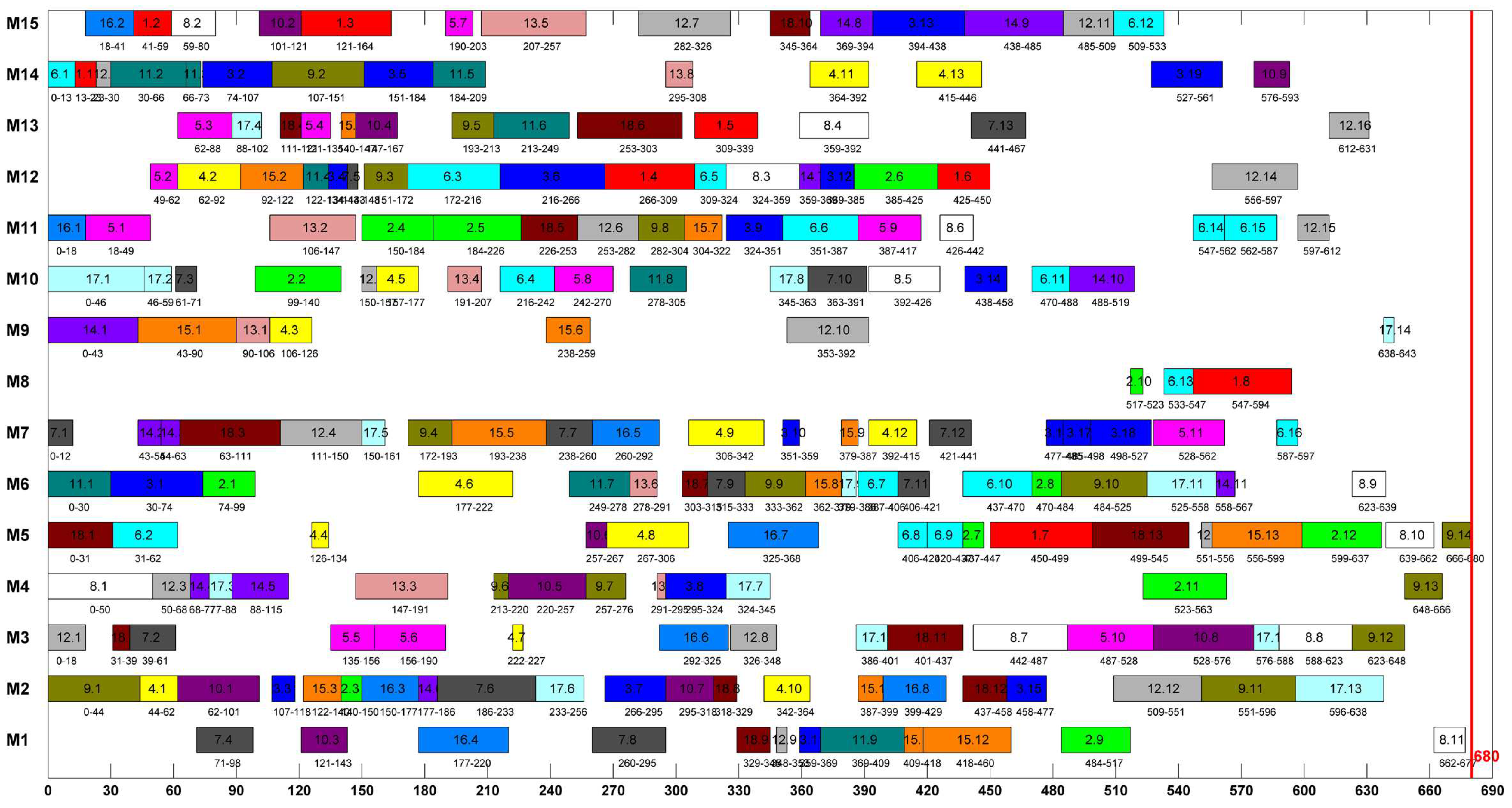
• Assign operations to the machines with low powers as much as possible. For example, the power values of machines 1, 3, 4, 6, 9, 10, 12, and 15 are larger than 15kw and only few operations are assigned to machines 1, 6, 9, and 10 according to Figure 8. In this way, the machine with low constant energy use will be assigned more operations to save energy; the negative effect is that the makespan criterion will deteriorate because more operations will accumulate and wait to be processed.
• Finish operation processing as early as possible on the machines with large powers. For example, operations processed by machines 1, 9, and 10 are sequenced compactly according to Figure 8 and the machines will be shut down once the machining procedures of the operations are finished; in this way, the idle energy consumptions on these machines can be reduced.
• From Figure 8, energy-efficient scheduling can also be realized by tight arrangements of operations on machines because this can edge out the idle time intervals on machines and therefore the idle energy consumption can be reduced.

6.2. Experiment 2

In this experiment, the energy consumption characteristics are discussed in different situations with different machine workloads (different $\beta$ values) using different types of machine tools (different $\alpha$ values). Instances in Kim’s benchmark can be classified into three categories, e.g., small-scale instances, medium-scale instances, and large-scale instances, according to the information in Table 2. In this experiment, Instances 1, 12, and 24 are selected to represent the small-scale, the medium-scale, and the large-scale instances. The energy consumption including both the cutting energy consumption and the idle energy consumption of the three instances are summarized in the histogram in Figure 10.

Figure 10a gives the energy consumption of the three instances using low automated machines ($\alpha =0.35$). It is easy to understand that the total energy consumption increases with the number of operations (also the scale of instances) because processing more operations means more energy consumption. For the idle energy consumption, marked in cyan color, there is no apparent fluctuation since the idle energy consumption takes a relative fixed percentage in each instance; more importantly, machines are not allowed to be turned off in this research unless all the operations are finished and this is the other reason there is no significant differences between idle energy consumptions of the instances in Figure 10a. since each machine has only two status—in machining state or in idle state—and all the 15 machines are used in all the three instances, the idle power consumption of machines can be deemed as a constant. For the cutting energy consumption, according to Figure 10a, it relates closely with the scale of instances and machine workloads. Similar situations can also be observed in Figure 10b,c where the fluctuation of idle energy consumptions is much less than that of cutting energy consumptions. However, with a higher automation level of machine tools, the idle energy consumptions in Figure 10b,c are larger than the case in Figure 10a. In cases of Figure 10b,c, the $\alpha$ values are set to 0.55 and 0.75, respectively, and we can intuitively see that the proportion of idle energy consumption to the whole energy consumption has increased. The cutting energy consumptions in Figure 10b,c are almost the same as the ones in Figure 10a; the reason is that the number of operations as well as the workload levels of the corresponding instances are the same in Figure 10a–c.

From the analysis presented above, an energy-efficient scheduling can be realized by reducing the idle energy consumptions of machine tools; that is, use of low automation level machine tools can improve the energy use rate. If we define the energy use rate as:

$$\frac{{\sum }_{k}MC{T}_k·Pcu{t}_k}{{\sum }_k\left[\left(M{C}_k-MC{T}_k\right)Pidl{e}_k\right]}$$

(14)

it can be found that the energy use rate can further be improved by increasing the number of jobs in a scheduling scheme because in this case the idle time intervals can be edged out and this will reduce the idle energy consumption. In Figure 10 when there are fewer jobs, such as in Instance 1, the energy use rate is close to 1 and this means that the idle energy consumption occupies a high proportion and the energy use in this case is inefficient. For the instance with more jobs (more operations), the energy use rate can be much higher because the extra operations occupy the idle time intervals in the Gantt chart. The extreme case is the energy consumption of Instance 24 in Figure 10a with $\alpha =0.35$ and $\beta =1$. With more operations and low automation level machine tools, it achieves a high energy use rate.

Figure 11 gives an intuitive normalized representation of the proportion the machining energy consumption and the idle energy consumption. According to Figure 11a,d,g, using low automation level machines can help improve the energy use rate because such machines are usually equipped with only basic components, e.g., coolant pumps and manual tool change devices, and hence consume less energy. For high-automation-level machines, however, they consume more energy even in non-cutting status because other components e.g., CNC systems, are not allowed to be turned off. The influence of machine workload on the energy consumption is also demonstrable; a large $\beta$ value means more energy will be consumed in processing the operation. With more operations and heavy workloads, e.g., cases c, f, and i, the energy use rate of the whole production will be improved. Also, it can be seen from Figure 11c,g that in the best case, about 80% of the total energy will be used in cutting processes; however, this value drops to about 55% in the worst case. In other words, about half of the total energy will be used in non-cutting processes in the worst case.

7. Conclusions

This research performs a study on the energy-efficient IPPS problem that has seldom been considered before. Due to the limitations in previous research where frequent machine turning “ons” and “offs” will cause damage to machine tools and also deteriorate the thermal balance of machine tools, in this research the machines in a job shop are not allowed to be shut down even in the idle time interval unless all the operations of that machine have been processed. A novel MILP model is established; due to the complexity in solving the MILP model, we then developed a multi-objective memetic algorithm to address this problem; in the proposed algorithm, the VNS method is applied to enhance the local search ability. Different scenarios about machine automation levels and workloads have been generated to study the characteristics of energy consumptions. Typical instances (Kim’s benchmark) are adopted in the experiments. Computational results show that the proposed multi-objective memetic algorithm can obtain more promising non-dominated solutions than the traditional NSGA-II algorithm. Compared with single-objective optimization method, multi-objective optimization results reveal the necessity to consider both energy efficiency and the makespan criterion in the IPPS problem.

According to the results under different scenarios, some managerial insights for energy consumption reduction (also carbon emission reduction) can be concluded as follows.

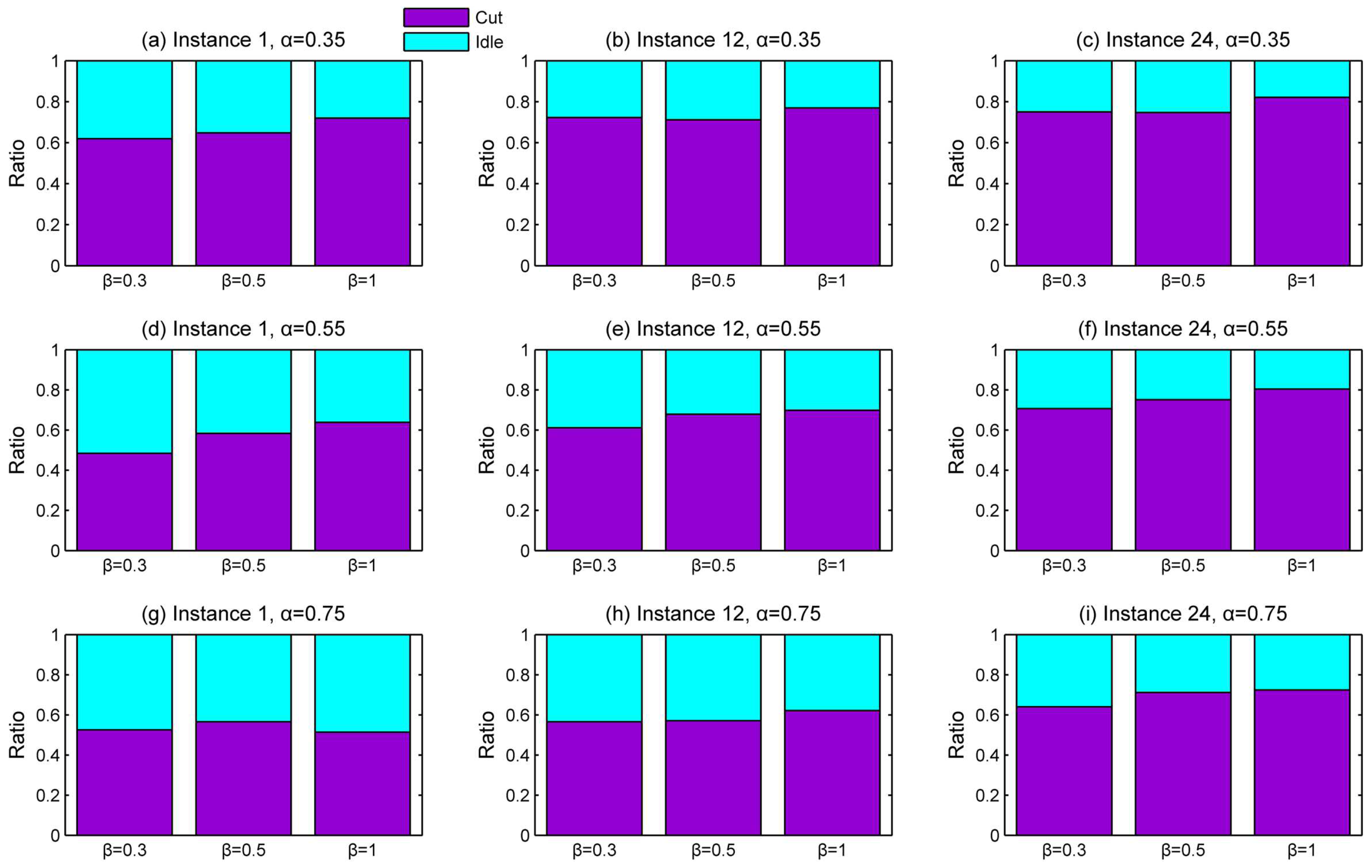
• Due to low constant energy use of machines with low automation levels, operations are suggested to be processed by machines with low automation levels. In such a case, the idle energy consumption can be reduced. This strategy can be applied to the cases where only few operations to be processed because there will be many idle time intervals.
• Increasing the number of operations or jobs is another way to improve energy use rate; there will be no idle time intervals between two operations on a machine and therefore, the idle energy consumption can be reduced.

However, in real-life production situations, the processing time of an operation is usually uncertain; therefore, the IPPS problem with deterministic processing times does not match the actual situation on the shop floor. The makespan as well as the energy consumption reduction for the IPPS problem with uncertain processing times will be considered as a further research direction and the fuzzy sets [59] can be used to describe the uncertain processing times. To reduce the coal-fired electricity consumption, the optimal scheduling method for the IPPS problem with time-sharing prices can also be considered.