Mechanistic Models of Inducible Synthetic Circuits for Joint Description of DNA Copy Number, Regulatory Protein Level, and Cell Load
Abstract
:1. Introduction
2. Materials and Methods
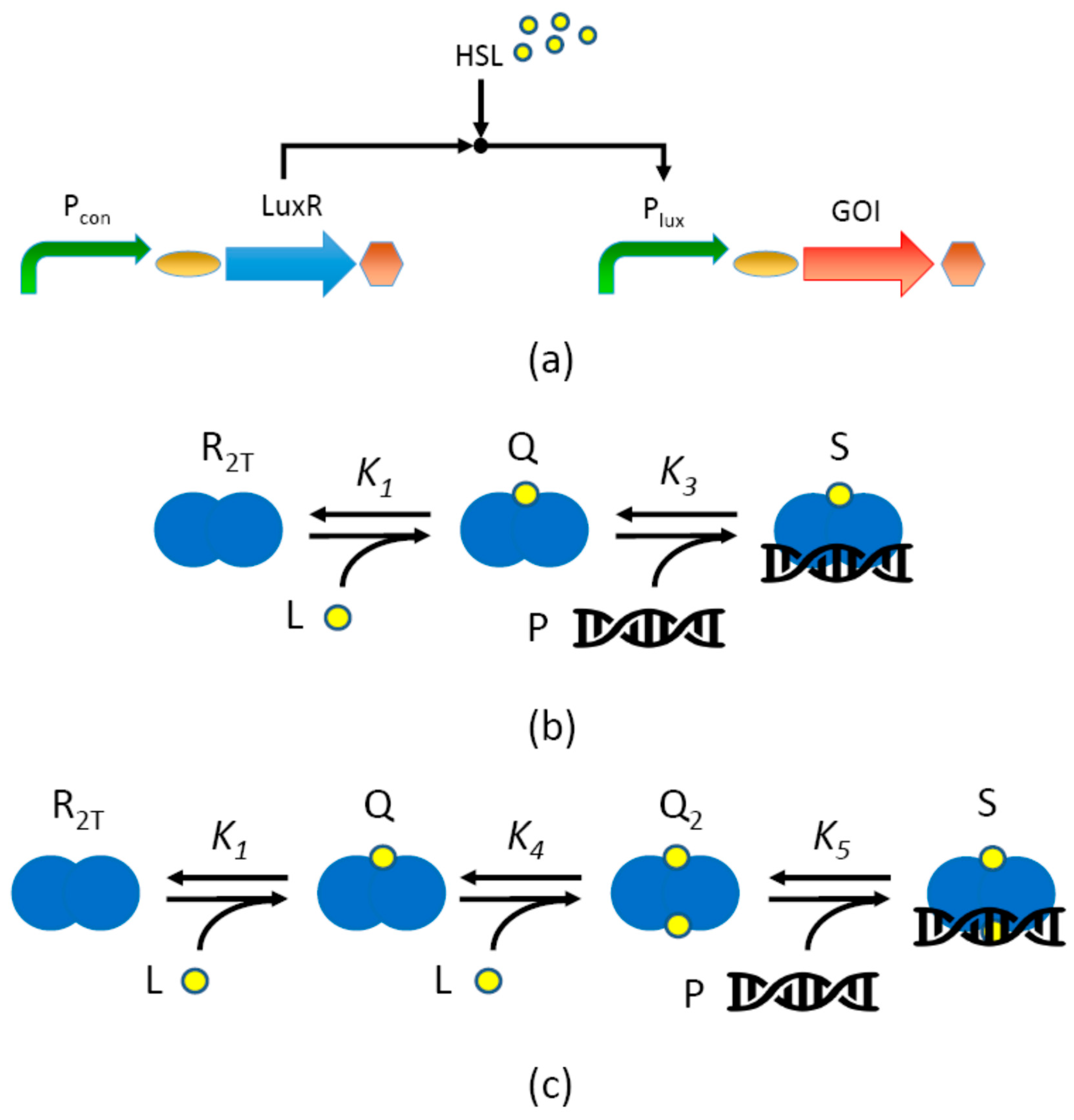
2.1. Inducible System Description
2.2. Model Definition
2.2.1. Empirical Michaelis–Menten Model (M0)
Assumptions
Derivation
Final Expression
2.2.2. Mechanistic Model with LuxR Abundance Assumption (M1)
Assumptions
Derivation
Final Expression
2.2.3. Mechanistic Model without LuxR Abundance Assumption (M2)
Assumptions and Final Expression
2.2.4. Modeling LuxR-HSL Hetero-Tetramerization (M1T, M2T)
Assumptions
Derivation
Final Expression
2.2.5. Modeling Cell Load (M1L, M2L)
Assumptions
Derivation
Final Expression
2.3. Model Analysis
2.3.1. Model Parametrization
2.3.2. A Priori Identifiability
2.3.3. A Posteriori Identifiability
2.3.4. Simulations
2.3.5. Analysis of Activation Curves
2.3.6. In Vivo Experiments
3. Results
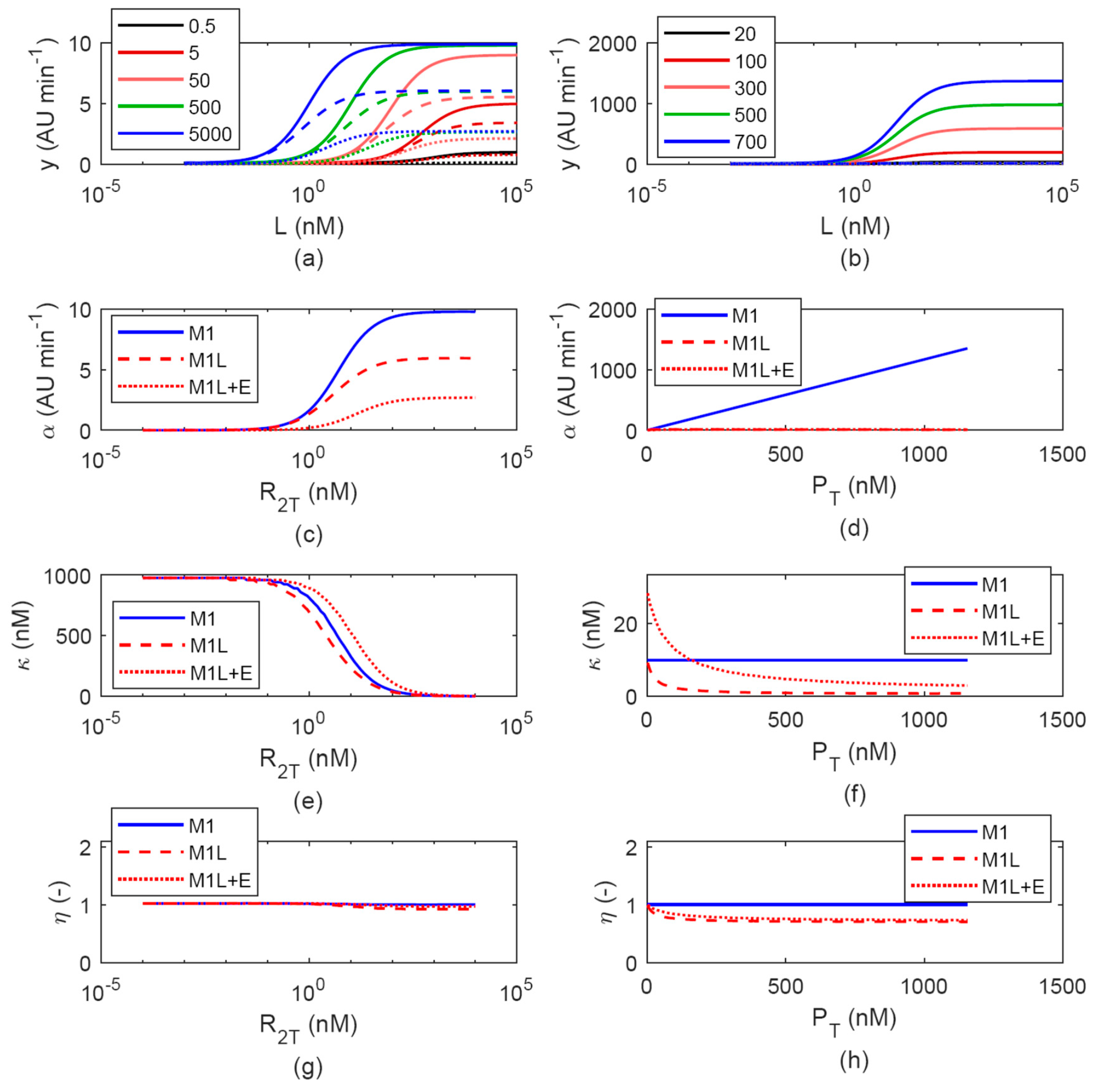
3.1. Simulated Output for Different Model Assumptions
3.1.1. Effect of LuxR Abundance Assumption: M1 vs. M2
3.1.2. Effects of Cell Load
3.1.3. Evaluation of LuxR-HSL Complex Formation Assumptions: M(1-2) vs. M(1-2)T
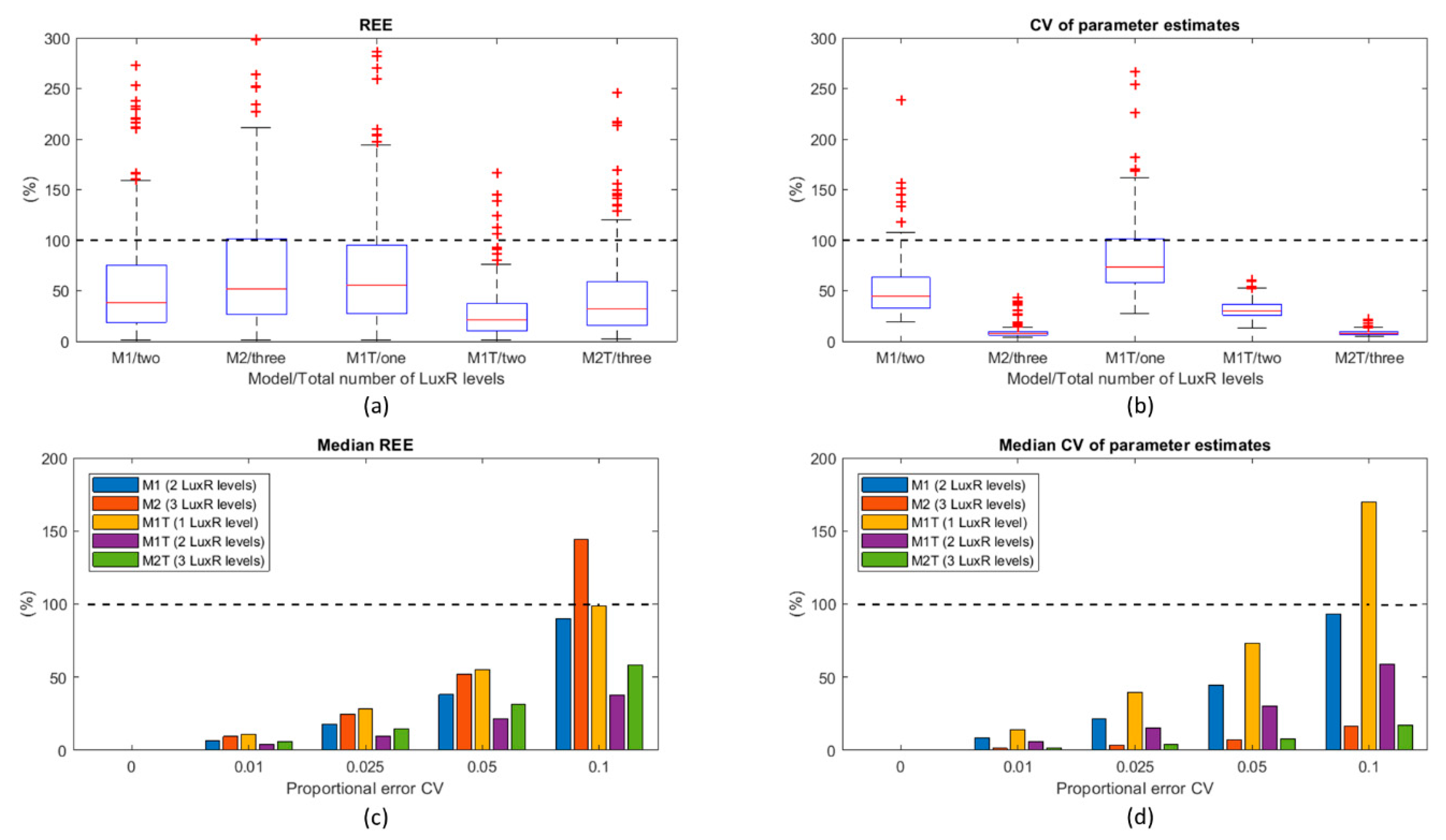
3.2. Model Identifiability
3.2.1. M1
3.2.2. M2
3.2.3. M1T
3.2.4. M2T
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peccoud, J. Synthetic Biology: Fostering the cyber-biological revolution. Synth. Biol. 2016, 1, ysw001. [Google Scholar] [CrossRef]
- Kitney, R.I.; Freemont, P.S. Engineering biology: A key driver of the bio-economy. IET: Eng. Biol. 2017, 1, 3–6. [Google Scholar] [CrossRef]
- Del Vecchio, D.; Qian, Y.; Murray, R.M.; Sontag, E.D. Future systems and control research in synthetic biology. Annu. Rev. Control 2018, 45, 5–17. [Google Scholar] [CrossRef]
- Schaerli, Y.; Isalan, M. Building synthetic gene circuits from combinatorial libraries: Screening and selection strategies. Mol. Biosyst. 2013, 9, 1559–1567. [Google Scholar] [CrossRef] [PubMed]
- Engstrom, M.D.; Pfleger, B.F. Transcription control engineering and applications in synthetic biology. Synth. Syst. Biotechnol. 2017, 2, 176–191. [Google Scholar] [CrossRef] [PubMed]
- Pasotti, L.; Zucca, S. Advances and computational tools towards predictable design in biological engineering. Comput. Math. Methods Med. 2014, 2014, 369681. [Google Scholar] [CrossRef] [PubMed]
- Way, J.C.; Collins, J.J.; Keasling, J.D.; Silver, P.A. Integrating biological redesign: Where synthetic biology came from and where it needs to go. Cell 2014, 157, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Carothers, M.; Keasling, J.D. Design of a dynamic sensor-regulator system for production of chemicals and fuels derived from fatty acids. Nat. Biotechnol. 2012, 30, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Lo, T.M.; Chng, S.H.; Teo, W.S.; Cho, H.S.; Chang, M.W. A two-layer gene circuit for decoupling cell growth from metabolite production. Cell Syst. 2016, 3, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Dragosits, M.; Nicklas, D.; Tagkopoulos, I. A synthetic biology approach to self-regulatory recombinant protein production in Escherichia coli. J. Biol. Eng. 2012, 6, 2. [Google Scholar] [CrossRef] [PubMed]
- Carr, S.B.; Beal, J.; Densmore, D.M. Reducing DNA context dependence in bacterial promoters. PLoS ONE 2017, 12, e0176013. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Huang, H.H.; Jiménez, J.I.; Del Vecchio, D. Resource competition shapes the response of genetic circuits. ACS Synth. Biol. 2017, 6, 1263–1272. [Google Scholar] [CrossRef] [PubMed]
- Bandiera, L.; Pasini, A.; Pasotti, L.; Zucca, S.; Mazzini, G.; Magni, P.; Giordano, E.; Furini, S. Experimental measurements and mathematical modeling of biological noise arising from transcriptional and translational regulation of basic synthetic gene circuits. J. Theor. Biol. 2016, 395, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Gyorgy, A.; Jiménez, J.I.; Yazbek, J.; Huang, H.H.; Chung, H.; Weiss, R.; Del Vecchio, D. Isocost lines describe the cellular economy of genetic circuits. Biophys. J. 2015, 109, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Ceroni, F.; Algar, R.; Stan, G.B.; Ellis, T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nat. Methods 2015, 12, 415–418. [Google Scholar] [CrossRef] [PubMed]
- Arkin, A.P. A wise consistency: Engineering biology for conformity, reliability, predictability. Curr. Opin. Chem. Biol. 2013, 17, 893–901. [Google Scholar] [CrossRef] [PubMed]
- Ang, J.; Harris, E.; Hussey, B.J.; Kil, R.; McMillen, D.R. Tuning response curves for synthetic biology. ACS Synth. Biol. 2013, 2, 547–567. [Google Scholar] [CrossRef] [PubMed]
- Trabelsi, H.; Koch, M.; Faulon, J.L. Building a minimal and generalizable model of transcription factor-based biosensors: Showcasing flavonoids. Biotechnol. Bioeng. 2018, 115, 2292–2304. [Google Scholar] [CrossRef] [PubMed]
- Endler, L.; Rodriguez, N.; Juty, N.; Chelliah, V.; Laibe, C.; Li, C.; Le Novere, N. Designing and encoding models for synthetic biology. J. R. Soc. Interface 2009, 6 (Suppl. 4), S405–S417. [Google Scholar] [CrossRef]
- Carbonell-Ballestero, M.; Duran-Nebreda, S.; Montañez, R.; Solé, R.; Macía, J.; Rodríguez-Caso, C. A bottom-up characterization of transfer functions for synthetic biology designs: Lessons from enzymology. Nucleic Acids Res. 2014, 42, 14060–14069. [Google Scholar] [CrossRef] [PubMed]
- Mileyko, Y.; Joh, R.I.; Weitz, J.S. Small-scale copy number variation and large-scale changes in gene expression. Proc. Natl. Acad. Sci. USA 2008, 105, 16659–16664. [Google Scholar] [CrossRef] [PubMed]
- Canton, B.; Labno, A.; Endy, D. Refinement and standardization of synthetic biological parts and devices. Nat. Biotechnol. 2008, 26, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Pasotti, L.; Bellato, M.; Casanova, M.; Zucca, S.; Cusella De Angelis, M.G.; Magni, P. Re-using biological devices: A model-aided analysis of interconnected transcriptional cascades designed from the bottom-up. J. Biol. Eng. 2017, 11, 50. [Google Scholar] [CrossRef] [PubMed]
- Gabor, A.; Villaverde, A.F.; Banga, J.R. Parameter identifiability analysis and visualization in large-scale kinetic models of biosystems. BMC Syst. Biol. 2017, 11, 54. [Google Scholar] [CrossRef] [PubMed]
- Berset, Y.; Merulla, D.; Joublin, A.; Hatzimanikatis, V.; van der Meer, J.R. Mechanistic modeling of genetic circuits for ArsR arsenic regulation. ACS Synth. Biol. 2017, 6, 862–874. [Google Scholar] [CrossRef] [PubMed]
- Rydenfelt, M.; Cox, R.S., 3rd; Garcia, H.; Phillips, R. Statistical mechanical model of coupled transcription from multiple promoters due to transcription factor titration. Phys. Rev. E 2014, 89, 012702. [Google Scholar] [CrossRef] [PubMed]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Kuhlman, T.; Phillips, R. Transcriptional regulation by the numbers: Applications. Curr. Opin. Genet. Dev. 2005, 15, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Phillips, R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Stevens, A.M.; Greenberg, E.P. Quorum sensing in Vibrio fischeri: Essential elements for activation of the luminescence genes. J. Bacteriol. 1997, 179, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Balagadde, F.K.; Song, H.; Ozaki, J.; Collins, C.H.; Barnet, M.; Arnold, F.H.; Quake, S.R.; You, L. A synthetic Escherichia coli predator-prey ecosystem. Mol. Syst. Biol. 2008, 4, 187. [Google Scholar] [CrossRef] [PubMed]
- Pasotti, L.; Bellato, M.; Politi, N.; Casanova, M.; Zucca, S.; Cusella De Angelis, M.G.; Magni, P. A synthetic close-loop controller circuit for the regulation of an extracellular molecule by engineered bacteria. IEEE Trans. Biomed. Circuits Syst. 2018, 13, 248–258. [Google Scholar] [CrossRef] [PubMed]
- Zucca, S.; Pasotti, L.; Politi, N.; Casanova, M.; Mazzini, G.; Cusella De Angelis, M.G.; Magni, P. Multi-faceted characterization of a novel LuxR-repressible promoter library for Escherichia coli. PLoS ONE 2015, 10, e0126264. [Google Scholar] [CrossRef] [PubMed]
- Zucca, S.; Pasotti, L.; Mazzini, G.; Cusella De Angelis, M.G.; Magni, P. Characterization of an inducible promoter in different DNA copy number conditions. BMC Bioinform. 2012, 13, S11. [Google Scholar] [CrossRef] [PubMed]
- Danino, T.; Mondragon-Palomino, O.; Tsimring, L.; Hasty, J. A synchronized quorum of genetic clocks. Nature 2010, 463, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Pasotti, L.; Quattrocelli, M.; Galli, D.; Cusella De Angelis, M.G.; Magni, P. Multiplexing and demultiplexing logic functions for computing signal processing tasks in synthetic biology. Biotechnol. J. 2011, 6, 784–795. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Del Vecchio, D. Effective interaction graphs arising from resource limitations in gene networks. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4417–4423. [Google Scholar]
- Pasotti, L.; Politi, N.; Zucca, S.; Cusella De Angelis, M.G.; Magni, P. Bottom-up engineering of biological systems through standard bricks: A modularity study on basic parts and devices. PLoS ONE 2012, 7, e39407. [Google Scholar] [CrossRef]
- Milo, R. What is the total number of protein molecules per cell volume? A call to rethink some published values. Bioessays 2013, 35, 1050–1055. [Google Scholar] [CrossRef] [PubMed]
- Magni, P.; Sparacino, G. Parameter estimation. In Modeling Methodology for Physiology and Medicine, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 83–110. [Google Scholar]
- Stefan, M.I.; Le Novere, N. Cooperative binding. PLoS Comput. Biol. 2013, 9, e1003106. [Google Scholar] [CrossRef] [PubMed]
- Colton, D.M.; Stabb, E.V.; Hagen, S.J. Modeling analysis of signal sensitivity and specificity by Vibrio fischeri LuxR variants. PLoS ONE 2015, 10, e0126474. [Google Scholar]
- Jayanthi, S.; Nilgiriwala, K.S.; Del Vecchio, D. Retroactivity controls the temporal dynamics of gene transcription. ACS Synth. Biol. 2013, 2, 431–441. [Google Scholar] [CrossRef] [PubMed]
- Borkowski, O.; Bricio, C.; Murgiano, M.; Rothschild-Mancinelli, B.; Stan, G.B.; Ellis, T. Cell-free prediction of protein expression costs for growing cells. Nat. Commun. 2018, 9, 1497. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Units | Models | Value |
|---|---|---|---|
| PU | nM | All | 1.66 |
| rT | nM a | All | 1.66 |
| n1 | - | All | 5 b |
| n2 | - a | All | 301 b |
| γX | min−1 | All | 0.01 c |
| σ | min−1 | All | 0.0167 |
| AU nM−1 min−1 | All | 0.0192 | |
| AU nM−1 min−1 | All | 1.907 | |
| K1 | nM−1 | M1, M1L, M2, M2L | 0.001 |
| M1T, M1TL, M2T, M2TL | 0.0055 | ||
| K3 | nM−1 | M1, M1L, M2, M2L | 0.2 |
| K4 | nM−1 | M1T, M2T, M1TL, M2TL | 0.001375 |
| K5 | nM−1 | M1T, M2T, M1TL, M2TL | 0.2 |
| JRFP | min AU−1 | M1L, M2L, M1TL, M2TL | 0.04 |
| E | - | M1L, M2L, M1TL, M2TL | 0 d |
| Condition | α (%) a | κ (nM) | η (-) | Reference |
|---|---|---|---|---|
| Medium copy b, no IPTG | 47 | 194.01 | 1.01 | [31] |
| Medium copy + E c, no IPTG | 27 | 474.1 | 0.98 | [31] |
| Medium copy, IPTG = 500 µM | 100 | 0.77 | 1.54 | [31] |
| Medium copy + E, IPTG = 500 µM | 68 | 0.99 | 1.29 | [31] |
| Low copy d, no ATc | 83 | 34.29 | 0.98 | This study |
| Low copy, ATc = 2.5 ng/ml | 92 | 11.32 | 1 | This study |
| Low copy, ATc = 5 ng/ml | 97 | 3.73 | 1.15 | This study |
| Low copy, ATc = 50 ng/ml | 100 | 1.52 | 1.39 | This study |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasotti, L.; Bellato, M.; De Marchi, D.; Magni, P. Mechanistic Models of Inducible Synthetic Circuits for Joint Description of DNA Copy Number, Regulatory Protein Level, and Cell Load. Processes 2019, 7, 119. https://doi.org/10.3390/pr7030119
Pasotti L, Bellato M, De Marchi D, Magni P. Mechanistic Models of Inducible Synthetic Circuits for Joint Description of DNA Copy Number, Regulatory Protein Level, and Cell Load. Processes. 2019; 7(3):119. https://doi.org/10.3390/pr7030119
Chicago/Turabian StylePasotti, Lorenzo, Massimo Bellato, Davide De Marchi, and Paolo Magni. 2019. "Mechanistic Models of Inducible Synthetic Circuits for Joint Description of DNA Copy Number, Regulatory Protein Level, and Cell Load" Processes 7, no. 3: 119. https://doi.org/10.3390/pr7030119
APA StylePasotti, L., Bellato, M., De Marchi, D., & Magni, P. (2019). Mechanistic Models of Inducible Synthetic Circuits for Joint Description of DNA Copy Number, Regulatory Protein Level, and Cell Load. Processes, 7(3), 119. https://doi.org/10.3390/pr7030119






