Simulation Study on the Influence of Gas Mole Fraction and Aqueous Activity under Phase Equilibrium
Abstract
:1. Introduction
2. Thermodynamic Framework
2.1. Thermodynamic Model of Vapor Phase
2.2. Thermodynamic Model of Hydrate Phase
2.3. Thermodynamic Model of Aqueous Phase
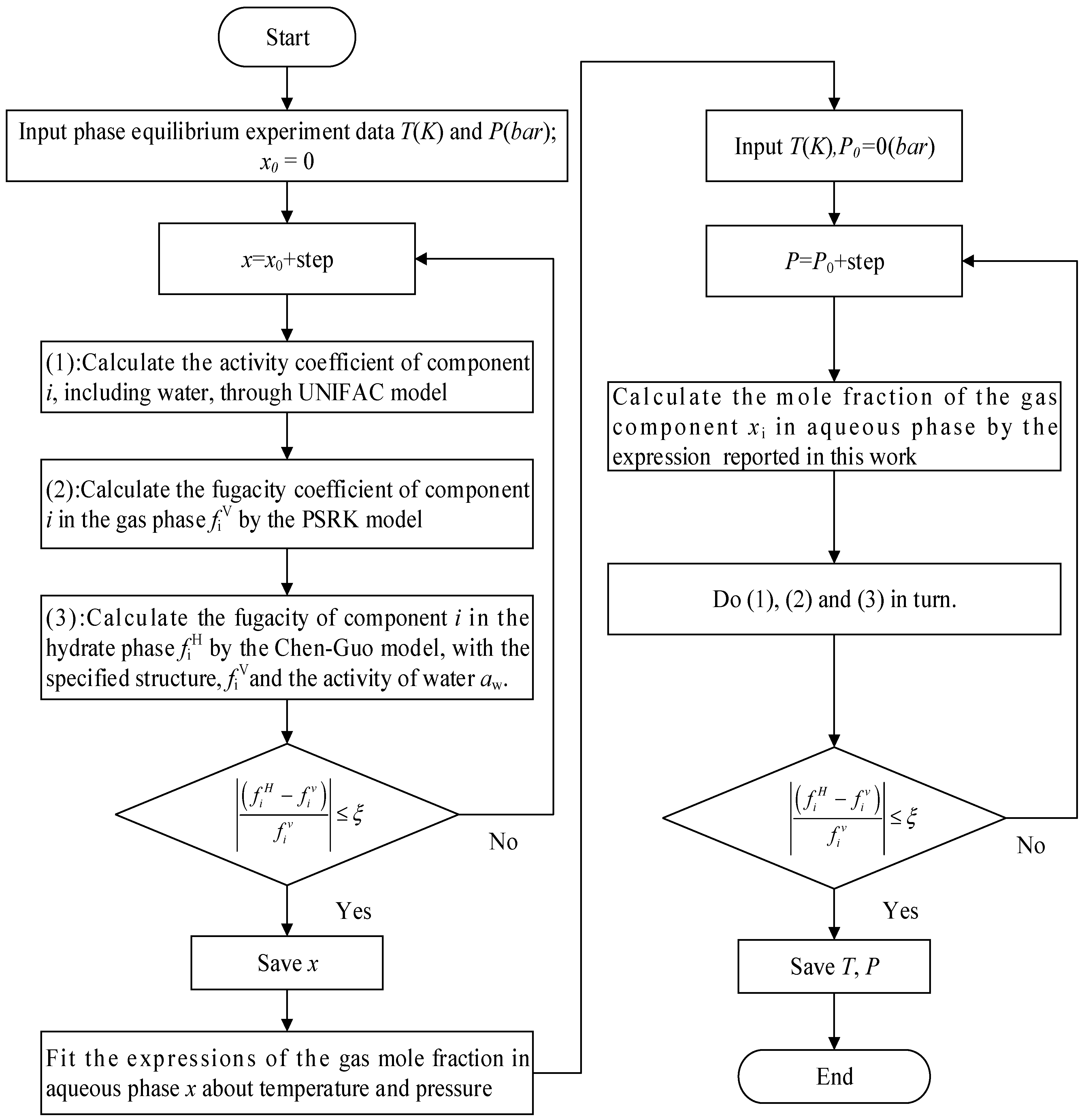
3. Calculation Procedure
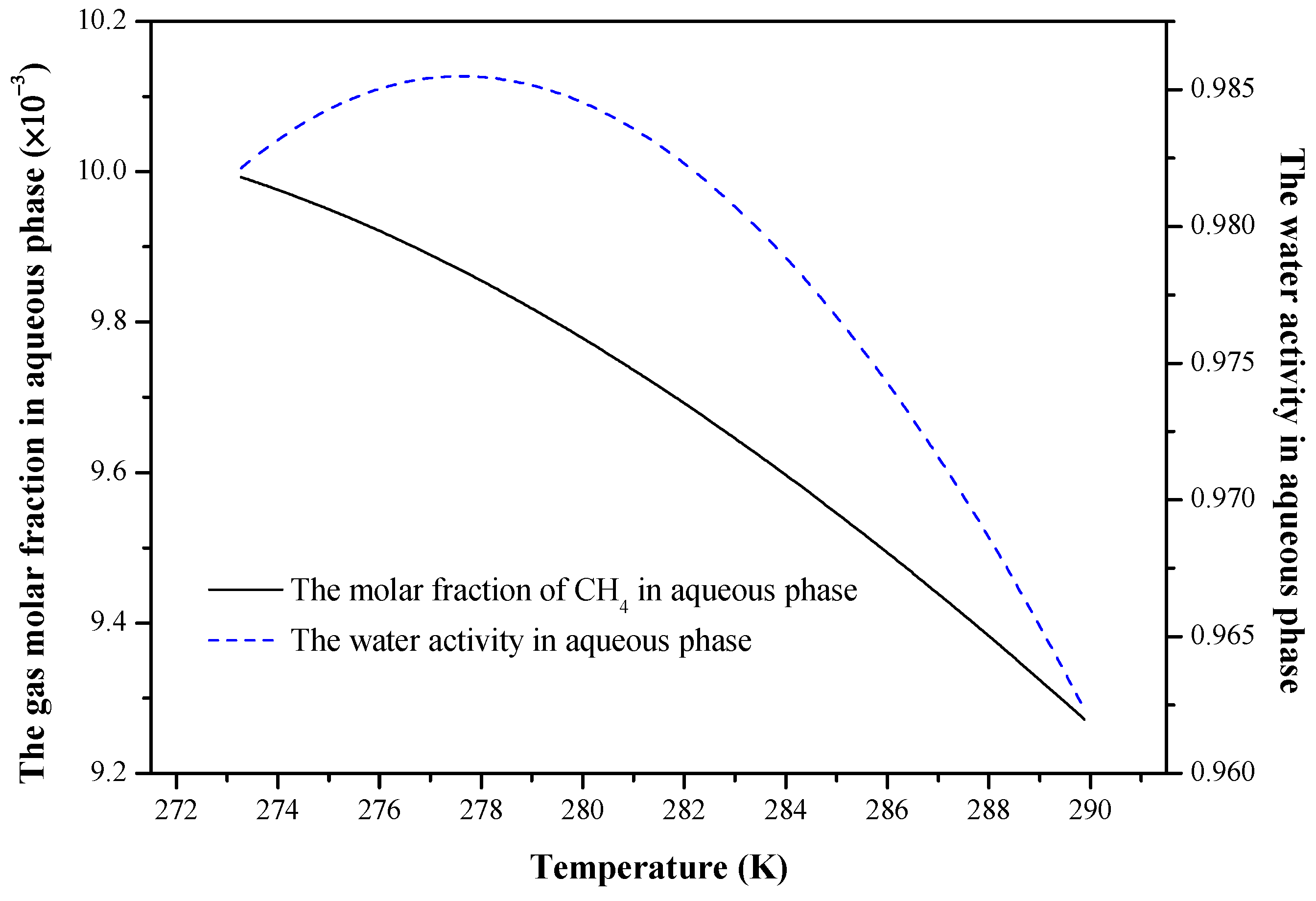
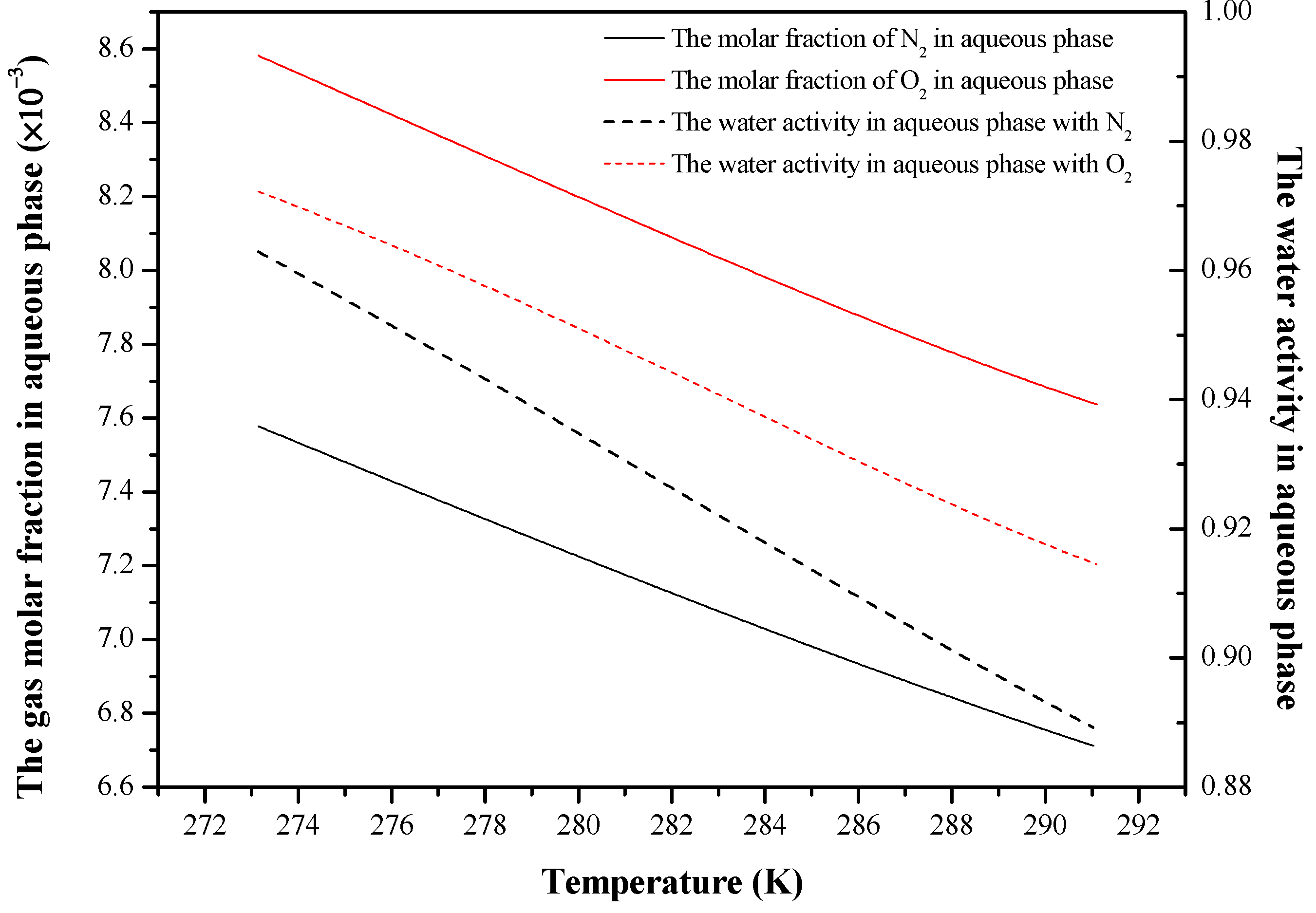
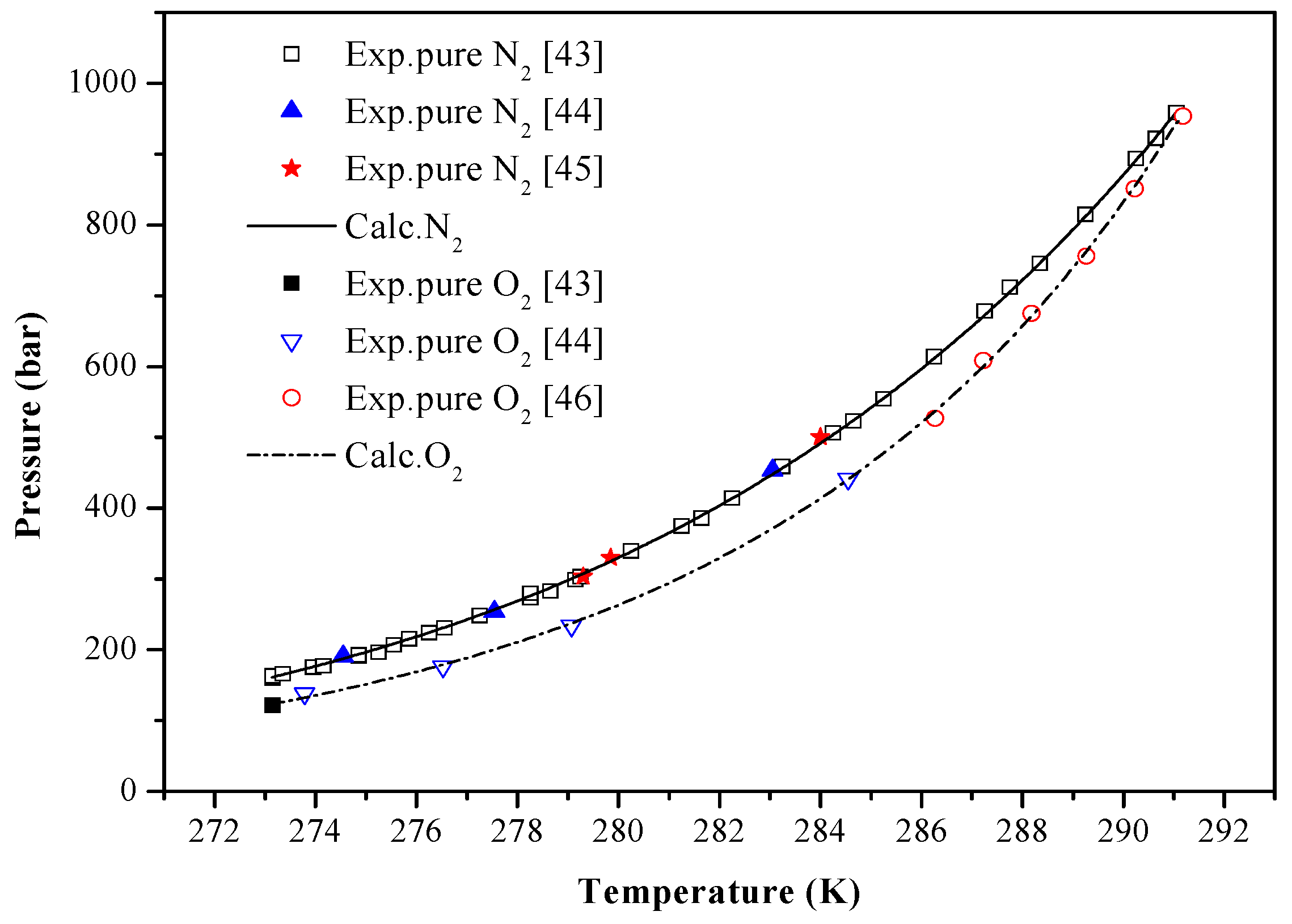
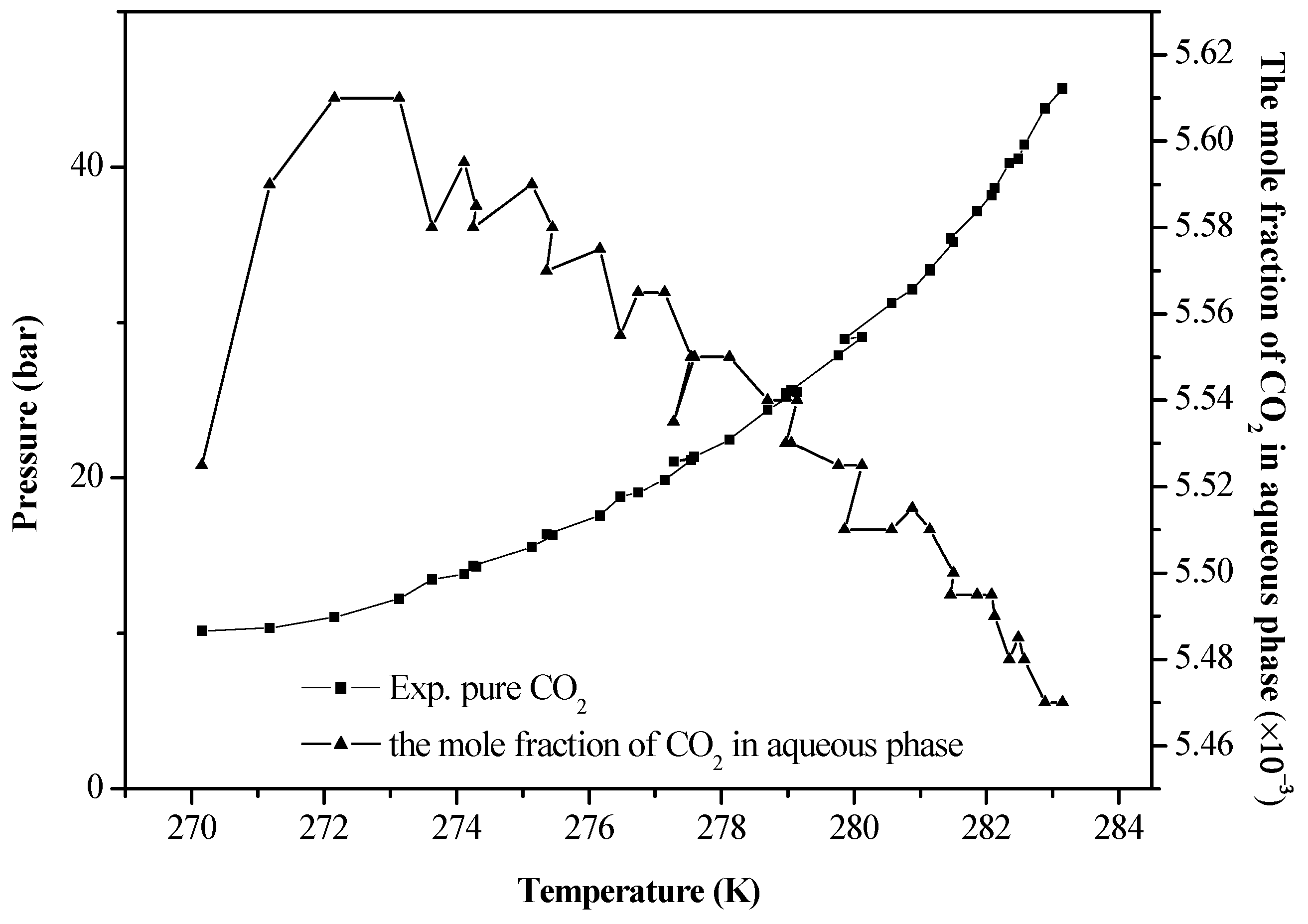
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gas, 3rd ed.; Chemical Industries, CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Carroll, J.J. Natural Gas Hydrates: A Guide for Engineers; Gulf Professional Publishing: Houston, TX, USA, 2009. [Google Scholar]
- Abdi-Khanghah, M.; Adelizadeh, M.; Naserzadeh, Z.; Barati, H.; Zhang, Z. Methane hydrate formation in the presence of ZnO nanoparticle and SDS: Application to transportation and storage. J. Nat. Gas Sci. Eng. 2018, 54, 120–130. [Google Scholar] [CrossRef]
- Aaron, D.; Tsouris, C. Separation of CO2 from Flue Gas: A Review. Sep. Sci. Technol. 2005, 40, 321–348. [Google Scholar] [CrossRef]
- Ogawa, T.; Ito, T.; Watanabe, K.; Tahara, K.-I.; Hiraoka, R.; Ochiai, J.-I.; Ohmura, R.; Mori, Y.H. Development of a novel hydrate-based refrigeration system: A preliminary overview. Appl. Therm. Eng. 2006, 26, 2157–2167. [Google Scholar] [CrossRef]
- Wang, X.; Dennis, M.; Hou, L. Clathrate hydrate technology for cold storage in air conditioning systems. Renew. Sustain. Energy Rev. 2014, 36, 34–51. [Google Scholar] [CrossRef]
- Xu, C.-G.; Li, X.-S. Research progress of hydrate-based CO2 separation and capture from gas mixtures. RSC Adv. 2014, 4, 18301–18316. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, Z.; Zhang, Z.; Shang, L.; Ma, S. Effect of silica sand size and saturation on methane hydrate formation in the presence of SDS. J. Nat. Gas Sci. Eng. 2018, 56, 266–280. [Google Scholar] [CrossRef]
- Khan, M.N.; Warrier, P.; Peters, C.J.; Koh, C.A. Review of vapor-liquid equilibria of gas hydrate formers and phase equilibria of hydrates. J. Nat. Gas Sci. Eng. 2016, 35, 1388–1404. [Google Scholar] [CrossRef]
- Taylor, F.W. The greenhouse effect and climate change. Rep. Prog. Phys. 1991, 54, 881. [Google Scholar] [CrossRef]
- Zhao, W.-L.; Zhong, D.-L.; Yang, C. Prediction of phase equilibrium conditions for gas hydrates formed in the presence of cyclopentane or cyclohexane. Fluid Phase Equilib. 2016, 427, 82–89. [Google Scholar] [CrossRef]
- van der Waals, J.H.; Platteeuw, J.C. Clathrate solutions. In Advances in Chemical Physics; Interscience Publishers Inc.: New York, NY, USA, 1959. [Google Scholar]
- Nasrifar, K.; Moshfeghian, M.; Maddox, R.N. Prediction of equilibrium conditions for gas hydrate formation in the mixtures of both electrolytes and alcohol. Fluid Phase Equilib. 1998, 146, 1–13. [Google Scholar] [CrossRef]
- Haghighi, H.; Chapoy, A.; Burgess, R.; Mazloum, S.; Tohidi, B. Phase equilibria for petroleum reservoir fluids containing water and aqueous methanol solutions: Experimental measurements and modelling using the CPA equation of state. Fluid Phase Equilib. 2009, 278, 109–116. [Google Scholar] [CrossRef]
- Martin, A.; Peters, C.J. Thermodynamic Modeling of Promoted Structure II Clathrate Hydrates of Hydrogen. J. Phys. Chem. B. 2009, 113, 7548–7557. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.J.; Guo, T.M. Thermodynamic modeling of hydrate formation based on new concepts. Fluid Phase Equilib. 1996, 122, 43–65. [Google Scholar] [CrossRef]
- Chen, G.J.; Guo, T.M. A new approach to gas hydrate modelling. Chem. Eng. J. 1998, 71, 141–151. [Google Scholar] [CrossRef]
- Sun, C.Y.; Chen, G.J. Modelling the hydrate formation condition for sour gas and mixtures. Chem. Eng. Sci. 2005, 60, 4879–4885. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sandler, S.I. Phase behavior of clathrate hydrates: A model for single and multiple gas component hydrates. Chem. Eng. Sci. 2003, 58, 27–41. [Google Scholar] [CrossRef]
- Ma, Q.L.; Chen, G.J.; Sun, C.Y.; Yang, L.Y.; Liu, B. Predictions of hydrate formation for systems containing hydrogen. Fluid Phase Equilib. 2013, 358, 290–295. [Google Scholar] [CrossRef]
- Ma, Q.L.; Chen, G.J.; Guo, T.M. Modelling the gas hydrate formation of inhibitor containing systems. Fluid Phase Equilib. 2003, 205, 291–302. [Google Scholar] [CrossRef]
- Liu, H.; Guo, P.; Du, J.; Wang, Z.; Chen, G.; Li, Y. Experiments and modeling of hydrate phase equilibrium of CH4/CO2/H2S/N2 quaternary sour gases in distilled water and methanol-water solutions. Fluid Phase Equilib. 2017, 432, 10–17. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. Aiche J. 2010, 21, 116–128. [Google Scholar] [CrossRef]
- Weidlich, U.; Gmehling, J. A modified UNIFAC model. 1. Prediction of VLE, hE, and .gamma..infin. Ind. Eng. Chem. Res. 1987, 26, 1372–1381. [Google Scholar] [CrossRef]
- Delavar, H.; Haghtalab, A. Prediction of hydrate formation conditions using GE-EOS and UNIQUAC models for pure and mixed-gas systems. Fluid Phase Equilib. 2014, 369, 1–12. [Google Scholar] [CrossRef]
- Delavar, H.; Haghtalab, A. Thermodynamic modeling of gas hydrate formation conditions in the presence of organic inhibitors, salts and their mixtures using UNIQUAC model. Fluid Phase Equilib. 2015, 394, 101–117. [Google Scholar] [CrossRef]
- Dehaghani, A.H.S.; Karami, B. A new predictive thermodynamic framework for phase behavior of gas hydrate. Fuel 2018, 216, 796–809. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sander, S.T. A Fugacity Model for Gas Hydrate Phase Equilibria. Ind. Eng. Chem. Res. 2000, 39, 3377–3386. [Google Scholar] [CrossRef]
- Heidemann, R.A.; Prausnitz, J.M. Equilibrium Data for Wet-Air Oxidation. Water Content and Thermodynamic Properties of Saturated Combustion Gases. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 375–381. [Google Scholar] [CrossRef]
- Sander, B.; Skjold-Jørgensen, S.; Rasmussen, P. Gas solubility calculations. I. Unifac. Fluid Phase Equilib. 1983, 11, 105–126. [Google Scholar] [CrossRef]
- Fredenslund, A.; Gmehling, J.; Rasmussen, P. Vapor-liquid equilibria using UNIFAC: A group contribution method. Fluid Phase Equilib. 1977, 1, 317. [Google Scholar]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Gmehling, J.; Li, J.; Fischer, K. Further development of the PSRK model for the prediction of gas solubilities and vapor-liquid-equilibria at low and high pressures II. Fluid Phase Equilib. 1997, 141, 113–127. [Google Scholar] [CrossRef]
- Fischer, K.; Gmehling, J. Further development, status and results of the PSRK method for the prediction of vapor-liquid equilibria and gas solubilities. Fluid Phase Equilib. 1996, 121, 185–206. [Google Scholar] [CrossRef]
- Holderbaum, T.; Gmehling, J. PSRK: A group contribution equation based on UNIFAC. Fluid Phase Equilib. 1991, 70, 251–265. [Google Scholar] [CrossRef]
- Sloan, E.D., Jr. Clathrate Hydrates of Natural Gases, 2nd ed.; CRC Press: New York, NY, USA, 1998. [Google Scholar]
- Holder, G.D.; Corbin, G.; Papadopoulos, K.D. Thermodynamic and Molecular Properties of Gas Hydrates from Mixtures Containing Methane, Argon, and Krypton. Ind. Eng. Chem. Fundam. 1980, 19, 282–286. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Sun, Q.; Guo, X.; Chapman, W.G.; Liu, A.; Yang, L.; Zhang, J. Vapor–hydrate two-phase and vapor–liquid–hydrate three-phase equilibrium calculation of THF/CH4/N2 hydrates. Fluid Phase Equilib. 2015, 401, 70–76. [Google Scholar] [CrossRef]
- Krichevsky, I.R.; Kasarnovsky, J.S. Thermodynamical Calculations of Solubilities of Nitrogen and Hydrogen in Water at High Pressures. J. Am. Chem. Soc. 1935, 57, 2168–2171. [Google Scholar] [CrossRef]
- Sloan, E.D. Clathrate Hydrates of Natural Gas; M. Dekker: New York, NY, USA, 2007. [Google Scholar]
- Ma, Z.W.; Zhang, P.; Bao, H.S.; Deng, S. Review of fundamental properties of CO2 hydrates and CO2 capture and separation using hydration method. Renew. Sustain. Energy Rev. 2016, 53, 1273–1302. [Google Scholar] [CrossRef]
- Van Cleeff, A.; Diepen, G.A.M. Gas hydrate of nitrogen and oxygen. Recueil des Travaux Chimiques des Pays-Bas 1960, 79, 582–586. [Google Scholar] [CrossRef]
- Mohammadi, A.H.; Tohidi, B.; Burgass, R.W. Equilibrium Data and Thermodynamic Modeling of Nitrogen, Oxygen, and Air Clathrate Hydrates. J. Chem. Eng. Data 2003, 48, 612–616. [Google Scholar] [CrossRef]
- Duc, N.H.; Chauvy, F.; Herri, J.-M. CO2 capture by hydrate crystallization—A potential solution for gas emission of steelmaking industry. Energy Convers. Manag. 2007, 48, 1313–1322. [Google Scholar] [CrossRef]
- Van Cleeff, A.; Diepen, G.A.M. Gas Hydrates of Nitrogen and Oxygen. II. Recueil des Travaux Chimiques des Pays–Bas 1965, 84, 1085–1093. [Google Scholar] [CrossRef]
- Walsh, M.R.; Beckham, G.T.; Koh, C.A.; Sloan, E.D.; Wu, D.T.; Sum, A.K. Methane Hydrate Nucleation Rates from Molecular Dynamics Simulations: Effects of Aqueous Methane Concentration, Interfacial Curvature, and System Size. J. Phys. Chem. C 2011, 115, 21241–21248. [Google Scholar] [CrossRef]
- Guo, G.J.; Rodger, P.M. Solubility of aqueous methane under metastable conditions: Implications for gas hydrate nucleation. J. Phys. Chem. B 2013, 117, 6498–6504. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Wu, Q.; Mu, C.; Chen, X. Nucleation Mechanisms of CO2 Hydrate Reflected by Gas Solubility. Sci. Rep. 2018, 8, 10441. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhang, B. Memory effect on the pressure-temperature condition and induction time of gas hydrate nucleation. J. Nat. Gas Chem. 2010, 19, 446–451. [Google Scholar] [CrossRef]



| Main Group | Sub Group | Number | Rk | Qk |
|---|---|---|---|---|
| H2O | H2O | 4 | 1.506 | 1.732 |
| CO2 | CO2 | 56 | 2.592 | 2.522 |
| CH4 | CH4 | 57 | 2.244 | 2.312 |
| O2 | O2 | 58 | 1.764 | 1.910 |
| N2 | N2 | 60 | 1.868 | 1.970 |
| Gas | Temperature Range (K) | Gas (56, 57, 58, 60) a |
|---|---|---|
| CO2 | 280–475 | 84.2 |
| CH4 | 275–375 | −80 |
| O2 | 250–330 | −260 |
| N2 | 210–330 | −250 |
| Gas | u0 | u1(×10−5) |
|---|---|---|
| CO2 | 980.1 | −1.6895 |
| CH4 | 1059.8 | −2.3172 |
| O2 | 1259.9 | −3.0295 |
| N2 | 1260.4 | −2.7416 |
| Guests | a | b (×105) | c (×107) | Np | R-Square |
|---|---|---|---|---|---|
| CH4 | 0.01713 | −2.58066 | −24.6488 | 500 | 0.99924 |
| CO2 | 0.00454 | 0.403588 | −49.4532 | 200 | 0.89458 |
| N2 | 0.0226 | −5.50785 | 1.49362 | 409 | 1 |
| O2 | 0.02468 | −5.90016 | 1.33948 | 200 | 0.99999 |
| Guests | Temperature (K) | P-Range (bar) | Np | Reference | AADP (%) |
|---|---|---|---|---|---|
| CH4 | 273.27–289.9 | 26.33–159.52 | 66 | [41] | 1.0634 |
| 276.81–281.3 | 37.79–62.02 | 5 | This work | 1.6317 | |
| CO2 | 270.15–283.15 | 10.19–45.05 | 41 | [42] | 1.5911 |
| N2 | 273.15–291.05 | 160.09–958.53 | 34 | [43] | 1.0224 |
| 274.55–283.05 | 190.93–453.55 | 3 | [44] | 1.4142 | |
| 279.30–284.00 | 303.00–500.00 | 3 | [45] | 1.5697 | |
| O2 | 273.15 | 121.50 | 1 | [43] | 1.6786 |
| 273.78–284.55 | 138.21–441.30 | 4 | [44] | 1.8001 | |
| 286.27–291.18 | 527.13–953.65 | 6 | [46] | 0.9462 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Wu, H.; Wen, J.; Guo, X.; Zhang, Y.; Wang, R. Simulation Study on the Influence of Gas Mole Fraction and Aqueous Activity under Phase Equilibrium. Processes 2019, 7, 58. https://doi.org/10.3390/pr7020058
Zhao W, Wu H, Wen J, Guo X, Zhang Y, Wang R. Simulation Study on the Influence of Gas Mole Fraction and Aqueous Activity under Phase Equilibrium. Processes. 2019; 7(2):58. https://doi.org/10.3390/pr7020058
Chicago/Turabian StyleZhao, Weilong, Hao Wu, Jing Wen, Xin Guo, Yongsheng Zhang, and Ruirui Wang. 2019. "Simulation Study on the Influence of Gas Mole Fraction and Aqueous Activity under Phase Equilibrium" Processes 7, no. 2: 58. https://doi.org/10.3390/pr7020058
APA StyleZhao, W., Wu, H., Wen, J., Guo, X., Zhang, Y., & Wang, R. (2019). Simulation Study on the Influence of Gas Mole Fraction and Aqueous Activity under Phase Equilibrium. Processes, 7(2), 58. https://doi.org/10.3390/pr7020058





