Splitting Triglycerides with a Counter-Current Liquid–Liquid Spray Column: Modeling, Global Sensitivity Analysis, Parameter Estimation and Optimization
Abstract
1. Introduction
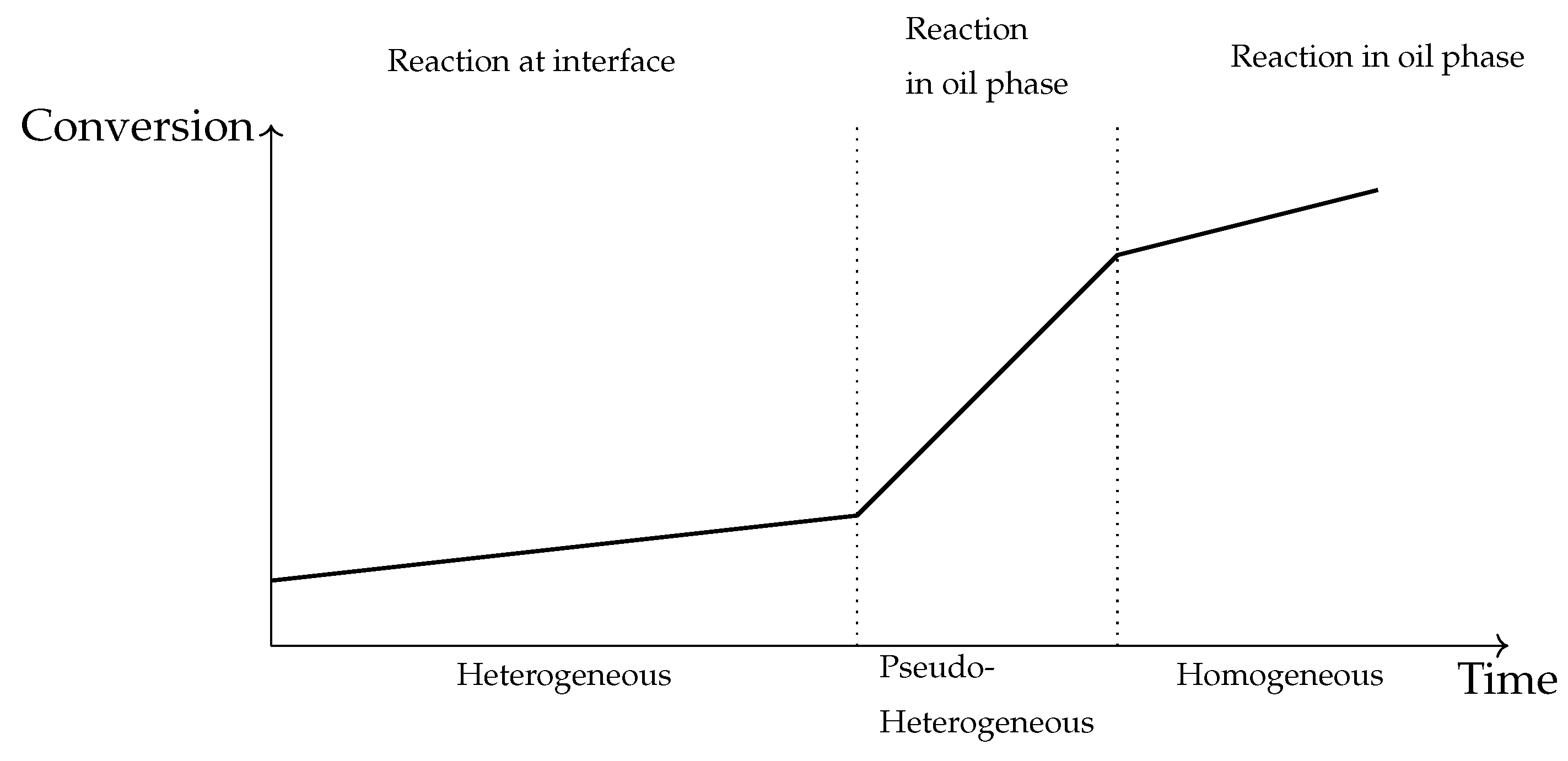
1.1. Hydrolysis Reaction
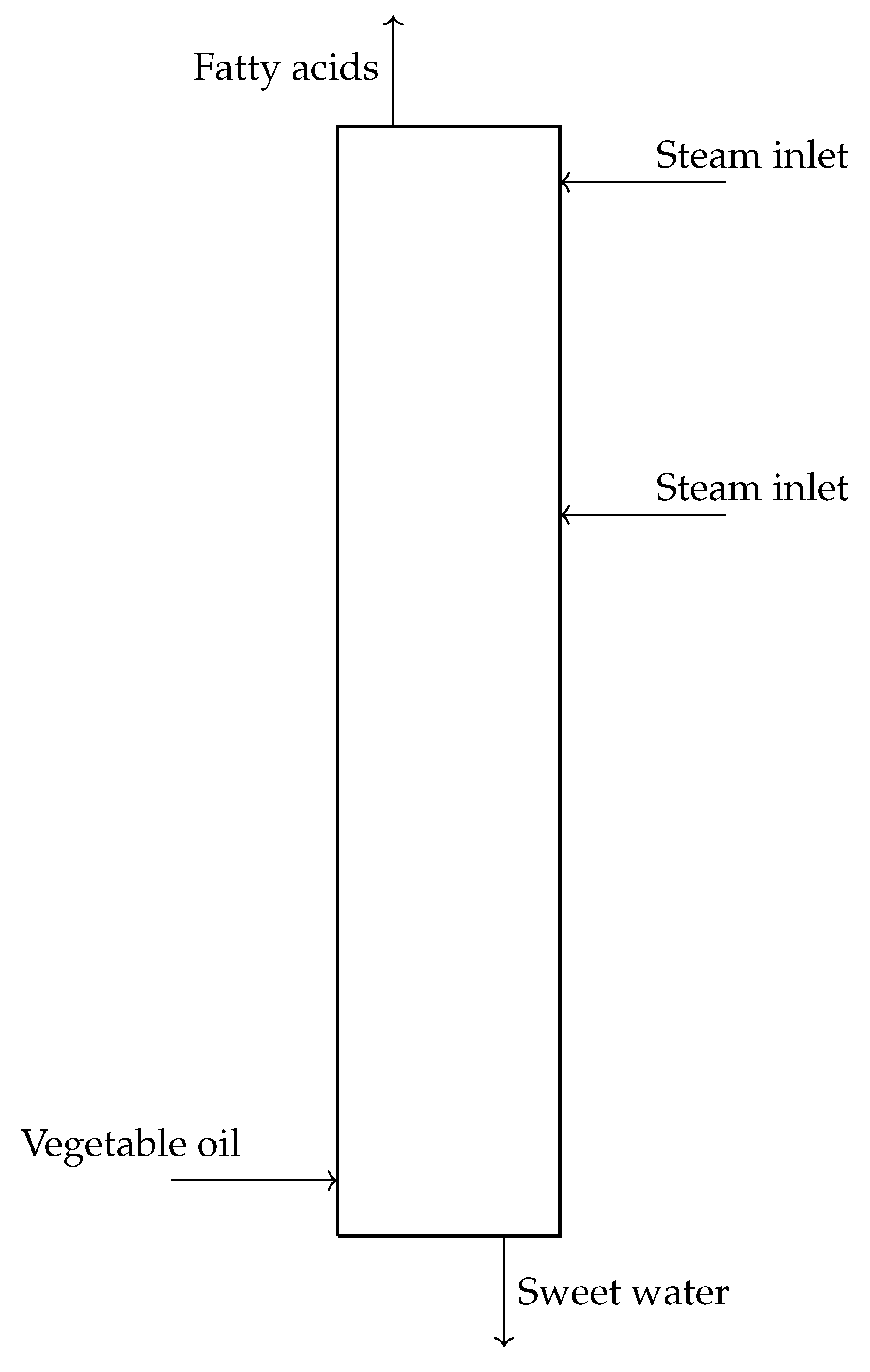
1.2. Spray Column
1.2.1. Research by Jeffreys et al.
1.2.2. Research by Rifai et al.
- The hydrolysis of triglycerides with water to fatty acids and glycerol follows the first order reaction to validate the model in this work with the experimental data set from Jeffreys et al.
- Constant mass flow rates are assumed for the continuous and dispersed phases in case of validating the model by Jeffreys et al.
- Variable mass flow rate is assumed for the continuous and dispersed phase and the model is then re-parameterized in respect to the mass-transfer rates, reaction rate and the backmixing coefficients.
- The finite volume model also takes backmixing into account as van Egmond and Goossens [20] showed that they obtain better results when considering axial dispersion.
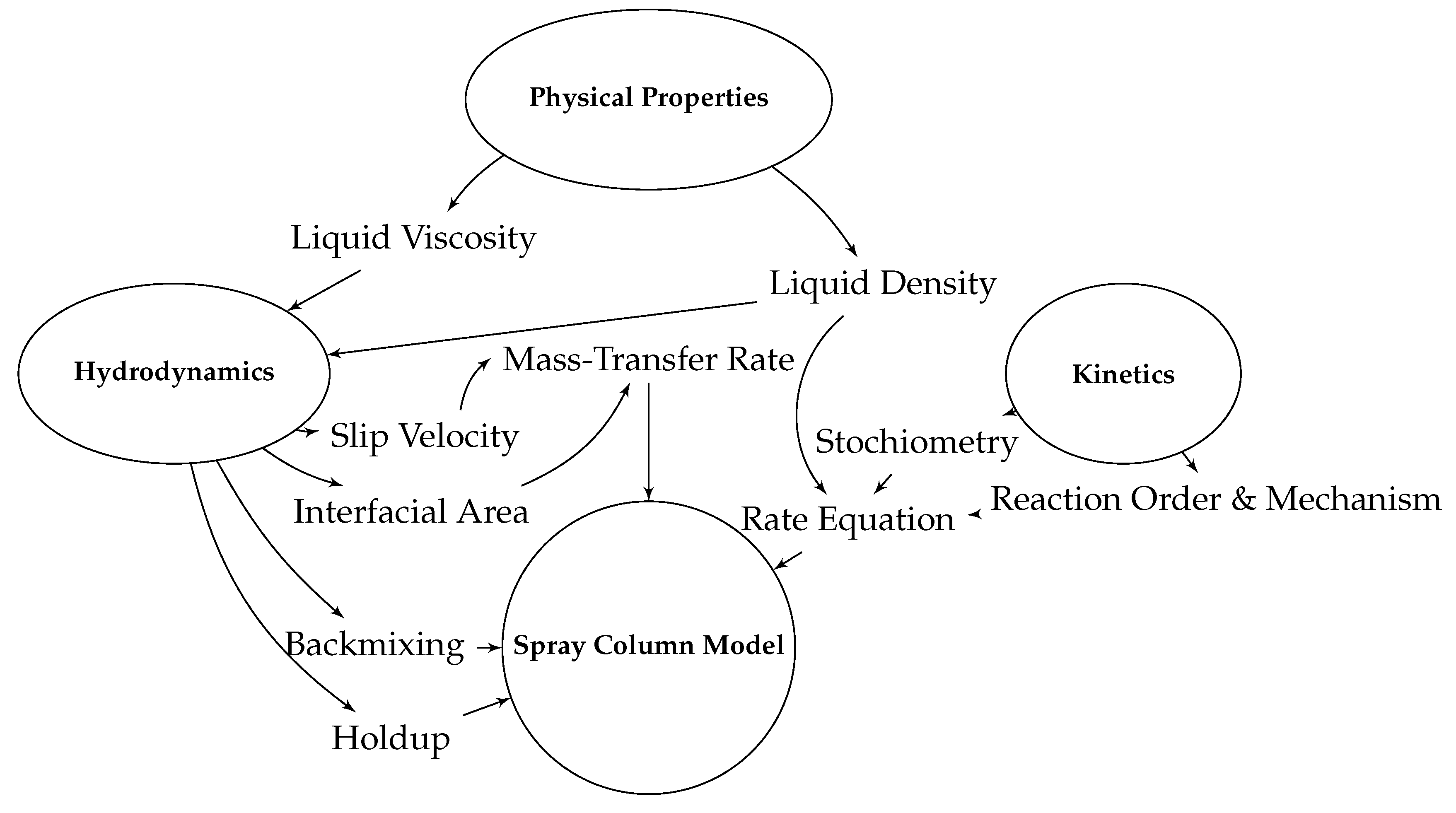
2. Methodology
2.1. Process Model of a Counter-Current Spray Column
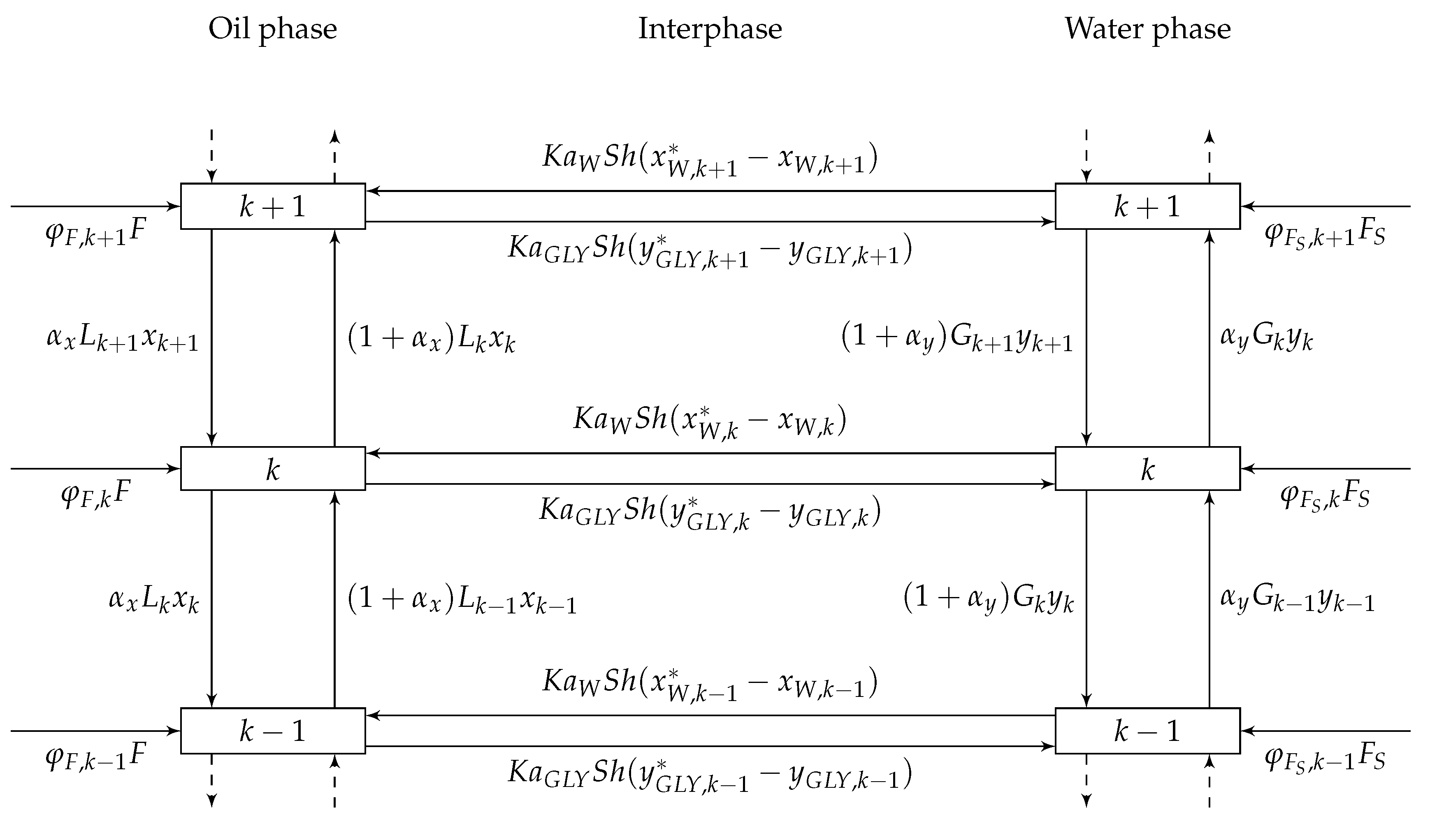
2.1.1. Material Balance
2.1.2. Phase Equilibrium
2.1.3. Solving the System of Equations
2.2. Parameter Estimation via Differential Evolution (DE)
- Specify population size, number of generations, crossover probability, mutation factor.
- Initialize vector population where parameters are uniformly distributed within their bounds.
- Evaluate the objective (cost) function for all individuals (vectors) and store in the fitness variable.
- Generation loop until number of generations or fitness of cost function is reached:
- 4.1.
- Mutation (Parameter mixing): Select a target vector, choose randomly three other vectors and create mutant vector where is called the mutant factor or differential weight.
- 4.2.
- Recombination: Generate trial vector by a probabilistic swapping (crossover) of elements from current target vector with mutant vector.
- 4.3.
- Replacement: Evaluate cost function and replace target vector with trial vector if the cost function is lower with the parameters from the trial vector.
- Parameter vector is returned with best fitness.
2.3. Multi-Criteria Optimization via Differential Evolution
3. Results
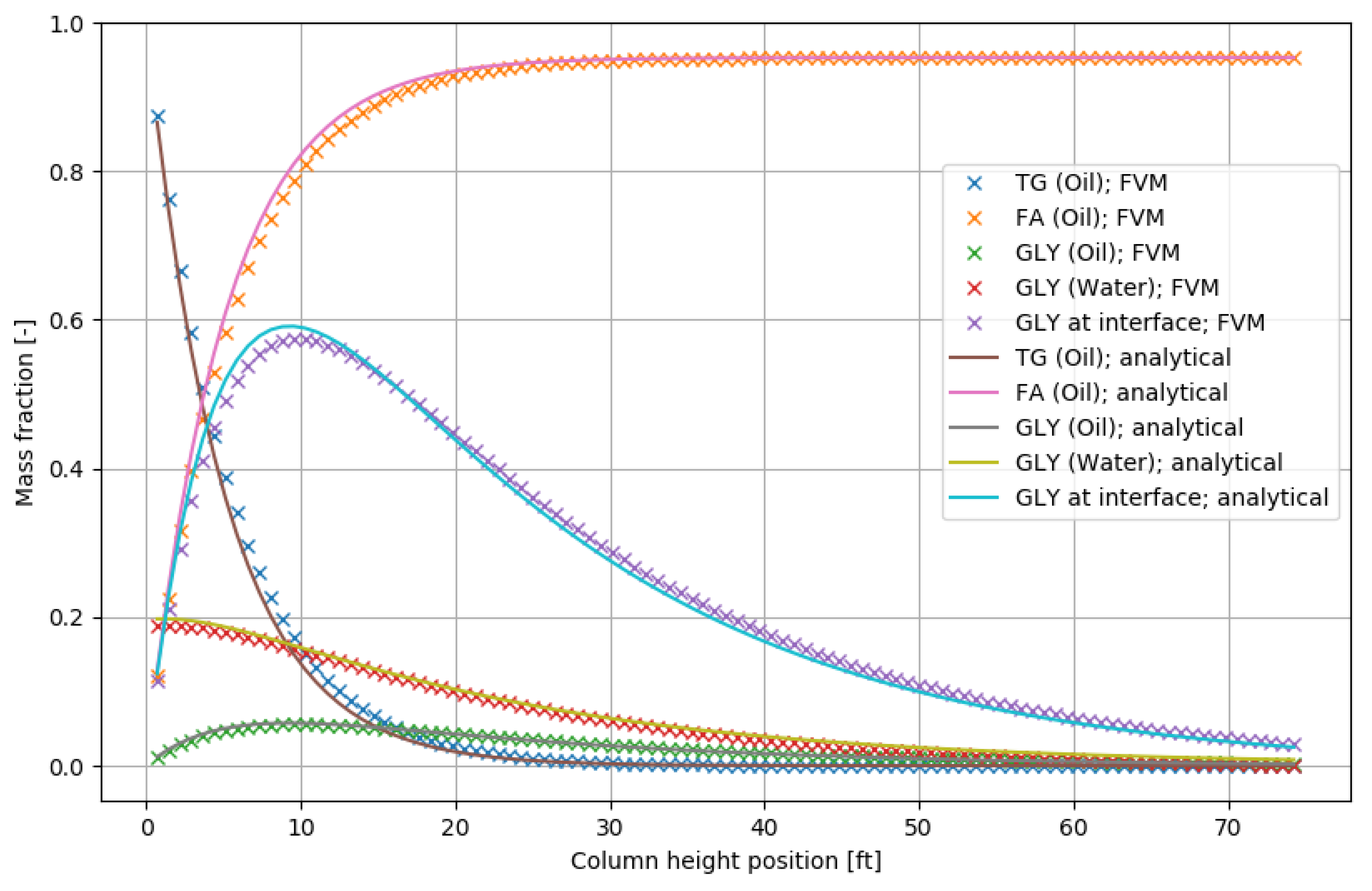
3.1. Model Validation
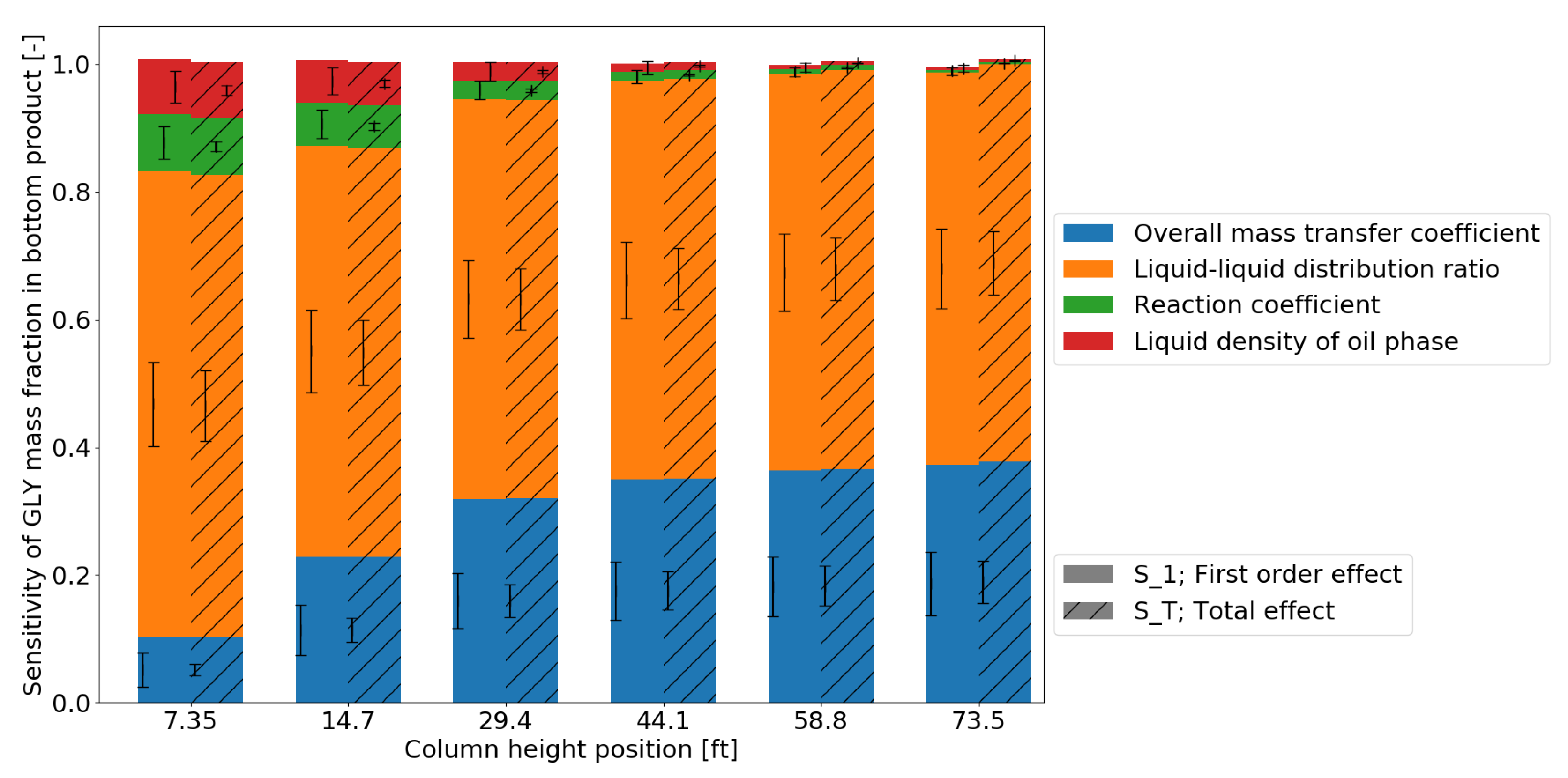
3.2. Global Sensitivity Analysis
3.3. Parameter Estimation
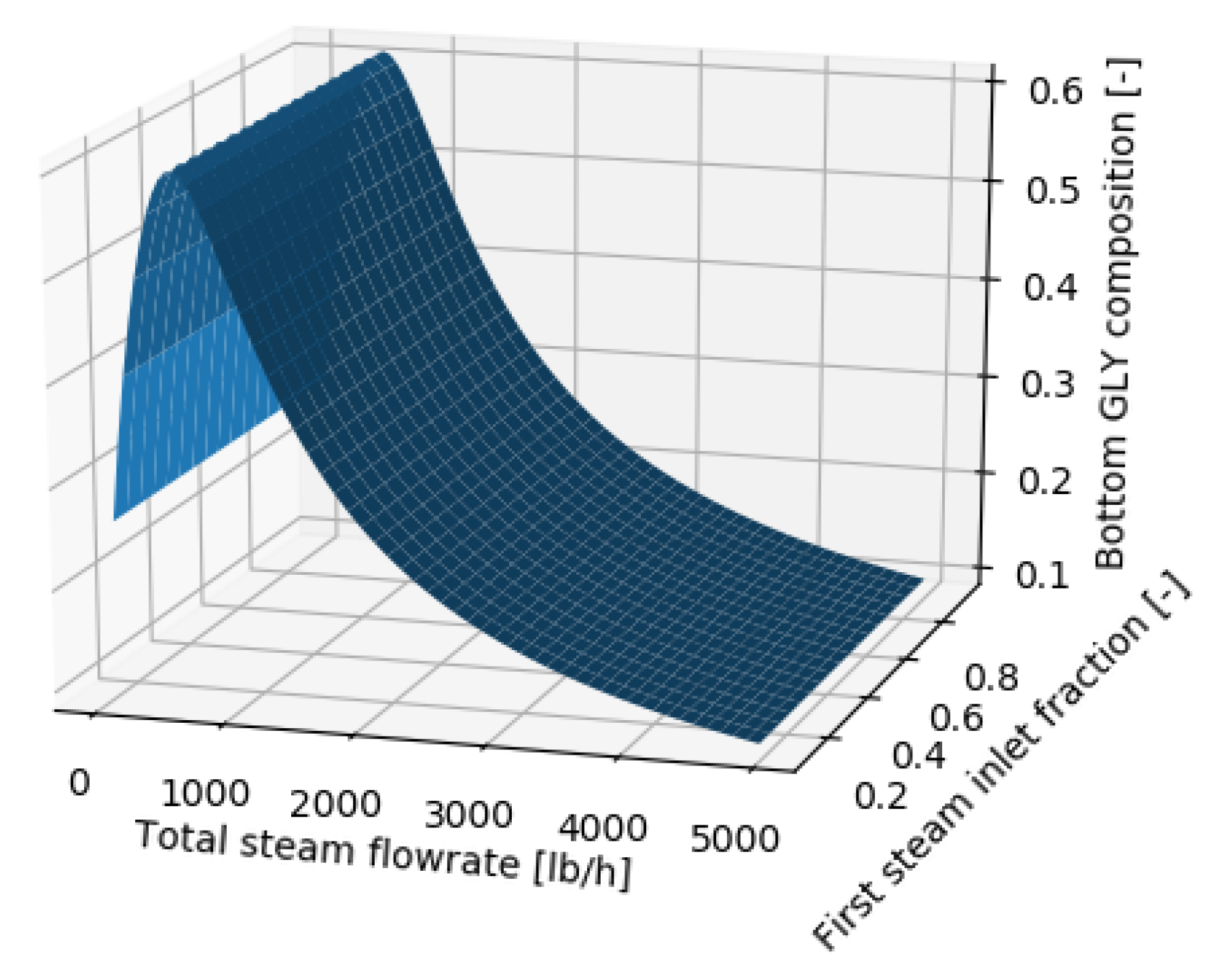
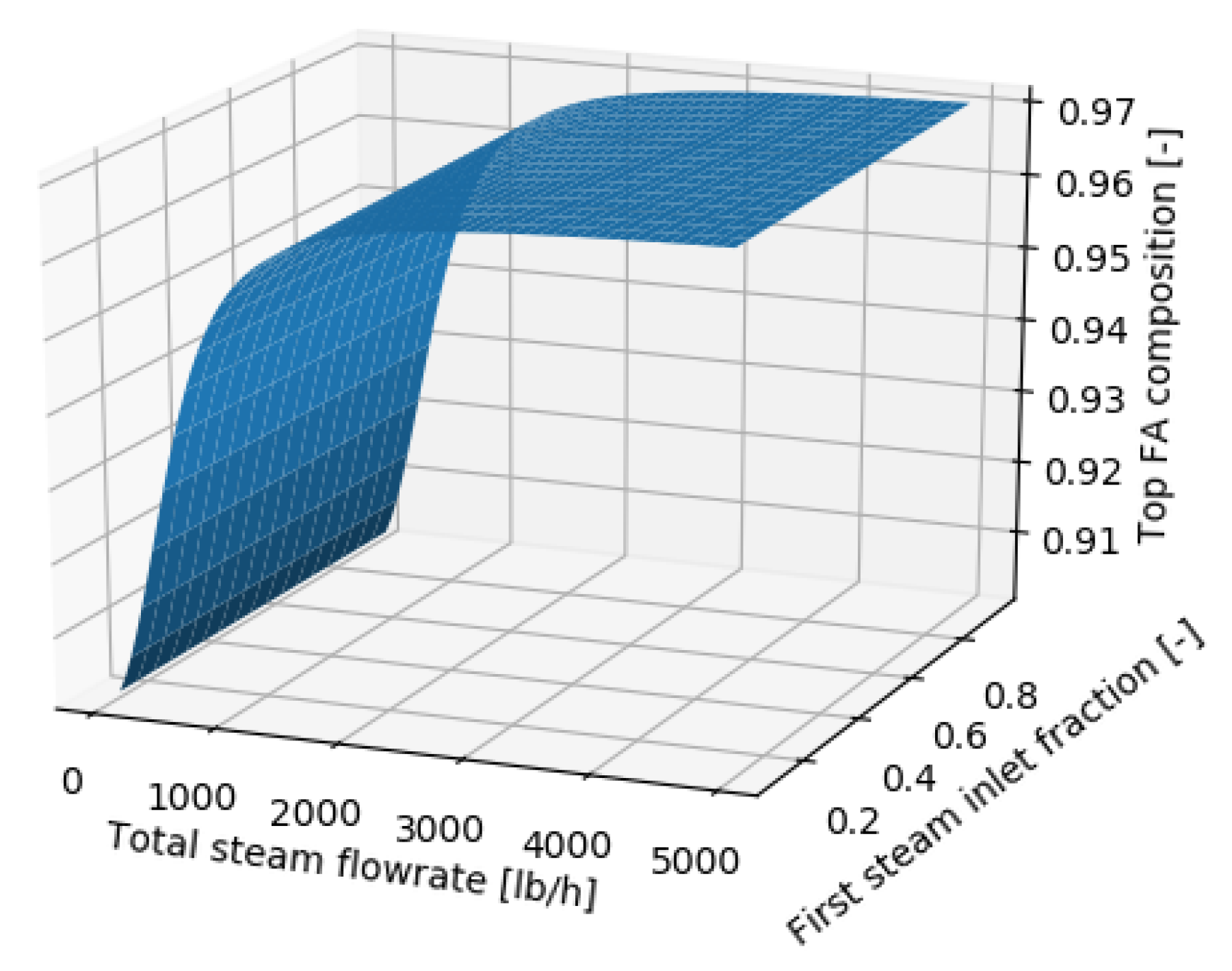
3.4. Multi-Criteria Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DE | Differential evolution |
| FA | Fatty acid |
| FVM | Finite volume model |
| G | Internal flow rate of aqueous phase at stage k [lb/h] |
| G | [lb/h] |
| GLY | Glycerol |
| H | Column height [ft] |
| h | Height of stage [ft] h = H/N |
| HTU | Height to transfer unit [ft] |
| Ka | Mass-transfer rate constant for species i [lb/(ft*h)] |
| K | Reaction equilibrium constant [−] |
| k | Forward reaction rate constant of species i [1/h] |
| L | Internal flow rate of oil phase at stage k [lb/h] |
| L | [lb/h] |
| m | Total mass of finite volume element system at stage k [lb] |
| N | Number of elements [−] |
| PDE | Partial differential equation |
| R | Fatty acid sidechain of triglyceride |
| r | Reaction rate of species i [1/h] |
| S | Cross-sectional column area [ft] |
| TAC | Total annual cost [$/a] |
| TG | Triglyceride |
| DG | Diglyceride |
| MG | Monoglyceride |
| W | Water |
| w | Ration between the required pounds of TG to produce one pound of FA |
| w | Ratio between the required pounds of TG to produce one pound of GLY |
| x | Mass fraction in oil phase of species i on stage k [−] |
| x | Mass fraction at oil interphase of species i on stage k [−] |
| y | Mass fraction in aqueous phase of species i on stage k [−] |
| y | Mass fraction at aqueous interphase of species i on stage k [−] |
| Eco indicator points for impact k and resource flow b | |
| Backmixing coefficient for oil phase [−] | |
| Backmixing coefficient for aqueous phase [−] | |
| Resource (e.g., material, energy) flows | |
| Fraction of column occupied by the continuous phase [−] | |
| Fraction of oil feed fed to column at stage k [−] | |
| Fraction of fed steam via column inlet at stage k [−] | |
| Density of oil feed [lb/ft] | |
| Slip velocity [ft/h] | |
| weighting factors in impact category d |
Appendix A. Data Study
| Type of Oil/Fat & Correlations | Type of Reaction | Unit | 225 C | 280 C |
|---|---|---|---|---|
| Coconut oil | ||||
| [12,13] | - | - | 27 | 10 |
| [15] | - | - | 29.6 | 8.14 |
| [12] | reversible 1st order | - | 0.458 | 1.160 |
| [13] | reversible 1st order | - | 0.7725 | 2.0596 |
| [15] | reversible 2nd order | - | 2.22 | 2.22 |
| [9] | irreversible 1st order | 1/min | 0.0201 | 0.0944 |
| [13] | reversible 1st order | 1.8605 × 10−4 | 0.0120 | |
| [15] | reversible 2nd order | kmol/(mmin) | 0.0118 | 0.0371 |
| Beef tallow fat | ||||
| [12,13] | - | - | 20 | 4.5 |
| [15] | - | - | 18.7 | 5.04 |
| [13] | reversible 1st order | - | 1.6795 | 5.7971 |
| [15] | reversible 2nd order | - | 2.22 | 2.22 |
| [9] | irreversible 1st order | 1/min | 0.0199 | 0.0855 |
| [13] | reversible 1st order | 0.0205 | 0.0997 | |
| [15] | reversible 2nd order | kmol/(mmin) | 0.0347 | 0.1355 |
| Peanut oil | ||||
| [15] | - | - | 30.0 | 9.7 |
| [15] | reversible 2nd order | - | 2.22 | 2.22 |
| [9] | irreversible 1st order | 1/min | 0.0151 | 0.0725 |
| [15] | reversible 2nd order | kmol/(mmin) | 0.0402 | 0.0988 |
| Type of TG | Unit | 225 C | 276 C | 280 C |
|---|---|---|---|---|
| C8:0 (Caprylic) | kg/m | 807.93 | 763.86 | 760.49 |
| lb/ft | 50.44 | 47.69 | 47.48 | |
| C12:0 (Lauric) | kg/m | 763.32 | 721.63 | 717.85 |
| lb/ft | 47.65 | 45.05 | 44.81 | |
| C18:0 (Stearic) | kg/m | 762.42 | 722.25 | 719.31 |
| lb/ft | 47.60 | 45.09 | 44.91 |
| Type of Oil | Unit | 200 C |
|---|---|---|
| Canola oil | kg/m | 806.6 |
| lb/ft | 50.4 | |
| Corn oil | kg/m | 807.8 |
| lb/ft | 50.4 | |
| Peanut oil | kg/m | 801.5 |
| lb/ft | 50.0 | |
| Soybean oil | kg/m | 807.4 |
| lb/ft | 50.4 |
| Substance | Unit | 225 C | 280 C |
|---|---|---|---|
| Coconut oil | |||
| kg/m | 738.0025 | 690.5853 | |
| lb/ft | 46.0720 | 43.1118 | |
| Water | |||
| kg/m | 833.7878 | 747.7287 | |
| lb/ft | 52.0517 | 46.6792 |
References
- Grand View Research. Oleochemicals Market Size, Share & Trends Analysis Report by Product (Fatty Acid, Glycerol, Fatty Alcohol), by Region (APAC, MEA, Europe, North America, CSA), and Segment Forecasts, 2018–2025; Technical Report; Grand View Research: San Francisco, CA, USA, 2018. [Google Scholar]
- Searchinger, T.; Heimlich, R.; Houghton, R.A.; Dong, F.; Elobeid, A.; Fabiosa, J.; Tokgoz, S.; Hayes, D.; Yu, T.H. Use of U.S. Croplands for Biofuels Increases Greenhouse Gases Through Emissions from Land-Use Change. Science 2008, 319, 1238–1240. [Google Scholar] [CrossRef] [PubMed]
- Fargione, J.; Hill, J.; Tilman, D.; Polasky, S.; Hawthorne, P. Land Clearing and the Biofuel Carbon Debt. Science 2008, 319, 1235–1238. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Guerra, E.; Gude, V.G. Assessment of Sustainability Indicators for Biodiesel Production. Appl. Sci. 2017, 7, 869. [Google Scholar] [CrossRef]
- Patil, T.A.; Raghunathan, T.S.; Shankar, H.S. Thermal Hydrolysis of Vegetable Oils and Fats. 2. Hydrolysis in Continuous Stirred Tank Reactor. Ind. Eng. Chem. Res. 1988, 27, 735–739. [Google Scholar] [CrossRef]
- Forero-Hernandez, H.; Jones, M.N.; Sarup, B.; Jensen, A.D.; Sin, G. A simplified kinetic and mass transfer modelling of the thermal hydrolysis of vegetable oils. Comput. Aided Chem. Eng. 2017, 40, 1177–1182. [Google Scholar] [CrossRef]
- Lascaray, L. Mechanism of Fat Splitting. Ind. Eng. Chem. 1949, 41, 786–790. [Google Scholar] [CrossRef]
- Lascaray, L. Industrial Fat Splitting. J. Am. Oil Chem. Soc. 1952, 29, 362–366. [Google Scholar] [CrossRef]
- Sturzenegger, A.; Sturm, H. Hydrolysis of Fats and High Temperatures. Ind. Eng. Chem. 1951, 43, 510–515. [Google Scholar] [CrossRef]
- Jeffreys, G.V.; Jenson, V.G.; Miles, F.R. The Analysis of a Continiuous Fat-Hydrolysing Column. Trans. Inst. Chem. Eng. 1961, 39, 389–396. [Google Scholar]
- Rifai, M.; Nashaie, S.; Kafafi, A. Analysis of a Countercurrent Tallow-Splitting Column. Trans. Inst. Chem. Eng. 1977, 55, 59–63. [Google Scholar]
- Namdev, P.D.; Patil, T.A.; Raghunathan, T.S.; Shankar, H.S. Thermal Hydrolysis of Vegetable Oils and Fats. 3. An Analysis of Design Alternatives. Ind. Eng. Chem. Res. 1988, 27, 739–743. [Google Scholar] [CrossRef]
- Attarakih, M.; Albaraghthi, T.; Abu-Khader, M.; Al-Hamamre, Z.; Bart, H. Mathematical modeling of high-pressure oil-splitting reactor using a reduced population balance model. Chem. Eng. Sci. 2012, 84, 276–291. [Google Scholar] [CrossRef]
- Alenezi, R.; Leeke, G.A.; Santos, R.C.D.; Khan, A.R. Hydrolysis kinetics of sunflower oil under subcritical water conditions. Chem. Eng. Res. Des. 2009, 87, 867–873. [Google Scholar] [CrossRef]
- Patil, T.A.; Butala, D.N.; Raghunathan, T.S.; Shankar, H.S. Thermal Hydrolysis of Vegetable Oils and Fats. 1. Reaction kinetics. Ind. Eng. Chem. Res. 1988, 27, 727–735. [Google Scholar] [CrossRef]
- Aniya, V.K.; Muktham, R.K.; Alka, K.; Satyavathi, B. Modeling and simulation of batch kinetics of non-edible karanja oil for biodiesel production. Fuel 2015, 161, 137–145. [Google Scholar] [CrossRef]
- Mills, V.; McClain, H.K. Fat Hydrolysis. Ind. Eng. Chem. 1949, 41, 1982–1985. [Google Scholar] [CrossRef]
- Minard, G.W.; Johnson, A.I. Limiting Flow and Holdup in a Spray Extraction Column. Chem. Eng. Prog. 1952, 48. [Google Scholar]
- Beyaert, B.O.; Lapidus, L.; Elgin, J.C. The Mechanics of Vertical Moving Liquid-Liquid Fluidized Systems: II. Countercurrent Flow. AIChE J. 1961, 7, 46–48. [Google Scholar] [CrossRef]
- Van Egmond, L.C.; Goossens, M.L. Berekningen aan Axiale Dispersie in een Operationele Vetsplitter; Technical Report; Laboratorium voor Chemische Technologie: Delft, The Netherlands, 1982. [Google Scholar]
- Ettouney, R.S.; El-Rifai, M.A.; Ghallab, A.O.; Anwar, A.K. Mass Transfer Fluid Flow Interactions in Perforated Plate Extractive Reactors. Sep. Sci. Technol. 2015, 50, 1794–1805. [Google Scholar] [CrossRef]
- Kermode, J. f90wrap. Available online: https://github.com/jameskermode/f90wrap (accessed on 9 March 2018).
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python. 2019. Available online: https://arxiv.org/abs/1907.10121 (accessed on 9 March 2018).
- Whitman, W.G. The two film theory of gas absorption. Int. J. Heat Mass Transf. 1962, 5, 429–433. [Google Scholar] [CrossRef]
- Nowak, U.; Weimann, L. A Family of Newton Codes for Systems of Highly Nonlinear Equations; Technical Report; Konrad-Zuse-Zentrum für Informationstechnik Berlin: Berlin, Germany, 1991. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, W.C.; Turner, T.L.; Roberts, W.L.; Stikeleather, L.F. Direct injection of superheated steam for continuous hydrolysis reaction. Chem. Eng. Process. Process Intensif. 2012, 59, 52–59. [Google Scholar] [CrossRef]
- Determining True Steam Prices. In Energy and Process Optimization for the Process Industries; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 17; pp. 366–385. [CrossRef]
- Goedkoop, M.; Spriensma, R. The Eco-indicator99: A Damage Oriented Method for Life Cycle Impact Assessment: Methodology Report; Technical Report; PRe Consultants B.V.: Amersfoort, The Netherlands, 2001. [Google Scholar]
- Thompson, M.; Ellis, R.; Wildavsky, A. Cultural Theory; Westview Press: Boulder, CO, USA, 1990. [Google Scholar]
- Hofstetter, P. Perspectives in Life Cycle Impact Assessment; Springer: Zurich, Switzerland, 1998. [Google Scholar] [CrossRef]
- Rangaiah, G.P.; Sharma, S. Differential Evolution in Chemical Engineering; World Scientific: Singapore, 2017. [Google Scholar] [CrossRef]
- Landress, L. Fatty Acids (North America); Technical Report; ICIS Pricing: London, UK, 2014. [Google Scholar]
- Landress, L. Glycerine (US Gulf); Technical Report; ICIS Pricing: London, UK, 2014. [Google Scholar]
- Malaysian Palm Oil Council (Oil). CPO vs SBO Prices. 2019. Available online: http://mpoc.org.my/daily-palm-oil-price/ (accessed on 9 March 2018).
- International, M. MEPS-World Stainless Steel Prices. 2018. Available online: http://www.meps.co.uk/world-price.htm#STEEL%20PRICE%20TABLES (accessed on 9 March 2018).
- Cadavid, J.; Godoy-Silva, R.; Narvaez, P.; Camargo, M.; Fonteix, C. Biodiesel production in a counter-current reactive extraction column: Modelling, parametric identification and optimisation. Chem. Eng. J. 2013, 228, 717–723. [Google Scholar] [CrossRef]
- Forero-Hernandez, H.; Jones, M.N.; Sarup, B.; Jensen, A.D.; Abildskov, J.; Sin, G. Comprehensive development, uncertainty and sensitivity analysis of a model for the hydrolysis of rapeseed oil. Comput. Chem. Eng. 2020, 133, 106631. [Google Scholar] [CrossRef]
- Rashid, M.M.; Mhaskar, P.; Swartz, C.L.E. Handling multi-rate and missing data in variable duration economic model predictive control of batch processes. AIChE J. 2017, 63, 2705–2718. [Google Scholar] [CrossRef]
- Diaz-Tovar, C.A.; Gani, R.; Sarup, B. Computer-Aided Modeling of Lipid Processing Technology. Ph.D. Thesis, Technical University of Denmark (DTU), Lyngby, Denmark, 2011. [Google Scholar]
- Perederic, O. Systematic Computer Aided Methods and Tools for Lipid Process Technology. Ph.D. Thesis, Technical University of Denmark (DTU), Lyngby, Denmark, 2018. [Google Scholar]
- Sahasrabudhe, S.N.; Rodriguez-Martinez, V.; O’Meara, M.; Farkas, B.E. Density, viscosity, and surface tension of five vegetable oils at elevated temperatures: Measurement and modeling. Int. J. Food Prop. 2017, 20, 1965–1981. [Google Scholar] [CrossRef]


| First Author | Reactor Type | Reaction Type and Order | Catalyst and Process Conditions | Model and Studied Parameters |
|---|---|---|---|---|
| Patil [5] | CSTR | Reversible & Pseudo-1st Order | None | Algebraic Equations |
| Forero-Hernandez [6] | Batch | None | ||
| Lascaray, 1949 [7] | Review | Review | Review; 100–220 C | - |
| Lascaray, 1952 [8] | Review | Review | Review; 100–220 C | - |
| Sturzenegger and Sturm [9] | Batch | Irreversible & Pseudo-1st Order | ZnO | |
| Jeffreys [10] | Spray column | Irreversible & Pseudo-1st Order | ZnO | Algebraic Equations |
| Rifai [11] | Spray Column | Reversible & 2nd Order? | ||
| Namdev [12] | Review | Reversible & Pseudo-1st Order | ||
| Attarakih [13] | Spray column | Reversible & Pseudo-1st Order | Reduced Population Balance Model |
| Aspect | Jeffreys et al. | Rifai et al. |
|---|---|---|
| Reaction kinetics | irreversible first order | reversible second order: |
| dh | dh | |
| Internal flowrates | assumed constant over column height | changes over column height |
| Water solubility | assumed constant over column height | changes over column height |
| Hydrodynamic model | - | Beyaert et al. [19] |
| Solution formulation | Analytical | System of non-linear differential equations |
| Experimental Run | Input | Output | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [lb/h] | [lb/h] | [lb/ft] | m [−] | [−] | [−] | [lb/h] | [lb/h] | [lb/h] | [lb/h] | |
| #1 | 7260 | 4600 | 45 | 10.32 | 0.1605 | 0.03 | 8050 | 3810 | 4205 | 7655 |
| #2 | 6490 | 4440 | 45.05 | 9.56 | 0.1705 | 0.037 | 7180 | 3750 | 4095 | 6835 |
| #3 | 6905 | 4300 | 45 | 11.38 | 0.189 | 0.027 | 7370 | 3835 | 4070 | 7140 |
| #4 | 7400 | 3980 | 45.1 | 11.67 | 0.182 | 0.019 | 7770 | 3610 | 3795 | 7585 |
| #5 | 6570 | 4480 | 44.9 | 8.32 | 0.227 | 0.027 | 7340 | 3710 | 4095 | 6955 |
| #6 | 8175 | 4120 | 45.05 | 10.32 | 0.188 | 0.024 | 8900 | 3395 | 3760 | 8540 |
| Cost | Unit | per 1000 lb Steam |
|---|---|---|
| Average boiler fuel | MMBtu | 1.56 |
| Fresh water | $ | 0.02 |
| Water treatment cost | $ | 0.74 |
| Water preheating and pumping | $ | 0.62 |
| Deareation steam | $ | 1.10 |
| FD fan | $ | 0.05 |
| C (variable cost) | $ | 11.9 |
| Boiler capital | MM$ | 20 |
| R depraciation factor | % of capital | 15 |
| Maintenance cost | % of capital | 2 |
| Two employees | $/a | 120,000 |
| Employee cost factor | - | 3 |
| C (fixed cost) | $ | 1.7 |
| C = C + C | $ | 13.6 |
| Impact Category | Steel [Points/lb] | Steam [Points/lb] | Electricity [Points/kWh] |
|---|---|---|---|
| Human health (d = 1) | |||
| Carcinogenics | |||
| Climate change | |||
| Ionizing radiation | |||
| Ozone layer depletion | |||
| Respiratory effects | |||
| Ecosystem (d = 2) | |||
| Acidification | |||
| Ecotoxicity | |||
| Resources (d = 3) | |||
| Land occupation | |||
| Fossil fuels | |||
| Mineral extraction |
| Section | Model Assumptions | Significant Variables and/or Parameters |
|---|---|---|
| 3.1. Model validation | - Constant internal flowrates | Process parameters by Jeffreys et al. |
| 3.2. Global sensitivity analysis | - Constant internal flowrates | Phenomena-based parameters |
| 3.3. Parameter estimation | - Variable internal flowrates | All relevant parameters (Table 8) |
| - Solubility and mass transfer | ||
| of water in and to oil phase | ||
| 3.4. Multi-criteria optimization | - Variable internal flowrates | Process operation variables |
| - No solubility and mass transfer | ||
| of water in and to oil phase |
| Parameter | Symbol | Nominal Value | Unit |
|---|---|---|---|
| Overall mass-transfer coefficient for glycerol | 14.21 | [lb/(fth)] | |
| Cross-sectional area of tower | S | 3.688 | [ft] |
| Mass flow of extract (aqueous phase) | G | 3760 | [lb/h] |
| Mass flow of raffinate (oil phase) | L | 8540 | [lb/h] |
| Glycerol distribution ratio/coefficient | 10.32 | [−] | |
| Forward reaction rate coefficient | k | 10.2 | [1/h] |
| Height of column | H | 73.5 | [ft] |
| Glycerol content in fat | 0.0853 | [−] | |
| Liquid density of fat | 45.05 | [lb/ft] | |
| Backmixing coefficient of cont. phase (oil) | 0.0 | [−] | |
| Backmixing coefficient of disp. phase (water) | 0.0 | [−] |
| Parameter | Re-Parameterized Model | Jeffreys et al. | ||||
|---|---|---|---|---|---|---|
| 43.64 | 19.06 | |||||
| 0.19 | - | |||||
| k | 77.14 | 10.2 | ||||
| 0.37 | 0.9 | |||||
| 0.19 | 0.1 | |||||
| 64.17 | 10.32 | |||||
| 27.40 | - | |||||
| Experiment | [−] | [−] | Deviation from exp. [%] | [lb/h] | [lb/h] | Deviation from exp. [%] |
| 1 | 0.1708 | 0.1605 | 6.4174 | 3879 | 3810 | 1.8110 |
| 2 | 0.1832 | 0.1705 | 7.4487 | 3741 | 3750 | −0.24 |
| 3 | 0.2072 | 0.189 | 9.6296 | 3686 | 3835 | −3.8853 |
| 4 | 0.2076 | 0.182 | 14.0659 | 3294 | 3610 | −8.7535 |
| 5 | 0.2265 | 0.227 | −0.2203 | 3983 | 3710 | 7.3585 |
| 6 | 0.2030 | 0.188 | 7.9787 | 3436 | 3395 | 1.2077 |
| [−] | [−] | [lb/h] | [lb/h] | |||
| 1 | 0.0000 | 0.03 | −100 | 7981 | 8050 | -0.8571 |
| 2 | 0.0000 | 0.037 | −100 | 7189 | 7180 | 0.1253 |
| 3 | 0.0000 | 0.027 | −100 | 7519 | 7370 | 2.0217 |
| 4 | 0.0000 | 0.019 | −100 | 8086 | 7770 | 4.0669 |
| 5 | 0.0000 | 0.027 | −100 | 7067 | 7340 | −3.7193 |
| 6 | 0.0000 | 0.024 | −100 | 8859 | 8900 | −0.4607 |
| [lb/h] | [lb/h] | [lb/h] | [lb/h] | |||
| 1 | 4236 | 4205 | 0.7372 | 7586 | 7655 | −0.9014 |
| 2 | 4088 | 4095 | −0.1709 | 6798 | 6835 | −0.5413 |
| 3 | 3990 | 4070 | −1.9656 | 7169 | 7140 | 0.4062 |
| 4 | 3634 | 3795 | −4.2424 | 7709 | 7585 | 1.6348 |
| 5 | 4228 | 4095 | 3.2479 | 6764 | 6955 | −2.7462 |
| 6 | 3775 | 3760 | 0.3989 | 8487 | 8540 | −0.6206 |
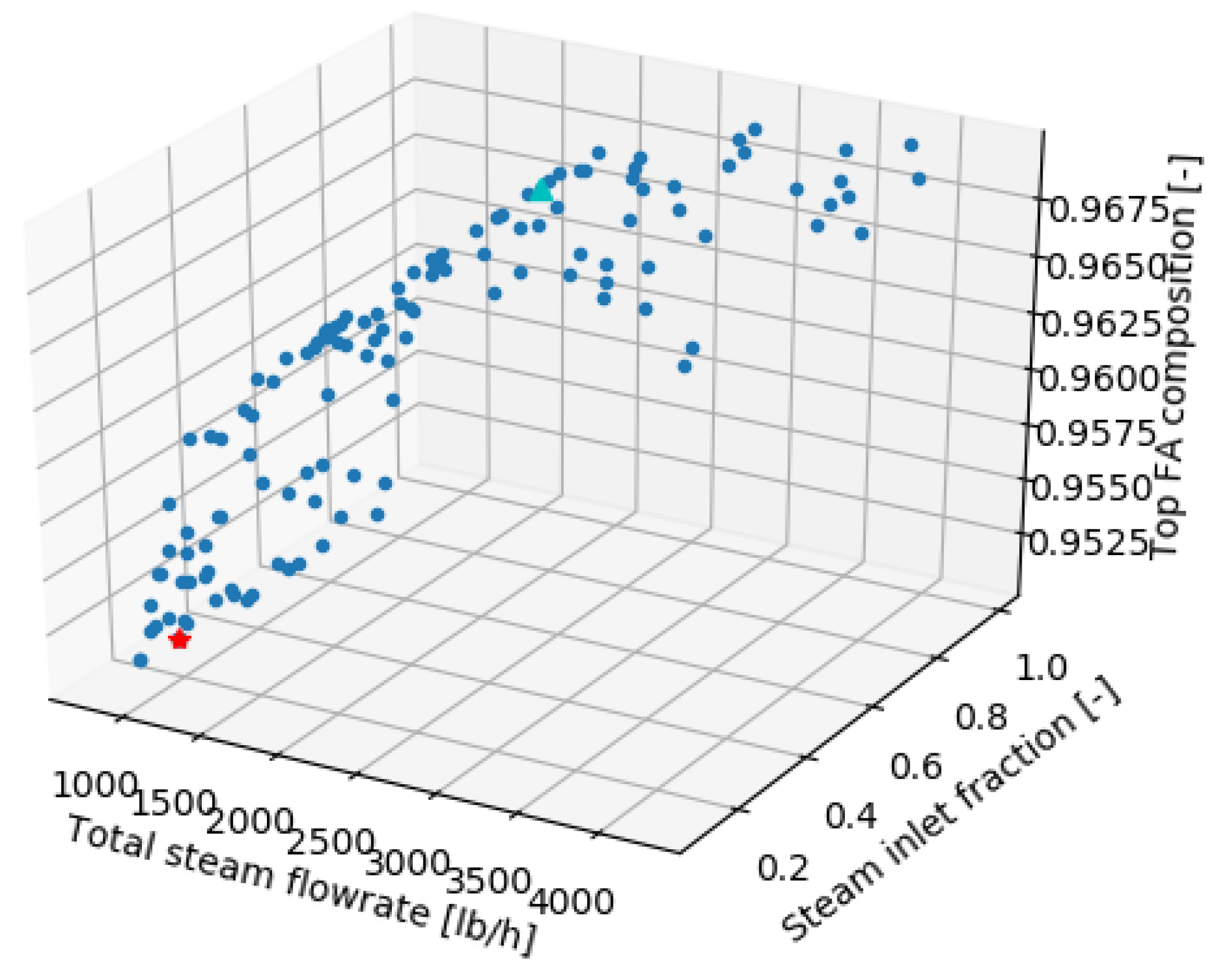
| Input and Objective | Unit | Value | Input Bounds |
|---|---|---|---|
| Input | |||
| Steam flowrate | lb/h | 786.55 | [50, 5000] |
| First steam inlet fraction | - | 0.27 | [0.1, 1.0] |
| Objective | |||
| Revenue | $/a | 47,410,513 | |
| Total annual cost (TAC) | $/a | 94,076 | |
| Raw material cost | $/a | 17,452,458 | |
| Profit | $/a | 29,863,978 | |
| Eco99 indicator | Points | 22,316 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, M.N.; Forero-Hernandez, H.; Zubov, A.; Sarup, B.; Sin, G. Splitting Triglycerides with a Counter-Current Liquid–Liquid Spray Column: Modeling, Global Sensitivity Analysis, Parameter Estimation and Optimization. Processes 2019, 7, 881. https://doi.org/10.3390/pr7120881
Jones MN, Forero-Hernandez H, Zubov A, Sarup B, Sin G. Splitting Triglycerides with a Counter-Current Liquid–Liquid Spray Column: Modeling, Global Sensitivity Analysis, Parameter Estimation and Optimization. Processes. 2019; 7(12):881. https://doi.org/10.3390/pr7120881
Chicago/Turabian StyleJones, Mark Nicholas, Hector Forero-Hernandez, Alexandr Zubov, Bent Sarup, and Gürkan Sin. 2019. "Splitting Triglycerides with a Counter-Current Liquid–Liquid Spray Column: Modeling, Global Sensitivity Analysis, Parameter Estimation and Optimization" Processes 7, no. 12: 881. https://doi.org/10.3390/pr7120881
APA StyleJones, M. N., Forero-Hernandez, H., Zubov, A., Sarup, B., & Sin, G. (2019). Splitting Triglycerides with a Counter-Current Liquid–Liquid Spray Column: Modeling, Global Sensitivity Analysis, Parameter Estimation and Optimization. Processes, 7(12), 881. https://doi.org/10.3390/pr7120881





