Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect
Abstract
1. Introduction
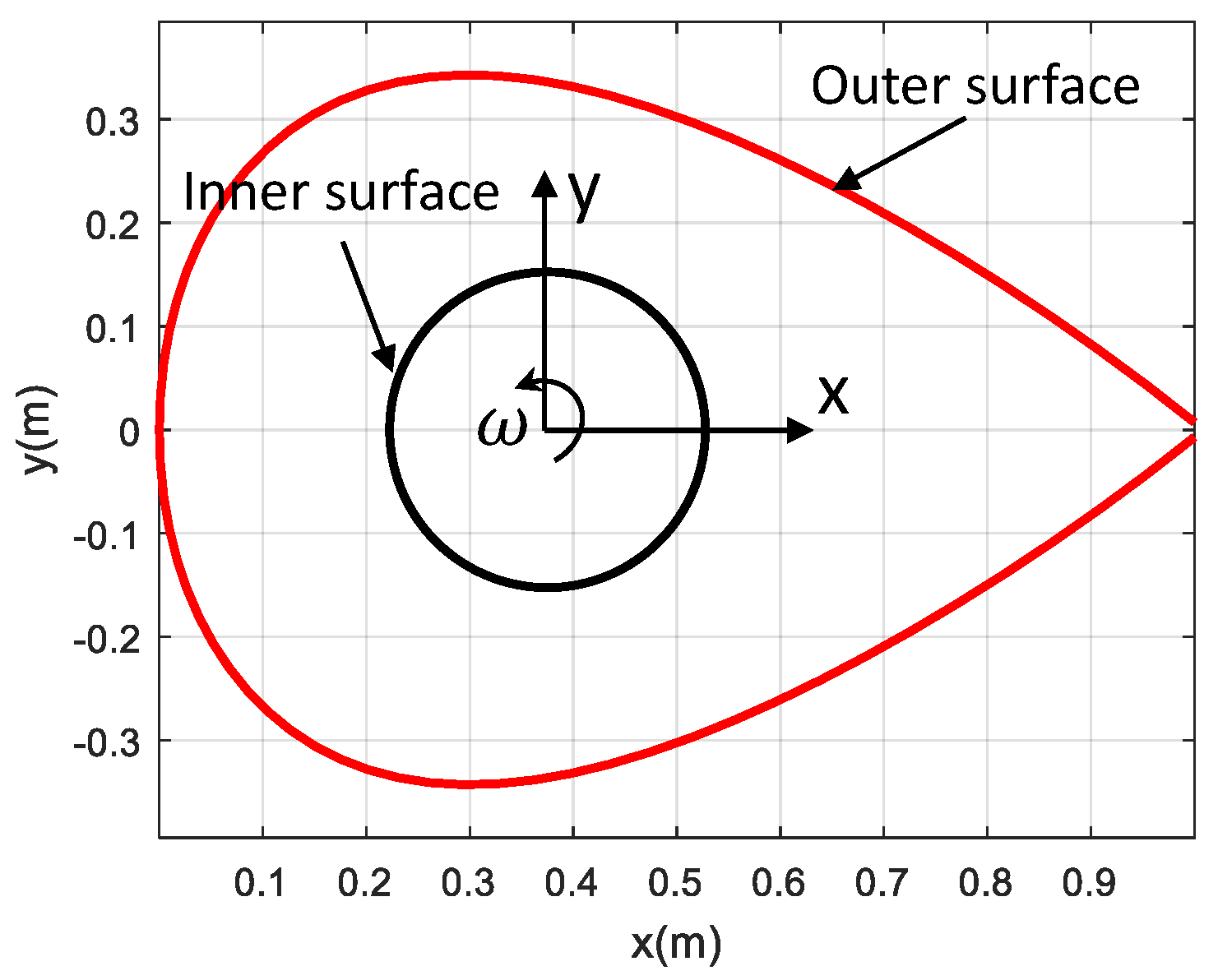
2. Heat Transfer Modeling of a Rotating Spacecraft Under Solar Radiation
3. Numerical Procedure: Meshless Method
3.1. Theoretical Background
3.2. Generation of the Point Cloud
3.3. Explicit Solver
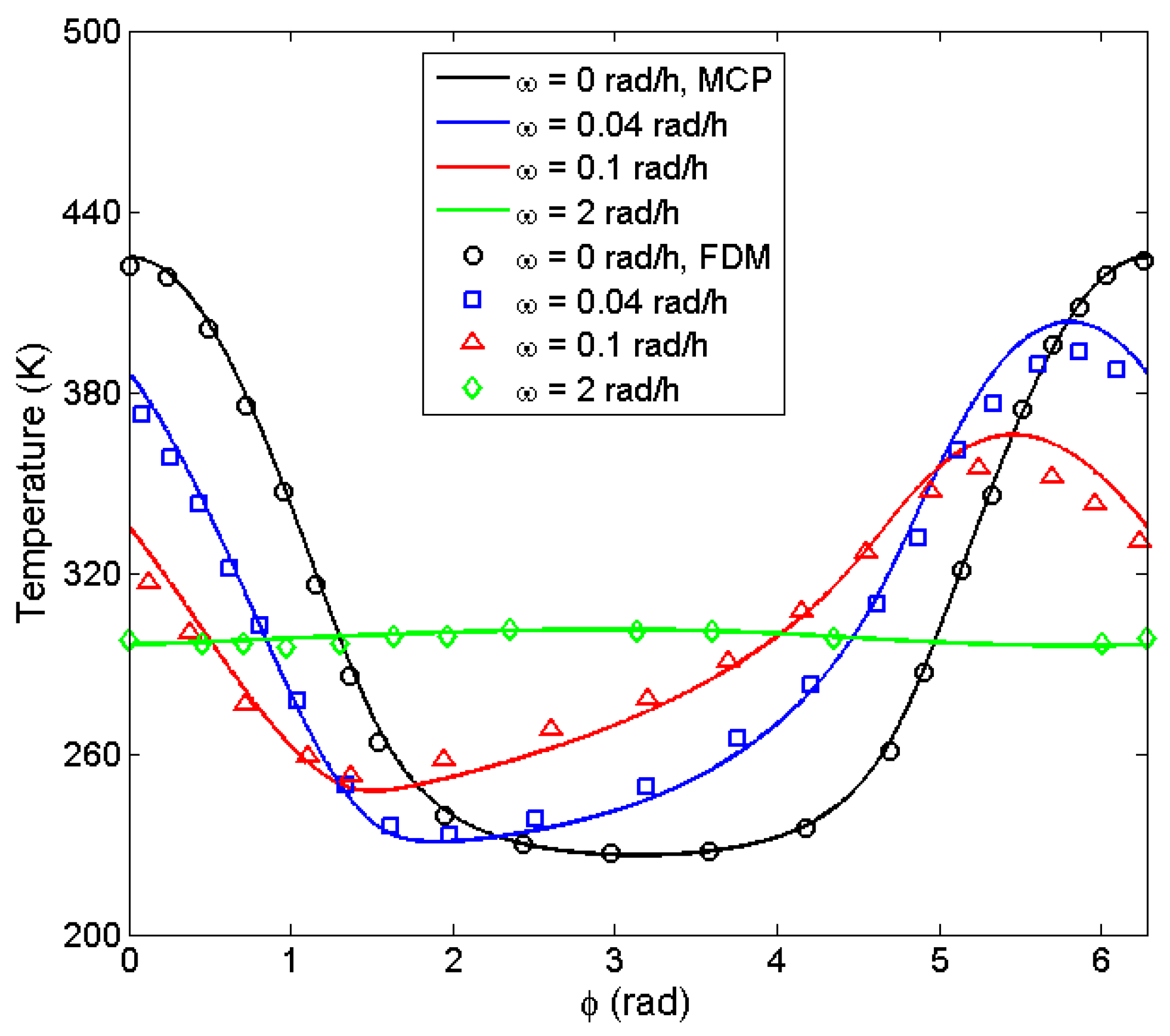
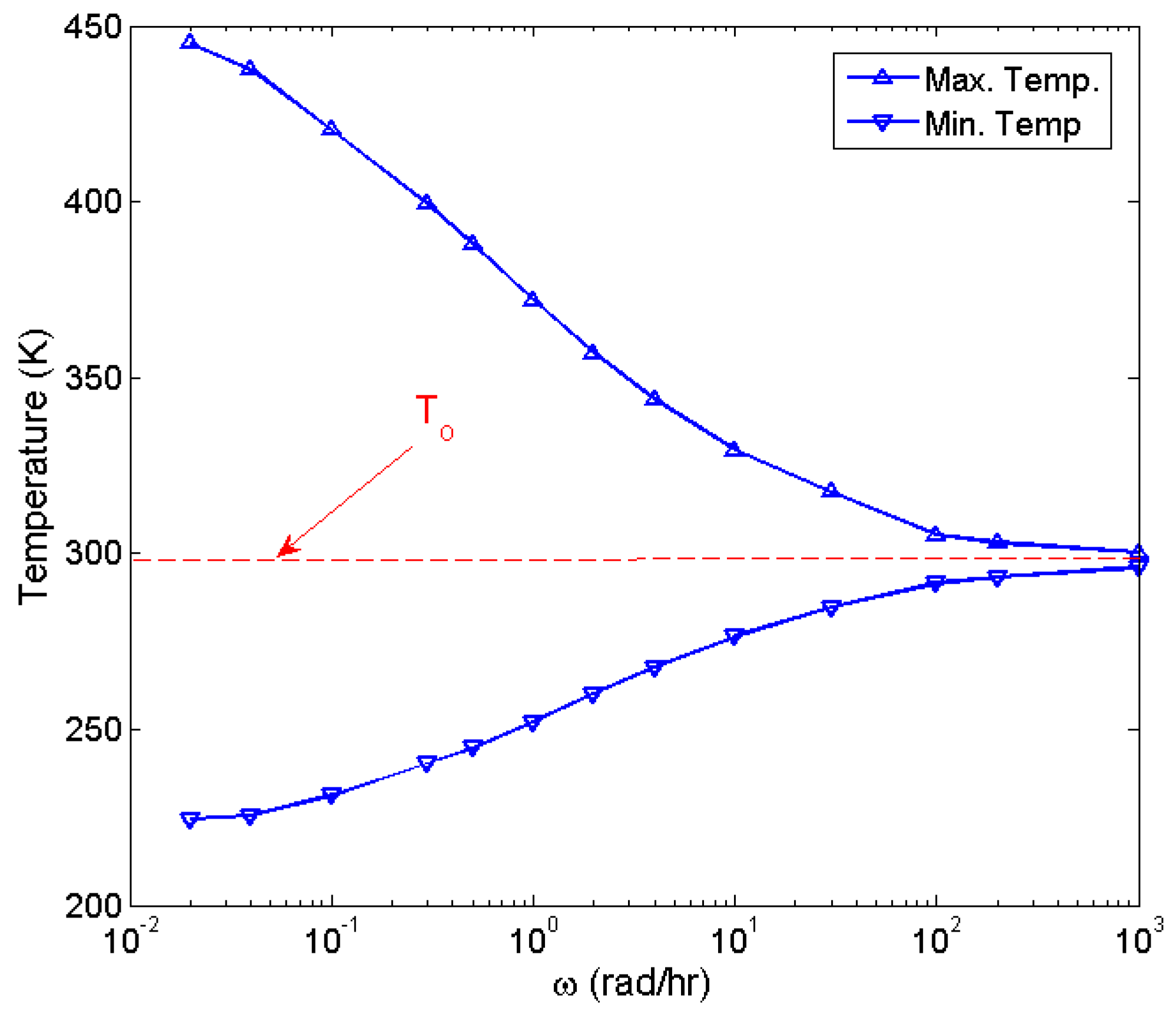
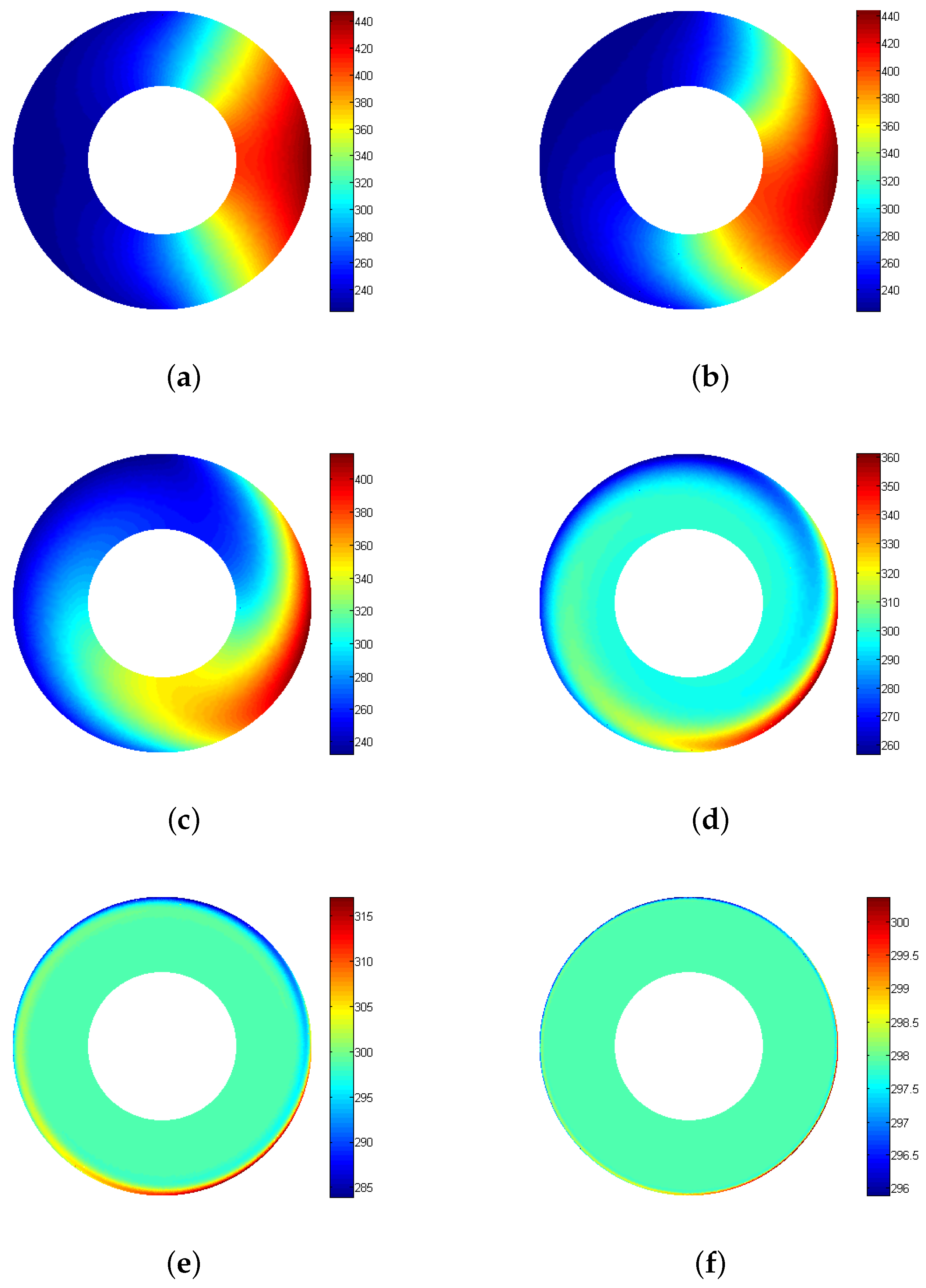
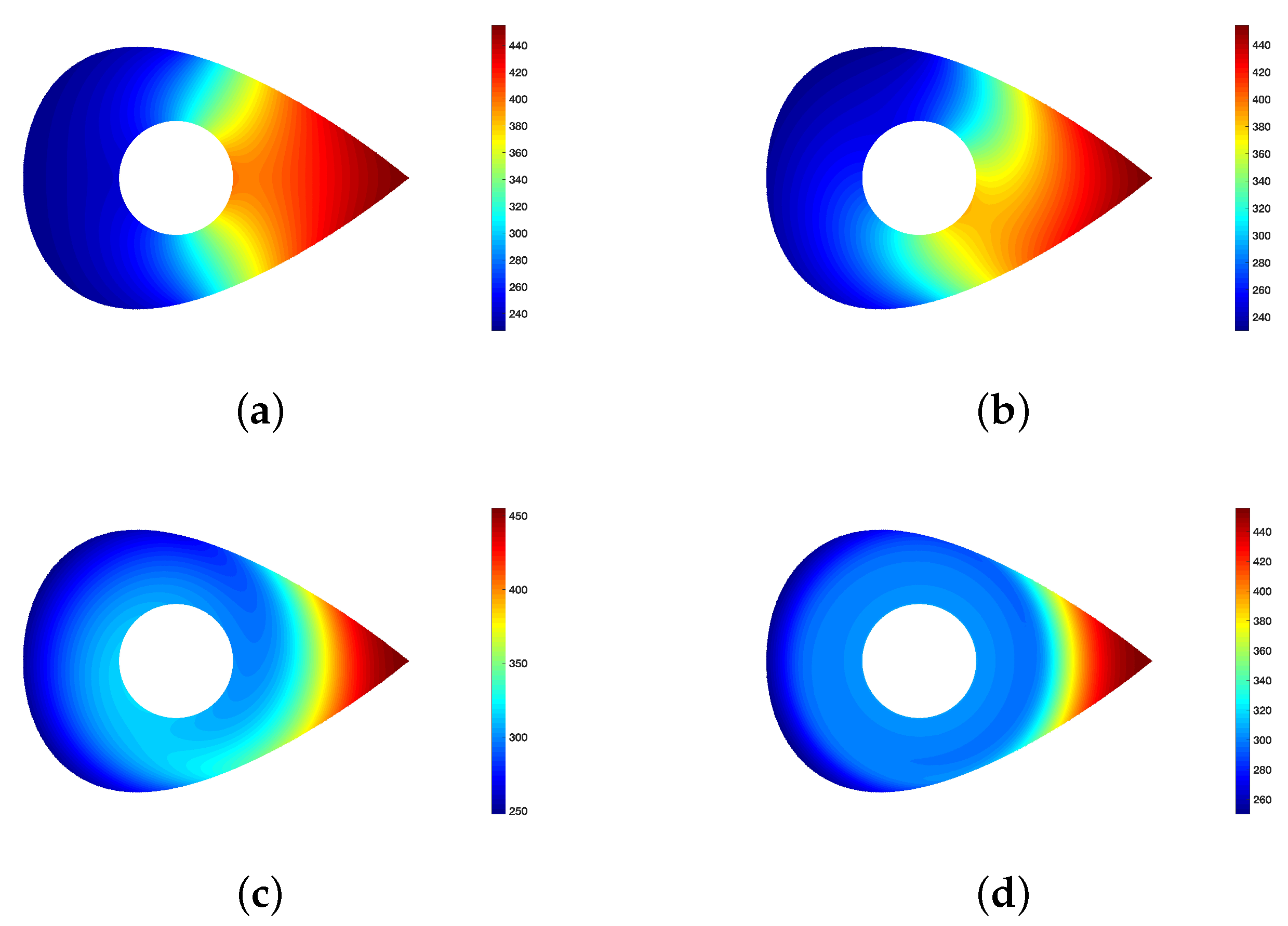
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schonberg, W.P. Studies of hypervelocity impact phenomena as applied to the protection of spacecraft operating in the MMOD environment. Procedia Eng. 2017, 204, 4–42. [Google Scholar]
- Deim, M.; Suderland, M.; Reiss, P.; Czupalla, M. Development and evaluation of thermal model reduction algorithms for spacecraft. Acta Astronaut. 2015, 110, 168–179. [Google Scholar] [CrossRef]
- Labibian, A.; Alikhani, A.; Pourtakdoust, S.H. Performance of a novel heat based model for spacecraft attitude. Aerosp. Sci. Technol. 2017, 70, 317–327. [Google Scholar] [CrossRef]
- Garmendia, I.; Anglada, E.; Vallejo, H.; Seco, M. Acurate calculation of conductive conductances in complex geometries for spacecraft thermal models. Adv. Space Res. 2016, 57, 1087–1097. [Google Scholar] [CrossRef]
- Fernandez-Rico, G.; Perez-Grande, I.; Sanz-Andres, A.; Torralbo, I.; Woch, J. Quasi-autonomous thermal model reduction for steady-state problems in space systems. Appl. Therm. Eng. 2016, 105, 456–466. [Google Scholar] [CrossRef]
- Perez-Grande, I.; Sanz-Andres, A.; Guerra, C.; Alonso, G. Analytical study of the thermal behaviour and stability of a small satellite. Appl. Therm. Eng. 2009, 29, 2567–2573. [Google Scholar] [CrossRef]
- Gadalla, M.A. Prediction of temperature variation in a rotating spacecraft in space environment. Appl. Therm. Eng. 2005, 25, 2379–2397. [Google Scholar] [CrossRef]
- Gadalla, M.A. Modeling of Thermal Analysis of Rotating Space Vehicles Subjected to Solar Radiation. In Proceedings of the 28th Intersociety Energy Conversion Engineering Conference (IECEC93), ACS, Atlanta, GA, USA, 8–13 August 1993. [Google Scholar]
- Gadalla, M.A.; Wahba, E. Computational modeling and analysis of thermal characteristics of a rotating spacecraft subjected to solar radiation. Heat Transf.-Asian Res. 2011, 40, 655–674. [Google Scholar] [CrossRef]
- Poncya, J.; Jubineau, F.; Angelo, F.D.; Perotto, V.; Juillet, J.J. Solar orbiter-heat shield and system technology. Acta Astronaut. 2009, 65, 1076–1088. [Google Scholar] [CrossRef]
- Corpino, S.; Caldera, M.; Nichele, F.; Masoero, M.; Viola, N. Thermal Design and analysis of a nanosatellite in low earth orbit. Acta Astronaut. 2015, 115, 247–261. [Google Scholar] [CrossRef]
- Farrahi, A.; Perez-Grande, I. Simplified analysis of the thermal behavior of a spinning satellite flying over sun-synchronous orbits. Appl. Therm. Eng. 2017, 125, 1146–1156. [Google Scholar] [CrossRef]
- Ross, R.G. Estimation of thermal conduction loads for structural supports of cryogenic spacecraft assemblies. Cryogenics 2004, 44, 421–424. [Google Scholar] [CrossRef]
- Guoliang, M.; Guiqing, J. Comprehensive analysis and estimation system on thermal environment, heat protection and thermal structure of spacecraft. Acta Astronaut. 2004, 54, 347–356. [Google Scholar] [CrossRef]
- Teofilatto, P. Preliminary aircraft design: Lateral handling qualities. Aircr. Des. 2001, 4, 63–73. [Google Scholar] [CrossRef]
- Shen, Z.; Li, H.; Liu, X.; Hu, G. Thermal shock induced dynamics of a spacecraft with a flexible deploying boom. Acta Astronaut. 2017, 141, 123–131. [Google Scholar] [CrossRef]
- Meese, E.A.; Norstrud, H. Simulation of convective heat flux and heat penetration for a spacecraft at re-entry. Aerosp. Sci. Technol. 2002, 6, 185–194. [Google Scholar] [CrossRef]
- Naumann, R.J. An analytical model for transport from quasi-steady and periodic acceleration on spacecraft. Int. J. Heat Mass Transf. 2000, 43, 2917–2930. [Google Scholar] [CrossRef]
- Pippin, G. Space environments and induced damage mechanisms in materials. Prog. Org. Coatings 2003, 47, 424–431. [Google Scholar] [CrossRef]
- Gaite, J.; Andres, A.S.; Grande, I.P. Nonlinear analysis of a simple model of temperature evolution in a satellite. Appl. Therm. Eng. 2009, 29, 2567–2573. [Google Scholar] [CrossRef]
- Charnes, A.; Raynor, S. Solar heating of a rotating cylindrical space vehicle. ARS 1960, 30, 479–483. [Google Scholar] [CrossRef]
- Wu, W.-F.; Liu, N.; Cheng, W.-L.; Liu, Y. Study on the effect of shape-stabilized phase change material on spacecraft thermal control in extreme thermal environment. Energy Convers. Manag. 2013, 69, 174–180. [Google Scholar] [CrossRef]
- Tkachenko, S.I.; Salmin, V.V.; Tkachenko, I.S.; Kaurov, I.V.; Korovin, M.D. Verifying parameters of ground data processing for the thermal control system of small spacecraft AIST based on telemetry data obtained by Samara. Orocrdia Eng. 2017, 185, 205–211. [Google Scholar] [CrossRef]
- Han, J.H.; Kim, C.G. Low earth orbit space environment simulation and its effects. Compos. Struct. 2006, 72, 218–226. [Google Scholar] [CrossRef]
- Azadi, E.; Fazelzadeh, S.A.; Azadi, M. Thermally induced vibrations of smart solar panel in a low-orbit satellite. Adv. Space Res. 2017, 59, 1502–1513. [Google Scholar] [CrossRef]
- Liu, L.; Cao, D.; Huang, H.; Shao, C.; Xu, Y. Thermal-structural analysis for an attitude maneuvering flexible spacecraft under solar radiation. Int. J. Mech. Sci. 2017, 126, 161–170. [Google Scholar] [CrossRef]
- Nicholes, L.D. Surface Temperature Distribution on Thin-Walled Bodies Subjected to Solar Radiation in Interplanetary Space; Technical Note D-584; NASA: Washington, DC, USA, 1961.
- Roberts, A.F. Heating of cylinders by radiation; approximate formulae for the temperature distribution. ASME 1964, 64-HT-39. [Google Scholar]
- Jenness, J.R. Temperature in a cylindrical satellite. Acta Astronaut. 1960, 5, 241–252. [Google Scholar]
- Torres, A.; Mishkinis, D.; Kaya, T. Mathematical modeling of a new satellite thermal architecture system connecting the east and west radiator panels and flight performance. Appl. Therm. Eng. 2014, 65, 623–632. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 275–389. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Schrader, B.; Reboux, S.; Sbalzarini, I.F. Discretization correction of general integral PSE operators for particle methods. J. Comput. Phys. 2010, 229, 4159–4182. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Cheeseman, B.L.; Ramaswamy, R.; Sbalzarini, I.F. Using DC PSE operator discretization in Eulerian meshless collocation methods improves their robustness in complex geometries. Comput. Fluids 2016, 136, 285–300. [Google Scholar] [CrossRef]
- Eldredge, J.D.; Leonard, A.; Colonius, T.A. A General Deterministic Treatment of Derivatives in Particle Methods. J. Comput. Phys. 2002, 180, 686–709. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Ghommem, M.; Kagadis, G.C.; Katsanos, K.; Loukopoulos, V.C.; Burganos, V.N.; Nikiforidis, G.C. Real-time tumor ablation simulation based on the dynamic mode decomposition method. Med. Phys. 2014, 41, 053301. [Google Scholar] [CrossRef]
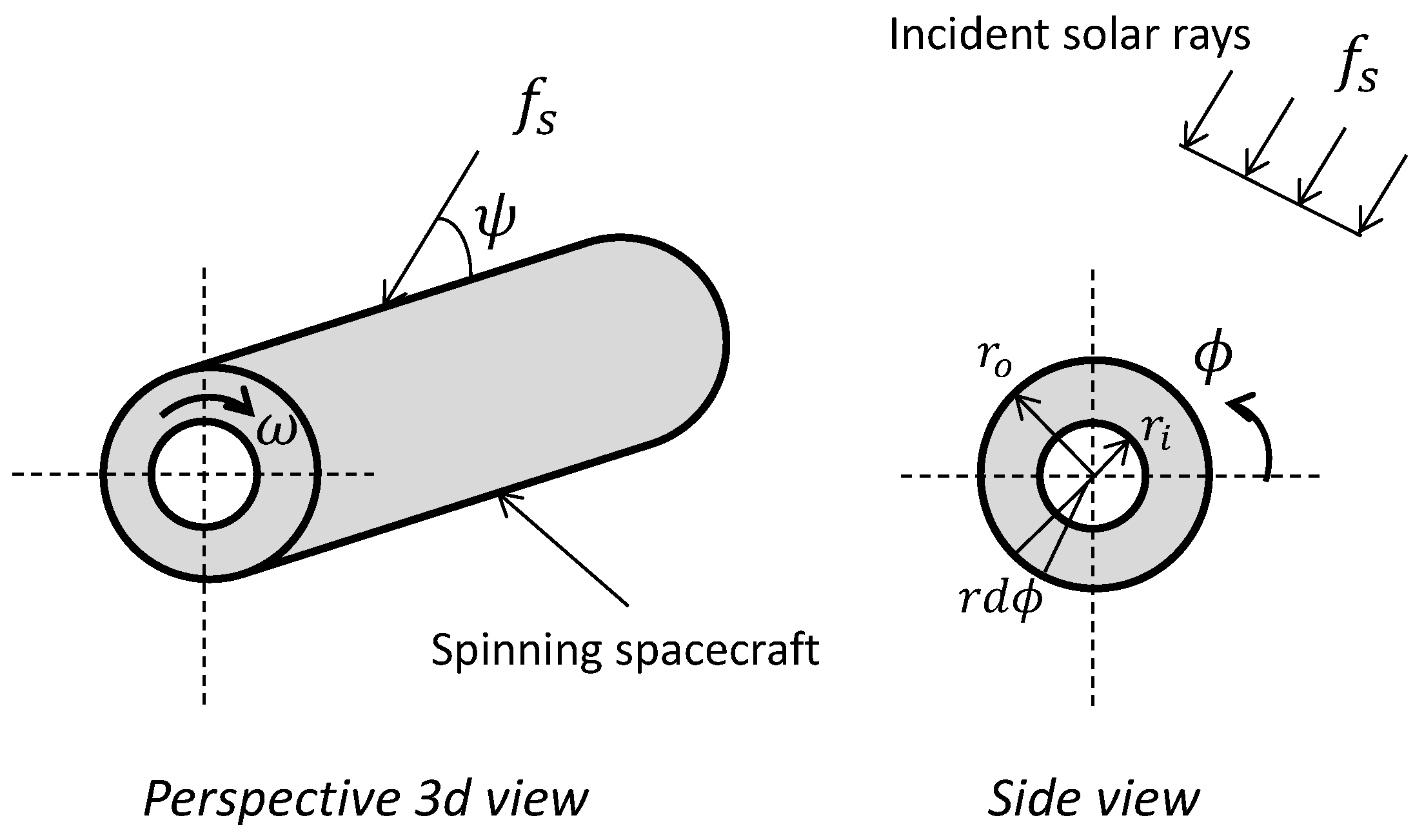
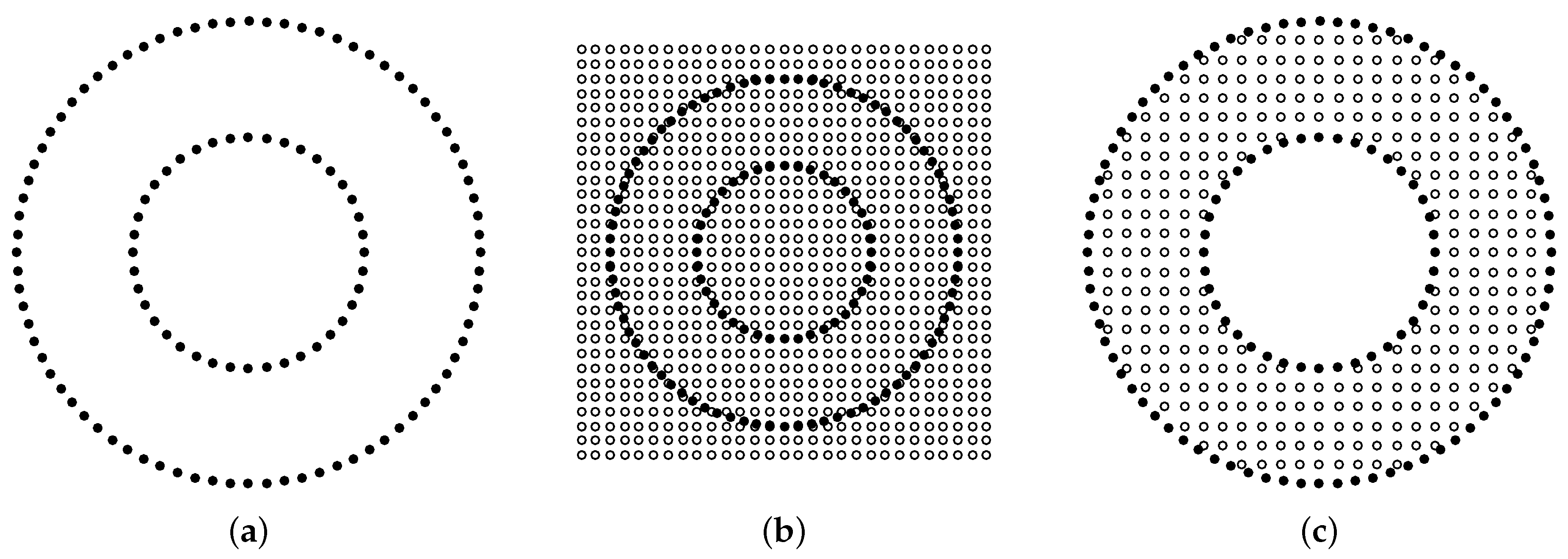
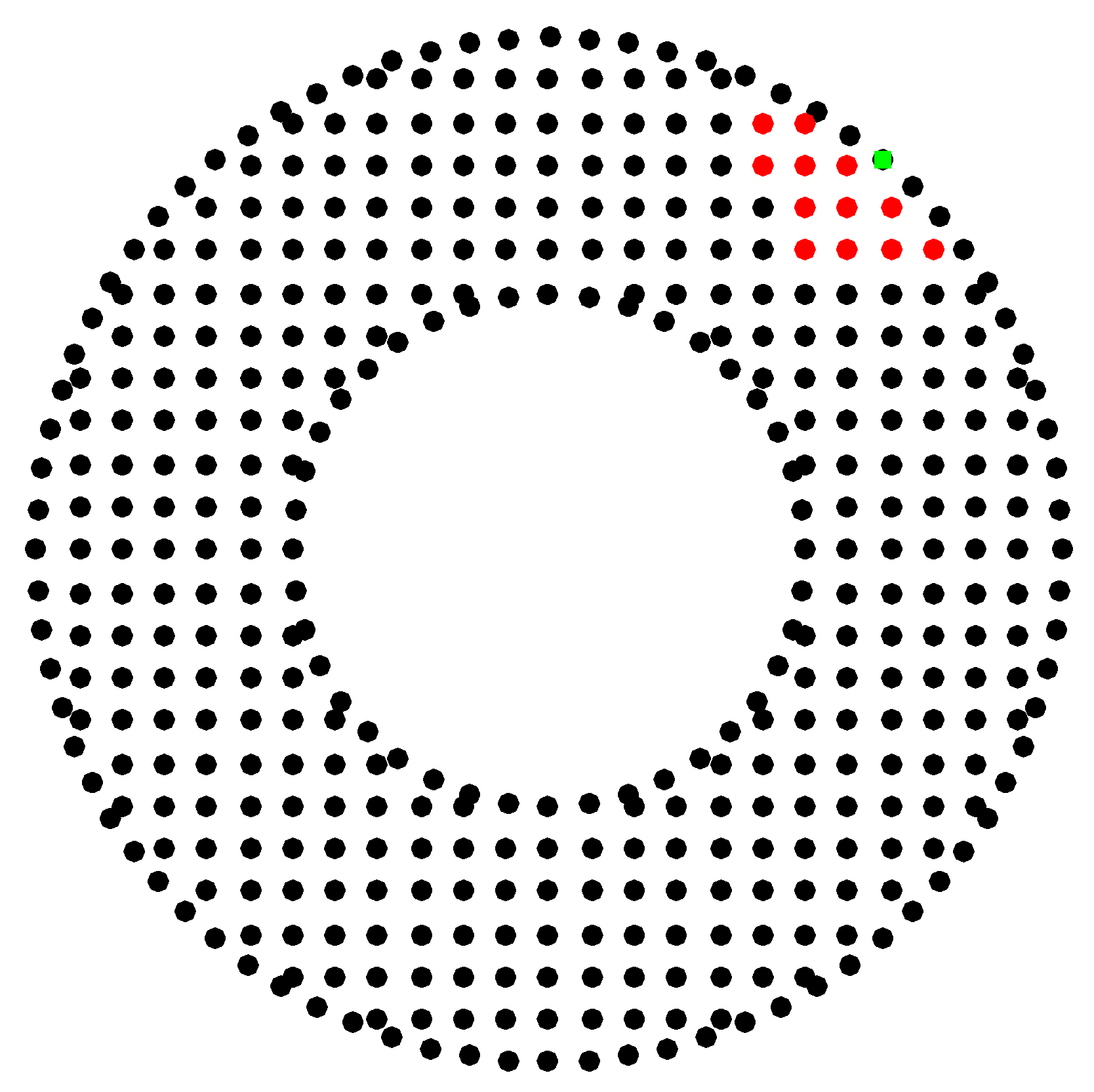
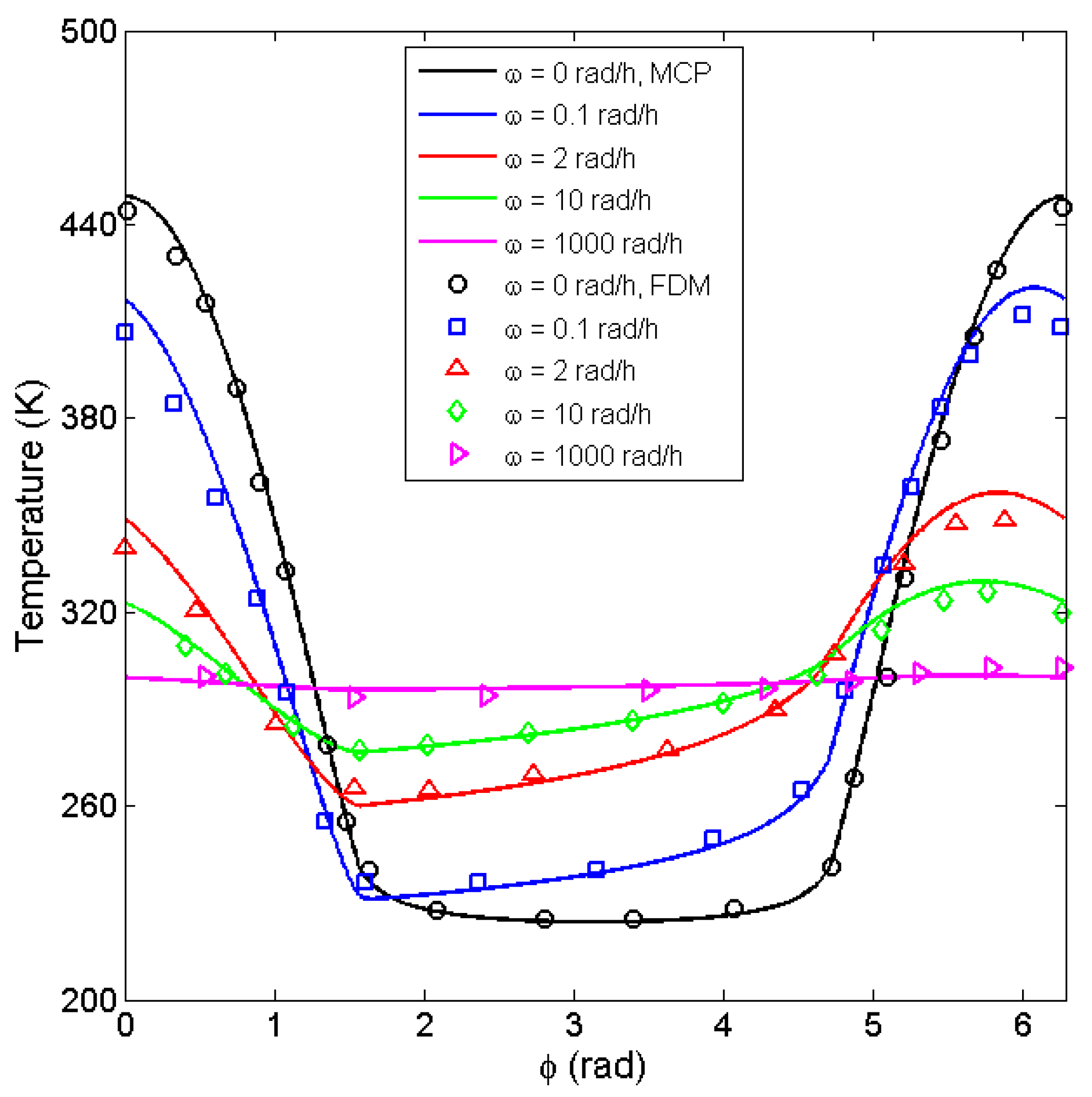
| Parameter | Symbol | Numerical Value |
|---|---|---|
| Outer radius | 0.3048 m | |
| Inner radius | 0.1524 m | |
| Inclination of the vehicle | ||
| Intensity of the sloar radiation | 1.4 kW/m2 | |
| Thermal conductivity | K | 0.173 W/m K |
| Absorptivity | 1 | |
| Emissivity | 1 | |
| Characteristic temperature | 297.46 K | |
| Non-dimensional radius | 0.8 and 1 | |
| Spinning speed | 0–1000 rad/h |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gadalla, M.; Ghommem, M.; Bourantas, G.; Miller, K. Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect. Processes 2019, 7, 807. https://doi.org/10.3390/pr7110807
Gadalla M, Ghommem M, Bourantas G, Miller K. Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect. Processes. 2019; 7(11):807. https://doi.org/10.3390/pr7110807
Chicago/Turabian StyleGadalla, Mohamed, Mehdi Ghommem, George Bourantas, and Karol Miller. 2019. "Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect" Processes 7, no. 11: 807. https://doi.org/10.3390/pr7110807
APA StyleGadalla, M., Ghommem, M., Bourantas, G., & Miller, K. (2019). Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect. Processes, 7(11), 807. https://doi.org/10.3390/pr7110807







