Reliability Evaluation Method Considering Demand Response (DR) of Household Electrical Equipment in Distribution Networks
Abstract
1. Introduction
- The load characteristic of two typical items of household electrical equipment is elaborately analyzed.
- An electricity price-based DR model and an incentive-based DR model are proposed for two typical items of high-power electrical equipment, considering charging behavior and thermodynamic property.
- A load shedding strategy is introduced to improve the traditional reliability evaluation method for distribution networks, while taking into account the capacity constraints.
- A reliability calculation method of distribution networks with shortage of power supply capacity and faults taken into consideration is presented.
2. DR Modeling
2.1. DR Modeling of EVs Based on Electricity Price
2.1.1. Optimization Objective
2.1.2. Constraints
2.2. DR Modeling of Air Conditioners Based on Incentive
2.2.1. Optimization Objective
2.2.2. Constraints
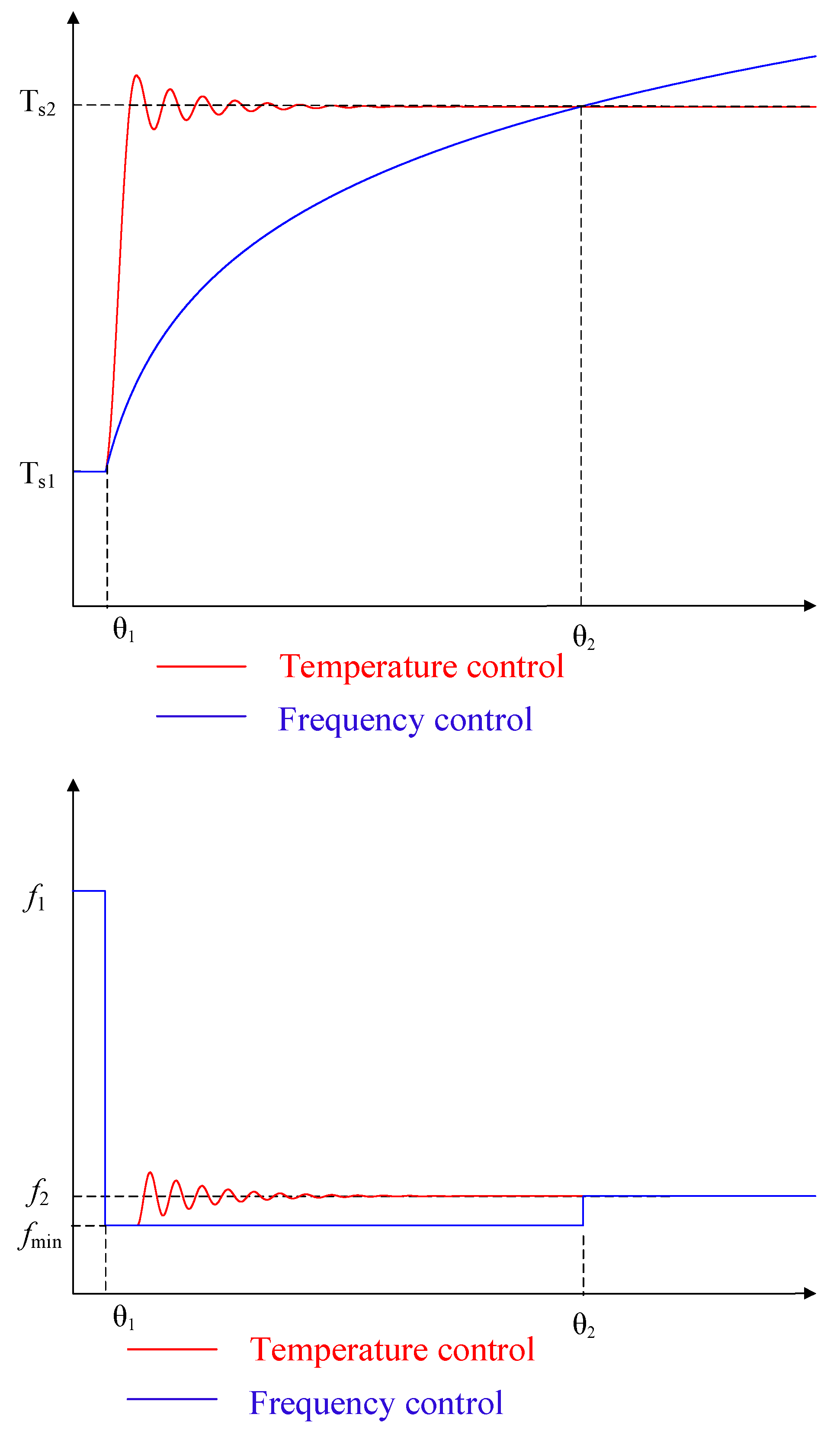
2.2.3. Control Method
3. Reliability Evaluation of Distribution Networks Considering DR
3.1. Model of Load Transfer Capacity
3.2. Load Shedding Strategy
4. Analysis of the Influence of DR on Distribution Network Reliability
4.1. Load Point Reliability Index
4.2. System Reliability Index
5. Improved Reliability Evaluation Method Based on Load Clustering
5.1. Improved Reliability Evaluation Method
- (1)
- When power supply capacity is insufficient in normal operation state, the load shedding strategy in Section 3.2 should be applied to supply power as much as possible with the feeder maximum capacity constraint respected. Calculate the system reliability indexes with and without DR, respectively.
- (2)
- When a failure occurs in the distribution network, parts of the loads of Type B cannot get power supply due to restricted transfer capacity if the maximum capacity limit of feeders are considered.
5.2. Reliability Calculation Method of Distribution Networks Considering Load Clustering
6. Case Study
6.1. Case 1
6.1.1. Residential Electricity Load Analysis
6.1.2. Analysis on DR of Residential Load
6.2. Case 2
6.2.1. Simulation Settings
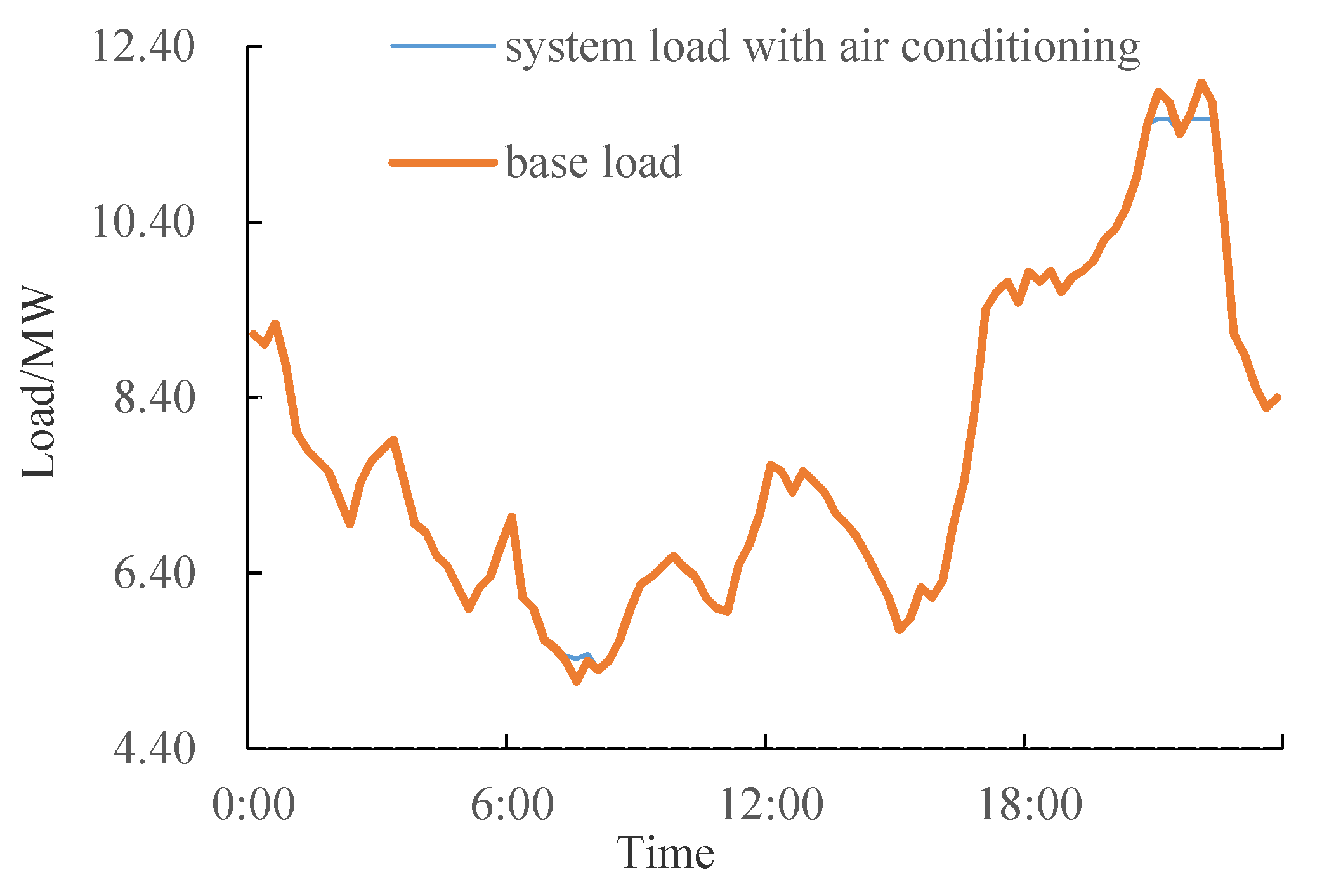
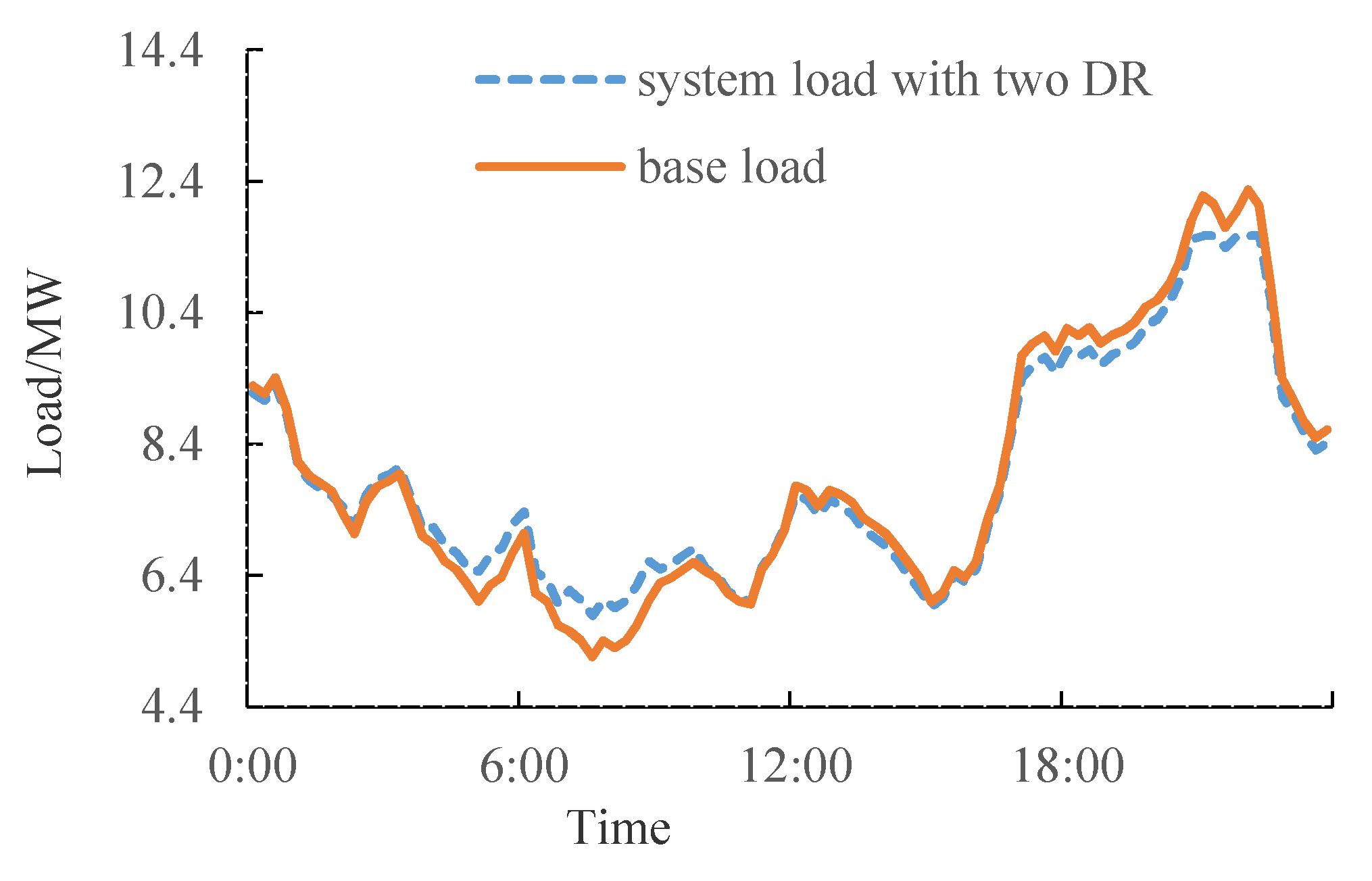
6.2.2. Load Profile Considering DR
6.2.3. Influence of Real-Time Electricity Price on DR
6.2.4. Reliability Evaluation Considering DR
- Case 1: DR is not taken into consideration.
- Case 2: DR based on electricity price and incentive is considered.
- Case 3: Case 1 with sufficient spare capacity of tie lines.
- Case 4: Case 2 with sufficient spare capacity of tie lines.
- The reliability index of the four cases is shown in Table 2.
7. Conclusions
- (1)
- DR can improve the load curve and reduce the peak loads. DR based on electricity price has a certain randomness and is greatly affected by real-time electricity price. Unreasonable real-time electricity price may lead to “peak-on-peak” or unnecessary load reduction.
- (2)
- Both DR based on electricity price and DR based on incentive can improve the reliability index of distribution networks. Compared with the reliability results attained by employing a single DR strategy, comprehensive DRs can improve reliability
- (3)
- DR has no influence on the distribution network reliability index if transmission capacity of tie lines is assumed to be infinite. Under the premise of considering the tie line capacity limit, DR reduces the peak loads of the systems and decreases the probability of insufficient power supply capacity in normal operation, and meanwhile increases the possibility of the load point being transferred when a failure occurs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Load Number (Class) | Average Load (kW) | Load Number (Class) | Average Load (kW) | Load Number (Class) | Average Load (kW) | Load Number (Class) | Average Load (kW) |
|---|---|---|---|---|---|---|---|
| LP1(II) | 165.9 | LP7(I) | 210.1 | LP13(III) | 250.1 | LP19(III) | 155.4 |
| LP2(III) | 180.8 | LP8(III) | 155.4 | LP14(III) | 155.4 | LP20(II) | 186.1 |
| LP3(III) | 250.1 | LP9(I) | 283.1 | LP15(II) | 186.1 | LP21(I) | 283.1 |
| LP4(III) | 243.1 | LP10(II) | 158.5 | LP16(II) | 158.5 | LP22(II) | 158.5 |
| LP5(I) | 207.0 | LP11(III) | 155.4 | LP17(III) | 250.1 | LP23(I) | 210.1 |
| LP6(II) | 165.9 | LP12(II) | 158.5 | LP18(III) | 243.1 |
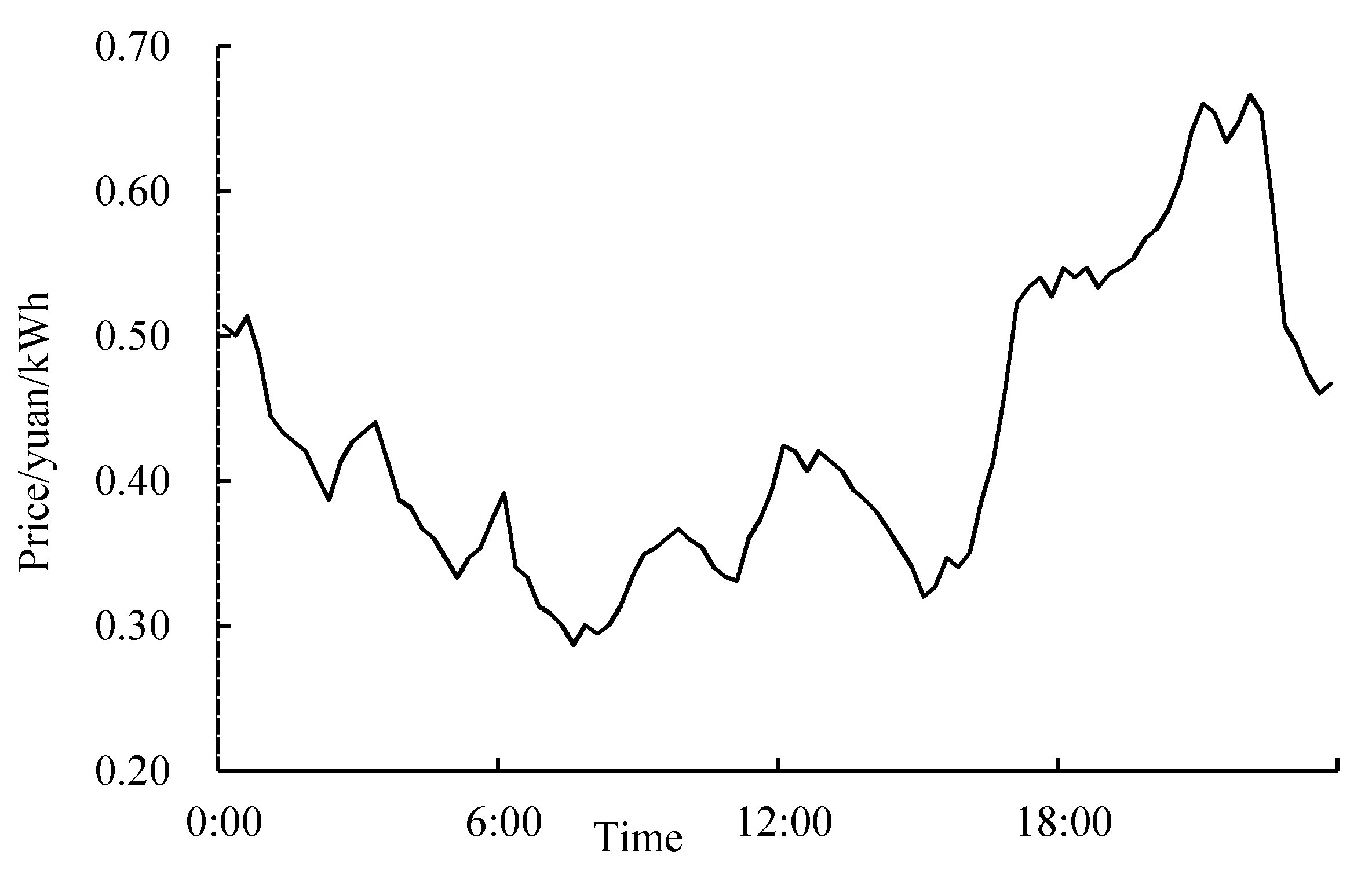
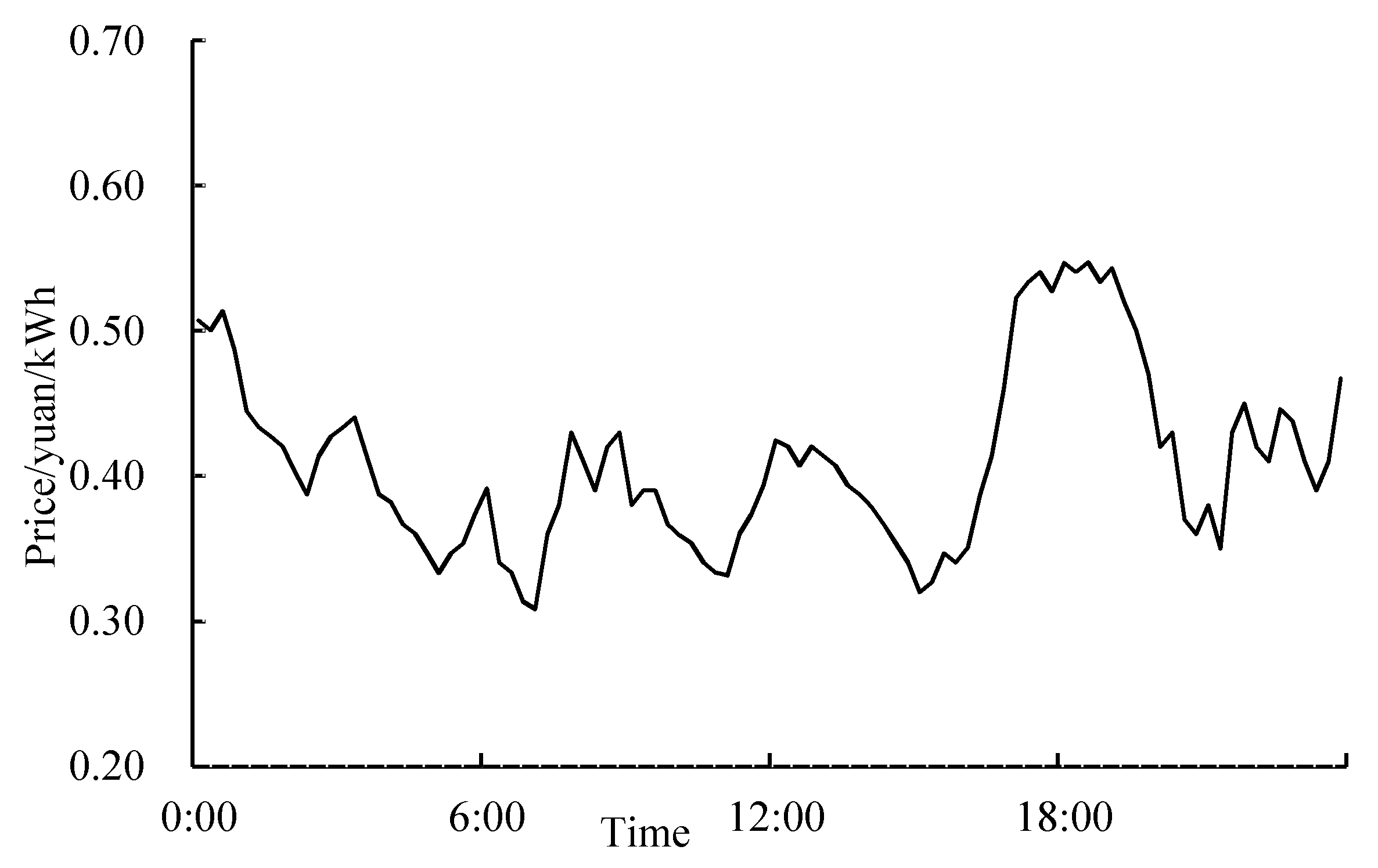
References
- Eissa, M.M. Developing incentive demand response with commercial energy management system (CEMS) based on diffusion model, smart meters and new communication protocol. Appl. Energy 2019, 236, 273–292. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Najafi, H.; Anvari-Moghaddam, A.; Guerrero, J. Study of the effect of time-based rate demand response programs on stochastic day-ahead energy and reserve scheduling in islanded residential microgrids. Appl. Sci. 2017, 7, 378. [Google Scholar] [CrossRef]
- Pinson, P.; Madsen, H. Benefits and challenges of electrical demand response: A critical review. Renew. Sustain. Energy Rev. 2014, 39, 686–699. [Google Scholar]
- Wang, F.; Zhou, L.; Ren, H.; Liu, X.; Talari, S.; Shafie-khah, M.; Catalão, J.P. Multi-objective optimization model of source-load-storage synergetic dispatch for building energy system based on TOU price demand response. IEEE Trans. Ind. Appl. 2018, 54, 1017–1028. [Google Scholar] [CrossRef]
- Sharifi, R.; Anvari-Moghaddam, A.; Fathi, S.H.; Guerrero, J.M.; Vahidinasab, V. Economic demand response model in liberalised electricity markets with respect to flexibility of consumers. IET Gener. Transm. Distrib. 2017, 11, 4291–4298. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chow, M.Y.; Chen, J.M. A survey on demand response in smart grids: Mathematical models and approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H.; Ding, Y.; Ye, H. An incentive-based demand response (DR) model considering composited DR resources. IEEE Trans. Ind. Electro. 2018, 66, 1488–1498. [Google Scholar] [CrossRef]
- Zhou, B.R.; Huang, Y.C.; Zhang, Y.J. Reliability analysis on microgrid considering incentive demand response. Autom. Electr. Power Syst. 2017, 41, 70–78. [Google Scholar]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Sharifi, R.; Moghaddam, A.A.; Fathi, S.H.; Vahidinasab, V. A flexible responsive load economic model for industrial demands. Processes 2019, 7, 147. [Google Scholar] [CrossRef]
- Sharifi, R.; Fathi, S.H.; Vahidinasab, V. A review on demand-side tools in electricity market. Renew. Sustain. Energy Rev. 2017, 72, 565–572. [Google Scholar] [CrossRef]
- Aalami, H.A.; Moghaddam, M.P.; Yousefi, G.R. Modelling and prioritizing demand response programs in power markets. Electr. Power Syst. Res. 2010, 80, 426–435. [Google Scholar] [CrossRef]
- Smith, R.; Meng, K.; Dong, Z.; Simpson, R. Demand response: A strategy to address residential air-conditioning peak load in Australia. J. Mod. Power Syst. Clean Energy 2013, 1, 223–230. [Google Scholar] [CrossRef]
- Reynolds, S.P.; Creighton, T.E. Time-of-use rates for very large customers on the pacific gas and electric company system. IEEE Trans. Power Appar. Syst. 1980, 99, 147–151. [Google Scholar] [CrossRef]
- Kai, M.; Hu, G.; Spanos, C.J. A cooperative demand response scheme using punishment mechanism and application to industrial refrigerated warehouses. IEEE Trans. Ind. Inform. 2015, 11, 1520–1531. [Google Scholar]
- Chen, C.; Kishore, S.; Wang, Z.; Alizadeh, M.; Scaglione, A. How will Demand Response aggregators affect electricity markets ?—A Cournot game analysis. In Proceedings of the 5th International Symposium on Communications Control and Signal Processing (ISCCSP), Roma, Italy, 2–4 May 2012; pp. 1–6. [Google Scholar]
- Zeng, B.; Jiang, W.Q.; Yang, Z.; Li, G. Optimal load dispatching method based on chance-constrained programming for household electrical equipment. Autom. Electr. Power Syst. 2018, 38, 27–33. [Google Scholar]
- Chen, Z.; Li, Y.Q.; Leng, Z.Y.; Lu, G.X. Refined modeling and energy management strategy of typical household high-power loads. Autom. Electr. Power Syst. 2018, 42, 135–143. [Google Scholar]
- Sharifi, R.; Anvari-Moghaddam, A.; Fathi, S.H.; Guerrero, J.M.; Vahidinasab, V. An optimal market-oriented demand response model for price-responsive residential consumers. Energy Eff. 2019, 12, 803–815. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Assi, C.; Maier, M.; Uddin, M.F. Smart microgrids: Optimal joint scheduling for electric vehicles and home appliances. IEEE Trans. Smart Grid 2014, 5, 239–250. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Guizani, M.; Alhussein, M.; Aurangzeb, K.; Ilahi, M. Towards dynamic coordination among home appliances using multi-objective energy optimization for demand side management in smart buildings. IEEE Access 2018, 6, 19509–19529. [Google Scholar] [CrossRef]
- Mohajeryami, S.; Moghaddam, I.N.; Doostan, M.; Vatani, B.; Schwarz, P. A novel economic model for price-based demand response. Electr. Power Syst. Res. 2016, 135, 1–9. [Google Scholar] [CrossRef]
- Mnatsakanyan, A.; Kennedy, S.W. A novel demand response model with an application for a virtual power plant. IEEE Trans. Smart Grid 2015, 6, 230–237. [Google Scholar] [CrossRef]
- Zhao, H.S.; Wang, Y.Y.; Chen, S. Impact of DR on distribution system reliability. Autom. Electr. Power Syst. 2015, 39, 49–55. [Google Scholar]
- Zhang, Y.B.; Ren, S.J.; Yang, X.D.; Bao, K.K.; Xie, L.Y.; Qi, J. Optimal configuration considering price-based demand response for stand-alone microgrid. Electr. Power Autom. Equip. 2017, 37, 55–62. [Google Scholar]
- Qi, X.J.; Cheng, Q.; Wu, H.B.; Yang, S.H.; Li, Z.X. Impact of incentive-based DR on operational reliability of distribution network. Trans. China Electrotech. Soc. 2018, 33, 5319–5326. [Google Scholar]
- Sharifi, R.; Fathi, S.H.; Vahidinasab, V. Customer baseline load models for residential sector in a smart-grid environment. Energy Rep. 2016, 2, 74–81. [Google Scholar] [CrossRef]
- Niu, W.J.; Li, Y.; Wang, B.B. Demand Response Based Virtual Power Plant Modeling Considering Uncertainty. Proc. CSEE 2014, 34, 3630–3637. [Google Scholar]
- Lei, M.; Wei, W.; Zeng, J.H.; Mo, S.Y. Effect of load control on power supply reliability considering demand response. Autom. Electr. Power Syst. 2018, 42, 53–59. [Google Scholar]
- Yang, J.R.; Shi, K.; Cui, X.Q.; Gao, C.W.; Cui, G.Y.; Yang, J.L. Peak Load Reduction Method of Inverter Air-conditioning Group Under DR. Autom. Electr. Power Syst. 2018, 42, 44–56. [Google Scholar]
- Kwac, J.; Flora, J.; Rajagopal, R. Household energy consumption segmentation using hourly data. IEEE Trans. Smart Grid 2014, 5, 420–430. [Google Scholar] [CrossRef]
- Billinton, R.; Jonnavithula, S. A test system for teaching overall power system reliability assessment. IEEE Trans. Power Syst. 1996, 11, 1670–1676. [Google Scholar] [CrossRef]
- Cao, X.L.; Yu, S.X.; Li, X.L.; Wang, W.; Liao, S.M. Theoretic and experimental study on domestic air-conditioner with R410A as refrigerant. J. Cent. South Univ. (Sci. Technol.) 2010, 41, 759–763. [Google Scholar]
- Transmission and Distribution Committee. IEEE Guide for Electric Power Distribution Reliability Indices Redline; IEEE: NY, USA, 2012. [Google Scholar]
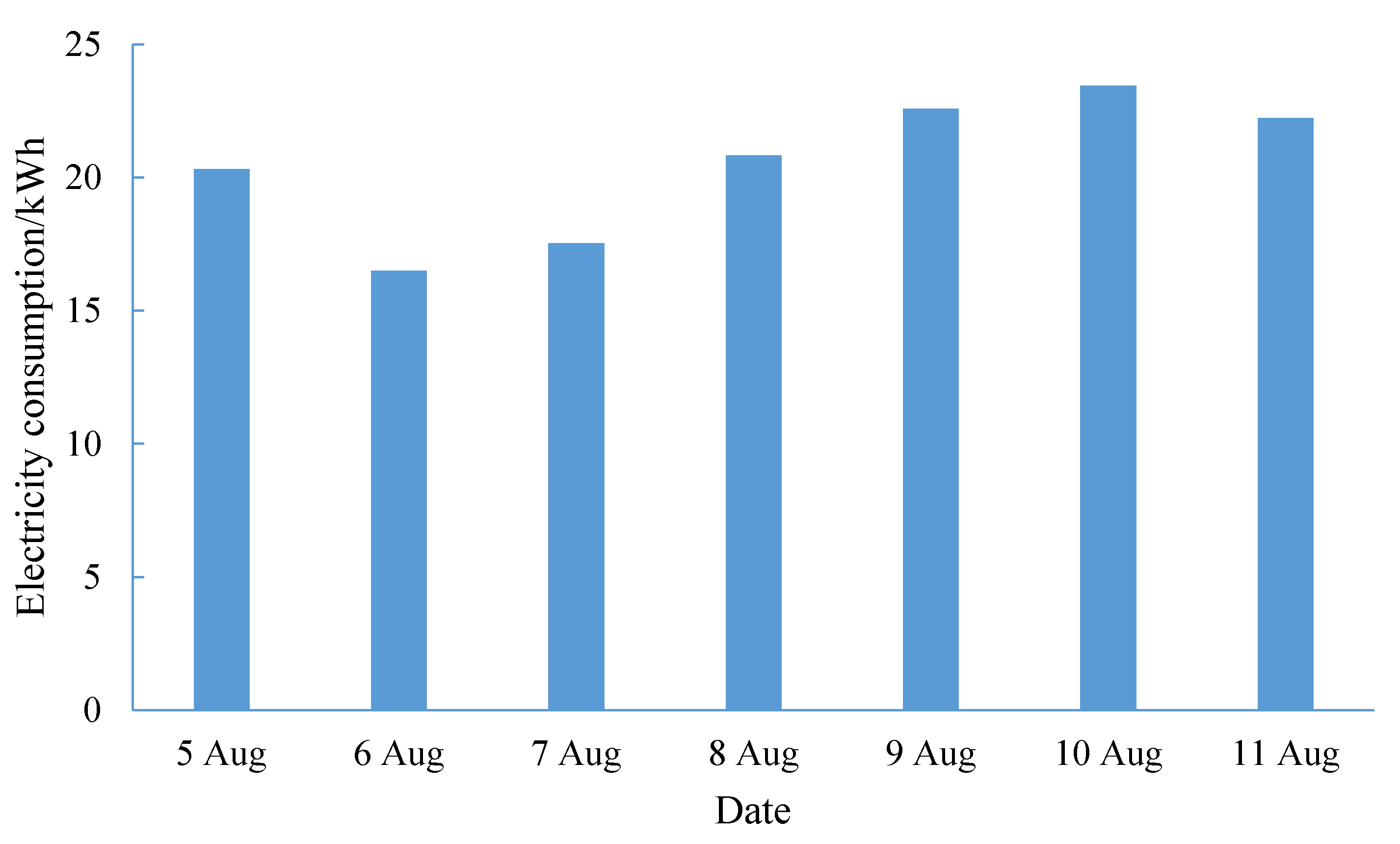
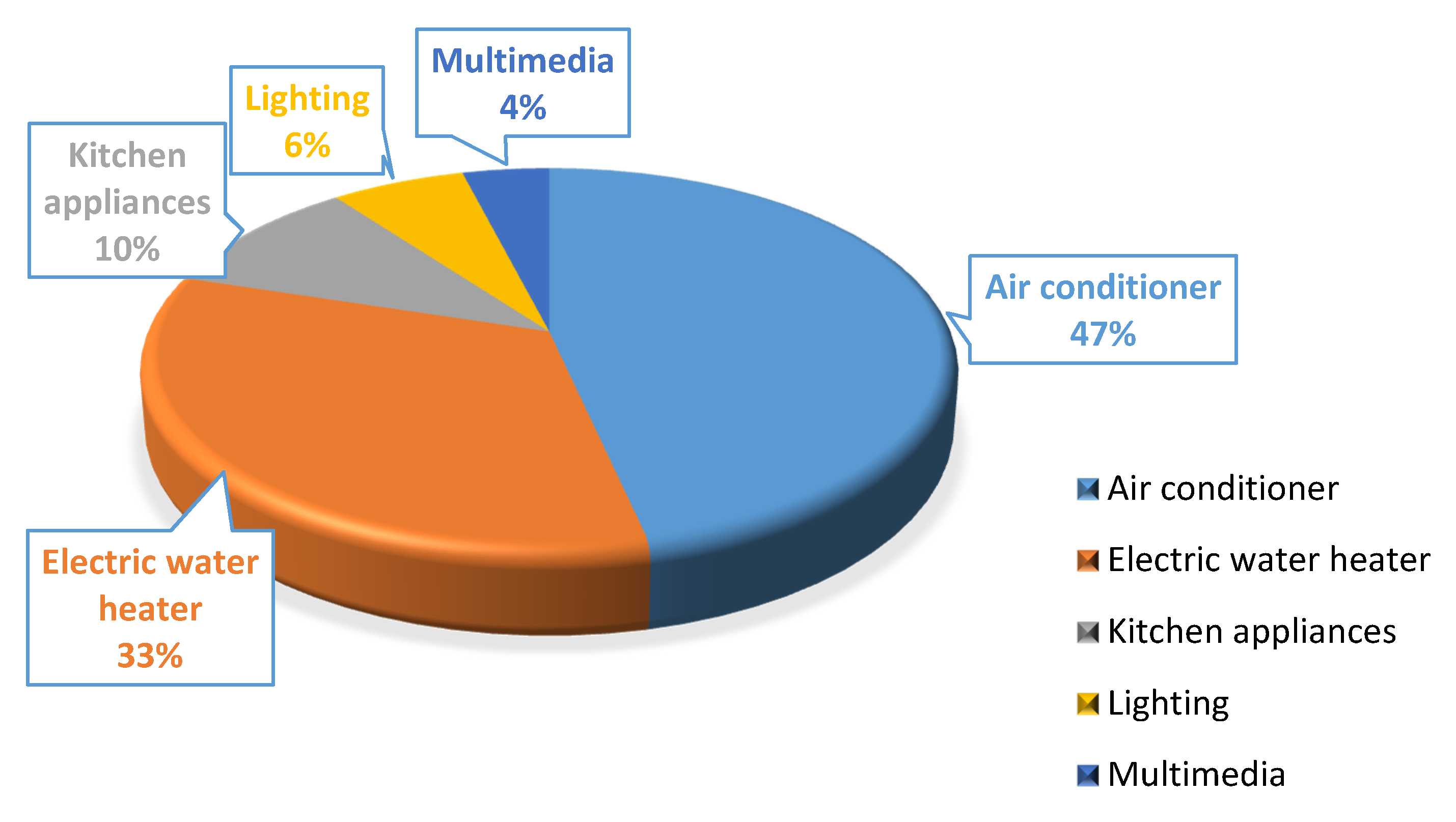
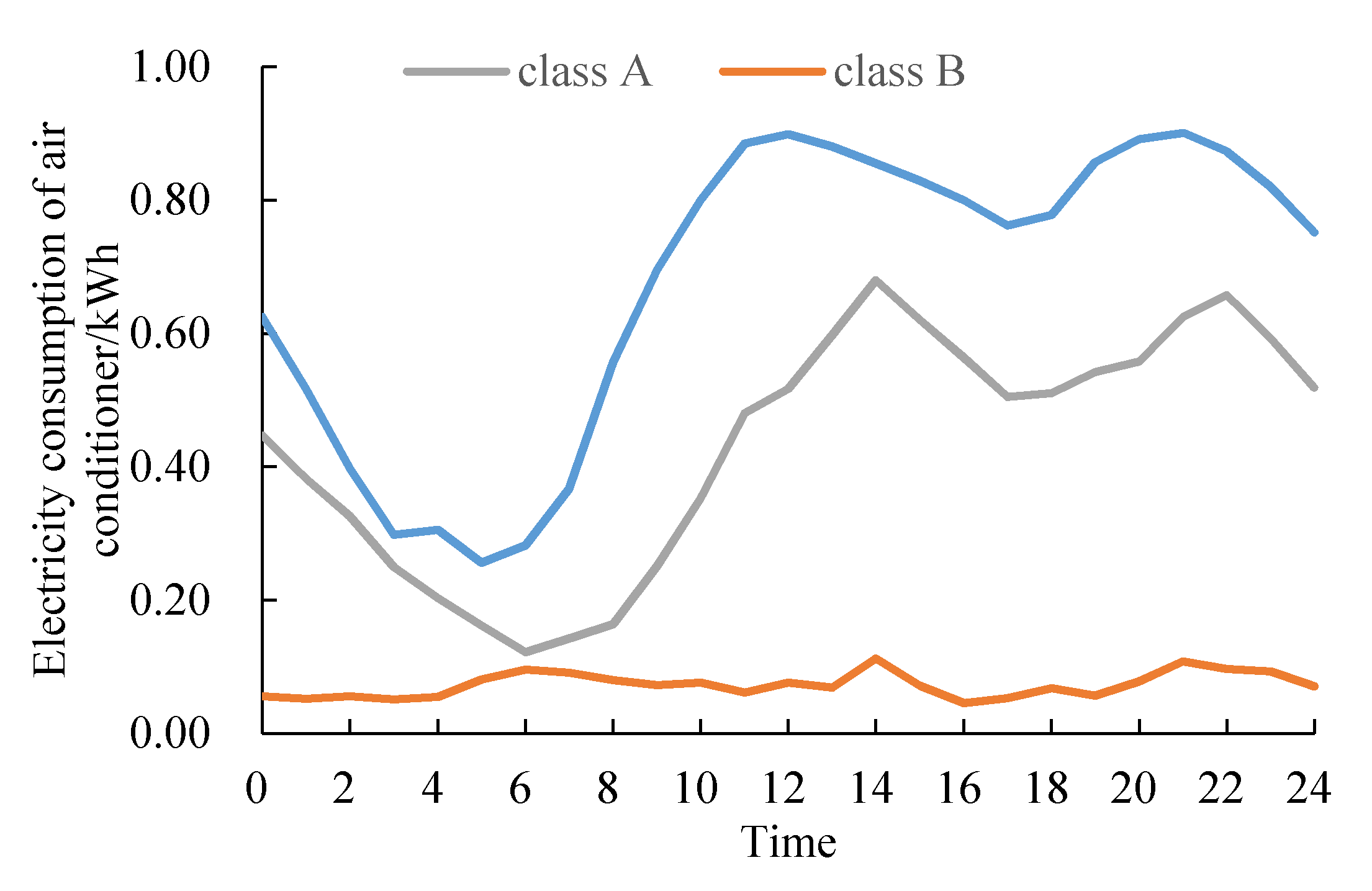

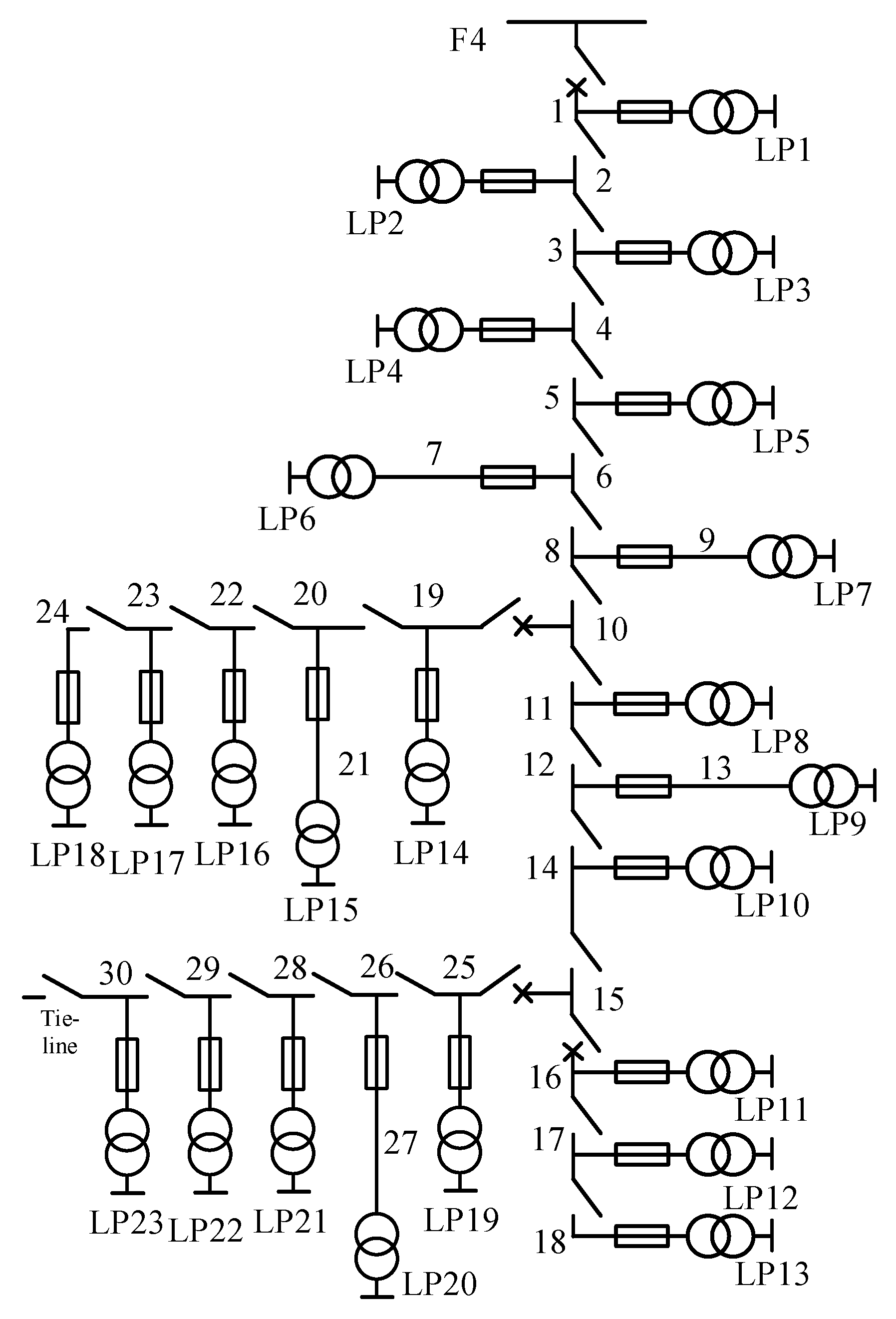
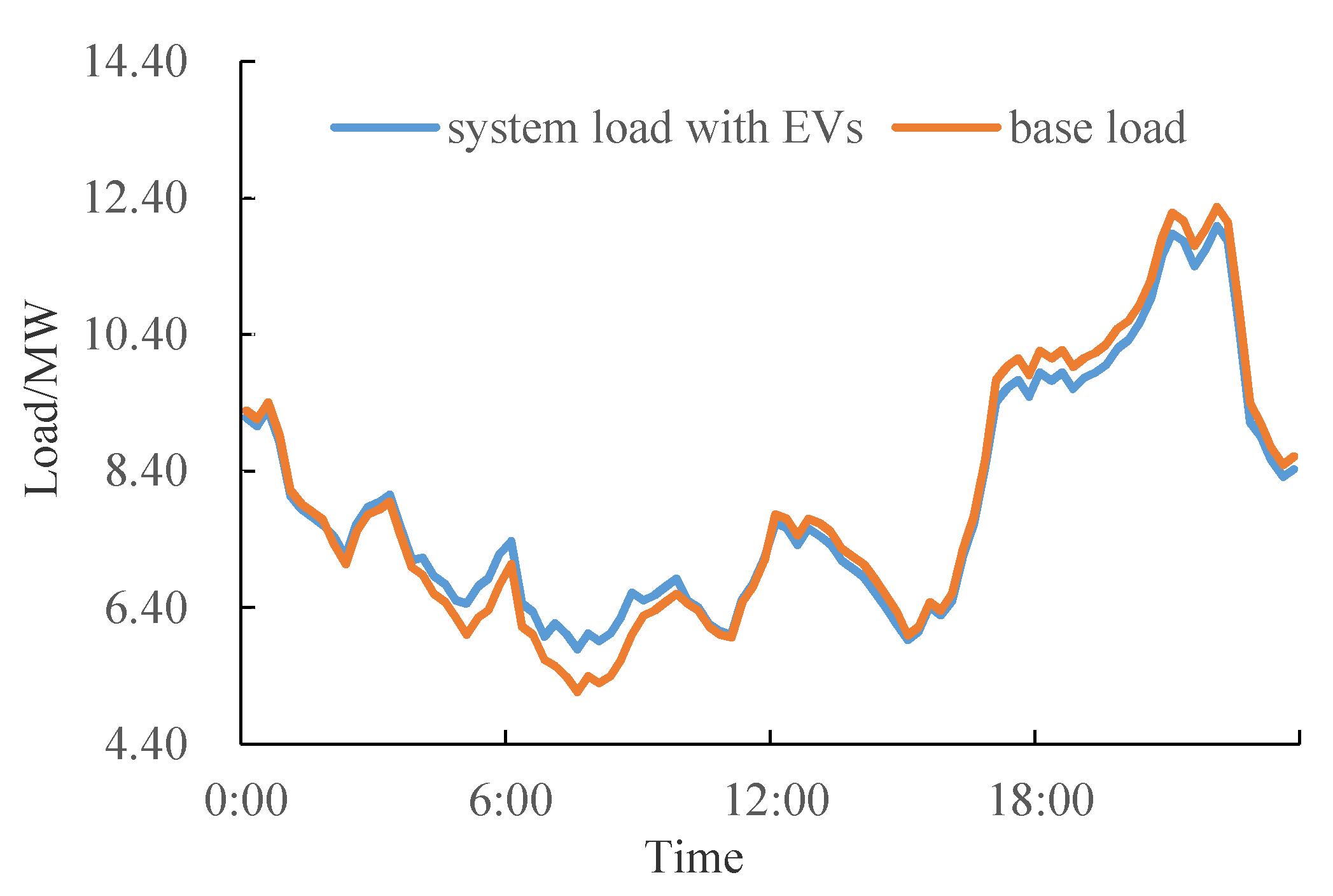

| Type | Daily Load Rate | Percent |
|---|---|---|
| A | 0.633253 | 56% |
| B | 0.647609 | 11% |
| C | 0.74984 | 33% |
| Case | SAIFI/(times/a) | SAIDI/(h/a) | CAIDI/(h/times) | ENS/(MW h/a) |
|---|---|---|---|---|
| 1 | 2.253 | 5.67 | 2.517 | 67.93 |
| 2 | 2.2052 | 5.2483 | 2.3798 | 59.31 |
| 3 | 2.2052 | 3.519 | 1.596 | 43.22 |
| 4 | 2.2052 | 3.519 | 1.596 | 40.76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Tang, J.; Sun, L.; Zhou, J.; Wang, X.; Mao, Y. Reliability Evaluation Method Considering Demand Response (DR) of Household Electrical Equipment in Distribution Networks. Processes 2019, 7, 799. https://doi.org/10.3390/pr7110799
Chen H, Tang J, Sun L, Zhou J, Wang X, Mao Y. Reliability Evaluation Method Considering Demand Response (DR) of Household Electrical Equipment in Distribution Networks. Processes. 2019; 7(11):799. https://doi.org/10.3390/pr7110799
Chicago/Turabian StyleChen, Hongzhong, Jun Tang, Lei Sun, Jiawei Zhou, Xiaolei Wang, and Yeying Mao. 2019. "Reliability Evaluation Method Considering Demand Response (DR) of Household Electrical Equipment in Distribution Networks" Processes 7, no. 11: 799. https://doi.org/10.3390/pr7110799
APA StyleChen, H., Tang, J., Sun, L., Zhou, J., Wang, X., & Mao, Y. (2019). Reliability Evaluation Method Considering Demand Response (DR) of Household Electrical Equipment in Distribution Networks. Processes, 7(11), 799. https://doi.org/10.3390/pr7110799





