Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities †
Abstract
1. Introduction
2. Methodology
2.1. Numerial Methods
2.2. Polymer Solution and Substrates Properties
3. Results
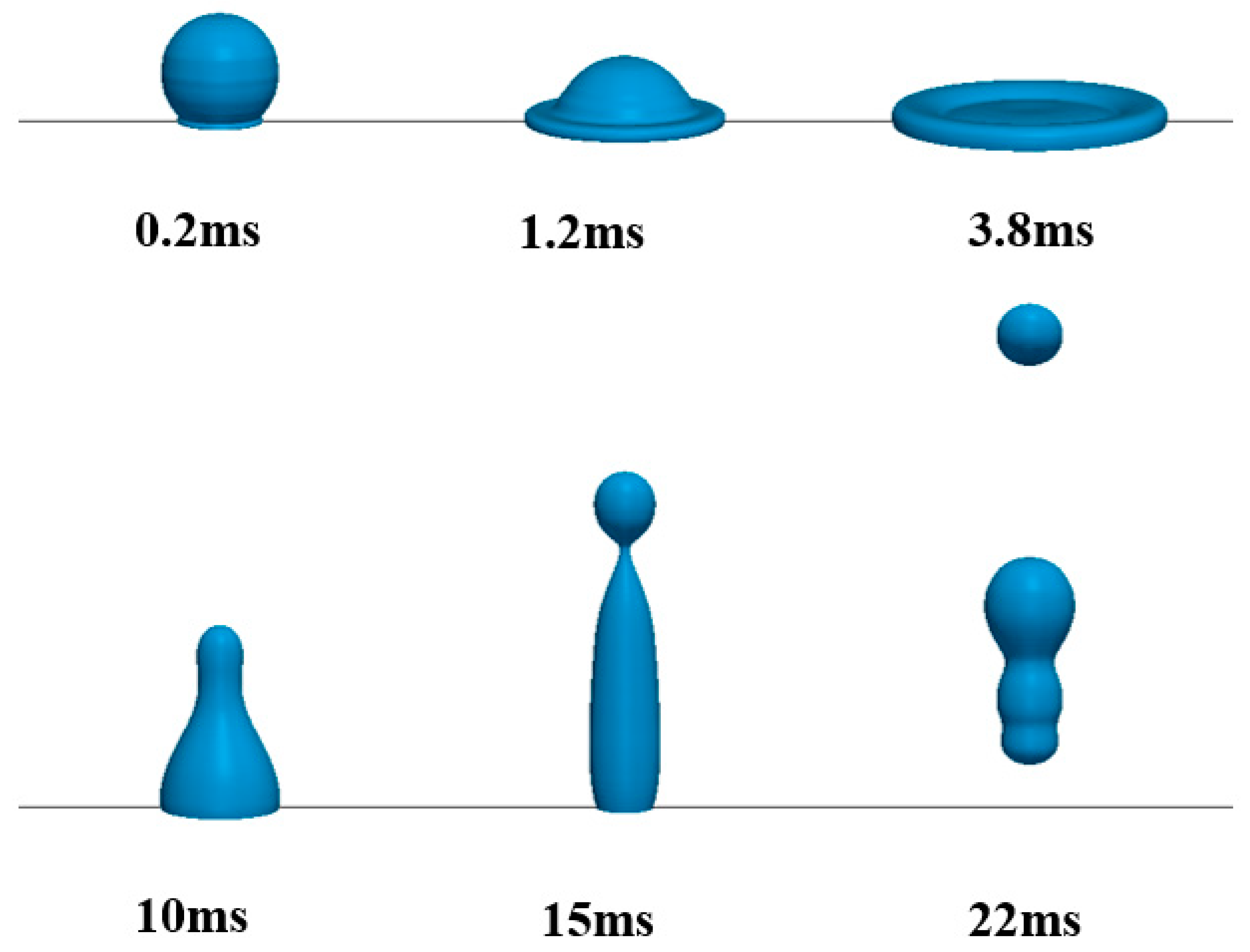
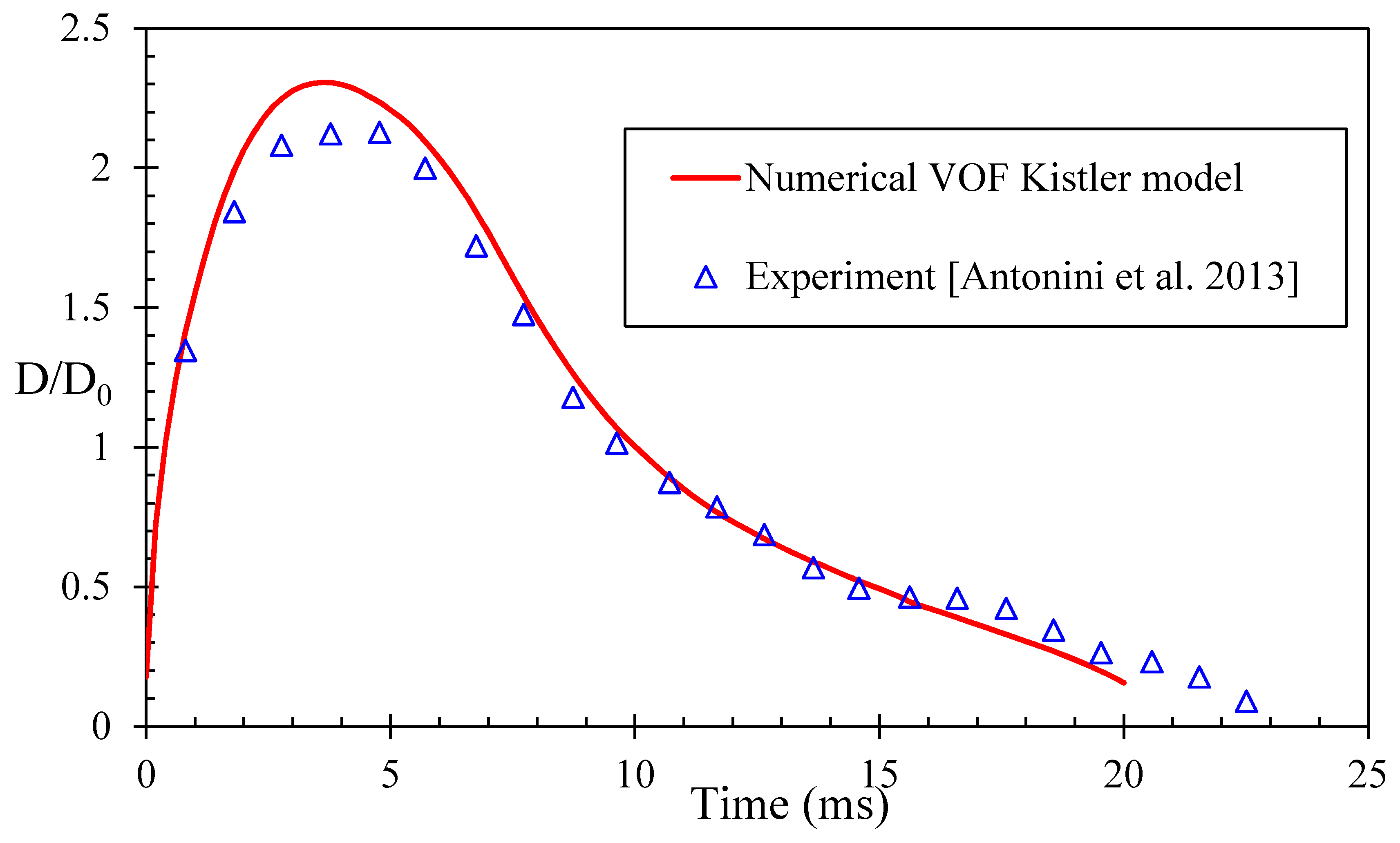
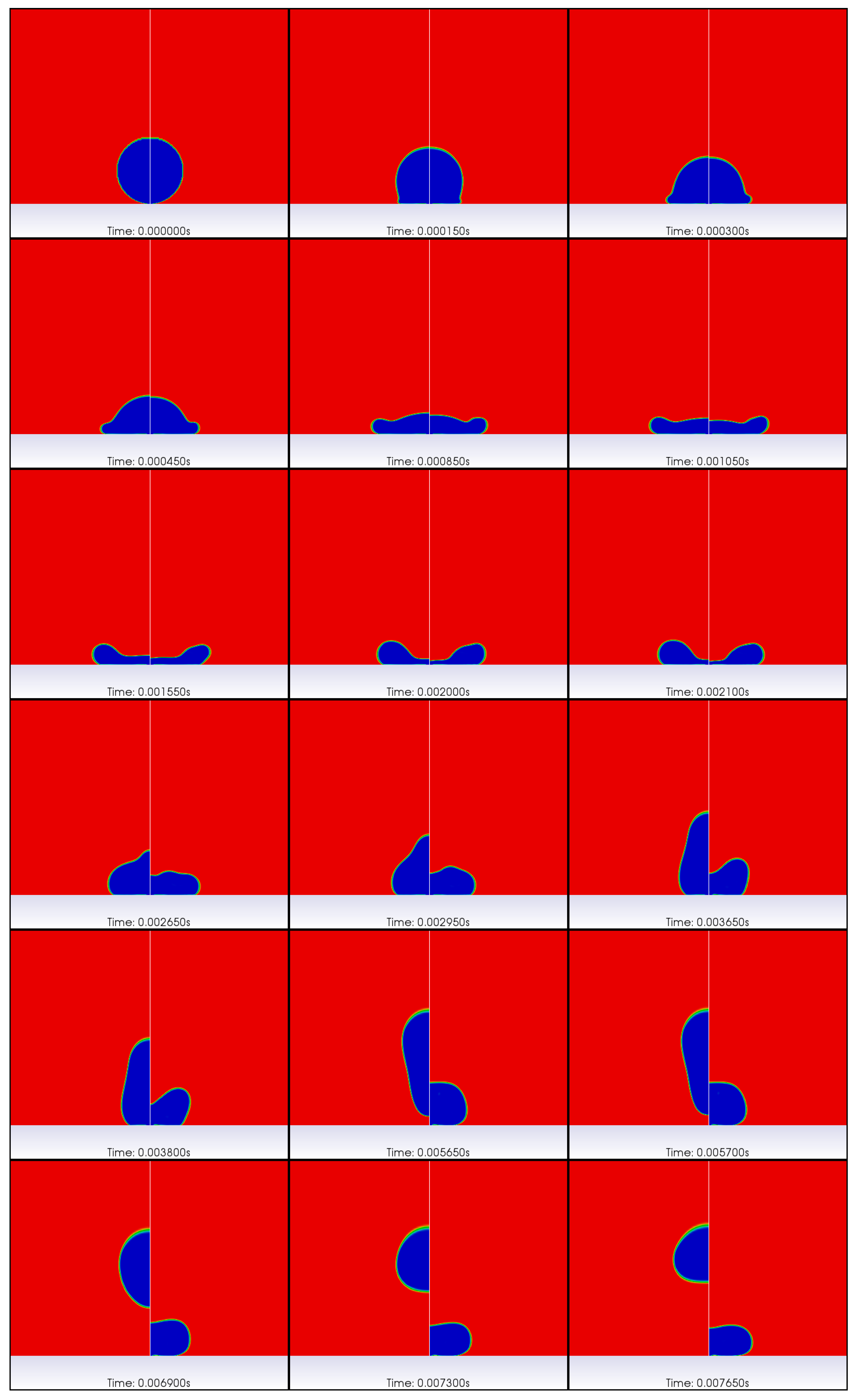
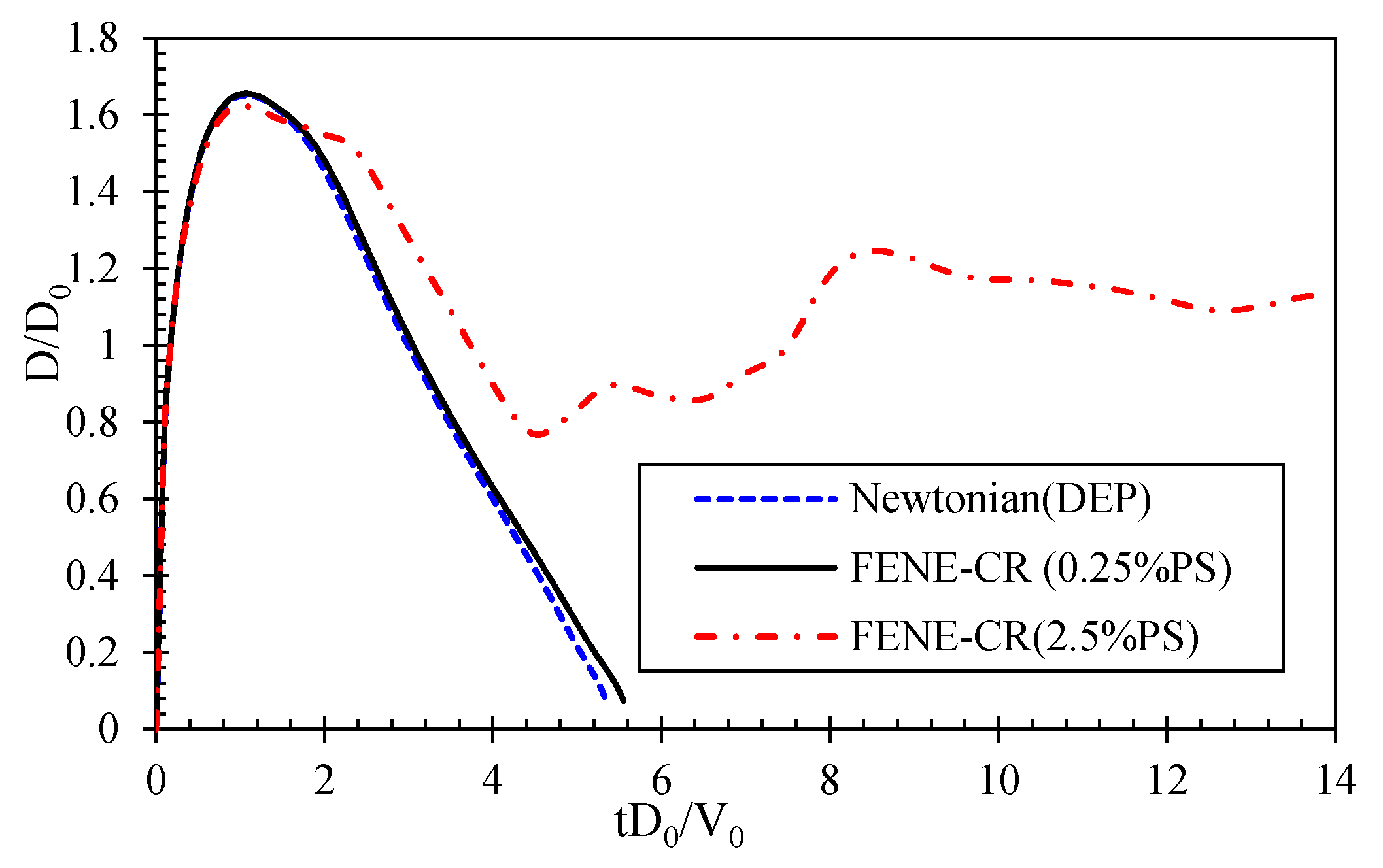
3.1. Validation of Newtonian Droplet Impact Dynamics
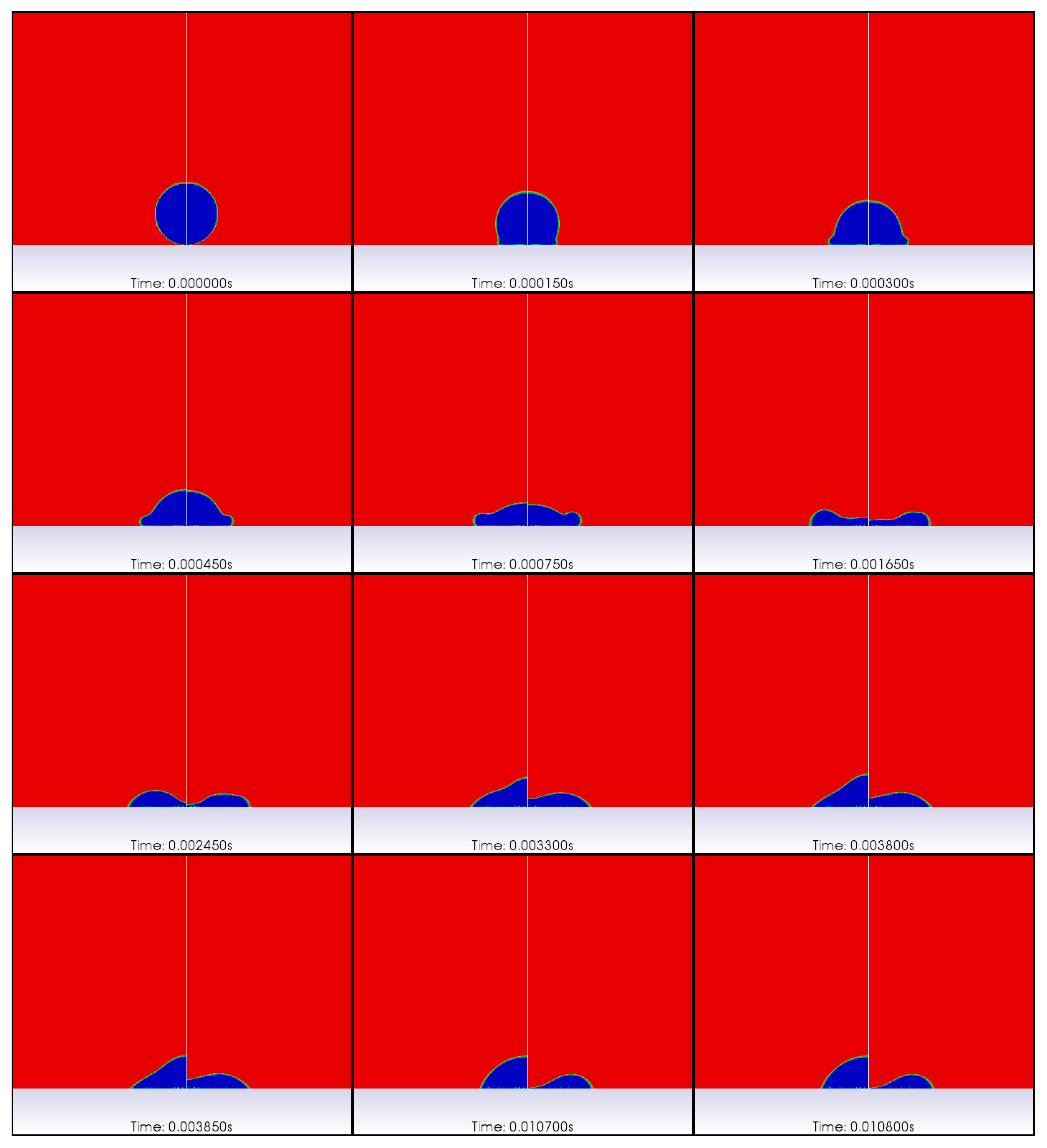
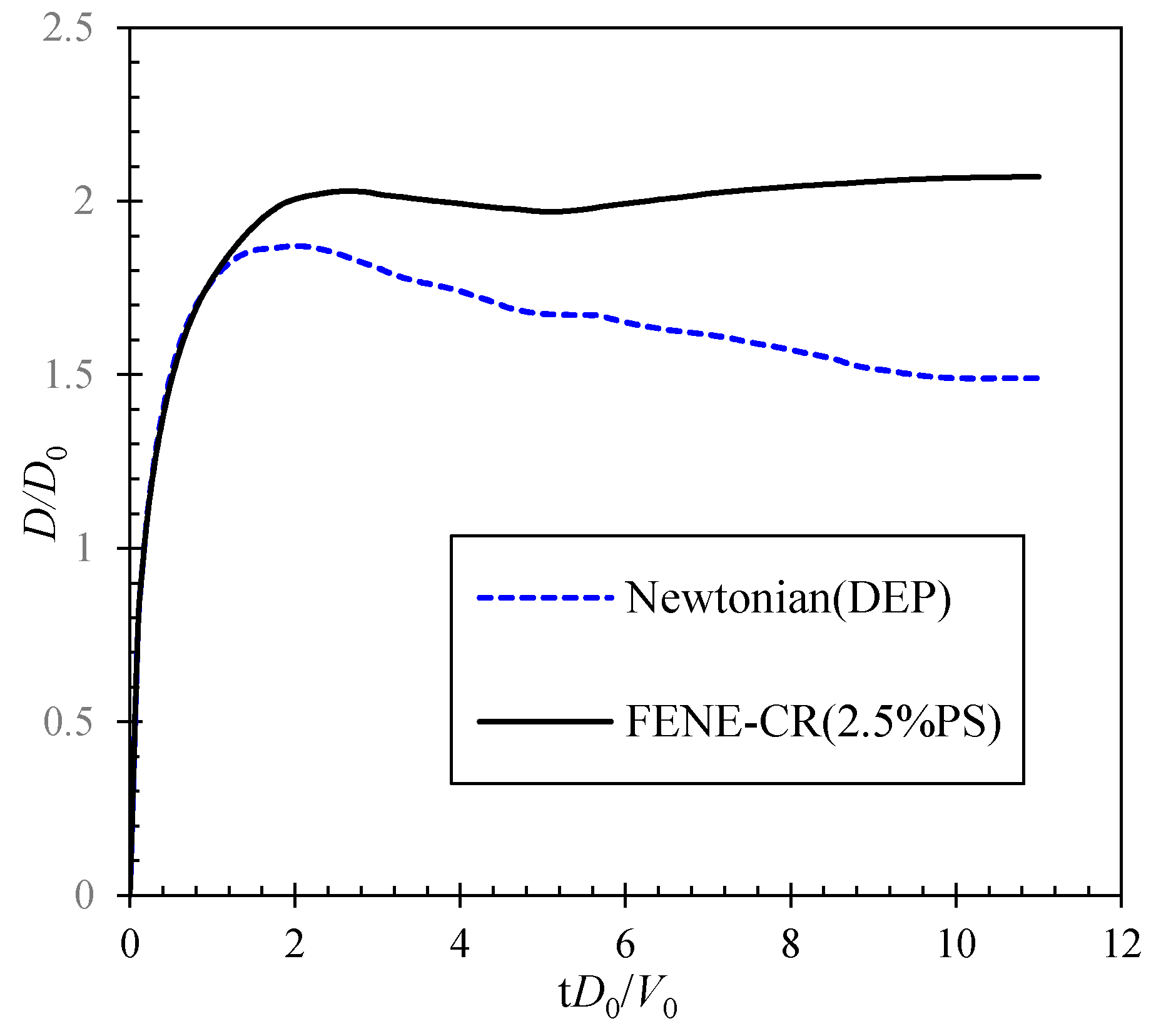
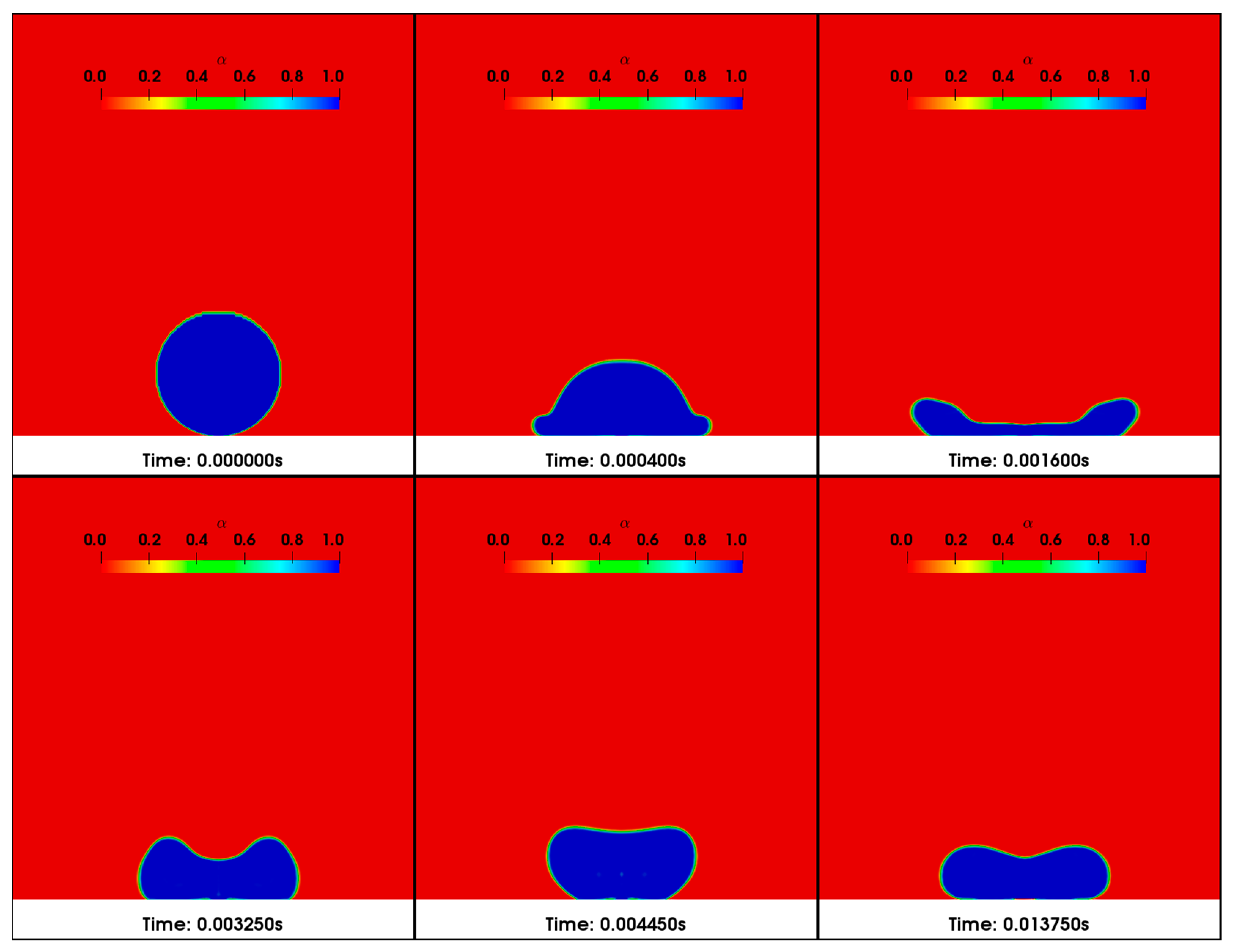
3.2. Impact of Polymer Solution Droplet
3.2.1. Hydrophilic Surface
3.2.2. Superhydrophobic Surface
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Mock, U.; Michel, T.; Tropea, C.; Roisman, I.; Rühe, J. Drop impact on chemically structured arrays. J. Phys. Condens. Matter 2005, 17, S595–S605. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Soucemarianadin, A.; Delattre, C.; Roux, D.C.D. Dynamic contact angle effects onto the maximum drop impact spreading on solid surfaces. Phys. Fluids 2009, 21, 122002. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys. Fluids 2012, 24, 102104. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.; Mackley, M.R.; Soucemarianadin, A. Towards an optimization of DOD printing of complex fluids. Int. Conf. Digit. Print. Technol. 2011, 2011, 86–92. [Google Scholar]
- Clemens, W.; Fix, W.; Ficker, J.; Knobloch, A.; Ullmann, A. From polymer transistors toward printed electronics. J. Mater. Res. 2004, 19, 1963–1973. [Google Scholar] [CrossRef]
- Xu, J.; Attinger, D. Drop on demand in a microfluidic chip. J. Micromech. Microeng. 2008, 18, 065020. [Google Scholar] [CrossRef]
- Ottnad, T.; Kagerer, M.; Irlinger, F.; Lueth, T.C. Modification and further development of a drop on demand printhead for wax enabling future 3D-printing and rapid prototyping. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 117–122. [Google Scholar]
- Joensson, H.N.; Andersson-Svahn, H. Droplet microfluidics—A tool for protein engineering and analysis. Lab Chip 2011, 11, 4144. [Google Scholar] [CrossRef]
- Tembely, M.; AlSumaiti, A.M.; Jouini, M.S.; Rahimov, K. The effect of heat transfer and polymer concentration on non-Newtonian fluid from pore-scale simulation of rock X-ray micro-CT. Polymers 2017, 9, 509. [Google Scholar] [CrossRef]
- Fukai, J.; Zhao, Z.; Poulikakos, D.; Megaridis, C.M.; Miyatake, O. Modeling of the deformation of a liquid droplet impinging upon a flat surface. Phys. Fluids A Fluid Dyn. 1993, 5, 2588–2599. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.J. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Shan, X.; Doolen, G. Multicomponent lattice-Boltzmann model with interparticle interaction. J. Stat. Phys. 1995, 81, 379–393. [Google Scholar] [CrossRef]
- Dalgamoni H., N. and Yong X. Axisymmetric lattice Boltzmann simulation of droplet impact on solid surfaces. Phys. Rev. E. 2018, 98, 013102. [Google Scholar] [CrossRef] [PubMed]
- Roisman, I.V.; Opfer, L.; Tropea, C.; Raessi, M.; Mostaghimi, J.; Chandra, S. Drop impact onto a dry surface: Role of the dynamic contact angle. Colloids Surf. A Physicochem. Eng. Asp. 2008, 322, 183–191. [Google Scholar] [CrossRef]
- Šikalo, Š.; Wilhelm, H.-D.; Roisman, I.V.; Jakirlić, S.; Tropea, C. Dynamic contact angle of spreading droplets: Experiments and simulations. Phys. Fluids 2005, 17, 062103. [Google Scholar] [CrossRef]
- Crochet, M.J.; Keunings, R. Finite element analysis of die swell of a highly elastic fluid. J. Nonnewton. Fluid Mech. 1982, 10, 339–356. [Google Scholar] [CrossRef]
- Morrison, N.F.; Harlen, O.G. Viscoelasticity in inkjet printing. Rheol. Acta 2010, 49, 619–632. [Google Scholar] [CrossRef]
- Tomé, M.F.; Paulo, G.S.; Pinho, F.T.; Alves, M.A. Numerical solution of the PTT constitutive equation for unsteady three-dimensional free surface flows. J. Nonnewton. Fluid Mech. 2010, 165, 247–262. [Google Scholar] [CrossRef]
- Fang, J.; Owens, R.G.; Tacher, L.; Parriaux, A. A numerical study of the SPH method for simulating transient viscoelastic free surface flows. J. Nonnewton. Fluid Mech. 2006, 139, 68–84. [Google Scholar] [CrossRef]
- Yu, J.-D.; Sakai, S.; Sethian, J.A. Two-phase viscoelastic jetting. J. Comput. Phys. 2007, 220, 568–585. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J. Phase-field simulations of dynamic wetting of viscoelastic fluids. J. Nonnewton. Fluid Mech. 2012, 189, 8–13. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.; MacKley, M.R.; Soucemarianadin, A. The matching of a “one-dimensional” numerical simulation and experiment results for low viscosity Newtonian and non-Newtonian fluids during fast filament stretching and subsequent break-up. J. Rheol. 2012, 56, 159–183. [Google Scholar] [CrossRef]
- Dong, H.; Carr, W.W.; Morris, J.F. An experimental study of drop-on-demand drop formation. Phys. Fluids 2006, 18, 072102. [Google Scholar] [CrossRef]
- Hoath, S.D.; Vadillo, D.C.; Harlen, O.G.; McIlroy, C.; Morrison, N.F.; Hsiao, W.-K.; Tuladhar, T.R.; Jung, S.; Martin, G.D.; Hutchings, I.M. Inkjet printing of weakly elastic polymer solutions. J. Nonnewton. Fluid Mech. 2014, 205, 1–10. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Tuladhar, T.R.; Mulji, A.C.; Jung, S.; Hoath, S.D.; Mackley, M.R. Evaluation of the inkjet fluid’s performance using the “Cambridge Trimaster” filament stretch and break-up device. J. Rheol. 2010, 54, 261–282. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Chilcott, M.D.; Rallison, J.M. Creeping flow of dilute polymer solutions past cylinders and spheres. J. Nonnewton. Fluid Mech. 1988, 29, 381–432. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Tembely, M.; Morrison, N.F.; Harlen, O.G.; MacKley, M.R.; Soucemarianadin, A. The matching of polymer solution fast filament stretching, relaxation, and break up experimental results with 1D and 2D numerical viscoelastic simulation. J. Rheol. 2012, 56, 1491–1516. [Google Scholar] [CrossRef]
- Mackley, M.R.; Butler, S.A.; Huxley, S.; Reis, N.M.; Barbosa, A.I.; Tembely, M. The observation and evaluation of extensional filament deformation and breakup profiles for Non Newtonian fluids using a high strain rate double piston apparatus. J. Nonnewton. Fluid Mech. 2017, 239, 13–27. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College of Science, Technology and Medicine, London, UK, 2002. [Google Scholar]
- Tembely, M.; Attarzadeh, R.; Dolatabadi, A. On the numerical modeling of supercooled micro-droplet impact and freezing on superhydrophobic surfaces. Int. J. Heat Mass Transf. 2018, 127, 193–202. [Google Scholar] [CrossRef]
- Kistler, S.F. Hydrodynamics of Wetting. In Wettability; Berg, J.C., Ed.; CRC Press: Boca Raton, FL USA, 1993. [Google Scholar]
- Yokoi, K.; Vadillo, D.; Hinch, J.; Hutchings, I. Numerical studies of the influence of the dynamic contact angle on a droplet impacting on a dry surface. Phys. Fluids 2009, 21, 072102. [Google Scholar] [CrossRef]
- Jadidi, M.; Tembely, M.; Moghtadernejad, S.; Dolatabadi, A. A coupled level set and volume of fluid method in openfoam with application to compressible two-phase flow. In Proceedings of the 22nd Annual Conference of the CFD Society of Canada, Toronto, ON, Canada, 1–4 June 2014. [Google Scholar]
- Graham, P.J.; Farhangi, M.M.; Dolatabadi, A. Dynamics of droplet coalescence in response to increasing hydrophobicity. Phys. Fluids 2012, 24, 112105. [Google Scholar] [CrossRef]
- Antonini, C.; Villa, F.; Bernagozzi, I.; Amirfazli, A.; Marengo, M. Drop Rebound after Impact: The Role of the Receding Contact Angle. Langmuir 2013, 29, 16045–16050. [Google Scholar] [CrossRef]
| Liquids | Interfacial Surface Tension (mN/m) | Viscosity (mPa.s) |
|---|---|---|
| DEP | 37 | 14 |
| DEP + 2.5% PS | 37 | 31 |
| Substrate | Equilibrium CA (°) | Advancing CA (°) |
|---|---|---|
| Hydrophilic (H) | 74 | 90 |
| Superhydrophobic (SH) | 154 | 162 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tembely, M.; Vadillo, D.; Soucemarianadin, A.; Dolatabadi, A. Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities. Processes 2019, 7, 798. https://doi.org/10.3390/pr7110798
Tembely M, Vadillo D, Soucemarianadin A, Dolatabadi A. Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities. Processes. 2019; 7(11):798. https://doi.org/10.3390/pr7110798
Chicago/Turabian StyleTembely, Moussa, Damien Vadillo, Arthur Soucemarianadin, and Ali Dolatabadi. 2019. "Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities" Processes 7, no. 11: 798. https://doi.org/10.3390/pr7110798
APA StyleTembely, M., Vadillo, D., Soucemarianadin, A., & Dolatabadi, A. (2019). Numerical Simulations of Polymer Solution Droplet Impact on Surfaces of Different Wettabilities. Processes, 7(11), 798. https://doi.org/10.3390/pr7110798





