Research on the Vertical Vibration Characteristics of Hydraulic Screw Down System of Rolling Mill under Nonlinear Friction
Abstract
:1. Introduction
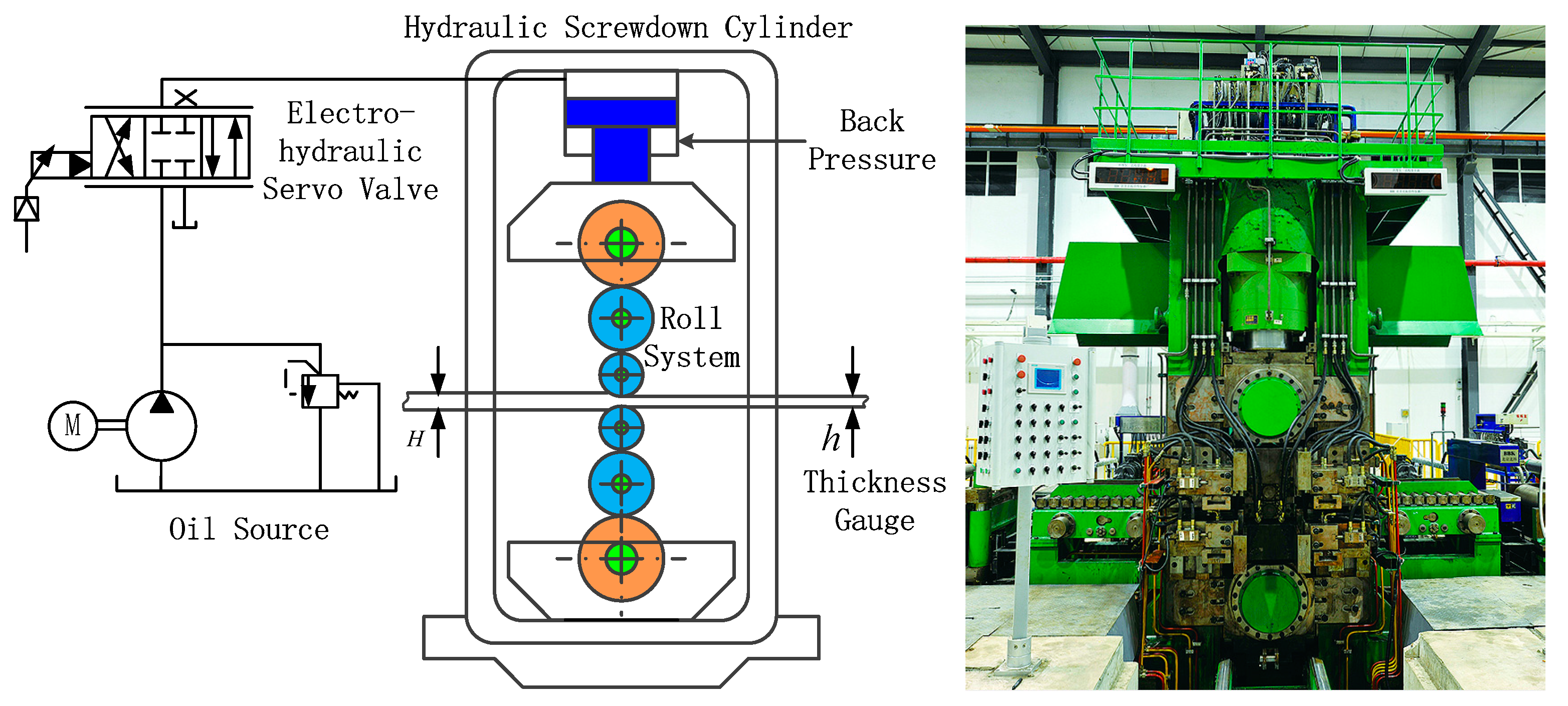
2. Principle of Hydraulic Screw Down System
3. Mathematical Model
3.1. Nonlinear Flow Equation of Four-Way Valve
- : port flow coefficient of four-way valve;
- : area grades of four-way valve;
- : spool displacement of four-way valve;
- : rod-less cavity pressure of hydraulic cylinder;
- : oil density.
3.2. Model of Servo Amplifier and Servo Valve
- : output of vibration controller;
- : gain of the servo amplifier;
- : output current of servo amplifier;
- : gain of servo valve.
3.3. Flow Equation of Hydraulic Cylinder
- : cross-sectional area of rod-less cavity of cylinder;
- : vibration displacement of cylinder piston rod;
- : leakage coefficient of hydraulic cylinder;
- : rod-less cavity volume of cylinder;
- : the initial stroke of the cylinder piston;
- : volume elastic modulus of oil.
3.4. Nonlinear Friction
- : average deformation of the sideburns;
- : stiffness coefficient of sideburns;
- : microscopic damping coefficient;
- : viscous damping coefficient;
- : coulomb force of friction;
- : maximum static friction force;
- : Stribeck speed.
- (1)
- When velocity , , the friction force is and is a constant. For the convenience of analysis, the constant is defined as , and .
- (2)
- When the velocity , can be expressed by Equation (6), and is continuously differentiable.
3.5. Balance Equation of Cylinder Piston Force
- : the effective area of rod cavity of cylinder;
- : equivalent total mass of piston and load;
- : viscous damping coefficient of piston;
- : spring stiffness of load;
- : nonlinear friction;
- : external force;
- : speed of hydraulic cylinder.
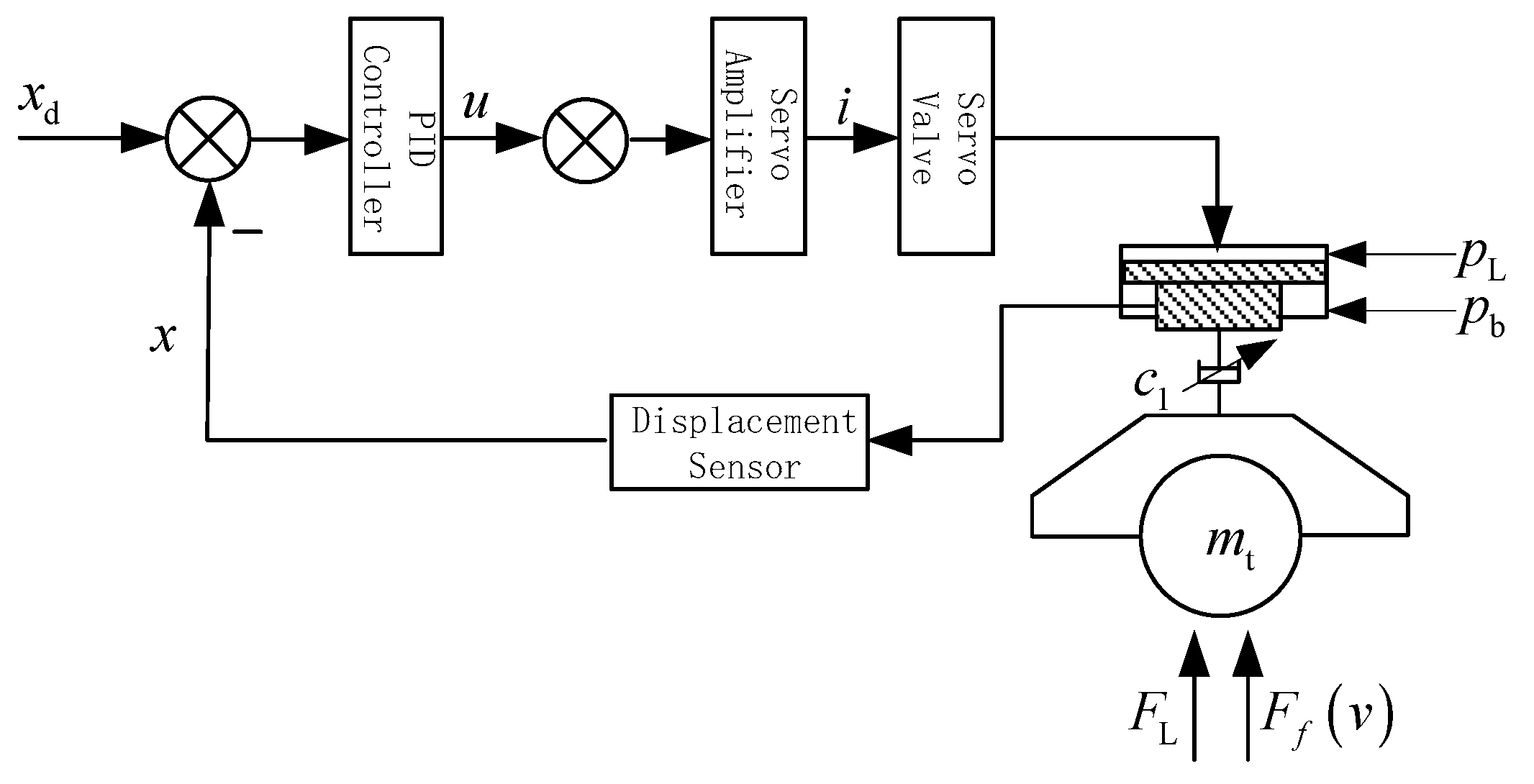
3.6. System State Equation
3.7. Vibration Controller
- : proportionality coefficient;
- : integral coefficient;
- : differential coefficient.
4. Numerical Simulation
4.1. The Parameters Selection of Simulation Model
4.2. Simulation Results and Analysis
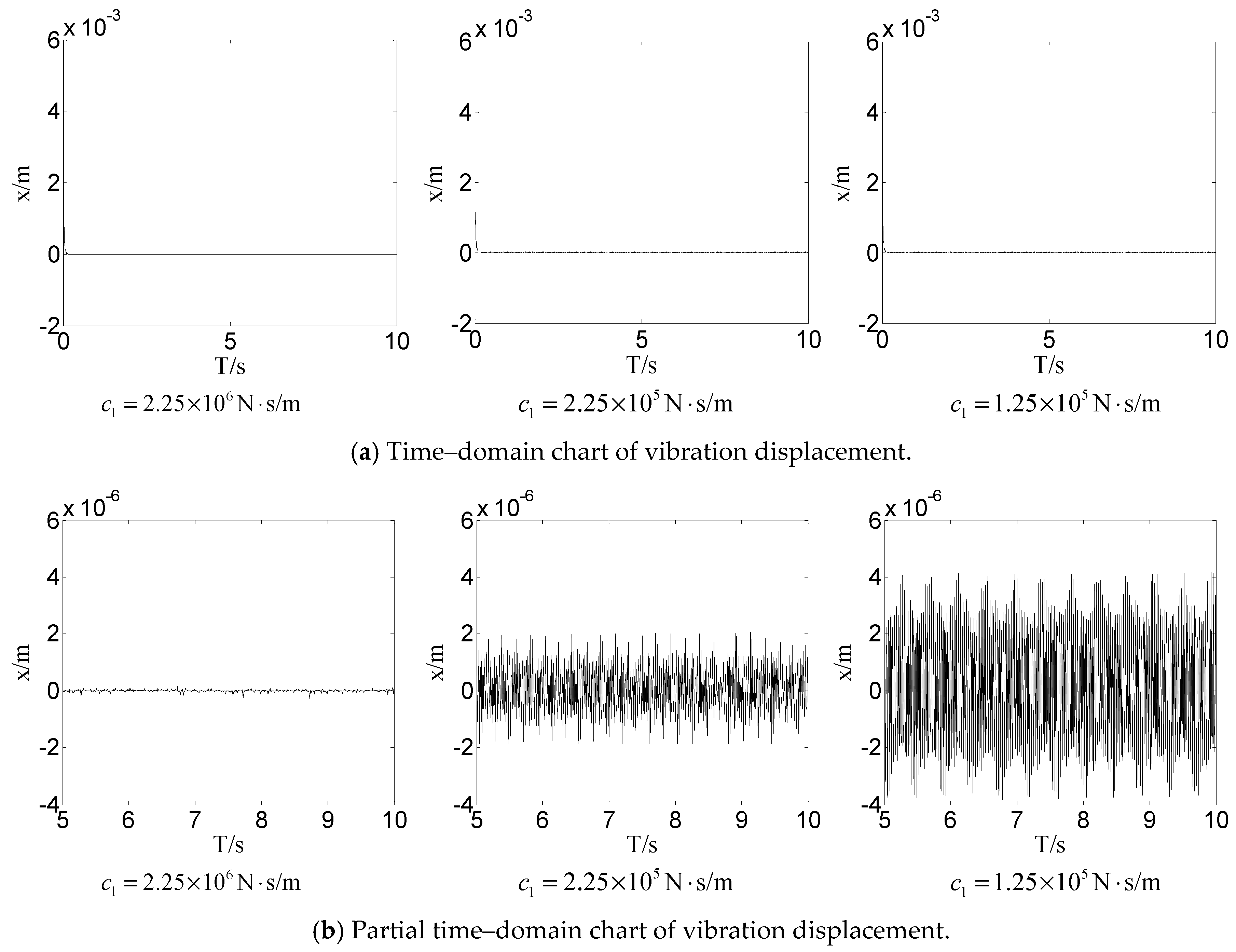
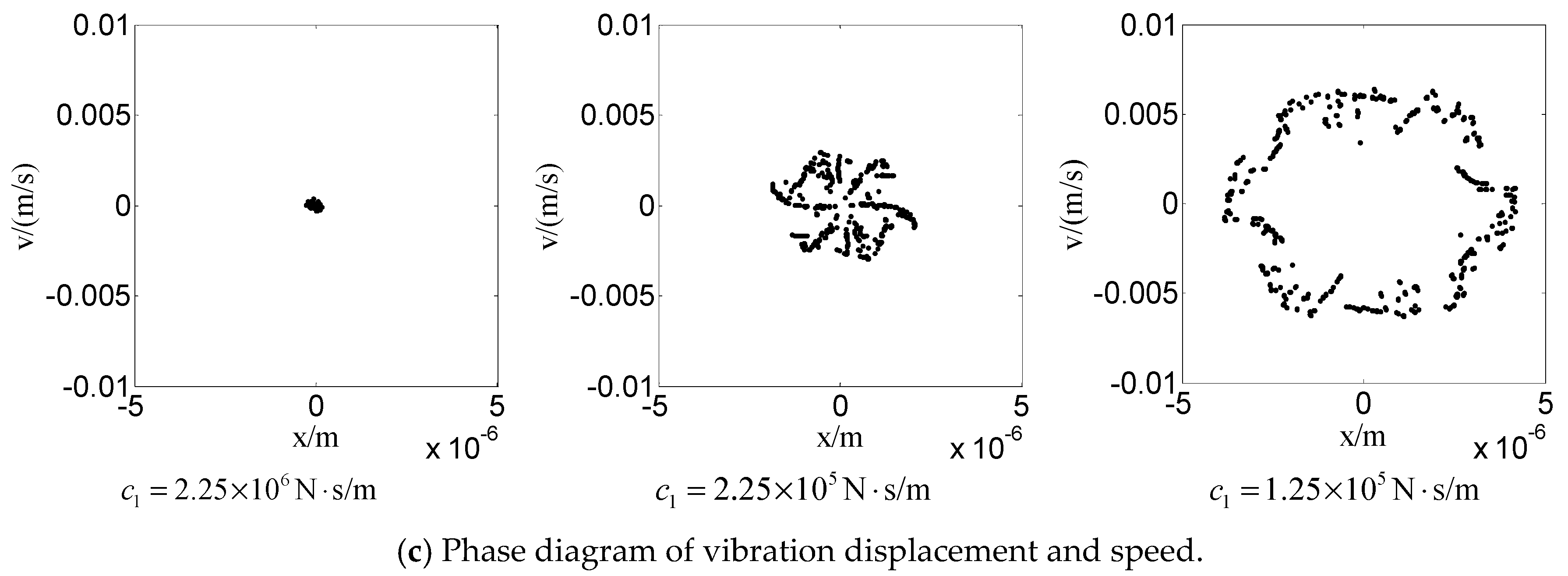
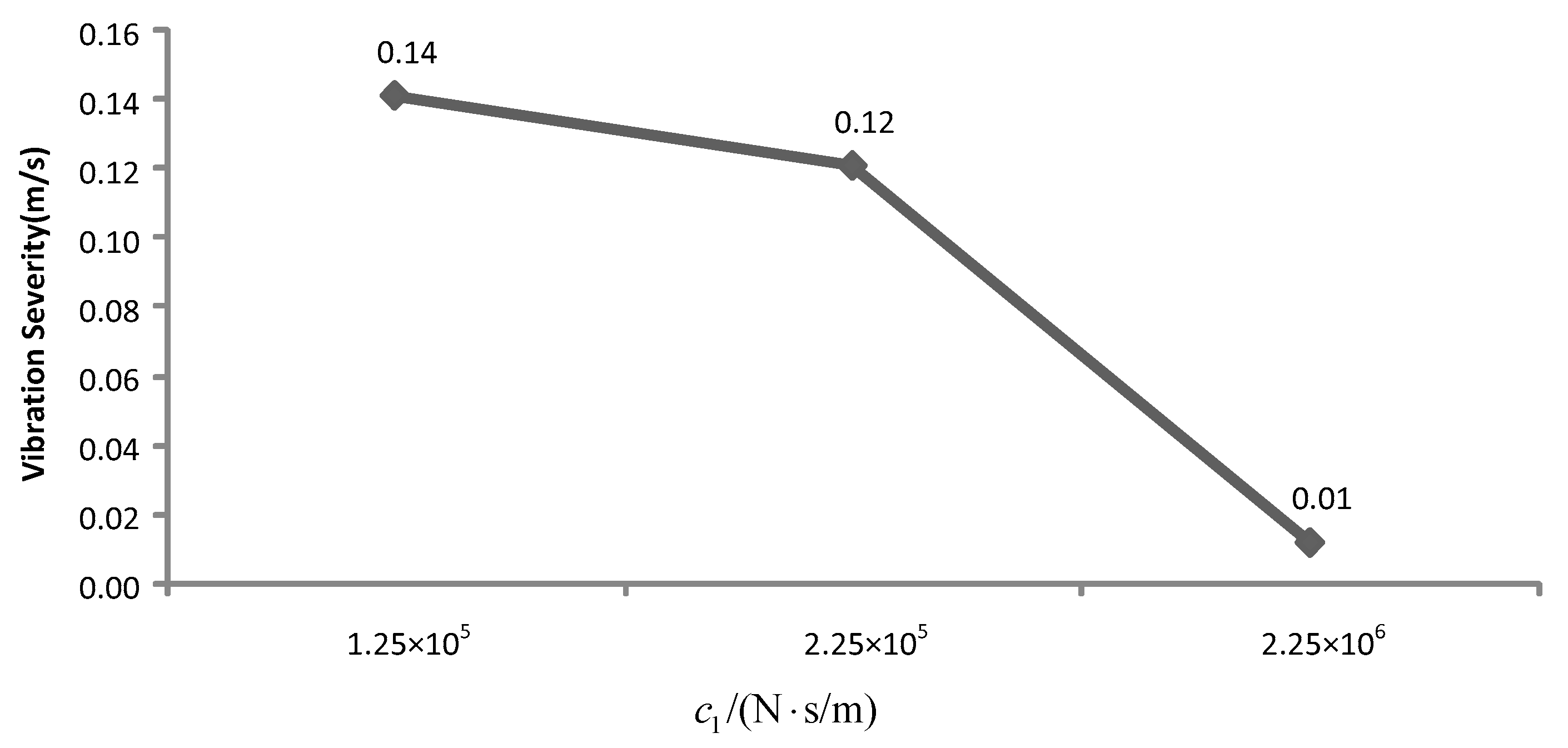
4.2.1. Influence of Different Equivalent Damping Coefficients on Nonlinear Dynamic Behavior
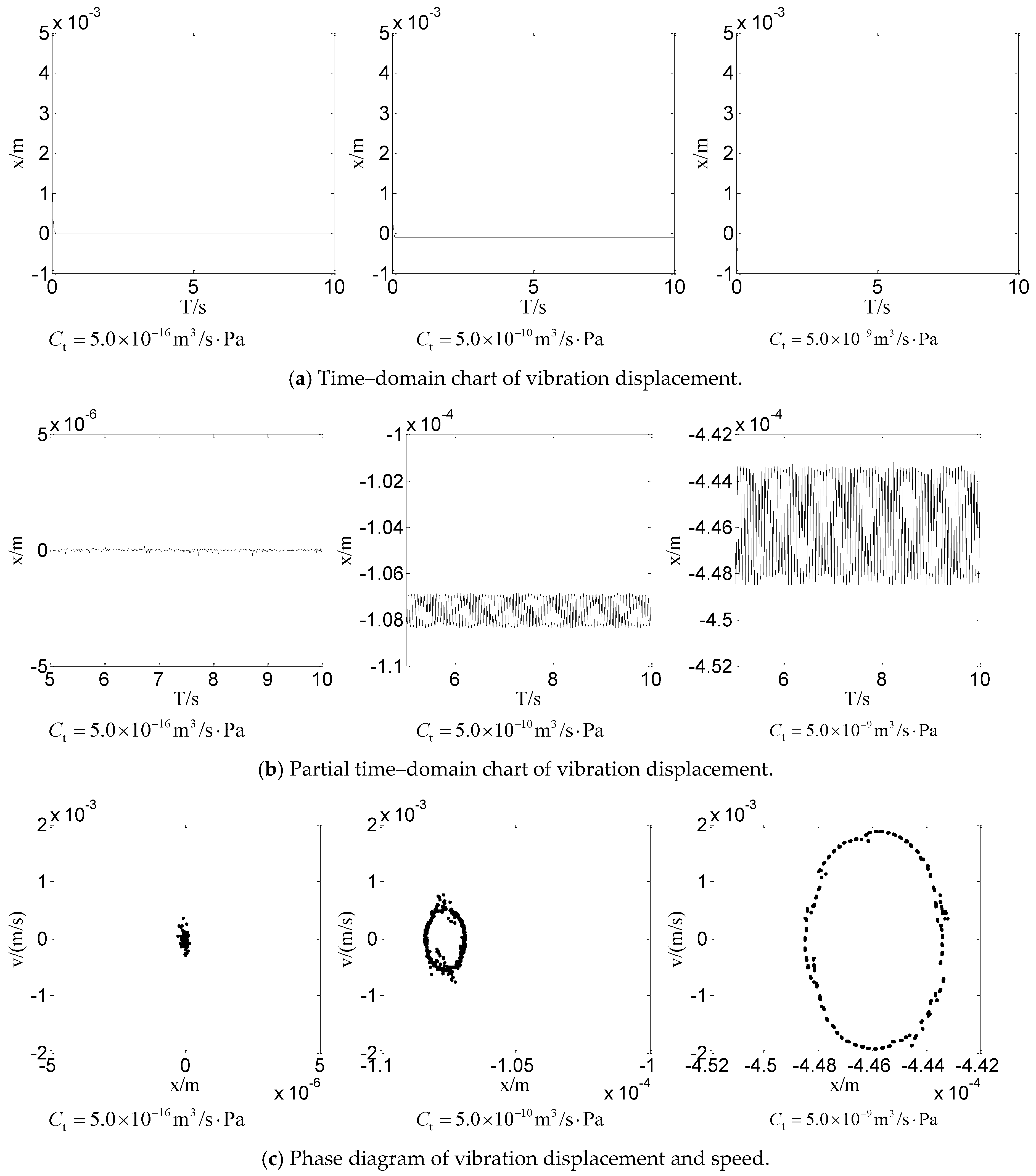
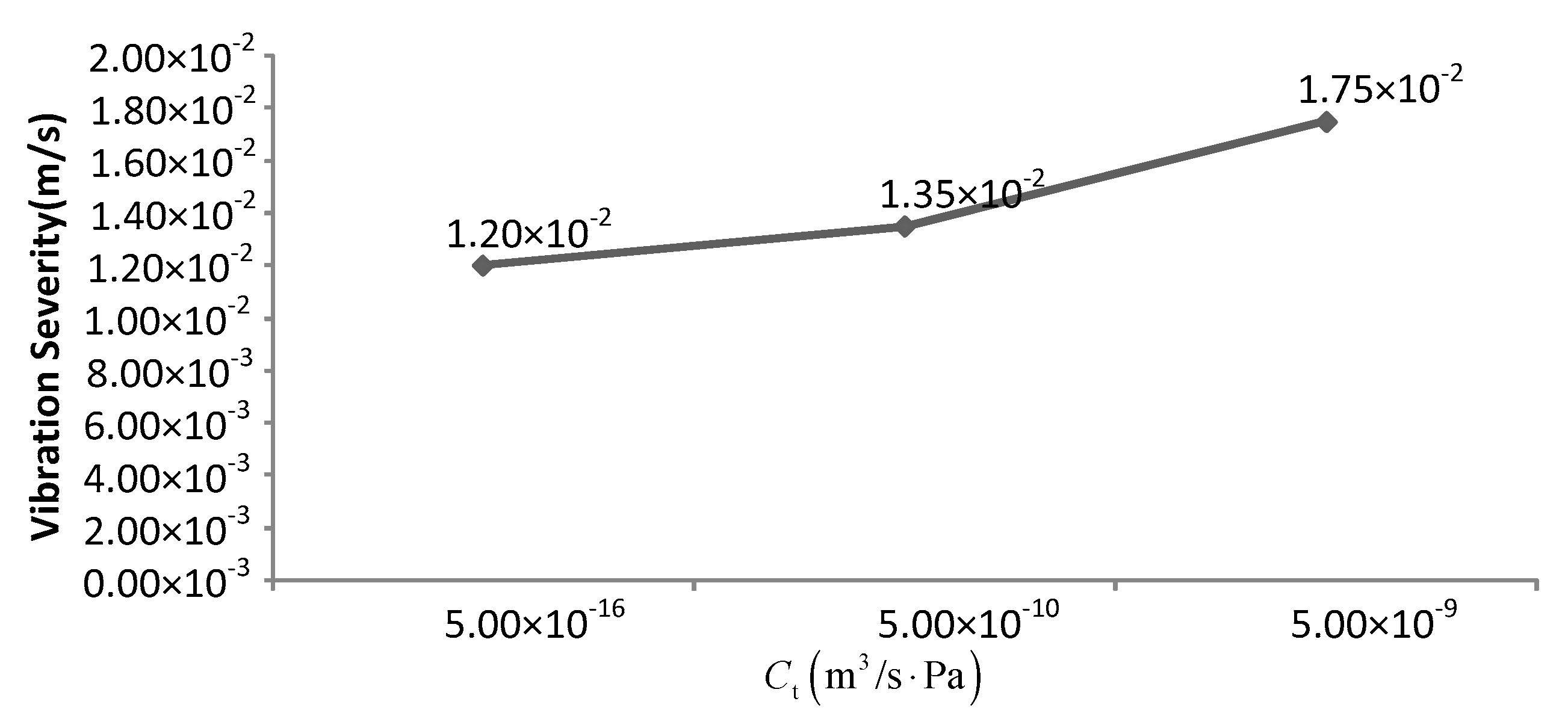
4.2.2. Influence of Different Leakage Coefficients on Nonlinear Dynamic Behavior
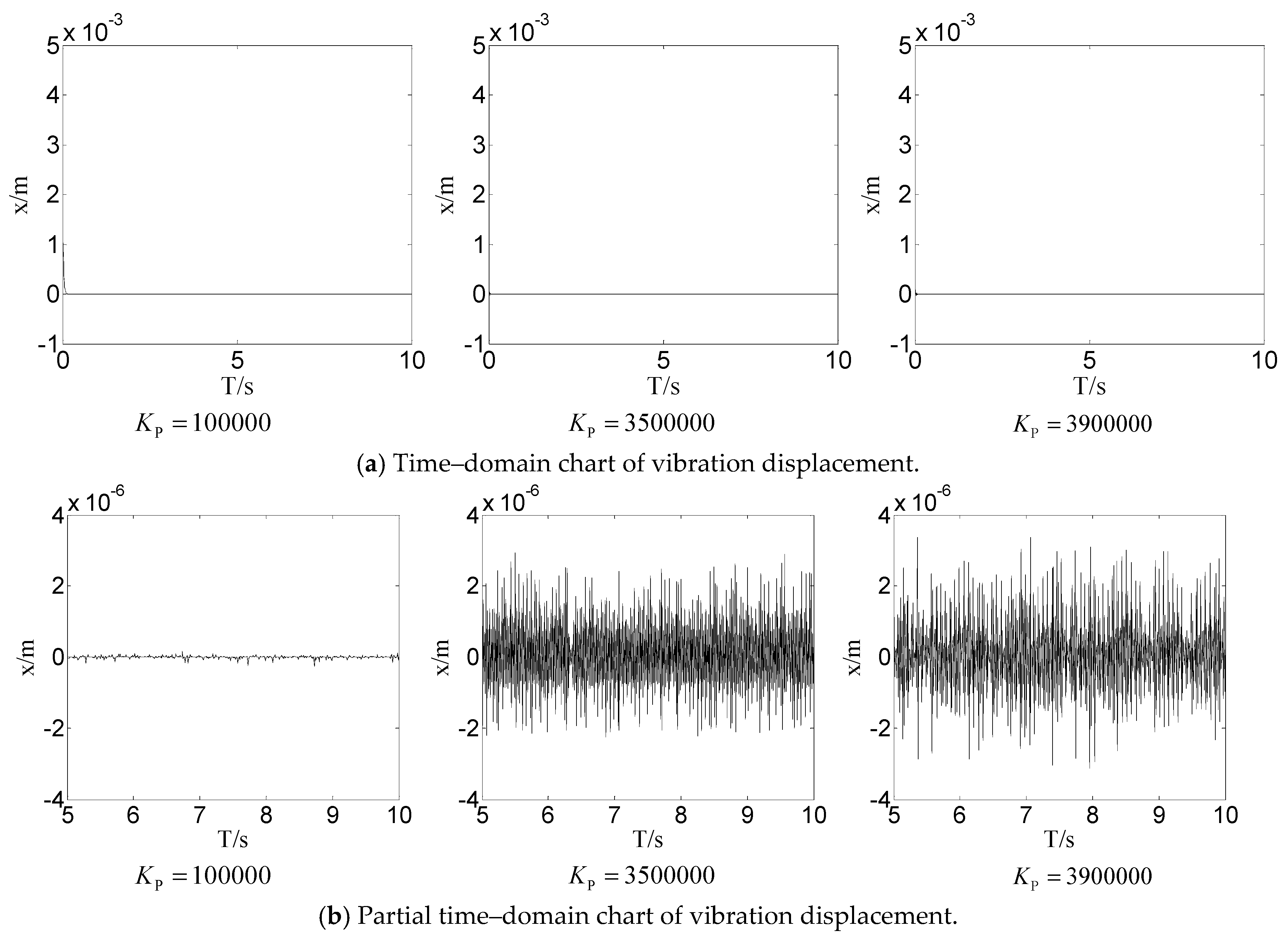
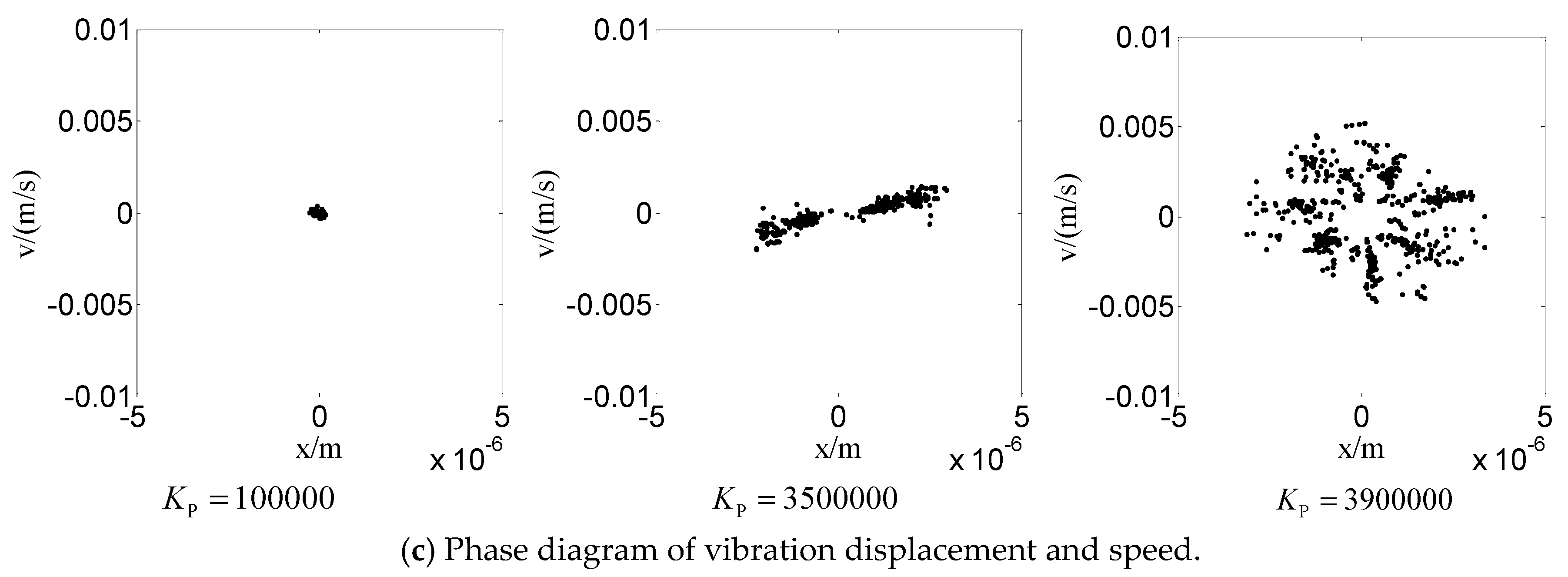
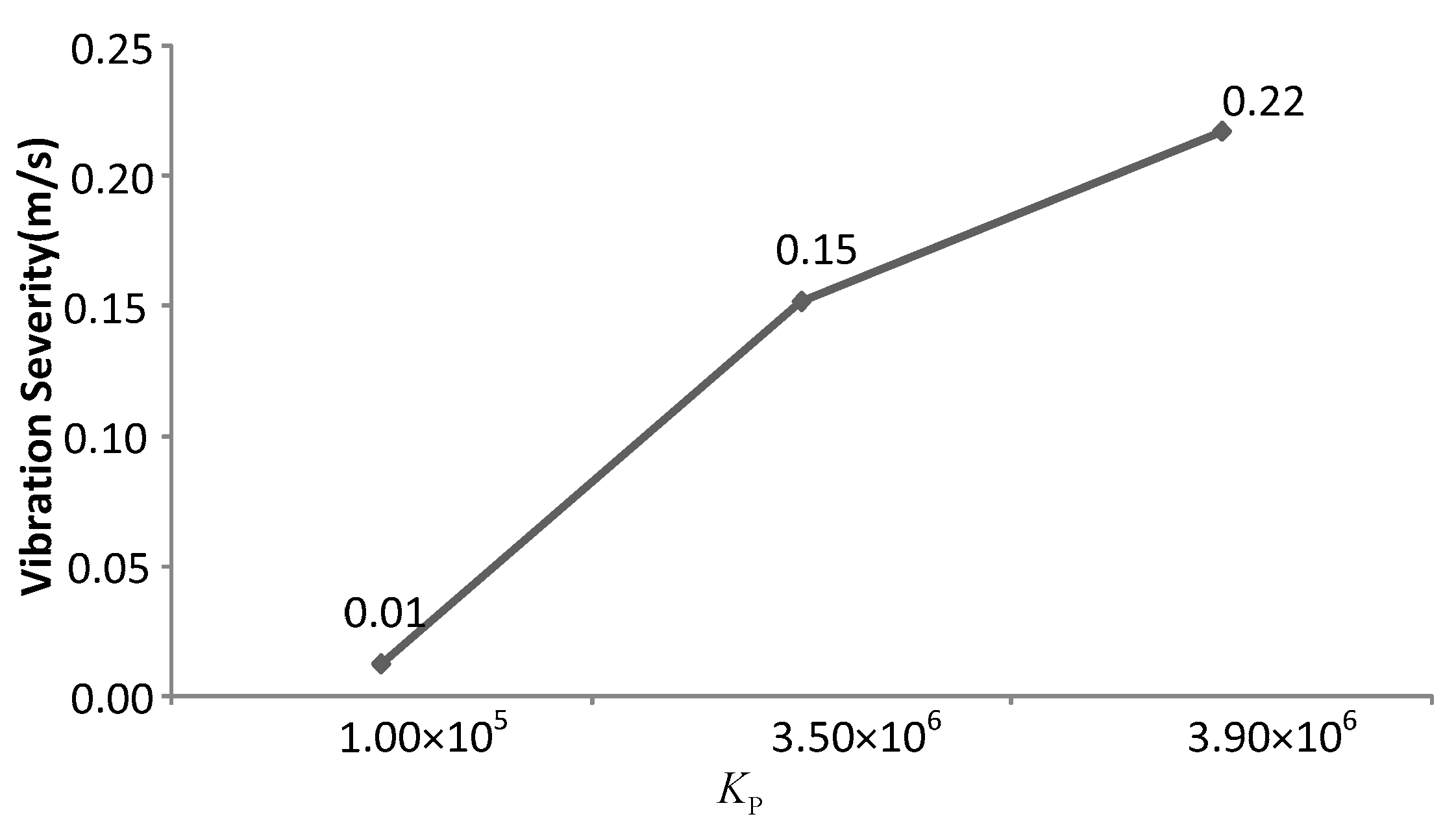
4.2.3. The Influences of Proportional Parameter of Vibration Controller on Nonlinear Dynamic Behavior
5. Conclusions
- (1)
- The friction force applied to the cylinder is nonlinear. The equivalent damping coefficient and internal leakage coefficient change with the working state and ambient temperature. The vibration model of the rolling mill is established by considering the influence of nonlinear friction and parameter uncertainty on the system characteristics.
- (2)
- When the vibration response of the hydraulic cylinder is analyzed by using a different damping coefficient, it is found that the vibration can be suppressed effectively by increasing the damping coefficient.
- (3)
- The hydraulic system will inevitably bring leakage problems with the aging of the sealing device. Through the analysis of the leakage coefficient, it is found that the vibration attenuation becomes slower and even periodic vibration appears with the increase of the leakage coefficient.
- (4)
- The controller is an effective mean to ensure accurate position control. Reasonable controller parameters can effectively suppress vibration, but fixed controller parameters will make negative effects on vibration suppression.
Author Contributions
Funding
Conflicts of Interest
References
- Prihod’ko, I.Y.; Krot, P.V.; Solov’yov, K.V.; Parsenyuk, E.A.; Chernov, P.P.; Pimenov, V.A.; Dolmatov, A.P.; Kharin, A.V. Vibration monitoring system and the new methods of chatter early diagnostics for tandem mill control. In Proceedings of the International Conference on Vibration in Rolling Mills, London, UK, 2006; pp. 87–106. [Google Scholar]
- Zhu, Y.; Tang, S.; Quan, L.; Jiang, W.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation characteristic research on the load vertical vibration of a hydraulic automatic gauge control system. Processes 2019, 7, 718. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute stability condition derivation for position closed-loop system in hydraulic automatic gauge control. Processes 2019, 7, 766. [Google Scholar]
- Yan, X.Q. Machinery-electric-hydraulic Coupling Vibration Control of Hot Continuous Rolling Mills. J. Mech. Eng. 2011, 47, 61–65. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.Q.; Gao, Y.J. Modeling and Simulation of Hydraulic Screw-down System in a Strip Mill. Chin. Hydraul. Pneum. 2004, 1, 21–24. [Google Scholar]
- Jiang, W.L.; Zhu, Y.; Zhang, Z.; Zhang, S. Nonlinear Vibration Mechanism of Electro-hydraulic Servo System and Its Experimental Verification. J. Mech. Eng. 2015, 51, 175–184. [Google Scholar] [CrossRef]
- Zhu, Y.; Qian, P.F.; Tang, S.G.; Jiang, W.L.; Li, W.; Zhao, J.H. Amplitude-frequency Characteristics Analysis for Vertical Vibration of Hydraulic AGC System under Nonlinear Action. AIP Adv. 2019, 9, 035019. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018, 139, 1–7. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B.; Zhu, S.Q. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Proccess. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W.D. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- He, X.; Jiao, W.; Wang, C.; Cao, W. Influence of surface roughness on the pump performance based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Qian, J.Y.; Gao, Z.X.; Liu, B.Z.; Jin, Z.J. Parametric study on fluid dynamics of pilot-control angle globe valve. ASME J. Fluids Eng. 2018, 114, 111103. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ.-Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Xuan, B.T.; Nur, H.; Hideki, Y. Modeling of dynamic friction behaviors of hydraulic cylinders. Mechatronics 2012, 22, 65–75. [Google Scholar]
- Yanada, H.; Khaing, W.; Endo, H.; Tran, X. Effect of friction model on simulation of hydraulic actuator. Proccess. J. Syst. Control Eng. 2014, 228, 690–698. [Google Scholar]
- Liu, B.; Li, P.; Liu, F.; Liu, H.; Jiang, J. Chaotic Prediction Control of Hydraulic Cylinder Nonlinear Stiffness Constrain System. China Mech. Eng. 2017, 28, 559–564. [Google Scholar]
- Yang, X.; Tong, C.N.; Yue, G.F.; Meng, J.J. Dynamic model of chatter for cold rolling. J. Iron Steel Res. Int. 2010, 17, 30–34. [Google Scholar] [CrossRef]
- Yang, X.; Tong, C.N. Coupling dynamic model and control of chatter in cold rolling. J. Dyn. Syst. Meas. Control 2012, 4, 0141001. [Google Scholar] [CrossRef]
- Bar, A.; Bar, O. Types of mid-frequency vibrations appearing during the rolling mill operation. J. Mater. Proccess. Technol. 2005, 162, 461–464. [Google Scholar] [CrossRef]
- Alborz, N.; Farhang, K. Vibration instability in a large motion bistable compliant mechanism due to stribeck friction. J. Vib. Acoust. 2018, 140, 061017. [Google Scholar]
- Ibrahim, R.A. Friction-induced vibration, chatter, squeal, and chaos-part II: Dynamics and modeling. Appl. Mech. Rev. 1994, 47, 227–253. [Google Scholar] [CrossRef]
- Leine, R.I.; Vancampen, D.H.; Kraker, A.D.E. Strick-slip vibrations induced by alternate friction models. Nonlinear Dyn. 1998, 16, 41–54. [Google Scholar] [CrossRef]
- Zhao, W.W.; Qiu, S.X.; Feng, C.Z. Study on the stick-slip phenomenon of hydraulic cylinder based on the LuGre friction model. Des. Res. 2017, 12, 88–92. [Google Scholar]
- Zhu, Y.; Jiang, W.L.; Hu, H.S.; Kang, H.Z. A Precise Frequency-domain Integral Method of Vibration Acceleration Signal. ICIC Control Express Lett. 2015, 9, 1617–1624. [Google Scholar]
- Zhu, Y.; Jiang, W.L.; Kong, X.D.; Zheng, Z.; Hu, H.S. An Accurate Integral Method for Vibration Signal Based on Feature Information Extraction. Shock Vib. 2015, 2015, 962793. [Google Scholar] [CrossRef]
- Khan, H.; Seraphin, C.A.; Sepehri, N. Nolinear observer-based fault detection technique for electro-hydraulic servo-positioning systems. Mechatronics 2005, 15, 1040–1041. [Google Scholar] [CrossRef]
- Liu, J.X.; Qiao, B.J.; Zhang, X.W. Adaptive vibration control on electrohydraulic shaking table system with an expanded frequency range: Theory analysis and experimental study. Mech. Syst. Signal Process. 2019, 132, 125. [Google Scholar] [CrossRef]
- Su, X. Modeling method and control performance of hydraulic AGC system. QinHuangdao 2018, 11, 37–43. [Google Scholar]
- Guan, C.; Pan, S.X. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters. Control Eng. Pract. 2008, 16, 1276. [Google Scholar] [CrossRef]

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| fs |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiang, W.; Zhu, Y.; Li, Z. Research on the Vertical Vibration Characteristics of Hydraulic Screw Down System of Rolling Mill under Nonlinear Friction. Processes 2019, 7, 792. https://doi.org/10.3390/pr7110792
Zhang Y, Jiang W, Zhu Y, Li Z. Research on the Vertical Vibration Characteristics of Hydraulic Screw Down System of Rolling Mill under Nonlinear Friction. Processes. 2019; 7(11):792. https://doi.org/10.3390/pr7110792
Chicago/Turabian StyleZhang, Yongshun, Wanlu Jiang, Yong Zhu, and Zhenbao Li. 2019. "Research on the Vertical Vibration Characteristics of Hydraulic Screw Down System of Rolling Mill under Nonlinear Friction" Processes 7, no. 11: 792. https://doi.org/10.3390/pr7110792
APA StyleZhang, Y., Jiang, W., Zhu, Y., & Li, Z. (2019). Research on the Vertical Vibration Characteristics of Hydraulic Screw Down System of Rolling Mill under Nonlinear Friction. Processes, 7(11), 792. https://doi.org/10.3390/pr7110792






