Stagnation Point Flow with Time-Dependent Bionanofluid Past a Sheet: Richardson Extrapolation Technique

Abstract

The study of laminar flow of heat and mass transfer over a moving surface in bionanofluid is of considerable interest because of its importance for industrial and technological processes such as fabrication of bio-nano materials and thermally enhanced media for bio-inspired fuel cells. Hence, the present work deals with the unsteady bionanofluid flow, heat and mass transfer past an impermeable stretching/shrinking sheet. The appropriate similarity solutions transform the boundary layer equations with three independent variables to a system of ordinary differential equations with one independent variable. The finite difference coupled with the Richardson extrapolation technique in the Maple software solves the reduced system, numerically. The rate of heat transfer is found to be higher when the flow is decelerated past a stretching sheet. It is understood that the state of shrinking sheet limits the rate of heat transfer and the density of the motile microorganisms in the stagnation region.

0. Highlights

• Validation of the general model has been achieved with the finite-difference coupled with the Richardson extrapolation and the shooting method in the Maple software.
• The far-field boundary conditions were chosen with the appropriate finite value to ensure that the numerical solution ideally approaches the asymptotic values.
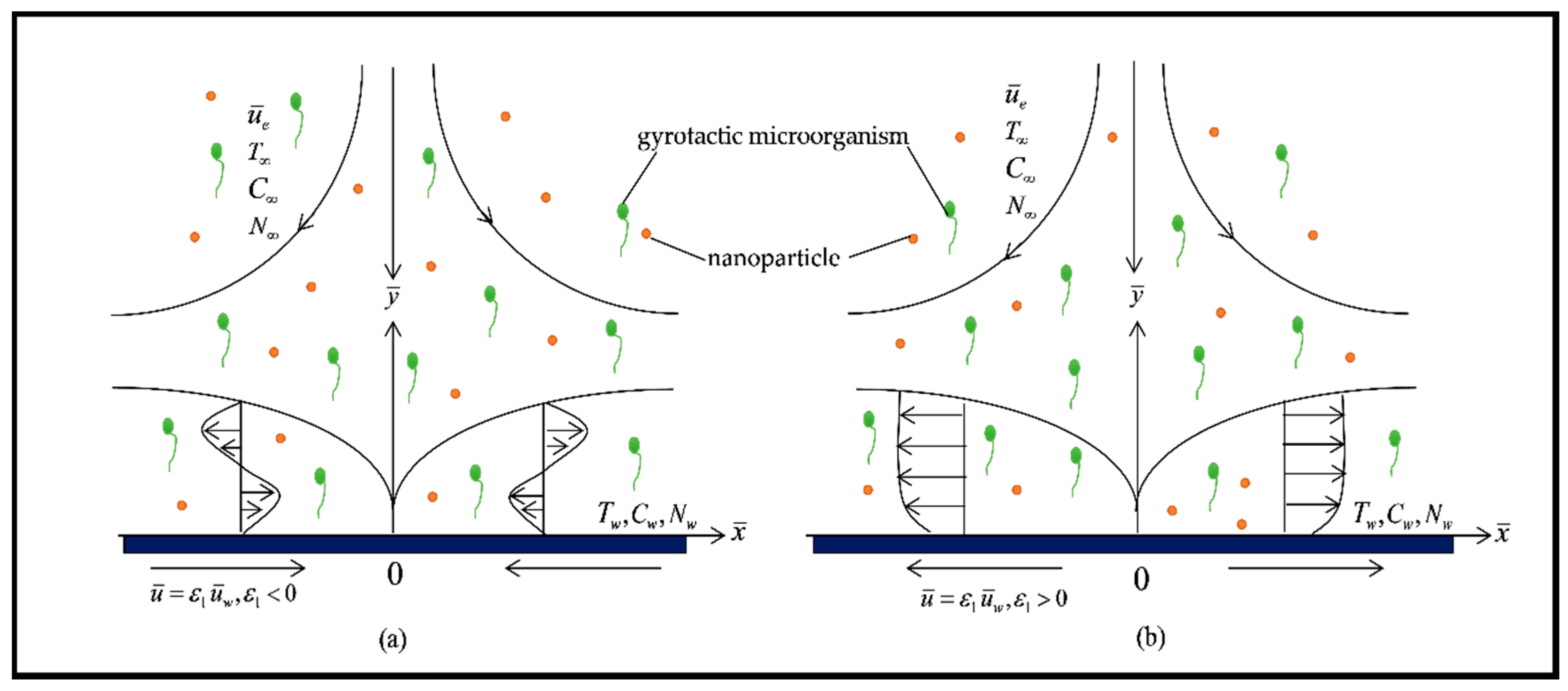
• The state of shrinking sheet limits the rate of heat transfer and the density of the motile microorganisms in the stagnation region.

1. Introduction

Nanofluid is a well-known smart fluid which has been found to be very useful in uplifting people’s lifestyle. This smart fluid is dilute liquid-suspended nanoparticles, where at least one of their primary measurements is smaller than 10 nm [1]. Nanofluid, as an advanced type of fluids, has been synthesized by dispersing nanoscale particles in conventional base fluids such as water, ethylene glycol, and oil [2]. Recent literature is densely occupied with the investigations of the fluid flow and heat transfer in the nanofluids due to their diverse applications in industry and engineering, compared to investigations about macro-sized materials [3,4]. Nanofluid detergent, nanofluid coolant, nano cryosurgery, and usage of nanofluid for industrial cooling are some of the remarkable applications involving nanofluid [1]. Nanofluid was proposed initially by Choi and Eastman [2] who proved that it has better heat transfer features compared to the conventional base fluids. The work of Buongiorno [5] molded the idea of nanofluid into a mathematical model that focuses on two main slip mechanisms (Brownian diffusion and thermophoresis), later known as the Buongiorno model, which became one of the benchmark models in the theoretical work of the boundary layer flow in a nanofluid. Moreover, the series of paper by Mahian et al. [6,7] provided a critical review on fundamentals, theory and applications of the mathematical modelling and simulations of nanofluid flows, and hence established a strong foundation in the theoretical works on nanofluids [8,9,10,11,12,13].

The industrial applications such as melt-spinning, wire-drawing, and production of plastic and rubber sheets provoked researchers to investigate the fluid flow and heat transfer past a moving surface. Sakiadis [14,15] formulated the problem of laminar and turbulent boundary layer flow along with a non-stop moving of the flat plate, which can be found in the continuous polymer sheet extrusion from a die. Then, Crane [16] extended the work of Sakiadis [14,15] by setting the sheet velocity to increase proportionally with the distance from a fixed source of flow and presented the closed form of two-dimensional Navier–Stokes equation’s analytic solution. Carragher and Crane [17] improved the work of Crane [16] by considering heat transfer property along with a continuous stretching sheet. Those works have been the mainstay for many numerical investigations which undergo various modifications in the scope of the boundary layer (see [18,19,20]). On the other hand, the fluid flow and heat transfer past a shrinking surface also received much attention from the researchers as they have various significant industrial applications [21,22,23,24,25,26,27]. The paper by Muhaimin et al. [28] acknowledged the shrinking surface applications such as shrinking transistors, non-radiated heat-shrinkable polyvinyl chloride (PVC) tubes and shrinking film. The numerical study of Davey [29] on the boundary layer flow past a shrinking surface which revealed the presence of dual solutions had initiated the development of the fluid flow and heat transfer past a shrinking surface. Goldstein [30] also focused on the backward boundary layer flow in a narrowing channel and discovered that the shrinking fluid flow postulates different physical behavior than the fluid flow caused by the stretching sheet.

Envision the behavior of the microorganisms which are slightly denser than water swimming upward. When more microorganisms accumulate at the upper region, that area becomes denser until at one point the suspensions turn out to be unbalanced. Consequently, the microorganisms tumble and form a bioconvection. In the experimental approach, two usual types of upswimming microorganisms: bottom-heavy alga (Chlamydomonas nivalis) and common soil bacterium Bacillus subtilis, are considered [31]. Different types of microorganisms own the subjective orientation of the mechanism [32]. For the theoretical study, the conventional mathematical model instituted bottom-heavy alga and oxytactic bacteria. The development of theoretical work in the field of bioconvection can be found in the following literature: [33,34,35,36,37,38,39,40,41,42,43,44,45]. Kuznetsov [46] commenced the problem of bioconvection boundary layer flow along a horizontal surface in a nanofluid containing a gyrotactic microorganism and presented the perturbation solutions. After that, Zaimi et al. [47] extended the work of Kuznetsov [46] by considering a stagnation-point bioconvection flow past a permeable stretching/shrinking surface in a nanofluid. Zaimi et al. [47] which had solved the problem numerically by using the shooting method in the Maple software and had presented dual solutions concluded that the influence of suction is essential to maintain a laminar boundary layer flow. The present paper aimed to broaden the research work of Zaimi et al. [47] by examining an unsteady stagnation-point flow past an impermeable stretching/shrinking sheet in a nanofluid containing gyrotactic microorganisms. The numerical solutions are produced via the Richardson extrapolation technique, and the effects of variations of the governing parameters on the physical quantities have been presented graphically and discussed in detail.

2. Mathematical Formulation

The present theoretical model considers an unsteady two-dimensional boundary layer flow and heat transfer at the stagnation region induced by a moving (stretching/shrinking) surface in a water-based nanofluid. Bionanofluid comprises of nanoparticles and motile gyrotactic microorganisms and allows the bioconvection process. In this investigation, water was chosen as the working fluid to keep the gyrotactic microorganisms alive, while the presence of the nanoparticles does not affect the gravitactic microorganisms’ swimming route and velocity. The nanosized (1–100 nm) metal nanoparticles which are made from metal precursors such as copper are considered in this investigation. Theoretically, the concentration of the nanoparticles is assumed to be ≤ 1% [5]. The physical configuration of the problem is shown in Figure 1.

The Cartesian coordinate frame is taken, where the $\overline{x}-$ direction remains along the stretching/shrinking surface, and the $\overline{y}-$ direction stands perpendicular to the surface. It is presumed that the sheet is stretching/shrinking with a velocity ${\overline{u}}_w={\epsilon }_{1}a\overline{x}{\left(1-A_1\overline{t}\right)}^{-1},$ in which $a$ is a positive constant with dimension $\left(s^{-1}\right)$, ${\epsilon }_1>0$ shows the stretching sheet, ${\epsilon }_1<0$ indicates the shrinking sheet while ${\epsilon }_1=0$ represents a stationary sheet. The ambient velocity is given as ${\overline{u}}_w=a\overline{x}{\left(1-A_1\overline{t}\right)}^{-1}$. In addition, the temperature, nanoparticle concentration and the density of microorganisms far away from the surface of the sheet are denoted as $T_{\infty },C_{\infty }$ and $N_{\infty },$ respectively. The temperature, nanoparticle concentration and the density of microorganisms at the wall of the moving surface are symbolized as $T_w,C_w$ and $N_w,$ respectively. It is assumed that $T_w>T_{\infty },C_w>C_{\infty },N_w>N_{\infty }$ and boundary conditions are applied to the surface of the sheet, with no-slip conditions. The thin moving sheet acts to heat the infinite body of fluid and retains a constant temperature throughout the process. The heating is adequately weak thus preserving the living gyrotactic microorganisms within the stagnation area. Based on these assumptions, the governing boundary layer equations can be given as follows [47]:

$$\frac{\partial \overline{u}}{\partial \overline{x}}+\frac{\partial \overline{v}}{\partial \overline{y}}=0,$$

(1)

$$\frac{\partial \overline{u}}{\partial \overline{t}}+\overline{u}\frac{\partial \overline{u}}{\partial \overline{x}}+\overline{v}\frac{\partial \overline{u}}{\partial \overline{y}}={\overline{u}}_e\frac{\partial {\overline{u}}_e}{\partial \overline{x}}+\frac{\partial {\overline{u}}_e}{\partial \overline{t}}+\upsilon \left(\frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}\right),$$

(2)

$$\frac{\partial T}{\partial \overline{t}}+\overline{u}\frac{\partial T}{\partial \overline{x}}+\overline{v}\frac{\partial T}{\partial \overline{y}}=\alpha \frac{{\partial }^{2}T}{\partial {\overline{y}}^2}+{\tau }_1\left[D_B\left(\frac{\partial T}{\partial \overline{y}}\frac{\partial C}{\partial \overline{y}}\right)+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial \overline{y}}\right)}^2\right],$$

(3)

$$\frac{\partial C}{\partial \overline{t}}+\overline{u}\frac{\partial C}{\partial \overline{x}}+\overline{v}\frac{\partial C}{\partial \overline{y}}=D_B\left(\frac{{\partial }^{2}C}{\partial {\overline{y}}^2}\right)+\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^{2}T}{\partial {\overline{y}}^2}\right),$$

(4)

$$\frac{\partial N}{\partial \overline{t}}+\overline{u}\frac{\partial N}{\partial \overline{x}}+\overline{v}\frac{\partial N}{\partial \overline{y}}+\frac{\tilde{b}{W}_c}{C_w-C_{\infty }}\left[\frac{\partial }{\partial \overline{y}}\left(N\frac{\partial C}{\partial \overline{y}}\right)\right]=D_n\left(\frac{{\partial }^{2}N}{\partial {\overline{y}}^2}\right).$$

(5)

Hence, the relevant boundary conditions are represented by

$$\begin{array}{lll}t\le 0:& \overline{v}=0,\hspace{1em}\overline{u}=0,\hspace{1em}T=T_{\infty },\hspace{1em}C=C_{\infty },\hspace{1em}N=N_{\infty }.& \\ t>0:& \overline{u}={\epsilon }_1{\overline{u}}_w\left(x,t\right)={\epsilon }_{1}a\overline{x}{\left(1-A_1\overline{t}\right)}^{-1}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}{A}_1\overline{t}\ne 1,\hspace{1em}\hspace{0.17em}\overline{v}=0,\hspace{1em}\hspace{0.17em}T=T_w,& \\ & C=\hspace{0.17em}{C}_w\hspace{0.17em},\hspace{0.17em}\hspace{1em}\hspace{0.17em}N=\hspace{0.17em}{N}_w& \mathrm{at}\overline{y}=0,\\ & \overline{u}={\overline{u}}_e\left(x,t\right)=a\overline{x}{\left(1-A_1\overline{t}\right)}^{-1}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}{A}_1\overline{t}\ne 1,\hspace{0.17em}\hspace{1em}\hspace{0.17em}T=T_{\infty }\hspace{0.17em},& \\ & C=C_{\infty },\hspace{1em}\hspace{0.17em}N=N_{\infty }& \mathrm{as} \overline{y}\to \infty ,\end{array}$$

(6)

where $\overline{u}$ and $\overline{v}$ are the velocity components along the $\overline{x}-$ and $\overline{y}-$ axes, respectively, $\overline{t}$ is time, $\upsilon$ is the kinematic viscosity, $T$ is the temperature, $\alpha$ is the thermal diffusivity of the nanofluid, $C$ is the nanoparticle volume fraction, ${\tau }_1={\left(\rho c\right)}_p/{\left(\rho c\right)}_f$ is the ratio between the heat capacity of the nanoparticle ${\left(\rho c\right)}_p$ and the heat capacity of the base fluid ${\left(\rho c\right)}_f$, $D_B$ is the Brownian diffusion coefficient, $D_T$ is the thermophoretic diffusion coefficient, $N$ is the number density of motile microorganisms, $D_n$ is the diffusivity of microorganism, $\tilde{b}$ is the chemotaxis constant, $W_c$ is the maximum cell swimming speed relative to the nanofluid and $A_1$ is a constant with dimension (time)⁻¹ which denotes the unsteadiness of the problem.

3. Similarity Differential Equations

Revised from Ali and Zaib [48], we adopt the following similarity transformations:

$$\begin{array}{l}\eta ={\left(\frac{a}{\upsilon (1-A_1\overline{t})}\right)}^{1/2}\overline{y},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi ={\left(\frac{a\upsilon }{1-A_1\overline{t}}\right)}^{1/2}\overline{x}f\left(\eta \right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\chi \left(\eta \right)=\frac{N}{N_w}.\end{array}$$

(7)

The substitution of the similarity solution (7) into the system (1)–(6), satisfies Equation (1) and the rest of the expressions are transformed as follows:

$$f^{‴}+f{f}^{″}-{f^{\prime }}^2+1+A\hspace{0.17em}\left[1-\left(\frac{1}{2}\eta f^{″}+f^{\prime }\right)\right]=0,$$

(8)

$${\theta }^{″}+\mathrm{Pr}f\hspace{0.17em}{\theta }^{\prime }+Nb\hspace{0.17em}{\theta }^{\prime }\hspace{0.17em}{\varphi }^{\prime }+Nt\hspace{0.17em}{{\theta }^{\prime }}^2-\frac{1}{2}\mathrm{Pr}A\hspace{0.17em}\eta \hspace{0.17em}{\theta }^{\prime }=0,$$

(9)

$${\varphi }^{″}+\frac{Nt}{Nb}{\theta }^{″}+Le\hspace{0.17em}\mathrm{Pr}\hspace{0.17em}f\hspace{0.17em}{\varphi }^{\prime }-\frac{1}{2}Le\hspace{0.17em}\mathrm{Pr}\hspace{0.17em}A\eta \hspace{0.17em}{\varphi }^{\prime }=0,$$

(10)

$${\chi }^{″}+Lb\hspace{0.17em}\mathrm{Pr}\hspace{0.17em}f{\chi }^{\prime }-Pe\left[\chi \hspace{0.17em}{\varphi }^{″}+{\varphi }^{\prime }{\chi }^{\prime }\right]-\frac{1}{2}Lb\hspace{0.17em}\mathrm{Pr}\hspace{0.17em}\eta \hspace{0.17em}A\hspace{0.17em}{\chi }^{\prime }=0,$$

(11)

along with the boundary conditions

$$\begin{array}{l}f\left(0\right)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}^{\prime }\left(0\right)={\epsilon }_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta \left(0\right)=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\varphi \left(0\right)=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\chi \left(0\right)=1,\\ f^{\prime }(\infty )=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta (\infty )=\hspace{0.17em}\hspace{0.17em}\varphi (\infty )=\chi (\infty )=0,\end{array}$$

(12)

where the Prandtl number (Pr), the Brownian motion parameter (Nb), the thermophoresis parameter (Nt), the Lewis number (Le), the bioconvection Lewis number (Lb) and the Péclet number (Pe) are defined as

$$\begin{array}{l}\mathrm{Pr}=\frac{\upsilon }{\alpha },\hspace{1em}Nb=\frac{\tau D_B\left(C_w-C_{\infty }\right)}{\alpha },\hspace{1em}Nt=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{\alpha T_{\infty }},\\ Le=\frac{\alpha }{D_B},\hspace{1em}Lb=\frac{\alpha }{D_n},\hspace{1em}Pe=\frac{\tilde{b}{W}_c}{D_n}.\end{array}$$

(13)

Meanwhile, $A>0$ corresponds to an accelerated flow and $A<0$ connotes a decelerated flow. For $A=0$, the flow is steady, i.e., the flow is independent of time.

4. Physical Quantities

The physical quantities of engineering interest in this study are the local skin friction coefficient $\left(C_{f_{\overline{x}}}\right)$, the local Nusselt number $\left(N{u}_{\overline{x}}\right)$, the local Sherwood number $\left(S{h}_{\overline{x}}\right)$, and the local density number of motile microorganisms $\left(N{n}_{\overline{x}}\right)$, defined as [47]

$$C_{f_{\overline{x}}}=\frac{\mu {\frac{\partial \overline{u}}{\partial \overline{y}}|}_{\overline{y}=0}}{\rho {\overline{u}}_e^2},\hspace{1em}N{u}_{{}_{\overline{x}}}=\frac{\overline{x}\left(-k{\frac{\partial T}{\partial \overline{y}}|}_{\overline{y}=0}\right)}{k(T_w-T_{\infty })},\hspace{0.17em}\hspace{1em}S{h}_{{}_{\overline{x}}}=\frac{\overline{x}\left(-D_B{\frac{\partial C}{\partial \overline{y}}|}_{\overline{y}=0}\right)}{D_B(T_w-T_{\infty })},\hspace{1em}N{n}_{\overline{x}}=\frac{\overline{x}\left(-D_n{\frac{\partial N}{\partial \overline{y}}|}_{\overline{y}=0}\right)}{D_n(N_w)}.$$

(14)

The substitution of Equation (7) into (14) yield the following expressions:

$${\mathrm{Re}}_{\overline{x}}^{1/2}{C}_{f_{\overline{x}}}=f^{″}(0),\hspace{1em}{\mathrm{Re}}_{\overline{x}}^{-1/2}N{u}_{\overline{x}}=-{\theta }^{\prime }(0),\hspace{1em}{\mathrm{Re}}_{\overline{x}}^{-1/2}S{h}_{\overline{x}}=-{\varphi }^{\prime }\left(0\right),\hspace{1em}{\mathrm{Re}}_{\overline{x}}^{-1/2}N{n}_{\overline{x}}=-{\chi }^{\prime }(0),$$

(15)

where the local Reynolds number is given as ${\mathrm{Re}}_{\overline{x}}=\frac{{\overline{u}}_e\overline{x}}{\upsilon }.$

5. Computational Method and Validation

The boundary value problem (8)–(12) was solved numerically by using a finite-difference technique, namely the Richardson extrapolation in the Maple software. This technique is a sequence acceleration method which is used to improve the rate of convergence of a sequence. The Richardson extrapolation (also known as post-processing procedure) is capable of producing a better accuracy to the exact solution obtained by averaging the computed numerical results on two embedded meshes [49]. The built-in command in Maple, dsolve uses the Richardson extrapolation technique to solve the boundary value problem efficiently. Based on the results of previous studies published by Zaimi et al. [47] and Ibrahim et al. [50], a comparison is made for the values of $f^{″}\left(0\right),-{\theta }^{\prime }\left(0\right)$ and $-{\varphi }^{\prime }\left(0\right)$, as shown in

Table 1. Comparison of $f^{″}\left(0\right),-{\theta }^{\prime }\left(0\right)$ and $-{\varphi }^{\prime }\left(0\right)$ when ${\epsilon }_1=1,Pe=1,Le=2,Sc=1,A=0,$ $Nt=Nb=0.5,$ and $\mathrm{Pr}=1$ in Equations (8)–(12) and setting $M=0$ and $A=1$ in Equations (18) and (21) of the paper by Ibrahim et al. [50].

	Ibrahim et al. [50]	Zaimi et al. [47]	Present Results
$f^{″}\left(0\right)$	0	0	0
$-{\theta }^{\prime }\hspace{0.17em}\left(0\right)$	0.4767	0.476737	0.476737
$-{\varphi }^{\prime }\left(0\right)$	1.0452	1.045154	1.045154

. There is an excellent agreement with the numerical values reported by previous literature which employed the shooting method. Numerically, the non-linear differential equation system (8)–(11) was solved by the conditions of associated boundary (12) by utilizing the finite-difference technique coupled with Richardson extrapolation numerical method. In this study, the specific range of the boundary layer thickness, ${\eta }_{\infty }$, was used in the computation and depends on the values of the parameters considered to ensure that all numerical solutions approach the asymptotic values correctly.

6. Results and Discussion

The computation process was carried out by setting $\mathrm{Pr}=6.8$ and $A=0.5$ to signify water-based nanofluid and decelerated flow, respectively. Figure 2a–c presents the temperature, concentration, and the density of motile microorganisms profiles as the Brownian motion parameter (Nb) varies for the case of stretching sheet $\left({\epsilon }_1=0.5\right)$ and shrinking sheet $\left({\epsilon }_1=-0.5\right).$ The temperature profiles as in Figure 2a convey that an increment in Nb at a stretching and shrinking sheet increases the bionanofluid temperature. The stretching sheet results in a thinner thermal boundary layer and steeper profiles compared to the profiles of the shrinking sheet. The state of shrinking sheet, which increases the fluid temperature, causes the temperature gradient to decline and reduces the rate of convective heat transfer. Figure 2b reveals that the decrement of the nanoparticle concentration as the values of Nb increase past a stretching and shrinking sheet. The increment in Nb creates continuous collisions between the nanoparticles and the water molecules, which induce the molecules to move more aggressively. Consequently, the nanoparticles, which had gained kinetic energy, move away from the surface of the moving sheet and result in the depletion of the concentration profiles as Nb increases. Physically larger values of Nb correlate with the nanoparticles of smaller sizes. This phenomenon promotes thermal conduction and macro-convection that has been explained in detail by Buongiorno [5], and also promotes nanoparticle species’ diffusion in nanofluid’s main body, i.e., more remote from a wall. Figure 2c illustrates the decrement of the density of motile microorganisms as the values of Nb increases. This trend is same for both cases of stretching and shrinking sheets. It is apparent from Figure 2c that the density of microorganisms at a surface sheet maximizes $\left(\chi =1\right)$ for the shrinking sheet; on the other hand, the density of microorganisms at a sheet surface is minimized as Nb is enhanced. From the results, it can be concluded that microorganisms have a propensity to swim further away from a sheet surface, especially in a condition where the sheet is shrinking in the boundary layer. Hence, this leads to making microorganisms’ density at the wall lower in contrast to the case of a stretching sheet. High Nb values enhance the thickness of the nanoparticle concentration boundary layer as they are dominant influencers; conversely, nanoparticle concentration (shrinking sheet) in the boundary layer is decreased by higher Nb values.

The effects of the thermophoresis (Nt) parameter towards the temperature, concentration, and the density of motile microorganisms’ profiles are plotted in Figure 3a–c, respectively for the stretching and shrinking sheet cases. Based on Figure 3a–c, increments are noted in temperature, concentration and microorganism density when the value of the thermophoresis parameter increases. The increment of Nt indicates a stronger thermophoretic force (due to the temperature gradient) which displaces the nanoparticles away from the hot sheet to quiescent fluid, which increases the concentration of the nanoparticles. The augmentation of the nanoparticles’ volume fraction greater than unit presented in Figure 3b is not acceptable because theoretically, the concentration of the nanoparticles should be ≤1 where $\varphi =1$ expresses that there is no fluid and the material entirely consists of solid particles. The concentration profiles for the shrinking case, as shown in Figure 3b, portray values of the nanoparticles’ concentration greater than one, and this is due to the concentration overshoot along the shrinking surface which forms the backward flow that later may disrupt the laminar flow.

Figure 4 suggests the depreciation of the concentration by the increment of the Lewis number (Le). The thickness of the concentration boundary layer decreases with an increment of Lewis number. The Lewis number encodes the thermal diffusion’s relative strength to the nanoparticle diffusion rates. If a condition happened to be $Le>1$, the thermal diffusivity would exceed the nanoparticle diffusivity. As a result, this leads to improvement in nanoparticles’ magnitudes in the stagnation regime, as well as accentuation in the concentration boundary layer thickness.

Figure 5 and Figure 6 show the distributions of the motile microorganism rescaled density function, $\chi \left(\eta \right)$ with diverse bioconvection Lewis (Lb) and Péclet (Pe) numbers for both cases of stretching and shrinking cases. Figure 5 and Figure 6 exhibit that an increment of Pe and Lb decreases the density of motile microorganisms. In parallel with this circumstance, the motile microorganism rescaled density function is usually enhanced by mounting bioconvection Lewis numbers. Pe connects a flow’s advection rate to its diffusion rate. Since $Pe=\tilde{b}{W}_c/D_n$, particularly when the chemotaxis is constant, it is directly proportional to the steady maximum cell swimming speed and inversely proportional to $D_n$ (microorganisms’ diffusivity). As Pe > 1, swimming movements have control over microorganisms’ species diffusivity. These eventually promote a decrease in the density of motile microorganism. Increasing bioconvection Lewis number’s (Lb) effects of aiding are held responsible for the decrement in microorganisms’ diffusivity relative to microorganism’s effective thermal diffusivity. Increasing bioconvection Lewis and Péclet (Pe) numbers suppressed a motile microorganism rescaled density boundary layer thickness.

The temperature gradient is observed to be enhanced with negative A (decelerated flow) and reduced when A = 0 (steady). The state of the stretching surface, however, results in a rise in temperature gradient for both negative and zero values of A, whereas the shrinking sheet wall results in a substantial drop in the temperature gradient (Figure 7). In Figure 8, the mass transfer rate response to variation of the unsteadiness parameter (A), Lewis number (Le) and wall stretching/shrinking (${\epsilon }_1$) effects is shown. With the negative values of ${\epsilon }_1$ (shrinking effect), the mass transfer rate is enhanced, whereas the opposite effect is sustained for positive values of ${\epsilon }_1$ (stretching effect) in the decelerating case. Microorganism gradient is enhanced in the case of the stretching sheet while it declines with the shrinking surface (Figure 9). For the Maple solutions, the effect of the unsteadiness parameter (A) and the stretching/shrinking parameter (${\epsilon }_1$) on the dimensionless velocity and velocity gradient are not significant.

7. Conclusions

This present work attempts to solve the problem of the unsteady stagnation-point and heat transfer past a stretching/shrinking sheet in a nanofluid containing gyrotactic microorganisms. The finite-difference method, namely the Richardson extrapolation technique in the Maple software, has been employed to solve the model in the form of ordinary differential equations. The numerical results were organized in terms of profiles and the physical quantities’ characteristics. This theoretical work is relevant to improve the performance of micro-scale mixing device, based on stable water suspensions of nanoparticles and microorganisms. The outcomes of the present investigation are summarized as follows:

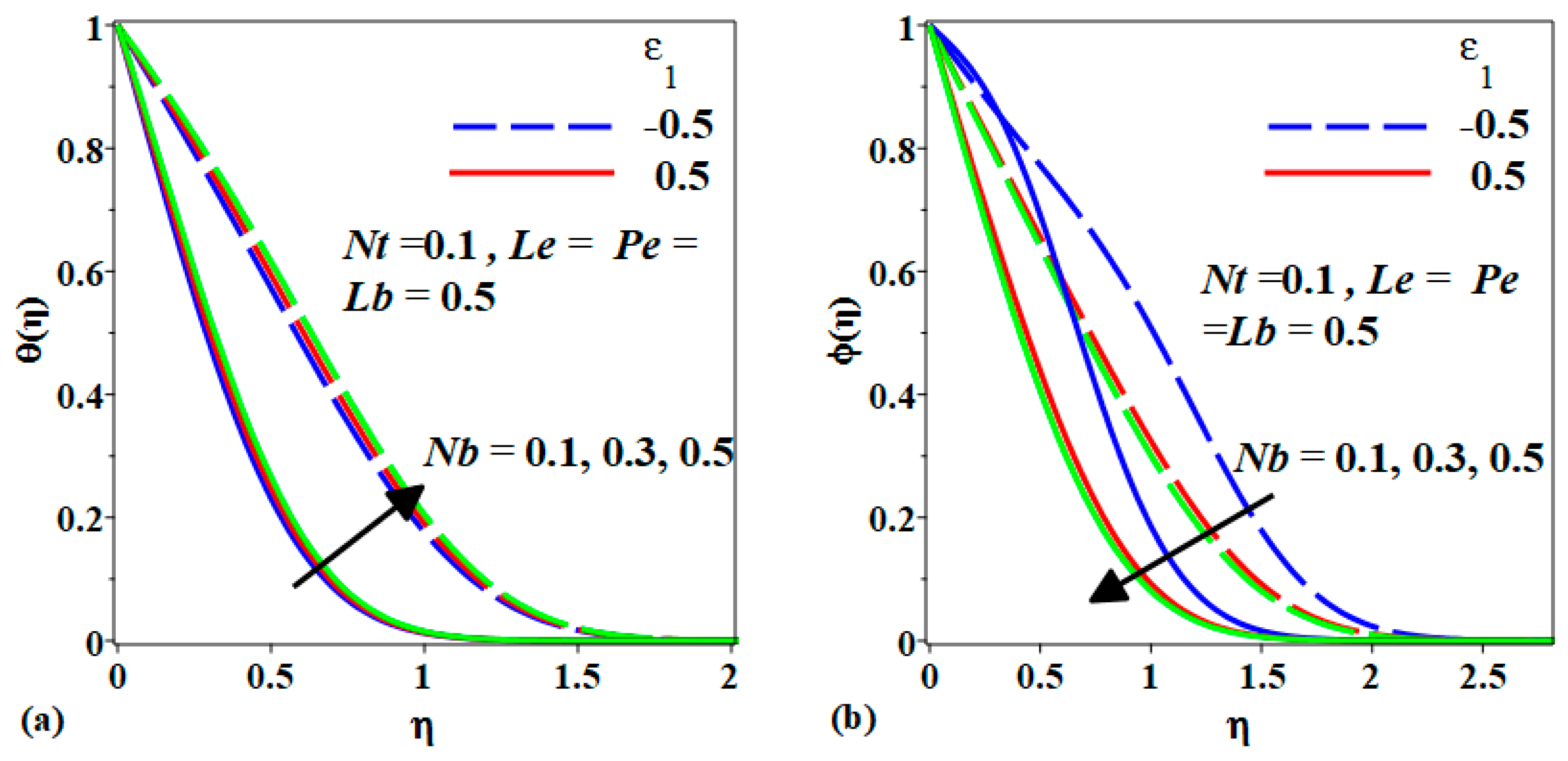
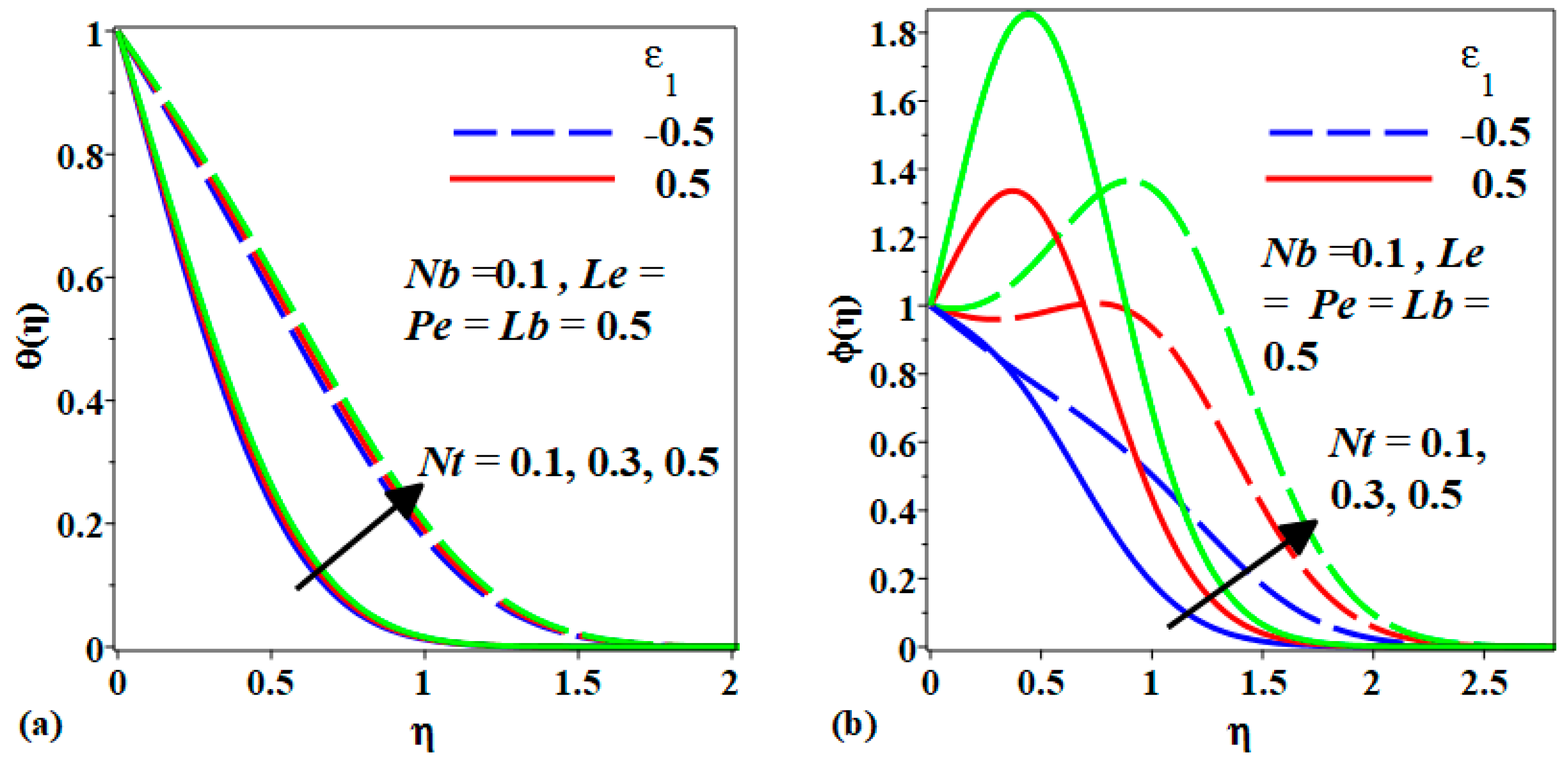
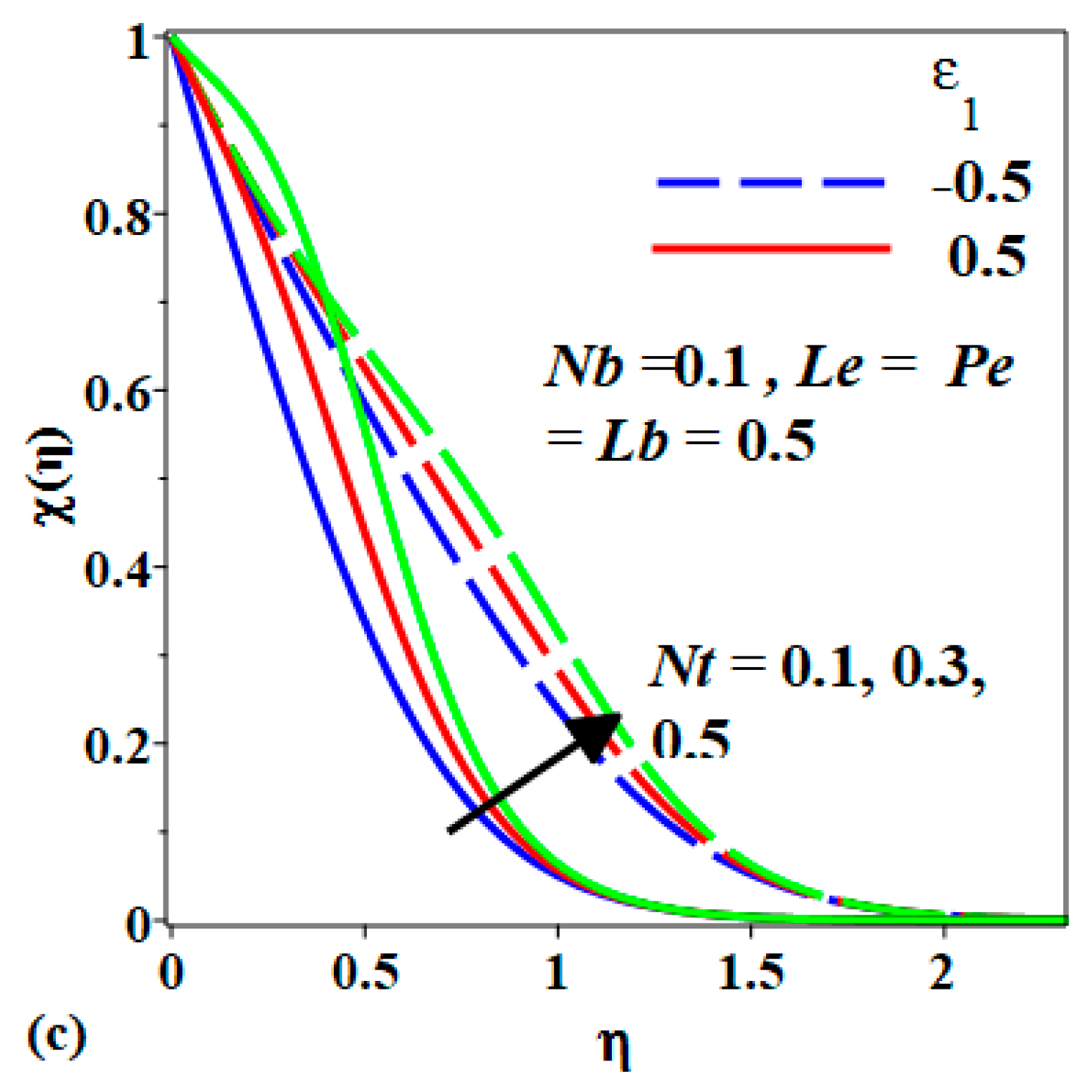
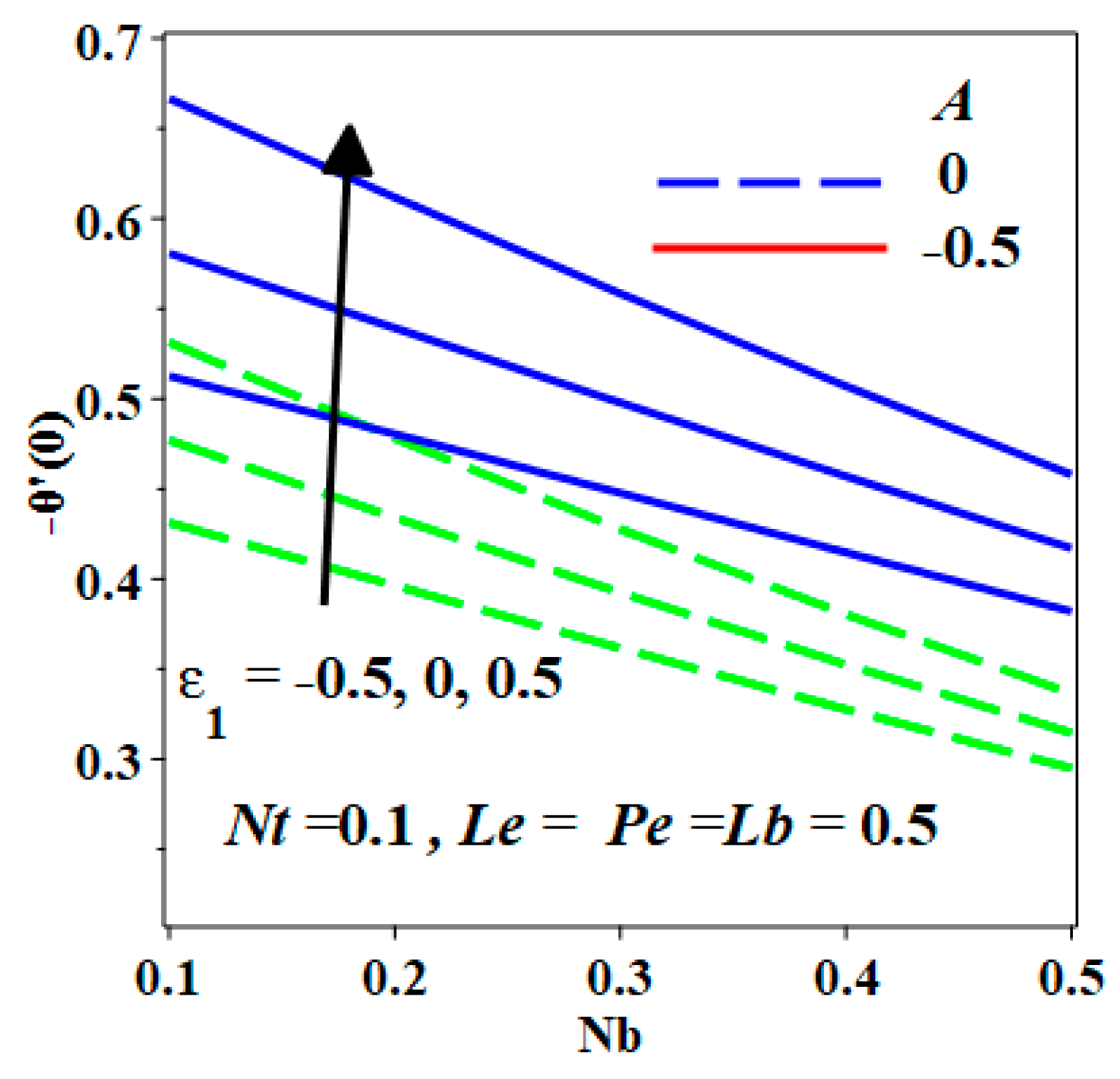
• The increment in Nb past a stretching or shrinking sheet increases the temperature of the bionanofluid temperature but decreases the nanoparticle concentration and the density of motile microorganisms,
• The enhancement in Nt improves the fluid temperature, concentration and the microorganism density in the stagnation region.
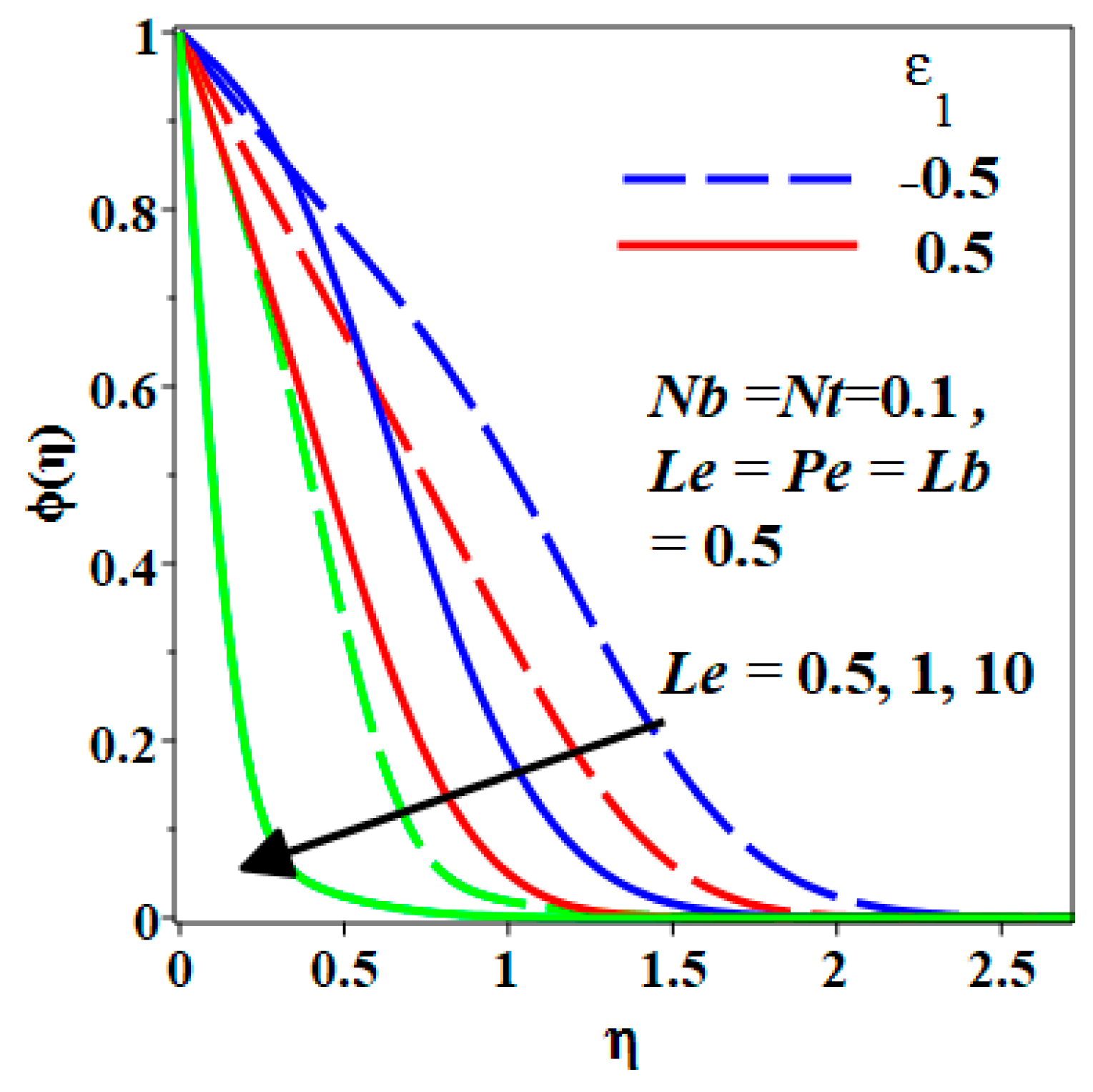
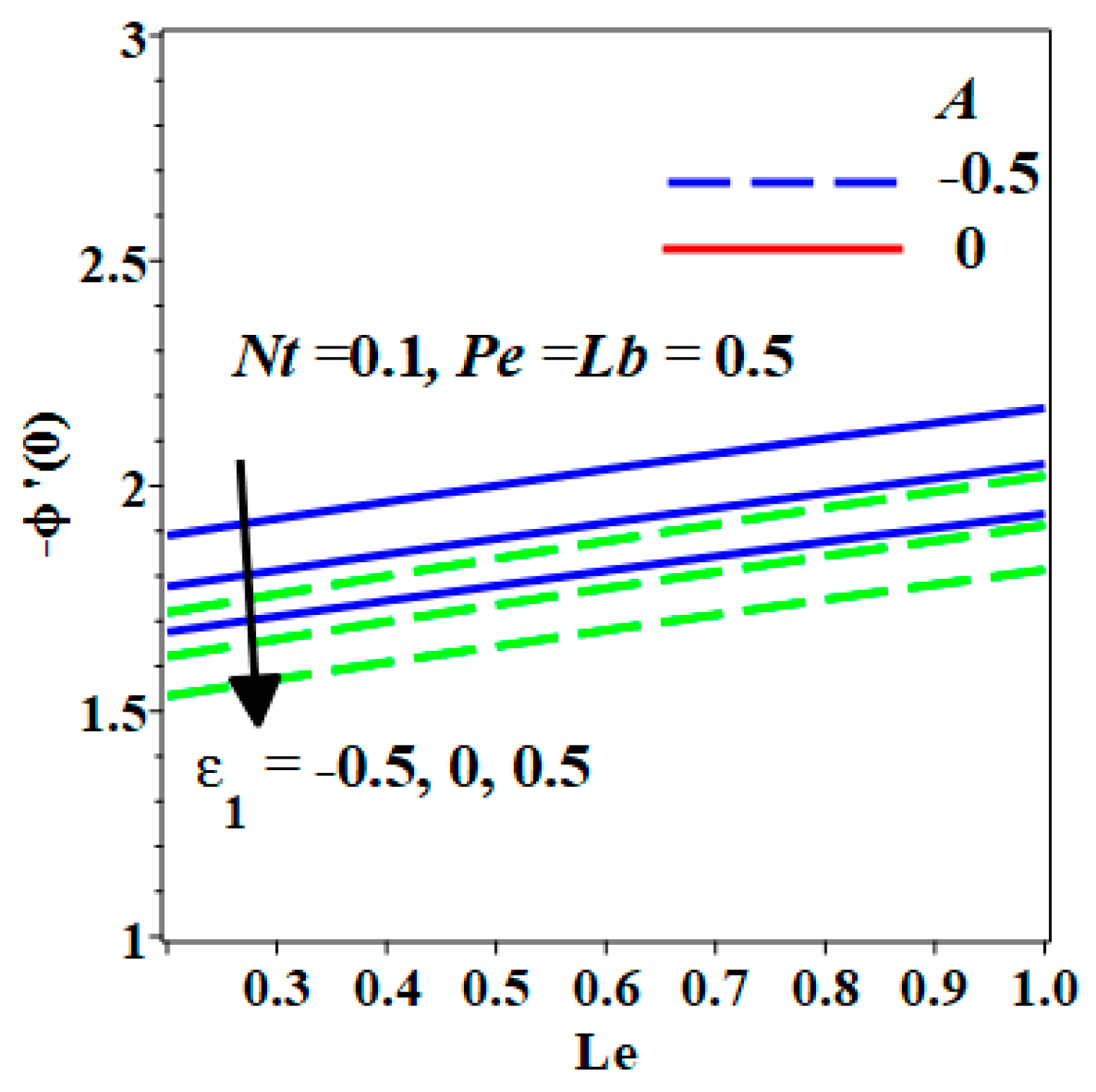
• The increment of Le affects the concentration of the nanoparticles, causing it to decrease.
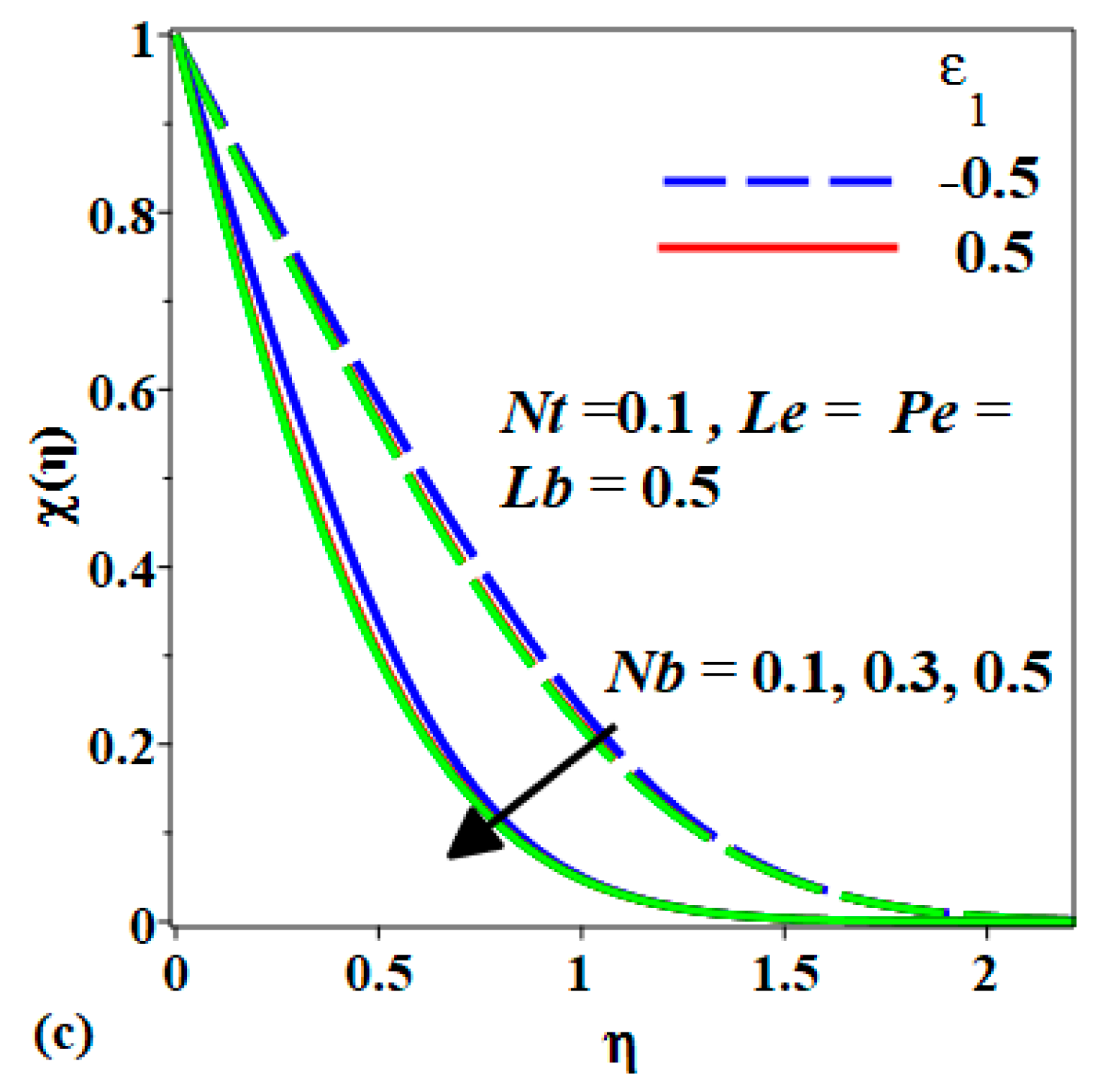
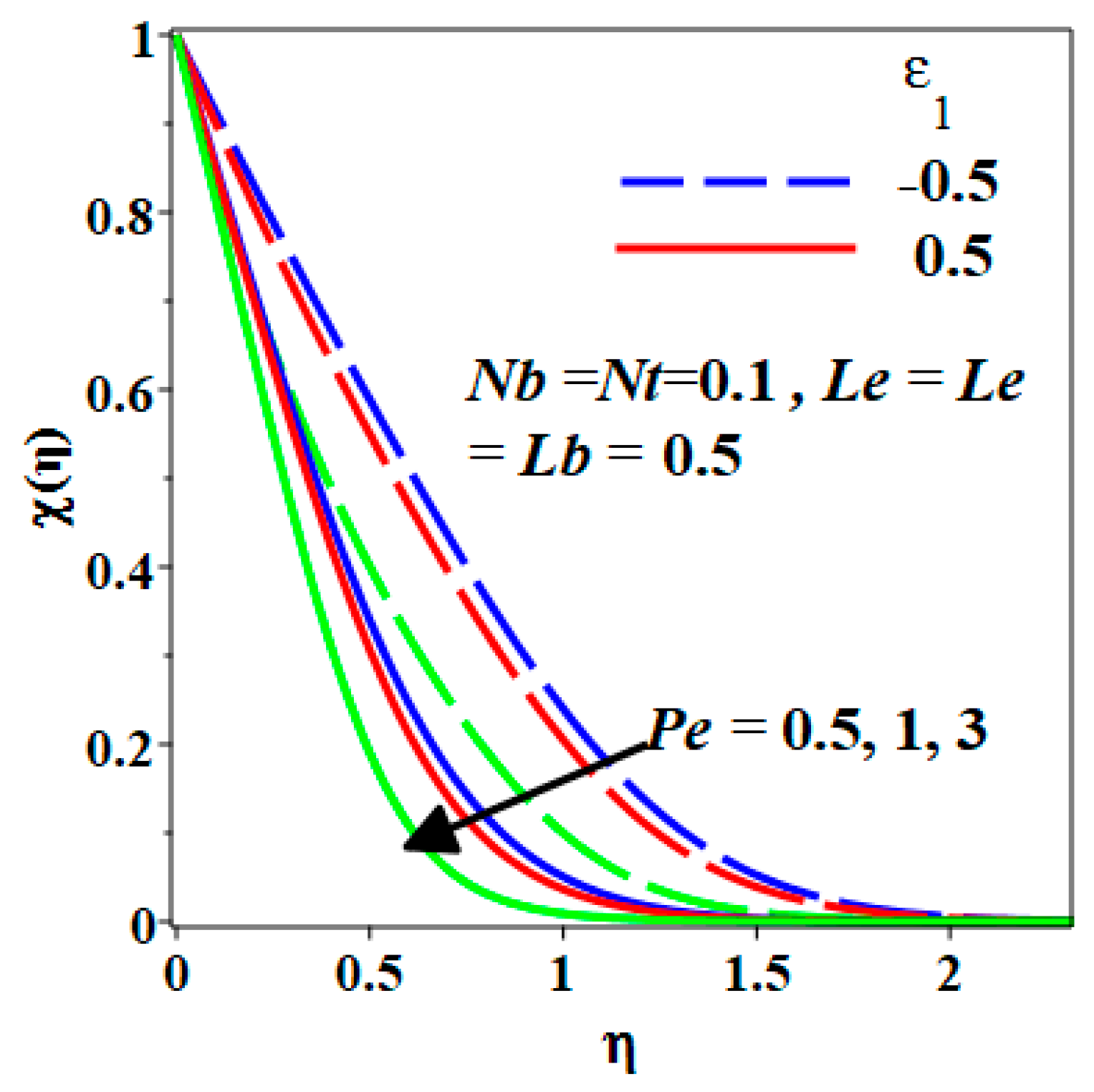
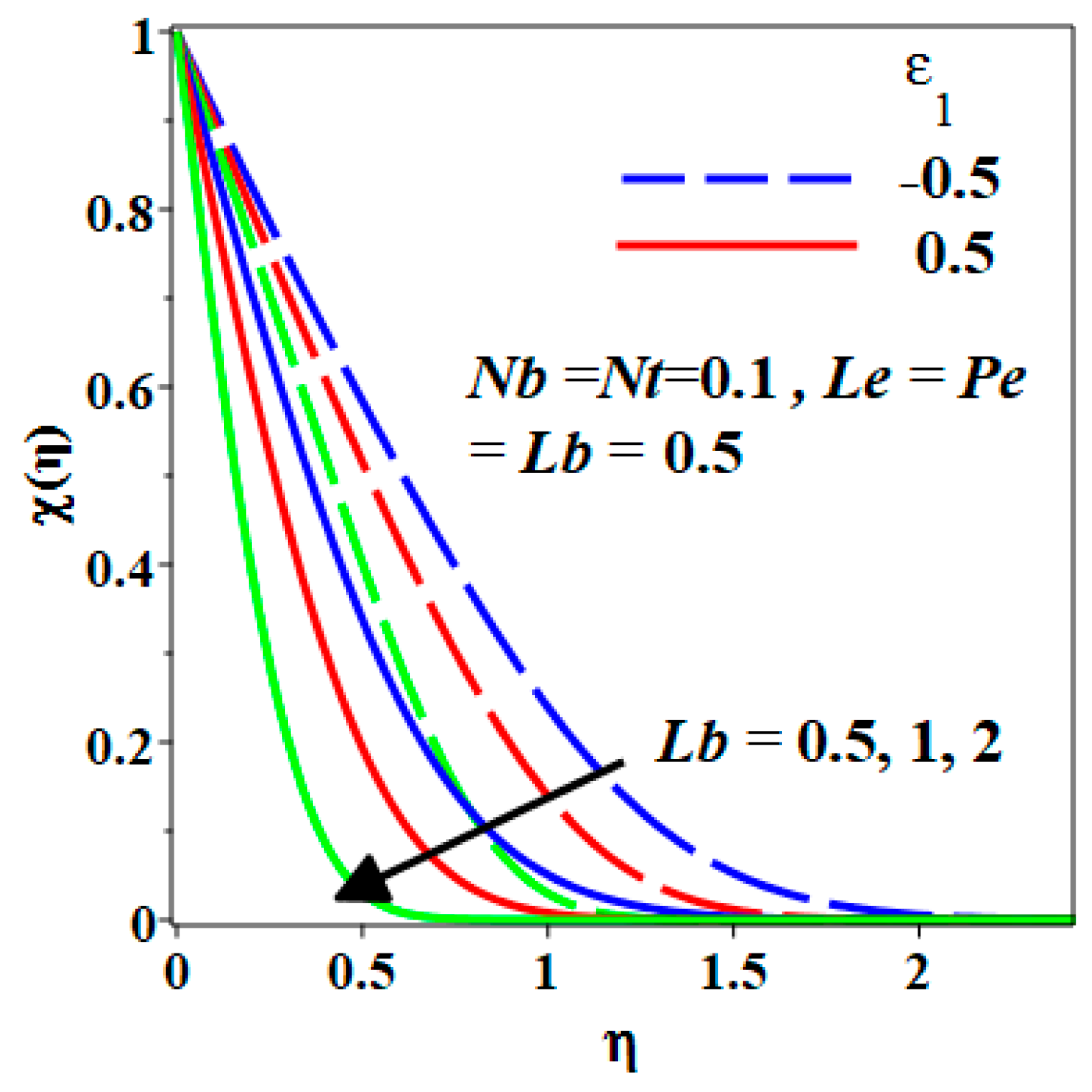
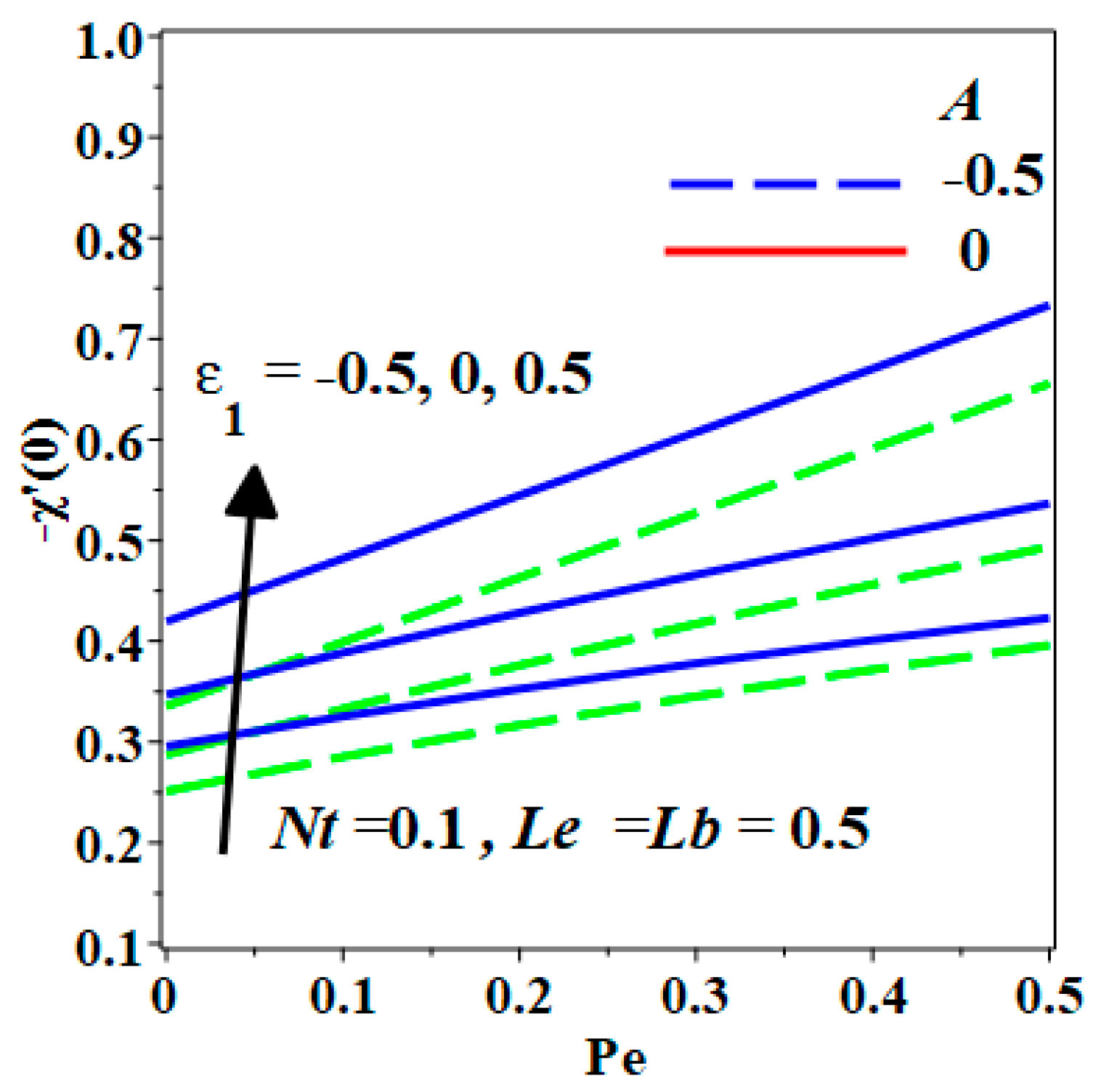
• The increment of Pe and Lb decreases the density of motile microorganisms past a stretching or shrinking sheet.
• The microorganism diffusivity is high in the case the stretching sheet but low in the case of the shrinking sheet.