Abstract
The current continuation aim is to explore the rheological consequences of Eyring Powell nanofluid over a moving surface in the presence of activation energy and thermal radiation. The bioconvection of magnetized nanoparticles is executed with the evaluation of motile microorganism. The most interesting Wu’s slip effects are also assumed near the surface. The evaluation of nanoparticles for current flow problems has been examined by using Buongiorno’s model. The governing equations for the assumed flow problem are constituted under the boundary layer assumptions. After converting these equations in dimensionless form, the famous shooting technique is executed. A detailed physical significance is searched out in the presence of slip features. The variation of physical quantities, namely velocity, nanoparticles temperature, nano particles concentration, motile microorganism density, skin friction coefficient, local Nusselt number and motile organism density number are observed with detailed physical aspects for various flow controlling parameters.
1. Introduction
In recent years, nanofluids have proven to be a more convent heat transfer media in contrast to the heat transfer liquids. Due to improved thermo-physical features, the nanoparticles are considered as a more constructive resource energy conversion and heat exchanger, which is quite necessitated in mechanical and engineering processes. The interaction of nanoparticles in base liquids can effectively enhance the cost-coefficient systems, which are related to the diverse mechanical and manufacturing processes. Beside this, the involvement of nano-materials in the era of medical sciences has been found to be quite progressive in recent decades, as these nano-sized particles can be more efficient in the diagnoses of different diseases like cancer tissue, artificial lungs, laser technology, chemotherapy, damage of defected cells etc. The foremost focus on thermo-physical properties of nanoparticles was put forward by Choi [1]. Later on, many miscellaneous attempts regarding the interaction of nanoparticles was made by numerous researchers in the past few years. Madhu and Kishan [2] examined the flow of non-Newtonian nanofluid in the stagnation point mixed convection flow over a moving surface. They employed the finite element numerical technique to execute the numerical treatment of the formulated problem. The enrolment of nanoparticles in the heat storage units and fins for heat exchangers has been determined by Sheikholeslami and co-workers [3]. Gupta et al. [4] incarcerated the features of thermal radiation and chemical reaction in the flow of nanofluid over an inclined configuration. Hayat et al. [5] performed a theoretical based analysis for nanoparticles suspension in Walters B fluid considered over a nonlinear moving geometry, which sustains a variable thickness. Another interesting contribution of the involvement of nanoparticles in circular jets was treated by Turkyilmazoglu [6]. In this analysis, some interesting analytical and numerical approach has been carried out via famous relevant techniques. Tlili et al. [7] simulated a forced convective flow of nanofluid over a horizontal cylinder in the presence of a magnetic force. The rotating flow of moving disk with Maxwell nanofluid in addition to heat absorption and generation features was reflected by Ahmed et al. [8]. Khan et al. [9] found that entropy generation effects the presence of hybrid nanoparticles. Ahmed et al. [10] investigated the flow of hybrid nanoparticles with micropolar fluid in stenosis arteries. The unsteady slip flow of Carreau nanofluid over a moving wedge in the presence of nonlinear thermal radiation features was focused by Khan et al. [11].
Despite the increasing significance of non-Newtonian fluids, comprehensive attempts have been made to visualize the rheology of non-Newtonian fluids because of their industrial and bioengineering applications. Many fluids like saliva, blood, synovial fluid, honey, silly putty, syrup and cosmetics, protracted a complex relationship for shear stress and deformation. The wade ranging significance of such nonlinear fluids insist the scientist to advise various non-Newtonian fluid models in the literature. Among these fluid models, Eyring Powell is one which reduces to viscous behavior at both high and low shear rates. The unique feature of this model is it does not attain any empirical relation but it is originated from kinetic theory of liquids. The shear thinning features can be depicted using this model. The bhumab body blood is treated as Eyring Powell fluid. This model was suggested by Powell and Eyring [12] in 1944. Later, various investigators analyzed the rheological features of this model with different flow configurations [13,14,15,16,17,18,19].
Exclusive investigations relating to the bioconvection of nanoparticles are explored in the current decade, since it involves a variety of significance in the science of biological systems and biotechnology. The basic source of this interesting phenomenon is the upward movement of microorganisms on average. The primly attention for the bioconvection of nanoparticles relates the combined features of pattern formulation and stratification density, which are generated due to self-propelled microorganisms, buoyancy forces, and nanoparticles. The microorganisms usually encompassed are the gravitaxis, gravitaxis, and oxytaxis organisms. The main benefit for combining the features of gyrotactic microorganisms and nanoparticles improve the mass transportation and stability of nanoparticles [20,21]. The basic thought of bioconvection was originated by Kuznetsov [22,23]. Siddiqa et al. [24] discussed the numerical computation of a problem that deals with the bioconvection of nanoparticles in wavy cone. Alsaedi et al. [25] directedthe interaction of magneto-nanoparticles along with gyrotactic microorganisms over permeable surface. The effect of Navier slip in nanofluid flow with gyrotactic microorganisms has been depicted by Khan et al. [26]. The impact of temperature dependent thermal conductivity and viscosity in bioconvection of nanoparticles immersed in saturated porous media was worked out by Xun et al. [27]. Waqas et al. [28] utilized the microorganisms’ effects in generalized second grade fluid over a stretched surface numerically. In another attempt, Waqas et al. [29] used convective boundary assumption for the flow of Maxwell nanofluid with motile microorganisms. Dero et al. [30] captured multiple solutions for bioconvection that involve nanoparticles in the presence of wall blowing and slip features [31,32,33,34,35,36].
In the current analysis, we aim to explore the bioconvection phenomenon in the steady flow of Eyring Powell nanofluid in presence of thermal radiation, activation energy and Wu’s slip (second order) slip features. The analysis has been performed over a stretched surface. The highly nonlinear formulated problem is solved numerically with shooting procedure. The insight observations for the declared problem are graphically explained.
2. Mathematical Modeling
Let us develop an unsteady and mixed convection flow of Eyring Powell nanofluid in presence of gyrostatic motile microorganism over a moving porous surface. The thermophoresis and Brownian features are entertained in the energy and concentration equations by using Buongiorno’s nanofluid model. The flow has been generated due to the moving wedge, which is subjected to the slip boundary conditions. The magnetic field effects are captured by employing it normal to the surface. Moreover, in the energy equation, the thermal radiation features are utilized by using famous Rosseland approximation theory. Following the cartesian coordinate system, velocity component is assumed in −direction and component is taken in −direction. Let , and explore the involvement of nanoparticles temperature, nanoparticles concentration and motile microorganisms respectively. The flow equation under such flow assumptions are written as [19,27,28]:
The boundary constraints flowing to the above flow equations are expressed as
We define slip boundary conditions in Equation (6) as follows
where , , , and are respectively expressed the Knudsen number, constants, free path for molecular mean and momentum coefficient. It is remarked that these slip conditions are termed as Wu’s slip conditions [37,38,39,40,41,42].
Using the Rosseland approximation, we have
where is the Stefan Boltzmann constant and is the absorption constant. For further analysis, we assume that the temperature gradients within the flow are small. As an implication of this assumption the term appearing in (16) may be linearized about the ambient temperature using Taylor series to give
Upon neglecting the higher-order terms, we get
In view of (16) and (18), Equation (13) takes the form
Before compute the solution of governing equations, first we convert these equations in dimensionless forms by introducing following variables
We introduce the stream function as follows
The inserting above quantities, the flow Equations (2)–(5) are converted in following forms
The transmuted boundary conditions are
In above equations and are dimensionless material fluid parameters, combined porosity and magnetic parameter, bio-convection Rayleigh number, buoyancy ratio parameter , mixed convection parameter, is the Prandtl number, Biot parameter, Lewis number , thermophoresis parameter, Brownian motion parameter, radiation parameter, , bioconvection constant, are Peclet number, is the bio-convection Lewis number, while , and first order and second order slip parameters respectively.
3. Numerical Solution
We employ the shooting numerical technique to compute the approximate solution of differential equations [43,44,45,46,47]. For this purpose the boundary value problem (12)–(15) is first converted into initial values problem as follows:
Similarly, the boundary conditions attained following forms:
The numerical computations are perfumed until excellent accuracy with 10−6 is obtained.
4. Validation of Solution
In order to verify the solution, the obtained results are compared in Table 1 with already available simulations [35,36]. Table 1 shows that a favorable agreement is noted with these studies.

Table 1.
Comparison of solution for with various values of when .
5. Analysis of Results
The aim of this section is to analyze the physical consequences of involved parameters. For this purpose, various graphs are prepared. Following the traditional theoretical scientific contributions for similar analysis, each parameter has assigned some values, while some fixed values have been accompanied to other remaining flow parameters like , , , , , , , , , , , , and .
Figure 1 reports the graphical results for combine parameter and mixed convection parameter on the distribution of velocity . The combine parameter involves the joint features of both magnetic force and porous medium. With the interaction of magnetic force, the movement of fluid particles resisted as magnetic field results Lorentz force. Similarly, the involvement of permeability of porous medium also reduces the particles motion and as a result the velocity distribution retarded. However, the existence of non-Newtonian parameter retains opposite effects i.e., the distribution of velocity increases with .
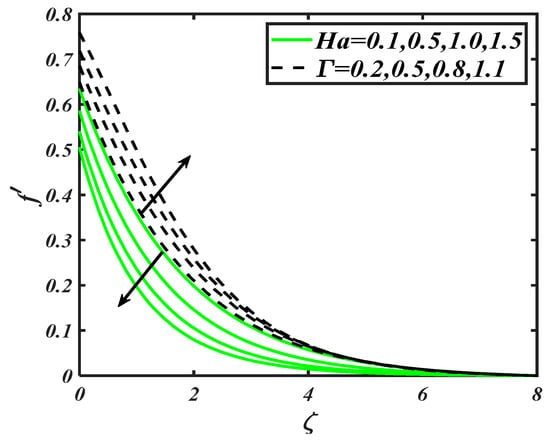
Figure 1.
Illustration of and on .
The significance of buoyancy ratio parameter and first order slip constant on has been visualized in Figure 2. The observation determined for variation of , shows that the increasing trend in is strictly altered effectively. The physical aspect of such an observation may include that bioconvection Rayleigh number involves the buoyancy ratio forces due to which the fluid particles movements decreases. Similarly, the interaction of first order slip also slows down the velocity distribution.
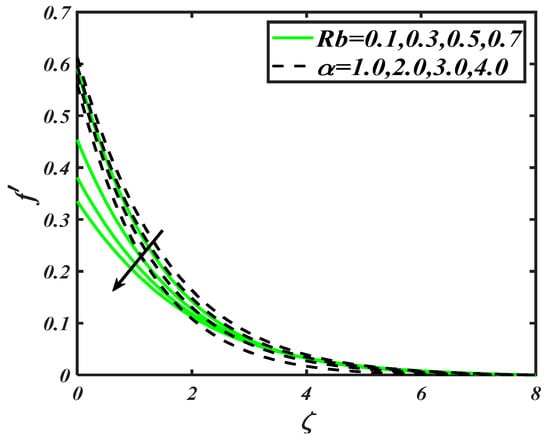
Figure 2.
Illustration of and on .
Figure 3 involves the impact of bioconvection Rayleigh number and second order slip factor on . The variation in both parameters depressed the velocity distribution. Physically, evaluation of bioconvection Rayleigh number sustains the buoyancy forces which are of resistive nature. Further, the decreasing trend for velocity in case of is more dominant as compared to .
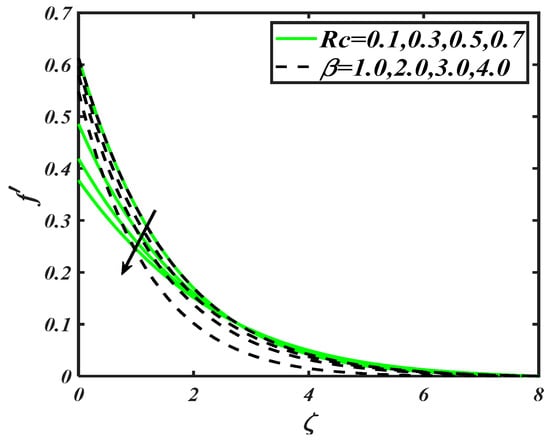
Figure 3.
Illustration of and on .
Figure 4 determines the variation in nanoparticles temperature against combined parameter and mixed convection parameter . It is observed that the nanoparticles temperature increases linearly with involvement of . Physically, both magnetic force and porous medium permeability enhance the nanoparticles temperature. However, with variation of , the temperature distribution impeded.
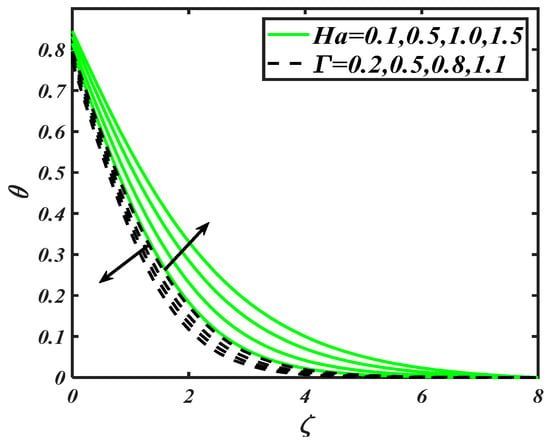
Figure 4.
Illustration of and on .
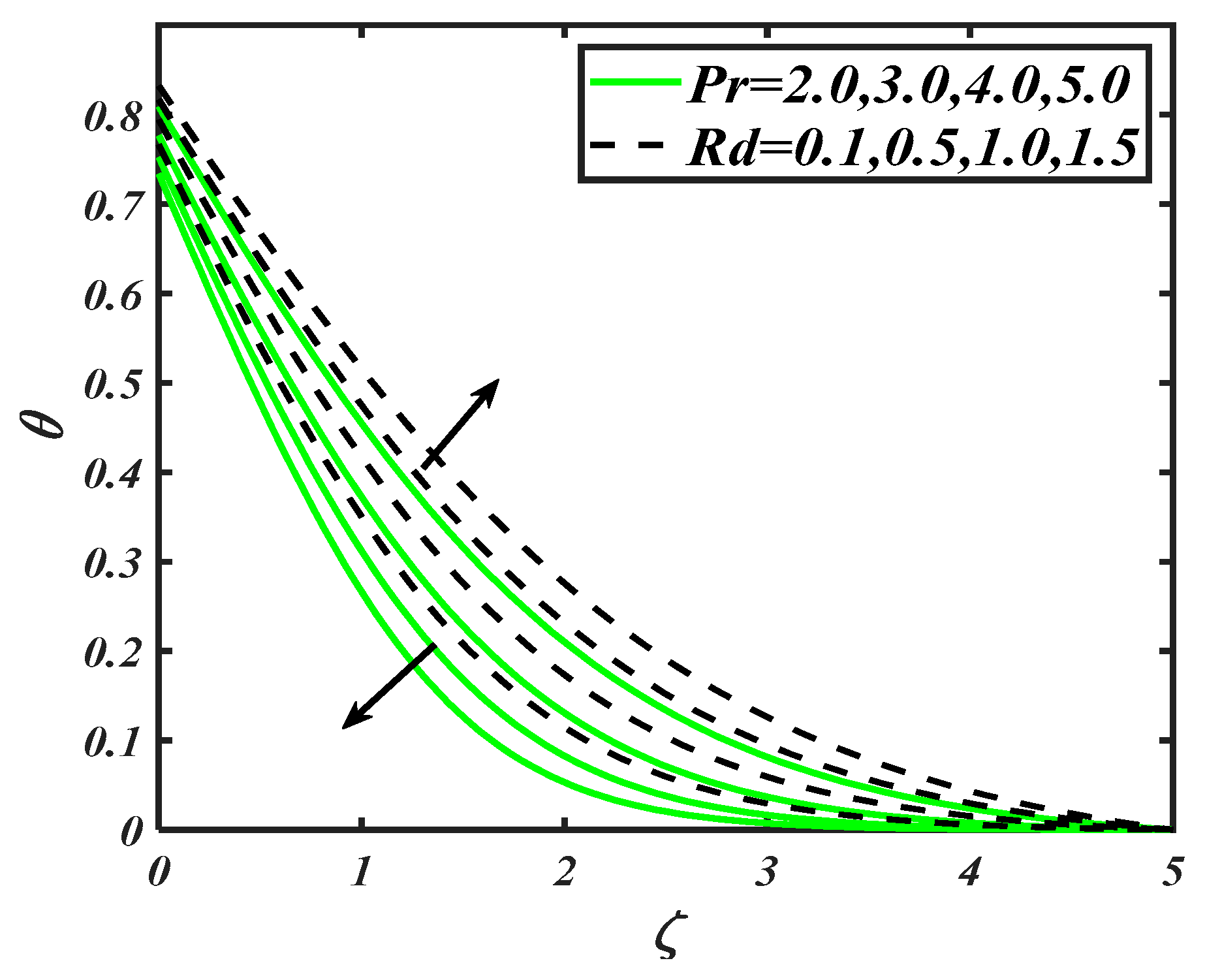
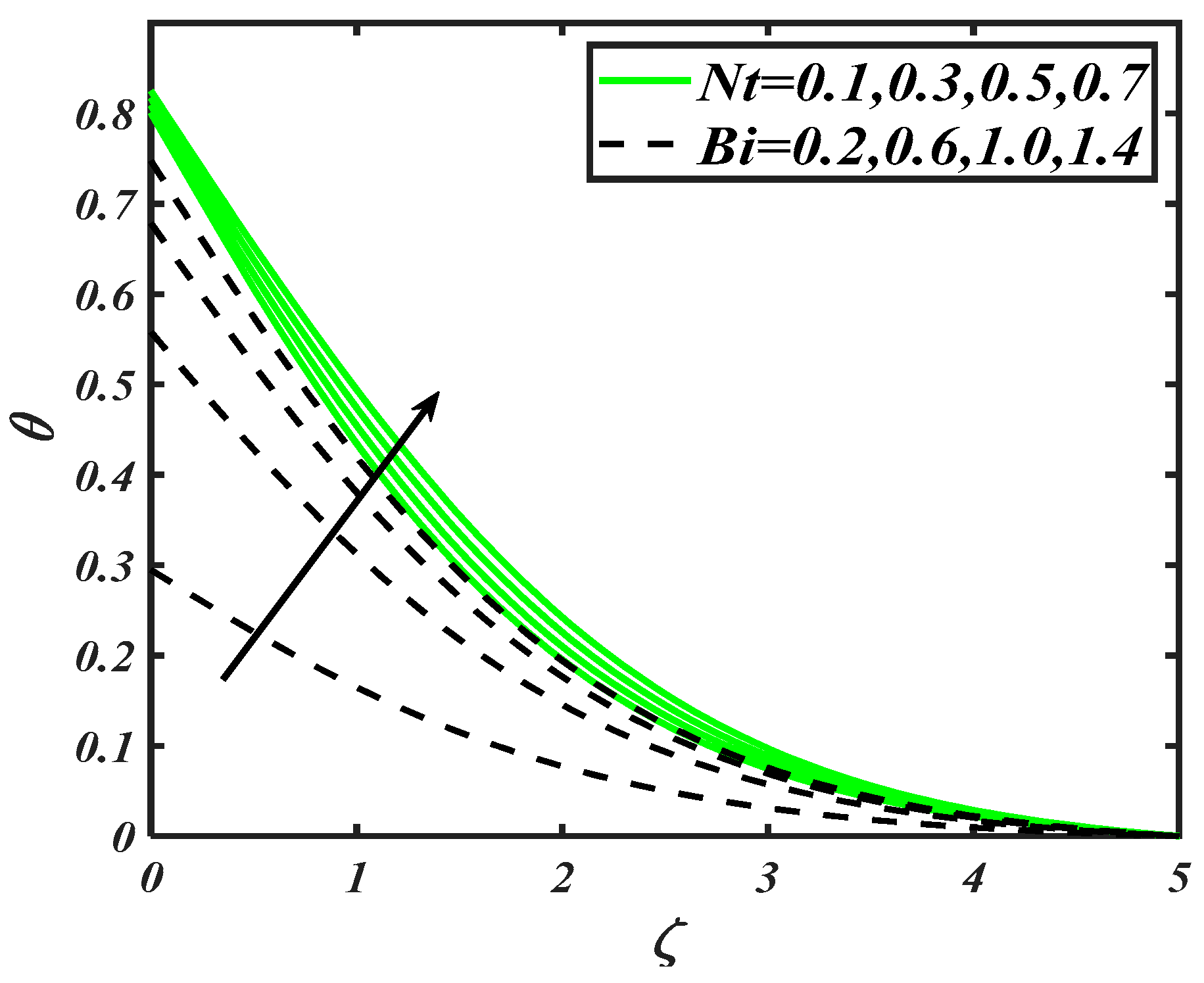
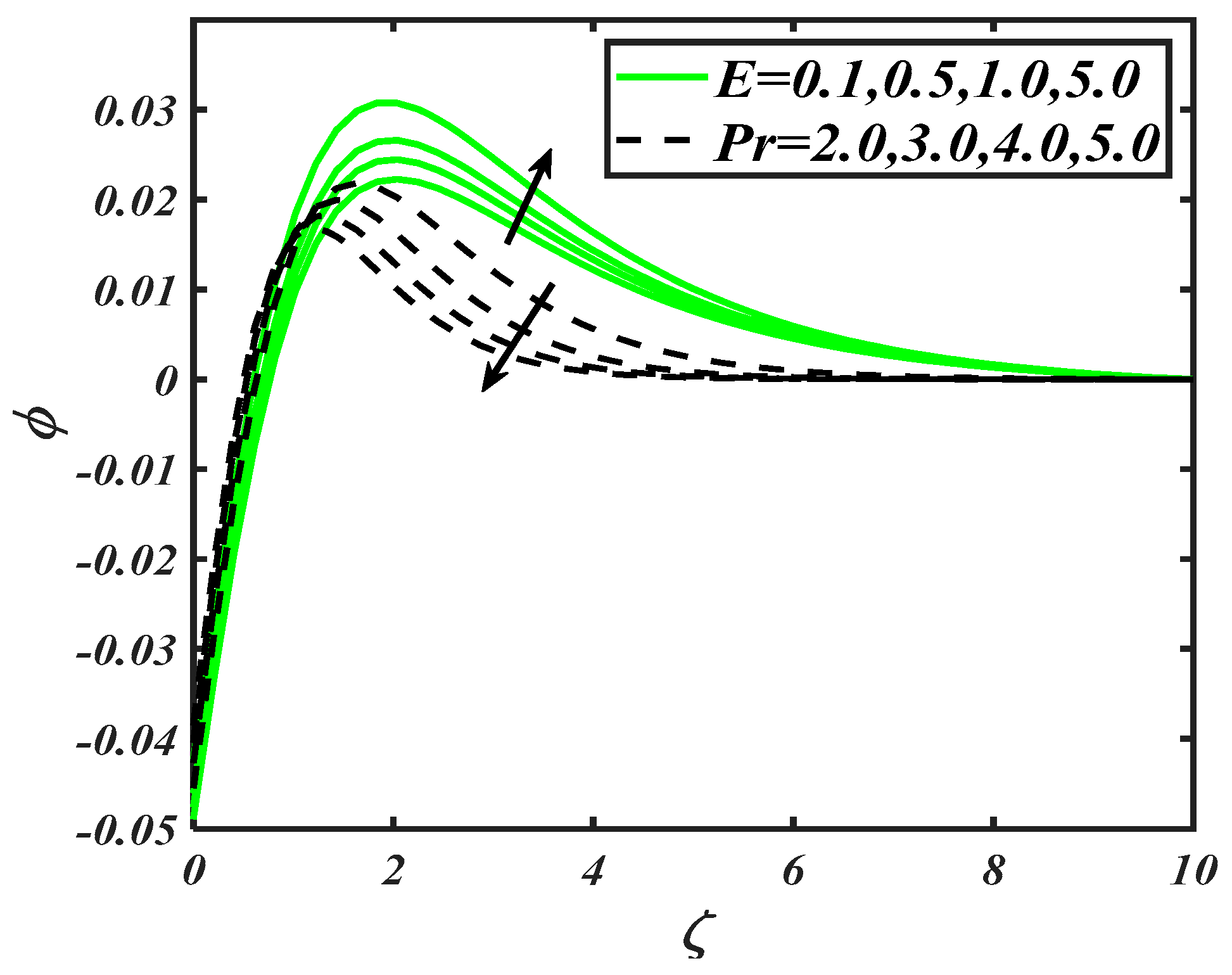
Figure 5 perceived the consequences of Prandtl number and radiation constant on . A decay in temperature distribution is carried out with variation of . The physical aspects of such a trend may include that is related to the thermal diffusivity inversely due to which decreases. On the other hand, increasing values of improve the nanoparticles particles distribution efficiently. Since radiation is considered an active mode of heat transportation, it enables it to raise the temperature of nanoparticles. From Figure 6, it is found that variation in reached at maximum level when both thermophoresis constant and thermal Biot number assigned maximum values. Thermophoresis phenomenon involves the migration of fluid particles due to the temperature difference, which yields an enhancement of temperature distribution. Also, thermal Biot number also plays a valuable role in the enhancement of nanoparticles temperature, as it is directly proportional to the heat transfer coefficient due to which increases.
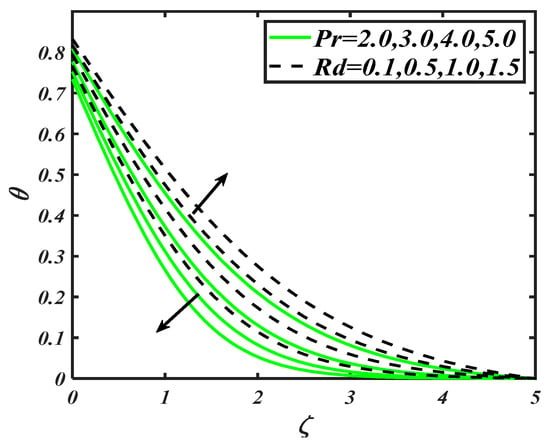
Figure 5.
Illustration of and on .
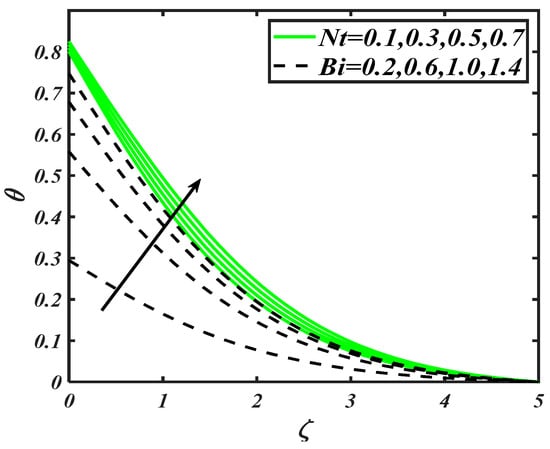
Figure 6.
Illustration of and on .
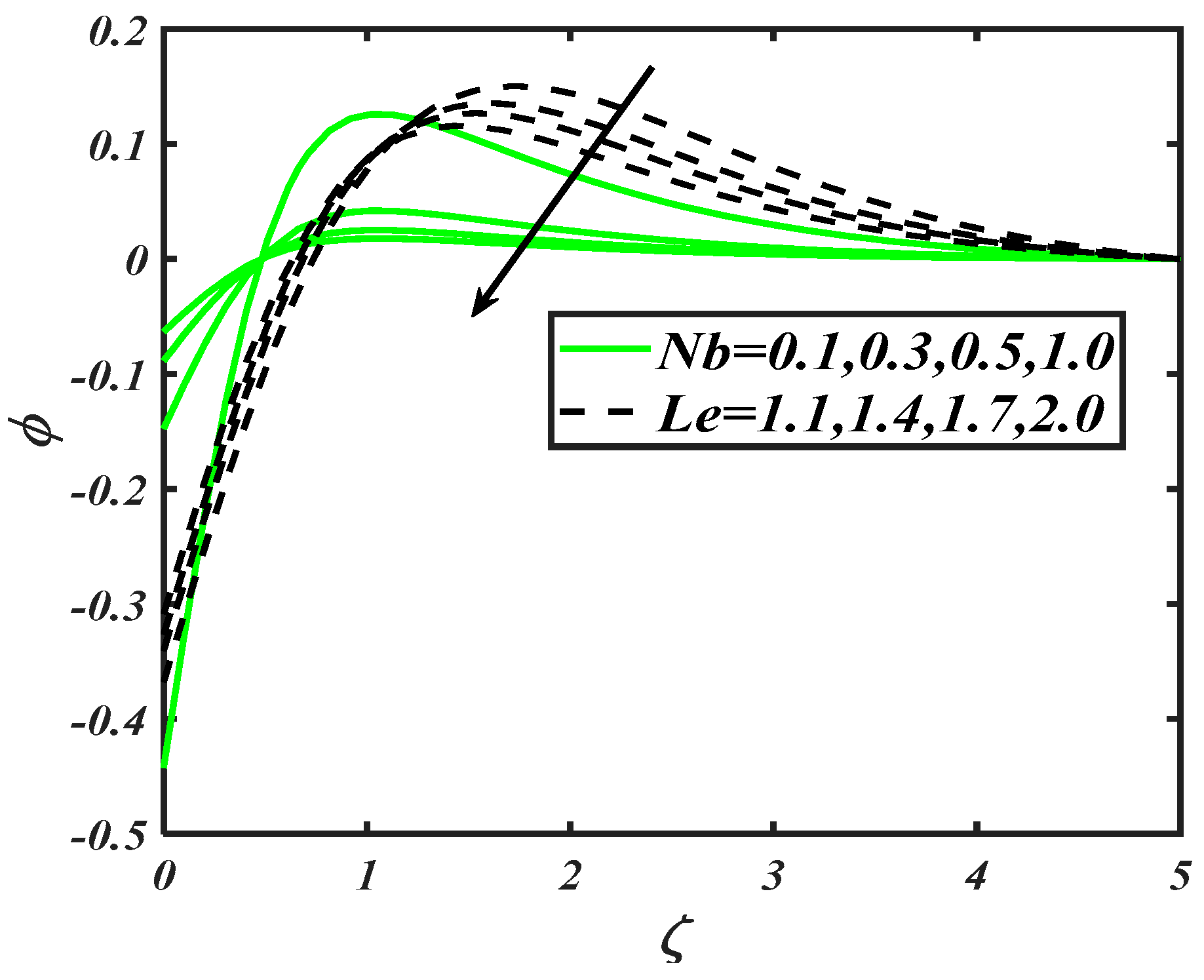
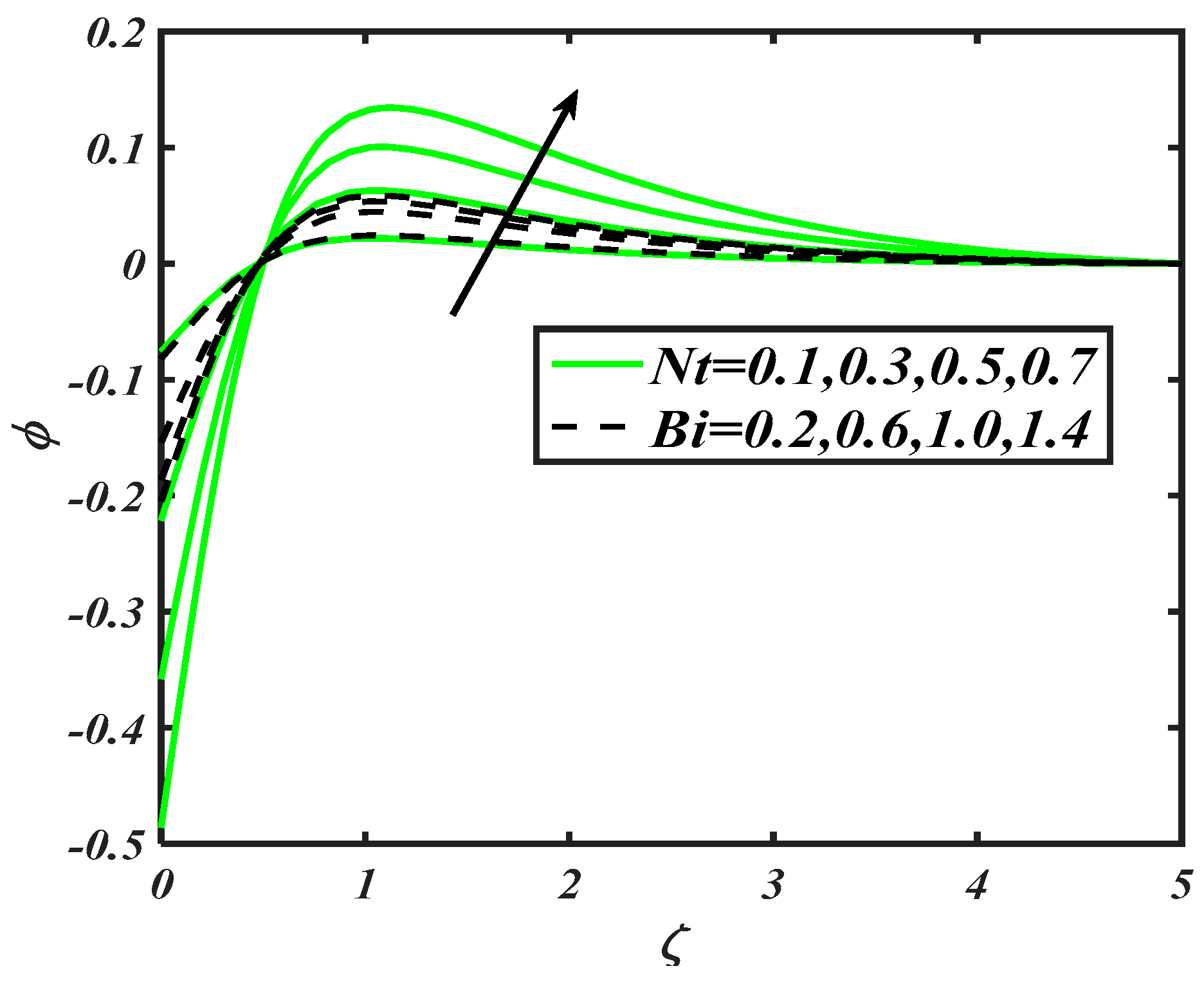
To examine the variation in nanoparticles concentration distribution against flow parameters namely Brownian constant , Lewis number , thermophoresis constant , Biot number , activation energy parameter and Prandtl number , Figure 7, Figure 8 and Figure 9 are prepared. Figure 7 visualized the graphical features for various prospective of Brownian constant and Lewis number . It is securitized that the decreases with variations of both as . Since the Brownian constant reflects the random movement of nanoparticles, which is altered for increasing values . Similarly, the nanoparticles concentration is also impeded for . Since accomplishes a reverse relationship with mass diffusivity, which causes a reduction in the nanoparticles concentration distribution. From Figure 8, it is noted that a maximum variation in has been observed, when and assigns maximum values. However, the increasing variation in is exclusively larger for . The role of activation energy and Prandtl number constants in distribution of is notified in Figure 9. With an increase of , the nanoparticles concentration distribution slows down. However, it grows up for activation energy parameter . Physical features behind this trend concluded the involvement of activation energy provided some extra energy, which enhanced the reaction process.
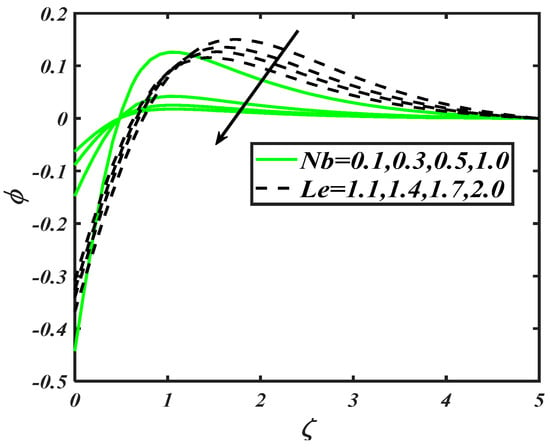
Figure 7.
Illustration of and on .
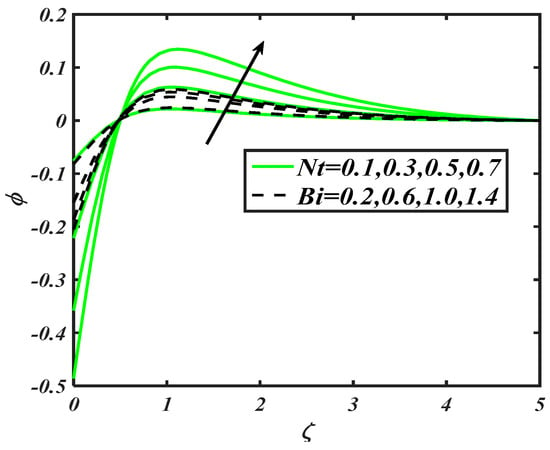
Figure 8.
Illustration of and on .
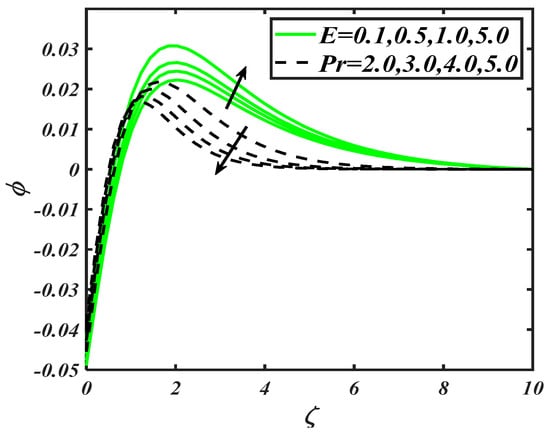
Figure 9.
Illustration of and on .
The motile microorganisms distribution is plotted in Figure 10 and Figure 11 for combined parameter , mixed convection constant , Peclet number and bioconvection Lewis number . The graphical inspected in Figure 10 taken account the effects of and . The motile microorganisms distribution raises with increment of . However, in case of , the distribution of motile microorganism increases. From Figure 11, it is notified that both Peclet number and bioconvection Lewis number decreases the motile microorganism distribution. The dimensionless Pecletnumber is inversely related to motile diffusivity. Therefore, higher values of accumulate lower motile diffusivity, which turn down the motile microorganisms’ distribution.
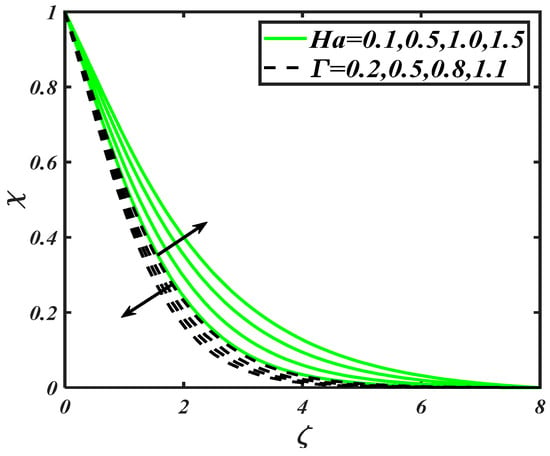
Figure 10.
Illustration of and on .
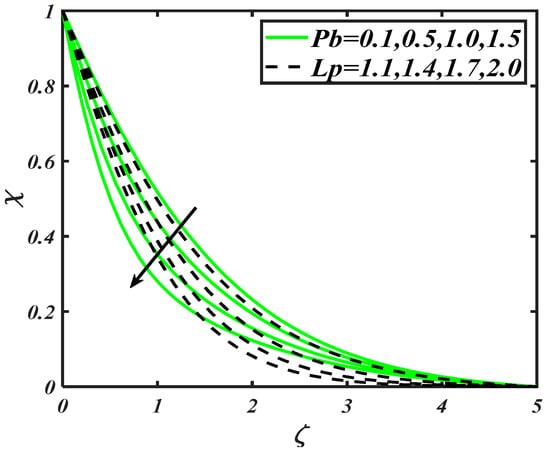
Figure 11.
Illustration of and over .
Table 2 determines the numerical variation of against values of , , , , , and . The numerical values of increase for , and in contrast to all remaining parameters. The variation in local Nusselt number has been captured for varying values of , , , , , , , and in Table 3. Maximum values of local Nusselt number are obtained with variation of while it decreases with all other parameters. From Table 4, we note that the local Sherwood number increases with variation of and . Finally, the variation in local motile density number has been iterated in Table 5. Carefully observing, we see that local motile density number decreases with slip parameters and while increasing trend has been noted for and .

Table 2.
Variation of skin friction coefficient for , , , , , and .

Table 3.
Variation in local Nusselt number for , , , , , , , and .

Table 4.
Variation in local Sherwood number for , , , , , and .

Table 5.
Variation of motile density number for of , , , , , , , and .
6. Concluding Remarks
We have incorporated the Wu’s slip effects, thermal radiation, and activation energy features in bioconvection of Powell Eyring nanofluid over a moving configuration. The formulated problem is solved numerically by incorporating the shooting technique. Some valuable observations from current analysis are summarized as:
- ❖
- A devaluate distribution of velocity has been observed for higher values of combine parameter, first order slip parameter and second order slip parameter.
- ❖
- The distribution of velocity attains maximum values with mixed convection parameter.
- ❖
- The nanoparticles temperature rises with thermophoresis parameter, Biot number and radiation parameter.
- ❖
- A decreasing variation in nanoparticles concentration has been figured out for mixed convection parameter and Brownian motion constant.
- ❖
- Both Peclet number and the bio-convection Lewis number retarded the motile microorganism distribution.
- ❖
- The observations presented here can be simulated to enhance the performances of various thermo-extrusion systems.
Author Contributions
A.M.A., S.U.K., H.W. and I.T. modeled the problem, numerically computed results, discussed the results physically, computed the tabulated results, wrote the manuscript, revised it and proof read it.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: IL, San Francisco, CA, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Madhu, M.; Kishan, N. Finite Element Analysis of heat and mass transfer by MHD mixed convection stagnation-point flow of a non-Newtonian power-law nanofluid towards a stretching surface with radiation. J. Egypt. Math. Soc. 2016, 24, 458–470. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.; Shafee, A.; Li, Z.; Elaraki, Y.G.; Tlili, I. Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. Int. J. Heat Mass Transf. 2019, 135, 470–478. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, D.; Singh, J. MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation. Int. J. Heat Mass Transf. 2018, 118, 378–387. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Ahmad, B. Magnetohydrodynamic (MHD) nonlinear convective flow of Walters-B nanofluid over a nonlinear stretching sheet with variable thickness. Int. J. Heat Mass Transf. 2017, 110, 506–514. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Free and circular jets cooled by single phase nanofluids. Eur. J. Mech. B-Fluid 2019, 76, 1–6. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. MHD Flow of Nanofluid Flow Across Horizontal Circular Cylinder: Steady Forced Convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J. Mol. Liq. 2019, 287, 110853. [Google Scholar] [CrossRef]
- Khan, M.I.; Alsaedi, A.; Hayat, T.; Khan, N.B. Modeling and computational analysis of hybrid class nanomaterials subject to entropy generation. Comput. Meth. Prog. Biol. 2019, 179, 104973. [Google Scholar] [CrossRef]
- Ahmed, A.; Nadeem, S. Effects of magnetohydrodynamics and hybrid nanoparticles on a micropolar fluid with 6-types of stenosis. Results Phys. 2017, 7, 4130–4139. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M.; Alshomrani, A.S. Unsteady slip flow of Carreaunanofluid over a wedge with nonlinear radiation and new mass flux condition. Results Phys. 2017, 7, 2261–2270. [Google Scholar] [CrossRef]
- Powell, R.E.; Eyring, H. Mechanisms for the relaxation theory of viscosity. Nature 1944, 154, 427–428. [Google Scholar] [CrossRef]
- Javed, T.; Ali, N.; Abbas, Z.; Sajid, M. Flow of an Eyring-Powell Non-Newtonian Fluid over a Stretching Sheet. Chem. Eng. Comm. 2013, 200, 327–336. [Google Scholar] [CrossRef]
- Khan, N.A.; Sultan, F. On the double diffusive convection flow of Eyring-Powell fluid due to cone through a porous medium with Soret and Dufour effects. AIP Adv. 2015, 5, 057140. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, N.; Hayat, T. Analytical and Numerical Study of Diffusion of Chemically Reactive Species in Eyring-Powell Fluid over an Oscillatory Stretching Surface. Bulg. Chem. Commun. 2017, 49, 320–330. [Google Scholar]
- Mallick, B.; Misra, J.C. Peristaltic flow of Eyring-Powell nanofluid under the action of an electromagnetic field. Eng. Sci. Technol. Int. J. 2019, 22, 266–281. [Google Scholar] [CrossRef]
- Akbar, N.S.; Ebaid, A.; Khan, Z.H. Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Malik, M.Y.; Khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 2015, 5, 117118. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, N.; Abbas, Z. Influence of Heat Generation/Absorption with Convective Heat and Mass Conditions in Unsteady Flow of Eyring Powell Nanofluid over Porous Oscillatory Stretching Surface. J. Nanofluids 2016, 5, 351–362. [Google Scholar] [CrossRef]
- Wang, S.; Ardekani, A.M. Unsteady swimming of small organisms. J. Fluid Mech. 2012, 702, 286–297. [Google Scholar] [CrossRef]
- Elfring, G.J.; Goyal, G. The effect of gait on swimming in viscoelastic fluids. J. Non-Newton Fluid 2016, 234, 8–14. [Google Scholar] [CrossRef][Green Version]
- Kuznetsov, A.V. The onset of nanofluidbioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluidbioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 100. [Google Scholar] [CrossRef] [PubMed]
- Siddiqa, S.; Begum, N.; Saleem, S.; Hossain, M.A.; Gorla, R.S.R. Numerical solutions of nanofluid bio-convection due to gyrotactic microorganisms along a vertical wavy cone. Int. J. Heat Mass Transf. 2016, 101, 608–613. [Google Scholar] [CrossRef]
- Khan, A.; Farooq, M.; Gull, N.; Hayat, T. Magnetohyrodynamic (MHD) stratified bio-convective flow of nanofluid due to gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 288–298. [Google Scholar]
- Khan, W.A.; Uddin, M.J.; Ismail, A.I.M. Free convection of non-Newtonian nanofluids in porous media with gyrotactic microorganisms. Trans. Porous Media 2013, 97, 241–252. [Google Scholar] [CrossRef]
- Xun, S.; Zhao, J.; Zheng, L.; Zhang, X. Bio convection in rotating system immersed in nanofluid with temperature dependent viscosity and thermal conductivity. Int. J. Heat Mass Transf. 2017, 111, 1001–1006. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bio convection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Shehzad, S.A.; Imran, M. Radiative flow of Maxwell nanofluid containing gyrotactic microorganisms and energy activation with convective Nield conditions. Heat Transf.-Asian Res. 2019, 48, 1663–1687. [Google Scholar] [CrossRef]
- Dero, S.; Uddin Md, J.; Rohni, A.M.R. Stefan Blowing and Slip Effects on Unsteady Nanofluid Transport Past a Shrinking Sheet: Multiple Solutions. Heat Transf. Asian Res. 2019. [Google Scholar] [CrossRef]
- Tlili, I. Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry 2019, 11, 438. [Google Scholar] [CrossRef]
- Goodarzi, M.; Tlili, I.; Tian, Z.; Safaei, M. Efficiency assessment of using graphene nanoplatelets-silver/water nanofluids in microchannel heat sinks with different cross-sections for electronics cooling. Int. J. Numer. Methods Heat Fluid Flow 2019. [CrossRef]
- Afridi, M.I.; Tlili, I.; Goodarzi, M.; Osman, M.; Khan, N.A. Irreversibility Analysis of Hybrid Nanofluid Flow over a Thin Needle with Effects of Energy Dissipation. Symmetry 2019, 11, 663. [Google Scholar] [CrossRef]
- Tlili, I. Tawfeeq Abdullah Alkanhal, Nanotechnology for water purification: Electrospun nanofibrous membrane in water and wastewater treatment. J. Water Reuse Desalin. 2019, 24. [Google Scholar] [CrossRef]
- Tlili, Iskander. Thermodynamic Study on Optimal Solar Stirling Engine Cycle Taking Into Account the Irreversibilities Effects. Energy Procedia. 2012, 584–591. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. Entropy Generation Due to MHD Stagnation Point Flow of a Nanofluid on a Stretching Surface in the Presence of Radiation. J. Nanofluids 2018, 7, 879–890. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Abel, M.S.; Siddalingappa, M. Second order slip flow and heat transfer over a stretching sheet with non-linear Navier boundary condition. Int. J. Therm. Sci. 2012, 58, 143–150. [Google Scholar] [CrossRef]
- Rosca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Shehzad, S.A.; Imran, M. Theoretical analysis for tangent hyperbolic nanoparticles with combined electrical MHD, activation energy and Wu’s slip features: A mathematical model. Phys. Scr. 2019. [Google Scholar] [CrossRef]
- Ibrahim, W. Magnetohydrodynamics (MHD) flow of a tangent hyperbolic fluid with nanoparticles past a stretching sheet with second order slip and convective boundary condition. Results Phys. 2017, 7, 3723–3731. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. MHD boundary layer flow and heat transfer over a stretching sheet with induced magnetic field. Heat Mass Transf. 2011, 47, 155–162. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Khan, I. Multiple slips effects on MHD SA-Al2O3 and SA-Cu non-Newtonian nanofluids flow over a stretching cylinder in porous medium with radiation and chemical reaction. Results Phys. 2018, 8, 213–222. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A. Thermodynamic Analysis of MHD Heat and Mass Transfer of Nanofluids Past a Static Wedge with Navier Slip and Convective Boundary Conditions. Arab. J. Sci. Eng. 2018, 1–13. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A.; Atawneh, S. Thermodynamic analysis of MHD Couette—Poiseuille flow of water—Based nanofluids in a rotating channel with radiation and Hall effects. J. Therm. Anal. Calorim. 2018, 132, 1899–1912. [Google Scholar] [CrossRef]
- Khan, W.A.; Rashad, A.M.; Abdou, M.M.M.; Tlili, I. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur. J. Mech.-B/Fluids 2019, 75, 133–142. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Therm. Eng. 2018, 12, 374–380. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).