Darcy–Forchheimer Radiative Flow of Micropoler CNT Nanofluid in Rotating Frame with Convective Heat Generation/Consumption

Abstract

Since 1991, from the beginning of the carbon nanotube era, this has been a focus point for investigation due to its synthetic and simple nature. Unique properties like good stiffness, high surface area, and resilience of carbon nanotubes (CNTs) have been investigated in many engineering applications such as hydrogen storage, composite material, energy storage, electrochemical super-capacitors, transistors, sensors, and field-emitting devices. Keeping in view these applications, we investigate single and multi-walled CNTs nanofluid flow having water as the base fluid between parallel and horizontal rotating plates with microstructure and inertial properties. The thermal radiation effect is considered for variable phenomenon of heat generation/consumption. The principal equations are first symmetrically transformed to a system of nonlinear coupled ordinary differential equations (ODEs), and then, Homotopy Analysis Technique (HAM) and numerical method are employed for solving these coupled equations. The obtained analytical and numerical results are explained graphically and through different tables. The HAM and numerical results show an excellent agreement. The Skin friction and the Nusselt number are numerically calculated and then analyzed with the already published results, and these results are found to be in agreement with one another. The impact of important parameters are shown graphically.

1. Introduction

The novel progress in nanotechnology has produced a pioneering and inventive kind of heat-carrying liquid called nanoliquids, which are formed by the dispersal of tiny solid particles (1 nm–100 nm) in classical liquids. There are different kinds of classical liquids like bio-fluid, polymeric mixture, numerous oils, lubricants, water, toluene, refrigerants, ethylene glycol, etc. which can carry heat through very short ranges and are broadly used for various engineering and technological purposes. In order to improve the heat transport rate of such liquids, the nanoparticles of different materials are scattered consistently in these classical fluids. Carbon nanotubes (CNTs) are nanomaterials with diameters below 100 nm. CNTs can be refined or produced to retain definite properties such as optical transmissions, electrical conductivity, and gas absorption. CNTs were introduced by Iijima [1]. Different CNTs studies based on structure, usage, characteristics, and shapes can be found in Ciraci et al. [2], Novoselov et al. [3] and Casari et al. [4]. CNTs have significant applications in nanotechnology, sensor devices, storage of gas, air refinement devices, conductive plastics, hard water, and many more. Due to such real-world applications, the investigators have shown great devotion to the field of nanotechnology [5,6,7]. CNTs based on nanoliquid flow over extending sheets has been studied by Imtiaz et al. [8]. Different features of CNTs in chemical reactions and in melting during Darcy–Forchheimer flow has been investigated by Hayat [9]. Mahanthesh and others [10] have inspected the magneto hydro dynamic (MHD) flow of CNT nanofluids by taking into consideration the impact of thermal energy. MHD slip flow with CNTs and convective heat energy transfer has been presented by Raja et al. [11]. Shah et al. [12] has analyzed the Darcy–Forchheimer radiative flow of CNTs in a circulating frame. Jawad et al. [13] examined the nonlinear thermal impact on the three-dimensional CNT flow with viscous dissipation. Sheikholeslami et al. [14,15,16] have numerically treated the nanofluid flow in porous media by considering different channels. Shah et al. [17,18,19] has studied the nanofluid flow by considering the impacts of Brownian motion, thermophoresis, and Hall current between parallel plates. The effects of radiations and heat source/sink on the flow of a nanofluid over a stretching surface has been given by Dawar et al. [20]. A more brief survey on the analysis of stretching surface can be found with different fluid models in Shah et al. [21] and Ameen et al. [22]. The Casson fluid flow with radiation impacts in rotating channels has been examined by Dawar et al. [23]. Sohail et al. [24] has analyzed Ferrofluid flow during the impact of magnet and drug targeting. This fluid is also discussed on the stretching surface by Zeeshan et al. [25]. Further analysis of Ferrofluid with different physical explorations can be found in Majeed et al. [26].

Eringon [27] has given for the first time the clue of micro-polar fluid, and then it was briefly explained by Lukaszewicz [28]. Mohammeadein and Gorla [29] have undertaken the MHD micro-polar fluid flow over a stretching surface. The Darcy–Forchheimer micro-polar nanofluid flow in a rotating frame which results in heat generation/absorption has examined by Khan et al. [30]. Many industrial as well as environmental systems, for example, geo-thermal energy and heat exchanger operating systems, contain the convective heat transfer flow on porous media. For investigation of all the relevant characteristics, Forchheimer [31] has explained the additional relation in momentum. Muskat [32] has called this additional relation the Forchheimer relation. The initial study on Darcian free convention flow has performed by Cheng et al. [33]. Later on, the appropriate similarity alternation has been suggested by Merkin [34]. The general form of the Merkin research was deliberated by Nakayama et al. [35]. The MHD flow of Darcy–Forchheimer nanofluid has been deliberated by Jawad et al. [36]. Further relevant studies can be found in Shah et al. [37], Khan et al. [38], Nasir et al. [39], Islam et al. [40] and Ellahi et al. [41]. Raju et al. [42] has determined the MHD flow of nanofluids over a cone. The uniform magnetic force effect on the thermal behavior of the water-based nanofluid has been explained by Sheikholeslami et al. [43]. Rehman et al. [44] has undertaken the MHD-flow of carbon micro-polar nanofluids in a rotating frame by taking into account the convective heat transfer during the flow. Some interesting studies related to nanofluid non-Newtonian flow field can be found in Hayat et al. [45], Tian et al. [46], Hsiao and Long [47] and Hsiao and Long [48]. The entropy production analysis during the carbon nanotube flows in a rotatory system by considering together the Hall and Ion-slip effects has been given by Feroz et al. [49]. A more brief survey on the entropy generation with different geometrical and analytical explorations can be found in Ellahi et al. [50,51]. Additional information about the relevant study can be explored in Sheikholeslami et al. [43], Ellahi et al. [52], Rehman et al. [44], Feroz et al. [49], Khan et al. [53] and Shah et al. [54].

In the current paper, single and multi-walled (CNT) nanofluid flow by taking water as the base fluid between parallel and horizontal rotating plates with microstructures and inertial properties is studied. Influences of nonlinear heat generation/absorption are presented. The important key factors are described in the output. Homotopy Analysis Technique (HAM) and the NDsolve [55,56,57,58,59,60] technique are used for solution purposes. In Section 2 the problem and geometry is explained. The results obtained are discussed in Section 3. The tables are presented and discussed in Section 4. This work is concluded in Section 5. Homotypic operators and theory are used in the solution section.

2. Problem Statement

Consider the steady flow of micro-polar nanofluid water-based carbon nanotubes among parallel plates. The geometry of the model is chosen such that both the nanofluid and plates are circulating around the y-axis with angular speed $\overline{\omega }$, as shown in Figure 1. The separation distance between the two plates is h. Equal and opposite forces are acting on the lower plate along x-axis which can stretch it with linear velocity $u=\alpha x$, where $\alpha >0$. A Darcy–Forchheimer model is assumed for the porosity. The temperature and concentration at the lower plates are taken as $T=T_h$ and $C=C_h$, respectively. Thermal radiation is assumed for irregular suction/injection. After applying these assumptions, the governing equations can be written as follows [9,10,18,19]:

$$u_x+v_y+w_z=0,$$

(1)

$$u{u}_x+v{u}_y+2w\overline{\omega }=-\frac{P_x}{{\rho }_f}+\left({\nu }_{nf}+\frac{\beta }{{\rho }_f}\right)\left(u_{xx}+u_{yy}\right)+\frac{\beta }{{\rho }_f}{N}_y-\frac{1}{{\rho }_f}\left(\frac{{\nu }_{nf}}{B}\right)u-\frac{1}{{\rho }_f}E{u}^2,$$

(2)

$$u{v}_x+v{v}_y=-\frac{P_y}{{\rho }_f}+\left(v_{xx}+v_{yy}\right)+\frac{\beta }{{\rho }_f}{N}_x,$$

(3)

$$u{w}_x+v{w}_y-2u\overline{\omega }=\left({\nu }_{nf}+\frac{\beta }{{\rho }_f}\right)\left(w_{xx}+w_{yy}\right)-\frac{1}{{\rho }_f}\left(\frac{{\nu }_{nf}}{B}\right)w-\frac{1}{{\rho }_f}E{w}^2,$$

(4)

$$u{T}_x+v{T}_y+w{T}_z={\alpha }^{*}\left(T_{xx}+T_{yy}+T_{zz}\right)+\frac{1}{{\left(\rho c\right)}_p}\left(q^{{}^{‴}}-q_y^{rd}\right),$$

(5)

$$u{N}_x+v{N}_y=-\frac{\gamma }{{\rho }_j}\left(N_{xx}+N_{yy}\right)-\frac{2\beta N}{{\rho }_j}+\frac{\beta }{{\rho }_j}\left(v_x-u_y\right).$$

(6)

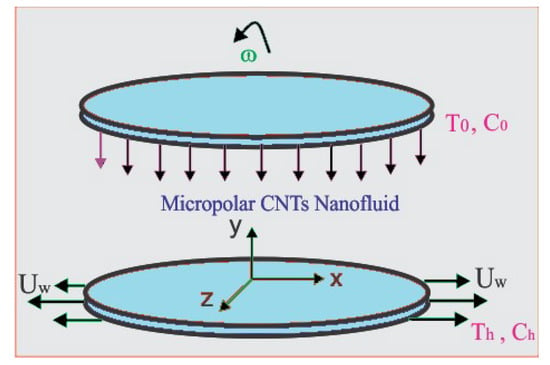
Figure 1. Geometrical sketch of the phenomenon.

In the above equations, ${\nu }_{nf}$, $\mu$, ${\rho }_f$, N, $\overline{\omega }$, $\beta$, B, $E=C_b{\left(bx\right)}^{-1/2}$, $C_b$, T, ${\alpha }^{*}$, $D_B$, $D_T$, $c_p$, ${\tau }^{*}$, and C represent kinematic viscosity, dynamic viscosity, density, micro rotational velocity, angular velocity, vertex viscosity, magnetic field strength, variable inertia coefficient, drag coefficient, temperature, thermal diffusivity, Brownian diffusion coefficient, thermophoretic diffusion coefficient, specific heat, fraction between nanofluid and heat capacity, and concentration of nanoparticles, respectively. The thermal radiation is mathematically defined as $q^{rd}=-\frac{16{\Theta }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y}$. After Taylor series expansion [12,18], we get

$$\frac{\partial q^{rd}}{\partial y}=-\frac{16T_0^3{\Theta }^{*}}{3k^{*}}\frac{\partial T^2}{{\partial }^{2}y}.$$

(7)

The term $q^{{}^{‴}}$ in Equation (5) is used for the irregular heat generation/consumption and is given as follows:

$$q^{{}^{‴}}=\frac{\beta u}{xv}\left(I(T-T_h)f^{{}^{\prime }}\left(\xi \right)+(T-T_h)J\right),$$

(8)

where I represents the temperature coefficient and J represents the space dependence of heat sink and source. The necessary boundary restriction are given by

$$\begin{array}{c}\hfill u=\alpha x,v=w=0,T=T_h,N=-\frac{\partial u}{\partial y}k\mathrm{at}y=0,\\ \hfill u=v=w=0,T=T_0,N=\frac{\partial u}{\partial y}k\mathrm{at}y=h.\end{array}$$

(9)

For the CNT nanofluids, the following model is presented by Xue [61].

$$\begin{array}{c}\hfill {\mu }_{nf}=\frac{{\mu }_f}{{(1-\phi )}^{2.5}},{\nu }_{nf}=\frac{{\mu }_{nf}}{{\rho }_{nf}},{\alpha }_{nf}=\frac{{\mu }_{n}f}{{\left(\rho c_p\right)}_{nf}},{\rho }_{nf}=(1-\phi ){\rho }_f+\phi {\rho }_{CNT},\\ \hfill {\left(\rho c_p\right)}_{nf}={\left(\rho c_p\right)}_f\left((1-\phi )+\left(\frac{{\left(\rho c_p\right)}_{CNT}}{{\left(\rho c_p\right)}_f}\right)\phi \right),\\ \hfill \frac{k_{nf}}{k_f}=\frac{1-\phi +2\phi \left(\frac{k_{CNT}}{k_{CNT}-k_f}\right)ln\left(\frac{k_{CNT}+k_f}{2k_f}\right)}{1-\phi +2\phi \left(\frac{k_f}{k_{CNT}-k_f}\right)ln\left(\frac{k_{CNT}+k_f}{2k_f}\right)}.\end{array}$$

(10)

Introducing the new transformation [18,19], we get

$$\begin{array}{c}\hfill u=\alpha x{f}^{{}^{\prime }}\left(\xi \right),v=-\alpha hf\left(\xi \right),N=-\frac{\alpha xG\left(\xi \right)}{h},\\ \hfill w=\alpha xg\left(\xi \right),\theta \left(\xi \right)=\frac{T-T_h}{T_0-T_h},\xi =\frac{y}{h}.\end{array}$$

(11)

Using Equation (10) in Equations (2)–(9), we get

$${\xi }_1\left(\left(\frac{1}{{\xi }_2}+P_1\right)f^{i\nu }+P_1{G}^{{}^{″}}-\gamma f^{{}^{\prime }}-2E_r{f}^{{}^{\prime }}{f}^{{}^{″}}\right)-\mathit{Re}(f^{{}^{\prime }}{f}^{{}^{″}}-f{f}^{{}^{‴}})-2N_r{g}^{{}^{\prime }}=0,$$

(12)

$${\xi }_1\left(\left(\frac{1}{{\xi }_2}+P_1\right)g^{{}^{″}}-\gamma g-E_r{g}^2\right)+\mathit{Re}(f{g}^{{}^{\prime }}-g{f}^{{}^{\prime }})+2N_r{f}^{{}^{\prime }}=0,$$

(13)

$$\frac{1}{{\xi }_1}\left({\xi }_3+\frac{4}{3}\mathit{Rd}\right){\theta }^{{}^{″}}-(I_1{f}^{{}^{\prime }}+J_1\theta )=0,$$

(14)

$${\xi }_1\left(P_2{G}^{{}^{″}}-P_1(2G+f^{{}^{″}})\right)-P_3\mathit{Re}(G{f}^{{}^{\prime }}-G^{{}^{\prime }}f)=0.$$

(15)

We have used the following symbols for simplification:

$$\begin{array}{c}\hfill {\xi }_1=\left((1-\phi )+\left(\frac{{\left(\rho c_p\right)}_{CNT}}{{\left(\rho c_p\right)}_f}\right)\phi \right),{\xi }_2={(1-\phi )}^{2.5},{\xi }_3=\frac{k_{nf}}{k_f}\end{array}$$

(16)

$$\begin{array}{c}\hfill f=g=0,f^{{}^{\prime }}=\theta =\phi =1,G=-k{f}^{{}^{″}},\mathrm{at}\xi =0,\\ \hfill f^{{}^{\prime }}=g=\theta =\phi =0,f=\delta =0,G=k{f}^{{}^{″}},\mathrm{at}\xi =1.\end{array}$$

(17)

In the above equations, the different parameters are defined as Rotation parameter ($N_r=\frac{2\overline{\omega }{h}^2}{{\nu }_{nf}}$), permeability ($\gamma =\frac{h^2{\nu }_{nf}}{aB}$), coefficient of inertia ($E_r=\frac{h^2{C}_b{B}^{-0.5}}{\rho }$), coupling ($P_1=\frac{\beta }{\mu }$), transpiration parameter ($\delta =\frac{{\nu }_0}{h}$), viscosity gradient ($P_2=\frac{{\nu }_s}{{\nu }_{nf}{h}^2}$), Reynold number ($\mathit{Re}=\frac{a{h}^2}{{\nu }_{nf}}$), micro-polar fluid constant ($P_3=\frac{j}{h^2}$), volume friction of nanofluid ($\phi$), thermal conductivity (k), and thermal radiation ($\mathit{Rd}=\frac{4T_0^3\eta }{{\left(\rho c_p\right)}_f\beta K}$). Here, $I_1$ and $J_1$ signify temperature- and space-dependent coefficients heat generation and absorption, where at $I_1>0$ and $J_1>0$, they link to inner heat source and, at $I_1<0$ and $J_1<0$, they correspond to inner heat sink. The skin friction $\left(C_f\right)$ and Nusselt number $\left(Nu\right)$ are defined as follows:

$$C_f={\xi }_1\left(\frac{1}{{\xi }_2}+P_1\right)f^{{}^{″}}\left(0\right)+P_{1}G\left(0\right),\mathit{Nu}=-\left({\xi }_3+\frac{4}{3}\mathit{Rd}\right){\theta }^{{}^{\prime }}\left(0\right).$$

(18)

3. Results and Discussion

This section is devoted to studying graphically the effects produced by different physical variables on profiles of velocity components ($f^{{}^{\prime }}\left(\xi \right)$, $g\left(\xi \right)$, $G\left(\xi \right)$) and temperature ($\theta \left(\xi \right)$) for single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs). These parameters are nanoparticle volume fraction $\phi$, permeability parameter $\gamma$, rotation parameter $N_r$, Reynolds number Re, inertial coefficient $E_r$, thermal radiation parameter $Rd$, coupling $P_1$, temperature-dependent coefficient $J_1$, and space-dependent parameter $I_1$.

The dependence of $f^{{}^{\prime }}\left(\xi \right)$ as well as $g\left(\xi \right)$ on $\phi$ is shown in Figure 2. From Figure 2a, it is clear that, with the escalating $\phi$, $f^{{}^{\prime }}\left(\xi \right)$ shows an increasing behavior in the domain $0.0\le \xi <0.5$, whereas it displays a reducing trend in the zone $0.5<\xi \le 1.0$. It is further evident that the increasing (decreasing) trend for SWCNTs is more rapid as compared to MWCNTs. Figure 2b shows that $g\left(\xi \right)$ varies inversely with respect to $\xi$ up to about $\xi =0.4$ and, beyond this value, shows an increase at fixed $\phi$. By increasing the value of $\phi$, $g\left(\xi \right)$ increases for both types of CNTs. Furthermore, the rate of variation of $g\left(\xi \right)$ is larger for MWCNTs as compared to SWCNTs. The effect of $\gamma$ on $f^{{}^{\prime }}\left(\xi \right)$ as well as $g\left(\xi \right)$ is depicted in Figure 2c,d, respectively. It is noted that $f^{{}^{\prime }}\left(\xi \right)$ displays dual behavior with the increasing $\gamma$. The profile of $f^{{}^{\prime }}\left(\xi \right)$ escalates in the zone $0\le \xi \le 0.5$, whereas it declines beyond it, that is, in the range $0.5<\xi \le 1$, with the higher $\gamma$ for both kinds of CNTs. From Figure 2d, it is clear that $g\left(\xi \right)$ enhances as we increase $\phi$ to larger values for both kinds of CNTs.

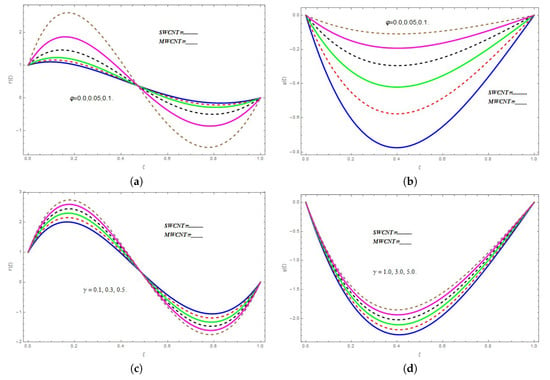
Figure 2. (a) Variation in $f^{{}^{\prime }}\left(\xi \right)$ with different values of $\phi$; (b) Variation in $g\left(\xi \right)$ with different values of $\phi$; (c) Impact of $\gamma$ on $f^{{}^{\prime }}\left(\xi \right)$; (d) Impact of $\gamma$ on $g\left(\xi \right)$

The dependence of the functions $f^{{}^{\prime }}\left(\xi \right)$ as well as $g\left(\xi \right)$ on $Re$ is depicted in Figure 3a,b. We observe from Figure 3a,c that $f^{{}^{\prime }}\left(\xi \right)$ shows the same dual behaviour as in the case of Figure 2a,c. The function $f^{{}^{\prime }}\left(\xi \right)$ increases in the range $0\le \xi \le 0.5$, whereas it reduces in the range $0.5\le \xi \le 1.0$ with larger $Re$. It is apparent from Figure 3b that $g\left(\xi \right)$ shows an increasing and measurable behaviour with respect to larger $Re$ only for intermediate values of $\xi$. The dependence of $f^{{}^{\prime }}\left(\xi \right)$ and $g\left(\xi \right)$ on $E_r$ is depicted in the Figure 3c,d, respectively. The angular form of Newton’s 2nd law indicates that the moment of inertia of a rotating system, which is the ratio of the net torque and angular acceleration, is a constant of motion. The higher values of inertial coefficient causes the fluid velocity to decline. The dual behavior is observed in both figures with the escalation in the inertial coefficient. This dual trend is a result of the frame rotation.

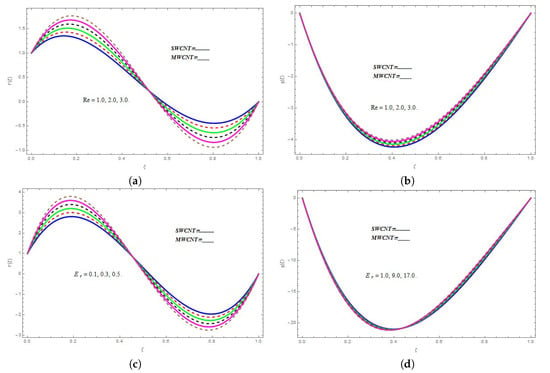
Figure 3. (a) Impact of $Re$ on $f^{{}^{\prime }}\left(\xi \right)$; (b) Impact of $Re$ on $g\left(\xi \right)$; (c) Impact of $E_r$ on $f^{{}^{\prime }}\left(\xi \right)$; (d) Impact of $E_r$ on $g\left(\xi \right)$

The influence of $N_r$ on both $f^{{}^{\prime }}\left(\xi \right)$ as well as $g\left(\xi \right)$ is displayed by Figure 4a,b. Within the restricted region, the escalating values of $N_r$ first result in a decrease and, after that, cause a growing behavior in the profile of $f^{{}^{\prime }}\left(\xi \right)$. In the $0\le \xi \le 0.6$ region, the increasing $N_r$ displays a declining impact of $f^{{}^{\prime }}\left(\xi \right)$ whereas, in the range $0.6\le \xi \le 1.0$, shows a rising impact of $f^{{}^{\prime }}\left(\xi \right)$, as shown in Figure 4a. The decreasing impact of $g\left(\xi \right)$ with the increasing values $N_r$ is evident from Figure 4b for both kinds of CNTs. Figure 4c,d demonstrates the effect produced by $P_1$ on profiles of both $f^{{}^{\prime }}\left(\xi \right)$ as well as $g\left(\xi \right)$. The coupling parameter defines the strength of the applied force in an interaction. It determines the strength of the interaction part with respect to the kinetic part. The escalating $P_1$ shows a dual behavior in the $f^{{}^{\prime }}\left(\xi \right)$ profile. $f^{{}^{\prime }}\left(\xi \right)$ increases in the domain $0\le \xi \le 0.55$, while it reduces in the zone $0.55\le \xi \le 1.0$ for SWCNTs as well as for MWCNTs. The rate of variation is faster for SWCNTs in comparison with MWCNTs. The dependence of $g\left(\xi \right)$ on $P_1$ is plotted in Figure 4d. This graph again depicts that $g\left(\xi \right)$ changes at a faster rate with increasing $P_1$ for SWCNTs.

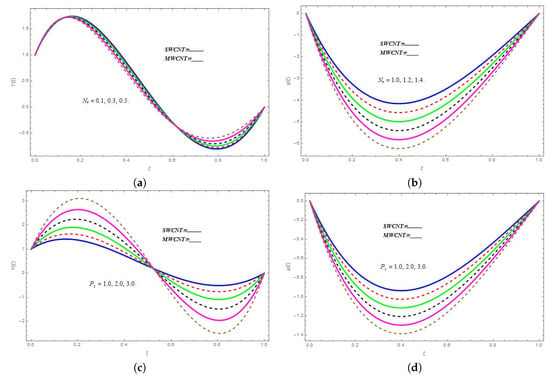
Figure 4. (a) Impact of $N_r$ on $f^{{}^{\prime }}\left(\xi \right)$; (b) Impact of $N_r$ on $g\left(\xi \right)$; (c) Impact of $P_1$ on $f^{{}^{\prime }}\left(\xi \right)$; (d) Impact of $P_1$ on $g^{(}\xi )$

The influence of $\phi$ on $\theta \left(\xi \right)$ is displayed in the Figure 5a. The rising values of $\phi$ shows an increasing trend in the $\theta \left(\xi \right)$ profile up to $\xi =0.8$, and then, the different curves start to overlap for both types of CNTs. The effect of $Rd$ on $\theta \left(\xi \right)$ is plotted in Figure 5b. The thermal radiations have a useful role in the heat energy transformation during the fluid flow process. The increasing thermal radiation values enhance the boundary layer flow rate, which results in the fluid temperature rising. Therefore, the temperature function $\theta \left(\xi \right)$ profile enhances for the higher values of $Rd$. Figure 5c,d depicts the influence of $J_1$ and $I_1$ on the temperature function $\theta \left(\xi \right)$. Both figures display the increasing effect of $J_1$ and $I_1$ on $\theta \left(\xi \right)$.

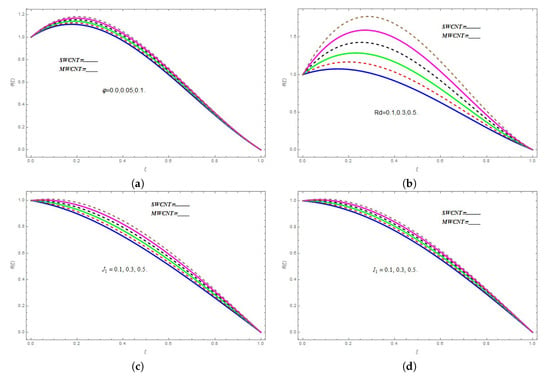
Figure 5. (a) Variations in $\theta \left(\xi \right)$ under different values of $\phi$; (b) Impact of $Rd$ on $\theta \left(\xi \right)$; (c)Impact of $J_1$ on $\theta \left(\xi \right)$; (d) Impact of $I_1$ on $\theta \left(\xi \right)$

The effect of $\phi$ on velocity function $G\left(\xi \right)$ is plotted in Figure 6a. The higher values of $\phi$ escalates the velocity function $G\left(\xi \right)$. Similar impacts of $P_1$ and $Re$ on velocity function $G\left(\xi \right)$ can be seen in Figure 6b,c, respectively.

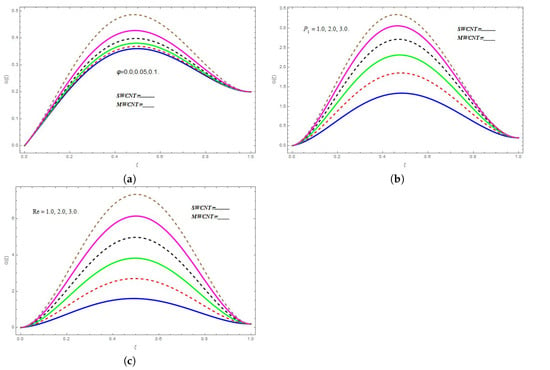
Figure 6. (a) Impact of $\phi$ on $G\left(\xi \right)$; (b) Variations in $G\left(\xi \right)$ under different values of $P_1$; (c) Impact of $Re$ on $G\left(\xi \right)$

The comparison between HAM results and numerical computations for the velocity and temperature profiles are displayed in Figure 7a–d. We see that the results obtained from analytical calculations and numerical computations are in excellent agreement for the undertaken study.

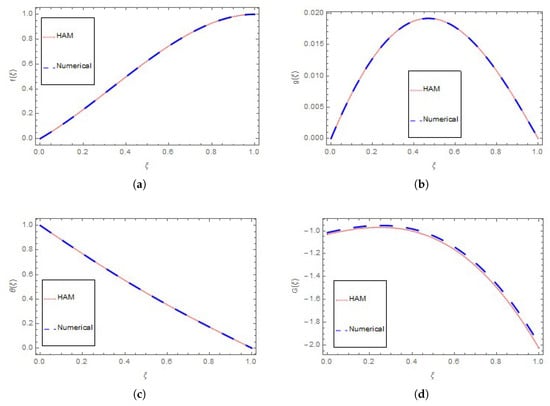
Figure 7. (a) Homotopy Analysis Method and Numerical method comparasion for $f\left(\xi \right)$; (b) Homotopy Analysis Method and Numerical method comparasion for $g\left(\xi \right)$; (c) Homotopy Analysis Method and Numerical method comparasion for $\theta \left(\xi \right)$; (d) Homotopy Analysis Method and Numerical method comparasion for $G\left(\xi \right)$

4. Tables Discussion

The comparison between analytical and numerical results for velocities, temperature, and concentration profiles is given in Table 1, Table 2, Table 3 and Table 4. From these tables, an excellent agreement between HAM and the numerical technique (ND-Solve Techniques) can be seen. The impact of physical quantities like $C_{fx}$, $C_{fy}$, and $N{u}_x$ for SWCNTs as well as for MWCNTs is shown in Table 5 and Table 6. The results obtained in the present study are then compared to the already published results [56]. It is found that both the present and published results are in agreement with each other.

Table 1. Comparision of HAM and Numerical results for $f\left(\xi \right)$.

$\mathit{\xi }$	HAM	Numerical Solution	Absolute Error
0.0	0.000000	0.000000	0.000000
0.2	0.232368	0.232374	6.268670 $\times {10}^{-6}$
0.4	0.496777	0.496789	0.000012
0.6	0.744737	0.744747	0.000010
0.8	0.928319	0.928323	3.595600 $\times {10}^{-6}$
1.0	1.000000	1.000000	6.712830 $\times {10}^{-6}$

Table 2. Comparision of HAM and Numerical results for $f\left(\xi \right)$.

$\mathit{\xi }$	HAM	Numerical Solution	Absolute Error
0.0	0.000000	0.000000	0.000000
0.2	0.012272	0.012272	1.023590 $\times {10}^{-7}$
0.4	0.018772	0.018772	1.820060 $\times {10}^{-8}$
0.6	0.017780	0.017780	1.174780 $\times {10}^{-7}$
0.8	0.010785	0.010785	1.308180 $\times {10}^{-7}$
1.0	−4.727530 $\times {10}^{-18}$	3.064270 $\times {10}^{-9}$	3.064270 $\times {10}^{-9}$

Table 3. Comparision of HAM and Numerical results for $f\left(\xi \right)$.

$\mathit{\xi }$	HAM	Numerical Solution	Absolute Error
0.0	1.000000	1.000000	0.000000
0.2	0.769682	0.769582	3.824810 $\times {10}^{-7}$
0.4	0.553068	0.553068	5.869700 $\times {10}^{-8}$
0.6	0.354231	0.354231	4.542170 $\times {10}^{-7}$
0.8	0.171895	0.171896	4.981640 $\times {10}^{-7}$
1.0	3.243540 $\times {10}^{-17}$	−1.553930 $\times {10}^{-8}$	1.553930 $\times {10}^{-9}$

Table 4. Comparision of HAM and Numerical results for $f\left(\xi \right)$.

$\mathit{\xi }$	HAM	Numerical Solution	Absolute Error
0.0	−1.030520	−1.015550	0.014980
0.2	−0.972080	−0.956321	0.015759
0.4	−1.001250	−0.982844	0.018401
0.6	−1.163130	−1.140120	0.023011
0.8	−1.495130	−1.465520	0.029607
1.0	−2.025290	−1.987240	0.038056

Table 5. Variation in skin-friction coefficient $C_{fx}$ and $C_{fy}$ for single-walled carbon nanotubes (SWCNTs) together with strong and weak concentrations $K=0$ and $K=0.5$ and the comparison with previous results for fixed values of $Rd=0.2$, $\delta =0.1$, and $Re=0.3$.

${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{E}}_{\mathit{r}}$	$\mathit{\gamma }$	${\mathit{N}}_{\mathit{r}}$	$\mathit{\phi }$	${\mathit{C}}_{\mathit{fx}}$ at K = 0 for SWCNT [56]	${\mathit{C}}_{\mathit{fx}}$ at K = 0 for SWCNT Present Values	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for SWCNT [56]	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for SWCNT Present Values
0.0	0.1	0.1	0.1	0.1	0.1	−1.47208	−1.93457	−1.47208	−1.14526
0.1						−1.58457	−1.72675	−1.52844	−1.19870
0.3						−2.03132	−1.99901	−1.75511	−1.24358
0.1	0.0					−1.58440	−1.64533	−1.52866	−1.99668
	0.3					−1.58453	−1.64337	−1.52849	−1.99650
	0.5					−1.58457	−1.64347	−1.52844	−1.99645
	0.1	0.1				−1.58265	−1.64555	−1.52558	−1.99660
		0.3				−1.59132	−1.64993	−1.53503	−2.10118
		0.5				−1.59977	−1.65001	−1.52849	−2.10110
		0.1	0.1			−1.58446	−1.64113	−1.53318	−2.10108
			0.3			−1.58477	−1.64783	−1.52848	−2.10318
			0.5			−1.58502	−1.65113	−1.52863	−2.10332
			0.1	0.1		−1.30696	−1.42001	−1.52863	−2.10337
				0.3		−1.02844	−1.34291	−1.52844	−2.10335
				0.5		−4.16259	−3.30023	−0.99212	−1.10002
				0.1	0.1	−2.95695	−3.14993	−4.01729	−3.80332
					0.3	−1.37247	−1.64793	−2.85298	−3.10300
					0.5	−1.44457	−1.64993	−1.32379	−1.23219
					0.1	−1.58457	−1.77903	−1.37935	−2.45332

Table 6. Variation in skin-friction coefficient $C_{fx}$ and $C_{fy}$ for multi-walled carbon nanotubes (MWCNTs) together with strong and weak concentrations $K=0$ and $K=0.5$ and the comparison with previous results for $Rd=0.3$, $\delta =0.1$, and $Re=0.4$.

${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{E}}_{\mathit{r}}$	$\mathit{\gamma }$	${\mathit{N}}_{\mathit{r}}$	$\mathit{\phi }$	${\mathit{C}}_{\mathit{fx}}$ at K = 0 for MWCNT [56]	${\mathit{C}}_{\mathit{fx}}$ at K = 0 for MWCNT Present Values	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for MWCNT [56]	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for MWCNT Present Values
0.0	0.1	0.1	0.1	0.1	0.1	−1.61091	−1.93457	−1.61091	−1.83452
0.1						1.73404	−1.72321	−1.67259	−1.77433
0.3						−2.22304	−1.99881	−1.92069	−2.10032
0.1	0.0					−1.73386	−1.68751	−1.67283	−1.88643
	0.3					−1.73399	−1.68761	−1.67265	−1.88653
	0.5					−1.73404	−1.83450	−1.67259	−1.88647
	0.1	0.1				−1.73212	−1. 83324	−1.67070	−1.88601
		0.3				−1.74161	−1. 89022	−1.67989	−2.10111
		0.5				−1.75087	−1.74332	−1.68882	−1.88765
		0.1	0.1			−1.73403	−1. 83350	−1.67259	−2.00111
			0.3			−1.73422	−1. 83551	−1.67277	−1.98321
			0.5			−1.73476	−1. 83551	−1.67329	−1.98319
			0.1	0.1		−1.73404	−1. 83534	−1.67259	−1.10337
				0.3		−1.43009	−1. 53448	−1.37949	−2.10335
				0.5		−1.12523	−1.22910	−1.08546	−1.10002
				0.1	0.1	−4.55171	−3.99643	−4.39269	−3.80332
					0.3	−3.23473	−3.54643	−3.12094	−3.10300
					0.5	−1.50199	−1.32011	−1.44871	−1.23219
					0.1	−1.44457	−1.23199	−1.37935	−2.45332

In Table 5, $C_{fx}$ and $C_{fy}$ are calculated for SWCNTs for a strong $K=0$ (weak $K=0.5$) concentration. It is observed that greater estimations of $P_1$, $E_r$, and $P_2$ reduces $C_{fx}$ and $C_{fy}$ for both the $K=0$ and $K=0.5$ cases while the opposite effect is found for $\gamma$, $N_r$, and $\phi$. In Table 6, $C_{fx}$ and $C_{fy}$ are calculated for MWCNTs for both $K=0$ and $K=0.5$. It is evident that higher estimations of $P_1$, $E_r$, and $P_2$ increase $C_{fx}$ and $C_{fy}$ for both $K=0$ and $K=0.5$ while opposite results are found for $\gamma$, $N_r$, and $\phi$.

In Table 7, the Nusselt number $N{u}_x$ for SWCNTs together with $K=0$ and $K=0.5$ are calculated. It is observed that higher estimations of $P_1$ increase $N{u}_x$ for $(K=0)$ while it decreases $N{u}_x$ for $(K=0.5)$, whereas increasing $P_2$ reduces $N{u}_x$ in the case of $(K=0)$ and enhances it for $(K=0.5)$. Furthermore, increasing values of $J_1$, $I_1$, and $Rd$ enhances $N{u}_x$ for $(K=0)$ while it reduces $N{u}_x$ for $(K=0.5)$. A higher value of $\phi$ reduces the heat flux. In Table 8, the Nusselt number $N{u}_x$ for MWCNTs together with $(K=0)$ and $(K=0.5)$ are calculated. Similar effects are observed as for that of Table 7 for MWCNTS in Table 8.

Table 7. Variation in the Nusselt numbers $N{u}_x$ for SWCNTs together with strong and weak concentrations $K=0$ and $K=0.5$ and the comparison with previous results for $E_r=0.3$, $\delta =0.2$, and $Re=0.2$.

${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{J}}_1$	${\mathit{I}}_1$	$\mathit{Rd}$	$\mathit{\phi }$	${\mathit{Nu}}_{\mathit{x}}$ at K = 0 for SWCNT [56]	${\mathit{Nu}}_{\mathit{x}}$ at K = 0 for SWCNT Present Values	${\mathit{Nu}}_{\mathit{x}}$ at K = 0.5 for SWCNT [56]	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for SWCNT Present Values
0.0	0.1	0.1	0.1	0.1	0.1	0.428266	0.938781	0.428266	0.938781
0.1						0.428328	0.938422	0.428259	0.938475
0.3						0.428217	0.938214	0.428230	0.938434
0.1	0.0					0.428278	0.937538	0.428261	0.937538
	0.3					0.428276	0.845373	0.428266	0.845473
	0.5					0.428274	0.845365	0.428259	0.845365
	0.1	0.1				……	0.648742	……	0.648546
		0.3				……	0.649931	……	0.649765
		0.5				……	0.650013	……	0.65563
		0.1	0.1			……	0.641131	……	0.641432
			0.3			……	0.6478321	……	0.647543
			0.5			……	0.651131	……	0.651665
			0.1	0.1		……	0.420010	……	0.423451
				0.3		……	0.342914	……	0.342914
				0.5		……	0.300233	……	0.300233
				0.1	0.1	0.433995	0.649936	0.433987	0.649936
					0.3	0.427375	0.642917	0.427370	0.642917
					0.5	0.425025	0.624327	0.425022	0.624327
					0.1	0.429519	0.779328	0.429512	0.779328

Table 8. Variation in $N{u}_x$ (the Nusselt numbers) for MWCNTs together with strong and weak concentrations $K=0$ and $K=0.5$ and the comparison with previous results for $E_r=0.2$, $\delta =0.1$, and $Re=0.3$.

${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{J}}_1$	${\mathit{I}}_1$	$\mathit{Rd}$	$\mathit{\phi }$	${\mathit{Nu}}_{\mathit{x}}$ at K = 0 for MWCNT [56]	${\mathit{Nu}}_{\mathit{x}}$ at K = 0 for MWCNT Present Values	${\mathit{Nu}}_{\mathit{x}}$ at K = 0.5 for MWCNT [56]	${\mathit{C}}_{\mathit{fy}}$ at K = 0.5 for MWCNT Present Values
0.0	0.1	0.1	0.1	0.1	0.1	0.429005	0.93457	0.429005	0.93878
0.1						0.429069	0.93675	0.428998	0.99883
0.3						0.429061	0.93901	0.428966	0.99958
0.1	0.0					0.429019	0.93533	0.428996	0.99968
	0.3					0.429015	0.93337	0.429005	0.99650
	0.5					0.429013	0.93347	0.429008	0.99045
	0.1	0.1				……	0.94557	……	0.99660
		0.3				……	0.94990	……	0.90118
		0.5				……	0.95032	……	0.90110
		0.1	0.1			……	0.94533	……	0.90108
			0.3			……	0.94783	……	0.90318
			0.5			……	0.95113	……	0.90332
			0.1	0.1		……	0.92021	……	0.90337
				0.3		……	0.94291	……	0.90333
				0.5		……	0.95023	……	0.90002
				0.1	0.1	0.430229	0.94993	0.430221	0.80332
					0.3	0.429013	0.94793	0.429007	0.80300
					0.5	0.427787	0.94993	0.427783	0.83219

The effect of $P_r$ (Prandtl number) on $N{u}_x$ (Nusselt number) in the case of $\phi =0$ (regular fluid) is displayed in Table 9. We see that the present results agree with the published results of Shah et al. [43,56]. In Table 10, some precarious physical characteristics of the CNTs are tabulated. Table 11 displays the impact of $\phi$ on the thermal conductivity $k_{nf}$. It is apparent that, for CNTs, the thermal conductivity changes with the increasing $\phi$.

Table 9. Influence of Prandtl number $Pr$ on Nusselt number $Nu$ at $\phi =0$.

$\mathit{P}\mathit{r}$	$\mathit{N}\mathit{u}$ [56] Results	$\mathit{N}\mathit{u}$ [43] Results	$\mathit{N}\mathit{u}$ Present Results
0.71	0.47	0.477	0.488
7.0	1.491	1.522	1.989
0.71	0.33	0.345	0.547

Table 10. Several physical characteristics of CNTs and different nanofluids.

Base Fluids	Nanofluids	${\mathit{c}}_{\mathit{p}}\left(\begin{array}{c}\frac{{\mathbf{K}}^{-1}}{\mathbf{Kg}}\end{array}\right)$	$\mathit{\rho }\left(\begin{array}{c}\frac{\mathbf{Kg}}{{\mathbf{m}}^3}\end{array}\right)$	$\mathit{k}\left(\begin{array}{c}\frac{\mathbf{W}}{\mathbf{mK}}\end{array}\right)$
Water		41.97 $\times {10}^2$	0.997 $\times {10}^3$	6.13 $\times {10}^{-1}$
Kerosene (lamp oil)		20.90 $\times {10}^2$	7.83 $\times {10}^{22}$	1.45 $\times {10}^{-1}$
Engine oil		19.10 $\times {10}^2$	8.84 $\times {10}^2$	1.44 $\times {10}^{-1}$
	SWCNT	0.425 $\times {10}^3$	2.6 $\times {10}^3$	6.6 $\times {10}^3$
	MWCNT	0.796 $\times {10}^3$	1.6 $\times {10}^3$	3 $\times {10}^3$

Table 11. Influence of the volume fraction $\phi$ on thermal conductivity $k_{nf}$.

$\mathit{\phi }$	${\mathit{k}}_{\mathit{nf}}$ for SWCNT	${\mathit{k}}_{\mathit{nf}}$ for MWCNT
0	14.5 $\times {10}^{-2}$	14.5 $\times {10}^{-2}$
0.01	17.4 $\times {10}^{-2}$	17.2 $\times {10}^{-2}$
0.02	20.4 $\times {10}^{-2}$	0.2 $\times {10}^{-2}$
0.03	23.5 $\times {10}^{-2}$	22.8 $\times {10}^{-2}$
0.04	26.6 $\times {10}^{-2}$	25.5 $\times {10}^{-2}$

5. Conclusions

The three-dimensional flow of Darcy–Forchheimer micro-polar nanofluid water-based carbon nanotubes in a rotatory frame has been examined in this research work. The impacts of rotation parameter, permeability parameter, coefficient of inertia, coupling parameter, viscosity gradient parameter, Reynold number, and thermal radiation are emphasized in this work. The fluid flow is studied under the assumptions of weak and strong concentrations. The key points are given as below:

• The upsurge in $Re$, $N_r$, $P_1$, $\phi$, and $E_r$ show dual behavior in the profile of $f^{{}^{\prime }}\left(\xi \right)$.
• The upsurge in $E_r$ exhibits dual behavior in the $g\left(\xi \right)$ profile.
• The higher $\phi$, $\gamma$, and $Re$ values escalate $g\left(\xi \right)$.
• The higher $N_r$ and $P_1$ values decline the $g\left(\xi \right)$ profile.
• The larger $\phi$, $P_1$, and $Re$ values cause an increase in $G\left(\xi \right)$.
• The higher $\phi$, $Rd$, $J_1$, and $I_1$ values result in a rise in the $\theta \left(\xi \right)$ profile.
• The upsurges in $P_1$, $E_r$, and $\gamma$ reduce $C_f$ for SWCNTs along the x and y-directions for both strong and weak concentrations, while it increases with the escalation in $N_r$.
• The higher values of $P_1$, $J_1$, $I_1$, and $Rd$ increase the Nusselt number $N{u}_x$ for strong concentrations while reduces it for weak concentrations for both SWCNTs and MWCNTs.