Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface
Abstract
1. Introduction
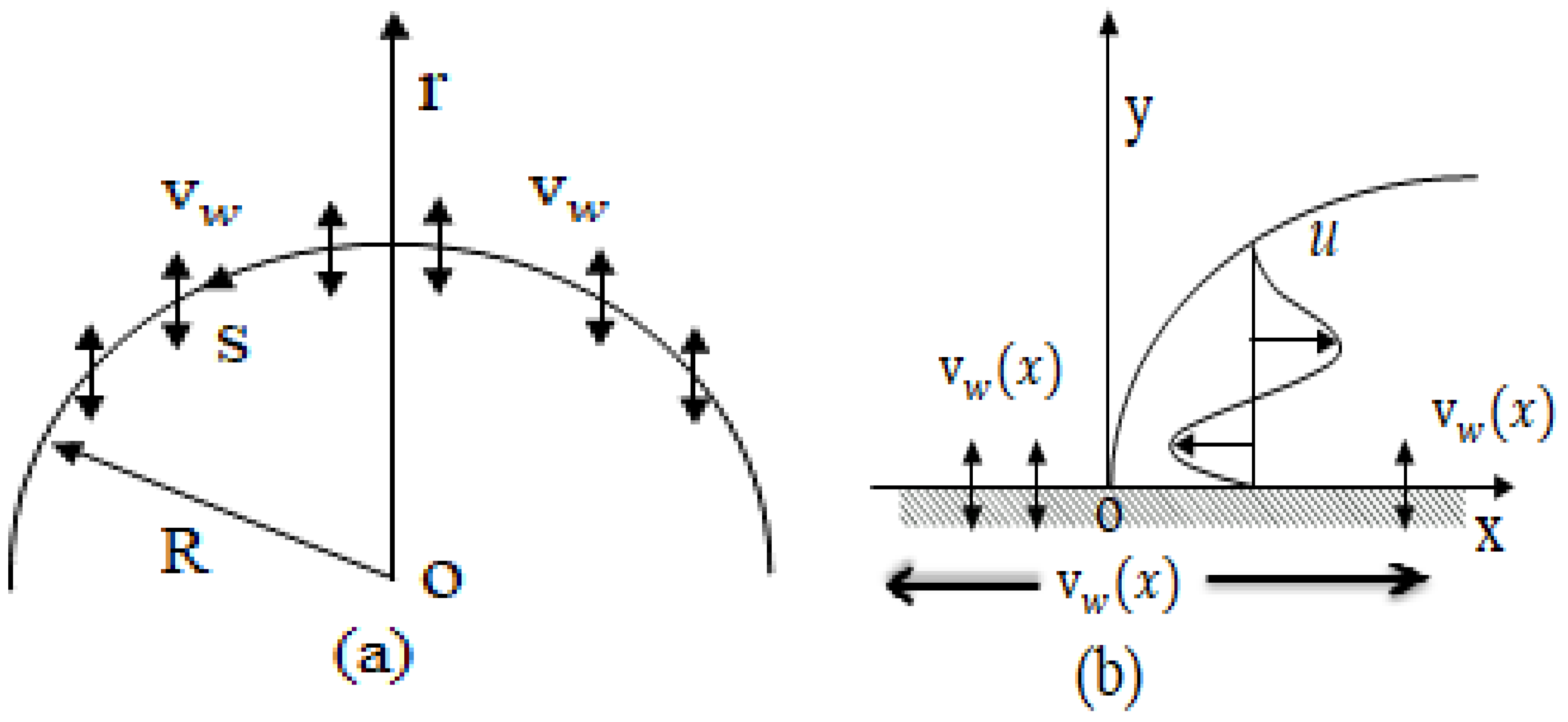
2. Mathematical Formulations
3. Results and Discussion
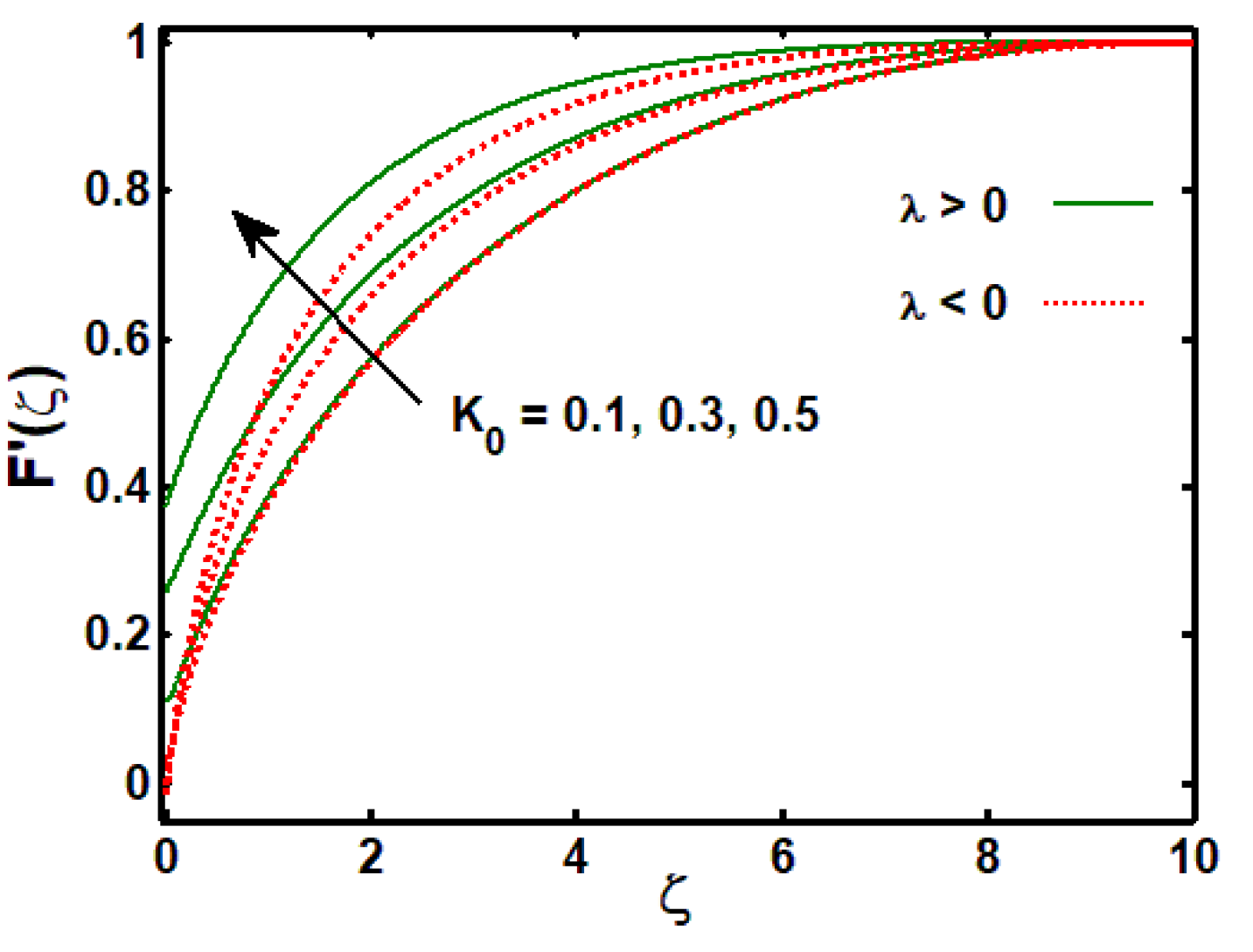
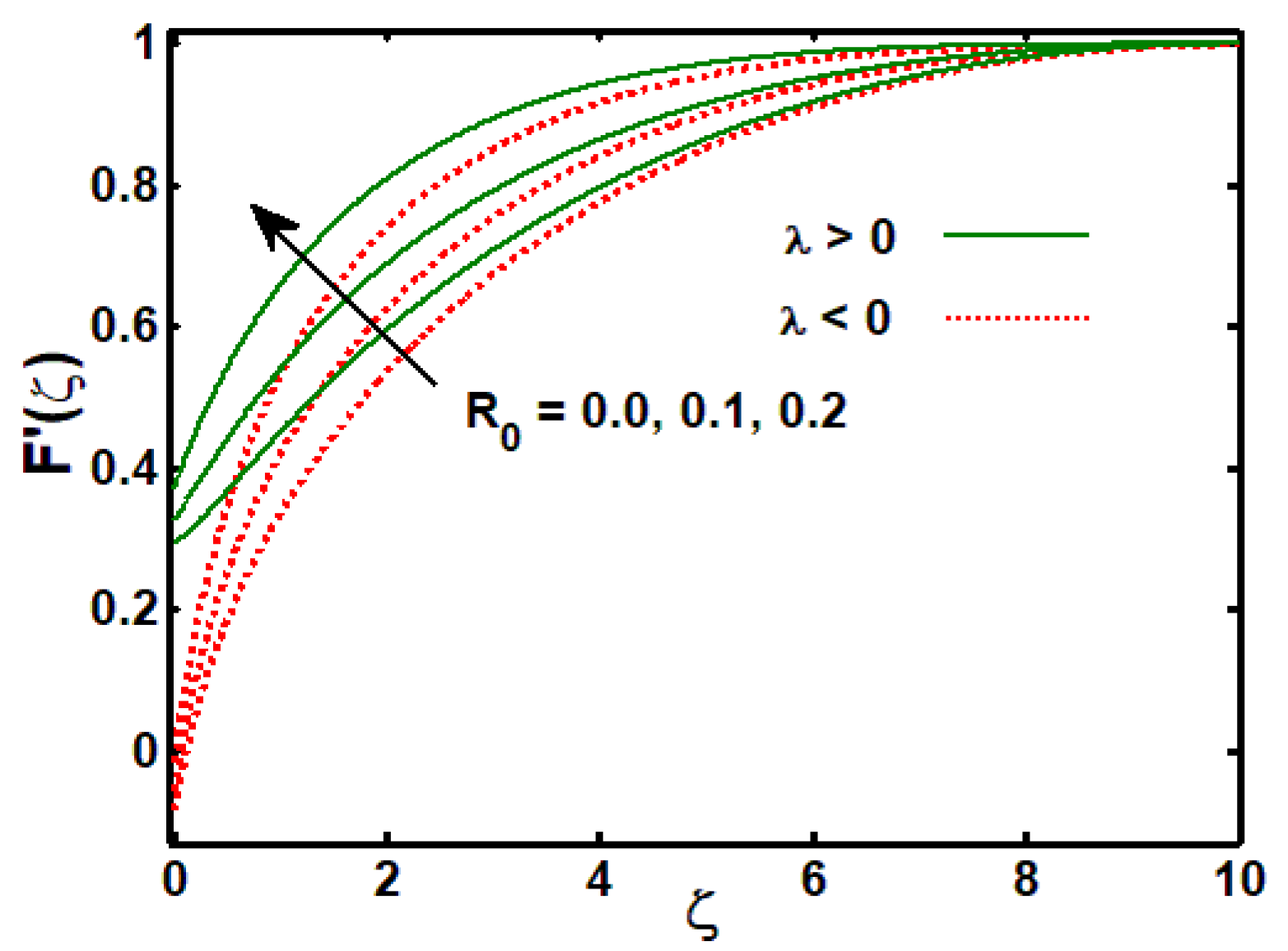
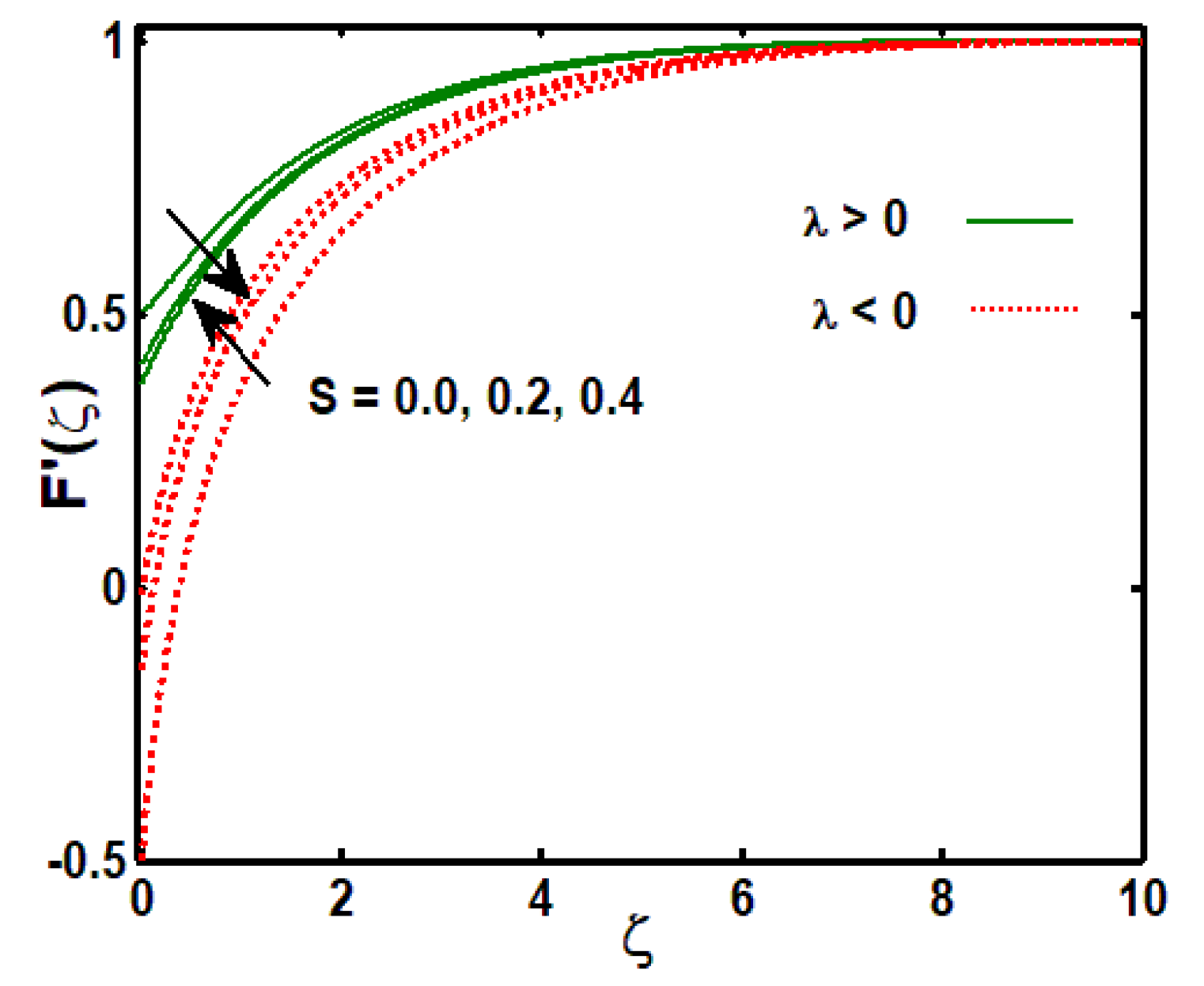
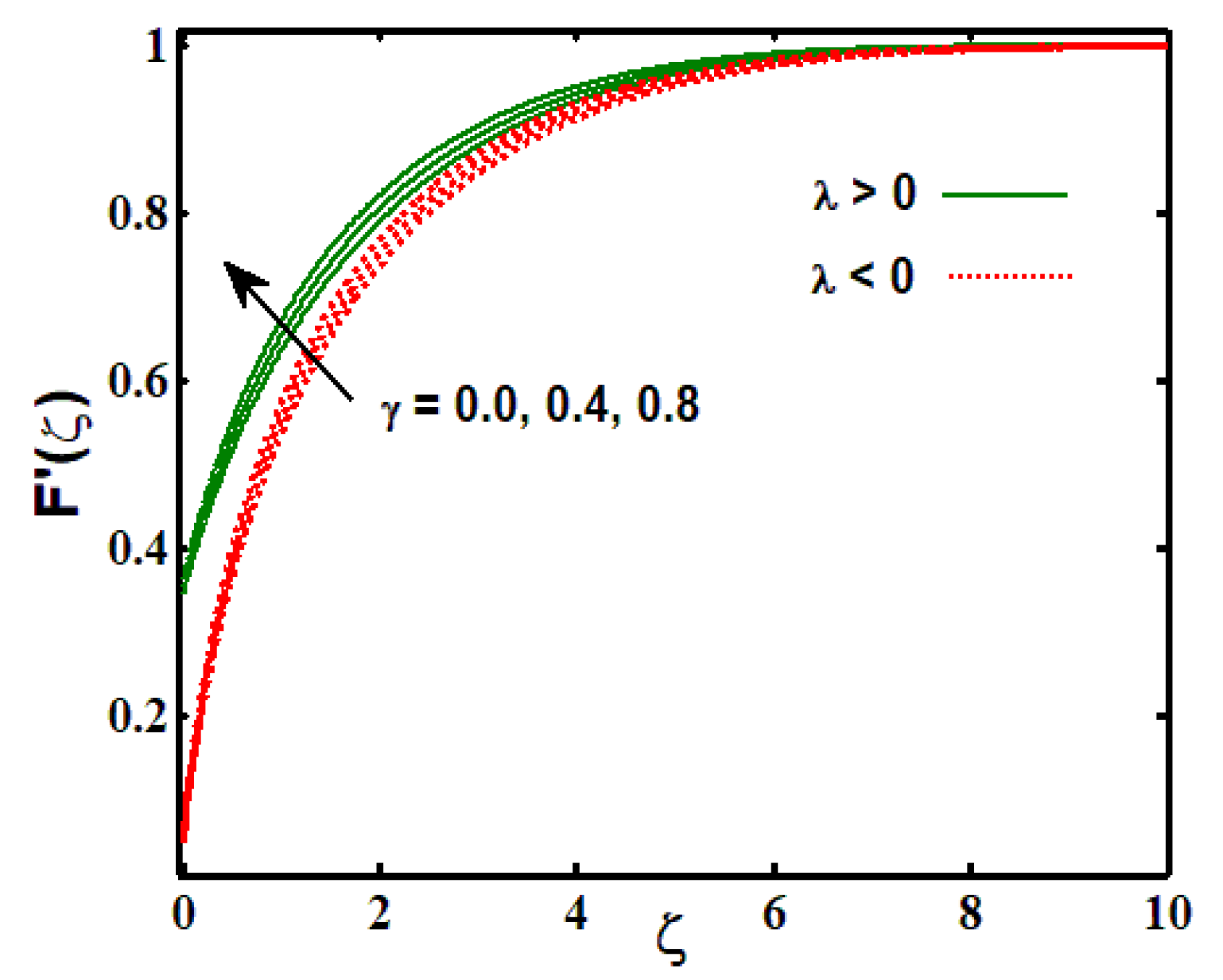
3.1. Influence of Physical Parameters on Velocity Profile
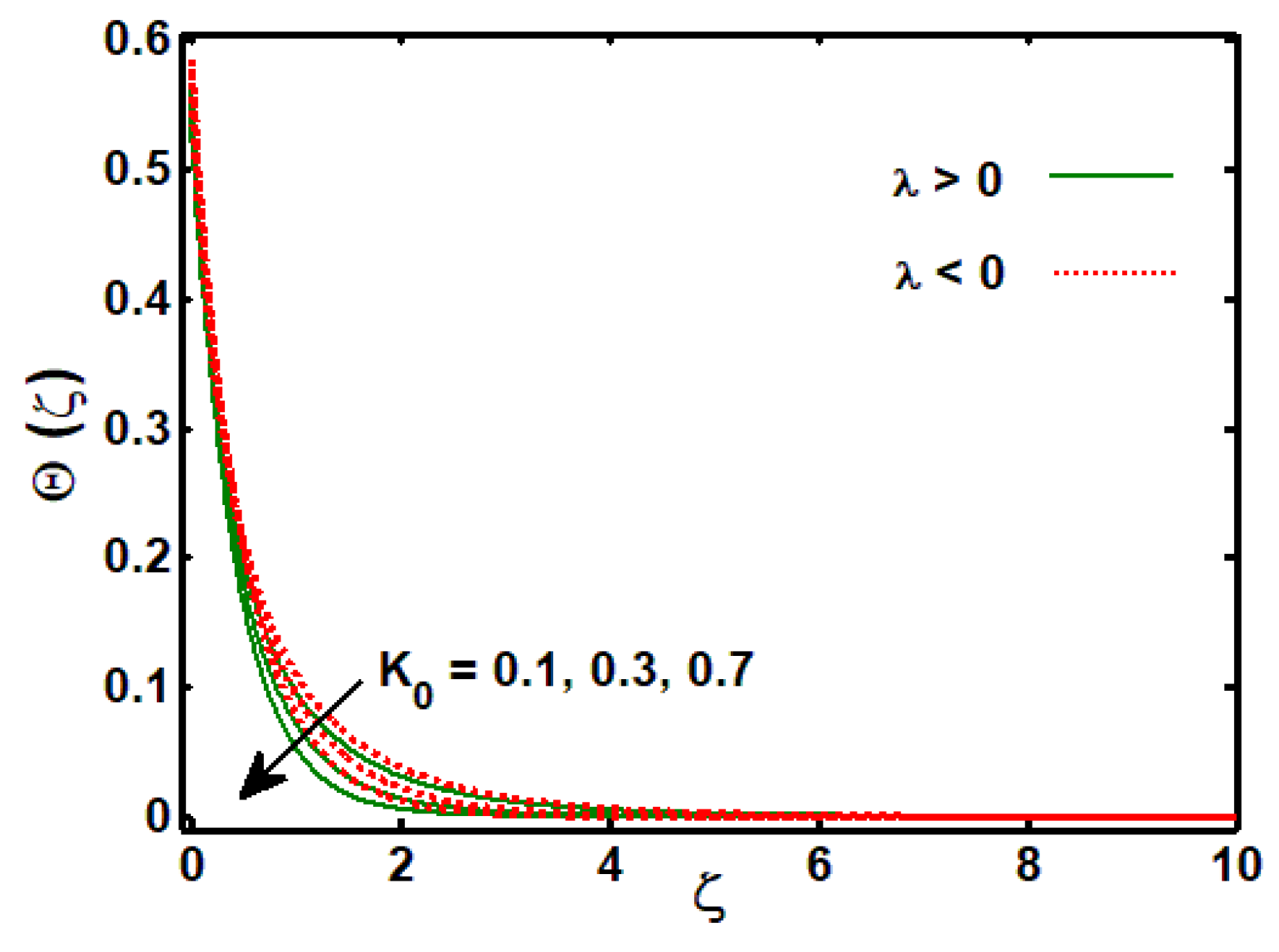
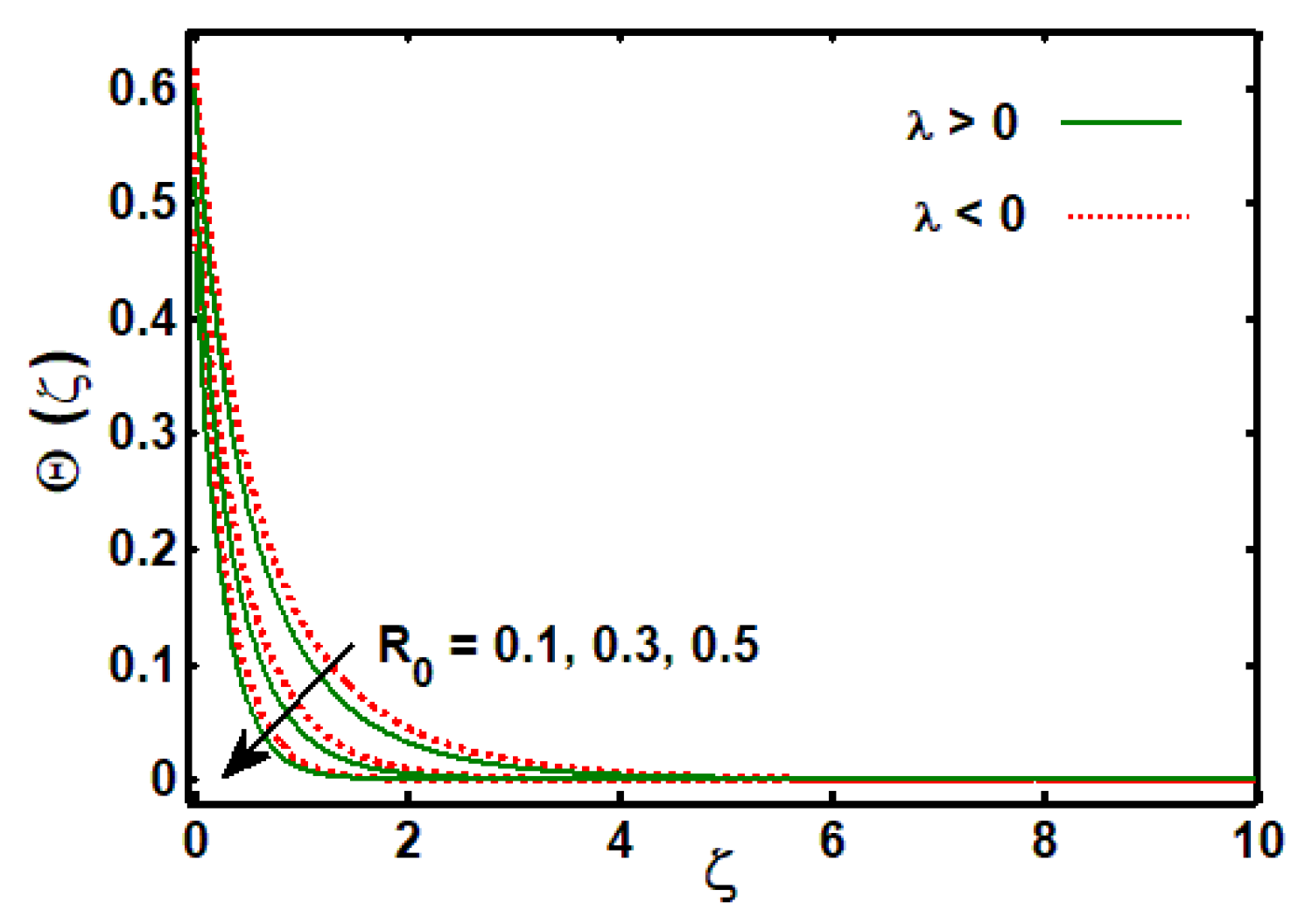
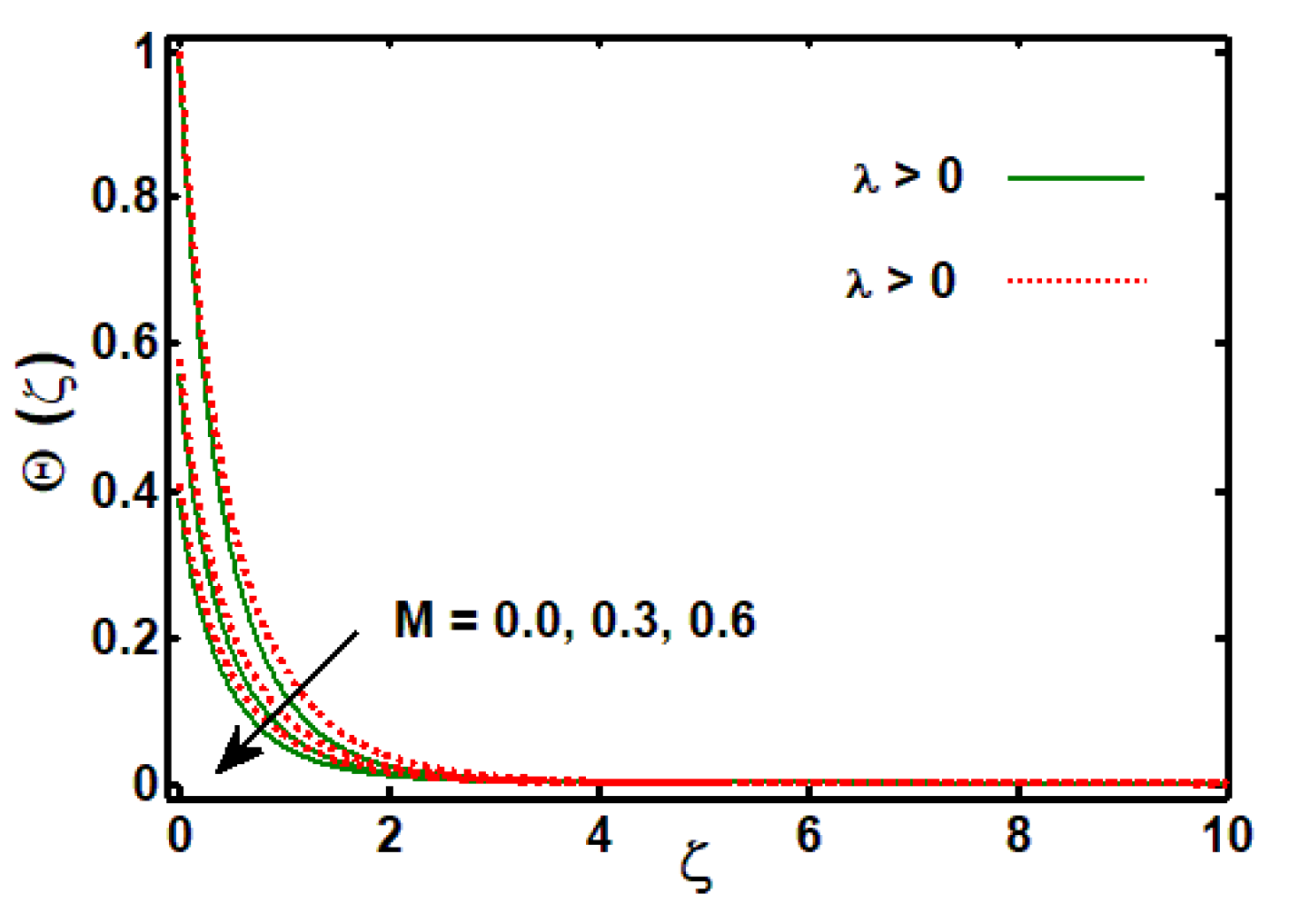
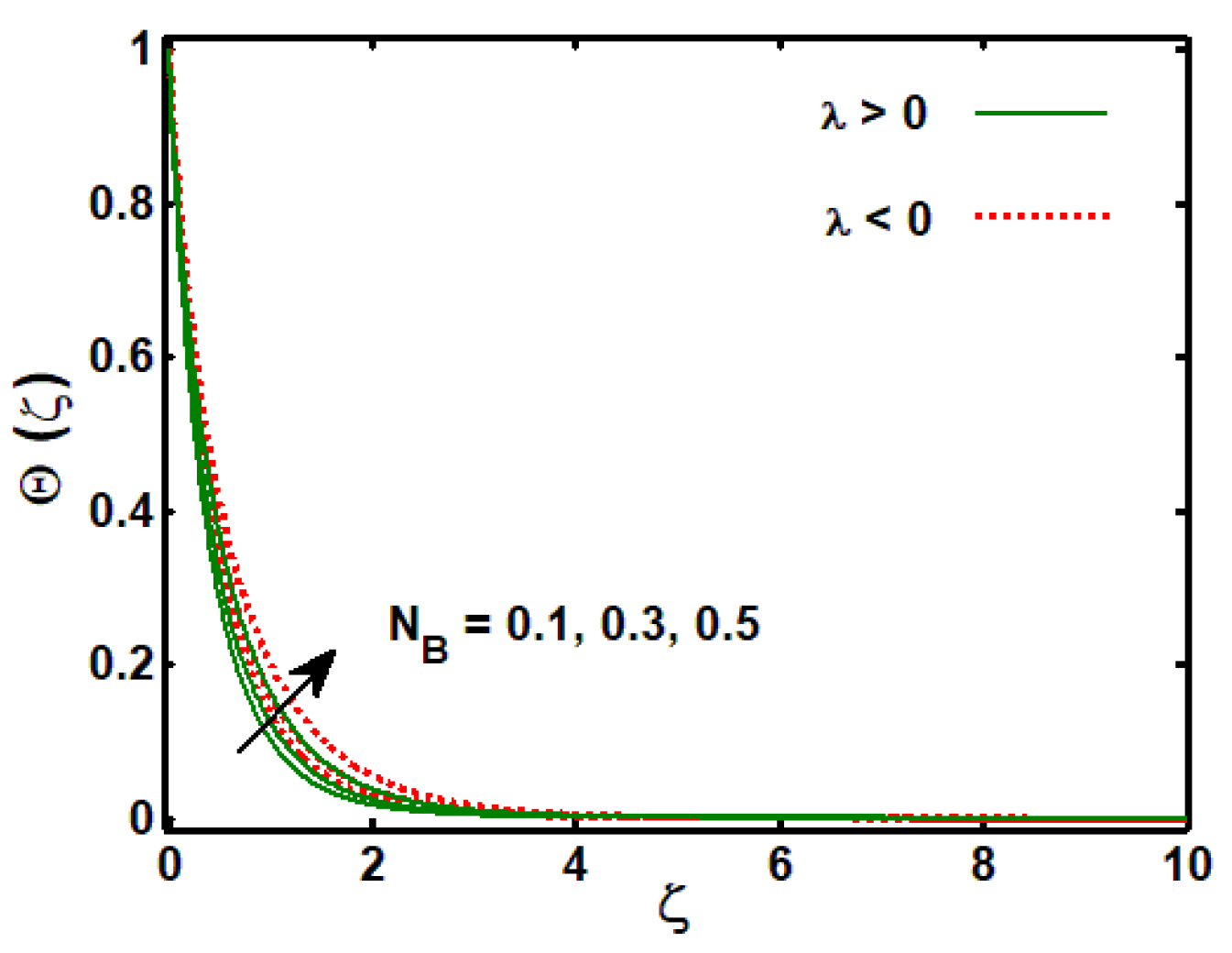
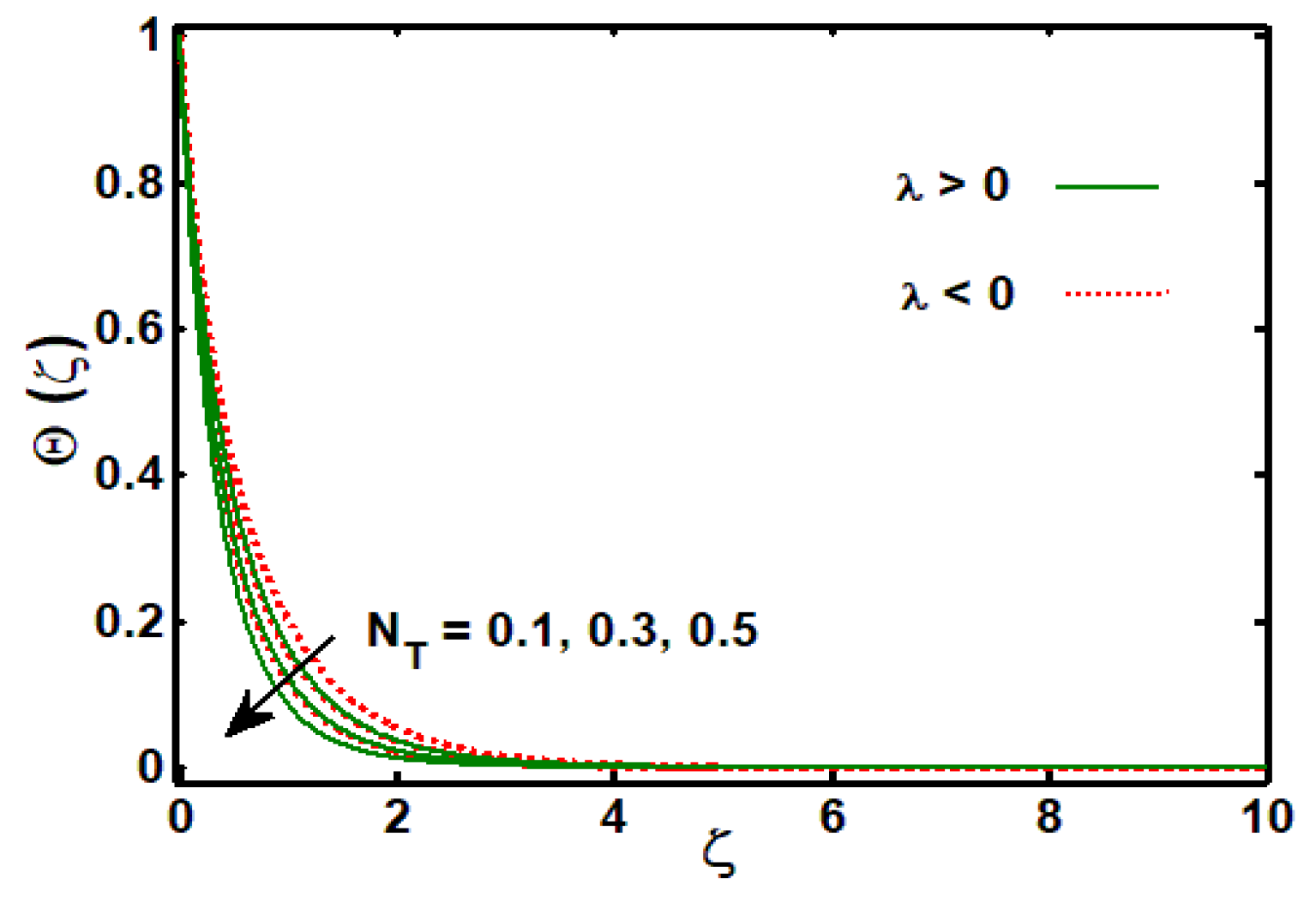
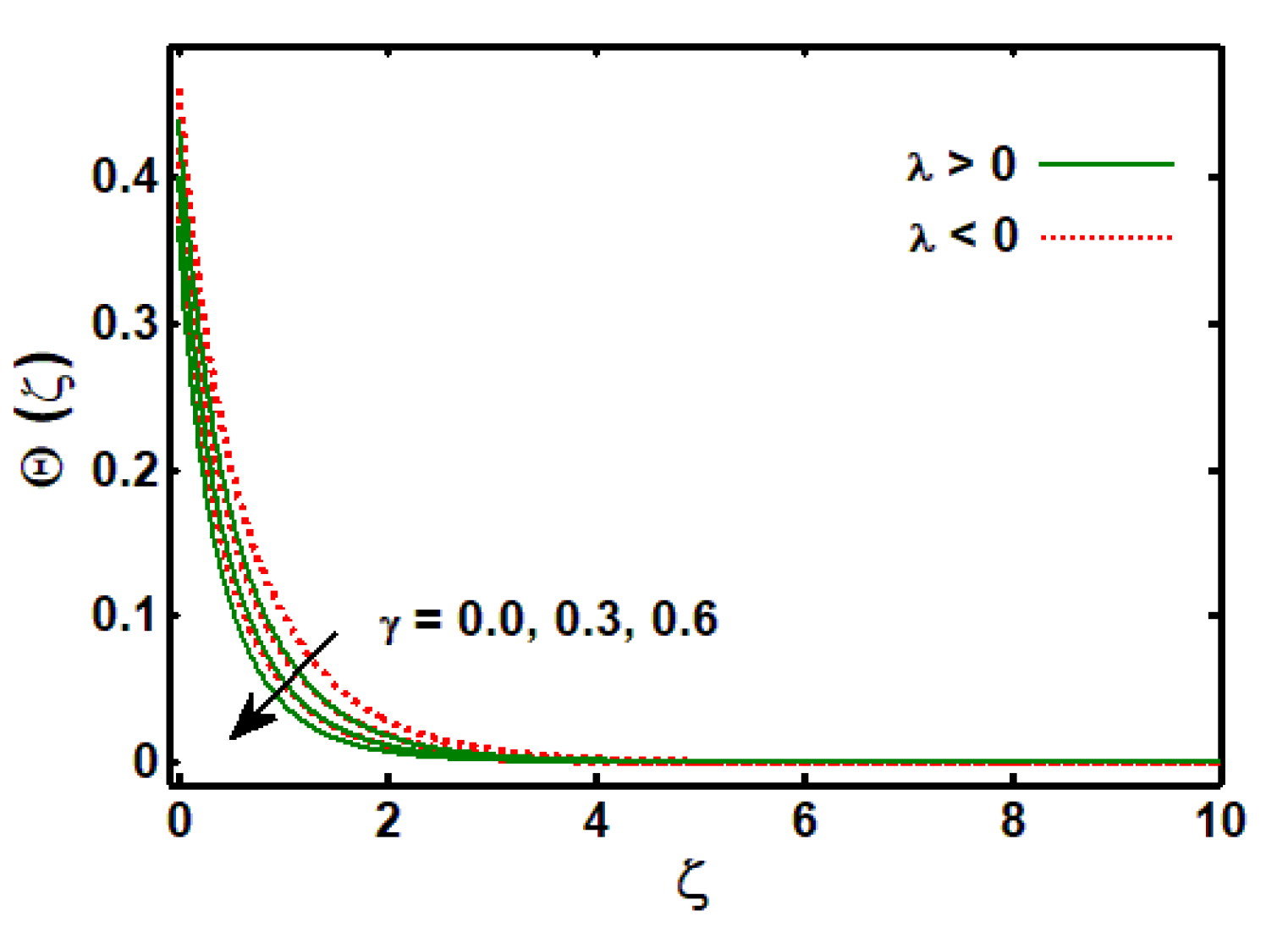
3.2. Effects of Physical Parameters on Temperature Profile
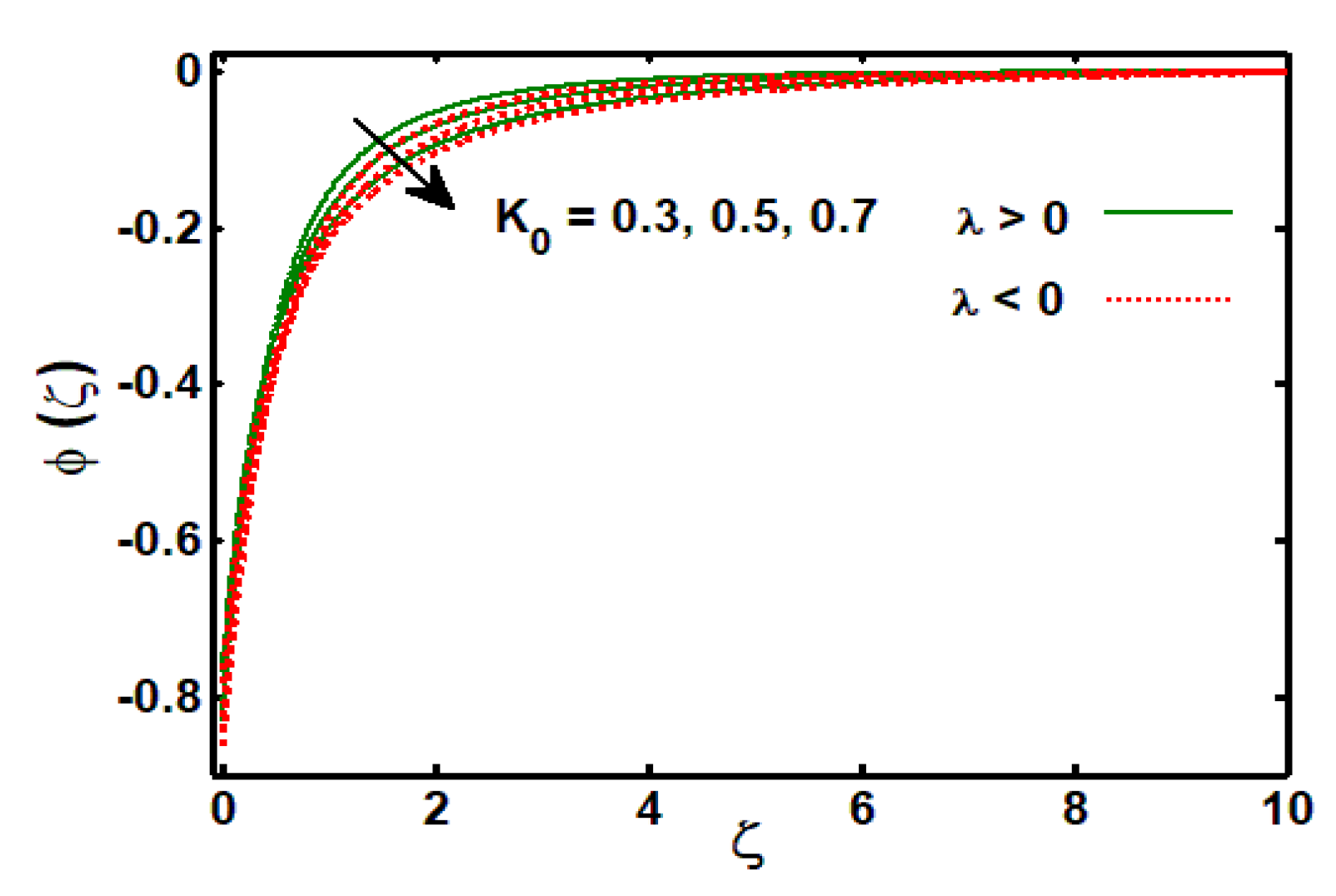
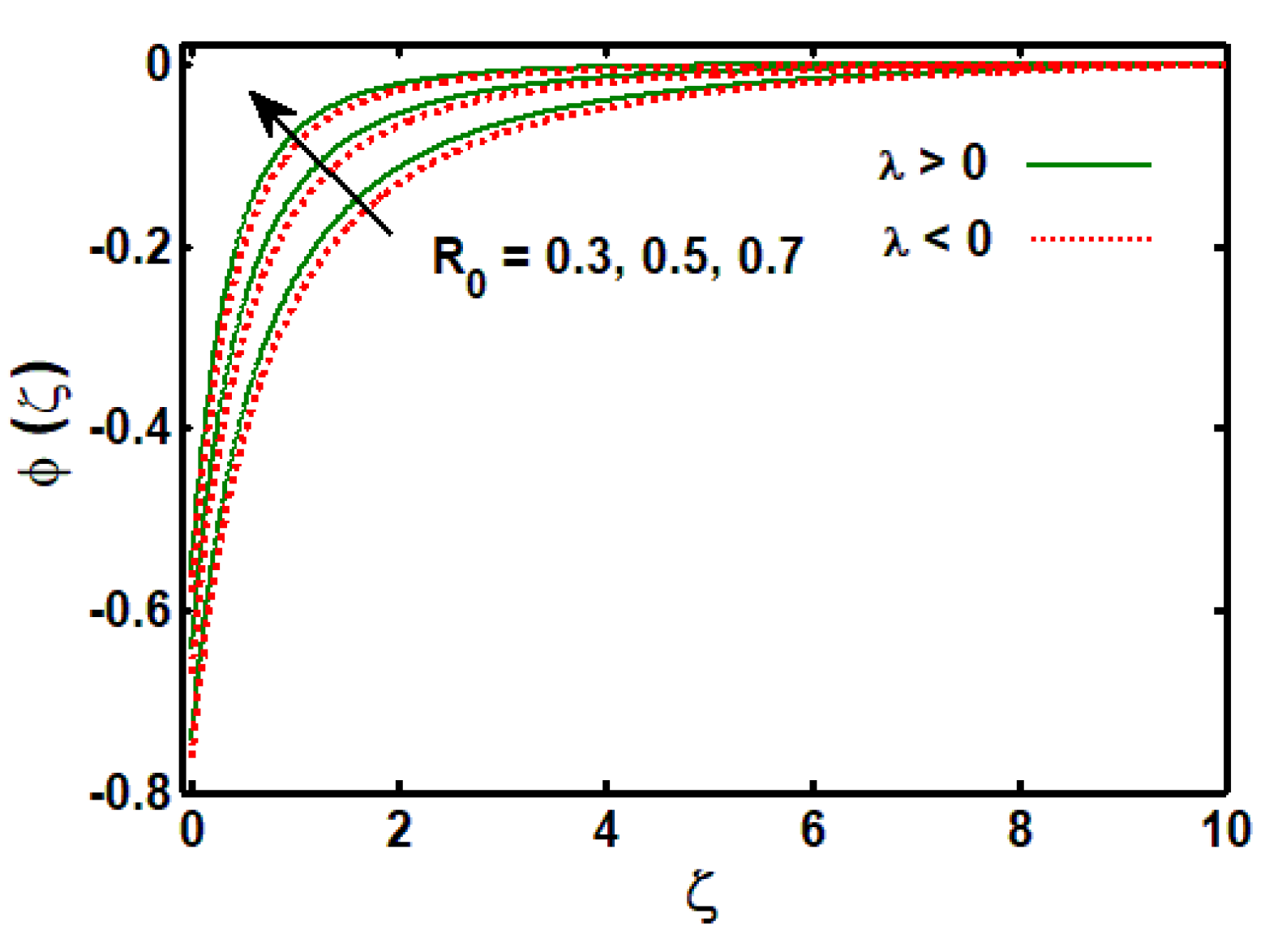
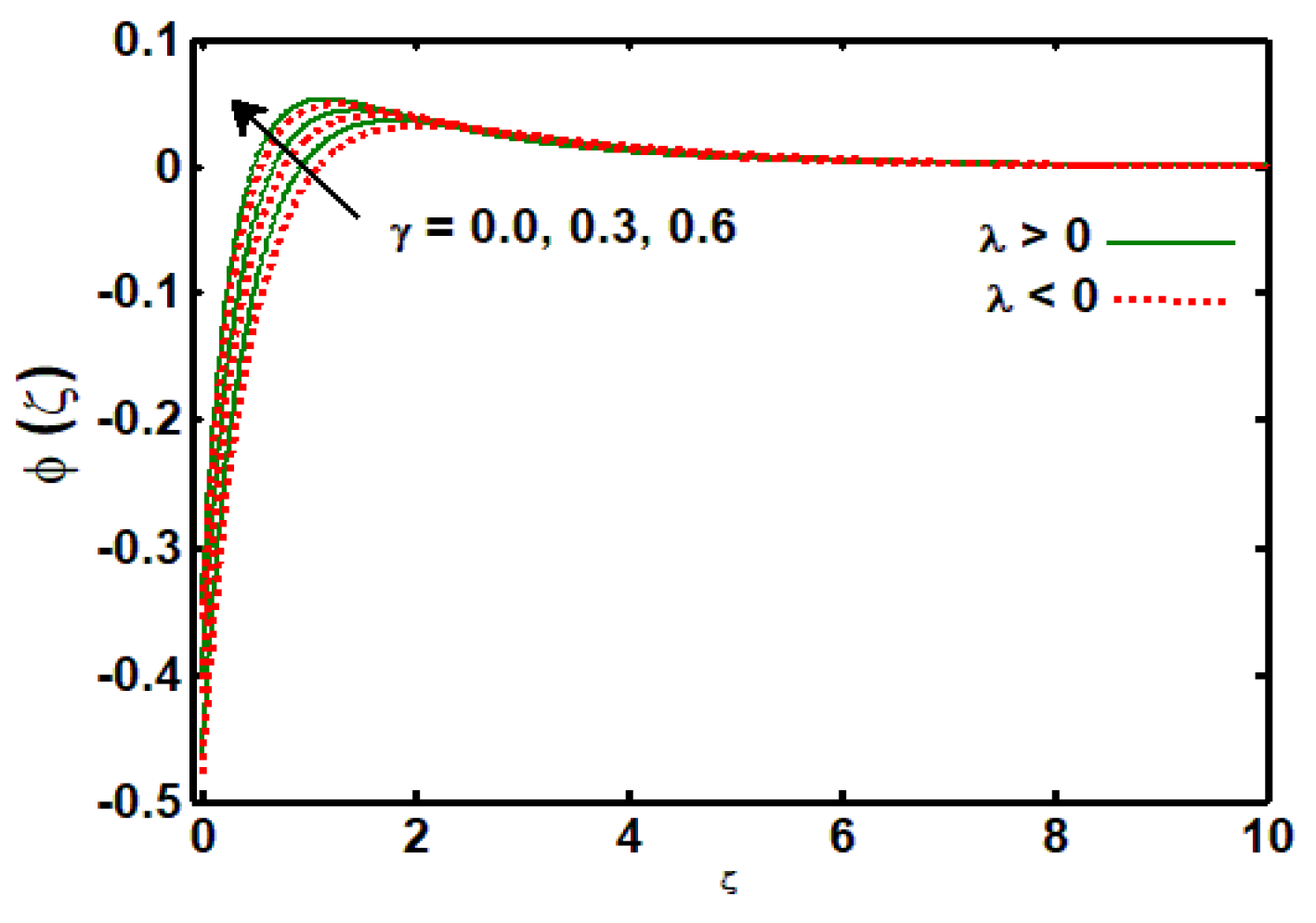
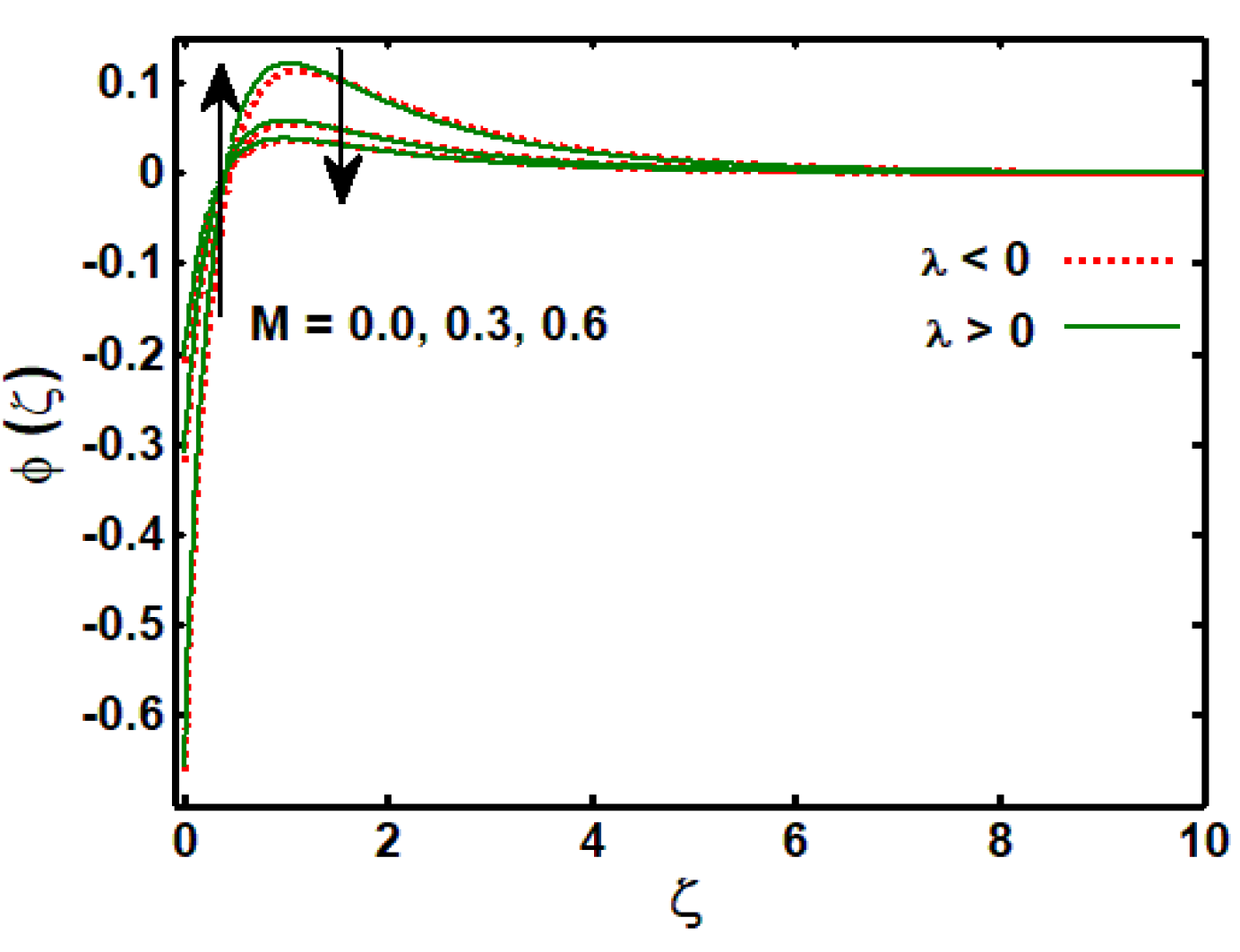
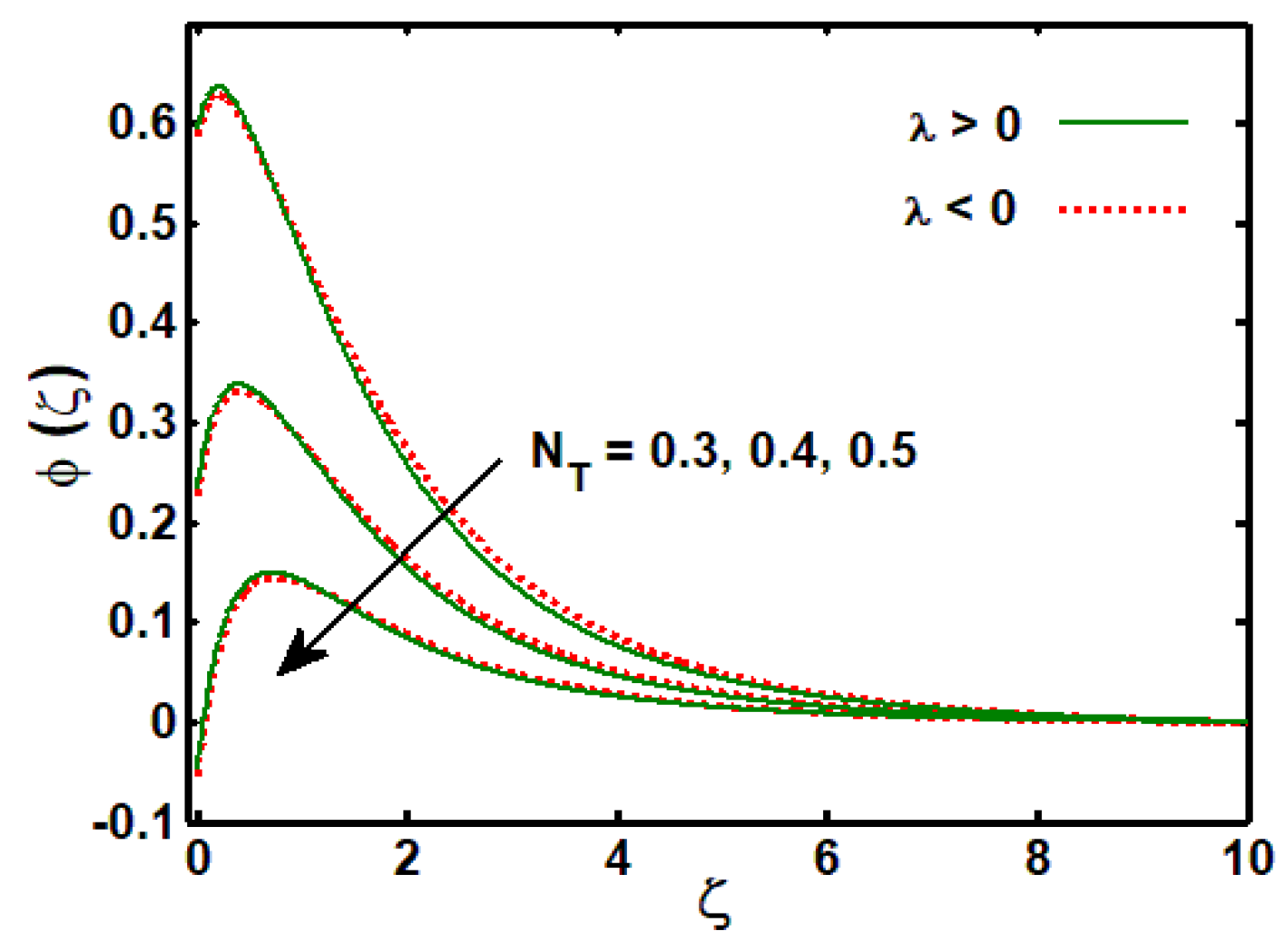
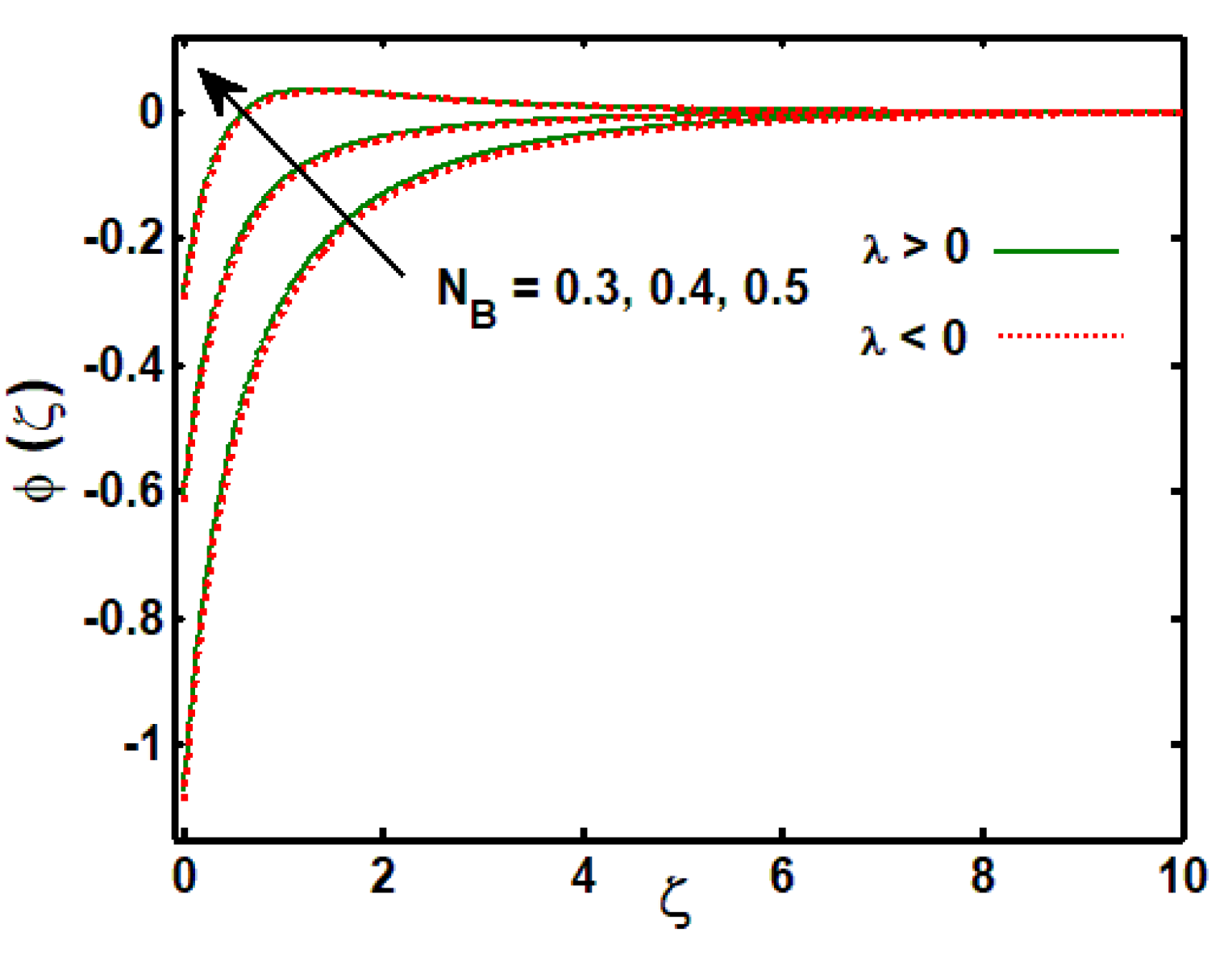
3.3. Effects of Physical Parameters on Concentration Profile
3.4. Numerical Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Physical parameters | |||
| Prandtl number | Wall temperature | ||
| Suction/Injection | Ambient temperature | ||
| Thermal slip | Fluid kinematic Viscosity | ||
| Curvature parameter | Thermal conductivity of fluid | ||
| Stretching parameter | λ | Stretching or shrinking parameter | |
| Temperature profile | Velocity slip | ||
| Velocity profile | Brownian motion parameter | ||
| Density | Thermo-phoresis parameter | ||
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Chiam, T.C. Stagnation-point flow towards a stretching plate. J. Phys. Soc. Jpn. 1994, 63, 2443–2444. [Google Scholar]
- Lin, C.R.; Chen, C.K. Exact solution of heat transfer from a stretching surface with variable heat flux. Heat Mass Transf. 1998, 33, 477–480. [Google Scholar] [CrossRef]
- Chen, C.H. Mixed convection cooling of a heated, continuously stretching surface. Heat Mass Transf. 2000, 36, 79–86. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Stagnation-point Flow towards a Stretching Surface. Can. J. Chem. Eng. 2003, 81, 258–263. [Google Scholar] [CrossRef]
- Ali, M.E. The buoyancy effects on the boundary layers induced by continuous surfaces stretched with rapidly decreasing velocities. Heat Mass Transf. 2004, 40, 285–291. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non–Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Wang, C. Analysis of viscous flow due to a stretching sheet with surface slip and suction. Nonlinear Anal. Real World Appl. 2009, 10, 375–380. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.; Gupta, A. Analytical solution of magnetohydrodynamic stagnation-point flow of a power-law fluid towards a stretching surface. Appl. Math. Comput. 2009, 215, 1696–1710. [Google Scholar] [CrossRef]
- Tie-Gang, F.; Ji, Z.; Yong-Fang, Z.; Hua, T. Unsteady viscous flow over an expanding stretching cylinder. Chin. Phys. Lett. 2011, 28, 124707. [Google Scholar]
- Wang, C. Natural convection on a vertical stretching cylinder. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1098–1103. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.; Hussain, A.; Awais, M.; Khan, I.; Khan, M. Analysis of tangent hyperbolic nanofluid impinging on a stretching cylinder near the stagnation point. Results Phys. 2017, 7, 426–434. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ahmad, S.; Shafee, A.; Suleman, M. Impact of Nonlinear Thermal Radiation and Entropy Optimization Coatings with Hybrid Nanoliquid Flow Past a Curved Stretched Surface. Coatings 2018, 8, 430. [Google Scholar] [CrossRef]
- Mamatha, S.; Raju, C.S.; Makinde, O.D. Radiative and Viscous Ohmic Dissipation on MHD Tangent Hyperbolic Fluid over a Convectively Heated Sheet in a Suspension of Dust Particles. Diffus. Found. 2018, 16, 177–190. [Google Scholar] [CrossRef]
- Nadeem, S.; Malik, M.Y.; Abbas, N. Heat transfer of three dimensional micropolar fluids on Riga plate. Can. J. Phys. 2019, 97, 579–587. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: DuPage County, IL, USA, 1995. [Google Scholar]
- Jang, S.P.; Choi, S.U.S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Öztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Santra, A.K.; Sen, S.; Chakraborty, N. Study of heat transfer due to laminar flow of copper–water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 2009, 48, 391–400. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I.; Khan, W. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Nadeem, S.; Maraj, E.N.; Akbar, N.S. Investigation of peristaltic flow of Williamson nanofluid in a curved channel with compliant walls. Appl. Nanosci. 2014, 4, 511–521. [Google Scholar] [CrossRef]
- Nadeem, S.; Shahzadi, I. Inspiration of induced magnetic field on nano hyperbolic tangent fluid in a curved channel. AIP Adv. 2016, 6, 015110. [Google Scholar] [CrossRef]
- Bibi, M.; Zeeshan, A.; Malik, M.Y.; Rehman, K.U. Numerical investigation of the unsteady solid-particle flow of a tangent hyperbolic fluid with variable thermal conductivity and convective boundary. Eur. Phys. J. Plus 2019, 134, 298. [Google Scholar] [CrossRef]
- Irshad, N.; Saleem, A.; Nadeem, S.; Shahzadi, I. Endoscopic Analysis of Wave Propagation with Ag-nanoparticles in Curved Tube Having Permeable Walls. Curr. Nanosci. 2018, 14, 384–402. [Google Scholar] [CrossRef]
- Rehman, K.U.; Shahzadi, I.; Malik, M.Y.; Al-Mdallal, Q.M.; Zahri, M. On heat transfer in the presence of nano-sized particles suspended in a magnetized rotatory flow field. Case Stud. Therm. Eng. 2019, 14, 100457. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Wang, C. Flow due to a stretching boundary with partial slip—An exact solution of the Navier–Stokes equations. Chem. Eng. Sci. 2002, 57, 3745–3747. [Google Scholar] [CrossRef]
- Wang, C. Stagnation slip flow and heat transfer on a moving plate. Chem. Eng. Sci. 2006, 61, 7668–7672. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Yao, S. Slip MHD viscous flow over a stretching sheet—An exact solution. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3731–3737. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Khan, A. Characteristics of three dimensional stagnation point flow of Hybrid nanofluid past a circular cylinder. Results Phys. 2018, 8, 829–835. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. On both MHD and slip effect in Micropolar Hybrid nanofluid past a circular cylinder under stagnation point region. Can. J. Phys. 2018, 97, 392–399. [Google Scholar] [CrossRef]
- Shahzadi, I.; Nadeem, S. Analysis of Ag/blood mediated transport in curved annulus with exclusive nature of convective boundary. Phys. Scr. 2019. [Google Scholar] [CrossRef]
- Nayak, M.K.; Hakeem, A.K.; Makinde, O.D. Time Varying Chemically Reactive Magneto-Hydrodynamic Non-Linear Falkner-Skan Flow Over a Permeable Stretching/Shrinking Wedge: Buongiorno Model. J. Nanofluids 2019, 8, 467–476. [Google Scholar] [CrossRef]
| For | For | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.3 | 0.4 | 0.4 | 0.5 | 0.5 | 0.4 | −0.6559 | 1.0014 | −1.0014 | 1.1634 | 0.9934 | −0.9934 |
| 0.2 | −0.6056 | 1.1639 | −1.1639 | 1.2110 | 1.1527 | −1.1527 | ||||||
| 0.3 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.4 | −0.4584 | 1.3642 | −1.3642 | 1.3488 | 1.3502 | −1.3502 | ||||||
| 0.3 | 0.1 | −0.9736 | 1.4909 | −1.4909 | 1.2485 | 1.4890 | −1.4890 | |||||
| 0.2 | −0.7471 | 1.3385 | −1.3385 | 1.2516 | 1.3315 | −1.3315 | ||||||
| 0.3 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.4 | −0.3472 | 1.2454 | −1.2454 | 1.3062 | 1.2264 | −1.2264 | ||||||
| 0.3 | 0.0 | −0.5593 | 1.1712 | −1.1712 | 1.2537 | 1.1572 | −1.1572 | |||||
| 0.2 | −0.5507 | 1.2244 | −1.2244 | 1.2622 | 1.2109 | −1.2109 | ||||||
| 0.4 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.6 | −0.5324 | 1.3269 | −1.3269 | 1.2802 | 1.3146 | −1.3146 | ||||||
| 0.4 | 0.0 | −0.5417 | 2.5835 | −2.5835 | 1.2710 | 2.5312 | −2.5312 | |||||
| 0.2 | −0.5417 | 1.7104 | −1.7104 | 1.2710 | 1.6873 | −1.6873 | ||||||
| 0.4 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.6 | −0.5417 | 1.0175 | −1.0175 | 1.2710 | 1.0093 | −1.0093 | ||||||
| 0.4 | 0.1 | −0.5417 | 1.3110 | −6.5549 | 1.2710 | 1.2980 | −6.4898 | |||||
| 0.3 | −0.5417 | 1.2991 | −2.1652 | 1.2710 | 1.2861 | −2.1435 | ||||||
| 0.5 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.7 | −0.5417 | 1.2449 | −0.8892 | 1.2710 | 1.2322 | −0.8801 | ||||||
| 0.5 | 0.1 | −0.5417 | 1.1503 | −0.2301 | 1.2710 | 1.1385 | −0.2277 | |||||
| 0.3 | −0.5417 | 1.2438 | −0.7463 | 1.2710 | 1.2311 | −0.7387 | ||||||
| 0.5 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.7 | −0.5417 | 1.2985 | −1.8179 | 1.2710 | 1.2855 | −1.7997 | ||||||
| 0.5 | 0.0 | −1.9708 | 1.2864 | −1.2864 | 4.6233 | 1.2388 | −1.2388 | |||||
| 0.2 | −0.8498 | 1.2786 | −1.2786 | 1.9939 | 1.2582 | −1.2582 | ||||||
| 0.4 | −0.5417 | 1.2764 | −1.2764 | 1.2710 | 1.2635 | −1.2635 | ||||||
| 0.6 | −0.3976 | 1.2754 | −1.2754 | 0.9328 | 1.2659 | −1.2659 | ||||||
| Parameter | BVP4C Method | Shooting Method | ND Solve Method | |||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 0.5 | 2.5835 | −2.5835 | 2.5835 | −2.5765 | 1.9865 | −2.4689 |
| 0.2 | 1.7104 | −1.7104 | 1.6812 | −1.7011 | 1.5864 | −1.6841 | ||
| 0.4 | 1.2764 | −1.2764 | 1.2584 | −1.2698 | 1.1981 | −1.2963 | ||
| 0.6 | 1.0175 | −1.0175 | 1.0115 | −1.0109 | 0.9987 | −1.0115 | ||
| 0.4 | 0.1 | 1.3110 | −6.5549 | 1.2986 | −6.4986 | 1.0982 | −6.3124 | |
| 0.3 | 1.2991 | −2.1652 | 1.2869 | −2.0985 | 1.1978 | −2.0258 | ||
| 0.5 | 1.2764 | −1.2764 | 1.2689 | −1.1989 | 1.2114 | −1.0638 | ||
| 0.7 | 1.2449 | −0.8892 | 1.2334 | −0.7995 | 1.1983 | −0.6987 | ||
| 0.5 | 0.1 | 1.1503 | −0.2301 | 1.1369 | −0.1968 | 1.0953 | −0.1657 | |
| 0.3 | 1.2438 | −0.7463 | 1.2589 | −0.7328 | 1.1896 | −0.6985 | ||
| 0.5 | 1.2764 | −1.2764 | 1.2765 | −1.2654 | 1.2546 | −1.1896 | ||
| 0.7 | 1.2985 | −1.8179 | 1.2893 | −1.7691 | 1.2789 | −1.7361 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alblawi, A.; Malik, M.Y.; Nadeem, S.; Abbas, N. Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface. Processes 2019, 7, 665. https://doi.org/10.3390/pr7100665
Alblawi A, Malik MY, Nadeem S, Abbas N. Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface. Processes. 2019; 7(10):665. https://doi.org/10.3390/pr7100665
Chicago/Turabian StyleAlblawi, Adel, Muhammad Yousaf Malik, Sohail Nadeem, and Nadeem Abbas. 2019. "Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface" Processes 7, no. 10: 665. https://doi.org/10.3390/pr7100665
APA StyleAlblawi, A., Malik, M. Y., Nadeem, S., & Abbas, N. (2019). Buongiorno’s Nanofluid Model over a Curved Exponentially Stretching Surface. Processes, 7(10), 665. https://doi.org/10.3390/pr7100665






