Component Characterization in a Growth-Dependent Physiological Context: Optimal Experimental Design
Abstract
1. Introduction
2. Materials and Methods
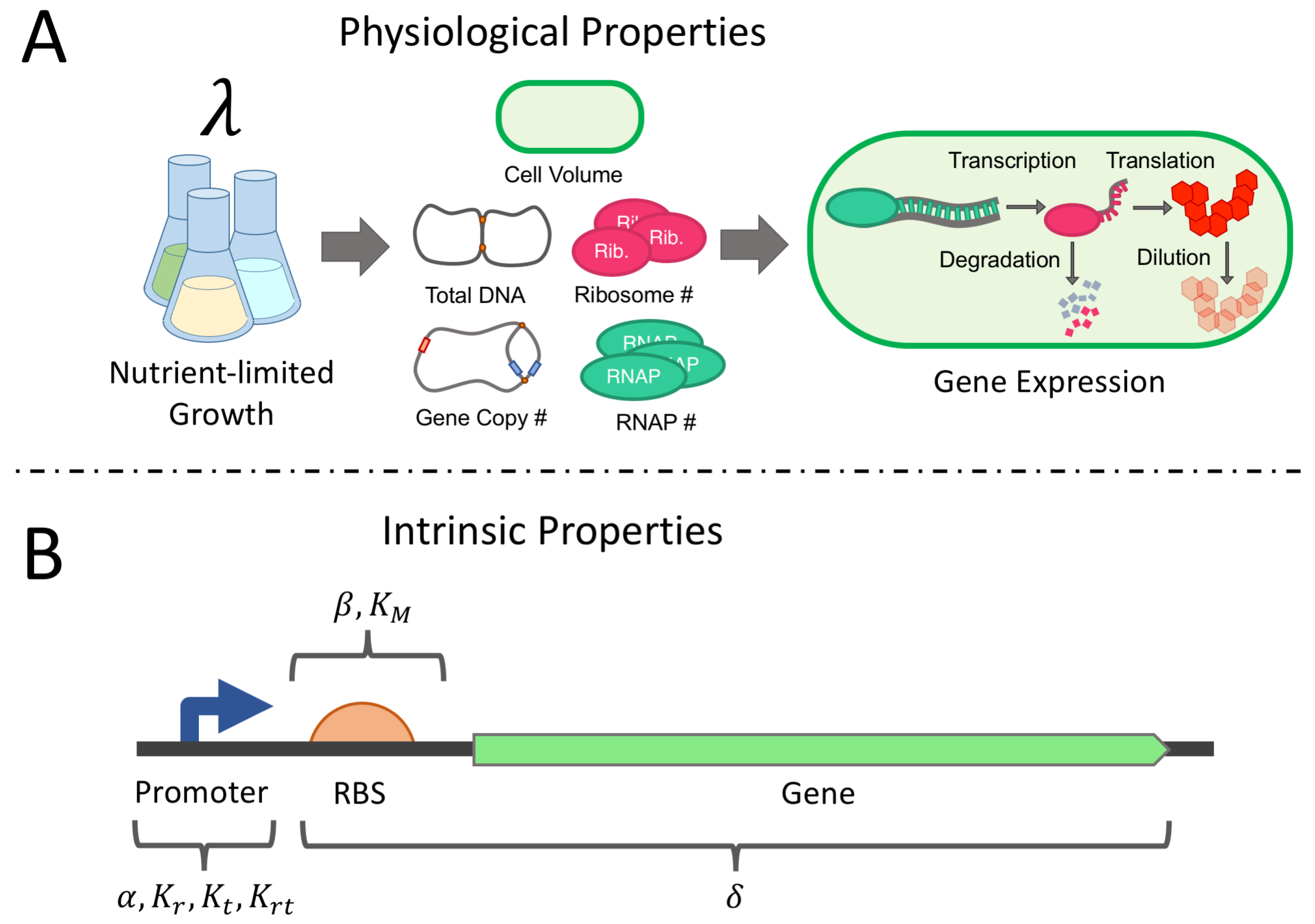
2.1. Derivation of the Physiological Gene Expression Model
2.1.1. Cell Volume and Mass, DNA Content, and Protein Mass
2.1.2. Total RNA Polymerase (RNAP)
2.1.3. Available RNAP
2.1.4. Transcription Rate
2.1.5. mRNA Degradation
2.1.6. Total and Free Ribosome Populations
2.1.7. Translation Rate
2.2. Optimal Experimental Design
3. Results
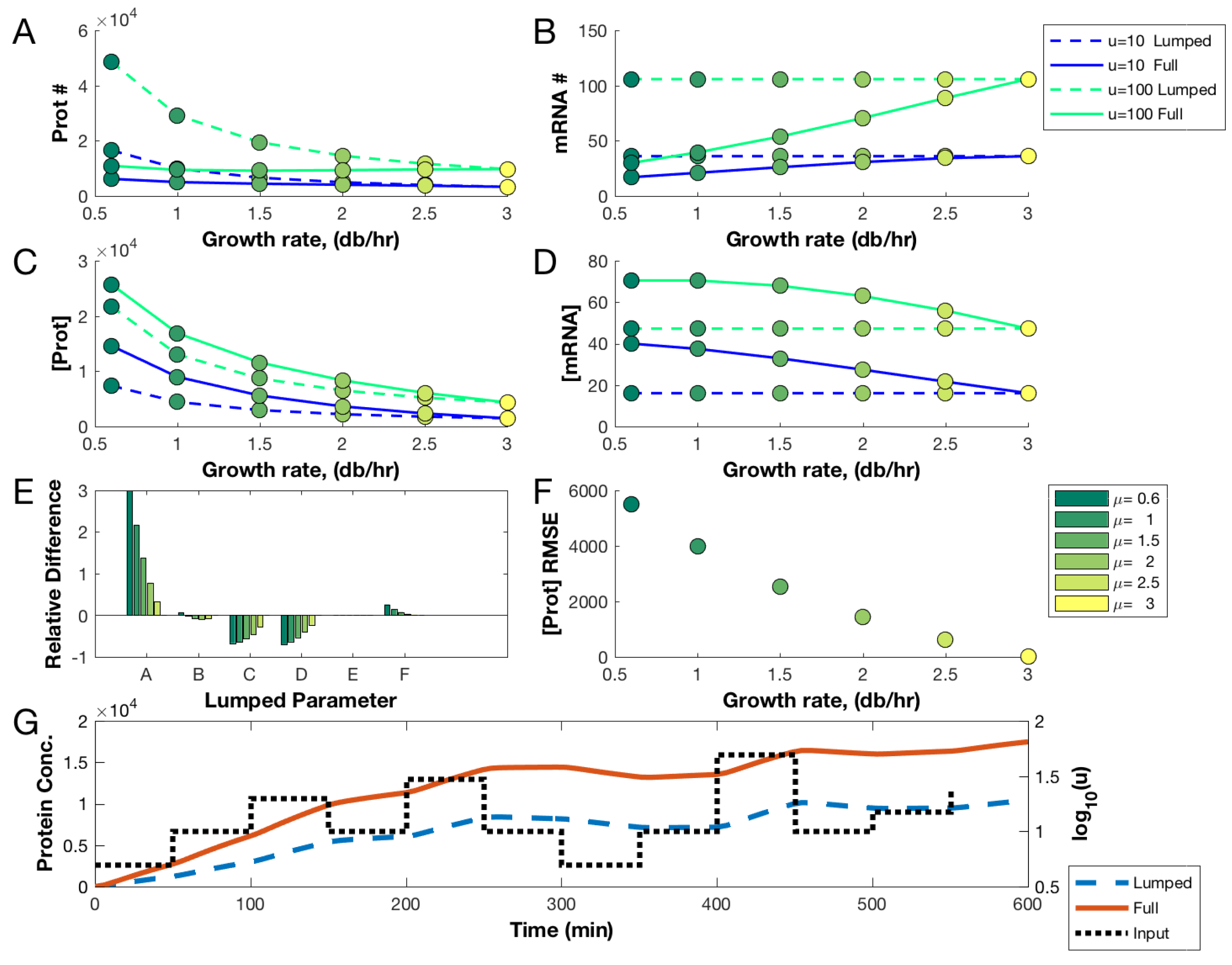
3.1. Comparing Lumped and Physiologically Aware Models
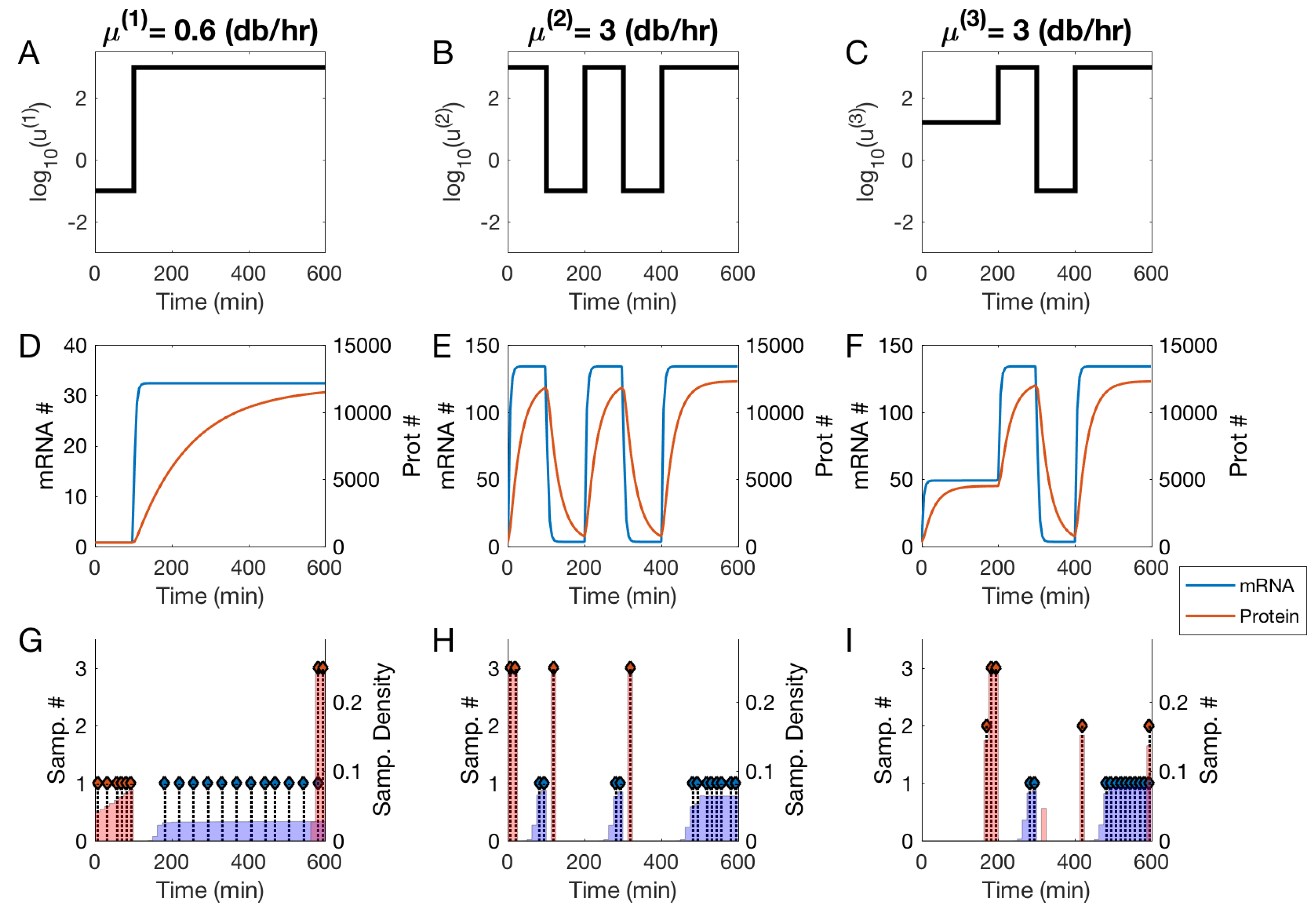
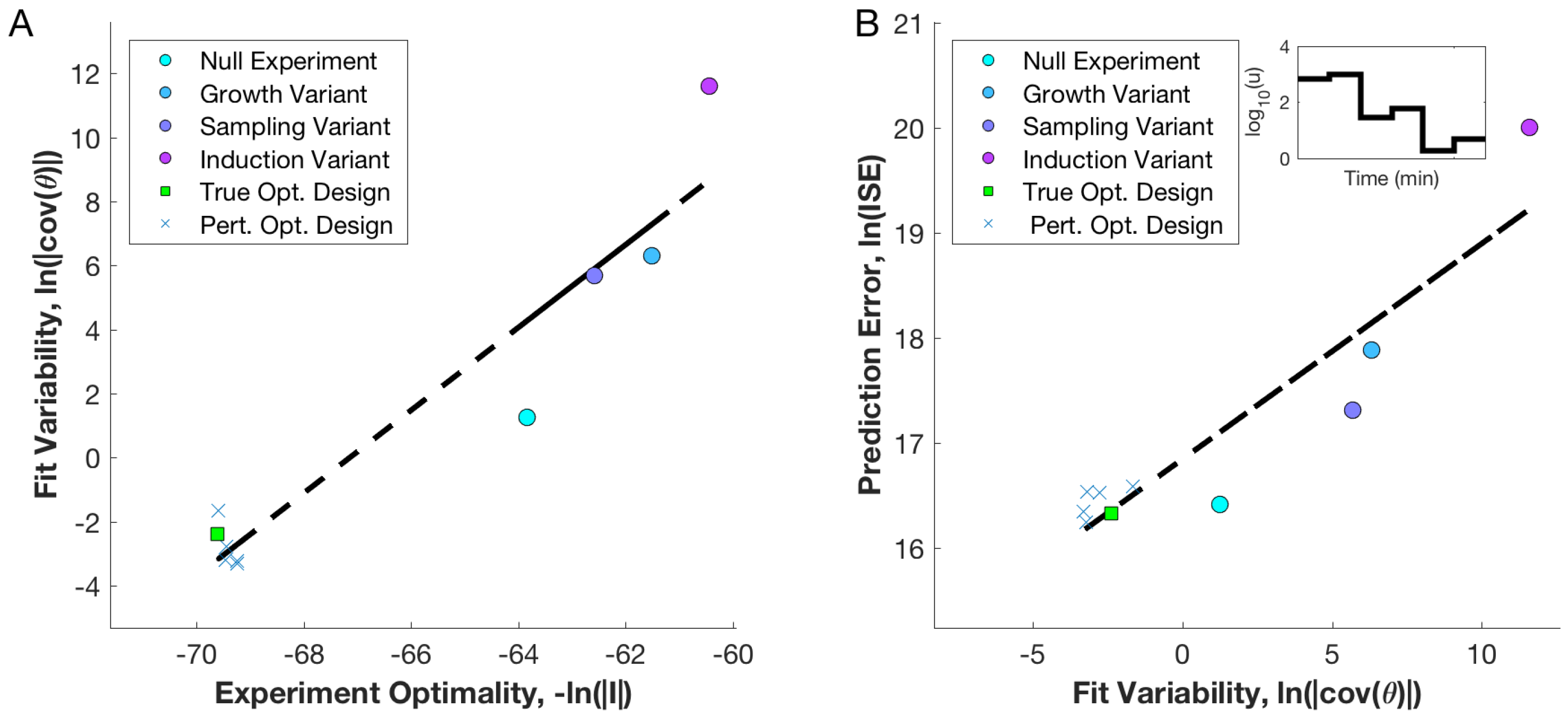
3.2. Null and Optimal Experimental Designs
3.3. Utility of Optimal Designs for Parameter Identification and Prediction
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Appleton, E.; Densmore, D.; Madsen, C.; Roehner, N. Needs and opportunities in bio-design automation: four areas for focus. Curr Opin. Chem. Biol. 2017, 40, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Beal, J. Bridging the gap: A roadmap to breaking the biological design barrier. Front. Bioeng. Biotechnol. 2015, 2, 87. [Google Scholar] [CrossRef] [PubMed]
- Guiziou, S.; Ulliana, F.; Moreau, V.; Leclere, M.; Bonnet, J. An Automated Design Framework for Multicellular Recombinase Logic. ACS Synth. Biol. 2018, 7, 1406–1412. [Google Scholar] [CrossRef] [PubMed]
- Otero-Muras, I.; Henriques, D.; Banga, J.R. SYNBADm: A tool for optimization-based automated design of synthetic gene circuits. Bioinformatics 2016, 32, 3360–3362. [Google Scholar] [CrossRef] [PubMed]
- Madec, M.; Pecheux, F.; Gendrault, Y.; Rosati, E.; Lallement, C.; Haiech, J. GeNeDA: An Open-Source Workflow for Design Automation of Gene Regulatory Networks Inspired from Microelectronics. J. Comput. Biol. 2016, 23, 841–855. [Google Scholar] [CrossRef] [PubMed]
- Huynh, L.; Tagkopoulos, I. Fast and accurate circuit design automation through hierarchical model switching. ACS Synth. Biol. 2015, 4, 890–897. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, G.; Jaramillo, A. AutoBioCAD: Full biodesign automation of genetic circuits. ACS Synth. Biol. 2012, 2, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Yaman, F.; Bhatia, S.; Adler, A.; Densmore, D.; Beal, J. Automated selection of synthetic biology parts for genetic regulatory networks. ACS Synth. Biol. 2012, 1, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Beal, J.; Weiss, R.; Densmore, D.; Adler, A.; Appleton, E.; Babb, J.; Bhatia, S.; Davidsohn, N.; Haddock, T.; Loyall, J.; et al. An end-to-end workflow for engineering of biological networks from high-level specifications. ACS Synth. Biol. 2012, 1, 317–331. [Google Scholar] [CrossRef]
- Beal, J.; Lu, T.; Weiss, R. Automatic compilation from high-level biologically-oriented programming language to genetic regulatory networks. PLoS ONE 2011, 6, e22490. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic circuit design automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed]
- Canton, B.; Labno, A.; Endy, D. Refinement and standardization of synthetic biological parts and devices. Nat. Biotechnol. 2008, 26, 787. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.R.; Rubin, A.J.; Davis, J.H.; Ajo-Franklin, C.M.; Cumbers, J.; Czar, M.J.; de Mora, K.; Glieberman, A.L.; Monie, D.D.; Endy, D. Measuring the activity of BioBrick promoters using an in vivo reference standard. J. Biol. Eng. 2009, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Davidsohn, N.; Beal, J.; Kiani, S.; Adler, A.; Yaman, F.; Li, Y.; Xie, Z.; Weiss, R. Accurate predictions of genetic circuit behavior from part characterization and modular composition. ACS Synth. Biol. 2014, 4, 673–681. [Google Scholar] [CrossRef] [PubMed]
- Cardinale, S.; Arkin, A.P. Contextualizing context for synthetic biology–identifying causes of failure of synthetic biological systems. Biotechnol. J. 2012, 7, 856–866. [Google Scholar] [CrossRef]
- Klumpp, S.; Zhang, Z.; Hwa, T. Growth rate-dependent global effects on gene expression in bacteria. Cell 2009, 139, 1366–1375. [Google Scholar] [CrossRef]
- Bremer, H.; Dennis, P. Modulation of Chemical Composition and Other Parameters of the Cell at Different Exponential Growth Rates. EcoSal Plus 2008, 3. [Google Scholar] [CrossRef]
- Scott, M.; Gunderson, C.W.; Mateescu, E.M.; Zhang, Z.; Hwa, T. Interdependence of cell growth and gene expression: Origins and consequences. Science 2010, 330, 1099–1102. [Google Scholar] [CrossRef]
- You, C.; Okano, H.; Hui, S.; Zhang, Z.; Kim, M.; Gunderson, C.W.; Wang, Y.P.; Lenz, P.; Yan, D.; Hwa, T. Coordination of bacterial proteome with metabolism by cyclic AMP signalling. Nature 2013, 500, 301. [Google Scholar] [CrossRef]
- Hui, S.; Silverman, J.M.; Chen, S.S.; Erickson, D.W.; Basan, M.; Wang, J.; Hwa, T.; Williamson, J.R. Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol. 2015, 11, 784. [Google Scholar] [CrossRef]
- Weiße, A.Y.; Oyarzún, D.A.; Danos, V.; Swain, P.S. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. USA 2015. [Google Scholar] [CrossRef] [PubMed]
- Carrera, J.; Rodrigo, G.; Singh, V.; Kirov, B.; Jaramillo, A. Empirical model and in vivo characterization of the bacterial response to synthetic gene expression show that ribosome allocation limits growth rate. Biotechnol. J. 2011, 6, 773–783. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.; Blanchard, A.E.; Lu, T. An integrative circuit–host modelling framework for predicting synthetic gene network behaviours. Nat. Microbiol. 2017, 2, 1658. [Google Scholar] [CrossRef] [PubMed]
- Gutenkunst, R.N.; Waterfall, J.J.; Casey, F.P.; Brown, K.S.; Myers, C.R.; Sethna, J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007, 3, e189. [Google Scholar] [CrossRef]
- Erguler, K.; Stumpf, M.P. Practical limits for reverse engineering of dynamical systems: A statistical analysis of sensitivity and parameter inferability in systems biology models. Mol. BioSyst. 2011, 7, 1593–1602. [Google Scholar] [CrossRef]
- Hagen, D.R.; White, J.K.; Tidor, B. Convergence in parameters and predictions using computational experimental design. Interface Focus 2013, 3, 20130008. [Google Scholar] [CrossRef]
- Apgar, J.F.; Witmer, D.K.; White, F.M.; Tidor, B. Sloppy models, parameter uncertainty, and the role of experimental design. Mol. BioSyst. 2010, 6, 1890–1900. [Google Scholar] [CrossRef]
- Bandara, S.; Schlöder, J.P.; Eils, R.; Bock, H.G.; Meyer, T. Optimal experimental design for parameter estimation of a cell signaling model. PLoS Comput. Biol. 2009, 5, e1000558. [Google Scholar] [CrossRef]
- Ruess, J.; Parise, F.; Milias-Argeitis, A.; Khammash, M.; Lygeros, J. Iterative experiment design guides the characterization of a light-inducible gene expression circuit. Proc. Natl. Acad. Sci. USA 2015, 112, 8148–8153. [Google Scholar] [CrossRef]
- Braniff, N.; Ingalls, B. New Opportunities for Optimal Design of Dynamic Experiments in Systems and Synthetic Biology. Curr. Opin. Syst. Biol. 2018, 9, 42–48. [Google Scholar] [CrossRef]
- Hoang, M.; Barz, T.; Merchan, V.; Biegler, L.; Arellano-Garcia, H. Simultaneous solution approach to model-based experimental design. AIChE J. 2013, 59, 4169–4183. [Google Scholar] [CrossRef]
- Janka, D.; Körkel, S.; Bock, H.G. Direct multiple shooting for nonlinear optimum experimental design. In Multiple Shooting and Time Domain Decomposition Methods; Springer: Berlin, Germany, 2015; pp. 115–141. [Google Scholar]
- Telen, D.; Vercammen, D.; Logist, F.; Van Impe, J. Robustifying optimal experiment design for nonlinear, dynamic (bio) chemical systems. Comput. Chem. Eng. 2014, 71, 415–425. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Alonso, A.A.; Banga, J.R. Computational procedures for optimal experimental design in biological systems. IET Syst. Biol. 2008, 2, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Kutalik, Z.; Cho, K.H.; Wolkenhauer, O. Optimal sampling time selection for parameter estimation in dynamic pathway modeling. Biosystems 2004, 75, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Braniff, N.; Reed, M.; Ingalls, B. Optimal experimental design for characterizing gene expression: Sample scheduling. IFAC-PapersOnLine 2018, 51, 48–51. [Google Scholar] [CrossRef]
- Si, F.; Li, D.; Cox, S.E.; Sauls, J.T.; Azizi, O.; Sou, C.; Schwartz, A.B.; Erickstad, M.J.; Jun, Y.; Li, X.; et al. Invariance of initiation mass and predictability of cell size in Escherichia coli. Curr. Biol. 2017, 27, 1278–1287. [Google Scholar] [CrossRef] [PubMed]
- Cooper, S.; Helmstetter, C.E. Chromosome replication and the division cycle of Escherichia coli Br. J. Mol. Biol. 1968, 31, 519–540. [Google Scholar] [CrossRef]
- Bremer, H.; Churchward, G. An examination of the Cooper-Helmstetter theory of DNA replication in bacteria and its underlying assumptions. J. Theor. Biol. 1977, 69, 645–654. [Google Scholar] [CrossRef]
- Kubitschek, H.E.; Baldwin, W.W.; Schroeter, S.J.; Graetzer, R. Independence of buoyant cell density and growth rate in Escherichia coli. J. Bacteriol. 1984, 158, 296–299. [Google Scholar]
- Basan, M.; Zhu, M.; Dai, X.; Warren, M.; Sévin, D.; Wang, Y.P.; Hwa, T. Inflating bacterial cells by increased protein synthesis. Mol. Syst. Biol. 2015, 11, 836. [Google Scholar] [CrossRef]
- Finn, R.D.; Orlova, E.V.; Gowen, B.; Buck, M.; van Heel, M. Escherichia coli RNA polymerase core and holoenzyme structures. EMBO J. 2000, 19, 6833–6844. [Google Scholar] [CrossRef] [PubMed]
- Bakshi, S.; Dalrymple, R.M.; Li, W.; Choi, H.; Weisshaar, J.C. Partitioning of RNA polymerase activity in live Escherichia coli from analysis of single-molecule diffusive trajectories. Biophys. J. 2013, 105, 2676–2686. [Google Scholar] [CrossRef] [PubMed]
- Klumpp, S.; Hwa, T. Growth-rate-dependent partitioning of RNA polymerases in bacteria. Proc. Natl. Acad. Sci. USA 2008, 105, 20245–20250. [Google Scholar] [CrossRef] [PubMed]
- Patrick, M.; Dennis, P.P.; Ehrenberg, M.; Bremer, H. Free RNA polymerase in Escherichia coli. Biochimie 2015, 119, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Stracy, M.; Lesterlin, C.; De Leon, F.G.; Uphoff, S.; Zawadzki, P.; Kapanidis, A.N. Live-cell superresolution microscopy reveals the organization of RNA polymerase in the bacterial nucleoid. Proc. Natl. Acad. Sci. USA 2015, 112, E4390–E4399. [Google Scholar] [CrossRef] [PubMed]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Phillips, R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Rydenfelt, M.; Cox III, R.S.; Garcia, H.; Phillips, R. Statistical mechanical model of coupled transcription from multiple promoters due to transcription factor titration. Phys. Rev. E 2014, 89, 012702. [Google Scholar] [CrossRef]
- Phillips, R. Napoleon is in equilibrium. Annu. Rev. Condens. Matter Phys. 2015, 6, 85–111. [Google Scholar] [CrossRef]
- Heyduk, E.; Kuznedelov, K.; Severinov, K.; Heyduk, T. A consensus adenine at position–11 of the nontemplate strand of bacterial promoter is important for nucleation of promoter melting. J. Biol. Chem. 2006, 281, 12362–12369. [Google Scholar] [CrossRef]
- Brunner, M.; Bujard, H. Promoter recognition and promoter strength in the Escherichia coli system. EMBO J. 1987, 6, 3139–3144. [Google Scholar] [CrossRef]
- Djordjevic, M.; Bundschuh, R. Formation of the open complex by bacterial RNA polymerase—A quantitative model. Biophys. J. 2008, 94, 4233–4248. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, M. Efficient transcription initiation in bacteria: An interplay of protein–DNA interaction parameters. Integr. Biol. 2013, 5, 796–806. [Google Scholar] [CrossRef] [PubMed]
- Stormo, G.D. Introduction to Protein-DNA Interactions: Structure, Thermodynamics, and Bioinformatics; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2013. [Google Scholar]
- Kushner, S. Messenger RNA Decay. EcoSal Plus 2007. [Google Scholar] [CrossRef] [PubMed]
- Jain, C.; Belasco, J.G. RNase E autoregulates its synthesis by controlling the degradation rate of its own mRNA in Escherichia coli: Unusual sensitivity of the rne transcript to RNase E activity. Genes Dev. 1995, 9, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Mudd, E.A.; Higgins, C.F. Escherichia coli endoribonuclease RNase E: Autoregulation of expression and site-specific cleavage of mRNA. Mol. Microbiol. 1993, 9, 557–568. [Google Scholar] [CrossRef] [PubMed]
- Jain, C.; Deana, A.; Belasco, J.G. Consequences of RNase E scarcity in Escherichia coli. Mol. Microbiol. 2002, 43, 1053–1064. [Google Scholar] [CrossRef] [PubMed]
- Ow, M.C.; Liu, Q.; Mohanty, B.K.; Andrew, M.E.; Maples, V.F.; Kushner, S.R. RNase E levels in Escherichia coli are controlled by a complex regulatory system that involves transcription of the rne gene from three promoters. Mol. Microbiol. 2002, 43, 159–171. [Google Scholar] [CrossRef]
- Chen, H.; Shiroguchi, K.; Ge, H.; Xie, X.S. Genome-wide study of mRNA degradation and transcript elongation in Escherichia coli. Mol. Syst. Biol. 2015, 11, 781. [Google Scholar] [CrossRef]
- Pedersen, S.; Reeh, S.; Friesen, J.D. Functional mRNA half lives in E. coli. Mol. Gen. Genet. MGG 1978, 166, 329–336. [Google Scholar]
- Selinger, D.W.; Saxena, R.M.; Cheung, K.J.; Church, G.M.; Rosenow, C. Global RNA half-life analysis in Escherichia coli reveals positional patterns of transcript degradation. Genome Res. 2003, 13, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Mackie, G.A. RNase E: At the interface of bacterial RNA processing and decay. Nat. Rev. Microbiol. 2013, 11, 45. [Google Scholar] [CrossRef] [PubMed]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; WH Freeman: New York, NY, USA, 2002. [Google Scholar]
- Dai, X.; Zhu, M.; Warren, M.; Balakrishnan, R.; Patsalo, V.; Okano, H.; Williamson, J.R.; Fredrick, K.; Wang, Y.P.; Hwa, T. Reduction of translating ribosomes enables Escherichia coli to maintain elongation rates during slow growth. Nat. Microbiol. 2017, 2, 16231. [Google Scholar] [CrossRef]
- Borkowski, O.; Goelzer, A.; Schaffer, M.; Calabre, M.; Mäder, U.; Aymerich, S.; Jules, M.; Fromion, V. Translation elicits a growth rate-dependent, genome-wide, differential protein production in Bacillus subtilis. Mol. Syst. Biol. 2016, 12, 870. [Google Scholar] [CrossRef] [PubMed]
- Kennell, D.; Riezman, H. Transcription and translation initiation frequencies of the Escherichia coli lac operon. J. Mol. Biol. 1977, 114, 1–21. [Google Scholar] [CrossRef]
- Seo, S.W.; Yang, J.S.; Kim, I.; Yang, J.; Min, B.E.; Kim, S.; Jung, G.Y. Predictive design of mRNA translation initiation region to control prokaryotic translation efficiency. Metab. Eng. 2013, 15, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Salis, H.M.; Mirsky, E.A.; Voigt, C.A. Automated design of synthetic ribosome binding sites to control protein expression. Nat. Biotechnol. 2009, 27, 946. [Google Scholar] [CrossRef]
- Olson, E.J.; Hartsough, L.A.; Landry, B.P.; Shroff, R.; Tabor, J.J. Characterizing bacterial gene circuit dynamics with optically programmed gene expression signals. Nat. Methods 2014, 11, 449–455. [Google Scholar] [CrossRef]
- De Leon, F.G.; Sellars, L.; Stracy, M.; Busby, S.J.; Kapanidis, A.N. Tracking low-copy transcription factors in living bacteria: The case of the lac repressor. Biophys. J. 2017, 112, 1316–1327. [Google Scholar] [CrossRef]
- Sager, S.; Bock, H.G.; Diehl, M. The integer approximation error in mixed-integer optimal control. Math. Progr. 2012, 133, 1–23. [Google Scholar] [CrossRef]
- Sager, S. Sampling decisions in optimum experimental design in the light of Pontryagin’s maximum principle. SIAM J. Control Optim. 2013, 51, 3181–3207. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Buzzard, G.T.; Rundell, A.E. Model-based design of experiments for cellular processes. Wiley Interdiscip. Rev. Syst. Biol. Med. 2013, 5, 181–203. [Google Scholar] [CrossRef] [PubMed]
- Wilks, S.S. Certain generalizations in the analysis of variance. Biometrika 1932, 24, 471–494. [Google Scholar] [CrossRef]
- Kreutz, C.; Timmer, J. Systems biology: Experimental design. FEBS J. 2009, 276, 923–942. [Google Scholar] [CrossRef] [PubMed]
- Vallisneri, M. Use and abuse of the Fisher information matrix in the assessment of gravitational-wave parameter-estimation prospects. Phys. Rev. D 2008, 77, 042001. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Prog. Comput. 2018, in press. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Prog. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Kiefer, J.; Wolfowitz, J. The equivalence of two extremum problems. Can. J. Math. 1960, 12, 234. [Google Scholar] [CrossRef]
- Bauer, I.; Bock, H.G.; Körkel, S.; Schlöder, J.P. Numerical methods for optimum experimental design in DAE systems. J. Comput. Appl. Math. 2000, 120, 1–25. [Google Scholar] [CrossRef]
- Galvanin, F.; Barolo, M.; Bezzo, F. Online model-based redesign of experiments for parameter estimation in dynamic systems. Ind. Eng. Chem. Res. 2009, 48, 4415–4427. [Google Scholar] [CrossRef]
- Bandiera, L.; Hou, Z.; Kothamachu, V.; Balsa-Canto, E.; Swain, P.; Menolascina, F. On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter. Processes 2018, 6, 148. [Google Scholar] [CrossRef]
- Gorochowski, T.E.; Borujeni, A.E.; Park, Y.; Nielsen, A.A.; Zhang, J.; Der, B.S.; Gordon, D.B.; Voigt, C.A. Genetic circuit characterization and debugging using RNA-seq. Mol. Syst. Biol. 2017, 13, 952. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Hair, S.M.; Sexton, J.T.; Landry, B.P.; Olson, E.J.; Igoshin, O.A.; Tabor, J.J. FlowCal: A user-friendly, open source software tool for automatically converting flow cytometry data from arbitrary to calibrated units. ACS Synth. Biol. 2016, 5, 774–780. [Google Scholar] [CrossRef] [PubMed]
- Beal, J.; Haddock-Angelli, T.; Gershater, M.; De Mora, K.; Lizarazo, M.; Hollenhorst, J.; Rettberg, R. Reproducibility of fluorescent expression from engineered biological constructs in E. coli. PLoS ONE 2016, 11, e0150182. [Google Scholar]
- Beal, J.; Haddock-Angelli, T.; Baldwin, G.; Gershater, M.; Dwijayanti, A.; Storch, M.; de Mora, K.; Lizarazo, M.; Rettberg, R. Quantification of bacterial fluorescence using independent calibrants. PLoS ONE 2018, 13, e0199432. [Google Scholar] [CrossRef] [PubMed]
- Venayak, N.; Anesiadis, N.; Cluett, W.R.; Mahadevan, R. Engineering metabolism through dynamic control. Curr. Opin. Biotechnol. 2015, 34, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Mannan, A.A.; Han, Y.; Oyarzún, D.A.; Zhang, F. Dynamic metabolic control: Towards precision engineering of metabolism. J. Ind. Microbiol. Biotechnol. 2018, 56, 535–543. [Google Scholar] [CrossRef]
- Tan, S.Z.; Prather, K.L. Dynamic pathway regulation: Recent advances and methods of construction. Curr. Opin. Chem. Biol. 2017, 41, 28–35. [Google Scholar] [CrossRef]
- Doong, S.J.; Gupta, A.; Prather, K.L. Layered dynamic regulation for improving metabolic pathway productivity in Escherichia coli. Proc. Natl. Acad. Sci. USA 2018, 115, 2964–2969. [Google Scholar] [CrossRef]
- Gupta, A.; Reizman, I.M.B.; Reisch, C.R.; Prather, K.L. Dynamic regulation of metabolic flux in engineered bacteria using a pathway-independent quorum-sensing circuit. Nat. Biotechnol. 2017, 35, 273. [Google Scholar] [CrossRef]
- Soma, Y.; Hanai, T. Self-induced metabolic state switching by a tunable cell density sensor for microbial isopropanol production. Metab. Eng. 2015, 30, 7–15. [Google Scholar] [CrossRef] [PubMed]
| Parameter Label | Intrinsic Parameter | Nominal Value | Feasible Range |
|---|---|---|---|
| Intrinsic Transcription Parameters | |||
| Promoter Escape Rate | 20 min−1 | [1–30] | |
| RNAP-Promoter Binding | 40 | [10–40] | |
| TF-Promoter Binding | [–] | ||
| TF-RNAP Interaction | [–] | ||
| Intrinsic mRNA Decay Parameters | |||
| mRNA Decay Rate | μm−3 min−1 | [–] | |
| Intrinsic Translation Parameters | |||
| Max. Initiation Rate | min−1 | [1–10] | |
| Half-saturating Constant | 750 μm−3 | [750–1500] | |
| Property Label | Physiological Property | Value at μ = 0.6 db/h | Value at μ = 3 db/h |
| Physiological Properties of Transcription | |||
| Gene Copy Number | g | 1.4 | 5.7 |
| Available RNAP | 1000 | 4000 | |
| Genome-lengths of DNA | G | 1.3 | 4.3 |
| Physiological Properties of mRNA Decay | |||
| RNase Concentration | 900 μm−3 min−1 | 900 μm−3 min−1 | |
| Physiological Properties of Translation | |||
| Free Ribosomes | 600 | 7000 | |
| General Physiological Properties | |||
| Cell Volume | V | 0.4 μm−3 | 2.24 μm−3 |
| Growth Rate | min−1 | min−1 | |
| Experiment | Growth Rates (db/h) | Induction Pattern (log10) | Sampling Schedule | Optimality |
|---|---|---|---|---|
| Null Experiment | {0.6,1.8,3} |  |  | −63.8 |
| Growth Variant | {2,2.5,3} |  |  | −61.5 |
| Sampling Variant | {0.6,1.8,3} |  |  | −62.6 |
| Induction Variant | {0.6,1.8,3} |  |  | −60.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braniff, N.; Scott, M.; Ingalls, B. Component Characterization in a Growth-Dependent Physiological Context: Optimal Experimental Design. Processes 2019, 7, 52. https://doi.org/10.3390/pr7010052
Braniff N, Scott M, Ingalls B. Component Characterization in a Growth-Dependent Physiological Context: Optimal Experimental Design. Processes. 2019; 7(1):52. https://doi.org/10.3390/pr7010052
Chicago/Turabian StyleBraniff, Nathan, Matthew Scott, and Brian Ingalls. 2019. "Component Characterization in a Growth-Dependent Physiological Context: Optimal Experimental Design" Processes 7, no. 1: 52. https://doi.org/10.3390/pr7010052
APA StyleBraniff, N., Scott, M., & Ingalls, B. (2019). Component Characterization in a Growth-Dependent Physiological Context: Optimal Experimental Design. Processes, 7(1), 52. https://doi.org/10.3390/pr7010052






