Simulating the Filtration Effects of Cement-Grout in Fractured Porous Media with the 3D Unified Pipe-Network Method
Abstract
1. Introduction
2. Mathematical Model
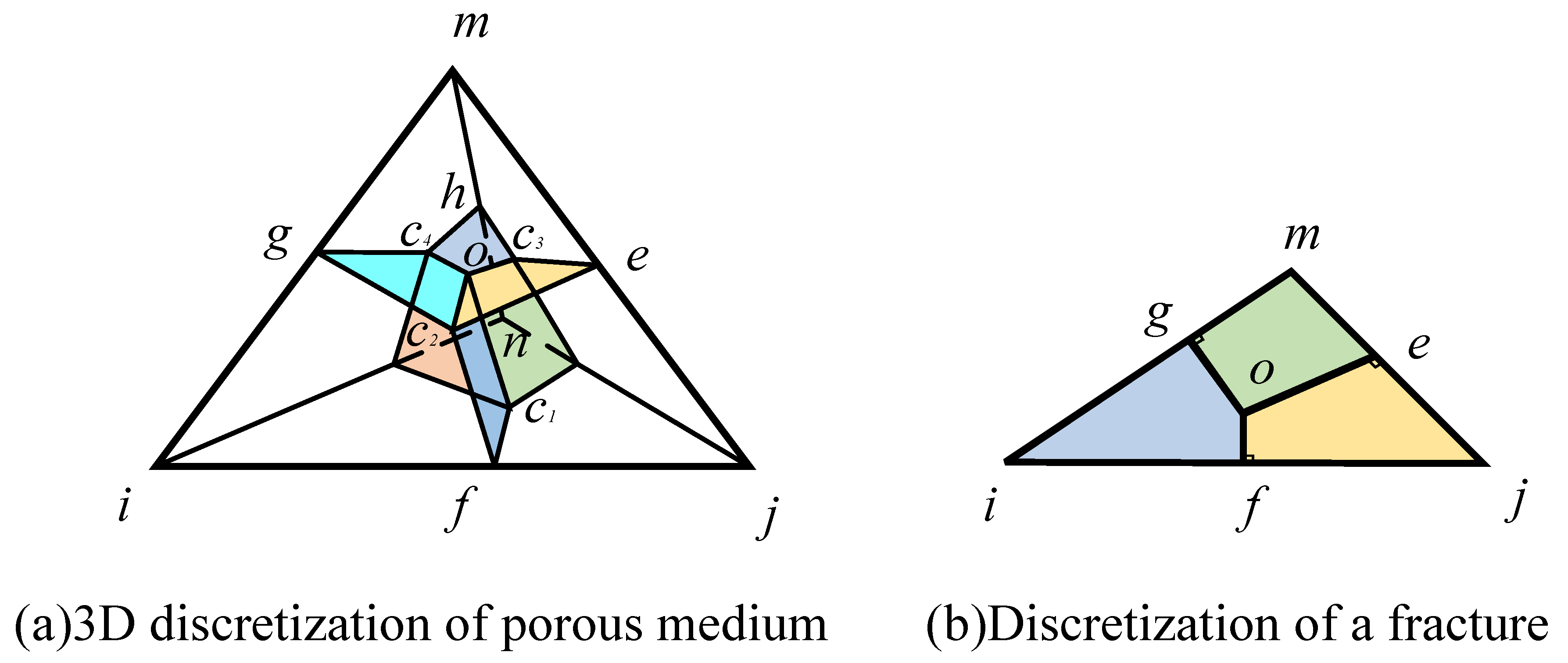
3. The Discretization Model for the 3D Unified Pipe-Network Method
Matrix Pipe-Network Model
4. Model Verification
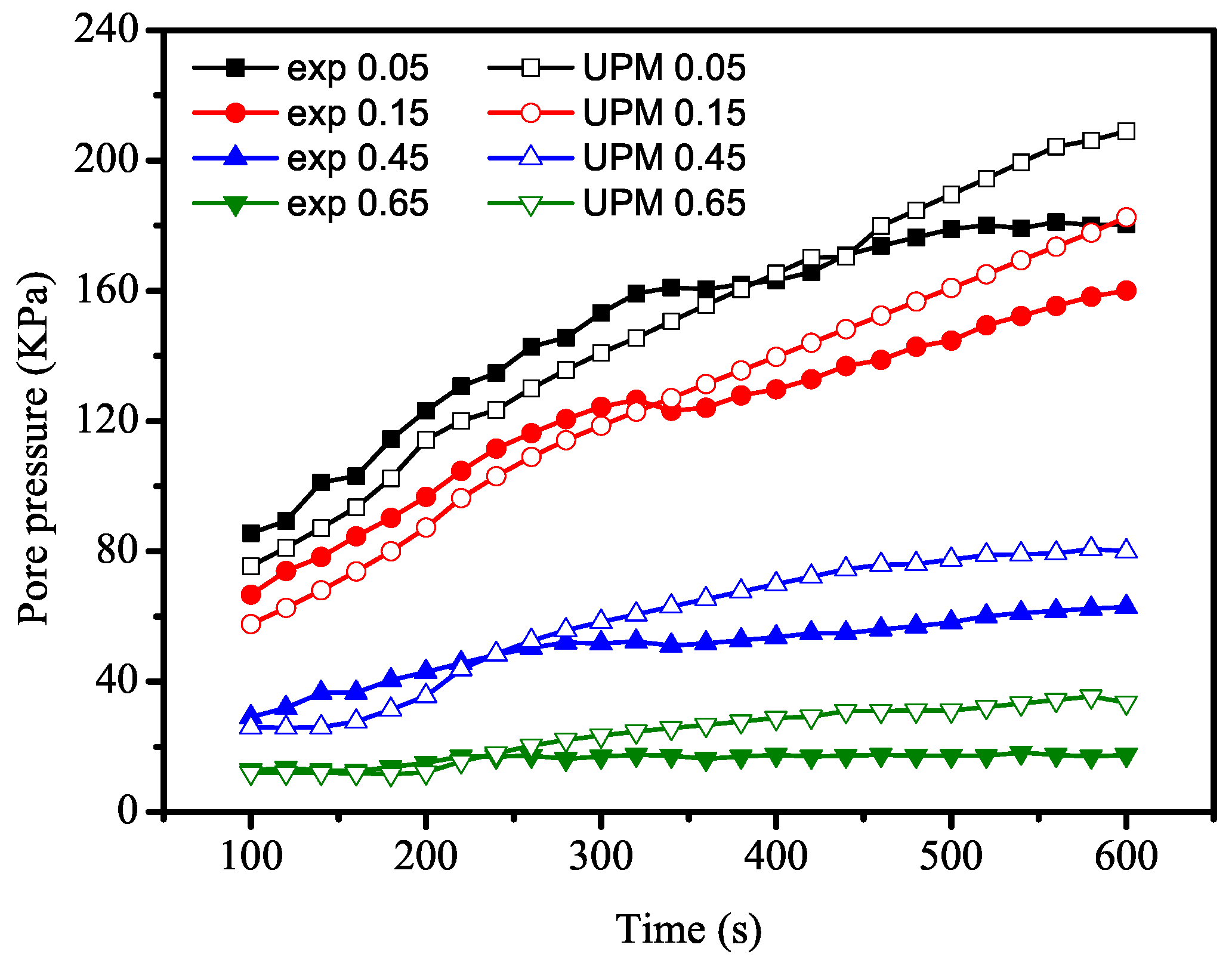
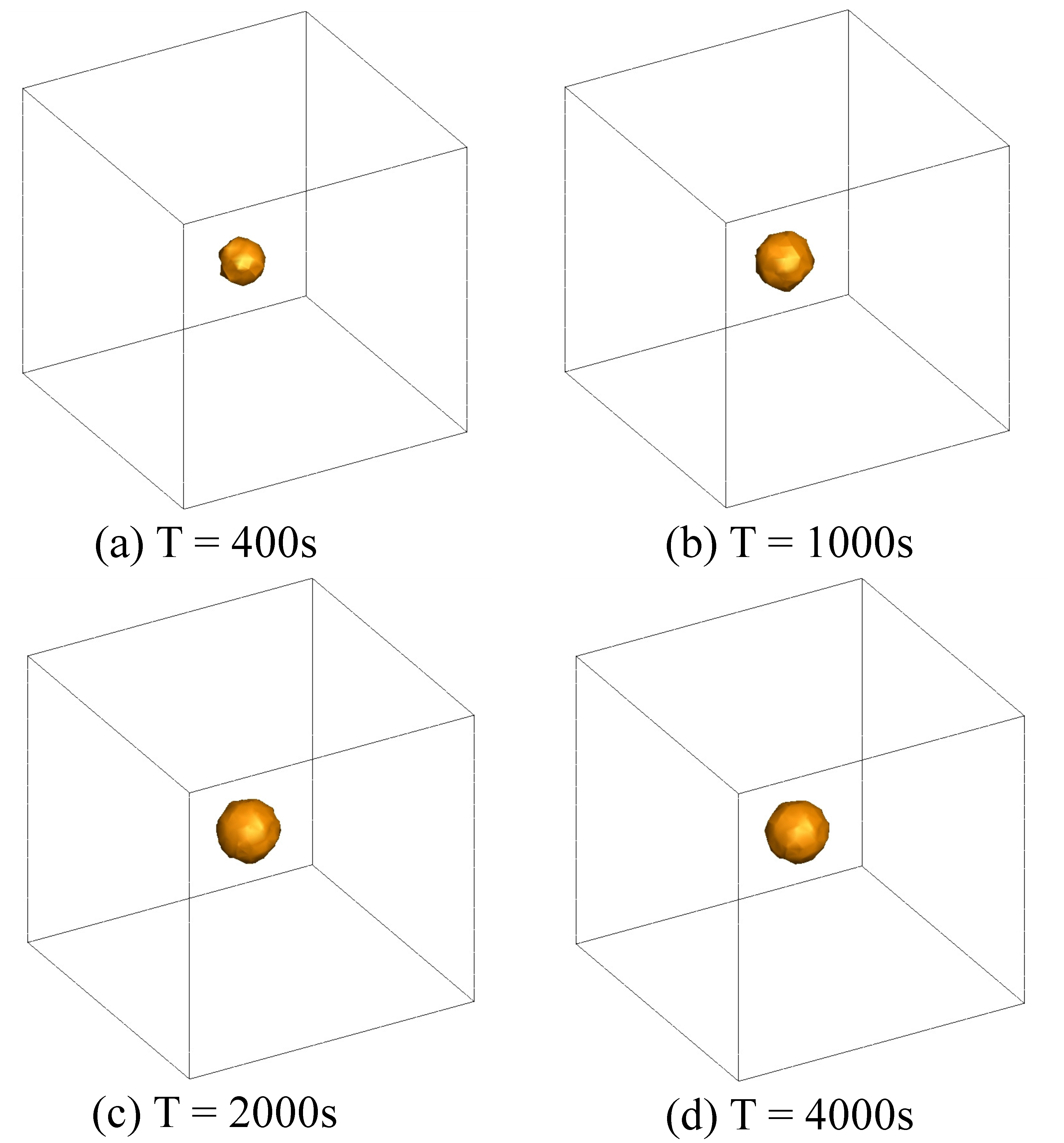
4.1. Experimental Verification
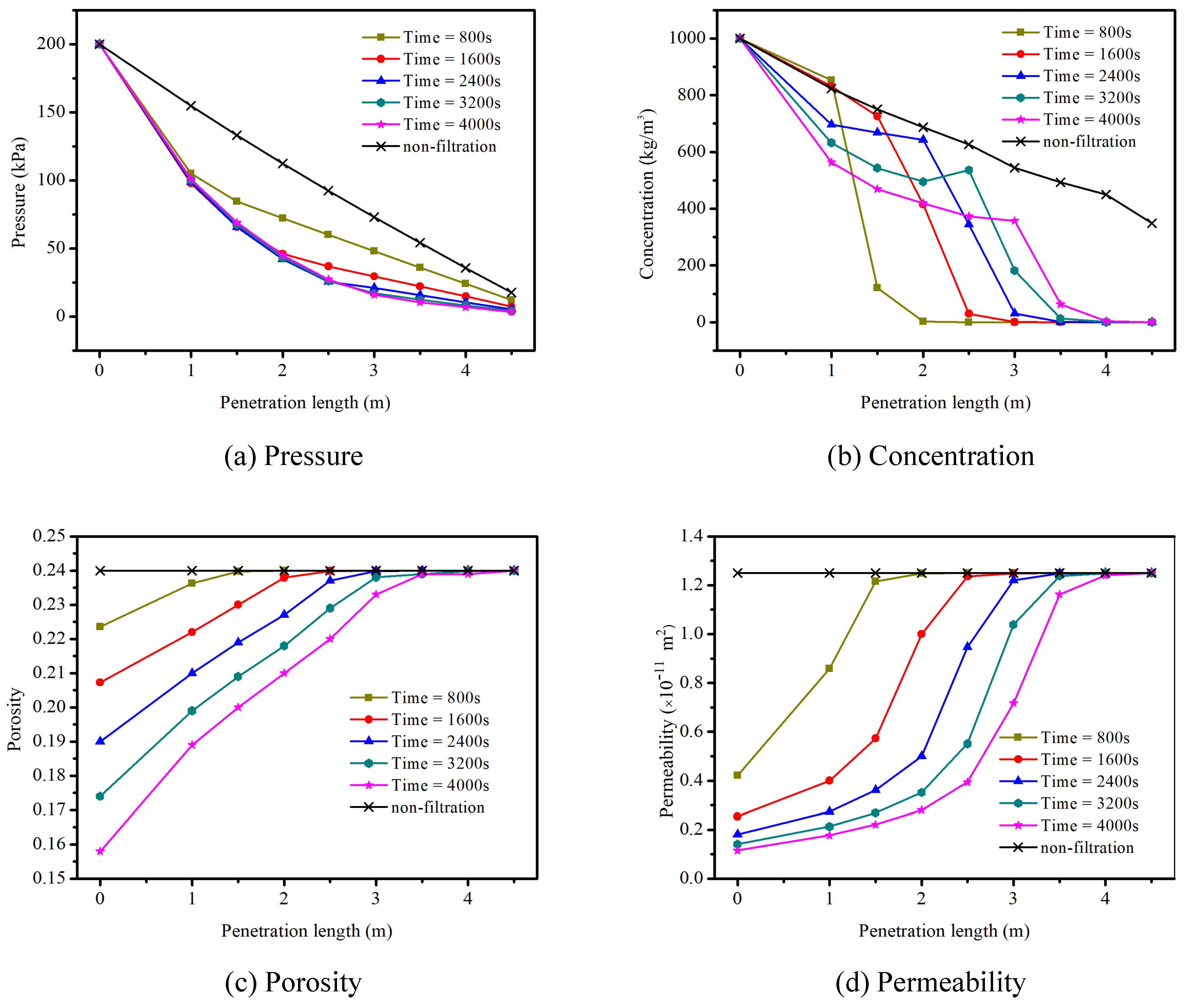
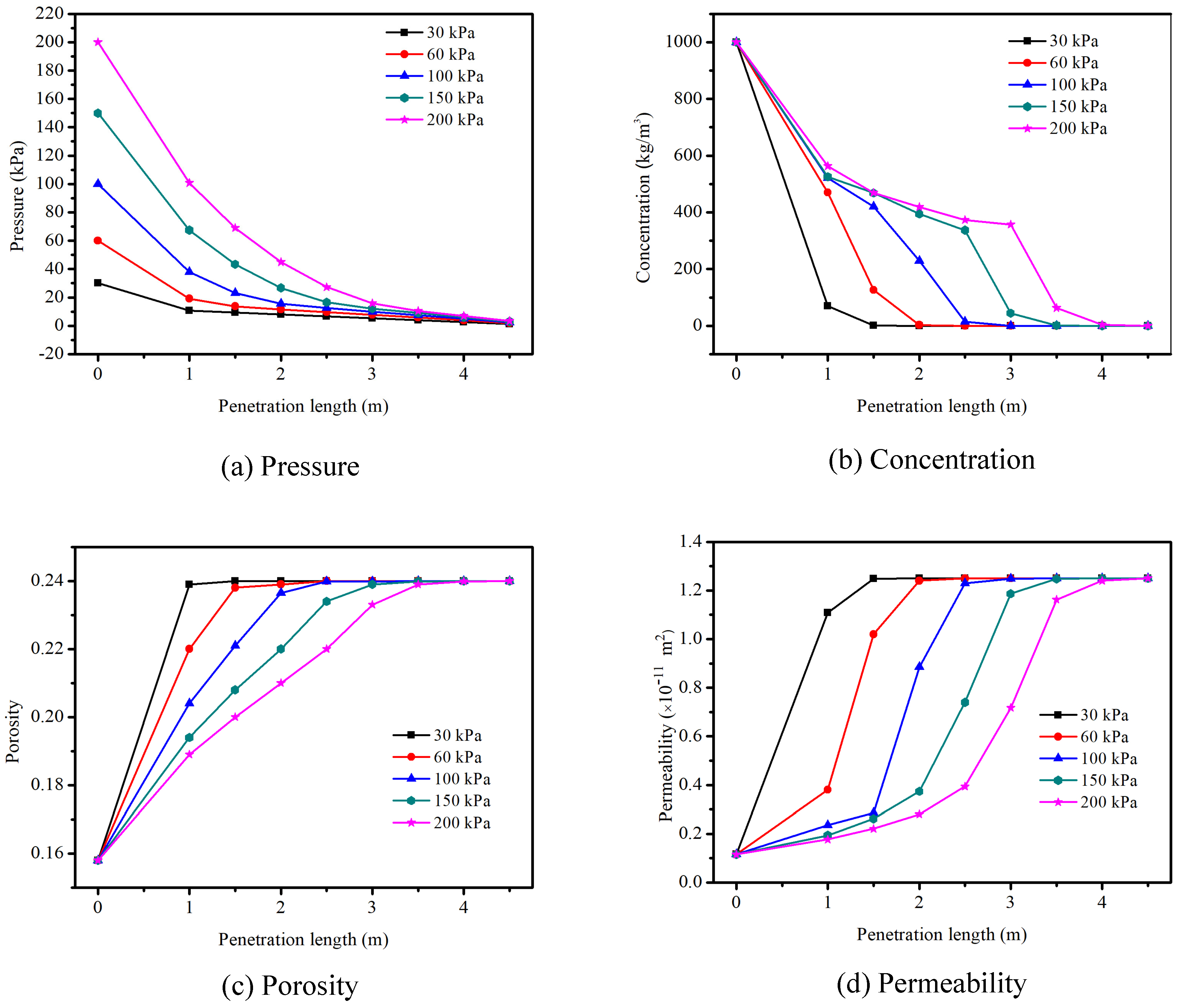
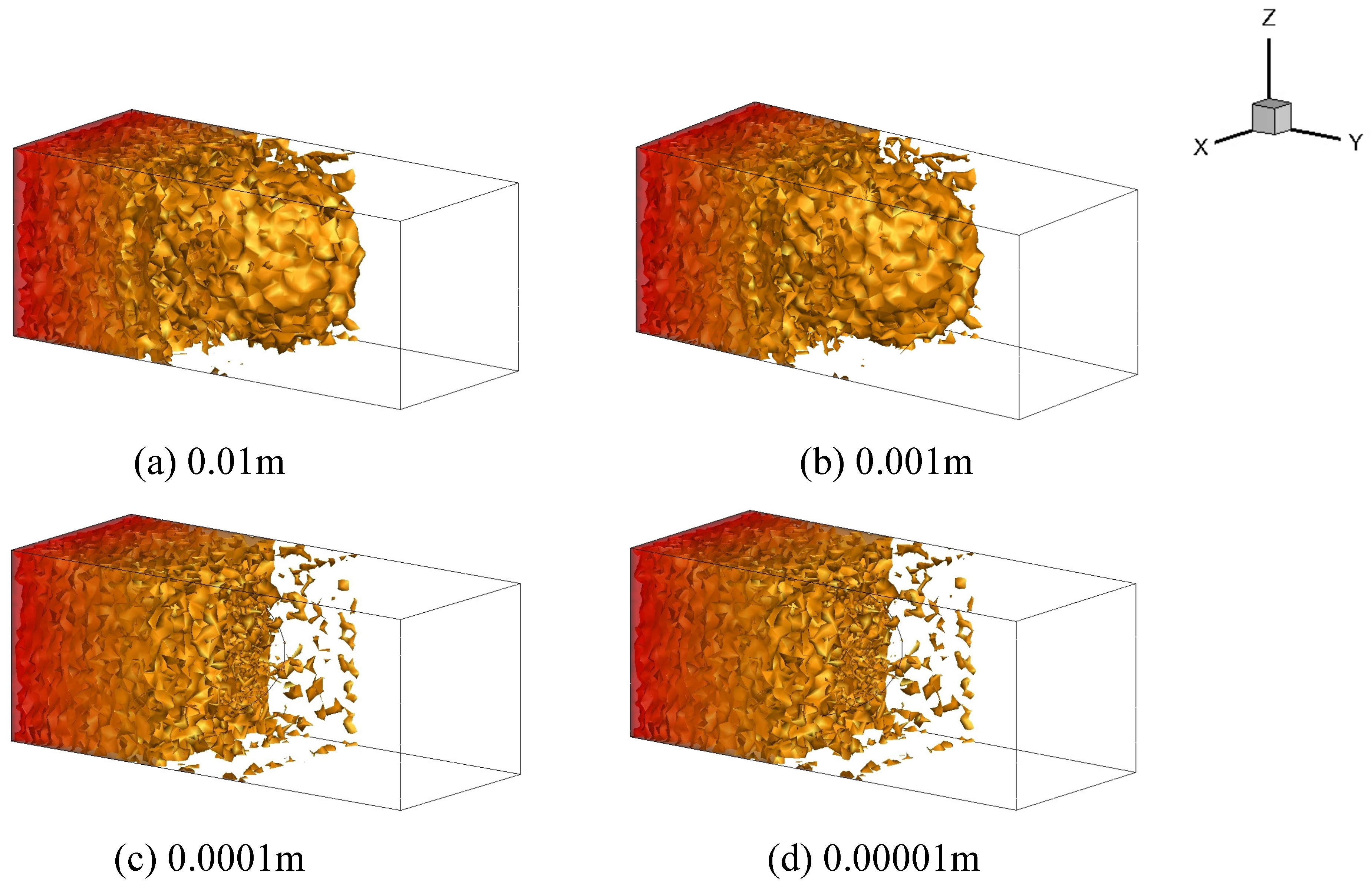
4.2. Sensitivity Analysis of Grout Filtration
4.2.1. Effects of the Grout Injection Pressure
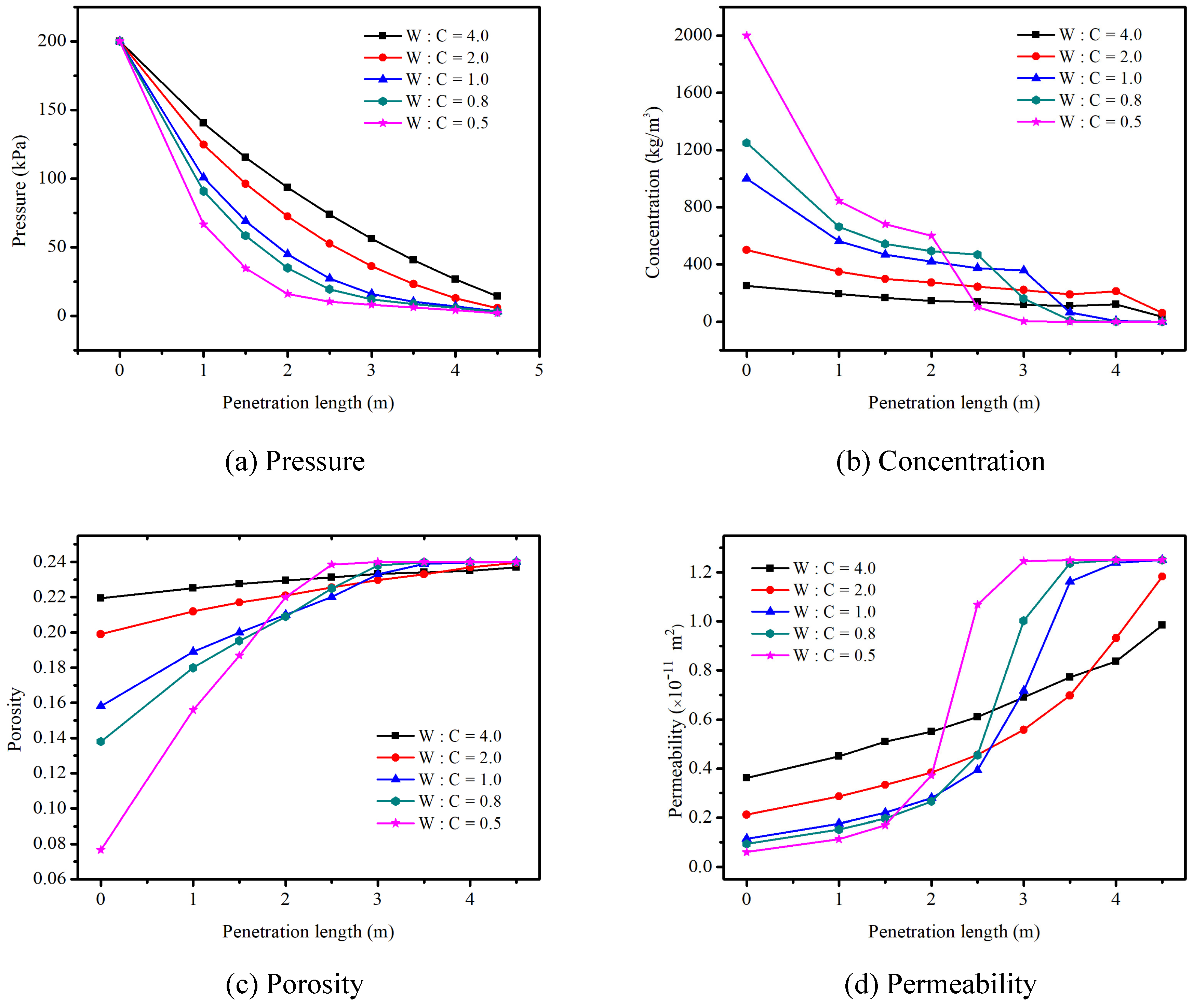
4.2.2. Effects of the Water–Cement Ratio
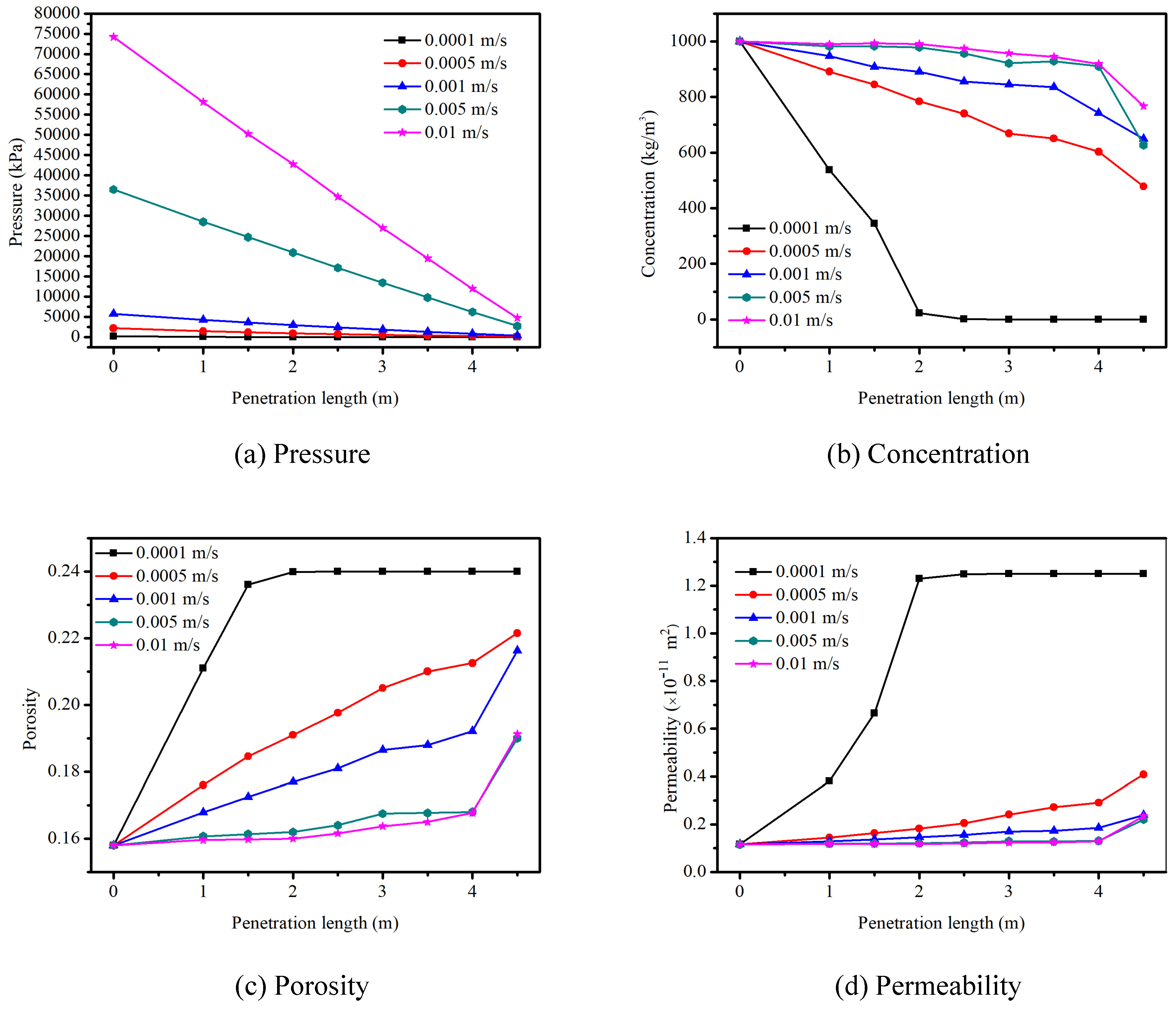
4.2.3. Effects of the Grout Injection Rate
5. Filtration in 3D Fractured Rock
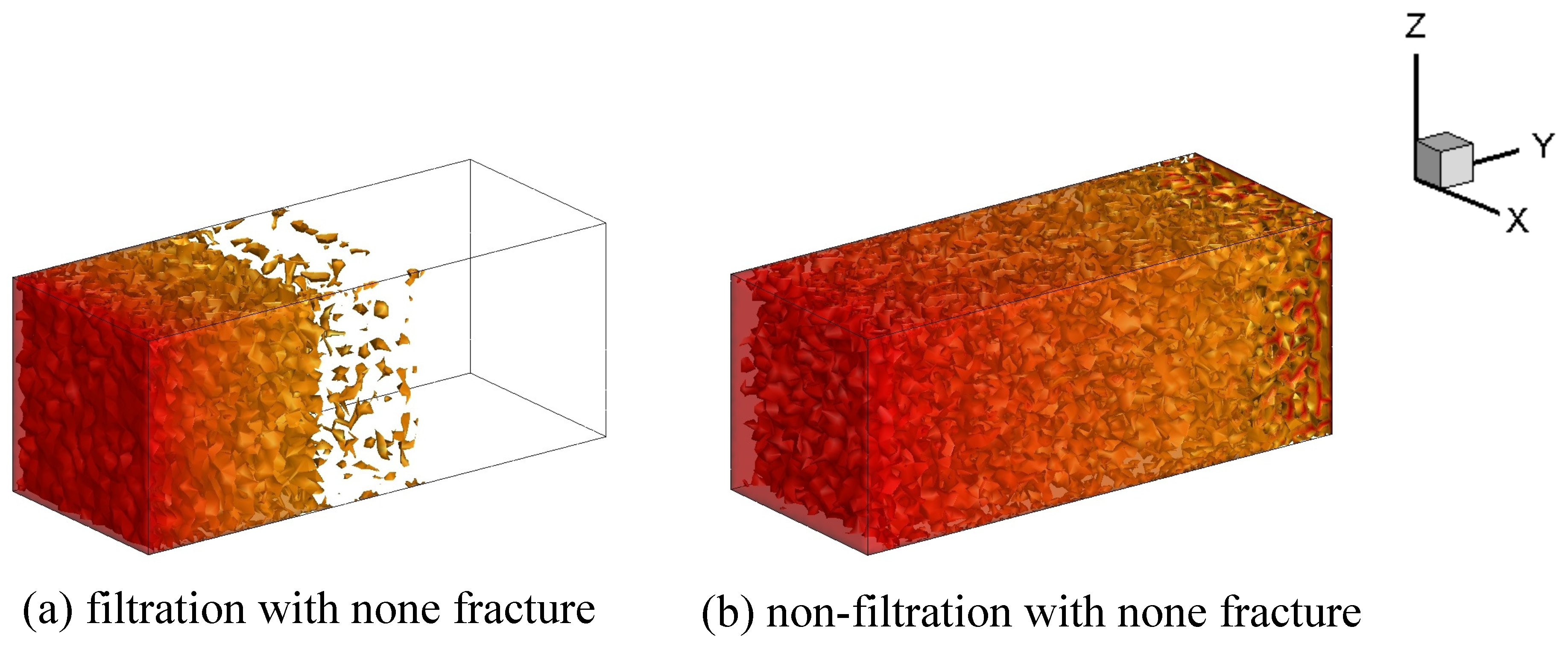
5.1. Effects of the Physical Properties of Fractures
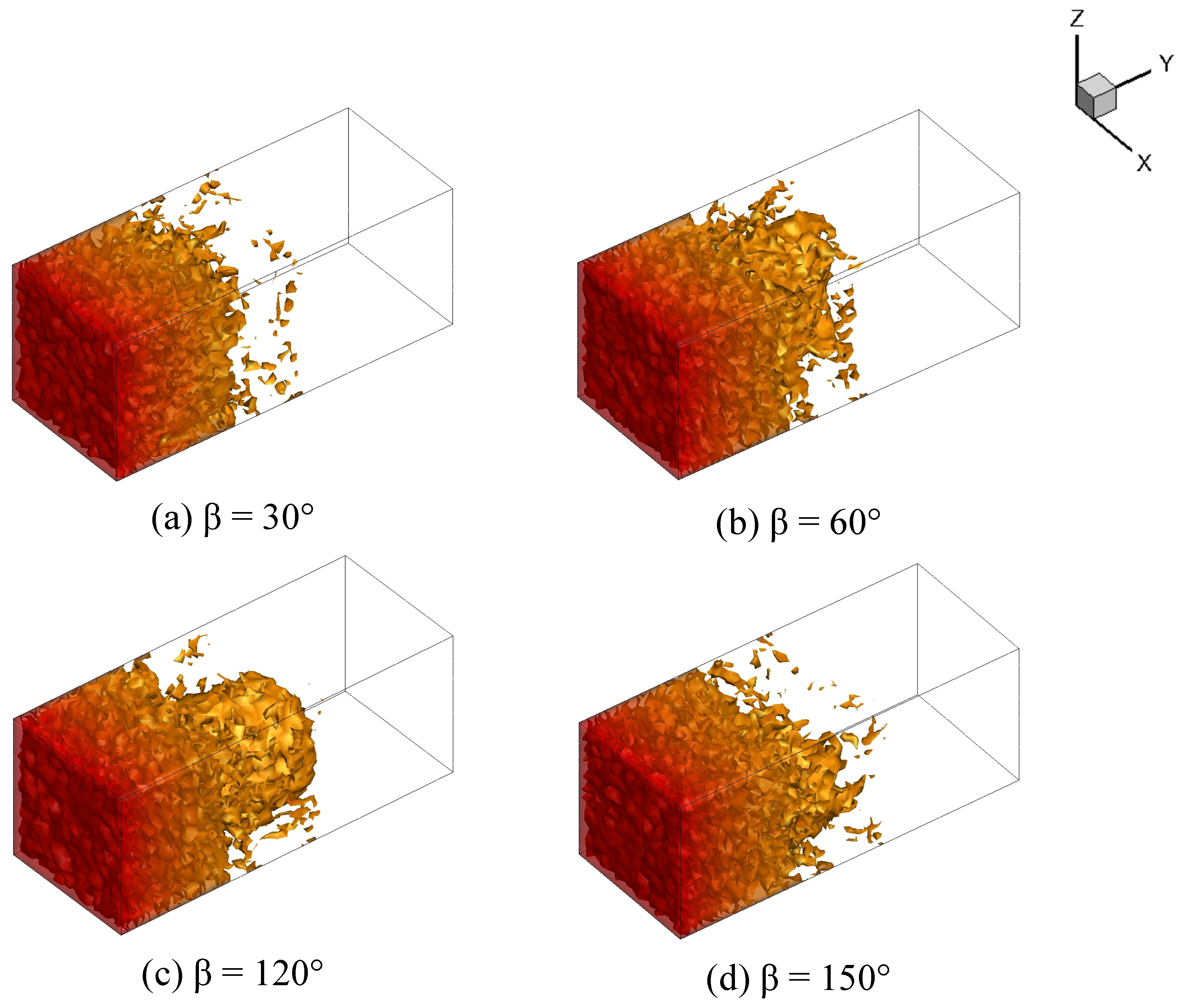
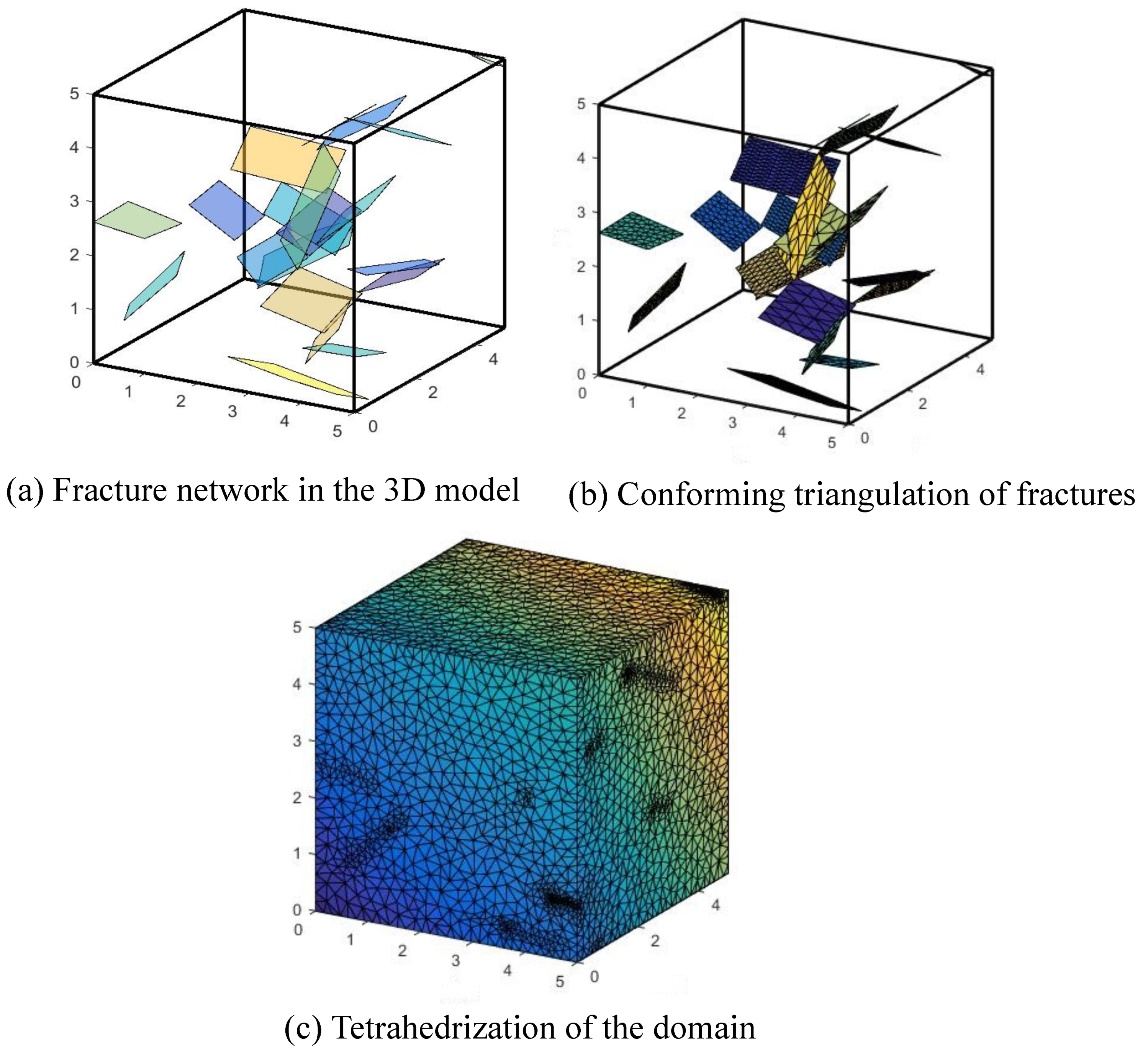
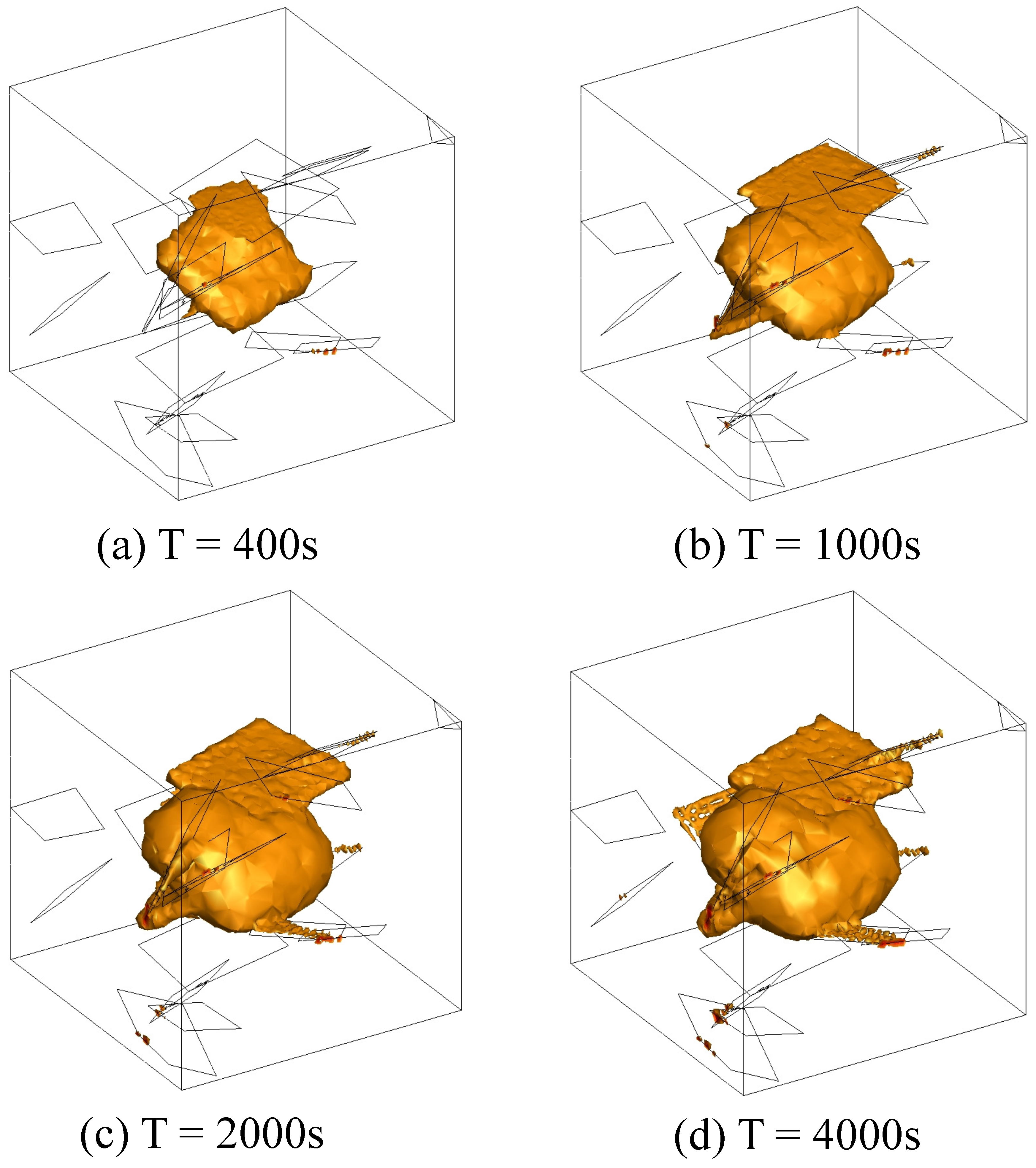
5.2. Effects of the Fracture Network
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UPM | Unified Pipe network Method |
References
- Arenzana, L.; Krizek, R.; Pepper, S. Injection of dilute microfine cement suspensions into fine sands. In Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, Brazil, 13–18 August 1989. [Google Scholar]
- Eriksson, M. Grouting field experiment at the äspö hard rock laboratory. Tunnel. Undergr. Space Technol. 2002, 17, 287–293. [Google Scholar] [CrossRef]
- Lees, E.L.D.; Naudts, A. New developments in permeation grouting: Design and evaluation. Concr. Int. 2000, 22, 47–52. [Google Scholar]
- Nikbakhtan, B.; Osanloo, M. Effect of grout pressure and grout flow on soil physical and mechanical properties in jet grouting operations. Int. J. Rock Mech. Min. Sci. 2009, 46, 498–505. [Google Scholar] [CrossRef]
- Ding, W.; Duan, C.; Zhu, Y.; Zhao, T.; Huang, D.; Li, P. The behavior of synchronous grouting in a quasi-rectangular shield tunnel based on a large visualized model test. Tunnel. Undergr. Space Technol. 2019, 83, 409–424. [Google Scholar] [CrossRef]
- Axelsson, M.; Gustafson, G. The penetracone, a new robust field measurement device for determining the penetrability of cementitious grouts. Tunnel. Undergr. Space Technol. 2010, 25, 1–8. [Google Scholar] [CrossRef]
- Zebovitz, S.; Krizek, R.; Atmatzidis, D. Injection of fine sands with very fine cement grout. J. Geotechn. Eng. 1989, 115, 1717–1733. [Google Scholar] [CrossRef]
- McDowell-Boyer, L.M.; Hunt, J.R.; Sitar, N. Particle transport through porous media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- Sharma, M.; Yortsos, Y. Transport of particulate suspensions in porous media: model formulation. AIChE J. 1987, 33, 1636–1643. [Google Scholar] [CrossRef]
- Kim, Y.S.; Whittle, A.J. Filtration in a porous granular medium: 1. Simulation of pore-scale particle deposition and clogging. Transp. Porous Med. 2006, 65, 53–87. [Google Scholar] [CrossRef]
- Axelsson, M.; Gustafson, G.; Fransson, A. Stop mechanism for cementitious grouts at different water-to-cement ratios. Tunnel. Undergr. Space Technol. 2009, 24, 390–397. [Google Scholar] [CrossRef]
- Hwang, H.; Yoon, J.; Rugg, D.; El Mohtar, C. Hydraulic conductivity of bentonite grouted sand. In Geo-Frontiers 2011: Advances in Geotechnical Engineering; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1372–1381. [Google Scholar]
- Eriksson, M.; Stille, H.; Andersson, J. Numerical calculations for prediction of grout spread with account for filtration and varying aperture. Tunnel. Undergr. Space Technol. 2000, 15, 353–364. [Google Scholar] [CrossRef]
- Abichou, T.; Benson, C.H.; Edil, T.B. Micro-structure and hydraulic conductivity of simulated sand-bentonite mixtures. Clays Clay Min. 2002, 50, 537–545. [Google Scholar] [CrossRef]
- Dupla, J.-C.; Canou, J.; Gouvenot, D. An advanced experimental set-up for studying a monodirectional grout injection process. Proc. Inst. Civ. Eng.-Ground Improv. 2004, 8, 91–99. [Google Scholar] [CrossRef]
- Draganović, A.; Stille, H. Filtration and penetrability of cement-based grout: Study performed with a short slot. Tunnel. Undergr. Space Technol. 2011, 26, 548–559. [Google Scholar] [CrossRef]
- Eriksson, M.; Stille, H. A Method for Measuring and Evaluating the Penetrability of Grouts. In Proceedings of the Third International Conference on Grouting and Ground Treatment, New Orleans, LA, USA, 10–12 February 2003; pp. 1326–1337. [Google Scholar]
- Bouchelaghem, F.; Vulliet, L.; Leroy, D.; Laloui, L.; Descoeudres, F. Mathematical and numerical filtration-advection-dispersion model of miscible grout propagation in saturated porous media. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 1195–1227. [Google Scholar] [CrossRef]
- Saada, Z.; Canou, J.; Dormieux, L.; Dupla, J.; Maghous, S. Modelling of cement suspension flow in granular porous media. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 691–711. [Google Scholar] [CrossRef]
- Yoneda, S.; Okabayashi, S.; Baba, O.; Tamura, M.; Mori, A. Permeating properties of ultra-fine cement grout. In Grouting and Deep Mixing; Balkema: Rotterdam, The Netherlands, 1996; pp. 107–113. [Google Scholar]
- Choo, C.-U.; Tien, C. Analysis of the transient behavior of deep-bed filtration. J. Colloid Interface Sci. 1995, 169, 13–33. [Google Scholar] [CrossRef]
- Herzig, J.; Leclerc, D.; Goff, P.L. Flow of suspensions through porous media-application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Chupin, O.; Saiyouri, N.; Hicher, P.-Y. Modeling of a semi-real injection test in sand. Comput. Geotech. 2009, 36, 1039–1048. [Google Scholar] [CrossRef]
- Rege, S.; Fogler, H. A Network Model for Deep Bed Filtration of Solids And Emulsions; Tech. Rep.; American Institute of Chemical Engineers: New York, NY, USA, 1988. [Google Scholar]
- Tarafdar, S.; Dey, A.; Gupta, B.S. A multiple state stochastic model for deep-bed filtration. Chem. Eng. Technol. Ind. Chem.-Plant Equip.-Process Eng.-Biotechnol. 1992, 15, 44–50. [Google Scholar] [CrossRef]
- Ghidaglia, C.; de Arcangelis, L.; Hinch, J.; Guazzelli, E. Transition in particle capture in deep bed filtration. Phys. Rev. E 1996, 53, R3028. [Google Scholar] [CrossRef]
- Nikiforov, A.; Nikanshin, D. Simulation of transfer of solid particles by a filtration flow. J. Eng. Phys. Thermophys. 1998, 71, 933–938. [Google Scholar] [CrossRef]
- Lee, J.; Koplik, J. Network model for deep bed filtration. Phys. Fluids 2001, 13, 1076–1086. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Jing, H.; Yu, L. Relationship between equivalent permeability and fractal dimension of dual-porosity media subjected to fluid–rock reaction under triaxial stresses. Fractals 2018, 26, 1850072. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Yu, L.; Jiang, Y.; Jing, H. A discrete-fracture-network fault model revealing permeability and aperture evolutions of a fault after earthquakes. Int. J. Rock Mech. Min. Sci. 2018, 107, 19–24. [Google Scholar] [CrossRef]
- Maghous, S.; Saada, Z.; Dormieux, L.; Canou, J.; Dupla, J. A model for in situ grouting with account for particle filtration. Comput. Geotech. 2007, 34, 164–174. [Google Scholar] [CrossRef]
- Bouchelaghem, F. Multi-scale modelling of the permeability evolution of fine sands during cement suspension grouting with filtration. Comput. Geotech. 2009, 36, 1058–1071. [Google Scholar] [CrossRef]
- Eriksson, M. Prediction of Grout Spread and Sealing Effect. Ph.D. Thesis, KTH Byggvetenskap, Stockholm, Switzerland, 2002. [Google Scholar]
- Areias, P.M.; Song, J.; Belytschko, T. Analysis of fracture in thin shells by overlapping paired elements. Comput. Methods Appl. Mech. Eng. 2006, 195, 5343–5360. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Li, F.-B. An improved stable xfem (is-xfem) with a novel enrichment function for the computational modeling of cohesive cracks. Comput. Methods Appl. Mech. Eng. 2015, 295, 77–107. [Google Scholar] [CrossRef]
- Saloustros, S.; Pela, L.; Cervera, M.; Roca, P. Finite element modelling of internal and multiple localized cracks. Comput. Mech. 2017, 59, 299–316. [Google Scholar] [CrossRef]
- Saloustros, S.; Cervera, M.; Pela, L. Challenges, tools and applications of tracking algorithms in the numerical modelling of cracks in concrete and masonry structures. Arch. Comput. Methods Eng. 2018, 1–45. [Google Scholar] [CrossRef]
- Cervera, M.; Pela, L.; Clemente, R.; Roca, P. A crack-tracking technique for localized damage in quasi-brittle materials. Eng. Fract. Mech. 2010, 77, 2431–2450. [Google Scholar] [CrossRef]
- Zhang, Y.; Lackner, R.; Zeiml, M.; Mang, H.A. Strong discontinuity embedded approach with standard sos formulation: Element formulation, energy-based crack-tracking strategy, and validations. Comput. Methods Appl. Mech. Eng. 2015, 287, 335–366. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X. Cracking elements: A self-propagating strong discontinuity embedded approach for quasi-brittle fracture. Finite Elem. Anal. Des. 2018, 144, 84–100. [Google Scholar] [CrossRef]
- Nikolić, M.; Ibrahimbegovic, A.; Miscevic, P. Brittle and ductile failure of rocks: Embedded discontinuity approach for representing mode i and mode ii failure mechanisms. Int. J. Numer. Methods Eng. 2015, 102, 1507–1526. [Google Scholar] [CrossRef]
- Cervera, M.; Barbat, G.; Chiumenti, M. Finite element modeling of quasi-brittle cracks in 2d and 3d with enhanced strain accuracy. Comput. Mech. 2017, 60, 767–796. [Google Scholar] [CrossRef]
- Cervera, M.; Chiumenti, M.; Codina, R. Mixed stabilized finite element methods in nonlinear solid mechanics: Part I: Formulation. Comput. Methods Appl. Mech. Eng. 2010, 199, 2559–2570. [Google Scholar] [CrossRef]
- Cervera, M.; Chiumenti, M.; Codina, R. Mixed stabilized finite element methods in nonlinear solid mechanics: Part II: Strain localization. Comput. Methods Appl. Mech. Eng. 2010, 199, 2571–2589. [Google Scholar] [CrossRef]
- Cervera, M.; Chiumenti, M.; Benedetti, L.; Codina, R. Mixed stabilized finite element methods in nonlinear solid mechanics. Part III: Compressible and incompressible plasticity. Comput. Methods Appl. Mech. Eng. 2015, 285, 752–775. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Nguyen, V.-P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018. [Google Scholar] [CrossRef]
- Wu, J.-Y. Robust numerical implementation of non-standard phase-field damage models for failure in solids article. Comput. Methods Appl. Mech. Eng. 2018. [Google Scholar] [CrossRef]
- Wu, J.; McAuliffe, C.; Waisman, H.; Deodatis, G. Stochastic analysis of polymer composites rupture at large deformations modeled by a phase field method. Comput. Methods Appl. Mech. Eng. 2016, 312, 596–634. [Google Scholar] [CrossRef]
- Nikolić, M.; Karavelić, E.; Ibrahimbegovic, A.; Miščević, P. Lattice element models and their peculiarities. Arch. Comput. Methods Eng. 2018, 25, 753–784. [Google Scholar] [CrossRef]
- Grassl, P. A lattice approach to model flow in cracked concrete. Cem. Concr. Compos. 2009, 31, 454–460. [Google Scholar] [CrossRef]
- Nikolić, M.; Do, X.N.; Ibrahimbegovic, A.; Nikolić, Ž. Crack propagation in dynamics by embedded strong discontinuity approach: Enhanced solid versus discrete lattice model. Comput. Methods Appl. Mech. Eng. 2018, 340, 480–499. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Fu, G.; Zhang, K. Investigation of the permeability anisotropy of 2d fractured rock masses. Eng. Geol. 2015, 196, 171–182. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Fan, L. Pipe network model for unconfined seepage analysis in fractured rock masses. Int. J. Rock Mech. Min. Sci. 2016, 88, 183–196. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, X.; Liu, R.; Xu, Z.; Li, S.; Zhang, Y. Transient analysis of grout penetration with time-dependent viscosity inside 3d fractured rock mass by unified pipe-network method. Water 2018, 10, 1122. [Google Scholar] [CrossRef]
- Bouchelaghem, F.; Vulliet, L.; Leroy, D.; Laloui, L.; Descoeudres, F. Real-scale miscible grout injection experiment and performance of advection–dispersion–filtration model. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 1149–1173. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Introduction to Modeling of Transport Phenomena in Porous Media; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Kim, Y.S.; Whittle, A.J. Filtration in a porous granular medium: 2. Application of bubble model to 1-d column experiments. Transp. Porous Media 2006, 65, 309–335. [Google Scholar] [CrossRef]
- Kim, Y.S.; Whittle, A.J. Particle network model for simulating the filtration of a microfine cement grout in sand. J. Geotech. Geoenviron. Eng. 2009, 135, 224–236. [Google Scholar] [CrossRef]
- Yoon, J.; Mohtar, C.S.E. A filtration model for evaluating maximum penetration distance of bentonite grout through granular soils. Comput. Geotech. 2015, 65, 291–301. [Google Scholar] [CrossRef]
- Bai, R.; Tien, C. Particle detachment in deep bed filtration. J. Colloid Interface Sci. 1997, 186, 307–317. [Google Scholar] [CrossRef] [PubMed]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Zhang, Y.; Pichler, C.; Yuan, Y.; Zeiml, M.; Lackner, R. Micromechanics-based multifield framework for early-age concrete. Eng. Struct. 2013, 47, 16–24. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeiml, M.; Pichler, C.; Lackner, R. Model-based risk assessment of concrete spalling in tunnel linings under fire loading. Eng. Struct. 2014, 77, 207–215. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeiml, M.; Maier, M.; Yuan, Y.; Lackner, R. Fast assessing spalling risk of tunnel linings under rabt fire: From a coupled thermo-hydro-chemo-mechanical model towards an estimation method. Eng. Struct. 2017, 142, 1–19. [Google Scholar] [CrossRef]
- Babuška, I. Error-bounds for finite element method. Numer. Math. 1971, 16, 322–333. [Google Scholar] [CrossRef]
- White, J.A.; Borja, R.I. Stabilized low-order finite element for coupled solid-deformation/fluid-diffusion and their application to fault zone transients. Comput. Methods Appl. Mech. Eng. 2008, 197, 4353–4366. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Li, T.; Zhu, H. Unified pipe network method for simulation of water flow in fractured porous rock. J. Hydrol. 2017, 547, 80–96. [Google Scholar] [CrossRef]
- Ren, F.; Ma, G.; Wang, Y.; Fan, L.; Zhu, H. Two-phase flow pipe network method for simulation of CO2 sequestration in fractured saline aquifers. Int. J. Rock Mech. Min. Sci. 2017, 98, 39–53. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Li, T.; Wang, Y.; Ren, F. Simulation of wormhole propagation in fractured carbonate rocks with unified pipe-network method. Comput. Geotech. 2018, 98, 58–68. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, G.; Ren, F.; Li, T. A constrained delaunay discretization method for adaptively meshing highly discontinuous geological media. Comput. Geosci. 2017, 109, 134–148. [Google Scholar] [CrossRef]



| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Injection grout velocity | u | ||
| Injection grout concentration | C | 1150 | |
| Water viscosity | |||
| Water density | 1000 | ||
| Rock density | 3000 | ||
| Initial matrix porosity | – | ||
| Intrinsic matrix permeability | 2 × | ||
| Hydrodynamic dispersion tensor of | 0 | ||
| Constant deposition coefficient | |||
| Constant negative scalar | b | – | |
| Gravitational acceleration constant | g |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Injection grout pressure | P | 200 | |
| Injection grout concentration | C | 1000 | |
| Water viscosity | |||
| Water density | 1000 | ||
| Rock density | 2940 | ||
| Initial matrix porosity | – | ||
| Intrinsic matrix permeability | × | ||
| Hydrodynamic dispersion tensor of | 0 | ||
| Constant deposition coefficient | |||
| Constant negative scalar | b | – | |
| Gravitational acceleration constant | g |
| Group | Fracture Number | Mean Length (m) | St dev | Dip Angle (Degree) | Dip Direction (Degree) | |
|---|---|---|---|---|---|---|
| 1 | 10 | x-axis | 1.2 | 0.5 | 16 | 40 |
| y-axis | 1 | 0.5 | ||||
| 2 | 10 | x-axis | 1.2 | 0.5 | 40 | 250 |
| y-axis | 1 | 0.5 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Yan, X.; Han, W.; Ma, G.; Zhang, Y. Simulating the Filtration Effects of Cement-Grout in Fractured Porous Media with the 3D Unified Pipe-Network Method. Processes 2019, 7, 46. https://doi.org/10.3390/pr7010046
Sun Z, Yan X, Han W, Ma G, Zhang Y. Simulating the Filtration Effects of Cement-Grout in Fractured Porous Media with the 3D Unified Pipe-Network Method. Processes. 2019; 7(1):46. https://doi.org/10.3390/pr7010046
Chicago/Turabian StyleSun, Zizheng, Xiao Yan, Weiqi Han, Guowei Ma, and Yiming Zhang. 2019. "Simulating the Filtration Effects of Cement-Grout in Fractured Porous Media with the 3D Unified Pipe-Network Method" Processes 7, no. 1: 46. https://doi.org/10.3390/pr7010046
APA StyleSun, Z., Yan, X., Han, W., Ma, G., & Zhang, Y. (2019). Simulating the Filtration Effects of Cement-Grout in Fractured Porous Media with the 3D Unified Pipe-Network Method. Processes, 7(1), 46. https://doi.org/10.3390/pr7010046






