Dynamic Sequence Specific Constraint-Based Modeling of Cell-Free Protein Synthesis
Abstract
1. Introduction
2. Results
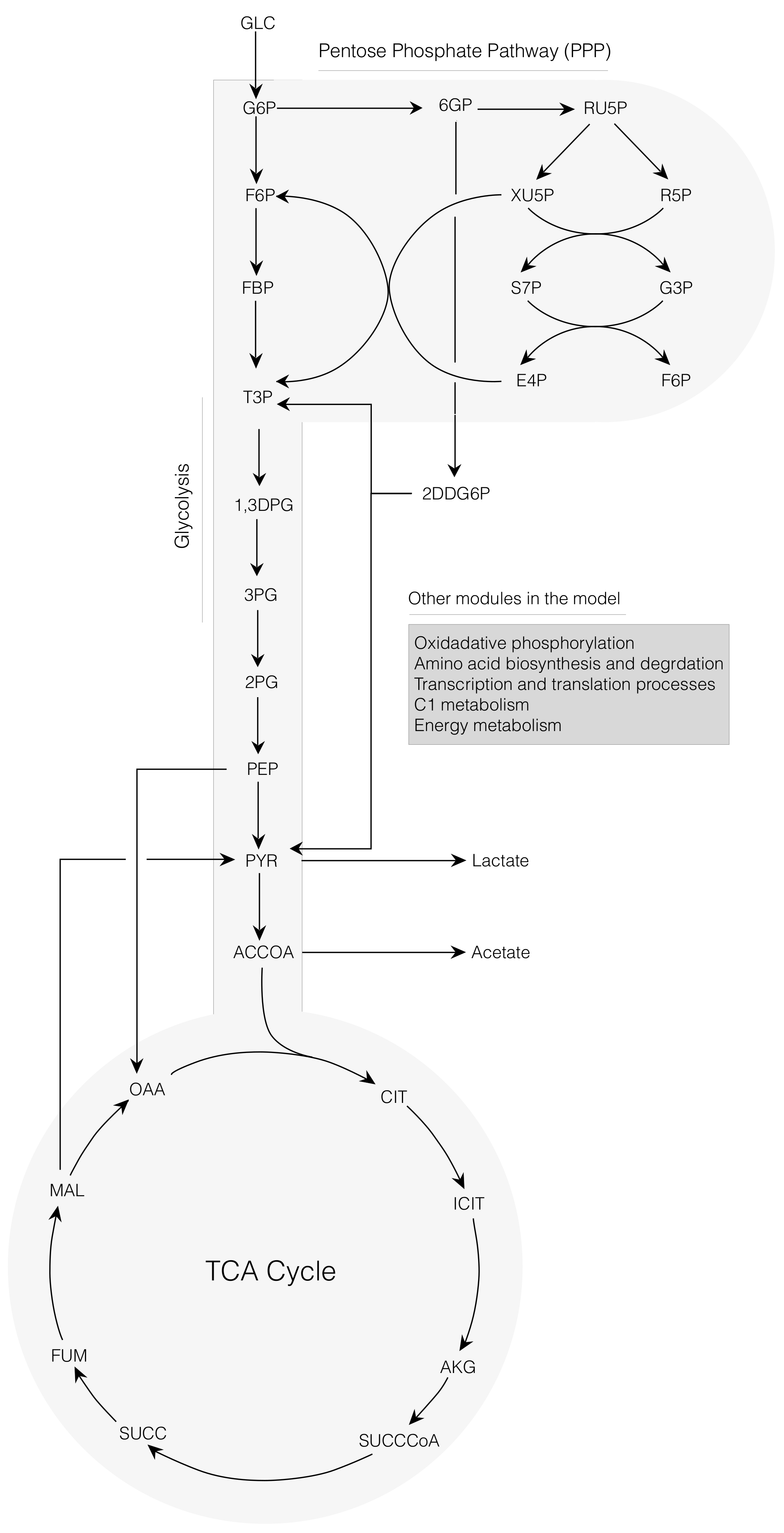
2.1. Cell-Free E. coli Metabolic Network
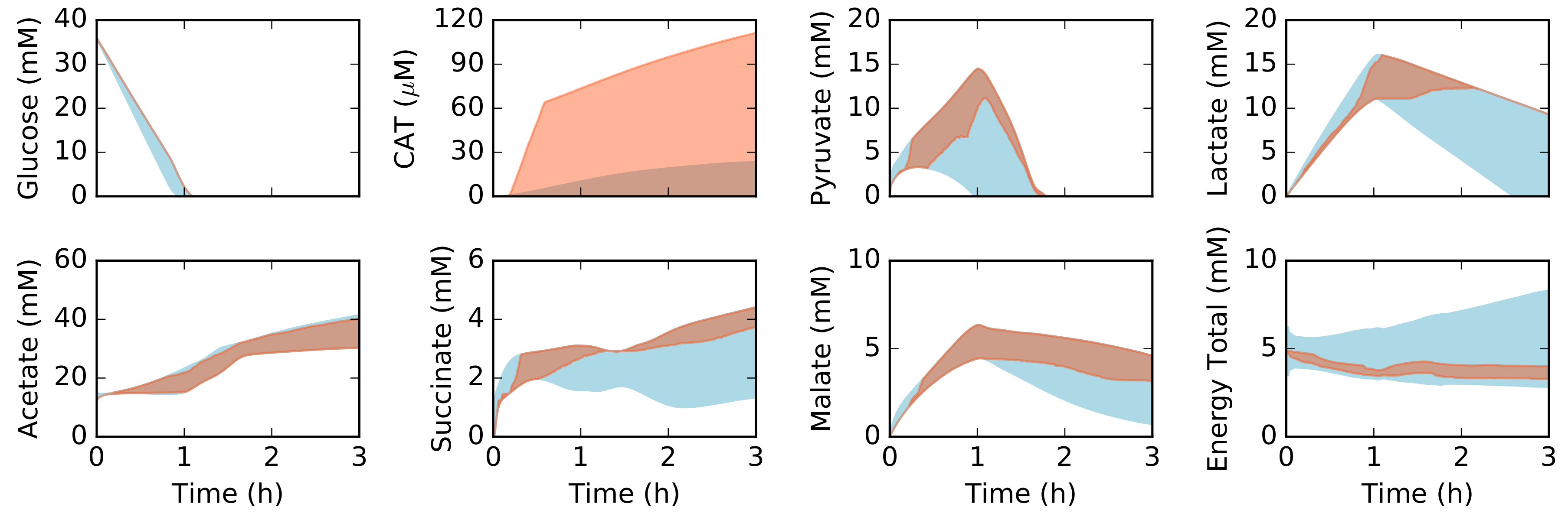
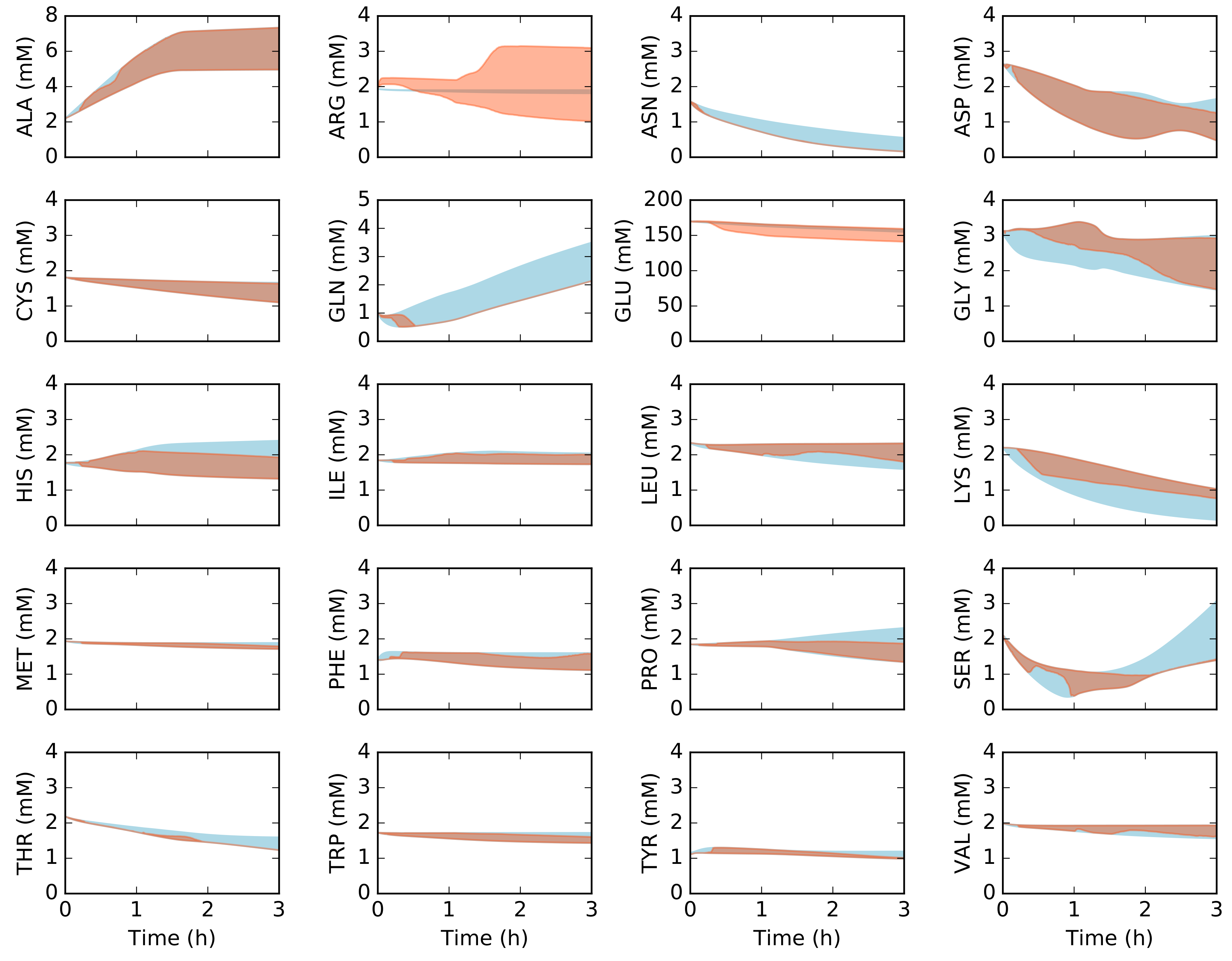
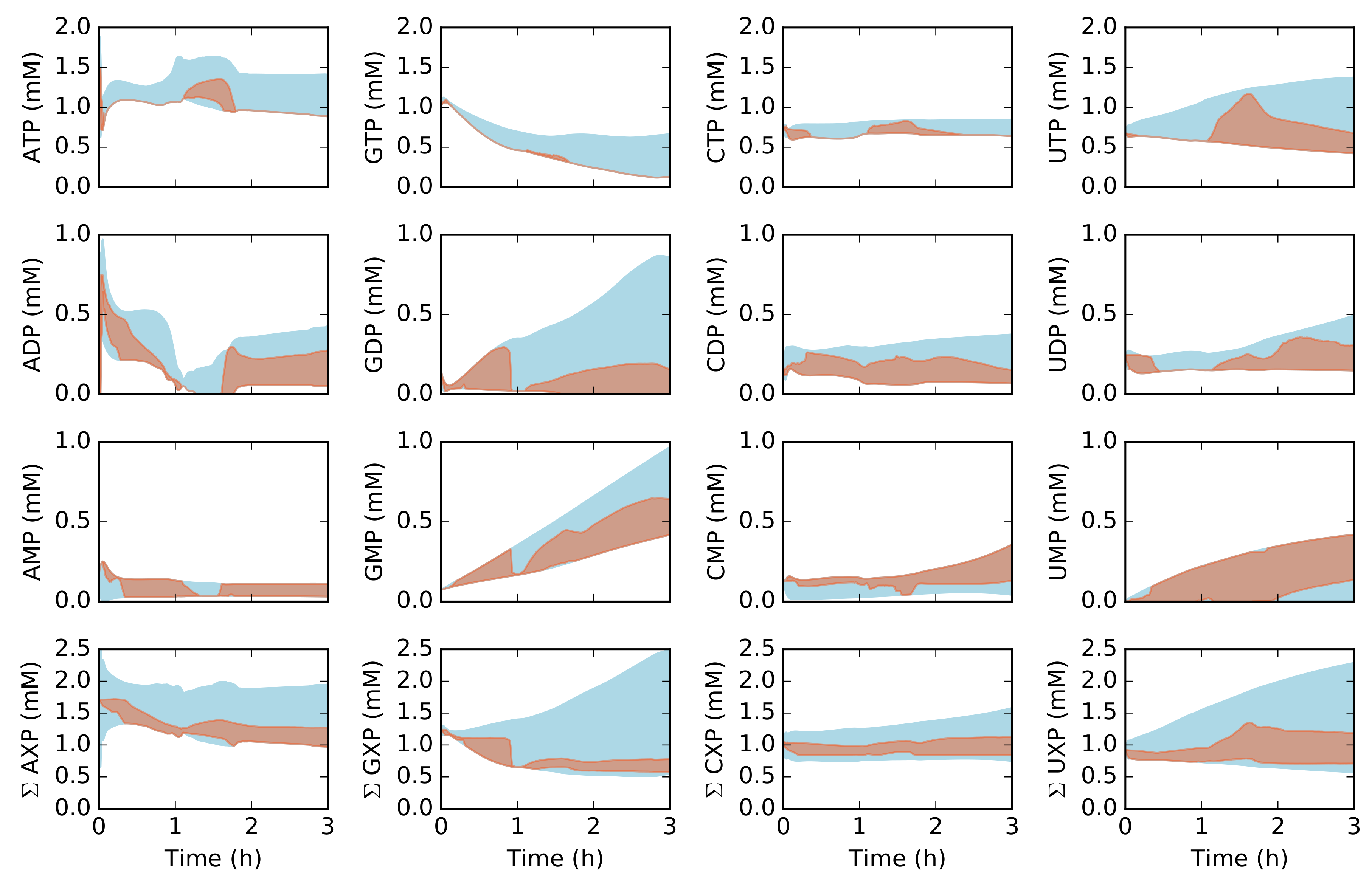
2.2. Dynamic Constrained Simulation of cell-free Protein Synthesis
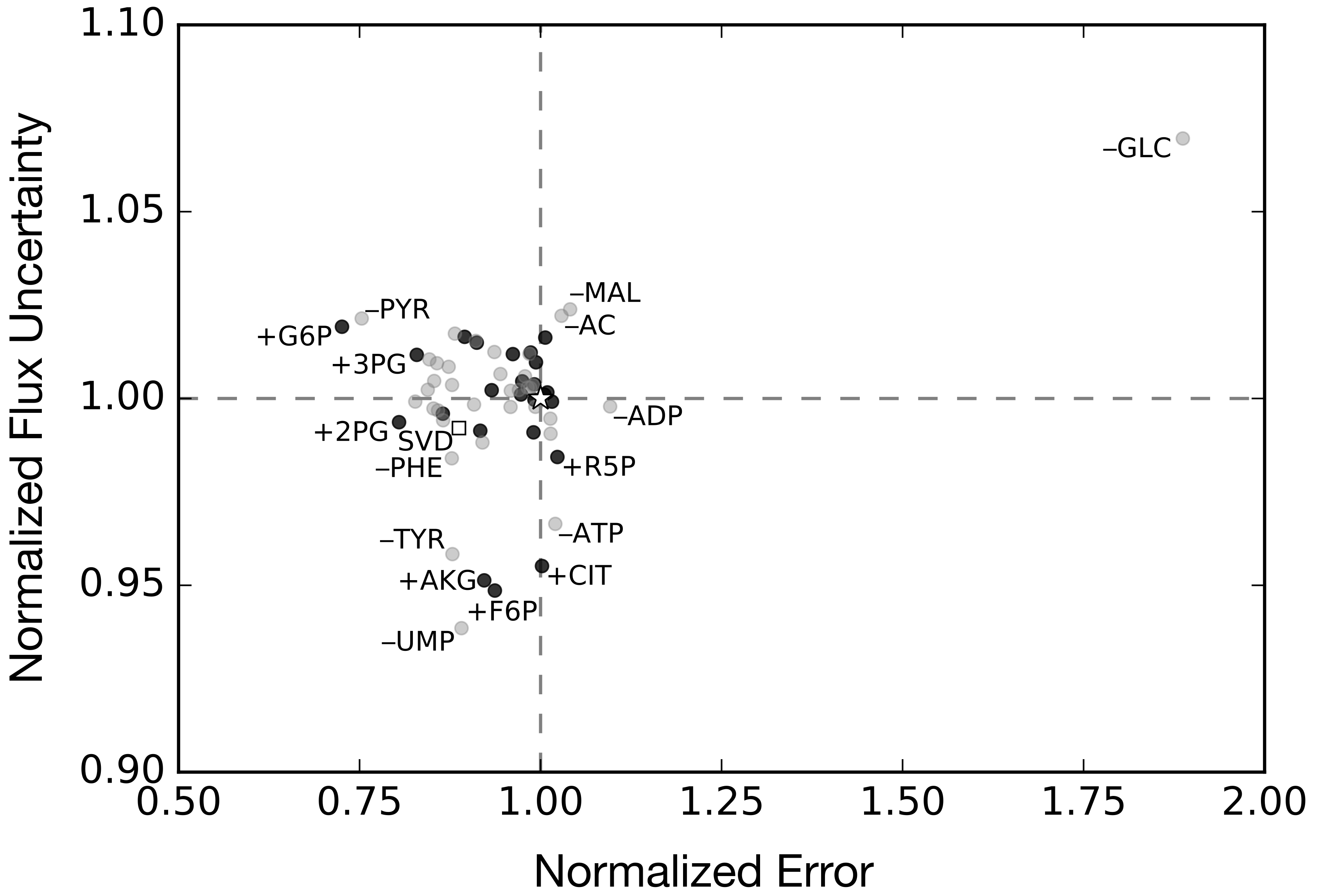
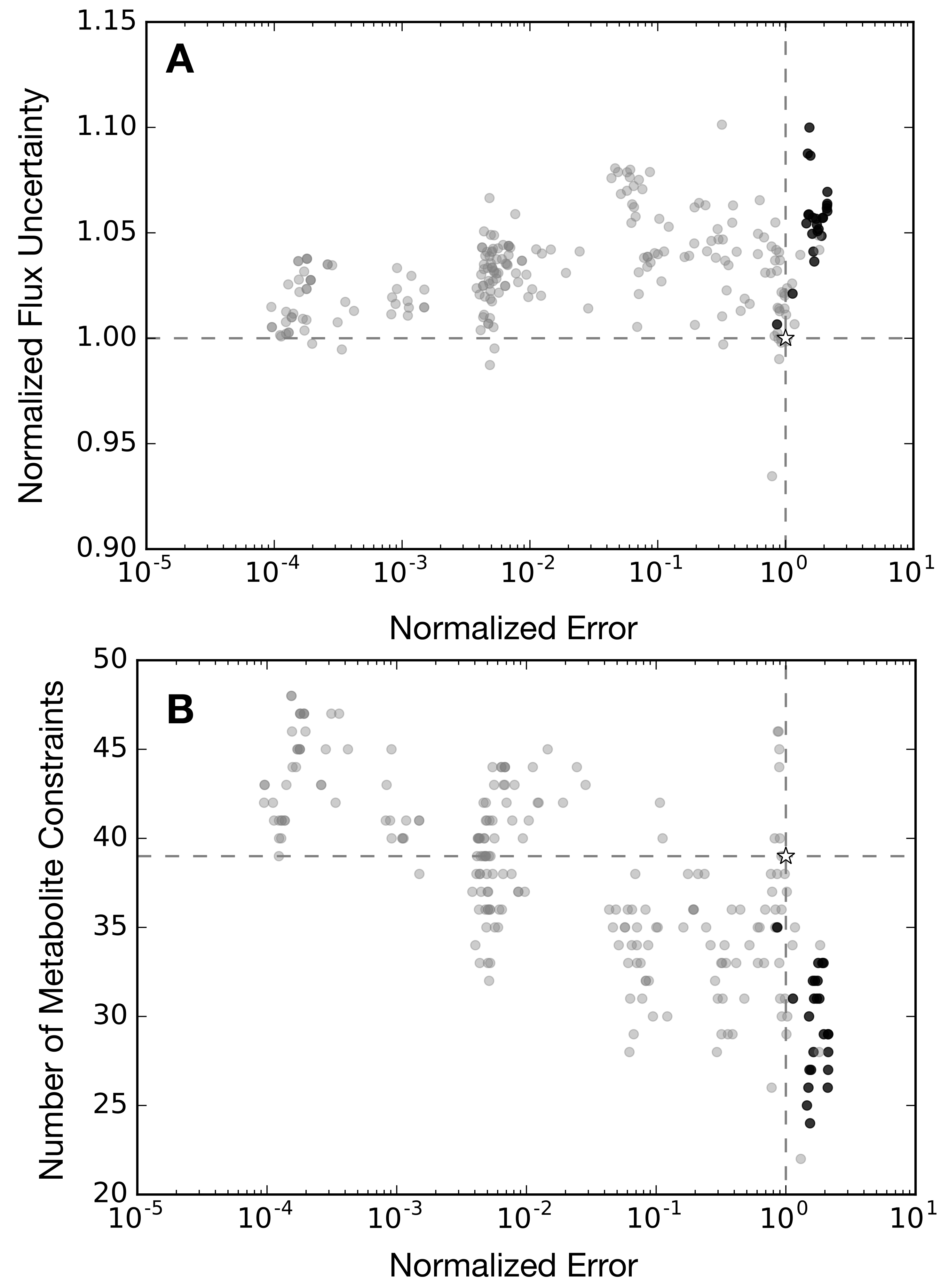
2.3. Alternative Measurement Sets
3. Discussion
4. Materials and Methods
4.1. Formulation and Solution of the Model Equations
4.2. Sampling of Transcription and Translation Parameters
4.3. Generation and Evaluation of Alternative Measurement Sets
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pardee, K.; Slomovic, S.; Nguyen, P.Q.; Lee, J.W.; Donghia, N.; Burrill, D.; Ferrante, T.; McSorley, F.R.; Furuta, Y.; Vernet, A.; et al. Portable, On-Demand Biomolecular Manufacturing. Cell 2016, 167, 248–259. [Google Scholar] [CrossRef] [PubMed]
- Jewett, M.C.; Calhoun, K.A.; Voloshin, A.; Wuu, J.J.; Swartz, J.R. An integrated cell-free metabolic platform for protein production and synthetic biology. Mol. Syst. Biol. 2008, 4, 220. [Google Scholar] [CrossRef] [PubMed]
- Matthaei, J.H.; Nirenberg, M.W. Characteristics and stabilization of DNAase-sensitive protein synthesis in E. coli extracts. Proc. Natl. Acad. Sci. USA 1961, 47, 1580–1588. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, M.W.; Matthaei, J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. USA 1961, 47, 1588–1602. [Google Scholar] [CrossRef] [PubMed]
- Spirin, A.; Baranov, V.; Ryabova, L.; Ovodov, S.; Alakhov, Y. A continuous cell-free translation system capable of producing polypeptides in high yield. Science 1988, 242, 1162–1164. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.M.; Swartz, J.R. Regeneration of adenosine triphosphate from glycolytic intermediates for cell-free protein synthesis. Biotechnol. Bioeng. 2001, 74, 309–316. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Welsh, J.P.; Swartz, J.R. Production and stabilization of the trimeric influenza hemagglutinin stem domain for potentially broadly protective influenza vaccines. Proc. Natl. Acad. Sci. USA 2014, 111, 125–130. [Google Scholar] [CrossRef] [PubMed]
- Hodgman, C.E.; Jewett, M.C. Cell-free synthetic biology: thinking outside the cell. Metab. Eng. 2012, 14, 261–219. [Google Scholar] [CrossRef] [PubMed]
- Jewett, M.C.; Swartz, J.R. Mimicking the Escherichia coli cytoplasmic environment activates long-lived and efficient cell-free protein synthesis. Biotechnol. Bioeng. 2004, 86, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Garamella, J.; Marshall, R.; Rustad, M.; Noireaux, V. The All E. coli TX-TL Toolbox 2.0: A Platform for Cell-Free Synthetic Biology. ACS Synth. Biol. 2016, 5, 344–355. [Google Scholar] [CrossRef] [PubMed]
- Lewis, N.E.; Nagarajan, H.; Palsson, B.Ø. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 2012, 10, 291–305. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J.S.; Palsson, B.Ø. The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. USA 2000, 97, 5528–5533. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.Ø. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Oh, Y.K.; Palsson, B.Ø.; Park, S.M.; Schilling, C.H.; Mahadevan, R. Genome-scale reconstruction of metabolic network in Bacillus subtilis based on high-throughput phenotyping and gene essentiality data. J. Biol. Chem. 2007, 282, 28791–28799. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Herrgård, M.J.; Thiele, I.; Reed, J.L.; Palsson, B.Ø. Reconstruction of biochemical networks in microorganisms. Nat. Rev. Microbiol. 2009, 7, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.Ø. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3, 119. [Google Scholar] [CrossRef] [PubMed]
- Hyduke, D.R.; Lewis, N.E.; Palsson, B.Ø. Analysis of omics data with genome-scale models of metabolism. Mol. Biosyst. 2013, 9, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.E.; Palsson, B.Ø. Sequence-based analysis of metabolic demands for protein synthesis in prokaryotes. J. Theor. Biol. 2003, 220, 1–18. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, E.J.; Lerman, J.A.; Chang, R.L.; Hyduke, D.R.; Palsson, B.Ø. Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol. Sys. Biol. 2013, 9, 693. [Google Scholar] [CrossRef]
- Mahadevan, R.; Edwards, J.S.; Doyle, F.J., 3rd. Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys. J. 2002, 83, 1331–1340. [Google Scholar] [CrossRef]
- Hjersted, J.L.; Henson, M.A.; Mahadevan, R. Genome-scale analysis of Saccharomyces cerevisiae metabolism and ethanol production in fed-batch culture. Biotechnol. Bioeng. 2007, 97, 1190–1204. [Google Scholar] [CrossRef] [PubMed]
- Hjersted, J.L.; Henson, M.A. Steady-state and dynamic flux balance analysis of ethanol production by Saccharomyces cerevisiae. IET Syst. Biol. 2009, 3, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Hanly, T.J.; Henson, M.A. Dynamic flux balance modeling of microbial co-cultures for efficient batch fermentation of glucose and xylose mixtures. Biotechnol. Bioeng. 2011, 108, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Henson, M.A.; Hanly, T.J. Dynamic flux balance analysis for synthetic microbial communities. IET Syst. Biol. 2014, 8, 214–229. [Google Scholar] [CrossRef] [PubMed]
- Höffner, K.; Harwood, S.M.; Barton, P.I. A reliable simulator for dynamic flux balance analysis. Biotechnol. Bioeng. 2013, 110, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.A.; Höffner, K.; Barton, P.I. DFBAlab: A fast and reliable MATLAB code for dynamic flux balance analysis. BMC Bioinform. 2014, 15, 409. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.A.; Barton, P.I. Dynamic Flux Balance Analysis Using DFBAlab. Methods Mol. Biol. 2018, 1716, 353–370. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, D.; Palsson, B.Ø; Feist, A.M. Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 2013, 9, 661. [Google Scholar] [CrossRef] [PubMed]
- Zomorrodi, A.R.; Suthers, P.F.; Ranganathan, S.; Maranas, C.D. Mathematical optimization applications in metabolic networks. Metab. Eng. 2012, 14, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Vilkhovoy, M.; Horvath, N.; Shih, C.H.; Wayman, J.; Calhoun, K.; Swartz, J.; Varner, J. Sequence Specific Modeling of E. coli Cell-Free Protein Synthesis. bioRxiv, 2017. [Google Scholar] [CrossRef]
- Horvath, N.; Vilkhovoy, M.; Wayman, J.A.; Calhoun, K.; Swartz, J.; Varner, J. Toward a Genome Scale Sequence Specific Dynamic Model of Cell-Free Protein Synthesis in Escherichia coli. bioRxiv, 2017. [Google Scholar] [CrossRef]
- Hu, C.Y.; Varner, J.D.; Lucks, J.B. Generating Effective Models and Parameters for RNA Genetic Circuits. ACS Synth. Biol. 2015, 4, 914–926. [Google Scholar] [CrossRef] [PubMed]
- Jewett, M.; Voloshin, A.; Swartz, J. Prokaryotic systems for in vitro expression. In Gene Cloning and Expression Technologies; Weiner, M., Lu, Q., Eds.; Eaton Publishing: Westborough, MA, USA, 2002; pp. 391–411. [Google Scholar]
- Varnerlab. Available online: http://www.varnerlab.org/downloads/ (accessed on 16 August 2018).
- Kigawa, T.; Muto, Y.; Yokoyama, S. Cell-free synthesis and amino acid-selective stable isotope labeling of proteins for NMR analysis. J. Biomol. NMR 1995, 6, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-Based Metabolic Flux Analysis. Biophys. J. 2006, 92, 1792–1805. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, J.J.; Dwivedi, V.; Reed, J.L. Quantitative Assessment of Thermodynamic Constraints on the Solution Space of Genome-Scale Metabolic Models. Biophys. J. 2013, 105, 512–522. [Google Scholar] [CrossRef] [PubMed]
- Zamboni, N.; Fendt, S.M.; Sauer, U. 13C-based metabolic flux analysis. Nat. Protoc. 2009, 4, 878–892. [Google Scholar] [CrossRef] [PubMed]
- Slomovic, S.; Pardee, K.; Collins, J.J. Synthetic biology devices for in vitro and in vivo diagnostics. Proc. Natl. Acad. Sci. USA 2015, 112, 14429–14435. [Google Scholar] [CrossRef] [PubMed]
- Andries, O.; Kitada, T.; Bodner, K.; Sanders, N.N.; Weiss, R. Synthetic biology devices and circuits for RNA-based ‘smart vaccines’: A propositional review. Expert Rev. Vaccines 2015, 14, 313–331. [Google Scholar] [CrossRef] [PubMed]
- Rustad, M.; Eastlund, A.; Marshall, R.; Jardine, P.; Noireaux, V. Synthesis of Infectious Bacteriophages in an E. coli-based Cell-free Expression System. J. Vis. Exp. 2017. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.J.; MacDonald, J.T.; Freemont, P.S. Cell-free synthetic biology for in vitro prototype engineering. Biochem. Soc. Trans. 2017, 45, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Pardee, K.; Green, A.A.; Ferrante, T.; Cameron, D.E.; DaleyKeyser, A.; Yin, P.; Collins, J.J. Paper-based synthetic gene networks. Cell 2014, 159, 940–954. [Google Scholar] [CrossRef] [PubMed]
- Savinell, J.M.; Palsson, B.O. Optimal selection of metabolic fluxes for in vivo measurement. I. Development of mathematical methods. J. Theor. Biol. 1992, 155, 201–214. [Google Scholar] [CrossRef]
- Savinell, J.M.; Palsson, B.O. Optimal selection of metabolic fluxes for in vivo measurement. II. Application to Escherichia coli and hybridoma cell metabolism. J. Theor. Biol. 1992, 155, 215–242. [Google Scholar] [CrossRef]
- Link, H.; Kochanowski, K.; Sauer, U. Systematic identification of allosteric protein-metabolite interactions that control enzyme activity in vivo. Nat. Biotechnol. 2013, 31, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Buescher, J.M.; Antoniewicz, M.R.; Boros, L.G.; Burgess, S.C.; Brunengraber, H.; Clish, C.B.; DeBerardinis, R.J.; Feron, O.; Frezza, C.; Ghesquiere, B.; et al. A roadmap for interpreting (13)C metabolite labeling patterns from cells. Curr. Opin. Biotechnol. 2015, 34, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Gadkar, K.G.; Varner, J.; Doyle, F.J., III. Model identification of signal transduction networks from data using a state regulator problem. Syst. Biol. 2005, 2, 17–30. [Google Scholar] [CrossRef]
- Mutalik, V.K.; Qi, L.; Guimaraes, J.C.; Lucks, J.B.; Arkin, A.P. Rationally designed families of orthogonal RNA regulators of translation. Nat. Chem. Biol. 2012, 8, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Westbrook, A.M.; Lucks, J.B. Achieving large dynamic range control of gene expression with a compact RNA transcription-translation regulator. Nucleic Acids Res. 2017, 45, 5614–5624. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.Y.; Takahashi, M.K.; Zhang, Y.; Lucks, J.B. Engineering a Functional Small RNA Negative Autoregulation Network with Model-Guided Design. ACS Synth. Biol. 2018, 7, 1507–1518. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, S.; Liu, L. Engineering redox balance through cofactor systems. Trends Biotechnol. 2014, 32, 337–343. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Yurkovich, J.T.; Lloyd, C.J.; Ebrahim, A.; Saunders, M.A.; Palsson, B.O. Principles of proteome allocation are revealed using proteomic data and genome-scale models. Sci. Rep. 2016, 6, 36734. [Google Scholar] [CrossRef] [PubMed]
- Moon, T.S.; Lou, C.; Tamsir, A.; Stanton, B.C.; Voigt, C.A. Genetic programs constructed from layered logic gates in single cells. Nature 2012, 491, 249–253. [Google Scholar] [CrossRef] [PubMed]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Phillips, R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.B.; Bailey, J.E. Genetically structured models forlac promoter–operator function in the Escherichia coli chromosome and in multicopy plasmids: Lac operator function. Biotechnol. Bioeng. 1984, 26, 1372–1382. [Google Scholar] [CrossRef] [PubMed]
- GNU Linear Programming Kit (GLPK). Version 4.52. GNU Project. 2016. Available online: https://www.gnu.org/software/glpk/ (accessed on 16 August 2018).
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Underwood, K.A.; Swartz, J.R.; Puglisi, J.D. Quantitative polysome analysis identifies limitations in bacterial cell-free protein synthesis. Biotechnol. Bioeng. 2005, 91, 425–435. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.C.; Bockmayr, A. Fast thermodynamically constrained flux variability analysis. Bioinformatics 2013, 29, 903–909. [Google Scholar] [CrossRef] [PubMed]
- Jaroentomeechai, T.; Stark, J.C.; Natarajan, A.; Glasscock, C.J.; Yates, L.E.; Hsu, K.J.; Mrksich, M.; Jewett, M.C.; DeLisa, M.P. Single-pot glycoprotein biosynthesis using a cell-free transcription-translation system enriched with glycosylation machinery. Nat. Commun. 2018, 9, 2686. [Google Scholar] [CrossRef] [PubMed]
| Description | Parameter | Value | Units | Reference |
|---|---|---|---|---|
| T7 RNA polymerase concentration | 1.0 | M | ||
| Ribosome concentration | 2 | M | [10] | |
| CAT mRNA length | 660 | nt | [36] | |
| CAT protein length | 219 | aa | [36] | |
| Transcription saturation coefficient | 100 | nM | estimated | |
| Transcription elongation rate | 25 | nt/s | [10] | |
| Translation saturation coefficient | 45 | M | estimated | |
| Translation elongation rate | 1.5 | aa/s | [10] | |
| T7 Promoter activity level | u | 0.9 | estimated | |
| Transcription rate | 123 | h−1 | calculated | |
| Polysome amplification constant | 10 | estimated | ||
| Translation rate | 247 | h−1 | calculated | |
| mRNA degradation time | 8 | min | BNID 106253 | |
| mRNA degradation rate | 5.2 | h−1 | calculated |
| Enzyme/Pathway | Reaction | Uncertainty |
|---|---|---|
| RNA polymerase | Translation | <0.01 |
| RNA polymerase | Translation initiation | <0.01 |
| tRNA charging of alanine | tRNA charging (ALA) | <0.01 |
| tRNA charging of cysteine | tRNA charging (CYS) | <0.01 |
| tRNA charging of aspartate | tRNA charging (ASP) | <0.01 |
| tRNA charging of histidine | tRNA charging (HIS) | <0.01 |
| tRNA charging of serine | tRNA charging (SER) | <0.01 |
| tRNA charging of tyrosine | tRNA charging (TYR) | <0.01 |
| tRNA charging of phenylalanine | tRNA charging (PHE) | <0.01 |
| tRNA charging of arginine | tRNA charging (ARG) | <0.01 |
| tRNA charging of glutamate | tRNA charging (GLU) | <0.01 |
| mRNA degradation | mRNA degradation | <0.01 |
| tRNA charging of tryptophan | tRNA charging (TRP) | <0.01 |
| tRNA charging of proline | tRNA charging (PRO) | <0.01 |
| tRNA charging of asparagine | tRNA charging (ASN) | <0.01 |
| tRNA charging of isoleucine | tRNA charging (ILE) | <0.01 |
| tRNA charging of glycine | tRNA charging (GLY) | <0.01 |
| tRNA charging of glutamine | tRNA charging (GLN) | <0.01 |
| tRNA charging of lysine | tRNA charging (LYS) | <0.01 |
| tRNA charging of threonine | tRNA charging (THR) | <0.01 |
| tRNA charging of valine | tRNA charging (VAL) | <0.01 |
| tRNA charging of methionine | tRNA charging (MET) | <0.01 |
| tRNA charging of leucine | tRNA charging (LEU) | <0.01 |
| Step 6 of AMP synthesis | R_A_syn_6 | <0.01 |
| Orotate synthase 1 | R_or_syn_1 | <0.01 |
| Metionine biosynthesis | R_met | 0.01 |
| Valine biosynthesis | R_val | 0.01 |
| Leucine biosynthesis | R_leu | 0.01 |
| Aldhyde-alcohol dehydrogenase | R_adhE_net | 0.01 |
| Malate dehydrogenase | R_mdh_net | 0.01 |
| Glycine biosynthesis | R_gly_deg | 0.02 |
| Threonine degradation 2 | R_thr_deg2 | 0.02 |
| Acetate kinase | R_ackA_net | 0.02 |
| Alanine biosynthesis | R_alaAC_net | 0.02 |
| Isoleucine biosynthesis | R_ile | 0.03 |
| Tyrosine biosynthesis | R_tyr | 0.03 |
| Histidine biosynthesis | R_his | 0.03 |
| Methylglyoxal degradation | R_mglx_deg | 0.03 |
| Transaldolase | R_talAB_net | 0.04 |
| Glycine cleavage system | R_gly_fol_net | 0.04 |
| Ribulose-phosphate 3-epimerase | R_rpe_net | 0.04 |
| Phosphate acetyltransferase | R_pta_net | 0.04 |
| Phosphoglycerate kinase | R_pgk_net | 0.05 |
| Glyceraldehyde-3-phosphate dehydrogenase | R_gapA_net | 0.05 |
| Fructose 1,6-bisphosphate aldolase | R_fbaA_net | 0.05 |
| Enolase | R_eno_net | 0.05 |
| Phenylalanine biosynthesis | R_phe | 0.05 |
| Transketolase 2 | R_tkt2_net | 0.06 |
| Fumarate hydratase | R_fum_net | 0.06 |
| Transketolase 1 | R_tkt1_net | 0.07 |
| Orotate synthase 2 | R_or_syn_2 | 0.07 |
| Phosphoglycerate mutase | R_gpm_net | 0.08 |
| Ribose-5-phosphate isomerase | R_rpi_net | 0.09 |
| CTP synthetase 1 | R_ctp_1 | 0.09 |
| CTP synthetase 2 | R_ctp_2 | 0.09 |
| Triosephosphate isomerase | R_tpiA_net | 0.1 |
| Step 7 of AMP synthesis | R_A_syn_7 | 0.15 |
| Step 12 of AMP synthesis | R_A_syn_12 | 0.17 |
| Lactate dehydrogenase | R_ldh_net | 0.17 |
| Step 5 of AMP synthesis | R_A_syn_5 | 0.2 |
| Methylenetetrahydrofolate reductase | R_mthfr2a | 0.2 |
| Glucose-6-phosphate dehydrogenase | R_zwf_net | 0.21 |
| Methylenetetrahydrofolate dehydrogenase | R_mthfd_net | 0.21 |
| UMP synthesis | R_ump_syn | 0.22 |
| OMP synthesis | R_omp_syn | 0.22 |
| Lysine degradation | R_lys_deg | 0.23 |
| Lysine biosynthesis | R_lys | 0.23 |
| Isocitrate dehydrogenase | R_icd_net | 0.23 |
| Threonine degradation 3 | R_thr_deg3 | 0.24 |
| Step 8 of AMP synthesis | R_A_syn_8 | 0.26 |
| Tryptophan degradation | R_trp_deg | 0.27 |
| Methylenetetrahydrofolate dehydrogenase | R_mthfc_net | 0.28 |
| Tryptophan biosynthesis | R_trp | 0.28 |
| Aconitase | R_acn_net | 0.33 |
| Phosphoglucose isomerase | R_pgi_net | 0.33 |
| Step e of folate synthesis | R_fol_e | 0.34 |
| Step 4 of AMP synthesis | R_A_syn_4 | 0.4 |
| GMP synthetase | R_gmp_syn | 0.44 |
| Step 9 of AMP synthesis | R_A_syn_9 | 0.48 |
| XMP synthase | R_xmp_syn | 0.53 |
| Step 3 of AMP synthesis | R_A_syn_3 | 0.6 |
| Step 10 of AMP synthesis | R_A_syn_10 | 0.63 |
| Step 2b of folate synthesis | R_fol_2b | 0.63 |
| Glutamate dehydrogenase | R_gdhA_net | 0.71 |
| Step 3 of folate synthesis | R_fol_3 | 0.74 |
| Step 4 of folate synthesis | R_fol_4 | 0.79 |
| Pyruvate formate lyase | R_pflAB | 0.8 |
| Step 2 of AMP synthesis | R_A_syn_2 | 0.81 |
| Step 2a of folate synthesis | R_fol_2a | 0.81 |
| Step 1 of folate synthesis | R_fol_1 | 0.99 |
| Glucokinase | R_glk_atp | 1 |
| Step 1 of AMP synthesis | R_A_syn_1 | 1 |
| Arginine degradation | R_arg_deg | 1.23 |
| Glycine biosynthesis | R_glyA | 1.33 |
| Phosphoribosylpyrophosphate synthase | R_prpp_syn | 1.34 |
| Chorismate synthesis | R_chor | 1.35 |
| Succinate thiokinase | R_sucCD | 1.55 |
| 2-Ketoglutarate dehydrogenase | R_sucAB | 1.55 |
| GABA degradation 1 | R_gaba_deg1 | 1.56 |
| GABA degradation 2 | R_gaba_deg2 | 1.56 |
| Glutamate degradation | R_glu_deg | 1.56 |
| Arginine biosynthesis | R_arg | 1.68 |
| Pyruvate dehydrogenase | R_pdh | 2.06 |
| Malate synthase | R_aceB | 2.3 |
| Threonine degradation 1 | R_thr_deg1 | 2.32 |
| Isocitrate lyase | R_aceA | 2.36 |
| Threonine biosynthesis | R_thr | 2.48 |
| Citrate synthase | R_gltA | 2.62 |
| 6-Phosphogluconate dehydrogenase | R_gnd | 2.62 |
| Cysteine biosynthesis | R_cysEMK | 4.59 |
| Cysteine degradation | R_cys_deg | 4.6 |
| Proline biosynthesis | R_pro | 5.45 |
| Proline degradation | R_pro_deg | 5.47 |
| 6-Phosphogluconate dehydrase | R_edd | 5.96 |
| 2-Keto-3-deoxy-6-phospho-gluconate aldolase | R_eda | 5.96 |
| Serine degradation | R_ser_deg | 6.43 |
| Nucleotide diphosphatase (ATP) | R_atp_amp | 6.53 |
| Nucleotide diphosphatase (UTP) | R_utp_ump | 6.53 |
| Nucleotide diphosphatase (GTP) | R_gtp_gmp | 6.53 |
| Nucleotide diphosphatase (CTP) | R_ctp_cmp | 6.53 |
| Cytidylate kinase | R_atp_cmp | 6.56 |
| Guanylate kinase | R_atp_gmp | 6.6 |
| UMP kinase | R_atp_ump | 6.62 |
| 6-Phosphogluconolactonase | R_pgl | 6.67 |
| Serine biosynthesis | R_serABC | 6.72 |
| NADH:ubiquinone oxidoreductase | R_nuo | 7.39 |
| NADH dehydrogenase 1 | R_ndh1 | 7.39 |
| NADH dehydrogenase 2 | R_ndh2 | 7.39 |
| Fumurate reductase | R_frd | 7.44 |
| Succinate dehydrogenase | R_sdh | 7.93 |
| Malic enzyme A | R_maeA | 7.99 |
| Malic enzyme B | R_maeB | 8.01 |
| Cytochrome oxidase bo | R_cyo | 8.03 |
| Cytochrome oxidase bd | R_cyd | 8.03 |
| ATP synthase | R_atp | 11.71 |
| PEP synthase | R_pps | 12.98 |
| Fructose-1,6-bisphosphate aldolase | R_fdp | 12.98 |
| Adenosinetriphosphatase | R_atp_adp | 12.98 |
| PEP carboxykinase | R_pck | 12.98 |
| Asparagine biosynthesis | R_asnB | 13 |
| Glutamate biosynthesis | R_gltBD | 13 |
| Glutamine degradation | R_gln_deg | 13 |
| Glutamine biosynthesis | R_glnA | 13.05 |
| Acetyl-CoA synthetase | R_acs | 13.06 |
| Inorganic pyrophosphatase | R_ppa | 13.08 |
| Adenylate kinase | R_adk_atp | 13.36 |
| PEP carboxylase | R_ppc | 14.22 |
| Phosphofructokinase | R_pfk | 14.9 |
| Pyruvate kinase | R_pyk | 15.89 |
| Transhydrogenase | R_pnt2 | 22.45 |
| Transhydrogenase | R_pnt1 | 25.5 |
| Aspartate degradation | R_asp_deg | 25.5 |
| Aspartate biosynthesis | R_aspC | 25.83 |
| Asparagine biosynthesis | R_asnA | 247.53 |
| Asparagine degradation | R_asn_deg | 247.53 |
| Enzyme | Reaction | Uncertainty |
|---|---|---|
| Step 6 of AMP synthesis | R_A_syn_6 | <0.01 |
| Orotate synthase 1 | R_or_syn_1 | <0.01 |
| Orotate synthase 2 | R_or_syn_2 | <0.01 |
| Aldhyde-alcohol dehydrogenase | R_adhE_net | <0.01 |
| RNA polymerase | Translation | <0.01 |
| tRNA charging of phenylalanine | tRNA charging (PHE) | <0.01 |
| tRNA charging of alanine | tRNA charging (ALA) | <0.01 |
| tRNA charging of glutamine | tRNA charging (GLN) | <0.01 |
| tRNA charging of threonine | tRNA charging (THR) | <0.01 |
| tRNA charging of aspartate | tRNA charging (ASP) | <0.01 |
| tRNA charging of glutamate | tRNA charging (GLU) | <0.01 |
| tRNA charging of histidine | tRNA charging (HIS) | <0.01 |
| tRNA charging of lysine | tRNA charging (LYS) | <0.01 |
| tRNA charging of tyrosine | tRNA charging (TYR) | <0.01 |
| tRNA charging of asparagine | tRNA charging (ASN) | <0.01 |
| tRNA charging of serine | tRNA charging (SER) | <0.01 |
| tRNA charging of methionine | tRNA charging (MET) | <0.01 |
| tRNA charging of isoleucine | tRNA charging (ILE) | <0.01 |
| tRNA charging of valine | tRNA charging (VAL) | <0.01 |
| tRNA charging of proline | tRNA charging (PRO) | <0.01 |
| tRNA charging of leucine | tRNA charging (LEU) | <0.01 |
| tRNA charging of arginine | tRNA charging (ARG) | <0.01 |
| tRNA charging of tryptophan | tRNA charging (TRP) | <0.01 |
| tRNA charging of cysteine | tRNA charging (CYS) | <0.01 |
| tRNA charging of glycine | tRNA charging (GLY) | <0.01 |
| RNA polymerase | Translation initiation | <0.01 |
| mRNA degradation | mRNA degradation | <0.01 |
| Glycine cleavage system | R_gly_fol_net | 0.01 |
| Transaldolase | R_talAB_net | 0.02 |
| Transketolase 1 | R_tkt1_net | 0.02 |
| Ribulose-phosphate 3-epimerase | R_rpe_net | 0.02 |
| Ribose-5-phosphate isomerase | R_rpi_net | 0.03 |
| Transketolase 2 | R_tkt2_net | 0.04 |
| Valine biosynthesis | R_val | 0.05 |
| Leucine biosynthesis | R_leu | 0.05 |
| Malate dehydrogenase | R_mdh_net | 0.06 |
| Triosephosphate isomerase | R_tpiA_net | 0.07 |
| Fructose 1,6-bisphosphate aldolase | R_fbaA_net | 0.07 |
| Glycine biosynthesis | R_gly_deg | 0.09 |
| Threonine degradation 2 | R_thr_deg2 | 0.09 |
| Phosphoglucose isomerase | R_pgi_net | 0.09 |
| Methylglyoxal degradation | R_mglx_deg | 0.09 |
| Methylenetetrahydrofolate dehydrogenase | R_mthfd_net | 0.13 |
| Glucose-6-phosphate dehydrogenase | R_zwf_net | 0.18 |
| Tyrosine biosynthesis | R_tyr | 0.2 |
| Enolase | R_eno_net | 0.2 |
| Phosphoglycerate mutase | R_gpm_net | 0.2 |
| Phosphoglycerate kinase | R_pgk_net | 0.21 |
| Glyceraldehyde-3-phosphate dehydrogenase | R_gapA_net | 0.21 |
| Methylenetetrahydrofolate dehydrogenase | R_mthfc_net | 0.28 |
| Metionine biosynthesis | R_met | 0.34 |
| Phosphate acetyltransferase | R_pta_net | 0.4 |
| Acetate kinase | R_ackA_net | 0.41 |
| Fumarate hydratase | R_fum_net | 0.43 |
| Phenylalanine biosynthesis | R_phe | 0.53 |
| Glucokinase | R_glk_atp | 1 |
| Step 5 of AMP synthesis | R_A_syn_5 | 1 |
| Step 7 of AMP synthesis | R_A_syn_7 | 1 |
| OMP synthesis | R_omp_syn | 1.09 |
| Isoleucine biosynthesis | R_ile | 1.13 |
| Alanine biosynthesis | R_alaAC_net | 1.49 |
| Step 8 of AMP synthesis | R_A_syn_8 | 1.76 |
| Methylenetetrahydrofolate reductase | R_mthfr2a | 1.85 |
| Isocitrate dehydrogenase | R_icd_net | 1.87 |
| Histidine biosynthesis | R_his | 1.95 |
| Step 4 of AMP synthesis | R_A_syn_4 | 2.02 |
| Threonine degradation 3 | R_thr_deg3 | 2.08 |
| CTP synthetase 1 | R_ctp_1 | 2.09 |
| CTP synthetase 2 | R_ctp_2 | 2.09 |
| Lysine biosynthesis | R_lys | 2.13 |
| Lysine degradation | R_lys_deg | 2.13 |
| Lactate dehydrogenase | R_ldh_net | 2.27 |
| Tryptophan degradation | R_trp_deg | 2.55 |
| Tryptophan biosynthesis | R_trp | 2.7 |
| Aconitase | R_acn_net | 2.82 |
| UMP synthesis | R_ump_syn | 2.85 |
| Step 3 of AMP synthesis | R_A_syn_3 | 3.07 |
| XMP synthase | R_xmp_syn | 4.04 |
| GMP synthetase | R_gmp_syn | 4.04 |
| Step 12 of AMP synthesis | R_A_syn_12 | 4.13 |
| Step e of folate synthesis | R_fol_e | 4.37 |
| Step 2 of AMP synthesis | R_A_syn_2 | 4.74 |
| Step 9 of AMP synthesis | R_A_syn_9 | 4.83 |
| Step 10 of AMP synthesis | R_A_syn_10 | 4.83 |
| Step 1 of AMP synthesis | R_A_syn_1 | 5.02 |
| Glutamate dehydrogenase | R_gdhA_net | 5.14 |
| Phosphoribosylpyrophosphate synthase | R_prpp_syn | 6.11 |
| Step 4 of folate synthesis | R_fol_4 | 6.24 |
| Step 3 of folate synthesis | R_fol_3 | 6.24 |
| Step 2b of folate synthesis | R_fol_2b | 7.03 |
| Step 2a of folate synthesis | R_fol_2a | 8.04 |
| Step 1 of folate synthesis | R_fol_1 | 9.04 |
| Glycine biosynthesis | R_glyA | 9.58 |
| Chorismate synthesis | R_chor | 13.98 |
| Arginine degradation | R_arg_deg | 14.97 |
| Succinate thiokinase | R_sucCD | 17.94 |
| GABA degradation 1 | R_gaba_deg1 | 17.95 |
| GABA degradation 2 | R_gaba_deg2 | 17.95 |
| Glutamate degradation | R_glu_deg | 17.95 |
| 2-Ketoglutarate dehydrogenase | R_sucAB | 18.06 |
| Arginine biosynthesis | R_arg | 18.14 |
| Threonine degradation 1 | R_thr_deg1 | 19.06 |
| Pyruvate formate lyase | R_pflAB | 19.97 |
| Threonine biosynthesis | R_thr | 22.23 |
| Malate synthase | R_aceB | 28.81 |
| Isocitrate lyase | R_aceA | 28.81 |
| Pyruvate dehydrogenase | R_pdh | 29.86 |
| 6-Phosphogluconate dehydrogenase | R_gnd | 31.9 |
| Citrate synthase | R_gltA | 32.2 |
| Cysteine biosynthesis | R_cysEMK | 48.93 |
| Cysteine degradation | R_cys_deg | 49.31 |
| Proline biosynthesis | R_pro | 61.2 |
| 2-Keto-3-deoxy-6-phospho-gluconate aldolase | R_eda | 61.86 |
| 6-Phosphogluconate dehydrase | R_edd | 61.86 |
| Proline degradation | R_pro_deg | 62.62 |
| Serine degradation | R_ser_deg | 68.5 |
| 6-Phosphogluconolactonase | R_pgl | 70.12 |
| Serine biosynthesis | R_serABC | 72.05 |
| Nucleotide diphosphatase (ATP) | R_atp_amp | 74.22 |
| Nucleotide diphosphatase (UTP) | R_utp_ump | 74.22 |
| Nucleotide diphosphatase (GTP) | R_gtp_gmp | 74.22 |
| Nucleotide diphosphatase (CTP) | R_ctp_cmp | 74.22 |
| Cytidylate kinase | R_atp_cmp | 74.74 |
| Guanylate kinase | R_atp_gmp | 76.11 |
| UMP kinase | R_atp_ump | 76.78 |
| NADH dehydrogenase 1 | R_ndh1 | 86.63 |
| NADH:ubiquinone oxidoreductase | R_nuo | 86.63 |
| Malic enzyme A | R_maeA | 86.77 |
| NADH dehydrogenase 2 | R_ndh2 | 87.01 |
| Fumurate reductase | R_frd | 87.01 |
| Malic enzyme B | R_maeB | 88.17 |
| Succinate dehydrogenase | R_sdh | 90.66 |
| Cytochrome oxidase bo | R_cyo | 92.08 |
| Cytochrome oxidase bd | R_cyd | 92.08 |
| ATP synthase | R_atp | 134.61 |
| PEP synthase | R_pps | 148.45 |
| Asparagine biosynthesis | R_asnB | 148.45 |
| Glutamine degradation | R_gln_deg | 148.45 |
| Glutamate biosynthesis | R_gltBD | 148.45 |
| Acetyl-CoA synthetase | R_acs | 148.45 |
| Adenosinetriphosphatase | R_atp_adp | 148.45 |
| Fructose-1,6-bisphosphate aldolase | R_fdp | 148.45 |
| PEP carboxykinase | R_pck | 148.45 |
| Glutamine biosynthesis | R_glnA | 149.67 |
| Inorganic pyrophosphatase | R_ppa | 150.79 |
| Adenylate kinase | R_adk_atp | 152.88 |
| PEP carboxylase | R_ppc | 158.68 |
| Phosphofructokinase | R_pfk | 161.64 |
| Pyruvate kinase | R_pyk | 170.95 |
| Transhydrogenase | R_pnt2 | 258.03 |
| Aspartate degradation | R_asp_deg | 286.46 |
| Transhydrogenase | R_pnt1 | 286.46 |
| Aspartate biosynthesis | R_aspC | 290.86 |
| Asparagine biosynthesis | R_asnA | 4421.48 |
| Asparagine degradation | R_asn_deg | 4421.48 |
| Metabolite | Symbol | Frequency |
|---|---|---|
| alpha-D-Glucose | GLC | 89.9% |
| Glucose 6-phosphate | G6P | 89.9% |
| Citrate | CIT | 85.7% |
| Isocitrate | ICIT | 84.9% |
| Fumarate | FUM | 84.5% |
| Fructose 6-phosphate | F6P | 83.6% |
| 6-Phospho-D-glucono-1,5-lactone | 6PGL | 81.5% |
| sedo-Heptulose 7-phosphate | S7P | 79.4% |
| Alanine | ALA | 77.7% |
| Guanosine triphosphate | GTP | 77.3% |
| Malate | MAL | 75.6% |
| D-Ribulose 5-phosphate | RU5P | 74.8% |
| Erythrose 4-phosphate | E4P | 73.1% |
| Adenosine diphosphate | ADP | 72.3% |
| alpha-Ketoglutarate | AKG | 71.8% |
| Uridine diphosphate | UDP | 70.2% |
| Succinate | SUCC | 69.7% |
| Cytidine monophosphate | CMP | 69.3% |
| Guanosine diphosphate | GDP | 67.2% |
| 6-Phospho-D-gluconate | 6PGC | 67.2% |
| Arginine | ARG | 66.8% |
| Ribose 5-phosphate | R5P | 66.4% |
| Methionine | MET | 65.5% |
| Glyoxylate | GLX | 65.5% |
| Glutamine | GLN | 63.9% |
| Phenylalanine | PHE | 63.4% |
| Valine | VAL | 62.6% |
| Glyceraldehyde 3-phosphate | G3P | 62.2% |
| Adenosine monophosphate | AMP | 62.2% |
| Proline | PRO | 60.1% |
| Fructose 1,6-diphosphate | FDP | 60.1% |
| Dihydroxyacetone phosphate | DHAP | 60.1% |
| Histidine | HIS | 59.7% |
| Glycine | GLY | 59.7% |
| Oxaloacetate | OAA | 58.4% |
| 2-Dehydro-3-deoxy-D-gluconate 6-phosphate | 2DDG6P | 58.4% |
| Chloramphenicol acetyltransferase | CAT | 56.3% |
| Cysteine | CYS | 55.5% |
| Acetate | AC | 54.2% |
| Succinyl coenzyme A | SUCCOA | 53.8% |
| Uridine monophosphate | UMP | 52.9% |
| Tryptophan | TRP | 52.5% |
| Lactate | LAC | 52.5% |
| Uridine triphosphate | UTP | 52.1% |
| Aspartate | ASP | 51.7% |
| Guanosine monophosphate | GMP | 50.8% |
| Asparagine | ASN | 50.4% |
| Cytidine diphosphate | CDP | 50.0% |
| Phosphoenolpyruvate | PEP | 48.3% |
| 3-Phosphoglycerate | 3PG | 47.9% |
| 2-Phosphoglycerate | 2PG | 47.1% |
| Lysine | LYS | 43.3% |
| Threonine | THR | 42.0% |
| Glutamate | GLU | 38.7% |
| Tyrosine | TYR | 37.0% |
| Adenosine triphosphate | ATP | 37.0% |
| D-Xylulose 5-phosphate | XU5P | 35.7% |
| Acetyl coenzyme A | ACCOA | 34.9% |
| Cytidine triphosphate | CTP | 33.2% |
| Serine | SER | 31.9% |
| Isoleucine | ILE | 29.8% |
| Leucine | LEU | 26.5% |
| Pyruvate | PYR | 21.8% |
| Metabolite | Symbol | Frequency |
|---|---|---|
| D-Xylulose 5-phosphate | XU5P | 100% |
| sedo-Heptulose 7-phosphate | S7P | 100% |
| D-Ribulose 5-phosphate | RU5P | 100% |
| Ribose 5-phosphate | R5P | 100% |
| Oxaloacetate | OAA | 100% |
| Isocitrate | ICIT | 100% |
| alpha-D-Glucose | GLC | 100% |
| Glucose 6-phosphate | G6P | 100% |
| Glyceraldehyde 3-phosphate | G3P | 100% |
| Fumarate | FUM | 100% |
| Fructose 1,6-diphosphate | FDP | 100% |
| Fructose 6-phosphate | F6P | 100% |
| Erythrose 4-phosphate | E4P | 100% |
| Dihydroxyacetone phosphate | DHAP | 100% |
| Citrate | CIT | 100% |
| Alanine | ALA | 100% |
| 6-Phospho-D-glucono-1,5-lactone | 6PGL | 100% |
| 6-Phospho-D-gluconate | 6PGC | 100% |
| 2-Dehydro-3-deoxy-D-gluconate 6-phosphate | 2DDG6P | 100% |
| Uridine triphosphate | UTP | 98.2% |
| alpha-Ketoglutarate | AKG | 98.2% |
| Succinate | SUCC | 94.7% |
| Arginine | ARG | 94.7% |
| 3-Phosphoglycerate | 3PG | 94.7% |
| Guanosine triphosphate | GTP | 91.2% |
| Uridine monophosphate | UMP | 89.5% |
| Glutamine | GLN | 87.7% |
| Cytidine monophosphate | CMP | 87.7% |
| Tyrosine | TYR | 82.5% |
| Threonine | THR | 82.5% |
| Aspartate | ASP | 80.7% |
| Cytidine diphosphate | CDP | 75.4% |
| Uridine diphosphate | UDP | 71.9% |
| Valine | VAL | 70.2% |
| Methionine | MET | 68.4% |
| Guanosine monophosphate | GMP | 68.4% |
| Glycine | GLY | 68.4% |
| Adenosine diphosphate | ADP | 68.4% |
| Tryptophan | TRP | 61.4% |
| Phenylalanine | PHE | 59.6% |
| Acetate | AC | 57.9% |
| Malate | MAL | 52.6% |
| Phosphoenolpyruvate | PEP | 50.9% |
| Leucine | LEU | 49.1% |
| Proline | PRO | 47.4% |
| Isoleucine | ILE | 47.4% |
| Histidine | HIS | 47.4% |
| Adenosine monophosphate | AMP | 45.6% |
| Glyoxylate | GLX | 43.9% |
| Lactate | LAC | 40.4% |
| Chloramphenicol acetyltransferase | CAT | 38.6% |
| Cysteine | CYS | 36.8% |
| Asparagine | ASN | 35.1% |
| Pyruvate | PYR | 33.3% |
| Glutamate | GLU | 31.6% |
| Succinyl coenzyme A | SUCCOA | 22.8% |
| Guanosine diphosphate | GDP | 22.8% |
| 2-Phosphoglycerate | 2PG | 22.8% |
| Cytidine triphosphate | CTP | 14% |
| Acetyl coenzyme A | ACCOA | 14% |
| Lysine | LYS | 7% |
| Adenosine triphosphate | ATP | 5.3% |
| Serine | SER | 0% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, D.; Horvath, N.; Varner, J. Dynamic Sequence Specific Constraint-Based Modeling of Cell-Free Protein Synthesis. Processes 2018, 6, 132. https://doi.org/10.3390/pr6080132
Dai D, Horvath N, Varner J. Dynamic Sequence Specific Constraint-Based Modeling of Cell-Free Protein Synthesis. Processes. 2018; 6(8):132. https://doi.org/10.3390/pr6080132
Chicago/Turabian StyleDai, David, Nicholas Horvath, and Jeffrey Varner. 2018. "Dynamic Sequence Specific Constraint-Based Modeling of Cell-Free Protein Synthesis" Processes 6, no. 8: 132. https://doi.org/10.3390/pr6080132
APA StyleDai, D., Horvath, N., & Varner, J. (2018). Dynamic Sequence Specific Constraint-Based Modeling of Cell-Free Protein Synthesis. Processes, 6(8), 132. https://doi.org/10.3390/pr6080132






