A Cybernetic Approach to Modeling Lipid Metabolism in Mammalian Cells
Abstract
1. Introduction
2. Materials and Methods
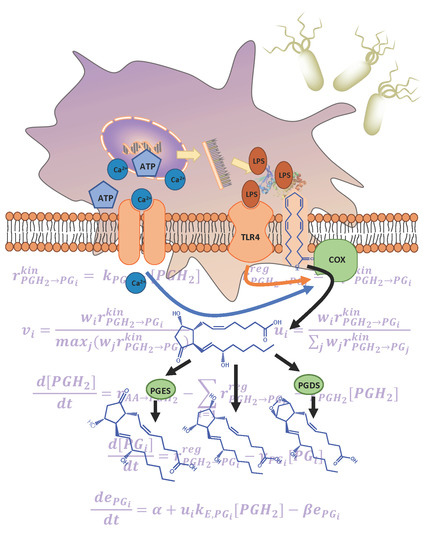
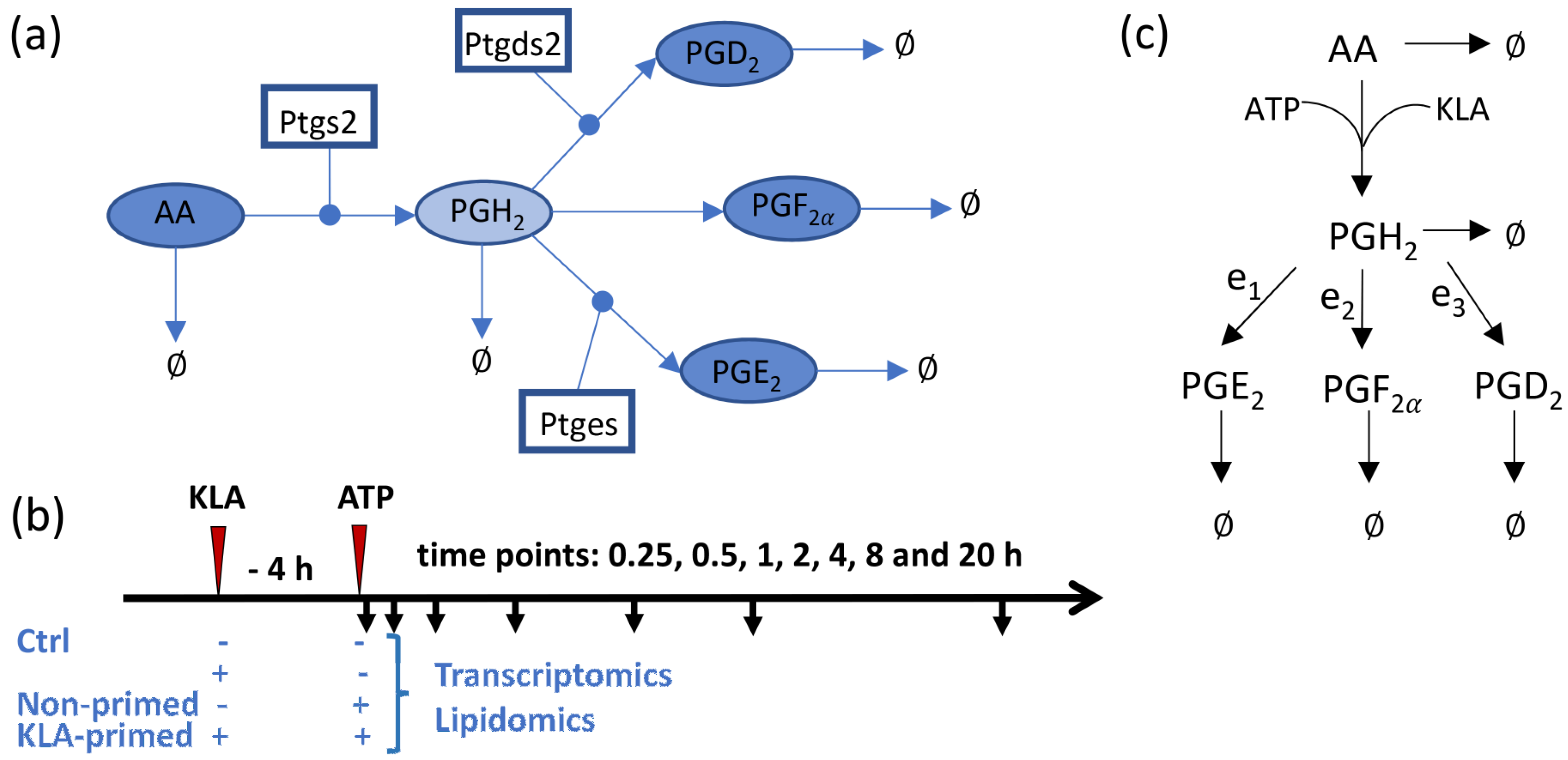
2.1. Development of the Kinetic Model
2.2. The Cybernetic Framework
2.3. Defining the Cybernetic Goal or Objective
2.4. Estimation of the Kinetic Rate Parameters and Uncertainty Analysis
3. Results
3.1. Development of the Kinetic Model for the COX Pathway
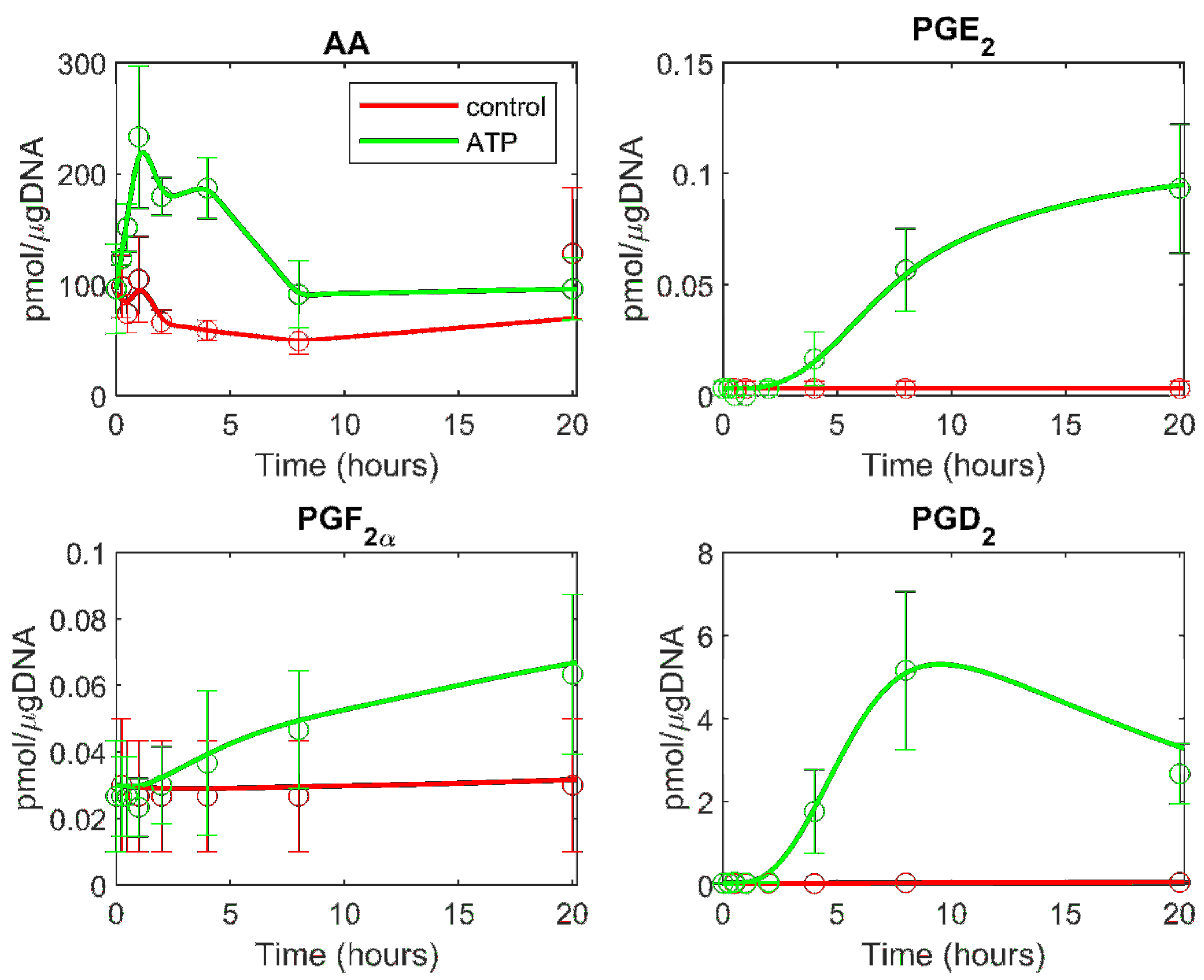
3.2. Prediction of the Eicosanoid Profile in KLA Primed ATP Stimulated Macrophages
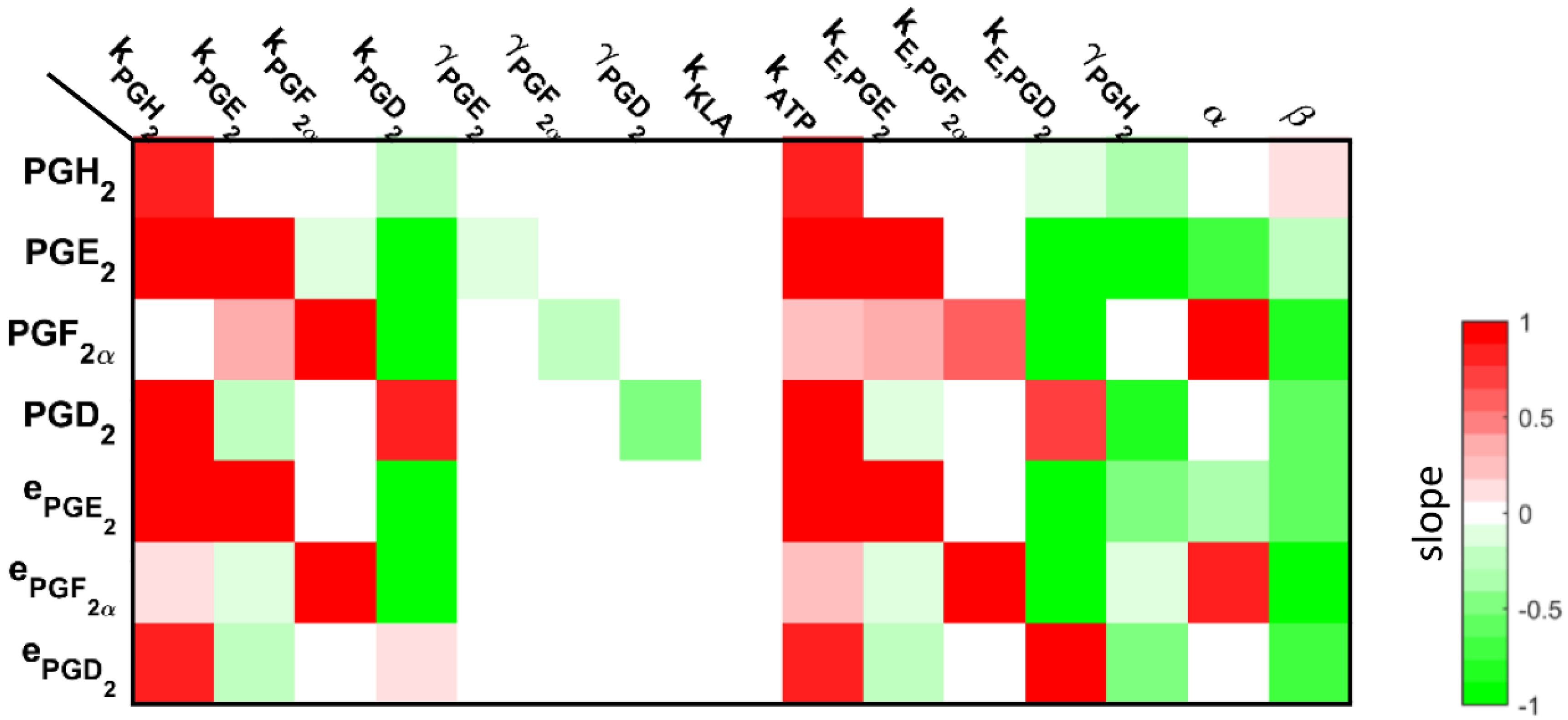
3.3. Understanding the Role of Regulation in the Cybernetic Variables
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| PARAMETER | SIMULATED | PREDICTED |
|---|---|---|
| KPGH2 | 0.0022 | 0.0016 |
| KPGE2 | 0.0044 | 0.0031 |
| KPGF2α | 0.0326 | 0.0339 |
| KPGD2 | 0.0533 | 0.0585 |
| 𝛾PGE2 | 0.0062 | 0.0044 |
| 𝛾PGF2α | 0.0205 | 0.0197 |
| 𝛾PGD2 | 0.1275 | 0.0893 |
| KKLA | 17.3923 | 0.0001 |
| KATP | 11.9112 | 8.3379 |
| KE,PGE2 | 8.0801 | 10.4215 |
| KE,PGF2α | 0.2078 | 0.1478 |
| KE,PGD2 | 0.2243 | 0.157 |
| 𝛾PGH2 | 0.2603 | 0.3384 |
| α | 0.2244 | 0.2918 |
| β | 0.7757 | 1.0082 |
| E0,PGE2 | 0.3974 | 0.5094 |
| E0,PGF2α | 0.0133 | 0.0105 |
| E0,PGD2 | 0.2601 | 0.3379 |
References
- Maurya, M.R.; Subramaniam, S. Computational Challenges in Systems Biology; Systems Biomedicine: Concepts and Perspectives; Elsevier: Oxford, UK, 2010; pp. 177–223. [Google Scholar]
- Gupta, S.; Ashok, R.D.; Merril, J.G.; Maurya, M.R.; Subramaniam, S. Omics Approaches to Macrophage Biology. In Macrophages: Biology and Role in the Pathology of Diseases; Springer: Berlin, Germany, 2014; pp. 587–615. [Google Scholar]
- Ramkrishna, D. A Cybernetic Perspective of Microbial Growth. In Foundations of Biochemical Engineering: Kinetics and thermodynamics in biological systems; American Chemical Society: Washington, DC, USA, 1982; pp. 161–178. [Google Scholar]
- Ramkrishna, D.; Song, H.S. Cybernetic Modeling for Bioreaction Engineering; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Dhurjati, P.; Flickinger, M.C.; Tsao, G.T. A cybernetic view of microbial growth: Modeling of cells as optimal strategists. Biotechnol. Bioeng. 1985, 27, 1–9. [Google Scholar] [PubMed]
- Kompala, D.S.; Ramkrishna, D.; Jansen, N.B.; Tsao, G.T. Investigation of bacterial growth on mixed substrates: Experimental evaluation of cybernetic models. Biotechnol. Bioeng. 1986, 28, 1044–1055. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishna, R.; Ramkrishna, D.; Konopka, A.E. Cybernetic modeling of growth in mixed, substitutable substrate environments: Preferential and simultaneous utilization. Biotechnol. Bioeng. 1996, 52, 141–151. [Google Scholar] [PubMed]
- Song, H.S.; Ramkrishna, D. Cybernetic models based on lumped elementary modes accurately predict strain-specific metabolic function. Biotechnol. Bioeng. 2011, 108, 27–40. [Google Scholar]
- Turner, B.G.; Ramkrishna, D.; Jansen, N.B. Cybernetic modeling of bacterial cultures at low growth rates: Mixed-substrate systems. Biotechnol. Bioeng. 1988, 32, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D.; Henne, K.L.; Morgan, J.A.; Konopka, A.E. Integrating cybernetic modeling with pathway analysis provides a dynamic, systems-level description of metabolic control. Biotechnol. Bioeng. 2008, 100, 542–559. [Google Scholar] [CrossRef] [PubMed]
- Koh, T.J.; DiPietro, L.A. Inflammation and wound healing: The role of the macrophage. Expert Rev. Mol. Med. 2011, 13, e23. [Google Scholar] [CrossRef] [PubMed]
- Remmerie, A.; Scott, C.L. Macrophages and lipid metabolism. Cell Immunol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Hubler, M.J.; Kennedy, A.J. Role of lipids in the metabolism and activation of immune cells. J. Nutr. Biochem. 2016, 34, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Funk, C.D. Prostaglandins and leukotrienes: Advances in eicosanoid biology. Science 2001, 294, 1871–1875. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, T. Lipid mediators in health and disease: Enzymes and receptors as therapeutic targets for the regulation of immunity and inflammation. Annu. Rev. Pharmacol. Toxicol. 2009, 49, 123–150. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.L.; DeWitt, D.L.; Garavito, R.M. Cyclooxygenases: Structural, cellular, and molecular biology. Annu. Rev. Biochem. 2000, 69, 145–182. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Maurya, M.R.; Stephens, D.L.; Dennis, E.A.; Subramaniam, S. An integrated model of eicosanoid metabolism and signaling based on lipidomics flux analysis. Biophys. J. 2009, 96, 4542–4551. [Google Scholar] [CrossRef] [PubMed]
- Kihara, Y.; Gupta, S.; Maurya, M.R.; Armando, A.; Shah, I.; Quehenberger, O.; Glass, C.K.; Dennis, E.A.; Subramaniam, S. Modeling of eicosanoid fluxes reveals functional coupling between cyclooxygenases and terminal synthases. Biophys. J. 2014, 106, 966–975. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Kihara, Y.; Maurya, M.R.; Norris, P.C.; Dennis, E.A.; Subramaniam, S. Computational modeling of competitive metabolism between omega3- and omega6-polyunsaturated fatty acids in inflammatory macrophages. J. Phys. Chem. B 2016, 120, 8346–8353. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Maurya, M.R.; Merrill, A.H., Jr; Glass, C.K.; Subramaniam, S. Integration of lipidomics and transcriptomics data towards a systems biology model of sphingolipid metabolism. BMC Syst. Biol. 2011, 5, 26. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Hide, I.; Ido, K.; Kohsaka, S.; Inoue, K.; Nakata, Y. Production and release of neuroprotective tumor necrosis factor by P2X7 receptor-activated microglia. J. Neurosci. 2004, 24, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Van der Bruggen, T.; Nijenhuis, S.; van Raaij, E.; Verhoef, J.; van Asbeck, B.S. Lipopolysaccharide-induced tumor necrosis factor alpha production by human monocytes involves the raf-1/MEK1-MEK2/ERK1-ERK2 pathway. Infect. Immun. 1999, 67, 3824–3829. [Google Scholar] [PubMed]
- Kanehisa, M.; Sato, Y.; Kawashima, M.; Furumichi, M.; Tanabe, M. KEGG as a reference resource for gene and protein annotation. Nucleic Acids Res. 2016, 44, D457–462. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, M.; Kanehisa, M. Using the KEGG database resource. Curr. Protoc. Bioinf. 2012, 38, 1.12.1–1.12.43. Available online: https://doi.org/10.1002/0471250953.bi0112s38 (accessed on 7 August 2018).
- Fahy, E.; Cotter, D.; Sud, M.; Subramaniam, S. Update of the LIPID MAPS comprehensive classification system for lipids. J. Lipid Res. 2009, 50, S9–S14. [Google Scholar] [CrossRef] [PubMed]
- Sud, M.; Fahy, E.; Cotter, D.; Brown, A.; Dennis, E.A.; Glass, C.K.; Merrill, A.H.Jr.; Murphy, R.C.; Raetz, C.R.; Russell, D.W.; et al. LMSD: LIPID MAPS structure database. Nucleic Acids Res. 2007, 35, D527–532. [Google Scholar] [CrossRef] [PubMed]
- Ogata, H.; Goto, S.; Sato, K.; Fujibuchi, W.; Boho, H.; Kanehisa, M. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 1999, 27, 29–34. [Google Scholar] [CrossRef] [PubMed]
- The LIPID MAPS Lipidomics Gateway. Available online: http://www.lipidmaps.org/ (accessed on 7 August 2018).
- Dennis, E.A.; Deems, R.A.; Harkewicz, R.; Quehenberger, O.; Brown, H.A.; Milne, S.B.; Myers, D.S.; Glass, C.K.; Hardiman, G.; Reichart, D.; et al. A mouse macrophage lipidome. J. Biol. Chem. 2010, 285, 39976–39985. [Google Scholar] [CrossRef] [PubMed]
- Dinasarapu, A.R.; Gupta, S.; Ram Maurya, M.; Fahy, E.; Min, J.; Sud, M.; Gersten, M.J.; Glass, C.K.; Subramaniam, S. A combined omics study on activated macrophages–enhanced role of STATs in apoptosis, immunity and lipid metabolism. Bioinformatics 2013, 29, 2735–2743. [Google Scholar] [CrossRef] [PubMed]
- Subramaniam, S.; Fahy, E.; Gupta, S.; Sud, M.; Byrnes, R.W.; Cotter, D.; Dinasarapu, A.R.; Maurya, M.R. Bioinformatics and systems biology of the lipidome. Chem. Rev. 2011, 111, 6452–6490. [Google Scholar] [CrossRef] [PubMed]
- DeVilbiss, F.T. Is Metabolism Goal-Directed? Investigating the Validaty of Modeling Biological Systems with Cybernetic Control via Omic Data. Ph.D Thesis, Purdue University, West Lafayette, IN, USA, 2016. [Google Scholar]
- Young, J.D.; Ramkrishna, D. On the matching and proportional laws of cybernetic models. Biotechnol. Prog. 2007, 23, 83–99. [Google Scholar] [CrossRef] [PubMed]
- DeVilbiss, F.; Mandli, A.; Ramkrishna, D. Consistency of cybernetic variables with gene expression profiles: A more rigorous test. Biotechnol. Prog. 2018. In press. [Google Scholar] [CrossRef] [PubMed]
- Jahan, N.; Maeda, K.; Matsouka, Y.; Sugimoto, Y.; Kurata, H. Development of an accurate kinetic model for the central carbon metabolism of Escherichia coli. Microb. Cell Fact 2016, 15, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Kotte, O.; Zaugg, J.B.; Heinemann, M. Bacterial adaptation through distributed sensing of metabolic fluxes. Mol. Syst. Biol. 2010, 6, 355–364. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Ramkrishna, D.; Pinchu, G.E.; Belaiev, A.S.; Konopka, A.E.; Frederickson, J.K. Dynamic modeling of aerobic growth of Shewanella oneidensis. Predicting triauxic growth, flux distributions, and energy requirement for growth. Metab. Eng. 2013, 15, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Ramkrishna, D. Prediction of dynamic behavior of mutant strains from limited wild-type data. Metab. Eng. 2012, 14, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.I.; Song, H.S.; Sunkara, S.R.; Lali, A.; Ramkrishna, D. Exacting predictions by cybernetic model confirmed experimentally: Steady state multiplicity in the chemostat. Biotechnol. Prog. 2012, 28, 1160–1166. [Google Scholar] [CrossRef] [PubMed]
- Balkwill, F.R.; Burke, F. The cytokine network. Immunol. Today 1989, 10, 299–304. [Google Scholar] [CrossRef]
- Boulet, L.; Ouellet, M.; Bateman, K.P.; Ethier, D.; Percival, M.D.; Riendeau, D.; Mancini, J.A.; Méthot, N. Deletion of microsomal prostaglandin E2 (PGE2) synthase-1 reduces inducible and basal PGE2 production and alters the gastric prostanoid profile. J. Biol. Chem. 2004, 279, 23229–23237. [Google Scholar] [CrossRef] [PubMed]
- Schomburg, I.; Chang, A.; Ebeling, C.; Gremse, M.; Heldt, C.; Huhn, G.; Schomburg, D. BRENDA, the enzyme database: Updates and major new developments. Nucleic Acids Res. 2004, 32, D431–433. [Google Scholar] [CrossRef] [PubMed]
- Lazarus, M.; Kubata, B.K.; Eguchi, N.; Fujitani, Y.; Urade, Y.; Hayaishi, O. Biochemical characterization of mouse microsomal prostaglandin E synthase-1 and its colocalization with cyclooxygenase-2 in peritoneal macrophages. Arch. Biochem. Biophys. 2002, 397, 336–341. [Google Scholar] [CrossRef] [PubMed]
- Tanioka, T.; Nakatani, Y.; Semmyo, N.; Murakami, M.; Kudo, I. Molecular identification of cytosolic prostaglandin E2 synthase that is functionally coupled with cyclooxygenase-1 in immediate prostaglandin E2 biosynthesis. J. Biol. Chem. 2000, 275, 32775–32782. [Google Scholar] [CrossRef] [PubMed]
- Chan, G.; Boyle, J.O.; Yang, E.K.; Zhang, F.; Sacks, P.G.; Shah, J.P.; Edelstein, D.; Soslow, R.A.; Koki, A.T.; Woerner, B.M. Cyclooxygenase-2 expression is up-regulated in squamous cell carcinoma of the head and neck. Cancer Res. 1999, 59, 991–994. [Google Scholar] [PubMed]
- Urade, Y.; Ujihara, M.; Horiguchi, Y.; Igarashi, M.; Nagata, A.; Ikai, K.; Hayaishi, O. Mast cells contain spleen-type prostaglandin D synthetase. J. Biol. Chem. 1990, 265, 371–375. [Google Scholar] [PubMed]
- Shimizu, T.; Yamamoto, S.; Hayaishi, O. Purification and properties of prostaglandin D synthetase from rat brain. J. Biol. Chem. 1979, 254, 5222–5228. [Google Scholar] [PubMed]
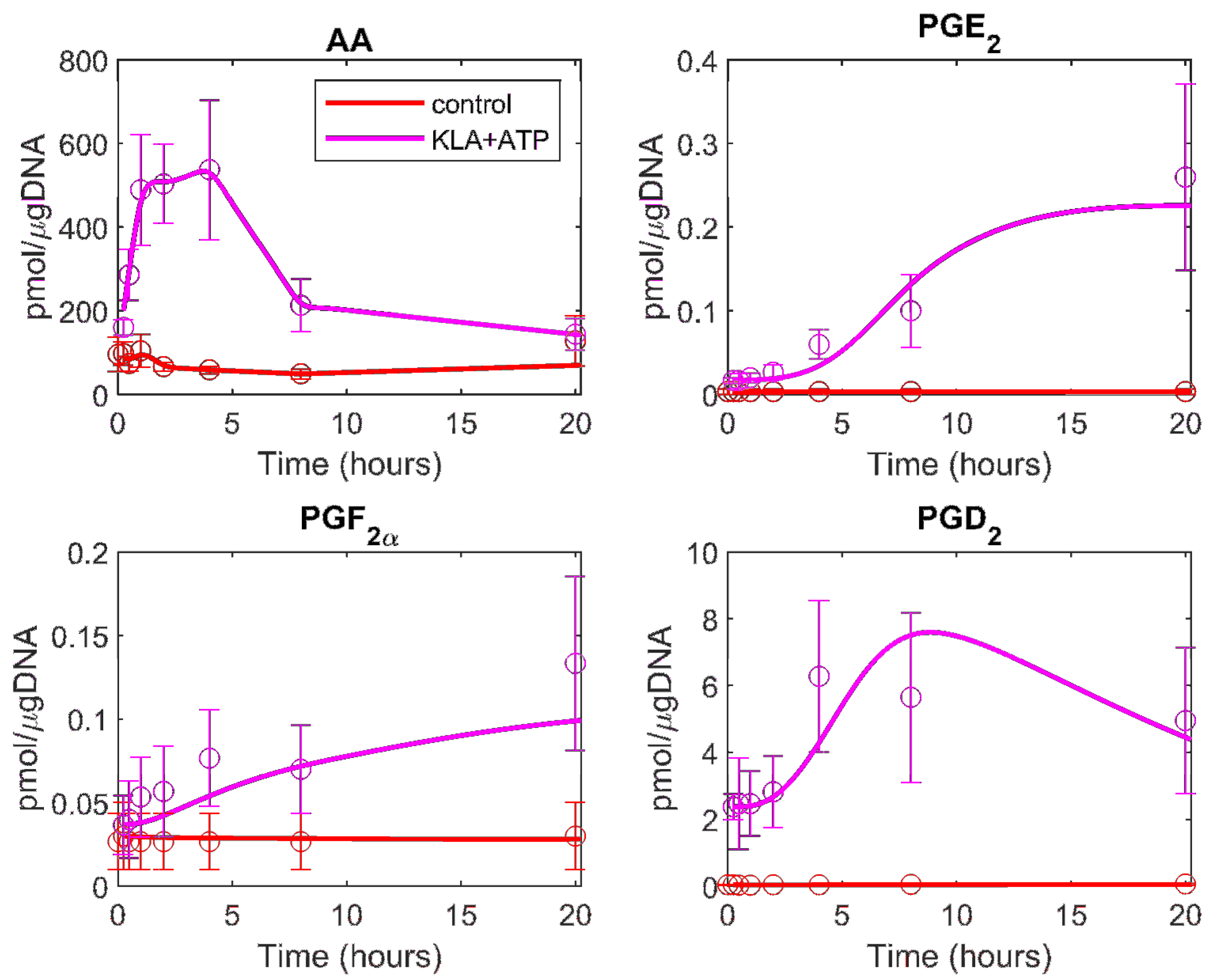
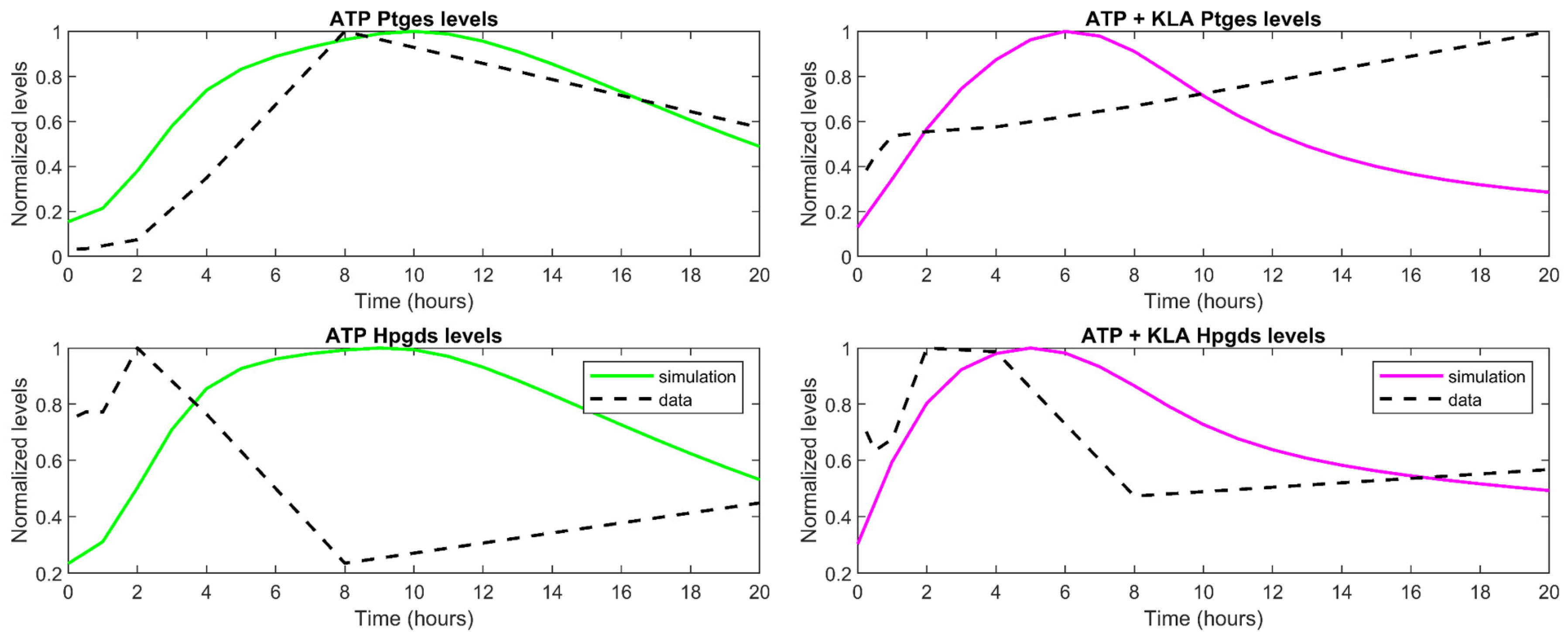
| Metabolite | Model Fit to ATP Data | Model Fit to KLA and ATP Data |
|---|---|---|
| PGE2 | 0.0312 | 0.2421 |
| PGF2α | 0.0470 | 0.0342 |
| PGD2 | 0.2636 | 0.1192 |
| Entrez ID | Pathway | Gene Symbol | Name |
|---|---|---|---|
| 64292 | PGH2 → PGE2 | Ptges | prostaglandin E synthase |
| 54486 | PGH2 → PGD2 | Hpgds/Ptgds2 | hematopoietic prostaglandin D2 synthase |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboulmouna, L.; Gupta, S.; Maurya, M.R.; DeVilbiss, F.T.; Subramaniam, S.; Ramkrishna, D. A Cybernetic Approach to Modeling Lipid Metabolism in Mammalian Cells. Processes 2018, 6, 126. https://doi.org/10.3390/pr6080126
Aboulmouna L, Gupta S, Maurya MR, DeVilbiss FT, Subramaniam S, Ramkrishna D. A Cybernetic Approach to Modeling Lipid Metabolism in Mammalian Cells. Processes. 2018; 6(8):126. https://doi.org/10.3390/pr6080126
Chicago/Turabian StyleAboulmouna, Lina, Shakti Gupta, Mano R. Maurya, Frank T. DeVilbiss, Shankar Subramaniam, and Doraiswami Ramkrishna. 2018. "A Cybernetic Approach to Modeling Lipid Metabolism in Mammalian Cells" Processes 6, no. 8: 126. https://doi.org/10.3390/pr6080126
APA StyleAboulmouna, L., Gupta, S., Maurya, M. R., DeVilbiss, F. T., Subramaniam, S., & Ramkrishna, D. (2018). A Cybernetic Approach to Modeling Lipid Metabolism in Mammalian Cells. Processes, 6(8), 126. https://doi.org/10.3390/pr6080126