A Coupled Thermal-Hydraulic-Mechanical Nonlinear Model for Fault Water Inrush
Abstract
1. Introduction
2. Governing Equations of Coupled THM Model
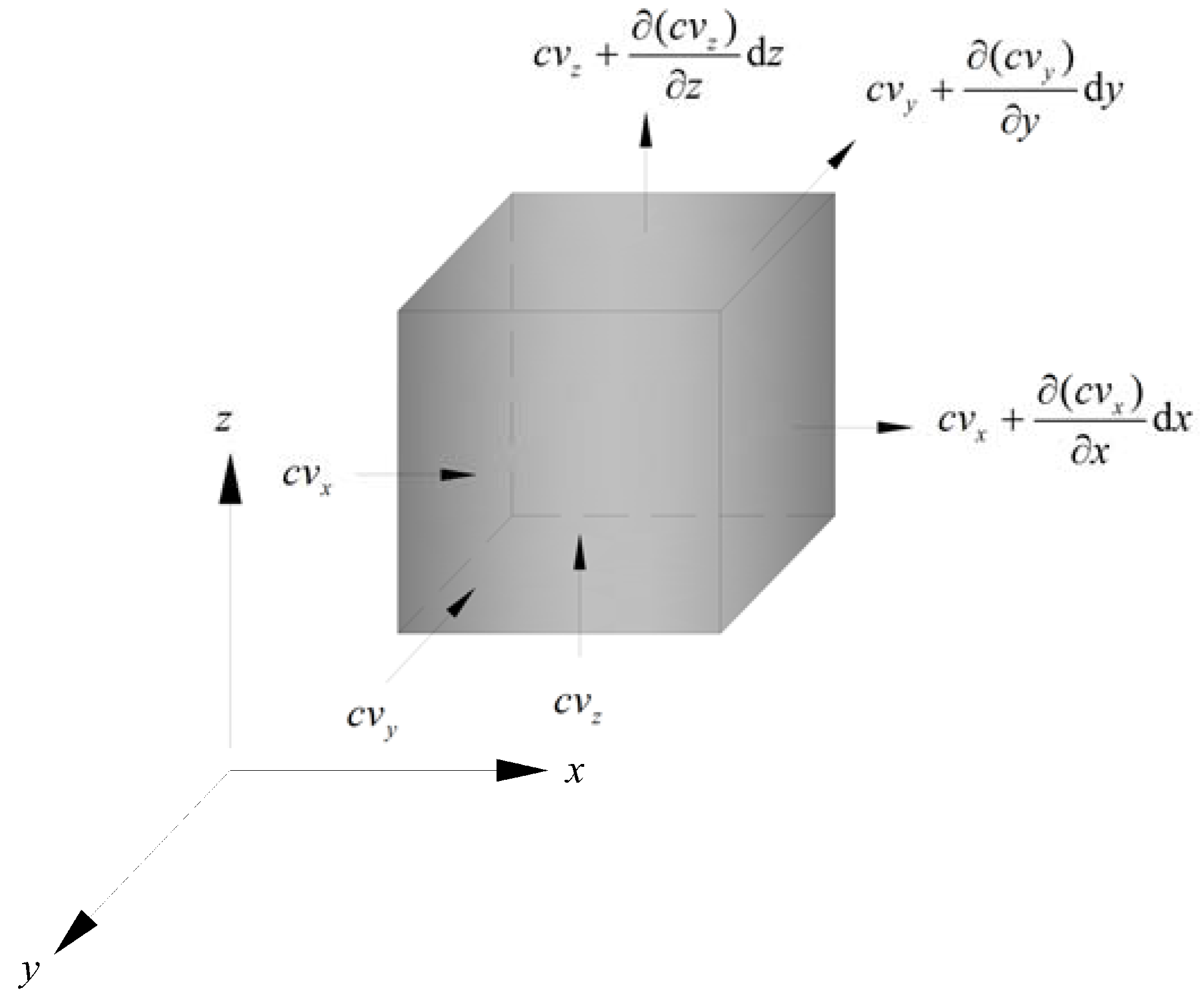
2.1. The Particle Transport Equation
2.2. The Nonlinear Flow Equation
2.3. The Mechanical Equation
2.4. The Heat Transfer Equation
3. Model Setup
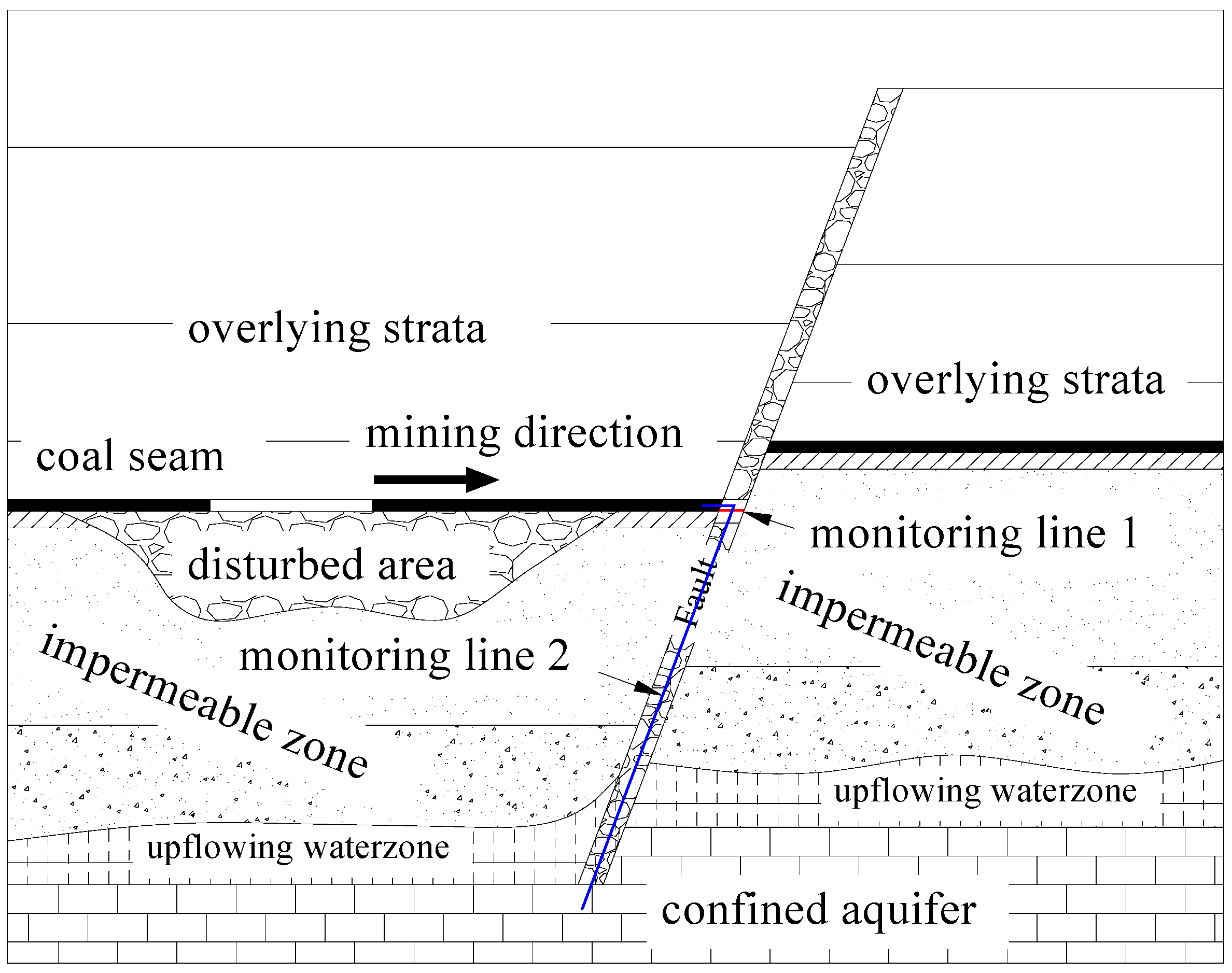
3.1. The Engineering Background and the Geologic Model
3.2. Boundary Condition Setting
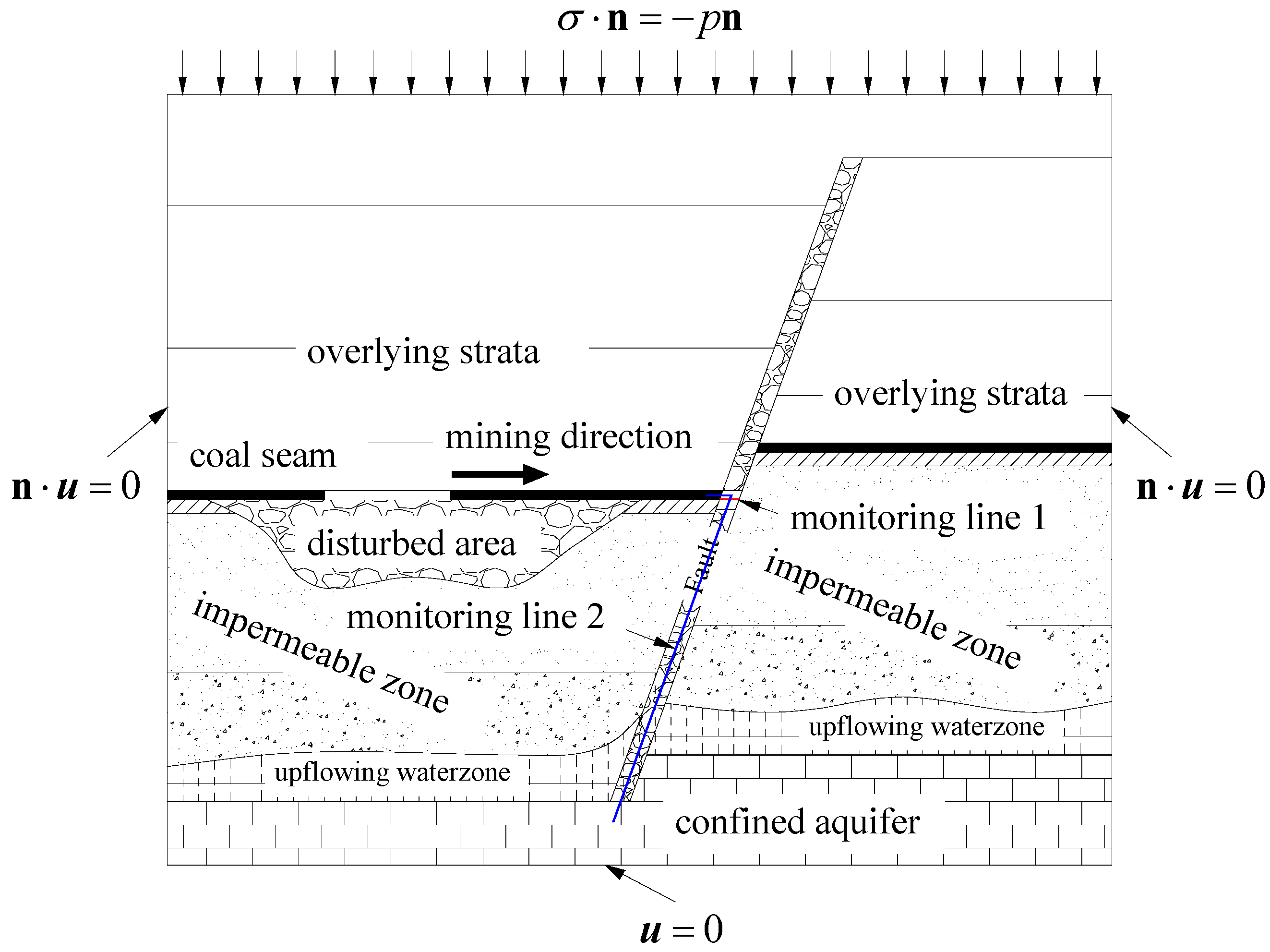
3.2.1. Mechanical Model
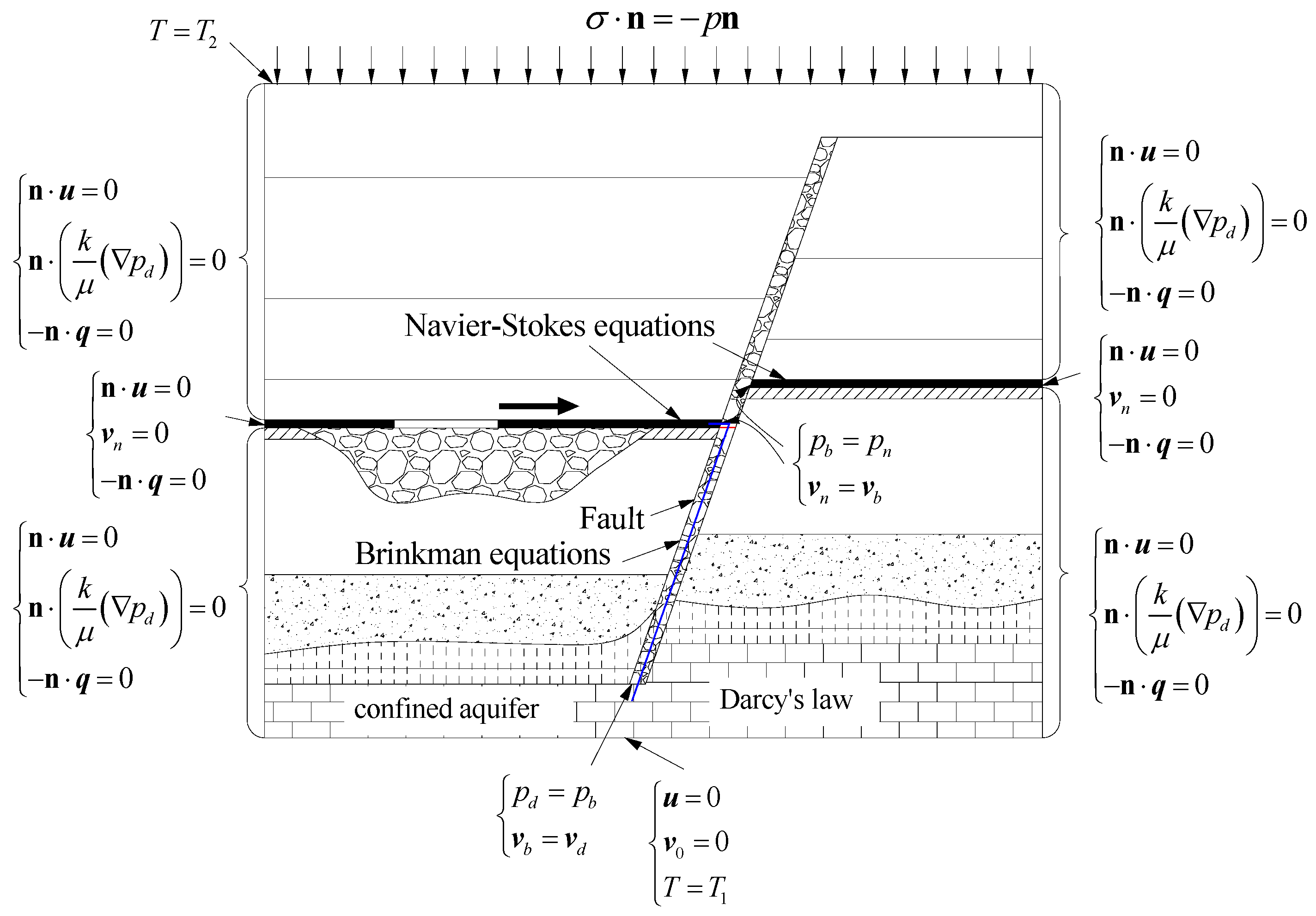
3.2.2. HM Coupling Model
3.2.3. THM Coupling Model
4. Results and Discussions
4.1. Simulation Results
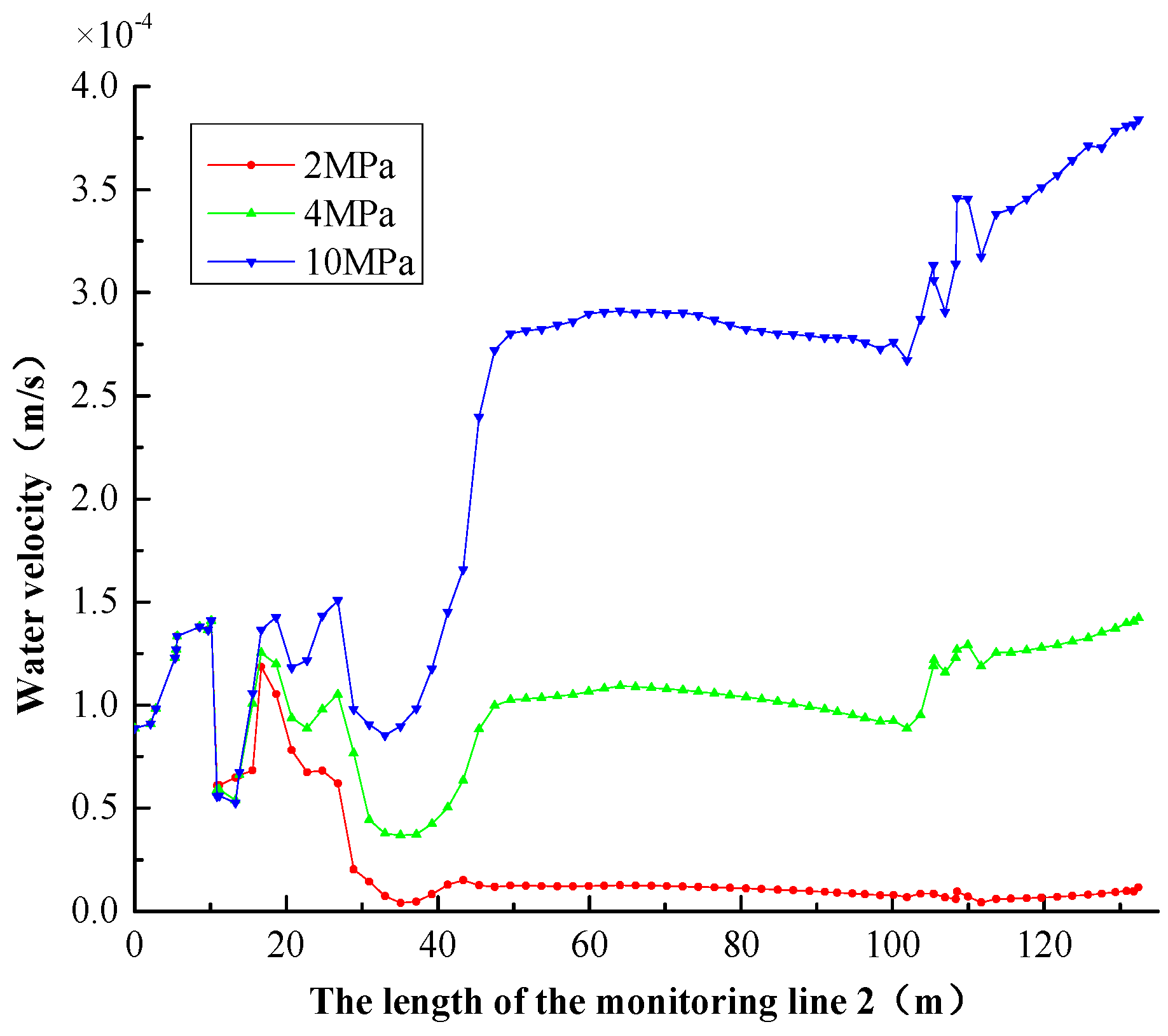
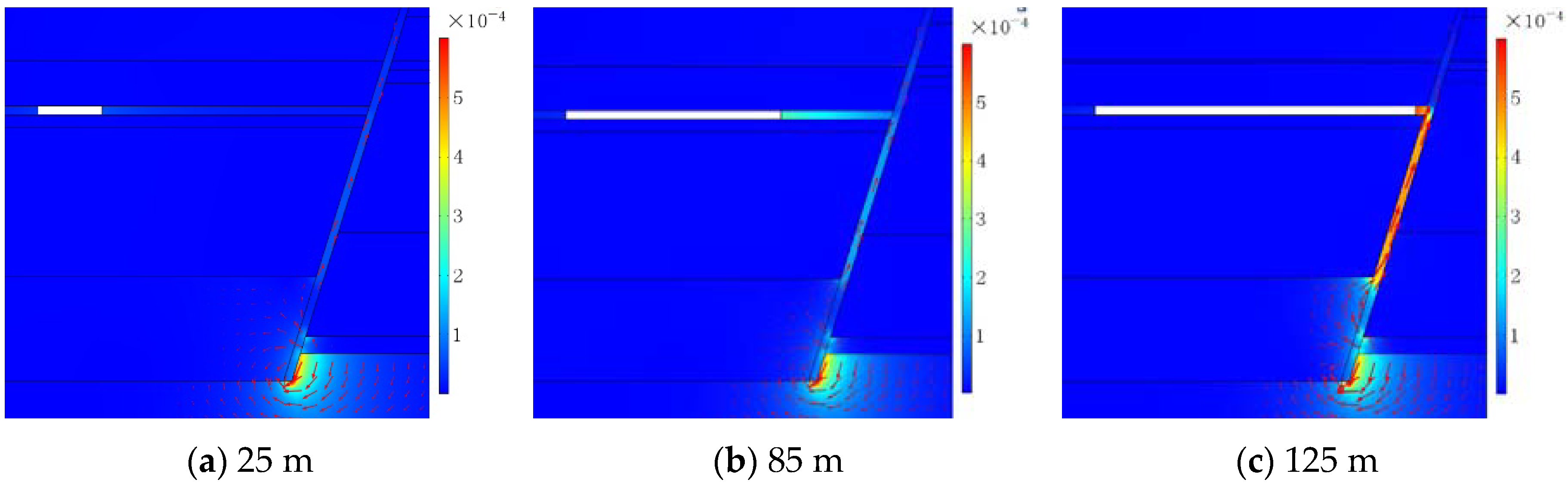
4.1.1. The Change Law of Water Velocity
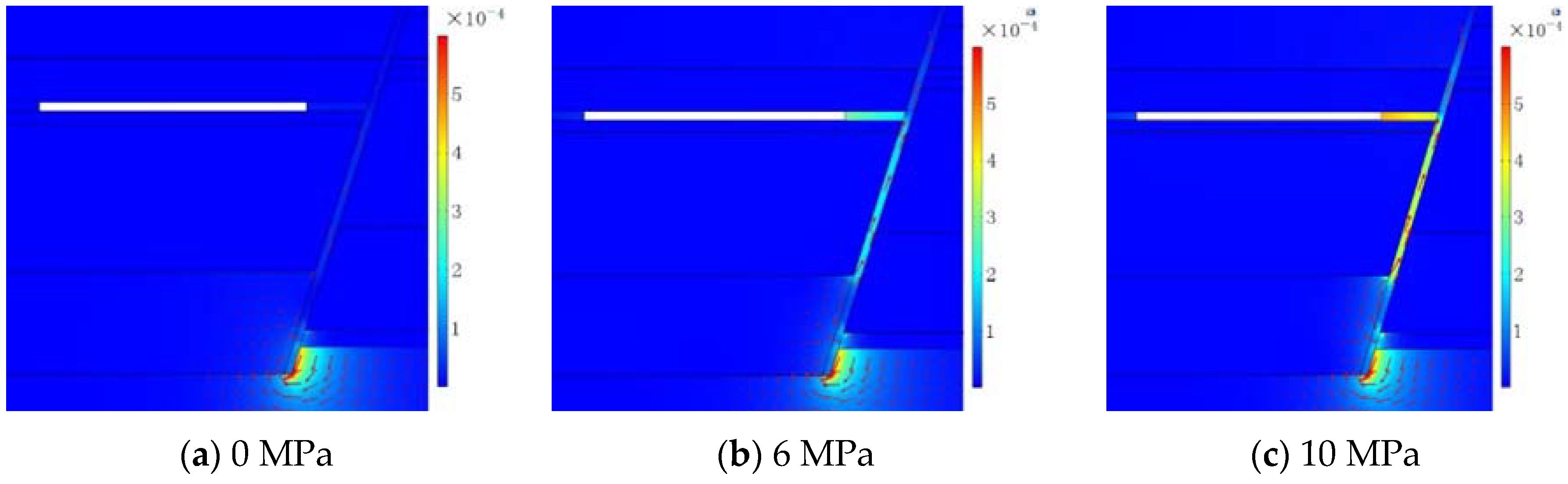
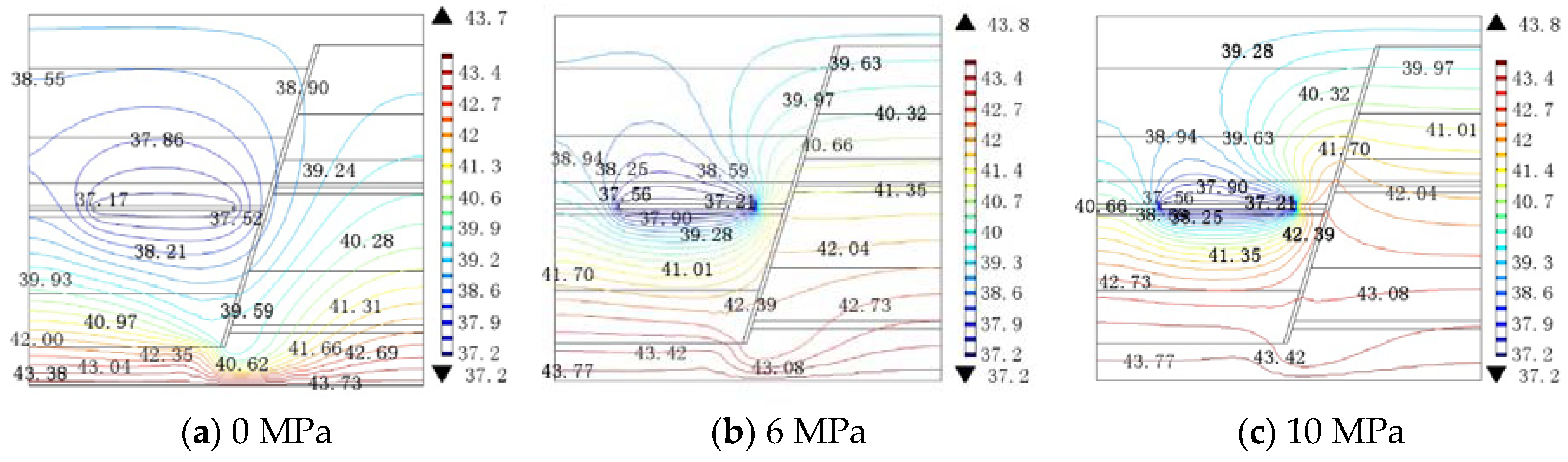
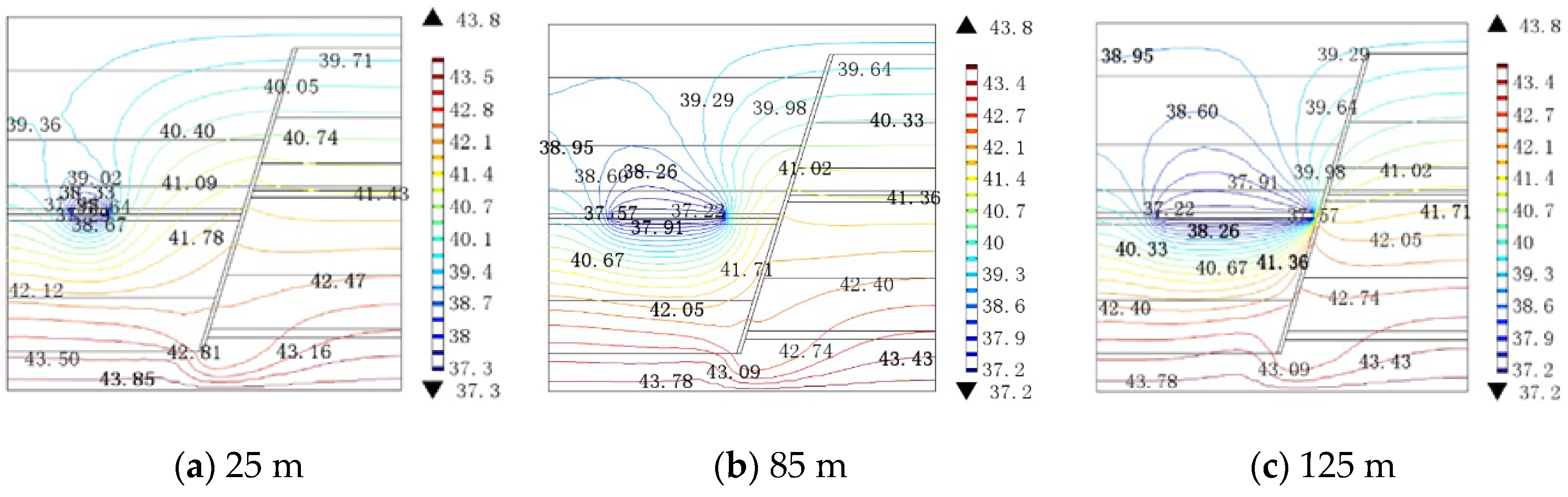
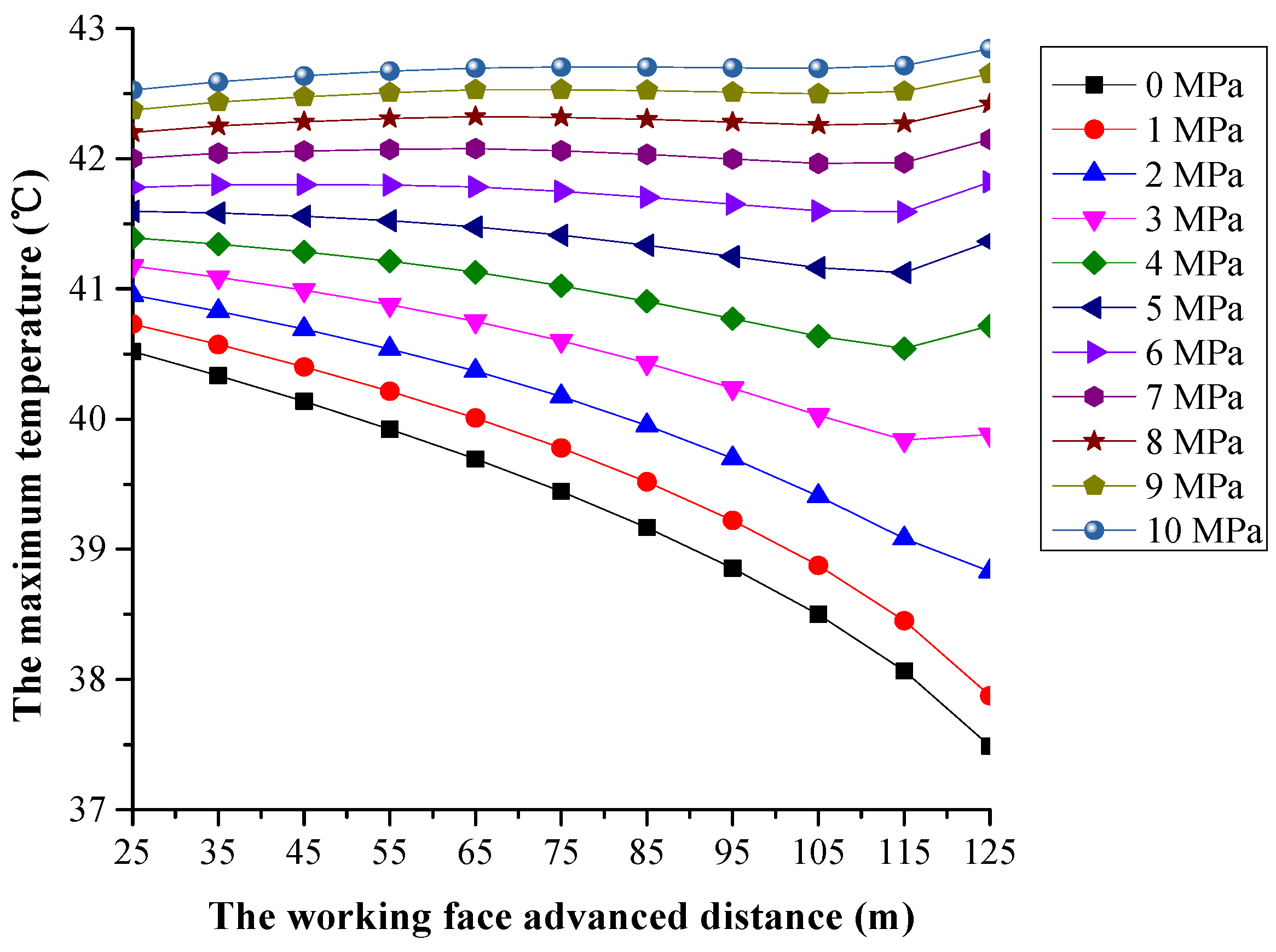
4.1.2. The Distribution of Temperature
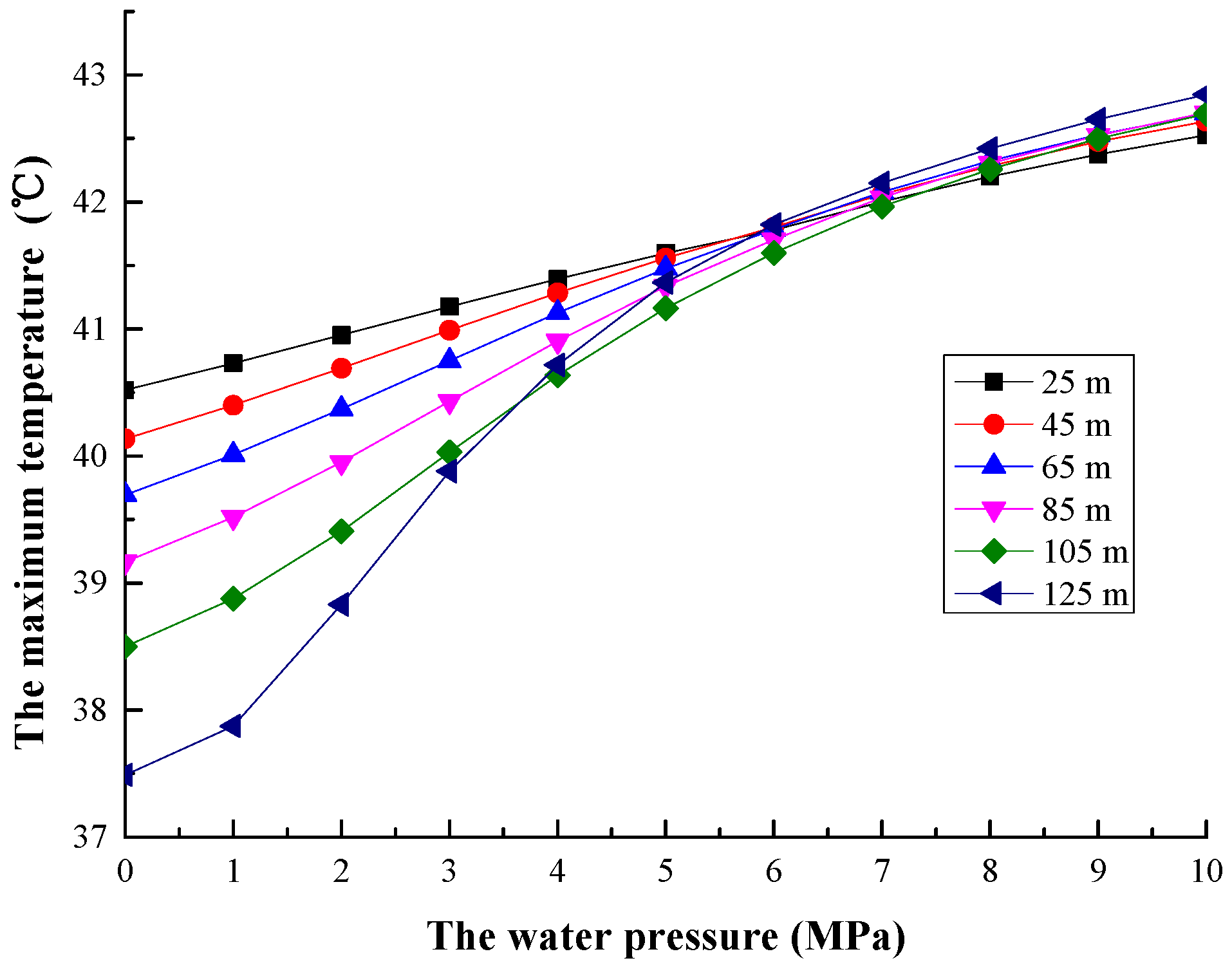
4.1.3. The Warning Level of Water Inrush
- There is some uncertainty in using this model to deal with engineering problems with low geothermal gradients.
- The disturbed area may extend the fault zone and aggravate fault activation, which was not considered in this model.
- The comparison between the measured results in reality and simulated results was not studied.
- Although this model was established based on the engineering background of a coal mine, it can be applied to tunneling in the vicinity of a fault. This model can be used as a method to study the water-rock-temperature interactions in tunneling in the vicinity of a fault. However, as the water inrush coefficient and the water-resisting thickness are applicable only in coal mines, they cannot be used to find the thresholds to divide the warning levels of fault water inrush in tunneling. A new method to divide the warning levels of fault water inrush in tunneling should be found if this model is used to predict fault water inrush in tunneling.
5. Conclusions
- The Darcy-Brinkman-NS equations can properly describe the nonlinear water flow process in the fractured zone of the fault. The water velocity increases with the increasing water pressure. The water velocity has a rapid increase at the junction of the confined aquifer, fault, and coal seam instead of a linear increase.
- Temperature change of the fault zone is subjected to the interaction of the water pressure and the working face advanced distance. At a lower water pressure, the influence of the working face advanced distance on the temperature of the fault zone is greater than that of the water pressure on the temperature. At a higher water pressure, the influence of water pressure on the temperature of the fault zone is greater than that of the working face advanced distance on the temperature. When the working face advanced distance is constant, the temperature of the fault zone increases with the increasing water pressure. The range of the temperature of the fault zone increases with the distance between the working face and the fault plane decreasing.
- The temperature change of the fault zone can reflect the change of the seepage field in the fault and confined aquifer. Monitoring the temperature rise of the fault zone, based on the conception of the water inrush coefficient and the water-resisting thickness of floor, the temperature increases of 1 and 2 °C were used as the thresholds to divide the warning levels of water inrush.
Author Contributions
Funding
Conflicts of Interest
References
- Andrés, C.; Ordóñez, A.; Álvarez, R. Hydraulic and Thermal Modelling of an Underground Mining Reservoir. Mine Water Environ. 2017, 36, 24–33. [Google Scholar] [CrossRef]
- Uhlík, J.; Baier, J. Model Evaluation of Thermal Energy Potential of Hydrogeological Structures with Flooded Mines. Mine Water Environ. 2012, 31, 179–191. [Google Scholar] [CrossRef]
- Xi, Y.; Li, J.; Liu, G.; Tao, Q.; Lian, W. A new numerical investigation of cement sheath integrity during multistage hydraulic fracturing shale gas wells. J. Nat. Gas Sci. Eng. 2018, 49, 331–341. [Google Scholar]
- Rutqvist, J.; Wu, Y.S.; Tsang, C.F.; Bodvarsson, G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Yang, C.S.; Xu, G. FEM Analyses for T-H-M-M Coupling Processes in Dual-Porosity Rock Mass under Stress Corrosion and Pressure Solution. J. Appl. Math. 2012, 10, 3129–3138. [Google Scholar] [CrossRef]
- Tsang, C.F.; Jing, L.; Stephansson, O.; Kautsky, F. The DECOVALEX III project: A summary of activities and lessons learned. Int. J. Rock Mech. Min. Sci. 2005, 42, 593–610. [Google Scholar] [CrossRef]
- Bond, A.E.; Bruský, I.; Cao, T.; Chittenden, N.; Fedors, R.; Feng, X.T.; Gwo, J.P.; Kolditz, O.; Lang, P.; McDermott, C.; et al. A synthesis of approaches for modelling coupled thermal–hydraulic–mechanical–chemical processes in a single novaculite fracture experiment. Environ. Earth Sci. 2017, 76, 1–19. [Google Scholar] [CrossRef]
- Graupner, B.J.; Shao, H.; Wang, X.R.; Nguyen, T.S.; Li, Z.; Rutqvist, J.; Chen, F.; Birkholzer, J.; Wang, W.; Kolditz, O.; et al. Comparative modelling of the coupled thermal–hydraulic-mechanical (THM) processes in a heated bentonite pellet column with hydration. Environ. Earth Sci. 2018, 77, 1–16. [Google Scholar] [CrossRef]
- Sheng, J. Fully coupled thermo-hydro-mechanical model of saturated porous media and numerical modeling. Chin. J. Rock Mech. Eng. 2006, 25, 3028–3033. [Google Scholar]
- Zhu, W.C.; Wei, C.H.; Tian, J.; Yang, T.H.; Tang, C.A. Coupled thermal-hydraulic-mechanical model during rock damage and its preliminary application. Rock Soil. Mech. 2009, 30, 3851–3857. [Google Scholar]
- Sun, J.; Wang, L.G.; Tang, F.R.; Shen, Y.F.; Gong, S.L. Micro seismic monitoring failure characteristics of inclined coal seam floor. Rock Soil. Mech. 2011, 32, 1589–1595. [Google Scholar]
- Bai, J.; Li, S.; Liu, R.; Zhang, Q.; Zhang, H.; Sha, F. Multi-field information monitoring and warning of delayed water bursting in deep rock fault. Chin. J. Rock Mech. Eng. 2015, 34, 2327–2335. [Google Scholar]
- Zhou, Q.; Herrera, J.; Hidalgo, A. The numerical analysis of fault-induced mine water inrush using the extended finite element method and fracture mechanics. Mine Water Environ. 2018, 37, 185–195. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, D.; Li, S.; Qiu, D.; Li, Z.; Zhu, J. A risk prediction method for water or mud inrush from water-bearing faults in subsea tunnel based on cusp catastrophe model. KSCE J. Civ. Eng. 2017, 21, 2607–2614. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Cherubini, C.; Giasi, C.I.; Pastore, N. Bench scale laboratory tests to analyze non-linear flow in fractured media. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 2511–2522. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Yu, L. A numerical approach for assessing effects of shear on equivalent permeability and nonlinear flow characteristics of 2-D fracture networks. Adv. Water Resour. 2018, 111, 289–300. [Google Scholar] [CrossRef]
- Yang, T.; Shi, W.; Li, S.; Xin, Y.; Yang, B. State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass. J. China Coal Soc. 2016, 41, 1598–1609. [Google Scholar]
- Yang, T.; Chen, S.; Zhu, W.; Meng, Z.; Gao, Y. Water inrush mechanism in mines and nonlinear flow model for fractured rocks. Chin. J. Rock Mech. Eng. 2008, 27, 1411–1416. [Google Scholar]
- Yang, T.H.; Shi, W.H.; Liu, H.L.; Yang, B.; Xin, Y.; Liu, Z.B. A non-linear flow model based on flow translation and its application in the mechanism analysis of water inrush through collapse pillar. J. China Coal Soc. 2017, 42, 315–321. [Google Scholar]
- Liu, W.; Zhao, J.; Li, Q. A MHC–NF Coupling Model for Water Inrush from Collapse Columns and Its Numerical Simulation. Geotech. Geol. Eng. 2018, 36, 2637–2647. [Google Scholar] [CrossRef]
- Yao, B.; Mao, X.; Wei, J.; Wang, D. Study on coupled fluid-solid model for collapse columns considering the effect of particle transport. J. China Univ. Min. Technol. 2014, 43, 30–35. [Google Scholar]
- Bear, J.; Bachmat, Y. Introduction to modeling of transport phenomena in porous media. Theory Appl. Transp. Porous Med. 1990, 4, 481–516. [Google Scholar]
- Zhou, Q.; Herrera-Herbert, J.; Hidalgo, A. Predicting the risk of fault-induced water inrush using the adaptive neuro-fuzzy inference system. Minerals 2017, 7, 1–15. [Google Scholar] [CrossRef]
- State Administration of Work Safety of China. Coal Mine Water Prevention and Control Regulations; China Coal Industry Publishing House: Beijing, China, 2009; pp. 84–85. (In Chinese) [Google Scholar]
- Li, W.; Liu, Y.; Qiao, W.; Zhao, C.; Yang, D.; Guo, Q. An improved vulnerability assessment model for floor water bursting from a Confined Aquifer Based on the Water Inrush Coefficient Method. Mine Water Environ. 2017, 37, 11–19. [Google Scholar] [CrossRef]
- He, M.; Lu, X.; Jing, H. Characters of surrounding rock mass in deep engineering and its nonlinear dynamic-mechanical design concept. Chin. J. Rock Mech. Eng. 2002, 21, 1215–1224. [Google Scholar]


| Rock | Thickness (m) | Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Permeability (m2) | Porosity |
|---|---|---|---|---|---|---|
| Sandstone 1 | 20 | 2660 | 9.896 | 8.051 | 1.1 × 10−14 | 0.05 |
| Sandstone 2 | 45 | 2650 | 9.756 | 7.257 | 1.2 × 10−14 | 0.06 |
| Main roof | 30 | 2480 | 8.730 | 4.264 | 1.8 × 10−13 | 0.12 |
| Immediate roof | 15 | 2502 | 8.872 | 6.031 | 1.7 × 10−14 | 0.10 |
| Coal seam | 3 | 1400 | 5.455 | 1.295 | 6.1 × 10−13 | 0.20 |
| Immediate floor | 4.2 | 2430 | 8.217 | 4.126 | 2 × 10−14 | 0.13 |
| Sandstone 3 | 50.3 | 2600 | 9.572 | 7.029 | 2.5 × 10−14 | 0.12 |
| Mudstone | 35 | 2490 | 8.530 | 4.162 | 2.1 × 10−13 | 0.21 |
| confined aquifer | 25 | 2620 | 10.417 | 5.952 | 5.1 × 10−11 | 0.28 |
| Fault | — | 1500 | 2 | 1.5 | 1.2 × 10−11 | 0.26 |
| The Working Face Advanced Distance | The Fitting Polynomial | 4.311 MPa | 7.185 MPa | 8.997 MPa | |||
|---|---|---|---|---|---|---|---|
| The Maximum Temperature | The Temperature Difference | The Maximum Temperature | The Temperature Difference | The Maximum Temperature | The Temperature Difference | ||
| 25 m | y = −5 × 10−5P4 + 0.0007P3 − 0.0048P2 + 0.2279P + 40.514 | 41.45 | 1.36 | 42.03 | 1.94 | 42.36 | 2.27 |
| 35 m | y = −1 × 10−5P4 − 0.0003P3 + 0.0025P2 + 0.2475P + 40.329 | 41.41 | 1.32 | 42.10 | 2.01 | 42.47 | 2.38 |
| 45 m | y = 5 × 10−5P4 − 0.0018P3 + 0.0115P2 + 0.2653P + 40.132 | 41.36 | 1.27 | 42.10 | 2.01 | 42.47 | 2.38 |
| 55 m | y = 0.0001P4 − 0.0034P3 + 0.0223P2 + 0.2793P + 39.919 | 41.30 | 1.21 | 42.08 | 1.99 | 42.42 | 2.33 |
| 65 m | y = 0.0002P4 − 0.0052P3 + 0.0346P2 + 0.2904P + 39.692 | 41.24 | 1.15 | 42.17 | 2.08 | 42.63 | 2.54 |
| 75 m | y = 0.0003P4 − 0.0076P3 + 0.0506P2 + 0.295P + 39.441 | 41.15 | 1.06 | 42.15 | 2.06 | 42.62 | 2.53 |
| 85 m | y = 0.0004P4 − 0.0106P3 + 0.0701P2 + 0.295P + 39.164 | 41.03 | 0.94 | 42.04 | 1.95 | 42.39 | 2.30 |
| 95 m | y = 0.0006P4 − 0.0144P3 + 0.0955P2 + 0.2883P + 38.854 | 40.93 | 0.84 | 42.11 | 2.02 | 42.62 | 2.53 |
| 105 m | y = 0.0008P4 − 0.0198P3 + 0.1294P2 + 0.2769P + 38.495 | 40.79 | 0.70 | 41.95 | 1.86 | 42.28 | 2.19 |
| 115 m | y = 0.0012P4 − 0.0284P3 + 0.18P2 + 0.2697P + 38.051 | 40.70 | 0.61 | 41.95 | 1.86 | 42.23 | 2.14 |
| 125 m | y = 0.0022P4 − 0.0474P3 + 0.2724P2 + 0.3337P + 37.432 | 40.90 | 0.81 | 42.17 | 2.08 | 42.38 | 2.29 |
| The Warning Level | The Water Inrush Coefficient (MPa/m) | The Water Pressure (MPa) | The Temperature Change (°C) |
|---|---|---|---|
| Safe | T ≤ 0.06 | P ≤ 4.311 | ΔT ≤ 1 |
| Dangerous | 0.06 < T ≤ 0.1 | 4.311 < P ≤ 7.185 | 1 < ΔT ≤ 2 |
| More dangerous | T > 0.1 | P > 7.185 | ΔT > 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhao, J.; Nie, R.; Liu, Y.; Du, Y. A Coupled Thermal-Hydraulic-Mechanical Nonlinear Model for Fault Water Inrush. Processes 2018, 6, 120. https://doi.org/10.3390/pr6080120
Liu W, Zhao J, Nie R, Liu Y, Du Y. A Coupled Thermal-Hydraulic-Mechanical Nonlinear Model for Fault Water Inrush. Processes. 2018; 6(8):120. https://doi.org/10.3390/pr6080120
Chicago/Turabian StyleLiu, Weitao, Jiyuan Zhao, Ruiai Nie, Yuben Liu, and Yanhui Du. 2018. "A Coupled Thermal-Hydraulic-Mechanical Nonlinear Model for Fault Water Inrush" Processes 6, no. 8: 120. https://doi.org/10.3390/pr6080120
APA StyleLiu, W., Zhao, J., Nie, R., Liu, Y., & Du, Y. (2018). A Coupled Thermal-Hydraulic-Mechanical Nonlinear Model for Fault Water Inrush. Processes, 6(8), 120. https://doi.org/10.3390/pr6080120





