Effects of Pulse Interval and Dosing Flux on Cells Varying the Relative Velocity of Micro Droplets and Culture Solution
Abstract
1. Introduction
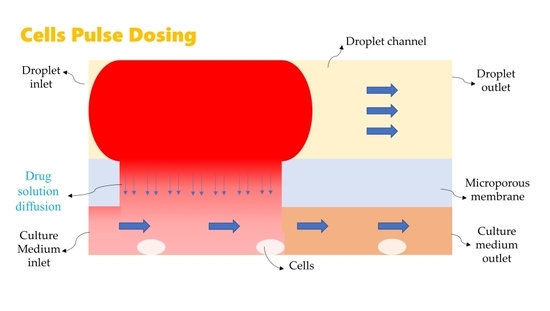
2. Computational Model
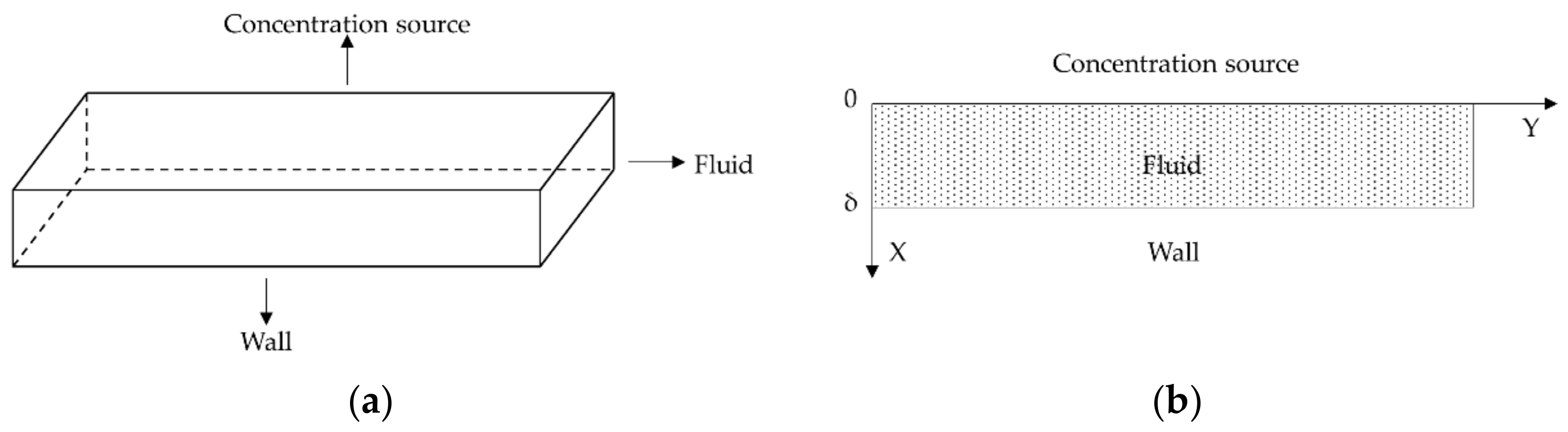
2.1. Mathematical Model
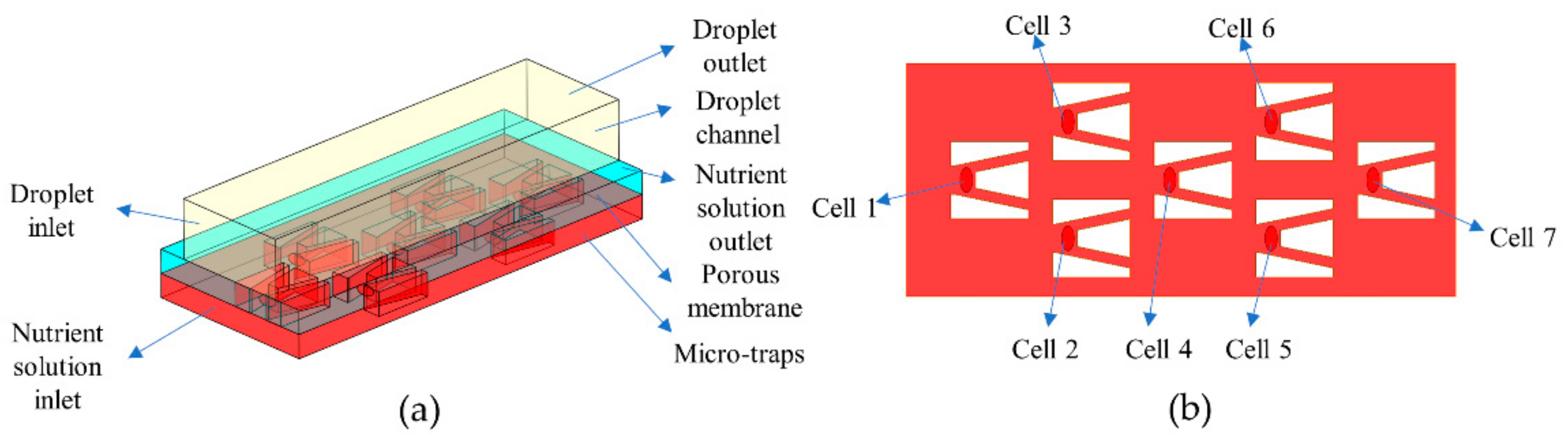
2.2. Numerical Simulation
3. Results and Discussion
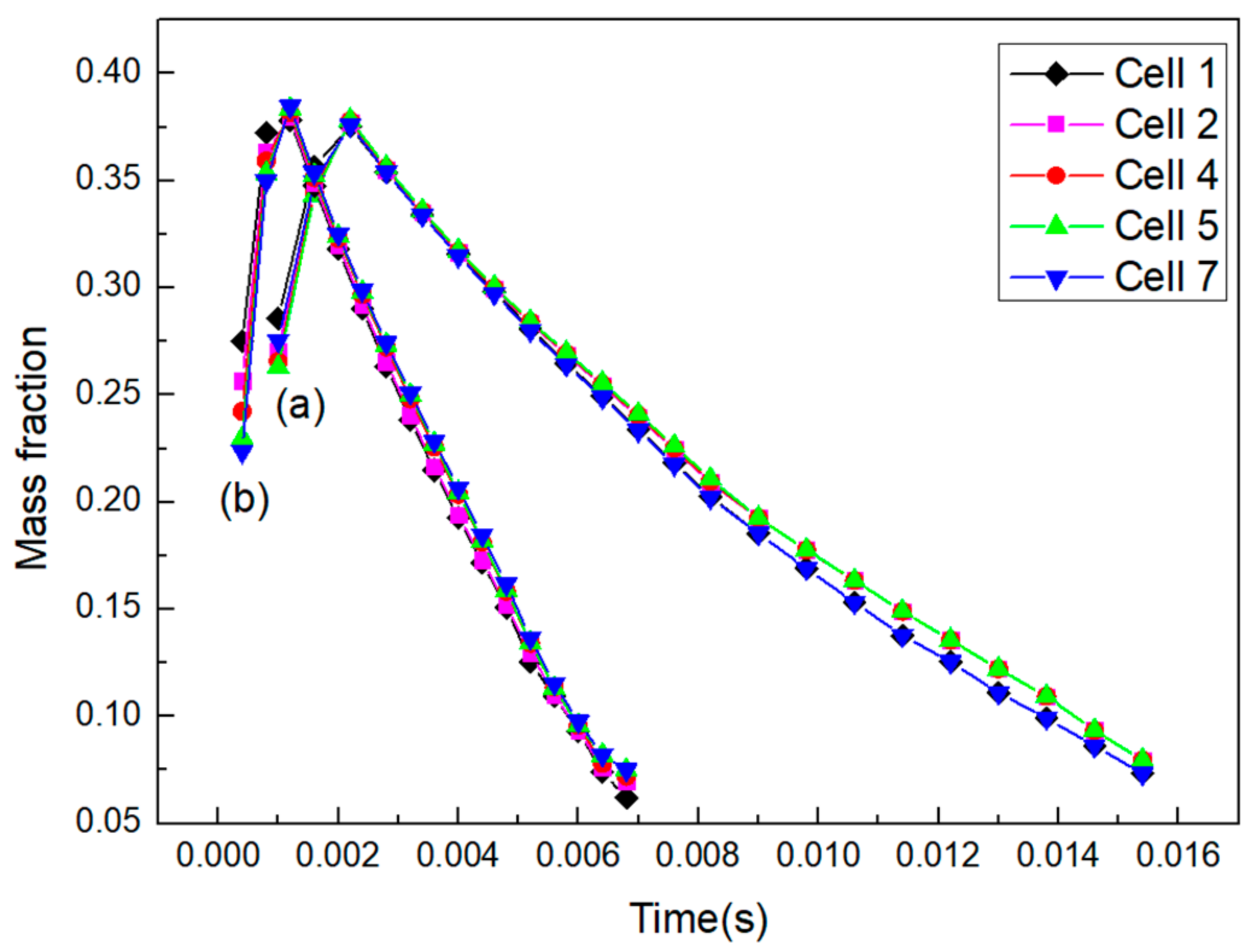
3.1. Area-Weighted Rhodamine Mass Fraction on Cell Surfaces
3.2. Pulse Time
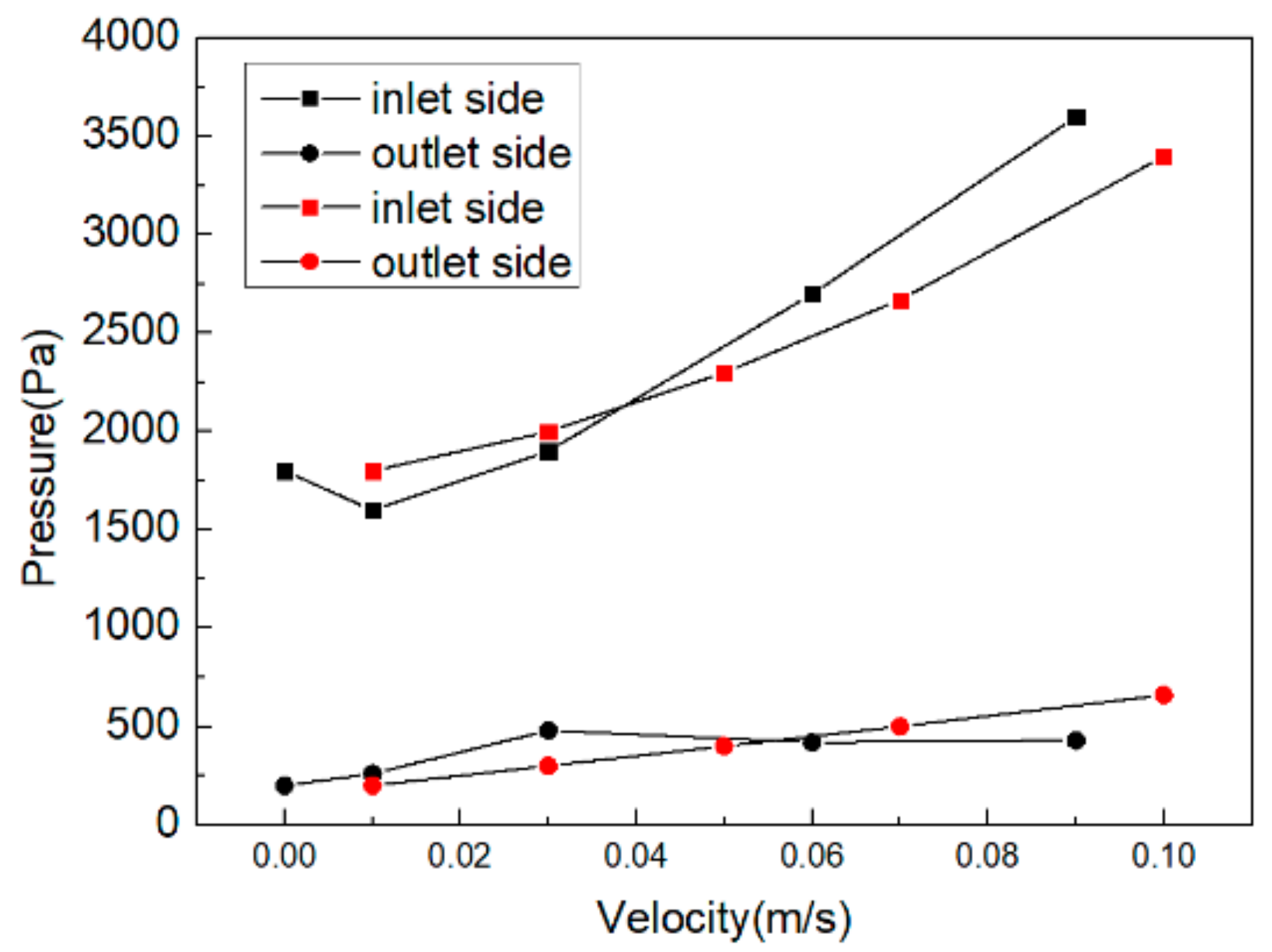
3.3. Pressure Field
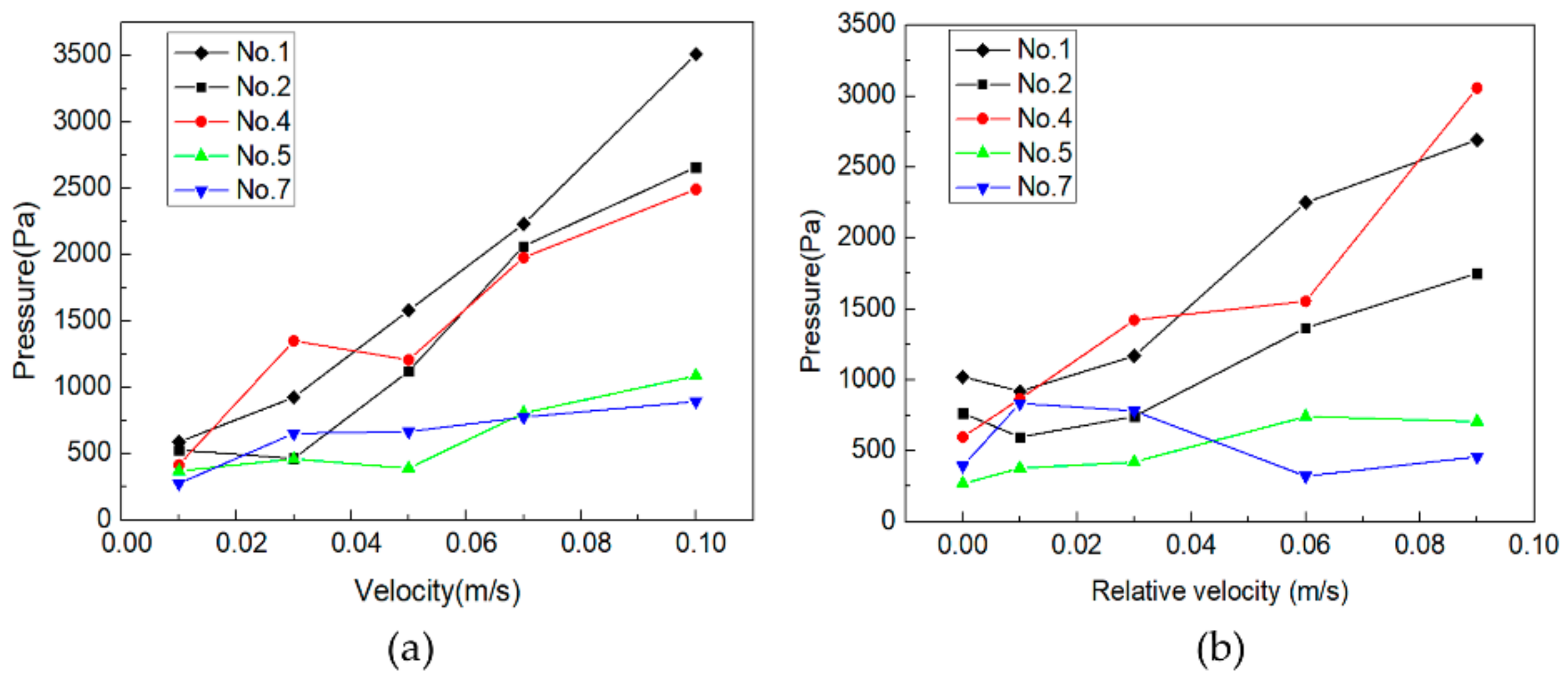
3.4. Combined Influence on Cell Dosing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Millet, L.J.; Gillette, M.U. New perspectives on neuronal development via microfluidic environments. Trends Neurosci. 2012, 35, 752–761. [Google Scholar] [CrossRef] [PubMed]
- Lion, N.; Rohner, T.C.; Dayon, L.; Arnaud, I.L.; Damoc, E.; Youhnovski, N.; Wu, Z.Y.; Roussel, C.; Josserand, J.; Jensen, H.; et al. Microfluidic systems in proteomics. Electrophoresis 2003, 24, 3533–3562. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; DeVoe, D.L.; Lee, C.S. Integration of polymeric membranes with microfluidic networks for bioanalytical applications. Electrophoresis 2001, 22, 3857–3867. [Google Scholar] [CrossRef]
- Benjamin, R.K.; Hochberg, F.H.; Fox, E.; Bungay, P.M.; Elmquist, W.F.; Stewart, C.F.; Gallo, J.M.; Collins, J.M.; Pelletier, R.P.; de Groot, J.F.; et al. Review of microdialysis in brain tumors, from concept to application: First annual Carolyn Frye-Halloran symposium. Neuro Oncol. 2004, 6, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Fair, R.B. Digital microfluidics: Is a true lab-on-a-chip possible? Microfluid. Nanofluid. 2007, 3, 245–281. [Google Scholar] [CrossRef]
- Chengfu, C.; Drew, K.L. Droplet-based microdialysis—Concept, theory, and design considerations. J. Chromatogr. A 2008, 1209, 29–36. [Google Scholar] [CrossRef]
- Lee, T.Y.; Hyun, K.A.; Kim, S.I.; Jung, H.I. An integrated microfluidic chip for one-step isolation of circulating tumor cells. Sens. Actuators B Chem. 2016, 238, 1144–1150. [Google Scholar] [CrossRef]
- Mao, H.; Cremer, P.S.; Manson, M.D. A sensitive, versatile microfluidic assay for bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 2003, 100, 5449–5454. [Google Scholar] [CrossRef] [PubMed]
- Dertinger, S.K.; Jiang, X.; Li, Z.; Murthy, V.N.; Whitesides, G.M. Gradients of substrate-bound laminin orient axonal specification of neurons. Proc. Natl. Acad. Sci. USA 2002, 99, 12542–12547. [Google Scholar] [CrossRef] [PubMed]
- Schiff, N.D.; Giacino, J.T.; Kalmar, K.; Victor, J.D.; Baker, K.; Gerber, M.; Fritz, B.; Eisenberg, B.; O’connor, J.; Kobylarz, E.J.; et al. Behavioural improvements with thalamic stimulation after severe traumatic brain injury. Nature 2007, 448, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Asaad, W.; Eskandar, E. The movers and shakers of deep brain stimulation. Nat. Med. 2008, 14, 17–18. [Google Scholar] [CrossRef] [PubMed]
- Fytagoridis, A.; Åström, M.; Wårdell, K.; Blomstedt, P. Stimulation-induced side effects in the posterior subthalamic area: Distribution, characteristics and visualization. Clin. Neurol. Neurosurg. 2013, 115, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Lopes, C.D.; Gomes, C.P.; Neto, E.; Sampaio, P.; Aguiar, P.; Pêgo, A.P. Microfluidic-based platform to mimic the in vivo peripheral administration of neurotropic nanoparticles. Nanomedicine 2016, 11, 3205–3221. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Tsutahara, M.; Kim, L.; Ha, M. Numerical simulations of droplet formation in a cross-junction microchannel by the lattice Boltzmann method. Int. J. Numer. Methods Fluids 2007, 57, 793–810. [Google Scholar] [CrossRef]
- Wu, L.; Tsutahara, M.; Kim, L.S.; Ha, M. Hree-dimensional lattice Boltzmann simulations of droplet formation in a cross-junction microchannel. Int. J. Multiph. Flow 2008, 34, 852–864. [Google Scholar] [CrossRef]
- Raj, R.; Mathur, N.; Buwa, V.V. Numerical simulations of liquid–liquid flows in microchannels. Ind. Eng. Chem. Res. 2010, 49, 10606–10614. [Google Scholar] [CrossRef]
- Raimondi, N.D.M.; Prat, L. Numerical study of the coupling between reaction and mass transfer for liquid–liquid slug flow in square microchannels. AICHE J. 2011, 57, 1719–1732. [Google Scholar] [CrossRef]
- Raimondi, N.M.; Prat, L.; Gourdon, C.; Cognet, P. Direct numerical simulations of mass transfer in square microchannels for liquid–liquid slug flow. Chem. Eng. Sci. 2008, 63, 5522–5530. [Google Scholar] [CrossRef]
- Pfaff, D.; Waters, E.; Khan, Q.; Zhang, X.; Numan, M. Minireview: Estrogen Receptor-Initiated Mechanisms Causal to Mammalian Reproductive Behaviors. Endocrinology 2012, 152, 1209–1217. [Google Scholar] [CrossRef] [PubMed]
- Serwer, L.P.; James, C.D. Challenges in drug delivery to tumors of the central nervous system: An overview of pharmacological and surgical considerations. Adv. Drug Deliv. Rev. 2012, 64, 590–597. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, L.H. Modern methods for delivery of drugs across the blood-brain barrier. Adv. Drug Deliv. Rev. 2012, 64, 640–665. [Google Scholar] [CrossRef] [PubMed]
- Monopoli, M.P.; Aberg, C.; Salvati, A.; Dawson, K.A. Biomolecular coronas provide the biological identity of nanosized materials. Nat. Nanotechnol. 2012, 7, 779–786. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, S.; Hattori, K.; Kanamori, T. Microfluidic serial dilution cell-based assay for analyzing drug dose response over a wide concentration range. Anal. Chem. 2010, 82, 8278–8282. [Google Scholar] [CrossRef] [PubMed]
- Mary, P.; Studer, V.; Tabeling, P. Microfluidic droplet-based liquid-liquid extraction. Anal. Chem. 2008, 80, 2680–2687. [Google Scholar] [CrossRef] [PubMed]
- Nerín, C.; Salafranca, J.; Aznar, M.; Batlle, R. Critical review on recent developments in solventless techniques for extraction of analytes. Anal. Bioanal. Chem. 2009, 393, 809–833. [Google Scholar] [CrossRef] [PubMed]
- Chua, Y.T.; Ji, G.; Birkett, G.; Lin, C.X.C.; Kleitz, F.; Smart, S. Nanoporous organosilica membrane for water desalination: Theoretical study on the water transport. J. Membr. Sci. 2015, 482, 56–66. [Google Scholar] [CrossRef]
- Peng, T.; Li, Q.; Chen, J.; Gao, X. Quantitative analysis of surface tension of liquid nano-film with thickness: Two stage stability mechanism, molecular dynamics and thermodynamics approach. Phys. A Stat. Mech. Appl. 2016, 462, 1018–1028. [Google Scholar] [CrossRef]
- Qu, J.; Wang, Q.; He, Z.X.; Jian, Q.U.; Qian, W.; Zhi-Xia, H.E.; Han, X.Y.; Zi-Cheng, H.U.; Tao, L. An experimental study of formation and flow charactristics of droplets in a rectangular microchannel. J. Shanghai Jiaotong Univ. 2015, 49, 86–90. [Google Scholar] [CrossRef]
- Chen, S.; Liu, K.; Liu, C.; Wang, D.; Ba, D.; Xie, Y.; Du, G.; Ba, Y.; Lin, Q. Effects of surface tension and viscosity on the forming and transferring process of microscale droplets. Appl. Surf. Sci. 2016, 388, 196–202. [Google Scholar] [CrossRef]
- Fujita, H.; Einaga, Y. Self-Diffusion and Viscoelasticity in Entangled Systems I. Self-Diffusion Coefficients. Polym. J. 1985, 17, 1131–1139. [Google Scholar] [CrossRef]
- Dunca, A.A.; Neda, M.; Rebholz, L.G. A mathematical and numerical study of a filtering-based multiscale fluid model with nonlinear eddy viscosity. Comput. Math. Appl. 2013, 66, 917–933. [Google Scholar] [CrossRef]
- Espin, L.; Kumar, S. Droplet spreading and absorption on rough, permeable substrates. J. Fluid Mech. 2015, 784, 465–486. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Culture medium density ρ1 | 1038 kg/m3 |
| Culture medium dynamic viscosity μ1 | 3.07 × 10−3 Pa·s |
| Rhodamine B solution density ρ2 | 1.053 kg/m3 |
| Rhodamine B solution dynamic viscosity μ2 | 1 × 10−3 Pa·s |
| Oil density ρ2 | 960 kg/m3 |
| Oil density dynamic viscosity μ3 | 0.012–0.096 Pa·s |
| Inlet velocity v0 | ≤0.1 m/s |
| Porosity ρ | 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, K.; Ning, J.; Chen, S.; Hao, M.; Wang, D.; Mei, Q.; Ba, Y.; Ba, D. Effects of Pulse Interval and Dosing Flux on Cells Varying the Relative Velocity of Micro Droplets and Culture Solution. Processes 2018, 6, 119. https://doi.org/10.3390/pr6080119
Wang Z, Liu K, Ning J, Chen S, Hao M, Wang D, Mei Q, Ba Y, Ba D. Effects of Pulse Interval and Dosing Flux on Cells Varying the Relative Velocity of Micro Droplets and Culture Solution. Processes. 2018; 6(8):119. https://doi.org/10.3390/pr6080119
Chicago/Turabian StyleWang, Zhanwei, Kun Liu, Jiuxin Ning, Shulei Chen, Ming Hao, Dongyang Wang, Qi Mei, Yaoshuai Ba, and Dechun Ba. 2018. "Effects of Pulse Interval and Dosing Flux on Cells Varying the Relative Velocity of Micro Droplets and Culture Solution" Processes 6, no. 8: 119. https://doi.org/10.3390/pr6080119
APA StyleWang, Z., Liu, K., Ning, J., Chen, S., Hao, M., Wang, D., Mei, Q., Ba, Y., & Ba, D. (2018). Effects of Pulse Interval and Dosing Flux on Cells Varying the Relative Velocity of Micro Droplets and Culture Solution. Processes, 6(8), 119. https://doi.org/10.3390/pr6080119