Abstract
The increasing variability in power plant load in response to a wildly uncertain electricity market and the need to to mitigate CO2 emissions, lead power plant operators to explore advanced options for efficiency optimization. Model-based, system-scale dynamic simulation and optimization are useful tools in this effort and are the subjects of the work presented here. In prior work, a dynamic model validated against steady-state data from a 605 MW subcritical power plant was presented. This power plant model was used as a test-bed for dynamic simulations, in which the coal load was regulated to satisfy a varying power demand. Plant-level control regulated the plant load to match an anticipated trajectory of the power demand. The efficiency of the power plant’s operation at varying loads was optimized through a supervisory control architecture that performs set point optimization on the regulatory controllers. Dynamic optimization problems were formulated to search for optimal time-varying input trajectories that satisfy operability and safety constraints during the transition between plant states. An improvement in time-averaged efficiency of up to 1.8% points was shown to be feasible with corresponding savings in coal consumption of 184.8 tons/day and a carbon footprint decrease of 0.035 kg/kWh.
1. Introduction
The excessive emissions of CO2 from fossil-fueled power plants contribute to the greenhouse effect and global warming. Increasing the efficiency of power generation cycles and integration with CO2 capture units are nowadays accepted as the most promising short-term approaches to reducing CO2 emissions while we transition to renewable and carbon free energy sources [1,2]. Efficiency improvements can be achieved through the optimization of power plant operating strategies or through modification of plant design. For instance, new fossil-fueled power plants use a combination of steam and gas turbines to generate electricity, resulting in thermal efficiencies as high as 61% [3]. Moreover, modern coal-fired Rankine cycle systems can achieve efficiencies as high as 47% using ultra-supercritical boilers [4]. For instance, the commercial power plant of Lnen (Germany) burns low-sulfur hard coal [5] at an efficiency of up to 46% in a 750 MW ultra-supercritical once-through boiler, operating at steam conditions of 600 C and 280 bar [6]. Nonetheless, subcritical coal-fired steam power plants that operate on the principle of the Rankine Cycle still supply more than one-third of the electricity demand in the US [7]. Subcritical power plants operating at pressures lower than 220 bar have a nominal efficiency of 37% [8]. Compared to supercritical and ultra-supercritical plants, the more common subcritical plants are advantageous in terms of lower installation costs, operating and maintenance experience [5,7]. Therefore, optimization of the efficiency of subcritical power plants is the first realistic step in our efforts to reduce CO2 emissions from the power sector.
Due to seasonal and daily fluctuations in power demand and new deployment programs focused on renewable energy, dynamic simulations and optimization are required for power plants in order to respond to the resulting time-varying power demand. The contribution of electricity generation from renewable energy sources throughout the world will expand from the current 21% to 29.8% by 2040 [7]. The impact of this increase in penetration of renewable sources has been explored by many researchers. For example, Shah et al. [9] showed that the higher penetration of large-scale photovoltaic plants in the power grid will lead to significant variation in the power flow across the grid and unstable power generation profiles for the balancing conventional plants. The work by Edmunds et al. [10] showed that today’s power plants are subject to more intense ramping operations due to the increasing variable renewable penetration. Critz et al. [11] focused on the challenges arising from the inability to accurately forecast renewable power generation. Correspondingly, Eser et al. [12] showed that the high penetration of renewable energy sources will result in an increase in periodic start-ups of thermal power plants. Thus, simulation of the dynamic behavior of the integrated electricity sector and, in particular, the dynamicity of the fossil-fueled power plants, which will provide the balanced power (between renewables input and market demand), is increasingly of interest to improve productivity and stability and reduce cost and emissions.
The efficiency of conventional fossil-fueled power plants that are based on the Rankine Cycle mostly depends on the steam temperature and pressure [4], with the majority of previous work on efficiency optimization of these plants focusing on steady-state analyses. The work by Fu et al. [13] showed an average efficiency increase of 0.1% points for every increment of 8 C in boiler feedwater temperature, every decrement of 4.5 C in flue gas temperature and every increment of 10 bar in main steam pressure, compared to a reference case with an efficiency of 45.5%. Sanpasertparnich and Aroonwilas [14] presented potential efficiency improvements of up to 8.88% points for subcritical coal-fired power plants. They identified the preheated air temperature, main steam temperature and pressure of stream extracted from the high-, intermediate-, and low-pressure turbines (HP, IP and LP, respectively), as being the most critical variables in the optimization of power plant performance. In work by Tzolakis et al. [15], an absolute net efficiency gain of 0.55% was shown to be feasible by reducing the mass flow rate of the steam exiting the HP turbines and increasing the mass flow rate of the steam exiting the IP and LP turbines. These significant efforts in the area of steady-state optimization of power plants paved the way for future work on dynamic optimization. Moreover, advancements in process modeling tools, such as Dymola [16] and gPROMS [17], have made it easier to simulate these processes dynamically. For instance, Chen et al. [18] developed a Dymola [16] dynamic model of a combined cycle power plant integrated with chemical-looping combustion, with the combustion process optimized in gPROMS [17] to maximize the power plant efficiency. Franke et al. [19] presented a model-based, dynamic optimization framework exploiting the Modelica language [20] to improve power plant performance. Their work illustrated the efficiency benefits of applying offline optimization results to online power plant operations. Lind and Sallberg [21] used modern acausal simulation and optimization tools to optimize the start-up procedure of a combined cycle power plant. Their analysis showed that the thermal stress in the heat recovery steam generator is the major constraint limiting the rapid start-up of the gas turbines to full load.
One practical approach to improve the efficiency of existing fossil-fueled power plants is to deploy supervisory control schemes targeted to efficiency optimization. Supervisory control architectures are often used to perform tasks of process optimization without changing the plant infrastructure and design. Skogestad [22] presented a systematic procedure for designing advanced control structures at the supervision level for complex chemical plants. The critical first steps in designing a supervisor logic are to define the operational and economic objectives and the available degrees of freedom. Common degrees of freedom include the set points of the regulatory controllers, system boundaries not controlled and system parameters tuned to a particular operating scheme. For instance, Lestage et al. [23] presented a linear supervisory control design for constrained real-time optimization of an ore grinding plant in which they optimized the set points of the local controllers to maximize throughput. Baillie and Bollas [24] presented the key steps in the development of a high-fidelity model for a chiller plant which was used in supervisory resilient control architectures for plant optimization under fault scenarios by Mittal et al. [25]. Obviously, supervisory control is a promising approach for the efficiency optimization of power plants, wherein there exists a large number of regulatory controllers that must be maintained for safety and performance reasons. In one such effort, Sez et al. [26] developed a supervisory algorithm based on adaptive predictive control to optimize the operation of the gas turbine of a combined cycle power plant in Chile. They showed the potential of 3% fuel consumption savings by manipulating variables such as the fuel flow, air flow and steam flow. Ponce et al. [27] presented a dynamic simulator of an integrated solar combined cycle power plant, incorporating a supervisory control strategy. Fuel savings of 1.7–3.7% were shown to be feasible through the manipulation of set points of the regulatory controllers of the steam pressure, gas turbine power and steam turbine power. These efforts focused mostly on the optimization of a few power plant components instead of solving a problem that maximizes the power plant efficiency by using all or most of the degrees of freedom. In this work, the optimization problem serving the supervisory controller deals with the integrated coal-fired steam power plant.
In prior work [28], a power plant model was developed and validated against steady-state data from a fossil-fueled subcritical power plant with a reheat, regenerative cycle [29]. The power plant modeled exhibited a full-load power generation of 605 MW at efficiency of 38.7%. The modeled power plant operates with nominal steam turbine conditions of 174 bar and 538 C, generated by the combustion of bituminous B coal. Conventional proportional-integral-derivative (PID) controllers were incorporated into the system model. Dynamic simulation of the power plant operating with step changes in fuel load showed that the controllers are robust in maintaining the controlled variables at set point. In this work, open-source data of time-varying power demand along with its forecast from the New England area are used to study this plant under realistic operating conditions [30]. A fuel load controller is implemented to meet the time-varying power demand, and controllers are added to adjust the air flow and water flow for a time-varying load. Supervisor control strategies are applied for static and dynamic optimization of the power plant’s efficiency. This optimization is accomplished by manipulating the set points of the regulatory controllers of the temperature of the superheated steam and preheated air, and the mass flow rates of steam extracted from the steam turbines. Steady-state and dynamic optimization results are compared and discussed in an effort to explore the value proposition of each. Previous work on power plant optimization focused on steady-state simulation and optimization. The main contribution of this work is to use dynamic optimization with embedded plant-level control to optimize the transient operation of power plants. This can enable plant operators to operate power plants efficiently at variable load demands which becomes increasingly important with the higher grid-penetration of renewables.
2. Power Plant Studied and Plant Model
The power plant studied and simulated in prior work [28] was the fossil fuel-fired subcritical power plant, shown in Figure 1, with operating conditions at full load, as reported by Singer [29]. The plant employs a reheat, regenerative cycle to produce 605 MW of electricity by burning fossil-fuel, with nominal turbine conditions of 174 bar and 538 C steam. The combustion of bituminous B coal [5] with preheated air produces hot flue gas that evaporates and superheats water. The feedwater is converted to high temperature superheated steam through a series of heat exchange steps in the boiler, including the economizer, evaporator, reheater, and superheater. The superheated steam produced in the boiler is expanded in a series of high-pressure (HP), intermediate-pressure (IP) and low-pressure (LP) turbines connected to a generator to convert the heat to mechanical torque and produce electricity. The steam exiting the last LP turbine is condensed in the condenser. The condensate is preheated in four heat exchange steps, including a deaerator and three water preheaters, which are supplied with steam streams extracted from the HP, IP and LP turbines. Three pumps, namely the condensate booster pump, condensate pump and boiler feed pump, are used to re-circulate the water after being condensed in the condenser. The preheated condensate re-enters the boiler under high pressure and closes the loop.
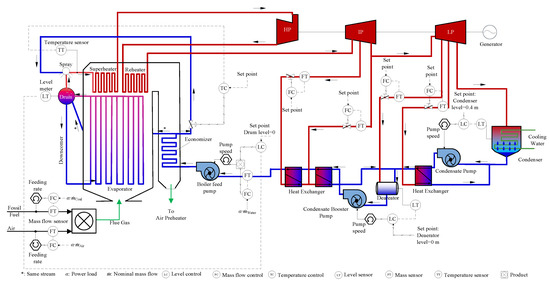
Figure 1.
Reheat regenerative cycle: 605 MW subcritical-pressure fossil power plant with a control system design [29].
The plant in Figure 1 was simulated with a dynamic power plant model developed in Dymola [16] using the Modelon ThermalPower library [31]. The Modelica language used in Dymola is a non-proprietary, object-oriented, equation-based language for the modeling of complex physical systems [20] that is well-suited for the objective of large-scale dynamic simulation of power plants. A comprehensive list of the operating data of the power plant was provided in prior work, and the plant model was provided as Supporting Information to that work [28]. The model of the plant operating at full load was shown to be in excellent agreement with steady-state data from the reference power plant. Figure 1 also shows the design of the control system of that plant, including controllers for safety regulation (marked with black solid lines), plant-level controllers (marked with blue dashed lines) and controllers for plant optimization (marked with red dotted lines). The regulatory control system, including the controllers of superheated steam temperature and of the water levels in the drum, condenser and deaerator, was discussed in detail in prior work [28]. This regulatory control system was tuned using bump tests and the dynamic responses of the model were assessed qualitatively in terms of robustness and plant stability. The multilayer control scheme designed in this work and the controllers required to meet the time-varying power load are discussed in the following text.
3. Power Plant Under Time-Varying Power Demand
Extensive studies of the power demand and its forecasting have resulted in excellent models of the power demand per market sector, such as gray-box prediction models, to forecast real-time electricity demand with an error less than 8% [32,33]. The forecasted power demand is typically used by utility companies to predict the grid load and maintain service reliability. In this work, the data of power demand (along with its forecast) in the New England area were used. In particular, the data from 17 April 2016 were used as a realistic sample of power demand fluctuations [30]. The duration for the temporal forecasted power demand studied was 24 h. To meet the full power load of the reference power plant (605 MW), the ISO New England data (maximum value is 18,000 MW) was uniformly scaled-down, as shown in Figure 2a. The underlying assumption in this normalization was that the power demand from one power plant is proportional to the total power consumed. Therefore, it was considered that a fraction of the total power demand (scaled by a constant factor) and its daily fluctuation needed to be met by one power plant. The reality with renewable inputs in the grid is, as mentioned, a more abruptly fluctuating load for the power plant. It is thus anticipated that the efficiency gains from the analysis presented herein are a lower bound to the potential efficiency gains when renewable energy becomes a more dominant contribution to the electric grid.
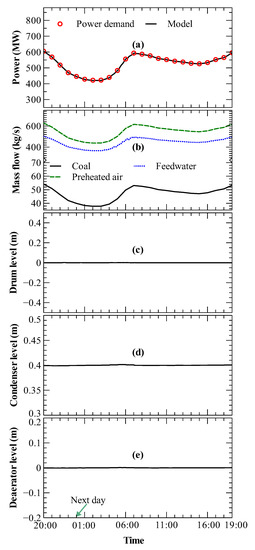
Figure 2.
Dynamic performance of the power plant model: (a) power demand and power generated by the plant model; (b) mass flow rates of coal, preheated air and feedwater; (c) water level in the drum; (d) water level in the condenser; (e) water level in the deaerator.
In prior work [28], the power plant model was validated dynamically, showing fast responses to sudden changes in coal load. The regulatory control system incorporated in the power plant model was shown to be robust in maintaining controlled variables at set points. Here, plant-level controllers were added to the plant model, as shown in Figure 1, to adjust the coal load, preheated air flow and feedwater flow so that the plant met the time-varying power load of Figure 2a. The mass flow rate of feedwater () circulating in the plant and the mass flow rate of preheated air () mixed with the fuel were assumed to be proportional to the power load [34]. The mass flow rates of feedwater and preheated air were set to adjust with the plant load, by multiplying the nominal and by the temporal power load change ratio. The mass flow rate of coal was adjusted by a PID fuel load controller to match the temporal power demand. Table 1 presents the tuning parameters of the feed-forward control of water and air feed rates and the PID controller of fuel load. The measurement for the fuel load controller was the power generation (P), the manipulated variable was the coal mass flow (), and the set point was the temporal profile of the normalized power demand of the New England area [30]. These new controllers were tuned following standard methodologies discussed elsewhere [28]. The plant time scale and response times to load changes were studied and shown to be in the order of seconds and always less than a minute. Figure 2a shows that the power generated by the plant model matched the power demand of the normalized New England area data [30]. Figure 2b shows the transient responses of , and to the dynamically varying power demands of Figure 2a. Figure 2c–e show that the safety-critical regulated variables (water levels in the drum, condenser and deaerator) were robustly controlled and exhibited negligible oscillations. The dynamic performance of the plant model over the entire 24-hour period suggests that the model provides a robust test-bed of the plant physics and its controls and thus, it was used in the following experiments for steady-state and dynamic optimization. Figure 2 also shows that power demand was rapidly and accurately matched by the feed-forward controller, as tuned with the settings of Table 1.

Table 1.
Controllers for the power plant in response to a time-varying power load *.
4. Optimization of an Integrated Power Plant
4.1. Objective and Optimization Variables
The objective of plant-level optimization is to maximize the efficiency of the power plant while operating at steady-state or to optimize the integral of the efficiency over time if the power plant is operating in a transient fashion. Another objective for plant-level optimization can be to reduce the plant’s settling time, but, as shown previously [28], the time scale of the plant studied here is small, making settling time reduction a secondary concern. This was accomplished by calculating the optimal set points for the regulatory controllers without violating the operability and safety constraints. The plant efficiency was calculated as [29]
where is the efficiency of the plant; is the mass flow rate of coal; is the lower heating value of coal; is the power generated by steam turbines; and is the power consumed by pumps. Here, high-volatile bituminous B coal with an average of 28 MJ/kg was used [5]. Other auxiliary energy losses were not not considered in Equation (1), as previous work has shown that auxiliary efficiency losses are small, often in the order of ∼2 MW for coal-fired steam cycles for plant sizes similar the one studied here [29,35]. As discussed in the introduction, the power plant efficiency of Equation (1) can be improved by manipulating several plant variables. Table 2 summarizes the optimization variables, range of variability and efficiency improvements achieved in relevant previous work. In the majority of previous analyses [13,14,15,36,37,38,39,40,41,42,43,44], plant efficiency optimization was performed by manipulating the temperature of superheated steam (). For example, Xiong et al. [41] showed that the higher superheated steam temperature increases the power generated by the HP turbine, improving cycle efficiency. Several other variables have been explored in the literature in regard to their capability to improve plant efficiency. Sanpasertparnich et al. [14,36] presented the impact of preheated air temperature () on power plant efficiency. Tzolakis et al. [15,42] optimized the plant efficiency at full load, by manipulating the mass flow extracted from steam turbines (, which included , and ). Other optimization variables, such as the moisture content of coal [45], the mass flow rate of feedwater [42], the isentropic efficiency of turbines [41], the temperature of flue gas exiting the boiler [43], and the pressure of steam extracted from turbines [14,36] require changes in the existing infrastructure and were not considered here. In summary, the common plant efficiency optimization variables , , and were chosen in this work. For the purpose of illustration, two optimization cases were considered. Case Study I presents plant optimization by manipulating and within an operation horizon of 24 h. Case Study II presents plant optimization by manipulating with an operation horizon of 4 h. This separation of optimization variables was done to allow for easy comparison with the trends reported in the literature and presented in Table 2. The results of each optimization problem are discussed in detail in the following section.

Table 2.
Review of power plant optimization efforts and respective variables *.
4.2. Supervisory Control
The control system of a plant is usually divided into several layers, typically separated by different time scale requirements and objectives. The control architecture includes regulatory control (seconds), supervisory control (minutes), local optimization (hours), site-wide optimization (days) and scheduling (weeks) [22]. Supervisory control can be designed to manipulate regulatory control set points and the remaining degrees of freedom of the plant (if any) to optimize the plant’s efficiency within constraints imposed by the local controllers [46]. The critical first steps in designing a supervisor logic are to define the operational and economic objectives and the available degrees of freedom. Common degrees of freedom include the set points of the regulatory controllers, uncontrolled system boundaries and system parameters tuned to a particular operating scheme.
Figure 3 illustrates a scheme for such a supervisory control strategy for the power plant studied. The control system includes the supervisory control, regulatory control and plant level control. The regulatory control structure includes optimization controllers (marked as red dotted lines in Figure 1), which are the regulatory controllers used for plant optimization and safety controllers (marked as black solid lines in Figure 1), which regulate the level of water in the drum, condenser and deaerator. The main function of the supervisory control is to update the set points of the optimization controllers () to maximize the plant’s efficiency as shown by Equation (1). The plant level controllers (marked with blue dashed lines in Figure 1) adjust the mass flow rates of coal, preheated air and feedwater according to the market power demand (). The set points of the control system include the set points of the safety controllers, plant-level controllers and optimization controllers, i.e., . These controllers manipulate the control inputs () to maintain the controlled variables at their set points. In principle, one should consider the disturbance () and measurement noise (), which are responsible for a difference () between the model () and power plant outputs (). An estimator could update the model’s parameters () and filter plant states () to eliminate this model-plant mismatch. In this work, disturbance and measurement noise were not considered, mostly to simplify the analysis, as the efficiency benefits are not affected by them (although the robustness of the supervisor will be). Therefore, and were considered negligible, and data filtering and state estimation (blocks in gray in Figure 3) are not discussed. The supervisory control updates the optimal according to an objective function maximizing Equation (1) in a formulation that includes the system model equations as discussed in the following text.
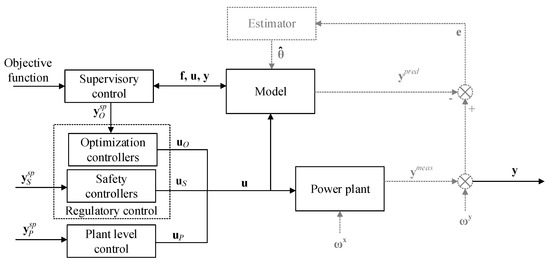
Figure 3.
Multilayer control scheme for the reheat regenerative cycle of a 605 MW subcritical-pressure coal-fired power plant. : set points of the optimization controllers; : set points of the safety controllers; : set points of the plant level controllers; : control input of the optimization controllers; : control input of the safety controllers; : control input of the plant level controllers; : control input; : disturbance; : measurement noise; : predicted outputs; : measured outputs; : system outputs; : error; : estimated model parameters; : system model.
4.3. Optimization Formulation
As described previously, the set points of the optimization controllers are manipulated by the supervisory layer as first-level variables to improve the plant’s efficiency (), Equation (1). This efficiency optimization also translates to coal consumption reduction and decrease of the plant carbon footprint. The intent of this work was to compare the steady-state and dynamic optimization results of the plant shown in Figure 2 to those of the plant operating under nominal conditions. This comparison also included an exploration of the added benefits of dynamic optimization, compared to those from steady-state optimal operation. First, steady-state optimization of the power plant operating at a full load of 605 MW was performed by calculating the optimal set points (constant with time) for the optimization controllers () and specifically, the set points of the superheat steam temperature controller, preheated air temperature controller and mass flow controllers of steam extracted from the steam turbines. The steady-state optimization problem formulation is shown in Equation (2):
where the plant efficiency is a function of power plant outputs () and admissible variable values () determined by the updated optimization controller set points ; is the vector of steady-state equations describing the system in terms of states, , admissible inputs, , and parameters, ; and describes the controller functions at steady-state to account for controller offset with being the measured system outputs, mapped to , , and through . All variables including unmeasured variables are constrained so that they do not violate plant safety and operability constraints.
Dynamic optimization was performed for the reference power plant operating under time- varying power demand normalized from the New England area data [30]. The objective was to maximize the integral of plant efficiency over a predetermined time horizon, . This was accomplished by calculating time-varying optimal set points for the optimization controllers. The generic formulation of the dynamic optimization problem solved for the power plant of Figure 1 is presented in Equation (3), where is the system of differential algebraic equations describing the conservation of mass and energy; is the vector of temporal state variables; is the vector of initial state variables; is the temporal set points of the optimization controllers; are the temporal system’s outputs; is the vector of control action time points with a constant interval, ; is the optimization horizon; and t is the time.
Table 3 shows the optimization variables’ bounds and time interval constraints for the problems of Equations (2) and (3) for the two cases studied. The set points of the controllers regulating , and (including , , and ) were manipulated by the supervisory control layer as degrees of freedom to seek an optimal input. In Case Study I, only the set points of and were manipulated. Although not shown in Figure 2, preheating of the air fed to the combustor to was accomplished by manipulating the mass flow of the economizer exhaust gas sent to the air preheater (with the balance being waste heat). In Case Study II, plant optimization was performed by manipulating the set points of , i.e., the set points of the mass flow rates of steam streams extracted from the first IP turbine (IP1), the second IP turbine (IP2), the first LP turbine (LP1), and the second LP turbine (LP2) (, , , and , respectively). The ranges of the admissible inputs, shown in Table 3, were based on common practice and previous work [13,14,15,27,36,38,41,42,43,45]. The optimization horizon, , was set to 24 h in Case Study I and 4 h in Case Study II, and the control action interval, , was set to 1 h. Large control actions were not penalized in the solved optimization problems, as the plant load profiles matched during the real-time plant optimization were relatively smooth. For instance, the temperature of the superheated steam feeding the steam turbine was seen to change gradually over time in response to load changes which is adequate for the protection of the steam turbines by thermal stress [14,36].

Table 3.
Inputs for the studied optimization problems.
5. Results
For each case study, the static optimization of the power plant operating at full load with the optimization formulation of Equation (2) is discussed first, followed by the dynamic optimization of the power plant operating under a time-varying power load with the optimization formulation of Equation (3). For the results discussed in the following text, the power plant was formulated with the object-oriented language Modelica [20], in the commercial software Dymola [16], and set point optimization was performed in Matlab [47] using an interior-point algorithm. The model developed in Dymola was flattened (from its object-oriented structure) and translated to a Functional Mockup Unit (FMU) file which includes all the variables and equations of the original plant model. Model exchange between the software packages of Dymola and Matlab was accomplished with use of the Functional Mockup Interface, a tool-independent standard for seamlessly integrating models in various simulation environments [48]. The Functional Mock-up Interface (FMI) enables model exchange of dynamic models in the form of xml-files and compiled C-code.
5.1. Case Study I: Optimization Variables and
Table 4 presents the steady-state optimization results at full load using the superheated steam temperature set point, , and that of the preheat air temperature, , as the optimization variables. The manipulation of and led to a power plant efficiency improvement from 38.3% to 40.23%. This efficiency improvement translates to a fuel saving of 3.78%, with the fuel flow rate decreasing from 56.38 kg/s to 54.25 kg/s. The carbon footprint of the plant also decreased from 0.8 kg/kWh to 0.77 kg/kWh. This efficiency optimization was accomplished by increasing from 200 C to 248 C, and increasing from 538 C to 560 C. This is consistent with earlier reports [13,14,27,38,41,42,43], showing that increasing and translates to efficiency improvements. The higher enabled the HP turbine to produce the same mechanical torque at a lower rate of coal consumption, while increasing recovered more waste heat from the boiler exhaust gas. It should be noted that the nominal steady-state data used as baseline in Table 4 were as reported by Singer [29] for the reference power plant and corresponded to the design point of this plant. In principle, the set points for and reported by Singer refer to an optimal plant configuration. The further improvement presented here could relate to better integrated plant-level optimization, model-plant differences and relaxation of plant constraints compared to the study reported in [29]. For an off-design operating point, the efficiency benefits of solving Equation (2) would, of course, have been much higher.

Table 4.
Steady-state optimization results of Case Study I.
The results of dynamic optimization for a horizon of 24 h of plant operation are presented in Figure 4. The data and plant performance results represent the response to the time-varying power demand normalized from the New England area data [30] shown in Figure 4a. In the absence of disturbances and noise, the solution to Equation (3) in the period 24 h) is equivalent to an off-line optimal control problem and is valid for the entirety of the time horizon considered. The optimization variables were and , but, in this case, they were updated in time intervals, h. Figure 4 presents the dynamic power plant performance under nominal and optimal operation conditions. The nominal dynamic operation is the result of constant at 538 C and at 200 C. Figure 4d,e shows that the controlled variables, and , were robustly controlled at their optimal set points by the regulatory controller. The values of and from the dynamic optimization solution were always higher than their respective nominal values. In particular, Figure 4d shows that the optimal trajectory was inversely proportional to that of the plant load. The optimal temporal, , for a plant load higher than maximum, was higher than the 560 C of the optimal steady-state at full load. This enhanced heat transfer from the flue gas side to the steam side in the superheater under low plant loads. Figure 4e shows that the optimal temporal profile of the temperature of air preheated by the flue gas exiting the boiler varyied proportionally to the plant load. The temperature of the exhaust gas was also proportional to the power load due to the time-varying mass flow rates of the feedwater, air and coal load. As Figure 4c shows, the improvement in time-averaged efficiency was 1.8% points. This efficiency improvement translates to a coal saving of 184.8 tons/day (Figure 4d) and time-averaged carbon footprint decrease of 0.0351 kg/kWh (Figure 4e). In summary, the optimized power plant can operate at a higher and , and this is consistent with the results of steady-state optimization.
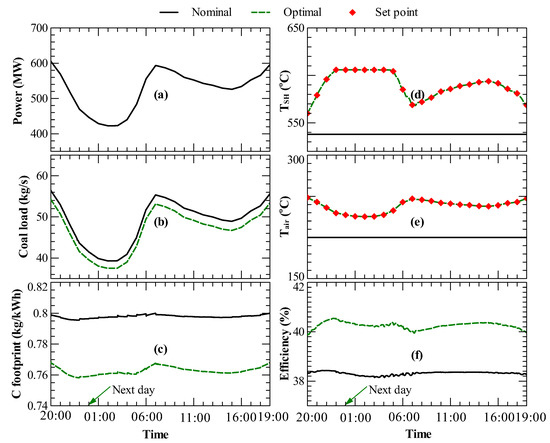
Figure 4.
Dynamic optimization results of Case Study I: (a) time-varying power load; (b) coal load; (c) carbon footprint; (d) temperature of preheated air; (e) temperature of superheated steam; (f) power plant efficiency.
Figure 5 presents the dynamic performance of the power plant operating with constant nominal set points for and , constant optimal and (from the steady-state optimization solution), and with time-varying optimal and (set by the dynamic optimization solution). The coal consumption and carbon footprint of the power plant operating with set points calculated by the static and dynamic optimization problem formulations were both lower those for the power plant under nominal operation conditions. The power plant operating with set points determined by dynamic optimization was the most efficient with the lowest coal consumption and the smallest carbon footprint. As shown in Table 5, the fuel saving accomplished by the power plant with steady-state optimization was 160.9 tons/day, whereas the fuel saving accomplished with dynamic set point optimization was 184.8 tons/day. The reduction in coal load and decrease in the carbon footprint of the dynamically optimal operation were pronounced when the power plant was operating at lower loads. At different loads, the plant had slightly different optimal regulatory control points compared to those of the steady-state optimization at full load, which are exploited by the formulation of Equation (3). As shown in Figure 4d, the values of calculated from Equation (3) at low loads were higher than the constant calculated from Equation (2) at full load. Dynamically optimizing improved the heat transfer in the superheater at low loads and converted more heat from the superheated steam to mechanical torque. This increase in mechanical torque led to improved power generation and efficiency. Moreover, the temperature profile of the preheated air in Figure 4e shows that the values of calculated from Equation (3) at low loads were lower than the constant calculated from Equation (2) at full load. At low loads, heat transfer between the water side and flue gas side in the boiler is enhanced, leading to a lower flue gas temperature, which, in turn, is used to preheat the air. Thus, the supervisor drives down to satisfy system constraints. Depending on the dynamic response times of the plant and the selection of the interval between control actions, , a multistep steady-state optimization problem could result in similar performance benefits to those of Equation (3). Nonetheless, Equation (3) is more generic and robust for use with a dynamic system. It should be noted that one could execute the same analysis but with an objective function that maximizes the profit for varying electricity prices. This would result in different plant load profiles, but the optimization procedure (not the objective function) and results would be similar.
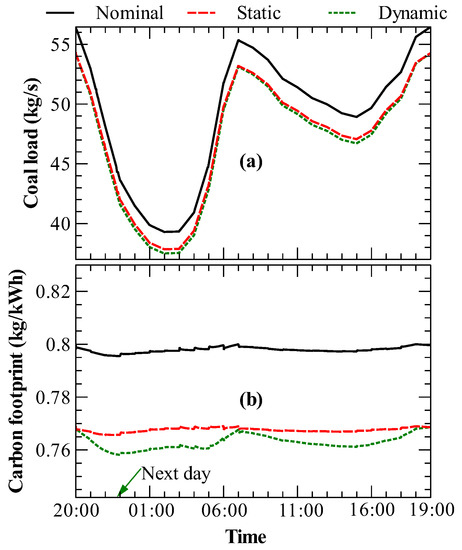
Figure 5.
Comparison of the dynamic performance of the power plant with nominal operation set points, steady-state optimal set points, and dynamic optimal set points: (a) coal load; (b) carbon footprint.

Table 5.
Comparison of static and dynamic optimization of the power plant for Case Study I *.
5.2. Case Study II: Optimization Variables , , and
As shown in Figure 1, four proportional–integral (PI) controllers were used to regulate the mass flow rates of steam extracted from the turbines. The parameters of these controllers are presented in Table 6. These controllers manipulate the respective valves to regulate the mass flow rates of streams extracted from the IP1, IP2, LP1 and LP2 turbines. In this case study, the supervisory control variables were the set points of the mass flow controllers of steam extracted from turbines, namely the set points of , , , and .

Table 6.
Proportional–integral (PI) controllers regulating the mass flow rates of steam extracted from turbines.
As before, steady-state optimization was first performed for the plant operating at full load. The set points of , , and were manipulated by the supervisory control layer to maximize the plant’s efficiency, as shown by Equation (2). The bounds of admissible inputs are shown in Table 3, with the optimal values presented in Table 7. The power plant efficiency was improved from 38.3% to 38.78%. The corresponding coal load decreased from 56.38 kg/s to 55.68 kg/s, and the carbon footprint decreased from 0.8 kg/kWh to 0.79 kg/kWh. Compared with the nominal case, the optimal case had a lower and higher , and , as shown in Table 7. The mass flow rate of steam extracted from the IP1 turbine was less than that of other steam turbine extractions. The IP1 turbine extraction had the highest pressure and temperature of all steam extractions. Thus, it would be better utilized for electricity production than water preheating. Meanwhile, the steam extracted from the IP2, LP1 and LP2 turbines would be better utilized for preheating the condensed feedwater to reach a higher temperature before entering the boiler. These results are consistent with the findings of the study by Chaibakhsh and Ghaffari [49] who proposed reducing (or removing) the high pressure and temperature steam extraction stream and increasing the steam extracted from the remaining IP and LP turbine stages.

Table 7.
Steady-state optimization results for Case Study II.
Dynamic optimization was performed for an optimization horizon of 4 h. The time period from 5 a.m. to 9 a.m. was used for the New England power demand data, as shown in Figure 6a. In this interval, the power plant iwa operating in response to a abrupt increase in power demand, with a power load change from 79.9% to 98.1%, followed by a decrease from 98.1% to 95.2%. This time interval includes the most abrupt change in power demand of the New England ISO data used as well as a change in the sign of change in power demand. To solve this problem, the power plant model was first initialized to steady-state at a load of 79.9% ( in Figure 6). As shown in Figure 6a, the power generated by the plant model matched the time-varying power demand which was accomplished by the plant load controllers shown in Figure 1.
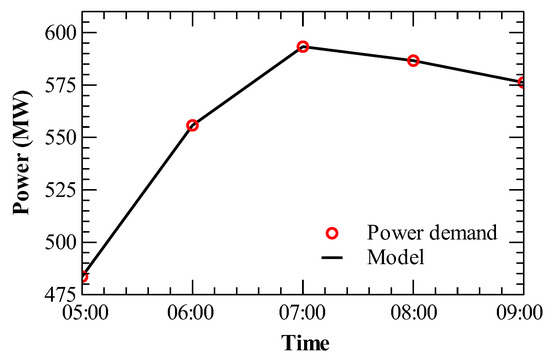
Figure 6.
Time-varying power demand and plant load for Case Study II.
Figure 7 presents the transient operation of the virtual power plant in response to nominal inputs and to those calculated with dynamic optimization for the power plant load of Figure 6. The supervisor updated the set points of the controllers regulating , , and to seek the maximum integral of efficiency over a time horizon of 4 h. The nominal operation of the power plant corresponds to constant set points for the mass flow rate of turbine extraction streams, shown in Table 7. For the optimal dynamic operation, these set points were treated as dynamic optimization variables that were updated every hour by the supervisory controller. Figure 7a shows that the mass flow rate of the steam streams extracted from the turbines was robustly maintained at the respective temporal set points (updated in 1 h intervals), set according to the dynamic optimization solution of the supervisor. Dynamic optimization requires the mass flow rate of IP1 steam extraction to be lower than that of the other steam extractions, similarly to the results for steady-state optimization. The optimal mass flow rates of all the steam extraction streams followed the load profile. This is because the total mass flow rate of water circulating in the steam cycle is proportional to the power load. The improvement in the time-averaged efficiency was 0.43% points, as shown in Figure 7b–d, which shows that the coal saving for four hours and the decrease in the time-averaged carbon footprint were 7.72 tons and 0.00859 kg/kWh, respectively. These benefits became more profound at higher plant loads which is in accordance with the relative contribution of the steam side of the plant to the overall power production.
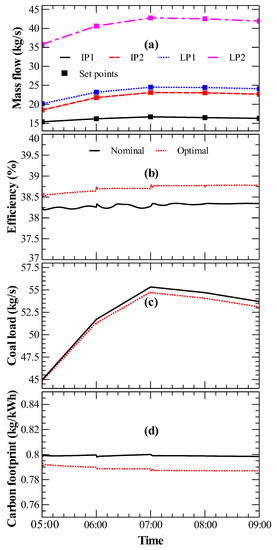
Figure 7.
Dynamic optimization results of Case Study II: (a) dynamic measurements and set points of mass flow rates of steam extracted from turbines; (b) coal load; (c) efficiency; (d) carbon footprint.
6. Conclusions
A dynamic power plant model was used as a test-bed for dynamic simulation and optimization in response to a variable plant load. Plant-level controllers were added to the plant model to meet the transient market power demand. Thereafter, optimization problems were formulated and solved with the objective of optimizing power plant efficiency at steady-state and dynamically. A supervisory control architecture was designed to manipulate the set points of regulatory controllers according to the solution of the optimization problems explored. The optimization variables and , and , chosen in this work after a comprehensive literature review, enabled an improvement in time-averaged efficiency of up to 1.95% points with corresponding savings in coal consumption of 184.7 tons/day and a carbon footprint decrease of 0.0352 kg/kWh. A comparison of the static and dynamic optimization formulations serving the supervisory controller showed that dynamic optimization offers higher time-averaged efficiency, fuel savings and CO reduction. Although the power plant model and regulatory control architecture have been validated in previous work [28], validation against transient power plant data would benefit this work in terms of the validity and accuracy of the estimated efficiency benefits.
Author Contributions
Conceptualization, G.M.B. and C.C.; Methodology, G.M.B.; Software, C.C.; Validation, C.C.; Investigation, C.C.; Resources, G.M.B.; Writing—Original Draft Preparation, C.C.; Writing—Review & Editing, G.M.B.; Visualization, C.C.; Supervision, G.M.B.; Project Administration, G.M.B; Funding Acquisition, G.M.B.
Funding
This material is based upon work supported by the National Science Foundation under Grant No. 1054718.
Acknowledgments
Chen Chen gratefully acknowledges support by the GE Graduate Fellowship for Innovation and helpful advice and guidance from Alstom Power. This work was partially sponsored by the United Technologies Corporation Institute for Advanced Systems Engineering (UTC-IASE) of the University of Connecticut. Any opinions expressed herein are those of the authors and do not represent those of the sponsor.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Han, L.; Bollas, G.M. Chemical-looping combustion in a reverse-flow fixed bed reactor. Energy 2016, 102, 669–681. [Google Scholar] [CrossRef]
- Han, L.; Bollas, G.M. Dynamic optimization of fixed bed chemical-looping combustion processes. Energy 2016, 112, 1107–1119. [Google Scholar] [CrossRef]
- Ibrahim, T.K.; Mohammed, M.K.; Awad, O.I.; Rahman, M.; Najafi, G.; Basrawi, F.; Abd Alla, A.N.; Mamat, R. The optimum performance of the combined cycle power plant: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 459–474. [Google Scholar] [CrossRef]
- Viswanathan, R.; Henry, J.; Tanzosh, J.; Stanko, G.; Shingledecker, J.; Vitalis, B.; Purgert, R. U.S. Program on Materials Technology for Ultra-Supercritical Coal Power Plants. J. Mater. Eng. Perform. 2005, 14, 281–292. [Google Scholar] [CrossRef]
- Hasler, D.; Rosenquist, W.; Gaikwad, R. New coal-fired power plant performance and cost estimates. In Sargent and Lundy Project; Environmental Protection Agency: Washington, DC, USA, 2009; pp. 1–82. [Google Scholar]
- Cziesla, F. Lünen—State-of-theArt Ultra Supercritical Steam Power Plant Under Construction Andreas Senzel. In Proceedings of the Power Generation Europe 2009, Cologne, Germany, 26–29 May 2009; pp. 1–21. [Google Scholar]
- U.S. Energy Information Administration. Energy Information Administration: Annual Energy Outlook 2018; U.S. Energy Information Administration: Washington, DC, USA, 2018.
- Masters, G.M. Renewable and Efficient Electric Power Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; p. 712. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R. Oscillatory stability analysis with high penetrations of large-scale photovoltaic generation. Energy Convers. Manag. 2013, 65, 420–429. [Google Scholar] [CrossRef]
- Edmunds, R.; Davies, L.; Deane, P.; Pourkashanian, M. Thermal power plant operating regimes in future British power systems with increasing variable renewable penetration. Energy Convers. Manag. 2015, 105, 977–985. [Google Scholar] [CrossRef]
- Critz, D.K.; Busche, S.; Connors, S. Power systems balancing with high penetration renewables: The potential of demand response in Hawaii. Energy Convers. Manag. 2013, 76, 609–619. [Google Scholar] [CrossRef]
- Eser, P.; Singh, A.; Chokani, N.; Abhari, R.S. Effect of increased renewables generation on operation of thermal power plants. Appl. Energy 2016, 164, 723–732. [Google Scholar] [CrossRef]
- Fu, C.; Anantharaman, R.; Jordal, K.; Gundersen, T. Thermal efficiency of coal-fired power plants: From theoretical to practical assessments. Energy Convers. Manag. 2015, 105, 530–544. [Google Scholar] [CrossRef]
- Sanpasertparnich, T.; Aroonwilas, A. Simulation and optimization of coal-fired power plants. Energy Procedia 2009, 1, 3851–3858. [Google Scholar] [CrossRef]
- Tzolakis, G.; Papanikolaou, P.; Kolokotronis, D.; Samaras, N.; Tourlidakis, A.; Tomboulides, A. Simulation of a coal-fired power plant using mathematical programming algorithms in order to optimize its efficiency. Appl. Therm. Eng. 2012, 48, 256–267. [Google Scholar] [CrossRef]
- Elmqvist, H.; Brück, D.; Otter, M. Dymola User’s Manual; Dynasim AB: Lund, Sweden, 1996. [Google Scholar]
- Process Systems Enterprise. gPROMS Advanced User Guide; Process Systems Enterprise Limited: London, UK, 2004. [Google Scholar]
- Chen, C.; Han, L.; Bollas, G.M. Dynamic Simulation of Fixed-Bed Chemical-Looping Combustion Reactors Integrated in Combined Cycle Power Plants. Energy Technol. 2016, 4, 1209–1220. [Google Scholar] [CrossRef]
- Franke, R.; Babji, B.; Antoine, M.; Isaksson, A. Model-based online applications in the ABB Dynamic Optimization framework. In Proceedings of the 6th International Modelica Conference, Bielefeld, Germany, 3–4 March 2008; pp. 279–285. [Google Scholar]
- Modelica Association. Modelica—A Unified Object-Oriented Language for Physical Systems Modeling. In Proceedings of the 12th European Conference on Object-Oriented Programming, Brussels, Belgium, 20–24 July 2010. [Google Scholar]
- Lind, A.; Sällberga, E.; Velutb, S. Start-up Optimization of a Combined Cycle Power Plant. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012. [Google Scholar]
- Skogestad, S. Control structure design for complete chemical plants. Comput. Chem. Eng. 2004, 28, 219–234. [Google Scholar] [CrossRef]
- Lestage, R.; Pomerleau, A.; Hodouin, D. Constrained real-time optimization of a grinding circuit using steady-state linear programming supervisory control. Powder Technol. 2002, 124, 254–263. [Google Scholar] [CrossRef]
- Baillie, B.P.; Bollas, G.M. Development, Validation, and Assessment of a High Fidelity Chilled Water Plant Model. Appl. Therm. Eng. 2017, 111, 477–488. [Google Scholar] [CrossRef]
- Mittal, K.; Wilson, J.; Baillie, B.; Gupta, S.; Bollas, G.; Luh, P.B. Supervisory Control for Resilient Chiller Plants under Condenser Fouling. IEEE Access 2017, 5, 14028–14046. [Google Scholar] [CrossRef]
- Sáez, D.; Ordys, A.; Grimble, M. Design of a supervisory predictive controller and its application to thermal power plants. Optim. Control Appl. Methods 2005, 26, 169–198. [Google Scholar] [CrossRef]
- Ponce, C.V.; Sáez, D.; Bordons, C.; Núñez, A. Dynamic simulator and model predictive control of an integrated solar combined cycle plant. Energy 2016, 109, 974–986. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Z.; Bollas, G.M. Dynamic modeling, simulation and optimization of a subcritical steam power plant. Part I: Plant model and regulatory control. Energy Convers. Manag. 2017, 145, 324–334. [Google Scholar] [CrossRef]
- Joseph, G.; Singer, P. (Eds.) Combustion Fossil Power: A Reference Book on Fuel Burning and Steam Generation, 4th ed.; Combustion Engineering: New York, NY, USA, 1991. [Google Scholar]
- ISO New England. Real-Time Maps and Charts; ISO New England: Holyoke, MA, USA, 2016. [Google Scholar]
- Casella, F.; Leva, A. Modelica open library for power plant simulation: Design and experimental validation. In Proceedings of the 2003 Modelica Conference, Linkoping, Sweden, 3–4 November 2003. [Google Scholar]
- Hsu, C.; Chen, C. Applications of improved grey prediction model for power demand forecasting. Energy Convers. Manag. 2003, 44, 2241–2249. [Google Scholar] [CrossRef]
- Akay, D.; Atak, M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy 2007, 32, 1670–1675. [Google Scholar] [CrossRef]
- Starkloff, R.; Alobaid, F.; Karner, K.; Epple, B.; Schmitz, M.; Boehm, F. Development and validation of a dynamic simulation model for a large coal-fired power plant. Appl. Therm. Eng. 2015, 91, 496–506. [Google Scholar] [CrossRef]
- ABB and Rocky Mountain Institute. ABB Energy Efficiency Handbook: Power Generation—Energy Efficient Design of Auxiliary Systems in Fossil-Fuel Power Plants; Technical Report; ABB and Rocky Mountain Institute: Basalt, CO, USA, 2009. [Google Scholar]
- Sanpasertparnich, T.; Aroonwilas, A.; Veawab, A. Improved Thermal Efficiency of Coal-Fired Power Station: Monte Carlo Simulation. In Proceedings of the 2006 IEEE EIC Climate Change Conference, Ottawa, ON, Canada, 10–12 May 2006; pp. 1–9. [Google Scholar] [CrossRef]
- Lizon-A-Lugrin, L.; Teyssedou, A.; Pioro, I. Appropriate thermodynamic cycles to be used in future pressure-channel supercritical water-cooled nuclear power plants. Nucl. Eng. Des. 2012, 246, 2–11. [Google Scholar] [CrossRef]
- Suresh, M.V.J.J.; Reddy, K.S.; Kolar, A.K. Thermodynamic Optimization of Advanced Steam Power Plants Retrofitted for Oxy-Coal Combustion. J. Eng. Gas Turbines Power 2011, 133, 063001. [Google Scholar] [CrossRef]
- Suresh, M.; Reddy, K.; Kolar, A.K. ANN-GA based optimization of a high ash coal-fired supercritical power plant. Appl. Energy 2011, 88, 4867–4873. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Dong, C.; Morosuk, T.; Tsatsaronis, G. Multi-objective optimization of coal-fired power plants using differential evolution. Appl. Energy 2014, 115, 254–264. [Google Scholar] [CrossRef]
- Xiong, J.; Zhao, H.; Zhang, C.; Zheng, C.; Luh, P.B. Thermoeconomic operation optimization of a coal-fired power plant. Energy 2012, 42, 486–496. [Google Scholar] [CrossRef]
- Koch, C.; Cziesla, F.; Tsatsaronis, G. Optimization of combined cycle power plants using evolutionary algorithms. Chem. Eng. Process 2007, 46, 1151–1159. [Google Scholar] [CrossRef]
- Espatolero, S.; Cortés, C.; Romeo, L.M. Optimization of boiler cold-end and integration with the steam cycle in supercritical units. Appl. Energy 2010, 87, 1651–1660. [Google Scholar] [CrossRef]
- Regulagadda, P.; Dincer, I.; Naterer, G.F. Exergy analysis of a thermal power plant with measured boiler and turbine losses. Appl. Therm. Eng. 2010, 30, 970–976. [Google Scholar] [CrossRef]
- Kakaras, E.; Ahladas, P.; Syrmopoulos, S. Computer simulation studies for the integration of an external dryer into a Greek lignite-fired power plant. Fuel 2002, 81, 583–593. [Google Scholar] [CrossRef]
- Tatjewski, P. Advanced Control of Industrial Processes; Advances in Industrial Control Series; Springer: London, UK, 2007. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB; MathWorks: Natick, MA, USA, 2013. [Google Scholar]
- MODELISAR Consortium. Functional Mock-up Interface for Model Exchange; Version 1.0; MODELISAR Consortium: Linköping, Sweden, 2010. [Google Scholar]
- Chaibakhsh, A.; Ghaffari, A. Steam turbine model. Simul. Model. Pract. Theory 2008, 16, 1145–1162. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).