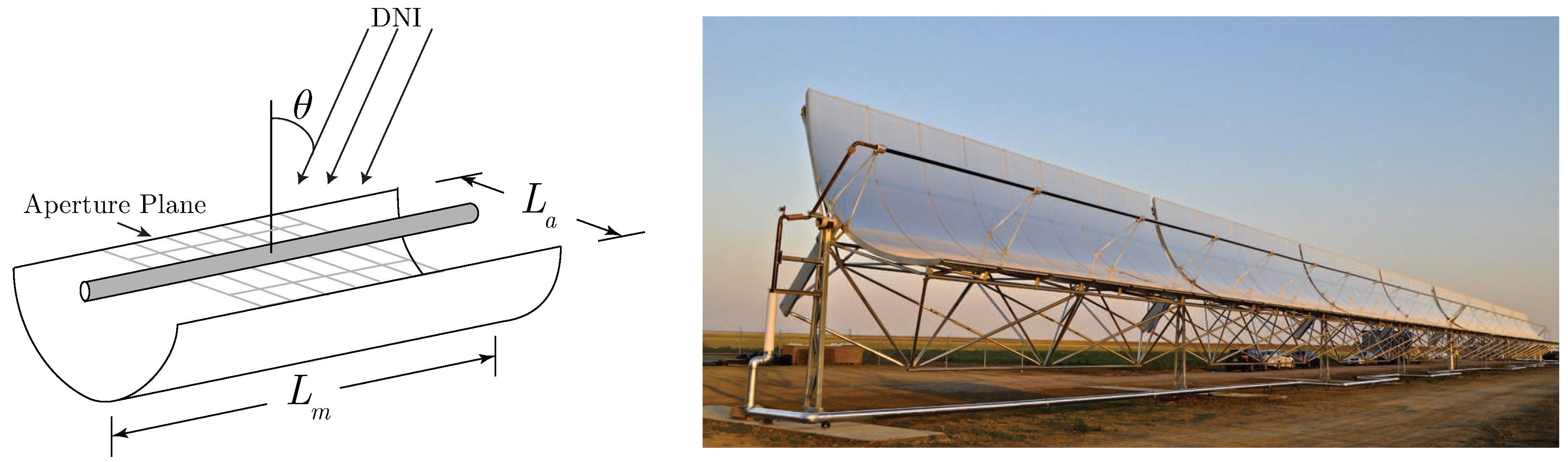
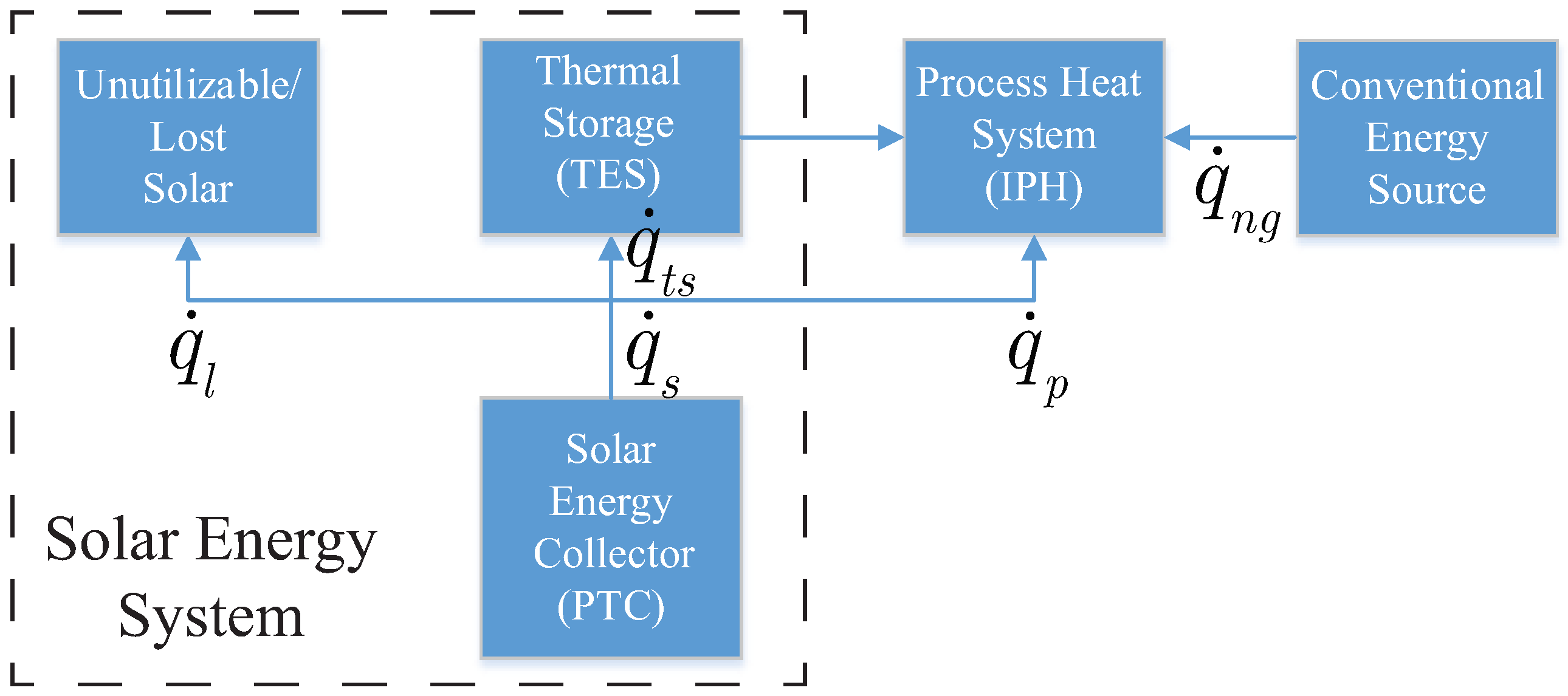
2.2. Process System Model
The process system of interest is represented by the block-flow diagram in
Figure 2. Physically, the system consists of the solar energy collector as the source of solar thermal energy for the system, the TES, the IPH system which exists as an energy demand, and the conventional (fossil) energy source for times of inadequate solar energy.
The process system model is developed from a high-level with the following simplifying assumptions:
Heat losses to the environment from piping and heat exchangers is negligible.
Heat losses to the environment from the TES is negligible.
The process system requires low to medium temperature IPH (i.e., ≤250 C).
Heat is always available at or above the minimum temperature as required by the IPH system.
The IPH system energy demand is not dependent on the state or design decisions of the solar energy system.
Under these assumptions, the process system model is developed from the overall energy balance on the entire system:
where
is the instantaneous thermal power provided by the solar system,
is the instantaneous thermal power provided by the conventional fossil-fuel (e.g., natural gas) heating system,
is the instantaneous thermal power demand by the industrial process (IPH),
is the instantaneous power supply/demand of the solar thermal energy storage system, and
is the lost solar thermal power due to meeting the IPH requirements and reaching the maximum thermal storage capacity (i.e., the unutilizable solar energy). Note that
can be both positive (charging state) and negative (discharging state).
The complicating details for accounting for energy in the system comes from the capacity limitations of the TES. For example, without TES, the solar array will simply deliver all its energy to the IPH system until the full power demand is met. At which point, the solar array will simply de-focus, or we account for the positive difference between the supply and demand as losses or unutilizable solar . The negative difference between the supply and demand is simply accounted for by the conventional heating system . However, with the existence of a TES device, the positive difference between solar thermal power supply and IPH demand can be stored and used in future times when the solar system alone cannot meet the IPH demand. This complicates the model since we assert a preference for solar energy over conventional energy sources, and hence must account for the finite capacity of the storage device and its stored capacity at each instant in time.
Rearranging Equation (
4) to focus on the storage device, we get:
where we have introduced
for ancillary energy accounting. Physically, this quantity is used for load balancing control (i.e., balancing energy supply and demand). Equivalently, we write:
assuming the TES device is empty at the start of the simulation. Applying the explicit Euler integration scheme with
as the discrete time step-size (1 h for standard solar data), we can write:
Next, we develop the model to account for the finite capacity of the TES device. Since we know that the energy capacity of the TES device at any instant can only take values between zero and the maximum capacity, we write:
where
is the storage capacity variable scaled in hours of peak process demand
, determined by the process operations schedule model (known a priori). The inner max binary operation accounts for the condition that if there was excess energy available from the combined solar array and TES at the previous time, then we should consider storing it for future use. The outer min binary operation accounts for the condition that, if we are considering storing energy, we can only store at or below the maximum TES capacity. Equivalently, we can write
where the mid operator selects the median value of the three arguments. Combining Equations (
5)–(
7), the overall energy balance becomes:
From this model, there are three possible states from the load-balancing perspective at each discrete time point i:
The PTC is not providing enough energy to meet the demand of the process (TES moves into the discharging state) and there is not enough energy in the TES to meet the demand of the process over this time step. In this case, conventional energy must be supplied to the process to meet the full demand of the process.
The PTC is providing enough energy to meet the demand of the process (TES moves into the charging state) and there is not enough available capacity to store all excess energy in the TES device. In this case, the excess energy must be rejected.
The TES is either in the discharging state with enough stored energy to meet the full demand, or it is in the charging state and has enough available capacity to store the solar energy in excess of the process demand.
With these relationships, we can write:
so that
and
are accurately accounted for. At any given discrete time point, we have the following relationship for load balancing:
Note that losses are accounted for here as simply the unutilizable solar power at any given time step and do not account for standard thermal losses to the environment which occur in thermal systems. As stated previously, heat losses for the TES are expected to be minimal over the timescale of charging/discharging cycles. This is valid for well-insulated systems that undergo complete or nearly-complete discharge over the course of the day. For systems that have long-term (i.e., many days or months) storage, this assumption will not be valid. Further, TES systems to be installed outdoors and above-ground may need special consideration of ambient environmental/weather conditions as large temperature swings and high winds may invalidate this assumption as significant heat transfer with the environment may occur. In all cases, some heat losses are expected during the course of operation of the physical systems which will result in an under-sized design proportional to the actual heat losses, under these assumptions.
Additionally, heat losses from piping and heat exchangers are expected to be minimal. Similarly, these assumptions are valid for well-insulated systems. To account for any of these losses, the design engineer may apply higher-fidelity models that take into account operating temperatures, heat exchanger designs, and overall heat transfer coefficients for the system(s) of concern. However, doing so at this stage significantly complicates the model from an optimization perspective and negatively impacts computational tractability. Alternatively, high-fidelity modeling may be used to estimate average losses for a particular geographic region and IPH temperature requirements. These losses can then be accounted for as an overall thermal efficiency and used to adjust the IPH demand accordingly, similar to the factor
in the optical efficiency model for the CST array in Equation (
1). Finally, to assess the performance of a CST system with respect to its ability to augment the use of conventional energy sources for IPH, we define the annual average solar fraction:
In terms of the discrete values calculated from Equation (
8) and the identities in Equation (
9), the solar fraction can be approximated numerically using:
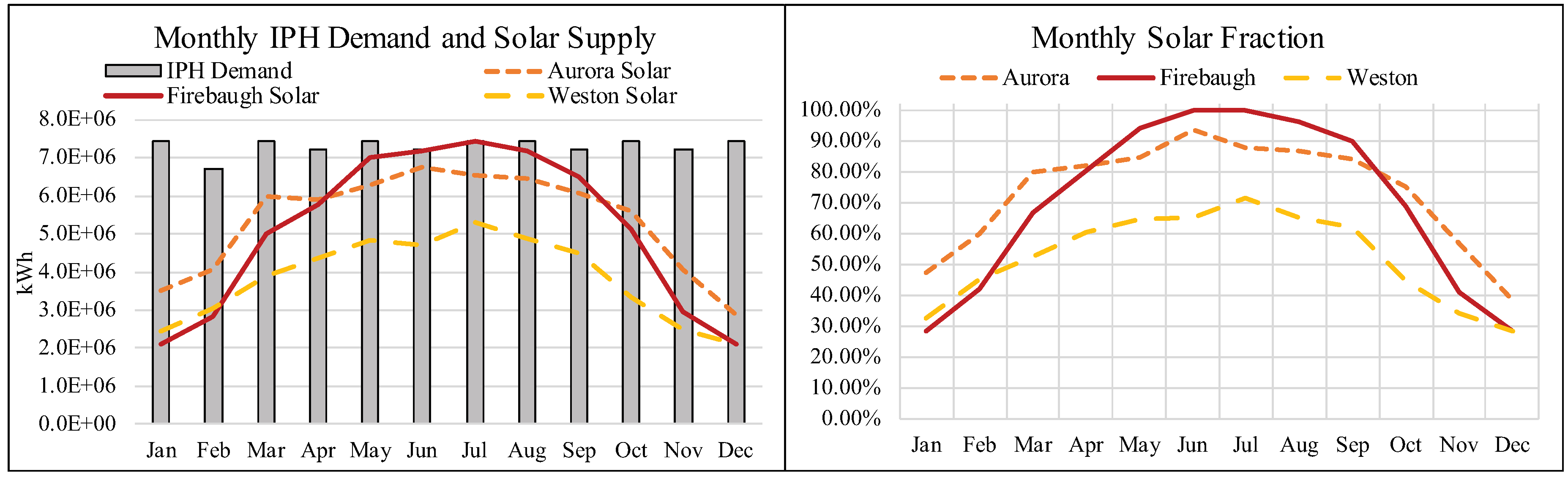
which represents the fraction of total energy consumed by the process that is supplied by the solar system over the entire time interval of interest (e.g., a TMY).
Lastly, although it was assumed that
is not a function of the state or design decisions of the solar energy system, it need not be constant. For the purposes of studying the effects of transient load demand on the solar hybridization strategy, we will consider the model:
which assumes
i is in hours (
) with
corresponding to 1:00 a.m. on 1 January,
is the mean IPH demand, and
is the fractional deviation from the mean IPH demand. For
, this models a constant IPH demand. For
, this model accounts for a dynamic ramp-up and ramp-down of demand with a maximum demand at local noon and a minimum demand at local midnight.
To use the developed models effectively within a simulation-based optimization framework, we present the following concavity result for .
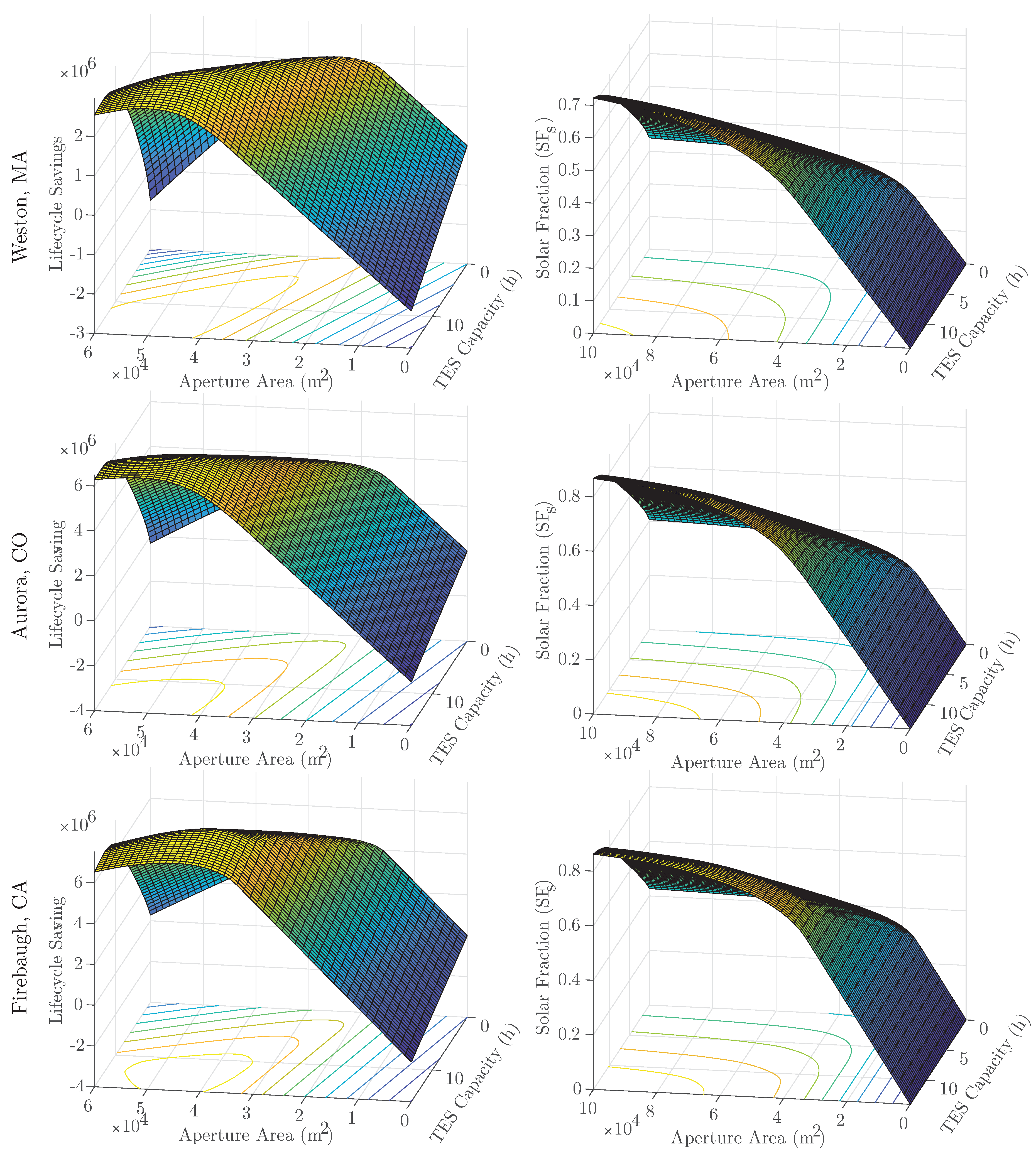
Theorem 1. Let be nonempty compact intervals. The solar fraction is a concave function on its domain.
Proof. From Equations (
7)–(
9) and the feasible system states, we can write
for the
case (or else
). The physical meaning of this case is that the solar system is producing more thermal power than can be used by the process or stored in the TES, and hence lost/rejected. We can see that
is an affine function of
and
is a convex function of
and
. Therefore,
is an affine function of
and
. Since
is the pointwise maximum of an affine function and a constant, it is convex. From Equation (
10), we have the summation of the terms:
which is an affine function of
subtracting a convex function of
and
, and hence concave. Finally, since
in Equation (
10) is a summation of concave functions (the denominator is not a function of
or
), it is concave. ☐
Smooth Approximation
Since the energy balance equations from the previous section involve min and max operators, differentiability of
as defined in Equation (
10) cannot be guaranteed. Since gradient-based optimization algorithms typically require all functions to be at least once-continuously differentiable, we must develop a smooth formulation. Consider the following operator:
as a smooth approximation of the binary max operator:
. The maximum error between the max operator and
is
and occurs at
. For
, the error approaches zero. Hence, for small
values, this approximation is not expected to introduce appreciable error into the model. A smooth approximation of
, as defined in Equation (
10), is given by:
Again, the motivation of the model development is for use within simulation-based (global) optimization. The following result ensures that the smooth approximation is concave and differentiable.
Theorem 2. Let be nonempty compact intervals. Then, the smooth solar fraction is concave and continuously differentiable.
Proof. Let
for some
i, and
. It is clear that
f is convex on
and
is affine. Therefore,
is convex for every
i. Further, both
f and
are continuously differentiable on their domains. Therefore,
is continuously differentiable on
. Since
is defined as the sum of the terms
with a constant denominator (with respect to
and
), it is concave and continuously differentiable on
. ☐
2.3. Economic Model
An economic analysis is at the heart of all new-technology investment decision-making. Therefore, successfully designing a solar-IPH hybridization strategy requires a thorough economic analysis to ensure an optimal venture. Often, such an analysis consists of a comparison of conventional energy prices and the levelized cost of electricity (LCOE) for electrical power systems or the levelized cost of heat (LCOH) for thermal systems. For IPH applications, the LCOH analysis is often appropriate. However, the LCOH is defined at a high-level as:
which cannot be guaranteed to be convex under appropriate assumptions. In contrast, we will develop the economic model of total lifecycle savings (LCS) which represents the total cost savings (which we wish to maximize) realized by hybridizing the IPH system with CSP.
The lifecycle savings is defined as the difference between the total lifetime cost of energy for a conventional system and that of the hybridized system, accounting for the time-value of money and energy-price inflation:
where
is simply the vector-form of our decision variables,
is the total lifetime of the project in years,
r is the discount rate,
is the cost of conventional fuel at year
i,
is the annualized cost of capital including debt service at year
i for financing model
k, and
is the annual operating and maintenance (O&M) cost of the CST-TES system at year
i. The solar hybridization design objective then is to maximize
, and hence, it is ideal if
is concave on its domain. The optimization problem formulation will be discussed in the next section.
The cost of conventional fuel at year
i is given by:
where
is the current specific thermal energy cost and
is an inflation rate on the fuel price. The O&M cost is typically estimated under a fixed-pricing model [
42] (i.e., cost per kWh of thermal energy produced).
The annualized capital expenditure and debt service of the CST-TES system at year
i is given by [
32]:
which assumes monthly-compounded interest at an annual rate of
, over the loan term
(in years). The term
is the total capital expenditure (debt principal), which can be calculated using different pricing models
k. The most common equipment pricing model has the form:
which accounts for discounts in volume pricing (economies of scale). The factors
and
are cost parameters which can be found in
Table A2. The exponents of
and
and the cost parameters are derived from various vendor quotes for commercially-available and custom-built equipment. Note, this model is concave in the variables
. Since this term is subtracted within
, concavity of
cannot be guaranteed using this model, in general, which complicates solving the optimal design problem (i.e., global optimization is required).
Alternatively, a fixed-pricing (linear) model can be used:
where
is the specific installed cost of the solar array (
$/m
aperture area) and
is the specific installed cost of thermal energy storage (
$/kWh). Taking
and
as a nominal specific cost for projects at a scale relevant to the design problem will yield results that are sufficiently accurate for initial design feasibility purposes but could lack the accuracy necessary for detailed design and economic analysis. Further, without a priori knowledge of the expected scale of a design, accurate cost estimates cannot be guaranteed with this model.
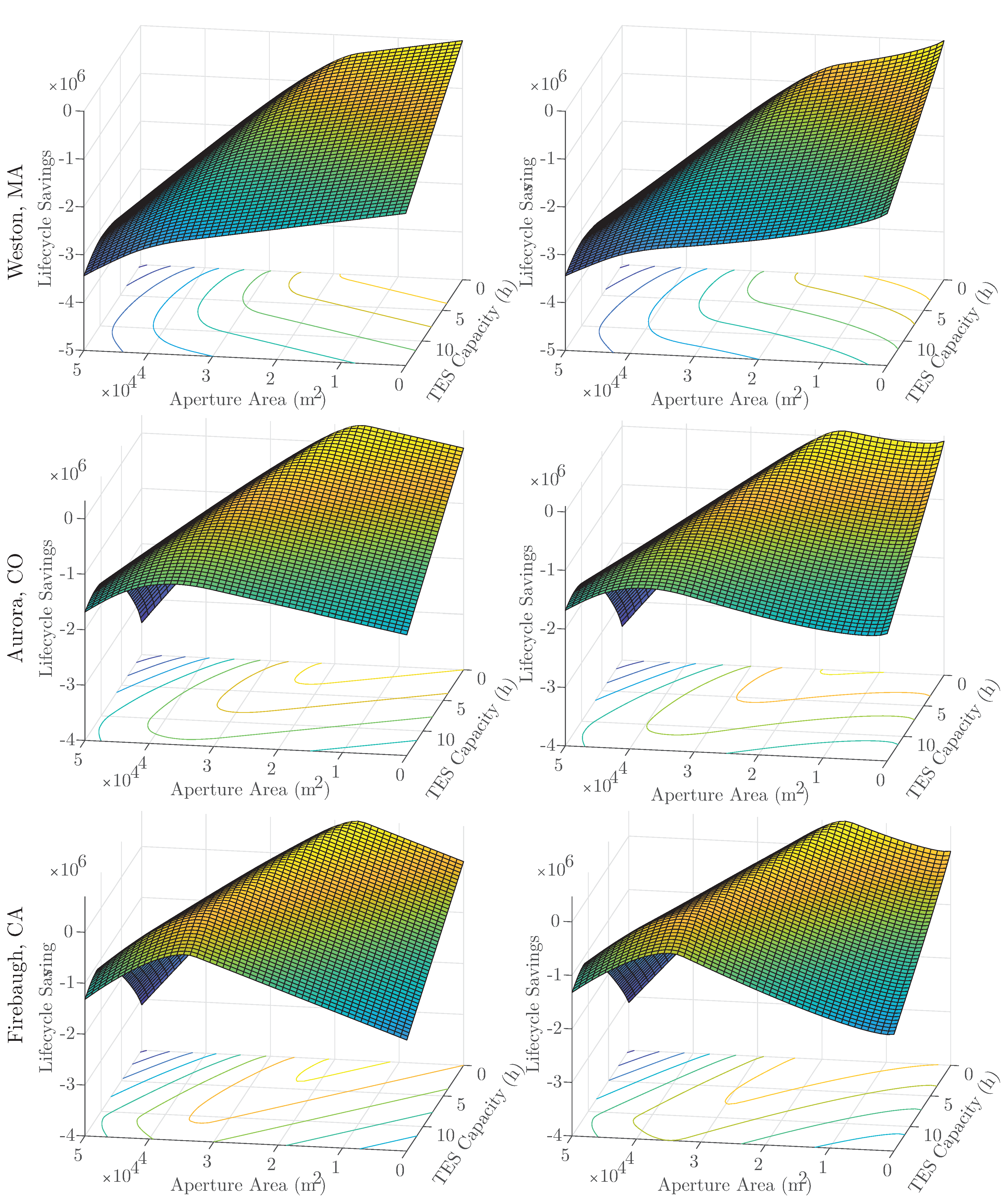
The following result details the construction of the
convex envelope of the concave discounted equipment pricing model in Equation (
14). The convex envelope is the tightest convex lower-bounding function that can be constructed for any nonconvex function on a domain of interest. The importance here is that it provides a rigorous lower bound on Equation (
14) over its domain of interest while providing the best-possible convex approximation of Equation (
14) over that domain.
Theorem 3. Consider the interval domain with . The convex envelope of Equation (
14)
on X is given bywith and Proof. Since
is separable, we can write
. Further, its convex envelope can be constructed as the sum of the convex envelopes of the separable factors
and
[
43]. The convex envelopes of these (univariate) factors are calculated simply as the secant lines between their endpoints:
☐
Corollary 1. Let , and . Then (
15)
is the convex envelope of Equation (
14)
on X. Proof. Since
, we have
and Equation (
16) reduces to
☐
From the above results, we have the following relationships between the models:
for
constructed via Corollary 1.
2.4. Optimization
The solar hybridization optimal design problem is formulated as a constrained nonlinear program (NLP) using the economic objective in Equation (
13) developed in the previous section. The model is formulated as
where
are
performance constraints that we may include, and
X is simply a two-component interval vector with
and
as lower- and upper-bounds on the variable vector
, respectively. In this work, we define only one constraint:
where
represents some minimum fraction of the total IPH energy supply that must come from solar (e.g., a social responsibility constraint or a tax-incentive constraint). However, this general formulation can accommodate any relevant set of constraints. The parameters of the optimization model in Equation (
19) can be found in
Table A2.
Theorem 4. The constrained NLP in Equation (
19)
with the inequality constraint and is a convex program. Proof. Since
is concave (Thm. 2) and
is convex for
and for all
i (Corollary 1),
is concave by design. Further, since
is concave, the function
is convex. Therefore, the feasible set
is convex. Since Equation (
19) is a concave maximization problem on a convex feasible set, it is a convex NLP. ☐
Note that, from Equation (
18), we have the following relationship between the optimal solution values:
for
constructed via Corollary 1. Therefore, we can use the fixed-pricing model in Equation (
15) for initial high-level economic feasibility studies, which will overestimate the value of the more precise discount-pricing model in Equation (
14). Further, given the result of Theorem 3, we can use Equation (
19) with
as a valid upper-bounding problem and solve the nonconvex program in Equation (
19) with
to global optimality by applying a spatial Branch-and-Bound algorithm (see
Appendix C). Therefore, for greater-detail engineering design and economic feasibility studies, a global optimum of Equation (
19) with
can be readily obtained using the models presented herein.