Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks
Abstract
1. Introduction
2. Simulation Methodology for Hydraulic Fracturing in Discontinuous Natural Fracture Networks
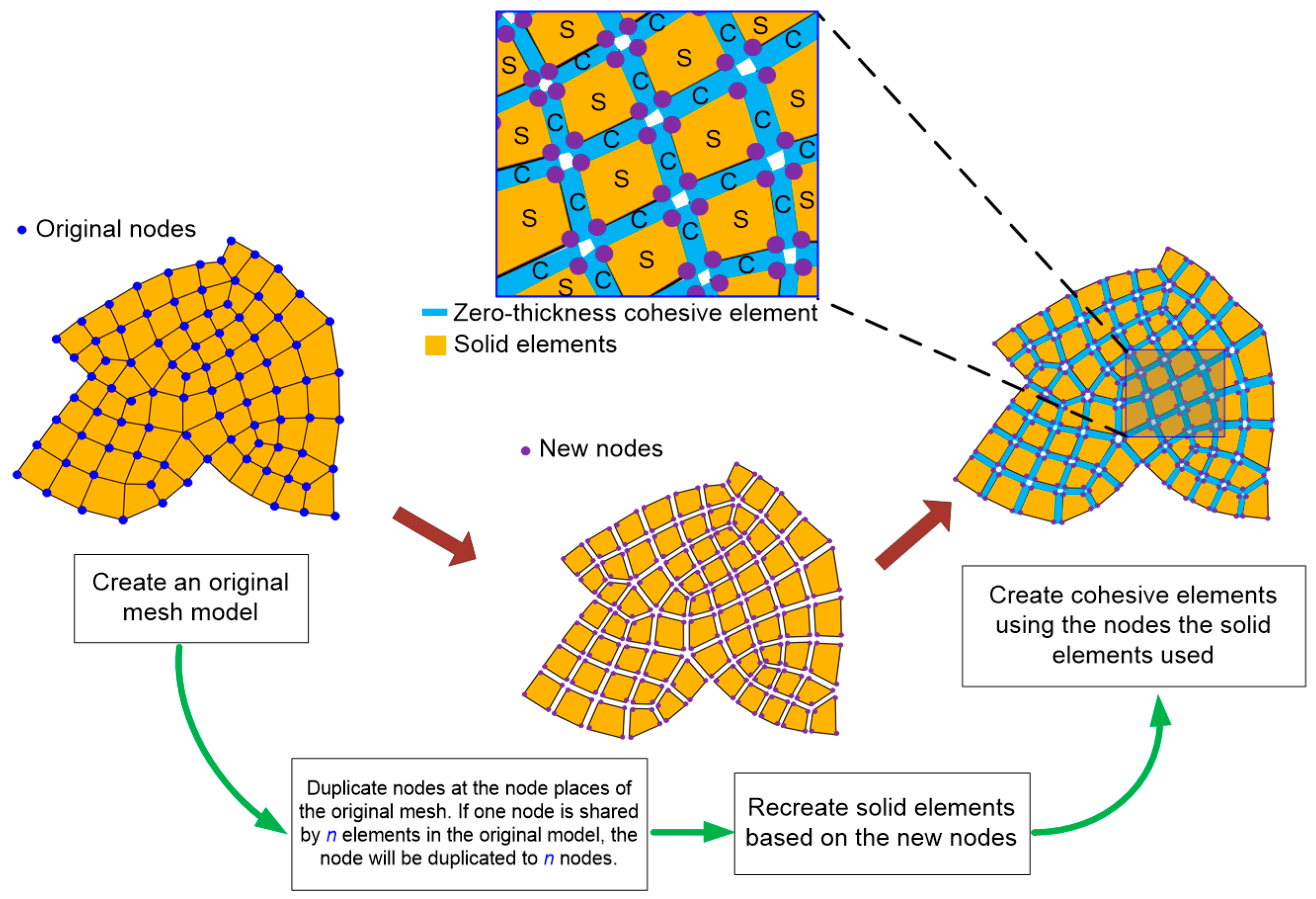
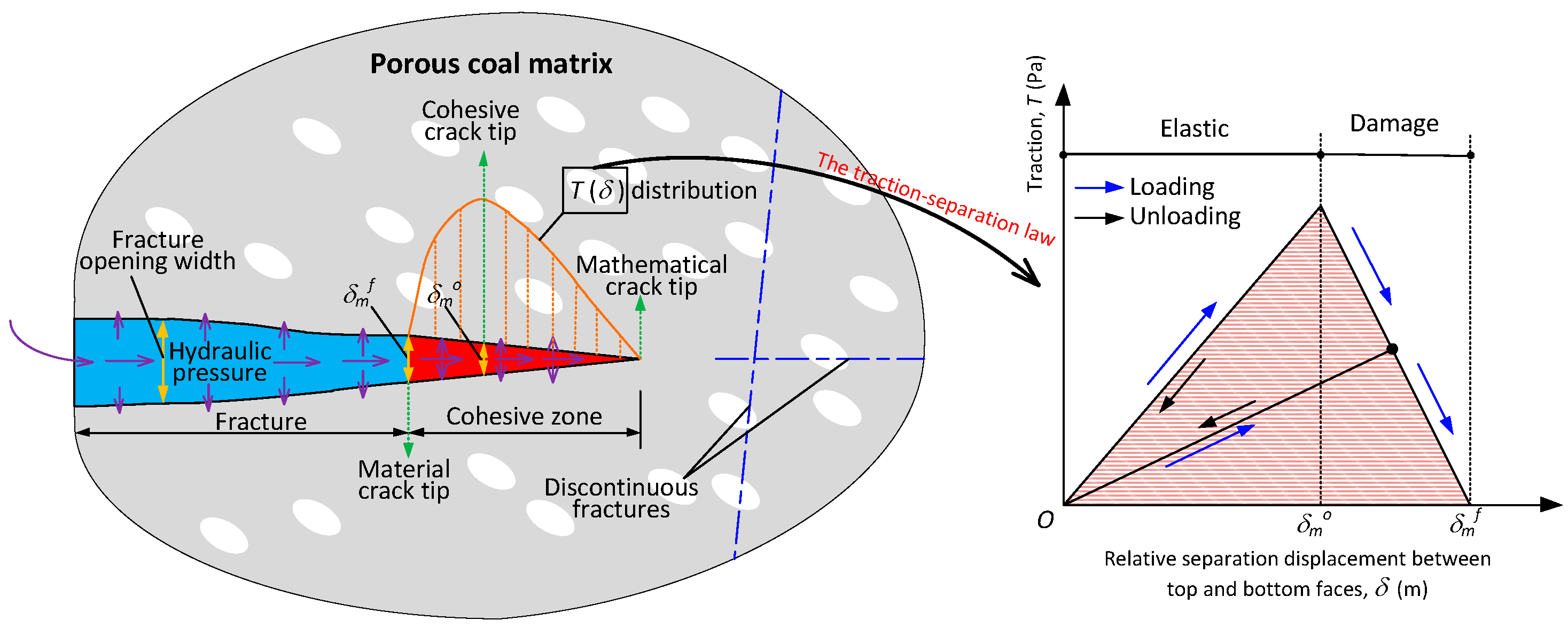
2.1. Concept and Methodology of the Hydraulic Fracturing Simulation Using the Cohesive Element Method
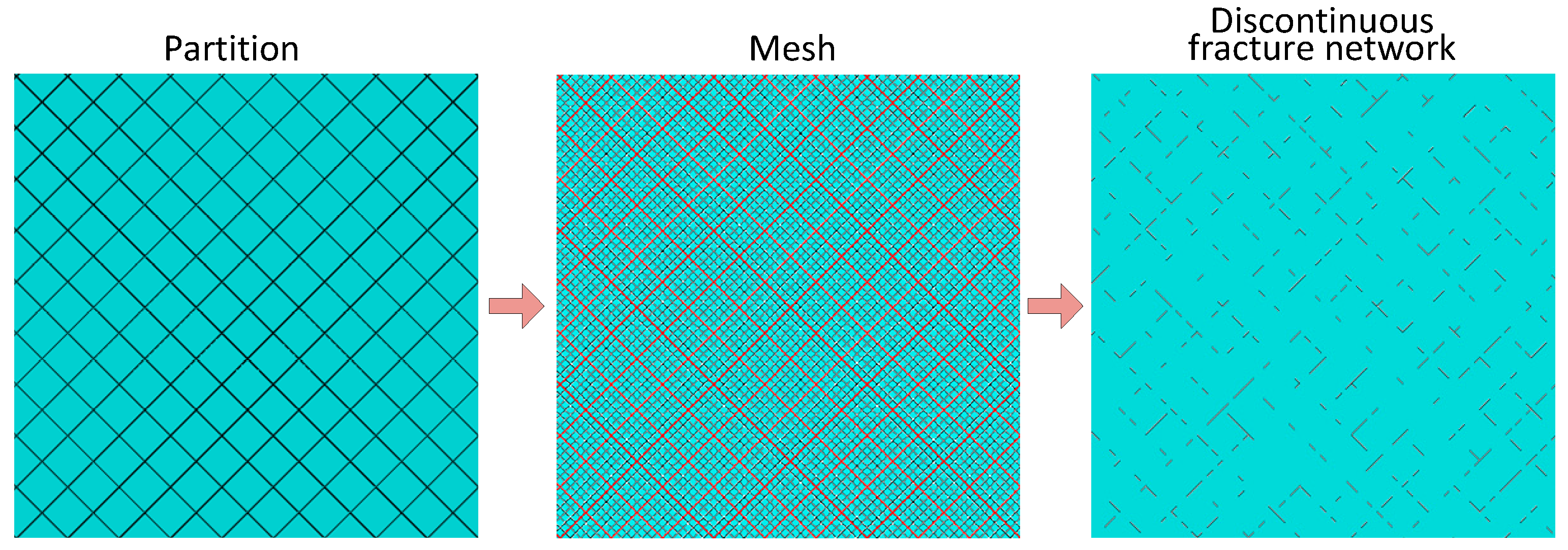
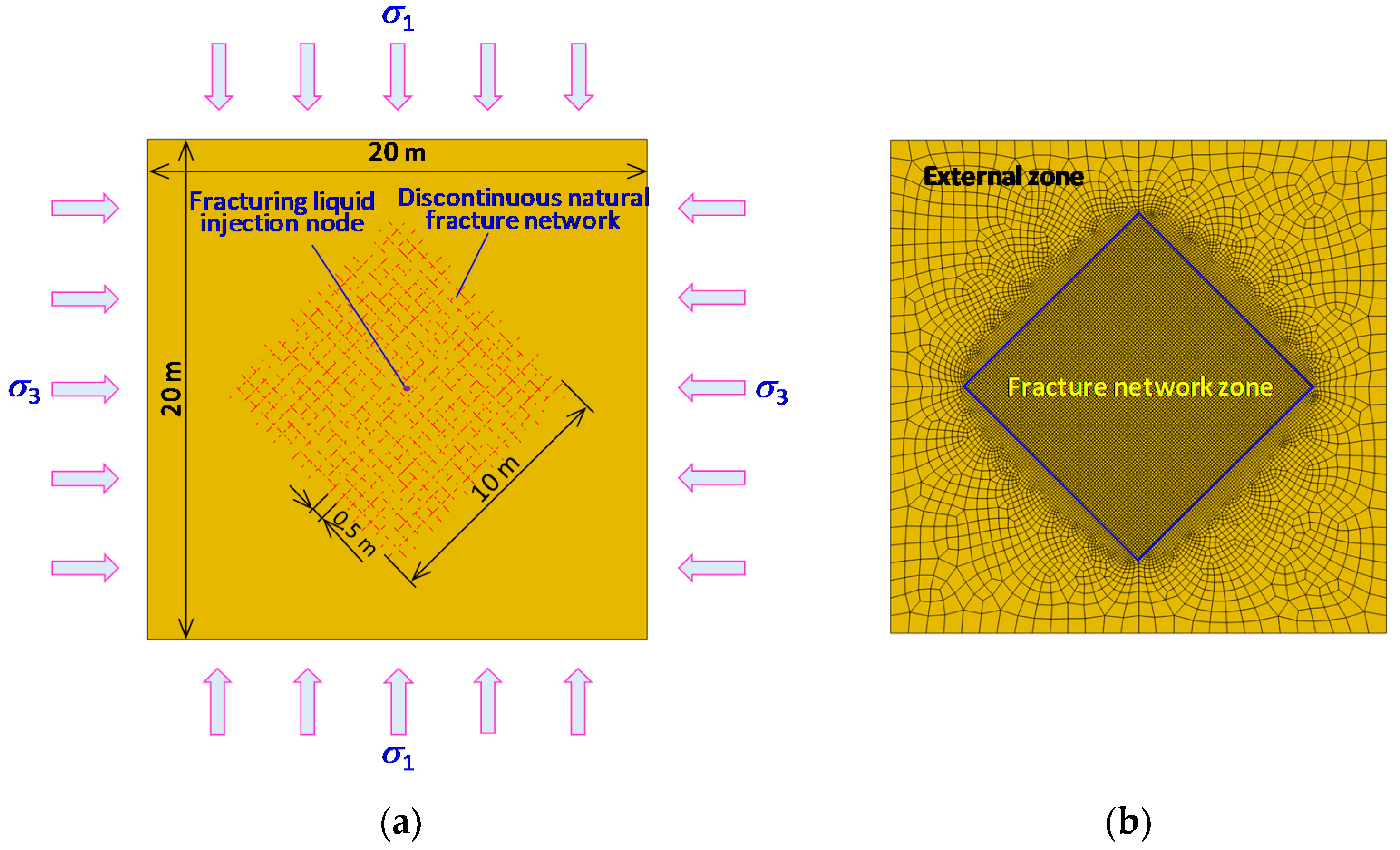
2.2. Discontinuous Natural Fracture Networks
- (1)
- A 2D plane model was created, then this plane was partitioned by two sets of lines that are orthogonal to each other.
- (2)
- This plane was meshed to generate solid elements.
- (3)
- CPPEs were embedded in this mesh model and numbered. The serial numbers of the CPPEs that were on the two sets of partition lines into set A were picked.
- (4)
- A certain proportion of elements from set A was randomly selected. By assigning very low mechanical properties, these selected elements were used to represent the discontinuous fractures. The above process for the creation of a discontinuous fracture network was executed using a Python script program in ABAQUS.
3. Seepage and Hydraulic Fracture Equations
3.1. Seepage–Stress Coupling Equation for the Coal Matrix
3.1.1. Discretized Equilibrium Equation
3.1.2. Continuity Equation of Seepage
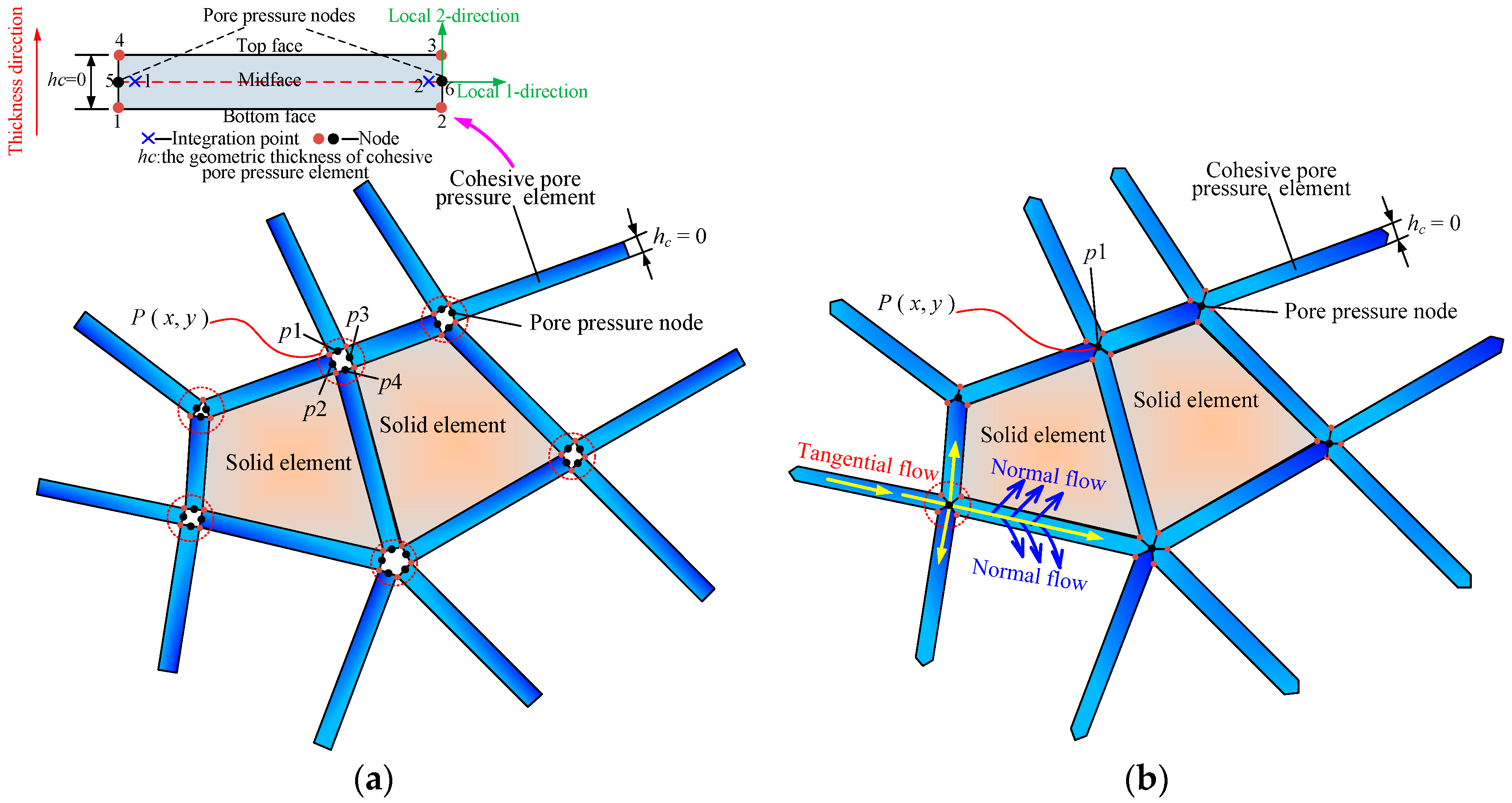
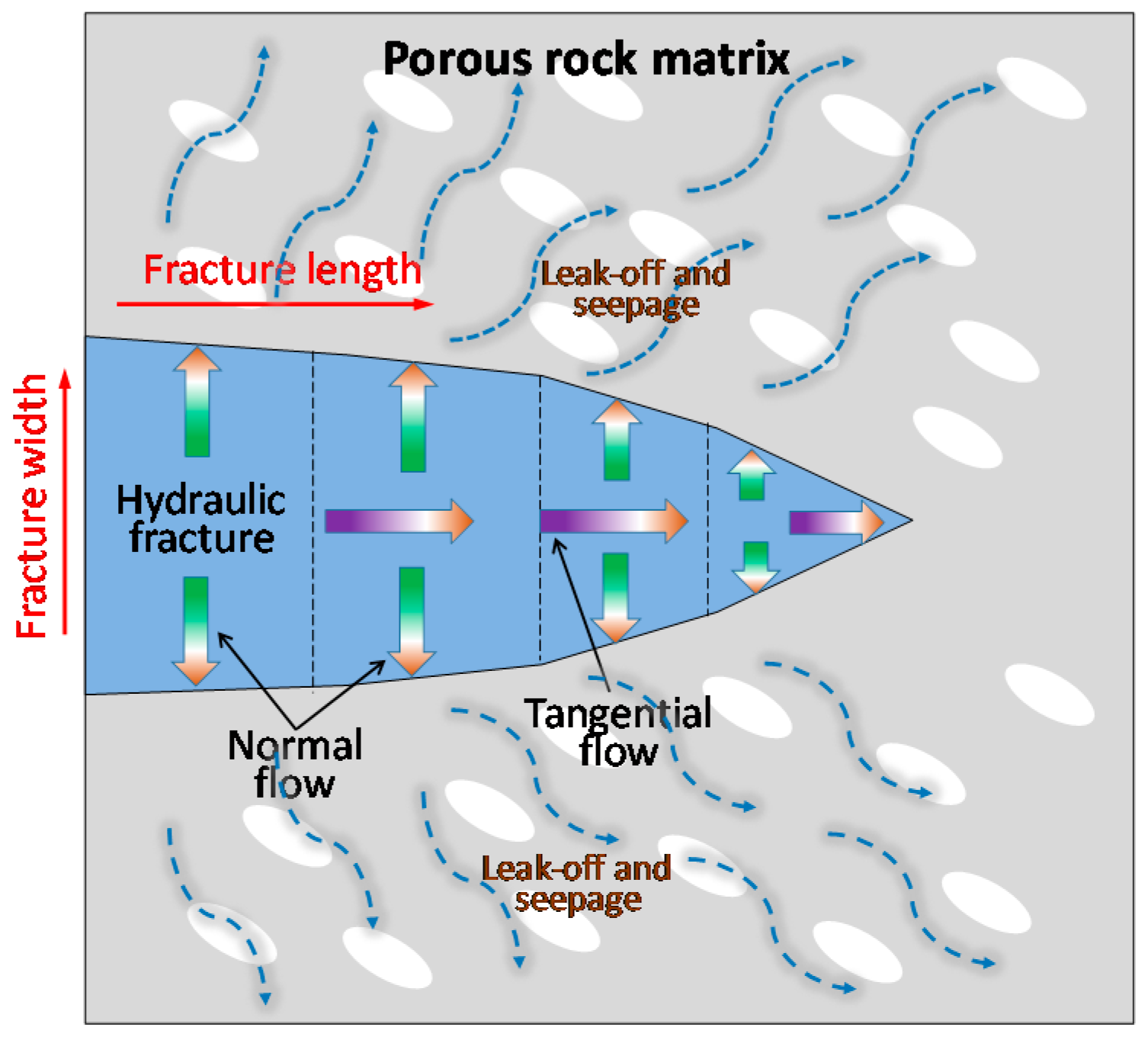
3.2. Flow Equation of the Fracturing Liquid Flow in CPPE
3.3. Damage Initiation and Evolution Law of Hydraulic Fractures
3.3.1. Damage Initiation
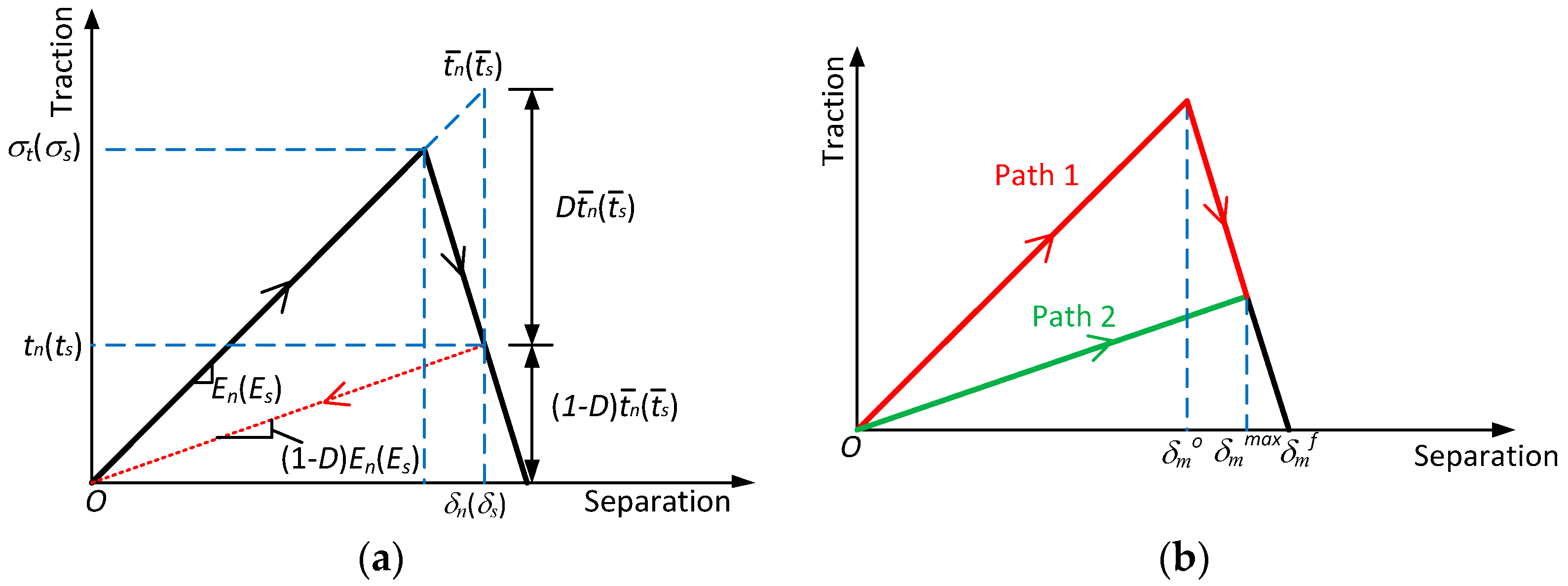
3.3.2. Damage Evolution
4. Numerical Simulation Procedure
4.1. The Mesh Model of Coal Seams with Discontinuous Natural Fracture Networks
4.2. Mechanical Properties of the Coal Matrix, Discontinuous Natural Fracture and Fracturing Liquid
4.3. Initial Conditions
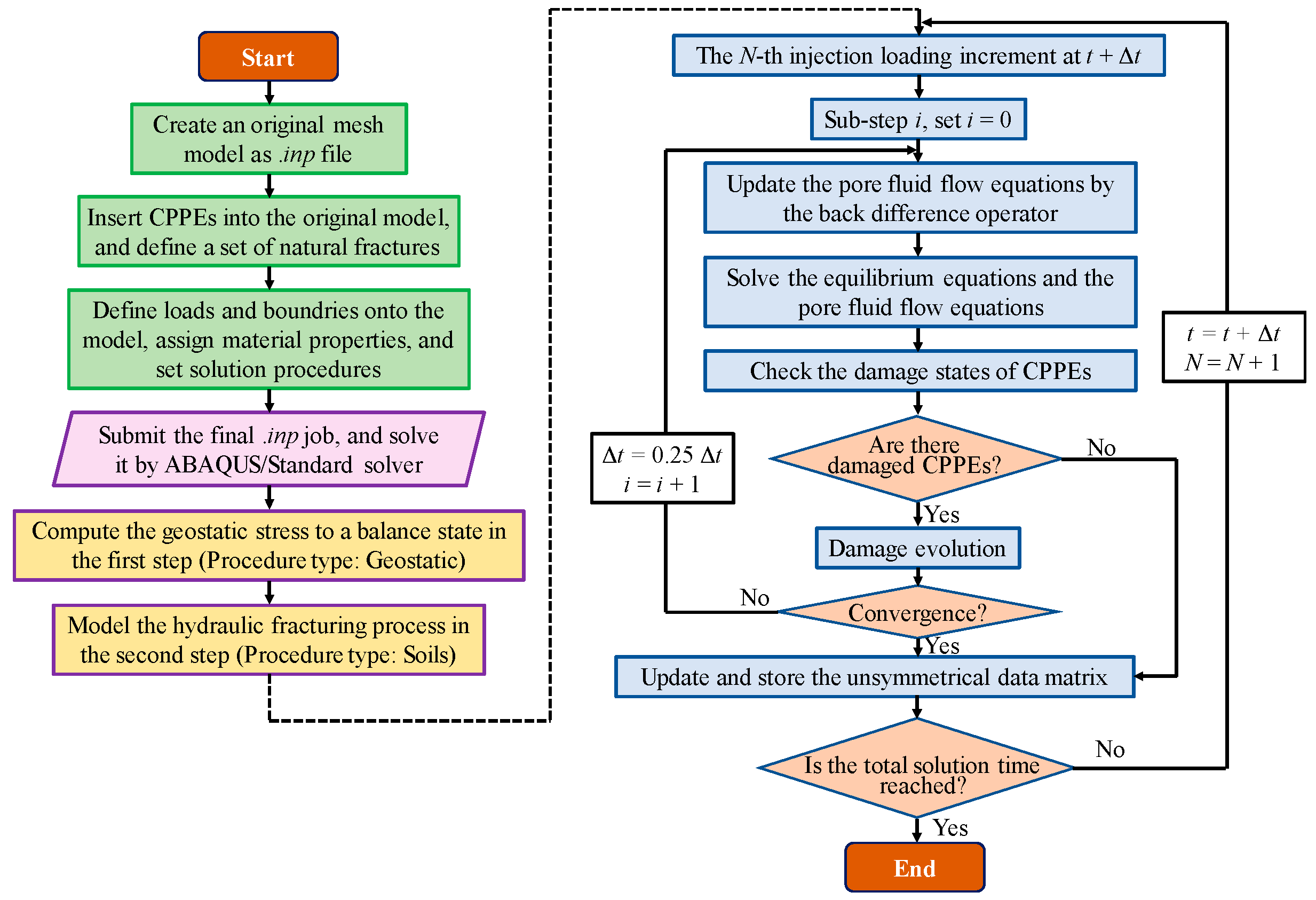
4.4. Solving Procedures, Convergence Criterion and Error Control
5. Results and Discussion
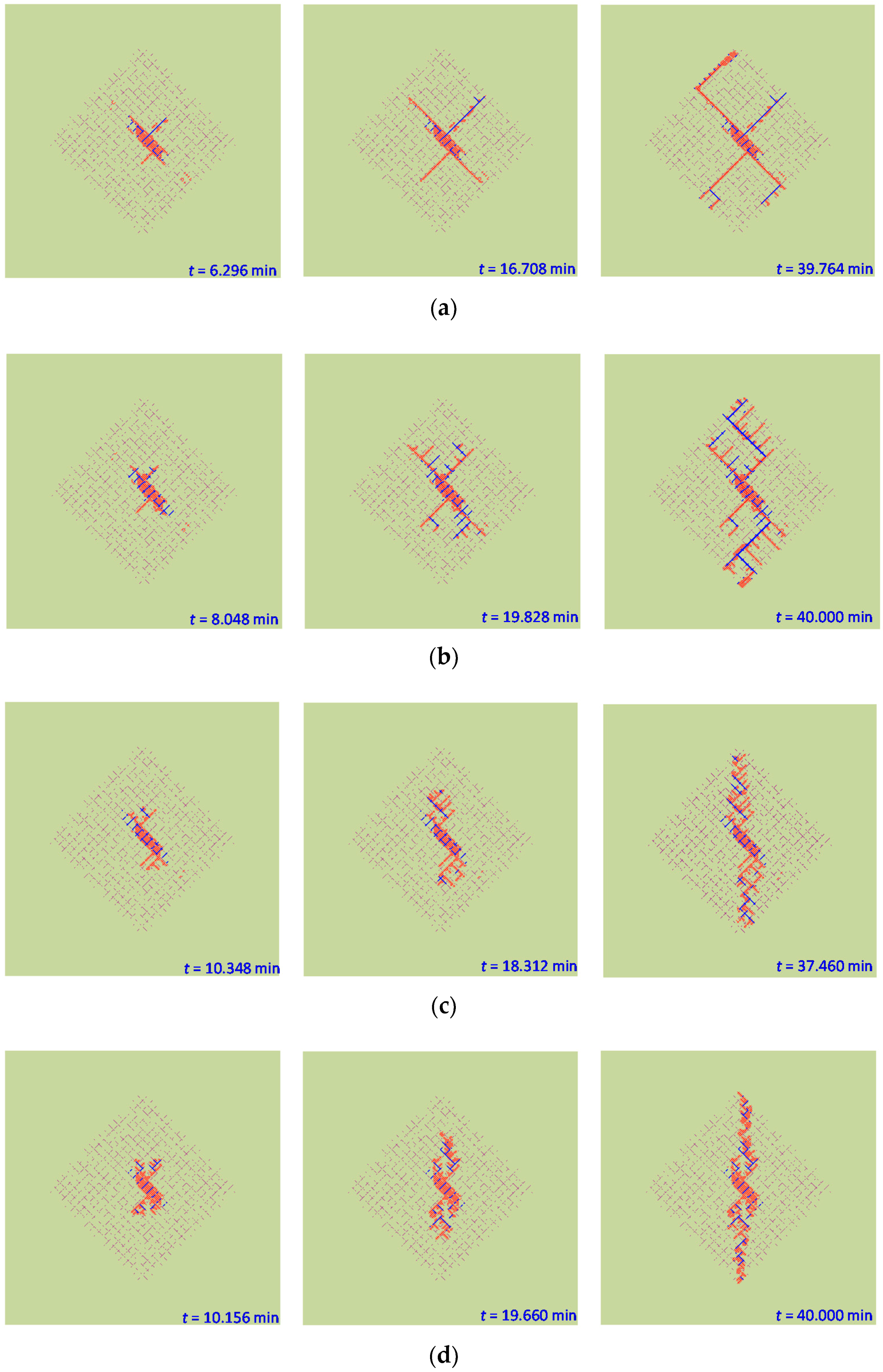
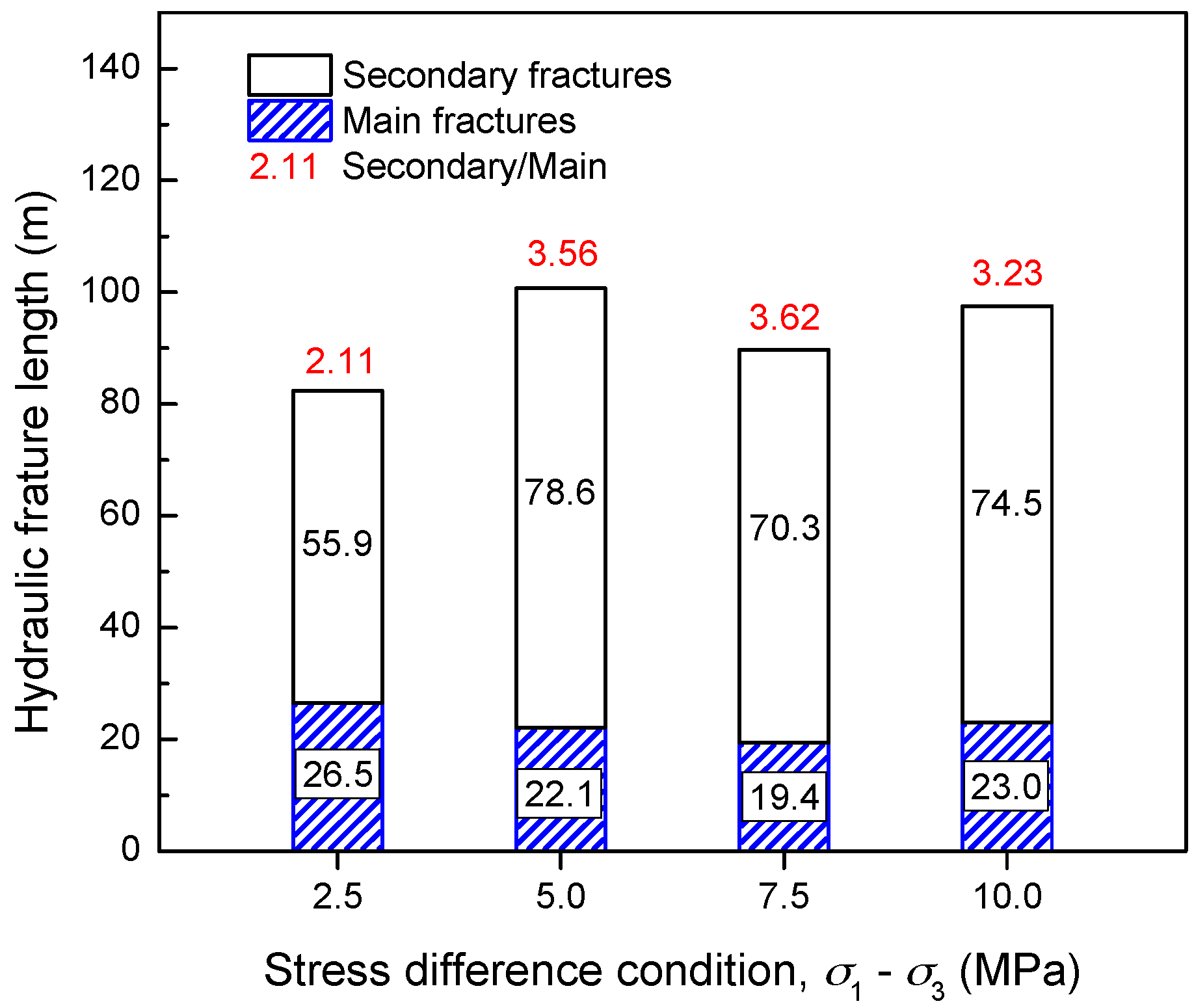
5.1. Hydraulic Fracture Network Characteristics
5.2. Growth Process of the Secondary Hydraulic Fractures
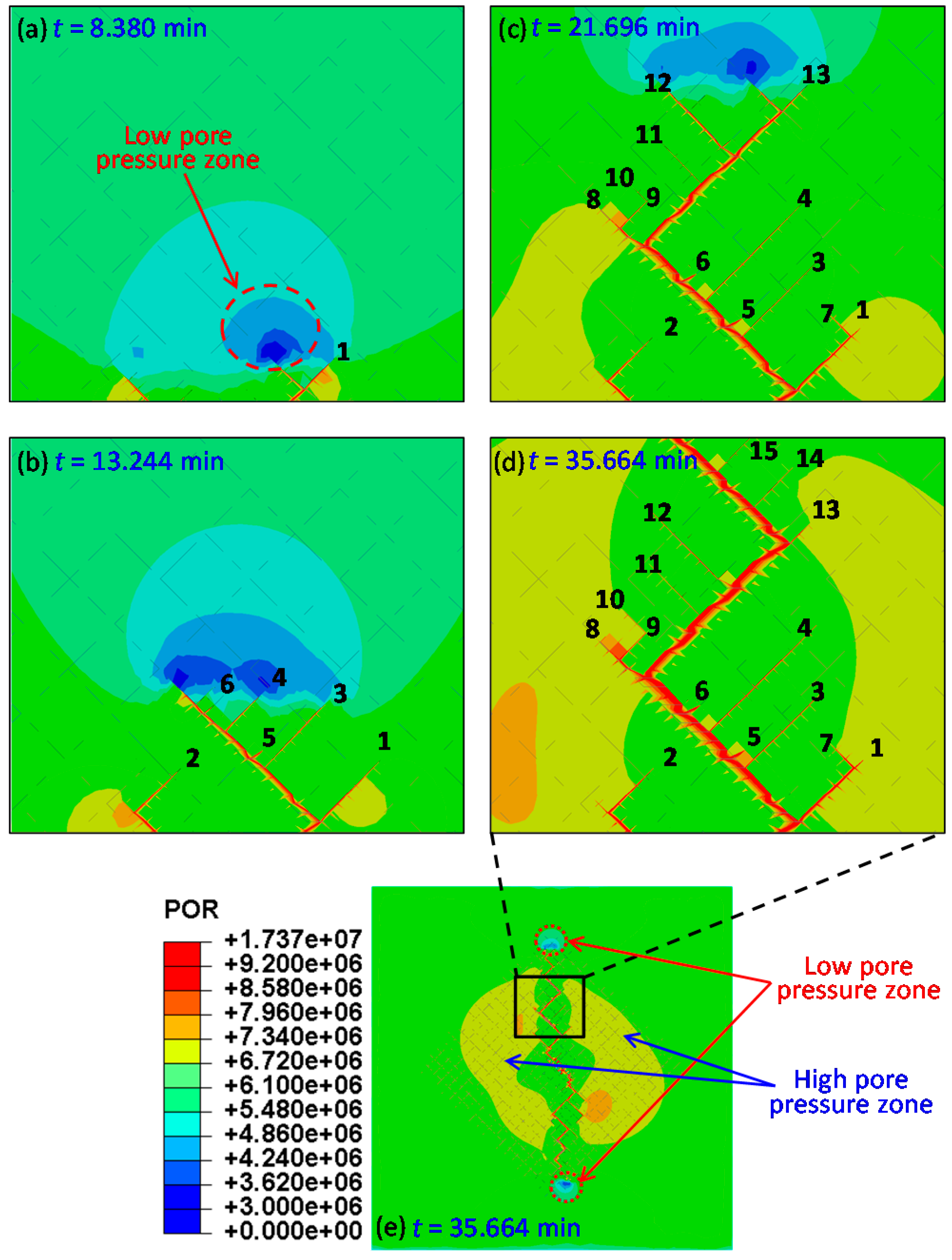
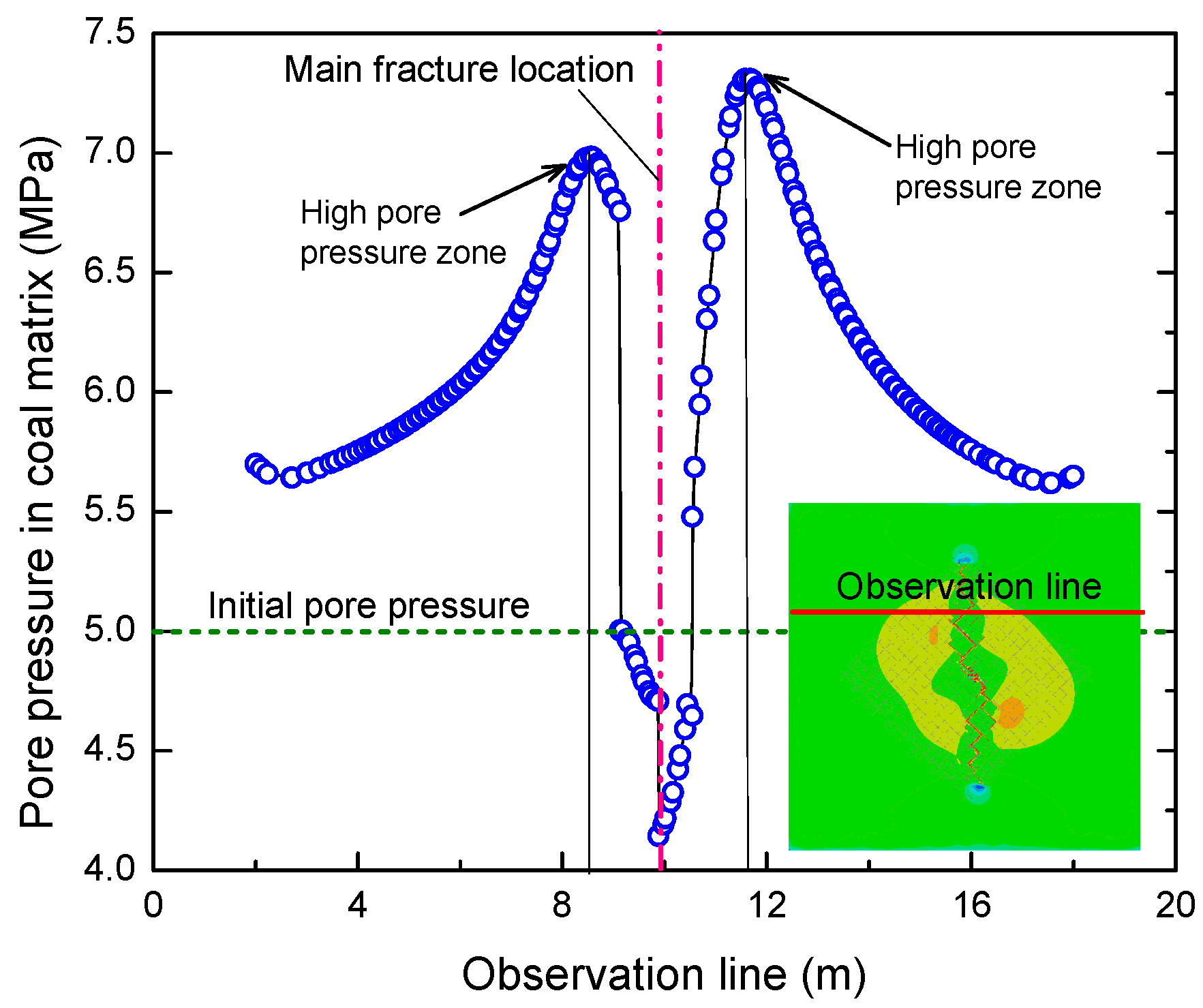
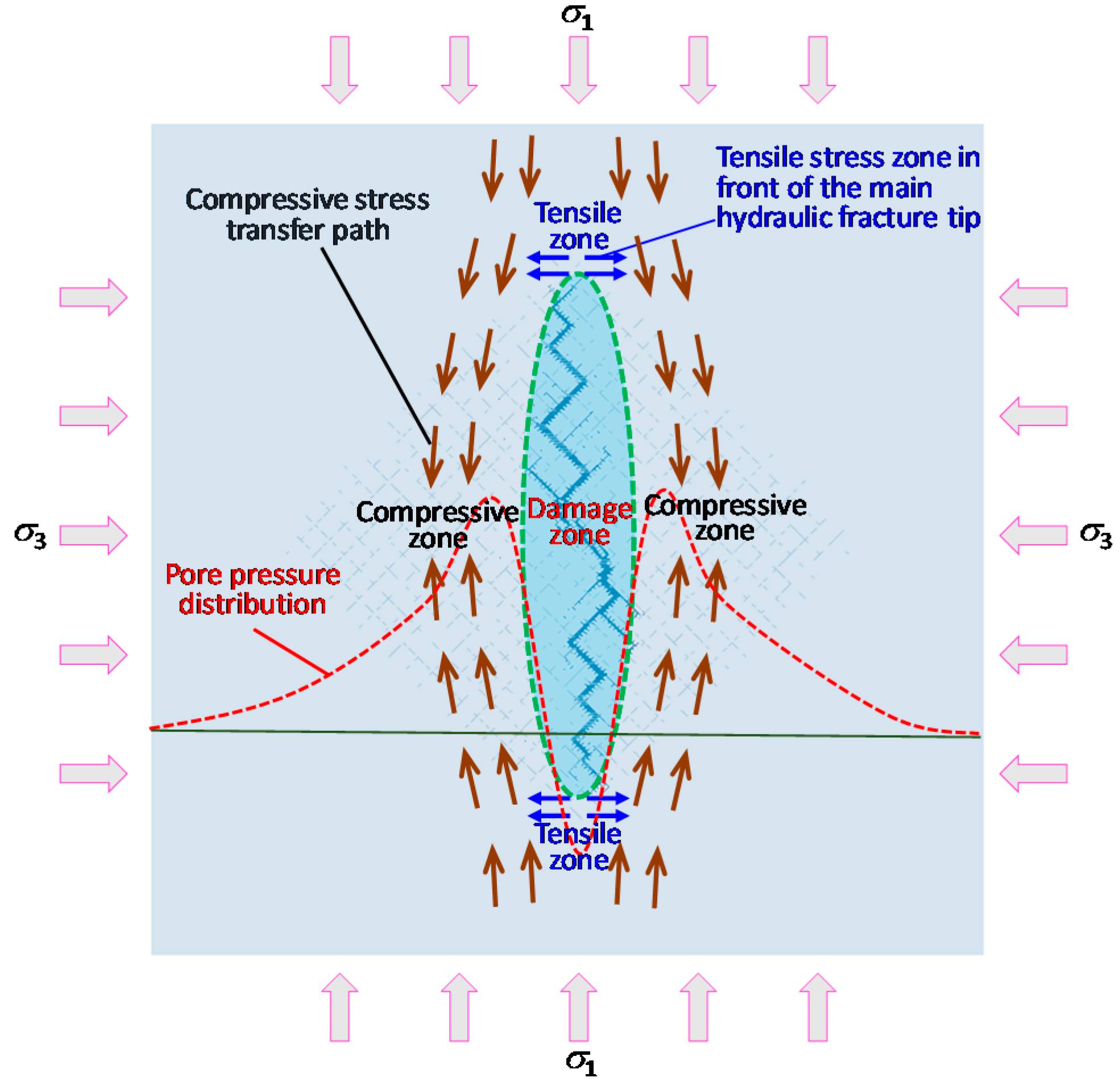
5.3. Pore Pressure Distribution Characteristics
5.4. Injection Fluid Pressure
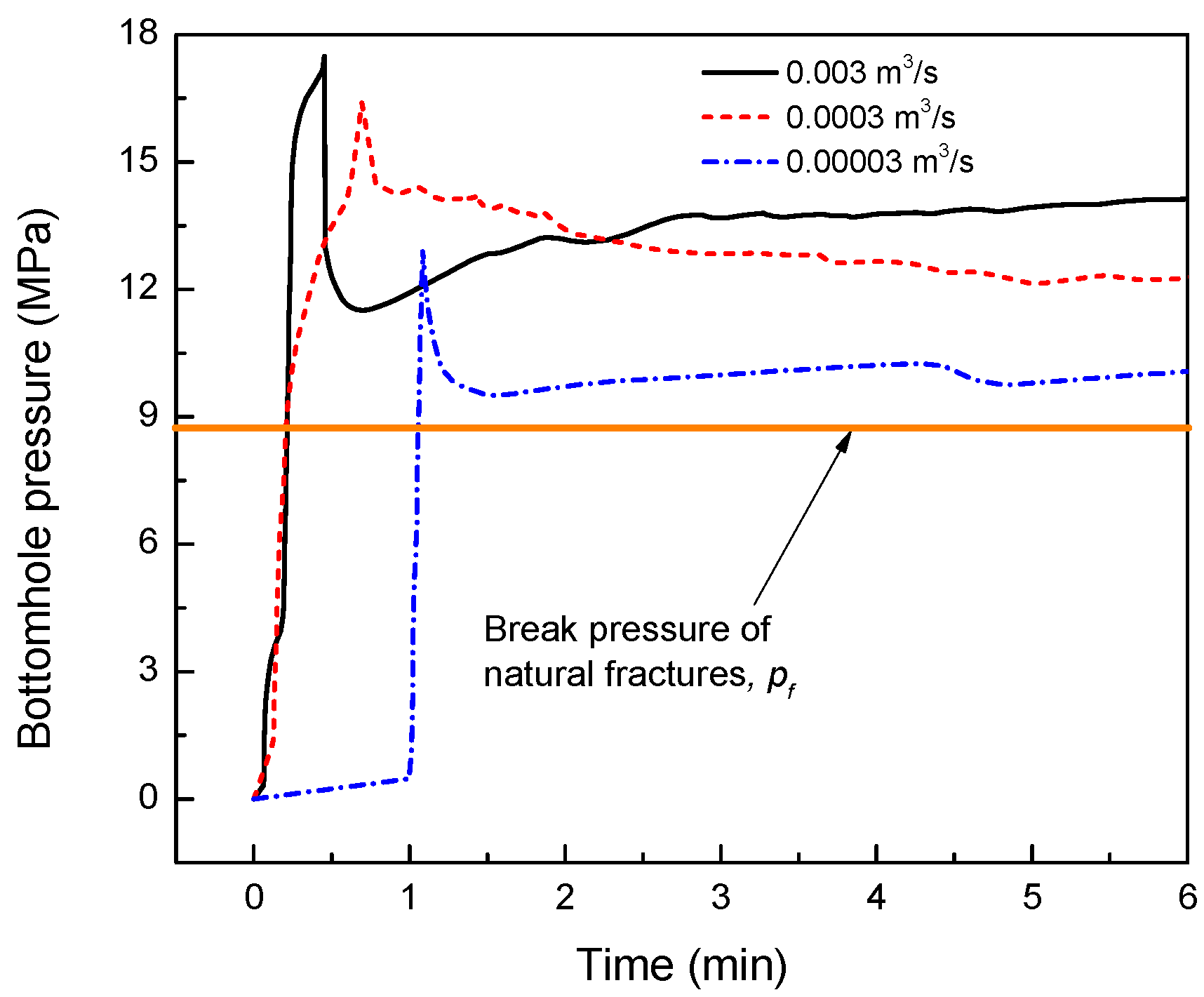
5.4.1. Effect of the Injection Rate on Bottomhole Pressure
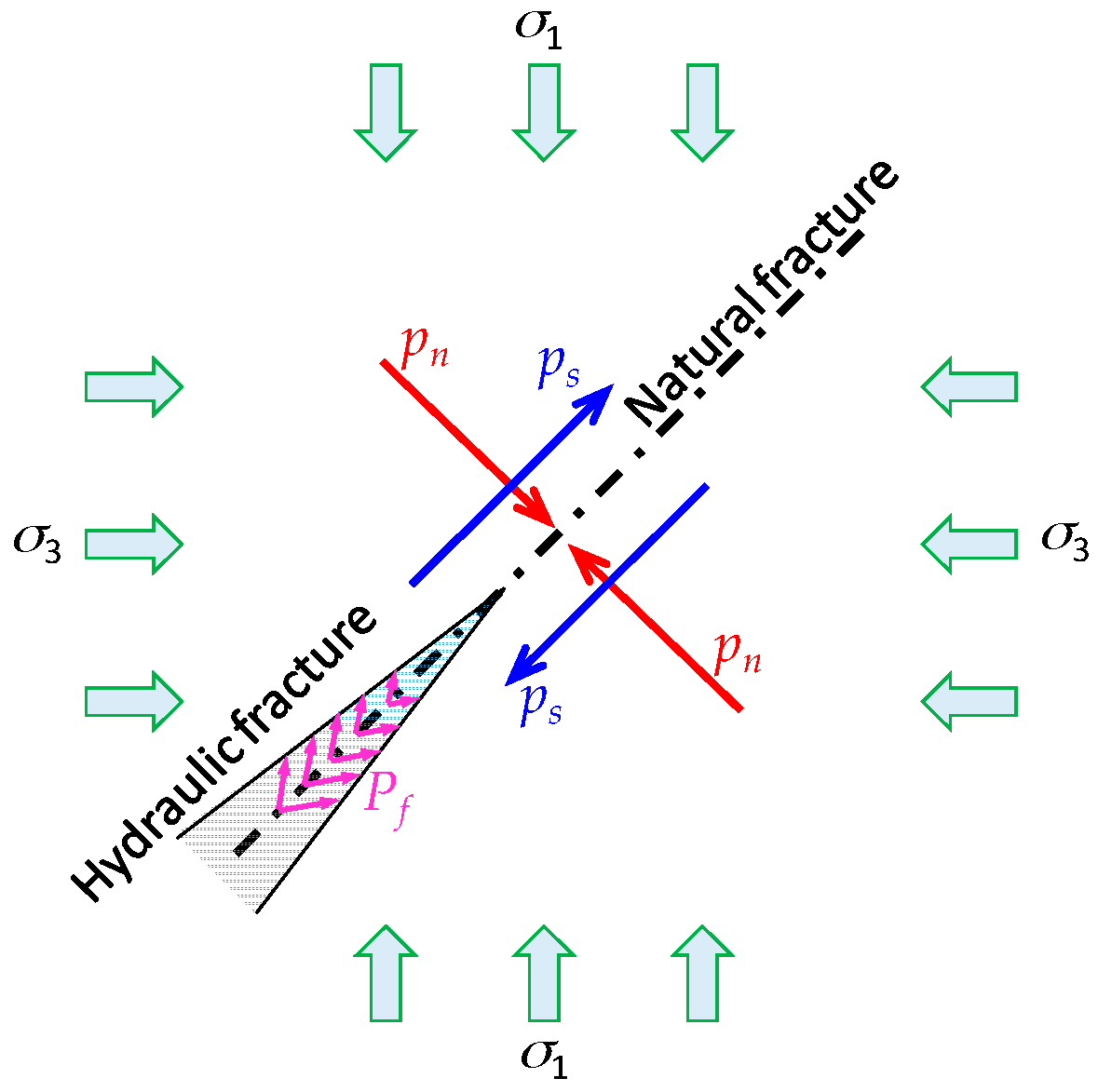
5.4.2. Break Pressure of the Discontinuous Natural Fracture
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moore, T.A. Coalbed methane: A review. Int. J. Coal Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- White, C.M.; Smith, D.H.; Jones, K.L.; Goodman, A.L.; Jikich, S.A.; LaCount, R.B.; DuBose, S.B.; Ozdemir, E.; Morsi, B.I.; Schroeder, K.T. Sequestration of carbon dioxide in coal with enhanced coalbed methane recovery a review. Energy Fuels 2005, 19, 659–724. [Google Scholar] [CrossRef]
- Cai, Y.D.; Liu, D.M.; Pan, Z.J.; Yao, Y.B.; Li, J.Q.; Qiu, Y.K. Pore structure and its impact on ch4 adsorption capacity and flow capability of bituminous and subbituminous coals from northeast china. Fuel 2013, 103, 258–268. [Google Scholar] [CrossRef]
- Cheng, W.M.; Liu, Z.; Yang, H.; Wang, W.Y. Non-linear seepage characteristics and influential factors of water injection in gassy seams. Exp. Therm. Fluid Sci. 2018, 91, 41–53. [Google Scholar] [CrossRef]
- Zou, Q.L.; Lin, B.Q.; Liu, T.; Zhou, Y.; Zhang, Z.; Yan, F.Z. Variation of methane adsorption property of coal after the treatment of hydraulic slotting and methane pre-drainage: A case study. J. Nat. Gas Sci. Eng. 2014, 20, 396–406. [Google Scholar] [CrossRef]
- Cheng, W.M.; Hu, X.M.; Xie, J.; Zhao, Y.Y. An intelligent gel designed to control the spontaneous combustion of coal: Fire prevention and extinguishing properties. Fuel 2017, 210, 826–835. [Google Scholar] [CrossRef]
- Zhou, G.; Fan, T.; Ma, Y.L. Preparation and chemical characterization of an environmentally-friendly coal dust cementing agent. J. Chem. Technol. Biotechnol. 2017, 92, 2699–2708. [Google Scholar] [CrossRef]
- Ni, G.H.; Cheng, W.M.; Lin, B.Q.; Zhai, C. Experimental study on removing water blocking effect (wbe) from two aspects of the pore negative pressure and surfactants. J. Nat. Gas Sci. Eng. 2016, 31, 596–602. [Google Scholar] [CrossRef]
- Wright, C.A.; Tanigawa, J.J.; Mei, S.; Li, Z. Enhanced hydraulic fracture technology for a coal seam reservoir in Central China. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, 14–17 November 1995; Society of Petroleum Engineers: Beijing, China, 1995. [Google Scholar] [CrossRef]
- Adachi, A.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Yuan, Z.G.; Wang, H.T.; Liu, N.P.; Liu, J.C. Simulation study of characteristics of hydraulic fracturing propagation of low permeability coal seam. Disaster Adv. 2012, 5, 717–720. [Google Scholar]
- Hou, B.; Chen, M.; Wang, Z.; Yuan, J.B.; Liu, M. Hydraulic fracture initiation theory for a horizontal well in a coal seam. Pet. Sci. 2013, 10, 219–225. [Google Scholar] [CrossRef]
- Li, D.Q.; Zhang, S.; Zhang, S.A. Experimental and numerical simulation study on fracturing through interlayer to coal seam. J. Nat. Gas Sci. Eng. 2014, 21, 386–396. [Google Scholar] [CrossRef]
- Eshiet, K.I.I.; Sheng, Y. Carbon dioxide injection and associated hydraulic fracturing of reservoir formations. Environ. Earth Sci. 2014, 72, 1011–1024. [Google Scholar] [CrossRef]
- Bredehoeft, J.; Wolff, R.; Keys, W.; Shuter, E. Hydraulic fracturing to determine the regional in situ stress field, piceance basin, colorado. Geol. Soc. Am. Bull. 1976, 87, 250–258. [Google Scholar] [CrossRef]
- Abou-Sayed, A.; Brechtel, C.; Clifton, R. In situ stress determination by hydrofracturing: A fracture mechanics approach. J. Geophys. Res. Solid Earth 1978, 83, 2851–2862. [Google Scholar] [CrossRef]
- Tenma, N.; Yamaguchi, T.; Zyvoloski, G. The hijiori hot dry rock test site, japan evaluation and optimization of heat extraction from a two-layered reservoir. Geothermics 2008, 37, 19–52. [Google Scholar] [CrossRef]
- Parker, R. The rosemanowes hdr project 1983–1991. Geothermics 1999, 28, 603–615. [Google Scholar] [CrossRef]
- Jeffrey, R.; Zhang, X.; Settari, A.; Mills, K.; Detournay, E. Hydraulic fracturing to induce caving: Fracture model development and comparison to field data. In DC Rocks 2001, The 38th US Symposium on Rock Mechanics (USRMS); American Rock Mechanics Association: Alexandria, VA, USA, 2001. [Google Scholar]
- Van As, A.; Jeffrey, R.G. Hydraulic fracturing as a cave inducement technique at northparkes mines. In Proceedings of the Massmin 2000, Brisbane, Austrilia, 29 October–2 November 2000; Australasian Institute of Mining and Metallurgy: Parkville Victoria, Australia, 2000; Volume 2000, pp. 165–172. [Google Scholar]
- Sun, R.J. Theoretical size of hydraulically induced horizontal fractures and corresponding surface uplift in an idealized medium. J. Geophys. Res. 1969, 74, 5995–6011. [Google Scholar] [CrossRef]
- Harper, J.A. The marcellus shale: An old “new” gas reservoir in Pennsylvania. Pa. Geol. 2008, 38, 2–13. [Google Scholar]
- Gandossi, L. An overview of hydraulic fracturing and other formation stimulation technologies for shale gas production. Eur. Comm. Jt. Res. Cent. Tech. Rep. 2013, 26347, 4–29. [Google Scholar]
- Montgomery, C.T.; Smith, M.B. Hydraulic fracturing: History of an enduring technology. J. Petrol. Technol. 2015, 62, 26–40. [Google Scholar] [CrossRef]
- McDaniel, B.W. Hydraulic fracturing techniques used for stimulation of coalbed methane wells. In Proceedings of the SPE Eastern Regional Meeting, Columbus, OH, USA, 31 October–2 November 1990; Society of Petroleum Engineers: Columbus, OH, USA, 1990. [Google Scholar] [CrossRef]
- Sampath, K.H.S.M.; Perera, M.S.A.; Ranjith, P.G.; Matthai, S.K.; Rathnaweera, T.; Zhang, G.; Tao, X. Ch4-CO2 gas exchange and supercritical CO2 based hydraulic fracturing as cbm production-accelerating techniques: A review. J. CO2 Util. 2017, 22, 212–230. [Google Scholar] [CrossRef]
- Ting, F.T.C. Origin and spacing of cleats in coal beds. J. Press. Vessel Technol. 1977, 99, 624–626. [Google Scholar] [CrossRef]
- Su, X.B.; Feng, Y.L.; Chen, J.F.; Pan, J.N. The characteristics and origins of cleat in coal from western north china. Int. J. Coal Geol. 2001, 47, 51–62. [Google Scholar] [CrossRef]
- Busse, J.; de Dreuzy, J.R.; Torres, S.G.; Bringemeier, D.; Scheuermann, A. Image processing based characterisation of coal cleat networks. Int. J. Coal Geol. 2017, 169, 1–21. [Google Scholar] [CrossRef]
- Golab, A.; Ward, C.R.; Permana, A.; Lennox, P.; Botha, P. High-resolution three-dimensional imaging of coal using microfocus X-ray computed tomography, with special reference to modes of mineral occurrence. Int. J. Coal Geol. 2013, 113, 97–108. [Google Scholar] [CrossRef]
- Rodrigues, C.F.; Laiginhas, C.; Fernandes, M.; de Sousa, M.J.L.; Dinis, M.A.P. The coal cleat system: A new approach to its study. J. Rock Mech. Geotech. Eng. 2014, 6, 208–218. [Google Scholar] [CrossRef]
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 16–18 May 1982; Society of Petroleum Engineers: Pittsburgh, PA, USA, 1982. [Google Scholar] [CrossRef]
- Dahi Taleghani, A.; Gonzalez-Chavez, M.; Yu, H.; Asala, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Petrol. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O.; Hofmann, H.; Zimmermann, G. Discrete element modelling of hydraulic fracture propagation and dynamic interaction with natural fractures in hard rock. Procedia Eng. 2017, 191, 1023–1031. [Google Scholar] [CrossRef]
- Damjanac, B.; Gil, I.; Pierce, M.; Sanchez, M.; Van As, A.; McLennan, J. A new approach to hydraulic fracturing modeling in naturally fractured reservoirs. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010; American Rock Mechanics Association: Salt Lake City, UT, USA, 2010. [Google Scholar]
- Wang, T.; Hu, W.R.; Elsworth, D.; Zhou, W.; Zhou, W.B.; Zhao, X.Y.; Zhao, L.Z. The effect of natural fractures on hydraulic fracturing propagation in coal seams. J. Petrol. Sci. Eng. 2017, 150, 180–190. [Google Scholar] [CrossRef]
- Deng, J.Q.; Yang, Q.; Liu, Y.R.; Liu, Y.; Zhang, G.X. 3d finite element modeling of directional hydraulic fracturing based on deformation reinforcement theory. Comput. Geotech. 2018, 94, 118–133. [Google Scholar] [CrossRef]
- Xu, L.L.; Cui, J.B.; Huang, S.P.; Tang, J.D.; Cai, L.; Yu, P. Analysis and application of fracture propagated model by hydraulic fracturing in coal-bed methane reservoir. J. China Coal Soc. 2014, 39, 2068–2074. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Zhang, G.Q. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Shilova, T.; Patutin, A.; Rybalkin, L.; Serdyukov, S.; Hutornoy, V. Development of the impermeable membranes using directional hydraulic fracturing. Procedia Eng. 2017, 191, 520–524. [Google Scholar] [CrossRef]
- He, Q.; Suorineni, F.T.; Ma, T.; Oh, J. Effect of discontinuity stress shadows on hydraulic fracture re-orientation. Int. J. Rock Mech. Min. Sci. 2017, 91, 179–194. [Google Scholar] [CrossRef]
- Liu, K.; Gao, D.L.; Wang, Y.B.; Yang, Y.C. Effect of local loads on shale gas well integrity during hydraulic fracturing process. J. Nat. Gas Sci. Eng. 2017, 37, 291–302. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, W.H.; Keer, L.M. An energy based analytical method to predict the influence of natural fractures on hydraulic fracture propagation. Eng. Fract. Mech. 2018, 189, 232–245. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Hou, B.; Han, K.; Zhou, Y.C.; Meng, S.Z. Experimental investigation on fracture initiation and non-planar propagation of hydraulic fractures in coal seams. Pet. Explor. Dev. 2017, 44, 470–476. [Google Scholar] [CrossRef]
- Guo, T.K.; Rui, Z.H.; Qu, Z.Q.; Qi, N. Experimental study of directional propagation of hydraulic fracture guided by multi-radial slim holes. J. Petrol. Sci. Eng. 2018, 166, 592–601. [Google Scholar] [CrossRef]
- Haimson, B.; Fairhurst, C. Initiation and extension of hydraulic fractures in rocks. SPE J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Schmitt, D.; Zoback, M. Poroelastic effects in the determination of the maximum horizontal principal stress in hydraulic fracturing tests—A proposed breakdown equation employing a modified effective stress relation for tensile failure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 499–506. [Google Scholar] [CrossRef]
- Schmitt, D.R.; Currie, C.A.; Zhang, L. Crustal stress determination from boreholes and rock cores: Fundamental principles. Tectonophysics 2012, 580, 1–26. [Google Scholar] [CrossRef]
- Atkinson, B.K. Fracture Mechanics of Rock; Academic Press Inc.: London, UK, 1987; Volume 2, pp. 33–45. [Google Scholar]
- McClure, M.W.; Horne, R.N. An investigation of stimulation mechanisms in enhanced geothermal systems. Int. J. Rock Mech. Min. Sci. 2014, 72, 242–260. [Google Scholar] [CrossRef]
- Perkins, T.; Kern, L. Widths of hydraulic fractures. J. Petrol. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Geertsma, J.; Klerk, F.D. A rapid method of predicting width and extent of hydraulically induced fractures. J. Petrol. Technol. 1969, 21, 1571–1582. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. SPE J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Warpinski, N.; Wolhart, S.; Wright, C. Analysis and prediction of microseismicity induced by hydraulic fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997; Society of Petroleum Engineers: Richardson, TX, USA, 2001. [Google Scholar] [CrossRef]
- Palmer, I.D.; Moschovidis, Z.A.; Cameron, J.R. Modeling shear failure and stimulation of the barnett shale after hydraulic fracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 23–25 January 2018; Society of Petroleum Engineers: College Station, TX, USA, 2007. [Google Scholar] [CrossRef]
- Rogers, S.; Elmo, D.; Dunphy, R.; Bearinger, D. Understanding hydraulic fracture geometry and interactions in the horn river basin through dfn and numerical modeling. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010; Society of Petroleum Engineers: Richardson, TX, USA, 2010. [Google Scholar] [CrossRef]
- Nagel, N.B.; Gil, I.; Sanchez-Nagel, M.; Damjanac, B. Simulating hydraulic fracturing in real fractured rocks-overcjavascript: Iterm()oming the limits of pseudo3D models. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 23–25 January 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar] [CrossRef]
- Weng, X.; Kresse, O.; Cohen, C.E.; Wu, R.; Gu, H. Modeling of hydraulic fracture network propagation in a naturally fractured formation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 23–25 January 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar] [CrossRef]
- Wu, R.; Kresse, O.; Weng, X.; Cohen, C.E.; Gu, H. Modeling of interaction of hydraulic fractures in complex fracture networks. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 23–25 January 2018; Society of Petroleum Engineers: The Woodlands, TX, USA, 2012. [Google Scholar] [CrossRef]
- Renshaw, C.E.; Pollard, D.D. An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic-materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 237–249. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at non-orthogonal angles. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010; American Rock Mechanics Association: Alexandria, VA, USA, 2010. [Google Scholar]
- Warpinski, N.; Lorenz, J.; Branagan, P.; Myal, F.; Gall, B. Examination of a cored hydraulic fracture in a deep gas well. SPE Prod. Facil. 1993, 8, 150–158. [Google Scholar] [CrossRef]
- Mahrer, K.D. A review and perspective on far-field hydraulic fracture geometry studies. J. Petrol. Sci. Eng. 1999, 24, 13–28. [Google Scholar] [CrossRef]
- Jeffrey, R.G.; Zhang, X.; Thiercelin, M.J. Hydraulic fracture offsetting in naturally fractures reservoirs: Quantifying a long-recognized process. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 5–7 February 2019; Society of Petroleum Engineers: Richardson, TX, USA, 2009. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous fluids. In Proceedings of the 4th World Petroleum Congress, Rome, Italy, 6–15 June 1955; Volume 2, pp. 579–586. [Google Scholar]
- Abé, H.; Mura, T.; Keer, L.M. Growth rate of a penny-shaped crack in hydraulic fracturing of rocks. J. Geophys. Res. 1976, 81, 5335–5340. [Google Scholar] [CrossRef]
- Settari, A.; Cleary, M.P. Three-dimensional simulation of hydraulic fracturing. J. Petrol. Technol. 1984, 36, 1177–1190. [Google Scholar] [CrossRef]
- Zhang, X.; Detournay, E.; Jeffrey, R. Propagation of a penny-shaped hydraulic fracture parallel to the free-surface of an elastic half-space. Int. J. Fract. 2002, 115, 125–158. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G. The role of friction and secondary flaws on deflection and re-initiation of hydraulic fractures at orthogonal pre-existing fractures. Geophys. J. Int. 2006, 166, 1454–1465. [Google Scholar] [CrossRef]
- Lecampion, B.; Detournay, E. An implicit algorithm for the propagation of a hydraulic fracture with a fluid lag. Comput. Methods Appl. Mech. Eng. 2007, 196, 4863–4880. [Google Scholar] [CrossRef]
- Dean, R.H.; Schmidt, J.H. Hydraulic-fracture predictions with a fully coupled geomechanical reservoir simulator. SPE J. 2009, 14, 707–714. [Google Scholar] [CrossRef]
- Ji, L.J.; Settari, A.; Sullivan, R.B. A novel hydraulic fracturing model fully coupled with geomechanics and reservoir simulation. SPE J. 2009, 14, 423–430. [Google Scholar] [CrossRef]
- Zhang, Z.; Ghassemi, A. Simulation of hydraulic fracture propagation near a natural fracture using virtual multidimensional internal bonds. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 480–495. [Google Scholar] [CrossRef]
- Chen, Z.R. Finite element modelling of viscosity-dominated hydraulic fractures. J. Petrol. Sci. Eng. 2012, 88–89, 136–144. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhang, Y.; Liu, J.S.; Zhang, B.Y. Numerical simulation of geofluid focusing and penetration due to hydraulic fracture. J. Geochem. Explor. 2010, 106, 211–218. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Numerical investigation on stress shadowing in fluid injection-induced fracture propagation in naturally fractured geothermal reservoirs. Rock Mech. Rock Eng. 2015, 48, 1439–1454. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Discrete element modeling of cyclic rate fluid injection at multiple locations in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2015, 74, 15–23. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A.; Stephansson, O. Discrete element modeling of fluid injection–induced seismicity and activation of nearby fault. Can. Geotech. J. 2015, 52, 1457–1465. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.N.; Stephansson, O. Numerical investigation on optimized stimulation of intact and naturally fractured deep geothermal reservoirs using hydro-mechanical coupled discrete particles joints model. Geothermics 2014, 52, 165–184. [Google Scholar] [CrossRef]
- Al-Busaidi, A.; Hazzard, J.F.; Young, R.P. Distinct element modeling of hydraulically fractured lac du bonnet granite. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Shimizu, H. Distinct Element Modeling for Fundamental Rock Fracturing and Application to Hydraulic Fracturing. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2010. [Google Scholar]
- Wang, T.; Zhou, W.B.; Chen, J.H.; Xiao, X.; Li, Y.; Zhao, X.Y. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. Int. J. Coal Geol. 2014, 121, 1–13. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Wang, T.; Elsworth, D.; He, Y.L.; Zhou, W.; Zhuang, L.; Zeng, J.; Wang, S.F. Controls of natural fractures on the texture of hydraulic fractures in rock. J. Petrol. Sci. Eng. 2018, 165, 616–626. [Google Scholar] [CrossRef]
- Huang, B. Research on Theory and Application of Hydraulic Fracture Weakening for Coal-Rock Mass. Ph.D. Thesis, China University of Mining Technology, Xuzhou, China, 2009. [Google Scholar]
- Zhao, H.F.; Wang, X.H.; Liu, Z.Y.; Yan, Y.J.; Yang, H.X. Investigation on the hydraulic fracture propagation of multilayers-commingled fracturing in coal measures. J. Petrol. Sci. Eng. 2018, 167, 774–784. [Google Scholar] [CrossRef]
- Nur, A.; Byerlee, J.D. An exact effective stress law for elastic deformation of rock with fluids. J. Geophys. Res. 1971, 76, 6414–6419. [Google Scholar] [CrossRef]
- Zhang, G.M.; Liu, H.; Zhang, J.; Wu, H.A.; Wang, X.X. Three-dimensional finite element numerical simulation of horizontal well hydraulic fracturing. Eng. Mech. 2011, 28, 101–106. [Google Scholar]
- Zhang, G.; Liu, H.; Zhang, J.; Biao, F.; Wu, H.; Wang, X. Simulation of hydraulic fracturing of oil well based on fluid-solid coupling equation and non-linear finite element. Acta Pet. Sin. 2009, 30, 113–116. [Google Scholar]
- Zhang, G.M.; Liu, H.; Zhang, J.; Wu, H.A.; Wang, X.X. Mathematical model and nonlinear finite element equation for reservoir fluid-solid coupling. Rock Soil Mech. 2010, 31, 1657–1662. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Shet, C.; Chandra, N. Analysis of energy balance when using cohesive zone models to simulate fracture processes. J. Eng. Mater. Technol. 2002, 124, 440–450. [Google Scholar] [CrossRef]
- Guo, T.K.; Qu, Z.Q.; Gong, D.Q.; Lei, X.; Liu, M. Numerical simulation of directional propagation of hydraulic fracture guided by vertical multi-radial boreholes. J. Nat. Gas Sci. Eng. 2016, 35, 175–188. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J.; Davila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Camanho, P.P. Failure Criteria for Fibre-Reinforced Polymer Composites. 2002. Available online: https://paginas.fe.up.pt/~stpinho/teaching/feup/y0506/fcriteria.pdf (accessed on 27 June 2018).
- Geng, Y.G.; Tang, D.Z.; Xu, H.; Tao, S.; Tang, S.L.; Ma, L.; Zhu, X.G. Experimental study on permeability stress sensitivity of reconstituted granular coal with different lithotypes. Fuel 2017, 202, 12–22. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Yu, L. A numerical approach for assessing effects of shear on equivalent permeability and nonlinear flow characteristics of 2-d fracture networks. Adv. Water Resour. 2018, 111, 289–300. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Abaqus 2017 Documentation. Available online: https://www.3ds.com/products-services/simulia/support/documentation/ (accessed on 27 June 2018).
- Liu, X. Mechanisms and Technical Features of Hydraulic Disturbance Method for Improvement of Coal and Rock Seams Permeability. Ph.D. Thesis, Henan Polytechnic University, Jiaozuo, China, 2015. [Google Scholar]

| Object | Mechanical Parameter | Value |
|---|---|---|
| Coal matrix | Elastic modulus (GPa) | 5 |
| Poisson’s ratio | 0.28 | |
| Tensile strength (MPa) | 0.77 | |
| Shear strength (cohesion) (MPa) | 6.42 | |
| Initial permeability (m/s) | 5 × 10−8 | |
| Initial porosity | 0.15 | |
| I-mode fracture energy (N/m) | 29.25 | |
| II-mode fracture energy (N/m) | 35.97 | |
| Initial leak-off coefficient (m/Pa·s) | 5 × 10−14 | |
| Discontinuous natural fractures | Tensile strength (MPa) | 0.005 |
| Shear strength (MPa) | 0.04 | |
| I-mode fracture energy (N/m) | 0.19 | |
| II-mode fracture energy (N/m) | 0.23 | |
| Initial leak-off coefficient (m/Pa·s) | 5 × 10−14 | |
| Fracturing liquid | Viscosity (Pa·s) | 0.005 |
| Density (kg/m3) | 1000 |
| Group | Minimum Principal Stress, σ3 (MPa) | Maximum Principal Stress, σ1 (MPa) | Stress Difference (MPa) |
|---|---|---|---|
| A | 10 | 12.5 | 2.5 |
| B | 10 | 15 | 5 |
| C | 10 | 17.5 | 7.5 |
| D | 10 | 20 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Li, H.; Li, D. Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks. Processes 2018, 6, 113. https://doi.org/10.3390/pr6080113
Wang S, Li H, Li D. Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks. Processes. 2018; 6(8):113. https://doi.org/10.3390/pr6080113
Chicago/Turabian StyleWang, Shen, Huamin Li, and Dongyin Li. 2018. "Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks" Processes 6, no. 8: 113. https://doi.org/10.3390/pr6080113
APA StyleWang, S., Li, H., & Li, D. (2018). Numerical Simulation of Hydraulic Fracture Propagation in Coal Seams with Discontinuous Natural Fracture Networks. Processes, 6(8), 113. https://doi.org/10.3390/pr6080113






