A High-Order Numerical Manifold Method for Darcy Flow in Heterogeneous Porous Media
Abstract
1. Introduction
2. Basic Theory of NMM
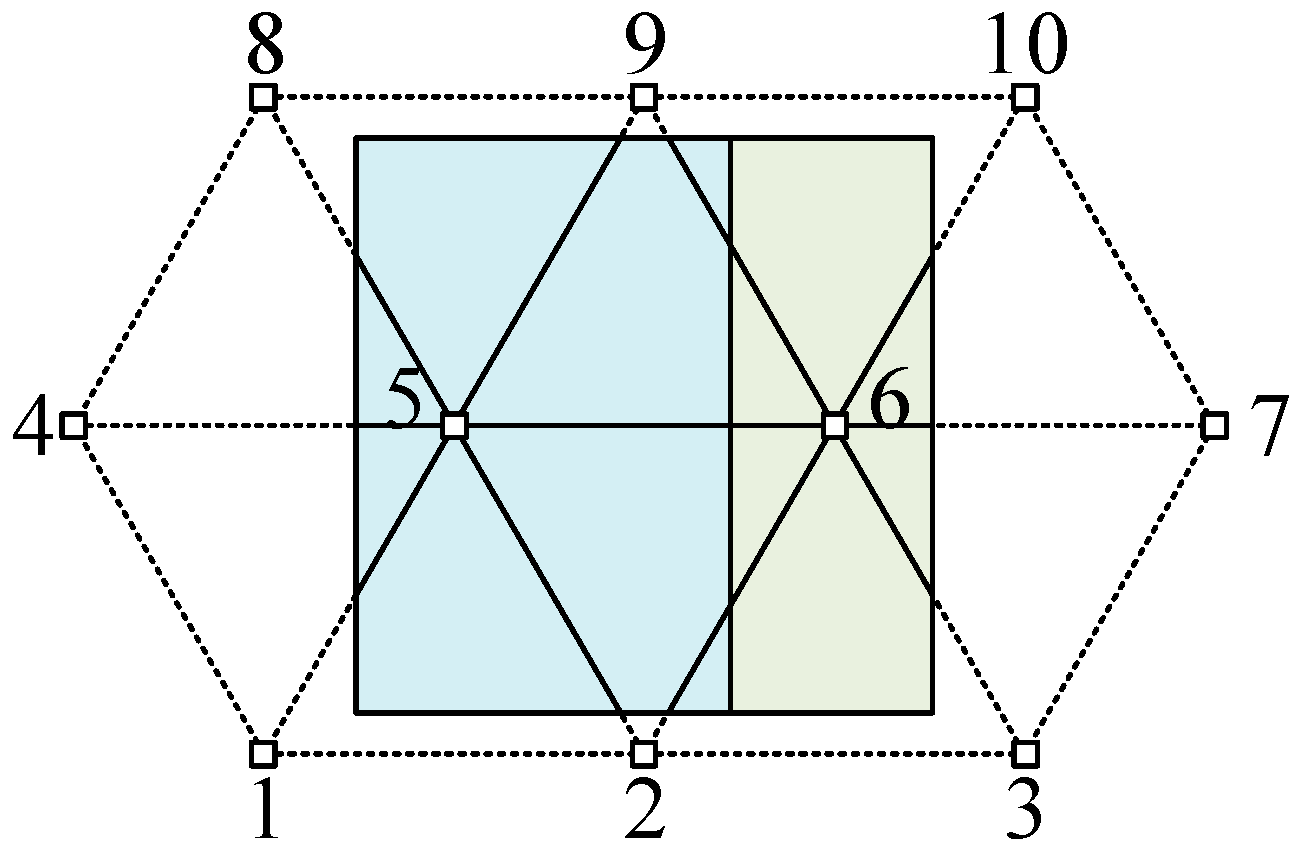
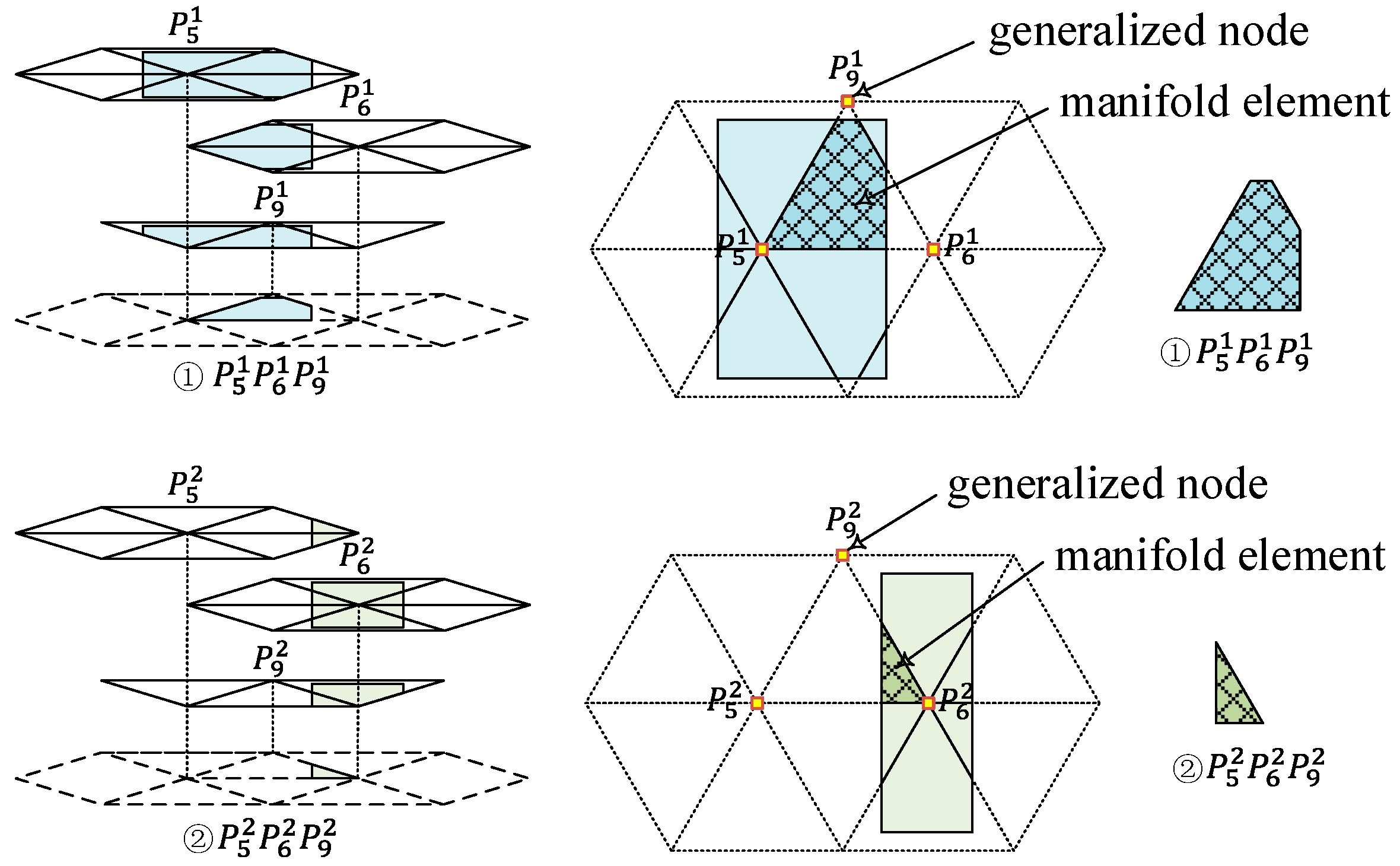
2.1. Dual Cover Systems and Manifold Elements
2.2. Local Approximation on Physical Covers
2.3. Global Approximation on Manifold Elements
3. Steady Darcy Flow in Heterogeneous Porous Media by NMM
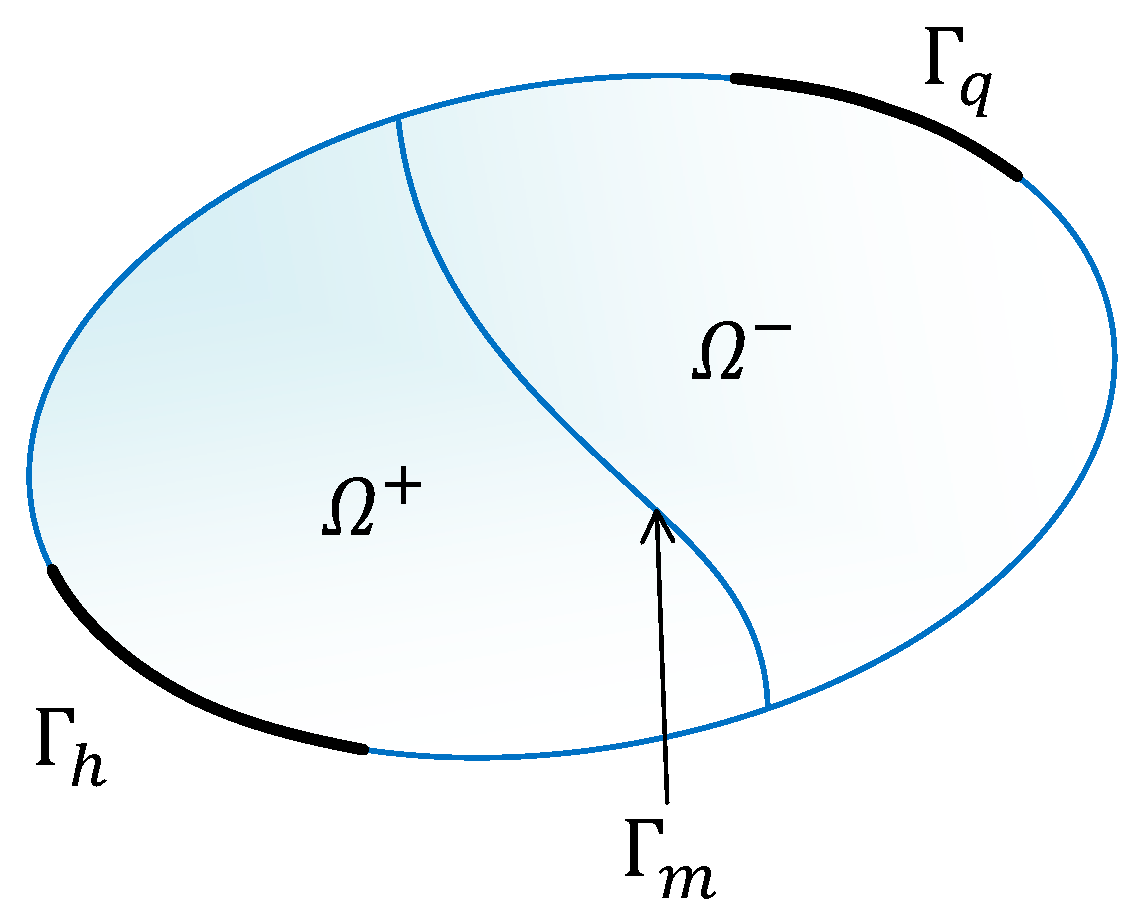
3.1. Governing Equations
3.2. NMM Interpolations
- (1)
- the Kronecker delta property ( ()),
- (2)
- the non-negative property ( ()),
- (3)
- the partition of the unity condition (),
- (4)
- and a nodal gradient of zero of the weight function.
3.3. Discrete Equations
3.4. Treatments for Boundaries and Material Interfaces
4. Numerical Examples
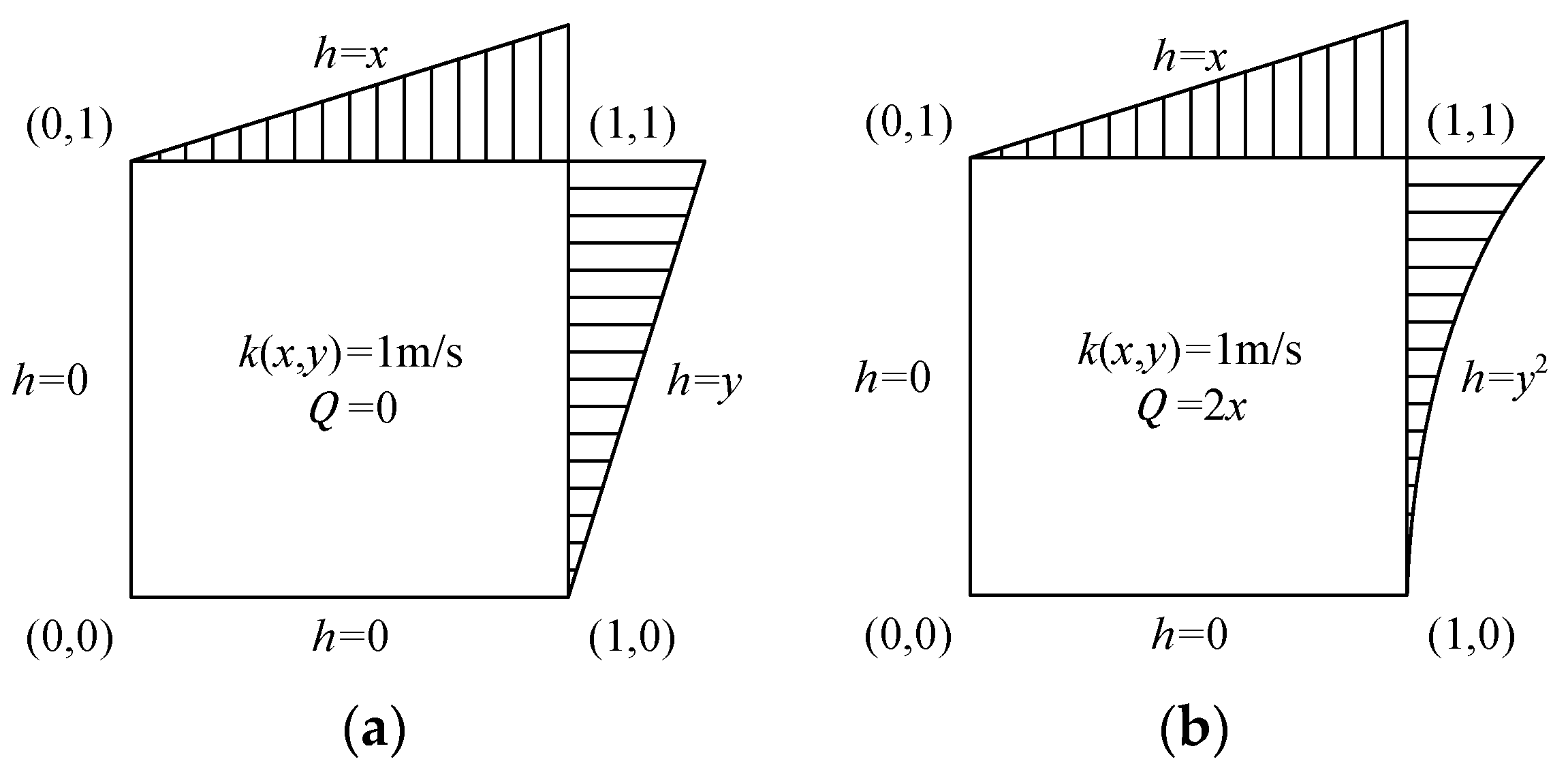
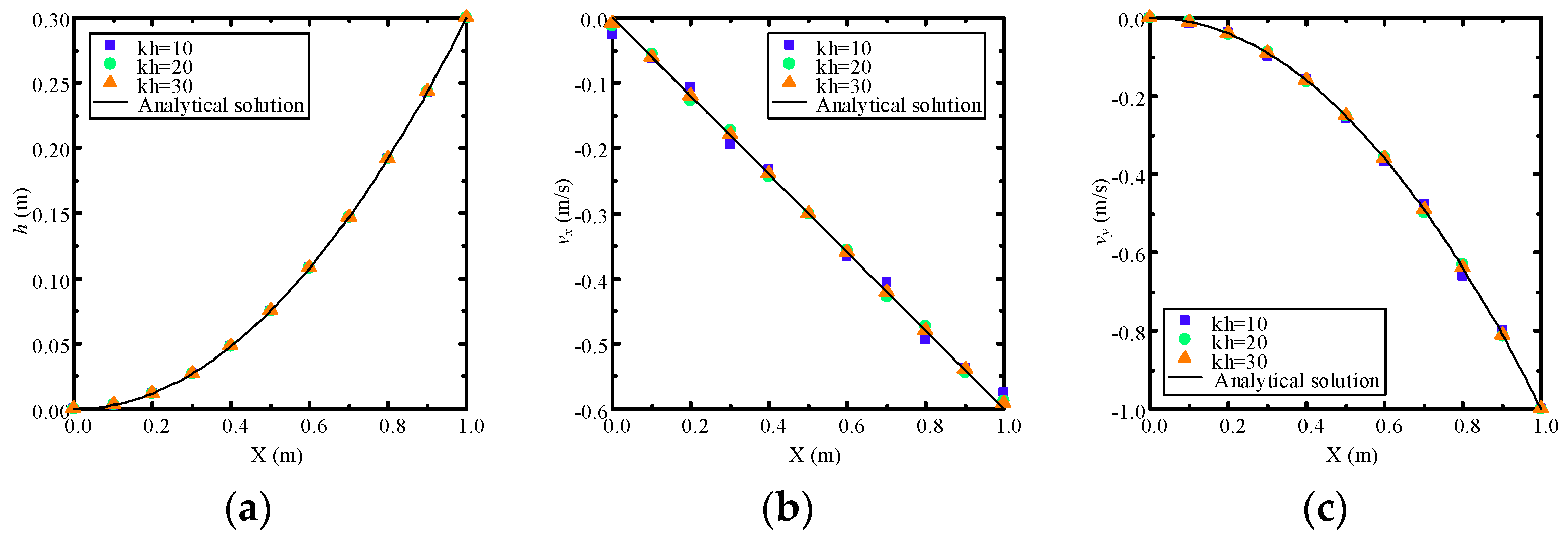
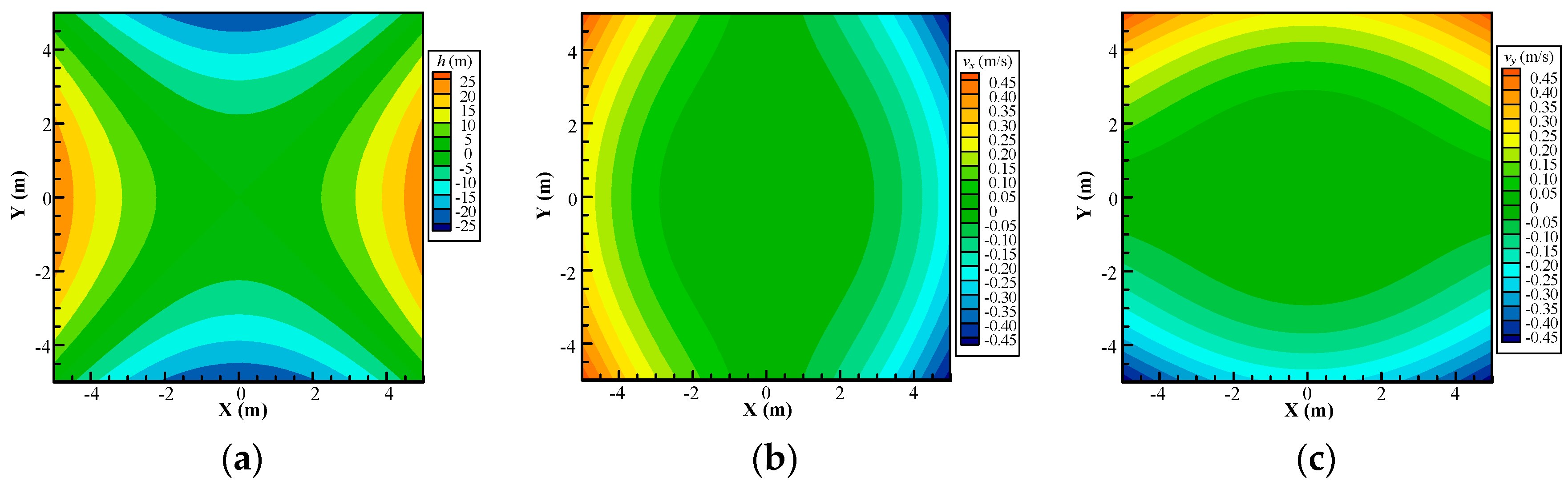
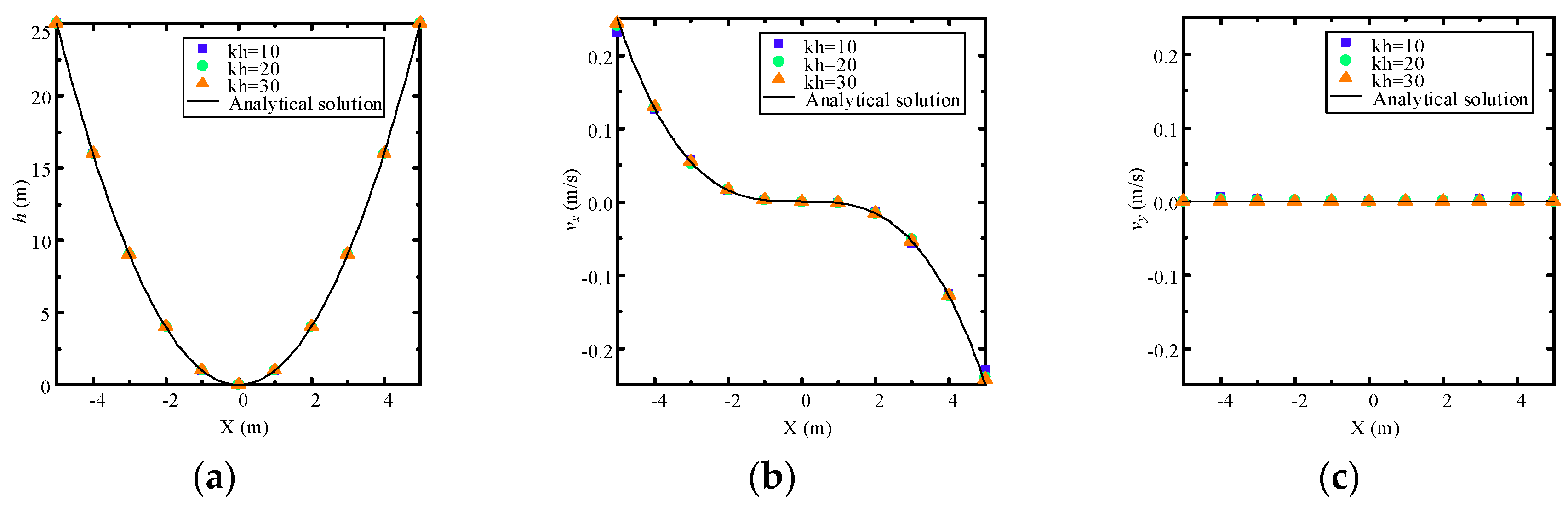
4.1. Example 1: Verification of Homogeneous Darcy Flow with an Analytical Solution
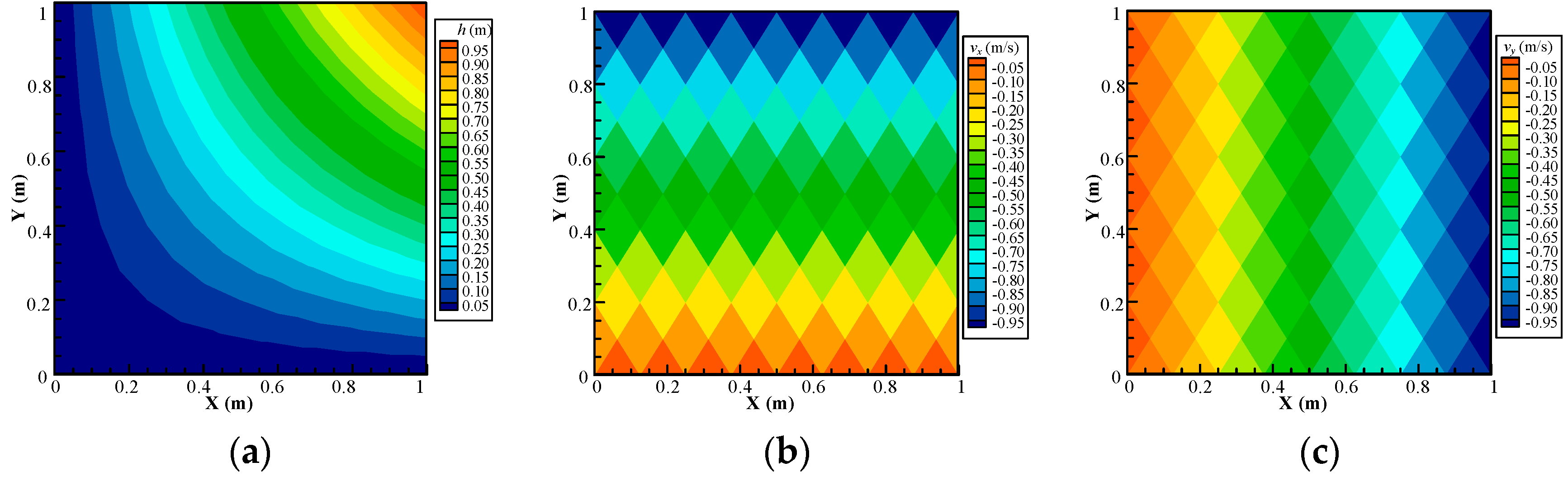
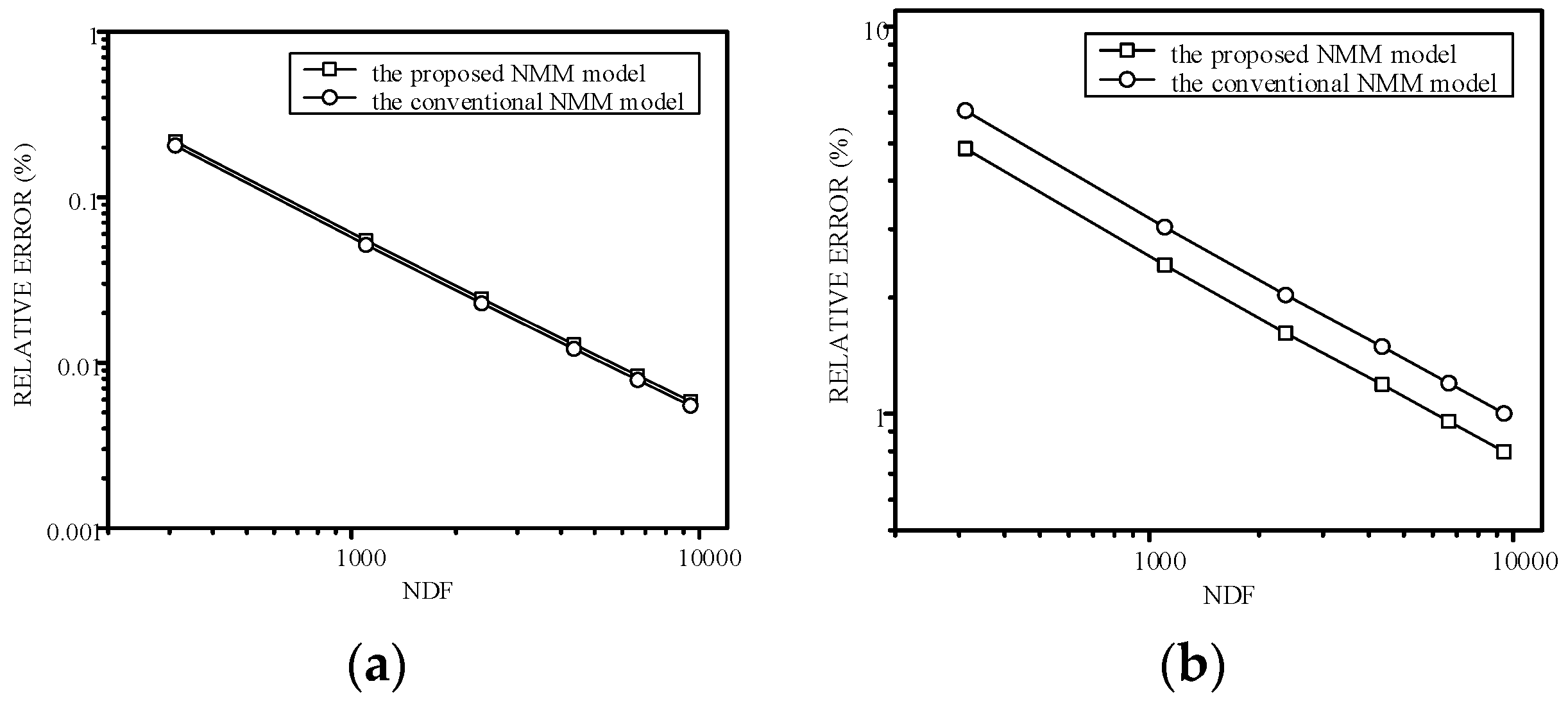
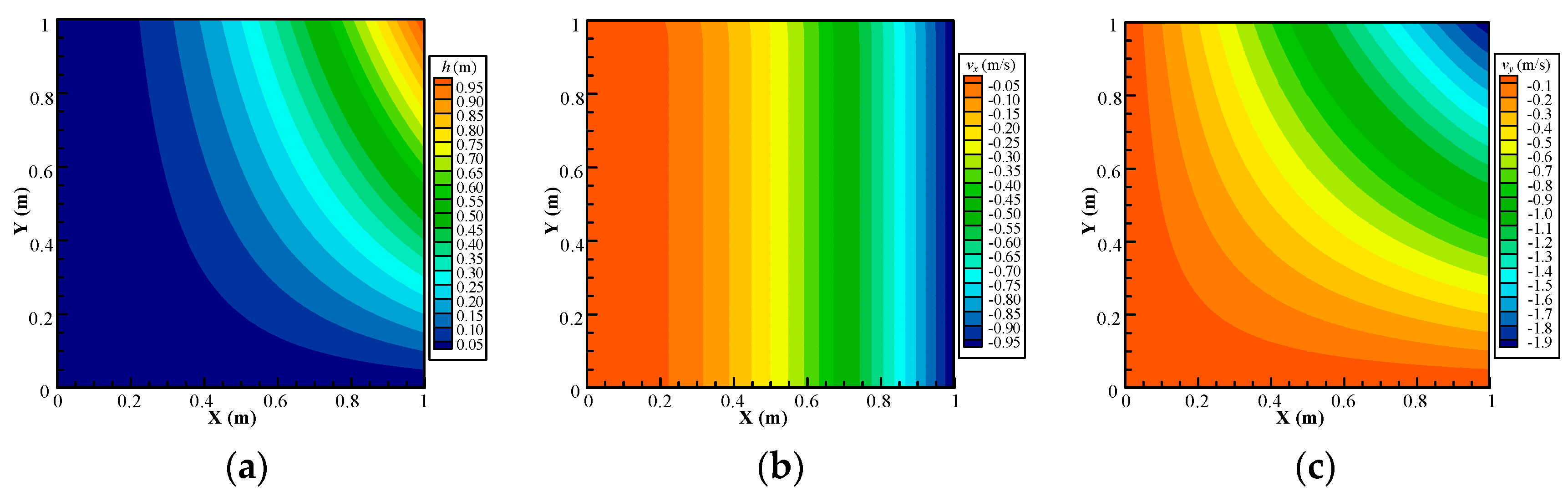
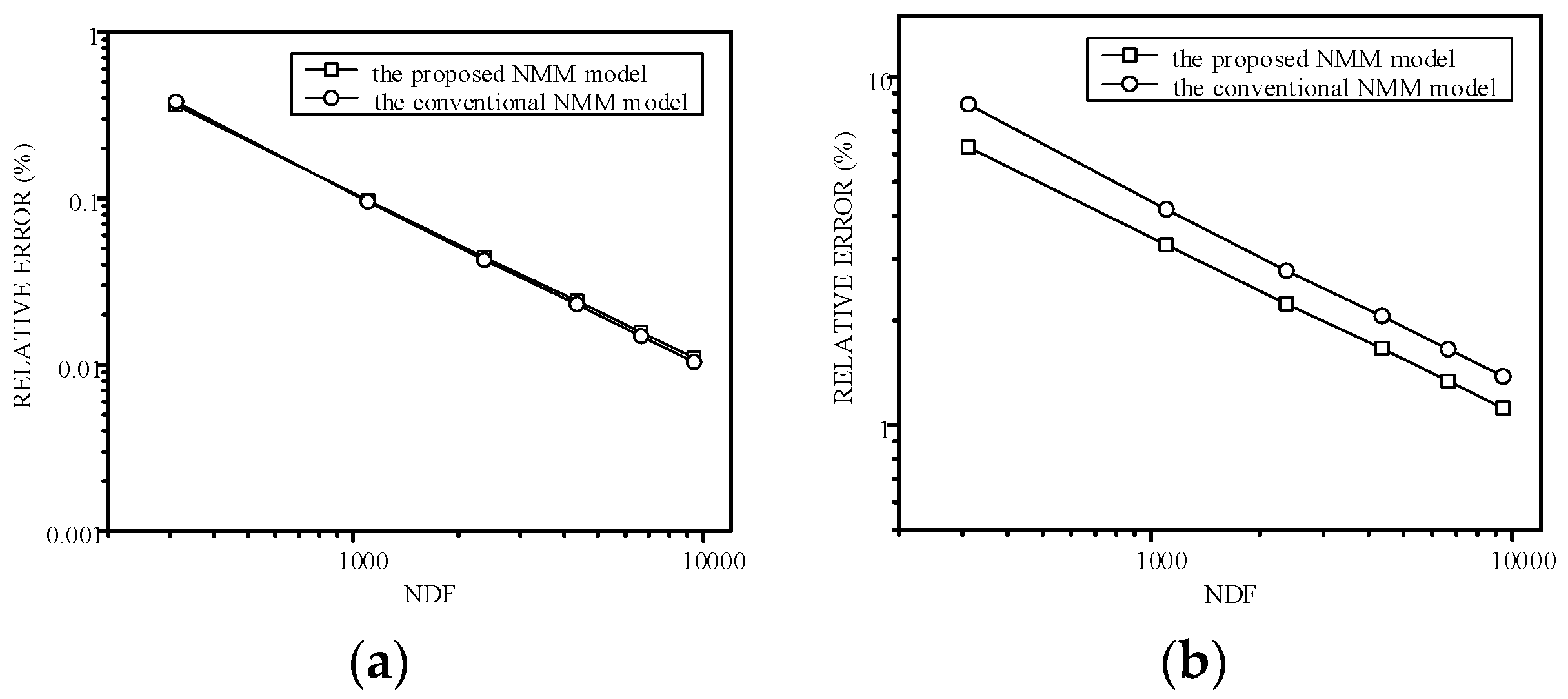
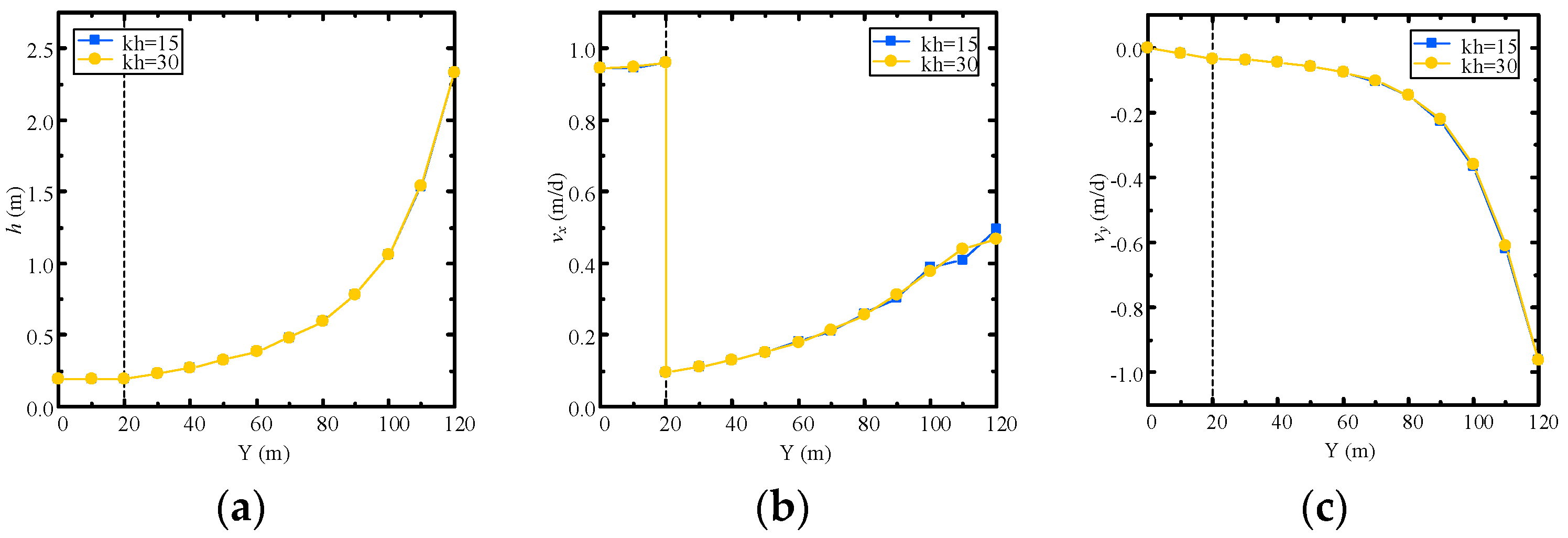
4.2. Example 2: Accuracy Darcy Velocity Solution for Continuous-Heterogeneous Media
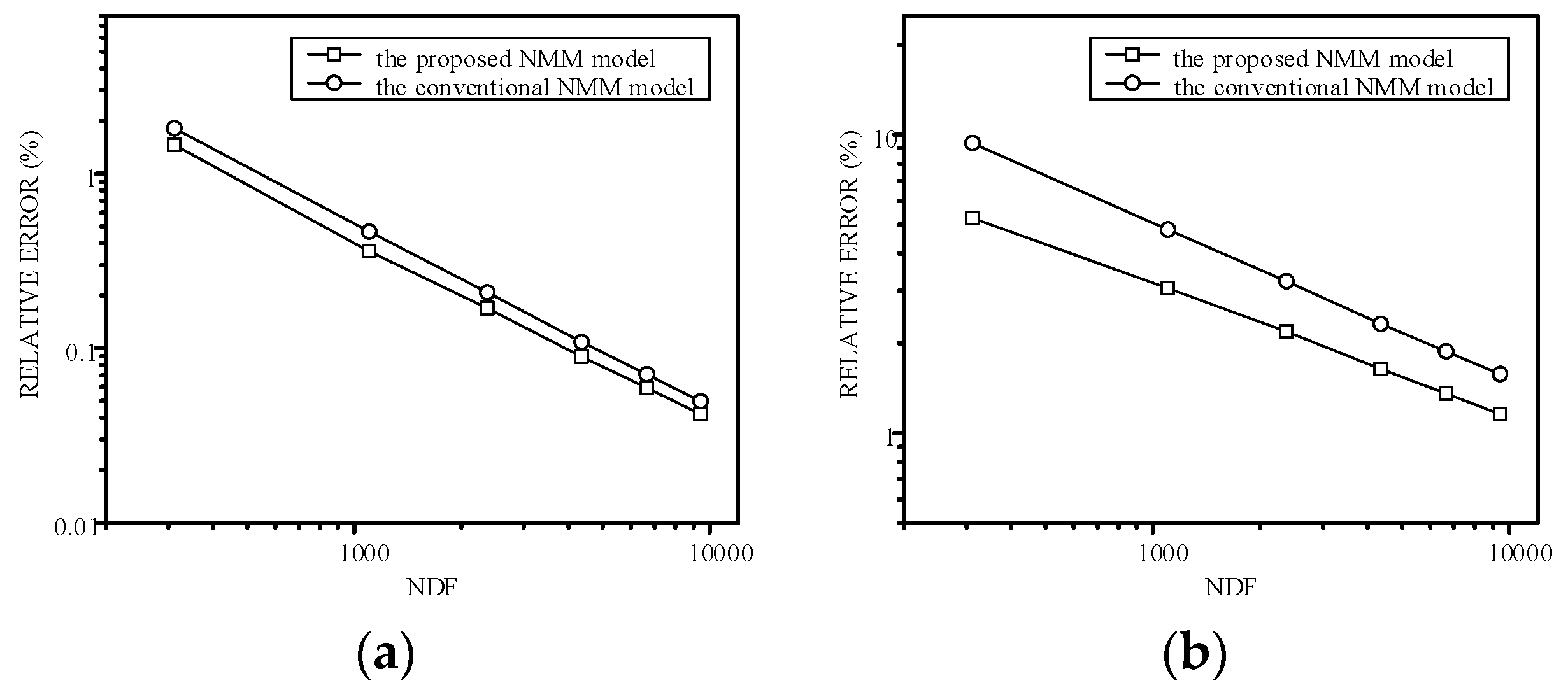
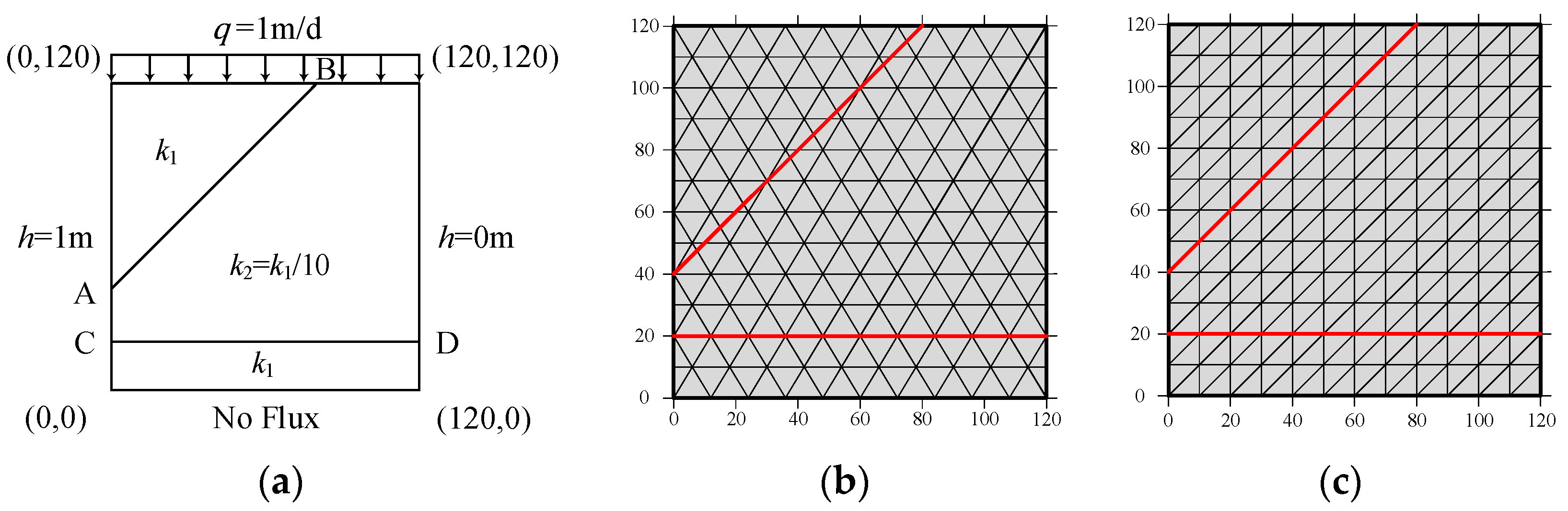
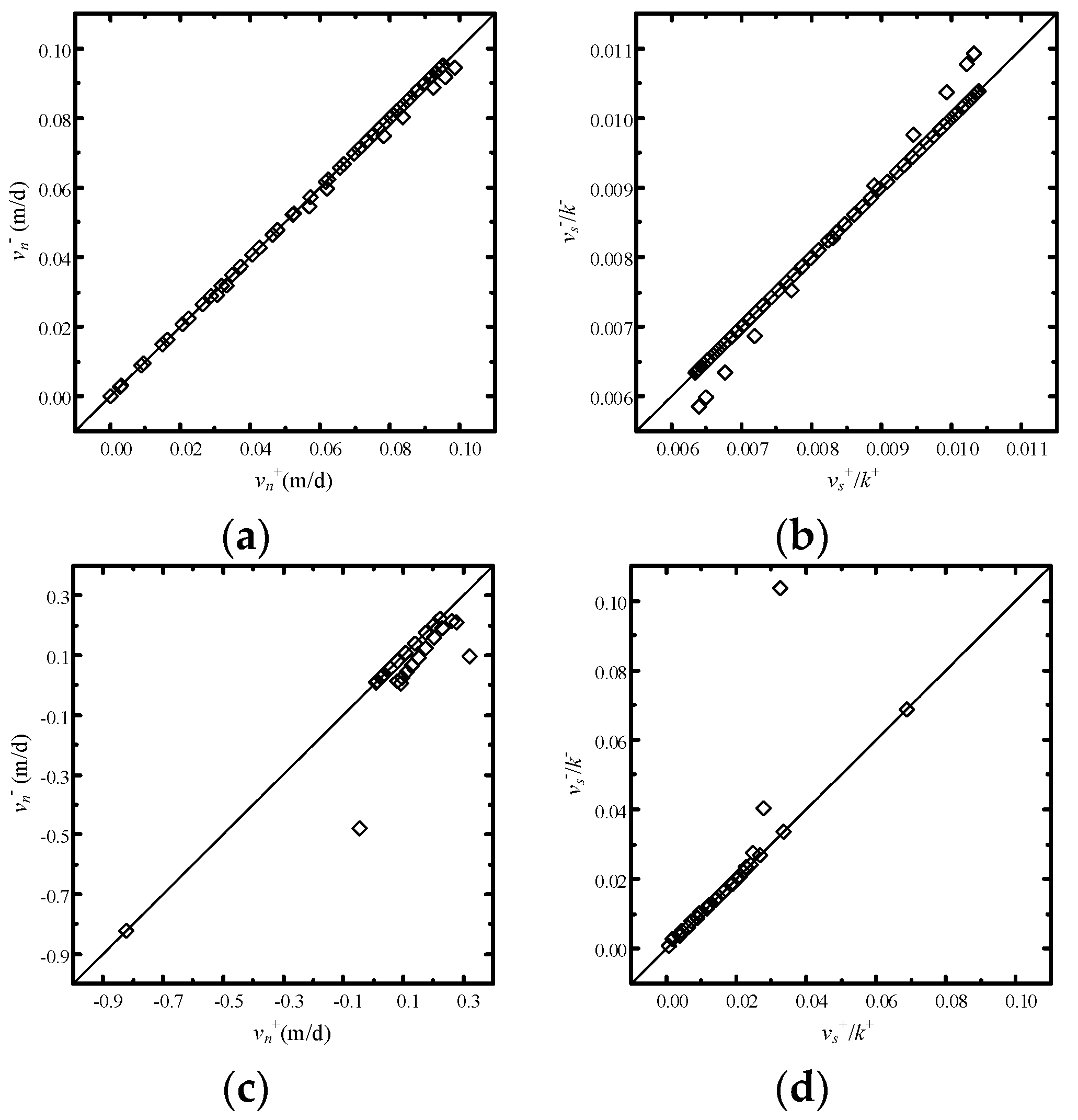
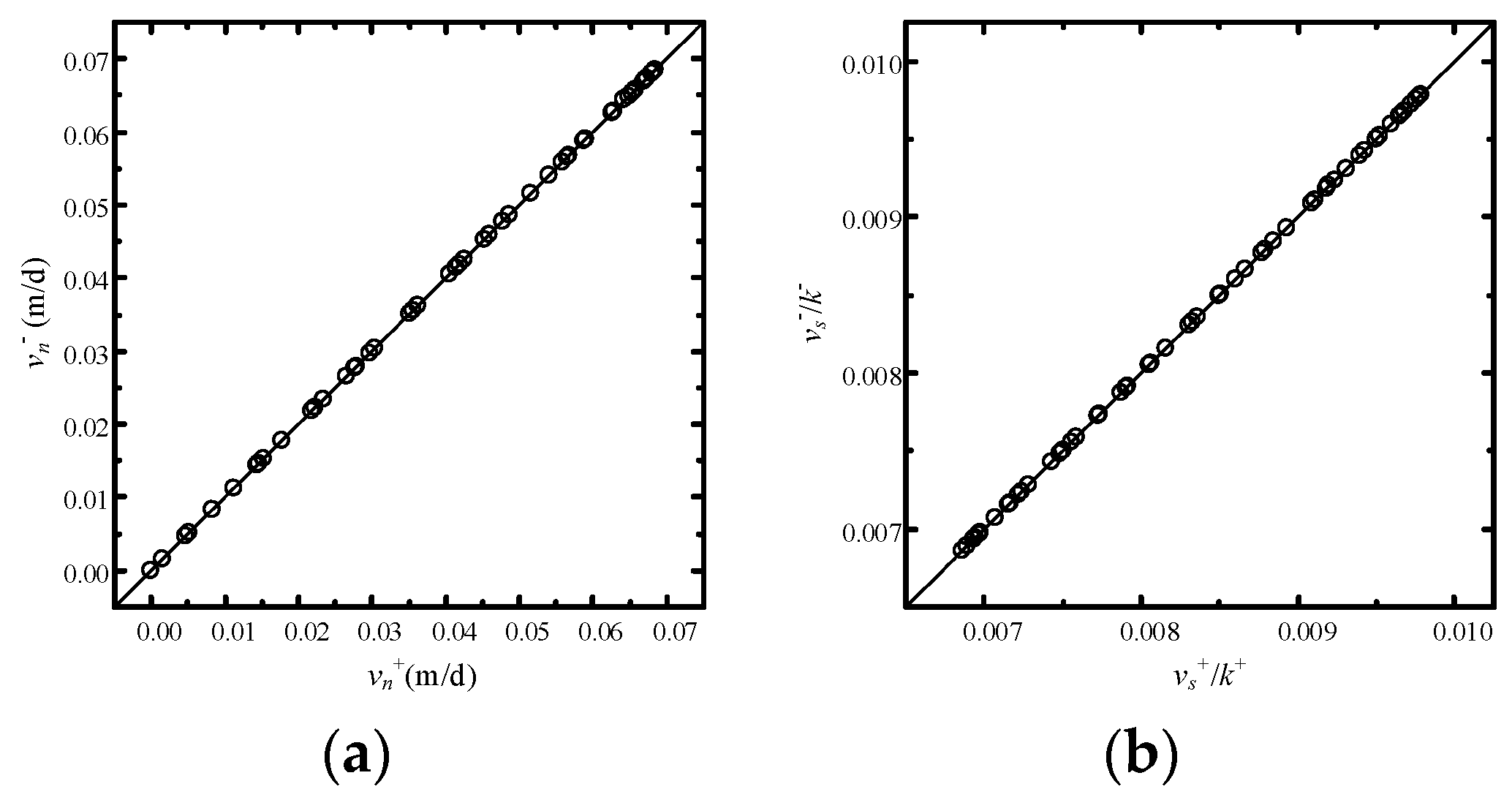
4.3. Example 3: Verification of Refraction Law for Discontinuous-Heterogeneous Media
5. Discussion and Conclusions
- (1)
- the solution of Darcy velocity is accurate, and continuous at each node;
- (2)
- the material interfaces exactly satisfy the refraction law, and thus the simulation results can be accurate and reliable; and
- (3)
- the pre-processing work is efficient, due to the two independent cover systems of NMM, in contrast with other numerical schemes. Especially for complex heterogeneous problems even with intersecting material interfaces, the proposed model provides a significant advantage.
Author Contributions
Funding
Conflicts of Interest
References
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Cainelli, O.; Bellin, A.; Putti, M. On the accuracy of classic numerical schemes for modeling flow in saturated heterogeneous formations. Adv. Water Resour. 2012, 47, 43–55. [Google Scholar] [CrossRef]
- Bellin, A.; Salandin, P.; Rinaldo, A. Simulation of dispersion in heterogeneous porous formations: Statistics, first-order theories, convergence of computations. Water Resour. Res. 1992, 28, 2211–2227. [Google Scholar] [CrossRef]
- Neuman, S.; Orr, S.; Levin, O.; Paleologos, E. Theory and high-resolution finite element analysis of 2-d and 3-d effective permeabilities in strongly heterogeneous porous media. In Proceedings of the 9th International Conference on Computational Methods in Water Resources, Denver, CO, USA, 1 June 1992. [Google Scholar]
- Ababou, R.; McLaughlin, D.; Gelhar, L.W.; Tompson, A.F. Numerical simulation of three-dimensional saturated flow in randomly heterogeneous porous media. Transp. Porous Media 1989, 4, 549–565. [Google Scholar] [CrossRef]
- Chin, D.A.; Wang, T. An investigation of the validity of first-order stochastic dispersion theories in isotropie porous media. Water Resour. Res. 1992, 28, 1531–1542. [Google Scholar] [CrossRef]
- Tompson, A.F.; Gelhar, L.W. Numerical simulation of solute transport in three-dimensional, randomly heterogeneous porous media. Water Resour. Res. 1990, 26, 2541–2562. [Google Scholar] [CrossRef]
- Batu, V. A finite element dual mesh method to calculate nodal darcy velocities in nonhomogeneous and anisotropic aquifers. Water Resour. Res. 1984, 20, 1705–1717. [Google Scholar] [CrossRef]
- Yeh, G.T. On the computation of Darcian velocity and mass balance in finite elements modeling of groundwater flow. Water Resour. Res. 1981, 17, 1529–1534. [Google Scholar] [CrossRef]
- Zhang, Z.; Xue, Y.; Wu, J. A cubic-spline technique to calculate nodal Darcian velocities in aquifers. Water Resour. Res. 1994, 30, 975–981. [Google Scholar] [CrossRef]
- D’Angelo, C.; Scotti, A. A mixed finite element method for darcy flow in fractured porous media with non-matching grids. ESAIM-Math 2012, 46, 465–489. [Google Scholar] [CrossRef]
- Masud, A.; Hughes, T.J.R. A stabilized mixed finite element method for darcy flow. Comput. Meth. Appl. Mech. Eng. 2002, 191, 4341–4370. [Google Scholar] [CrossRef]
- Mosé, R.; Siegel, P.; Ackerer, P.; Chavent, G. Application of the mixed hybrid finite element approximation in a groundwater flow model: Luxury or necessity? Water Resour. Res. 1994, 30, 3001–3012. [Google Scholar] [CrossRef]
- Zhou, Q.; Bensabat, J.; Bear, J. Accurate calculation of specific discharge in heterogeneous porous media. Water Resour. Res. 2001, 37, 3057–3069. [Google Scholar] [CrossRef]
- Xie, Y.F.; Wu, J.C.; Xue, Y.Q.; Xie, C.H.; Ji, H.F. A domain decomposed finite element method for solving darcian velocity in heterogeneous porous media. J. Hydrol. 2017, 554, 32–49. [Google Scholar] [CrossRef]
- Shi, G.H. Manifold method of material analysis. In Proceedings of the Transactions of the 9th Army Conference on Applied Mathematics and Computing, Minneapolis, MN, USA, 18–21 June 1991; pp. 57–76. [Google Scholar]
- Shi, G.H. Modeling rock joints and blocks by manifold method. In Proceedings of the 33th U.S. Symposium on Rock Mechanics, Santa Fe, NM, USA, 3–5 June 1992; pp. 639–648. [Google Scholar]
- Ma, G.W.; An, X.M.; Zhang, H.H.; Li, L.X. Modeling complex crack problems using the numerical manifold method. Int. J. Fract. 2009, 156, 21–35. [Google Scholar] [CrossRef]
- Zhang, H.H.; Li, L.X.; An, X.M.; Ma, G.W. Numerical analysis of 2-d crack propagation problems using the numerical manifold method. Eng. Anal. Bound. Elem. 2010, 34, 41–50. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wong, L.N.Y. Frictional crack initiation and propagation analysis using the numerical manifold method. Comput. Geotech. 2012, 39, 38–53. [Google Scholar] [CrossRef]
- Zheng, H.; Xu, D.D. New strategies for some issues of numerical manifold method in simulation of crack propagation. Int. J. Numer. Methods Eng. 2014, 97, 986–1010. [Google Scholar] [CrossRef]
- Ning, Y.J.; An, X.M.; Ma, G.W. Footwall slope stability analysis with the numerical manifold method. Int. J. Rock Mech. Min. Sci. 2011, 48, 964–975. [Google Scholar] [CrossRef]
- He, L.; An, X.M.; Ma, G.W.; Zhao, Z.Y. Development of three-dimensional numerical manifold method for jointed rock slope stability analysis. Int. J. Rock Mech. Min. Sci. 2013, 64, 22–35. [Google Scholar] [CrossRef]
- An, X.M.; Ning, Y.J.; Ma, G.W.; He, L. Modeling progressive failures in rock slopes with non-persistent joints using the numerical manifold method. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 679–701. [Google Scholar] [CrossRef]
- Fan, L.F.; Yi, X.W.; Ma, G.W. Numerical manifold method (NMM) simulation of stress wave propagation through fractured rock mass. Int. J. Appl. Mech. 2013, 5, 20. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wong, L.N.Y.; Fan, L.F. Dynamic study on fracture problems in viscoelastic sedimentary rocks using the numerical manifold method. Rock Mech. Rock Eng. 2013, 46, 1415–1427. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Wu, Z.J. Application of the numerical manifold method to model progressive failure in rock slopes. Eng. Fract. Mech. 2014, 119, 1–20. [Google Scholar] [CrossRef]
- Zhao, G.F.; Zhao, X.B.; Zhu, J.B. Application of the numerical manifold method for stress wave propagation across rock masses. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 92–110. [Google Scholar] [CrossRef]
- Ohnishi, Y.; Tanaka, M.; Koyama, T.; Mutoh, K. Manifold method in saturated-unsaturated unsteady groundwater flow analysis. In Proceedings of the Third International Conference on Analysis of Discontinuous Deformation (ICADD-3), Vail, CO, USA, 3–4 June 1999; pp. 221–230. [Google Scholar]
- Zhang, Z.R.; Zhang, X.W.; Yan, J.H. Manifold method coupled velocity and pressure for navier-stokes equations and direct numerical solution of unsteady incompressible viscous flow. Comput. Fluids 2010, 39, 1353–1365. [Google Scholar] [CrossRef]
- Jiang, Q.H.; Deng, S.S.; Zhou, C.B.; Lu, W.B. Modeling unconfined seepage flow using three-dimensional numerical manifold method. J. Hydrodyn. 2010, 22, 554–561. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, M.S.; Zhou, Q.L.; Rutqvist, J. Energy-work-based numerical manifold seepage analysis with an efficient scheme to locate the phreatic surface. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1633–1650. [Google Scholar] [CrossRef]
- Hu, M.S.; Wang, Y.; Rutqvist, J. On continuous and discontinuous approaches for modeling groundwater flow in heterogeneous media using the numerical manifold method: Model development and comparison. Adv. Water Resour. 2015, 80, 17–29. [Google Scholar] [CrossRef]
- Hu, M.S.; Wang, Y.; Rutqvist, J. An effective approach for modeling fluid flow in heterogeneous media using numerical manifold method. Int. J. Numer. Methods Fluids 2015, 77, 459–476. [Google Scholar] [CrossRef]
- Hu, M.S.; Wang, Y.; Rutqvist, J. Development of a discontinuous approach for modeling fluid flow in heterogeneous media using the numerical manifold method. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1932–1952. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, F.; Li, C.G. Primal mixed solution to unconfined seepage flow in porous media with numerical manifold method. Appl. Math. Model. 2015, 39, 794–808. [Google Scholar] [CrossRef]
- Yang, Y.T.; Zheng, H. A three-node triangular element fitted to numerical manifold method with continuous nodal stress for crack analysis. Eng. Fract. Mech. 2016, 162, 51–75. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Sun, G.H.; Zheng, H. Modeling complex crack problems using the three-node triangular element fitted to numerical manifold method with continuous nodal stress. Sci. China Technol. Sci. 2017, 60, 1537–1547. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]







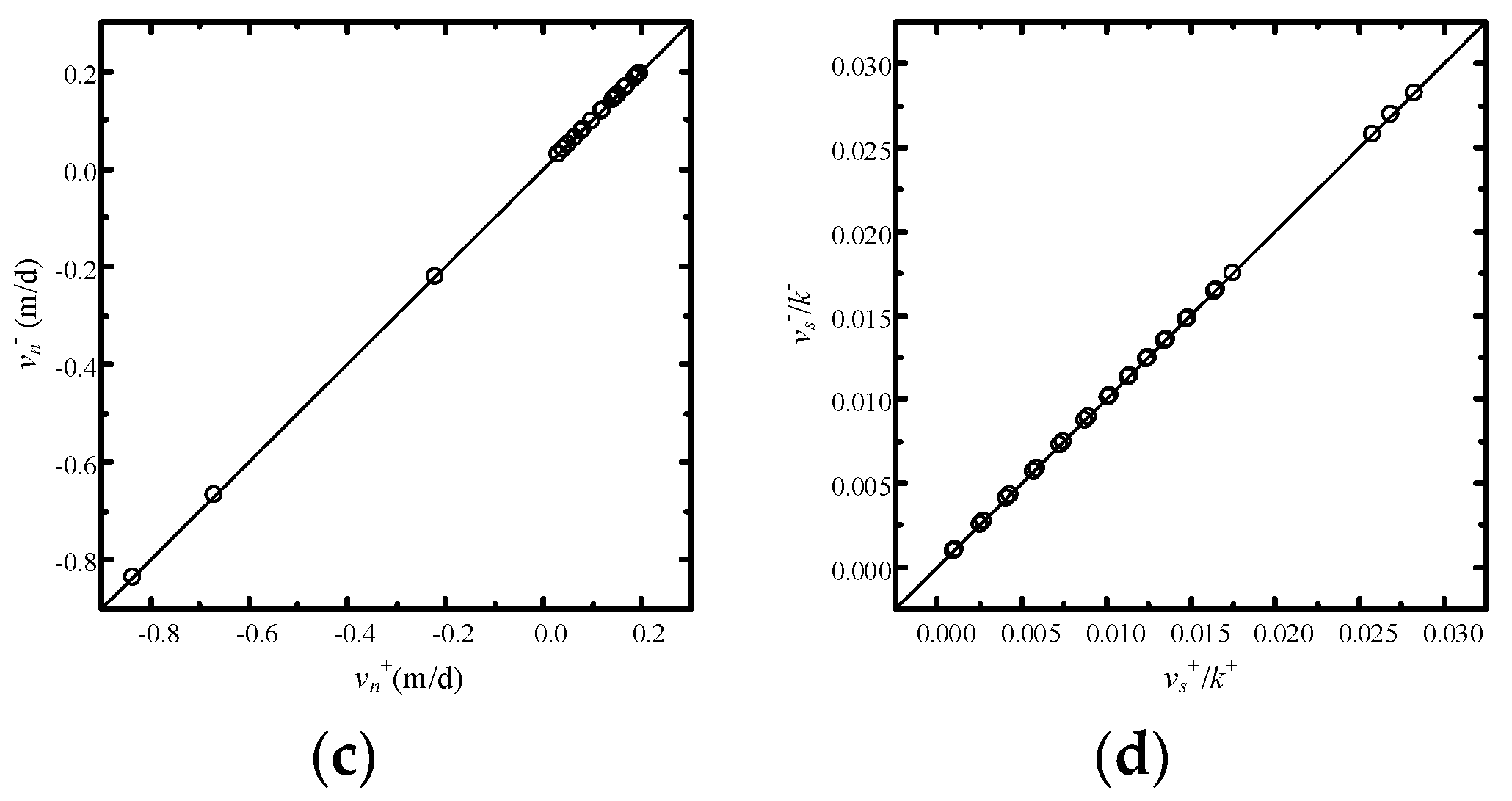
| kh 1 | L2 Error of Hydraulic Head | L2 Error of Darcy Velocity | ||
|---|---|---|---|---|
| Relative Error | Convergence Rate | Relative Error | Convergence Rate | |
| 5 | 2.18 × 10−3 | – | 4.84 × 10−2 | – |
| 10 | 5.47 × 10−4 | −1.10 | 2.42 × 10−2 | −0.55 |
| 15 | 2.44 × 10−4 | −1.06 | 1.61 × 10−2 | −0.53 |
| 20 | 1.29 × 10−4 | −1.04 | 1.19 × 10−2 | −0.50 |
| 25 | 8.36 × 10−5 | −1.03 | 9.55 × 10−3 | −0.52 |
| 30 | 5.86 × 10−5 | −1.02 | 7.98 × 10−3 | −0.52 |
| kh | L2 Error of Hydraulic Head | L2 Error of Darcy Velocity | ||
|---|---|---|---|---|
| Relative Error | Convergence Rate | Relative Error | Convergence Rate | |
| 5 | 2.05 × 10−3 | – | 6.07 × 10−2 | – |
| 10 | 5.14 × 10−4 | −1.10 | 3.04 × 10−2 | −0.55 |
| 15 | 2.29 × 10−4 | −1.06 | 2.03 × 10−2 | −0.53 |
| 20 | 1.21 × 10−4 | −1.04 | 1.49 × 10−2 | −0.50 |
| 25 | 7.84 × 10−5 | −1.03 | 1.20 × 10−2 | −0.52 |
| 30 | 5.49 × 10−5 | −1.02 | 1.00 × 10−2 | −0.52 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Wang, Y.; Feng, D. A High-Order Numerical Manifold Method for Darcy Flow in Heterogeneous Porous Media. Processes 2018, 6, 111. https://doi.org/10.3390/pr6080111
Zhou L, Wang Y, Feng D. A High-Order Numerical Manifold Method for Darcy Flow in Heterogeneous Porous Media. Processes. 2018; 6(8):111. https://doi.org/10.3390/pr6080111
Chicago/Turabian StyleZhou, Lingfeng, Yuan Wang, and Di Feng. 2018. "A High-Order Numerical Manifold Method for Darcy Flow in Heterogeneous Porous Media" Processes 6, no. 8: 111. https://doi.org/10.3390/pr6080111
APA StyleZhou, L., Wang, Y., & Feng, D. (2018). A High-Order Numerical Manifold Method for Darcy Flow in Heterogeneous Porous Media. Processes, 6(8), 111. https://doi.org/10.3390/pr6080111




