Modelling of a Naphtha Recovery Unit (NRU) with Implications for Process Optimization
Abstract
:1. Introduction
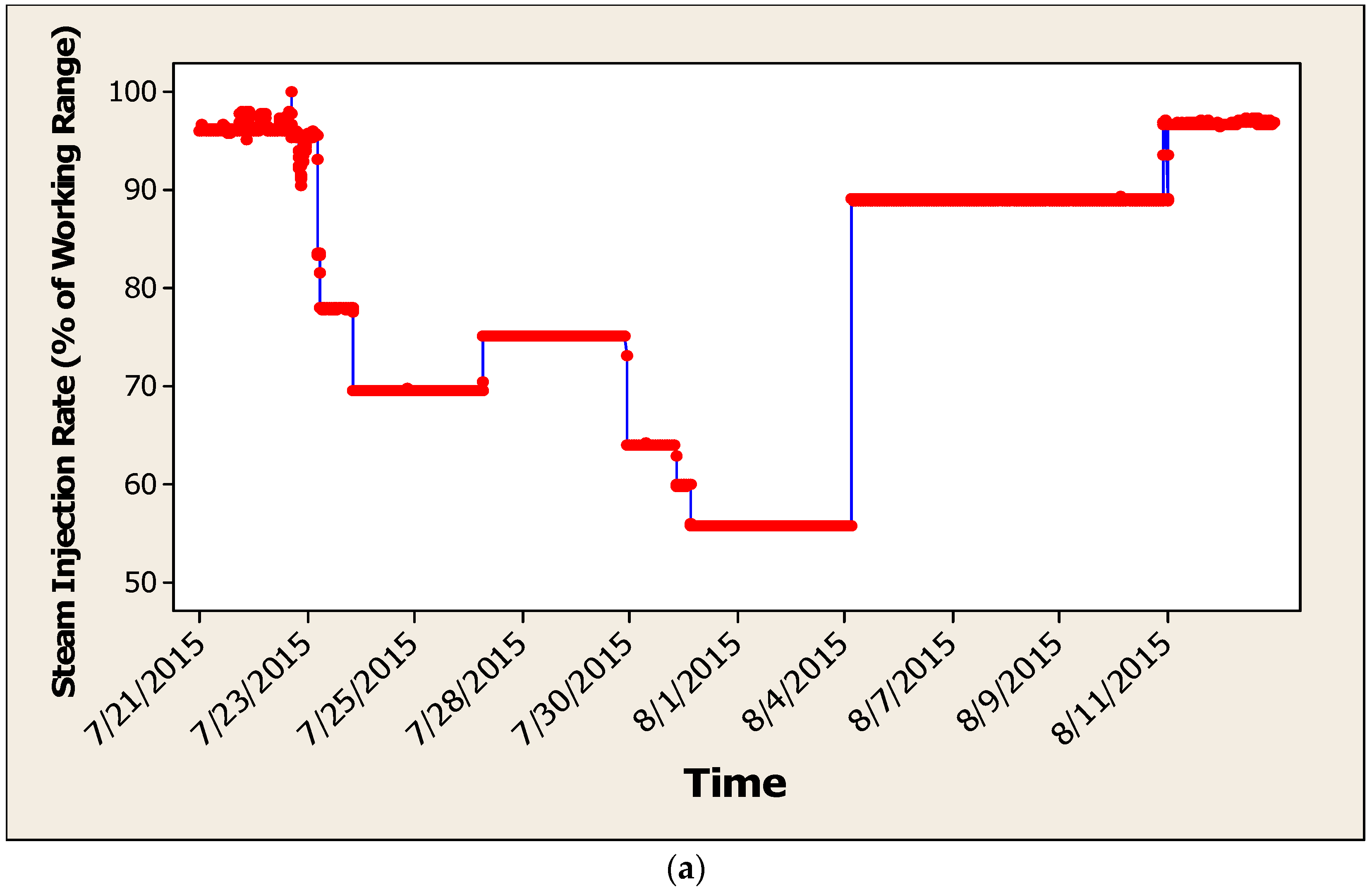
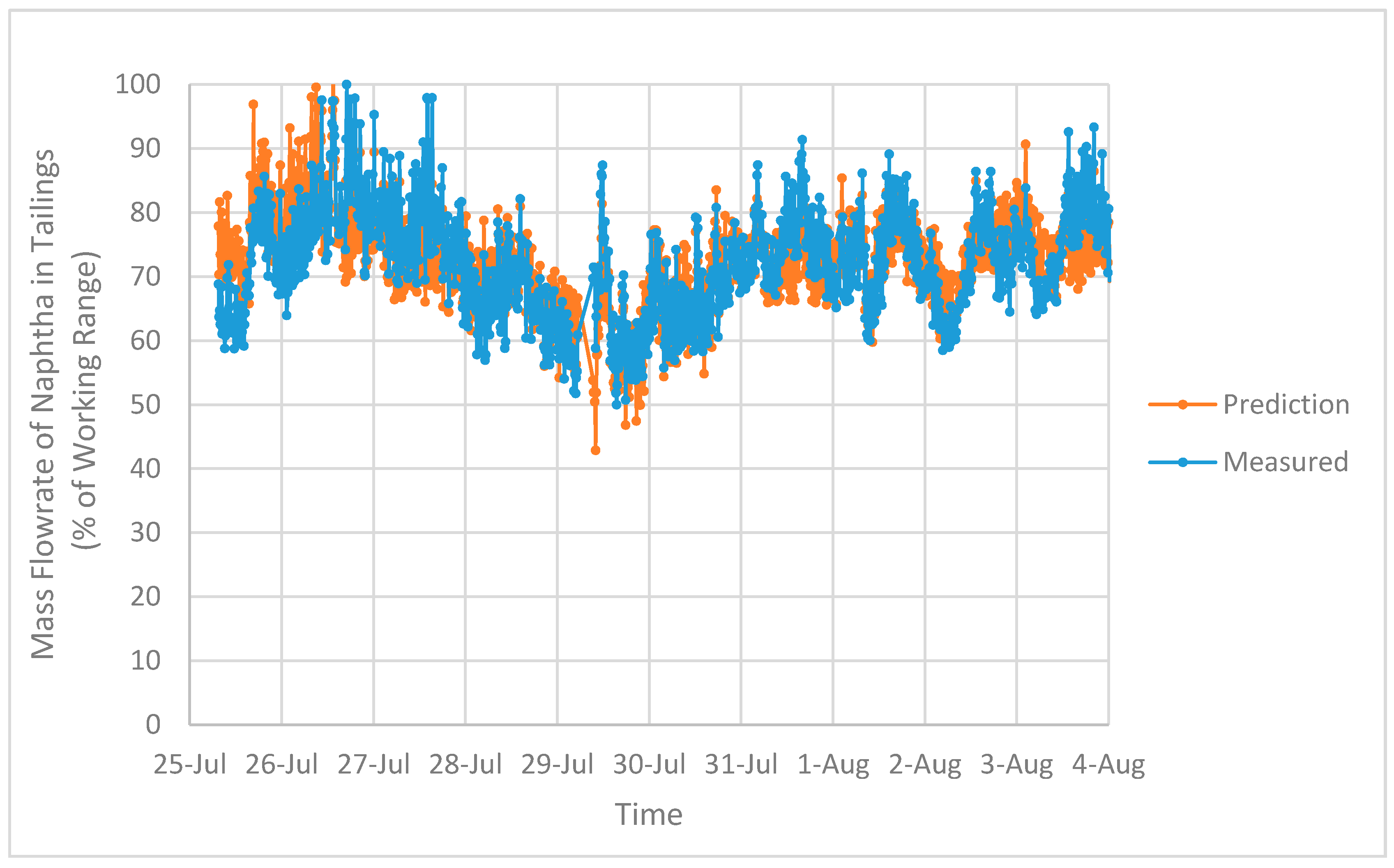
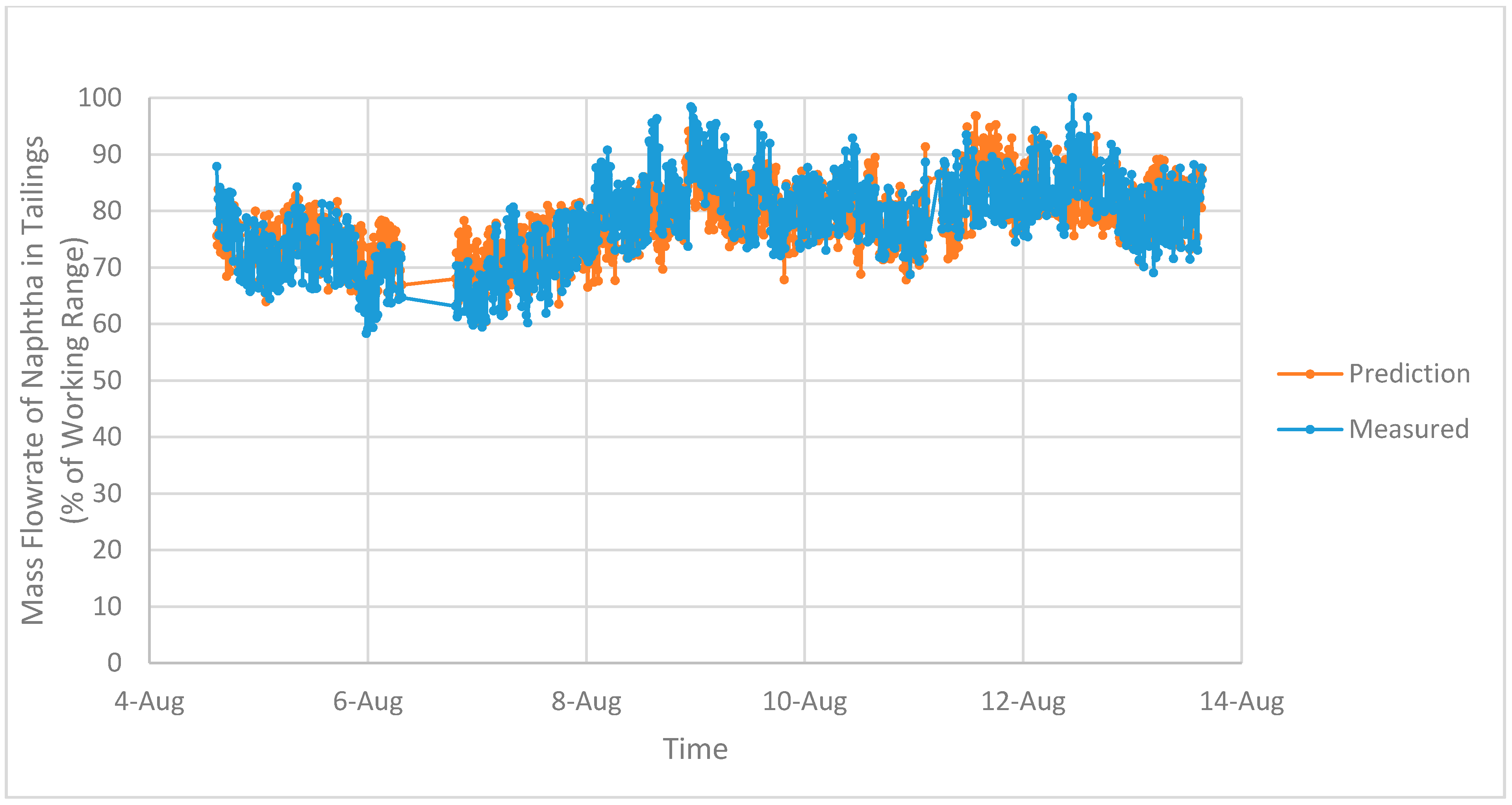
2. Performance Test on the NRU
3. Statistical Modelling of the NRU Using Minitab® (V16)
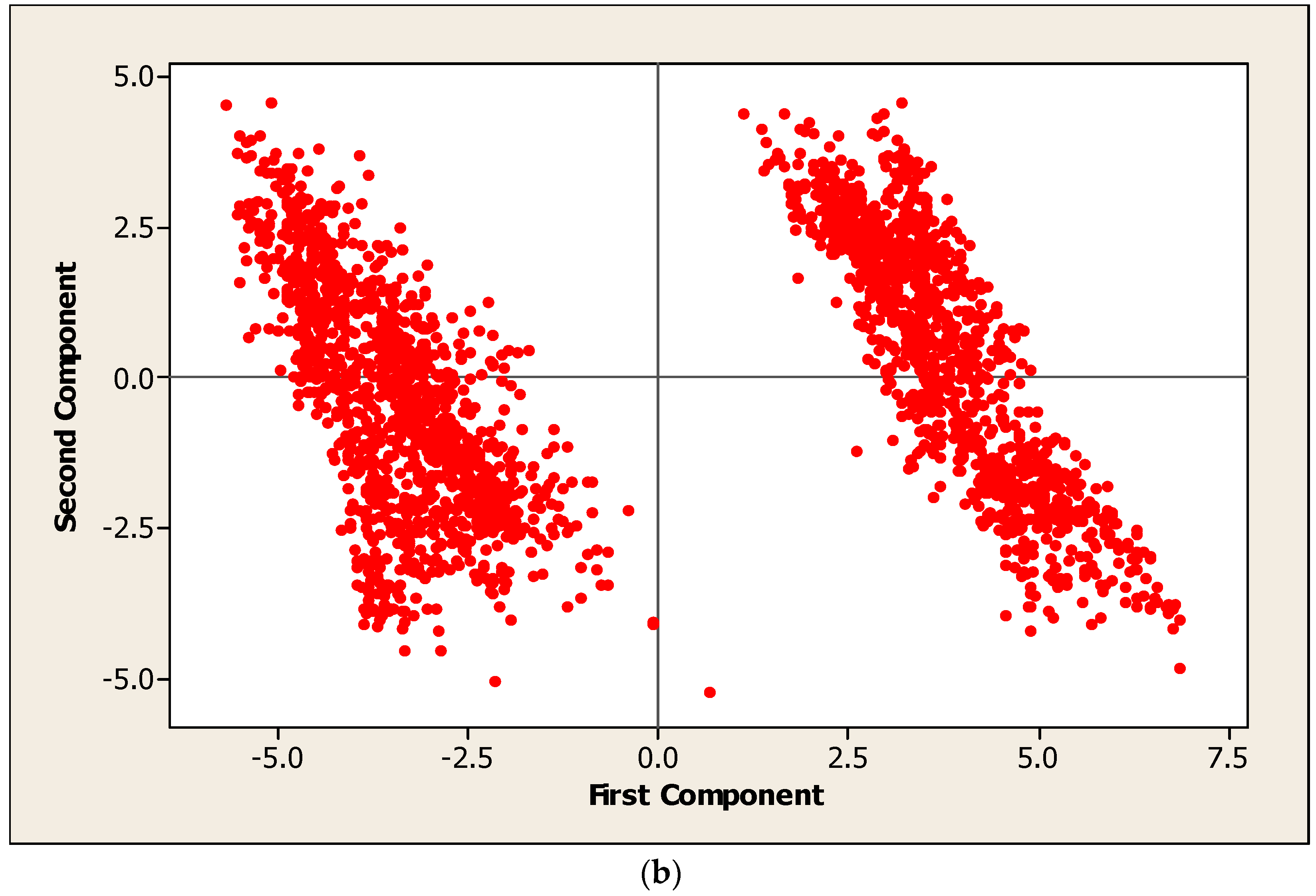
3.1. Principal Component Analysis (PCA)
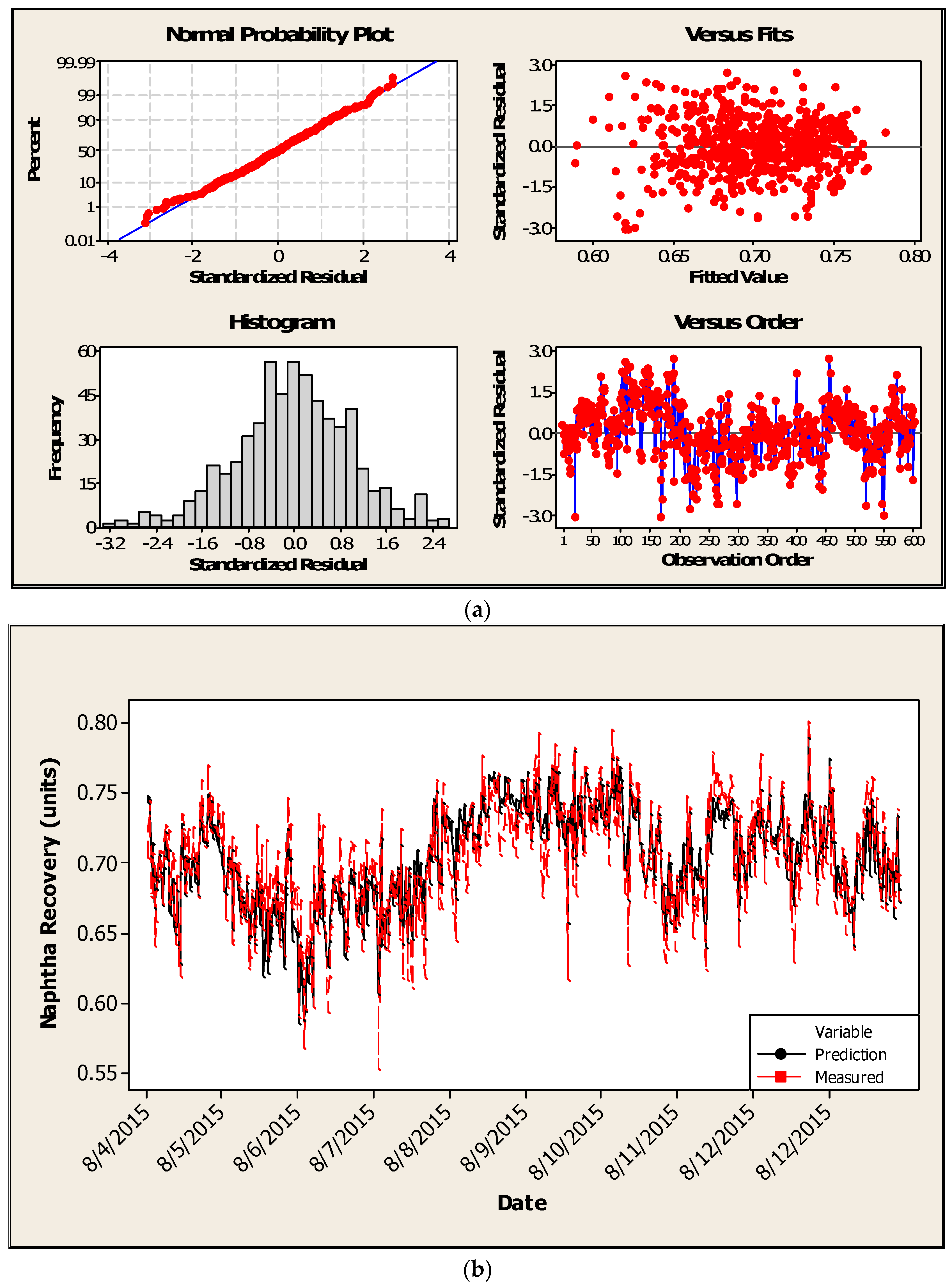
3.2. Linear Regression Models
4. First-Principles Modelling of the NRU in Aspen Plus® (V8.6)
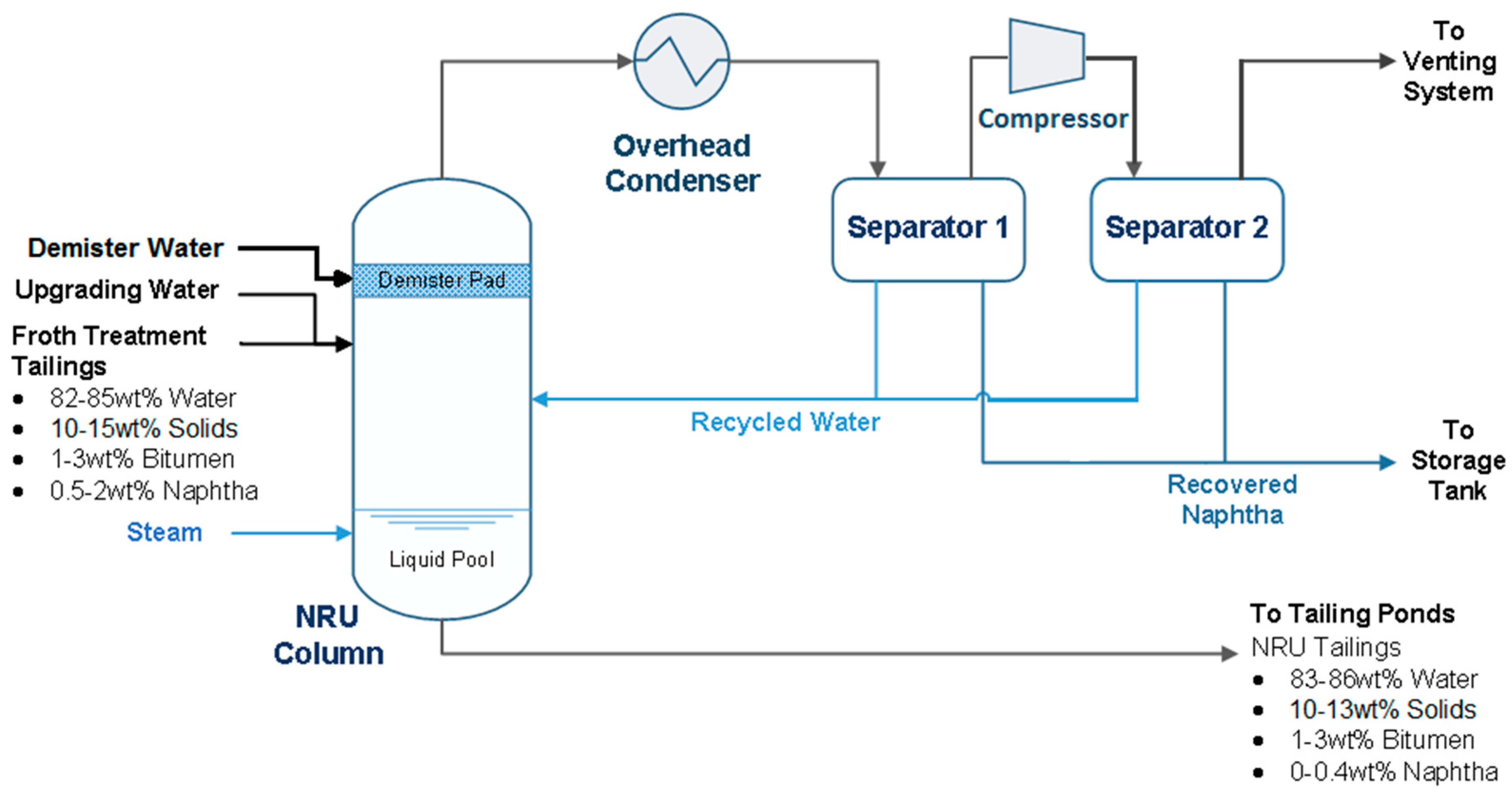
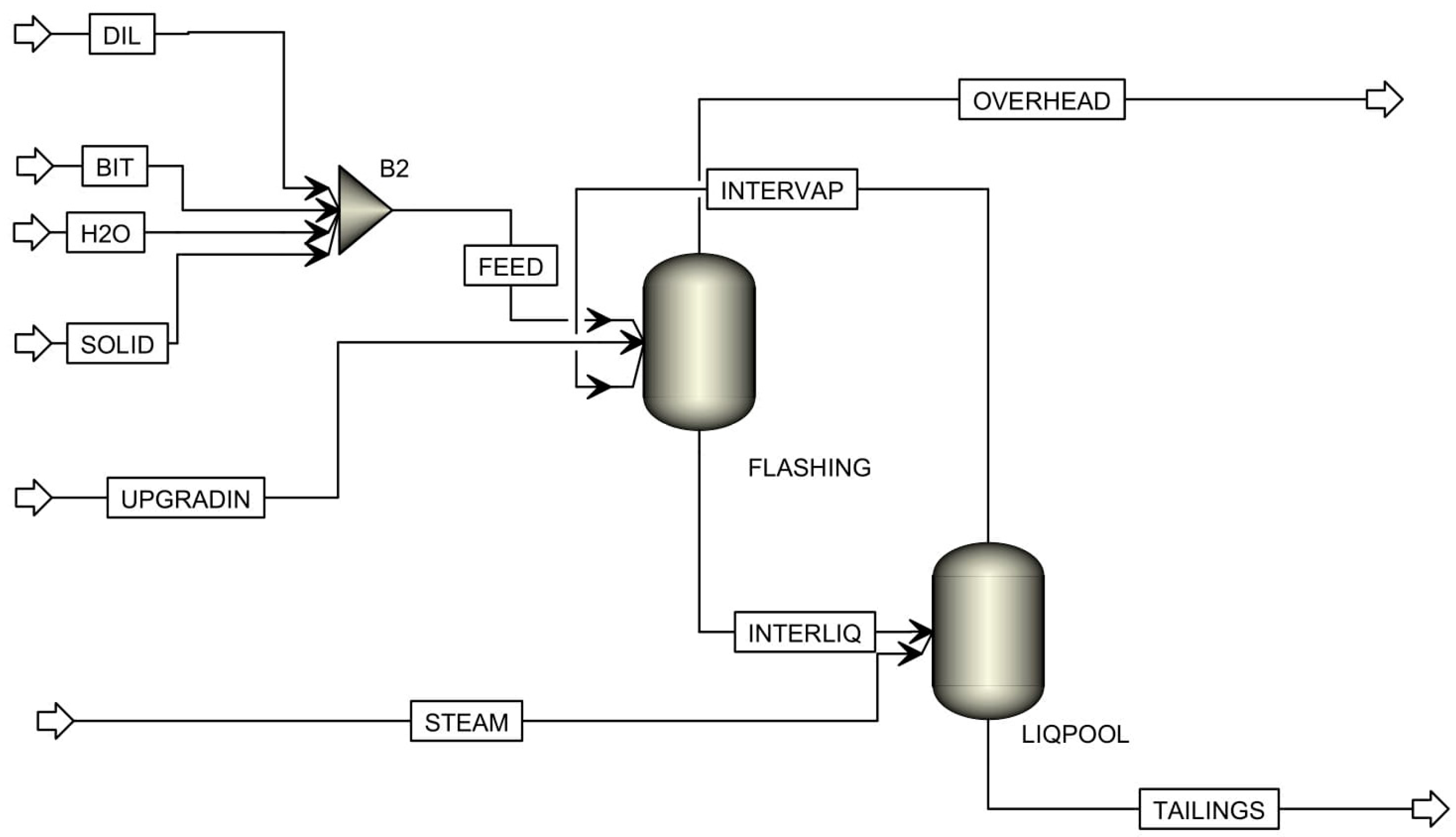
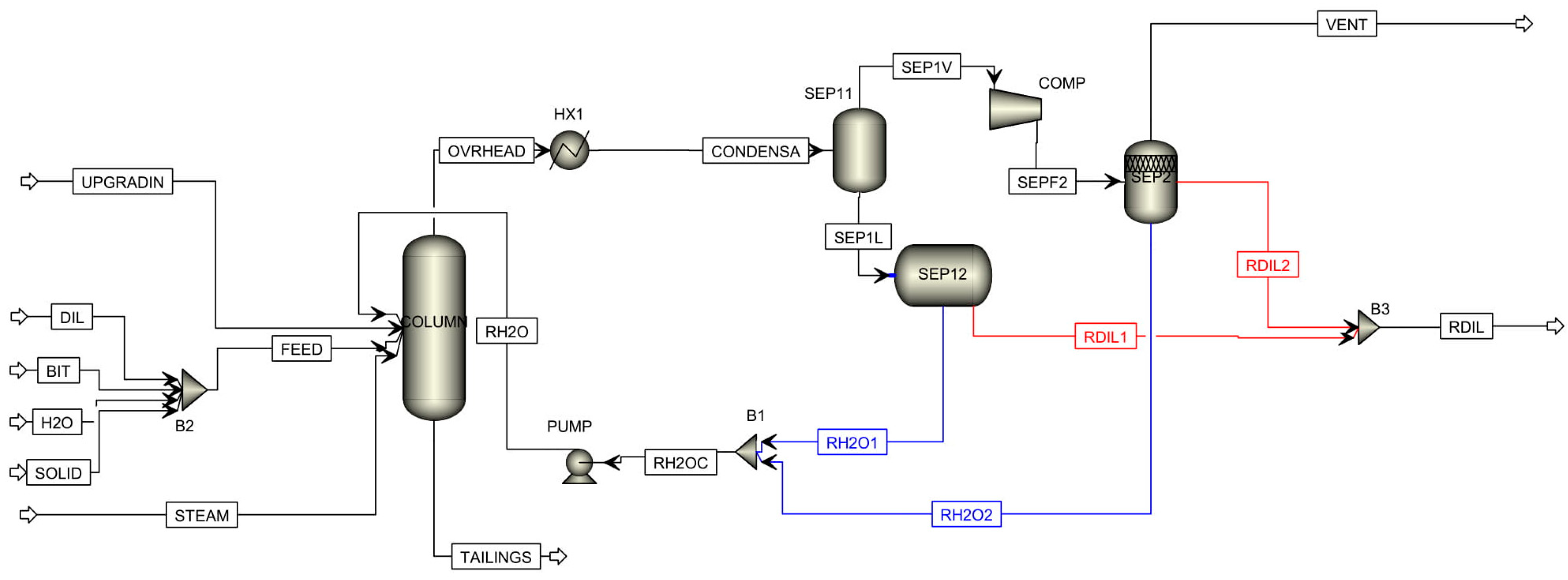
4.1. Conceptual Design of the NRU Column
4.2. Conceptual Design of the Overhead System
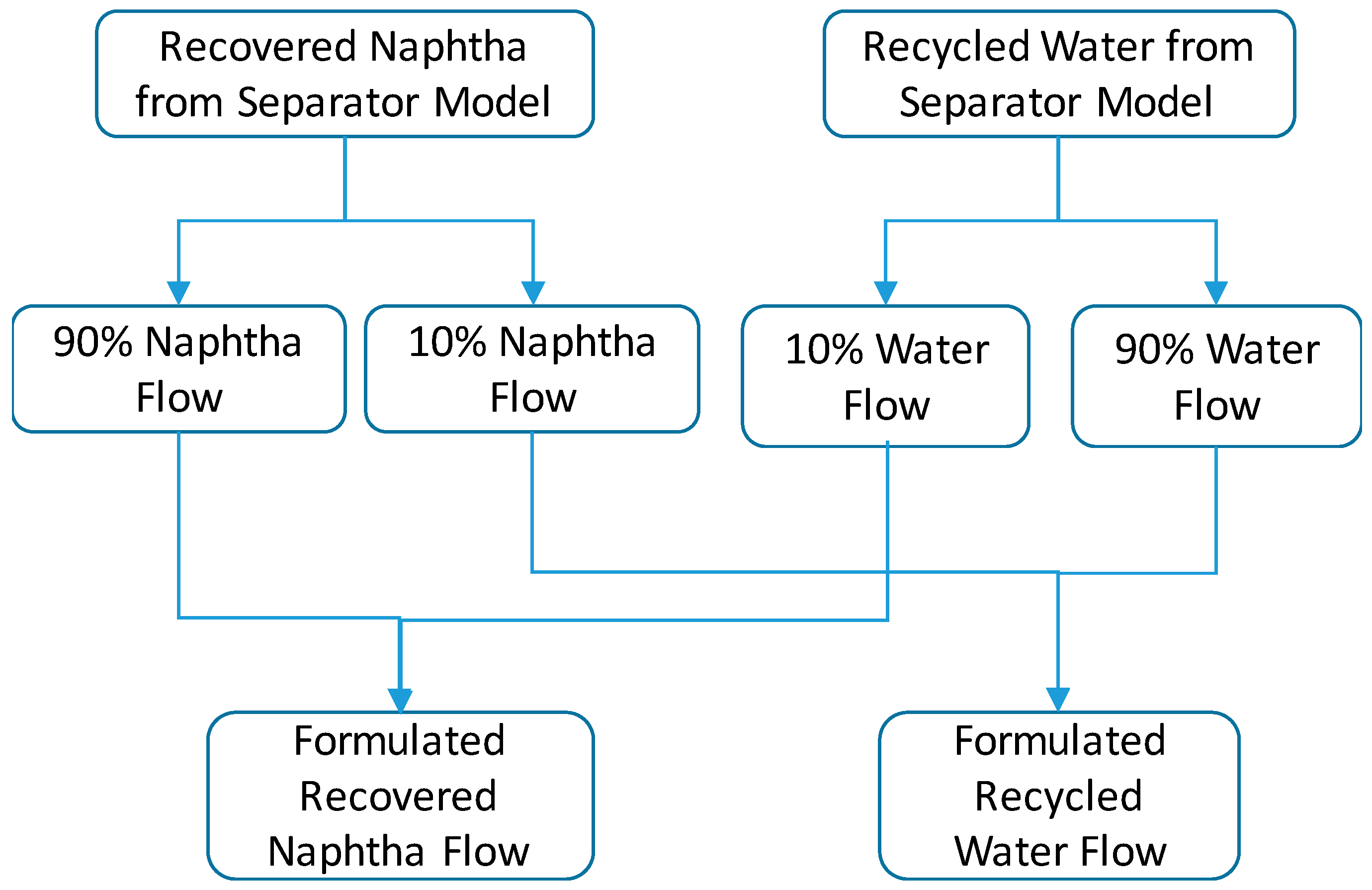
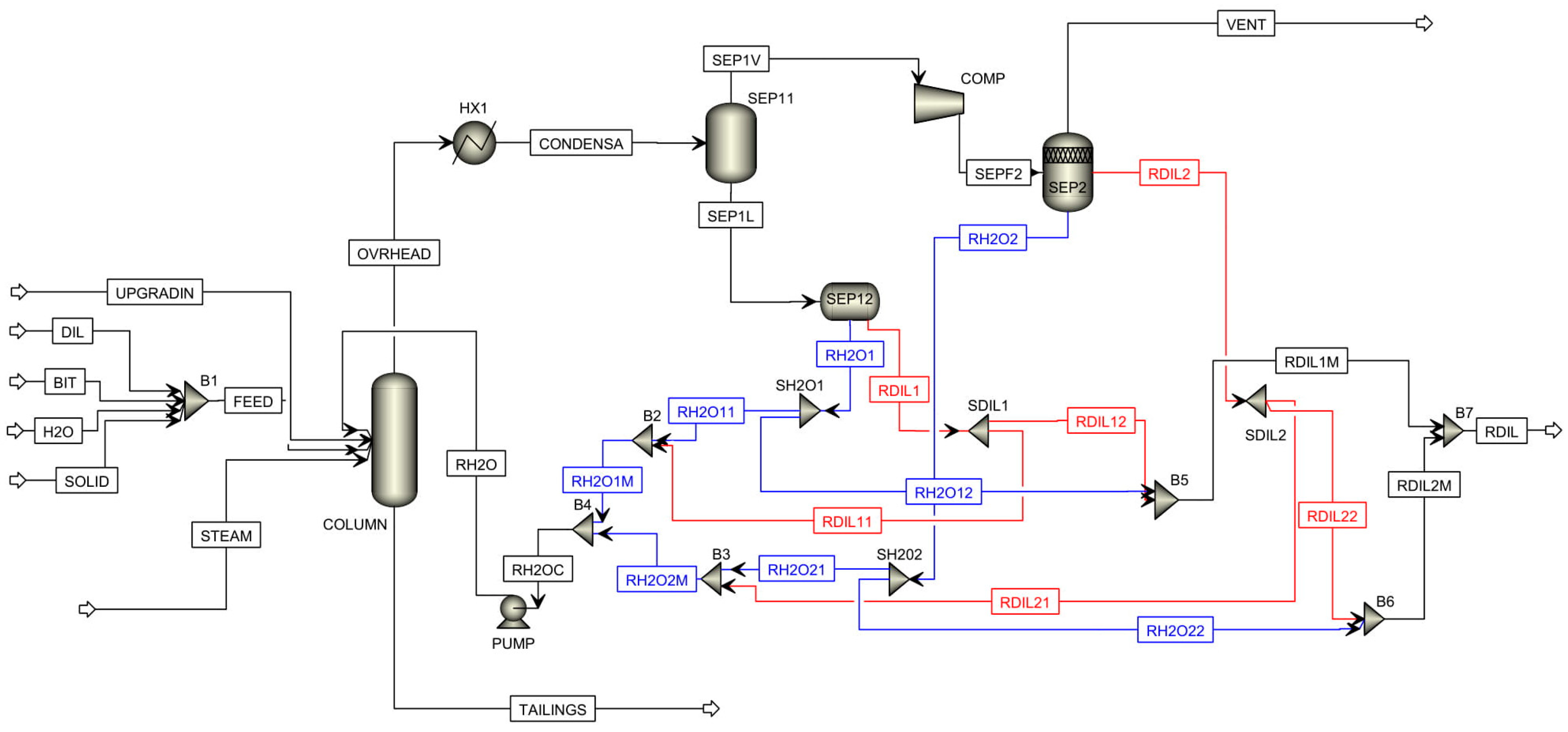
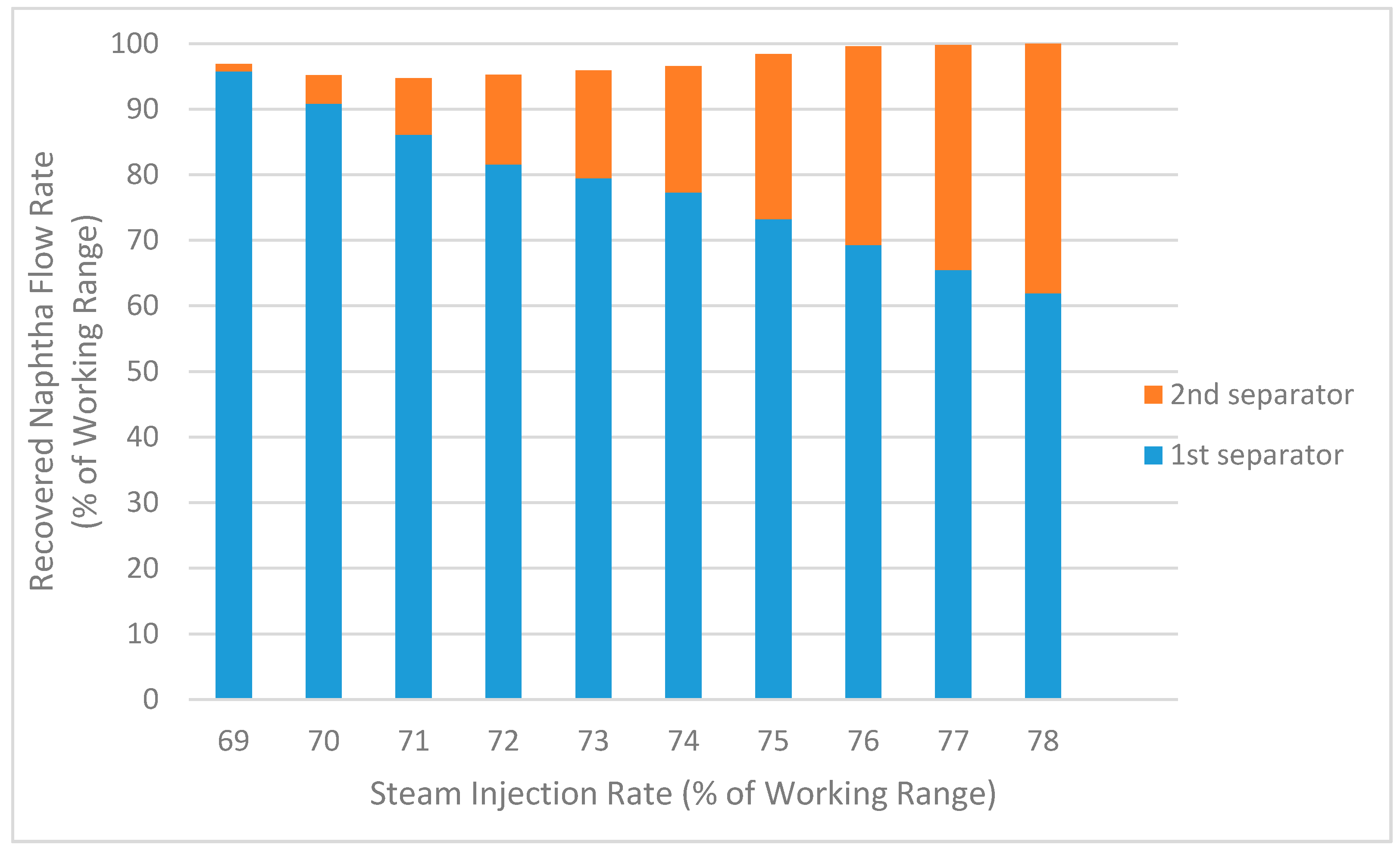
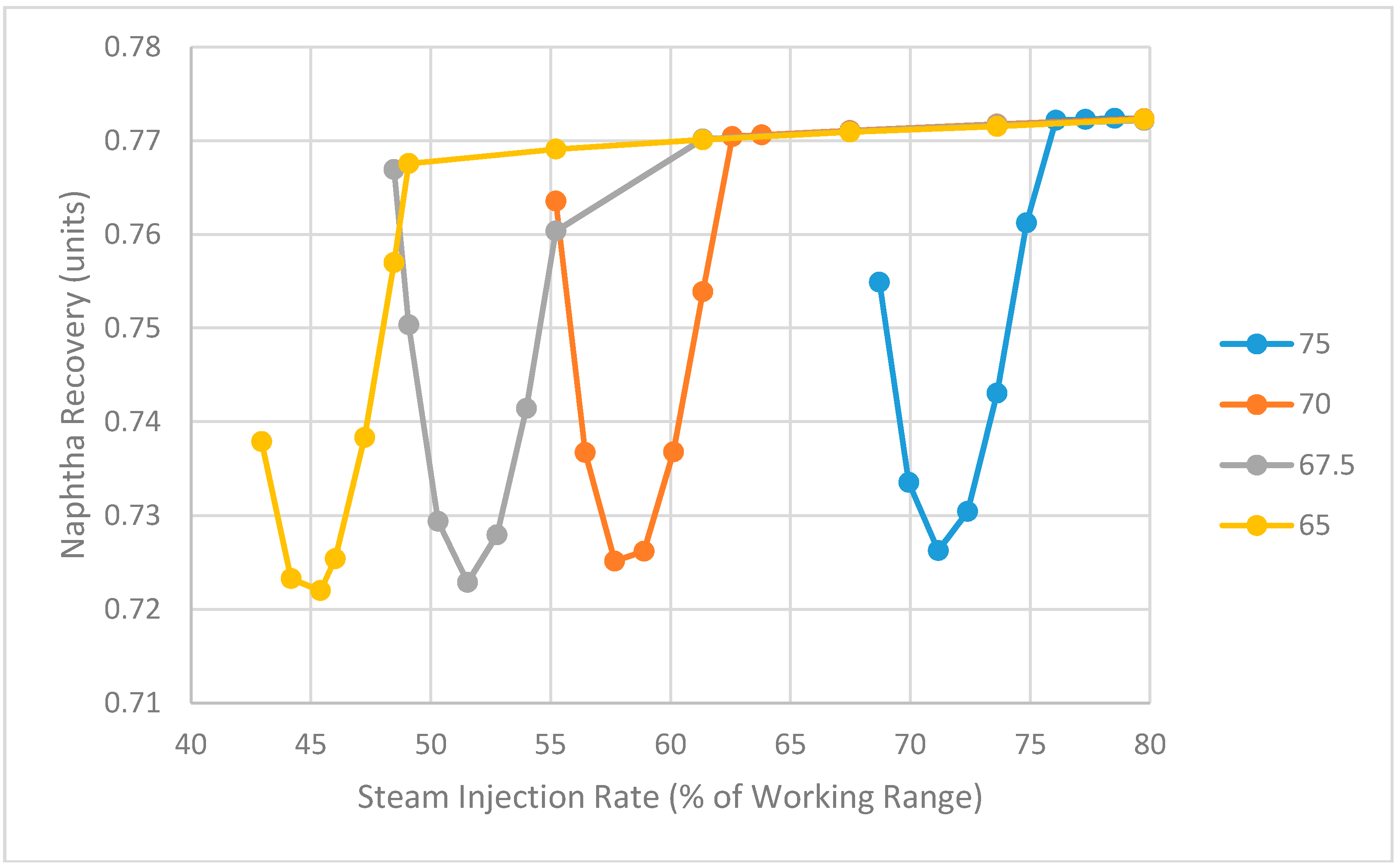
5. Implications for Process Optimization
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Speight, J.G. Oil Sand Production Processes; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- Khatibisepehr, S.; Huang, B.; Domlan, E.; Naghoosi, E.; Zhao, Y.; Miao, Y.; Shao, X.; Khare, S.; Keshavarz, M.; Feng, E.; et al. Soft sensor solutions for control of oil sands processes. Can. J. Chem. Eng. 2013, 91, 1416–1426. [Google Scholar] [CrossRef]
- Long, Y.; Dabros, T.; Hamza, H. Analysis of solvent-diluted bitumen from oil sands froth treatment using NIR spectroscopy. Can. J. Chem. Eng. 2004, 82, 776–781. [Google Scholar] [CrossRef]
- Feng, E.; Domlan, E.; Kadali, R. Spectroscopic measurements in oil sands industry—From laboratories to real-time applications. In Proceedings of the 9th International Symposium on Advanced Control of Chemical Processes, The International Federation of Automatic Control, Whistler, BC, Canada, 7–10 June 2015; pp. 199–204. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principle component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Kourti, T.; MacGregor, J.F. Process analysis, monitoring and diagnosis, using multivariate projection methods. Chemom. Intell. Lab. Syst. 1995, 28, 3–21. [Google Scholar] [CrossRef]
- Zhao, S.J.; Zhang, J.; Xu, Y.M. Monitoring of processes with multiple operating modes through multiple principle component analysis models. Ind. Eng. Chem. Res. 2004, 43, 7025–7035. [Google Scholar] [CrossRef]
- Khatibisepehr, S.; Huang, B.; Xu, F.; Espejo, A. A Bayesian approach to design of adaptive multi-model inferential sensors with application in the oil sand industry. J. Process Control 2012, 22, 1913–1929. [Google Scholar] [CrossRef]
- Mahapatra, P.; Bequette, B.W. Design and control of an elevated-pressure air separations unit for IGCC power plants in a process simulator environment. Ind. Eng. Chem. Res. 2013, 52, 3178–3191. [Google Scholar] [CrossRef]
- Sistu, P.B.; Bequette, B.W. Model predictive control of processes with input multiplicities. Chem. Eng. Sci. 1995, 50, 921–936. [Google Scholar] [CrossRef]





| Measured Variables | Description | Units | Measured Variables | Description | Units |
|---|---|---|---|---|---|
| Feed flow rate | bbl/h | Water composition in tailings | wt.% | ||
| Feed temperature | °F | Solid composition in tailings | wt.% | ||
| Naphtha composition in feed | wt.% | Recycled water flowrate | USGPM | ||
| Bitumen composition in feed | wt.% | Recycled water density | SG | ||
| Water composition in feed | wt.% | Water composition in recycled water | wt.% | ||
| Solid composition in feed | wt.% | Hydrocarbon composition in recycled water | wt.% | ||
| Steam injection rate | MLB/h | Recovered naphtha flowrate | USGPM | ||
| Upgrading water flow rate | bbl/h | Recovered naphtha density | SG | ||
| Demister water flow rate | USGPM | Water composition in recovered naphtha | wt.% | ||
| Tailings flow rate | USGPM | Hydrocarbon composition in recovered naphtha | wt.% | ||
| Tailings temperature | °F | Cooling water flowrate | USGPM | ||
| Naphtha composition in tailings | wt.% | Cooling water inlet temperature | °F | ||
| Bitumen composition in tailings | wt.% | Cooling water outlet temperature | °F |
| Measured Variables | Description | Units | Measured Variables | Description | Units |
|---|---|---|---|---|---|
| NRU column bottom temperature | °F | NRU column top pressure | psi | ||
| NRU column bottom pressure | psi | Second separator temperature | °F | ||
| NRU column top temperature | °F | Overhead compressor suction pressure | psi |
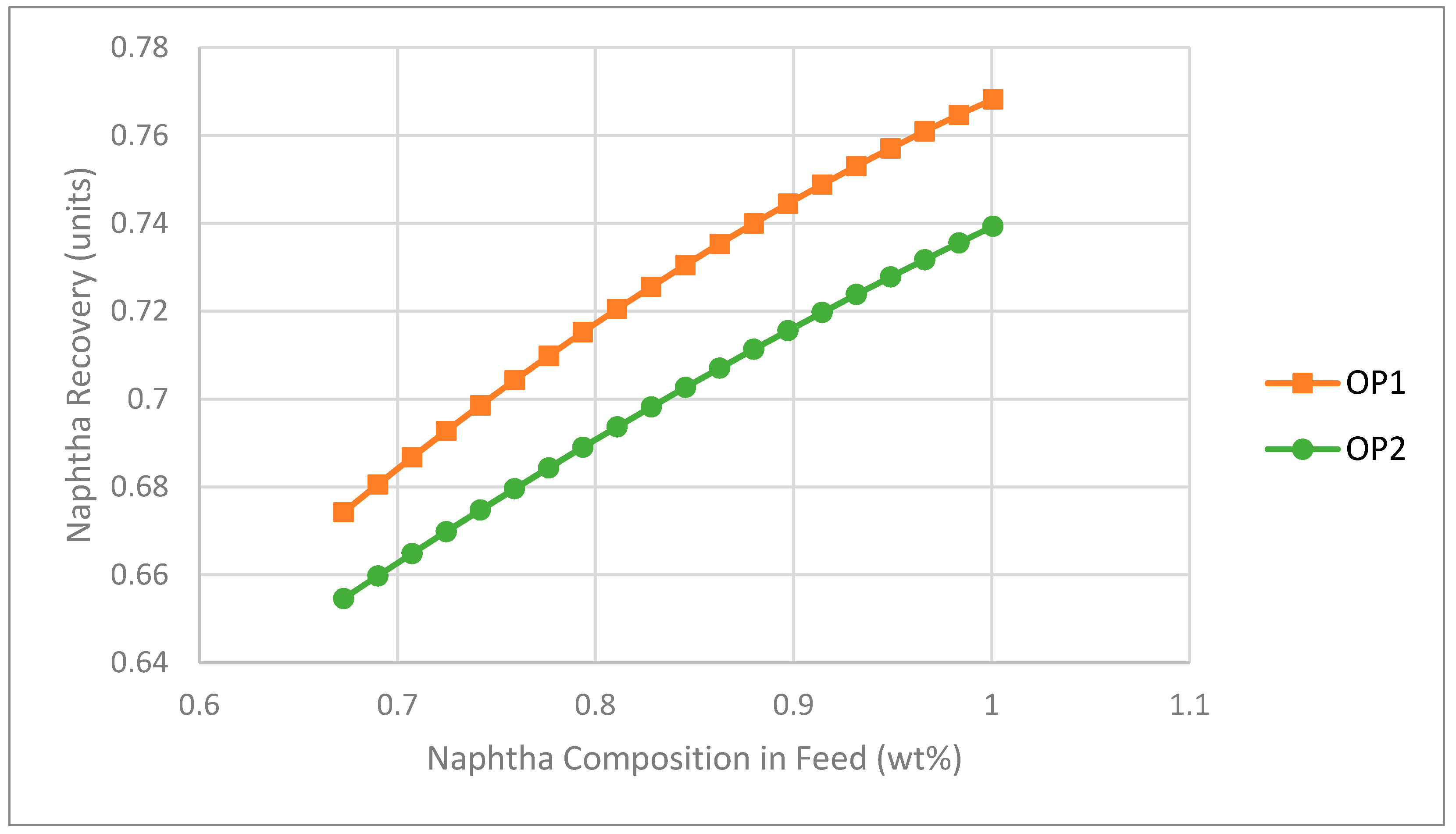
| LS Model | NRprediction = 0.347 + 0.735 NF − 0.264 (NF)2 − 0.077 SF | |
|---|---|---|
| R square | Training Set | Testing Set |
| 0.927 | 0.912 | |
| Validation 1 | NRmeasured = −0.0095 + 1.011 NRprediction | |
| LS Model | NRprediction = 0.605 + 0.475 NF − 0.129 (NF)2 − 0.375 SF | |
|---|---|---|
| R square | Training Set | Testing Set |
| 0.810 | 0.817 | |
| Validation 1 | NRmeasured = 0.0264 + 0.963 NRprediction | |
| Component | Mass Fraction (Total = 100) |
|---|---|
| n-Pentane | 0.25 |
| Benzene | 0.27 |
| Methylcyclopentane | 5.25 |
| n-Hexane | 9.23 |
| Toluene | 2.38 |
| Methylcyclohexane | 9.32 |
| n-Heptane | 9.33 |
| 2-Methylhexane | 8.43 |
| m-Xylene | 3.21 |
| Ethylbenzene | 0.79 |
| 1-Methyl-1-ethycyclopentane | 5.90 |
| n-Octane | 6.42 |
| 2-Methylheptane | 8.60 |
| 2,3-Dihydroindene | 0.50 |
| 1-Ethyl-3-methylbenzene | 3.66 |
| tert-Butylcyclopentane | 1.83 |
| n-Nonane | 4.33 |
| 2,2,5-Trimethylhexane | 11.71 |
| n-Decane | 4.13 |
| C10-Naphthene | 1.18 |
| 1,3-Dimethyl-4-ethylbenzene | 0.46 |
| Isobutylcyclohexane | 0.30 |
| 3,6-Dimethyloctane | 1.82 |
| n-Undecane | 0.70 |
| Industrial Unit | Symbol | Simulation Model | Specification | ||
|---|---|---|---|---|---|
| Variable | Value | Unit | |||
| NRU Column | COLUMN | RadFrac | Number of Stage | 2 | stage |
| Pressure @ 1st stage | 2.7 | psi | |||
| Pressure Drop | 0.3 | psi | |||
| Overhead Condenser | HX1 | HEATER | Pressure | 2.5 | psi |
| Duty | −75 | MMBTU/h | |||
| Compressor | COMP | Compr(Isentropic) | Discharge Pressure | 3.8 | psi |
| Pump | PUMP | Pump | Discharge Pressure | 2.7 | psi |
| First Separator | SEP11 | Flash 2 | Pressure | 2.5 | psi |
| Duty | 0 | MMBTU/h | |||
| SEP12 | Decanter | Pressure | 2.5 | psi | |
| Temperature | 82 | ||||
| Second Separator | SEP2 | Flash 3 | Temperature | 100 | |
| Pressure | 3.8 | psi | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Cluett, W.R. Modelling of a Naphtha Recovery Unit (NRU) with Implications for Process Optimization. Processes 2018, 6, 74. https://doi.org/10.3390/pr6070074
Du J, Cluett WR. Modelling of a Naphtha Recovery Unit (NRU) with Implications for Process Optimization. Processes. 2018; 6(7):74. https://doi.org/10.3390/pr6070074
Chicago/Turabian StyleDu, Jiawei, and William R. Cluett. 2018. "Modelling of a Naphtha Recovery Unit (NRU) with Implications for Process Optimization" Processes 6, no. 7: 74. https://doi.org/10.3390/pr6070074
APA StyleDu, J., & Cluett, W. R. (2018). Modelling of a Naphtha Recovery Unit (NRU) with Implications for Process Optimization. Processes, 6(7), 74. https://doi.org/10.3390/pr6070074





