Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost
Abstract
1. Introduction
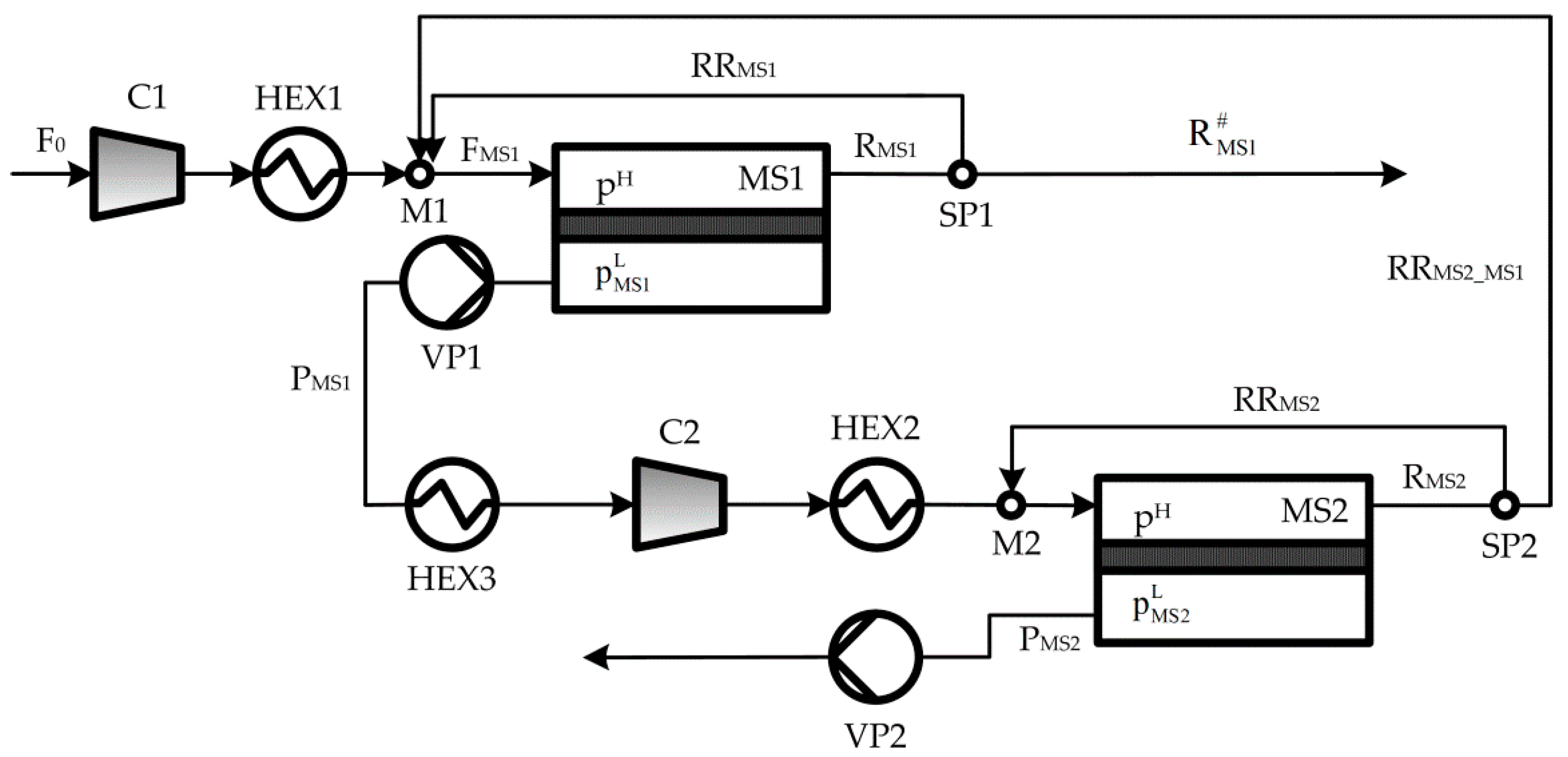
2. Process Description
3. Process Modeling
3.1. Assumptions and Process Mathematical Model
3.2. Cost Model
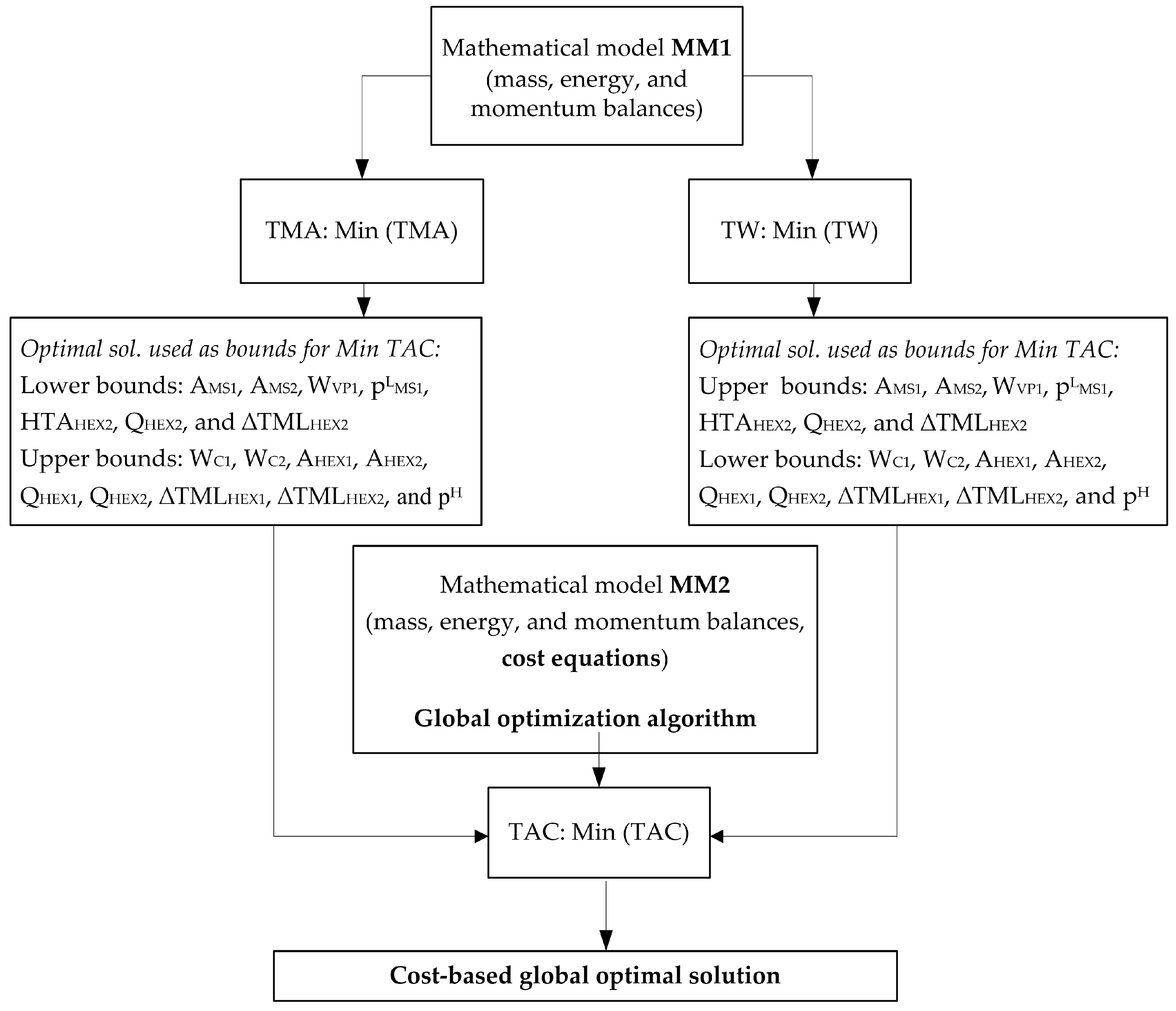
4. Problem Statement
- Minimal TAC.
- Optimal TAC distribution between the annualized capital expenditures (CAPEX) and operating expenditures (OPEX).
- Optimal sizes of the process units (membrane unit areas, heat exchanger areas, compressor and vacuum-pump power capacities).
- Optimal values of temperature, pressure, composition, and flow rate of all process streams.
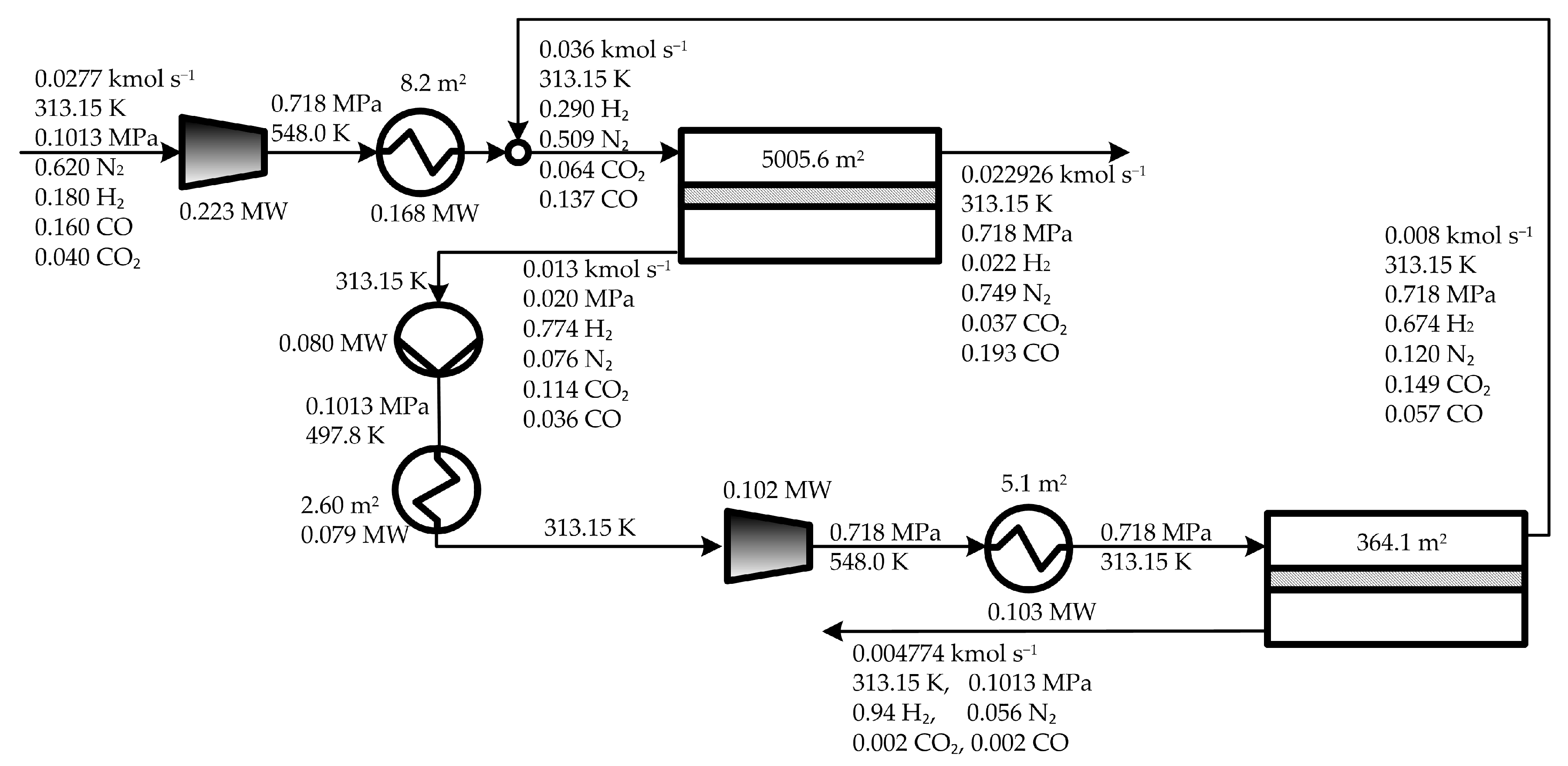
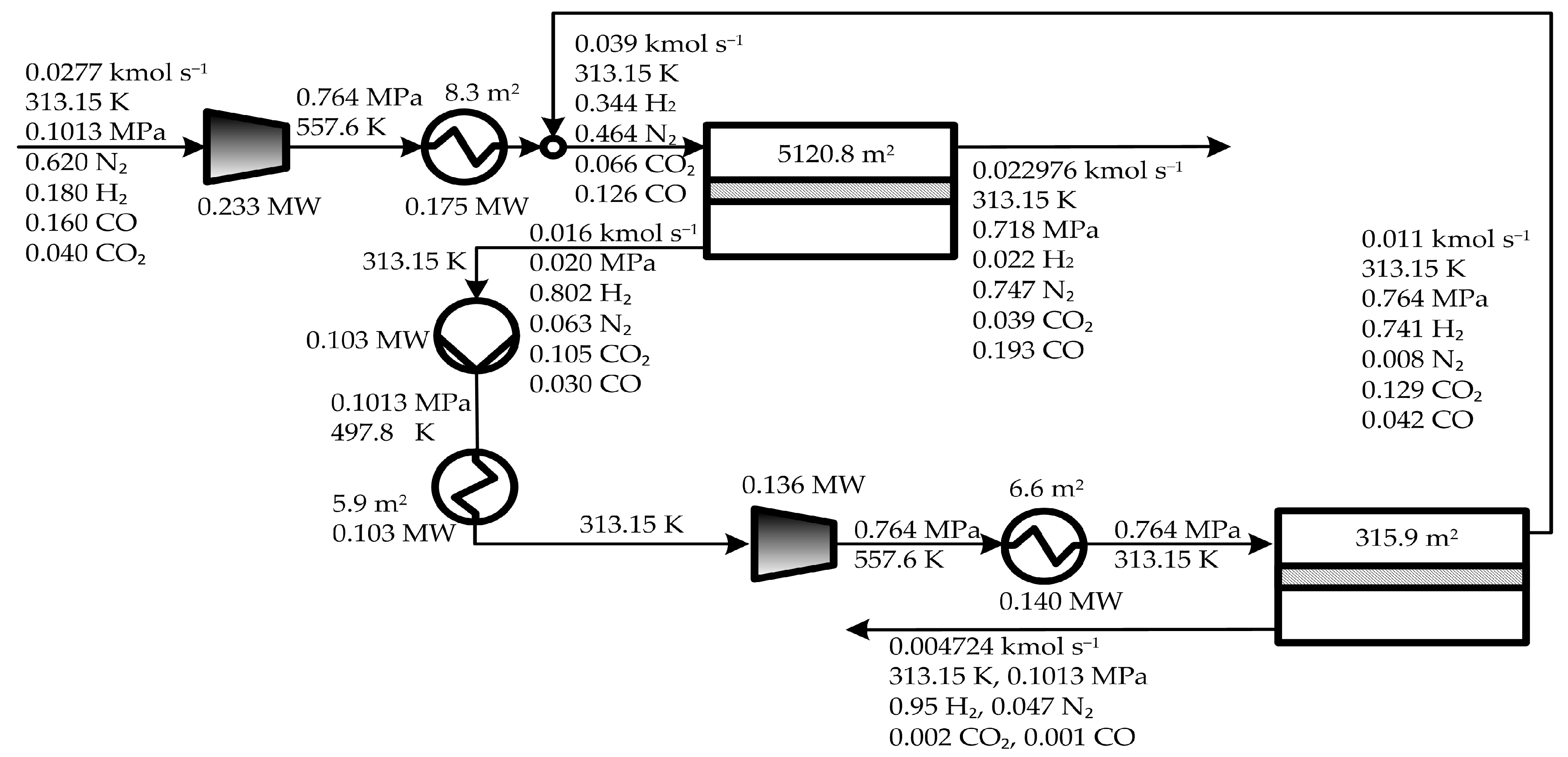
5. Results and Discussion
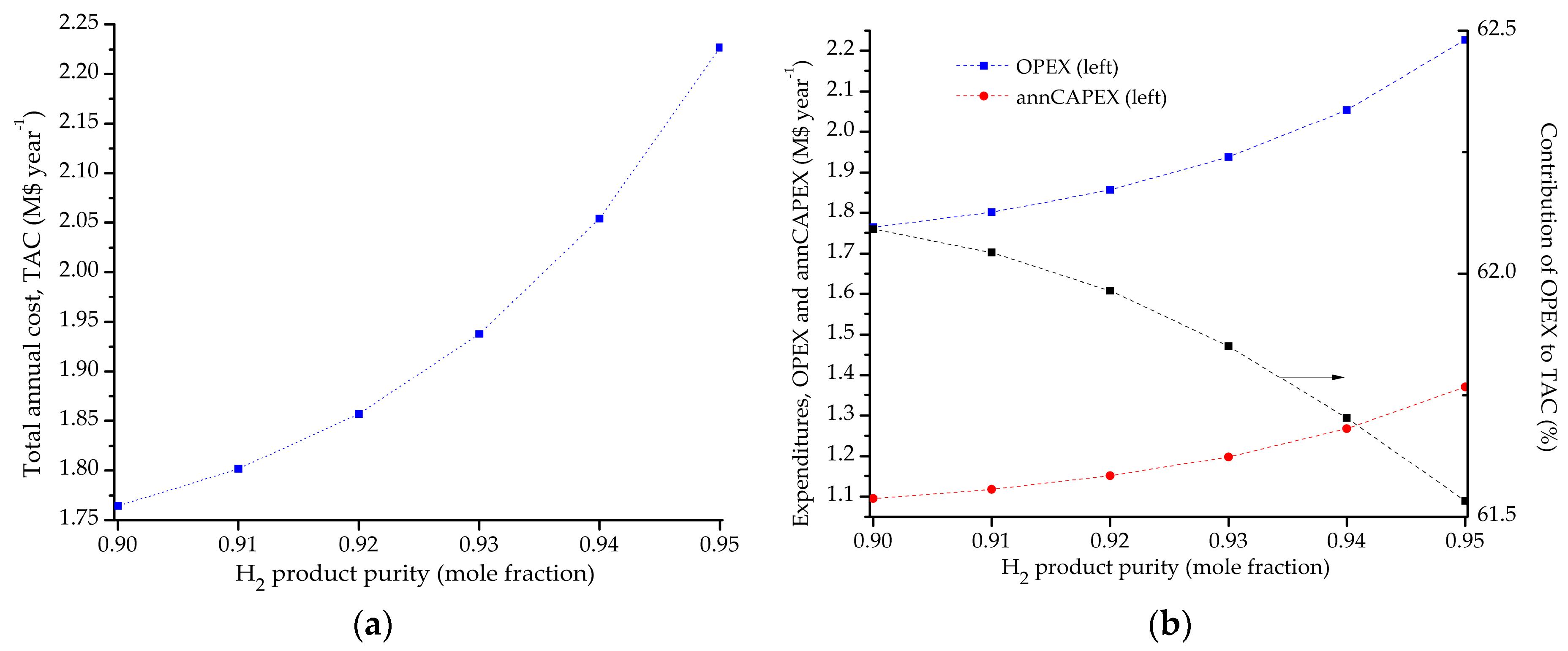
5.1. Optimal Solutions Corresponding to the Minimization of the Total Annual Cost
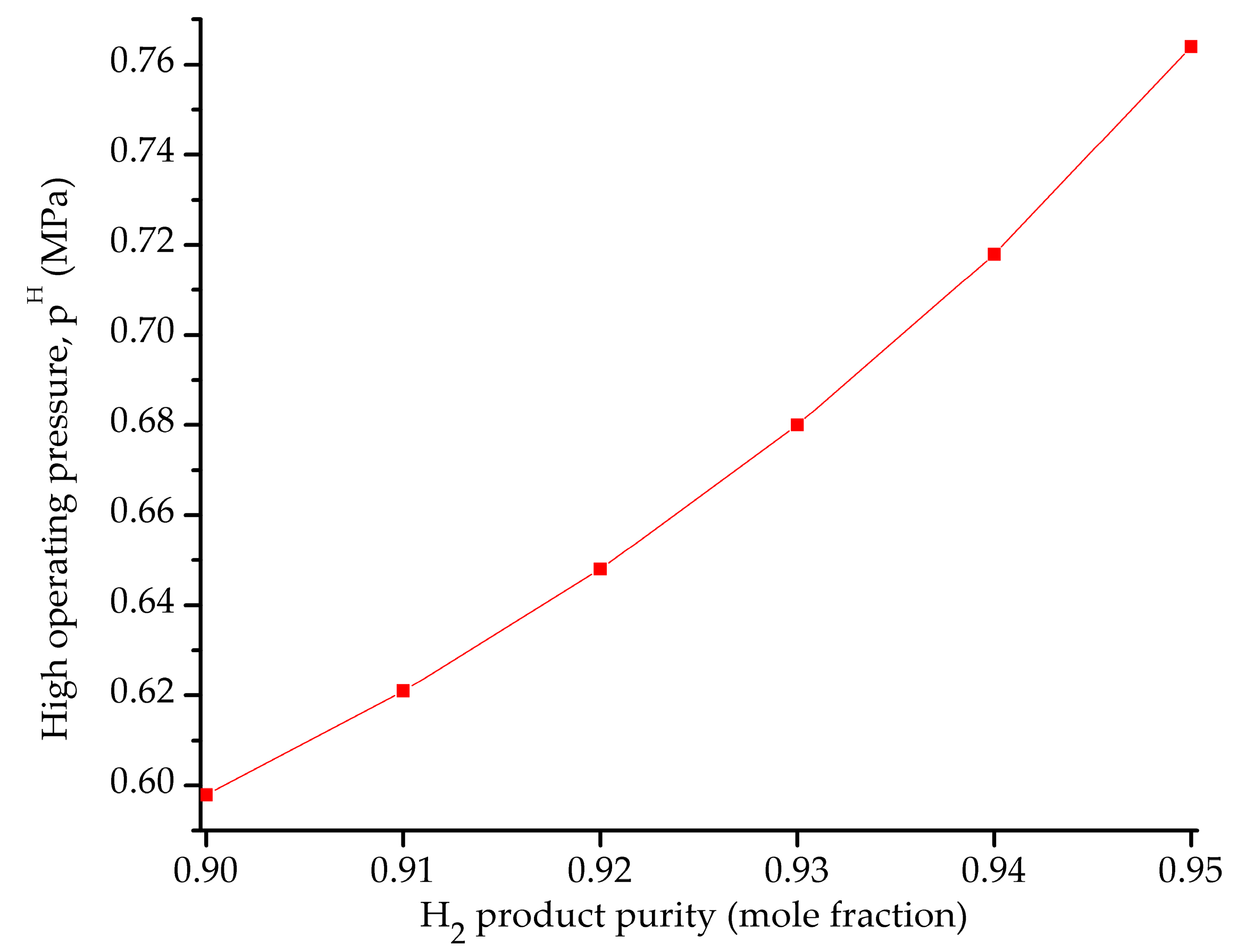
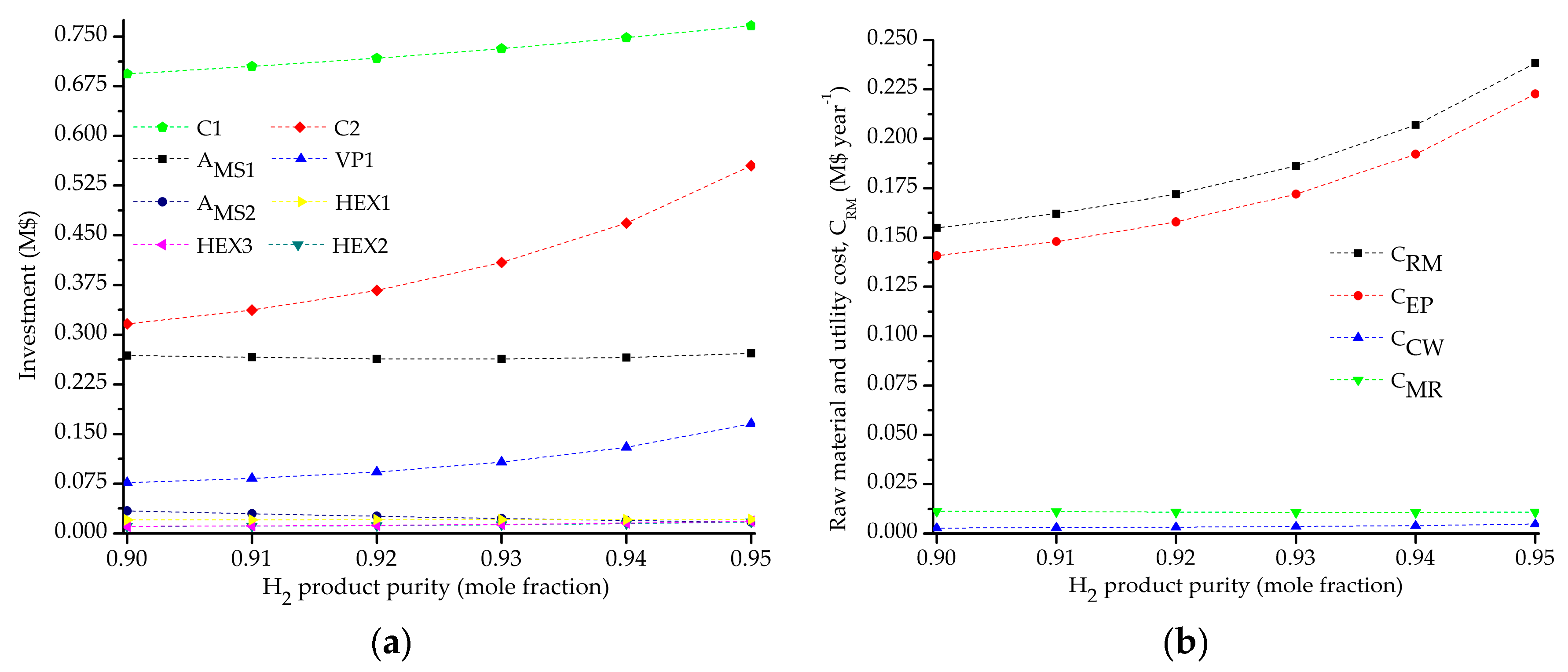
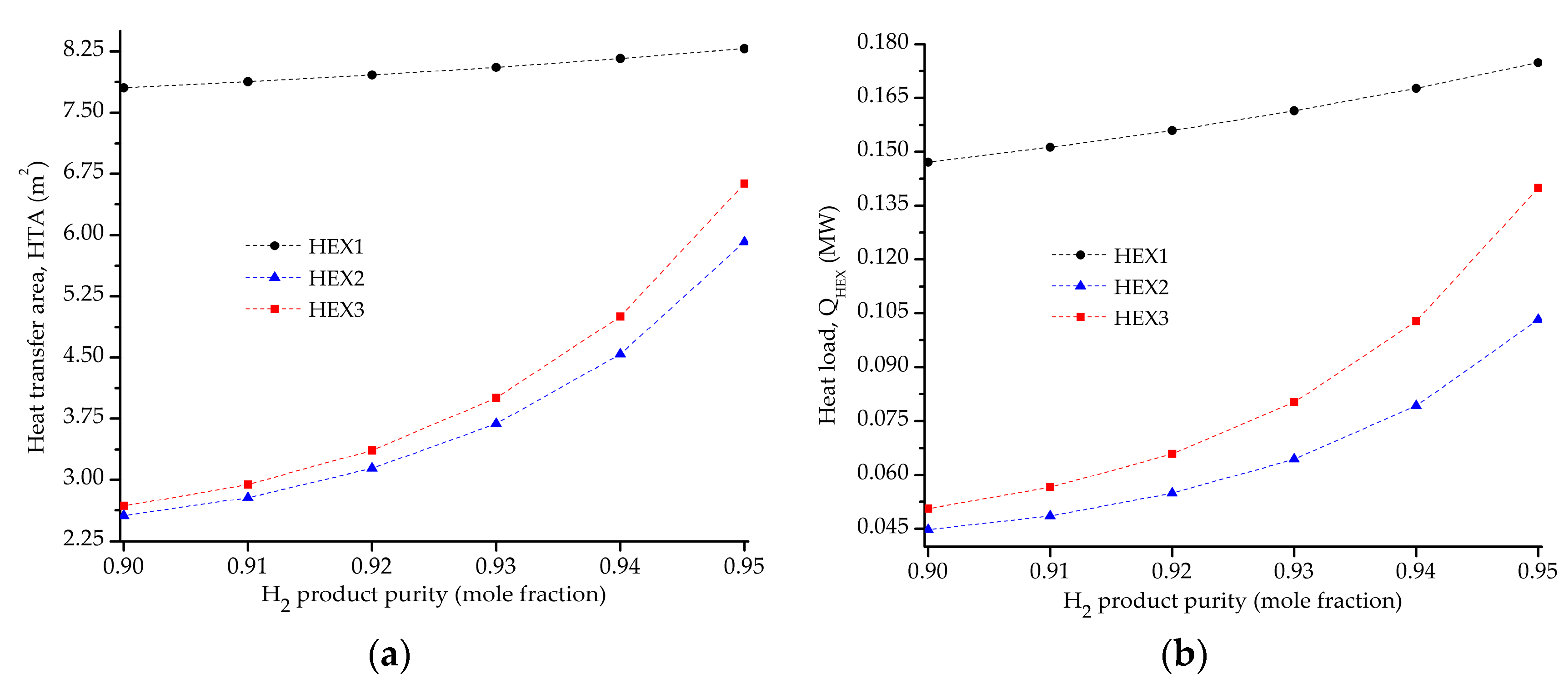
5.2. Influence of the Objective Functions on the Optimal Design and Operating Conditions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AMS# | membrane area required in the membrane stage MS#, m2 |
| annCAPEX | annualized capital expenditures, M$ year−1 |
| CAPEX | capital expenditures, M$. |
| CRF | capital recovery factor, year−1 |
| CRM | raw material and utility cost, M$ year−1 |
| cruCW | specific cost of the cooling water, M$ kg−1 |
| cruEE | specific cost of the electricity, M$ kW−1 |
| cruMR | specific cost of the membrane replacement, M$ m−2 |
| F0 | feed flow rate, kmol s−1 |
| FMS# | feed flow rate in the membrane stage MS#, kmol s−1 |
| IMS# | investment for membrane area of the stage MS#, M$ |
| IHEX# | investment for the heat exchanger HEX#, M$ |
| IVP# | investment for the vacuum pump VP#, M$. |
| IC# | investment for the compressor C#, M$ |
| OPEX | operating expenditures, M$ year−1 |
| pH | high operating pressure (retentate side), MPa |
| pLMS# | operating pressure in the permeate side of the membrane stage MS#, MPa |
| PMS# | permeate flow rate obtained in the membrane stage MS#, kmol s−1 |
| RMS# | retentate flow rate obtained in the membrane stage MS#, kmol s−1 |
| TAC | total annual cost, M$ year−1 |
| T0 | feed temperature, K |
| Tout C# | outlet temperature from the compressor C# associated with the membrane stage MS#, K |
| TMS# | operating temperature in the membrane stage MS#, K |
| Tout HEX# | outlet temperature from the heat exchanger HEX#, K |
| TW | total power, MW |
| WC# | power required by the compressor C# associated with the membrane stage MS#, MW |
| WVP# | power required by the vacuum pump VP# in the membrane stage MS#, MW |
| xi,0 | mole fraction of component i in the feed stream, dimensionless |
| xMS#,i | inlet composition of the component i in the membrane stage MS#, dimensionless |
| xMS#,i,j | mole fraction of the component i in the retentate stream of the membrane stage MS# at the discretization point j, dimensionless |
| xMS#,R,i | mole fraction of the component i in the retentate stream leaving the membrane stage MS#, dimensionless |
| yMS#,i | mole fraction of the component i in the permeate stream leaving the membrane stage MS#, dimensionless |
| yMS1,i,j | mole fraction of the component i in the permeate stream of the membrane stage MS# at the discretization point j, dimensionless |
Appendix A. Process Mathematical Model
Appendix A.1. Main Model Assumptions
- All components can permeate.
- The component permeability is not affected by the operating pressure.
- The pressure drop is negligible at both membrane sides.
- The pressure of the feed and retentate streams is the same.
- Plug-flow pattern is considered at both membrane sides.
- Each membrane module operates isothermally.
- The Fick’s first law is used.
Appendix A.2. Mathematical Model
Appendix A.2.1. Mass Balances
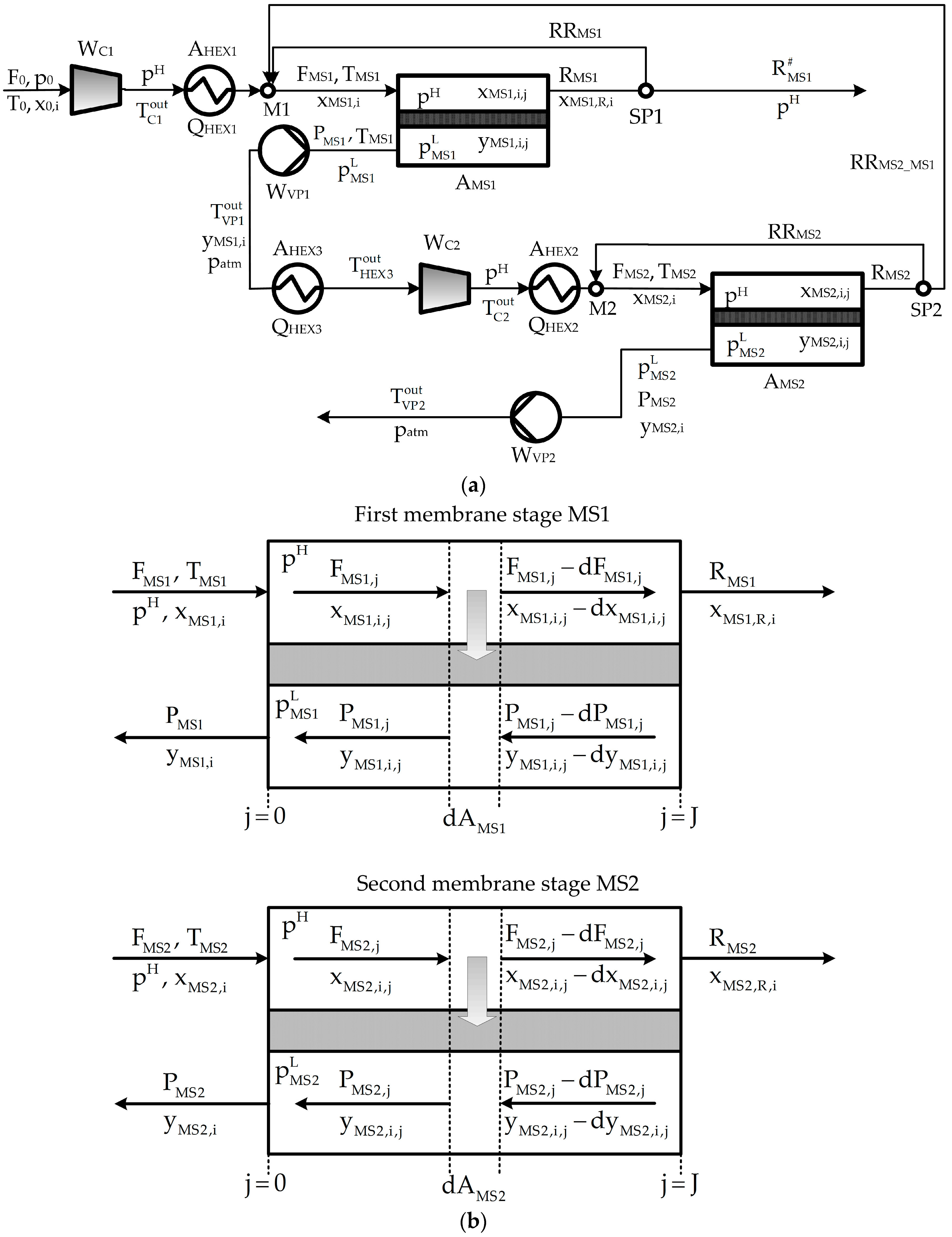
Appendix A.2.2. Power Requirement
Appendix A.2.3. Energy Balances and Transfer Areas of Heat Exchangers
Appendix A.2.4. Connecting Constraints
Appendix A.2.5. Performance Variables
References
- Benson, J.; Celin, A. Recovering hydrogen—And profits—From hydrogen-rich offgas. Chem. Eng. Prog. 2018, 114, 55–59. [Google Scholar]
- Favre, E. Polymeric Membranes for Gas Separation. In Comprehensive Membrane Science and Engineering; Drioli, E., Giorno, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; Volume II, pp. 155–212. ISBN 978-0-444-53204-6. [Google Scholar]
- Edlund, D. Hydrogen Membrane Technologies and Application in Fuel Processing. In Hydrogen and Syngas Production and Purification Technologies; Liu, K., Song, C., Subramani, V., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 2009; pp. 357–384. ISBN 978-0-471-71975-5. [Google Scholar]
- Baker, R. Membrane Technology in the Chemical Industry: Future Directions. In Membrane Technology; Pereira Nunes, S., Peinemann, K.-V., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 2001; pp. 268–295. ISBN 978-3-527-60038-0. [Google Scholar]
- Shalygin, M.G.; Abramov, S.M.; Netrusov, A.I.; Teplyakov, V.V. Membrane recovery of hydrogen from gaseous mixtures of biogenic and technogenic origin. Int. J. Hydrog. Energy 2015, 40, 3438–3451. [Google Scholar] [CrossRef]
- Ramírez-Santos, Á.A.; Bozorg, M.; Addis, B.; Piccialli, V.; Castel, C.; Favre, E. Optimization of multistage membrane gas separation processes. Example of application to CO2 capture from blast furnace gas. J. Membr. Sci. 2018, 566, 346–366. [Google Scholar] [CrossRef]
- Ohs, B.; Lohaus, J.; Wessling, M. Optimization of membrane based nitrogen removal from natural gas. J. Membr. Sci. 2016, 498, 291–301. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Zarca, G.; Urtiaga, A.; Biegler, L.T.; Ortiz, I. An optimization model for assessment of membrane-based post-combustion gas upcycling into hydrogen or syngas. J. Membr. Sci. 2018, 563, 83–92. [Google Scholar] [CrossRef]
- Ahmad, F.; Lau, K.K.; Shariff, A.M.; Murshid, G. Process simulation and optimal design of membrane separation system for CO2 capture from natural gas. Comput. Chem. Eng. 2012, 36, 119–128. [Google Scholar] [CrossRef]
- Chowdhury, M.H.M.; Feng, X.; Douglas, P.; Croiset, E. A new numerical approach for a detailed multicomponent gas separation membrane model and AspenPlus simulation. Chem. Eng. Technol. 2005, 28, 773–782. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Jafari, M.; sari, A.; Babalou, A.A. Performance investigation of membrane process in natural gas sweetening by membrane process: modeling study. Chem. Prod. Process Model. 2016, 11, 23–27. [Google Scholar] [CrossRef]
- Giordano, L.; Roizard, D.; Bounaceur, R.; Favre, E. Energy penalty of a single stage gas permeation process for CO2 capture in post-combustion: A rigorous parametric analysis of temperature, humidity and membrane performances. Energy Procedia 2017, 114, 636–641. [Google Scholar] [CrossRef]
- Turi, D.M.; Ho, M.; Ferrari, M.C.; Chiesa, P.; Wiley, D.E.; Romano, M.C. CO2 capture from natural gas combined cycles by CO2 selective membranes. Int. J. Greenh. Gas Control 2017, 61, 168–183. [Google Scholar] [CrossRef]
- Arias, A.M.; Mussati, M.C.; Mores, P.L.; Scenna, N.J.; Caballero, J.A.; Mussati, S.F. Optimization of multi-stage membrane systems for CO2 capture from flue gas. Int. J. Greenh. Gas Control 2016, 53, 371–390. [Google Scholar] [CrossRef]
- Franz, J.; Scherer, V. An evaluation of CO2 and H2 selective polymeric membranes for CO2 separation in IGCC processes. J. Membr. Sci. 2010, 359, 173–183. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Zhang, C.; Zhao, S.; Qiao, Z.; Li, P.; Wang, J.; Wang, S. Parametric analysis and potential prediction of membrane processes for hydrogen production and pre-combustion CO2 capture. Chem. Eng. Sci. 2015, 135, 202–216. [Google Scholar] [CrossRef]
- Arias, A.M. Minimization of Greenhouse Gases (GHGs) Emissions in the Energy Sector Employing Non-Conventional Technologies. Ph.D. Thesis, Universidad Tecnológica Nacional, Córdoba, Argentina, 2017. [Google Scholar]
- Abu-Zahra, M.R.M.; Niederer, J.P.M.; Feron, P.H.M.; Versteeg, G.F. CO2 capture from power plants: Part II. A parametric study of the economical performance based on mono-ethanolamine. Int. J. Greenh. Gas Control 2007, 1, 135–142. [Google Scholar] [CrossRef]
- Rao, A.B.; Rubin, E.S. A technical, economic, and environmental assessment of amine-based CO2 capture technology for power plant greenhouse gas control. Environ. Sci. Technol. 2002, 36, 4467–4475. [Google Scholar] [CrossRef] [PubMed]
- General Algebraic Modeling System (GAMS); Release 24.2.1; GAMS Development Corporation: Fairfax, VA, USA, 2013.
- Drud, A. CONOPT 3 Solver Manual; ARKI Consulting and Development A/S: Bagsvaerd, Denmark, 2012. [Google Scholar]
- Puranik, Y.; Sahinidis, N.V. Domain reduction techniques for global NLP and MINLP optimization. Constraints 2017, 22, 338–376. [Google Scholar] [CrossRef]
- Sherali, H.D.; Totlani, R.; Loganathan, G.V. Enhanced lower bounds for the global optimization of water distribution networks. Water Resour. Res. 1998, 34, 1831–1841. [Google Scholar] [CrossRef]
- Ruiz, J.P.; Grossmann, I.E. A New Theoretical Result for Convex Nonlinear Generalized Disjunctive Programs and its Applications. In Computer Aided Chemical Engineering; Bogle, I.D.L., Fairweather, M., Eds.; 22 European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2012; Volume 30, pp. 1197–1201. [Google Scholar]
- Kirst, P.; Stein, O.; Steuermann, P. Deterministic upper bounds for spatial branch-and-bound methods in global minimization with nonconvex constraints. TOP 2015, 23, 591–616. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Feed specification | |
| Flow rate, kmol h−1 | 100 |
| Temperature, K | 313.15 |
| Pressure, kPa | 101.32 |
| Composition (mole fraction) | |
| CO2 | 0.04 |
| CO | 0.16 |
| H2 | 0.18 |
| N2 | 0.62 |
| Membrane material (Polymer) | |
| Permeance (mole m−2 s−1 MPa−1) | |
| CO2 | 8.444 × 10−3 |
| CO | 7.457 × 10−4 |
| H2 | 2.871 × 10−2 |
| N2 | 4.078 × 10−4 |
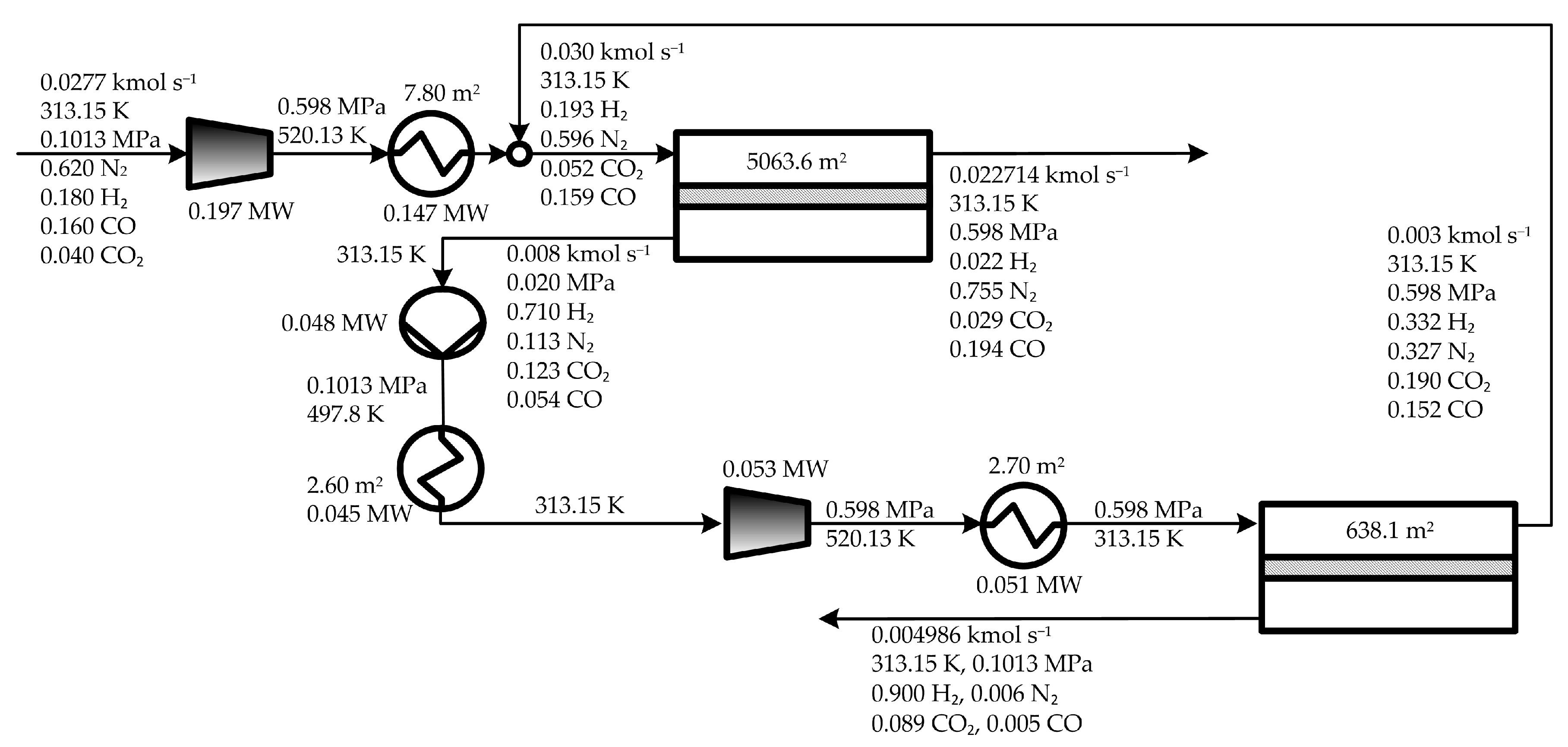
| Cost Item | Min TMA (osTMA) | Min. TAC (osTAC) | Min TW (osTW) |
|---|---|---|---|
| TAC (M$ year−1) | 1.851 | 1.764 | 2.116 |
| OPEX (M$ year−1) | 1.158 | 1.095 | 1.262 |
| annCAPEX (M$ year−1) | 0.692 | 0.669 | 0.853 |
| CINV (M$) | 1.481 | 1.431 | 1.826 |
| IC1 | 0.852 | 0.694 | 0.489 |
| IC2 | 0.365 | 0.316 | 0.274 |
| IMA_MS1 | 0.134 | 0.269 | 0.831 |
| IVP1 | 6.93 × 10−2 | 7.67 × 10−2 | 0.1043 |
| IHEX1 | 2.19 × 10−2 | 2.03 × 10−2 | 0.018 |
| IMA_MS2 | 1.84 × 10−2 | 3.40 × 10−2 | 8.49 × 10−2 |
| IHEX3 | 1.10 × 10−2 | 1.07 × 10−2 | 1.14 × 10−2 |
| IHEX2 | 9.87 × 10−3 | 1.04 × 10−2 | 1.26 × 10−2 |
| CRM (M$ year−1) | 0.193 | 0.155 | 0.139 |
| CE | 0.183 | 0.141 | 0.102 |
| CMR | 5.71 × 10−3 | 1.14 × 10−2 | 3.46 × 10−2 |
| CCW | 3.66 × 10−3 | 2.79 × 10−3 | 2.06 × 10−3 |
| Cost Item | Min TMA (osTMA) | Min. TAC (osTAC) | Min TW (osTW) |
|---|---|---|---|
| TMA (m2) | 2854.23 | 5701.66 | 17316.96 |
| MAMS1 | 2510.80 | 5063.60 | 15714.90 |
| MAMS2 | 343.43 | 638.06 | 1602.06 |
| TW (MW) | 0.387 | 0.298 | 0.216 |
| WC1 | 0.277 | 0.197 | 0.110 |
| WC2 | 6.75 × 10−2 | 5.32 × 10−2 | 4.20 × 10−2 |
| WVP1 | 4.29 × 10−2 | 4.75 × 10−2 | 6.46 × 10−2 |
| HTAHEX1 (m2) | 8.839 | 7.802 | 6.378 |
| HTAHEX2 (m2) | 2.305 | 2.6 | 3.5 |
| HTAHEX3 (m2) | 2.813 | 2.680 | 2.997 |
| QHEX1 (MW) | 0.210 | 0.147 | 8.09 × 10−2 |
| QHEX2 (MW) | 4.10 × 10−2 | 4.50 × 10−2 | 6.00 × 10−2 |
| QHEX3 (MW) | 6.68 × 10−2 | 5.05 × 10−2 | 3.80 × 10−2 |
| ∆TMLHEX1 (K) | 85.533 | 67.908 | 45.676 |
| ∆TMLHEX2 (K) | 62.871 | 62.871 | 61.236 |
| ∆TMLHEX3 (K) | 85.533 | 67.908 | 45.676 |
| pH (MPa) | 1.01320 | 0.59834 | 0.30396 |
| pLMS1 (MPa) | 2.00 × 10−2 | 2.00 × 10−2 | 2.10 × 10−2 |
| pLMS2 (MPa) | 0.10132 | 0.10132 | 0.10132 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mores, P.L.; Arias, A.M.; Scenna, N.J.; Caballero, J.A.; Mussati, S.F.; Mussati, M.C. Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost. Processes 2018, 6, 221. https://doi.org/10.3390/pr6110221
Mores PL, Arias AM, Scenna NJ, Caballero JA, Mussati SF, Mussati MC. Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost. Processes. 2018; 6(11):221. https://doi.org/10.3390/pr6110221
Chicago/Turabian StyleMores, Patricia L., Ana M. Arias, Nicolás J. Scenna, José A. Caballero, Sergio F. Mussati, and Miguel C. Mussati. 2018. "Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost" Processes 6, no. 11: 221. https://doi.org/10.3390/pr6110221
APA StyleMores, P. L., Arias, A. M., Scenna, N. J., Caballero, J. A., Mussati, S. F., & Mussati, M. C. (2018). Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost. Processes, 6(11), 221. https://doi.org/10.3390/pr6110221






