Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application
Abstract
:1. Introduction
2. Experimental Method
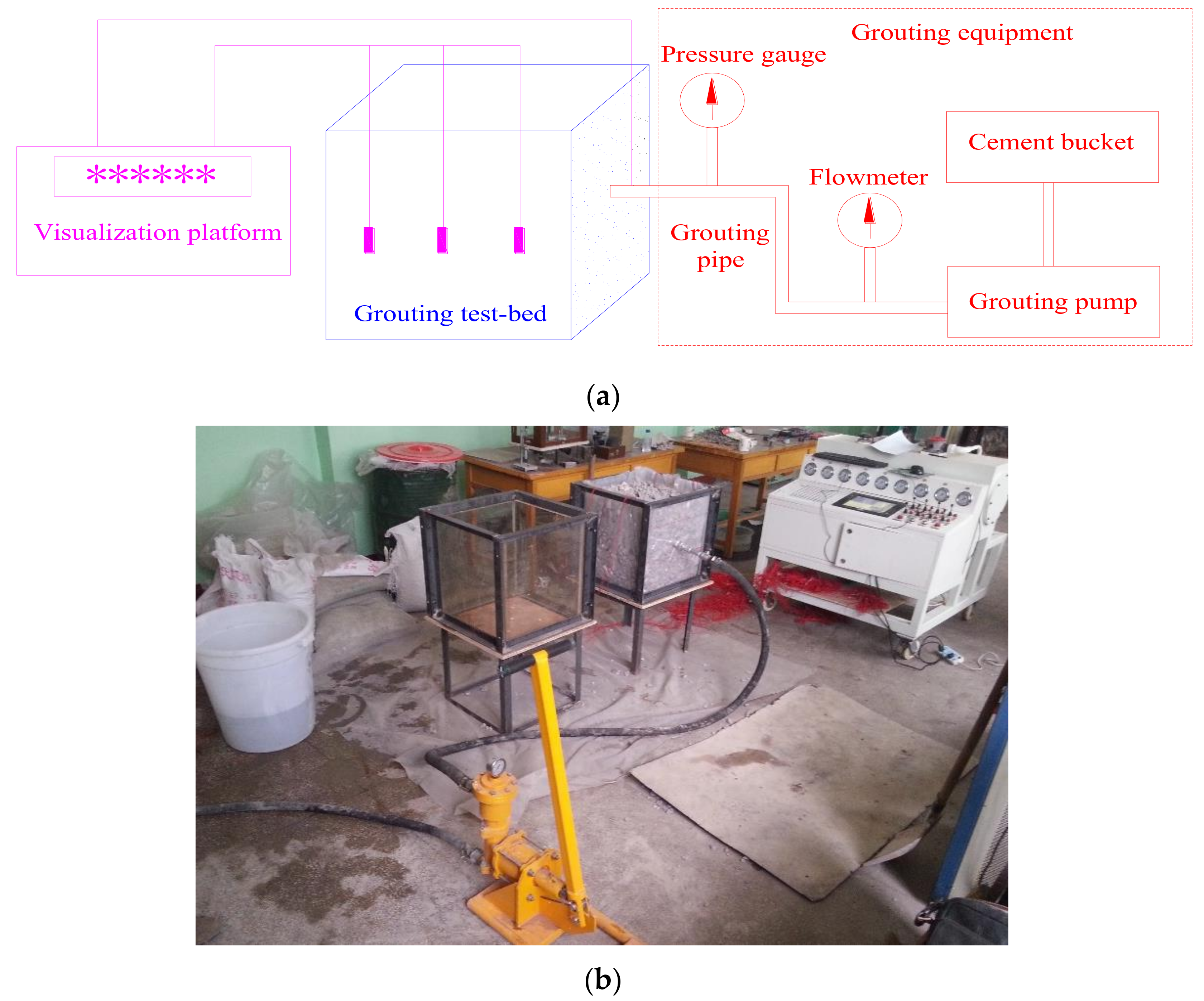
2.1. Experimental System
2.2. Experimental Plan
2.3. Experimental Procedure
- (1)
- Stones with different particle sizes of 8–10 mm, 15–30 mm and 35–50 mm were selected and mixed evenly to simulate the fractured porous rock mass. Different porosities were obtained by controlling the ratios of stones with different diameters, as shown in Table 3.
- (2)
- The mixed stone material was loaded into the grouting test-bed, and the sensors were arranged at the corresponding position of the grouting test-bed during the loading process.
- (3)
- The coordinates of the sensors were put into visualization platform. After inputting the coordinates, the green dots were displayed at the corresponding positions on the screen. During the grouting process, the green dots became red dots when the grout reached the corresponding sensor position.
- (4)
- Grouts with different water-cement ratios were prepared according to the experimental requirements. After that, the grout was stirred for 15 min in the grout bucket. The amount of grout in each experiment was 40 kg.
- (5)
- The grouting system was connected, the grouting pipe was inserted into the grouting hole, and then the grouting experiment began. The grouting pressure must be controlled within the required experimental range.
- (6)
- After grouting, the grouting pipe was pulled out from the grouting hole, the hole packer was stuffed into the grouting hole, then the grouting equipment was cleaned.
3. Result Analysis
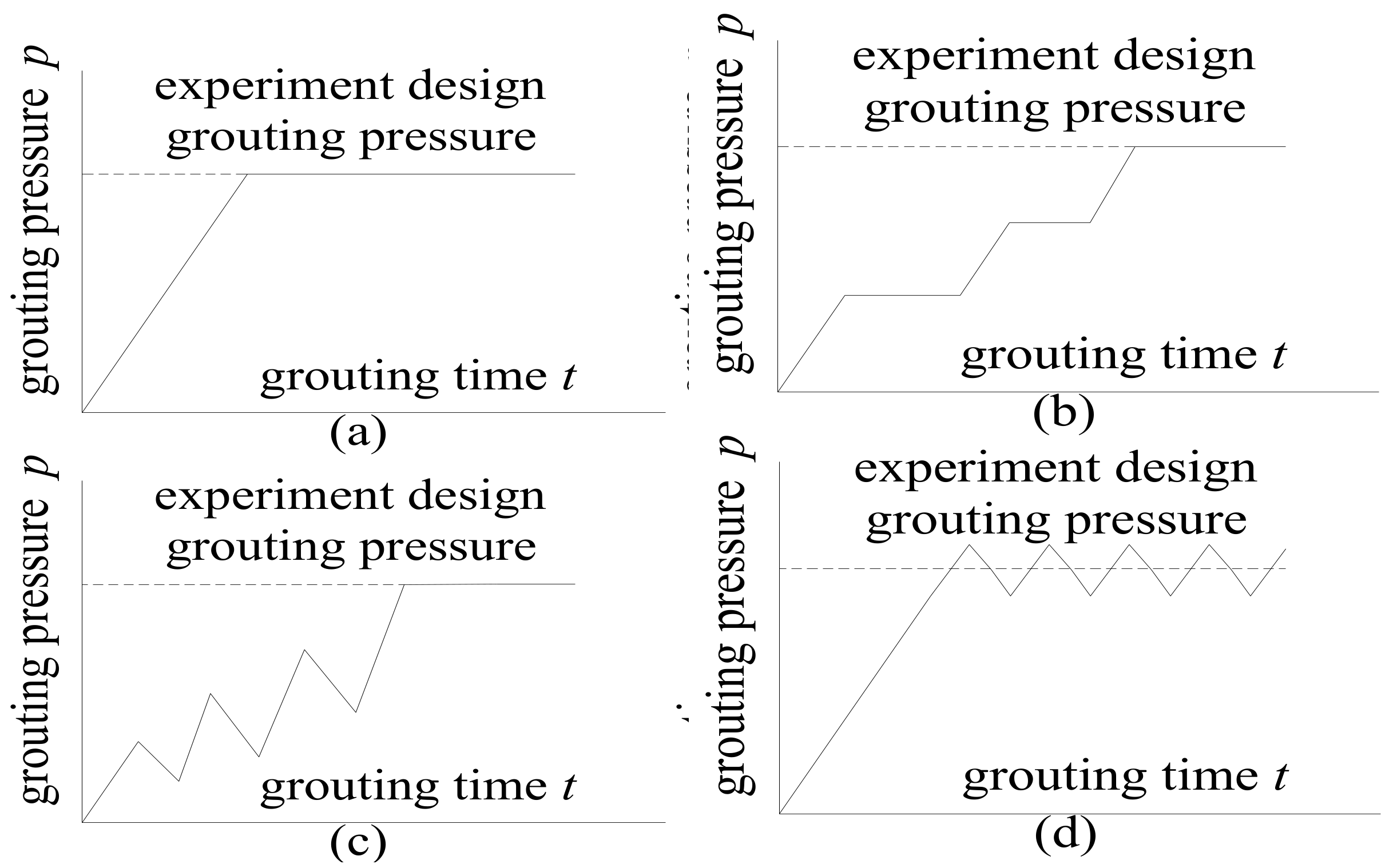
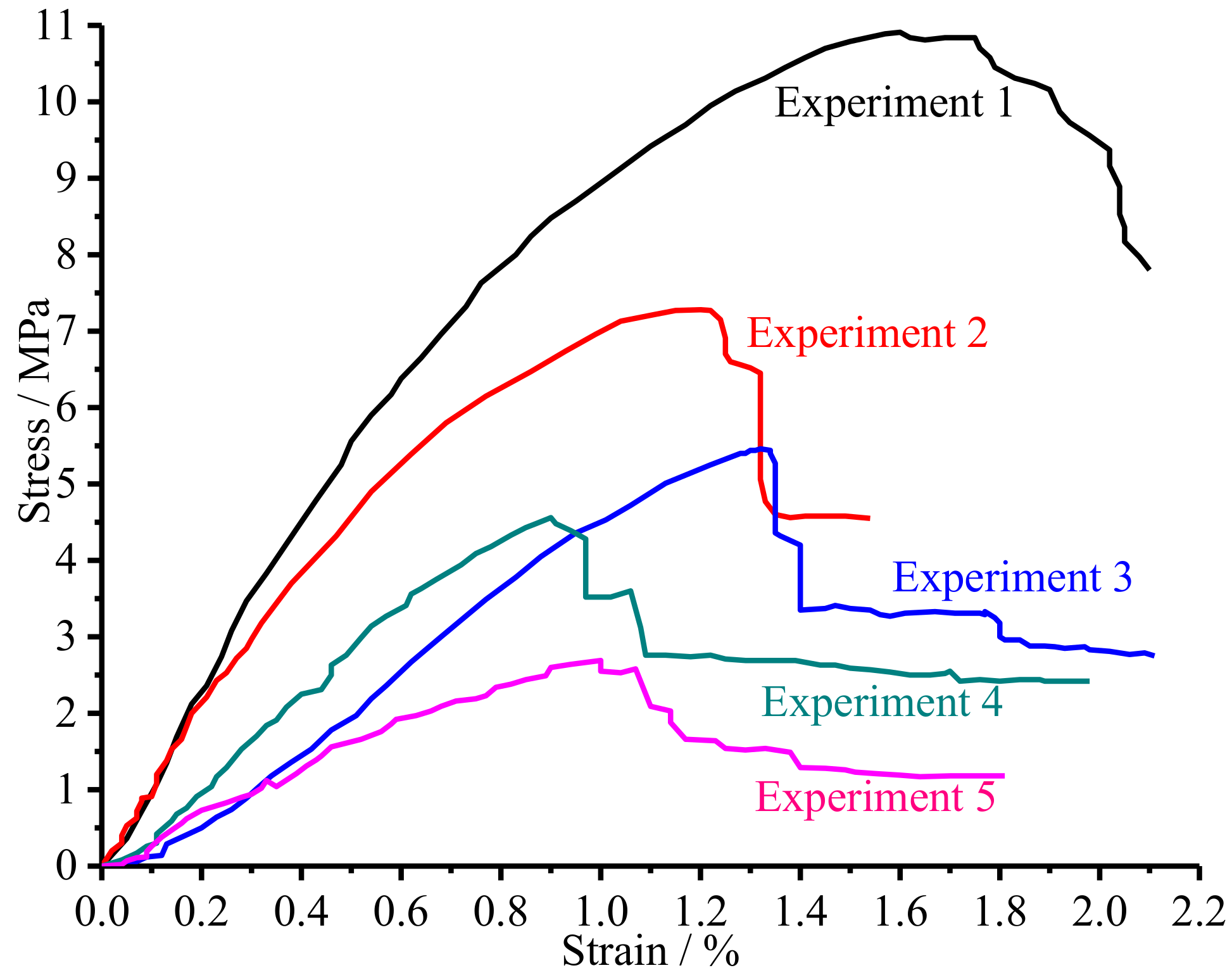
3.1. Grouting Pressure Variation Forms
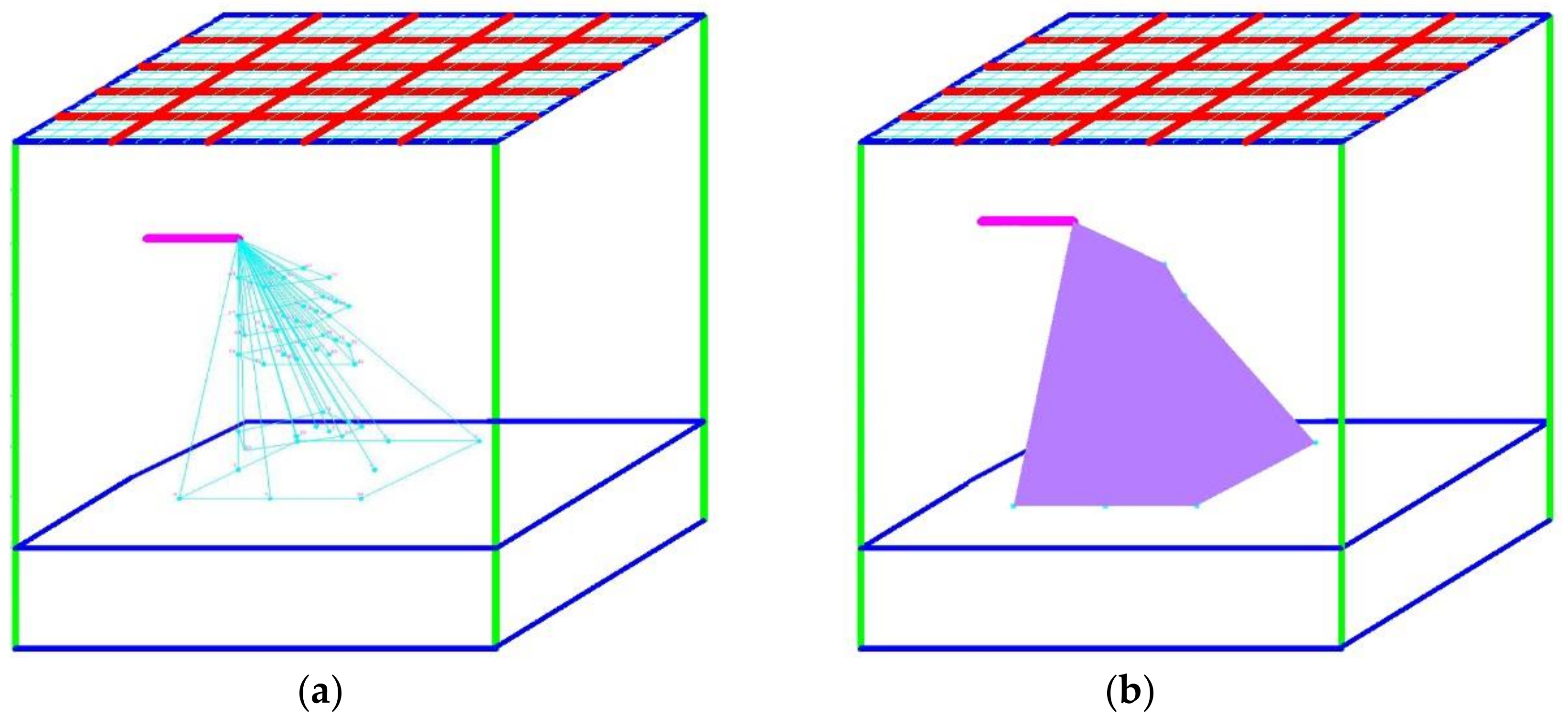
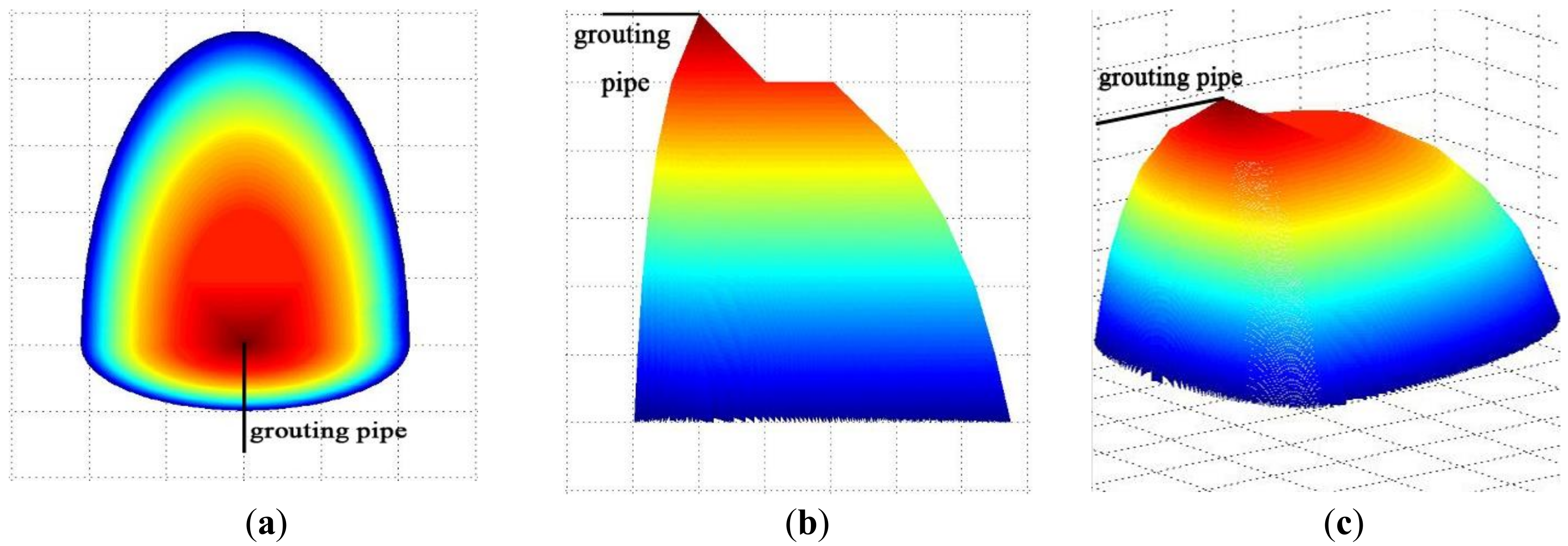
3.2. Grout Diffusion Pattern
3.3. Grouting Effect Testing
4. Field Application Effect and Analysis
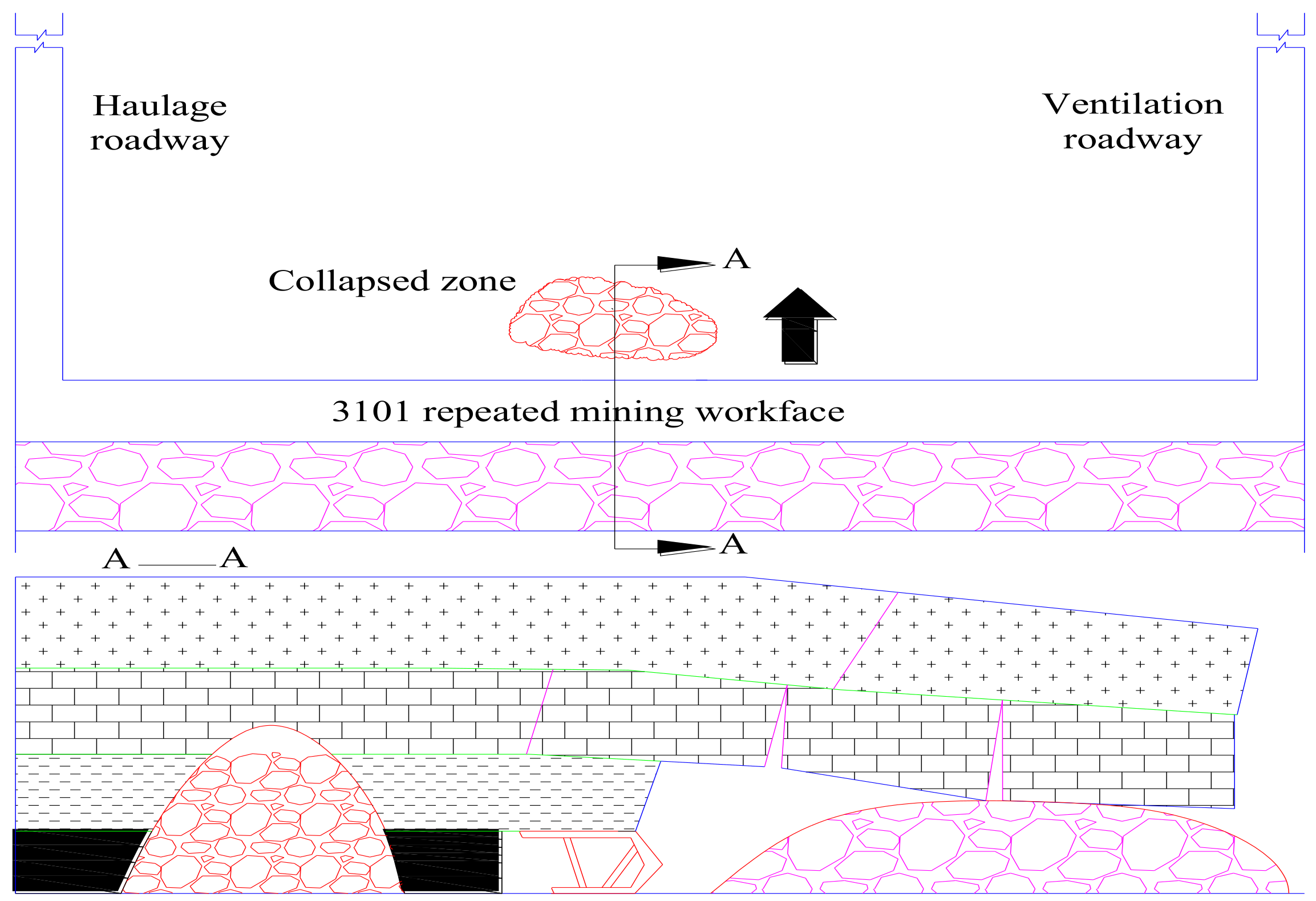
4.1. Engineering Geological Conditions
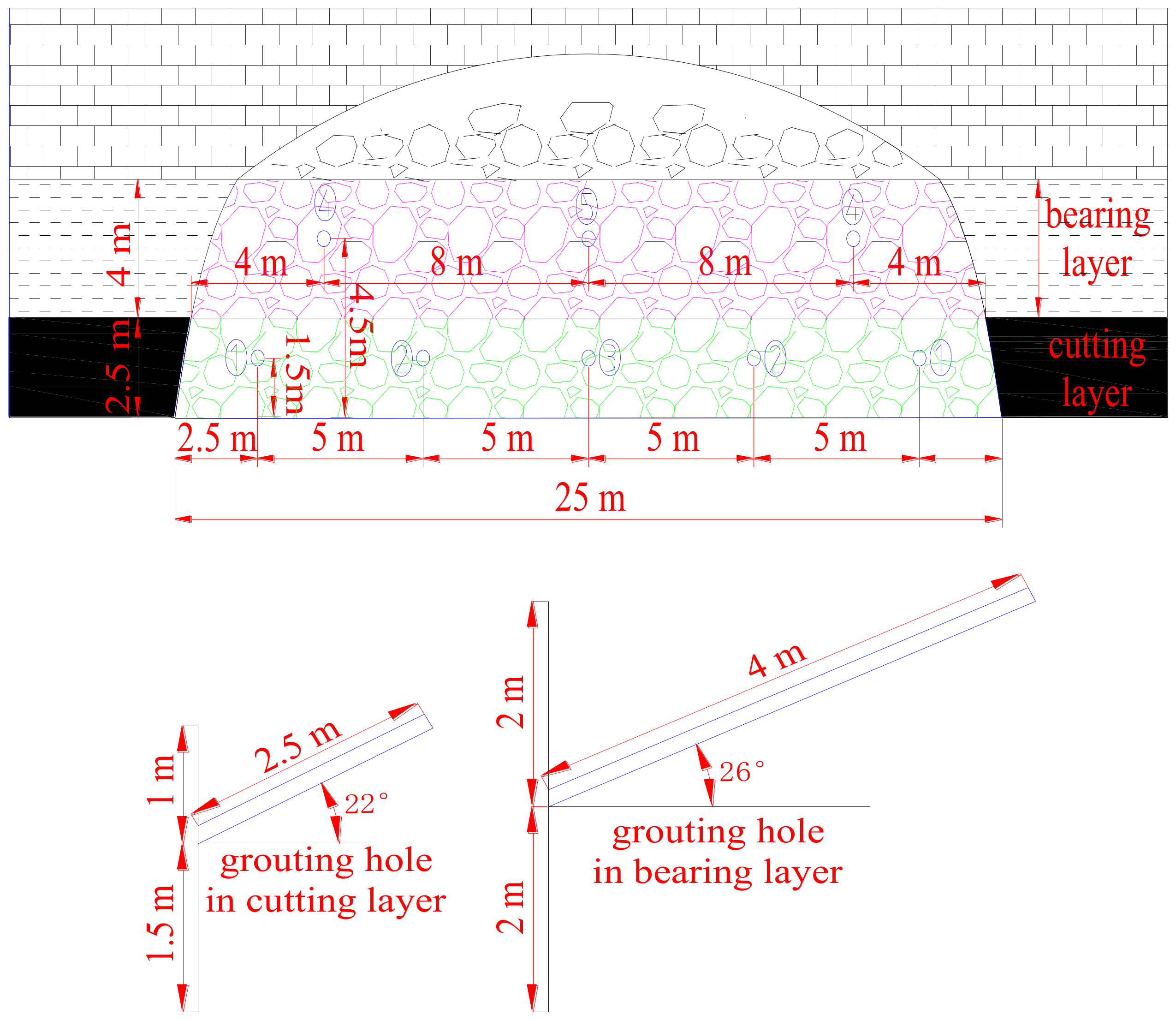
4.2. Grouting Parameters Selection
4.3. Arrangement of Layered Progressive Grouting
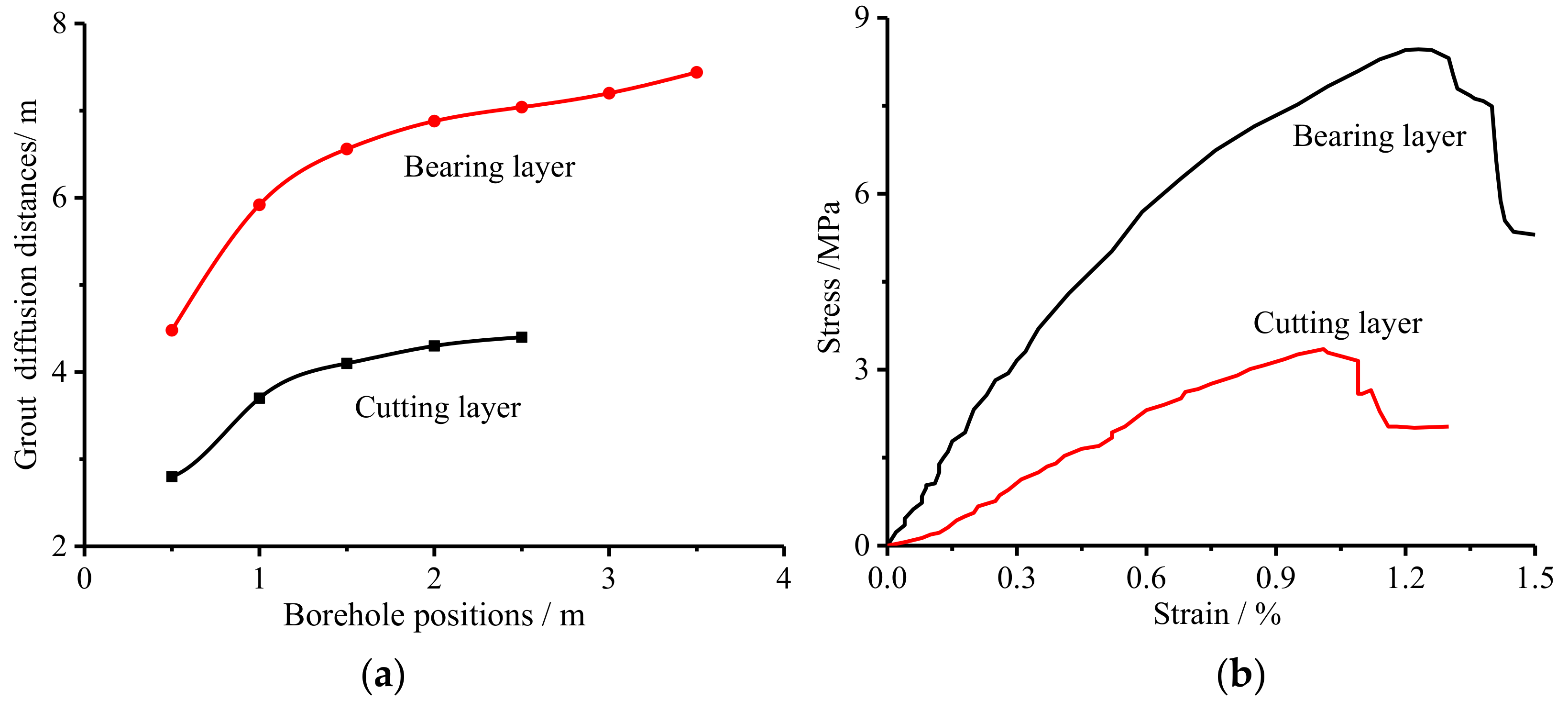
4.4. Application Effect Testing and Analysis
5. Discussion
- (1)
- When grouting in a fractusred porous rock mass, the main diffusion method of grouting is infiltration. The resistance of grout diffusion is mainly caused by friction in the grout and friction between the grout and rock mass medium. The diffusion resistance is small and can be maintained at a low level for an extended period of time. The grouting volume is mainly controlled by the volume and porosity of the fractured rock mass. In engineering practice, the distribution range of the fractured porous rock mass can first be measured, and then the grouting quantity and other related parameters can be calculated. In general, the grouting zone is not a standard sphere, and the equivalent grouting diffusion radius can be used to represent the grouting range.
- (2)
- Grouting in a fractured porous rock mass can improve the strength of the rock mass because grouting can change the properties of the rock mass. On one hand, the grout can improve the surface mechanical properties of the rock mass, reduce the sliding ability of the fractured rock mass, and enhance the tensile and shear strength parameters. On the other hand, the grout can enter the pores of the rock mass and fill the gaps and cracks in the rock mass. Because of the cohesion of the grout, the cohesion and internal friction angle of the rock mass are improved, and the fractured porous rock mass becomes a strong bearing capacity consolidation body, which is difficult to destroy.
6. Conclusions
- (1)
- To study the law of grouting diffusion in a fractured rock mass, this paper developed a visualization platform of the grouting diffusion range and a three-dimensional grouting experimental system. It can monitor the grout diffusion range, diffusion time, grout pressure, etc.
- (2)
- The grouting pressure has four kinds of variation forms in the grouting experiment: linear growth; cyclic growth; fluctuation stability and slow growth.
- (3)
- The flow pattern of the grout in the fractured porous rock mass has a parabolic shape from the grouting hole to the bottom. The lower the level is, the larger the diffusion range of the grout is. In the horizontal direction, the grout diffusion surface around the grouting hole had an asymmetrical circular surface. When the height of the grouting pipe, initial velocity of the grout, outlet angle and pore connectivity are determined, the shape of diffusion surface is certain.
- (4)
- The grouting pressure has the greatest influence on the grouting diffusion radius, followed by the grouting horizon and water-cement ratio. The grouting permeability coefficient has the least influence on the grouting diffusion radius.
- (5)
- The uniaxial compressive strength is significantly different in different experiments. The grout water-cement ratio has the greatest influence on the strength of the grouted gravel, followed by the grouting permeability. The grouting pressure coefficient has the least amount of influence on the grouting diffusion radius.
- (6)
- The results of the study were applied to old mining caving zone grouting reinforcement engineering. According to the results, the grouting parameters were designed and a layered progressive grouting method was proposed. Borehole observation and a core mechanical property test were performed to analyze the application effect. The working face traversed the old mining caving zone safely and smoothly. A good grouting effect was achieved.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Gong, P.; Zhang, X.; Lian, Q.; Li, J.; Duan, D. Characteristics and control of roof fracture in caving zone for residual coal mining face. Chin. J. Rock Mech. Eng. 2016, 35, 1–9. [Google Scholar]
- Liu, C.; Gong, P.L.; Wang, K.; Zhang, X.Q.; Liu, Y.D. Roof stability for repeated mining workface passing through abandoned parallel gateway. J. China Coal Soc. 2015, 40, 314–322. [Google Scholar]
- Ghosh, G.K.; Sivakumar, C. Application of underground microseismic monitoring for ground failure and secure longwall coal mining operation: A case study in an Indian mine. J. Appl. Geophys. 2018, 150, 21–39. [Google Scholar] [CrossRef]
- Riedel, I.; Guéguen, P. Modeling of damage-related earthquake losses in a moderate seismic-prone country and cost-benefit evaluation of retrofit investments: Application to France. Nat. Hazards 2018, 90, 639–662. [Google Scholar] [CrossRef]
- Xia, X.; Huang, Q. Study on the dynamic height of caved zone based on porosity. J. Min. Saf. Eng. 2014, 31, 102–107. [Google Scholar]
- Feng, G.; Jia, K.; Shang, B. Application and prospect of super-high-water packing material in mining engineering. Coal Sci. Technol. 2015, 43, 5–9. [Google Scholar]
- Marwan, A.; Zhou, M.M.; Abdelrehim, M.Z.; Meschke, G. Optimization of artificial ground freezing in tunneling in the presence of seepage flow. Comput. Geotech. 2016, 75, 112–125. [Google Scholar] [CrossRef]
- Li, S.J.; Wang, L.G.; Lu, Y.L.; Zhang, B. Slurry diffusion within cracked wall rock during the bolt-grouting process. J. China Univ. Min. Technol. 2011, 40, 874–880. [Google Scholar]
- Di Nucci, C. Unsteady free surface flow in porous media: One-dimensional model equations including vertical effects and seepage face. C. R. Mec. 2018, 346, 366–383. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Maglione, R.; Tsamantaki, C. Optimal determination of rheological parameters for Herschel-Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling. J. Pet. Sci. Eng. 2006, 5, 203–224. [Google Scholar] [CrossRef]
- Shucai, L.; Zhuo, Z.; Rentai, L. Analysis of diffusion of grout in porous media considering infiltration effects. Chin. J. Rock Mech. Eng. 2015, 34, 2401–2409. [Google Scholar]
- Huang, Y.; Wang, L.; Lu, Y. Study on the law of slurry diffusion within roadway surrounding rock during the whole section bolt-grouting process. J. Min. Saf. Eng. 2015, 32, 240–246. [Google Scholar]
- Saada, Z.; Canou, J.; Dormieux, L.; Dupla, J.C.; Maghous, S. Modeling of cement suspension flow in granular porous media. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 691–711. [Google Scholar] [CrossRef]
- Rafi, J.Y.; Stille, H. Basic mechanism of elastic jacking and impact of fracture aperture change on grout spread, transmissivity and penetrability. Tunn. Undergr. Space Technol. 2015, 49, 174–187. [Google Scholar] [CrossRef]
- Shimada, H.; Hamanaka, A.; Sasaoka, T.; Matsui, K. Behavior of grouting material used for floor reinforcement in underground mines. Int. J. Mech. Sci. 2014, 28, 133–148. [Google Scholar]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock: New methods for calculation of penetration length Part I. Tunn. Undergr. Space Technol. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock: New methods for calculation of penetration length Part II. Tunn. Undergr. Space Technol. 2008, 23, 9–17. [Google Scholar] [CrossRef]
- Minto, J.M.; MacLachlan, E.; El Mountassir, G.; Lunn, R.J. Rock fracture grouting with microbially induced carbonate precipitation. Water Resour. Res. 2016, 52, 8810–8827. [Google Scholar] [CrossRef]
- Minto, J.M.; MacLachlan, E.; El Mountassir, G.; Lunn, R.J. Study on grouting simulation experiment and its application. Chin. J. Geotech. Eng. 1997, 19, 28–33. [Google Scholar]
- Fang, K.T.; Ma, C.X. Orthogonal and Uniform Experimental Design; Science Press: Beijing, China, 2001. [Google Scholar]
- Liang, D.; Jiang, Z.; Cao, D. Calculation of hydraulic conductivity in high water-pressure test. J. Min. Saf. Eng. 2016, 33, 324–328. [Google Scholar]
- Yang, Z.Q.; Niu, X.D.; Hou, K.P.; Zhou, Z.H.; Liang, W. Study of grouting diffusion parameters in gravel soil. Rock Soil Mech. 2015, 36, 397–402. [Google Scholar]






| Experiment Number | Porosity n | Water-Cement Ratio m | Grouting Pressure p (MPa) | Dynamic Viscosity Coefficient η (Pa·s) | Grout Density ρ (kg/m3) | Permeability e (m2) | Permeability Coefficient k (m/s) |
|---|---|---|---|---|---|---|---|
| 1 | 0.459 | 0.5:1 | 0.3 | 37 | 1823 | 2.33 × 10−6 | 0.001124 |
| 2 | 0.455 | 0.6:1 | 0.5 | 20 | 1734 | 1.41 × 10−6 | 0.001195 |
| 3 | 0.447 | 0.7:1 | 0.2 | 13 | 1662 | 5.24 × 10−7 | 0.000656 |
| 4 | 0.426 | 0.8:1 | 0.4 | 8 | 1603 | 1.27 × 10−7 | 0.000249 |
| 5 | 0.466 | 0.9:1 | 0.6 | 6 | 1512 | 4.27 × 10−6 | 0.010553 |
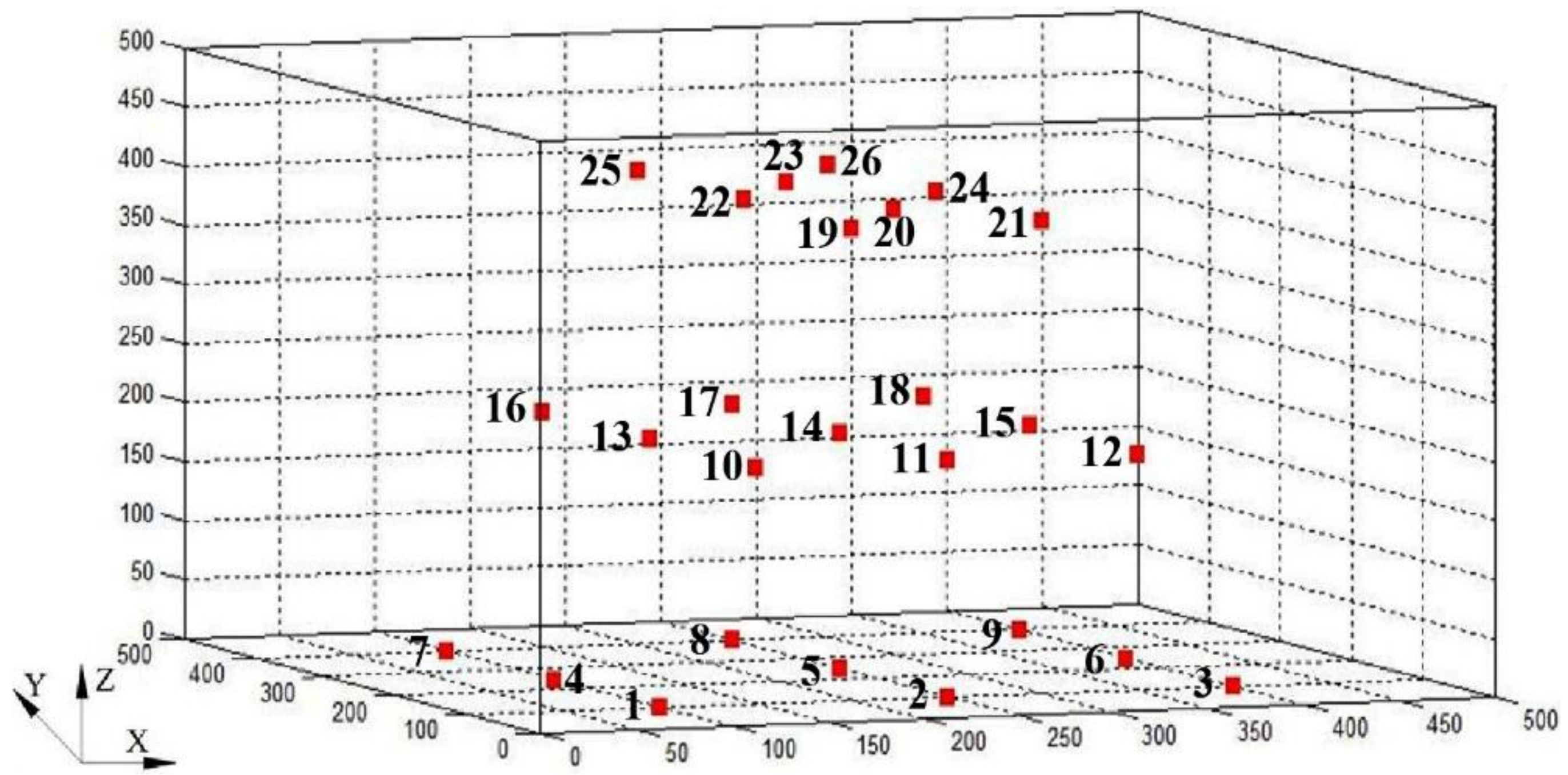
| Signal Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sensor coordinate | X | 100 | 250 | 400 | 100 | 250 | 400 | 100 | 250 | 400 | 150 | 250 | 350 | 150 |
| Y | 100 | 100 | 100 | 250 | 250 | 250 | 400 | 400 | 400 | 100 | 100 | 100 | 250 | |
| Z | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 200 | 200 | 200 | 200 | |
| Signal Number | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| Sensor coordinate | X | 250 | 350 | 150 | 250 | 350 | 200 | 250 | 300 | 200 | 250 | 300 | 200 | 300 |
| Y | 250 | 250 | 400 | 400 | 400 | 100 | 175 | 100 | 250 | 325 | 250 | 400 | 400 | |
| Z | 200 | 200 | 200 | 200 | 200 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | |
| Experiment Number | The Proportions of Stones with Different Particle Sizes (%) | Porosity | ||
|---|---|---|---|---|
| 8–10 mm | 15–30 mm | 35–50 mm | ||
| 1 | 0 | 50 | 50 | 0.459 |
| 2 | 20 | 50 | 30 | 0.455 |
| 3 | 60 | 30 | 10 | 0.447 |
| 4 | 100 | 0 | 0 | 0.426 |
| 5 | 0 | 0 | 100 | 0.466 |
| Experiment Number | Range of Grout Diffusion for Different Level (mm) | ||
|---|---|---|---|
| 50 mm | 200 mm | 300 mm | |
| 1 | 145 | 181 | 206 |
| 2 | 157 | 196 | 224 |
| 3 | 123 | 154 | 175 |
| 4 | 149 | 186 | 212 |
| 5 | 173 | 216 | 246 |
| Experiment Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Compressive strength (MPa) | 10.91 | 7.28 | 5.46 | 4.56 | 2.69 |
| Action Layer | Diffusion Radius R (m) | Bearing Pressure P (MPa) | Grouting Amount Q (m3) | Porosity n | Water-Cement Ratio m | Grouting Pressure p (MPa) | Grouting Time t (min) | Permeability k (m/s) |
|---|---|---|---|---|---|---|---|---|
| Bearing layer | 4 | 8 | 34.48 | 0.52 | 0.7:1 | 3 | 100 | 0.115 |
| Cutting layer | 2.5 | 3 | 13.48 | 0.52 | 0.9:1 | 1.5 | 30 | 0.226 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Cheng, X.; Luan, H.; Wang, T.; Zhang, M.; Hao, R. Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application. Processes 2018, 6, 191. https://doi.org/10.3390/pr6100191
Jiang D, Cheng X, Luan H, Wang T, Zhang M, Hao R. Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application. Processes. 2018; 6(10):191. https://doi.org/10.3390/pr6100191
Chicago/Turabian StyleJiang, Donghai, Xianzhen Cheng, Hengjie Luan, Tongxu Wang, Mingguang Zhang, and Ruiyun Hao. 2018. "Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application" Processes 6, no. 10: 191. https://doi.org/10.3390/pr6100191
APA StyleJiang, D., Cheng, X., Luan, H., Wang, T., Zhang, M., & Hao, R. (2018). Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application. Processes, 6(10), 191. https://doi.org/10.3390/pr6100191






