Modeling the Separation of Microorganisms in Bioprocesses by Flotation
Abstract
:1. Introduction
2. Modeling Approaches
2.1. Aggregation Kernel
2.1.1. Frequency of Encounters
2.1.2. Encounter Efficiency
2.2. Spatial Models
2.2.1. Two-Zone Model
2.2.2. One-Way Coupling
2.3. Heteroaggregation Modeling
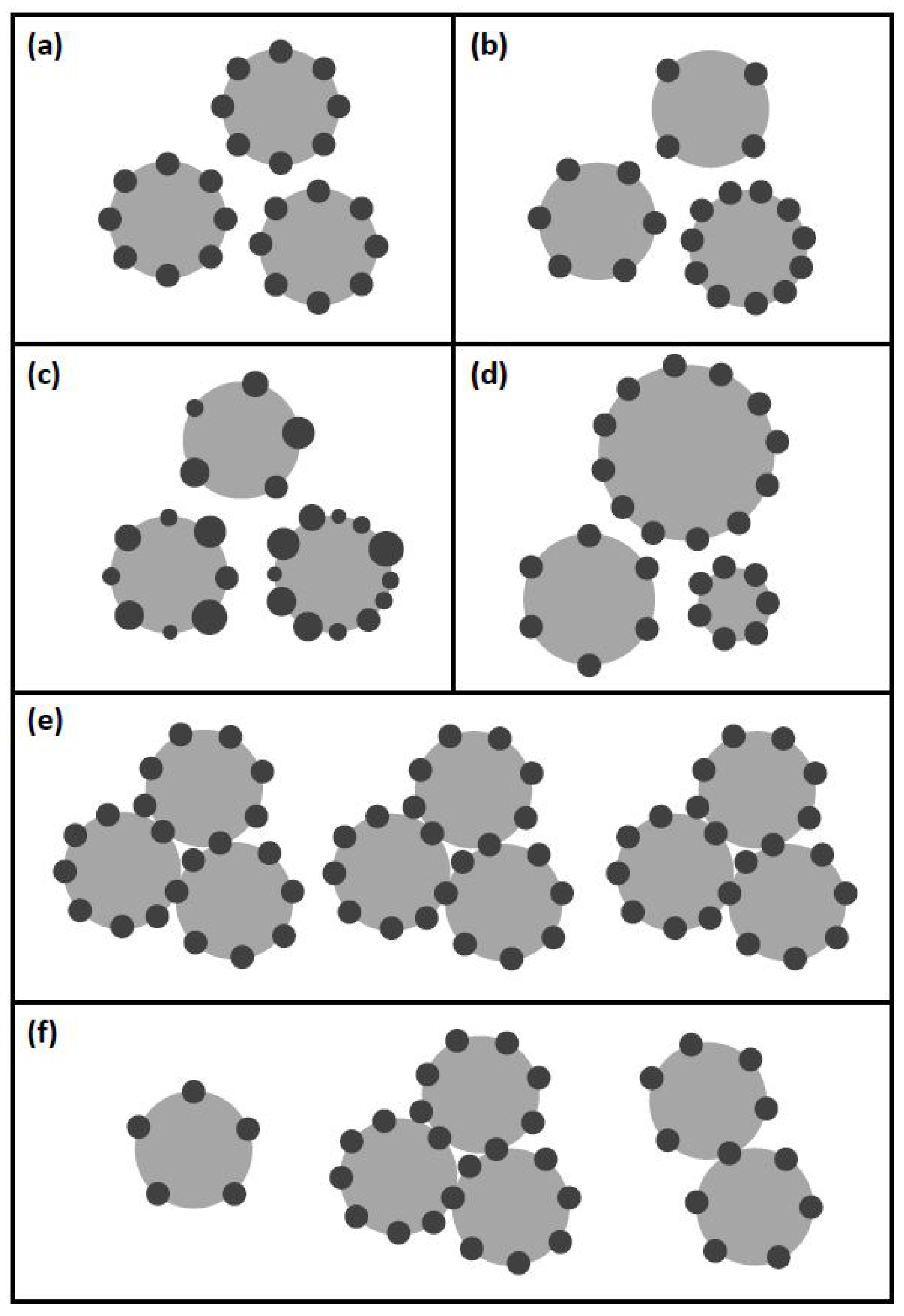
2.3.1. Averaged
2.3.2. Not Averaged
2.3.3. Poly.Cells
2.3.4. Poly.Bubbles
2.3.5. Clustering
2.3.6. Clustering Averaged
3. Numerical Methods
4. Results and Discussion
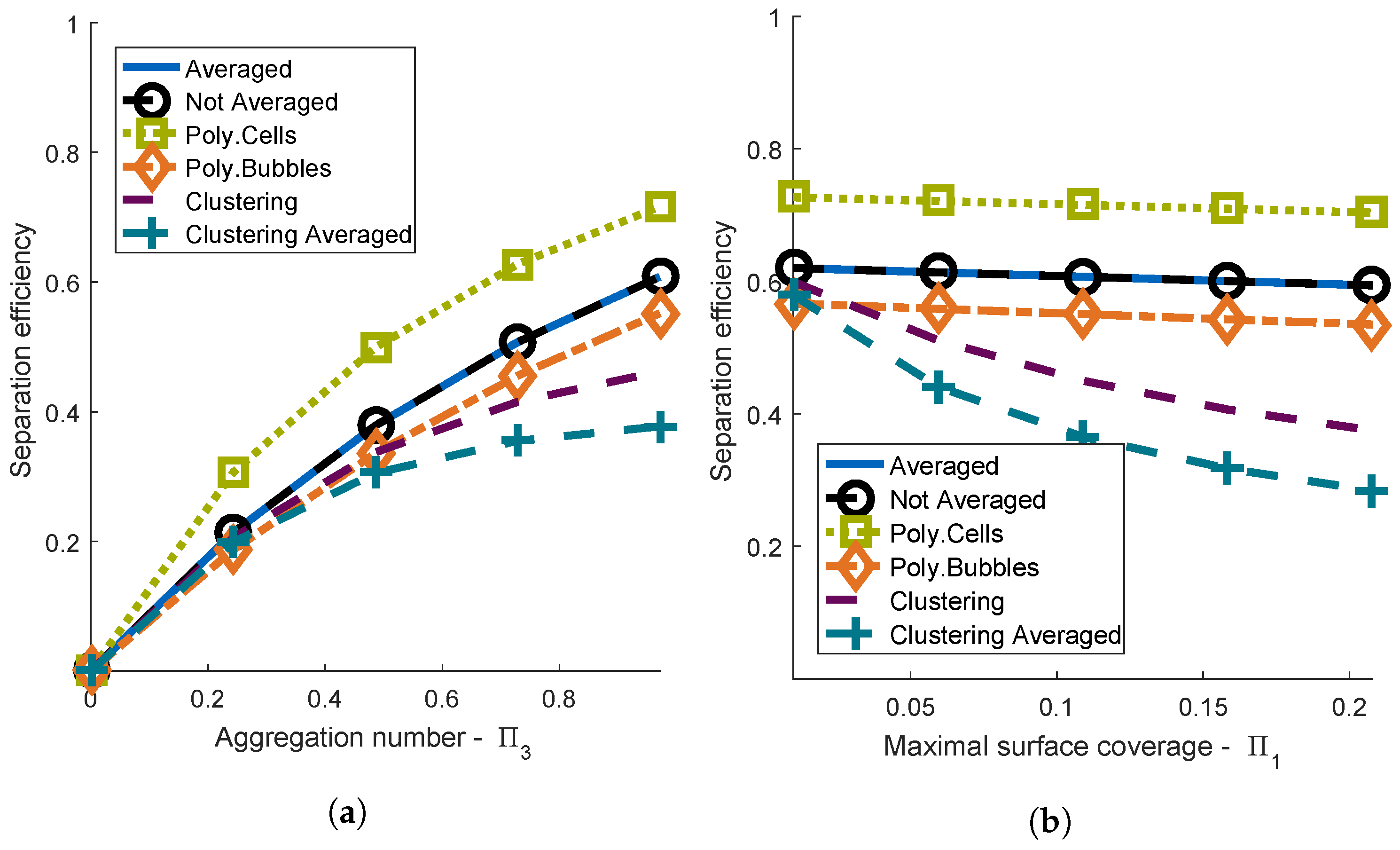
4.1. Comparison of the Different Aggregation Models
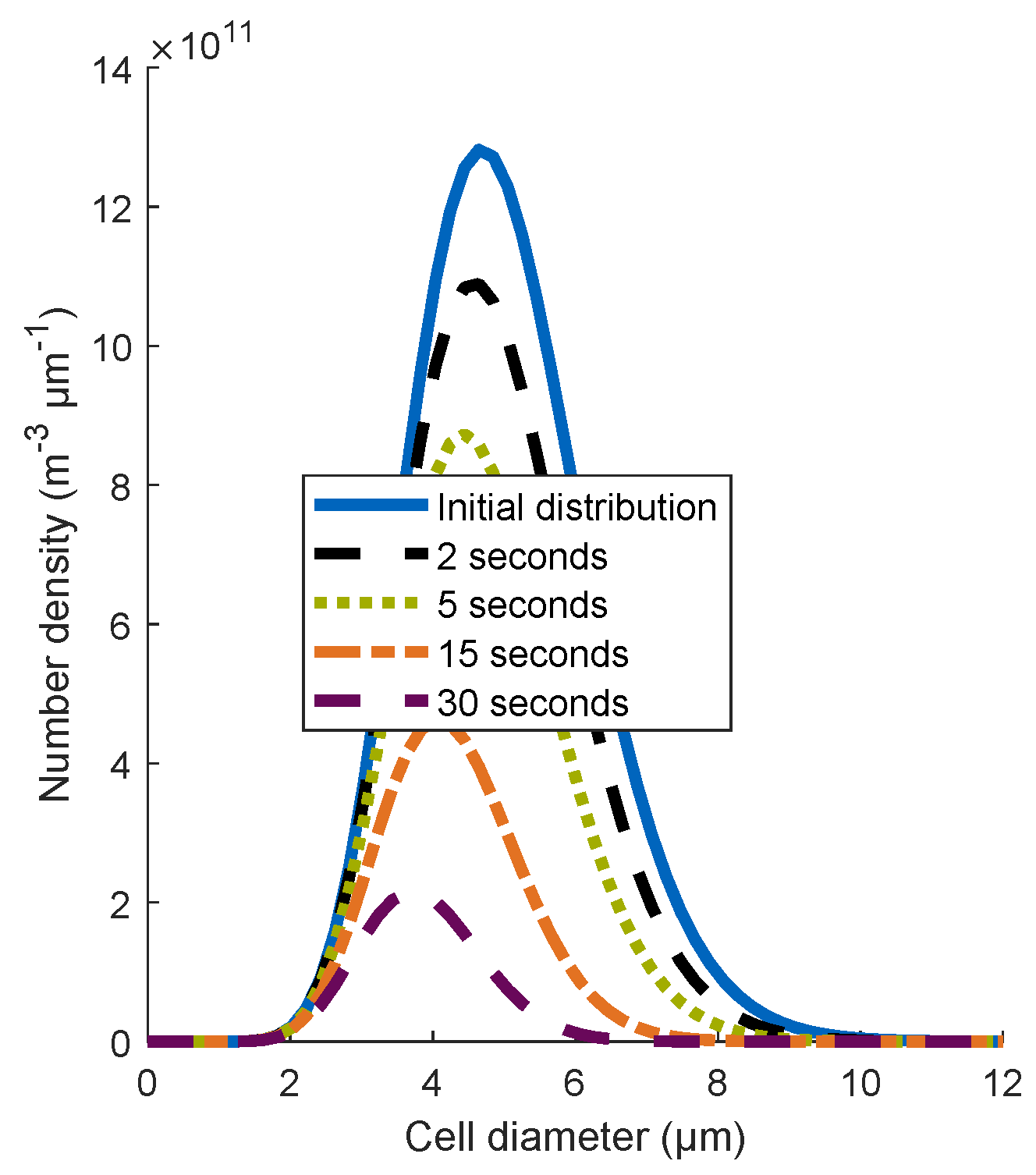
4.1.1. Influence of the Cell Size Distribution
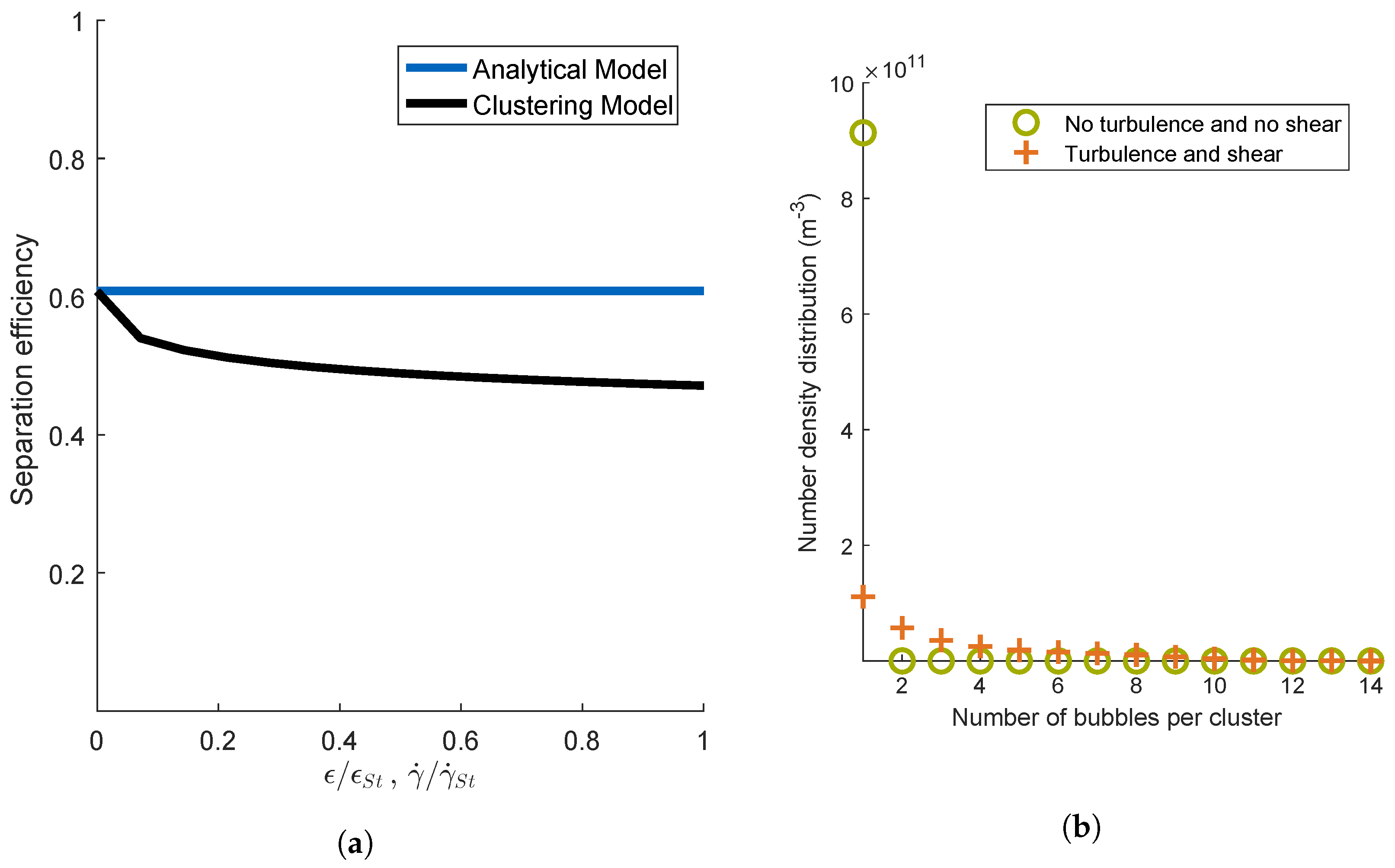
4.1.2. Mechanisms Leading to the Formation of Clusters
4.1.3. Scope of Aggregation Models
4.2. One-Way Coupling
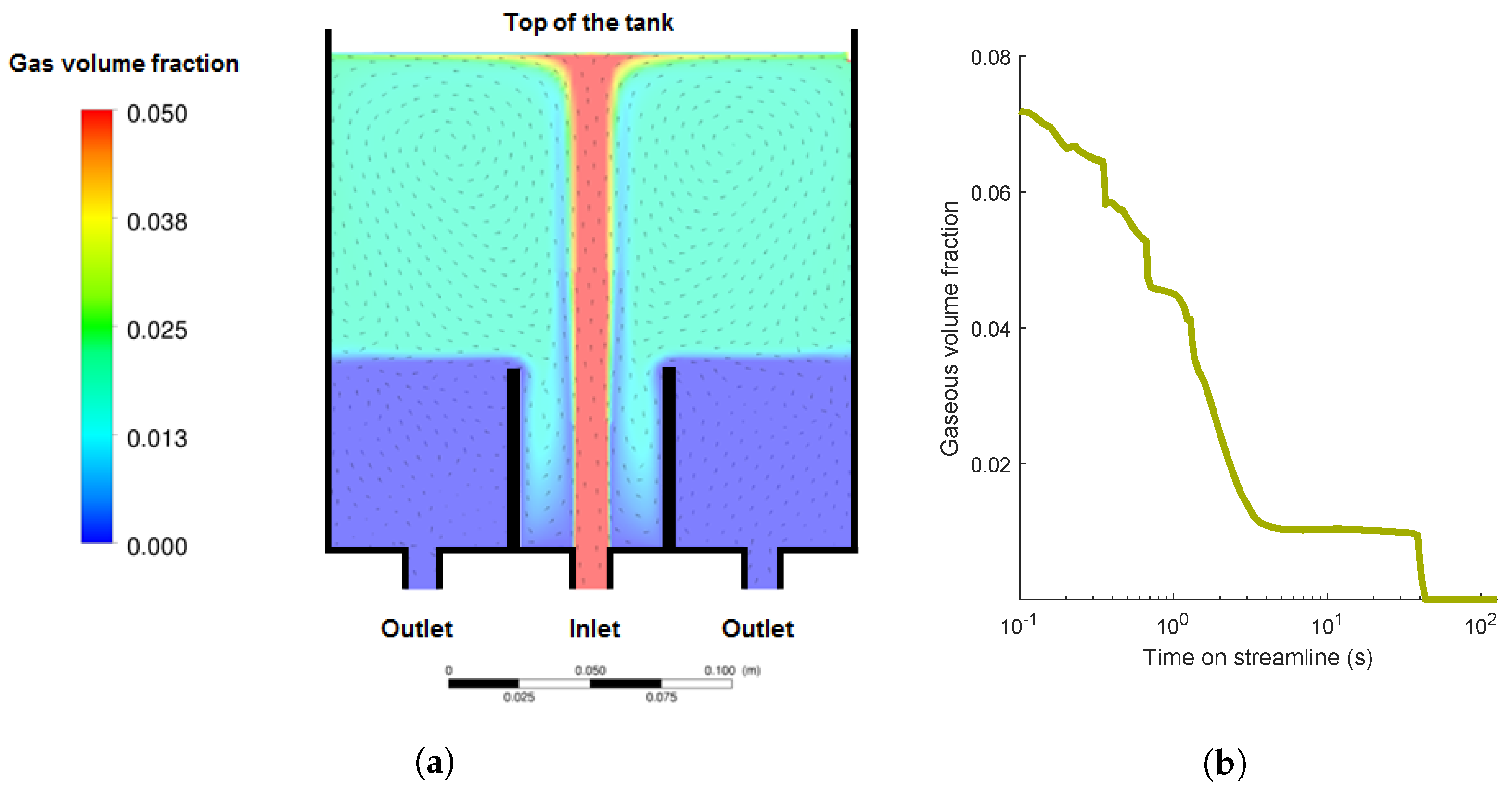
4.2.1. Gas Volume Fraction
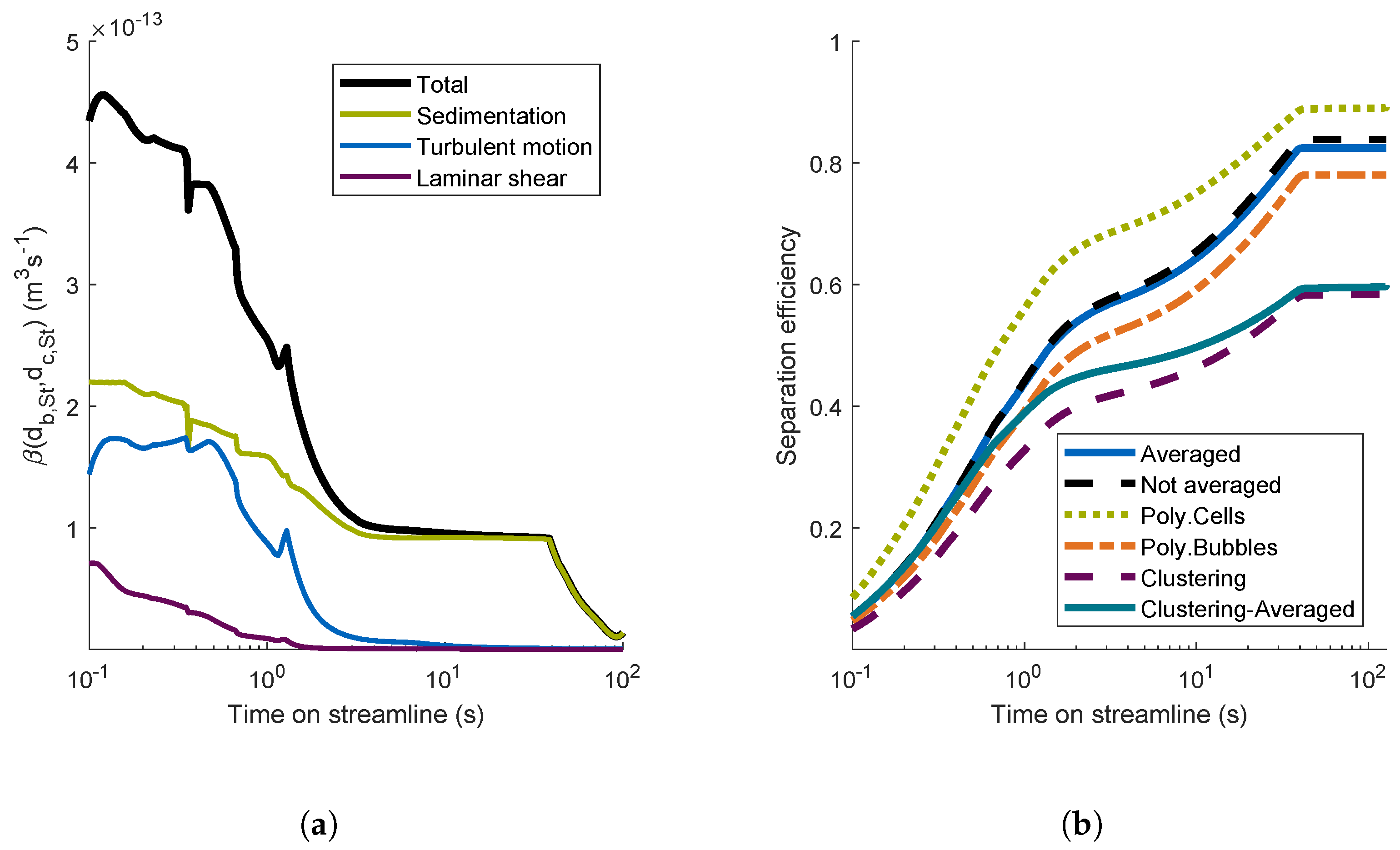
4.2.2. Aggregation Mechanisms
4.2.3. Comparison of Different Aggregation Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Model Averaged-Algebraic Solution for Two-Zone Model
Appendix A.1. Aggregation Equation
Appendix A.2. Collision Efficiency Due to Surface Coverage
Appendix A.3. Non-Dimensionalization
Appendix A.4. Analytical Solution
Appendix B. Encounter Efficiency Due to Surface Coverage for Clustering
References
- Larkum, A.W.; Ross, I.L.; Kruse, O.; Hankamer, B. Selection, breeding and engineering of microalgae for bioenergy and biofuel production. Trends Biotechnol. 2012, 30, 198–205. [Google Scholar] [CrossRef] [PubMed]
- Sarris, D.; Papanikolaou, S. Biotechnological production of ethanol: Biochemistry, processes and technologies. Eng. Life Sci. 2016, 16, 307–329. [Google Scholar] [CrossRef]
- Christenson, L.; Sims, R. Production and harvesting of microalgae for wastewater treatment, biofuels, and bioproducts. Biotechnol. Adv. 2011, 29, 686–702. [Google Scholar] [CrossRef] [PubMed]
- Chisti, Y. Biodiesel from microalgae. Biotechnol. Adv. 2007, 25, 294–306. [Google Scholar] [CrossRef] [PubMed]
- Merkel, T.; Königsson, S.; Thorsson, C.; Münkel, R. Flocculation inside disc-stack centrifuges to improve biomass separation (Result of EU project PRODIAS). Chem. Ing. Tech. 2018, 90, 1267–1267. [Google Scholar] [CrossRef]
- Grima, E.M.; Belarbi, E.H.; Fernández, F.A.; Medina, A.R.; Chisti, Y. Recovery of microalgal biomass and metabolites: process options and economics. Biotechnol. Adv. 2003, 20, 491–515. [Google Scholar] [CrossRef] [Green Version]
- Barros, A.I.; Gonçalves, A.L.; Simões, M.; Pires, J.C. Harvesting techniques applied to microalgae: A review. Renew. Sustain. Energy Rev. 2015, 41, 1489–1500. [Google Scholar] [CrossRef] [Green Version]
- Soetaert, W.; Vandamme, E.J. Industrial Biotechnology: Sustainable Growth and Economic Success; WILEY-VCH: Weinheim, Germany, 2010. [Google Scholar]
- Milledge, J.J.; Heaven, S. Disc stack centrifugation separation and cell disruption of microalgae: A technical note. Environ. Nat. Resour. Res. 2011, 1, 17–24. [Google Scholar] [CrossRef]
- Hutahaean, J.; Cilliers, J.; Brito-Parada, P.R. A multi-criteria decision framework for the selection of biomass separation equipment. Chem. Eng. Technol. 2018. [Google Scholar] [CrossRef]
- Cilliers, J. Hydrocyclones for Particle Size Separation; UMIST: Manchester, UK, 2000. [Google Scholar]
- Vega, D.; Brito-Parada, P.; Cilliers, J. Optimising small hydrocyclone design using 3D printing and CFD simulations. Chem. Eng. J. 2018, 350, 653–659. [Google Scholar] [CrossRef]
- Habibian, M.; Pazouki, M.; Ghanaie, H.; Abbaspour-Sani, K. Application of hydrocyclone for removal of yeasts from alcohol fermentations broth. Chem. Eng. J. 2008, 138, 30–34. [Google Scholar] [CrossRef]
- Ndikubwimana, T.; Chang, J.; Xiao, Z.; Shao, W.; Zeng, X.; Ng, I.S.; Lu, Y. Flotation: A promising microalgae harvesting and dewatering technology for biofuels production. Biotechnol. J. 2016, 11, 315–326. [Google Scholar] [CrossRef] [PubMed]
- Hanotu, J.; Bandulasena, H.; Zimmerman, W.B. Microflotation performance for algal separation. Biotechnol. Bioeng. 2012, 109, 1663–1673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanotu, J.; Karunakaran, E.; Bandulasena, H.; Biggs, C.; Zimmerman, W.B. Harvesting and dewatering yeast by microflotation. Biochem. Eng. J. 2014, 82, 174–182. [Google Scholar] [CrossRef]
- Shawwa, A.R.; Smith, D.W. Dissolved air flotation model for drinking water treatment. Can. J. Civ. Eng. 2000, 27, 373–382. [Google Scholar] [CrossRef]
- Edzwald, J.K. Dissolved air flotation and me. Water Res. 2010, 44, 2077–2106. [Google Scholar] [CrossRef] [PubMed]
- Fukushi, K.; Tambo, N.; Matsui, Y. A Kinetic-Model for Dissolved Air Flotation in Water and Waster-Water Treatment. Water Sci. Technol. 1995, 31, 37–47. [Google Scholar] [CrossRef]
- Zhang, X.; Hewson, J.C.; Amendola, P.; Reynoso, M.; Sommerfeld, M.; Chen, Y.; Hu, Q. Critical evaluation and modeling of algal harvesting using dissolved air flotation. Biotechnol. Bioeng. 2014, 111, 2477–2485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwak, D.H.; Yoo, S.J.; Lee, E.J.; Lee, J.W. Evaluation on simultaneous removal of particles and off-flavors using population balance for application of powdered activated carbon in dissolved air flotation process. Water Sci. Technol. 2010, 61, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Lee, J.; Choi, D.; Kim, S.; Kwak, D. Flotation efficiency of activated sludge flocs using population balance model in dissolved air flotation. Korean J. Chem. Eng. 2006, 23, 271–278. [Google Scholar] [CrossRef]
- Laamanen, C.A.; Ross, G.M.; Scott, J.A. Flotation harvesting of microalgae. Renew. Sustain. Energy Rev. 2016, 58, 75–86. [Google Scholar] [CrossRef]
- Leppinen, D.; Dalziel, S.; Linden, P. Modelling the global efficiency of dissolved air flotation. Water Sci. Technol. 2001, 43, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Kwak, D.H.; Jung, H.J.; Kwon, S.B.; Lee, E.J.; Won, C.H.; Lee, J.W.; Yoo, S.J. Rise velocity verification of bubble-floc agglomerates using population balance in the DAF process. J. Water Supply Res. Technol.-AQUA 2009, 58, 85–94. [Google Scholar] [CrossRef]
- Matsui, Y.; Fukushi, K.; Tambo, N. Modeling, simulation and operational parameters of dissolved air flotation. J. Water Serv. Res. Technol.-AQUA 1998, 47, 9–20. [Google Scholar] [CrossRef]
- Lakghomi, B.; Lawryshyn, Y.; Hofmann, R. A model of particle removal in a dissolved air flotation tank: Importance of stratified flow and bubble size. Water Res. 2015, 68, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Leppinen, D.; Dalziel, S. Bubble size distribution in dissolved air flotation tanks. J. Water Suppl. Res. Technol.-AQUA 2004, 53, 531–543. [Google Scholar] [CrossRef]
- Gulden, S.; Riedele, C.; Rollié, S.; Kopf, M.H.; Nirschl, H. Online bubble size analysis in micro flotation. Chem. Eng. Sci. 2018, 185, 168–181. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karapantsios, T.D.; Matis, K.A. CFD model for the design of large scale flotation tanks for water and wastewater treatment. Ind. Eng. Chem. Res. 2007, 46, 6590–6599. [Google Scholar] [CrossRef]
- Edzwald, J.K. Principles and applications of dissolved air flotation. Water Sci. Technol. 1995, 31, 1–23. [Google Scholar] [CrossRef]
- Saffman, P.; Turner, J. On the collision of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Meyer, C.; Deglon, D. Particle collision modeling—A review. Miner. Eng. 2011, 24, 719–730. [Google Scholar] [CrossRef]
- Pedocchi, F.; Piedra-Cueva, I. Camp and Stein’s Velocity Gradient Formalization. J. Environ. Eng. 2005, 131, 1369–1376. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar] [CrossRef]
- Nguyen, A.; Ralston, J.; Schulze, H. On modelling of bubble-particle attachment probability in flotation. Int. J. Miner. Process. 1998, 53, 225–249. [Google Scholar] [CrossRef]
- Nguyen, A. Hydrodynamics of liquid flows around air bubbles in flotation: A review. Int. J. Miner. Process. 1999, 56, 165–205. [Google Scholar] [CrossRef]
- Sasic, S.; Sibaki, E.K.; Strom, H. Direct numerical simulation of a hydrodynamic interaction between settling particles and rising microbubbles. Eur. J. Mech. B Fluids 2014, 43, 65–75. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle-bubble collision models—A review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- Rollié, S.; Briesen, H.; Sundmacher, K. Discrete bivariate population balance modelling of heteroaggregation processes. J. Colloid Interface Sci. 2009, 336, 551–564. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Harshe, Y.M.; Lattuada, M. Influence of the Potential Well on the Breakage Rate of Colloidal Aggregates in Simple Shear and Uniaxial Extensional Flows. Langmuir 2015, 31, 5712–5721. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Zeng, Q.; Yu, A. Calculation of Noncontact Forces between Silica Nanospheres. Langmuir 2013, 29, 2175–2184. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, M.; Peuker, U.A. Hydrophobicity of Minerals Determined by Atomic Force Microscopy—A Tool for Flotation Research. Chem. Ing. Tech. 2014, 86, 865–873. [Google Scholar] [CrossRef]
- Ditscherlein, L.; Gulden, S.J.; Müller, S.; Baumann, R.P.; Peuker, U.A.; Nirschl, H. Measuring interactions between yeast cells and a micro-sized air bubble via atomic force microscopy. J. Colloid Interface Sci. 2018, 532, 689–699. [Google Scholar] [CrossRef] [PubMed]
- Ta, C.; Beckley, J.; Eades, A. A multiphase CFD model of DAF process. Water Sci. Technol. 2001, 43, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Buffo, A. Multivariate Population Balance for Turbulent Gas-Liquid Flows. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2012. [Google Scholar]
- Hecht, K.J.; Krause, U.; Hofinger, J.; Bey, O.; Nilles, M.; Renze, P. Prediction of gas density effects on bubbly flow hydrodynamics: New insights through an approach combining population balance models and computational fluid dynamics. AIChE J. 2018, 64, 3764–3774. [Google Scholar] [CrossRef]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakaguchi, T. Drag coefficients of single bubbles under normal and micro gravity conditions. JSME Int. J. Ser. B-Fluids Therm. Eng. 1998, 41, 472–479. [Google Scholar] [CrossRef]
- Kumar, J.; Peglow, M.; Warnecke, G.; Heinrich, S.; Morl, L. Improved accuracy and convergence of discretized population balance for aggregation: The cell average technique. Chem. Eng. Sci. 2006, 61, 3327–3342. [Google Scholar] [CrossRef]
- Iyer-Biswas, S.; Crooks, G.E.; Scherer, N.F.; Dinner, A.R. Universality in stochastic exponential growth. Phys. Rev. Lett. 2014, 113, 028101. [Google Scholar] [CrossRef] [PubMed]
| Encounter Frequency | Due to: | Eq. |
| Laminar shear | (4) | |
| Sedimentation | (5) | |
| Turbulence | (6) | |
| Encounter Efficiency Due to Surface Coverage | For Model: | Eq. |
| Averaged | (7) | |
| Not Averaged | (8) | |
| Poly.Cells | (9) | |
| Poly.Bubbles | (10) | |
| Clustering | (11) | |
| Clustering Averaged | (12) | |
| (13) | ||
| Hydrodynamic encounter efficiency | (14) |
| Parameter | Abbreviation | Value | Unit |
|---|---|---|---|
| Residence time | 10 | s | |
| Gas volume fraction | 0.03 | - | |
| Bubble diameter | 40 | m | |
| Cell diameter | 5 | m | |
| Cell concentration of feed | 10 | ||
| Ratio recycle flow to total flow | - | ||
| Viscosity fluid | mPa · s | ||
| Turbulent dissipation rate | |||
| Shear rate | s |
| Properties | Averaged | Not Averaged | Poly.Cells | Poly.Bubbles | Clustering | Clustering Averaged |
|---|---|---|---|---|---|---|
| Cells polydisperse | No | No | Yes | No | No | No |
| Bubbles polydisperse | No | No | No | Yes | No | No |
| Loading averaged | Yes | No | No | No | No | Yes |
| Clustering considered | No | No | No | No | Yes | Yes |
| Simulation time | Very low | Low | Medium | Medium | Very high | Low |
| Complexity | Very low | Low | Medium | Medium | High | Low |
| Standard deviation of bubble diameter | Small | Small | Small | High | Small | Small |
| Standard deviation of cell diameter | Small | Small | High | Small | Small | Small |
| Influence of clustering | Negligible | Negligible | Negligible | Negligible | Important | Important |
| Cells have to be smaller than bubbles | Yes | Yes | Yes | Yes | No | No |
| Difficulty of direct coupling to CFD simulations | Low | High | High | High | Very high | Medium |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmideder, S.; Kirse, C.; Hofinger, J.; Rollié, S.; Briesen, H. Modeling the Separation of Microorganisms in Bioprocesses by Flotation. Processes 2018, 6, 184. https://doi.org/10.3390/pr6100184
Schmideder S, Kirse C, Hofinger J, Rollié S, Briesen H. Modeling the Separation of Microorganisms in Bioprocesses by Flotation. Processes. 2018; 6(10):184. https://doi.org/10.3390/pr6100184
Chicago/Turabian StyleSchmideder, Stefan, Christoph Kirse, Julia Hofinger, Sascha Rollié, and Heiko Briesen. 2018. "Modeling the Separation of Microorganisms in Bioprocesses by Flotation" Processes 6, no. 10: 184. https://doi.org/10.3390/pr6100184
APA StyleSchmideder, S., Kirse, C., Hofinger, J., Rollié, S., & Briesen, H. (2018). Modeling the Separation of Microorganisms in Bioprocesses by Flotation. Processes, 6(10), 184. https://doi.org/10.3390/pr6100184





