Toward a Comprehensive and Efficient Robust Optimization Framework for (Bio)chemical Processes
Abstract
1. Introduction
2. Background of Probability-Based Robust Optimization
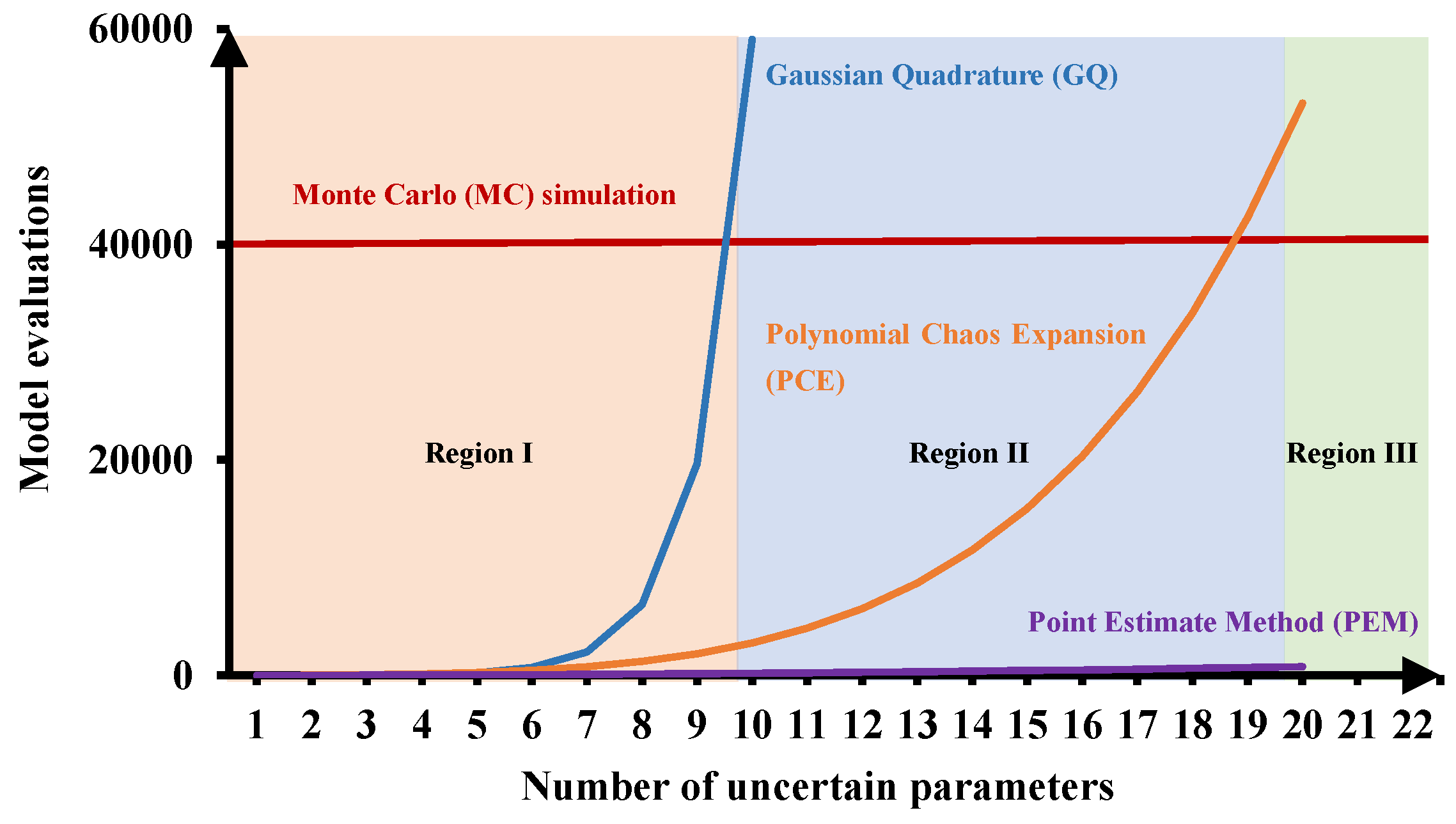
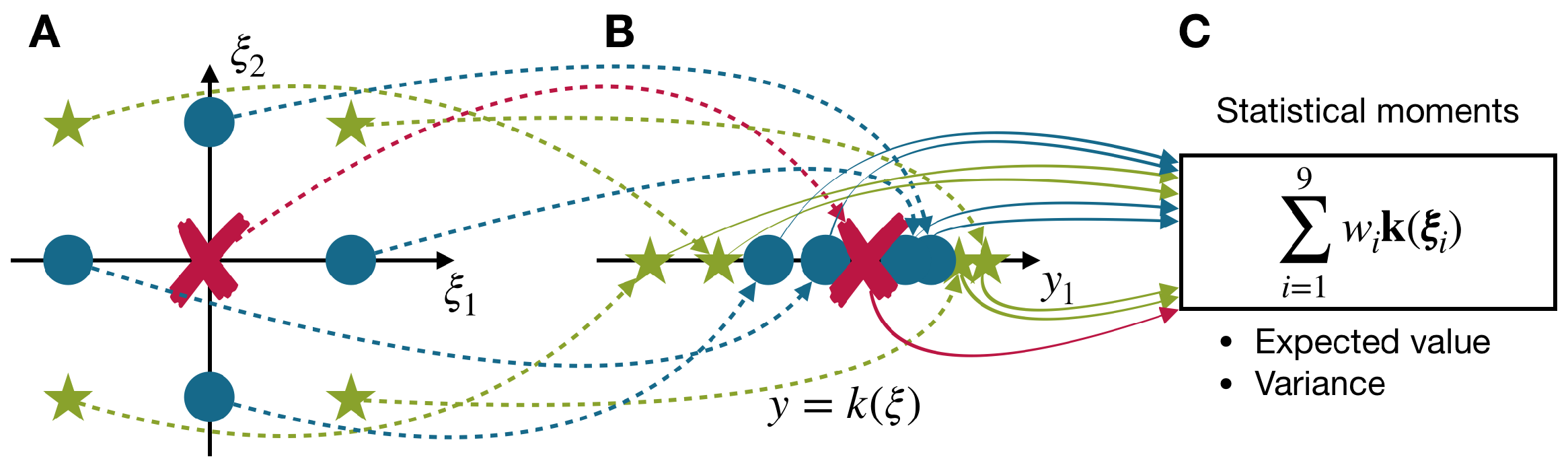
3. Point Estimate Method
3.1. Basics of the Point Estimate Method
3.2. Sampling Strategy for Independent/Correlated Random Variables of Arbitrary Distributions
| Algorithm 1 Sampling for correlated random variables |
Initialization: Random variables , ; have marginal cumulative density functions and correlation matrix ;
|
4. Moment Method for Approximating Robust Inequality and Equality Constraints
4.1. Categorization of the Constraints
4.2. Robust Formulation of Soft Inequality Constraints
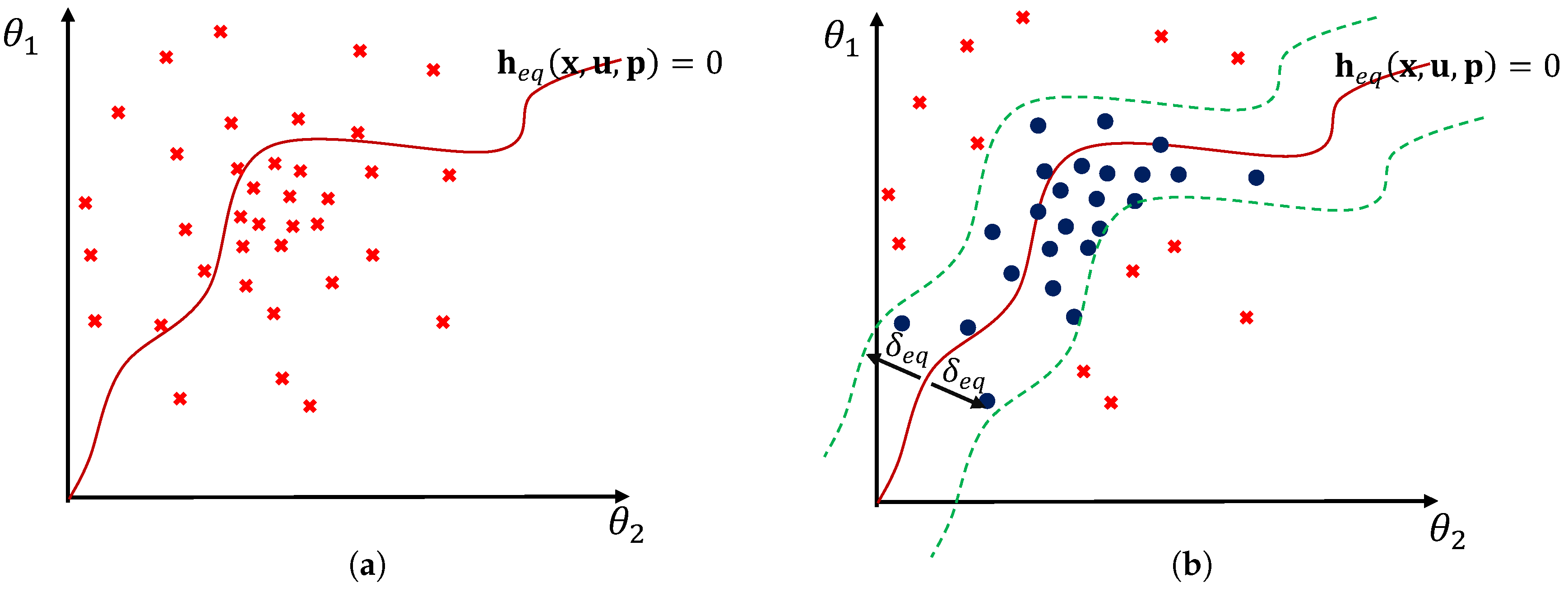
4.3. Robust Formulation of soft Equality Constraints
5. Robust Optimization with the PEM
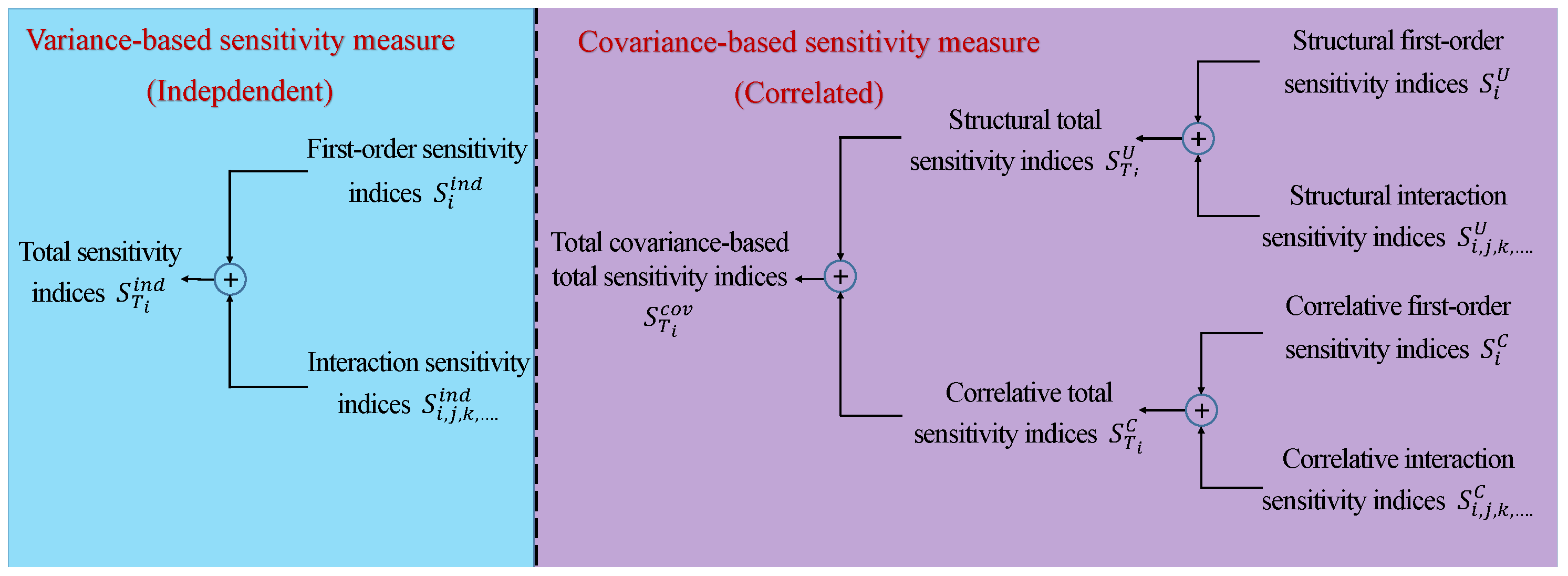
6. Global Sensitivity Analysis
7. Case Studies
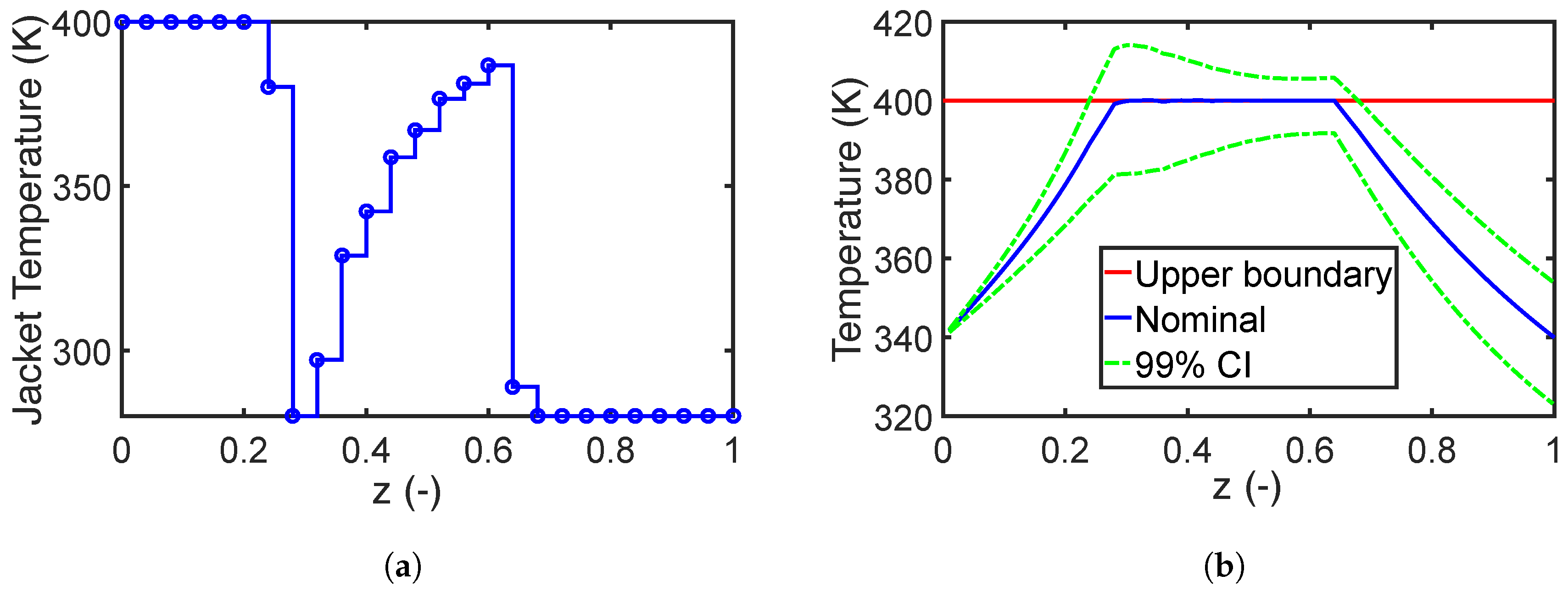
7.1. Case Study 1: A Jacket Tubular Reactor
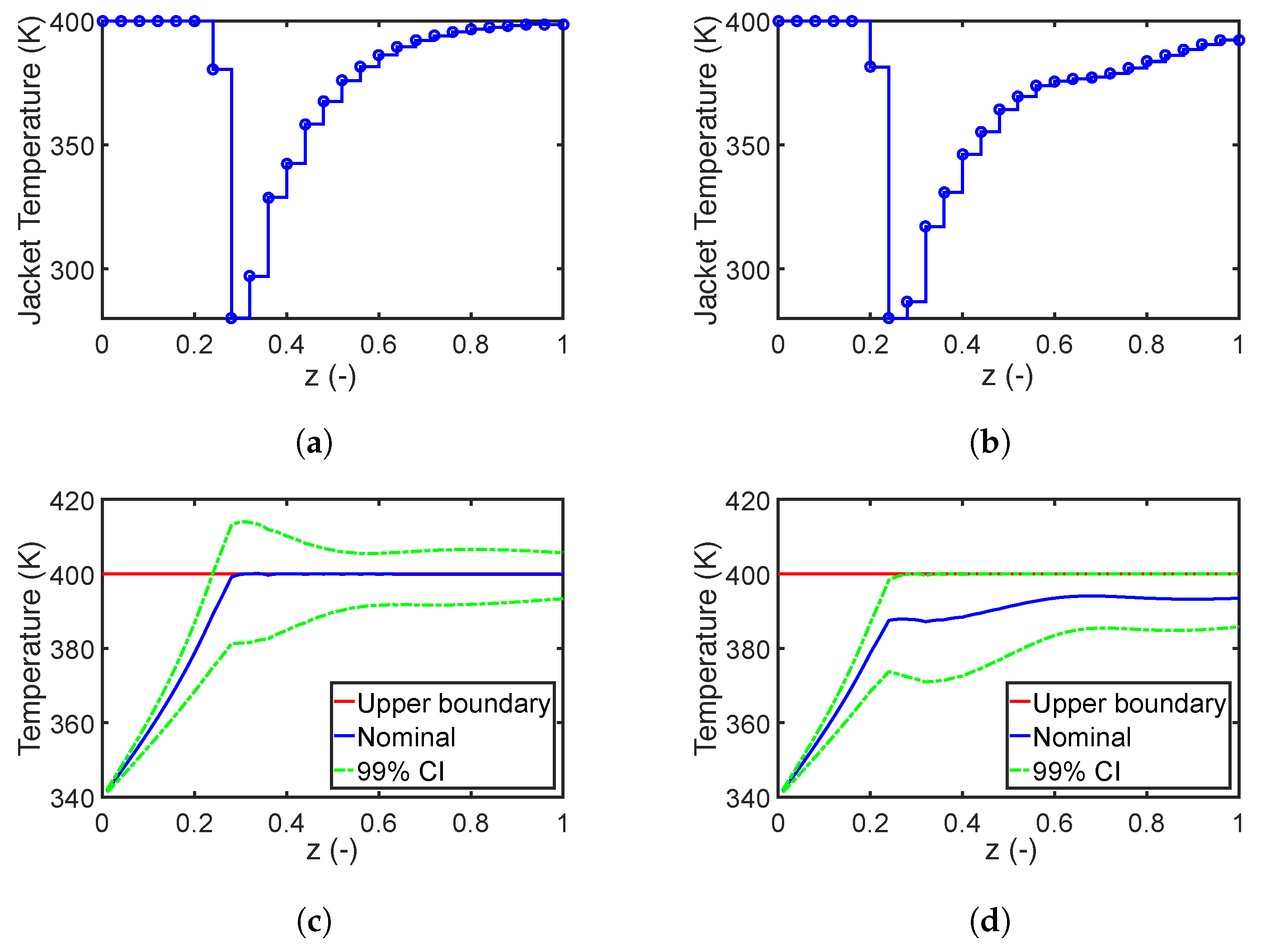
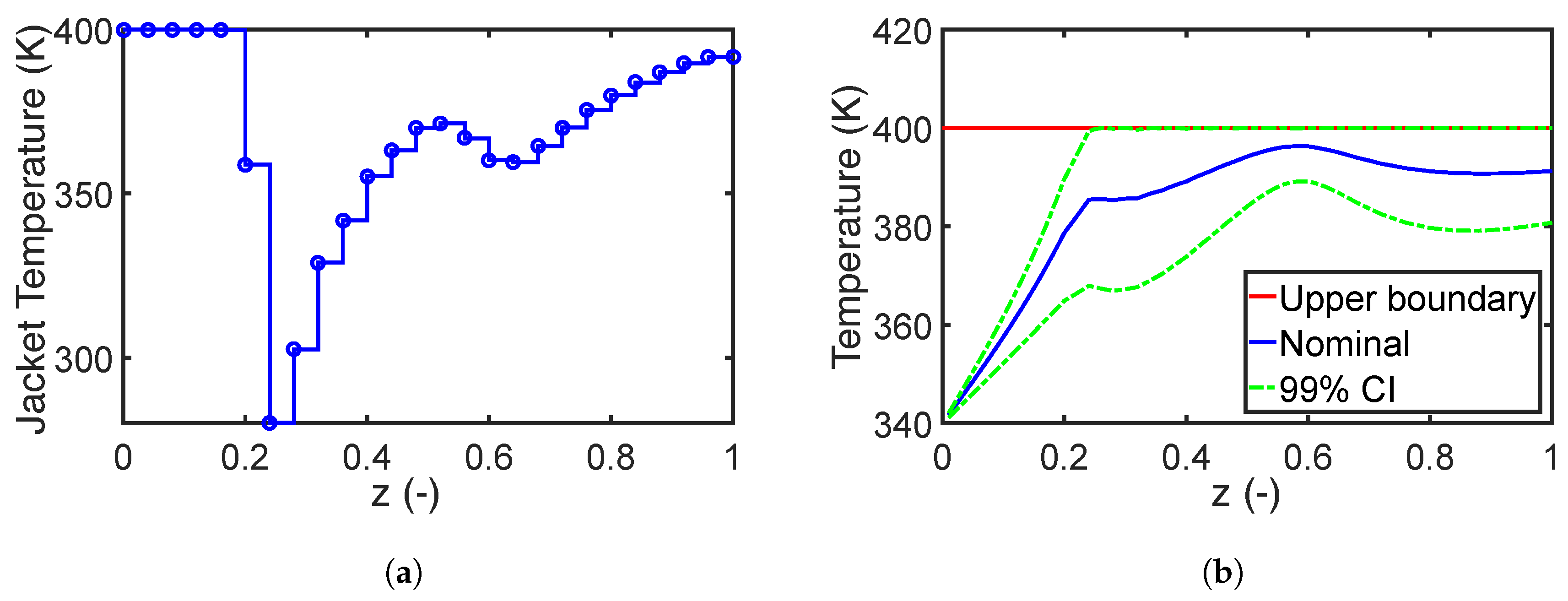
7.1.1. Robust Design with Parameter Correlation
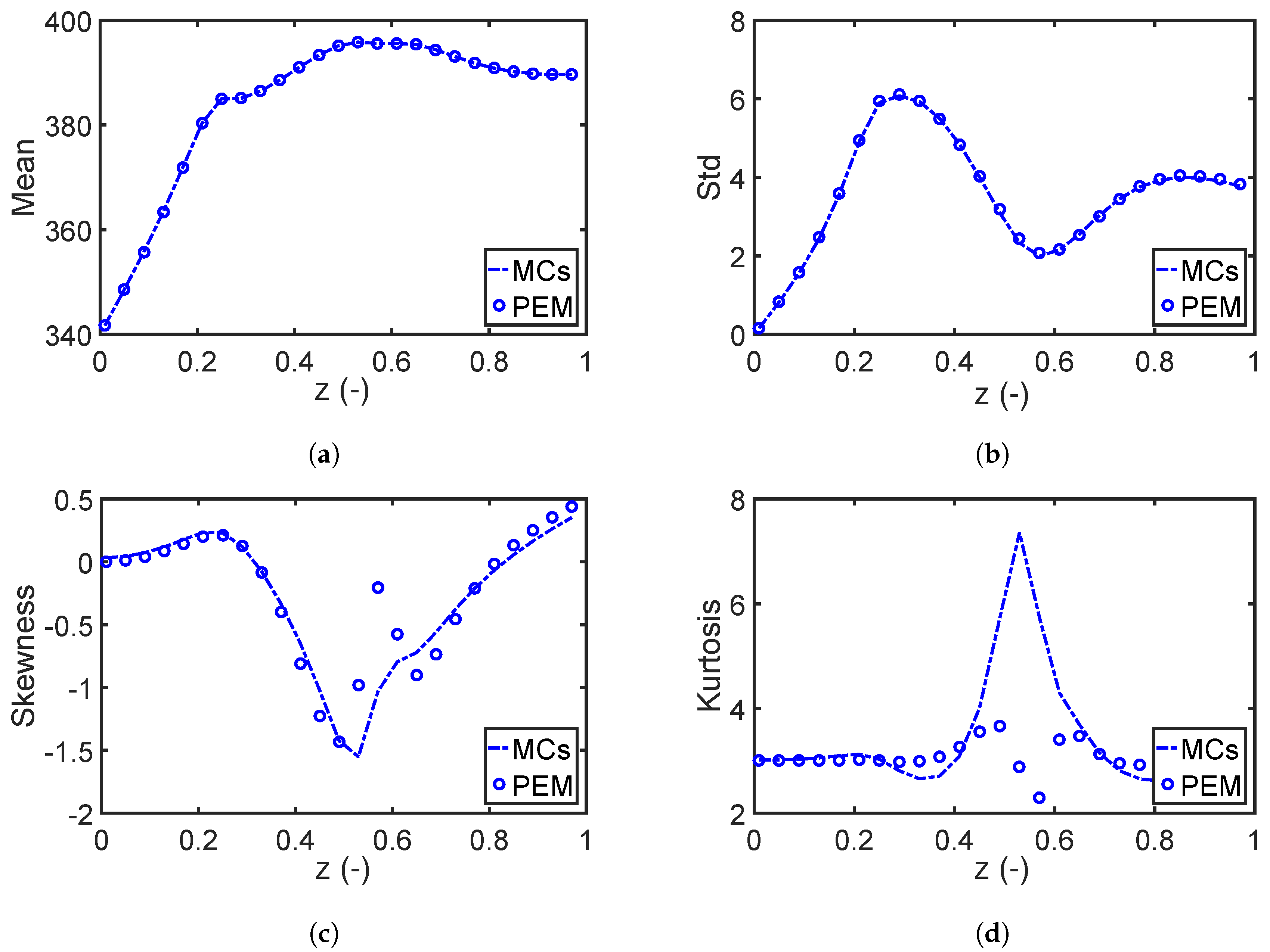
7.1.2. Performance of the Fourth Moment Method
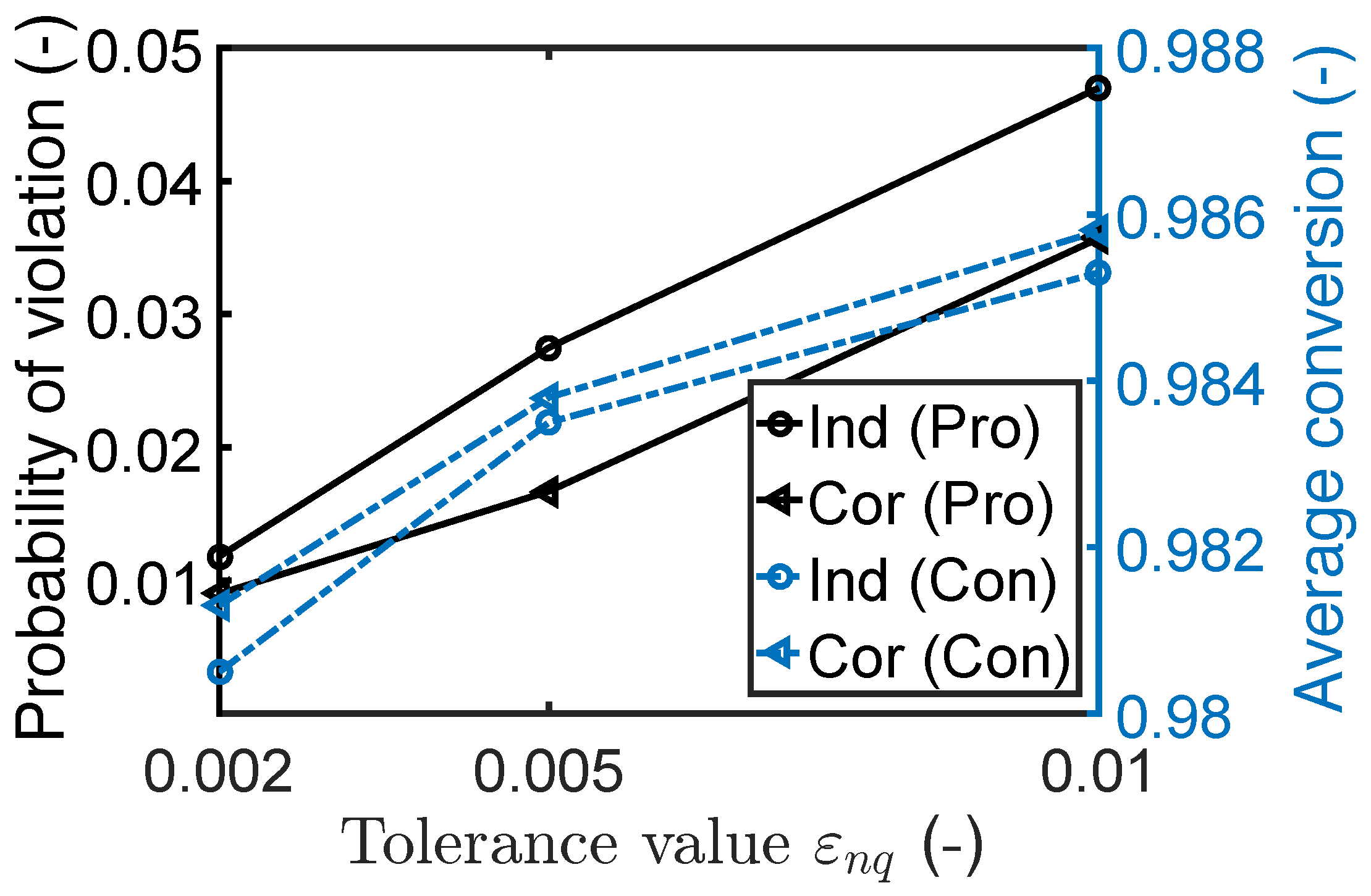
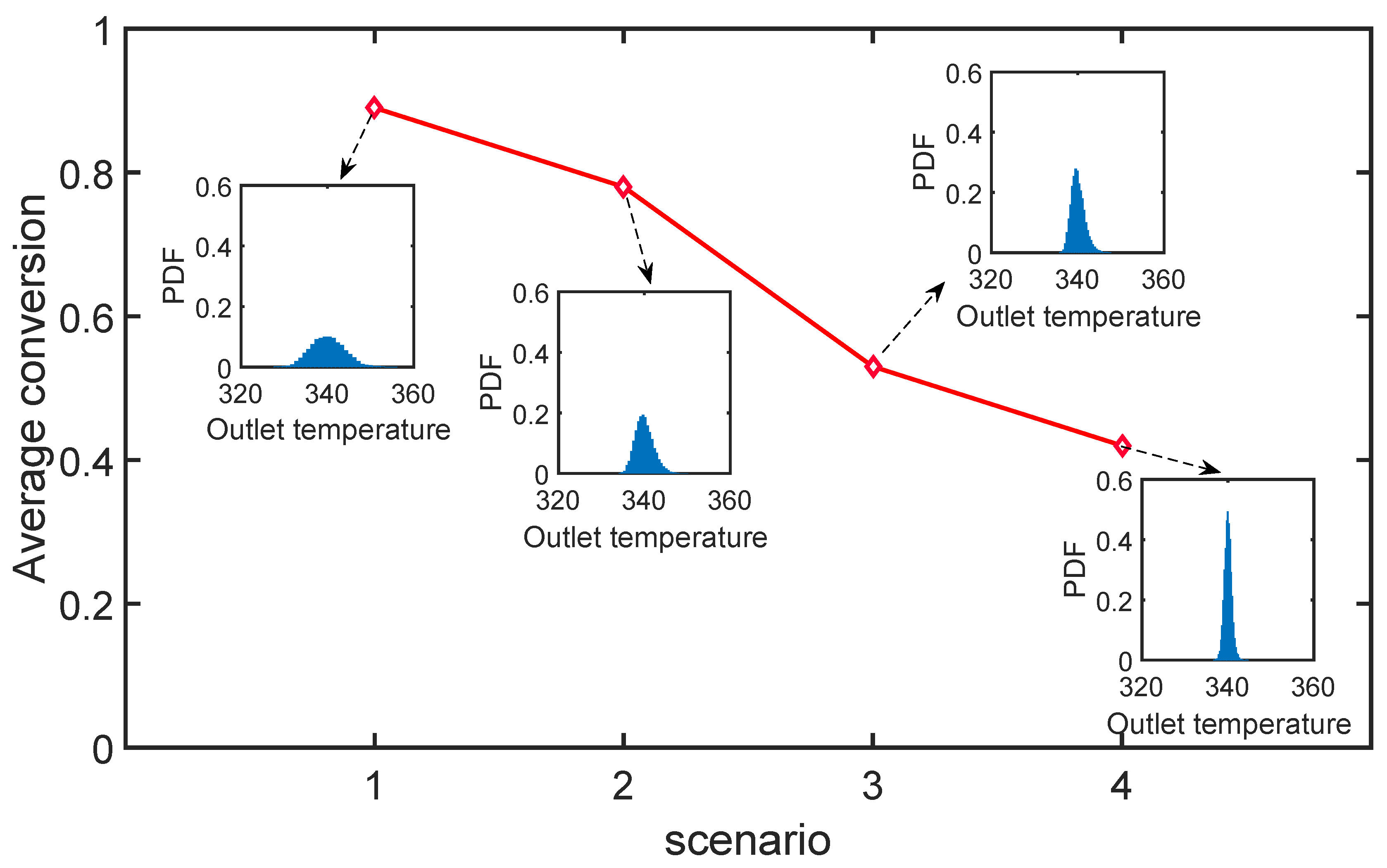
7.1.3. Impact of Robust Equality Constraints
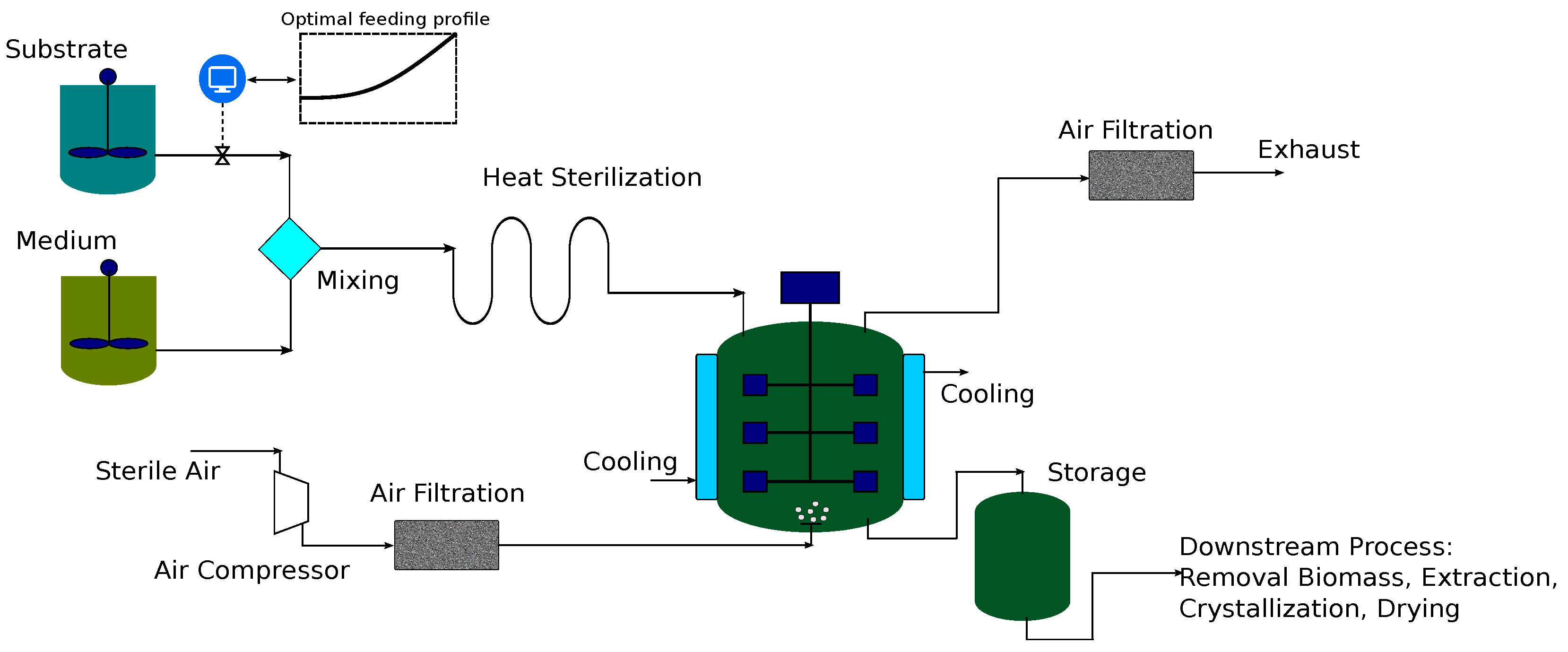
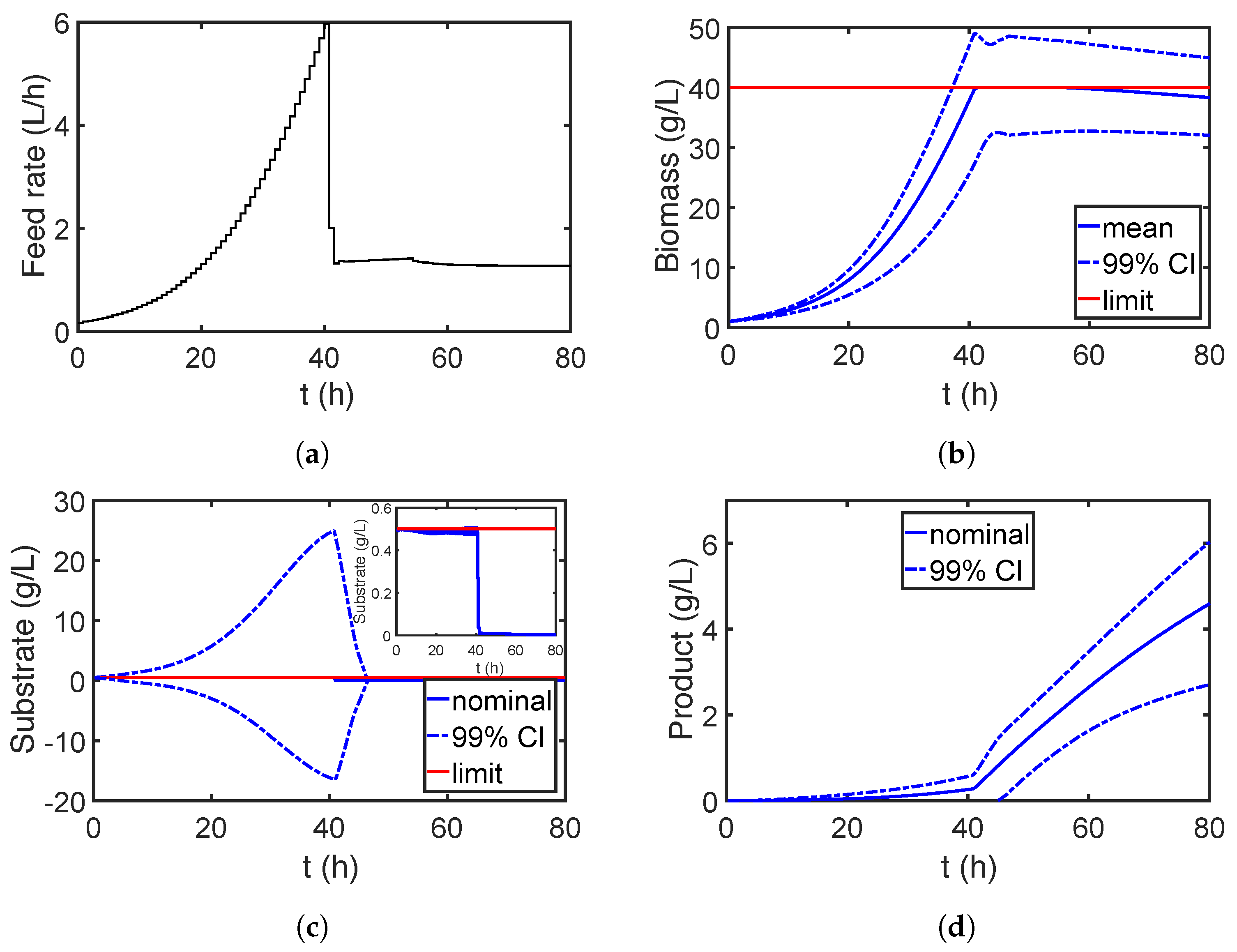
7.2. Case Study 2: Fed-Batch Bioreactor for Fermentation of Penicillin
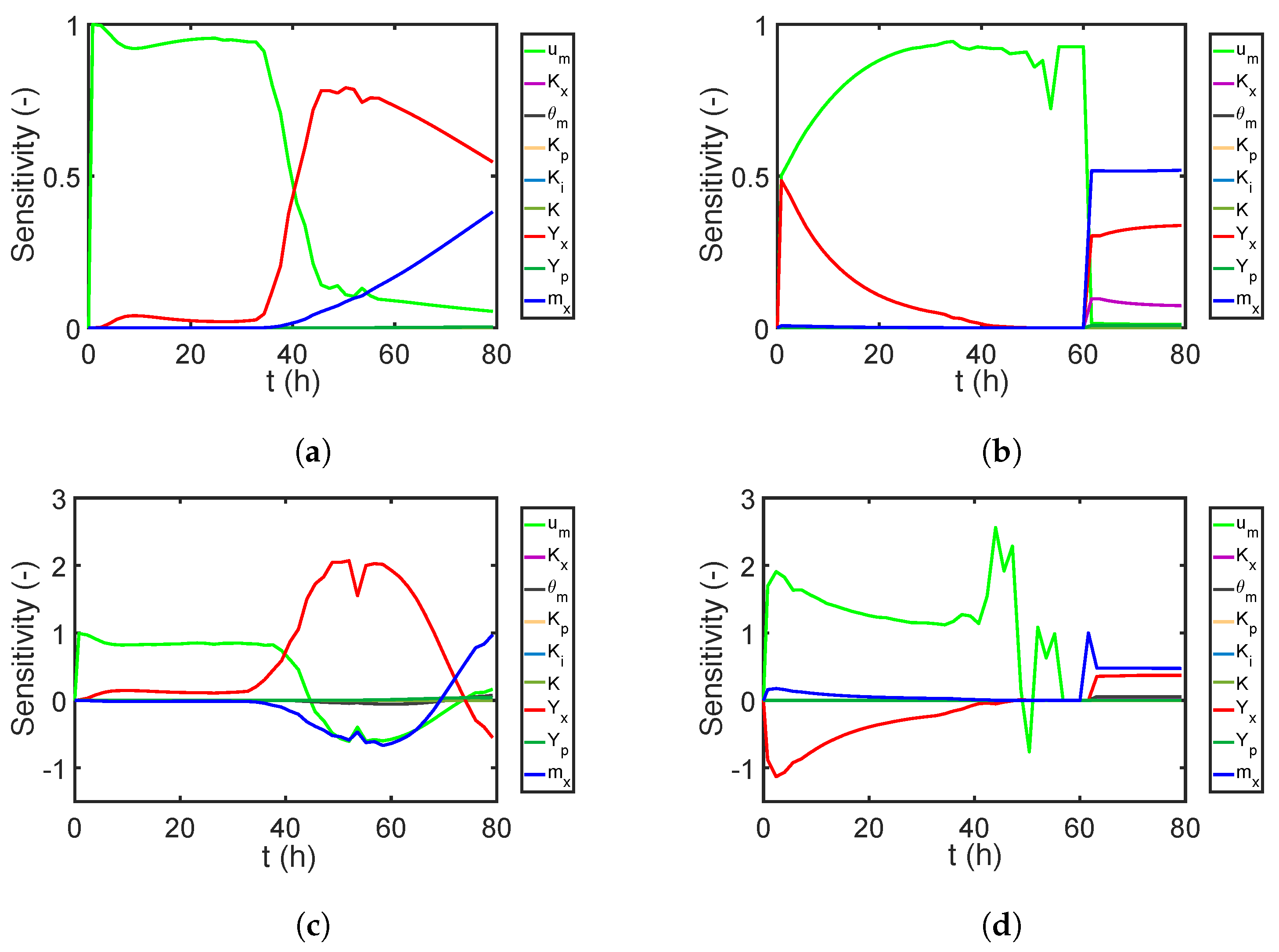
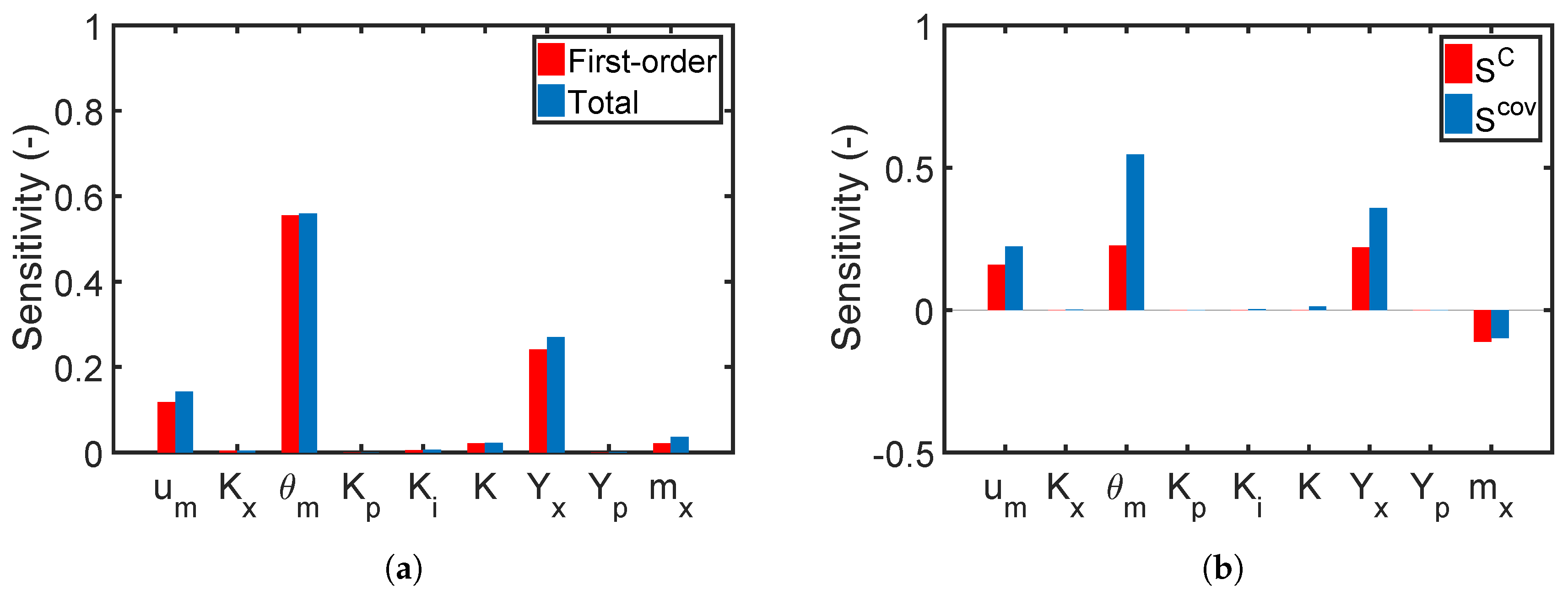
7.2.1. Global Sensitivity Analysis
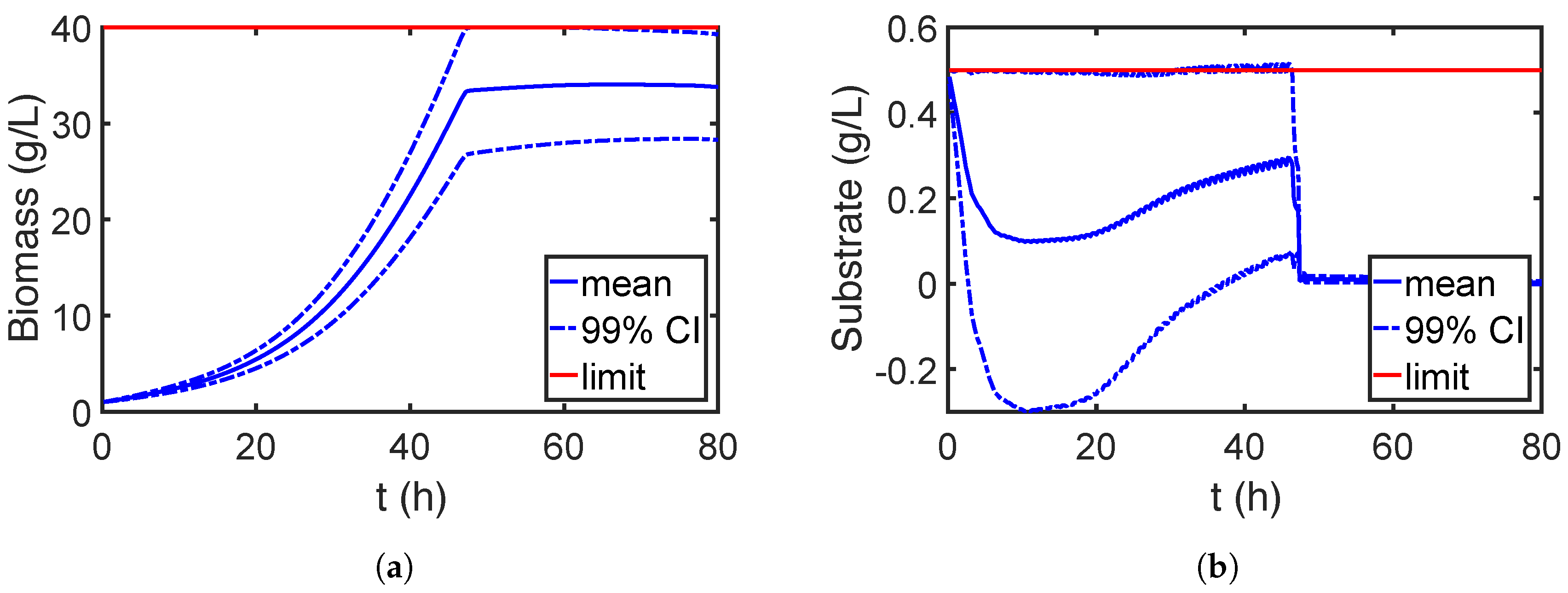
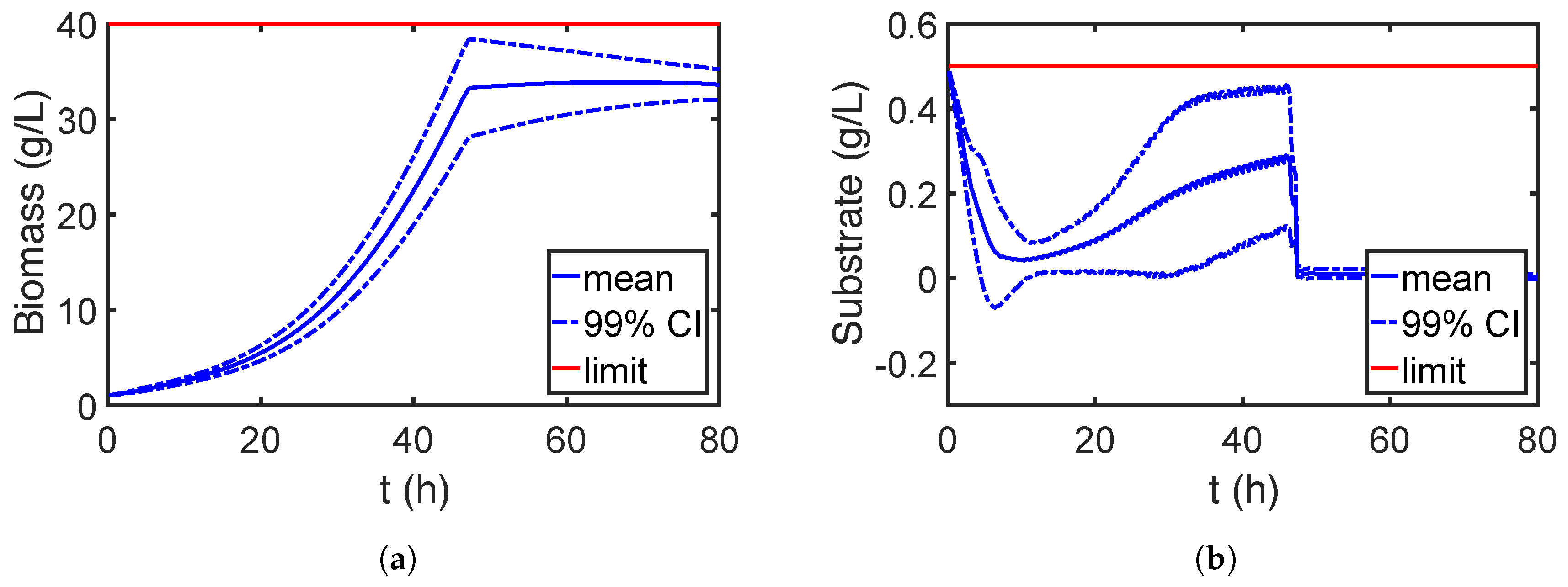
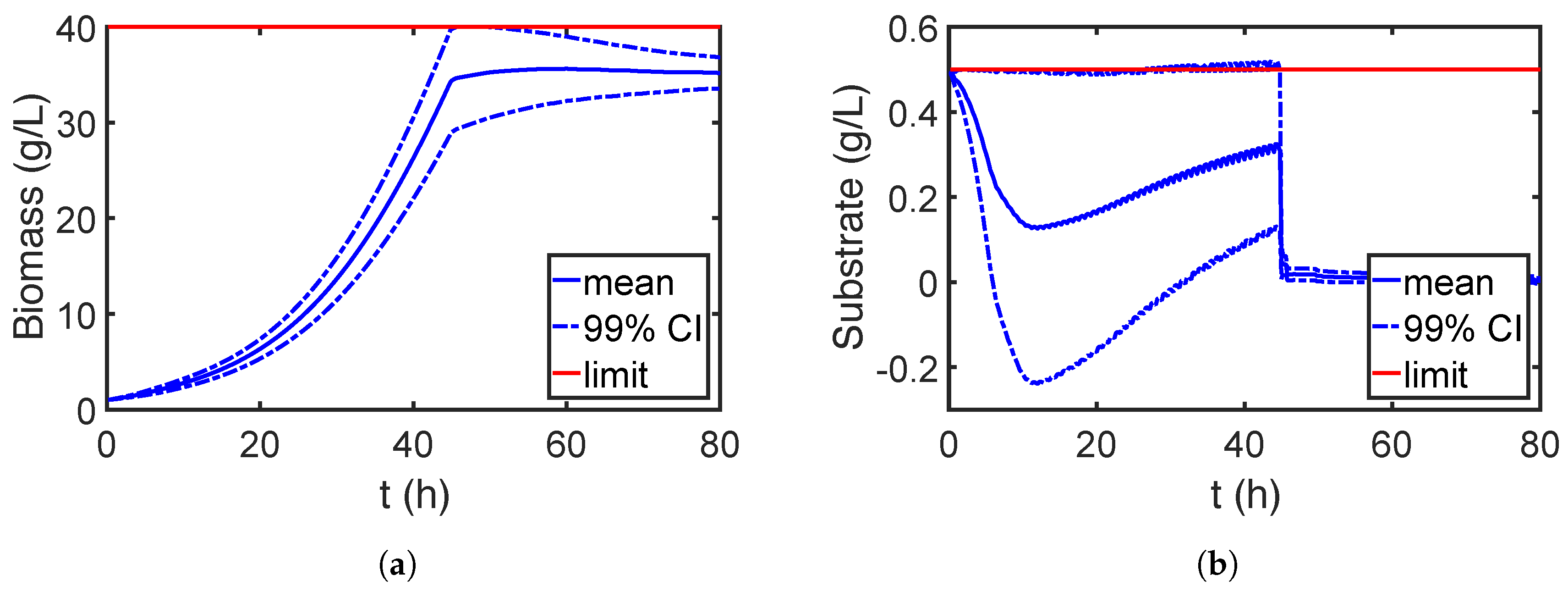
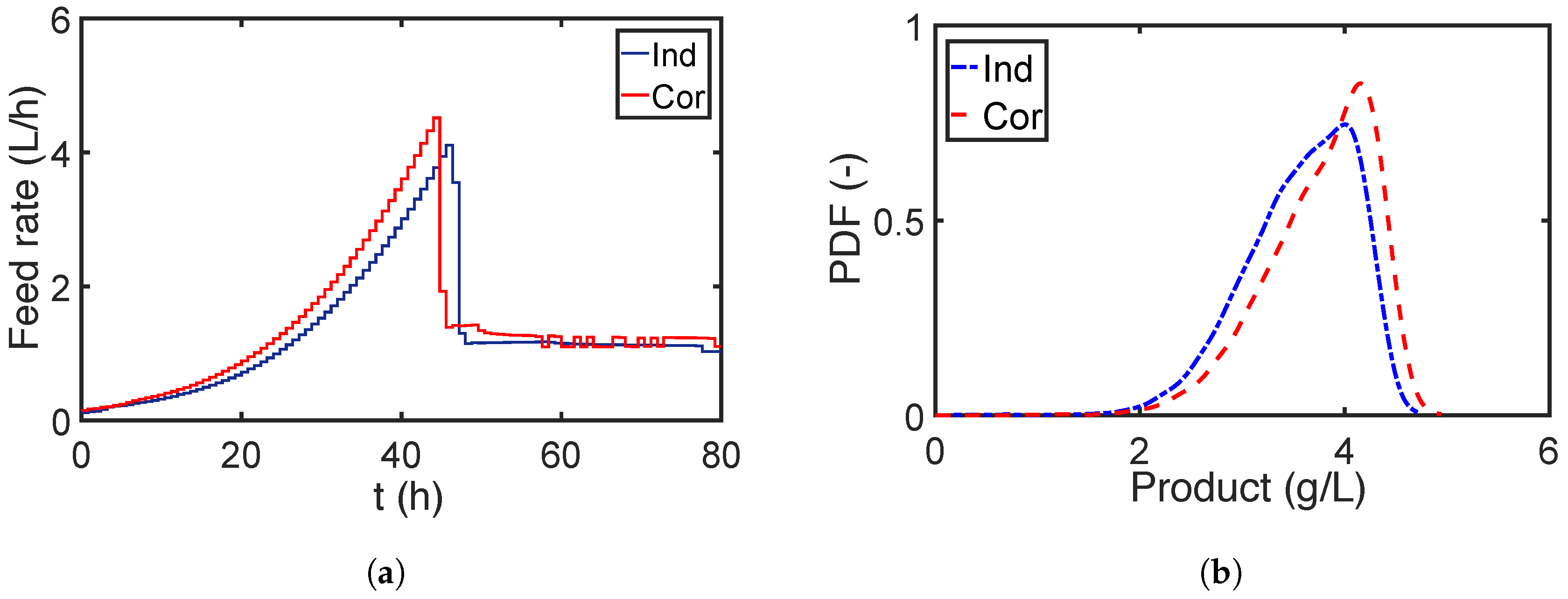
7.2.2. Robust Optimization
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications To Chemical Processes; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Schenkendorf, R. Optimal Experimental Design for Paramter Identification and Model Selection. Ph.D. Thesis, Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2014. [Google Scholar]
- Mortier, S.T.F.; Van Bockstal, P.J.; Corver, J.; Nopens, I.; Gernaey, K.V.; De Beer, T. Uncertainty analysis as essential step in the establishment of the dynamic Design Space of primary drying during freeze-drying. Eur. J. Pharm. Biopharm. 2016, 103, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, G.; Clausing, D. Robust quality. Harv. Bus. Rev. 1990, 68, 65–75. [Google Scholar]
- Vallerio, M.; Telen, D.; Cabianca, L.; Manenti, F.; Van Impe, J.; Logist, F. Robust multi-objective dynamic optimization of chemical processes using the Sigma Point method. Chem. Eng. Sci. 2016, 140, 201–216. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R.; Krewer, U. Robust design of chemical processes based on a one-shot sparse polynomial chaos expansion concept. Comput. Aided Chem. Eng. 2017, 40, 613–618. [Google Scholar]
- Nagy, Z.K.; Braatz, R.D. Worst-case and distributional robustness analysis of finite-time control trajectories for nonlinear distributed parameter systems. IEEE Trans. Control Syst. Technol. 2003, 11, 694–704. [Google Scholar] [CrossRef]
- Ghaoui, L.E.; Oks, M.; Oustry, F. Worst-case value-at-risk and robust portfolio optimization: A conic programming approach. Oper. Res. 2003, 51, 543–556. [Google Scholar] [CrossRef]
- Janak, S.L.; Lin, X.; Floudas, C.A. A new robust optimization approach for scheduling under uncertainty: II. Uncertainty with known probability distribution. Comput. Chem. Eng. 2007, 31, 171–195. [Google Scholar] [CrossRef]
- Venter, G.; Haftka, R. Using response surface approximations in fuzzy set based design optimization. Struct. Multidiscipl. Optim. 1999, 18, 218–227. [Google Scholar] [CrossRef]
- Beyer, H.G.; Sendhoff, B. Robust optimization–a comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, And Applications; SIAM: Philadelphia, PA, USA, 2013; Volume 12. [Google Scholar]
- Shi, J.; Biegler, L.T.; Hamdan, I.; Wassick, J. Optimization of grade transitions in polyethylene solution polymerization process under uncertainty. Comput. Chem. Eng. 2016, 95, 260–279. [Google Scholar] [CrossRef]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Mesbah, A.; Streif, S. A probabilistic approach to robust optimal experiment design with chance constraints. IFAC-PapersOnLine 2015, 48, 100–105. [Google Scholar] [CrossRef]
- Nimmegeers, P.; Telen, D.; Logist, F.; Van Impe, J. Dynamic optimization of biological networks under parametric uncertainty. BMC Syst. Biol. 2016, 10, 86. [Google Scholar] [CrossRef] [PubMed]
- Paulson, J.A.; Mesbah, A. An efficient method for stochastic optimal control with joint chance constraints for nonlinear systems. Int. J. Robust Nonlinear Control 2017. [Google Scholar] [CrossRef]
- Golub, G.H.; Welsch, J.H. Calculation of Gauss quadrature rules. Math. Comput. 1969, 23, 221–230. [Google Scholar] [CrossRef]
- Xie, X.; Krewer, U.; Schenkendorf, R. Robust Optimization of Dynamical Systems with Correlated Random Variables using the Point Estimate Method. IFAC-PapersOnLine 2018, 51, 427–432. [Google Scholar] [CrossRef]
- Freund, H.; Maußner, J. Optimization Under Uncertainty in Chemical Engineering: Comparative Evaluation of Unscented Transformation Methods and Cubature Rules. Chem. Eng. Sci. 2018, 183, 329–345. [Google Scholar]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley: New York, NY, USA, 2000; Volume 1. [Google Scholar]
- Reizman, B.J.; Jensen, K.F. An automated continuous-flow platform for the estimation of multistep reaction kinetics. Org. Process Res. Dev. 2012, 16, 1770–1782. [Google Scholar] [CrossRef]
- Sudret, B.; Caniou, Y. Analysis of covariance (ANCOVA) using polynomial chaos expansions. In Proceedings of the 11th International Conference on Structural Safety & Reliability, New York, NY, USA, 16–20 June 2013. [Google Scholar]
- Valkó, É.; Varga, T.; Tomlin, A.; Busai, Á.; Turányi, T. Investigation of the effect of correlated uncertain rate parameters via the calculation of global and local sensitivity indices. J. Math. Chem. 2018, 56, 864–889. [Google Scholar] [CrossRef]
- López-Benito, A.; Bolado-Lavín, R. A case study on global sensitivity analysis with dependent inputs: The natural gas transmission model. Reliab. Eng. Syst. Saf. 2017, 165, 11–21. [Google Scholar] [CrossRef]
- Valkó, É.; Varga, T.; Tomlin, A.; Turányi, T. Investigation of the effect of correlated uncertain rate parameters on a model of hydrogen combustion using a generalized HDMR method. Proc. Combust. Inst. 2017, 36, 681–689. [Google Scholar] [CrossRef]
- Xie, X.; Ohs, R.; Spieß, A.; Krewer, U.; Schenkendorf, R. Moment-Independent Sensitivity Analysis of Enzyme-Catalyzed Reactions with Correlated Model Parameters. IFAC-PapersOnLine 2018, 51, 753–758. [Google Scholar] [CrossRef]
- Lebrun, R.; Dutfoy, A. Do Rosenblatt and Nataf isoprobabilistic transformations really differ? Probab. Eng. Mech. 2009, 24, 577–584. [Google Scholar] [CrossRef]
- Logist, F.; Smets, I.; Van Impe, J. Derivation of generic optimal reference temperature profiles for steady-state exothermic jacketed tubular reactors. J. Process Control 2008, 18, 92–104. [Google Scholar] [CrossRef]
- Telen, D.; Vallerio, M.; Cabianca, L.; Houska, B.; Van Impe, J.; Logist, F. Approximate robust optimization of nonlinear systems under parametric uncertainty and process noise. J. Process Control 2015, 33, 140–154. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Ono, T. Moment methods for structural reliability. Struct. Saf. 2001, 23, 47–75. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Lerner, U.N. Hybrid Bayesian Networks for Reasoning About Complex Systems. Ph.D. Thesis, Stanford University Stanford, Stanford, CA, USA, 2002. [Google Scholar]
- Schenkendorf, R. A general framework for uncertainty propagation based on point estimate methods. In Proceedings of the Second european conference of the prognostics and health management society, phme14, Nantes, France, 8–10 July 2014. [Google Scholar]
- Maußner, J.; Freund, H. Optimization under uncertainty in chemical engineering: Comparative evaluation of unscented transformation methods and cubature rules. Chem. Eng. Sci. 2018, 183, 329–345. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A General Method for Approximating Nonlinear Transformations of Probability Distributions; Robotics Research Group, Department of Engineering Science, University of Oxford: Oxford, UK, 1996. [Google Scholar]
- Schenkendorf, R.; Groos, J.C. Global sensitivity analysis applied to model inversion problems: A contribution to rail condition monitoring. Int. J. Progn. Health Manag. 2015, 6, 1–14. [Google Scholar]
- Schenkendorf, R.; Mangold, M. Qualitative and quantitative optimal experimental design for parameter identification of a map kinase model. IFAC Proc. Vol. 2011, 44, 11666–11671. [Google Scholar] [CrossRef]
- Telen, D.; Logist, F.; Van Derlinden, E.; Van Impe, J.F. Robust optimal experiment design: A multi-objective approach. IFAC Proc. Vol. 2012, 45, 689–694. [Google Scholar] [CrossRef]
- Schenkendorf, R.; Xie, X.; Rehbein, M.; Scholl, S.; Krewer, U. The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design. Processes 2018, 6, 27. [Google Scholar] [CrossRef]
- Lebrun, R.; Dutfoy, A. A generalization of the Nataf transformation to distributions with elliptical copula. Probab. Eng. Mech. 2009, 24, 172–178. [Google Scholar] [CrossRef]
- Rangavajhala, S.; Mullur, A.; Messac, A. The challenge of equality constraints in robust design optimization: Examination and new approach. Struct. Multidiscipl. Optim. 2007, 34, 381–401. [Google Scholar] [CrossRef]
- Ostrovsky, G.; Ziyatdinov, N.; Lapteva, T. Optimal design of chemical processes with chance constraints. Comput. Chem. Eng. 2013, 59, 74–88. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Foundations of the Theory of Probability: Second English Edition; Courier Dover Publications: Mineola, NY, USA, 2018. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Boukouvala, F.; Niotis, V.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012, 42, 30–47. [Google Scholar] [CrossRef]
- Rehrl, J.; Gruber, A.; Khinast, J.G.; Horn, M. Sensitivity analysis of a pharmaceutical tablet production process from the control engineering perspective. Int. J. Pharm. 2017, 517, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Kiparissides, A.; Kucherenko, S.; Mantalaris, A.; Pistikopoulos, E. Global sensitivity analysis challenges in biological systems modeling. Ind. Eng. Chem. Res. 2009, 48, 7168–7180. [Google Scholar] [CrossRef]
- Wang, Z.; Ierapetritou, M. Global sensitivity, feasibility, and flexibility analysis of continuous pharmaceutical manufacturing processes. Comput. Aided Chem. Eng. 2018, 41, 189–213. [Google Scholar]
- Lin, N.; Xie, X.; Schenkendorf, R.; Krewer, U. Efficient global sensitivity analysis of 3D multiphysics model for Li-ion batteries. J. Electrochem. Soc. 2018, 165, A1169–A1183. [Google Scholar] [CrossRef]
- Li, G.; Rabitz, H.; Yelvington, P.E.; Oluwole, O.O.; Bacon, F.; Kolb, C.E.; Schoendorf, J. Global sensitivity analysis for systems with independent and/or correlated inputs. J. Phys. Chem. A 2010, 114, 6022–6032. [Google Scholar] [CrossRef] [PubMed]
- Mara, T.A.; Tarantola, S.; Annoni, P. Non-parametric methods for global sensitivity analysis of model output with dependent inputs. Environ. Model. Softw. 2015, 72, 173–183. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Xie, X.; Schenkendorf, R.; Krewer, U. Efficient sensitivity analysis and interpretation of parameter correlations in chemical engineering. Reliab. Eng. Syst. Saf. 2018. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in Matlab. In Proceedings of the Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis (ISUMA), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar]
- Biegler, L.T. An overview of simultaneous strategies for dynamic optimization. Chem. Eng. Process. Process Intensif. 2007, 46, 1043–1053. [Google Scholar] [CrossRef]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A symbolic package for automatic differentiation and optimal control. In Recent Advances in Algorithmic Differentiation; Springer: New York, NY, USA, 2012; pp. 297–307. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Duff, I.S. MA57—A code for the solution of sparse symmetric definite and indefinite systems. ACM Trans. Math. Softw. (TOMS) 2004, 30, 118–144. [Google Scholar] [CrossRef]
- Rossner, N.; Heine, T.; King, R. Quality-by-design using a gaussian mixture density approximation of biological uncertainties. IFAC Proc. Vol. 2010, 43, 7–12. [Google Scholar] [CrossRef]
- Bajpai, R.; Reuss, M. A mechanistic model for penicillin production. J. Chem. Technol. Biotechnol. 1980, 30, 332–344. [Google Scholar] [CrossRef]
- San, K.Y.; Stephanopoulos, G. Optimization of fed-batch penicillin fermentation: A case of singular optimal control with state constraints. Biotechnol. Bioeng. 1989, 34, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Hahn, J. Necessary condition for applying experimental design criteria to global sensitivity analysis results. Comput. Chem. Eng. 2013, 48, 280–292. [Google Scholar] [CrossRef]
| Parameters | Unit | Nominal Value | Uncertainty |
|---|---|---|---|
| - | 0 | - | |
| - | 0 | - | |
| s−1 | 0.058 | ||
| s−1 | 0.2 | ||
| v | ms−1 | 0.1 | - |
| - | 16.66 | - | |
| - | 0.25 | - |
| Second Moment Method | Fourth Moment Method | |||||
|---|---|---|---|---|---|---|
| Number of | Independent | Correlated | Independent | Correlated | ||
| violations | 470 | 357 | 440 | 385 | ||
| Probability | 0.047 | 0.036 | 0.044 | 0.039 | ||
| Parameters | Unit | Nominal Value | Parameters | Unit | Nominal Value |
|---|---|---|---|---|---|
| 1/h | 0.11 | 1/h | 0.029 | ||
| - | 0.006 | g/L | 400 | ||
| 1/h | 0.004 | t | h | 0–80 | |
| g/L | 0.0001 | g/L | 1 | ||
| g/L | 0.1 | g/L | 0.5 | ||
| K | 1/h | 0.01 | g/L | 0 | |
| - | 0.47 | L | 250 | ||
| - | 1.2 |
| Independent | Correlated | ||
|---|---|---|---|
| X | 146 | 35 | |
| S | 572 | 554 | |
| performance | 3.63 | 3.76 | |
| X | 19 | 2 | |
| S | 378 | 369 | |
| performance | 3.53 | 3.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Schenkendorf, R.; Krewer, U. Toward a Comprehensive and Efficient Robust Optimization Framework for (Bio)chemical Processes. Processes 2018, 6, 183. https://doi.org/10.3390/pr6100183
Xie X, Schenkendorf R, Krewer U. Toward a Comprehensive and Efficient Robust Optimization Framework for (Bio)chemical Processes. Processes. 2018; 6(10):183. https://doi.org/10.3390/pr6100183
Chicago/Turabian StyleXie, Xiangzhong, René Schenkendorf, and Ulrike Krewer. 2018. "Toward a Comprehensive and Efficient Robust Optimization Framework for (Bio)chemical Processes" Processes 6, no. 10: 183. https://doi.org/10.3390/pr6100183
APA StyleXie, X., Schenkendorf, R., & Krewer, U. (2018). Toward a Comprehensive and Efficient Robust Optimization Framework for (Bio)chemical Processes. Processes, 6(10), 183. https://doi.org/10.3390/pr6100183






