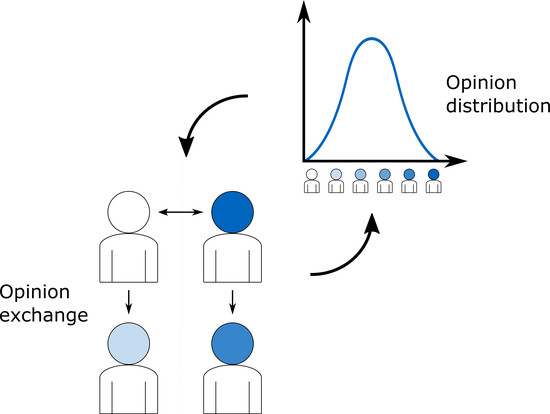
Population Balance Modeling and Opinion Dynamics—A Mutually Beneficial Liaison?
Abstract
1. Introduction
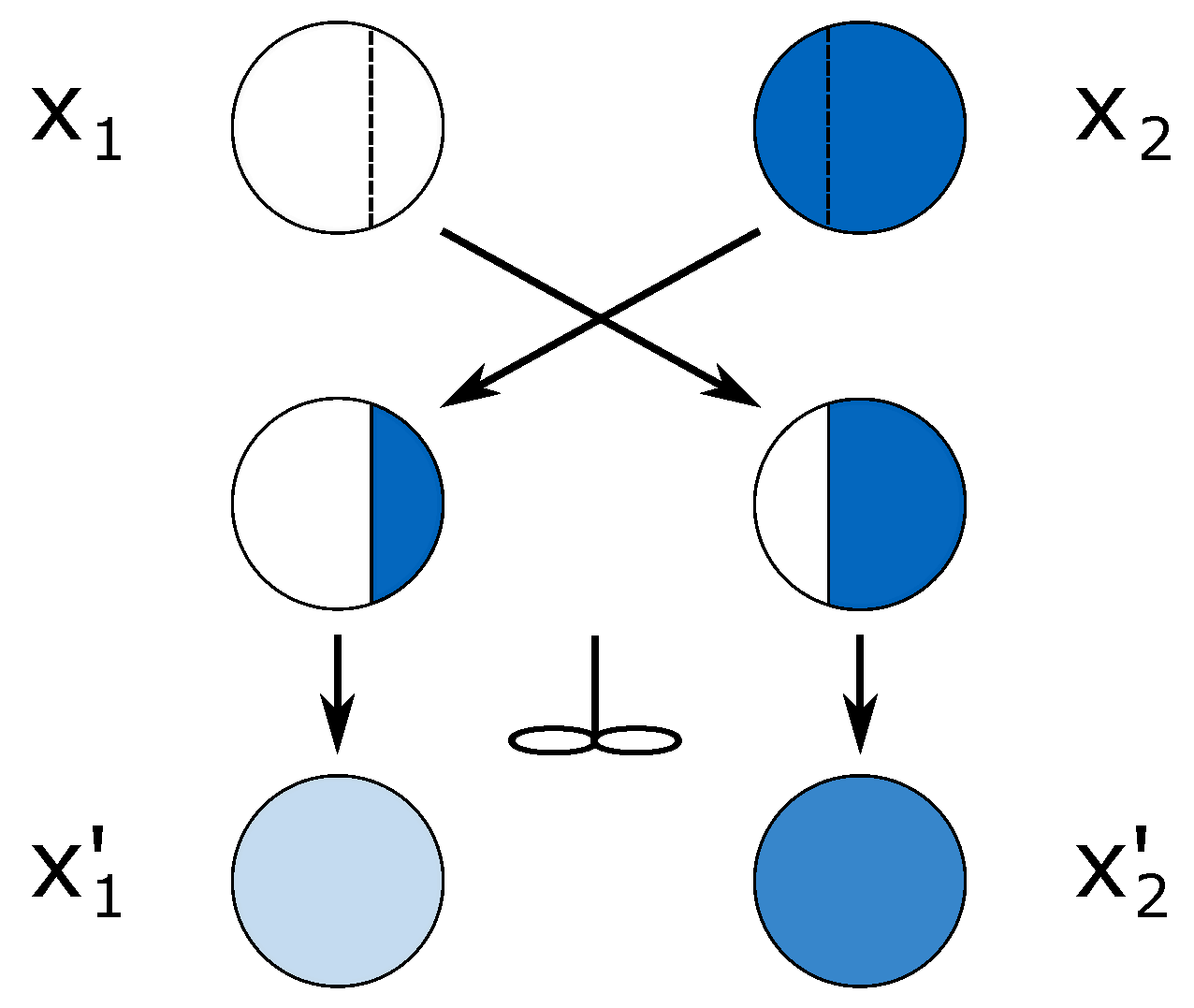
2. Population Balance Model
2.1. Model Formulation
2.2. Initial Distribution
2.3. Model Analysis
2.4. Numerical Methods
3. Numerical Results
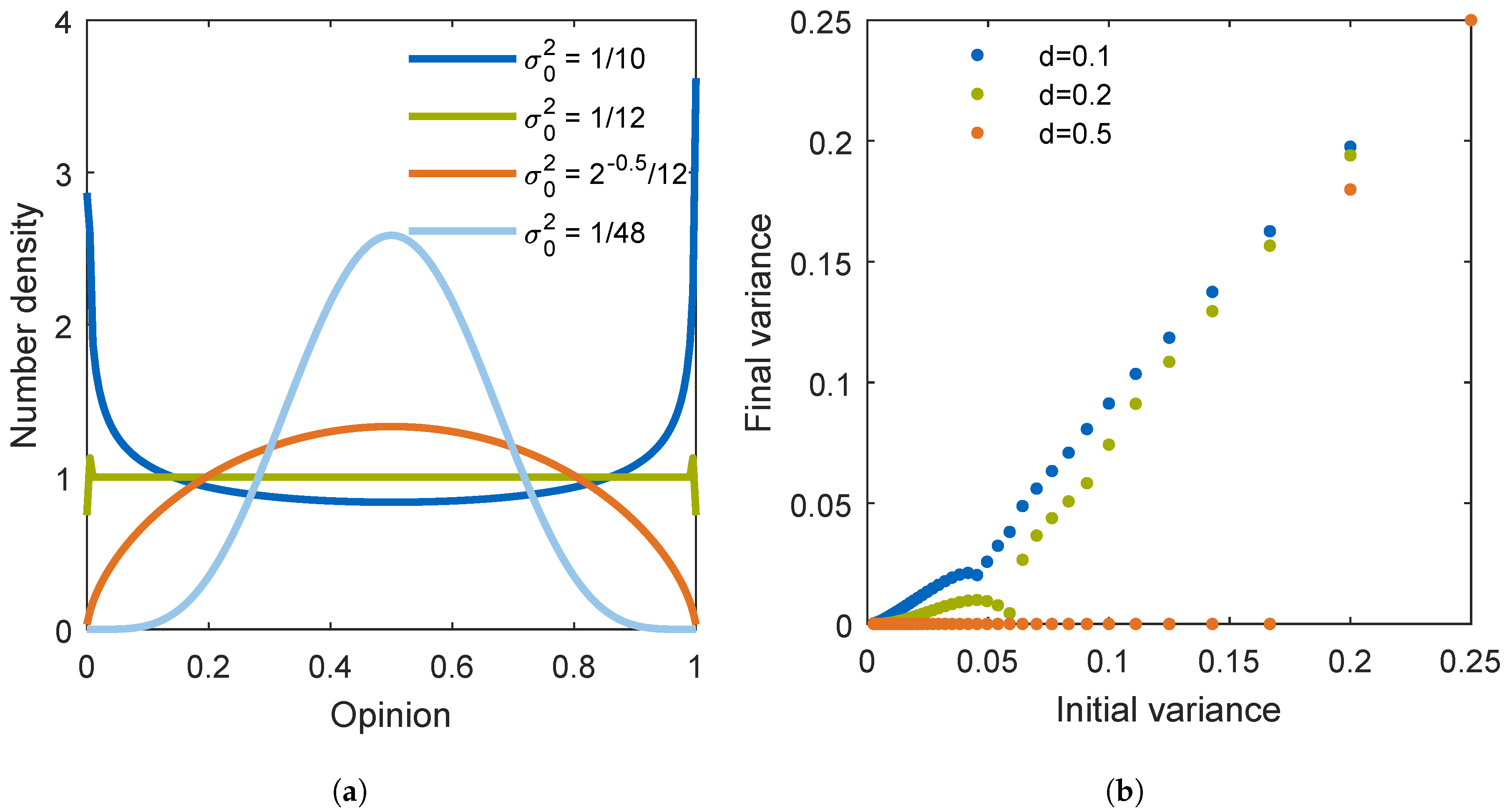
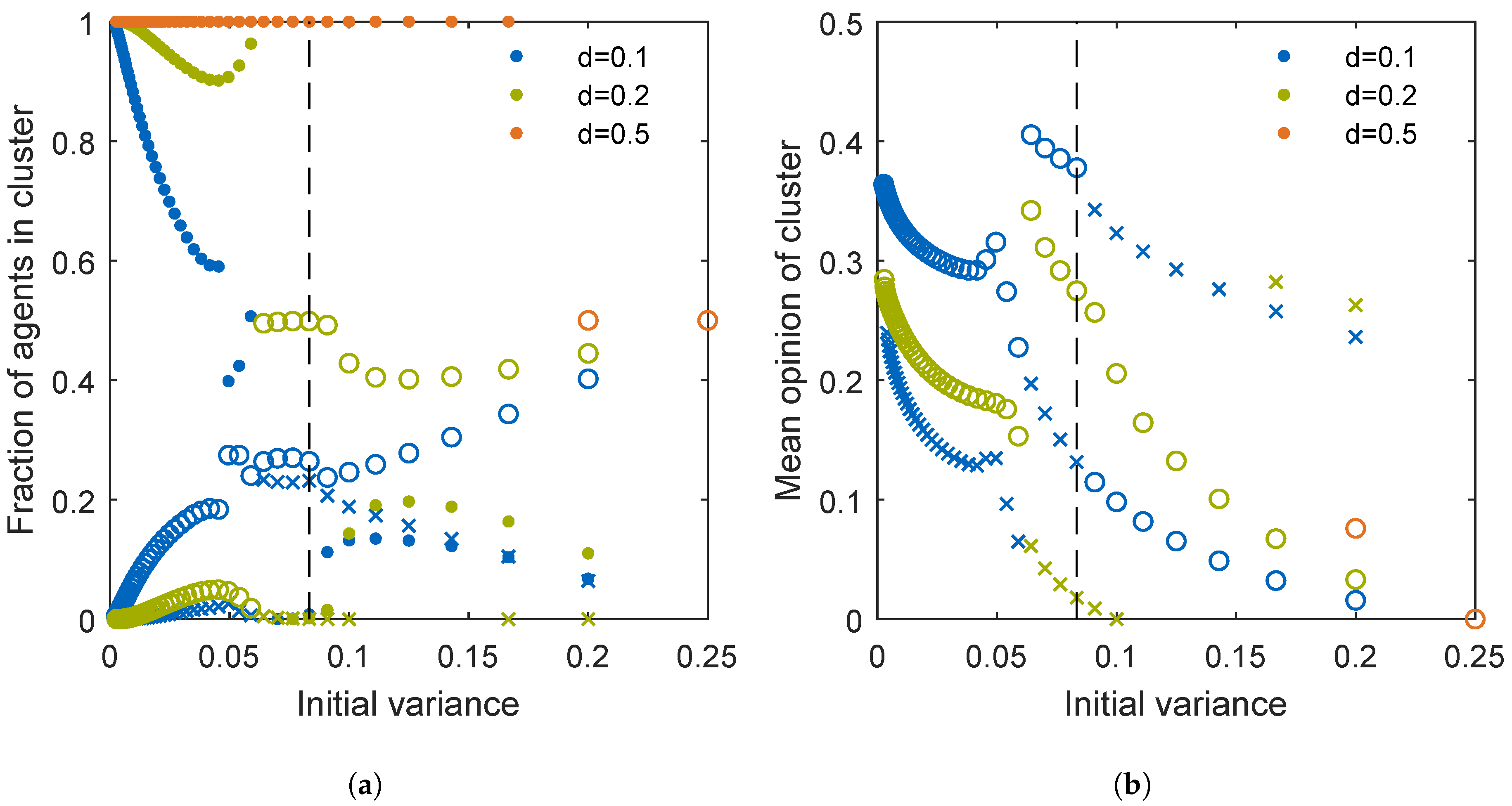
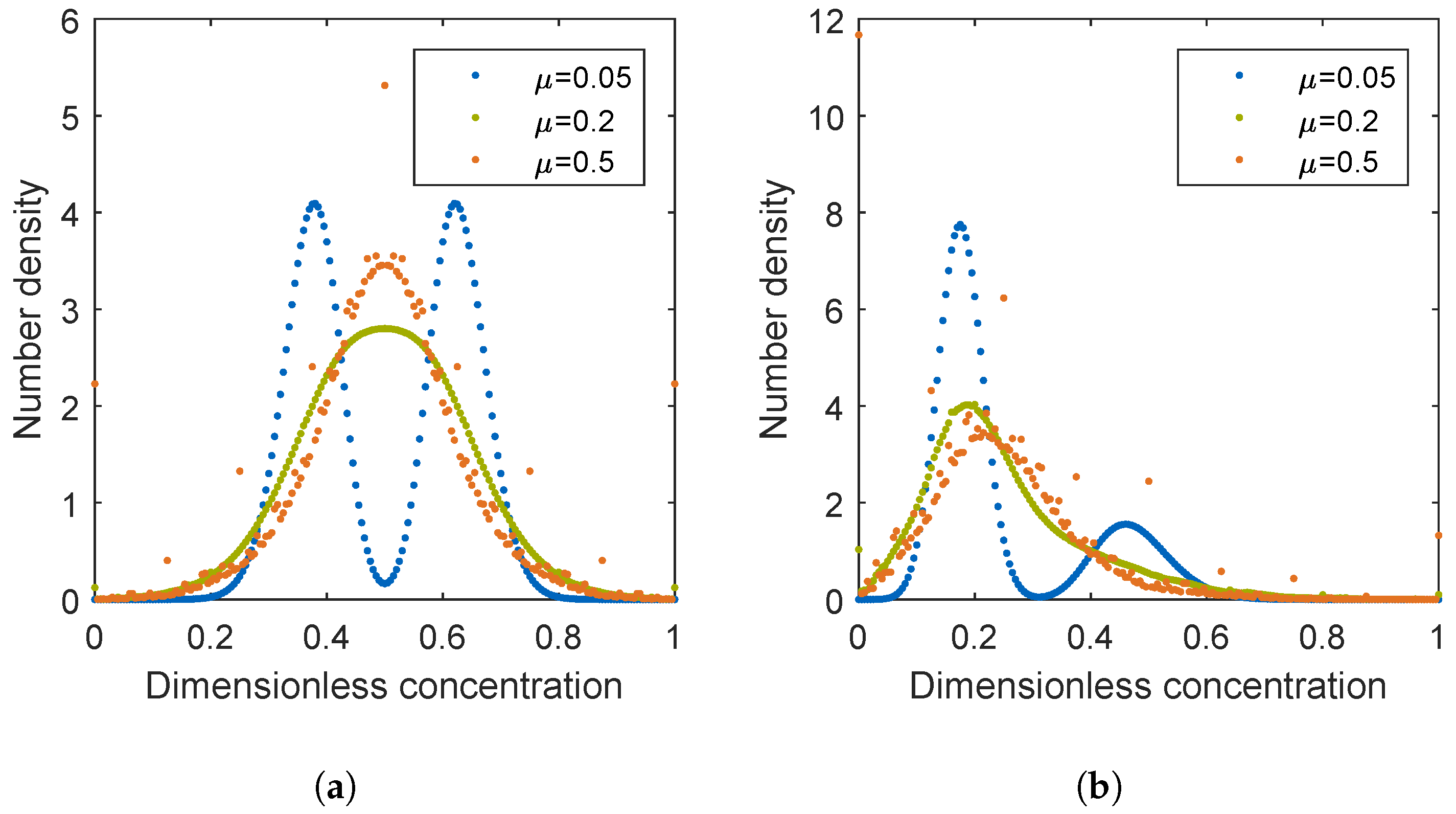
3.1. Uniform Initial Distribution
3.2. Influence of Initial Distribution
4. Transfer to Engineering
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DW model | Deffuant-Weisbuch model |
| PB | population balance |
| PBE | population balance equation |
| PBM | population balance model |
Appendix A. Derivation of Population Balance Equation

Appendix B. Moment Analysis
Appendix B.1. Definition of Moments
Appendix B.2. Transformation to a Square Integration Domain for the Source Term
Appendix B.3. Derivation of Ordinary Differential Equation for the Moments
Appendix B.4. Constant Number of Agents
Appendix B.5. Constant Total Belief
Appendix B.6. Ordinary Differential Equation for the Variance
Appendix B.7. Exponential Decay of Variance for d = 1
Appendix B.8. Variance for an Arbitrary d
References
- Ramkrishna, D. Population Balances; Academic Press: London, UK, 2000. [Google Scholar]
- Ramkrishna, D.; Singh, M.R. Population Balance Modeling: Current Status and Future Prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef] [PubMed]
- Sporleder, F.; Borka, Z.; Solsvik, J.; Jakobsen, H.A. On the population balance equation. Rev. Chem. Eng. 2012, 28, 149–169. [Google Scholar] [CrossRef]
- Nopens, I.; Biggs, C. Advances in population balance modelling. Chem. Eng. Sci. 2006, 61, 1–2. [Google Scholar] [CrossRef]
- Nopens, I.; Briesen, H.; Ducoste, J. Celebrating a milestone in Population Balance Modeling. Chem. Eng. Sci. 2009, 64, 627. [Google Scholar] [CrossRef]
- Kumar, S.; Briesen, H. Population balances in the league of mass, momentum, and energy balances. Chem. Eng. Sci. 2012, 70, 1–3. [Google Scholar] [CrossRef]
- Lorenz, J. Continuous Opinion Dynamics under Bounded Confidence: A Survey. Int. J. Mod. Phys. C 2007, 18, 1819–1838. [Google Scholar] [CrossRef]
- Sîrbu, A.; Loreto, V.; Servedio, V.D.P.; Tria, F. Participatory Sensing, Opinions and Collective Awareness. In Participatory Sensing, Opinions and Collective Awareness; Loreto, V., Haklay, M., Hotho, A., Servedio, V.D., Stumme, G., Theunis, J., Tria, F., Eds.; Chapter Opinion Dynamics: Models, Extensions and External Effects; Springer: Cham, Swizerland, 2017; pp. 363–401. [Google Scholar]
- Schweitzer, F. Sociophysics. Phys. Today 2018, 71, 40–46. [Google Scholar] [CrossRef]
- Gargiulo, F.; Lottini, S.; Mazzoni, A. The saturation threshold of public opinion: Are aggressive media campaigns always effective? arXiv, 2008; arXiv:0807.3937. [Google Scholar]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Weisbuch, G.; Deffuant, G.; Amblard, F.; Nadal, J.P. Interacting Agents and Continuous Opinions Dynamics. In Heterogenous Agents, Interactions and Economic Performance; Cowan, R., Jonard, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 225–242. [Google Scholar]
- Urbig, D.; Lorenz, J.; Herzberg, H. Opinion Dynamics: The Effect of the Number of Peers Met at Once. J. Artif. Soc. Soc. Simul. 2008, 11, 4. [Google Scholar]
- Zhang, J.; Hong, Y. Convergence analysis of heterogeneous Deffuant–Weisbuch model. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 1124–1129. [Google Scholar]
- Zhang, J.; Hong, Y. Convergence Analysis of the Long-range Deffuant–Weisbuch Dynamics. IFAC Proc. Vol. 2013, 46, 141–146. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, G. Convergence rate of the asymmetric Deffuant–Weisbuch dynamics. J. Syst. Sci. Complex. 2015, 28, 773–787. [Google Scholar] [CrossRef]
- Kayal, S. Unsupervised image segmentation using the Deffuant–Weisbuch model from social dynamics. Signal Image Video Process. 2017, 11, 1405–1410. [Google Scholar] [CrossRef]
- Carletti, T.; Fanelli, D.; Grolli, S.; Guarino, A. How to make an efficient propaganda. Europhys. Lett. 2006, 74, 222. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence: Models, analysis and simulation. J. Artif. Soc. Soc. Simul. 2002, 5, 1–24. [Google Scholar]
- Lorenz, J. Heterogeneous bounds of confidence: Meet, discuss and find consensus! Complexity 2010, 15, 43–52. [Google Scholar] [CrossRef]
- Toscani, G. Kinetic models of opinion formation. Commun. Math. Sci. 2006, 4, 481–496. [Google Scholar] [CrossRef]
- Boudin, L.; Salvarani, F. A kinetic approach to the study of opinion formation. Math. Model. Numer. Anal. 2009, 43, 507–522. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Boudin, L.; Salvarani, F. Modelling opinion formation by means of kinetic equations. In Mathematical Modeling of Collective Behavior in Socio-Economic and Life Sciences; Naldi, G., Pareschi, L., Toscani, G., Eds.; Birkhäuser Boston: Boston, MA, USA, 2010; pp. 245–270. [Google Scholar]
- Boudin, L.; Monaco, R.; Salvarani, F. Kinetic model for multidimensional opinion formation. Phys. Rev. E 2010, 81, 036109. [Google Scholar] [CrossRef] [PubMed]
- Kou, G.; Zhao, Y.; Peng, Y.; Shi, Y. Multi-Level Opinion Dynamics under Bounded Confidence. PLoS ONE 2012, 7, e43507. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. Deffuant model with general opinion distributions: First impression and critical confidence bound. Complexity 2013, 19, 38–49. [Google Scholar] [CrossRef]
- Antonopoulos, C.G.; Shang, Y. Opinion formation in multiplex networks with general initial distributions. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ben-Naim, E.; Krapivsky, P.; Redner, S. Bifurcations and patterns in compromise processes. Phys. D 2003, 183, 190–204. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Chen, Z.; Pruss, J.; Warnecke, H.J. A population balance model for disperse systems: Drop size distribution in emulsion. Chem. Eng. Sci. 1998, 53, 1059–1066. [Google Scholar] [CrossRef]
- Attarakih, M.; Bart, H.; Faqir, N. Numerical solution of the bivariate population balance equation for the interacting hydrodynamics and mass transfer in liquid–liquid extraction columns. Chem. Eng. Sci. 2006, 61, 113–123. [Google Scholar] [CrossRef]
- Attarakih, M.; Abu-Khader, M.; Bart, H.J. Modeling and dynamic analysis of a rotating disc contactor (RDC) extraction column using one primary and one secondary particle method (OPOSPM). Chem. Eng. Sci. 2013, 91, 180–196. [Google Scholar] [CrossRef]
- Bommarius, A.S.; Holzwarth, J.F.; Wang, D.I.C.; Hatton, T.A. Coalescence and Solubilizate Exchange in a Cationic 4-component Reversed Micellar System. J. Phys. Chem. 1990, 94, 7232–7239. [Google Scholar] [CrossRef]
- Niemann, B.; Rauscher, F.; Adityawarman, D.; Voigt, A.; Sundmacher, K. Microemulsion-assisted precipitation of particles: Experimental and model-based process analysis. Chem. Eng. Process. 2006, 45, 917–935. [Google Scholar] [CrossRef]
- Voigt, A.; Adityawarman, D.; Sundmacher, K. Size and distribution prediction for nanoparticles produced by microemulsion precipitation: A Monte Carlo simulation study. Nanotechnology 2005, 16. [Google Scholar] [CrossRef] [PubMed]
- Hatton, T.A.; Bommarius, A.S.; Holzwarth, J.F. Population-dynamics of Small Systems. 1. Instantaneous and Irreversible Reactions in Reversed Micelles. Langmuir 1993, 9, 1241–1253. [Google Scholar] [CrossRef]
- Natarajan, U.; Handique, K.; Mehra, A.; Bellare, J.R.; Khilar, K.C. Ultrafine metal particle formation in reverse micellar systems: Effects of intermicellar exchange on the formation of particles. Langmuir 1996, 12, 2670–2678. [Google Scholar] [CrossRef]
- Bandyopadhyaya, R.; Kumar, R.; Gandhi, K.S. Simulation of precipitation reactions in reverse micelles. Langmuir 2000, 16, 7139–7149. [Google Scholar] [CrossRef]
- Kumar, A.R.; Hota, G.; Mehra, A.; Khilar, K.C. Modeling of nanoparticles formation by mixing of two reactive microemulsions. AICHE J. 2004, 50, 1556–1567. [Google Scholar] [CrossRef]
- Jain, R.; Mehra, A. Monte Carlo models for nanoparticle formation in two microemulsion systems. Langmuir 2004, 20, 6507–6513. [Google Scholar] [CrossRef] [PubMed]
- Ethayaraja, M.; Bandyopadhyaya, R. Population balance models and Monte Carlo simulation for nanoparticle formation in water-in-oil microemulsions: Implications for CdS synthesis. J. Am. Chem. Soc. 2006, 128, 17102–17113. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Kumar, S. Effect of mixing on nanoparticle formation in micellar route. Chem. Eng. Sci. 2006, 61, 192–204. [Google Scholar] [CrossRef]
- Pruim, R. Foundations and Applications of Statistics: An Introduction Using R; Pure and Applied Undergraduate Texts; American Mathematical Society: Providence, RI, USA, 2011; Volume 13. [Google Scholar]
- Lacks, D.J.; Sankaran, R.M. Contact electrification of insulating materials. J. Phys. D 2011, 44, 453001. [Google Scholar] [CrossRef]
- Landauer, J.; Foerst, P. Triboelectric separation of a starch-protein mixture—Impact of electric field strength and flow rate. Adv. Powder Technol. 2018, 29, 117–123. [Google Scholar] [CrossRef]
- Prokhorov, A. Delta-function. In Encyclopedia of Mathematics; Kluwer Academic Publisher: Norwell, MA, USA, 2011. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuhn, M.; Kirse, C.; Briesen, H. Population Balance Modeling and Opinion Dynamics—A Mutually Beneficial Liaison? Processes 2018, 6, 164. https://doi.org/10.3390/pr6090164
Kuhn M, Kirse C, Briesen H. Population Balance Modeling and Opinion Dynamics—A Mutually Beneficial Liaison? Processes. 2018; 6(9):164. https://doi.org/10.3390/pr6090164
Chicago/Turabian StyleKuhn, Michael, Christoph Kirse, and Heiko Briesen. 2018. "Population Balance Modeling and Opinion Dynamics—A Mutually Beneficial Liaison?" Processes 6, no. 9: 164. https://doi.org/10.3390/pr6090164
APA StyleKuhn, M., Kirse, C., & Briesen, H. (2018). Population Balance Modeling and Opinion Dynamics—A Mutually Beneficial Liaison? Processes, 6(9), 164. https://doi.org/10.3390/pr6090164