Discrete Symbiotic Organisms Search with Adaptive Mutation for Simultaneous Optimization of Features and Hyperparameters and Its Application

Abstract

Effective engineering modeling requires simultaneously addressing feature selection and hyperparameter interdependence, a challenge exacerbated by high-dimensional data characteristics in complex engineering modeling. Traditional optimization methods typically address these two aspects separately, which limits overall model performance. This study introduces a hybrid framework to enhance the performance of extreme gradient boosting (XGBoost) in engineering applications. The framework comprises two main phases: first, preliminary feature selection guided by prior domain knowledge and statistical analysis to reduce data dimensionality while preserving interpretability; second, a discrete symbiotic organisms search algorithm with adaptive feature mutation (DMSOS) simultaneously optimizes feature subsets and XGBoost hyperparameters. The DMSOS employs a discretization strategy to separate feature selection from hyperparameter tuning, facilitating focused searches within distinct spaces. An adaptive mutation mechanism dynamically adjusts exploration intensity based on iteration progress and feature importance. Additionally, evaluations on 1414 field-measured blasting vibration data demonstrate that the proposed DMSOS-XGBoost model achieves superior prediction performance, with an r² of 0.96696 and RMSE of 0.02636, outperforming models optimized via traditional sequential approaches. Further interpretability analysis highlights spatial geometry and explosive load as critical features, offering actionable insights for environmental risk management. This research provides a valuable methodological reference for engineering modeling scenarios requiring simultaneous optimization of features and hyperparameters.

1. Introduction

The main challenge in engineering and construction for resource exploitation is the need to address both complex geological conditions and a changing external environment. These issues typically arise from intricate interactions among multiple variables and their prevalent nonlinear relationships [1,2]. For instance, in geotechnical engineering, the inherent uncertainty and spatial variability of geological conditions can directly impact the project’s initial design, construction safety, and subsequent maintenance [3,4]. In mining engineering, blasting is a necessary operation for efficient and economical production in mining [5]. The intensity of vibrations is influenced by numerous parameters from the source to the propagation path [6,7]. Even minor prediction errors in vibration can cause structural damage or lead to legal disputes, making it particularly crucial to accurately predict and pre-emptively control the intensity and impact range of blasting vibrations [8]. Traditional solutions, including empirical methods, field testing, and numerical analysis, all have inherent limitations [9]. Empirical methods are limited because they consider only a few factors, making them unsuitable for complex and variable environments. Field tests rely on specific equipment, involve considerable time and economic costs, and do not allow for forward-looking predictive analysis. Although numerical analysis can economically simulate engineering problems, it still faces challenges in constructing complex field models. These limitations naturally motivate the use of data-driven artificial intelligence (AI) approaches, in which machine learning algorithms can capture nonlinear multivariate relationships and provide interpretable feature contributions. Given these advantages, AI modeling methods have enabled multi-parameter modeling with greater efficiency, becoming essential tools for solving complex engineering problems [10,11,12,13].

As feature dimensionality increases during the modeling process, redundant or irrelevant variables may trigger the curse of dimensionality. In this context, the importance of feature selection as an indispensable step in model construction cannot be ignored [14]. Effective feature selection not only enhances model performance and interpretability but also significantly improves computational efficiency. The essence of feature selection methods lies in defining the mechanisms for subset search and subset evaluation. In general, according to their interaction with the learner, feature selection methods can be categorized into filter methods, wrapper methods, and embedded methods [15]. Filter methods select features before model training by using statistical analysis to evaluate the importance of features, thereby retaining key features or eliminating those deemed unimportant. This approach offers the advantages of broad applicability and high computational efficiency, but it may not always identify the feature subset that maximizes model performance. In contrast, wrapper methods assess feature subsets based on algorithm performance, often selecting more optimal subsets than filter methods, but at the cost of higher computational costs. Embedded methods integrate feature selection within the model training process, offering lower computational costs compared to wrapper methods and better performance than filter methods. However, the outcomes of embedded methods depend on the specific model used, and different models may lead to different feature selection results. Based on search strategy, feature selection can be divided into exhaustive search, sequential search, and random search [16]. In the context of random search, the metaheuristic algorithms, such as genetic algorithms [17], particle swarm optimization [18], ant colony optimization [19], grey wolf optimizer [20], and butterfly optimization [21], have seen widespread use in recent years due to their excellent global optimization capabilities in feature selection [14,22,23,24,25].

However, in the study of engineering problems, the application of metaheuristic methods for feature selection remains relatively limited. Researchers often instead use other methods to select feature subsets or directly use the full feature set for model training. For instance, Zhou et al. [26] employed the Pearson chi-square test to assess the independence of features from the output variable, selecting five key features for random forest and Bayesian network models to predict ground vibrations. Hu [27] applied the maximum information coefficient method to evaluate the contributions of various factors to the liquefaction potential, identifying 13 significant factors influencing gravelly soil liquefaction through a filtering method. Demir and Sahin [28] explored the use of recursive feature elimination, Boruta, and stepwise regression to enhance the performance of tree-based algorithms, finding that the Boruta method performed best in predicting soil liquefaction. Nguyen et al. [29] analyzed the correlations among features before developing a prediction model, but ultimately chose to use the complete feature set to predict peak vibration speeds in open-pit coal mines due to weak correlations. Hajihassani et al. [30] directly utilized nine features to predict vibrations and air overpressure caused by blasting, without performing feature selection.

On the other hand, metaheuristic algorithms have been widely adopted to optimize model hyperparameters. For instance, Azimi et al. [31] utilized genetic algorithms to optimize the architecture of an artificial neural network, improving the prediction accuracy of blasting vibration in open-pit copper mines. He et al. [32] employed the grey wolf optimizer (GWO), whale optimization algorithm (WOA), and tunicate swarm algorithm (TSA) to search for the optimal hyperparameters of a random forest (RF) model, and found that the RF-TSA model provided a robust solution for predicting overbreak caused by tunnel blasting. Tang and Na [33] used particle swarm optimization and grid search to optimize the hyperparameters of four different machine learning models for predicting ground settlement in various tunnels. Qiu et al. [34] fine-tuned hyperparameters of the XGBoost model using GWO, WOA, and Bayesian optimization, and compared the resulting models with an unoptimized baseline, demonstrating that hyperparameter optimization can significantly enhance predictive performance. Furthermore, metaheuristic algorithms such as particle swarm optimization, ant colony algorithm, and artificial bee colony have also been utilized to enhance the performance of models, providing effective support for solving engineering problems [35,36,37,38].

Although numerous methods have been proposed for feature selection and hyperparameter optimization, these two processes are often conducted independently, which can lead to suboptimal performance of the final model. When seeking the best model, the optimal feature subset and the best model hyperparameters should be solved simultaneously. For a specific feature subset, there exists a corresponding set of optimal hyperparameters; similarly, for a given set of hyperparameters, there is a corresponding optimal feature subset.

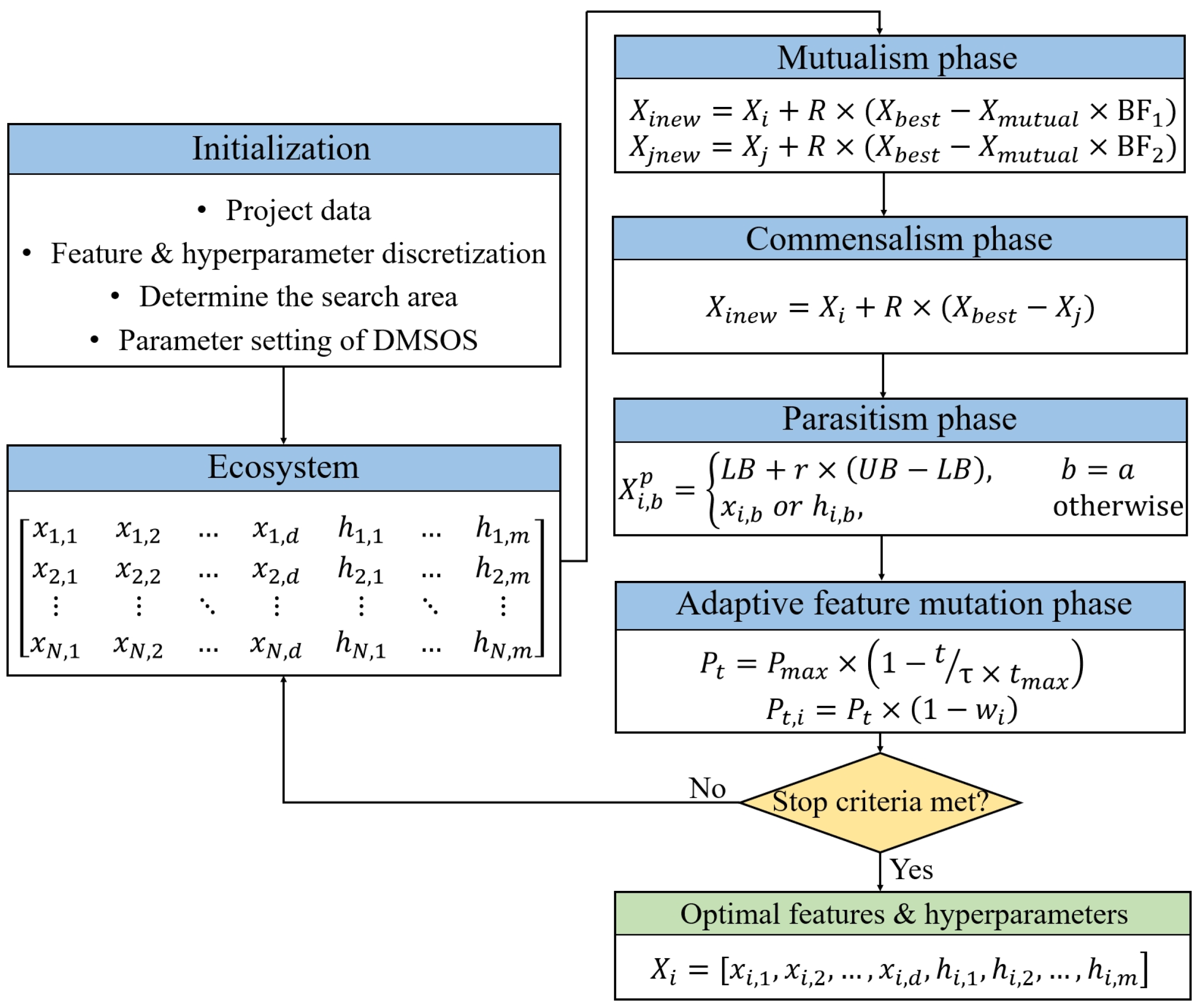
Therefore, this study proposes a systematic framework that integrates feature selection and hyperparameter optimization. First, a preliminary feature selection method is developed to eliminate redundant variables based on prior knowledge and statistical analysis. Second, a novel discrete symbiotic organisms search algorithm with adaptive feature mutation (DMSOS) is introduced. This algorithm simultaneously optimizes features and hyperparameters for the XGBoost model, enhanced by a mutation strategy based on time and weight to balance exploration and exploitation during optimization. Finally, the proposed DMSOS-XGBoost model is validated based on the blasting vibration data of a shaft project and compared with other sequential modeling strategies, and the feature importance analysis of the model provides guidance for field construction.

2. Methodology

2.1. Preliminary Feature Selection

In complex and variable engineering environments, effective feature selection is essential for constructing reliable predictive models. The purpose of feature selection is to filter out the optimal subset from the original feature set, aiming to eliminate irrelevant or redundant features [24]. This section presents a preliminary feature selection method that is guided by engineering theory, employing a mathematical model to evaluate both the relationships between features and the target output and the interactions among features. The goal is to identify and remove features that are highly correlated with other features and have a weak correlation with the target output.

2.1.1. Evaluation Criteria

The evaluation criteria are used to determine whether a feature should be removed. Specifically, the constructed mathematical model is used to compute a score for the currently selected feature set, which is defined as follows:

$${\mathrm{F}}_{score}={\displaystyle \frac{\sum _{i=1}^N{w}_i\left|c_{x_i,t}\right|}{\sum _{i=1}^N{w}_i^2+\lambda /N\sum _{i\ne j}|c_{x_i,x_j}|}}$$

(1)

where F_score represents the score of the feature set, a higher score indicates a more optimal feature set. N is the number of features. $\left|c_{x_i,t}\right|$ denotes the absolute value of the statistical correlation between feature x_i and the target variable t, and $\left|c_{x_i,x_j}\right|$ represents the absolute value of the statistical correlation between feature x_i and feature x_j. w_i is the weight assigned to feature x_i. λ is a penalty parameter ranging from 0 to 1, used to adjust the impact of correlation among features to suit different operating conditions. When λ = 0, only the correlation between the features and the target variable is taken into account.

The relationships among features and between features and the target variable are calculated based on the Pearson correlation coefficient [39]. The correlation between feature x_i and feature x_j is computed using the following formula:

$$c_{x_i,x_j}={\displaystyle \frac{\sum _{k=1}^n(x_{i,k}-{\overline{x}}_i)(x_{j,k}-{\overline{x}}_j)}{\sqrt{\sum _{k=1}^n(x_{i,k}-{\overline{x}}_i{)}^2\sum _{k=1}^n(x_{j,k}-{\overline{x}}_j{)}^2}}}$$

(2)

where x_i,k represents the value of the k-th sample in feature x_i, ${\overline{x}}_i$ is the mean value of the samples for feature x_i, and n is the total number of samples. Similarly, the correlation $c_{x_{i,t}}$ between a feature and the target variable can be obtained in a similar manner. The weight of feature x_i is determined by the square of its correlation with the target variable and is normalized. The formula is as follows:

$$w_i={\displaystyle \frac{|c_{x_{i,t}}{|}^2}{\sum _{k=1}^N|c_{x_{k,t}}{|}^2}}$$

(3)

2.1.2. Filtering Process

Feature Grouping

To avoid inadvertently removing key features that are theoretically supported and critical to prediction outcomes during the feature selection process, the established engineering theories are utilized to guide feature selection. These theories serve as prior knowledge to categorize features based on the nature of their impact on the target variable. For example, when predicting blasting vibrations, features can be grouped according to the engineering structure and charge characteristics of the blasting source, spatial geometrical characteristics of the propagation process, and the physical and mechanical characteristics of the monitoring points. By integrating prior knowledge, this grouping strategy avoids cross-group comparisons during feature removal, focusing instead on analyzing relationships within the same group. In addition, feature selection is an NP-hard problem, under the assumption that 12 features are evenly distributed to 4 groups, the number of candidate feature subsets that need to be evaluated is reduced from 4095 to 2401.

Feature Selection Process

Within each feature group, the internal correlations among the features are first calculated. Starting with the pair of features with the highest correlation across all feature groups, the correlation of these two features with the target variable is evaluated, and the feature with the lower correlation is identified as a potential candidate for removal. Subsequently, the score of the feature subset after removing this feature is calculated. If the F_score does not decrease, then the removal of the feature is confirmed; if the F_score decreases, the feature is retained. The analysis then continues with the next pair of highly correlated features, repeating the F_score evaluation process until a preset correlation threshold is reached. It is important to note that at least one feature is retained in each feature group to ensure that the group’s potential impact on the target variable is not lost. The flowchart for this method is shown in Figure 1.

From the perspective of feature selection theory, the above procedure can be regarded as a filter-type preliminary selection strategy that combines prior engineering knowledge with a relevance-redundancy trade-off. Compared with modern filter methods such as minimum redundancy-maximum relevance or HSIC-Lasso, the proposed F_score index is constructed from Pearson correlation and normalized feature weights, making the evaluation criterion transparent and easy to interpret. In contrast to wrapper or embedded approaches such as Boruta or SHAP-based selection, which repeatedly train a learning model to assess candidate features, the present preliminary feature selection is model-agnostic, serving only to remove clearly redundant or weakly informative variables before the stage of simultaneous feature selection and hyperparameter optimization. This design reduces the size of the search space, lowers computational cost, and preserves the physical interpretability of feature groups.

2.2. Simultaneous Optimization of Features and Hyperparameters

2.2.1. Symbiotic Organisms Search Algorithm

Inspired by the symbiotic relationships between organisms in ecosystems, Cheng and Prayogo proposed a novel metaheuristic algorithm that simulates the symbiotic interaction strategies organisms use to survive in ecosystems, known as the symbiotic organisms search algorithm (SOS) [40]. Initially, the SOS algorithm was developed to solve continuous engineering optimization problems [40]. Subsequent studies have shown that SOS outperforms many competing algorithms on a range of benchmark functions and engineering design problems, contributing to its growing popularity and widespread adoption across practical applications [41,42,43,44].

2.2.2. Discrete Symbiotic Organisms Search Algorithm with Adaptive Feature Mutation (DMSOS)

The operations within each search phase of the SOS algorithm are required to maintain connexity, ensuring that there are searchable paths between every pair of solutions. However, this study involves the simultaneous optimization of features and hyperparameters, both of which involve discrete variables. To address this limitation of the standard SOS algorithm, this section introduces the newly proposed DMSOS algorithm, which establishes an ecosystem decision matrix containing simultaneous decision vectors for features and hyperparameters. The algorithm discretizes vector dimensions through a specially designed transfer function and implements adaptive feature mutation based on time and weight for the feature vectors, ultimately achieving simultaneous optimization of features and hyperparameters of the model. The flowchart of the DMSOS algorithm is given in Figure 2, and the corresponding steps are described in detail below.

Discretization of Features and Hyperparameters

Since the SOS algorithm primarily searches for solutions in continuous spaces, it is mathematically incompatible with the discrete decision variables in this study, including binary feature inclusion (0/1) and integer hyperparameters. Therefore, the search is redesigned as a discrete optimization process by introducing a discretization scheme for features and hyperparameters, as shown in Figure 3.

Binary encoding is used to represent the selection status of each feature, where “1” indicates the selection of the feature, and “0” indicates non-selection. This encoding can be expressed as a binary vector with a length equal to the total number of features. Typically, the binary discretization of features involves mapping the continuous output values of the algorithm to the [0, 1] interval, and a fixed threshold (e.g., 0.5) is used to decide whether to select a feature. While this method is straightforward, it cannot effectively adjust the feature flip probability in response toa significant change in output values. Therefore, a novel transformation function is proposed to ensure that the probability of feature flipping approaches 100% when there is a large change in output values, while this probability is greatly reduced when the changes are minimal. To achieve this, the Gaussian function is modified, and a new V-shaped transformation function is designed to map the function’s output values to the [0, 1] interval, which is used to calculate the probability of changes in feature states:

$$T\left({\Delta x}_i\right)=1-e^{-\mathrm{k}{{(\Delta x}_i)}^2}$$

(4)

where Δx_i represents the change in the i-th feature following a particular evaluation update, k is an adjustable parameter that controls the sensitivity of the function, with higher values of k making the feature more likely to change its current state. The transformation function is illustrated in Figure 4. Whether the state of a feature changes in the next phase is determined by the equation:

$$x_i^{t+1}=\left\{\begin{array}{l}1-x_i^t, T\left({\Delta x}_i^t\right)> r\\ x_i^t, \mathrm{otherwise}\end{array}\right.$$

(5)

where $x_i^t$ represents the current binary state of the i-th feature, $x_i^{t+1}$ is the binary state of that feature after the t-th evaluation update, and r is a random value within the range [0, 1].

In many algorithms, hyperparameters often need to be specified in integer form, such as the depth and number of trees in the random forest algorithm. For the integer-type discretization of hyperparameters, whether to round up or down is determined by comparing the decimal part of a real number with a random value, thus converting the continuous real number into an integer:

$$p_i^t=h_i^t-⌊h_i^t⌋$$

(6)

$$h_i^{t+1}=\left\{\begin{array}{l}⌈h_i^t⌉, p_i^t>r\\ ⌊h_i^t⌋, \mathrm{otherwise}\end{array}\right.$$

(7)

where $p_i^t$ represents the probability that the i-th hyperparameter will be rounded up after the t-th evaluation update, calculated from the decimal part of the current value of the hyperparameter $h_i^t$. $⌊h_i^t⌋$ is the floor function, and $⌈h_i^t⌉$ is the ceiling function. r is a random value within the range [0, 1]. In Equation (7), whether $h_i^{t+1}$ is ultimately rounded up or down is determined by comparing $p_i^t$ with r.

Initialization

The feature set is converted into binary form, and the hyperparameters in the model are categorized as either integer or real types, establishing the search range for the hyperparameters. Concurrently, the maximum number of iterations and the size of the ecosystem (eco_size) for the DMSOS algorithm are set. The objective is to obtain the optimal features and hyperparameters, thereby enhancing the performance of the final model. To achieve this, a random generator is employed to construct a decision matrix, which initializes the ecosystem and sustains the subsequent search process.

$$\mathrm{Decision} \mathrm{matrix}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{X}_1\\ X_2\end{array}\\ ⋮\end{array}\\ X_{\mathrm{N}}\end{array}\right]=\left[\begin{array}{ccccccc}{x}_{\mathrm{1,1}}& x_{\mathrm{1,2}}& \cdots & x_{1,d}& h_{\mathrm{1,1}}& \cdots & h_{1,m}\\ x_{\mathrm{2,1}}& x_{\mathrm{2,2}}& \cdots & x_{2,d}& h_{\mathrm{2,1}}& \cdots & h_{2,m}\\ ⋮& ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ x_{N,1}& x_{N,2}& \cdots & x_{N,d}& h_{N,1}& \cdots & h_{N,m}\end{array}\right]$$

(8)

The decision matrix has dimensions of N × M, where N represents the number of decision vectors X, and M is the total length of each decision vector. Here M = d + m, d is the length of the feature vector, and m is the length of the hyperparameter vector. Within this framework, each decision vector X can be viewed as an organism within the ecosystem, representing a candidate solution to the problem:

$$X_i=[x_{i,1},x_{i,2},\dots ,x_{i,d},h_{i,1},h_{i,2},\dots ,h_{i,m}]$$

(9)

where $X_i$ represents the i-th organism within the ecosystem, and each organism contains two distinct types of elements: x represents the binary feature dimensions, and h represents the model hyperparameter dimensions, which include both integers and real types. The decision matrix is the fundamental architecture that enables the simultaneous optimization of features and hyperparameters. It defines the joint search space and provides a unified representation on which the search phases of DMSOS operate. By updating entire rows of this matrix, the algorithm simultaneously modifies the feature subset and the associated hyperparameters for each organism, ensuring that feature selection and hyperparameter tuning are explored and evaluated jointly rather than in isolation.

Mutualism Phase

For each organism $X_i$, another organism $X_j$ is randomly selected from the ecosystem. The mutualism relationship between these two organisms is represented by the following formula:

$$X_{inew}=X_i+R\times (X_{best}-X_{mutual}\times {\mathrm{B}\mathrm{F}}_1)$$

(10)

$$X_{jnew}=X_j+R\times (X_{best}-X_{mutual}\times {\mathrm{B}\mathrm{F}}_2)$$

(11)

where R represents an M-dimensional vector of random numbers generated from rand(0, 1). X_best denotes the organism with the best performance in the current ecosystem, $X_{mutual}$ signifies the mutualistic symbiotic traits exhibited by two organisms to enhance their survival advantage, calculated as $X_{mutual}={\displaystyle \frac{X_i+X_j}{2}}$. The benefit factors BF₁ and BF₂ are randomly set to 1 or 2, reflecting the degree of benefit derived from the interactive effects. In this phase, the current organism is only replaced by the new organism if the latter performs better.

Commensalism Phase

Similarly, the organism $X_i$ randomly selects another organism $X_j$ from the ecosystem, and benefits from the interaction without causing harm to the other party. This commensalism relationship is mathematically represented as:

$$X_{inew}=X_i+R\times (X_{best}-X_j)$$

(12)

where R in Equation (12) is an M-dimensional vector of random numbers generated from rand(−1, 1). The current $X_i$ is replaced by $X_{inew}$ only if the latter performs better.

Parasitism Phase

In this phase, the organism $X_i$ randomly selects several dimensions a from its decision vector, and updates the element values on these selected dimensions to random values, thereby producing a parasitic version, $X_i^p$. The generation process of this parasite can be described by the mathematical model:

$$X_{i,b}^p=\left\{\begin{array}{l}LB+r\times \left(UB-LB\right), b=a\\ x_{i,b} or h_{i,b}, \mathrm{otherwise}\end{array}\right.$$

(13)

where r is a random value within the range [0, 1], and LB (lower bound) and UB (upper bound) represent the boundaries of the respective dimensions in the decision vector. Subsequently, another organism $X_j$, randomly selected from the ecosystem, serves as the host for the parasite $X_i^p$. If the parasite performs better than its host, the host will be replaced; otherwise, the parasite will not survive in the ecosystem.

Adaptive Feature Mutation Phase

During the parasitism phase, the original algorithm explores solutions by replicating organisms and randomly altering the values of some of their dimensions. However, this process carries the risk of modifying an insufficient number of dimensions, and for binary features, random modifications within boundary limits may not effectively change the feature states. In particular, during the early and middle stages of the optimization process, if the number of dimensions randomly altered is too few, the algorithm’s ability to explore optimal solutions in a broader space may be restricted, thereby reducing its global optimization capability.

Therefore, in the subsequent phase, adaptive probability mutations are applied to the binary values of feature dimensions in the organism $X_i$, producing a mutated organism $X_i^m$. This approach aims to foster a diverse ecosystem of features, thereby enhancing the algorithm’s capability to optimize the feature set and helping to avoid entrapment in local optima. Initially, the mutation probabilities for different iterative search periods are calculated as follows:

$$P_t=max\left\{0, P_{max}\times \left(1-{\displaystyle \raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\tau \times t_{max}$}\right.}\right)\right\}$$

(14)

where $P_t$ represents the probability of feature mutation, $P_{max}$ is the maximum mutation probability, and τ is the percentage parameter controlling the final cutoff time for mutations. t is the current iteration number, and $t_{max}$ is the maximum number of iterations. Mathematically,$P_t$ is a monotone decreasing function of t. At the beginning of the search, $P_t {\approx P}_{max}$ so that features are allowed to strong exploration, while as t approaches $t_{max}$, $P_t$ gradually decays to 0, reducing the expected number of mutations and favouring exploitation around promising solutions.

Furthermore, during the same iteration period, the mutation probabilities differ among various features, with those features having a greater impact on the target output being assigned lower mutation probabilities and thus becoming more stable. Therefore, the mutation probability for the i-th feature in the decision vector during the t-th iteration is calculated using the following equation:

$$P_{t,i}=P_t\times \left(1-w_i\right)$$

(15)

where w_i denotes the weight of feature x_i, calculated in accordance with Equation (3). Since w_i ∈ [0, 1], Equation (15) ensures that $P_{t,i}$ ∈ [0, $P_t$]. Features with larger weights have smaller mutation probabilities, while less important features have larger $P_{t,i}$ and are more frequently perturbed. Hence, the expected mutation probability will decrease as the iteration and feature importance increase, which encodes the balance between exploration and exploitation. The mutation result for feature x_i is determined by the following function:

$$x_{t+1,i}=\left\{\begin{array}{l}1-x_{t,i}, r<P_{t,i}\\ x_{t,i}, otherwise\end{array}\right.$$

(16)

where r is a random value within the range [0, 1], each feature bit is flipped with probability $P_{t,i}$ and kept unchanged otherwise. In this selection mechanism, if the performance of the mutated organism $X_i^m$ exceeds that of the original organism $X_i$, indicating that the mutant is better adapted to the ecosystem, then the original organism is replaced. Otherwise, the mutant is removed.

The pseudocode of the DMSOS algorithm is presented in Figure 5. The algorithm introduces two key adaptations that fundamentally modify the SOS process to address simultaneous discrete optimization challenges. First, a new V-shaped transfer function is employed in place of the continuous updates in SOS; it maps continuous changes into feature flipping probabilities, ensuring that significant variations in the search space lead to a high likelihood of switching feature states, which cannot be achieved by the standard SOS. Second, the adaptive feature mutation injects directed randomness into the search. Unlike the purely random perturbations in the parasitism phase, it uses time-decaying and feature weight sensitive mutation probabilities. This strategy promotes population diversity and broad exploration in the early iterations, while stabilizing in the later stage to support local refinement. Overall, these enhancements enable the algorithm to simultaneously search feature subsets and hyperparameters more effectively, improving final solution quality by avoiding local optima and yielding more robust feature configurations.

2.3. Extreme Gradient Boosting (XGBoost)

XGBoost is a powerful supervised learning algorithm proposed by Chen and Guestrin [45]. The core concept of the algorithm is an ensemble learning method based on gradient boosting, which enhances the overall predictive capability of the model by combining multiple weak learners. XGBoost model predicts outputs through an ensemble of regression trees, with the model output represented as the sum of the outputs from all the trees:

$${\hat{\mathrm{y}}}_i={\sum }_{k=1}^K{f}_k\left(x_i\right)$$

(17)

where $f_k$ represents the prediction function of the k-th tree, and K is the total number of trees. ${\hat{\mathrm{y}}}_i$ is the predicted value for sample i, and $x_i$ is the feature of sample i. The model’s performance is enhanced by optimizing an objective function that includes regularization terms. This objective function is defined as:

$$L\left(\varphi \right)={\sum }_{i=1}^{n}l(y_i,{\hat{\mathrm{y}}}_i)+{\sum }_{k=1}^K\Omega \left(f_k\right)$$

(18)

$$\Omega \left(f_k\right)=\gamma T+{\displaystyle \frac{1}{2}}\lambda |w{|}^2$$

(19)

where $l(y_i,{\hat{\mathrm{y}}}_i)$ is a differentiable convex loss function used to quantify the error between the predicted value ${\hat{\mathrm{y}}}_i$ and the actual value y_i. $\Omega \left(f_k\right)$ is the regularization term, with γ controlling the complexity of the trees, λ as the L2 regularization parameter for leaf weights, T representing the number of leaf nodes in the tree, and w is the vector of weights for the leaf nodes. In each iteration, XGBoost adds a new tree $f_t$ by minimizing an objective function of the following form:

$$L^{\left(t\right)}={\sum }_{i=1}^n\left[l\right(y_i,{\hat{\mathrm{y}}}_i^{(t-1)}+f_t\left(x_i\right))+\Omega (f_t\left)\right]$$

(20)

The detailed explanation of the XGBoost algorithm can refer to the original paper [45]. The overall analysis process of this study is illustrated in Figure 6. Initially, preliminary feature selection is conducted on the dataset as described in Section 2.1, and then the data is randomly split into 80% for training and 20% for testing. In the model optimization process, the training set is utilized for simultaneous optimization by the DMSOS algorithm described in Section 2.2, in which each organism is encoded as a joint decision vector consisting of a binary feature mask and the integer and real-valued hyperparameters of the XGBoost model outlined in Section 2.3. For each candidate decision vector, the feature mask is used to select a subset of input variables, then XGBoost is trained with the corresponding hyperparameters, and the average root mean square error (RMSE) over five-fold cross-validation on the training set is evaluated as the fitness value. During the iterative search, the mutualism, commensalism, and parasitism phases of DMSOS update this joint decision vector via the discrete transfer function and adaptive mutation mechanism, so that the feature subset and hyperparameters are refined simultaneously toward an optimal combination, while overfitting is controlled through cross-validation. Finally, the performance of the DMSOS-XGBoost model is evaluated using the remaining test set.

3. Application and Results

3.1. Data Description

To evaluate the model’s performance in practical application, blasting vibration data were collected from a shaft construction project at a gold mine (Figure 7). Vibration peaks were extracted from each blast, combined with construction diaries and a survey of the surrounding environment, a total of 1414 data samples were gathered, each containing 13 input features and one target variable, as shown in

Table 1. Attributes and range of the dataset.

Parameter	Unit	Min	Max	Mean	Type
Horizontal distance from blast source (D)	m	181.95	1340.9	765.79	Feature
Altitude of geophone (A)	m	2	38	8.88	Feature
Depth difference from blast source (H)	m	696.7	864.7	770.02	Feature
Straight-line distance from blast source (R)	m	754.95	1577.36	1129.56	Feature
Explosive charge per-delay (Q)	kg	57.6	232	114.06	Feature
Hole spacing (HS)	mm	606	1063	913.57	Feature
Circles diameter (CD)	mm	2000	11,200	6742.86	Feature
Hole angle (HA)	°	88	90	89.71	Feature
Charge per hole (CPH)	kg	4	6.4	5.14	Feature
Hole depth (HD)	mm	4500	4700	4528.57	Feature
Free surface area (FSA)	m2	29.53	158.34	95.5	Feature
Number per circle (NPC)	-	9	58	24.29	Feature
Rebound value (RD)	-	19	40.5	26.02	Feature
Peak particle velocity (PPV)	cm/s	0.0059	0.9083	0.117	Target

. The entire dataset was then randomly divided into 80% training and 20% testing sets, and the density distributions of the training, testing, and complete dataset is illustrated in Figure 8. As depicted in Figure 6, during the training of the predictive model, five-fold cross-validation (CV) was used to optimize the DMSOS-XGBoost hyperparameters by minimizing the mean RMSE across validation folds. The final model performance on the testing set was quantified with r² and RMSE to assess the agreement between predictions and observations.

3.2. Preliminary Feature Selection Results

According to the different modes of influence on vibration, features were categorized into four groups: engineering structure related to the blasting source, spatial geometry associated with propagation, explosive charge characteristics, and physical and mechanical properties at the monitoring points (

Table 2. Result of feature grouping in preliminary feature selection.

Group Number	Feature Grouping	Description
Group 1	HS, CD, HA, HD, FSA, NPC	Blasthole layout and geometric parameters
Group 2	D, H, A, R	Spatial relationship parameters
Group 3	Q, CPH	Explosive charge parameters
Group 4	RD	Rock mass property parameter

). The correlations among the features within each group were calculated, and the results are displayed in Figure 9. The correlations between features were arranged in ascending order based on their absolute values and divided into five intervals, as shown in

Table 3. Range division based on absolute values of correlation coefficients.

Range	Feature Pair	Correlation Level
0~0.2	HA-HD, H-R, HS-CD, HS-FSA	Very weak
0.2~0.4	H-A, D-H	Weak
0.4~0.6	HA-FSA, CD-HA, HS-HD, R-A, HS-NPC, HD-NPC	Moderate
0.6~0.8	Q-CPH, HS-HA, D-A, CD-HD, HD-FSA	Strong
0.8~1.0	CD-FSA, D-R, HA-NPC, FSA-NPC, CD-NPC	Very strong

. In this study, a threshold of 0.8 for strong correlation was adopted to guide feature selection, because correlation coefficients $\left|\theta \right|$≥ 0.8 are commonly interpreted as indicating a strong association and are therefore suitable for flagging redundancies between input variables. In addition, the penalty parameter λ controls the trade-off between relevance and redundancy. When λ = 0, only the correlation between each feature and the target is considered, whereas larger λ values place more emphasis on penalizing inter-feature redundancy. To keep the relevance and redundancy terms on a comparable scale, preliminary tests in this study showed that setting λ = 0.5 effectively removed redundant features without excessively discarding informative ones. To clearly illustrate the selection process, the corresponding calculations and steps are detailed in

Table 4. The preliminary feature selection process.

Index	Feature Pair	Absolute Correlation	Absolute Correlation with PPV	Feature Removed	Fscore (Initial Score 0.515)	Removed
1	CD	0.999	0.379	CD	0.600	Yes
	FSA		0.381
2	D	0.982	0.548	R	0.599	No
	R		0.484
3	HA	0.899	0.277	HA	0.693	Yes
	NPC		0.374
4	FSA	0.881	0.381	NPC	0.815	Yes
	NPC		0.374
5	CD	0.879	0.379	NPC	0.815	Yes
	NPC		0.374

. The final result of the preliminary feature selection was the removal of features CD, HA, and NPC.

3.3. Simultaneous Optimization Results

In this section, the DMSOS algorithm was utilized to simultaneously optimize feature subsets and XGBoost hyperparameters. The optimized features build on the preliminary feature selection results from Section 3.2, and the recommended search ranges for the five primary hyperparameters are listed in

Table 5. Overview of five primary hyperparameters in the XGBoost.

Hyperparameters	Recommended Range	Type	Description
max_depth	[3, 10]	Integer	Maximum depth of a tree; default = 6.
min_child_weight	[1, 10]	Integer	Minimum sum of instance weight required in a child node to allow a split; default = 1.
num_boost_round	[10, 1000]	Integer	Number of boosting iterations.
eta	[0.001, 1]	Real	Learning rate; default = 0.3.
gamma	[0, 1]	Real	Minimum loss reduction required to make a further split; default = 0.

. To determine suitable parameter values of DMSOS for this study, a single-factor sensitivity analysis was conducted for four parameter settings. The results are presented in Figure 10, where each polyline represents one parameter combination and the red curves correspond to combinations that achieve better performance. Another critical DMSOS setting is the number of decision vectors in the decision matrix, which represents the size of the ecosystem (eco_size). Based on previous studies, eco_size is examined at values of 10, 20, 40, 60, 80, and 100 [46,47]. The detailed parameter settings of DMSOS are summarized in

Table 6. Parameter settings of the DMSOS algorithm.

Parameters	Recommended Value	Description
Iterations	300	Maximum number of iterations per run.
eco_size	10, 20, 40, 60, 80, 100	The size of the ecosystem.
k	4	Controls the sensitivity of the transformation function.
$P_{max}$	0.8	Upper bound of the mutation probability.
τ	0.9	Controls the cutoff point of the mutation.

. Considering the randomness of the algorithm, each eco_size is executed in five independent runs, with a maximum of 300 iterations per run to ensure convergence while avoiding excessive computation.

The convergence behavior and final performance for different eco_sizes are shown in Figure 11. Figure 11a presents the best convergence curves for different eco_sizes over five runs, while Figure 11b shows the final fitness of various eco_sizes. Although the configuration with an eco_size of 100 did not converge the fastest, it achieved the lowest fitness value. Therefore, the configuration with an eco_size of 100 was selected, and its optimized decision vector for the feature set and hyperparameters was adopted as the optimal solution to enhance the predictive model’s performance.

Additionally, this study introduced the standard SOS algorithm for comparison, which employs a rounding principle for discretizing features and hyperparameters, with all dimensions clipped to the upper and lower bounds. Apart from this necessary discretization step, the SOS algorithm does not have an adaptive mutation stage, and its basic parameter settings were kept consistent with DMSOS, ensuring that both algorithms operated within the same search space under identical basic conditions. As shown in Figure 12a, the DMSOS algorithm achieved lower fitness values compared to the SOS algorithm. Figure 12b reveals the changes in the number of selected features over iterations, where the DMSOS algorithm selected two more features than the SOS algorithm. Figure 12c,d depict the selection process of individual features during iterations for both algorithms. In comparison, the DMSOS updated the feature set more frequently in the early stages of iterations and reached convergence more quickly. Furthermore, for comparison with other classical algorithms, the standard GA and PSO were improved based on the same feature and hyperparameter discretization procedure as well as the adaptive mutation strategy, and the comparison results are presented in

Table 7. The comparison results of different algorithms.

Algorithm	Fitness Value	Running Time (s)	Performance Ranking
SOS	0.026386	8952	4
DMSOS	0.026215	11,653	1
GA	0.026318	5637	3
PSO	0.026283	5246	2

. It can be seen that DMSOS exhibits the best overall performance, although its running time is longer than that of the other algorithms. Given that, in blasting engineering, even minor prediction errors can lead to structural damage or subsequent legal disputes, this additional computational cost is acceptable from the perspective of engineering safety and reliability. The final optimization results of the DMSOS algorithm are listed in

Table 8. Final optimization results for features and hyperparameters.

Optimization Objective	Synchronized Optimization Results
Hyperparameters	max_depth	min_child_weight	num_boost_round	eta	gamma
	4	1	356	0.08167	0
Features	A, H, R, Q, CPH, HD, FSA

.

3.4. Performance Comparison

Different model construction strategies are compared to quantify the effects of feature selection and hyperparameter tuning in engineering practice. Specifically, AFDH-XGBoost: all features with default hyperparameters. PFDH-XGBoost: a preliminary feature subset with default hyperparameters. PFOH-XGBoost: a preliminary feature subset with individually optimized hyperparameters. DHOF-XGBoost: an optimally selected feature subset under fixed hyperparameters. DMSOS-XGBoost: the proposed approach that simultaneously optimizes both the feature subset and hyperparameters.

During the construction of the predictive model, the complete feature set includes 13 features described in Section 3.1, while the preliminary feature subset comprises the 10 features retained after preliminary feature selection in Section 3.2. The model’s training data utilizes the training set divided in Section 3.1, and the testing set is used to evaluate the predictive performance of different models. Based on previous research on the XGBoost algorithm, the five main hyperparameters of the predictive model are set by default as follows: max_depth is 6, min_child_weight is 1, num_boost_round is 100, eta is 0.3, and gamma is 0 [45,48]. The DMSOS algorithm is adjusted to achieve either individual optimization of hyperparameters or features. For only optimizing hyperparameters, the feature dimensions within the decision vector are fixed, allowing the hyperparameter dimensions to optimize the hyperparameters. For only optimizing features, the hyperparameter dimensions are fixed while only the features are optimized. The parameter settings of the individual optimization process remained consistent with the DMSOS algorithm described in Section 3.3. Each optimization method was executed five times to obtain the best fitness results, and the optimized hyperparameters or feature subset were determined by the corresponding decision vector. The results of the individual optimizations are presented in

Table 9. Results of hyperparameters optimization and features optimization.

Strategy	Objective	Independent Optimization Results
Fixed features	Hyperpara-meters	max_depth	min_child_weight	num_boost_round	eta	gamma
		4	1	572	0.06605	0
Fixed Hyper-parameters	Features	H, R, Q, HS, RD

, and the results of the simultaneous optimization of the feature set and hyperparameters are reported in Table 8.

The performance of the five prediction models is summarized in

Table 10. Performance comparison of different prediction models.

Evaluation Index	RMSE		r2
	Training Set	Test Set	Training Set	Test Set
AFDH-XGBoost	0.00397	0.03138	0.99920	0.95316
PFDH-XGBoost	0.00397	0.03138	0.99920	0.95316
PFOH-XGBoost	0.00887	0.02814	0.99599	0.96233
DHOF-XGBoost	0.00390	0.03090	0.99922	0.95458
DMSOS- XGBoost	0.01239	0.02636	0.99218	0.96696

Note: Boldface indicates the best performance in each metric.

. Although the DHOF-XGBoost model exhibits excellent performance on the training set, showing the lowest RMSE and highest r² value, its performance is not the best on the test set. The evaluation indices of AFDH-XGBoost and PFDH-XGBoost are identical, which may be attributed to the inherent feature selection capability of the XGBoost algorithm, indicating that the excluded features have no significant impact on model performance. This also demonstrates that preliminary feature selection effectively removes redundant features. On the test set, both PFOH-XGBoost and DHOF-XGBoost outperform PFDH-XGBoost, suggesting that both hyperparameter optimization and feature optimization play positive roles in model construction. Further comparison shows that PFOH-XGBoost’s predictive performance surpasses that of DHOF-XGBoost, which indicates that in this study, individual optimization of hyperparameters yields greater benefits than optimizing the feature set alone. Figure 13 presents a bar graph of the evaluation indices for each model on both the training and testing datasets. AFDH-XGBoost, PFDH-XGBoost and DHOF-XGBoost all achieve low training RMSE and high training r², but their generalization performance degrades more noticeably on the test set. PFOH-XGBoost partially alleviates this gap, while DMSOS-XGBoost not only attains the lowest RMSE and highest r² on the test set, but also shows the smallest discrepancy between training and testing metrics, indicating a more balanced trade-off between bias and variance. It is worth noting that DMSOS-XGBoost does not obtain the smallest error on the training set. Because its fitness function is defined as the average RMSE over 5-fold cross-validation rather than the in-sample error of a single fitted model. This design, together with the simultaneous optimization of features and hyperparameters, implicitly penalizes over complex configurations that overfit individual folds and favors solutions with stable performance across folds. As a result, DMSOS-XGBoost achieves slightly higher training error but better generalization on the test set, indicating that the improvement is driven by enhanced robustness rather than random fluctuations.

Figure 14 illustrates the sample-wise prediction errors for the first 40 samples in the test set, providing a detailed view of prediction deviations that complement the aggregate evaluation indices in Figure 13. It further demonstrates that the DMSOS-XGBoost model aligns more closely with the actual values and exhibits smaller errors. Overall, for the practical application considered in this study, the performance of each predictive model is ranked from highest to lowest as follows: DMSOS-XGBoost, PFOH-XGBoost, DHOF-XGBoost, PFDH-XGBoost, AFDH-XGBoost.

4. Feature Importance Analysis

Based on the preceding analysis, distinct performance differences have emerged among the models. To explain the differences, it is crucial to investigate how each model utilizes input features to make predictions. Although tree-based global explanation provides the overall impact of features, it lacks the contribution of particular features to individual predictions. To address this limitation, this study employs the SHapley Additive exPlanations (SHAP) method to interpret each predictive model. SHAP is an innovative explanation method that directly measures local feature interaction effects and offers a comprehensive understanding of the global model structure by aggregating local explanations of each prediction [49].

Figure 15 presents the global SHAP-based feature importance for all models. In the first three predictive models (AFDH-XGBoost, PFDH-XGBoost and PFOH-XGBoost), seven features make significant contributions, with the D, Q, and H consistently ranked among the most influential variables. This pattern is consistent with classical vibration attenuation theory, in which the geometric spreading of waves and the input explosive energy jointly control the PPV level. In contrast, in the DHOF-XGBoost and DMSOS-XGBoost models, the number of strongly contributing features is reduced to five, indicating that redundant or weakly informative variables have been largely eliminated and that the prediction relies on a smaller set of physically meaningful features. The global importance patterns of AFDH-XGBoost and PFDH-XGBoost are also very similar, explaining their comparable predictive performance and suggesting that the preliminary feature selection step does not change the dominant physical controls on vibration. Across all models, feature Q is always identified as highly important, which is physically reasonable because the explosive charge directly determines the input energy of the blast and thus the overall vibration amplitude. In contrast, the DMSOS-XGBoost model not only captures the energy input and geometric attenuation, but also particularly highlights the critical contribution of feature A to the prediction outcomes, which indicates that the model successfully captures the elevation amplification effect in blasting vibration propagation. By assigning higher importance to A, DMSOS-XGBoost captures these site-specific propagation and amplification effects more clearly than the other models.

As shown in Figure 16a, a local analysis was performed on the 24th sample point in Figure 14 to explore the causes of significant prediction errors in a single forecast. These errors represent localized residuals from a minority of samples, and their impact on the overall fitting quality is not significant. As shown in Figure 16b–f, the contributions of features in the local explanation waterfall plots for the AFDH-XGBoost and PFDH-XGBoost models were consistent, leading to the same prediction value. In this particular prediction sample, spatial geometry features D, H, and R, along with the explosive charge feature Q, made significant positive contributions, resulting in a prediction value higher than the actual value. Similarly, in the DHOF-XGBoost model, contributions from all features were also positive, which resulted in significant prediction errors. In the PFOH-XGBoost and DMSOS-XGBoost models, features Q and CPH from the explosive charge feature group had negative contributions to the prediction results, which offset part of the positive contributions from the spatial geometry feature group, thus bringing the prediction closer to the actual value.

In summary, spatial geometric relationships and the explosive charge are key factors in vibration control. In engineering construction, to ensure the safety of structures near blasting sources, safe distances must be strictly maintained. For immovable structures, appropriate adjustment of the explosive charge can be employed to minimize potential impacts on these structures and the surrounding environment. Additionally, particular attention should be paid to protecting structures in high-altitude areas, as these regions may experience more intense vibration effects, thereby increasing safety risks during construction.

5. Discussion

Although the proposed hybrid framework has been successfully validated and practically applied in an engineering project, several limitations remain. These limitations also highlight potential directions for future research.

Despite achieving the best overall performance, DMSOS requires a higher computational budget due to repeated fitness evaluations throughout the search process. Each evaluation requires training an XGBoost model under cross-validation, which dominates the overall runtime. By comparison, the additional operations introduced by DMSOS, such as the discretization process and the adaptive mutation mechanism, are lightweight relative to model training. Therefore, the total runtime is mainly governed by the ecosystem size, the maximum number of iterations, and the number of cross-validation folds. From an engineering standpoint, this extra cost is acceptable because improved predictive accuracy helps reduce the risk of blasting vibration, which could otherwise lead to structural damage or subsequent disputes. In practice, the computational burden can be alleviated through several strategies, such as reducing the number of cross-validation folds, employing early stopping rules when rapid decisions are needed, or leveraging parallel computing. These approaches offer flexible trade-offs between computational efficiency and solution quality.

The sensitivity of parameter settings requires further investigation. Both the preliminary feature selection and the DMSOS algorithm involve several parameter settings, such as the correlation threshold for the filtering process, the adaptive mutation probability strategy, and the bounds of the hyperparameter search space. In this study, these settings were mainly determined through preliminary trials or empirical selection, without a comprehensive parameter sensitivity analysis. Therefore, the impact of different parameter configurations on the feature and hyperparameter optimization results has not been quantified. Future research will involve a comprehensive sensitivity analysis and explore adaptive control strategies for DMSOS, thereby reducing the dependence on manual parameter tuning.

Comparative analysis with other algorithms and evaluation on multiple datasets would better demonstrate the overall performance of the proposed method. The primary objective of this study was to improve the original SOS algorithm, enabling it to simultaneously optimize features and model hyperparameters, thereby providing more reliable guidance for field construction, and offering a reference for improving other algorithms facing simultaneous optimization challenges. However, while DMSOS shows improvements over the original SOS and other sequential modeling approaches, its performance relative to other optimization algorithms remains to be fully verified. Furthermore, validation relied on measurement data from a single engineering project with limited feature diversity. Future work should include systematic testing on datasets with varying dimensionalities and noise characteristics, along with statistical comparisons between DMSOS and other optimization algorithms.

Further validation is needed regarding the generalizability of the engineering applications. Although validated with blasting vibration data, whether the identified optimal parameters and selected features can be generalized to other mining regions remains to be verified. Subsequent work will extend the application to multiple mining areas, varying operational conditions, and other geotechnical engineering problems to evaluate its broader applicability.

In summary, this study reduced data dimensionality through preliminary feature selection and simultaneously addressed the interdependency between features and hyperparameters in complex engineering modeling. These efforts effectively enhanced the performance of the predictive model. Future research focusing on parameter sensitivity, computational efficiency, and generalizability across different scenarios will further enhance the reliability and applicability of the proposed hybrid framework in diverse engineering contexts.

6. Conclusions

This study addresses the problem of high-dimensional data complexity and hyperparameter interdependence in engineering modeling. By integrating a preliminary feature selection stage with a discrete optimization scheme, a unified framework is constructed to improve predictive performance in blast vibration prediction and related engineering problems.

(1)

A preliminary feature selection method based on prior knowledge and statistical analysis is introduced. By constructing a mathematical model within the constraints of engineering theory, redundant features that are highly correlated with other features and weakly correlated with the target output are effectively identified and eliminated. In processing blast vibration data, the method eliminates three redundant features, which reduces the dimensionality of the input space and lowers the computational cost of subsequent model training without sacrificing the dominant physical information.

(2)

Discrete symbiotic organisms search algorithm with adaptive feature mutation (DMSOS) is developed to simultaneously optimize the input features and hyperparameters of the XGBoost model. The DMSOS algorithm overcomes the limitation that SOS algorithms can only work in the continuous domain by designing a discretization process for feature and hyperparameter optimization and an adaptive mutation strategy based on iteration time and feature weights. These adaptations enable DMSOS to operate over mixed discrete and integer domains, enhance convergence behavior, and yield higher quality solutions.

(3)

In the application to blasting vibration prediction, the DMSOS-XGBoost model successfully identified the optimal feature subset and hyperparameters through the simultaneous optimization process. The model demonstrated superior performance, achieving an r² of 0.96696 and RMSE of 0.02636, surpassing other predictive models constructed using traditional sequential strategies. The feature importance analysis based on SHAP indicates that spatial geometric relationships and explosive charge parameters are the key factors for vibration control, providing interpretable guidance for construction safety in the field.