Migration Laws of Acidic Gas Overflow in High Temperature and High Pressure Gas Wells

Abstract

Most existing ultra-deep gas wells are characterized by high temperature, high pressure, and high sulfur content. During development, they face serious challenges such as unclear mechanisms of acid gas-induced blowouts and difficulties in wellbore pressure inversion, posing significant challenges to well control operations. To reveal the reasons behind the tendency of acidic gases to trigger blowouts and to clarify the impact of different concentrations of acidic gases on the flow behavior of annular fluids, this study considers the effects of solubility and phase changes on the physical properties of acidic gases. A method replacing critical parameters with pseudo-critical parameters is used to analyze the variation trends of gas density, solubility, and other properties along the well depth. A mathematical model for the annular flow of acidic gas overflow incorporating solubility phase change effects is established. The model is numerically solved using a four-point difference scheme, exploring the essential characteristics of gas flow in the annulus after overflow, and discussing the distribution patterns of physical properties of acidic gases, as well as dynamic parameters such as wellbore pressure and temperature along the well depth. Numerical simulations show that the physical properties of acidic gases change significantly with well depth: the more acidic gas present in the wellbore, the smaller the deviation factor, and the greater the density and viscosity, with parameter changes exceeding 40% near the pseudo-critical point for binary mixtures with 40% H₂S. Compared to pure methane, mixed fluids containing acidic gas experience more than 20% volume expansion near the wellhead for ternary mixtures with 20% CO₂ and 20% H₂S, and the flow velocity increases by more than 10% for mixtures with ≥30% acidic gas content, leading to a higher risk of a sudden pressure drop during well control. This study clarifies the migration patterns of acidic gas overflow in HPHT (high pressure, high temperature) gas wells, providing valuable guidance for optimizing well control design, improving well control emergency plans, and developing well-killing measures.

1. Introduction

The deep to ultra-deep conventional gas resources in major basins of PetroChina amount to 20 trillion cubic meters, indicating enormous exploration potential [1,2]. However, with increasing well depths, high-temperature, high-pressure, and high-sulfur conditions pose significant challenges to well control safety [3,4].

Table 1. Acid gas deep well blowout statistics (H₂S and CO₂ content are reported in g/m³ at standard conditions (1 atm, 20 °C)).

Well Number.	Time	Depth (m)	Formation	Ejected Medium	H2S Content (g/m3)	CO2 Content (g/m3)	Casualties (People)
Luojia 16H	December 2003	4050	Feixianguan Formation	Gas	151.0	--	243
Tazhong823	December 2005	5550	Ordovician	Oil and Gas	22.0	--	--
Luojia 2	March- 2006	3404	Feixianguan Formation	Gas	125.5	106.88	--
Zhonggu70	March- 2018	7413	Yingshan Formation	Oil and Gas	4000	--	--
Tazhong 726-2X	December 2018	5594	Ordovician	Gas	500–4800	--	--

presents statistical data on blowouts caused by acidic gas influx [5], revealing that once gas invasion occurs in natural gas containing acidic components, there is a high probability of severe accidents [6,7,8]. Therefore, it is imperative to investigate the migration mechanisms of acidic gas under high-temperature and high-pressure conditions in ultra-deep wells [9], ensuring the safe and efficient development of acidic gas reservoirs [10,11].

Today, researchers both domestically and internationally have conducted extensive studies on wellbore gas kicks and gas pollution [12,13,14].

In 2012, ref. [15] considered the unique physical properties of high-sulfur gases and potential phase changes occurring in the wellbore, developing a mathematical model for wellbore flow and heat transfer during high-sulfur gas overflow. They coupled temperature, pressure, and physical property parameters of high-sulfur gases, and proposed a solution method. The study analyzed the wellbore pressure and gas properties during the ascent of gases with different H₂S contents, concluding that high-sulfur gases can easily lead to well control issues. In 2016, ref. [16] developed a temperature field model for CO₂ in the wellbore and fractures to calculate the phase change of fluid and variations in thermophysical parameters during fracturing. The study analyzed the location of CO₂ phase transitions from liquid to supercritical state, finding that the transition point shifted from inside the wellbore toward the fractures. In 2017, ref. [17] established a multiphase flow analysis model for wellbore considering factors such as wellbore temperature, fluid compressibility, annulus pressure loss, throttling pipeline friction loss, and gas slippage in order to determine the optimal casing depth and select the appropriate casing grade. Neglecting the effects of wellbore temperature and fluid compressibility and designing casing based on a single bubble model is unreliable, and in offshore oil wells, the frictional loss of throttling pipelines is an important factor that should be considered in casing design. In 2019, ref. [18] considered the effect of solubility on gas migration and established a semi analytical model of annular air invasion based on a drift model. For two scenarios of single bubble migration and constant gas invasion rate, gas invasion behavior was simulated in water-based drilling fluid and oil-based drilling fluid, respectively. Mud pit increment and wellhead pressure were determined to be two key indicators for gas invasion detection. Ref. [19] performed extensive experiments using detailed data on gas and brine compositions in the Sarawak Basin, Malaysia. He estimated the initial CO₂ solubility in brine reservoirs at 423.15 K and 36.0 MPa in the Sarawak Basin. In 2019, ref. [20] conducted a quantitative analysis of the dissolution process of H₂S in NaCl solution, using normalized Raman peak intensities (peak area ratios and peak height ratios) to quantify the solubility of H₂S in the solution.

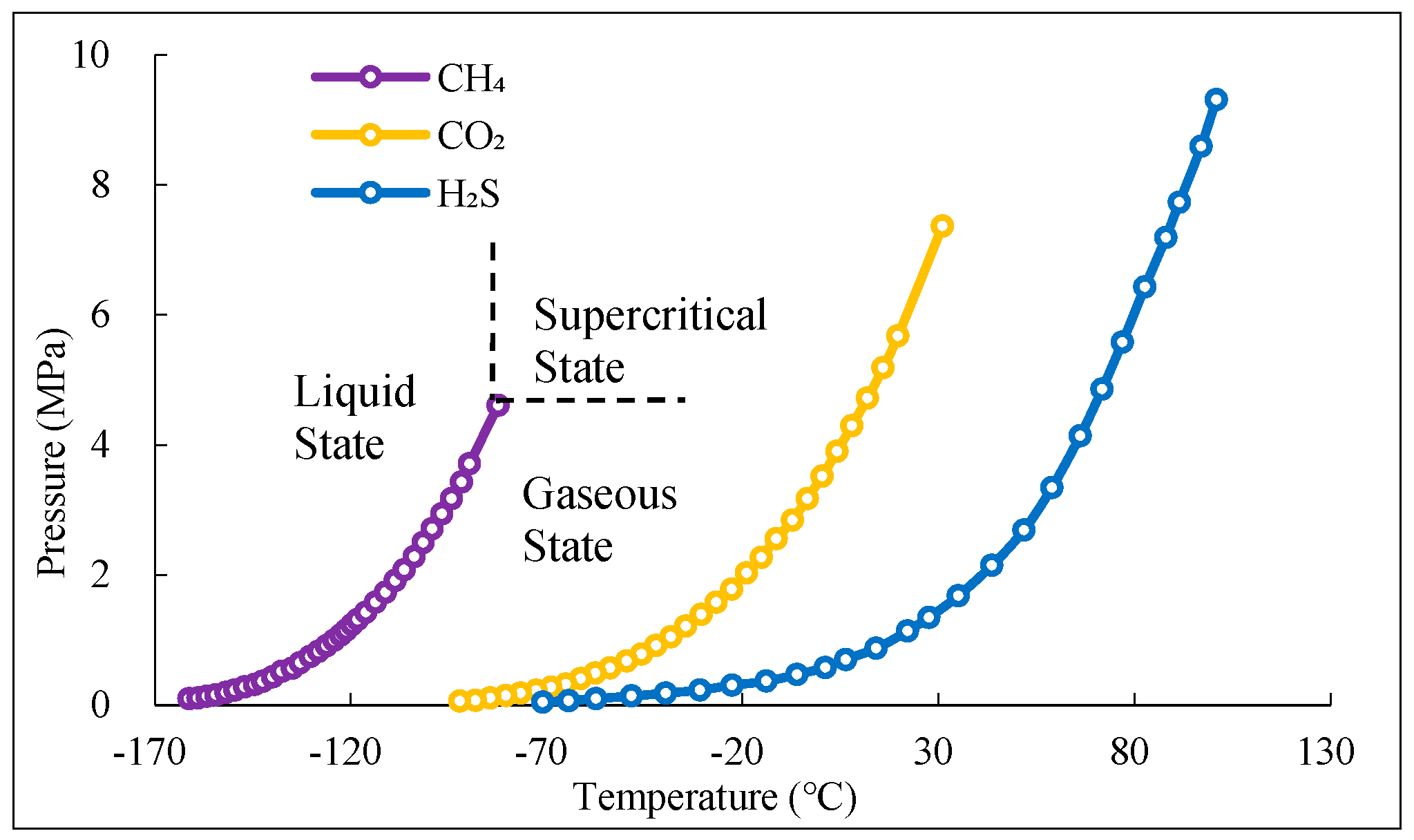
It is evident that experimental investigations on supercritical acidic gases have primarily focused on CH₄, CO₂, and their mixtures. However, due to the high toxicity of H₂S, experimental studies on supercritical H₂S and CO₂–H₂S mixtures are relatively limited. Given the challenges of conducting experiments with H₂S, simulation and numerical modeling methods are commonly used. Moreover, most existing work focuses on how acidic gases and their mixtures dissolve in water-based systems. In contrast, there is limited understanding of how these gases—especially hydrogen sulfide (H₂S)—behave in organic solvents.

In the study of annular multiphase flow, extensive efforts have been made to explore its characteristics and underlying mechanisms [21,22].

In 2017, Na [23] coupled wellbore temperature, pressure, and hydrate dissociation effects to establish a dynamic model for wellbore temperature, pressure, multiphase flow, and hydrate mass transfer during offshore natural gas hydrate drilling. In 2017, ref. [24] introduced a new method to measure pressure drop and liquid hold-up to improve the closure relationships of the MAST multiphase flow simulator, which had been validated using a series of laboratory and field data collected by TEA Sistemi. In 2018, ref. [25] found that gas diffusion in the annulus is the main parameter affecting the peak pressure of the casing. Considering the two extreme cases of single bubbles and dispersed bubbles rising along the annulus, ignoring the influence of annulus friction, casing pressure calculation models were established separately. The study found that under the same conditions, there is a significant difference in the casing pressure calculated by the two models, especially for situations where the bottomhole pressure is low. Karami and Akbari used commercial OLGA software to simulate the development law of gas invasion, and found that gas diffusion was most significant at low cycle displacements; When the circulation displacement is high, the time for gas invasion to reach the wellhead is the fastest. Ref. [26] proposed a multiphase flow model for real-time calculations used in managed pressure drilling (MPD) control, considering gas solubility in the drilling fluid. The model accounts for the real-time adjustment of wellhead pressure and its impact on gas migration and phase changes. In 2020, ref. [27] noted that existing two-phase flow models for the annulus rarely consider the effects of liquid viscosity, leading to poor predictions. The study examined the impact of liquid viscosity on two-phase flow regimes in vertical pipes and proposed two flow regime transitions: bubble flow (BL) and dispersed bubble flow (DB) for different bubble sizes. In 2019, ref. [28] considered the compressibility and rheology of drilling fluids and established a transient compressible isothermal mathematical model to predict the mud pit increment and wellbore pressure transfer during gas invasion. Research has shown that the greater the compressibility of the fluid, the greater the difference between the increment of the mud pit and the volume of gas invasion. The rheological properties of the drilling fluid greatly affect gas invasion detection and pressure transmission. Ref. [29] used CFD software to simulate gravity-driven gas–liquid two-phase flow and analyzed the variation in gravity displacement rates within fractures under two boundary conditions. Additionally, they developed a simplified model for gravity displacement in dual-boundary fractures, based on gas–liquid two-phase flow theory.

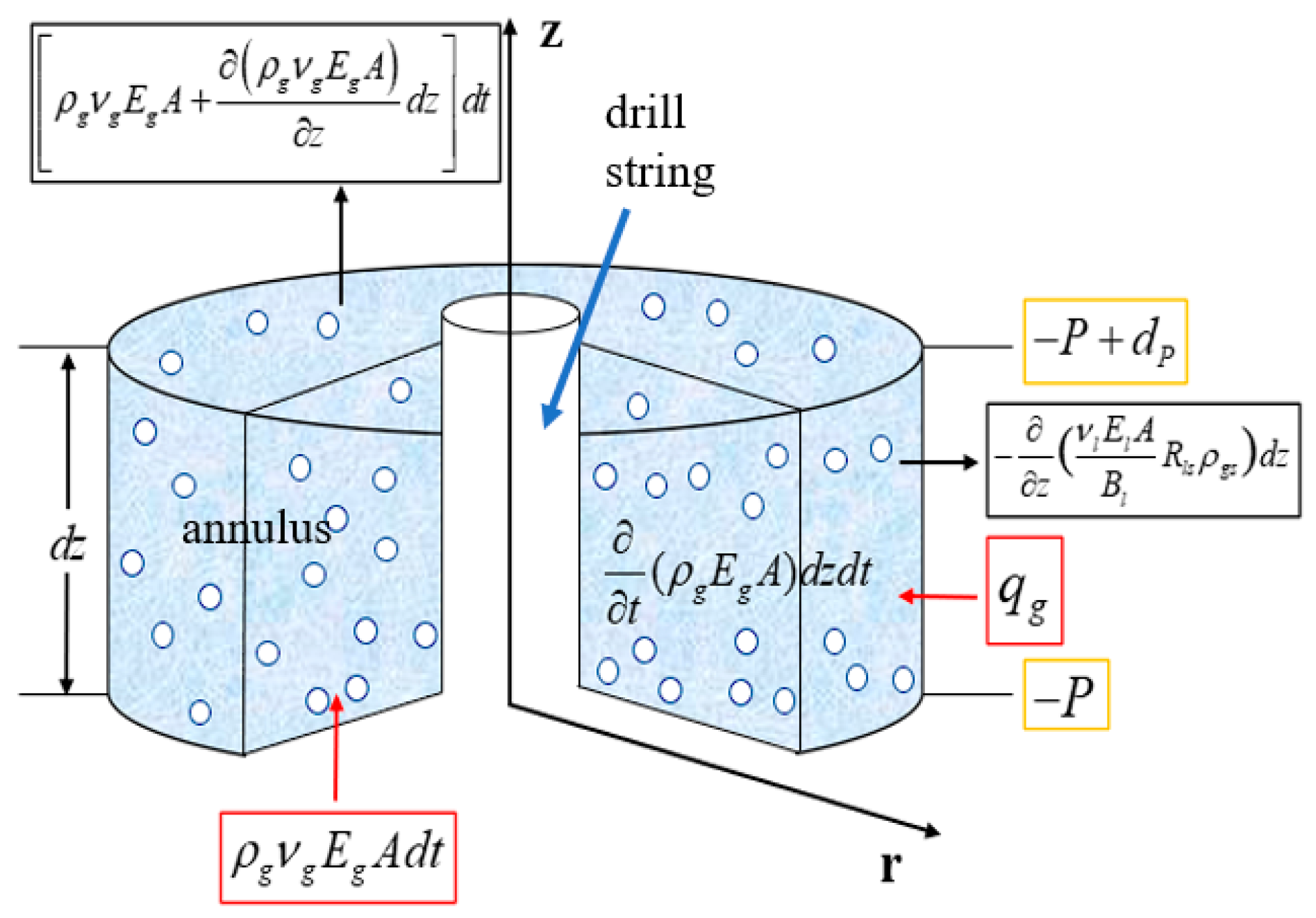
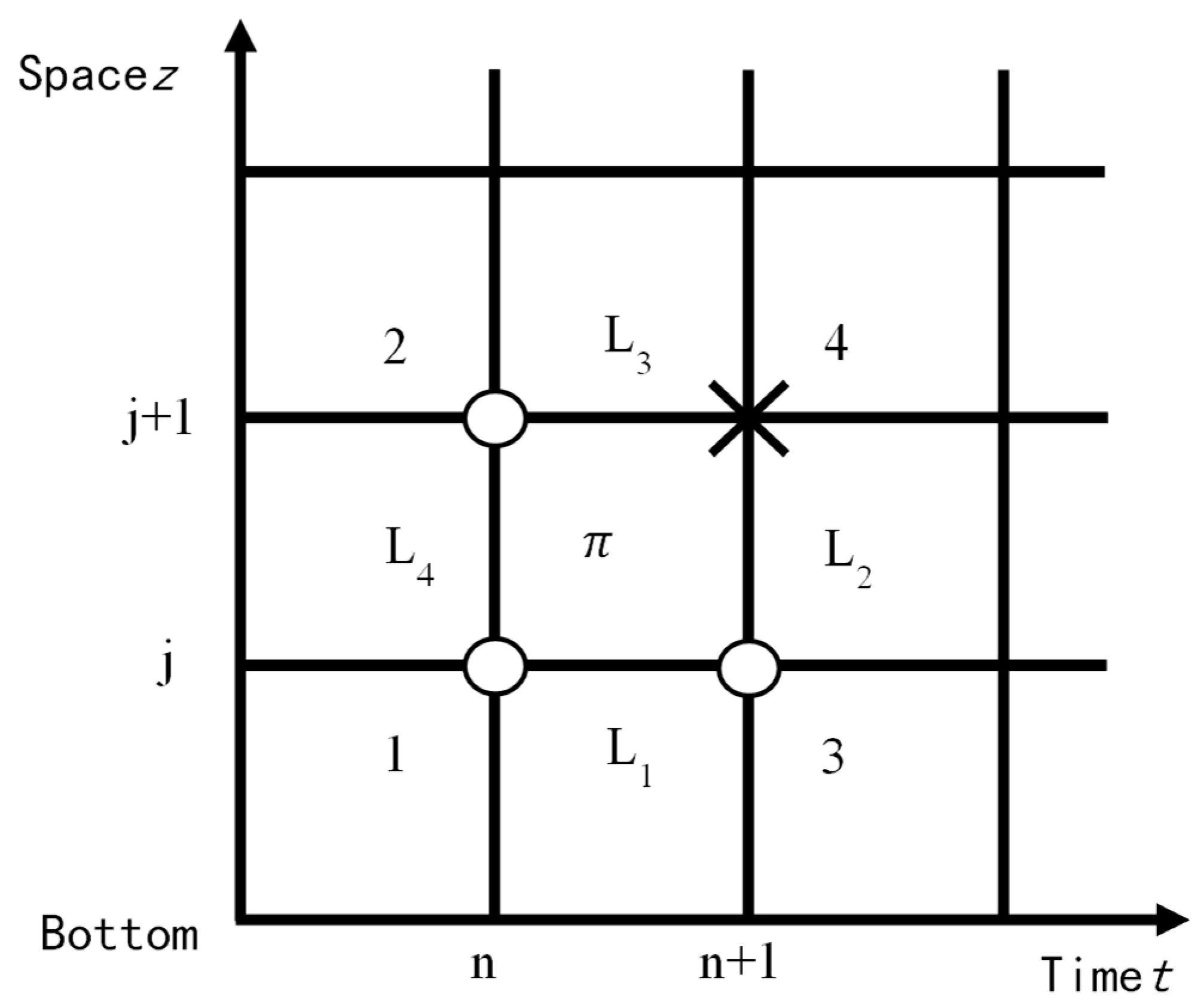
It is evident that studies on annular multiphase flow have primarily relied on simulation and numerical modeling, with a strong emphasis on single-component systems. However, most of these studies do not consider the effects of H₂S invasion and the solubility of acidic gases in drilling fluids on transient multiphase flow in the annulus. A few studies analyze the impact of acidic gases by considering their phase behavior, but the fundamental causes are not discussed. This paper establishes a flow model based on the solubility of acidic gases and critical parameters, solving it using a four-point difference scheme. The model reveals the expansion and flow velocity variation in acidic gases at the wellhead and quantifies the significant impact of H₂S on well control, providing theoretical support for the safety of well control in ultra-deep wells.

2. Fundamental Physical Property Analysis

2.1. Properties of Supercritical Fluids

Figure 1 presents the temperature-pressure phase diagram for pure gases. In addition to the conventional liquid and gas regions, a supercritical fluid region is also observed. The three lines in the figure represent the gas–liquid equilibrium lines for CH₄, CO₂, and H₂S, respectively. The endpoint of each line indicates the critical point of the corresponding substance. When the temperature and pressure of a substance exceed its critical temperature and critical pressure, the substance is in a supercritical state. Fluids in this state are referred to as supercritical fluids.

A comparison of the properties of the three gases in

Table 2. Compares the characteristics of different state bodies.

Fluid Types	Density (kg/m3)	Viscosity (Pa·s)	Diffusion Coefficient (m2/s)	Thermal Conductivity (W/m·k)
Gas	1	1~3 × 10−5	5~200 × 10−6	5~30 × 10−3
Supercritical fluid	200~700	2~10 × 10−4	0.01~1 × 10−6	30~70 × 10−3
Liquid	1000	1~10 × 10−2	0.4~3 × 10−9	70~250 × 10−3

reveals that the density, viscosity, diffusion coefficient, and thermal conductivity of supercritical fluids lie between those of gaseous and liquid fluids. The density of supercritical fluids is similar to that of liquid fluids, while their viscosity is similar to that of gaseous fluids.

2.2. Pseudo-Critical Point

The pseudo-critical properties of gas mixtures with known components are determined using the calculation method proposed by [30] coefficient formula is applied for correction. The pseudo-critical parameters for gases with different components, as calculated, are shown in

Table 3. Quasi-critical parameters of gas mixtures of different components.

Gas Composition		Pseudo-Critical Temperature (°C)	Pseudo-Critical Pressure (MPa)
Binary Mixture	$50\%{\mathrm{CH}}_4+50\%{\mathrm{H}}_2\mathrm{S}$	−15.47	2.14
	$70\%{\mathrm{CH}}_4+30\%{\mathrm{H}}_2\mathrm{S}$	−51.16	2.90
	$90\%{\mathrm{CH}}_4+10\%{\mathrm{H}}_2\mathrm{S}$	−78.56	4.66
	$50\%{\mathrm{CH}}_4+50\%{\mathrm{CO}}_2$	−44.84	5.51
	$70\%{\mathrm{CH}}_4+30\%{\mathrm{CO}}_2$	−67.51	4.96
	$90\%{\mathrm{CH}}_4+10\%{\mathrm{CO}}_2$	−82.87	4.59
Ternary Mixture	$70{\%\mathrm{CH}}_4+20\%{\mathrm{H}}_2\mathrm{S}+10\%{\mathrm{CO}}_2$	−57.32	5.12
	$70{\%\mathrm{CH}}_4+15\%{\mathrm{H}}_2\mathrm{S}+15\%{\mathrm{CO}}_2$	−60.31	5.08
	$70{\%\mathrm{CH}}_4+10\%{\mathrm{H}}_2\mathrm{S}+20\%{\mathrm{CO}}_2$	−63.19	5.01

. It can be observed that the pseudo-critical points of mixed acidic gases with varying H₂S and CO₂ content differ significantly, and the difference decreases with an increase in CH₄ content.

2.3. Solubility of Acidic Gases

The variation in solubility with well depth is shown in Figure 2.

The drilling fluid formula used in the calculation is: 4% bentonite + (0.2–0.3%) zwitterionic polymer strong encapsulator + (2–4%) sulfonated phenolic resin + (2–4%) lignite resin + (0.4–0.6%) sodium hydroxide + (3–5%) sulfonated tannin + (0.3–0.5%) sodium carbonate + (1–2%) sulfonated asphalt + (20–25%) sodium chloride + (0.2–0.4%) polyanionic cellulose.

As shown in the figure, under the same wellbore temperature and pressure conditions, the solubility of CH₄ is significantly lower than that of CO₂ and H₂S, indicating that CH₄ is almost insoluble in water. Therefore, the effect of CH₄ solubility is neglected when developing the flow model.

3. Acidic Gas Annular Flow Model

An annular flow model for acidic gases is established by considering gas solubility. The basic assumptions of the model are as follows [31]:

(1)

The fluid flow in the annulus is one-dimensional and continuous.

(2)

The inner wall of the annulus is rigid, and complex situations such as abnormal high pressure, lost circulation, and wellbore collapse are not considered.

(3)

The fluid invading the wellbore from the formation is gas, with formation water and oil invasion neglected.

(4)

Fluids in the annulus do not react with each other; only physical changes occur, with no chemical reactions.

(5)

Neglecting heat changes caused by fluid phase transitions and neglecting the effects of other heat sources.

(6)

Differences between acidic natural gas mixtures released by drilling fluids and those generated by the reservoir are neglected.

3.1. Mass and Momentum Conservation Equations

The solubility is calculated using the equation of state method proposed by [32,33].

$$\ln m_i=\ln y_{i}P-{\displaystyle \frac{{\mu }_i^{l\left(0\right)}\left(T,P\right)-{\mu }_i^{v\left(0\right)}\left(T\right)}{RT}}+\ln {\phi }_i\left(T,P,y\right)-\ln {\gamma }_i\left(T,P,m\right)$$

(1)

where $m_i$ is the molar concentration of gas i in the liquid phase, $\mathrm{mol}/\mathrm{kg}$; $y_i$ is the mole fraction of gas i in the gas phase, dimensionless; P is the absolute pressure, MPa; T is the absolute temperature, K; ${\mu }_i^{l\left(0\right)}$ is the chemical potential of gas i in the liquid phase; ${\mu }_i^{v\left(0\right)}$ is the chemical potential of gas i in the gas phase; R is the molar gas constant, with a value of $0.08314467\mathrm{bar}\cdot 1/\mathrm{mol}\cdot K$; ${\phi }_i$ is the fugacity coefficient, dimensionless; ${\gamma }_i$ is the activity coefficient, dimensionless.

A physical model, as shown in Figure 3, is established. Taking the upward flow direction in the annulus as the positive direction, a differential segment dz is analyzed, with a cross-sectional area of A.

According to the law of mass conservation: Influx Gas + Formation-Generated Gas + Gas Released from Drilling Fluid—Outflow Gas = Total Change. The terms are detailed in

Table 4. Mass components of dz cell.

Gas Mass Inflow at the Lower Surface	${\rho }_g{v}_g{E}_{g}Adt$
Gas Mass Generated by Formation within the Differential Element	$q_{g}dzdt$
Gas Mass Released from Drilling Fluid within the Differential Element	$\left[-{\displaystyle \frac{\partial }{\partial z}}\left({\displaystyle \frac{v_l{E}_{l}Adt}{B_l}}{R}_{ls}{\rho }_{gs}\right)dz\right]dt$
Free Gas Mass Outflow at the Upper Surface	$\left[{\rho }_g{v}_g{E}_{g}A+{\displaystyle \frac{\partial \left({\rho }_g{v}_g{E}_{g}A\right)}{\partial z}}dz\right]dt$
Total Change within the Differential Element	${\displaystyle \frac{\partial \left({\rho }_g{E}_{g}A\right)}{\partial t}}dzdt$

Where A is the cross-sectional area of the annulus, m²; ${\rho }_g$ is the density of free gas, $\mathrm{kg}/{\mathrm{m}}^3$; $v_g$ is the upward velocity of free gas, $\mathrm{m}/\mathrm{s}$; $E_g$ is the volume fraction of free gas, dimensionless; $q_g$ is the mass of gas generated by the reservoir per unit depth per unit time, $\mathrm{kg}/\left(\mathrm{m}\cdot \mathrm{s}\right)$; $v_l$ is the upward velocity of the liquid phase, $\mathrm{m}/\mathrm{s}$; $E_l$ is the volume fraction of the liquid phase, dimensionless; $R_{ls}$ is the solubility of gas in the drilling fluid, ${\mathrm{m}}^3/{\mathrm{m}}^3$; ${\rho }_{gs}$ is the density of gas under standard conditions, $\mathrm{kg}/{\mathrm{m}}^3$.

.

The continuity equation for the mixed acidic gas is:

$${\displaystyle \frac{\partial }{\partial t}}({\rho }_g{E}_{g}A)+{\displaystyle \frac{\partial }{\partial z}}({\rho }_g{\nu }_g{E}_{g}A+{\displaystyle \frac{{\nu }_l{E}_{l}A}{B_l}}{R}_{ls}{\rho }_{gs})=q_g$$

(2)

Similarly, the continuity equation for the liquid phase is:

$${\displaystyle \frac{\partial }{\partial t}}({\rho }_l{E}_{l}A)+{\displaystyle \frac{\partial }{\partial z}}({\rho }_l{\nu }_l{E}_{l}A-{\displaystyle \frac{{\nu }_l{E}_{l}A}{B_l}}{R}_{ls}{\rho }_{gs})=0$$

(3)

where ${\rho }_l$ is the density of the liquid phase, $\mathrm{kg}/{\mathrm{m}}^3$.

According to the law of momentum conservation, the combined effects of fluid weight, acceleration, viscous friction between the fluid and the wellbore wall, and momentum exchange between the mixed acidic gas and the drilling fluid within the differential element are balanced, yielding the total momentum equation:

$$\begin{array}{l}{\displaystyle \frac{\partial }{\partial t}}({\rho }_l{\nu }_l{E}_{l}A+{\rho }_g{\nu }_g{E}_{g}A)+{\displaystyle \frac{\partial }{\partial z}}({\rho }_l{\nu }_l^2{E}_{l}A+{\rho }_g{\nu }_g^2{E}_{g}A)\\ +Ag\left({\rho }_l{E}_l+{\rho }_g{E}_g\right)+{\displaystyle \frac{d\left(AP\right)}{dz}}+{\displaystyle \frac{d\left(AFr\right)}{dz}}=0\end{array}$$

(4)

where F_r is the annular frictional pressure drop, MPa.

3.2. Auxiliary Equations and Boundary Conditions

(1) Drift Flux Model Physical Equation:

$${\nu }_g=C_0\left[{\nu }_g{E}_g+{\nu }_l(1-E_g)\right]+{\nu }_{rg}$$

(5)

where C₀ the gas distribution coefficient, dimensionless; v_rg is the gas-phase drift velocity, m/s.

(2) Gas Phase Equation of State:

$${\rho }_g=3486.6{\displaystyle \frac{P{\rho }_{\mathrm{gs}}}{Z\left(T+273\right)}}$$

(6)

In this equation, Z is the compressibility factor, dimensionless.

(3) Flow Pattern Identification and Friction Calculation:

The flow pattern identification and friction calculation formulas used in this study are shown in

Table 5. Flow pattern discriminant and friction calculation formula.

Flow Pattern	Identification Criterion	Friction Calculation
Single-phase Flow	Influx gas completely dissolved	$Fr=32.4{\displaystyle \frac{f_0{\rho }_{l}L{Q}^2}{{\left(D-d\right)}^3{\left(D+d\right)}^2}}$
Bubble Flow	$\left\{\begin{array}{l}{v}_{sg}<0.429v_{sl}+0.357v_{0\infty }\\ v_{0\infty }=1.53{\left[g\left({\rho }_l-{\rho }_g\right)\sigma /{\rho }_l^2\right]}^{0.25}\end{array}\right.$	$Fr=2f_m{v}_m^2{\rho }_m/g_{c}d$
Slug Flow	$\left\{\begin{array}{l}{v}_{sg}\ge 0.429v_{sl}+0.357v_{0\infty }\\ {\rho }_g{v}_{sg}^2<25.4\log \left({\rho }_l{u}_{sl}^2\right)-38.9\begin{array}{cc}& \end{array}\left({\rho }_l{v}_{sl}^2\ge 74.4\right)\\ {\rho }_g{v}_{sg}^2<0.0051{\left({\rho }_l{u}_{sl}^2\right)}^{1.7}\begin{array}{cc}& \end{array}\left({\rho }_l{v}_{sl}^2<74.4\right)\end{array}\right.$	$Fr=2f_m{E}_l{v}_m^2{\rho }_m/g_{c}d$
Churn Flow	$\left\{\begin{array}{l}{v}_{sg}<3.1{\left[\sigma g\left({\rho }_l-{\rho }_g\right)/{\rho }_g^2\right]}^{0.25}\\ {\rho }_g{v}_{sg}^2>25.4\log \left({\rho }_l{v}_{sl}^2\right)-38.9\begin{array}{cc}& \end{array}\left({\rho }_l{v}_{sl}^2>74.4\right)\\ {\rho }_g{v}_{sg}^2<0.0051{\left({\rho }_l{v}_{sl}^2\right)}^{1.7}\begin{array}{cc}& \end{array}\left({\rho }_l{v}_{sl}^2<74.4\right)\end{array}\right.$
Annular Flow	$v_{sg}>{\left[3.1\sigma g\left({\rho }_l-{\rho }_g\right)/{\rho }_g^2\right]}^{0.25}$	$Fr=2f_c{v}_g^2{\rho }_c/d$

Where $v_{sg}$ is the apparent velocity of the gas phase, m/s; $v_{sl}$ is the apparent velocity of the liquid phase, m/s; $v_{0\infty }$ is the bubble rise limit velocity, m/s; $\sigma$ is the gas–liquid surface tension, N/m.

. The specific derivation process and calculation of relevant parameters are introduced in the studies by [34,35].

(4) Acidic Natural Gas Compressibility Factor

The method used when the pressure is less than 35 MPa and greater than or equal to 35 MPa is shown in

Table 6. Calculation formula of compression coefficient of acid natural gas.

Pressure	The Calculation Formulas
$\mathrm{P}<35 \mathrm{MPa}$	$Z=1+\left(0.31506-{\displaystyle \frac{1.0467}{T_{pr}}}-{\displaystyle \frac{0.5783}{T_{pr}^2}}\right){\rho }_{pr}+(0.535-{\displaystyle \frac{0.6123}{T_{pr}}}){\rho }_{pr}^2+{\displaystyle \frac{0.6815{\rho }_{pr}^3}{T_{pr}^3}}$
	$\left\{\begin{array}{l}{\rho }_{pr}={\displaystyle \frac{0.27P_{pr}}{Z{T}_{pr}}}\\ T_{pr}={\displaystyle \frac{T}{T_c}}\\ P_{pr}={\displaystyle \frac{P}{P_c}}\end{array}\right.$
$\mathrm{P}\ge 35 \mathrm{MPa}$	$\left\{\begin{array}{l}Z={\displaystyle \frac{1+{\rho }_{pr}+{\rho }_{pr}^2-{\rho }_{pr}^3}{{\left(1-{\rho }_{pr}\right)}^3}}-(14.76t-9.76t^2+4.58t^3){\rho }_{pr}+(90.7t-242.2t^2+42.4t^3){\rho }_{pr}(1.18+2.82t)\\ Z={\displaystyle \frac{0.06125P_{pr}t\exp (-1.2{(1-t)}^2)}{{\rho }_{pr}}}\end{array}\right.$
	$t={\displaystyle \frac{1}{T_{pr}}}={\displaystyle \frac{T_{pc}}{T}}$

Where $T_c$ is the critical temperature of the gas, K; $P_c$ is the critical pressure of the gas, MPa; $T_{pr}$ is the pseudo-critical temperature of the gas, K; $P_{pr}$ is the pseudo-critical pressure of the gas, MPa; ${\rho }_{pr}$ is the pseudo-critical density of the gas, kg/m³.

.

3.3. Initial Conditions

The initial conditions refer to the fluid flow state and pressure distribution in the annulus at the initial moment. When there is no acidic gas invasion into the annulus at t = 0, the fluid in the annulus is a single-phase flow. The flow state and pressure distribution in the annulus at any given time are determined by the boundary conditions. The initial conditions and boundary conditions are shown in

Table 7. Initial and boundary conditions.

Initial Conditions	Boundary Conditions
$\left\{\begin{array}{l}{E}_{\mathrm{g}}\left(0,z\right)=0\\ {\nu }_{sg}\left(0,z\right)=0\\ {\nu }_{sl}\left(0,z\right)={\displaystyle \frac{Q_l}{A_j}}\\ {\rho }_l=const\\ P(0,z)=P(z)\end{array}\right.$	$\left\{\begin{array}{l}{E}_g\left(t,0\right)={\displaystyle \frac{Q_g\left(t,0\right)}{C_0\left(Q_l+Q_g\left(t,0\right)\right)+A{\nu }_{rg}}}\\ E_l\left(t,0\right)=1-E_g\left(t,0\right)\\ {\nu }_{sg}\left(t,0\right)={\displaystyle \frac{Q_g\left(t,0\right)}{A}}\\ {\nu }_{sl}\left(t,0\right)={\displaystyle \frac{Q_l}{A}}\\ P(t,N)=0\end{array}\right.$

Where P(t, N) is the pressure at the wellhead node, MPa.

.

4. Model Solution

4.1. Grid Division

The spatial domain is divided using a fixed-step grid division method. The step size and total number of spatial grids in the defined domain are given by:

$$\left\{\begin{array}{l}\Delta z=z_{j+1}-z_j\\ N=INT({\displaystyle \sum _j\frac{z}{\Delta z}})\end{array}\right.$$

(7)

where $j=1,2,3,\dots ,N$.

For the time domain, non-uniform step sizes can be used by dividing the spatial grid step size by the current grid fluid velocity. The step size for each time grid and the total number of time grids are given by:

$$\left\{\begin{array}{l}\Delta t={\displaystyle \frac{\Delta z}{\nu }}\\ N=INT({\displaystyle \sum _i\frac{t}{\Delta t}})\end{array}\right.$$

(8)

where $i=1,2,3,\dots ,N$.

4.2. Governing Equations for Model Solution

(1)

Single-Phase Gas Blowout Model

Considering a single bubble representation of gas in a riser, the pressure in the gas relates to the gas volume as:

$$p_g{\nu }_{\mathrm{g}}=M_g{c}_g^2(T)$$

(9)

where M_g is the gas mass and C_g(T) is the sound velocity of the gas, depending on temperature T.

Consider a control volume covering the gas bubble and an incompressible liquid column above. Setting the liquid velocity equal to the head of the gas bubble, we can employ a momentum balance the gas and liquid of the control volume to obtain:

$${\displaystyle \frac{\partial v_g}{\partial t}}\left(h_g{\rho }_l+{\displaystyle \frac{M_g}{A}}\right)=p_g-p_c-{\rho }_{l}g{h}_g-F_r{v}_g^2\left(h_g{\rho }_l+{\displaystyle \frac{M_g}{A}}\right)$$

(10)

where h_g is the distance of the bubble head to the top of the riser, m; P_g is the pressure in the gas bubble (assumed uniform), MPa; P_b is the applied back-pressure (equal to atmospheric when no riser gas handler is used), MPa; g is the acceleration of gravity, m/s².

Expressing the gas volume rate of change as the difference in velocity between the bubble head v_G and tail C_m we obtain the system of equations.

$${\displaystyle \frac{\partial v_g}{\partial t}}={\displaystyle \frac{p_g(V_{\mathrm{g}})-p_c-{\rho }_{l}g{h}_g}{h_g{\rho }_l+\frac{M_g}{A}}}-F_r{v}_g^2$$

(11)

$${\displaystyle \frac{\partial v_g}{\partial t}}=A(v_g-C_m)$$

(12)

$${\displaystyle \frac{\partial h_g}{\partial t}}=-v_g$$

(13)

And the closure relations:

$$p_g={\displaystyle \frac{M_g{c}_g^2(T)}{v_g}}$$

(14)

$$C_m={\displaystyle \frac{C_0{Q}_0}{A}}+v_{\infty }$$

(15)

where Q₀ is the flowrate into the bottom of the riser.

We note that the mode associated with the acceleration, Equation (9), would be expected to have a large eigenvalue (meaning it tends rapidly to its equilibrium) due to acceleration terms tending to be small is such a context. The consequence is that the system may become stiff, and some care must be taken in implementation. Immediate equilibrium could be imposed on (9) to avoid this, and without expecting significant loss of accuracy; however, we will avoid doing this as the resulting expression becomes quite involved.

Finally, using $h_{g0}=h_g+{\displaystyle \frac{v_g}{A}}$ to denote the position of the tail of the gas bubble, we can write the pressure at the BOP as:

$$p_{BOP}=p_g+(L-h_{g0}){\rho }_g\left(g+{\displaystyle \frac{F_r{Q}_0}{A}}\right)$$

(16)

(2)

The difference equation

Difference equation for the gas phase continuity equation:

$$\begin{array}{l}{\left(A{\rho }_g{E}_g{v}_g+{\displaystyle \frac{A{\rho }_{gs}{E}_g{v}_g{R}_{ls}}{B_g}}\right)}_{j+1}^{n+1}-{\left(A{\rho }_g{E}_g{v}_g+{\displaystyle \frac{A{\rho }_{gs}{E}_g{v}_g{R}_{ls}}{B_g}}\right)}_j^{n+1}\\ ={\displaystyle \frac{\Delta z}{2\Delta t}}\left[{\left(A{\rho }_g{E}_g\right)}_j^n+{\left(A{\rho }_g{E}_g\right)}_{j+1}^n-{\left(A{\rho }_g{E}_g\right)}_j^{n+1}-{\left(A{\rho }_g{E}_g\right)}_{j+1}^{n+1}\right]+{\displaystyle \frac{\Delta z}{2}}\left[{\left(q_g\right)}_j^{n+1}+{\left(q_g\right)}_{j+1}^{n+1}\right]\end{array}$$

(17)

Difference equation for the liquid phase continuity equation:

$$\begin{array}{l}{\left(A{\rho }_l{E}_l{v}_l-{\displaystyle \frac{A{\rho }_{gs}{E}_l{v}_l{R}_{ls}}{B_l}}\right)}_{j+1}^{n+1}-{\left(A{\rho }_l{E}_l{v}_l-{\displaystyle \frac{A{\rho }_{gs}{E}_l{v}_l{R}_{ls}}{B_l}}\right)}_j^{n+1}\\ ={\displaystyle \frac{\Delta z}{2\Delta t}}\left[{\left(A{\rho }_l{E}_l\right)}_j^n+{\left(A{\rho }_l{E}_l\right)}_{j+1}^n-{\left(A{\rho }_l{E}_l\right)}_j^{n+1}-{\left(A{\rho }_l{E}_l\right)}_{j+1}^{n+1}\right]\end{array}$$

(18)

Momentum equation

The difference format for the momentum equation is:

$$p_{j+1}^{n+1}-p_j^{n+1}=T_A+T_B+T_C+T_D$$

(19)

where

$$T_A={\displaystyle \frac{\Delta z}{2\Delta t}}\left[\begin{array}{l}{\left({\rho }_g{E}_g{v}_{g}A+{\rho }_l{E}_l{v}_{l}A\right)}_j^n+{\left({\rho }_g{E}_g{v}_{g}A+{\rho }_l{E}_l{v}_{l}A\right)}_{j+1}^n\\ -{\left({\rho }_g{E}_g{v}_{g}A+{\rho }_l{E}_l{v}_{l}A\right)}_j^{n+1}-{\left({\rho }_g{E}_g{v}_{g}A+{\rho }_l{E}_l{v}_{l}A\right)}_{j+1}^{n+1}\end{array}\right]$$

(20)

$$T_B={\left({\rho }_g{E}_g{v}_g^{2}A+{\rho }_l{E}_l{v}_l^{2}A\right)}_j^{n+1}-{\left({\rho }_g{E}_g{v}_g^{2}A+{\rho }_l{E}_l{v}_l^{2}A\right)}_{j+1}^{n+1}$$

(21)

$$T_C=-{\displaystyle \frac{\Delta z}{2}}\left[{\left({\rho }_g{E}_{g}Ag+{\rho }_l{E}_{l}Ag\right)}_j^{n+1}+{\left({\rho }_g{E}_{g}Ag+{\rho }_l{E}_{l}Ag\right)}_{j+1}^{n+1}\right]$$

(22)

$$T_D=-{\displaystyle \frac{\Delta z}{2}}\left[{\left(A\left|{\displaystyle \frac{dP}{dz}}\right|\right)}_j^{n+1}+{\left(A\left|{\displaystyle \frac{dFr}{dz}}\right|\right)}_{j+1}^{n+1}\right]$$

(23)

(3)

Boundary conditions

Discretize the initial conditions and boundary conditions as shown in

Table 8. Discretization of initial and boundary conditions.

Dispersion of Initial Conditions

Boundary Conditions

$\left\{\begin{array}{l}{\left(E_g\right)}_j^0=0\\ {\left(v_{sg}\right)}_j^0=0\\ {\left(v_{sl}\right)}_j^0={\displaystyle \frac{Q_l}{A_j}}\\ {\left({\rho }_l\right)}_j^0=const\\ {\left(P\right)}_j^0=P\left(z_j\right)\end{array}\right.$

$\left\{\begin{array}{l}{\left(E_g\right)}_0^n={\displaystyle \frac{{\left(Q_g\right)}_0^n}{C_0{\left(Q_l+Q_g\right)}_0^n+A\left(0\right){\left(v_{rg}\right)}_0^n}}\\ {\left(E_l\right)}_0^n=1-{\left(E_g\right)}_0^n\\ {\left(v_{sg}\right)}_0^n={\displaystyle \frac{{\left(Q_g\right)}_0^n}{A\left(0\right)}}\\ {\left(v_{sl}\right)}_0^n={\displaystyle \frac{{\left(Q_l\right)}_0^n}{A\left(0\right)}}\\ {\left(P\right)}_N^n=0\end{array}\right.$

.

4.3. Solution Process

After discretizing the equations, the difference equations for the gas–liquid continuity equation and momentum equation of the acid gas circulation model are obtained. In this study, the difference equations are solved step by step using a four-point difference grid format, as shown in Figure 4. In the figure, “○” is the known parameter, and “×” is the parameter to be determined.

Taking the calculation of flow parameters at node 4 in the figure as an example, the detailed calculation process is as follows:

(1)

Estimate the pressure value at node 4 ($P_4^{\ast }$).

(2)

Based on the estimated pressure, use the PVT state Equation (6) to calculate the gas density at node 4 (${\rho }_{g4}$).

(3)

Estimate the gas content at node 4 ($E_{g4}^{\ast }$).

(4)

Based on the estimated gas content, use the gas and liquid continuity Equations (2) and (3) to calculate the gas and liquid flow velocities ($v_g$) and ($v_l$).

(5)

Based on the gas and liquid flow velocities, use the drift flow Equation (5) to calculate the actual gas content at node 4 ($E_{g4}$).

(6)

Perform an error analysis on the calculated gas content. If $\left|E_{g4}^{\ast }-E_{g4}\right|<\epsilon$, then the estimate in step (3) is reasonable, and proceed to the next step.

(7)

Otherwise, re-estimate the gas content and repeat the calculations in steps (3) to (6) until the desired accuracy is reached.

(8)

Based on the gas–liquid flow velocity and gas content, the pressure at node 4 is calculated using the mixed momentum Equation (4). The calculated pressure at node 4 is then compared with the estimated pressure in step (1). If $\left|P_4^{\ast }-P_4\right|<\epsilon$, the estimated pressure is considered reasonable, and the calculation for the node is complete. The flow parameters calculated at the node are then used as the known conditions for the next node. If $\left|P_4^{\ast }-P_4\right|>\epsilon$, the pressure must be re-estimated. The calculation steps should be repeated until the pressure calculation error meets the required precision.

(9)

Repeat this iterative process for the entire time and space domain until the solution for the entire fixed domain is obtained, and the flow parameters at all nodes are determined.

4.4. Model Validation

When acidic gas overflow occurs, due to its inherent toxicity, the risk associated with on-site data collection is high, making the operation challenging. Therefore, this study validates the accuracy of the proposed model by comparing the computational results with previously measured data from overflow wells. Specifically, the work by [36], which collected data on overflow conditions in wells with high H₂S concentrations across different regions, including key parameters such as annular pressure, Increase in mud pit volume, and overflow gas composition. The well he studied was actually drilled to a well depth of 4049.68 m, with a vertical depth of 3381 m, and a Φ244.5 mm casing installed down to a well depth of 2479 m. The drilling fluid density was 1.43 g/m³, and the H₂S content was 151 g/cm³ (approximately 10% of the volume content under standard conditions). The computational results of this study were compared with these field-measured data, as shown in Figure 5. As shown in the figure, the overall trend of annular pressure is to decrease with decreasing well depth, but the annular pressure at the same well depth decreases with increasing time. As the content of acidic gas increases, the volume of the mud pit gradually decreases at the same time. However, the volume of the mud pit shows a trend of first remaining flat and then decreasing sharply with increasing time. This indicates that the solubility of acidic gas significantly affects the overflow volume. The comparison results indicate that the trends of the model calculations are largely consistent with the measured data, with a maximum error within ±5%, further demonstrating the high accuracy and reliability of the acidic gas annular flow model developed in this study.

Ref. [37] simulated the behavior of riser gas under a Rapid Gas Handling (RGH) system, which closes and regulates pressure to 20 bar. A comparison chart (Figure 6) is provided to illustrate the differences between their results and those obtained from the model presented in this study. As shown in the figure, the results obtained from the model in this study closely align with the bubble pressure and ROP pressure predicted by Aarsnes’s model, with a deviation within ±10%. This demonstrates the model’s accuracy and its applicability to practical production calculations.

5. Calculation Example

5.1. Basic Parameters

The X1 well of Z oil field is used as the basis for the calculations in this paper. The designed depth of the well is 11,100 m: the first section depth is 1500 m, the second section depth is 5900 m, the third section depth is 8000 m, the fourth section depth is 10,000 m, and the fifth section depth is 11,100 m. The outer diameter of the annulus is taken as the drill bit diameter (168.3 mm), and the inner diameter of the annulus is taken as the drill collar outer diameter (101.6 mm). During the fifth section, the drill string assembly inside the well consists of:

168.3 mm drill bit + rod drill string (9 m) + float valve (0.5 m) + 127 mm spiral drill collar (189 m) + 101.6 mm heavy drill pipe (144 m) × 101.6 mm inclined drill pipe × S135I (3000 m) + 101.6 mm inclined drill pipe × V150 (2000 m) + 149.2 mm inclined drill pipe × V150I (3057 m) + 149.2 mm inclined drill pipe × V150 (2700 m). The basic input parameters are shown in

Table 9. Basic input parameters.

Parameters	Values	Parameters	Values
Relative density of H2S	1.189 kg/m3	Drilling fluid replacement	0.012 m3/s
Relative density of CO2	1.535 kg/m3	Formation temperature gradient	0.03 °C/m
Relative density of natural gas	0.717 kg/m3	Surface temperature	20 °C
Viscosity of drilling fluid	0.04 Pa·s	Surface pressure	0.1 MPa
Density of drilling fluid	1510 kg/m3	Kick flow rate	0.5 m3/s
Formation pressure gradient	0.012 MPa/m

.

5.2. Study on the Variation in Acidic Gas Properties with Well Depth

Figure 7 shows the trend of the deviation factor of mixed acidic gases with different compositions as a function of well depth. It can be observed that the deviation factor changes more dramatically near the pseudo-critical point with higher H₂S and CO₂ content, and the minimum value tends to shift towards the wellhead.

From Figure 7a, the deviation factor of the component with 40% H₂S content changes by more than 0.5, while the deviation factor of the component with 40% CO₂ content also changes dramatically near the pseudo-critical point, but to a lesser extent than that of the component with 40% H₂S content. From Figure 7b, the component with a higher H₂S content has its minimum deviation factor shifting more to the left, indicating that the higher the H₂S content in the mixed acidic gas, the shallower the well depth at which the minimum deviation factor occurs during ascent along the wellbore.

Figure 8 shows the variation trend of different components of mixed acidic gas properties (density, viscosity) with well depth. From Figure 8a, the density of mixed gas follows a similar trend to pure CH₄, both increasing with well depth; the rate of increase is initially fast and then slows down. At the same well depth, the density of the mixed gas is significantly greater than that of pure CH₄, and since CO₂ has the highest density among the three gases, the composition with a higher CO₂ content will have a slightly higher density than the one with a higher H₂S content.

From Figure 8b, it is observed that the viscosity of mixed acidic gas is noticeably higher than that of pure CH₄, and its variation pattern is like that of pure CH₄. Overall, the viscosity of mixed fluid with more CO₂ is slightly higher than that of mixed fluid with more H₂S.

5.3. Migration Pattern of Acidic Gas in the Annular Space

The variation in volume fraction of mixed acidic gases with different components as a function of well depth is shown in Figure 9. As seen from Figure 9, below 1500 m depth, the volume fraction of different components of mixed acidic gas remains relatively unchanged. However, above 1500 m, the volume fraction increases rapidly with decreasing depth.

From Figure 9a, it can be observed that when the gas reaches the wellhead, the higher the H₂S content in the binary mixed gas, the larger its volume fraction. This indicates that the mixed gas with higher H₂S content experiences more significant volume expansion when it returns to normal conditions. This is because, in the high-temperature and high-pressure environment below 1500 m, H₂S is completely dissolved in the drilling fluid, while CH₄ has lower solubility. However, under conditions where temperature and pressure exceed its critical point, CH₄ remains in a supercritical state during the ascent, resulting in a smaller gas-phase volume fraction, less than 0.1. When the depth is less than 1500 m, the solubility of H₂S gradually decreases with the reduction in temperature and pressure, leading to its gradual exsolution from the drilling fluid, and the gas volume fraction gradually increases.

From Figure 9b, it can be observed that the component with higher H₂S content undergoes expansion at a shallower depth and at a faster rate. At the wellhead, the gas-phase volume fraction of the component with higher H₂S content is greater than that of the component with higher CO₂ content. This is because H₂S has a higher solubility than CO₂, and it exsolves later. Additionally, since its deviation factor is smaller than that of CO₂, its volume expansion is more significant.

The variation in flow velocity for different components of mixed acidic gas with well depth is shown in Figure 10. As seen from the figure, the flow velocity of mixed fluid containing acidic gas increases more rapidly near the wellhead, approximately 1 m/s faster than pure CH₄. The mixed phase velocity of the component with higher H₂S content increases slightly later than that of the component with higher CO₂ content, but near the wellhead, the mixed phase velocity increases more rapidly. The reason for this is that the higher the acidic gas content, the smaller the deviation factor in the supercritical state. As temperature and pressure decrease, the gas properties near the critical point change more dramatically.

Figure 11 shows the wellbore pressure variation after the intrusion of two-component mixed acidic gas. From Figure 11a, the bottom-hole pressure of the well for different mixed acidic gas components sharply decreases with the overflow time. However, the CH₄-H₂S mixed gas experiences a later point of rapid pressure drop and a greater overall pressure drop than the CH₄-CO₂ mixed gas. This is because H₂S has a higher solubility than CO₂, and thus exsolves later in the wellbore. Additionally, due to the smaller deviation factor of the CH₄-H₂S mixture at the critical point compared to the CH₄-CO₂ mixture, gas expansion is more intense at the wellhead, further lowering the liquid column pressure. Therefore, H₂S overflow leads to a larger bottom-hole pressure drop.

Figure 11b shows that the overflow annular pressure of the three gas mixtures changes more slowly at greater depths. Near the wellhead, the annular pressure drops gradient increases. This is because the components containing acidic gases reduce the deviation factor at the supercritical point, and as the temperature and pressure near the wellhead decrease, the components with acidic gases expand more intensely, resulting in an intensified overflow and a greater decrease in wellbore pressure.

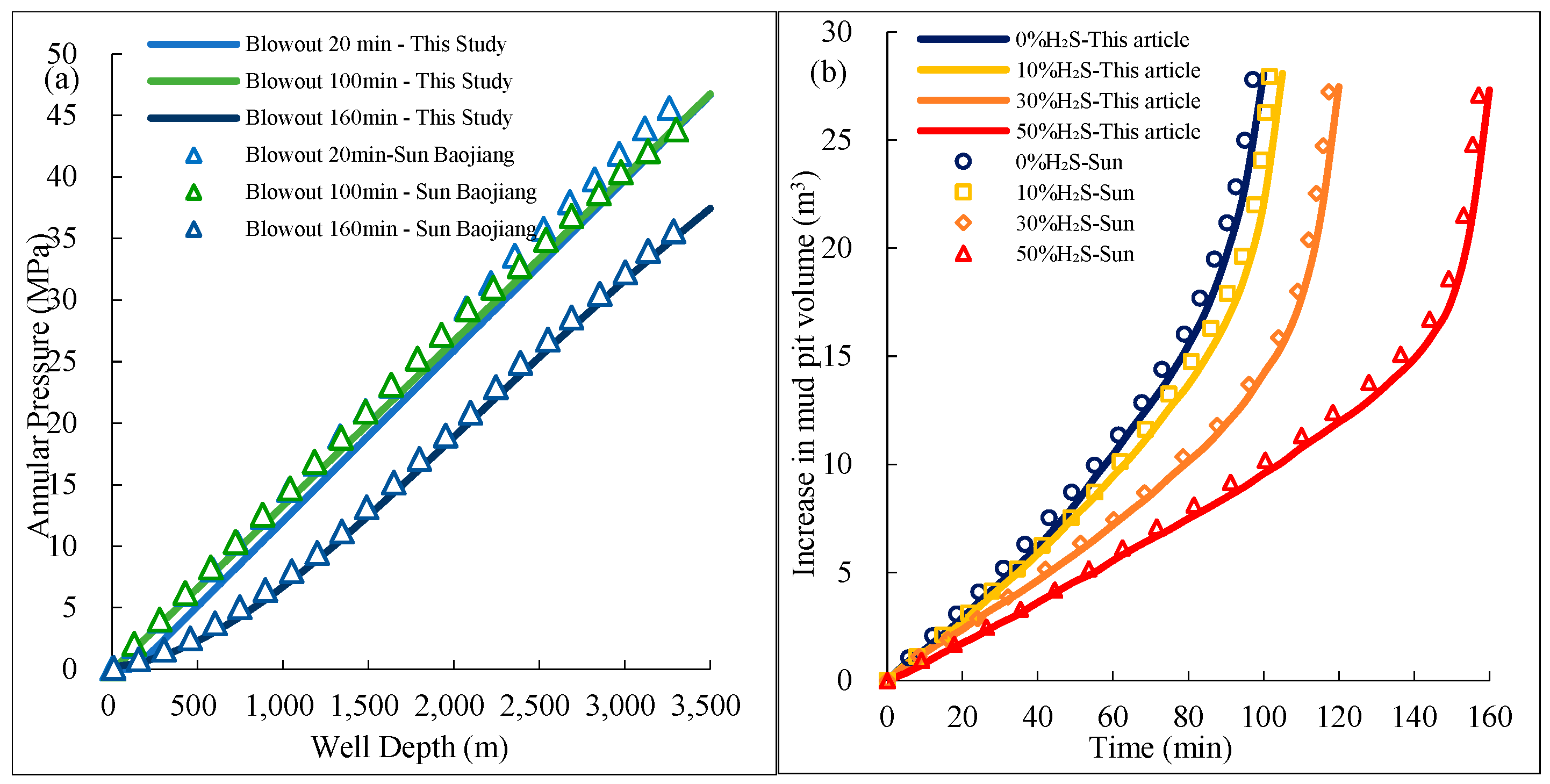
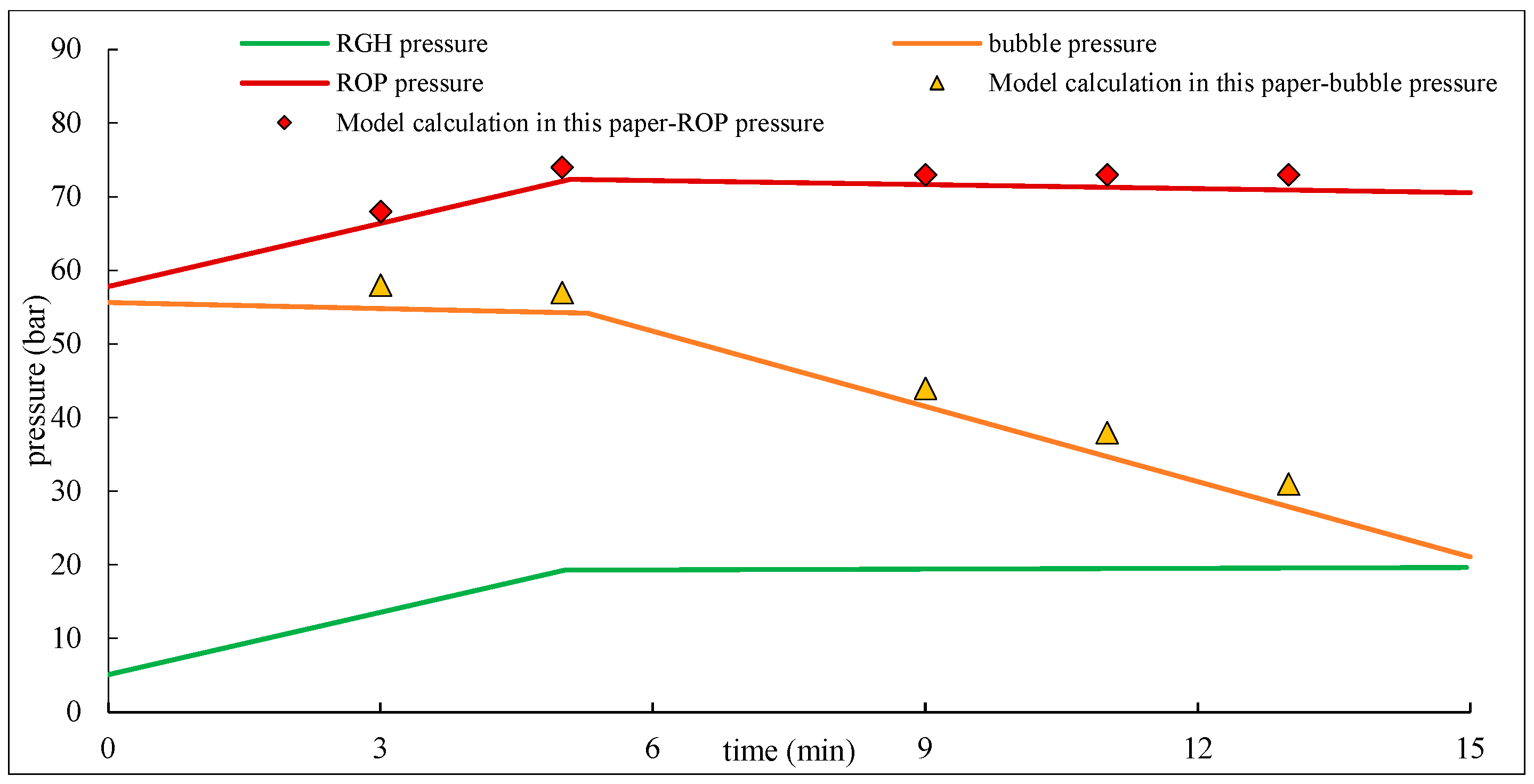
6. Discussion

The migration laws of acidic gas overflow obtained in this study provide important practical guidance for well control safety in HPHT gas wells. The results can be applied in three main aspects: well control design, emergency planning, and well-killing operations.

In terms of well control design optimization, the simulations show that acidic gas exsolution and rapid expansion near the wellhead lead to nonlinear pressure drops and accelerated flow velocities. In engineering design, this requires incorporating larger design safety margins in wellhead equipment and casing strength to accommodate sudden annular pressure fluctuations. And selecting drilling fluids with improved H₂S and CO₂ solubility to delay gas exsolution and reduce the intensity of overflow expansion.

Compared to CO₂, the invasion of H₂S is more dangerous because of its higher solubility and delayed but stronger dissolution. This means that we should strengthening on-site safety equipment, including emergency ventilation, breathing apparatus, and protective shelters, to address the higher probability of H₂S release during overflow.

The findings indicate that H₂S intrusion produces greater wellhead expansion and mud pit displacement, which requires us to adjust the well killing strategy, such as: Kill mud density calculations should be corrected for acidic gas solubility and pseudo-critical behavior rather than methane-only assumptions. Foam or polymer-enhanced drilling fluids can be considered to suppress bubble growth and improve stability during acid gas kicks.

Field cases and model results suggest that when H₂S concentration exceeds “20–30% in the invading gas phase”, migration behavior changes significantly: solubility increases sharply, exsolution is delayed to shallower depths, and volume expansion near the wellhead intensifies. This threshold marks the point at which overflow transitions from manageable to high-risk. Engineering practice should therefore treat influxes with H₂S content above 20% as high-risk scenarios requiring enhanced monitoring, higher mud density margins, and stricter surface safety protocols. For H₂S concentrations above “40%”, the model predicts critical nonlinear effects: compressibility factor reductions >0.5 and wellhead volume expansion exceeding 20% compared to methane. Such conditions should be considered “severe hazard,” and pre-planned contingency measures must be activated immediately.

7. Conclusions

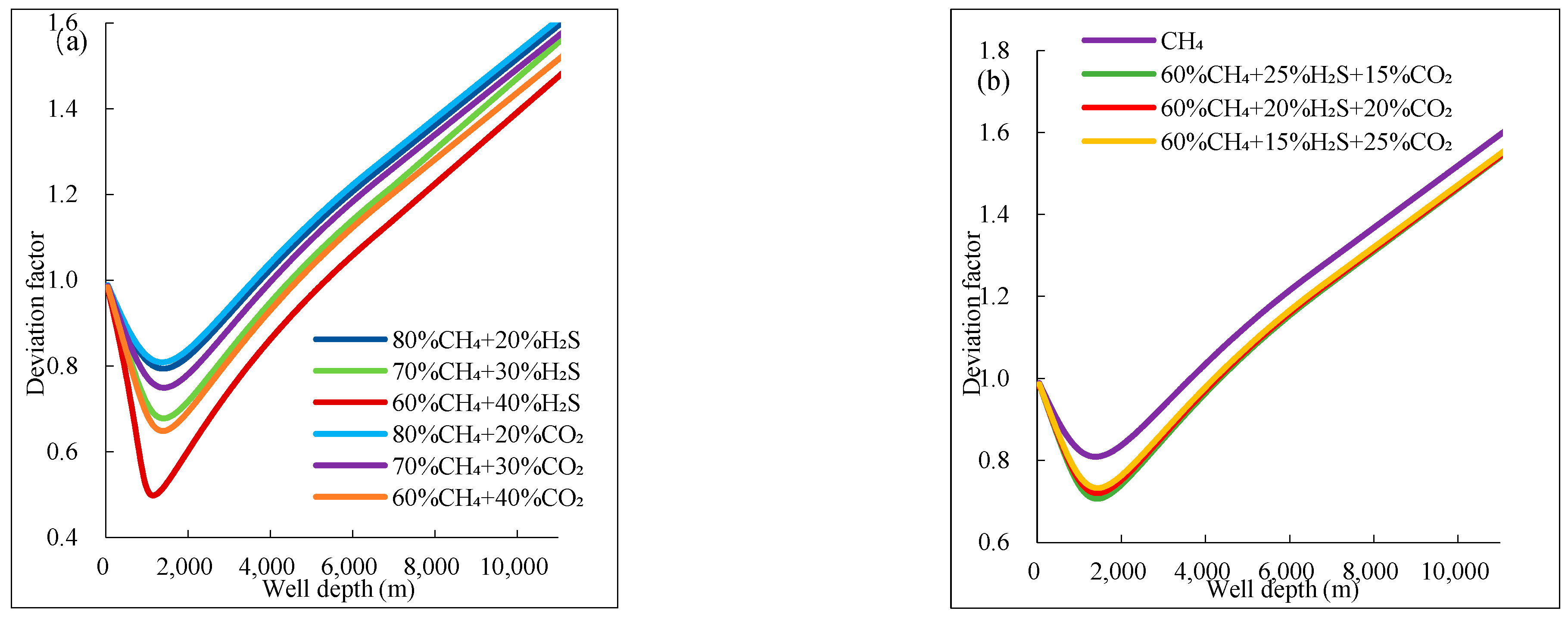
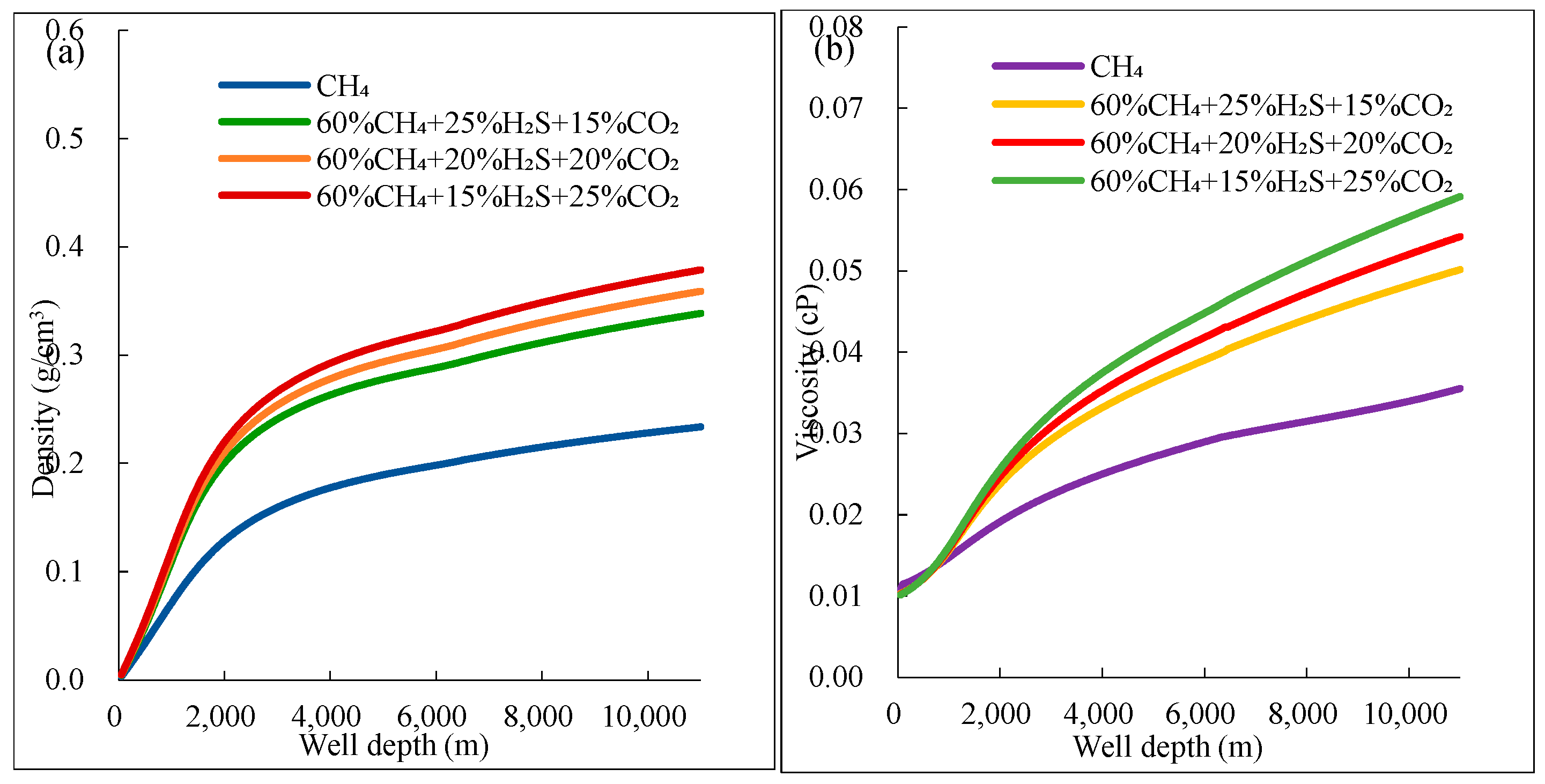
(1) For gas mixtures with >30% H₂S, the compressibility factor decreases by 40–50% near the pseudo-critical point, while density increases by 35–45% and viscosity rises by 20–30% compared to pure CH₄. These changes are most severe at depths of 1000–1500 m, where temperature/pressure approach pseudo-critical conditions.

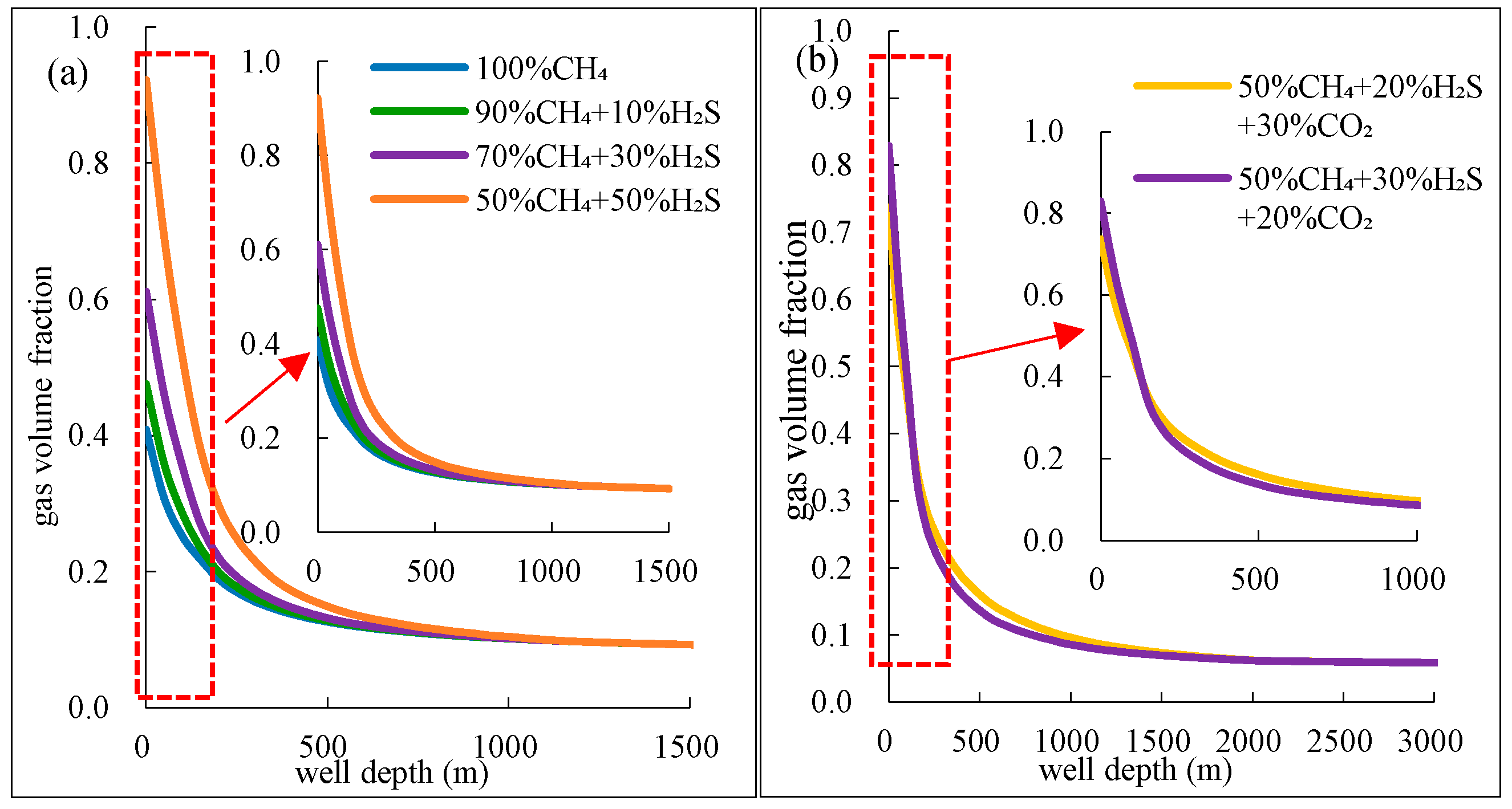
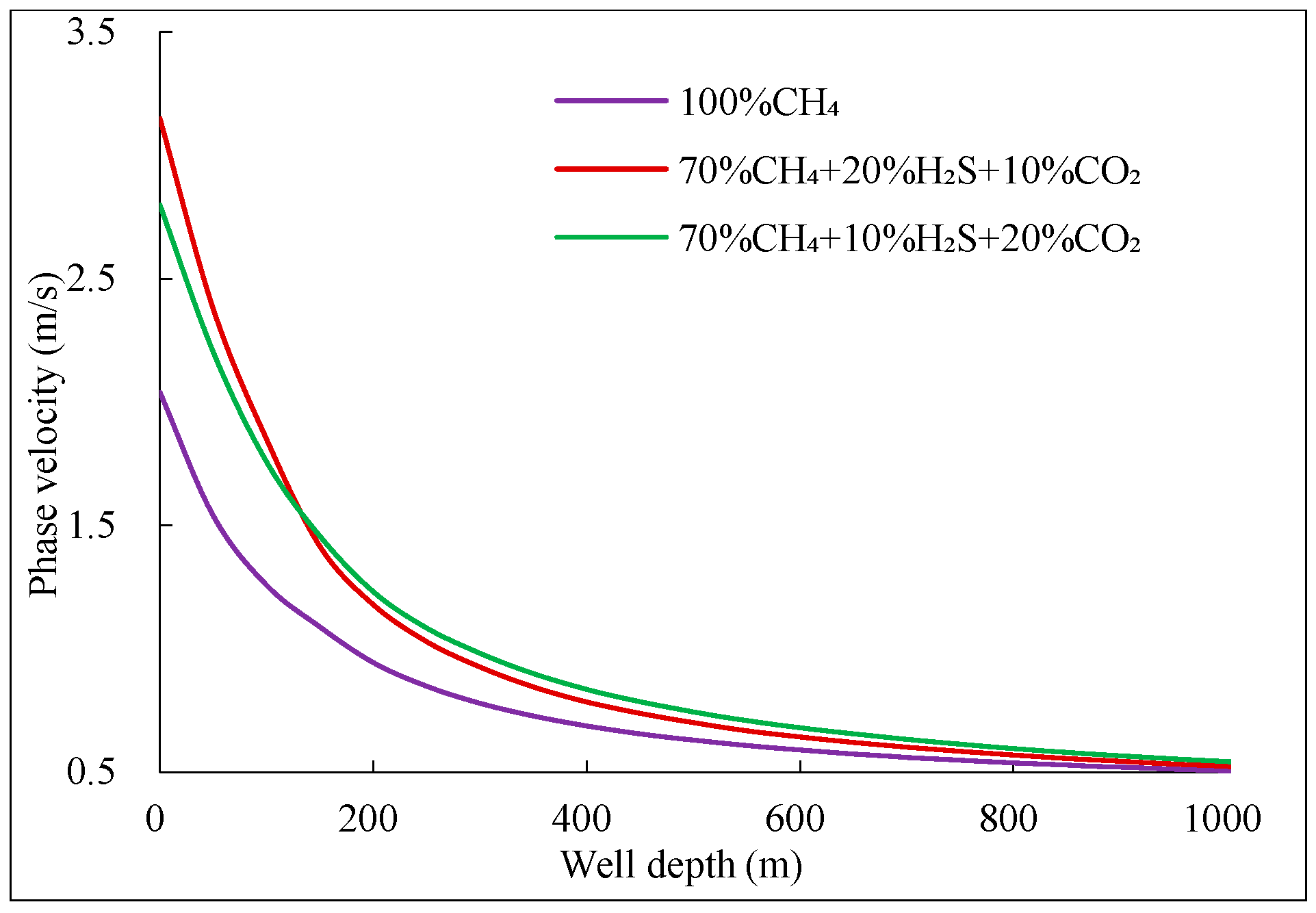
(2) For mixtures with ≥20% H₂S, the gas phase volume fraction expands by 20–25% at the wellhead, and flow velocity surges by 10–15% due to abrupt exsolution below 1500 m. Ternary mixtures (e.g., 20% CO₂ + 20% H₂S) show 30% greater expansion than binary mixtures (e.g., 40% CO₂).

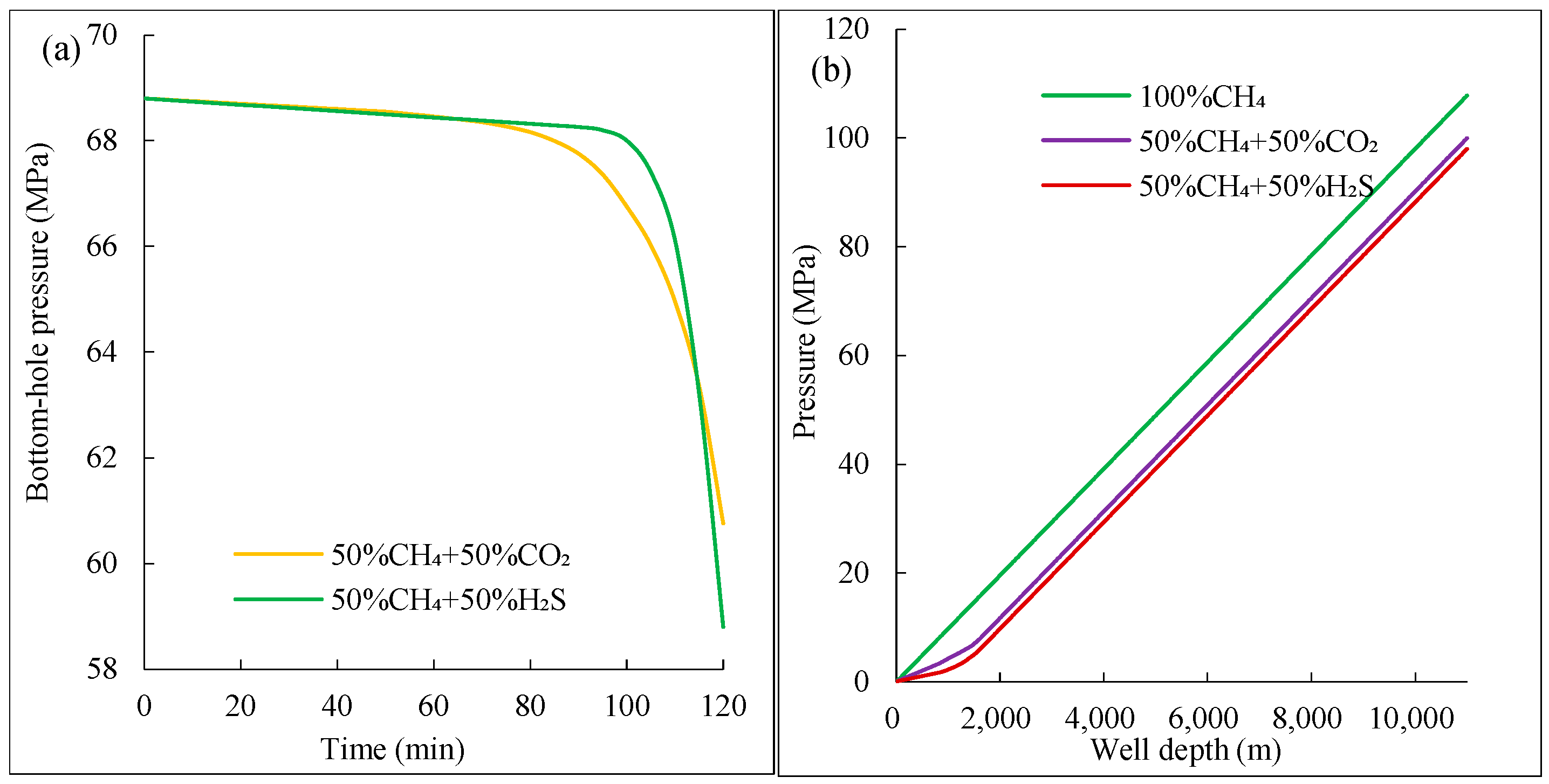
(3) Annular pressure drops nonlinearly by 15–20% near the wellhead for mixtures with >15% acidic gas, due to greater solubility in drilling fluid and increased expansion near the wellhead as temperature and pressure decrease, thereby exacerbating well control risks.

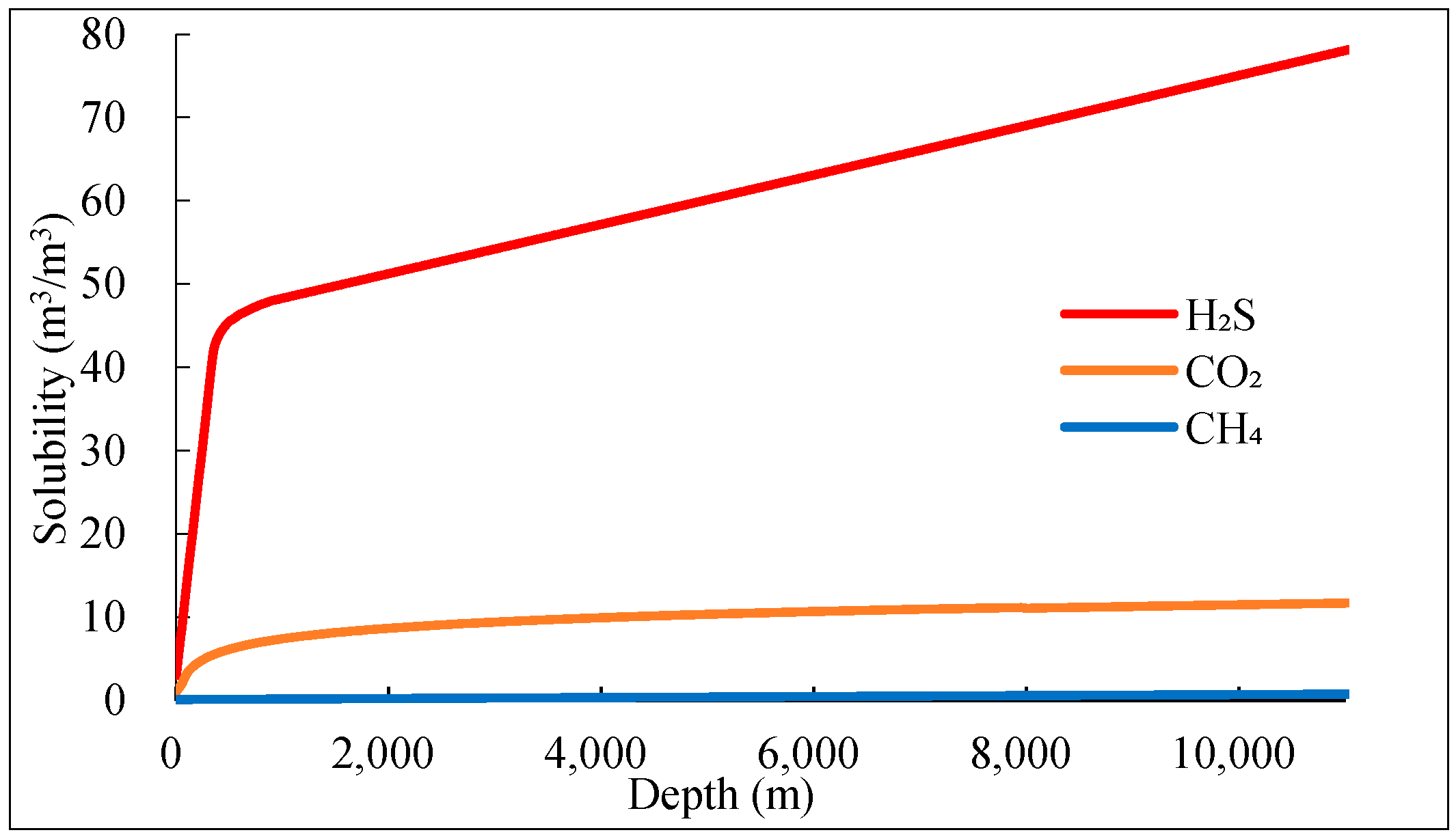
(4) The greater the density of acidic gases, the larger the increase in mud pit volume. Compared to CO₂-rich gases, H₂S intrusion causes more significant volume expansion due to its lower compressibility coefficient, resulting in greater displacement of drilling fluid near the wellhead. Therefore, H₂S has the greatest impact on well control (difficulty in overflow monitoring, pressure control, etc.), followed by CO₂, and CH₄ has the least impact.