Application of the NOA-Optimized Random Forest Algorithm to Fluid Identification—Low-Porosity and Low-Permeability Reservoirs
Abstract
1. Introduction
2. Research Background
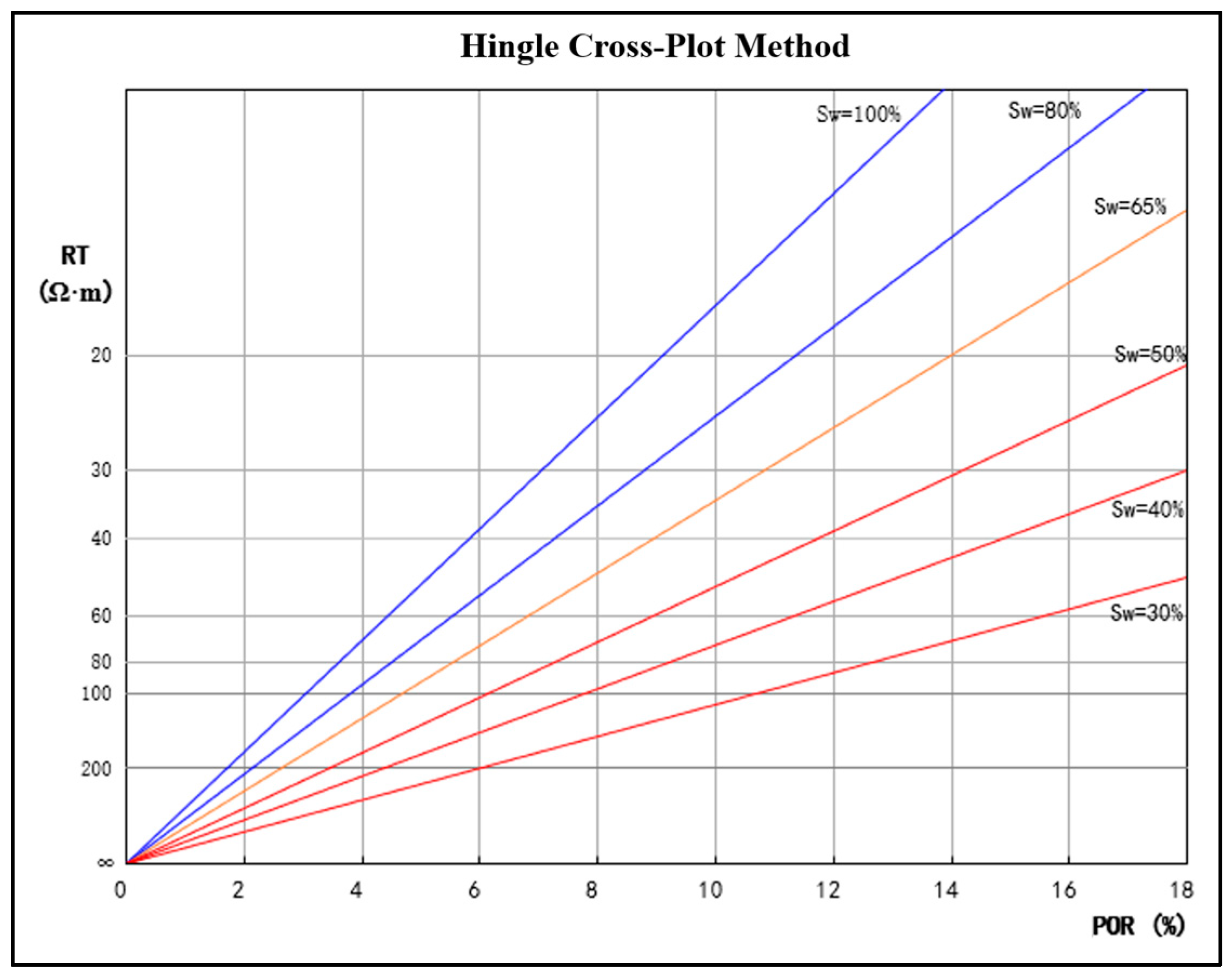
3. Hingle Cross-Plot Method
3.1. Principle
3.2. Nutcracker Optimization Algorithm (NOA)
4. Data Processing and Result Analysis
4.1. Hingle Intersection Diagram Method
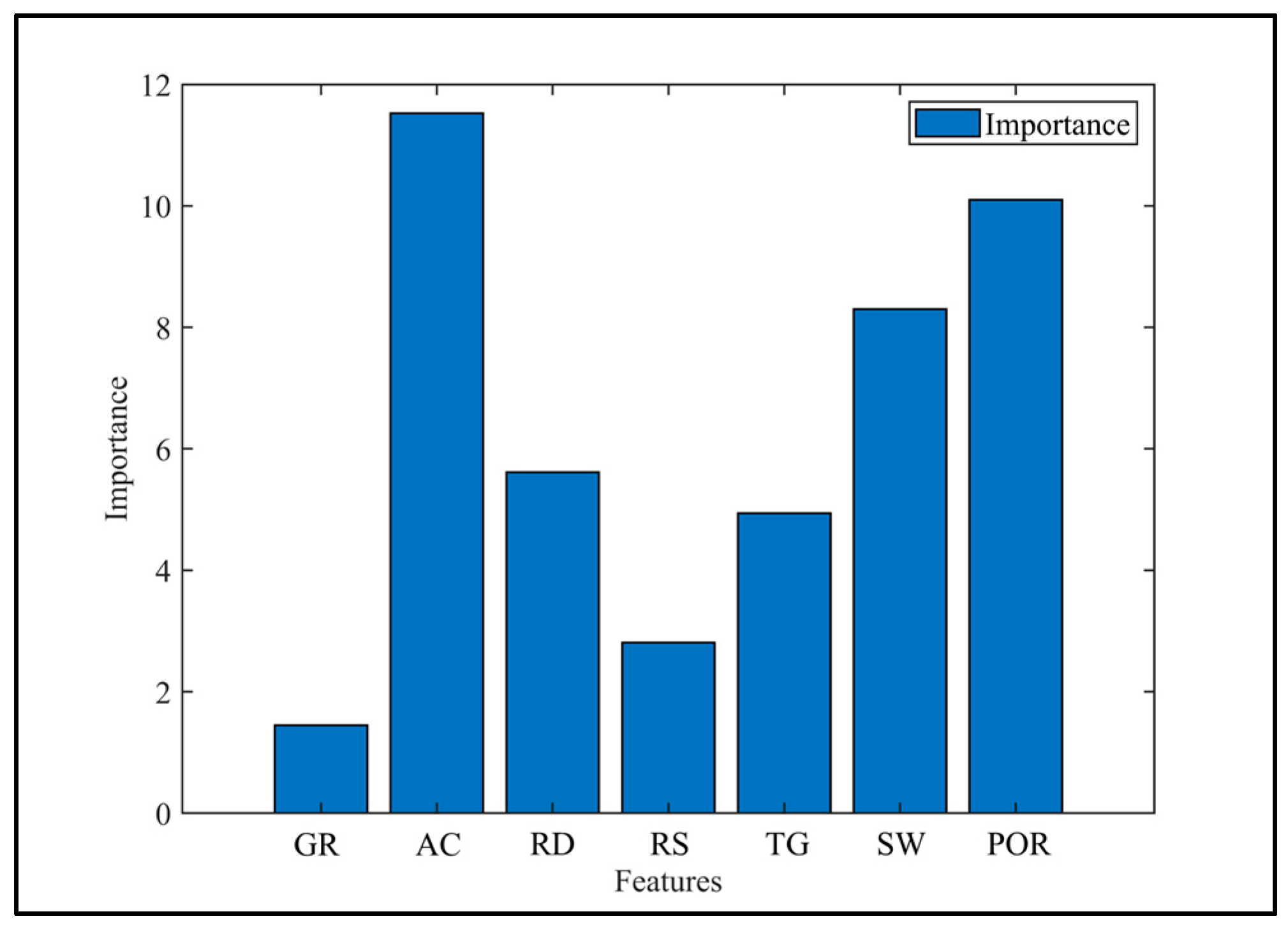
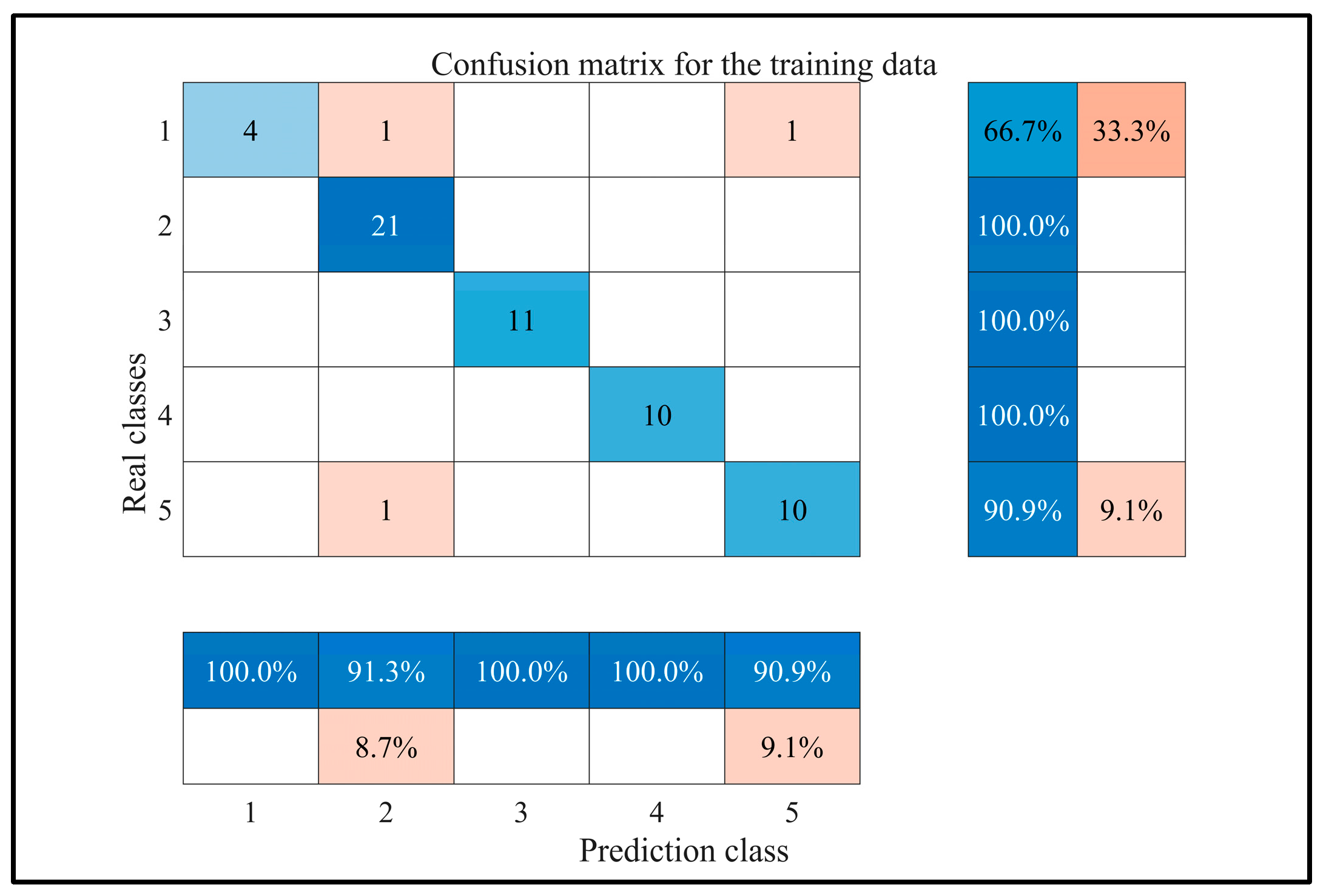
4.2. NOA-Optimized Random Forest Classification Method
5. Application Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.-H. Research on Logging Evaluation Methods for Low Permeability Reservoirs. Master’s Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Li, N.; He, X.J.; Gao, X.L. Overview and prospect of the logging evaluation technology on low porosity and permeability reservoirs. World Well Logging Technol. 2013, 8–11, 14. (In Chinese) [Google Scholar]
- Hong, Y.M. Logging Data Processing and Comprehensive Interpretation; China University of Petroleum Press: Dongying, China, 2007; pp. 165–195. (In Chinese) [Google Scholar]
- Du, Y.-Y.; Wang, Y.; Li, Y.-F.; Wei, T.; Li, X.-J.; Wang, J.-W.; Lu, Z.-Y.; Li, L.-X.; Tan, H.-Q. Research status and outlook of the mud logging and well logging data comprehensive recognition for the low porosity and permeability of the reservoir fluid properties. Prog. Geophys. 2018, 33, 0571–0580. (In Chinese) [Google Scholar]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design prob-lems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Yuan, J.-Y.; Chan, Q.-L.; Chen, Y.-B.; Yan, C.-F. Petroleum Geological Character and Favorable Exploration Domains of Qaidam Basin. Nat. GAS Geosci. 2018, 33, 571–580. [Google Scholar]
- Hanson, D.A.; Ritts, D.B.; Zinniker, D.; Michael Moldowan, J.; Biffi, U. Upper Oligocene Lacustrine Source Rocks and Petroleum Systems of the Northern Qaidam Basin, Northwest China. GeoScienceWorld 2001, 85, 601–619. [Google Scholar]
- Dang, Y.; Yin, C.; Zhao, D. Sedimentary facies of the Paleogene and Neogene in western Qaidam Basin. J. Palaeogeogr. 2004, 297–306. [Google Scholar]
- Mei, Z. Sedimentary Facies and Palaeogeographic Reconstruction; Northwestern University Press: Xi’an, China, 1994; pp. 195–198. [Google Scholar]
- Yong, S.; Zhang, C. Logging Data Processing and Comprehensive Interpretation; Petroleum University Press: Beijing, China, 1996; pp. 211–212. [Google Scholar]
- Wang, T.; Nie, Y.; Wang, S.; Wang, S.; Wu, Q.-C.; Zhang, S.-H.; Huang, Y.-Z. Depth control of ROV using the improved LADRC based on nutcracker optimization algorithm. Ocean. Eng. 2024, 309, 118370. [Google Scholar] [CrossRef]
- Jameel, M.; Abouhawwash, M. Revolutionizing optimization: An innovative nutcr-acker optimizer for single and multi-objective problems. Appl. Soft Comput. 2024, 164, 112019. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, H.; Zhang, B. Multi-Unmanned Aerial Vehicle Path Planning Based on Improved Nutcracker Optimization Algorithm. Drones 2025, 9, 116. [Google Scholar] [CrossRef]
- Li, X. Research on Logging Evaluation Technology for Low Saturation Oil Formation in Yaojia Formation West of the Changyuan, Daqing Oilfield. Master’s Thesis, China University of Petroleum, Beijing, China, 2022. [Google Scholar]
- Wu, J.; Zhang, H.-R.; Hu, X.-Y.; Yang, D. Comprehensive Evaluation Method of Low-Resistivity Reservoirs in Gravelly Sandstone with Complex Pore Structure in Beibuwan Basin. Spec. Oil Gas Reserv. 2023, 30, 67–76. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Pan, S.-W.; Zheng, Z.-C.; Lei, J.-Y.; Wang, Y.-L. Porosity Prediction of Sandstone Reservoirs Based on Hybrid Optimization XGBoost Algorithm. Comput. Appl. Softw. 2023, 40, 103–109+206. [Google Scholar]
- Cui, J.-F.; Yang, J.-L.; Wang, M.; Wang, X.; Wu, Y.; Xu, C.-Q. Shale porosity prediction based on random forest algorithm. Pet. Geol. Recovery Effic. 2023, 30, 13–21. [Google Scholar]
- Cheng, X.; Zhou, J.; Fu, H.-C.; Luo, X.-M. Applicability and Application of Machine Learning Algorithm in Logging Interpretation. Northwestern Geol. 2023, 56, 336–348. [Google Scholar]
- Lu, P. Research on Porosity and Permeability Model of Tight Sandstone Reservoirs Based on Machine Learning. Ph.D. Thesis, Northwest University, Xi’an, China, 2022. [Google Scholar]
- Wang, G.-Y.; Song, J.-G.; Xu, F.; Zhang, W.; Liu, T.; Chen, X.-F. Random Forests lithology prediction method for imbalanced data sets. Oil Geophys. Prospect. 2021, 56, 679–687+669. [Google Scholar]





| Well Number | Core Analysis Porosity | Core Analysis Permeability | ||
|---|---|---|---|---|
| Range (%) | Average (%) | Range (mD) | Average (mD) | |
| 33 | 7.0~11.0 | 9.52 | 0.100~147.100 | 6.740 |
| 31 | 9.7~12.0 | 10.73 | 0.031~112.600 | 6.290 |
| 26 | 5.4~11.4 | 9.59 | 0.004~255.200 | 6.279 |
| 36 | 6.5~11.9 | 9.54 | 0.002~29.500 | 1.595 |
| 12 | 7.0~11.1 | 9.71 | 0.033~128.698 | 3.293 |
| 5 | 6.0~16.3 | 12.57 | 0.010~156.170 | 6.544 |
| 3 | 10.2~15.5 | 14.51 | 0.103~27.976 | 3.749 |
| 21 | 7.0~13.4 | 10.07 | 0.100~78.400 | 7.721 |
| 14 | 6.1~13.1 | 9.44 | 0.002~147.61 | 5.239 |
| Test Zone Number | Oil Test Conclusion | Test Zone Number | Oil Test Conclusion |
|---|---|---|---|
| 1 | Oil–water coexistence layer | 18 | Oil–water coexistence layer |
| 2 | Oil–water coexistence layer | 19 | Oil–water coexistence layer |
| 3 | Oil–water coexistence layer | 20 | Oil–water coexistence layer |
| 4 | Oil-bearing layer | 21 | Oil–water coexistence layer |
| 5 | Oil-bearing layer | 22 | Oil–water coexistence layer |
| 6 | Oil-bearing layer | 23 | Oil–water coexistence layer |
| 7 | Oil-bearing layer | 24 | Oil–water coexistence layer |
| 8 | Oil-bearing layer | 32 | Oil–water coexistence layer |
| 10 | Oil-bearing layer | 33 | Oil–water coexistence layer |
| 14 | Oil–water coexistence layer | 34 | Oil-bearing layer |
| 15 | Oil–water coexistence layer | 35 | Oil–water coexistence layer |
| 16 | Oil–water coexistence layer | 36 | Oil–water coexistence layer |
| 17 | Oil–water coexistence layer |
| Fluid Type | Porosity/% | Oil Saturation/% |
|---|---|---|
| Oil-bearing layer | ≥12 | ≥58 |
| Oil–water coexistence layer | ≥8 | ≥35 |
| Oil-bearing water layer | ≥8 | ≥10 |
| Water layer | >8 | <10 |
| Dry layer | <8 | / |
| Model Parameters | Optimization Range | Optimal Value |
|---|---|---|
| ntree | 10~500 | 10 (10.0) |
| mtry | 1~10 | 6 (6.4098) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Q.; Lu, Y.; Yang, X.; Li, Y.; Zhang, W.; Yang, Q.; Tian, Z.; Deng, R. Application of the NOA-Optimized Random Forest Algorithm to Fluid Identification—Low-Porosity and Low-Permeability Reservoirs. Processes 2025, 13, 2132. https://doi.org/10.3390/pr13072132
Tang Q, Lu Y, Yang X, Li Y, Zhang W, Yang Q, Tian Z, Deng R. Application of the NOA-Optimized Random Forest Algorithm to Fluid Identification—Low-Porosity and Low-Permeability Reservoirs. Processes. 2025; 13(7):2132. https://doi.org/10.3390/pr13072132
Chicago/Turabian StyleTang, Qunying, Yangdi Lu, Xiaojing Yang, Yuping Li, Wei Zhang, Qiangqiang Yang, Zhen Tian, and Rui Deng. 2025. "Application of the NOA-Optimized Random Forest Algorithm to Fluid Identification—Low-Porosity and Low-Permeability Reservoirs" Processes 13, no. 7: 2132. https://doi.org/10.3390/pr13072132
APA StyleTang, Q., Lu, Y., Yang, X., Li, Y., Zhang, W., Yang, Q., Tian, Z., & Deng, R. (2025). Application of the NOA-Optimized Random Forest Algorithm to Fluid Identification—Low-Porosity and Low-Permeability Reservoirs. Processes, 13(7), 2132. https://doi.org/10.3390/pr13072132






