Intelligent Interpretation of Sandstone Reservoir Porosity Based on Data-Driven Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Preparation and Processing
2.2. Selection of Machine Learning Algorithms
2.2.1. One-Versus-One Support Vector Machines (OVO SVMs)
2.2.2. Random Forest (RF)
2.2.3. eXtreme Gradient Boosting (XGBoost)
2.2.4. Categorical Boosting (CatBoost)
2.3. Establishment of Intelligent Interpretation Model for Porosity
3. Case Study
3.1. Data Acquisition and Data Cleaning
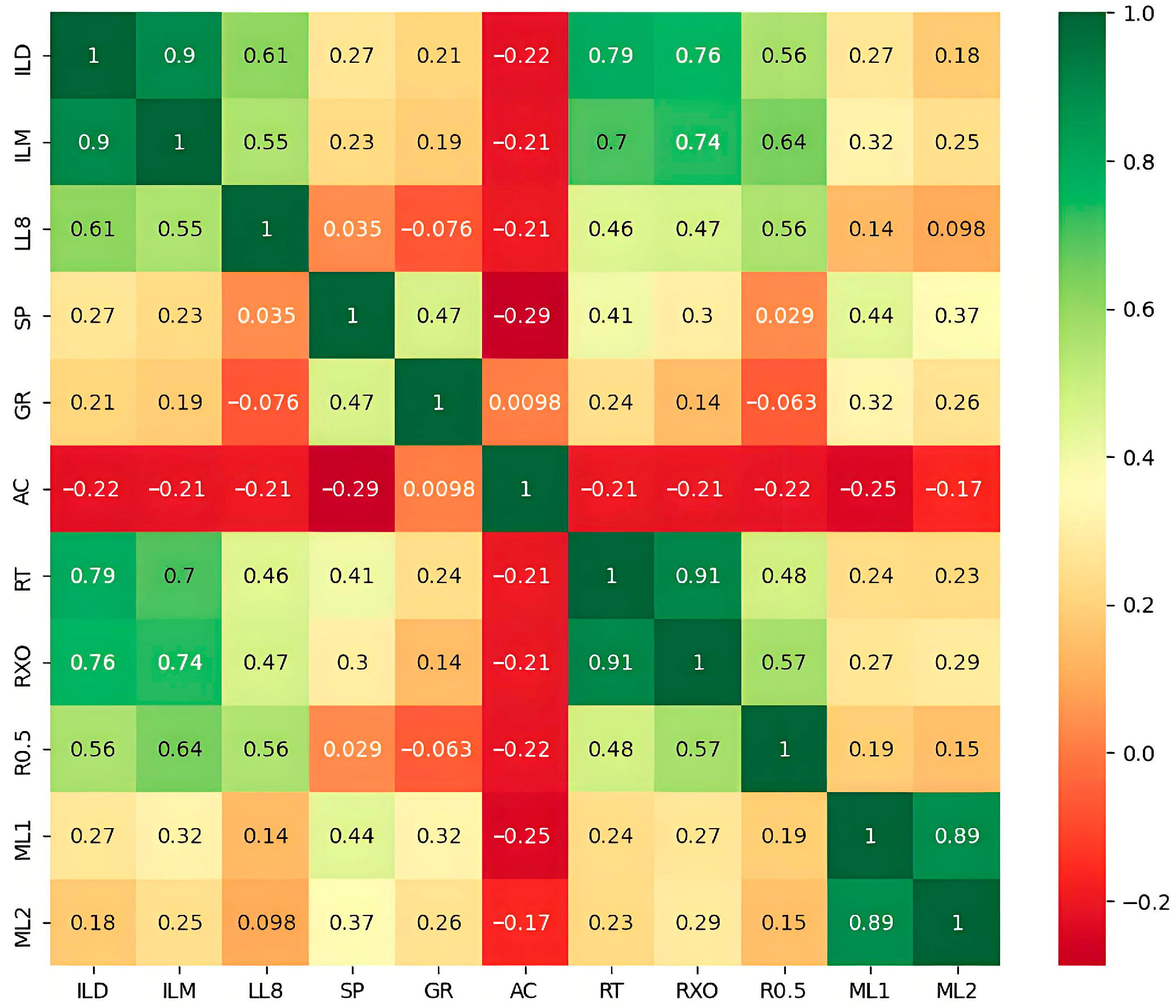
3.2. Correlation Analysis
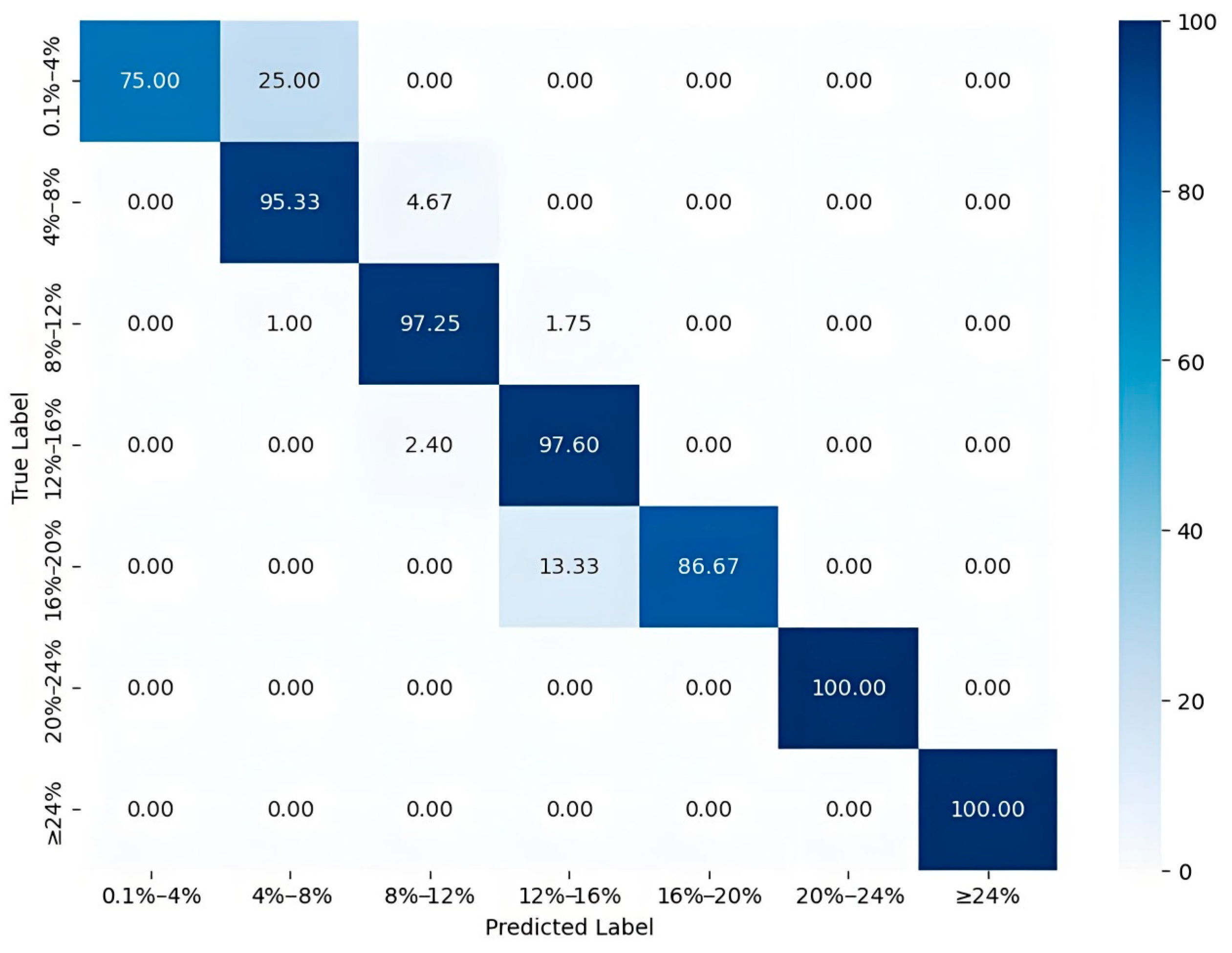
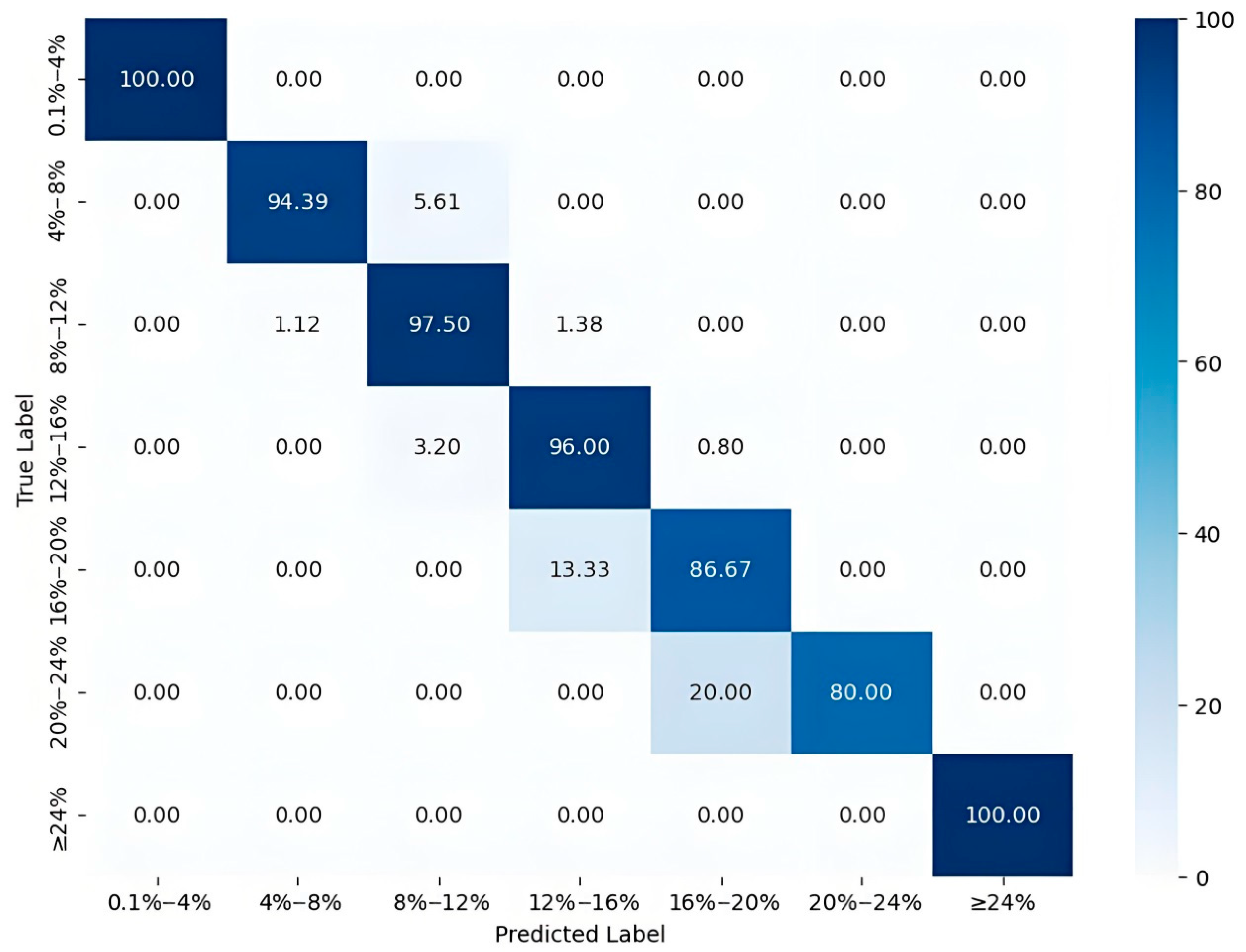
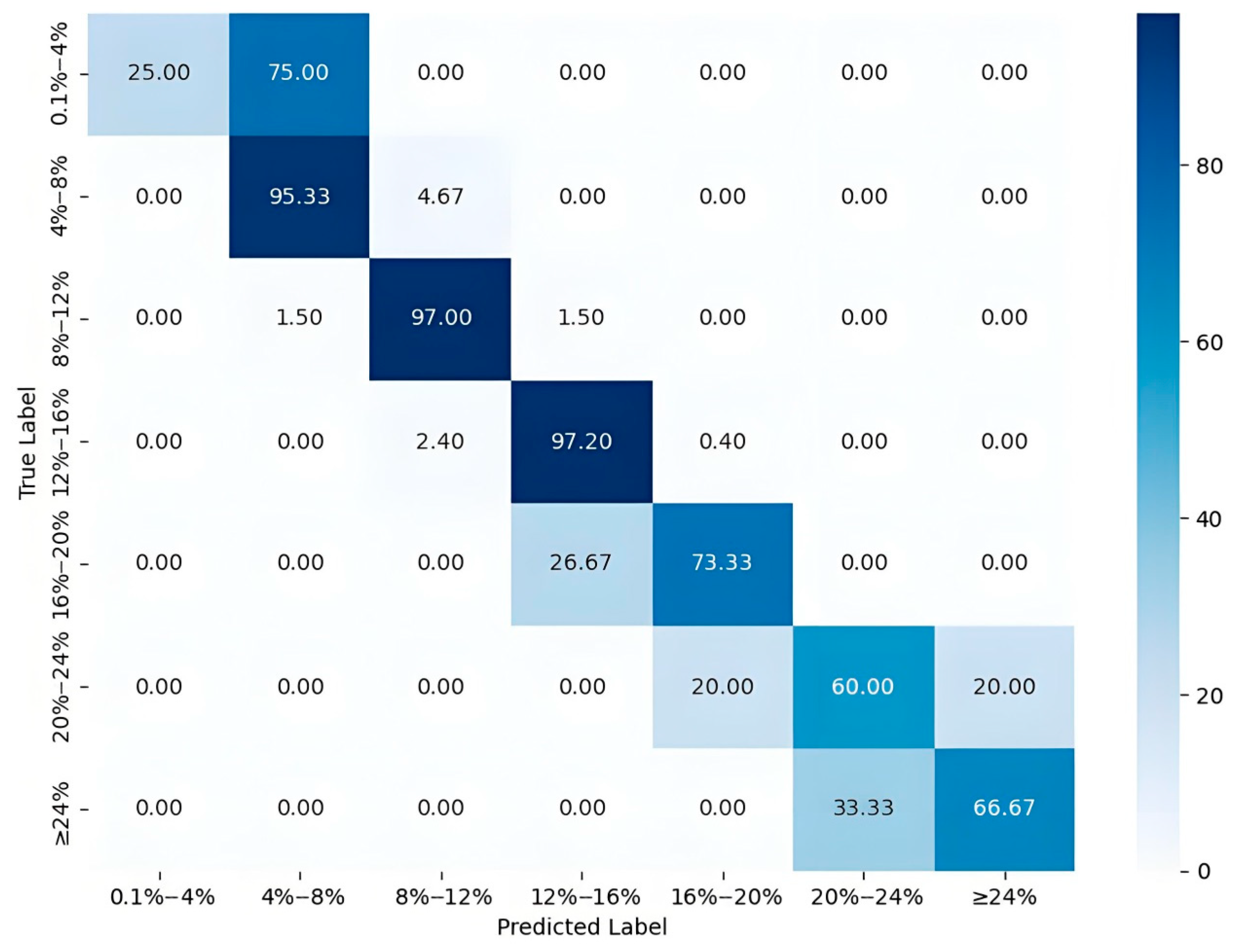
3.3. Intelligent Interpretation Model of Porosity Based on Different Algorithms
3.3.1. The OVO SVM Porosity Interpretation
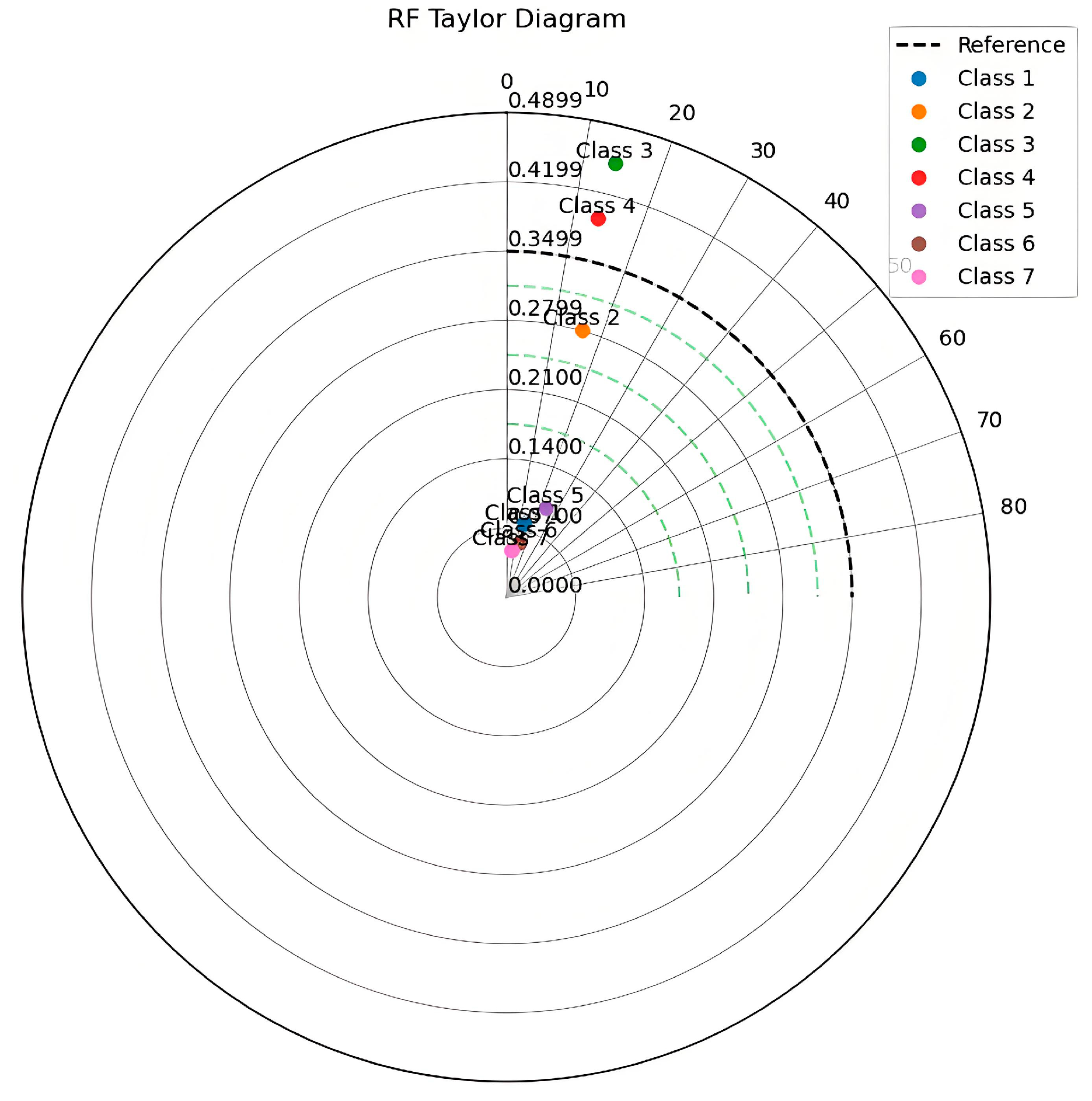
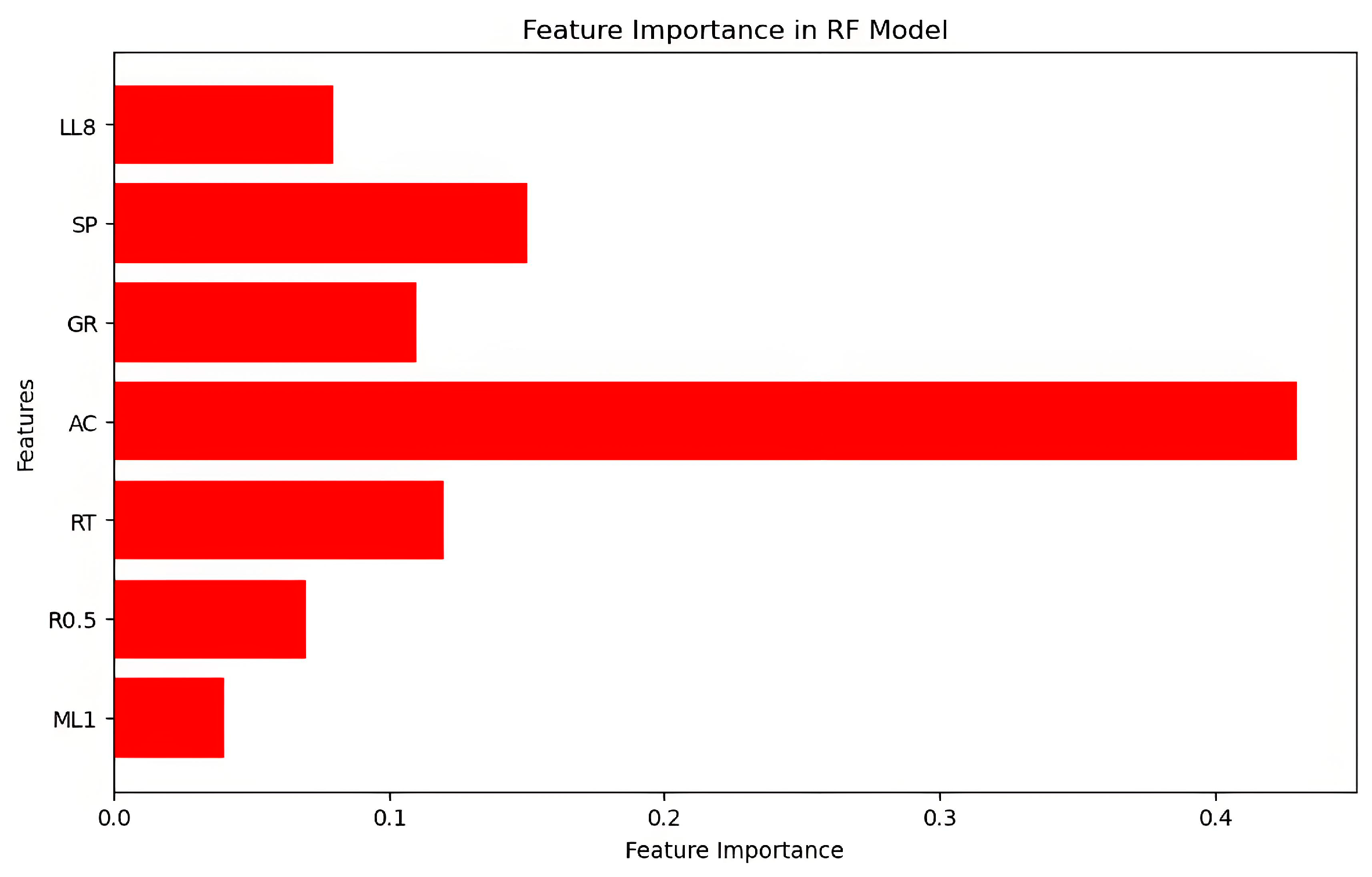
3.3.2. The RF Porosity Interpretation
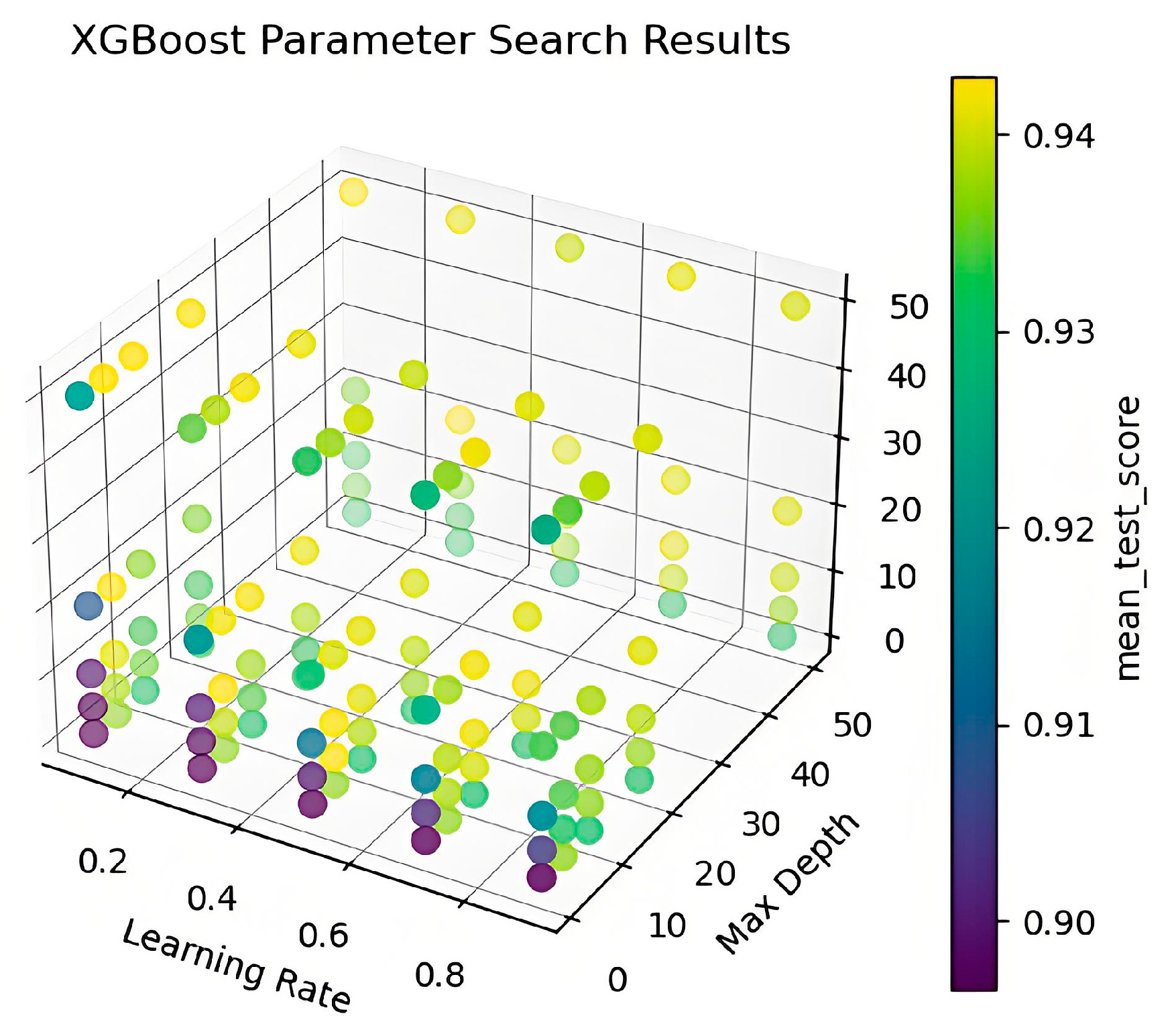
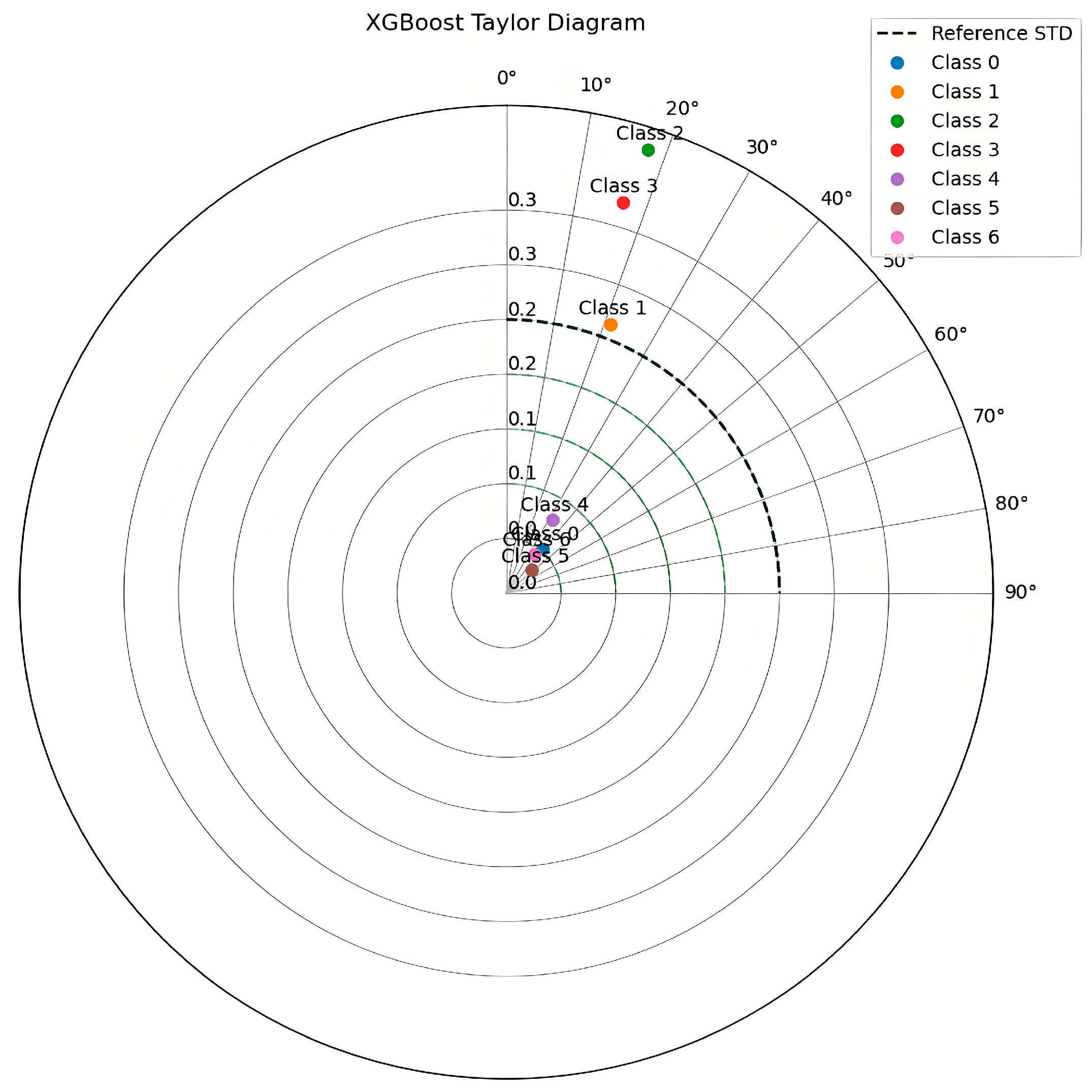
3.3.3. The XGBoost Porosity Interpretation
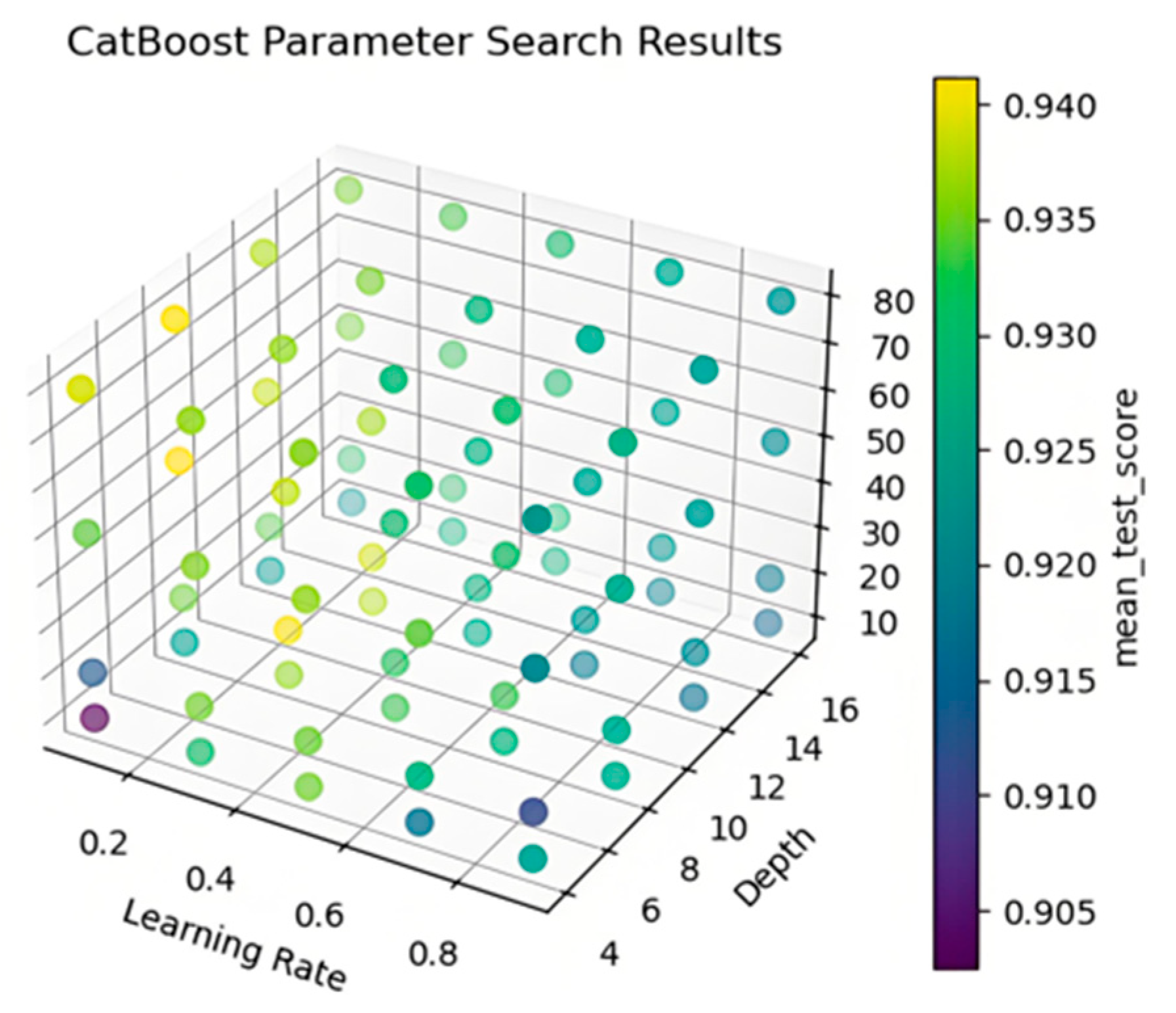
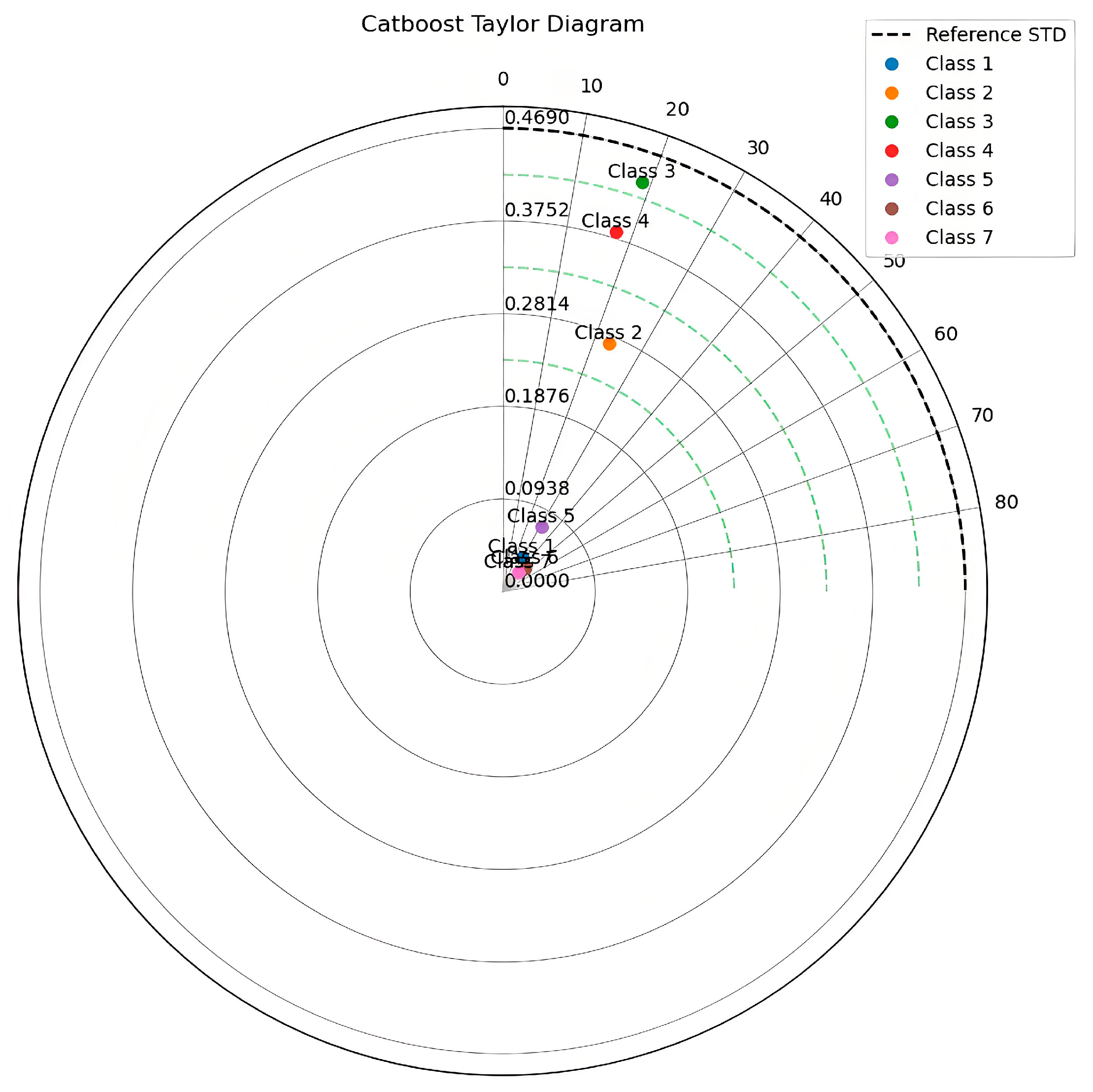
3.3.4. The CatBoost Porosity Interpretation
3.4. Porosity Interpretation
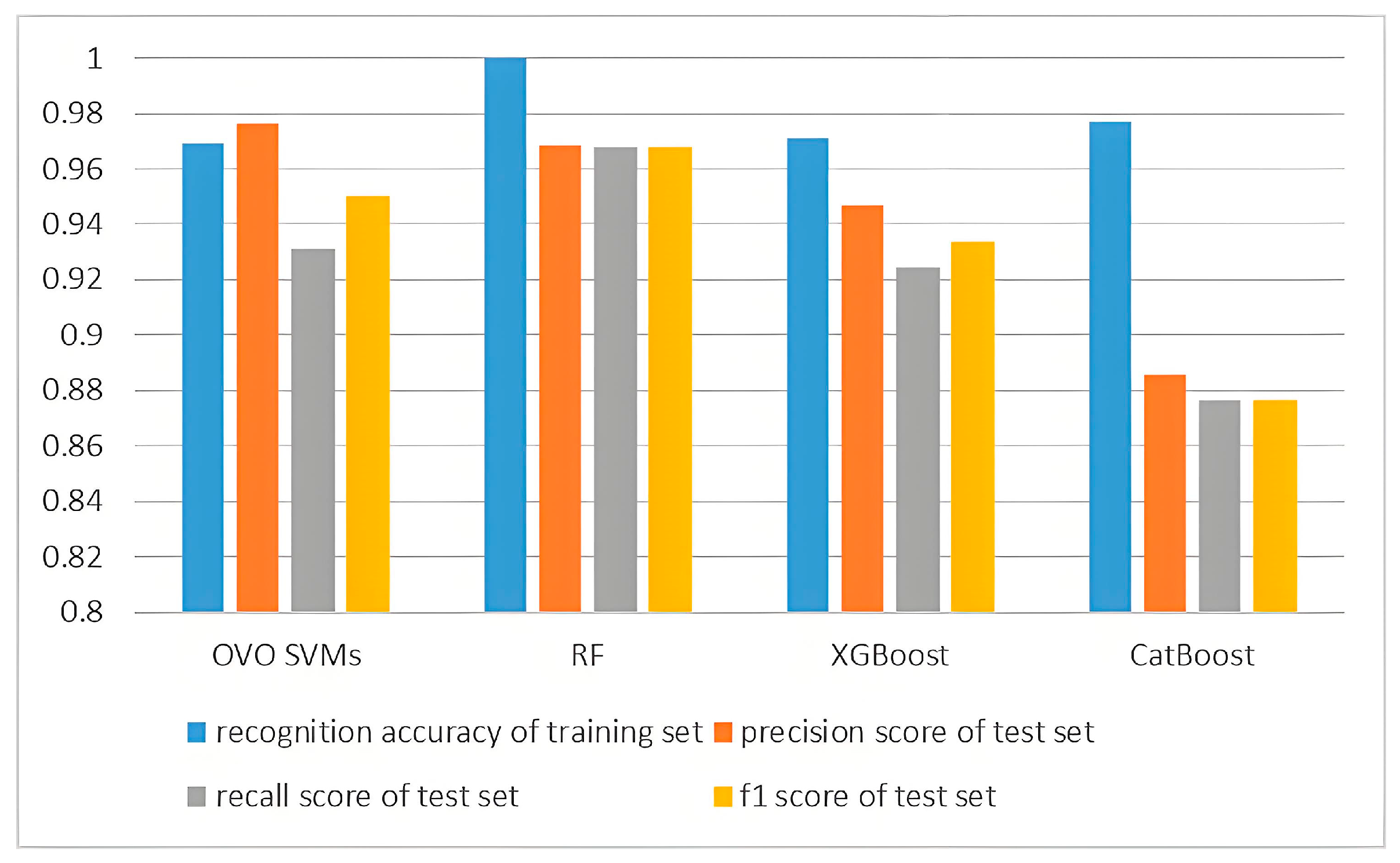
4. Results and Discussion
5. Conclusions
- (a)
- Before initiating model training, conducting a thorough correlation analysis of the input data is a crucial step in avoiding data redundancy and reducing data dimensionality, thereby enhancing computational accuracy and shortening model training time.
- (b)
- The rational application of grid search combined with cross-validation methods for model parameter optimization is of utmost importance, as it directly influences whether the model parameter optimization can achieve a globally optimal solution rather than merely a locally optimal one.
- (c)
- In the reservoir case studied in this paper, through a comprehensive comparison of the recognition accuracy of the training set, precision, recall, and F1 scores of the test set, we ultimately selected the RF model as the tool for porosity interpretation. This model demonstrated the highest recognition accuracy on the training set and also achieved the highest recall and F1 scores on the test set, with a precision score exceeding 96%, showcasing exceptional performance.
- (d)
- Given the diverse data structures and information categories, various machine learning algorithms each exhibit their unique advantages. Therefore, when interpreting reservoir porosity in different blocks, we should construct interpretation models based on multiple machine learning algorithms and select the optimal model for practical application.
- (e)
- The methodology proposed in this study can be applied to other sandstone reservoirs; however, its application necessitates reconstructing the model and re-optimizing parameters using data from the new study area, reflecting certain limitations in generalizability. To address this issue, our team is currently focusing on the development of transfer learning algorithms based on an unsupervised domain adaptation framework. This method is intended to be employed in future work to interpret sandstone reservoir porosity, with the aim of enhancing the applicability of the methodology and increasing the scientific significance of related research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Li, Q.; Chen, M.; Ren, L.; Huang, G.; Li, C.; Zhang, Z. Optimization of models for a rapid identification of lithology while drilling-A win-win strategy based on machine learning. J. Pet. Sci. Eng. 2019, 176, 321–341. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, R.; Chen, M.; Chen, B.; Wang, X.; Li, Q.; Ren, L. Identification of Porosity and Permeability While Drilling Based on Machine Learning. Arab. J. Sci. Eng. 2021, 46, 7031–7045. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, R. Application of Principal Component Analysis and Least Square Support Vector Machine to Lithology Identification. Well Logging Technol. 2009, 33, 425–429. [Google Scholar]
- Li, R.; Zhong, Y. Dentification Method of Oil/Gas/Water Layer Based on Least Square Support Vector Machine. Nat. Gas Explor. Dev. 2009, 32, 15–18+72. [Google Scholar]
- Song, Y.; Zhang, J.; Yan, W.; He, W.; Wang, D. A new identification method for complex lithology with support vector machine. J. Daqing Pet. Inst. 2007, 31, 18–20. [Google Scholar]
- Li, X.; Li, H. A new method of identification of complex lithologies and reservoirs: Task-driven data mining. J. Pet. Sci. Eng. 2013, 109, 241–249. [Google Scholar] [CrossRef]
- Xie, Y.; Zhu, C.; Zhou, W.; Li, Z.; Liu, X.; Tu, M. Evaluation of machine learning methods for formation lithology identification: A comparison of tuning processes and model performances. J. Pet. Sci. Eng. 2018, 160, 182–193. [Google Scholar] [CrossRef]
- Dong, S.; Wang, Z.; Zeng, L. Lithology identification using kernel Fisher discriminant analysis with well logs. J. Pet. Sci. Eng. 2016, 143, 95–102. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R. Integration of spectral, spatial and morphometric data into lithological mapping: A comparison of different Machine Learning Algorithms in the Kurdistan Region, NE Iraq. J. Asian Earth Sci. 2017, 146, 90–102. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Ebadi, M.; Hosseini, S.M. Machine learning-based models for predicting permeability in tight carbonate reservoirs. J. Pet. Sci. Eng. 2020, 192, 107273. [Google Scholar]
- Rahimi, M.; Riahi, M.A. Reservoir facies classification based on random forest and geostatistics methods in an offshore oilfield. J. Appl. Geophys. 2022, 201, 104640. [Google Scholar] [CrossRef]
- Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial Neural Networks in the domain of reservoir characterization: A review from shallow to deep models. Comput. Geosci. 2020, 135, 104357. [Google Scholar] [CrossRef]
- Zhu, L.; Wei, J.; Wu, S.; Zhou, X.; Sun, J. Application of unlabelled big data and deep semi-supervised learning to significantly improve the logging interpretation accuracy for deep-sea gas hydrate-bearing sediment reservoirs. Energy Rep. 2022, 8, 2947–2963. [Google Scholar] [CrossRef]
- Liu, G.; Gong, R.; Shi, Y.; Wang, Z.; Mi, L.; Yuan, C.; Zhong, J. Construction of well logging knowledge graph and intelligent identification method of hydrocarbon bearing formation. Pet. Explor. Dev. 2022, 49, 572–585. [Google Scholar] [CrossRef]
- Alatefi, S.; Azim, R.A.; Alkouh, A.; Hamada, G. Integration of Multiple Bayesian Optimized Machine Learning Techniques and Conventional Well Logs for Accurate Prediction of Porosity in Carbonate Reservoirs. Processes 2023, 11, 1339. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S.; Aleksandrov, A.N. Analysis of reservoir rock permeability changes due to solid precipitation during waterffooding using artiffcial neural network. J. Pet. Explor. Prod. Technol. 2025, 15, 17. [Google Scholar] [CrossRef]
- Ghanizadeh, A.R.; Ghanizadeh, A.; Asteris, P.G.; Fakharian, P.; Armaghani, D.J. Developing bearing capacity model for geogrid-reinforced stone columns improved soft clay utilizing MARS-EBS hybrid method. Transp. Geotech. 2023, 38, 100906. [Google Scholar] [CrossRef]
- Ali, A.; Aliyuda, K.; Elmitwally, N.; Bello, A.M. Towards more accurate and explainable supervised learning-based prediction of deliverability for underground natural gas storage. Appl. Energy 2022, 327, 120098. [Google Scholar] [CrossRef]
- Ali, A. Data-driven based machine learning models for predicting the deliverability of underground natural gas storage in salt caverns. Energy 2021, 229, 120648. [Google Scholar] [CrossRef]
- Aliyuda, K.; Howell, J.; Hartley, A.; Ali, A. Stratigraphic controls on hydrocarbon recovery in clastic reservoirs of the Norwegian Continental Shelf. Pet. Geosci. 2021, 27, petgeo2019-133. [Google Scholar] [CrossRef]
- Li, H.; Tan, Q.; Deng, J.; Dong, B.; Li, B.; Guo, J.; Zhang, S.; Bai, W. A Comprehensive Prediction Method for Pore Pressure in Abnormally High-Pressure Blocks Based on Machine Learning. Processes 2023, 11, 2603. [Google Scholar] [CrossRef]
- Delavar, M.R.; Ramezanzadeh, A. Pore Pressure Prediction by Empirical and Machine Learning Methods Using Conventional and Drilling Logs in Carbonate Rocks. Rock Mech. Rock Eng. 2023, 56, 535–564. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Zhang, L. A data-driven approach for shale gas production forecasting based on machine learning. Energy 2020, 211, 118689. [Google Scholar]
- Kang, L.; Guo, W.; Zhang, X.; Liu, Y.; Shao, Z. Differentiation and Prediction of Shale Gas Production in HorizontalWells: A Case Study of the Weiyuan Shale Gas Field, China. Energies 2022, 15, 6161. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, C.; Cheng, Y.; Luo, X.; Qiu, X. Using a Deep Neural Network with Small Datasets to Predict the Initial Production of Tight Oil Horizontal Wells. Electronics 2023, 12, 4570. [Google Scholar] [CrossRef]
- Wang, Z.; Tang, H.; Cai, H.; Hou, Y.; Shi, H.; Li, J.; Yang, T.; Feng, Y. Production prediction and main controlling factors in a highly heterogeneous sandstone reservoir: Analysis on the basis of machine learning. Energy Sci. Eng. 2022, 10, 4674–4693. [Google Scholar] [CrossRef]
- Wang, K.; Xie, M.; Liu, W.; Li, L.; Liu, S.; Huang, R.; Feng, S.; Liu, G.; Li, M. New Method for Capacity Evaluation of Offshore Low-Permeability Reservoirs with Natural Fractures. Processes 2024, 12, 347. [Google Scholar] [CrossRef]
- Gao, M.; Wei, C.; Zhao, X.; Huang, R.; Yang, J.; Li, B. Production Forecasting Based on Attribute-Augmented Spatiotemporal Graph Convolutionttal Network for a Typical Carbonate Reservoir in the Middle East. Energies 2023, 16, 407. [Google Scholar] [CrossRef]
- Sun, J.; Li, Q.; Chen, M.; Ren, L. Optimization of model for identification of oil /gas and water layers while drilling based on machine. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2019, 34, 79–85, 90. [Google Scholar]
- Chang, Y.W.; Hsieh, C.J.; Chang, K.W.; Ringgaard, M.; Lin, C.-L. Training and testing low-degree polynomial data mappings via linear SVM. J. Mach. Learn. Res. 2010, 11, 1471–1490. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fakharian, P.; Nouri, Y.; Ghanizadeh, A.R.; Jahanshahi, F.S.; Naderpour, H.; Kheyroddin, A. Bond strength prediction of externally bonded reinforcement on groove method (EBROG) using MARS-POA. Compos. Struct. 2024, 349–350, 118532. [Google Scholar] [CrossRef]
- Nouri, Y.; Ghanizadeh, A.R.; Jahanshahi, F.S.; Fakharian, P. Data-driven prediction of axial compression capacity of GFRP-reinforced concrete column using soft computing methods. J. Build. Eng. 2025, 101, 111831. [Google Scholar] [CrossRef]
- Van den Bossche, J.; Bostoen, R.; Ongenae, F. A systematic review on data cleaning for fraud detection. Knowl. Inf. Syst. 2019, 60, 139–163. [Google Scholar]
- Zaki, M.J.; Meira, A., Jr. Fundamentals of Data Mining Algorithms; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rubicondo, J.G., Jr.; Caires, E.; Barbon, S. Data cleaning: A review of literature and case studies. Data Sci. J. 2019, 18, 8. [Google Scholar]





| Depth | ILD | ILM | LL8 | SP | GR | AC | RT | RXO | R0.5 | ML1 | ML2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2319.125 | 0.158097 | 0.31127 | 0.260079 | 0.268738 | 0.153086 | 0.198764 | 0.300401 | 0.352655 | 0.949788 | 0.104695 | 0.125684 |
| 2319.250 | 0.153399 | 0.286822 | 0.271505 | 0.269231 | 0.147443 | 0.195926 | 0.308435 | 0.36692 | 0.91825 | 0.088032 | 0.085521 |
| 2319.375 | 0.147734 | 0.258977 | 0.260385 | 0.26997 | 0.140037 | 0.193524 | 0.315476 | 0.379313 | 0.880461 | 0.129992 | 0.127416 |
| 2319.500 | 0.140306 | 0.228678 | 0.221904 | 0.270935 | 0.135096 | 0.193306 | 0.321289 | 0.389241 | 0.837252 | 0.190682 | 0.181097 |
| 2319.625 | 0.130939 | 0.197886 | 0.164352 | 0.272088 | 0.133687 | 0.198546 | 0.325685 | 0.396381 | 0.789591 | 0.222265 | 0.220757 |
| 2319.750 | 0.120564 | 0.170567 | 0.104484 | 0.273379 | 0.140387 | 0.210991 | 0.328517 | 0.400683 | 0.738402 | 0.251911 | 0.243474 |
| 2319.875 | 0.110404 | 0.148911 | 0.060793 | 0.274778 | 0.159436 | 0.231079 | 0.329576 | 0.402097 | 0.684951 | 0.286981 | 0.268704 |
| 2320.000 | 0.100757 | 0.132651 | 0.036448 | 0.276272 | 0.180248 | 0.256624 | 0.328587 | 0.400628 | 0.630979 | 0.286551 | 0.28751 |
| 2320.125 | 0.091939 | 0.120813 | 0.023516 | 0.277838 | 0.203529 | 0.282825 | 0.325442 | 0.39655 | 0.575928 | 0.346724 | 0.33769 |
| 2320.250 | 0.084441 | 0.112462 | 0.016824 | 0.279412 | 0.2321 | 0.305314 | 0.319656 | 0.389395 | 0.52201 | 0.364809 | 0.384799 |
| 2320.375 | 0.07815 | 0.106703 | 0.013812 | 0.280956 | 0.252558 | 0.320162 | 0.312312 | 0.379963 | 0.470374 | 0.170208 | 0.206699 |
| 2320.500 | 0.07292 | 0.102917 | 0.012877 | 0.28245 | 0.265608 | 0.325838 | 0.303755 | 0.368527 | 0.421516 | 0.13419 | 0.121346 |
| 2320.625 | 0.068934 | 0.100436 | 0.01315 | 0.28385 | 0.273017 | 0.32169 | 0.29434 | 0.35523 | 0.375767 | 0.114427 | 0.103136 |
| 2320.750 | 0.065878 | 0.098742 | 0.014168 | 0.285162 | 0.271958 | 0.307498 | 0.284225 | 0.340207 | 0.333638 | 0.099421 | 0.090418 |
| OVO SVM Optimal Parameters | RF Optimal Parameters | XGBoost Optimal Parameters | CatBoost Optimal Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C | gamma | n_estimators | max_features | n_estimators | max_depth | learning_rate | iterations | depth | learning_rate |
| 2000 | 0.001 | 40 | 5 | 20 | 5 | 0.1 | 50 | 8 | 0.1 |
| Class | STD_Pred | Correlation | RMSE |
|---|---|---|---|
| Class 1 | 0.051594 | 0.853779 | 0.046386 |
| Class 2 | 0.280806 | 0.929577 | 0.106865 |
| Class 3 | 0.449875 | 0.950449 | 0.146594 |
| Class 4 | 0.394054 | 0.955654 | 0.120511 |
| Class 5 | 0.096226 | 0.908963 | 0.046845 |
| Class 6 | 0.052204 | 0.975684 | 0.017938 |
| Class 7 | 0.048500 | 0.987033 | 0.008129 |
| Class | STD_Pred | Correlation | RMSE |
|---|---|---|---|
| Class 1 | 0.076198 | 0.972555 | 0.019327 |
| Class 2 | 0.280992 | 0.962624 | 0.077907 |
| Class 3 | 0.453123 | 0.969993 | 0.114383 |
| Class 4 | 0.394744 | 0.972066 | 0.095784 |
| Class 5 | 0.098780 | 0.918795 | 0.044239 |
| Class 6 | 0.057242 | 0.977919 | 0.014829 |
| Class 7 | 0.048382 | 0.993852 | 0.005757 |
| Class | STD_Pred | Correlation | RMSE |
|---|---|---|---|
| Class 1 | 0.044073 | 0.781405 | 0.060956 |
| Class 2 | 0.221556 | 0.932605 | 0.114025 |
| Class 3 | 0.357986 | 0.952606 | 0.205588 |
| Class 4 | 0.313091 | 0.958208 | 0.140226 |
| Class 5 | 0.066571 | 0.847971 | 0.070348 |
| Class 6 | 0.026577 | 0.672535 | 0.057876 |
| Class 7 | 0.036586 | 0.819678 | 0.041750 |
| Class | STD_Pred | Correlation | RMSE |
|---|---|---|---|
| Class 1 | 0.040124 | 0.878011 | 0.050366 |
| Class 2 | 0.273869 | 0.920221 | 0.113165 |
| Class 3 | 0.438619 | 0.946722 | 0.152930 |
| Class 4 | 0.381907 | 0.954257 | 0.122389 |
| Class 5 | 0.076752 | 0.858772 | 0.060329 |
| Class 6 | 0.032695 | 0.741480 | 0.046068 |
| Class 7 | 0.025201 | 0.795544 | 0.033822 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Tang, K.; Ren, L.; Zhang, Y.; Zhang, Z. Intelligent Interpretation of Sandstone Reservoir Porosity Based on Data-Driven Methods. Processes 2025, 13, 2775. https://doi.org/10.3390/pr13092775
Sun J, Tang K, Ren L, Zhang Y, Zhang Z. Intelligent Interpretation of Sandstone Reservoir Porosity Based on Data-Driven Methods. Processes. 2025; 13(9):2775. https://doi.org/10.3390/pr13092775
Chicago/Turabian StyleSun, Jian, Kang Tang, Long Ren, Yanjun Zhang, and Zhe Zhang. 2025. "Intelligent Interpretation of Sandstone Reservoir Porosity Based on Data-Driven Methods" Processes 13, no. 9: 2775. https://doi.org/10.3390/pr13092775
APA StyleSun, J., Tang, K., Ren, L., Zhang, Y., & Zhang, Z. (2025). Intelligent Interpretation of Sandstone Reservoir Porosity Based on Data-Driven Methods. Processes, 13(9), 2775. https://doi.org/10.3390/pr13092775







