Effect of Burial Depth, Cavern Shape, and Sealing Layer on the Mechanical Behaviour of Abandoned Mines for Compressed Air Energy Storage

Abstract

As renewable energy adoption intensifies, the demand for efficient and large-scale storage technologies such as compressed air energy storage (CAES) has become critical. Abandoned mine caverns present a cost-effective and sustainable option for CAES, enabling the reuse of existing underground spaces while minimizing new excavation. This study aims to quantitatively evaluate the stability of abandoned mine caverns for CAES under varying burial depths (150 m, 300 m, 450 m), cavern geometries (rectangular, trapezoidal, straight-wall arch, and circular) and sealing layer (steel, polymer) in Class II rock mass conditions. Finite element modelling employing ABAQUS was employed to simulate excavation, lining installation, and high-pressure gas storage, incorporating an analysis of surrounding rock strain, plastic zone development, and sealing layer performance. Results indicate that geometry and burial depth are dominant factors controlling deformation, with straight-wall arch caverns inducing relatively minimal disturbance to the ground surface after excavation and lining, and circular caverns showing the highest stability after pressurization. Steel sealing layers significantly improve structural performance, while polymer layers have a limited effect. The findings provide engineering guidance for the safe retrofit and design of CAES facilities in abandoned mines.

1. Introduction

The growing integration of intermittent renewable energy sources such as wind and solar has intensified the demand for large-scale, flexible, and cost-effective energy storage technologies. Compressed air energy storage (CAES) stands out for its scalability, grid-balancing capability, and rapid response, making it particularly suitable for peak shaving and frequency regulation services [1,2].

Reutilising abandoned mines as underground storage caverns offers a cost-efficient and environmentally sustainable approach, minimising excavation needs and capital investment when supporting the energy transition [3,4,5]. Recent projects, such as the 300 MW/1200 MWh CAES facility in Jiangsu, China, reflect growing global interest in this technology [6].

CAES systems are typically classified as isothermal, diabatic, or adiabatic, depending on their thermal energy management during compression and expansion. Hybrid configurations incorporating Concentrated Solar Power (CSP) and other renewables have also been explored to enhance round-trip efficiency and operational flexibility [7,8]. Significant research has been dedicated to optimising cavern geometry, lining systems, thermal regulation, and sealing integrity [9,10,11].

Nevertheless, the mechanical stability and sealing reliability of underground caverns under long-term cyclic pressurisation, especially repurposing mine shafts, are great challenges. Previous studies have involved thermo-mechanical coupling [12,13,14], air leakage through sealing interfaces [15,16], and the permeability of concrete and rock surrounding lined caverns [17]. Others are related to multi-objective optimisation frameworks for prestressed liners [18] and crack evolution under pressure cycling [19].

A wide range of sealing materials—including metallic liners, polymer membranes, shotcrete, and bentonite-based barriers—have been employed in underground gas storage applications. However, under cyclic high-pressure loading, comparative assessments of their deformation compatibility, gas migration resistance, and long-term sealing performance remain limited. In this context, Cui et al. [20] conducted a series of studies on bentonite, providing critical insights into its applicability as a sealing material. They developed a coupled thermal–hydraulic–gas transport model to quantify the temperature-dependent behaviour of gas migration in saturated bentonite, and designed a novel apparatus for accurately measuring gas transport in ultralow-permeability geomaterials [21]. Their experiments further revealed that bentonite exhibits successive gas breakthrough phenomena under rigid boundary conditions [22], and that alkaline environments can significantly degrade swelling capacity and sealing efficiency [23]. These findings offer valuable theoretical and experimental support for the use of bentonite-based sealing systems in CAES caverns, especially where flexibility, self-sealing, and chemical resilience are required.

However, there are still some issues. Most studies focus on fixed geometries (e.g., circular or horseshoe-shaped), lacking a comparative analysis across alternative shapes (rectangular, trapezoidal, straight-wall arch) with equal cross-sectional areas [11,13,24]. Moreover, the influence of the burial depth on plastic deformation, surface subsidence, and strain localisation is underexplored [12,25]. Meanwhile, sealing material diversity is underrepresented, which is a limited evaluation of mechanical performance differences between rigid metallic liners and flexible polymer coatings under high-pressure cycling [15,16,17]. Stress concentration at corners or vault–wall junctions in non-circular shapes is also neglected, despite its implications for fatigue damage and early leakage [18,19].

In order to quantitatively assess the plastic zones, strain fields, and stress localisation of CAES caverns that are equal in cross-sectional area with different shapes and sealing materials, this study develops a finite element framework in ABAQUS to simulate the mechanical behaviour of four typical cavern geometries, including rectangular, trapezoidal, straight-wall arch, and circular, across three burial depths (150 m, 300 m, 450 m) under 10 MPa gas storage pressure. The model separately simulates excavation and pressurisation phases to assess deformation evolution and stress concentration. Furthermore, a comparative analysis of steel versus polymer sealing layers is conducted to explore material selection in diverse geological settings. The findings could provide theoretical insight and practical guidance for cavern retrofitting, site selection, and sealing system configuration, particularly in engineering about repurposing abandoned mining infrastructure.

2. Finite Element Analysis of CAES Cavern

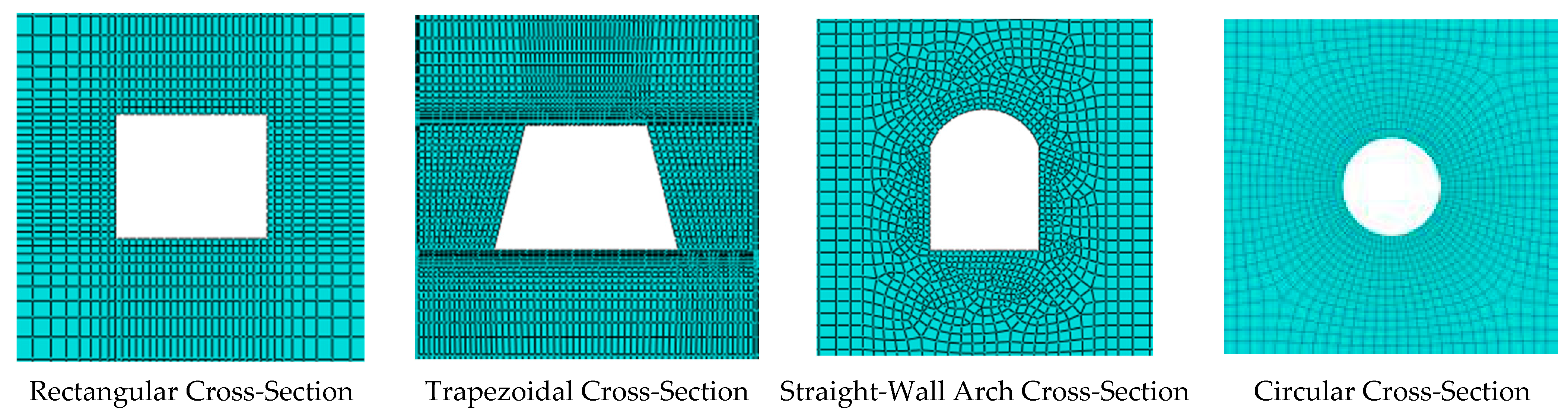
2.1. Cavern Shape of Abandoned Mines for CAES

The geometry of the cavern cross-section of the abandoned mines significantly influences the performance and safety of CAES systems [18]. The semi-circular arch section offers structural simplicity, ease of construction, and suitability for environments characterized by high roof pressure and low lateral pressure. Consequently, it is commonly employed for gas storage caverns and air transmission channels. However, under conditions of high lateral pressure, supplemental support is typically required to ensure stability.

In contrast, horseshoe-shaped sections of the abandoned mines exhibit superior resistance to both substantial roof and lateral pressures. This makes them well-suited for installations in soft, expansive surrounding rock, where they provide enhanced safety and durability. Their construction, however, is more complex.

Ultimately, selecting the optimal cavern cross-section shape of the abandoned mines is critical for maximizing the efficiency and safety of CAES installations [19]. To accommodate complex geologic conditions, operational requirements (mining requirements), and economic constraints, various shapes, including semi-circular arches, horseshoe shapes, circular arches, and circular interfaces, are utilized during mine cavern excavation [11].

2.2. CAES Cavern Dimensions

In abandoned mine caverns, a variety of cross-sectional geometries can be encountered. In this study, four representative configurations, including rectangular, trapezoidal, straight-wall arch, and circular, were selected for comparative analysis, with their cross-sectional areas kept equal to each other. The rectangular section has a width of 10 m and a height of 8 m. The trapezoidal section has upper and lower base widths of 8 m and 12 m, with a height of 8 m. The circular section has a radius of approximately 5.05 m, and the vaulted portion of the straight-wall arch section is formed by a segment of a circle.

The cross-sectional area S of a straight-wall arch section with an arched roof is given by the following equation:

S = D(H + 0.241 h),

(1)

where D is the net width of the roadway, H is the height of the wall, and h is the height of the arch [26]. After calculation, section D of the circular arc arch is 8 m, H is 8 m, and h is 2.67 m.

The burial depth of all caverns is 150 m, 300 m, and 450 m, respectively. In order to simplify the analysis, the thickness of concrete lining is uniformly set to 50 cm without considering the interference effect between caverns.

The design of lining thickness should integrate both surrounding rock classification and cavern geometry, drawing on the findings of Jiang et al. [19] and relevant design standards. For Class II rock masses, a lining thickness of 50 cm is recommended. To minimise the influence of thickness variations on simulation results, this study adopts a uniform 50 cm thickness in all numerical models.

2.3. Numerical Simulation Schemes for CAES

In order to construct the numerical analysis model of tunnel-type caverns, the distance between the left, right, and top and bottom boundaries of the model is set to be three times the diameter of the cavern, so as to weaken the boundary effect on the calculation results. The distance from the top of the cavern to the ground surface is determined based on the designed burial depth to evaluate the surface deformation response. The simulation adopts a two-dimensional planar model, assuming that the section is in a plane strain state. Owing to the substantial length-to-width ratio of caverns, their mechanical behaviour can be appropriately represented under the plane strain assumption, wherein two-dimensional modelling achieves markedly higher computational efficiency than three-dimensional simulations without compromising analytical reliability [11,27]. For the boundary conditions, horizontal (x-direction) displacement constraints are imposed on the left and right boundaries of the model, vertical (y-direction) displacement constraints are imposed on the lower boundary, and the surface boundary is set as a free boundary. The mesh division is based on structured quadrilateral cells, and the mesh division of the cavern area located at a burial depth of 150 m is shown in Figure 1.

The numerical simulation procedure comprises three phases. First, the geostatic stress equilibrium is established through applying gravitational loading prior to excavation. Second, excavation and lining construction triggers stress redistribution. Third, the sealing layer models are established for analysing their effects on the mechanical behaviour of the abandoned mines. But, it should be noted that sealing layer analyses were only conducted on the circular cavern. Finally, 10 MPa air pressure is imposed in the CAES cavern to assess the development of the surrounding rock plastic zone and reinforced concrete lining deformation. According to Wang et al. [28], several completed CAES facilities in China, including the Pingjiang project in Hunan (2017), the Suichang project in Zhejiang (2019), the Hanwula Wind Farm project in Inner Mongolia (2012), and the Zhangjiakou project in Hebei (2022), are operating with a maximum storage pressure of 10 MPa. Therefore, this study adopts 10 MPa as the maximum internal pressure in the numerical simulations to ensure consistency with the operational conditions of typical large-scale CAES projects in China.

2.4. Constitutive Model and Parameters of the CAES Cavern

It is assumed that the surrounding rock material conforms to the properties of an ideal elastic–plastic material [29], based on the Mohr–Coulomb yield criterion, which has been widely applied for granite in underground engineering stability analysis:

$$({\sigma }_1-{\sigma }_3) = 2\mathrm{ccos}\phi +({\sigma }_1+{\sigma }_3)\sin \phi$$

(2)

where, σ₁ indicates the maximum principal stress (MPa), σ₃ is the minimum principal stress (MPa), c is the cohesive force of rock (MPa), and φ is the internal friction angle of rock (°).

Based on the engineering geological survey report and relevant standards (“Code for Design of Road Tunnel” JTG D70-2004 [30]), the physical and mechanical parameters of the surrounding rock are determined as shown in

Table 1. Physical and mechanical parameters of surrounding rock.

Surrounding Rock Classification	Unit Weight γ/kN/m3	Elastic Modulus E/GPa	Poisson’s Ratio μ	Internal Friction Angle φ/°	Cohesion c/MPa	Tensile Strength σₜ/MPa
II	25	30	0.2	60	2.0	2

.

The strength parameter of concrete lining is taken with reference to the Specification for design of hydraulic tunnel (DL/T5195-2004, People’s Republic of China [31]), and it is assumed to be an elastic material [11], as shown in

Table 2. Physical and mechanical properties of concrete lining.

Concrete Strength	Lining Thickness/cm	Unit Weight γ/kN/m3	Elastic Modulus E/GPa	Poisson’s Ratio μ
C30	25	25	30	0.167

.

CAES caverns typically employ steel linings or polymeric materials as sealing layers. In this study, butyl rubber is adopted as the representative polymeric sealing material. Key parameters including density and elastic modulus are empirically assigned based on established material properties [32,33], as listed in

Table 3. Physical and mechanical parameters of CAES sealing layer.

Sealing Type	Density ρ/kg/m3	Elastic Modulus E/GPa	Poisson’s Ratio μ	Coefficient of Thermal Expansion α	Thermal Conductivity λ/W/(m·K)
Steel Lining	7800	2 × 105	0.3	1.7 × 10−5	45
Polymer Materials	920	1.5	0.5	4.8 × 10−4	0.091

.

3. Calculation Results and Discussion

3.1. Cavern Stability After Excavation and Lining Installation

3.1.1. Rectangular Cavern

Under different burial depth conditions, the degree of plasticity development of the rectangular cavern after excavation and lining application is similar overall. The distribution of plastic zones in the rectangular cavern with 10 m width and 8 m height is shown in Figure 2. When the burial depth is 150 m, the surrounding rock has no obvious plastic zone, and the surface settlement is about 0.73 mm. When the burial depth increases to 300 m, the surrounding rock of the cavern basically maintains its elasticity, there is a local plasticity extension only in the four corners of the area, and the plastic zone extends to the inside of the surrounding rock for about 0.5 m. When the burial depth increases to 450 m, the surface settlement increases to 1.03 mm, the scope of the plastic zone of the surrounding rock of the wall is obviously expanded, and the maximum extension depth reaches 1 m.

3.1.2. Trapezoid Cavern

For trapezoidal caverns with an upper width of 8 m, lower width of 12 m, and height of 8 m, the distribution of plastic zones after excavation and lining application remains consistent across varying burial depths, as illustrated in Figure 3. At burial depths of 150 m and 300 m, no significant plastic zones were observed. At a burial depth of 450 m, localized plastic zones emerged near the two corners of the lower base, with a maximum tangential strain of 4.16 × 10⁻⁵ in the surrounding rock. Surface settlement increased linearly with depth, measuring 0.64 mm, 1.32 mm, and 2.00 mm at depths of 150 m, 300 m, and 450 m, respectively.

3.1.3. Straight-Wall Arch Cavern

Under the conditions of different burial depths, the plastic zones of the surrounding rock after the excavation of the straight-wall arch-shaped cavern have little change in general. The distribution of plastic zones after excavation and lining is shown in Figure 4, from which it can be seen that, at a burial depth of 150 m, the surrounding rock of the cavern basically maintains its elastic state after excavation and lining, and there is no obvious plastic zone. At a burial depth of 300 m, the surrounding rock of the cavern locally (mainly located in the surface layer of the cave wall) shows a small range of plastic zones. The corresponding surface settlements are 0.41 mm and 0.87 mm, respectively. When the burial depth is increased to 450 m, the surrounding rocks at the two corners of the bottom plate of the cavern form a local plastic zone, and the surface settlement increases to 1.33 mm.

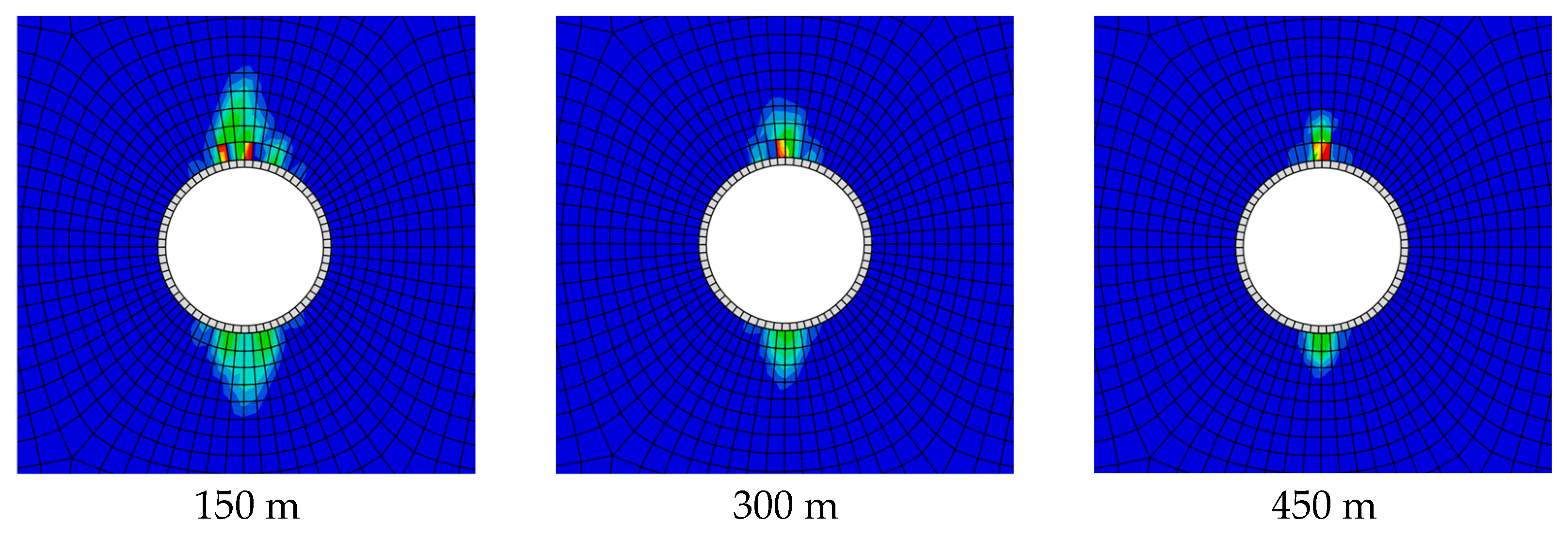
3.1.4. Circular Cavern

Under different burial depths, the circular cavern remained elastic after excavation and lining, and no significant plastic damage area is observed. For the circular cavern with a radius of 5.64 m, the surface settlement shows an increasing trend with the increase in burial depth. When the burial depth is 150 m, 300 m, and 450 m, the maximum surface settlement caused by excavation is about 0.86 mm, 1.75 mm, and 2.64 mm, respectively.

3.2. Comparison of the Mechanical Properties of the Surrounding Rock After Excavation and Lining Construction

As can be seen in Figure 5, the maximum strain around the hole of the circular cavern remains relatively stable after excavation and lining at different burial depths. When the burial depth is shallow, the maximum strain around the hole of each hole shape is less different. As can be seen from Figure 6, after excavation and lining, the straight-wall arch-shaped cavern has less disturbance to the ground surface, while the circular cavern is relatively larger.

3.3. Post-Pressurization Cavern Stability and Deformation

3.3.1. Rectangular Cavern

Under the action of 10 MPa air pressure, with the increase in burial depth, the shear-type plastic zone in the surrounding rock of the rectangular cavern gradually expands, and its evolution distribution is shown in Figure 7. The results show that the change in burial depth has limited influence on the range of plastic zones after air pressure. At 150 m and 300 m burial depth, the plastic zones are mainly distributed in the four corners of the rectangular cavern due to the fact that the self-weight of the surrounding rock is less than 10 MPa gas pressure, and corresponding surface bulges of about 1.00 mm and 0.34 mm appear respectively. With the increase in burial depth to 450 m, the self-weight of the surrounding rock slightly exceeds the air pressure, which leads to the obvious contraction of the plastic zone. The plastic zones in the four corners are significantly weakened, and the deformation of the ground surface turns to settlement, with a value of 0.32 mm.

After the gas pressure is added, the surrounding rock of the cavern is in a state of tension, and the maximum value of the first principal stress of the surrounding rock of the rectangular cavern with burial depths of 150 m, 300 m, and 450 m is 13.8 MPa, 5.8 MPa, and 1.75 MPa, respectively. It can be seen that tension damage occurs at the burial depths of 150 m and 300 m.

The location of the maximum peri-cavity strain corresponds closely to the distribution of the plastic zone, with the peak strain predominantly concentrated around the four corners of the cavern. This is accompanied by the development of plastic strain, ultimately forming distinct plastic zones. Such pronounced plastic deformation in these regions arises primarily from stress concentration effects. The peri-cavity rock strains at the corners of the cavern are relatively similar in magnitude, whereas the minimum peri-cavity strains occur at the midpoints of the four sides. These side regions are subjected to comparatively lower stress than the corners, resulting in reduced plastic strain.

At a burial depth of 150 m, the tensile strain values of the peri-cavity rock at the upper and lower corners of the rectangle are 1.18 × 10⁻³ and 0.98 × 10⁻³, respectively, with the maximum and minimum values at the four corners being 1.18 × 10⁻³ and 0.59 × 10⁻⁴. At a burial depth of 300 m, the corresponding tensile strain values at the upper and lower corners are 1.44 × 10⁻⁴ and 1.20 × 10⁻⁴, with the maximum and minimum values at the four corners being 1.44 × 10⁻⁴ and 0.72 × 10⁻⁴. At a burial depth of 450 m, the tensile strain values at the upper and lower corners are 1.45 × 10⁻⁴ and 1.21 × 10⁻⁴, with the maximum and minimum values at the four corners being 1.45 × 10⁻⁴ and 0.73 × 10⁻⁴. These results indicate that, across all examined burial depths, the maximum peri-cavity strain is approximately twice that of the minimum peri-cavity strain.

Furthermore, the influence of burial depth on peri-cavity rock strain is considerably more pronounced at shallower depths, whereas its variation becomes progressively less significant with increasing depth. For a rectangular cavern measuring 10 m in width and 8 m in height, increasing the burial depth from 150 m to 300 m results in an 88.1% reduction in the maximum peri-cavity rock strain. A subsequent increase to 450 m induces only a marginal variation, with the maximum strain remaining essentially unchanged.

Figure 8 shows the distribution of internal forces on the concrete lining of the rectangular cavity under compressed air. The axial force and shear force on the lining structure are relatively small, the internal force response is mainly dominated by the bending moment, and the bending moment shows a decreasing trend with the increase in burial depth. Calculation results show that the lining shear force is larger than the normal range.

3.3.2. Trapezoid Cavern

The distribution of plastic zones of shear damage in the trapezoidal cavern under 10 MPa air pressure under different burial depth conditions is shown in Figure 9. The results show that the influence of burial depth on the range of plastic zones is limited. At the burial depths of 150 m and 300 m, the plastic deformation is mainly concentrated in the two corners of the perimeter rock of the upper top and lower bottom of the cavern, and there are 0.98 mm and 0.45 mm bulges on the surface, respectively. When the burial depth is increased to 450 m, the plastic zone of the surrounding rock is significantly reduced, and the degree of plastic development is significantly weakened compared with the state after excavation and lining, while 0.34 mm of subsidence occurs on the surface.

After gas pressure, the surrounding rock of the cavern is in a tensile state, and the maximum values of the first principal stress of the surrounding rock of the trapezoidal cavern with burial depths of 150 m, 300 m, and 450 m are 0.86 MPa, 0.19 MPa, and 1.34 MPa, respectively. It can be seen that there is no tensile damage in the burial depths of 150 m, 300 m, and 450 m.

In the same trapezoidal cavern, there are large differences in the surrounding rock strain at different locations, with the maximum strain occurring at the two corners of the lower bottom and the minimum strain at the centre of the upper top. For the trapezoidal cavern with the upper top of 8 m, the lower bottom of 12 m, and the height of 8 m, the peri-cavity strains at the two corners of the top plate, the two corners of the bottom plate, and the centre of the top plate are 1.93 × 10⁻³, 1.60 × 10⁻³, and 1.61 × 10⁻⁴, respectively, under the burial depth of 150 m.

The change in burial depth after gas compression has a large effect on the peri-cavity rock strain. When the burial depth increased from 150 m to 300 m, the maximum peri-cavity strain decreased by 88.5%; while when the burial depth was further increased to 450 m, the maximum strain value was about doubled compared with that at 300 m.

The internal force distribution of the concrete lining in the trapezoidal cavern under compressed air conditions is shown in Figure 10. Under the condition of a consistent cross-sectional area, the values of the axial force, shear force, and bending moment of the trapezoidal cavity are higher than those of the rectangular cavity. It can be seen that the rectangular cavern is more advantageous from the perspective of lining force rationality.

3.3.3. Straight-Wall Arch Cavern

Figure 11 demonstrates the distribution of plastic zones when shear damage occurs after compression gas in the straight-wall arch cavern. The burial depths of the cavern are 150 m, 300 m, and 450 m. With the increase in the burial depth, the range of the plastic zone of the arch top is gradually reduced, and the surface deformation bulges 0.87 mm and 0.21 mm for burial depths of 150 m and 300 m, and settles at 0.43 mm for a burial depth of 450 m.

The peripheral rock of the cavern may be in a tension state after gas compression, and the maximum values of the first principal stress of the peripheral rock of the straight-wall arch cavern with burial depths of 150 m, 300 m, and 450 m are 0.91 MPa, 0.54 MPa, and 0.19 MPa, respectively. It can be seen that the peripheral rock has not been tensile-damaged under the burial depths of 150 m, 300 m, and 450 m.

The maximum rock strain around the hole in the straight-wall arch cavern at different burial depths is located at the top of the arch and the two corners of the floor, and the rock strain around the hole decreases with the increase in burial depth. Comparatively speaking, the maximum value of rock strain around the vault decreases from 1.15 × 10⁻³ at the burial depth of 150 m to 1.90 × 10⁻⁴ at the burial depth of 300 m, and decreases to 1.00 × 10⁻⁴ at the burial depth of 450 m.

The maximum internal force value of the concrete lining after compressed air in the straight-wall arch cavity is shown in Figure 12. Compared with the rectangular and trapezoidal cavity, the axial force, shear force, and bending moment of the straight-wall arch cavity decrease with the increase in burial depth. But, there is an increase at a burial depth of 450 m, which indicates that a burial depth of 300 m is more suitable.

3.3.4. Circular Cavern

Figure 13 shows the distribution characteristics of the plastic zone after compression of the straight-wall arch cavern under different burial depth conditions. When the burial depth is 150 m and 300 m, the plastic zone caused by inflation is mainly concentrated in the upper and lower sides, and the surface bulges by 1.01 mm. When the burial depth is increased to 300 m and 450 m, the range of the plastic zones at the top and bottom of the arch is obviously reduced, the surface deformation is changed to subsidence, and the corresponding amounts of subsidence are 0.50 mm and 1.78 mm, respectively.

There is a risk of tension in the surrounding rock of the circular cavern after inflation. The maximum values of the first principal stress of the surrounding rock are 1.21 MPa, 1.15 MPa, and 1.24 MPa at burial depths of 150 m, 300 m, and 450 m, respectively, and it can be seen that the surrounding rock has not been tensile-damaged.

The strain distribution characteristics of the surrounding rock around the cavern are highly consistent with the range of the plastic zone, and the maximum strain appears in the top part of the arch, followed by the bottom of the arch, and the difference between the two is relatively small. but the strain in the side wall area is the lowest. At the burial depth of 150 m, the tensile strain of the arch of the cavern with a diameter of 5.64 m is 8.67 × 10⁻⁴. When the burial depth is increased to 300 m and 450 m, the tensile strain of the arch is 9.91 × 10⁻⁴ and 8.01 × 10⁻⁴, respectively, which shows that the change in the burial depth of the circular cavern has less effect on the peripheral strains of the cavern.

The internal force distribution of the concrete lining of the circular cavern under compressed air conditions is shown in Figure 14. Compared with other hole-shaped caverns, the axial force, shear force, and bending moment of the circular cavern decrease with the increase in burial depth as in the case of the rectangular cavern. However, when the burial depth is 450 m, the bending moment of the circular cavern is smaller than that of the rectangular one, which indicates that the circular cavern is more reasonable under the same cross-sectional area.

3.4. Comparison of Mechanical Properties of Surrounding Rock After Gas Compression

According to the analysis of Figure 15, the maximum circumferential strain values of the circular cavern are similar after experiencing compressed air under each burial depth condition. From Figure 16, it can be seen that the maximum value of the first principal stress of the surrounding rock is similar between the circular cavern and the straight-wall arch-shaped cavern under different burial depths after gas compression. The circular cavern has better overall stability under compressed air working conditions, which are more suitable for the selection of cavern type in CAES projects. At the same time, all types of caverns can realize good stability under reasonable support conditions, and have feasibility in engineering applications.

Rectangular and trapezoidal caverns typically have large stress concentrations in the corner or edge areas. Rectangular structures, in particular, have higher stresses in the corners, which can lead to fatigue or rupture of the lining material. Trapezoidal structures, although they can improve the stress distribution to some extent, may still generate uneven pressure in the upper part or on both sides. In contrast, a circular cavern can distribute the external pressure uniformly over the entire cavern wall. This uniform stress distribution not only improves the stability and safety of the structure, but also reduces the risk of possible cracks, thus extending the service life of the cavern. In addition, the circular structure has no corners and the overall structure is much tighter, which helps to improve impermeability and reduce the risk of gas leakage. The circular section of the cavern chamber maintains a better seal in cases of high-pressure gas storage, ensuring the safety of the system.

4. Influence of Sealing Layer

4.1. Steel Sealing Layer

Figure 17 shows the plastic zones of shear damage after the inflation of the steel sealing layer in circular caverns with different burial depths. When the burial depth is 150 m, the plastic zone caused by inflating is concentrated at the top and bottom of the cavern, and the corresponding surface uplift is 0.99 mm. When the burial depths are 300 m and 450 m, the plastic zones of the top and bottom of the cavern are obviously reduced, and the amount of surface subsidence is 0.41 mm and 1.67 mm.

The maximum rock strain around the hole in the straight-wall arch cavern at different burial depths is located at the top of the arch and the two corners of the floor, and the rock strain around the hole decreases with the increase in burial depth. Comparatively speaking, the maximum value of rock strain around the vault decreases from 6.75 × 10⁻⁴ at 150 m burial depth to 6.53 × 10⁻⁴ at 300 m burial depth, and decreases to 4.98 × 10⁻⁴ at 450 m burial depth.

4.2. Sealing Layer of Polymer Material

The distribution of shear damage plastic zones formed by inflating the circular cavern after sealing it with a polymer material at different burial depths is shown in Figure 18. At the burial depth of 150 m, a significant plastic zone appeared at the top and bottom of the arch, and the amount of surface uplift reached 1.34 mm. When the burial depth was 300 m and 450 m, the amount of surface uplift at this time was 1.10 mm and 0.97 mm.

The maximum rock strain around the hole in the straight-wall arch cavern at different burial depths is located at the top of the arch and the two corners of the floor, and the rock strain around the hole decreases with the increase in burial depth. Comparatively speaking, the maximum value of rock strain around the vault increases from 1.13 × 10⁻³ at the burial depth of 150 m to 1.24 × 10⁻³ at the burial depth of 300 m, and increases to 1.50 × 10⁻³ at the burial depth of 450 m.

4.3. Analysis of Sealing Layer Effects

As shown in Figure 19, after applying the steel sealing layer, the maximum strain around the hole of the circular cavern after compressed air decreases with the increase in the burial depth, and, compared to that without a sealing layer, the maximum strain around the hole is significantly reduced. Additionally, the amount of surface settlement and bulging is reduced compared to that without a steel lining sealing layer; after applying polymer material, due to the large plasticity of polymer material, the maximum strain around the hole increases with the increase in burial depth and increases compared with the value without a sealing layer, and the amount of surface bulging decreases with the increase in burial depth.

Xia et al. [32] reported that, under typical operating conditions (operating pressure 4.5–10.0 MPa, surrounding rock elastic modulus 14 GPa), steel liners made of the same material can meet the service life requirements of CAES caverns under cyclic loading. Their findings indicate that liner fatigue life increases with higher surrounding rock modulus, but decreases with greater operating pressure and larger initial crack size. Zhou et al. [33] found that butyl rubber (IIR), ethylene–propylene–diene monomer (EPDM), natural rubber (NR), and fiberglass-reinforced plastic (FRP) all satisfy both airtightness and mechanical performance requirements, making them suitable sealing layer materials for CAES caverns. In this study, the sealing layer analysis is based on a single 10 MPa pressurization, focusing on the influence of different sealing materials on surrounding rock strain, without considering cyclic loading effects such as polymer creep or steel crack propagation. Therefore, the conclusions primarily reflect the short-term rock response under pressurization, and the long-term effects of sealing layer materials under operational conditions require further investigation.

5. Conclusions

This paper carries out the calculation of mechanical properties of the surrounding rock and lining of rectangular, trapezoidal, and straight-wall arch-shaped caverns after excavation and lining and after gas compression, and obtains the surrounding rock strains of rectangular, trapezoidal, and straight-wall arch-shaped gas compression caverns with different depths of burial in Class II surrounding rock under 10 MPa gas pressure. Meanwhile, the optimization scheme of the cave shape is obtained through comparison with the circular cave chamber. The influence of the sealing layer on the cave chamber after gas compression is investigated, and the following conclusions are obtained:

(1)

Burial depth has a greater influence on the stability of the cavern. When the burial depth is 150 m, the threat to the stability of the cavern caused by the gas pressure condition is greater than that after excavation and lining. When the burial depth is increased to 450 m, the stability is lower after excavation and lining. When the burial depth is 300 m, the degree of development of the plastic zone triggered by the two conditions of excavation and gas pressure is comparable, and the overall stability is better than that under the conditions of 150 m and 450 m burial depth, which shows a better safety. Overall, the stability of rectangular and straight-wall arch caverns with a burial depth of 450m and 300m is relatively high. Compared with other cavern shapes, the circular cavern shows better applicability in compressed air energy storage underground engineering, and thus is more suitable as the choice of cavern shape for energy storage.

(2)

Cavern shape is one of the important factors controlling the strain level of rock around the cavern. Among all the calculated cavern shapes, the trapezoidal cavern has the highest maximum peri-cavity strain value (1.60 × 10⁻³~1.93 × 10⁻³), followed by the rectangular cavern (1.08 × 10⁻³~1.18 × 10⁻³). The straight-wall arch-shaped cavern is slightly lower than the rectangular cavern (1.05 × 10⁻³~1.15 × 10⁻³), and the circular cavern has the smallest peri-cavity strain (8.01 × 10⁻⁴~9.91 × 10⁻⁴).

(3)

In this study, it was found that the shape of the cavern and the burial depth were the main influencing factors of the surrounding rock strain. The surrounding rock strains are different for different cavern shapes. When the sectional area and burial depth are the same, the maximum strains around the hole of the rectangular, trapezoidal, straight-wall arch and circular caverns are not much different. While the stability of the circular cavern is the best, the cave modification can be closer to the circular cavern to meet the requirements of different geological conditions.

(4)

Different sealing conditions have a certain impact on the stability of the compressed air energy storage cavern. The steel sealing layer can enhance the stability of the cavern after compressed air storage, while polymer material as a sealing layer is corrosion-resistant in comparison, and the stability of the cavern is similar to that of the sealing layer, so that the appropriate sealing material can be selected according to the actual working conditions.

(5)

This study is derived from simulations conducted under Class II surrounding rock conditions. There are still some disadvantages. In weaker rock masses, and commonly in such cases as Class III–IV conditions, the optimal cavern geometry may vary. Moreover, the effects of thermal fields under cyclic charge–discharge conditions also were not considered. Future work will include systematically mechanical behaviour and sensitivity analyses in the light of varying rock mass and temperature parameters to assess the performance of different cavern geometries under a wider range of geological conditions.