Research on Hole-Cleaning Technology Coupled with Prevention and Removal of Cuttings Bed
Abstract
1. Introduction
1.1. Background and Significance
1.2. State of the Art
1.2.1. Research on Key Drilling Parameter Influences
1.2.2. Research Status of Mathematical Models
1.2.3. Advances in Cleaning Tool Development
1.2.4. Research Innovation Positioning
2. Materials and Methods
2.1. Materials
2.1.1. Cutting Samples
- Density: 2.25 g/cm3.
- Particle size distribution: 0.1–5 mm.
- Clay mineral composition: 35% montmorillonite, 10% illite, and 5% kaolinite.
- Compressive strength: 12–18 MPa.
2.1.2. Drilling Fluid Properties
- Density: 1.9 g/cm3.
- Plastic viscosity: 30–50 mPa·s.
- Flow behavior index: 0.65.
- Consistency index: 0.45 Pa·sn.
- Gel strength: 2.337 Pa.
2.2. Methods
2.2.1. Numerical Simulation of Cutting Transport
- Turbulence Model: The Realizable k-ε model with enhanced wall treatment to capture near-wall flow characteristics.
- Cuttings Properties: Density 2.25 g/cm3; sphericity factor 0.6; and particle size distribution = 0.1–5 mm.
- Inlet condition: Velocity inlet with cuttings concentration = 0.05 kg/m3.
- Outlet condition: Pressure outlet with free flow.
- Wall condition: No-slip boundary for the wellbore and drill pipe walls: roughness = 0.05 mm.
2.2.2. Parameters and Optimization
Necessity of Parameter Optimization
Single-Factor Optimization Design
Orthogonal Simulation Design
2.2.3. Mechanical Cuttings Removal Tool Design
Tool Structure and Material Specifications
- Groove geometry: Trapezoidal cross-section with a depth of 8 mm, width of 12 mm, and helix angle of 30°.
- Body dimensions: Outer diameter 190 mm and length 500 mm, with threaded connections of 4½ IF for compatibility with standard drill pipes.
- Material: A 4140-alloy steel with a wear-resistant coating to withstand abrasive cuttings in J Block.
Working Mechanism
- Shearing action: A groove-induced flow creates shear stress at the bed surface, breaking cohesive bonds between fine clay-rich cuttings.
- Lifting effect: Eddies generate upward velocity components that suspend dislodged cuttings, enhancing their transport via the main annular flow.
Theoretical Basis for Spacing Calculation
- Drill string collision effect: Horizontal wellbores induce frequent collisions between the drill string and wellbore, reducing actual slip velocity by ~30% compared to vertical conditions [36].
- Tool-induced turbulence: The helical groove sub enhances local flow velocity, extending the effective transport distance of dislodged cuttings.
3. Results
3.1. Parameter Optimization Results
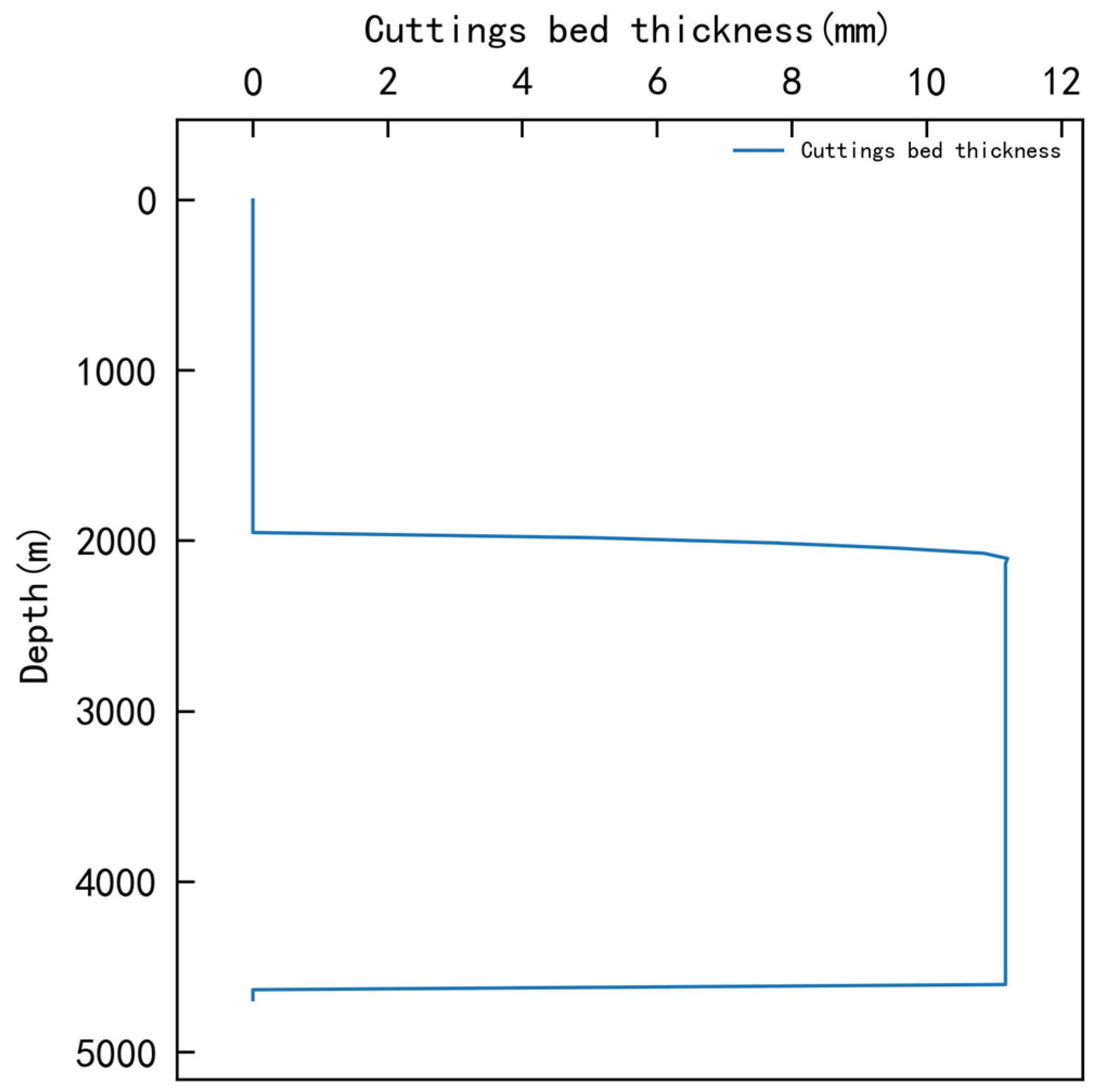
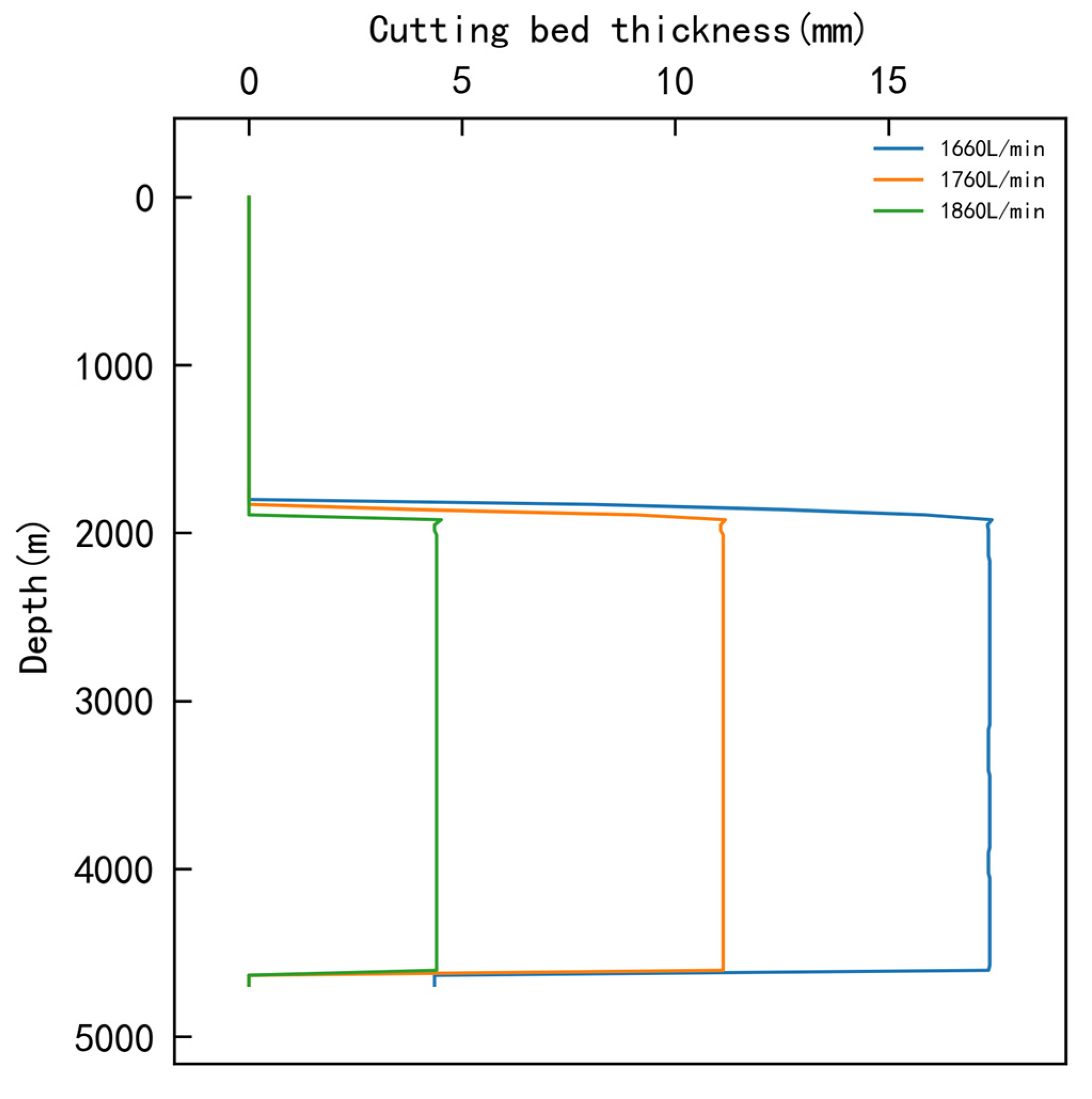
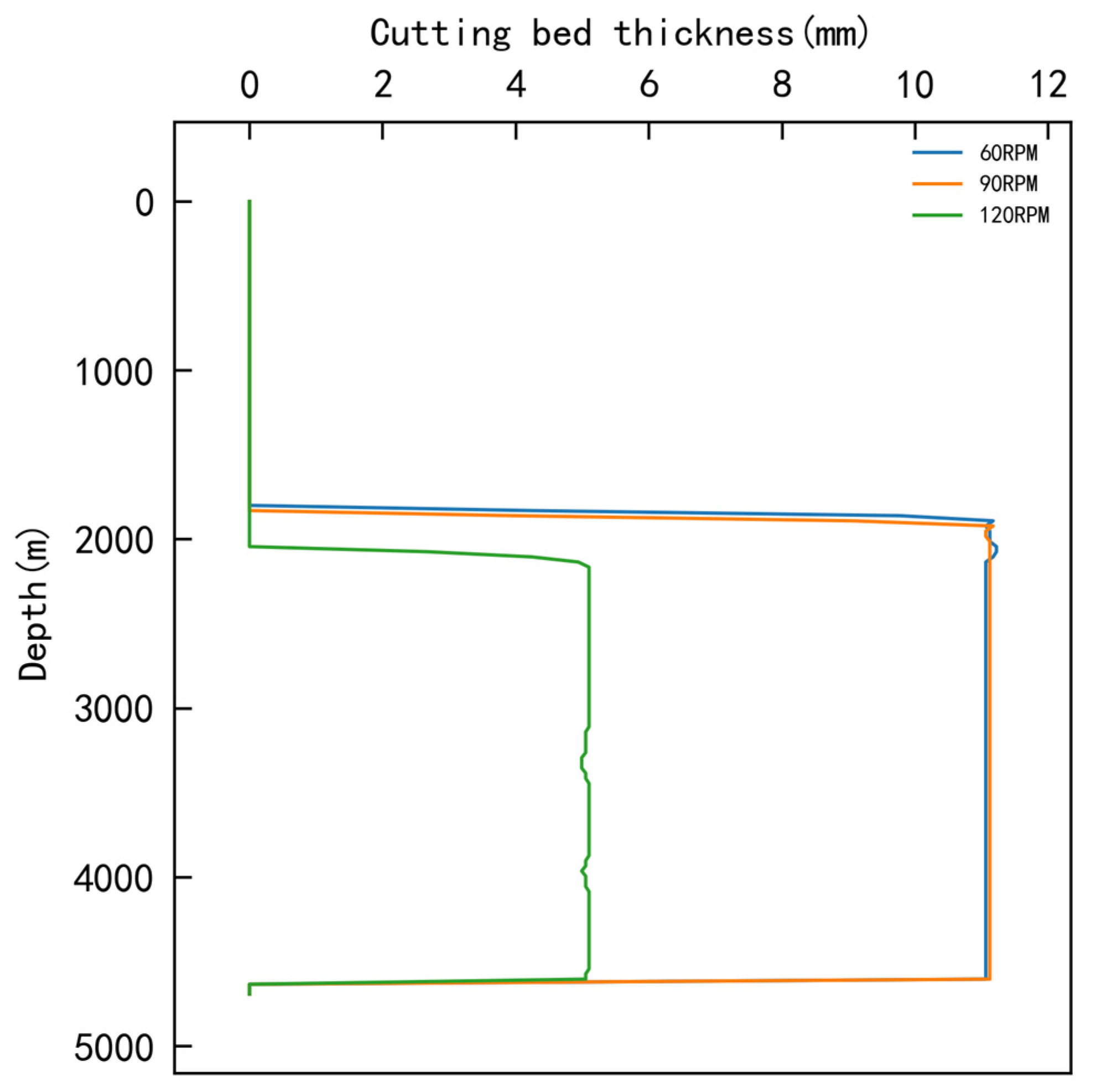
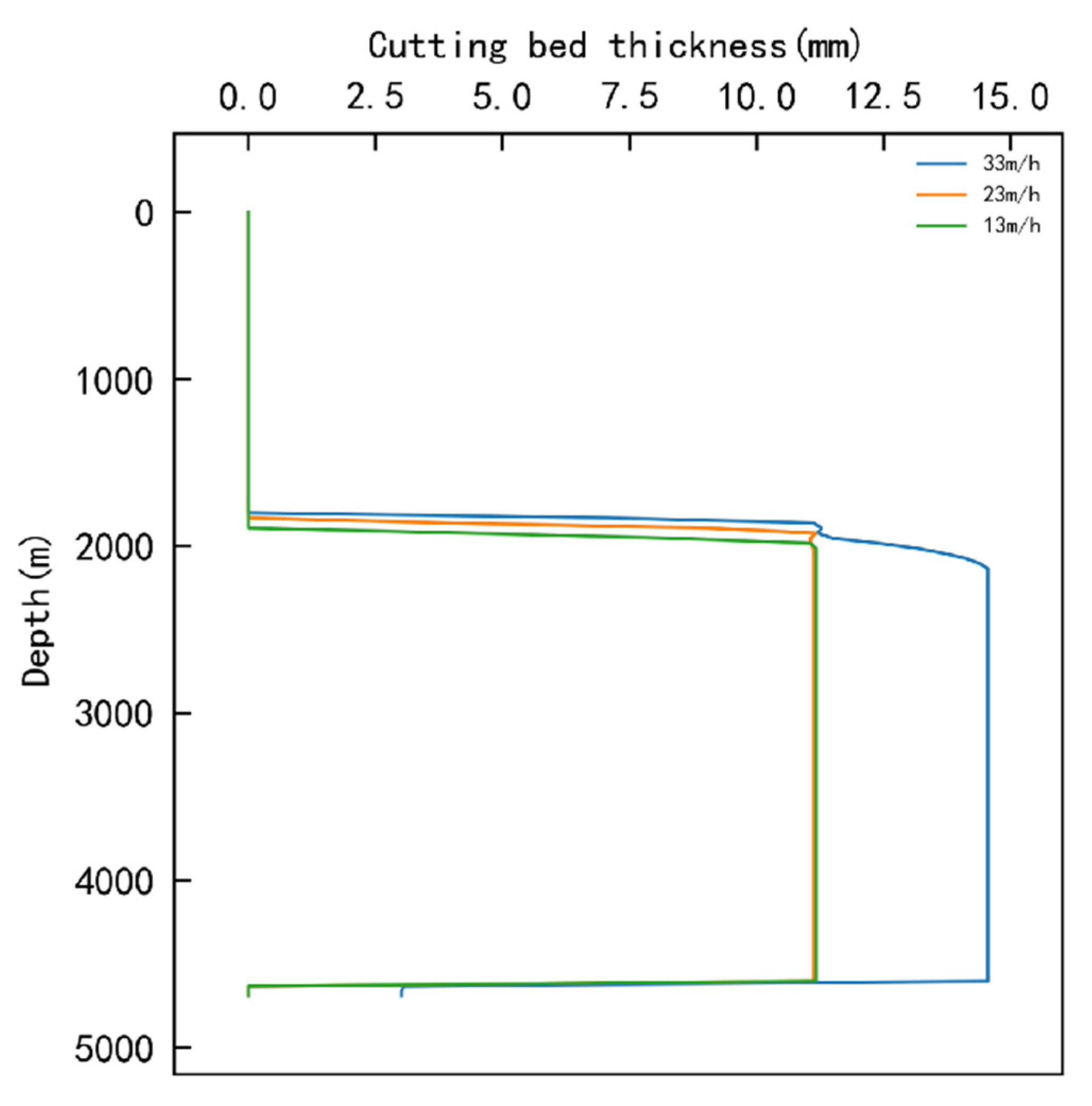
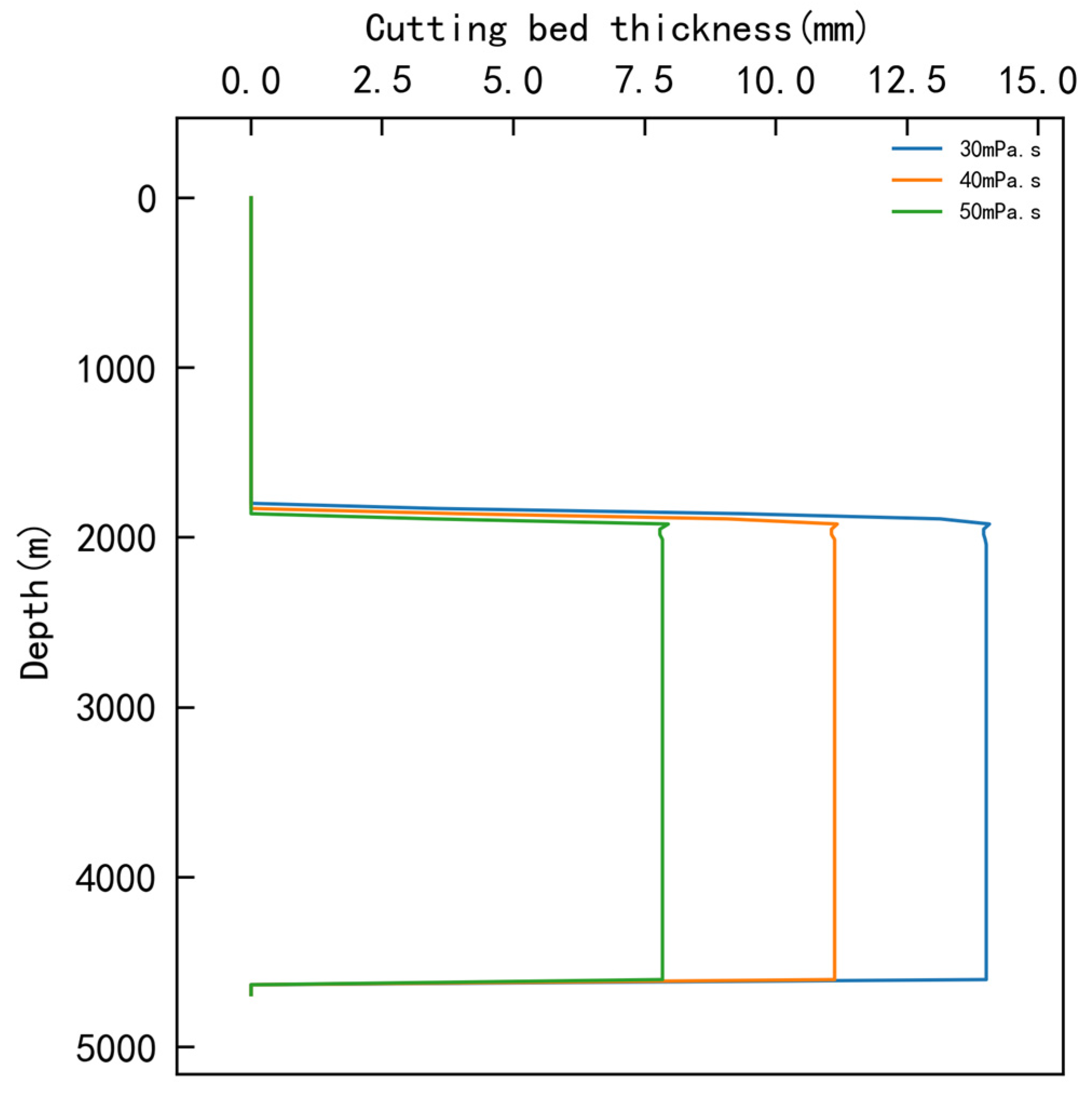
3.1.1. Single-Factor Optimization Results
3.1.2. Orthogonal Optimization Results
Optimal Parameter Combination
Influence Ranking of Factors
Synergistic Effect
3.2. Optimal Spacing Calculation Results
- (1)
- Input Parameters of Well J64-2H:
- Hole diameter = 215.9 mm; drill pipe outer diameter = 127 mm → hydraulic diameter = 215.9 − 127 = 88.9 mm.
- Optimized flow rate = 1860 L/min → annular velocity = 1.254 m/s.
- Average diameter of cuttings = 4.2 mm; corrected slip velocity in horizontal section = 0.005218 m/s.
- Well inclination = 90° (horizontal section) → = 1.
- Tool factors: = 1.12 and = 1.28.
- (2)
- Calculation Process and Results:
- (3)
- Field Adjustment:
3.3. Field Application Validation
- (1)
- Horizontal section drilling parameters: Flow rate ≥ 1860 L/min; rotation speed ≥ 120 RPM; and ROP ≤ 13 m/h.
- (2)
- Installation of spiral groove cuttings removal subs was conducted, spaced at approximately every two stands (the closest practical spacing to the calculated 60.49 m), totaling 34 subs.
- (3)
| Condition | Interval (m) | WOB (Ton) | Sliding Friction (Ton) | Pick-up Drag After Orienting (Ton) |
|---|---|---|---|---|
| Before App | 3702–3706 | 10–12 | 30 | 30 |
| 3725–3730 | 10–12 | 40 | 30 | |
| 3792–3795 | 10 | 40 | 35 | |
| 3822–3829 | 8–10 | 50 | 40 | |
| After App | 4017–4021 | 6–10 | 10 | 24 |
| 4041–4047 | 6–10 | 12 | 24 | |
| 4070–4076 | 6–10 | 12 | 24 | |
| 4110–4115 | 6–10 | 14 | 24 | |
| 4214–4218 | 6–10 | 12 | 24 | |
| 4226–4230 | 6–10 | 14 | 25 |
| Condition | Interval (m) | WOB (Ton) | Rotational Torque (kN·m) |
|---|---|---|---|
| Before App | 3706–3725 | 10–12 | 20 |
| 3730–3792 | 10 | 22 | |
| 3795–3822 | 8–10 | 24 | |
| 3829–3841 | 8 | 24 | |
| After App | 4021–4041 | 6 | 10–20 |
| 4047–4054 | 6–8 | 10–18 | |
| 4076–4082 | 6–8 | 10–18 | |
| 4115–4214 | 6–8 | 10–16 | |
| 4218–4226 | 6–8 | 10–16 | |
| 4230–4269 | 6–8 | 10–18 |
- (1)
- Before Application: Severe drag was encountered during oriented sliding drilling. A weight on bit (WOB) of 8–12 tons was needed to achieve differential back-up pressure across the mud motor. Pick-up drag after completing oriented sections ranged from 30 to 40 tons. Rotating torque ranged from 20 to 24 kN·m.
- (2)
- After Application: During oriented drilling, adding 6–10 tons of WOB achieved motor differential back-up pressure. Pick-up drag after orienting decreased to 10–20 tons. Rotating torque decreased to 10–16 kN·m, with some intervals up to 18–20 kN·m.
4. Discussion
4.1. Comparative Analysis with Previous Research
- (1)
- Advancements in Model Correction: This study reduced the error of the Moore cuttings slip velocity model from ±20% to ±5% by introducing a horizontal section drill string collision correction factor. This aligns with Chen Ye’s [38] conclusion regarding the impact of drill string collision on secondary cuttings fragmentation, but our work quantitatively establishes the direct influence of the correction factor on slip velocity, addressing the neglect of dynamic collisions in horizontal wells using traditional models. In contrast, prediction models for cuttings bed height, such as that formulated by Zongyu et al. [43], which omit drill string collision parameters, exhibit prediction deviations of 15–20% in Block J.
- (2)
- Synergistic Effect of Parameter Optimization: The optimal parameter combination (flow rate ≥ 1860 L/min; rotation speed ≥ 120 RPM; and ROP ≤ 13 m/h) reduced the cuttings input rate by 43.48%, significantly suppressing bed formation. This finding corroborates Gharib’s conclusion that an increased flow rate enhances cuttings transport capacity. However, our study is the first to demonstrate, through orthogonal simulation, the necessity of synergistic optimization of flow rate, rotation speed, and ROP. Only increasing the flow rate in Block J’s high-level clay formations risks wellbore instability, while the tri-parameter synergy maximizes cleaning efficiency and ensures wellbore stability.
- (3)
- Engineering Innovation in Mechanical Removal: The subspacing model resolves the issue of cuttings re-sedimentation. By introducing the carrying factor (α) and acceleration factor (β), the model quantifies the influence of tool disturbance range on cutting transport distance. While Nour et al. [44] proposed machine learning for optimizing tool spacing, their model relies on historical data and does not account for real-time drilling parameter variations. In contrast, our model can be directly embedded within drilling control systems for dynamic adjustment. Compared to Akhshik (2015)’s CFD-DEM model [12], our model demonstrated the following. (1) Computational efficiency: Our model has a 2 h/parameter set vs. 48 h for CFD-DEM, making it suitable for real-time field adjustment in J Block; (2) Field applicability: Our simplified formula integrates into conventional drilling software while CFD-DEM requires specialized teams; and (3) Accuracy balance: a ±5% error in J Block high-level clay conditions meets engineering needs.
4.2. Practical Significance of the Technological Breakthrough
4.3. Limitations of the Study
- (1)
- Model Applicability Boundary: The modified Moore model performs inadequately in sections with dogleg severity (DLS) > 7°/30 m. High DLS exacerbates drill string eccentricity, altering annular flow patterns. The current model lacks an eccentricity correction term.
- (2)
- Tool Performance Dependency: The carrying factor (α) and acceleration factor (β) require laboratory calibration for specific sub-designs. In practice, if tool wear exceeds 15%, α can decrease to 0.98–1.05, potentially causing spacing errors of up to ±8 m.
- (3)
- Limited Coupling with Dynamic Mud Properties: This study assumed stable drilling fluid properties. However, as noted by David et al. [45], fluid properties are prone to dynamic changes in shale formations with high clay contents. Plastic viscosity fluctuations exceeding 20% could adversely impact the prediction accuracy of cuttings slip velocity.
5. Conclusions
- (1)
- Develop an Adaptive Spacing Model: Integrate real-time downhole torque monitoring data to establish a dynamic feedback mechanism for adjusting sub spacing.
- (2)
- Extend the Model for High-DLS Sections: Introduce a drill string eccentricity correction coefficient to establish quantitative relationships between DLS, eccentricity, and slip velocity.
- (3)
- Integrate into Intelligent Drilling Systems: Embed the parameter optimization and mechanical removal modules within intelligent drilling platforms. Combine this with Gharib’s drilling fluid digital twin concept to achieve closed-loop control of the entire hole-cleaning process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Li, Y.; Pan, S.Q.; Zhao, Z.F.; Jing, Z.H.; Wang, X.T. Astronomical Cyclological Constraints on Carboniferous-Permian Organic Matter Enrichment in North China. J. Sedimentol. 2024. [Google Scholar] [CrossRef]
- Zhao, L.; Xian, B.Z.; Yu, Z.Y.; Shi, F.H.; Fang, H.L. Study on the enrichment of organic matter in continental shale under the constraint of astronomical cycles: A case study of the lower Lianger subcommittee in the Fuxing area of Sichuan Basin. Acta Sedimentol. Sin. 2023, 8. [Google Scholar] [CrossRef]
- Chen, C.; Guan, Q.; Chen, X.; Li, C.D.; Ye, Y.H.; Wu, J.; Jiao, K.; Liang, H.R.; Wan, Y. Driving Mechanism of Shale Organic Matter Enrichment in Wufeng Formation-Longmaxi Formation in Weiyuan Area under Astronomical Orbital Period. Pet. Geol. Dev. Daqing 2025. [Google Scholar] [CrossRef]
- Wei, W.; Wenbin, S.H.I.; Xiaoping, F.U.; Xie, J.T.; Ni, K. Oil and gas enrichment regularity of conti-nental shale of Lianggaoshan Formation of Middle Jurassic in Fuling area, Sichuan Ba-sin. Nat. Gas Geosci. 2022, 33, 764–774. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Yang, G.; Tao, S.; Ni, C.; Zhang, B.; He, X.; Lin, J.; Huang, D.; Liu, M.; et al. New research progress of Jurassic tight oil in cen-tral Sichuan Basin, SW China. Pet. Explor. Dev. 2016, 43, 954–964. [Google Scholar] [CrossRef]
- Zecheng, W.; Yizuo, S.H.I.; Long, W.E.N.; Jiang, H.; Jiang, Q.; Huang, S.; Xie, W.; Li, R.; Jin, H.; Zhang, Z.; et al. Exploring the potential of oil and gas re-sources in Sichuan Basin with Super Basin Thinking. Pet. Explor. Dev. 2022, 49, 977–990. [Google Scholar]
- Xinhua, M.A.; Jun, X.I.E. The progress and prospects of shale gas exploration and devel-opment in southern Sichuan Basin, SW China. Pet. Explor. Dev. 2018, 45, 172–182. [Google Scholar]
- Pedrosa, C.; Saasen, A.; Ytrehus, J.D. Fundamentals and physical principles for drilled cuttings transport—Cuttings bed sedimentation and erosion. Energies 2021, 14, 545. [Google Scholar] [CrossRef]
- Qu, J.; Sun, X.; Yan, T.; Chen, Y.; Hu, Q. A novel prediction model for cuttings bed height in horizontal and deviated wells. J. Nat. Gas Sci. Eng. 2021, 95, 104192. [Google Scholar] [CrossRef]
- Li, X.; Fan, Y.; Li, J.; Su, X.; Zhan, S.; Hu, G.; He, Y.; Zhang, M. Research on the Influence of a Cuttings Bed on Drill String Fric-tion Torque in Horizontal Well Sections. Processes 2022, 10, 2061. [Google Scholar] [CrossRef]
- Pedrosa, C.; Lund, B.; Opedal, N.; Ytrehus, J.D.; Saasen, A. Experimental bench-scale study on cuttings-bed erosion in horizontal wells. J. Energy Resour. Technol. 2023, 145, 053101. [Google Scholar] [CrossRef]
- Akhshik, S.; Behzad, M.; Rajabi, M. CFD–DEM approach to investigate the effect of drill pipe rotation on cuttings transport behavior. J. Pet. Sci. Eng. 2015, 127, 229–244. [Google Scholar] [CrossRef]
- Al-Rubaii, M.; Al-Shargabi, M.; Al-Shehri, D.; Yadav, A.S. Hole Cleaning during Drilling Oil and Gas Wells: A Review for Hole-Cleaning Chemistry and Engineering Parameters. Ad-Vances Mater. Sci. Eng. 2023, 2023, 6688500. [Google Scholar] [CrossRef]
- Mahmoud, H.; Hamza, A.; Nasser, M.S.; Hussein, I.A.; Ahmed, R.; Karami, H. Hole cleaning and drilling fluid sweeps in horizontal and deviated wells: Comprehensive review. J. Pet. Sci. Eng. 2020, 186, 106748. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, J.; Guan, N.; Zhu, H. Cuttings Transport Characteristics and Multi-Objective Optimization Design of a Novel Hole Cleaning Tool. Geoenergy Sci. Eng. 2025, 254, 214053. [Google Scholar] [CrossRef]
- Chen, D.C.K. New drilling optimization technologies make drilling more efficient. In Proceedings of the PETSOC Canadian International Petroleum Conference, Calgary, AB, Canada, 8–10 June 2004. PETSOC, 2004: PETSOC-2004-020. [Google Scholar]
- Boyou, N.; Haddad, A.S.; Rafati, R.; Aboulrous, A.A.; Alsabagh , A. Comprehensive Review on Wellbore Cleaning: Analyzing Factors, Simulation Models, and Emerging Technologies for Enhanced Drilling Efficiency. J. Pet. Min. Eng. 2024, 26, 7–36. [Google Scholar] [CrossRef]
- Ramsey, M.S. Practical Wellbore Hydraulics and Hole Cleaning: Unlock Faster, More Effi-Cient, and Trouble-Free Drilling Operations; Gulf Professional Publishing: Houston, TX, USA, 2019. [Google Scholar]
- Dosunmu, A.; Orun, C.; Anyanwu, C.; Ekeinde, E. Optimization of hole cleaning using dynamic real-time cuttings monitoring tools. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 4–6 August 2025. SPE 2015: SPE-178373-MS. [Google Scholar]
- Wang, H.; Huang, H.; Bi, W.; Ji, G.; Zhou, B.; Zhuo, L. Deep and ultra-deep oil and gas well drilling technolo-gies: Progress and prospect. Nat. Gas Ind. B 2022, 9, 141–157. [Google Scholar] [CrossRef]
- Katende, A.; Segar, B.; Ismail, I.; Sagala, F.; Saadiah, H.H.A.R.; Samsuri, A. The effect of drill–pipe rotation on improving hole cleaning using polypropylene beads in water-based mud at different hole angles. J. Pet. Explor. Prod. Technol. 2020, 10, 1253–1262. [Google Scholar] [CrossRef]
- Yeo, L.; Feng, Y.; Seibi, A.; Temani, A.; Liu, N. Optimization of hole cleaning in horizontal and inclined wellbores: A study with computational fluid dynamics. J. Pet. Sci. Eng. 2021, 205, 108993. [Google Scholar] [CrossRef]
- Sanchez, R.A.; Azar, J.J.; Bassal, A.A.; Martins, A.L. Effect of Drillpipe Rotation on Hole Cleaning During Directional-Well Drilling. SPE J. 1999, 4, 101–108. [Google Scholar] [CrossRef]
- Saasen, A.; Løklingholm, G. The effect of drilling fluid rheological properties on hole cleaning. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Galveston, TX, USA, 26–28 February 2002. SPE 2002: SPE-74558-MS. [Google Scholar]
- Adari, R.B.; Miska, S.; Kuru, E.; Bern, P.; Saasen, A. Selecting drilling fluid properties and flow rates for effective hole cleaning in high-angle and horizontal wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 1–4 October 2000. SPE 2000: SPE-63050-MS. [Google Scholar]
- Orun, C.B.; Akpabio, J.U.; Agwu, O.E. Drilling fluid design for depleted zone drilling: An integrated review of laboratory, field, modelling and cost studies. Geoenergy Sci. Eng. 2023, 226, 211706. [Google Scholar] [CrossRef]
- Caenn, R.; Darley, H.C.H.; Gray, G.R. Composition and Properties of Drilling and Comple-Tion Fluids; Gulf Professional Publishing: Houston, TX, USA, 2011. [Google Scholar]
- Zhou, Y.; He, Y.; Li, Z.; Ju, G. Hole cleaning performance of v-shaped hole cleaning device in horizontal well drilling: Numerical modeling and experiments. Appl. Sci. 2022, 12, 5141. [Google Scholar] [CrossRef]
- Kjøsnes, I.; Løklingholm, G.; Saasen, A.; Syrstad, S.O.; Agle, A.; Solvange, K.-A. Successful water based drilling fluid design for optimizing hole cleaning and hole stability. In Proceedings of the SPE/IADC Middle East Drilling Technology Conference and Exhibition, Abu Dhabi, United Arab Emirates, 20–22 October 2003. SPE 2003: SPE-85330-MS. [Google Scholar]
- Luo, Y.; Bern, P.A.; Chambers, B.D. Flow-rate predictions for cleaning deviated wells. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, New Orleans, LA, USA, 18–21 February 1992. SPE 1992: SPE-23884-MS. [Google Scholar]
- Noah, A.Z. Optimizing drilling fluid properties and flow rates for effective hole clean-ing at high-angle and horizontal wells. J. Appl. Sci. Res. 2013, 9, 705–718. [Google Scholar]
- Sayindla, S.; Lund, B.; Ytrehus, J.D.; Saasen, A. Hole-cleaning performance comparison of oil-based and water-based drilling fluids. J. Pet. Sci. Eng. 2017, 159, 49–57. [Google Scholar] [CrossRef]
- Busahmin, B.; Saeid, N.H.; Alusta, G.; Zahran, E.-S.M.M. Review on hole cleaning for horizontal wells. ARPN J. Eng. Appl. Sci. 2017, 12, 4697–4708. [Google Scholar]
- Shirangi, M.G.; Aragall, R.; Osgouei, R.E.; May, R.; Furlong, E.; Dahl, T.G.; Thompson, C.A.; Furlong, T. Development of digital twins for drilling fluids: Local velocities for hole clean-ing and rheology monitoring. J. Energy Resour. Technol. 2022, 144, 123003. [Google Scholar] [CrossRef]
- Iyoho, A.W.; Horeth, I.J.M.; Veenkant, R.L. A computer model for hole-cleaning analy-sis. J. Pet. Technol. 1988, 40, 1183–1192. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, J.; Xu, B.; Zhu, H. Numerical simulation and experimental study of hole cleaning. Tunn. Undergr. Space Technol. 2024, 147, 105697. [Google Scholar] [CrossRef]
- Cayeux, E.; Mesagan, T.; Tanripada, S.; Zidan, M.; Fjelde, K.K.K. Real-time evaluation of hole-cleaning condi-tions with a transient cuttings-transport model. SPE Drill. Complet. 2014, 29, 5–21. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, X.; Yan, T.; Yao, D.; Duan, R. Experimental study on micron-sized sand particles transport in the water flow path of hydrates production wellbore. J. Nat. Gas Sci. Eng. 2020, 73, 103088. [Google Scholar] [CrossRef]
- Ji, G.; Wang, H.; Huang, H.; Meng, Z.; Cui, L.; Guo, W. Design and test of a cuttings bed remover for horizontal wells. Nat. Gas Ind. B 2021, 8, 412–419. [Google Scholar] [CrossRef]
- Peng, S.; Huang, W.J.; Gao, D.L. Hole cleaning evaluation and installation spacing opti-mization of cuttings bed remover in extended-reach drilling. Pet. Sci. 2024, 21, 2005–2022. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Hu, Z.; Feng, D.; Zhu, T.; Bian, R.; Jiang, T.; Jin, Z. Lithofacies types and assemblage features of continental shale strata and their implications for shale gas exploration: A case study of the Middle and Lower Jurassic strata in the Sichuan Basin. Nat. Gas Ind. B 2020, 7, 358–369. [Google Scholar] [CrossRef]
- Saasen, A.; Omland, T.H.; Ekrene, S.; Brévière, J.; Villard, E.; Kaageson-Loe, N.; Tehrani, A.; Cameron, J.; Freeman, M.A.; Growcock, F.; et al. Automatic measurement of drilling fluid and drill-cuttings properties. SPE Drill. Complet. 2009, 24, 611–625. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Wu, B.C.; Shi, J.G.; Xi, C.M.; Wei, K. A Multiparameter Coupled Prediction Model for Annular Cuttings Bed Height in Horizontal Wells. Geofluids 2022, 2022. [Google Scholar] [CrossRef]
- Nour, M.; Elsayed, K.S.; Mahmoud, O. A supervised machine learning model to select a cost-effective directional drilling tool. Sci. Rep. 2024, 14, 26624. [Google Scholar] [CrossRef]
- David, C.E.; Zimmerman, W.R. Pore structure model for elastic wave velocities in fluid-saturated sandstones. J. Geophys. Res. Solid Earth 2012, 117, B7. [Google Scholar] [CrossRef]


| Block | TD (m) | HLS Length (m) | ROP (m/h) | Vertical Sec. (d) | Build/Tangent + HLS (d) | Drilling Cycle (d) | Trouble Time (%) | Remarks |
|---|---|---|---|---|---|---|---|---|
| J Block | 4626 | 1667 | 6.15 | 14.49 | 54 | 101 | 13.3 | Early development |
| Adjacent 2013 | 4215 | 1532 | 5.02 | 20 | 40 | 85 | 4.64 | Early development |
| Adjacent 2025 | 4956 | 2132 | 20.62 | 6.3 | 25.2 | 28.9 | 2.63 | Mature technology |
| Factor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Flow rate (L/min) | 1660 | 1760 | 1860 |
| Rotating speed (RPM) | 60 | 90 | 120 |
| ROP (m/h) | 13 | 23 | 33 |
| Plastic viscosity (mPa·s) | 30 | 40 | 50 |
| No. | Flow Rate L/min | Rotating Speed RPM | ROP m/h | Plastic Viscosity mPa·s | Cuttings Bed Thickness mm |
|---|---|---|---|---|---|
| 1 | 1660 | 60 | 13 | 30 | 19.22 |
| 2 | 1660 | 90 | 23 | 40 | 18.28 |
| 3 | 1660 | 120 | 33 | 50 | 17.37 |
| 4 | 1760 | 60 | 23 | 50 | 11.17 |
| 5 | 1760 | 90 | 33 | 30 | 15.09 |
| 6 | 1760 | 120 | 13 | 40 | 11.73 |
| 7 | 1860 | 60 | 33 | 40 | 11.14 |
| 8 | 1860 | 90 | 13 | 50 | 4.4 |
| 9 | 1860 | 120 | 23 | 30 | 6.23 |
| Factor | Level 1 Mean (mm) | Level 1 Mean (mm) | Level 1 Mean (mm) | Range (mm) | Order of Influence |
|---|---|---|---|---|---|
| Flow rate (L/min) | 18.29 | 12.66 | 10.59 | 7.7 | 1 |
| Rotating speed (RPM) | 13.84 | 12.57 | 11.78 | 2.06 | 2 |
| ROP (m/h) | 11.78 | 11.89 | 14.53 | 2.75 | 4 |
| Plastic viscosity (mPa·s) | 13.51 | 13.53 | 11.17 | 2.36 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Song, X.; Xie, Y.; Liu, J.; Han, H.; Deng, Q.; Geng, H. Research on Hole-Cleaning Technology Coupled with Prevention and Removal of Cuttings Bed. Processes 2025, 13, 2604. https://doi.org/10.3390/pr13082604
Yang D, Song X, Xie Y, Liu J, Han H, Deng Q, Geng H. Research on Hole-Cleaning Technology Coupled with Prevention and Removal of Cuttings Bed. Processes. 2025; 13(8):2604. https://doi.org/10.3390/pr13082604
Chicago/Turabian StyleYang, Dong, Xin Song, Yingjian Xie, Jianli Liu, Hu Han, Qiao Deng, and Hao Geng. 2025. "Research on Hole-Cleaning Technology Coupled with Prevention and Removal of Cuttings Bed" Processes 13, no. 8: 2604. https://doi.org/10.3390/pr13082604
APA StyleYang, D., Song, X., Xie, Y., Liu, J., Han, H., Deng, Q., & Geng, H. (2025). Research on Hole-Cleaning Technology Coupled with Prevention and Removal of Cuttings Bed. Processes, 13(8), 2604. https://doi.org/10.3390/pr13082604






